1 引言
随着市政交通的快速发展,城市干道的交通路况日益复杂,路面塌陷、裂缝危害等道路病害问题层出不穷,存在一定的交通隐患,这一问题为实时、高效检测路面结构情况的研究提出了挑战。
传统对于路面结构的测量方法包含取芯法,即从道路上钻取芯样,评定结构质量,但是取芯的成本高、效率低,且破坏了路面结构,是传统测量方法的重大弊端。以探地雷达(Ground Penetrating Radar,简称GPR)技术为代表的电磁勘探方法解决了取芯的弊端,成为道路检测、地下勘探等领域的主流技术方法[1-2]。
探地雷达技术主要是利用发射天线向地下发射高频超宽带电磁波,电磁波在不同的介质层结构中存在着反射、折射、散射等特性[3- 4],根据接收天线获得的GPR回波信号,可以推演出地下介质的厚度、介电常数等结构信息,具有探测的无损性与高效性。
GPR方法的工作原理可以分为波形正演与波形反演两个部分。正演方法,即根据实验的模型结构,利用时域有限差分(finite-difference time-domain,简称FDTD)生成相应的回波信号,进行后续信号处理与波形反演。波形反演主要是根据GPR回波信号,构建模型结构的空间分布,获取各层介质的相对介电常数与层厚信息。
GPR波形反演方法得到了许多的研究与发展,其中对于层状介质分层的波形反演算法,可以大致分类为时域反演与频域反演。时域方法包含有共中心点方法[5](common middle point,简称CMP)、速度谱方法[6-7]等。Liu在文献[8]中基于CMP,引入射线路径,建立了滑行波模型。Kao在文献[9]中基于CMP构建了地下多层介质滑行波模型,利用分层介质面反射波的首达时,反演出层状介质的相对介电常数和层厚信息,但是这种方法无法有效反演相对介电常数,且利用滑行波模型反演参数的误差较大。刘四新在文献[10]中基于速度谱,绘制了地下结构的速度谱图,通过速度拾取与Dix方程实现了对地下介质波速信息的精确反演。频域反演算法主要通过构建频域正演模型,将反射系数序列频谱与介质层厚、介电常数等指标相互关联,实现参数反演[11-12]。
本文所研究的共中心点参数反演算法属于时域反演的内容,基于传统的CMP算法,通过构造电磁波的传播方程,实现第一介质层的相对介电常数与层厚的反演,基于电磁波传播时间的代价函数,通过遗传算法,实现多层介质层的参数反演。
2 共中心点模型
2.1 单层介质模型
共中心点方法是利用收发间距改变的B-scan数据,构造不同收发间距下电磁波的传播距离方程,反演出第一层的相对介电常数与层厚信息。如图1所示,对于单层介质的CMP模型,在天线收发间隔2L下,Tx端发射的电磁波以Q1→P→Q2的路径传播至Rx端。
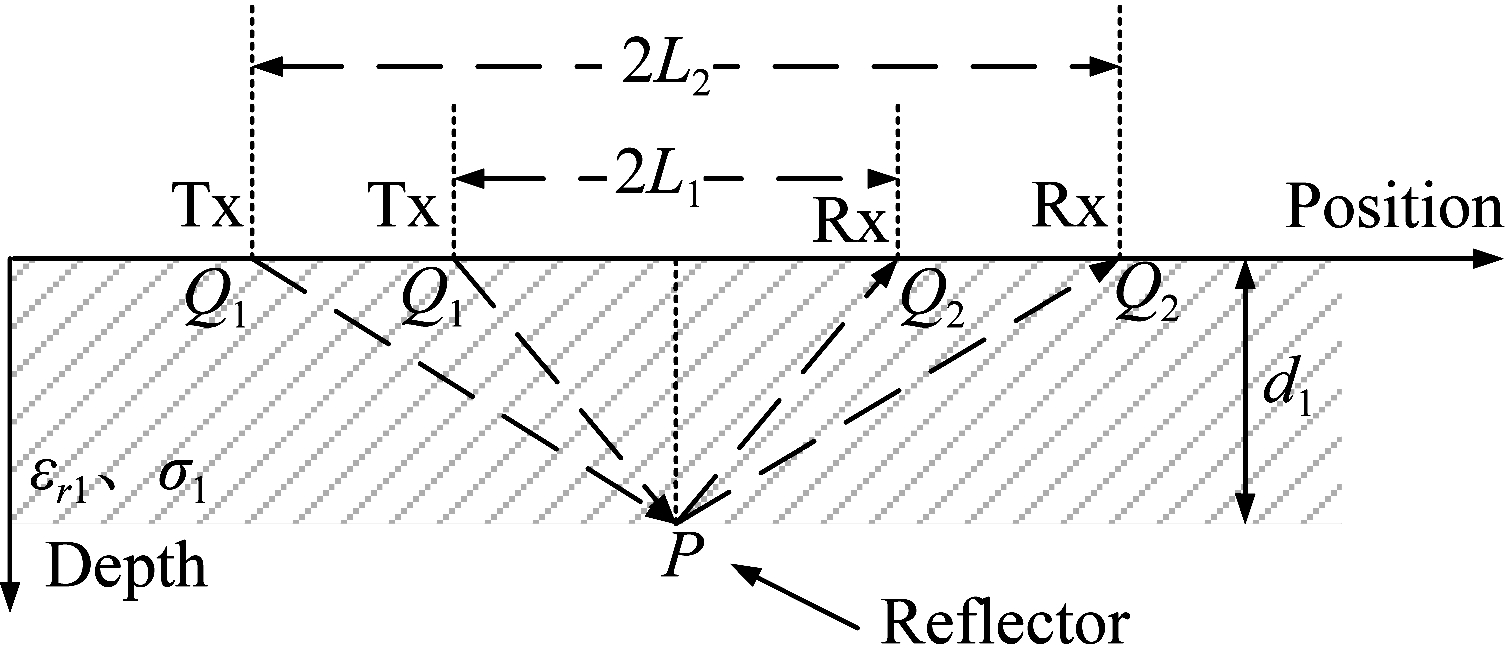
图1 单层介质的CMP模型
Fig.1 CMP model of single layer medium
根据反射波的传播路径,构造传播距离的方程
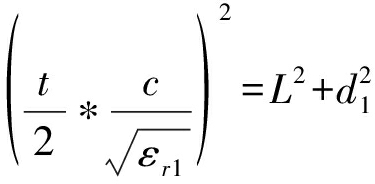
(1)
其中d1为第一层介质层的厚度,εr1为第一层的相对介电常数,c为光速,L为收发间距的一半,t为反射波自Tx端至Rx端的传播时间。
由式(1),通过不同收发间距的传播方程,推导得到单层介质层的相对介电常数与层厚表达式。根据N道A-scan数据,对所有相对介电常数与层厚的反演参数取均值,可以得到
(2)
(3)
2.2 多层介质模型
多层模型的电磁波传播过程存在折射现象,传播路径复杂,可以通过引入优化算法,建立代价函数,通过迭代寻优的方式找到层厚与相对介电常数。在满足雷达方程所限制的测量范围内,对于n层介质的CMP模型,如图2所示,根据电磁波在介质中的传播路径,建立所对应的传播时间方程
(4)
由式(4)可以进一步推导出传播距离方程
(5)
其中Δti为第i层底面反射波与空气直达波的到达时之差。
当已知前n-1层的介质参数时,由斯涅尔定律可以将前n层中的折射点位置表示为εrn与dn的表达式。于是,对于m道A-scan数据,构造n层介质参数反演的代价函数,即建立最小二乘误差函数δ(εrn,dn)
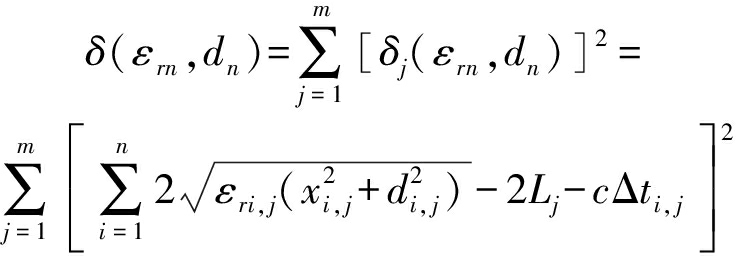
(6)
其中,εri, j、di, j为第j道A-scan中第i层的相对介电常数与厚度,xi, j为第j道A-scan中第i层底面的折射点位置,Δti, j为第j道A-scan中第i层底面反射波与空气直达波的到达时之差,Lj为第j道A-scan的天线收发间距的一半。
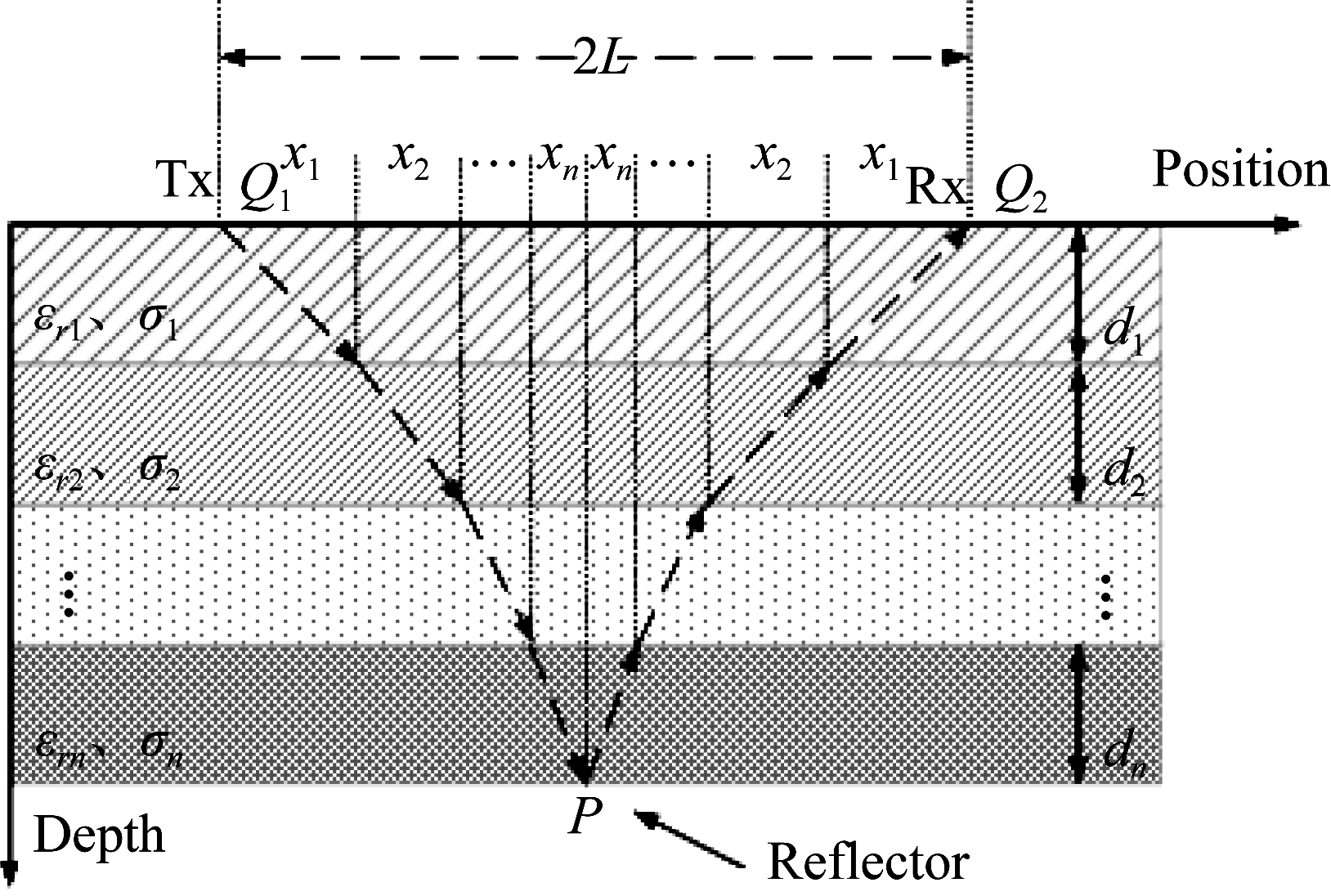
图2 n层介质的CMP模型
Fig.2 CMP model of n layer medium
2.3 折射点优化
如图3所示,由斯涅尔定律可以建立如下方程
(7)
即有
(8)
根据
的限制条件,求解折射点需要计算复杂的一元四次方程。
在文献[13]中,Mast 提出了一种利用一次代数运算代替求解复杂的一元四次方程,如图3所示,根据电磁波折射的几何模型,折射点坐标可由下式近似得到
(9)
其中c1为电磁波在空气中的波速,c2为电磁波在介质中的波速。
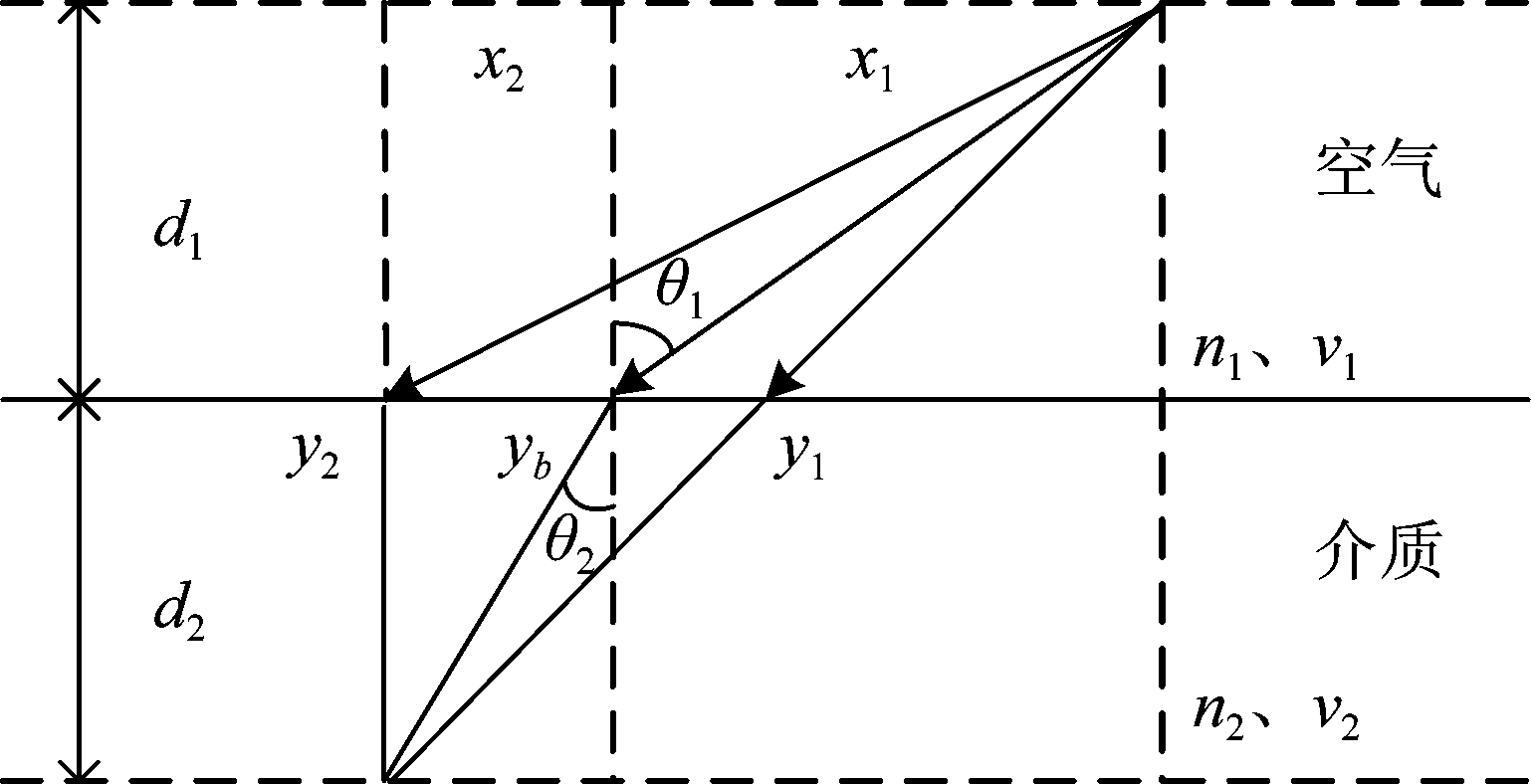
图3 折射点近似的几何关系图
Fig.3 Approximate geometrical relation of refraction points
3 优化算法
3.1 遗传算法
遗传算法[14]属于一种高效率的仿生类优化算法,算法结构来源于达尔文的进化论思想,利用物种遵循的自然进化过程来求取问题的最优解。
这里以介质层厚与相对介电常数[d,ε]作为优化对象,采取浮点编码法,以d=[d,ε]T、D=[d1,d2,…,dM]作为个体与种群(个体总量为M)的编码方式,采取式(6)的适应度函数,用以表征种群个体的优秀程度,评判和寻找模型的最优解。遗传步骤中采取固定值的选择、交叉、变异概率与自适应的变异范围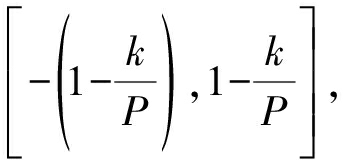
其中k为当前迭代次数,P为总迭代次数。
根据道路地下材料分层的先验条件,在参数的约束范围内按照编码方式随机获取个体染色体,构成初代种群。初始化后的初代种群,进行适应度函数计算,并根据适应度数值大小采取轮盘赌选择法,经过单点交叉、基本位变异的遗传步骤构成高适应度的子代,再进行种群迭代,直至达到终止条件,输出层厚与相对介电常数的理想解[d,ε]。
3.2 代价函数
3.2.1 折射模型
基于n层介质的CMP模型,采取Mast近似的方法求取折射点位置,由式(6),建立电磁波传播方程的最小二乘误差函数δ(εrn,dn)
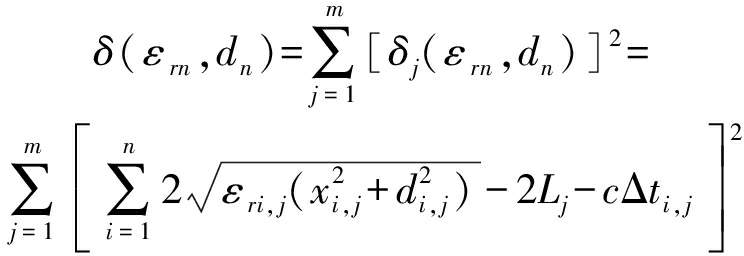
(10)
其中,εri, j、di, j为第j道A-scan中第i层的相对介电常数与厚度,xi, j为第j道A-scan中第i层底面的折射点位置,Δti, j为第j道A-scan中第i层底面反射波与空气直达波的到达时之差,Lj为第j道A-scan的天线收发间距的一半,c为光速。
3.2.2 垂直入射模型
由于代价函数中引入了折射点位置,折射点位置的求取涉及一元四次方程的求解问题,若采取近似求取的方法,会导致折射点存在一定的偏差,在多层情况下误差较大,优化算法可能无法得到理论值。
于是,基于n层介质的CMP模型,从收发间距为0 m的A-scan中,提取第j道A-scan中第i层底面反射波传播时间ti, j,构建代价函数
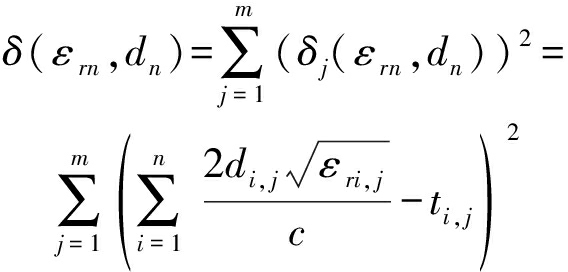
(11)
3.3 优化模型
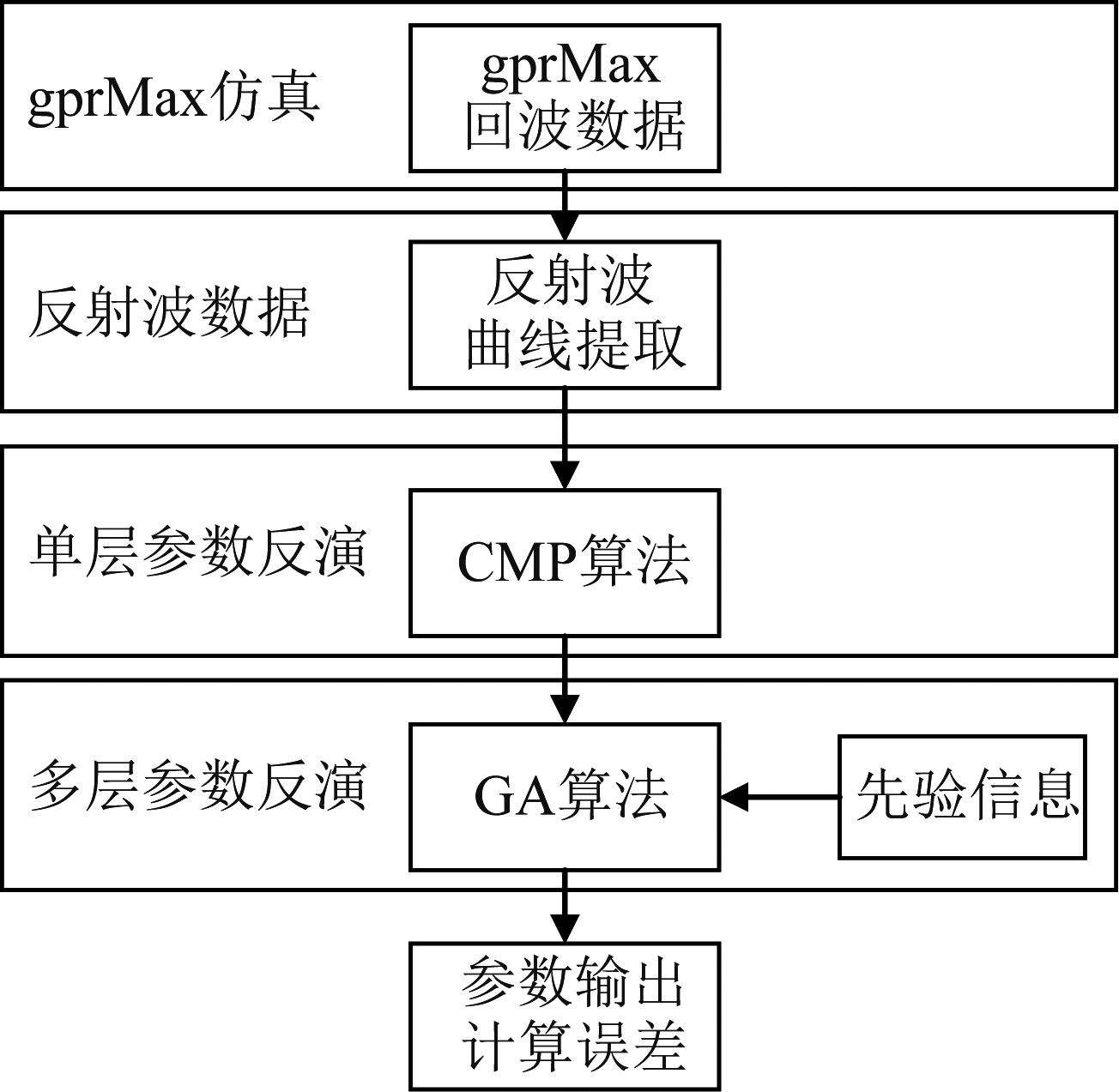
图4 基于遗传算法的优化模型
Fig.4 Optimization model A based on genetic algorithm
基于地下多层介质模型,构建如图4的基于遗传算法的优化模型,通过反射波曲线提取获取不同介质层的反射波到达时,构建起反演算法的数据基础,以折射模型或垂直入射模型的代价函数作为优化目标,模型使用常规CMP方法反演第一层参数,使用遗传算法反演多层参数。
在优化模型的多层参数反演步骤中,采取逐层反演的机制,根据单层CMP方法反演得到的参数信息进行第二层、第三层等的逐层迭代,每次迭代均采取相同的优化算法流程,实现对地下多层参数的反演。
4 算法仿真
4.1 代价函数
使用gprMax[15]作为仿真软件,采取表1的仿真参数与图5的仿真模型,遗传算法设置种群个体数为1000,总迭代次数为200。
表1 仿真参数
Tab.1 Simulation parameters
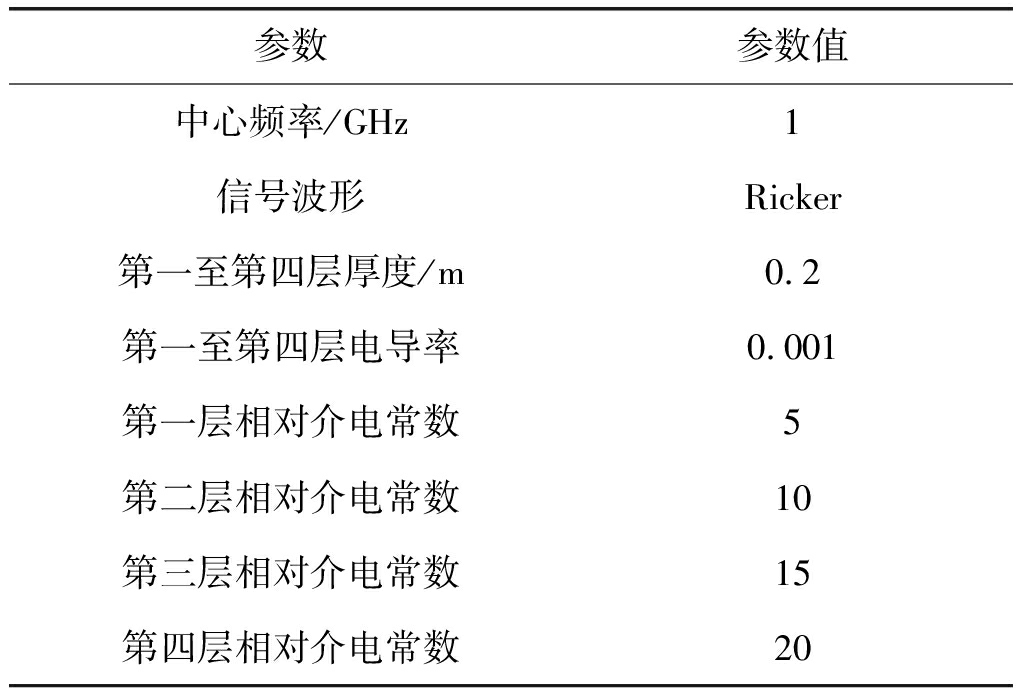
参数参数值中心频率/GHz1信号波形Ricker第一至第四层厚度/m0.2第一至第四层电导率0.001第一层相对介电常数5第二层相对介电常数10第三层相对介电常数15第四层相对介电常数20
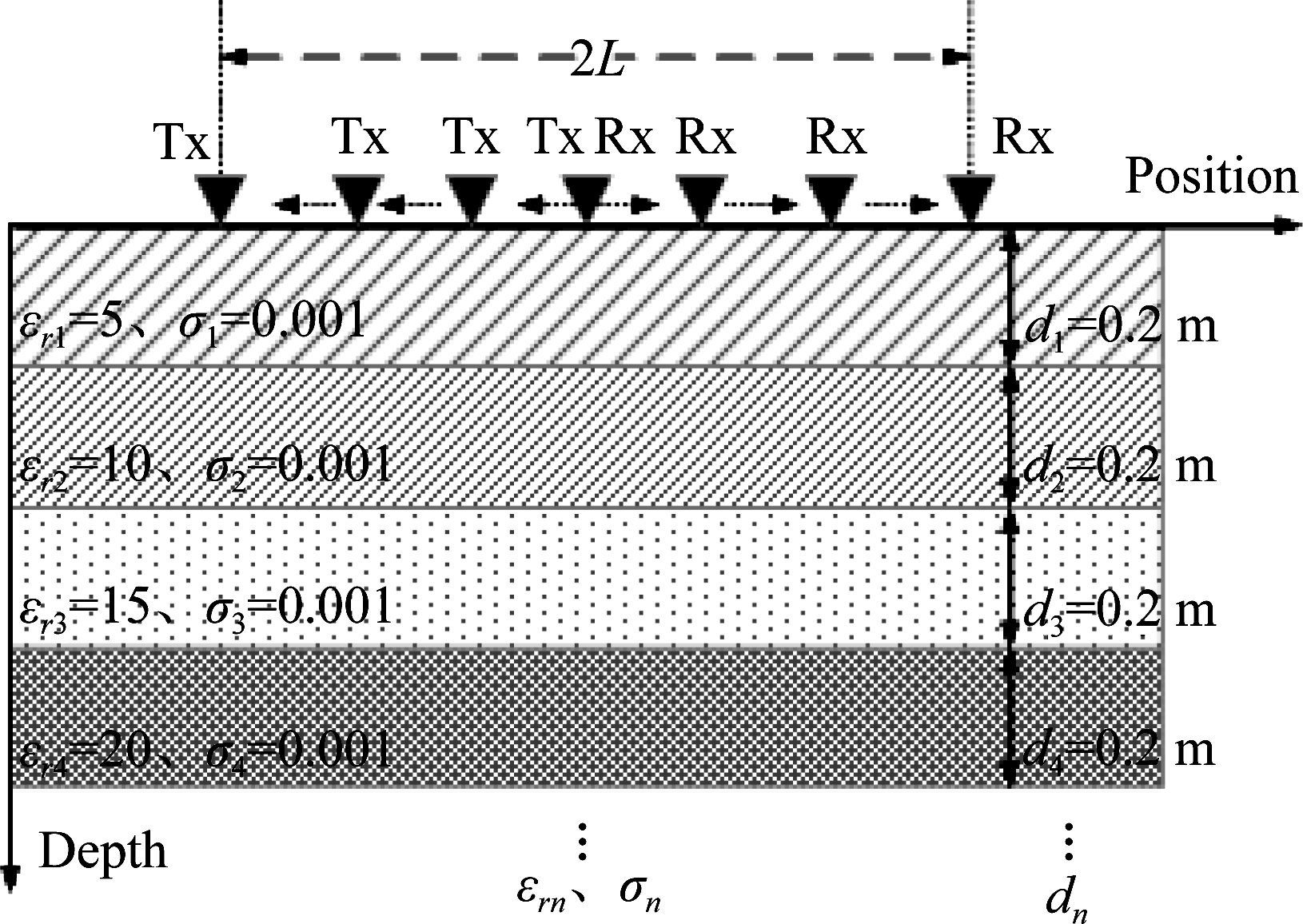
图5 仿真模型
Fig.5 Simulation model
为了验证代价函数内是否存在大量局部极值点,在相对介电常数与层厚的先验范围内以很小步进间隔的穷举法绘制网格,计算节点代价值,得到极小值分布。如图6所示,基于垂直入射模型,采取式(11)所示的代价函数,可以看出代价函数存在着大量的极值点,极值点之间的数值差距较小,均位于10-21的量级。其中,极小值位置的相对介电常数与层厚构成线性关系,且斜率很大,意味着当层厚变化较小时,介电常数往往会有很大的波动。这解释了参数反演方法易出现层厚参数反演准确率高,而介电常数较大误差的问题。
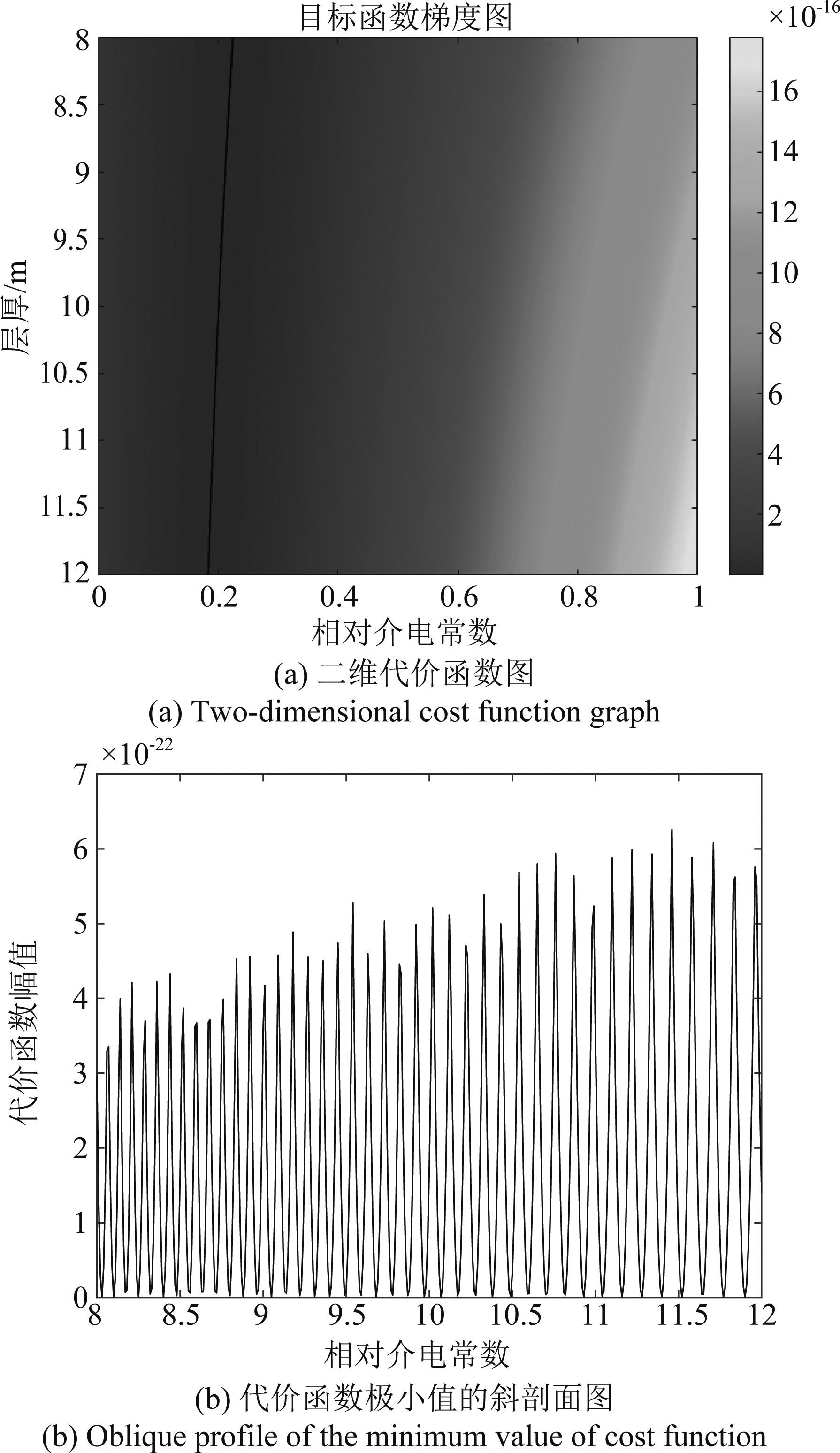
图6 代价函数图
Fig.6 The cost function diagram
4.2 优化模型仿真
根据表1仿真数据,采取图5的仿真模型,进行算法的仿真实验。首先,基于单层的介质模型,利用不同收发间距下的电磁波传播方程,进行CMP方法的参数反演,得到表2的仿真结果。
表2 单层介质模型仿真结果
Tab.2 Simulation results of single layer medium model
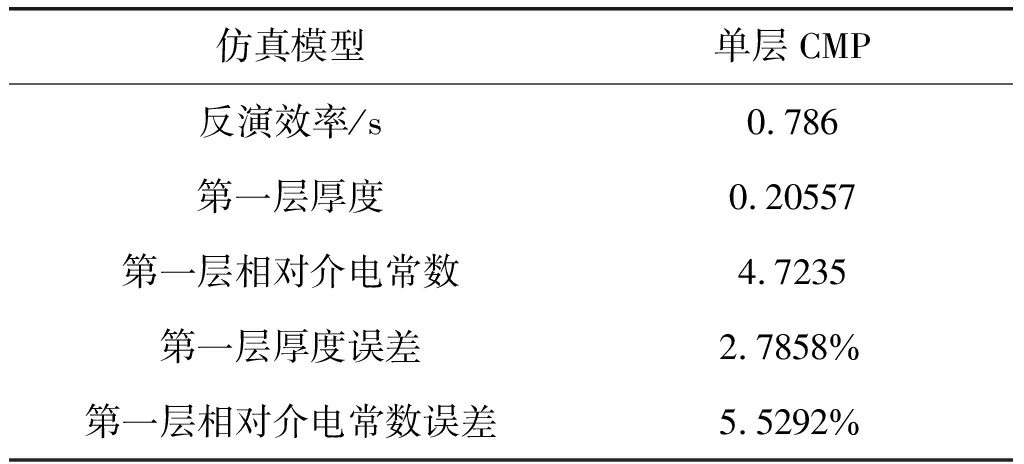
仿真模型单层CMP反演效率/s0.786第一层厚度0.20557第一层相对介电常数4.7235第一层厚度误差2.7858%第一层相对介电常数误差5.5292%
文献[16]中介绍了一种应用于空耦情况下的扩展CMP(XCMP)方法,它基于第一层介质参数已知的情况下,如图7所示,构建双层介质模型的传播方程,利用反射波的时间差与折射定律,求解出分层界面的折射点位置与第二层介质参数。但是,XCMP方法需要已知第一层参数,并且局限于第二层的参数反演,无法适用于多层情况。
图7 XCMP的双层介质模型
Fig.7 Double layer medium model for XCMP
于是,在采取表2中单层CMP方法反演第一层参数的基础上,基于图5中双层介质模型进行基于遗传算法的优化模型方法的参数反演,利用XCMP方法作为对比,得到表3的仿真结果。
表3 双层介质模型仿真结果
Tab.3 Simulation results of double layer medium model
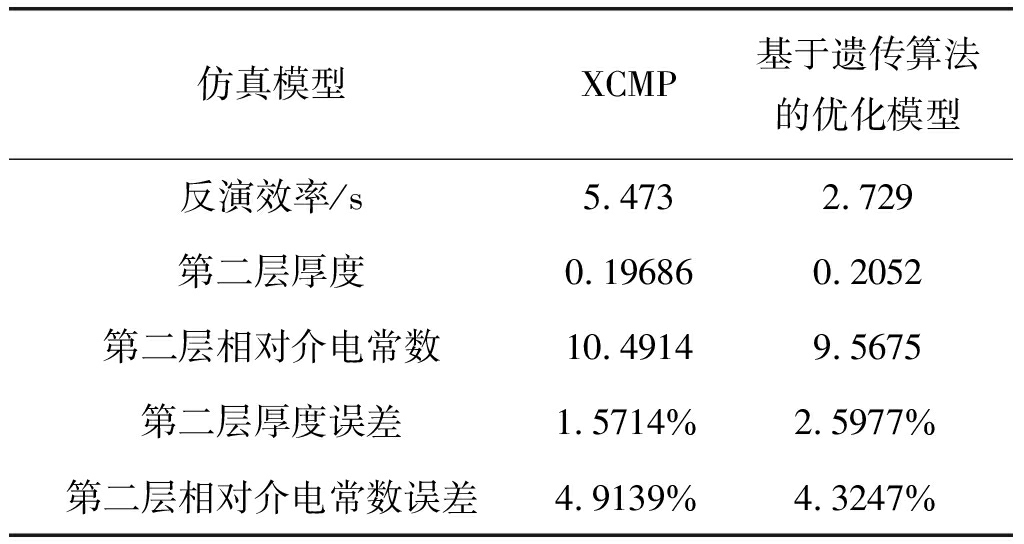
仿真模型XCMP基于遗传算法的优化模型反演效率/s5.4732.729第二层厚度0.196860.2052第二层相对介电常数10.49149.5675第二层厚度误差1.5714%2.5977%第二层相对介电常数误差4.9139%4.3247%
由表3的结果可以看出, XCMP方法由于涉及了一元四次方程的折射点位置求解,反演效率较低,但在厚度反演方面取得了不错的准确率。本文所提出的基于遗传算法的优化模型利用Mast折射点近似与遗传算法,得到了很好的反演效率,并且在反演精度方面,达到了与XCMP相近的反演效果。
表4 多层介质模型仿真结果
Tab.4 Simulation results of multilayered medium model
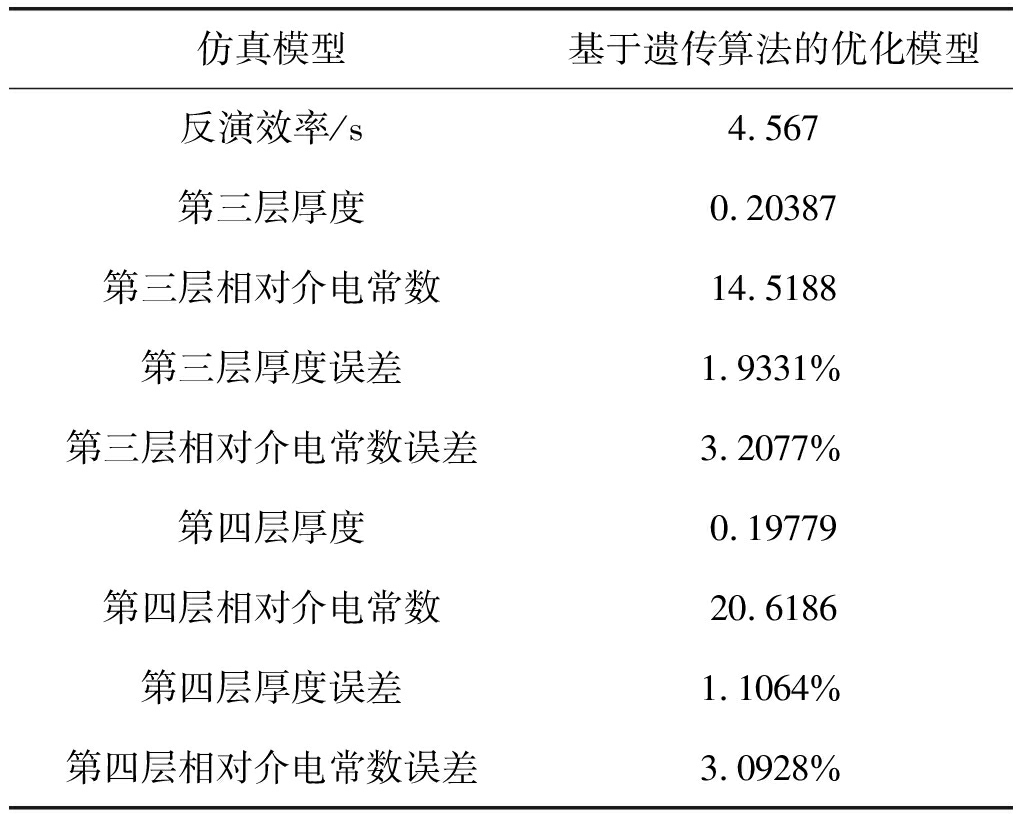
仿真模型基于遗传算法的优化模型反演效率/s4.567第三层厚度0.20387第三层相对介电常数14.5188第三层厚度误差1.9331%第三层相对介电常数误差3.2077%第四层厚度0.19779第四层相对介电常数20.6186第四层厚度误差1.1064%第四层相对介电常数误差3.0928%
由表1与图5的仿真模型,将双层介质模型拓展为四层的多层介质模型,此时XCMP方法不再适用,采取本文所提方法进行仿真实验。根据表4的仿真结果,基于遗传算法的优化模型具有着很好的反演效率与较优的准确率,可以将厚度误差控制在3%以内,介电常数误差控制在5%以内。在实际中,由于大部分探地雷达采取发射和接收天线整体安装的形式,因此实测时需要搭配矢量网络分析仪,设置测量迹线,进行CMP数据的采集。
5 结论
针对实时、高效、无损的检测道路结构情况,探地雷达技术的CMP方法作为道路勘测的主流方法,得到了广泛研究与发展。常规的CMP方法可以解决单层介质的参数反演,但是针对地下多层介质的道路情况,算法需要求解折射点位置的一元四次方程,严重影响了探地雷达测量的实时性与高效率,并且参数反演误差较大。本文提出的基于遗传算法的探地雷达层状介质参数反演算法,将CMP方法与遗传算法相互结合,实现了对地下多层介质结构的参数反演。经过实验验证,算法取得了较好的反演效率与准确率,提出的优化模型可以将厚度误差控制在3%以内,相对介电常数误差控制在5%以内。
[1] 叶奇玲. 基于GPR信号的路基结构特征提取和病害识别[D]. 南京: 南京邮电大学, 2019.
YE Qiling. Analysis and identification of concrete structural defects in GPR images[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2019.(in Chinese)
[2] ZOU Lilong, YI Li, SATO M. On the use of lateral wave for the interlayer debonding detecting in an asphalt airport pavement using a multistatic GPR system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4215- 4224.
[3] BOHIDAR R N, HERMANCE J F. The GPR refraction method[J]. GEOPHYSICS, 2002, 67(5): 1474-1485.
[4] CHEN C C. Lateral waves in ground penetrating radar applications[C]∥2012 14th International Conference on Ground Penetrating Radar (GPR). Shanghai, China. IEEE, 2012: 39- 41.
[5] 袁明德. 探地雷达检测中如何计算速度[J]. 物探与化探, 2003, 27(3): 220-222,236.
YUAN Mingde. The speed calculation in ground-penetrating radar detection[J]. Geophysical and Geochemical Exploration, 2003, 27(3): 220-222,236.(in Chinese)
[6] LIU Hai, XIE Xiongyao, CUI Jie, et al. Groundwater level monitoring for hydraulic characterization of an unconfined aquifer by common mid-point measurements using GPR[J]. Journal of Environmental and Engineering Geophysics, 2014, 19(4): 259-268.
[7] WANG Honghua, LIU Hai, CUI Jie, et al. Velocity analysis of CMP gathers acquired by an array GPR system ‘Yakumo’: Results from field application to tsunami deposits[J]. Exploration Geophysics, 2018, 49(5): 669- 674.
[8] LIU C R, LI J, GAN X, et al. New model for estimating the thickness and permittivity of subsurface layers from GPR data[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(6): 315.
[9] KAO C P, LI Jing, WANG Ying, et al. Measurement of layer thickness and permittivity using a new multilayer model from GPR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2463-2470.
[10] 刘四新, 蔡佳琪, 傅磊, 等. 利用探地雷达精确探测铁路路基含水率[J]. 地球物理学进展, 2017, 32(2): 878- 884.
LIU Sixin, CAI Jiaqi, FU Lei, et al. Accurate detection of moisture content of subgrade by GPR[J]. Progress in Geophysics, 2017, 32(2):878- 884.(in Chinese)
[11] HUANG Zhonglai, ZHANG Jianzhong. Determination of parameters of subsurface layers using GPR spectral inversion method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7527-7533.
[12] 黄忠来, 张建中. 利用探地雷达频谱反演层状介质几何与电性参数[J]. 地球物理学报, 2013, 56(4): 1381-1391.
HUANG Zhonglai, ZHANG Jianzhong. An inversion method for geometric and electric parameters of layered media using spectrum of GPR signal[J]. Chinese Journal of Geophysics, 2013, 56(4): 1381-1391.(in Chinese)
[13] JOHANSSON E M, MAST J E. Three-dimensional ground-penetrating radar imaging using synthetic aperture time-domain focusing[C]∥SPIE’s 1994 International Symposium on Optics, Imaging, and Instrumentation. Proc SPIE 2275, Advanced Microwave and Millimeter-Wave Detectors, San Diego, CA, USA. 1994, 2275: 205-214.
[14] 肖美华, 薛锦云. 遗传算法机理的研究及应用[J]. 计算机工程, 2003, 29(20): 137-139.
XIAO Meihua, XUE Jinyun. Research and Application of Genetic Algorithm Theory[J]. Computer Engineering, 2003, 29(20): 137-139.(in Chinese)
[15] GIANNOPOULOS A. Modelling ground penetrating radar by GprMax[J]. Construction and Building Materials, 2005, 19(10): 755-762.
[16] LENG Zhen, AL-QADI I L. An innovative method for measuring pavement dielectric constant using the extended CMP method with two air-coupled GPR systems[J]. NDT & E International, 2014, 66: 90-98.
