1 引言
由于我国人口密集,地形复杂,流动性大,对交通便利的要求极高,于是我国有非常多的桥梁,目前我国的公路桥梁已超80万座,位居世界第一,但是由于桥梁的使用年数增高,以及服役条件恶劣所引发的安全问题引起了人们的重视,其安全问题主要源于此等建筑物容易受到外界因素导致发生振动,引起形变,发生严重形变时,会发生安全问题导致无法正常运行,从而被迫维修,对人们的安全威胁,以及经济的损失,都是不可忽略的,甚至引发毁灭性的灾难,于是在建造时期确保建筑符合安全系数,以及在正常运行时期及时发现危险,这是重中之重的问题。
合成孔径雷达能够进行全天时、全天候的高分辨率成像[1],而且雷达图像具有相位信息,可以通过对相位信息进行分析,提取振动形变信息,雷达可以进行非接触式,高精度的形变量提取,于是雷达成为对桥梁振动形变检测的重要工具之一。桥梁主要的评估参数就是其振动幅度以及频率,而得到这些参数的途径就是对其在运行中产生的振动信号进行分析,但是桥梁,铁路,隧道,多数存在于干扰较强的环境,振动信号难以被检测到,更不容易检测到振动信号的基频,于是能否顺利的确认振动目标的距离位置,并且在对应位置上检测出信号的振动频率,成为了检测桥梁安全道路上的一大绊脚石。
传统的振动目标检测方法通常对原始雷达信号先进行形变量反演,再从反演后的振动信号上对振动信号及其频率进行检测,但是当目标处于较复杂的环境,在杂波的作用下,反演后的振动信号难以呈现出振动信号自身的特征,所以振动信号的基频不容易被检测出来,因此要通过形变反演这一途径对振动信号进行检测,通常需要对杂波进行抑制。在信号处理方面,传统的方法如杂波图对消[2]、脉冲对消[3]、差分对消只能抑制静止杂波[4],并且在对消后,会大大削减目标信号的能量,造成信号的不真实。有文献指出时间自适应滤波方法[5]对杂波抑制有一定效果,但是无法抑制雷达系统自身工作频率对信号的影响。还有的方法在硬件电路上对杂波进行抑制,如载波自适应对消技术[6],该技术对消电路反应时间极短,可以满足高精度振动检测,也不会被系统自身工作频率影响,但是硬件难度非常高,甚至超过雷达自身的硬件难度,难以实现。所以在形变反演后的信号上面对振动目标进行检测所受到的条件限制较多。
于是对雷达原始信号直接进行分析成为了更好的途径,对原始信号进行处理可以提高信噪比,一般在背景较简单,目标能量足够的情况下,在一维距离像上便可以对目标振动信号所在位置进行检测,但是桥梁通常处于复杂的环境,一维距离像中难以分辨目标。有文献指出振动目标雷达回波信号可以被转换为正弦调制信号[7],对振动目标检测可以被代替为杂波噪声环境下正弦调制信号的检测问题,并且提出一种基于广义似然比检验的振动目标检测算法[8],该算法抗杂波噪声能力较强,但是需要对参数进行三维搜索,运算量过大。也有文献指出,利用自相关法[9]可实现对振动目标的检测,并且可以估计出振动频率,但是当目标背景较复杂时、同一个距离单元出现多个振动目标时,该算法就无法用于检测振动信号。
因此,本文提出一种基于CA-CFAR[10]桥梁振动目标位置及频率检测方法,首先对雷达回波信号进行处理,利用CA-CFAR在距离多普勒域对振动目标进行检测,得到目标所在距离单元,其次提取目标所在距离单元的振动频谱,再次利用CA-CFAR对振动信号频域峰值进行检测,之后利用振动信号自身具有多次谐波、周期性的特点,找到振动信号的基频,完成对振动目标的检测。该方法在原始信号上进行检测,可以规避各种通过形变反演后的信号进行检测所形成的条件限制。而且本文在距离多普勒域对振动目标距离单元进行检测,可以利用振动信号在频域的特点,避免运动目标等非振动信号的干扰,优于在单纯的一维距离信号上面进行检测。
本文的后续章节安排如下,第2部分介绍振动信号的信号模型,对振动信号进行了仿真。第3部分对于提出的检测方法的原理进行论述。第4部分利用仿真的数据以及信标仪的真实数据对检测方法的有效性以及适用性进行验证。最后,对本文的内容进行了总结。
2 振动目标信号模型
振动目标信号模型可表示为:
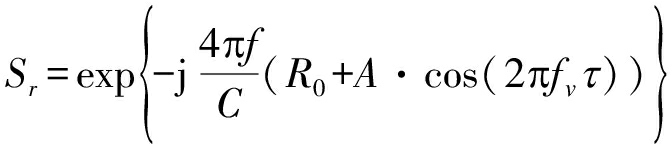
(1)
其中, f为快时间频率,τ为脉冲时间,A为目标振幅, fv为目标振动频率,R0为振动目标到雷达的距离。
将信号模型中相位表示为φp,即:
(2)
在一般情况的下,通过雷达波遇到目标反射后的相位差变化[11],相位如式(2),先对信号进行形变量反演,再去检测振动信号,最能够体现振动信号的特征,也可以更加清晰的判断目标是否为振动信号,但是在复杂环境中,信号的相位非常容易发生变化,导致形变反演不准确,无法判断目标是否为振动信号。
为了更加清晰的呈现振动信号的特征,根据式(1)所给出的振动信号模型,下面给出振动信号的一维距离信号、多普勒频率信号、形变量反演的仿真图,更加直观的去解释信号模型。如图1所示,振动目标距离为20 m,振动频率为10 Hz,振幅为0.005 mm。

图1 振动信号仿真
Fig.1 Vibration signal simulation
如图1所示,可以清晰的看出目标所在位置为20 m处,也就是式(1)中R0的含义。并且在图1(b)多普勒频率信号中,由于振动信号自身的多次谐波特征,各个峰值以10 Hz为距离,均匀分布,峰值之间的距离10 Hz也就是fv为目标振动频率。在图1(c)形变反演信号中,可以看到信号呈现周期性的特征,上下浮动幅度为0.01 mm,也就是振动信号的幅度A。
3 基于CA-CFAR振动目标位置及频率检测方法原理
总体方案流程图如图2所示。

图2 总流程图
Fig.2 General flow-chart
在背景不复杂的情况下,在原始数据的一维距离向上即可检测到目标所在的距离单元,在形变反演后的信号可以检测出信号的振动频率,但是应用在实际场景如桥梁情况下,在噪声与杂波的影响下,在一维距离向上难以检测到振动目标,形变反演也难以体现振动信号的特征,于是需要在信号的距离多普勒域对振动目标所在距离单元进行检测。在目标所在位置的多普勒频率信号中对信号频率进行检测。首先利用CA-CFAR的方法,在距离多普勒域上对每个距离单元上的多普勒频率进行检测,通过比较每个距离单元频率点的个数,来确定振动目标所在距离单元,从而完成自动检测目标距离单元的研究目标。通过上一步得到的目标距离单元,提取目标距离单元的多普勒频率信号,再次利用CA-CFAR对频谱进行检测,在检测结果中,利用振动信号自身具有多次谐波、周期性的特征,对振动目标基频进行检测。
3.1 数据预处理
原始数据处理的流程图如图3所示。
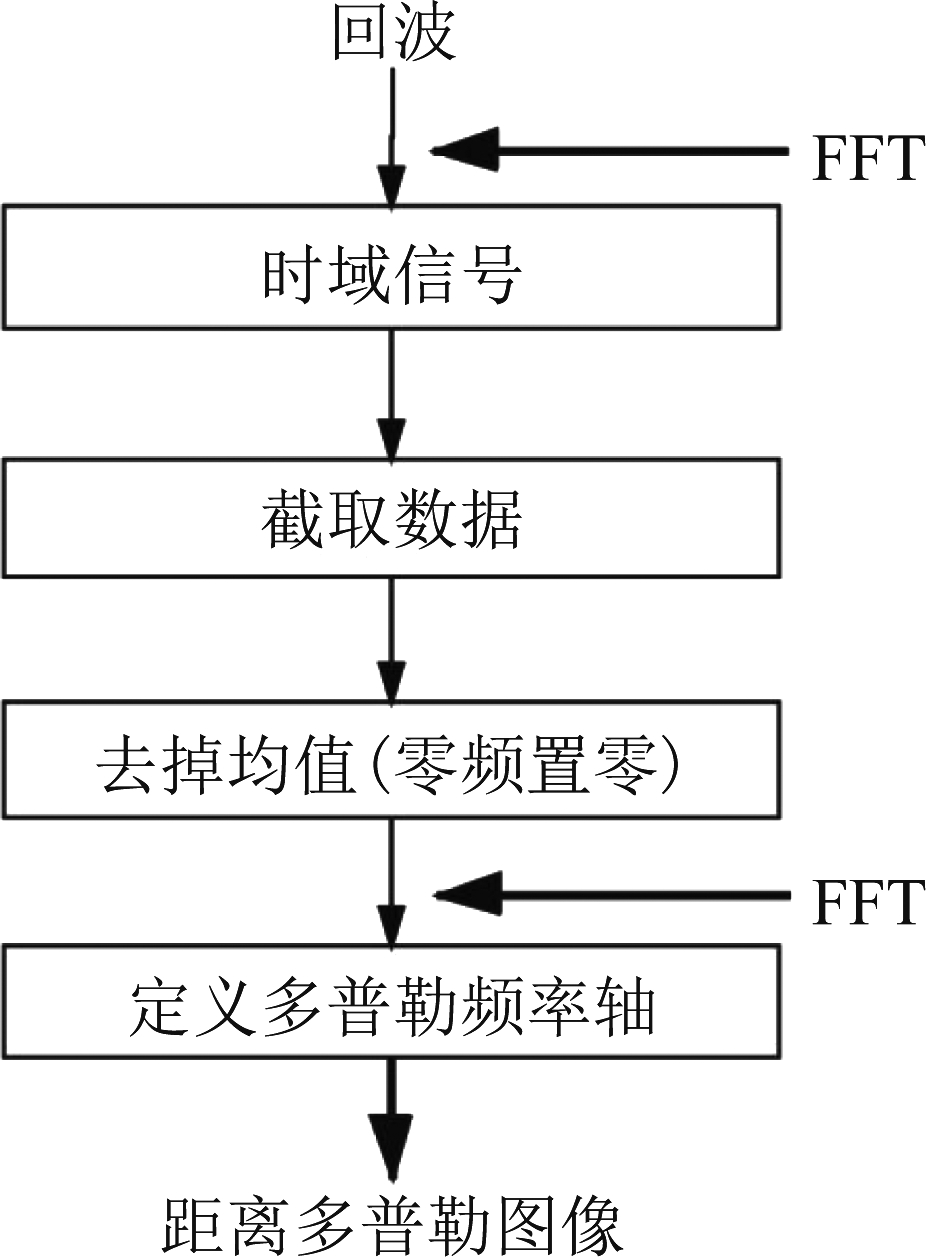
图3 数据处理流程图
Fig.3 Data processing flow chart
首先对频域回波进行傅里叶变换,得到时域信号,然后截取我们所要检测的部分数据,由于信号零频的能量很强,容易影响检测结果,于是需要去掉均值或者将零频置零减少干扰,之后再次进行傅里叶变换,重新得到处理后的频域信号,之后根据带宽与点数定义多普勒频域轴,最后就可以得到所需的距离多普勒信号。
3.2 目标距离单元检测
本文中,利用CA-CFAR在距离多普勒域对目标距离单元进行检测,CA-CFAR的主要原理如图4所示。
图4 CA-CFAR模型
Fig.4 The model of CA-CFAR
如图4所示,该图为CA-CFAR算法的滑窗模型,其中X为检测单元,即通过比较阈值来检测目标是否存在的单元。T为训练单元,滞后于检测单元的称为滞后训练单元,领先于检测单元的称为前导训练单元,一般情况下,通过合并前导与滞后训练单元,然后取所有训练单元的平均作为阈值,与检测单元进行比较。G为保护单元,当目标较强时,目标信号通常会散射到周围的训练单元中,会影响阈值的设定。于是设置保护单元,保护单元不参与阈值计算,有效避免了目标能量散射的情况。其中,保护单元与训练单元的数量根据实际场景的复杂程度而定。
如图5所示第一步,将图4所示的检测滑窗,也就是图5示意图中的红色滑窗X,使用在距离多普勒域的每一个距离单元上,从最左侧第一个距离点数(第一列)开始,对一个距离点数(每一列)上的多普勒频率进行CA-CFAR检测,直到滑窗X检测完最后一个距离点数后结束。由于目标通常会将能量散射到周围的距离单元上,于是会在多个距离上检测到多个频点,因此需要进行第二步,统计每一列所检测到的频点个数,计算出频点最多的一列,就是振动目标所在的位置,记录当前距离。
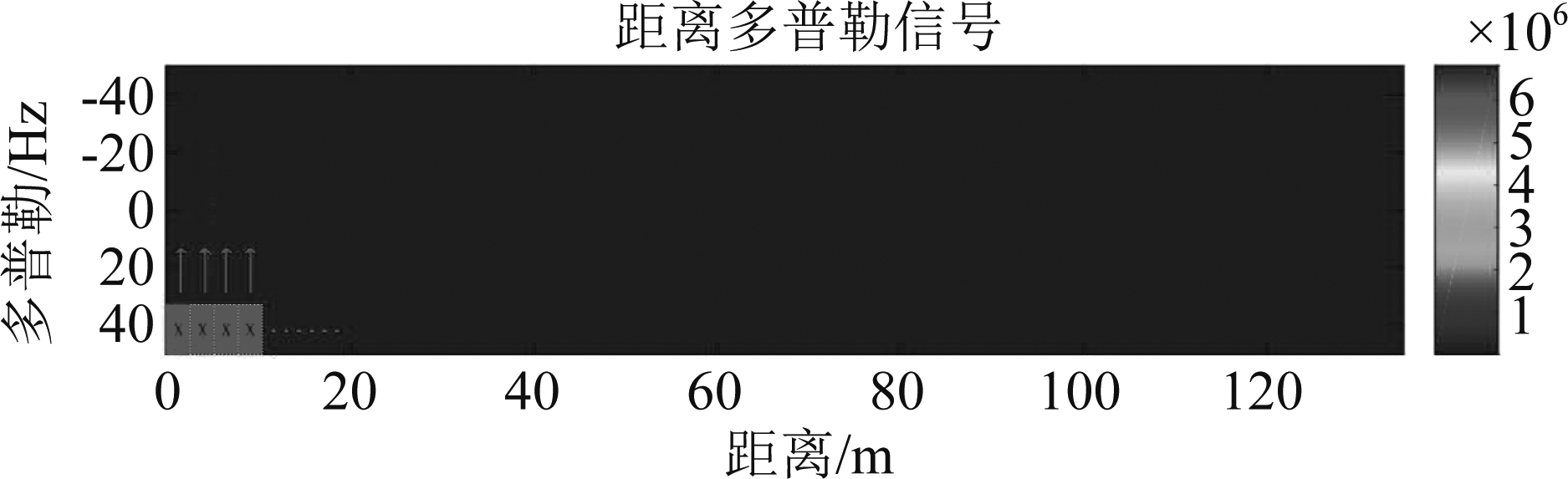
图5 CA-CFAR检测示意图
Fig.5 CA-CFAR Detection Schematic
3.3 振动目标频率检测
在确认了目标所在的距离单元后,提取目标所在距离单元的多普勒信号,利用CA-CFAR对该信号进行检测,再次将图4所示的检测滑窗,沿着多普勒频率轴进行检测,得到检测结果后,将频率峰值标记出,观察检测点的分布,观察检测点是否符合振动信号多次谐波的特征,通过检测点之间的间距,得到振动目标的振动频率。
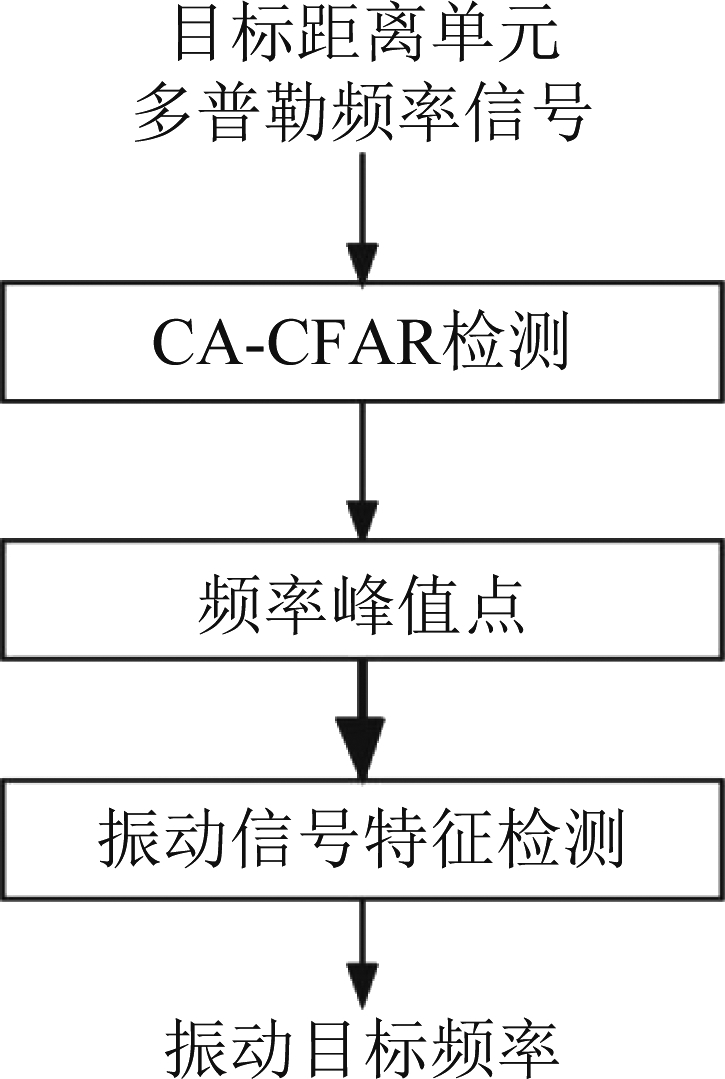
图6 频率检测流程图
Fig.6 Frequency detection process chart
4 仿真与实测数据验证
4.1 仿真实验4.1.1 复杂环境下振动信号仿真实验
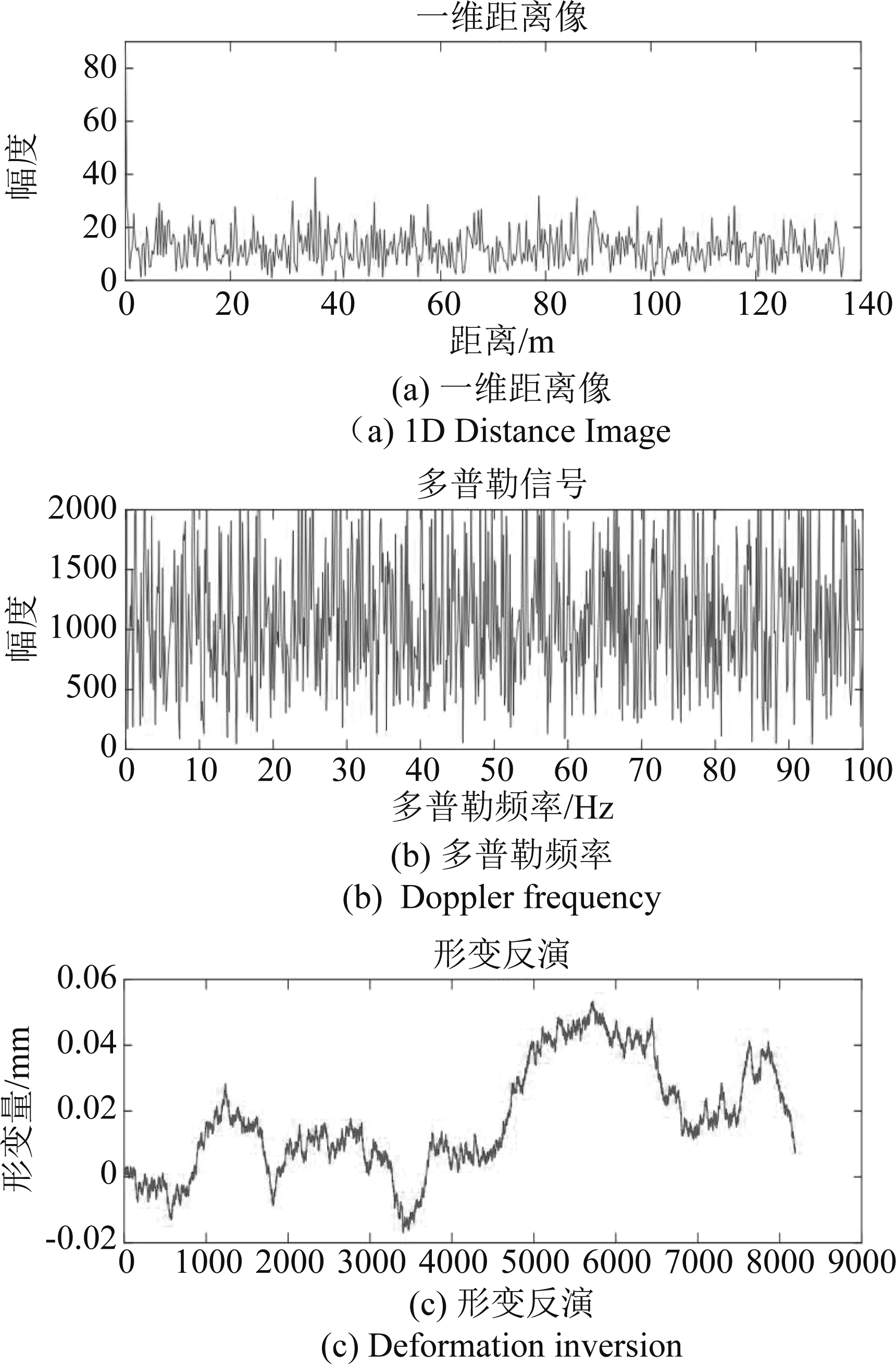
图7 振动信号仿真(加入杂波、噪声)
Fig.7 Vibration signal simulation (add clutter, noise)
为了证明在复杂环境中,难以从形变反演中提取振动信号,下面给出加入杂波与噪声以模仿真实环境的仿真图,其中,振动目标距离为20 m,振动频率为10 Hz,振幅为0.01 mm,与第2章振动信号模型示意图的参数一致。
由此可见,在噪声与杂波的影响下,难以从上述的三种信号图像中检测到振动目标的信息。本节从信号模型上说明了振动信号特征以及在外界环境影响下信号发生的变化,通过仿真实验,验证了该变化的存在。
4.1.2 振动目标距离以及频率检测仿真实验
为了验证本文所提算法的可行性以及适用范围,下面进行了振动目标检测仿真实验,仿真场景内只包含一个振动目标回波。设置雷达系统工作与振动目标参数,以及场景参数,如表1所示。为了模拟真实监测场景,在仿真的回波信号中加入对应的噪声以及杂波。
表1 仿真参数
Tab.1 Simulation parameters

参数参数值起始频率/GHz77信号带宽/MHz560脉冲重复频率/Hz2000目标振动频率/Hz4目标振幅/m0.005目标距离/m20噪声/dB-30杂波1000
根据上述参数设置进行振动目标场景回波仿真,之后对回波进行处理,在距离多普勒域对利用CA-CFAR对振动目标进行检测,完成对目标距离单元的自动检测,并且利用振动信号自身的特征,对振动信号的基频进行检测。
仿真结果如图8所示,在振动回波模型的基础上为了模拟真实场景,加入了常数1000的杂波以及-30 dB的噪声,检测结果为在20 m处存在振动目标,与设定的20 m目标距离参数相符,验证了本算法在杂波与噪声的作用下检测目标距离单元的准确性。图8(c)可以看出在目标位置上的多普勒频率峰值点呈现等差数列,并且表2给出了20个频率峰值点的变量数据以及相对应的幅度值,峰值频率数据取了后两位小数,幅度值取了整数方便观察,可以更加清楚地看到幅值呈以4为差值的等差数列分布,但是由于误差的原因,会在同一个频率检测到多个点,但是不影响数据呈现振动信号的周期性。因此验证了本算法在杂波与噪声作用下振动信号频率检测的准确性。
表2 频率变量数据
Tab.2 Frequency variable data

频率/Hz3.914.158.0615.8716.1120.0223.9327.8328.0831.98幅度/dB28113463131701282835964662873531频率/Hz35.8936.1340.0443.9547.8548.105255.9156.1560.06幅度/dB1201214836689150566228345516101526
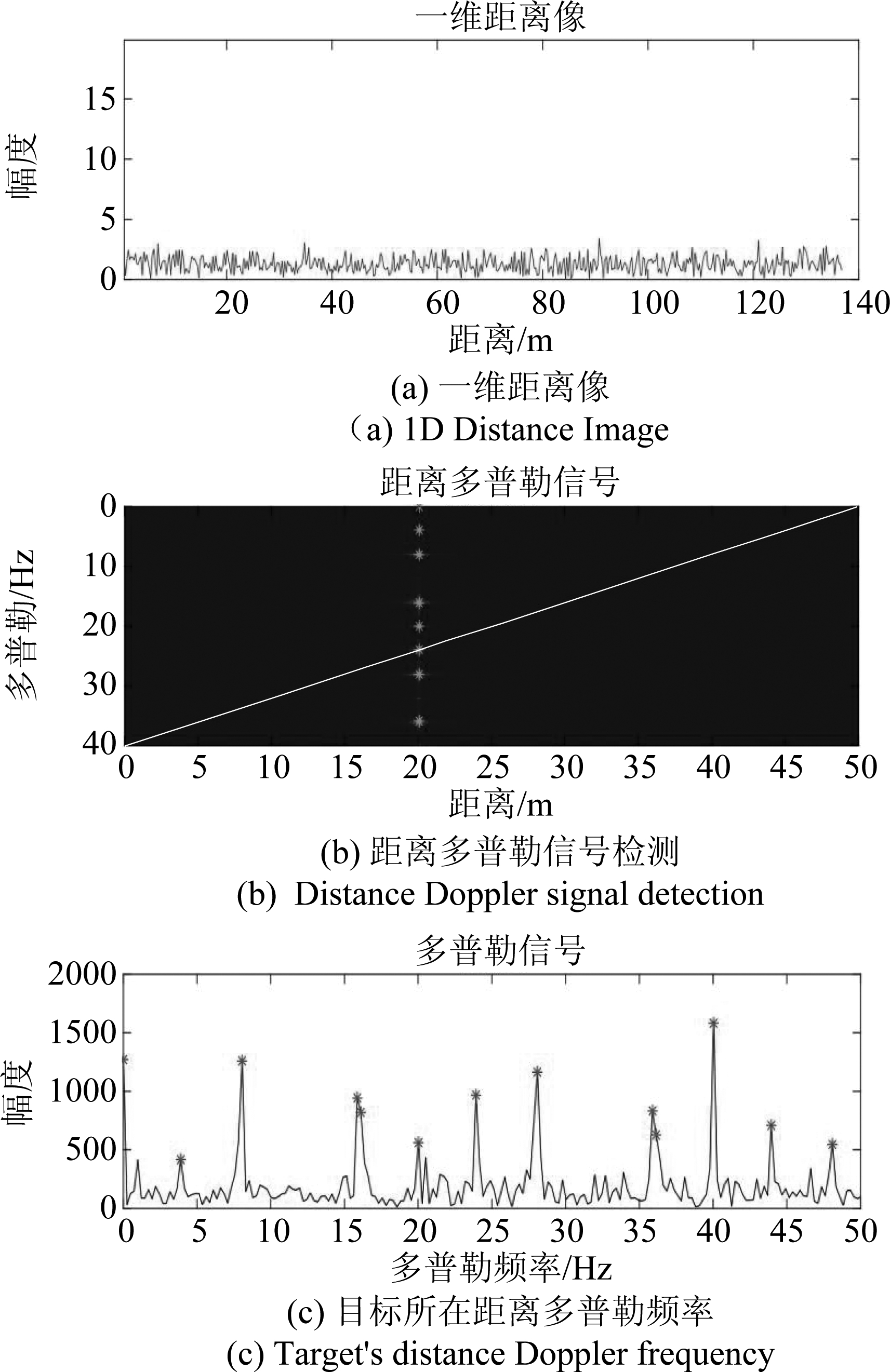
图8 仿真振动目标检测
Fig.8 Simulation Vibration Target Detection
4.2 信标仪定量化实验
为了模拟真实的桥梁振动场景,进行了振动信标仪检测试验,先给出了雷达以及信标仪的参数,采用77G毫米波雷达,以及振动频率为2 Hz,振动幅度为0.1 mm的振动信标仪,实际测试设备布点如图9所示,实验地点为西黄村一处广阔平台,信标仪放置在雷达正前方5 m处。如表3所示。之后给出了振动目标的一维距离像、距离多普勒信号图、所在距离单元多普勒频率图。

图9 实验场景
Fig.9 Experimental scene
表3 信标仪定量化参数
Tab.3 Quantitative Parameters of Vibration Instrument
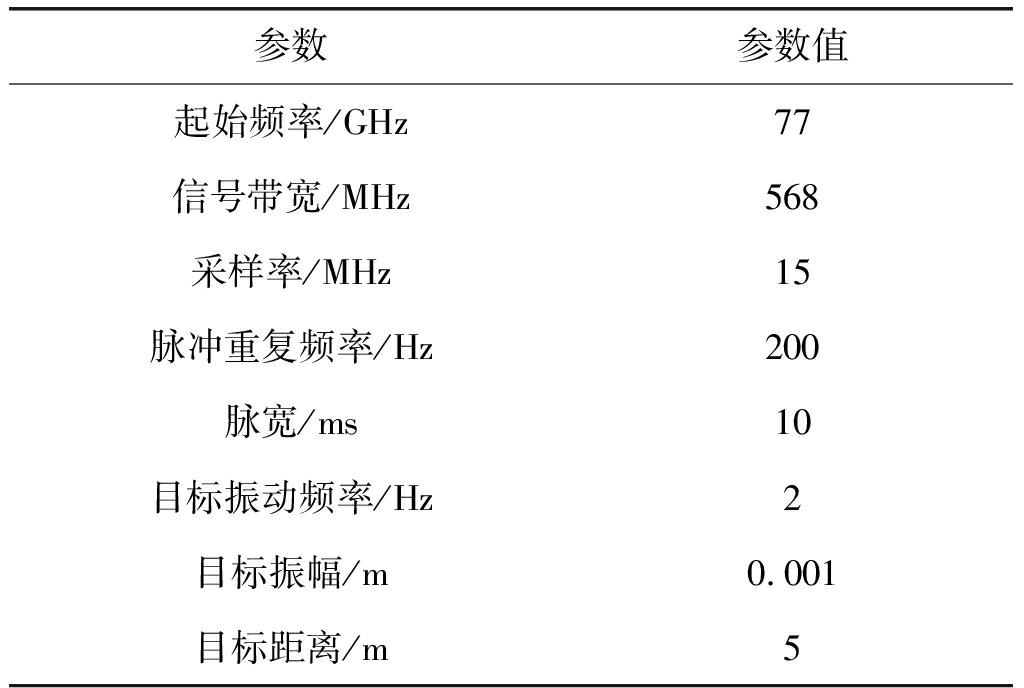
参数参数值起始频率/GHz77信号带宽/MHz568采样率/MHz15脉冲重复频率/Hz200脉宽/ms10目标振动频率/Hz2目标振幅/m0.001目标距离/m5
由于目标背景比较单一,可以在一维距离信号中看出目标位置,但是无法获得振动频率,在本文检测算法的作用下,在图9(b)依然可以看出目标所在距离为5 m,之后提取该距离处的多普勒频率信号,对其进行检测,得到图9(c),可以看出峰值点呈现较强的规律性,符合振动信号周期性的标准,之后从表4中可以看到所取的20个峰值频点以及对应的幅度值,峰值频率呈等差数列,差值约为2,与信标仪设定的2 Hz振动频率相符,可以说明检测到了振动频率为2 Hz的振动信号,于是本文算法得以验证。
表4 频率变量数据
Tab.4 Frequency variable data

频率/Hz2.054.106.108.1512.1912.2414.2416.2918.3420.34幅度/dB682334784100638545118154107162频率/Hz22.3924.4426.4928.4930.5332.5834.5836.6338.6840.73幅度/dB134225234864304294229337480265
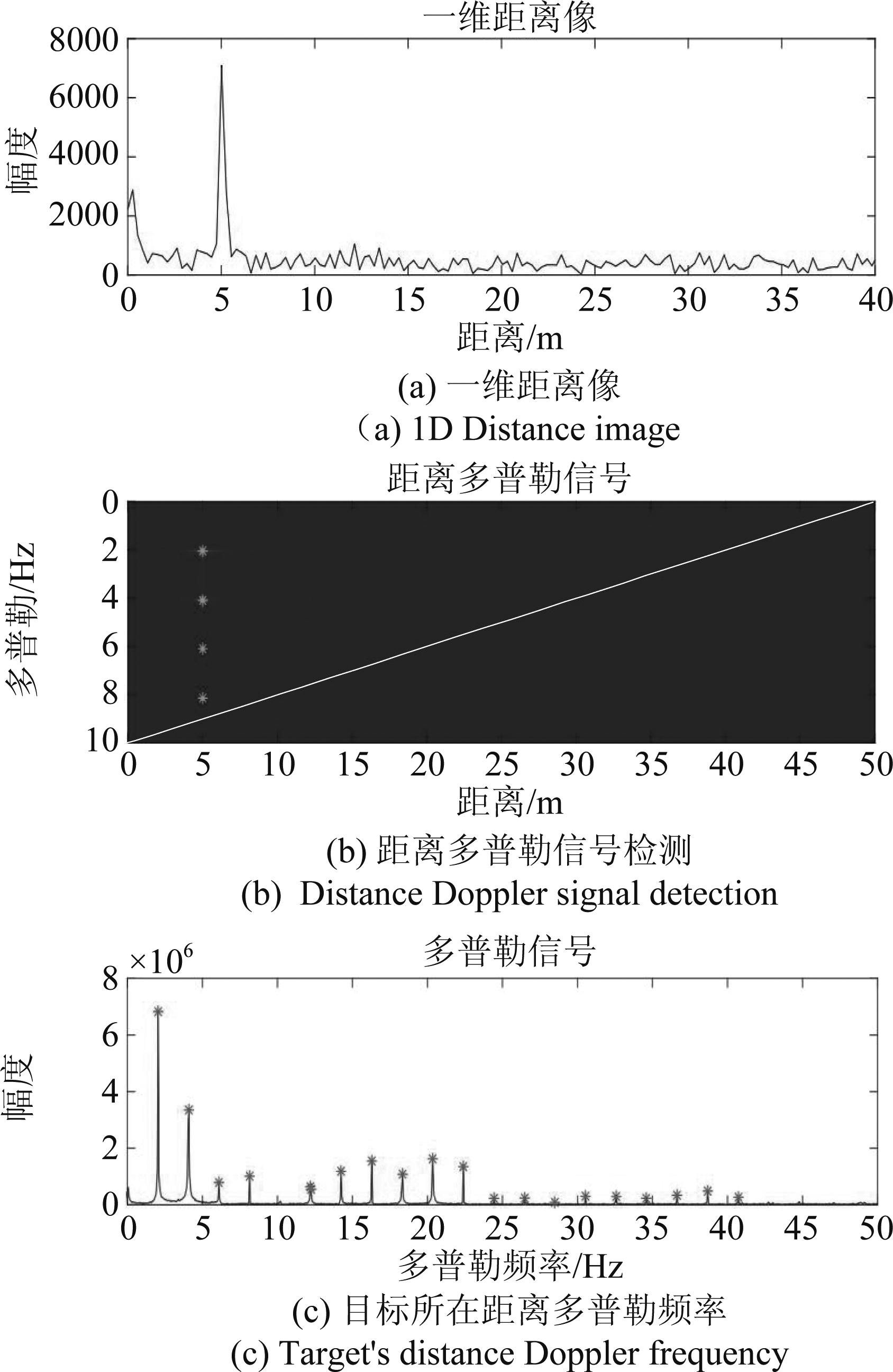
图10 信标仪定量化检测
Fig.10 Quantitative Detection of Vibrator
5 结论
在利用雷达对桥梁振动信号所在位置与频率进行检测时,在一维距离像中难以看出目标所在距离,在外界环境的影响下,通过形变量反演不容易检测到振动信号的频率。本文提出基于CA-CFAR的桥梁振动信号位置与频率检测方法,对目标距离单元的自动检测,对目标的基频进行精准的检测,并且通过仿真实验以及信标仪定量化实验对该算法进行了验证,结果符合预期,验证了算法的有效性以及准确性。该方法在桥梁振动检测应用上面可以实现定位桥体振幅较大的位置以及检测出该位置的振动频率,确定其是否符合安全标准。本文在CA-CFAR对信号进行检测的期间,会出现漏检以及检测到多个峰值的情况,在多普勒频率检测图中,会出现漏检情况:也就是在振动信号特征的影响下,本该出现等差数列排序的频点,但是没有检测到某个等差位置上的频点。也会出现虚检情况,也就是检测到不符合振动信号特征、非规律性的频点,这两种问题是由于对训练单元以及保护单元的数量设置还没有明确的标准,后期会继续推进。
[1] 秦玉亮, 王建涛, 王宏强, 等. 弹载合成孔径雷达技术研究综述[J]. 信号处理, 2009, 25(4): 630- 635.
QIN Yuliang, WANG Jiantao, WANG Hongqiang, et al. Overview on missile-borne synthetic aperture radar[J]. Signal Processing, 2009, 25(4): 630- 635.(in Chinese)
[2] 冯大政, 曹杨, 毛依娜,等. 用于MIMO雷达的两维多脉冲对消器[P]. CN101907702A,2010-12- 08.
FENG Dazheng, CAO Yang, MAO Yina, et al. 2D multi-pulse canceller for MIMO radar[P]. CN101907702A,2010-12- 08.(in Chinese)
[3] 张敬松, 潘健. 通用型雷达动态杂波图对消系统[J]. 现代雷达, 2007, 29(4): 31-33.
ZHANG Jingsong, PAN Jian. Cancellation system of general radar dynamic clutter map[J]. Modern Radar, 2007, 29(4): 31-33.(in Chinese)
[4] 曾涛, 卢峄灵, 向寅, 等. 一种强杂波环境下雷达目标微振动信号提取方法[J]. 信号处理, 2019, 35(6): 935-943.
ZENG Tao, LU Yiling, XIANG Yin, et al. A micro-oscillation signal extraction method for radar target in strong clutter environment[J]. Journal of Signal Processing, 2019, 35(6): 935-943.(in Chinese)
[5] 钱鉴, 府锡东, 郭文锋. 一种载波对消提高相位调制度的新技术[J]. 微波学报, 2019, 35(4): 1-5.
QIAN Jian, FU Xidong, GUO Wenfeng. Novel technique for enhancing modulation depth through carrier cancellation[J]. Journal of Microwaves, 2019, 35(4): 1-5.(in Chinese)
[6] 贺峰. 宽带/超宽带雷达运动人体目标检测与特征提取关键技术研究[D]. 长沙: 国防科学技术大学, 2011.
HE Feng. Researches on key techniques of wide band/ultra-wide band radar detection and signature extraction of locomotor human targets[D]. Changsha: National University of Defense Technology, 2011.(in Chinese)
[7] 周阳, 沈爱国, 毕大平. 双通道SAR振动目标快速检测[J]. 遥感学报, 2020, 24(9): 1143-1156.
ZHOU Yang, SHEN Aiguo, BI Daping. A fast detection algorithm of vibration targets for Dual-Channel SAR[J]. Journal of Remote Sensing, 2020, 24(9): 1143-1156.(in Chinese)
[8] DENG B, WANG H Q, LI X, et al. Generalised likelihood ratio test detector for micro-motion targets in synthetic aperture radar raw signals[J]. IET Radar, Sonar & Navigation, 2011, 5(5): 528.
[9] SUN Zhaoqiang, LI Baozhu, LU Yaobing. Research on micro-motion and micro-Doppler of ballistic targets[C]∥2009 IET International Radar Conference. Guilin. IET, 2009: 1- 4.
[10] 李健, 孙光才, 邢孟道, 等. 基于卷积构型的单元平均CFAR目标检测算法[J]. 电波科学学报, 2018, 33(1): 56- 63.
LI Jian, SUN Guangcai, XING Mengdao, et al. A cell averaging CFAR detector based on convolution for target detection in SAR images[J]. Chinese Journal of Radio Science, 2018, 33(1): 56- 63.(in Chinese)
[11] 王翔, 潘中明, 王波. 基于雷达的斜拉索索力非接触遥测技术研究[J]. 世界桥梁, 2019, 47(3): 49-53.
WANG Xiang, PAN Zhongming, WANG Bo. Study of non-contact remote cable force testing techniques based on radar[J]. World Bridges, 2019, 47(3): 49-53.(in Chinese)




