1 引言
随着现代化设备的发展,无线传感器网络已经应用于水下复杂的信道环境[1- 4]。声源定位技术是水下无线传感器网络的核心技术,它在水下目标检测、水下机器人作业和深海探测等诸多领域都有广泛应用[5- 6]。水下声源定位主要包括到达时间(Time of arrival, TOA)、到达时间差(Time difference of arrival, TDOA)、到达频率差(Frequency difference of arrival, FDOA)和到达角度(Angle of arrival, AOA)等[7-10]。
在水下定位中,TDOA定位不需要保持目标和传感器之间的时间同步,因此被越来越多的学者所关注。传统的TDOA定位算法包括两阶段加权最小二乘算法[11](Two-stage weighted least squares, TSWLS)和泰勒[12](Taylor)算法。这两种算法各具有优势,前者不需要初始迭代位置且是封闭形式的,后者需要初始迭代位置且定位精度高。文献[13]提出了观测传感器最少的TDOA算法,将最大似然估计(Maximum likelihood estimation, MLE)和两阶段加权最小二乘算法结合使用。TDOA定位求解的是目标的位置,运动目标的速度估计需要利用FDOA定位来进行[14]。文献[15]提出了一种基于TDOA/FDOA的两阶段加权最小二乘算法,第一阶段粗略估计目标的位置和速度,第二阶段进行误差补偿。文献[16]提出了一种基于TDOA/FDOA的迭代加权最小二乘算法,相对于文献[15]的算法,定位精度有了显著提高。文献[17]提出了一种利用TDOA和FDOA测量的移动源定位的半定凸松弛算法,该算法利用凸优化方法求解目标位置和速度估计值,定位精度比TSWLS算法高很多。
在上述文献的基础上,本文结合TSWLS算法不需要初始迭代解和Taylor算法迭代精度高的优势,提出了一种基于TDOA/FDOA的泰勒加权最小二乘算法。文献[12]提出了目标到传感器距离的泰勒展开式,文献[9]对距离变化率的泰勒展开式进行了求解,本文综合以上文献对TDOA/FDOA的测量值进行泰勒展开,并构造定位方程。首先,通过加权最小二乘算法求解目标粗估计位置和速度;然后,通过求解TDOA和FDOA测量值的泰勒展开式构造定位误差方程,用迭代的方法不断更新目标估计位置和速度;最后,当定位误差足够小或达到最大迭代次数的时候,算法停止运行并输出目标估计位置和速度。已有的Taylor算法只能计算目标的位置,本文针对利用泰勒算法计算目标位置和速度的问题进行研究。
2 定位场景
在三维水下定位场景中,运动目标的位置坐标为u=[x,y,z]T,它的速度坐标为
目标的位置和速度是待求解的参数。假设有M个传感器参与定位,第i个传感器的位置以及速度坐标为si=[xi,yi,zi]T和
其中i=1,2,…,M。不妨设第一个传感器是参考传感器,它的位置以及速度坐标为s1=[x1,y1,z1]T和
传感器的位置以及速度坐标是已知的。
传感器i到水下目标的距离可以表示为
(1)
式中||*||表示欧几里得范数。
如果目标发射的声波传播至传感器i(i≠1)和参考传感器的真实时延差为
水下声波传播的速度为v。则它们得到的真实的TDOA测量值可以写为
(2)
对方程(1)两端关于时间求导可以得到距离变化率为
(3)
考虑方程(2)关于时间的导数,传感器i(i≠1)和参考传感器提取的FDOA测量值可以表示为
(4)
参考传感器和其余传感器的真实TDOA测量值的向量形式记为
和它们的真实FDOA测量值的向量形式可以表示为
在实际的水下环境中,测量值往往伴随着噪声,因此实际得到的TDOA和FDOA的测量值向量可以写为γ=γ0+Δγ和
这里实际得到的TDOA测量值和它们的噪声向量分别为γ=[r2,1,r3,1,…,rM,1]T和Δγ=[Δr2,1,Δr3,1,…,ΔrM,1]T。实际得到的FDOA测量值和它们的噪声向量记为
和
假设Δγ和
的所有元素均服从均值为0且方差为常数的高斯分布,则它们的协方差矩阵可以写为Qγ=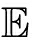
[ΔγΔγT]和
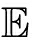
这里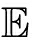为期望函数。
3 基于泰勒加权最小二乘算法的水下目标定位
3.1 初始目标位置和速度估计
将方程(2)改写为
两边完全平方后,带入方程(1)可以得到
i=2,3,…,M
(5)
方程(5)是非线性的,将
作为一个未知量可以构成一组线性方程。对方程(5)两边关于时间求导可以得到FDOA测量方程,具体如下所示
(6)
引入TDOA测量值噪声向量Δγ后,TDOA方程(5)可以写为
(7)
式中
其中Δri是距离噪声。方程(7)取约等式的原因是忽视了Δri,12项。
引入TDOA/FDOA测量值噪声向量Δγ和后,FDOA方程(6)可以表示为
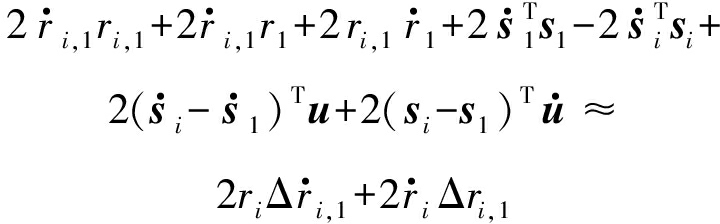
(8)
式中
其中
是距离变化率噪声。方程(8)取约等式的原因是忽视了
项。
定义待求变量
并考虑所有的传感器组成的TDOA/FDOA联合定位方程组,可以构造以下矩阵方程
h-Gθ=Bn
(9)
式中
(10)
G=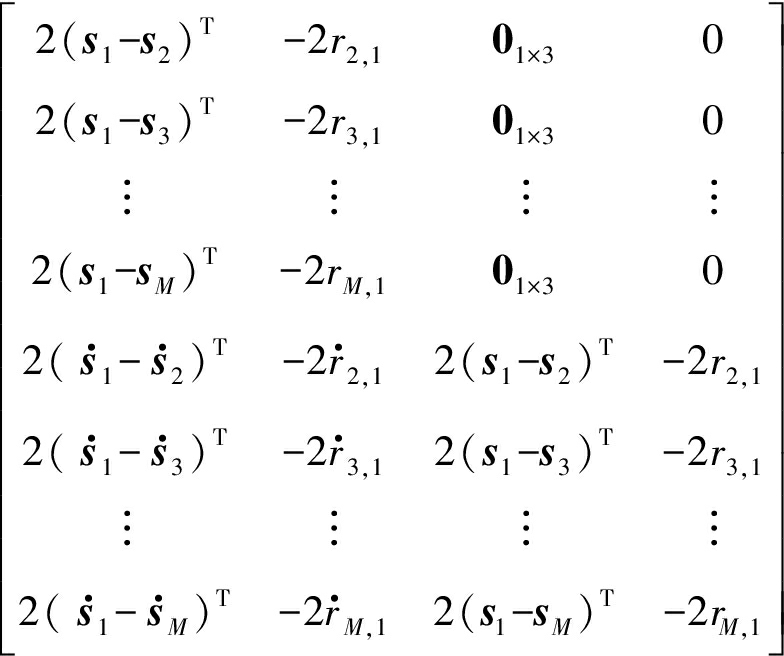 
(11)
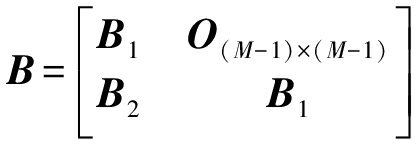
(12)
B1=2diag(r2,r3,…,rM)
(13)
(14)
和
表示零向量,下标表示它的维度。O(M-1)×(M-1)表示所有元素都为零的矩阵。diag(*)表示将*对角化,对角线以外的元素全为0。
矩阵方程(9)的加权最小二乘解可以写为
θ1=(GTW-1G)-1GTW-1h
(15)
式中
是权值矩阵,它可以写为
其中协方差矩阵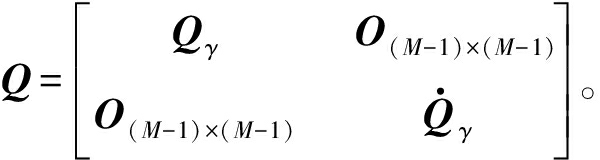
特别的,权值矩阵W的求解需要知道ri和
的取值,所以需要用协方差矩阵Q代替W进行方程(15)的第一次求解目标估计位置和速度,用目标估计位置和速度计算ri和的取值。
3.2 泰勒展开算法
利用加权最小二乘算法求得估计值θ1后,我们构造定位误差向量
于是有
和
传感器i到目标的距离的一阶泰勒展开式为
i=1,2,…,M
(16)
式中距离估计值
和ρa,b=(a-b)/||a-b||,a和b是维度相同的向量。
对方程(16)关于时间求导于是有[9]
(17)
式中
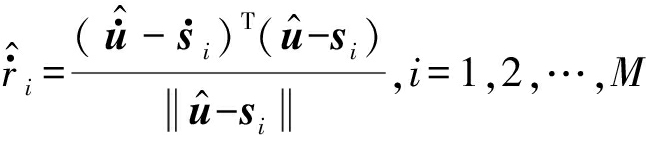
(18)
由此,我们可以构造以下方程
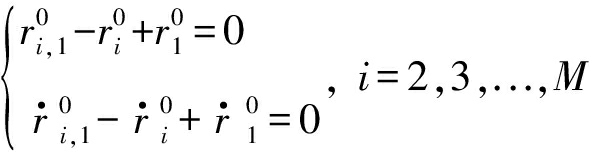
(19)
引入TDOA和FDOA噪声向量以及方程(16)和(17),方程(19)可以写为如下两个方程
(20)
(21)
式中
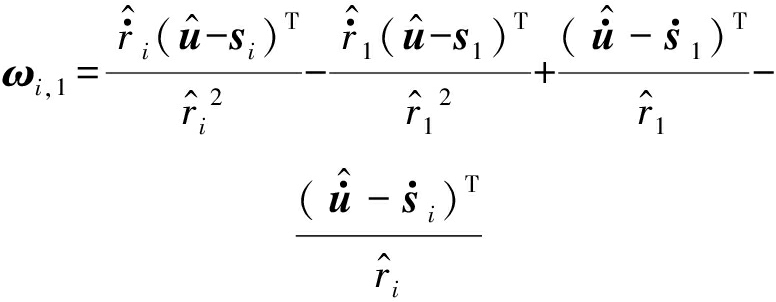
(22)
考虑所有的传感器组成的方程组,方程(20)和(21)的矩阵形式可以写为
R-PΔθ=n
(23)
式中
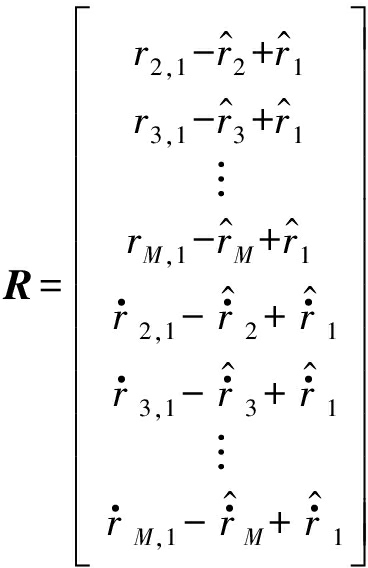
(24)
(25)
方程(23)的定位误差估计值可以用如下方程求得
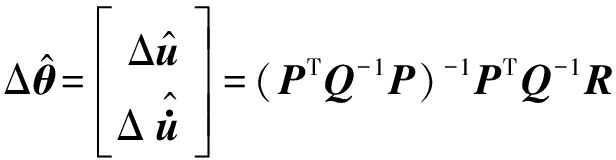
(26)
于是最终的泰勒迭代估计结果为
和
将求解的位置估计值
和速度估计值
带回到方程(23)中,直至
或达到了最大迭代次数时,算法停止运算并输出最终估计位置和估计速度
这里δ=10- 6。
值得注意的是,本文通过引入文献[9]的方程,将泰勒算法从TDOA定位领域扩展到TDOA/FDOA定位领域,使得泰勒算法不但能计算目标位置,而且能计算目标速度。本文提出的泰勒加权最小二乘算法通过加权最小二乘算法求解初始值,再将初始值带入泰勒算法进行反复迭代,本文算法在噪声较小时能够收敛。算法框图如图1所示。
图1 所提算法框图
Fig.1 Block diagram of the proposed algorithm
4 克拉美罗下界
克拉美罗下界表示无偏估计所能达到的最佳的估计效果,常用于判断是否达到克拉美罗下界来验证算法的精确度。TDOA/FDOA定位的克拉美罗下界的表达式如下所示[15]
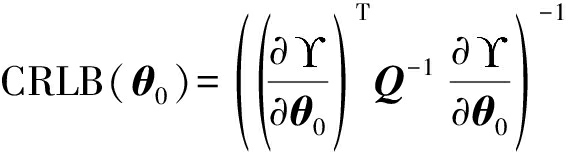
(27)
式中
和
方程(27)中的一些细节如下所示
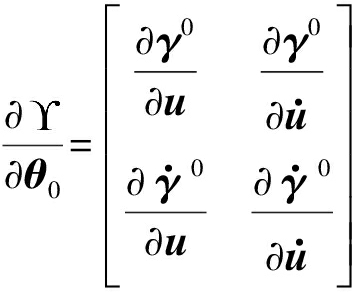
(28)
式中
(29)
(30)
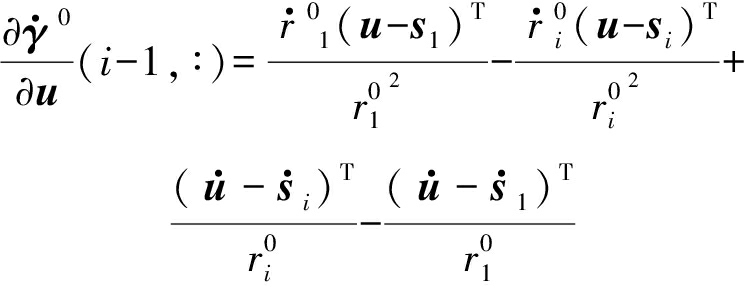
(31)
(32)
本文算法每次迭代的协方差矩阵可以表示为[8]
(33)
文献[15]证明了在低噪声情况下加权最小二乘算法的解是收敛到真实值附近的。观察方程(25)和(28)可以得到
(34)
(35)
于是可以得到在低噪声条件下,每次泰勒迭代本文算法都能更加接近克拉美罗下界。
5 仿真
在本节中总共有两组仿真,第一组水下定位场景中,目标是高速移动的物体比如鱼雷或潜水艇等;第二组水下定位场景中,目标是缓慢移动的物体,比如水下无人潜航器或水下机器人等。假设TDOA和FDOA测量值噪声服从均值为零和方差为常数的高斯分布,且它们的协方差矩阵记为
(36)
式中σ2为TDOA和FDOA测量值的方差。
仿真通过多次蒙特卡罗随机实验来计算目标位置和速度估计值的误差,用来评价算法性能的指标有均方根误差(Root mean square error, RMSE)和偏差(Bias),其中均方根误差定义为
(37)
和偏差定义为
ϑ)||/L
(38)
式中ϑ为真实值,
为估计量,在本文仿真中L=10000。
仿真1 对高速移动目标的定位
在水下定位场景中,有五个传感器参与定位,水下目标为速度极快的鱼雷等敌对目标,目标与传感器的分布如表1所示。仿真的对比算法有加权最小二乘(Weighted Least Squares, WLS)算法、TSWLS算法[15]和克拉美罗下界。仿真1中所有算法的位置估计的均方根误差和偏差如图2所示,速度估计的均方根误差和偏差如图3所示。
图2和图3的横坐标表示噪声方差的10倍对数形式,单位为分贝(dB),具体取值范围为-40 dB到10 dB。从图2中的均方根误差曲线可以看出,所提算法的均方根误差远小于WLS算法的均方根误差。位置噪声方差在-40 dB到0 dB时,所提算法均方根误差和TSWLS算法相同,但位置噪声方差在0 dB到10 dB之间时,所提算法的均方根误差要远低于TSWLS算法。此外,在位置噪声方差为-40 dB到10 dB区间内,所提算法恒接近克拉美罗下界。从图2中的偏差曲线可以看出,位置噪声方差在-40 dB到-20 dB时,所提算法的偏差和TSWLS算法相同,且都优于WLS算法。位置噪声方差大于-20 dB时,所提算法的偏差是最小的。
从图3的均方根误差曲线可以看出,当速度噪声方差在-40 dB到10 dB时所提算法的均方根误差恒接近克拉美罗下界,是优于WLS算法和TSWLS算法的。由图3的偏差曲线可以看出,当速度噪声方差在-40 dB到-10 dB时,所提算法与TSWLS算法的偏差差不多。当速度噪声方差在-10 dB到10 dB时,所提算法的偏差低于-10 dB且是最优的。
图4和图5展示了所提算法和对比算法在σ2=9时的累积分布函数(Cumulative distribution function, CDF)。
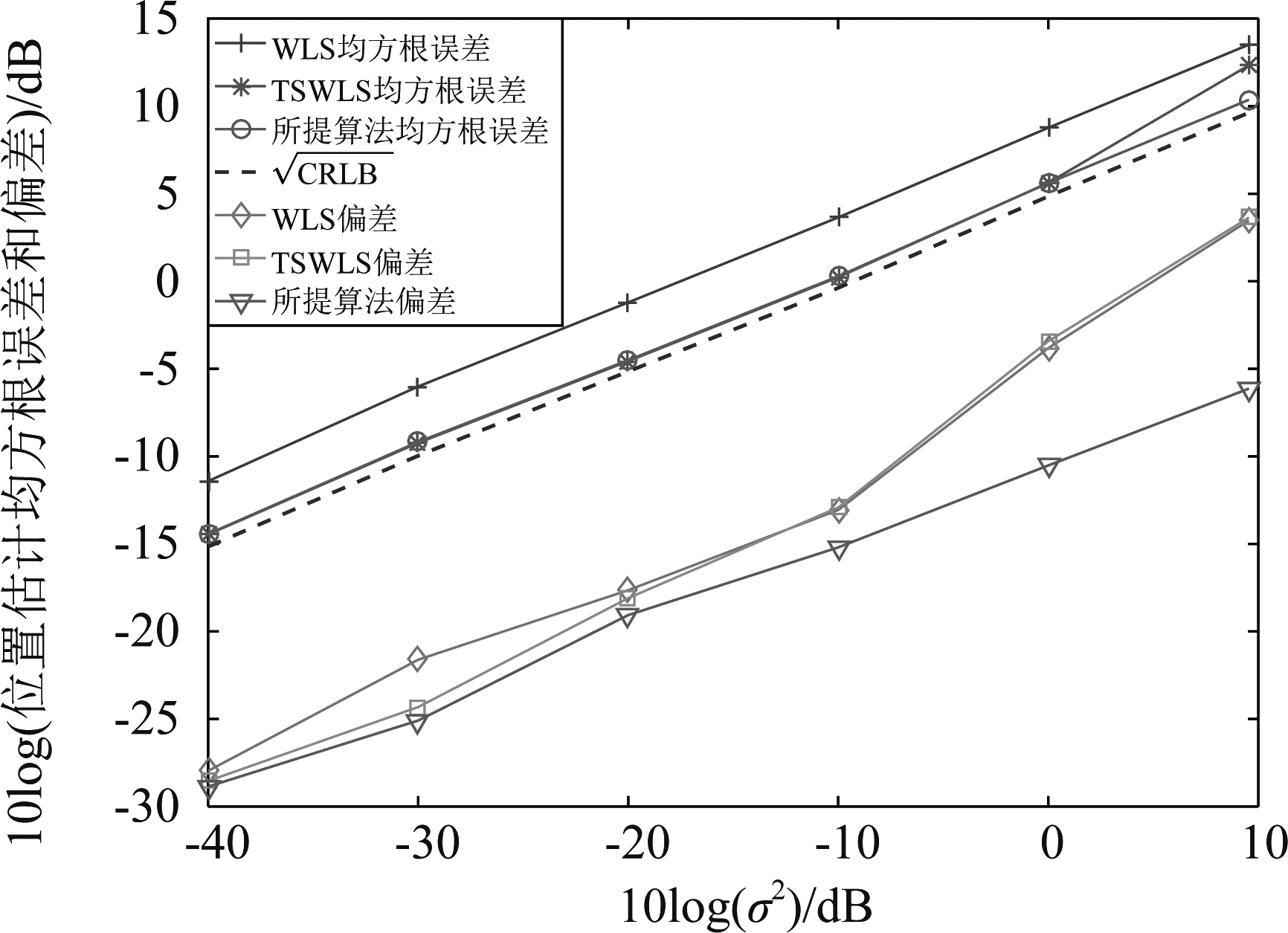
图2 仿真1中所有算法位置估计的均方根误差和偏差
Fig.2 RMSE and Bias of position estimation of all algorithms in simulation 1
图3 仿真1中所有算法速度估计的均方根误差和偏差
Fig.3 RMSE and Bias of velocity estimation of all algorithms in simulation 1
图4和图5的横坐标分别表示位置误差和速度误差的对数形式,单位为dB。从图4可以看出,在位置噪声方差σ2=9时,所提算法的误差分布相对均匀,最大位置误差在1.5 dB左右,是优于TSWLS算法的。从图5中可以看出,在速度噪声方差σ2=9时,所提算法的累积分布函数曲线上升趋势最快,且最快到达1,这表明所提算法是最优的。
表1 仿真1中目标与传感器的分布
Tab.1 The distribution of target and sensors in simulation 1
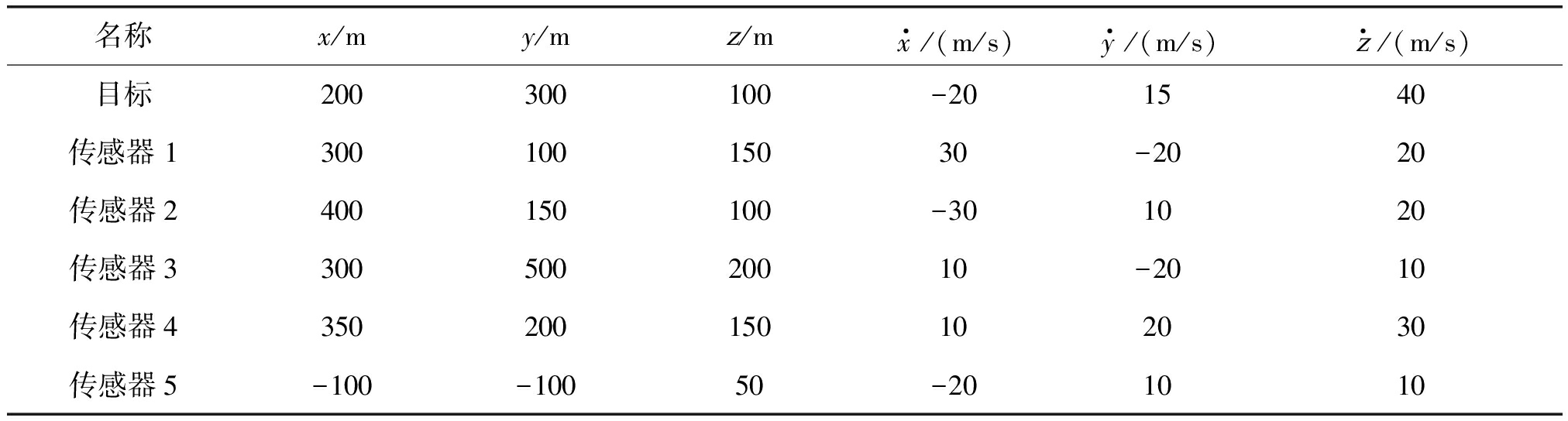
名称x/my/mz/mx·/(m/s)y·/(m/s)z·/(m/s)目标200300100-201540传感器 130010015030-2020传感器2400150100-301020传感器330050020010-2010传感器4350200150102030传感器5-100-10050-201010
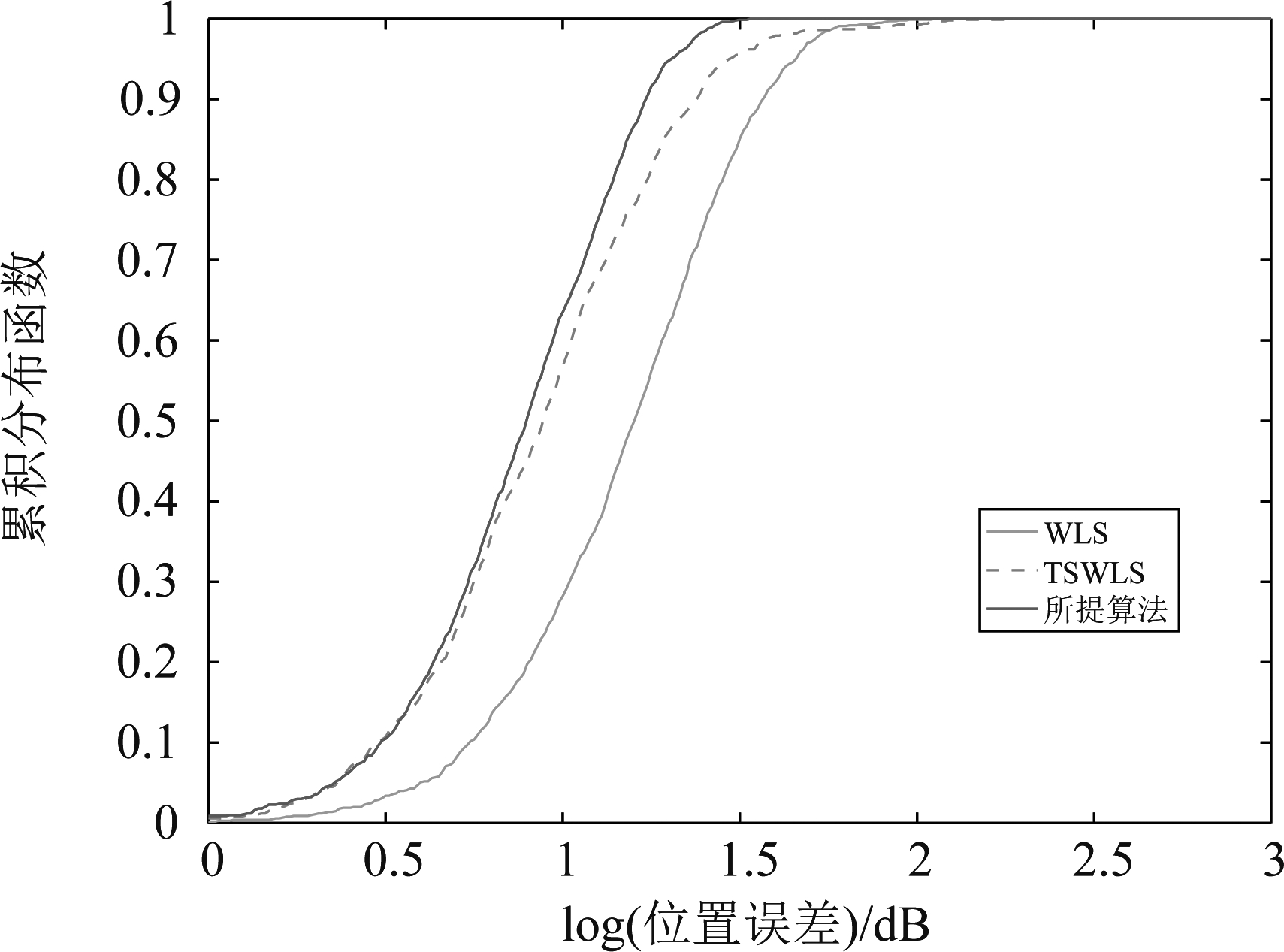
图4 仿真1中所提算法在位置噪声方差σ2=9 时的累积分布函数
Fig.4 The CDF of the proposed algorithm in simulation 1 when the positional noise varianceσ2=9
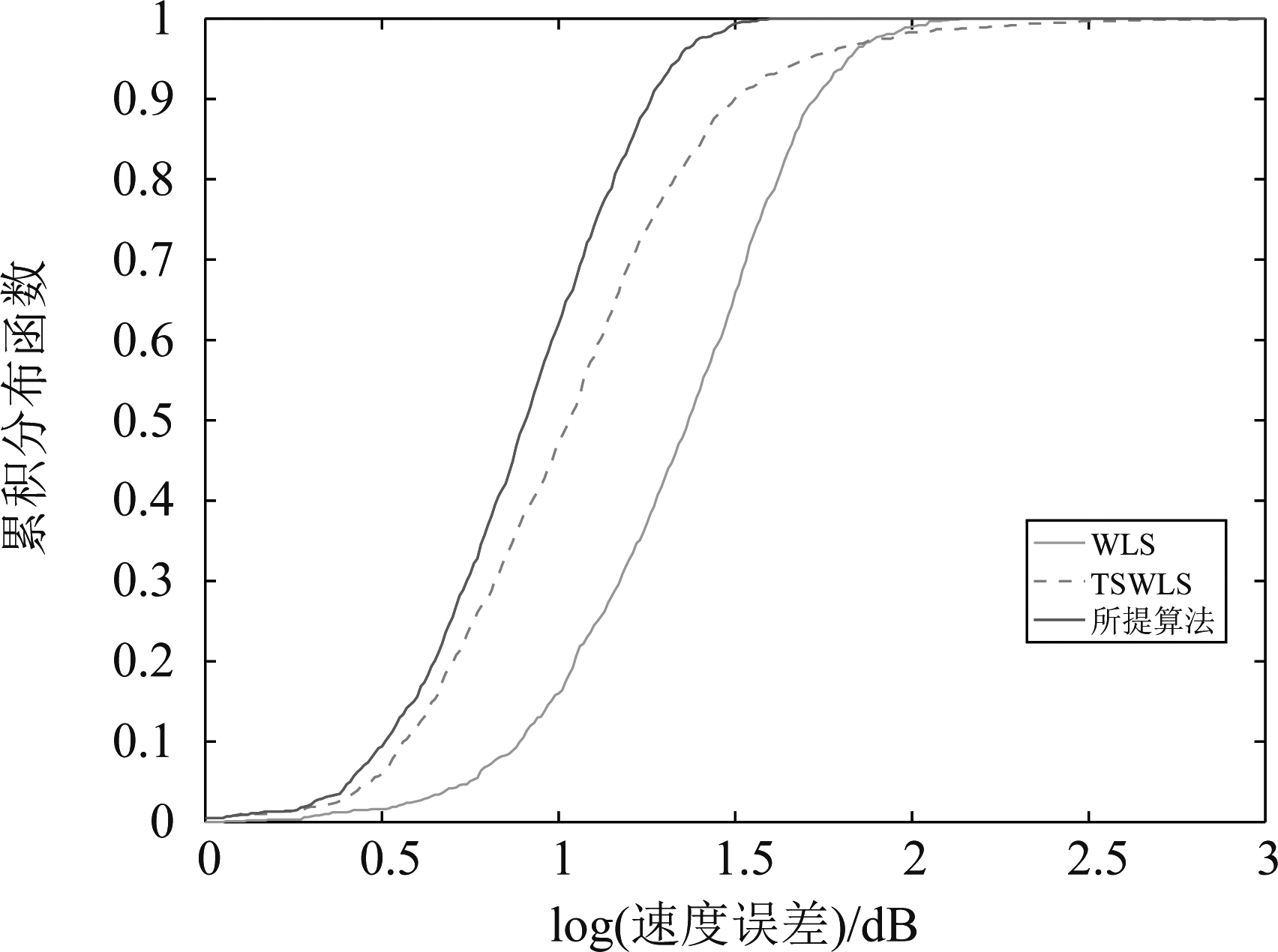
图5 仿真1中所提算法在速度噪声方差σ2=9 时的累积分布函数
Fig.5 The CDF of the proposed algorithm in simulation 1 when the velocity noise varianceσ2=9
仿真2 对低速移动目标的定位
在此水下定位场景中,同样有五个传感器参与定位,目标是速度缓慢的无人潜航器等的合作目标,目标与传感器的分布如表2所示。仿真2中本文算法的位置估计的均方根误差和偏差如图6所示,速度估计的均方根误差和偏差如图7所示。
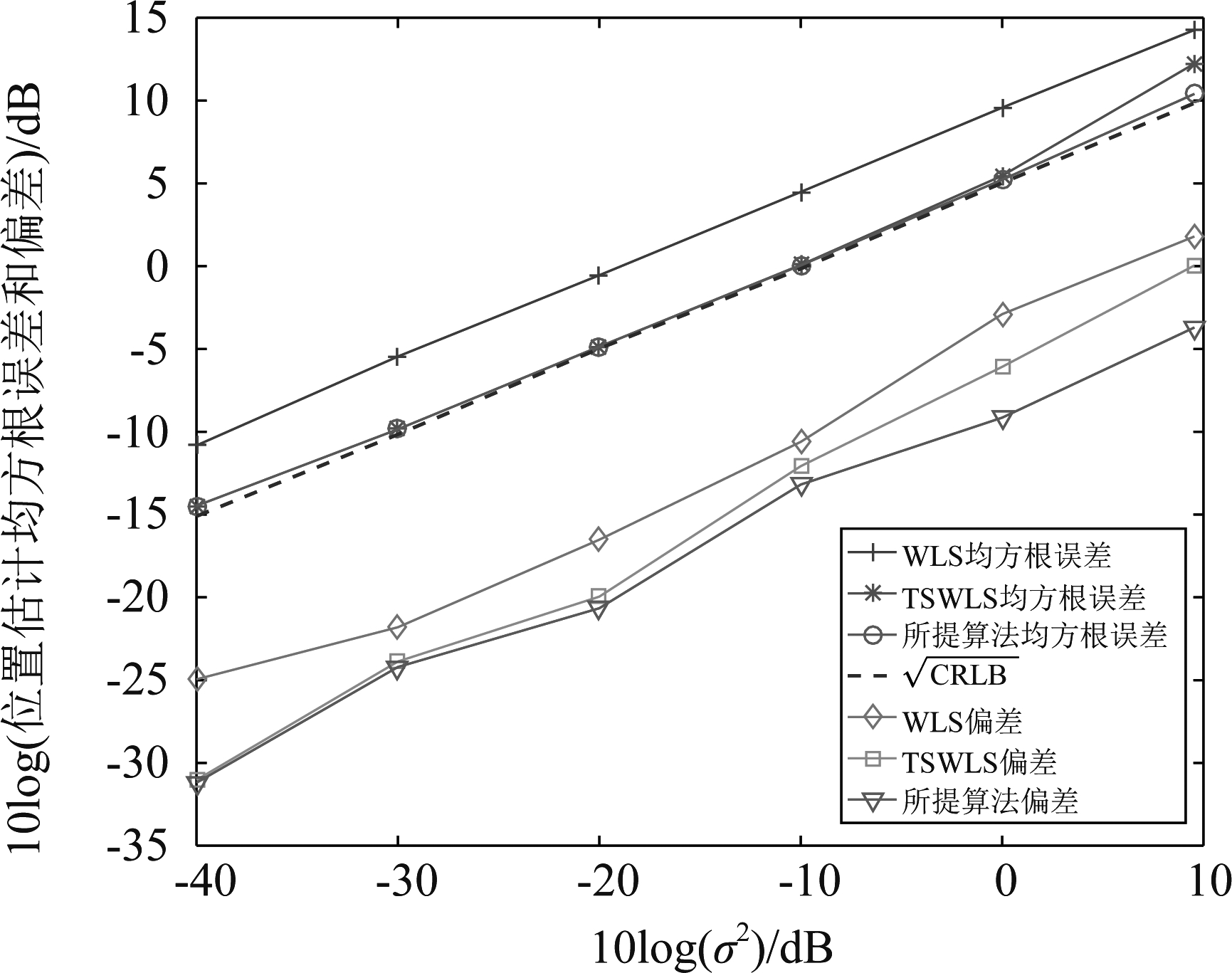
图6 仿真2中本文算法位置估计的均方根误差和偏差
Fig.6 RMSE and Bias of the position estimation of the algorithm in the simulation 2
图6的位置估计的均方根误差曲线表明,本文算法位置估计的均方根误差在位置噪声方差小于0 dB时约等于克拉美罗下界,在位置噪声方差大于0 dB时,略高于克拉美罗下界。总体来看,本文算法位置估计的均方根误差曲线是最优的。从图6的偏差曲线可以看出,在位置噪声方差为-40 dB到-20 dB时,本文算法位置估计的偏差与TSWLS算法相同,但位置噪声方差大于-20 dB时,本文算法位置估计的偏差小于TSWLS算法。
表2 仿真2中目标与传感器的分布
Tab.2 The distribution of target and sensors in simulation 2
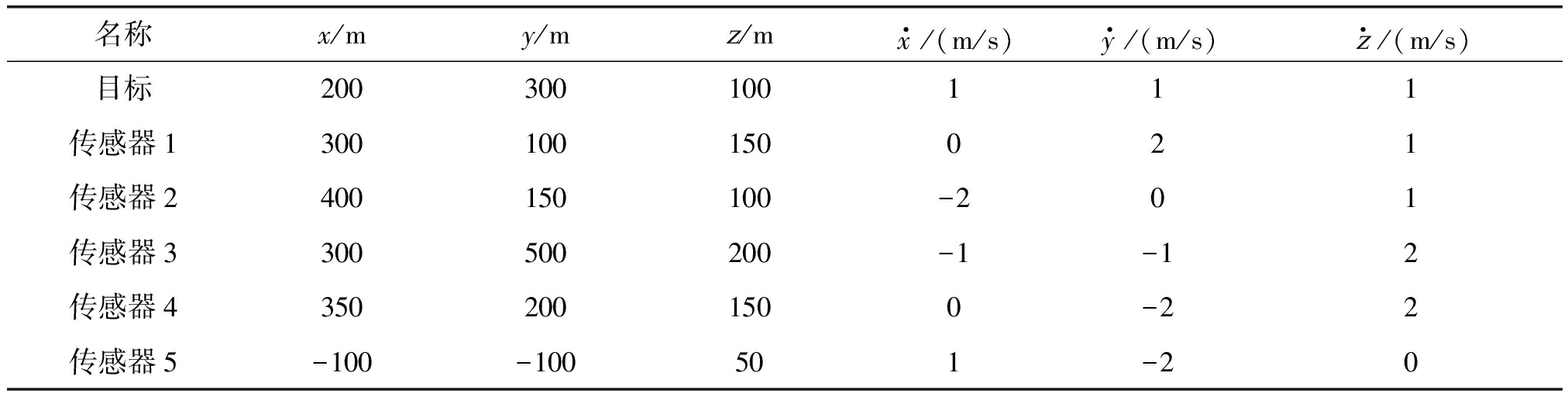
名称x/my/mz/mx·/(m/s)y·/(m/s)z·/(m/s)目标200300100111传感器1300100150021传感器2400150100-201传感器3300500200-1-12传感器43502001500-22传感器5-100-100501-20
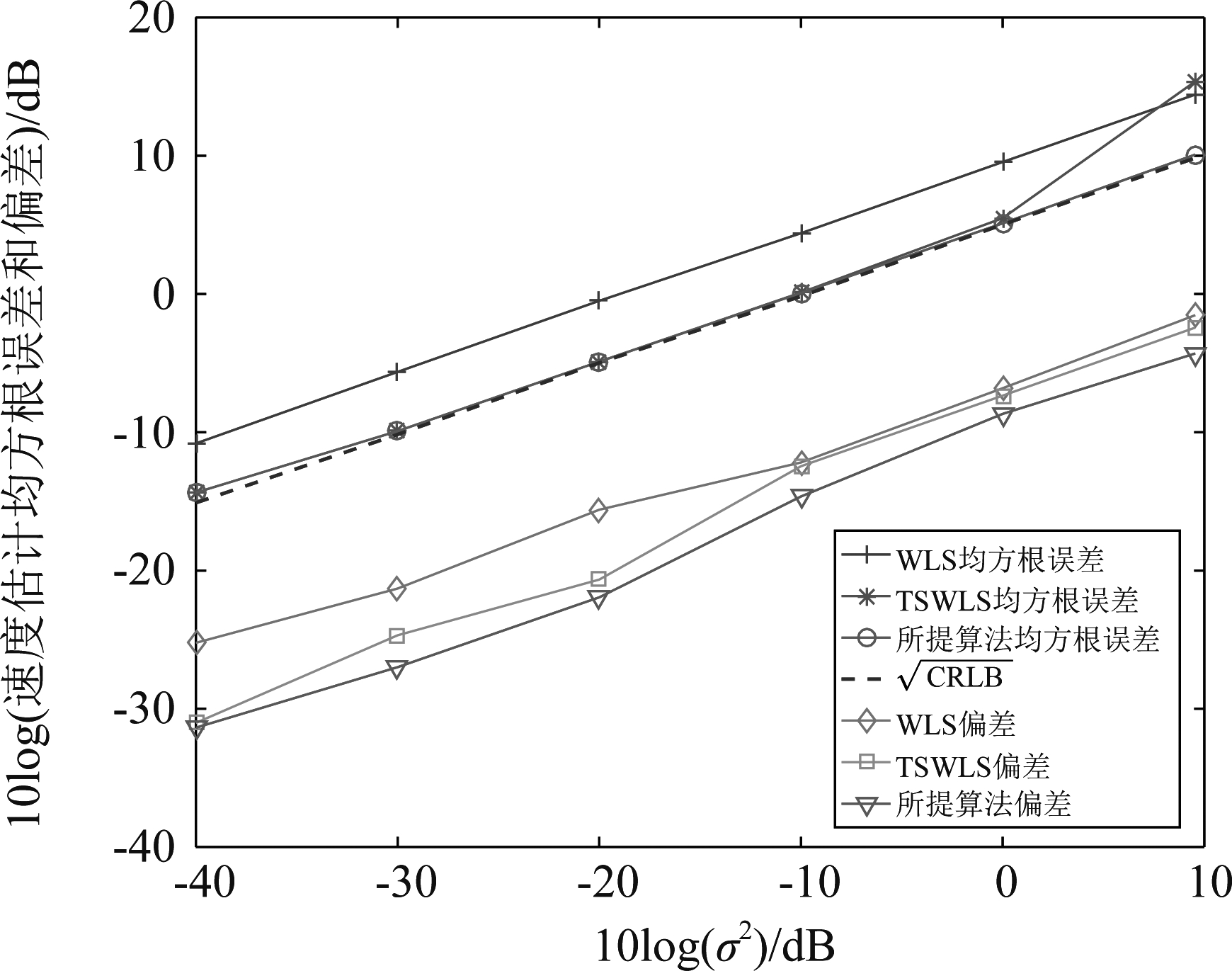
图7 仿真2中本文算法速度估计的均方根误差和偏差
Fig.7 RMSE and Bias of the velocity estimation of the algorithm in the simulation 2
从图7的速度估计的均方根误差曲线可以看出,当噪声方差小于10 dB时,本文算法速度估计的均方根误差恒等于克拉美罗下界,这表明了算法的优越性。从图7的速度估计的偏差曲线可以看出,速度噪声方差在-40 dB到10 dB范围内时,本文算法速度估计的偏差是最低的。
图8和图9展示了本文算法和对比算法在σ2=9时的累积分布函数。
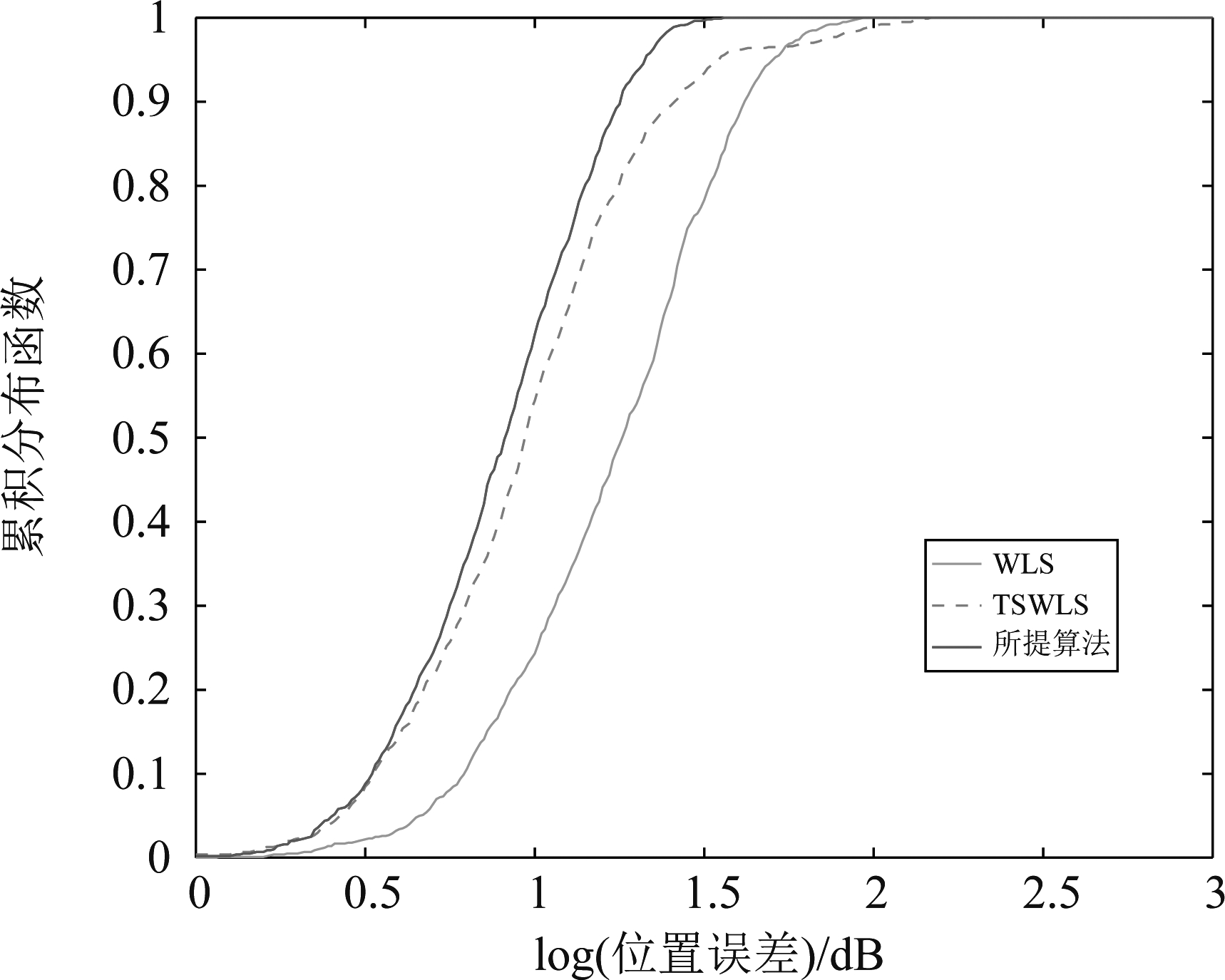
图8 仿真2中本文算法在位置噪声方差σ2=9时的 累积分布函数
Fig.8 The CDF of the algorithm in the simulation 2 when the position noise varianceσ2=9
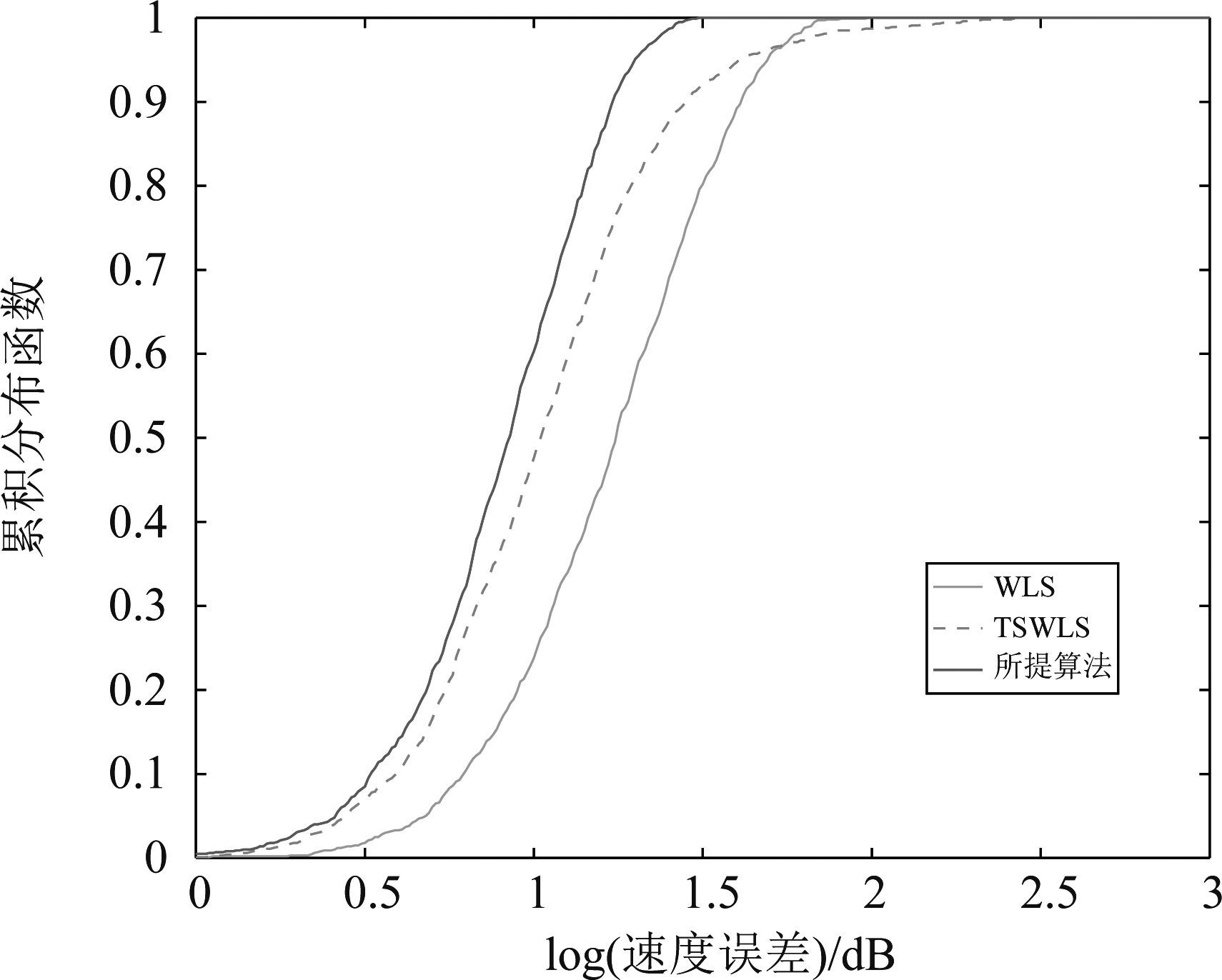
图9 仿真2中本文算法在速度噪声方差σ2=9 时的累积分布函数
Fig.9 The CDF of the algorithm in the simulation 2 when the velocity noise varianceσ2=9
从图8和图9中可以看出,无论是本文算法的位置误差还是速度误差的累积分布函数,曲线上升的速度都是最快的,且最先到达概率1。这表明本文算法的误差分布更加均匀。
仿真1和仿真2验证了算法的性能,本文提出的泰勒加权最小二乘算法综合了两阶段加权最小二乘算法和泰勒算法的优势,利用加权最小二乘算法求解初值,再用泰勒算法迭代,仿真表明本文算法是有效的。
6 结论
针对水下定位场景中,两阶段加权最小二乘算法因为忽视噪声平方项而造成的定位不精确问题,本文提出了一种基于TDOA/FDOA的泰勒加权最小二乘算法。本文算法将泰勒算法从只用于TDOA定位扩展到应用于TDOA/FDOA联合定位,并通过加权最小二乘算法求解迭代初值。仿真表明,在噪声方差小于10 dB时,本文算法的位置和速度估计的均方根误差能够接近或约等于克拉美罗下界。
[1] SALVO ROSSI P, CIUONZO D, EKMAN T, et al. Energy detection for MIMO decision fusion in underwater sensor networks[J]. IEEE Sensors Journal, 2015, 15(3): 1630-1640.
[2] LI Chao, XU Yongju, XU Chaonong, et al. DTMAC: A delay tolerant MAC protocol for underwater wireless sensor networks[J]. IEEE Sensors Journal, 2016, 16(11): 4137- 4146.
[3] IQBAL Z, LEE H N. Spatially concatenated channel-network code for underwater wireless sensor networks[J]. IEEE Transactions on Communications, 2016, 64(9): 3901-3914.
[4] HAN Guangjie, ZHANG Chenyu, SHU Lei, et al. Impacts of deployment strategies on localization performance in underwater acoustic sensor networks[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1725-1733.
[5] 梁国龙, 赵天白, 邹男, 等. 基于Chan算法的水下测控设备组网数据融合技术研究[J]. 电子与信息学报, 2018, 40(5): 1181-1186.
LIANG Guolong, ZHAO Tianbai, ZOU Nan, et al. An underwater measurement and control network centralized data fusion localization algorithm based on Chan-algorithm[J]. Journal of Electronics & Information Technology, 2018, 40(5): 1181-1186.(in Chinese)
[6] 王领, 申晓红, 康玉柱, 等. 水声传感器网络信号到达时间差目标定位的最小二乘法估计性能[J]. 兵工学报, 2020, 41(3): 542-551.
WANG Ling, SHEN Xiaohong, KANG Yuzhu, et al. Least squares estimation performance for TDOA target localization in underwater acoustic sensor networks[J]. Acta Armamentarii, 2020, 41(3): 542-551.(in Chinese)
[7] 刘开华, 魏冲冲, 于洁潇. 联合TOA和DOA的浅海多径定位算法[J]. 天津大学学报(自然科学与工程技术版), 2018, 51(2): 129-134.
LIU Kaihua, WEI Chongchong, YU Jiexiao. Joint TOA and DOA localization algorithm in shallow ocean multipath environment[J]. Journal of Tianjin University (Science and Technology), 2018, 51(2): 129-134.(in Chinese)
[8] JIANG Feng, ZHANG Zhenkai, ESMAEILI NAJAFABADI H. Deep sea TDOA localization method based on improved OMP algorithm[J]. IEEE Access, 2019, 7: 168151-168161.
[9] JIANG Feng, ZHANG Zhenkai, ESMAEILI NAJAFABADI H, et al. Underwater TDOA/FDOA joint localisation method based on cross-ambiguity function[J]. IET Radar, Sonar & Navigation, 2020, 14(8): 1256-1266.
[10] 王旭东, 董文杰, 吴楠. 基于TDOA/AOA混合的高精度室内可见光定位算法[J]. 系统工程与电子技术, 2019, 41(10): 2371-2377.
WANG Xudong, DONG Wenjie, WU Nan. Hybrid TDOA/AOA algorithm based high accuracy indoor visible light positioning[J]. Systems Engineering and Electronics, 2019, 41(10): 2371-2377.(in Chinese)
[11] CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915.
[12] FOY W H. Position-location solutions by Taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(2): 187-194.
[13] AMIRI R, BEHNIA F, NOROOZI A. An efficient estimator for TDOA-based source localization with minimum number of sensors[J]. IEEE Communications Letters, 2018, 22(12): 2499-2502.
[14] 周龙健, 罗景青, 孔辉, 等. 相参短脉冲辐射源双站TDOA/FDOA直接定位算法[J]. 信号处理, 2017, 33(5): 695-702.
ZHOU Longjian, LUO Jingqing, KONG Hui, et al. Direct positioning maximum likelihood estimator using bistatic stations TDOA and FDOA for coherent short-pulse emitter[J]. Journal of Signal Processing, 2017, 33(5): 695-702.(in Chinese)
[15] HO K C, XU Wenwei. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453-2463.
[16] QU Xiaomei, XIE Lihua, TAN Wenrong. Iterative constrained weighted least squares source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(15): 3990- 4003.
[17] WANG Yunlong, WU Ying. An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements[J]. IEEE Communications Letters, 2017, 21(1): 80- 83.
