1 引言
信源定位是阵列信号处理领域的一个重要研究方向,在通信、军事、航空技术等方面有着广泛的应用。早期的信源定位估计主要针对远场源[1],由于远场源的位置只取决于来波方向,故远场源定位又称之为波达方向(DOA, direction of arrival)估计,而随着基于麦克风阵列的声源定位、雷达探测以及移动通信等领域的发展,目标信号源定位于菲涅尔区域[2-3]的情况日益增多,近场源的参数估计变得越来越重要。
学者们以DOA估计中经典的多重信号分类(MUSIC, multiple signal classification)算法和基于旋转不变技术的信号参数估计(ESPRIT, estimating signal parameter via rotational invariance techniques)算法为基础,提出了一系列算法[4-12]以解决近场源的参数估计问题。文献[5]提出了一种二维MUSIC方法同时估计近场源的角度和距离,该方法需要进行二维谱峰搜索,运算复杂度很高。近年来,为了提高参数估计的精度和对噪声的稳定性,学者们提出一些基于高阶累量矩阵的算法[6- 8],它们大都需要构造两个矩阵,然后对这两个矩阵分别使用ESPRIT方法或者MUSIC方法估计近场的角度和距离。文献[6]构造了两个高阶累量矩阵,并用MUSIC方法对两个矩阵分别进行一维谱峰搜索估计角度和距离。文献[7- 8]构造了一个高阶累量矩阵和一个协方差矩阵,其中文献[7]对两个矩阵分别用MUSIC方法进行一维谱峰搜索估计参数,文献[8]对高阶累量矩阵用ESPRIT方法估计近场角度,免去了一次谱峰搜索,但是对协方差矩阵仍然用MUSIC方法进行一维谱峰搜索估计近场距离。这些算法虽然避免了二维谱峰搜索,而且由于高阶累积量对高斯噪声具有较强的鲁棒性,算法的估计分辨率有所提高,但是它们要同时构造两个矩阵,运算复杂度较高,而且仍然需要进行一维谱峰搜索。之后,文献[9]提出了一种只需构造一个非Hermitian高阶累量矩阵和进行一次奇异值分解就可以估计近场源角度和距离的算法。该算法利用累积量奇异向量,先后用MUSIC方法一维谱峰搜索估计参数。相比于文献[6- 8]需要同时构造两个矩阵的估计算法,该算法一定程度上降低了计算量,但是其仍然需要两次一维谱峰搜索。
文献[10-11]提出了仅基于协方差矩阵的算法,其中文献[11]提出了使用Root-MUSIC方法估计距离参数的算法,该算法在文献[10]的基础上,用多项式求根代替距离估计时的一维谱峰搜索。与基于高阶累积量的算法相比,二者的运算量较小,但是在阵元数目为L时它们的最大可分辨信源数仅为L/2,并且其在分辨率和参数估计精度方面还有待进一步提高。
对于以上文献的不足,本文提出了一种新算法以实现近场源参数的快速估计。基于文献[9],本文提出的算法首先构造一个非厄米特的四阶累量矩阵,然后对于近场源的角度和距离均利用类Root-MUSIC算法[12]进行估计,具体来说是对累积量奇异值分解之后,分别用其右奇异向量和左奇异向量得到角度估计和距离估计的闭式解。文献[6- 8]中基于高阶累积量的方法不能通过一个矩阵分离近场的角度和距离参数,需要额外地构造协方差矩阵或者构造另外一个累量矩阵,而本文算法仅需构造这一个非厄米特的高阶累积量与进行一次奇异值分解,就能对近场的角度和距离参数进行参数估计,降低了计算量,并且不仅能实现参数的自动配对,与文献[9]相比闭式解还避免了谱峰搜索的过程,进一步减少了运算量。本文提出的算法与文献[10-11]相比,在对近场源参数估计时不仅有效减少了阵列的孔径损失,当阵元数目为L时最大可分辨信源数可达到L-1,而且还有较高的分辨率和参数估计精度。
此外,本文提出的算法除了能针对纯近场源进行有效参数估计外,还能容易地推广到同时包含远场近场信号的混合源场源场景中。在此场景中,第一步估计远场信号DOA时,本文提出的算法与文献[8]的算法相比无需构造新的矩阵,而是利用类Root-MUSIC算法对混合场源估计出所有DOA,再通过简单的子空间正交性来区分远近场。接下来对于估计出的远场信号无需再估计距离,按照纯近场情况进一步估计出近场源的距离即完成所有的参数估计。而文献[7]中的算法在面对混合场源时需要用MUSIC算法通过谱峰搜索得到所有场源的距离,然后再把距离估计结果为无穷大的场源判断为远场源,二者相比本文所提算法在纯近场的基础上没有增加过多的计算量。实验结果表明,本文提出的算法在分辨率、估计精度上都有较大的优越性。
2 系统模型
假设有K个独立的窄带近场信号源,接收端是有L=2N+1个阵元的线性对称均匀阵列,阵元之间的间距为d,其中阵列的中心为相位参考点。线性阵列示意图如图1所示。
那么第l个阵元接收到的信号可以表示为
(1)
其中sk(t)是第k个信源信号,nl(t)是加到第l个阵元的高斯白噪声,τlk是指第k个信源信号在被阵列接收时第l个阵元与第0个阵元之间的相位差。
(2)
其中式中θk和rk表示第k个近场源信号的方向和距离,λ是波长。根据菲涅耳区域的定义,信源与传感器阵列之间的距离rk应满足0.62(D3/λ)1/2<rk<2D2/λ,其中D=(L-1)d/λ为阵列孔径。在(2)的基础上使用二阶泰勒展开式,τlk可进一步写成
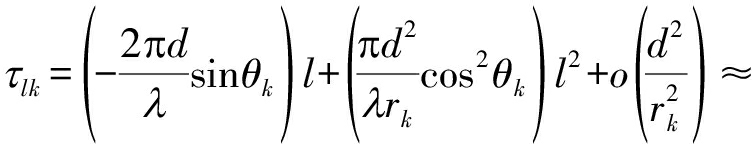ωkl+φkl2
(3)
其中ωk和φk分别定义如下
(4)
(5)
那么t时刻,阵列接收信号x(t)可以表示为
x(t)=ANsN(t)+n(t)
(6)
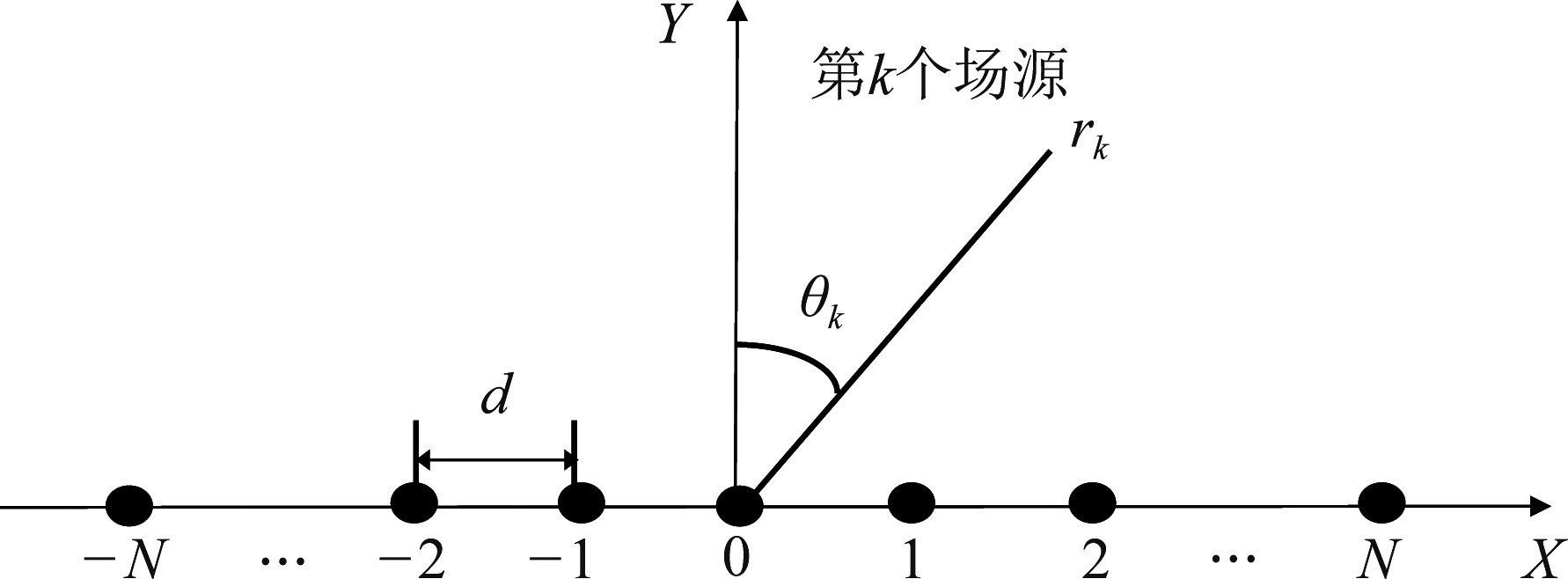
图1 线性对称均匀阵列示意图
Fig.1 The diagram of symmetrical uniform array
式中
x(t)=[x-N(t),…,x0(t),…,xN(t)]T
(7)
AN=[a(θ1,r1),…,a(θk,rk),…,a(θK,rK)]
(8)
sN(t)=[s1(t),s2(t),…,sK(t)]T
(9)
n(t)=[n-N(t),…,n0(t),…,nN(t)]T
(10)
其中阵列流型AN的列向量a(θk,rk)表示近场源的导向矢量,由角度θ和距离r共同确定,具体可以表示为
a(θk,rk)=[ejχ-N,…,ejχ0,…,ejχN]T
(11)
其中χn=ωkn+φkn2,n∈[-N,N]。
3 算法原理
3.1 角度估计
对于阵列接收信号可以构造四阶累量矩阵如下
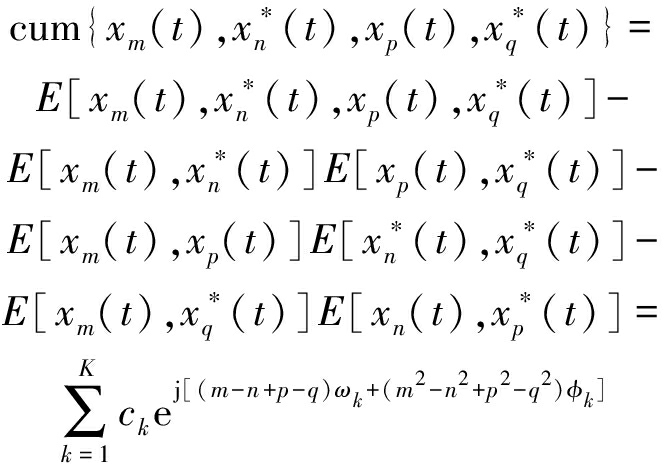
(12)
并且
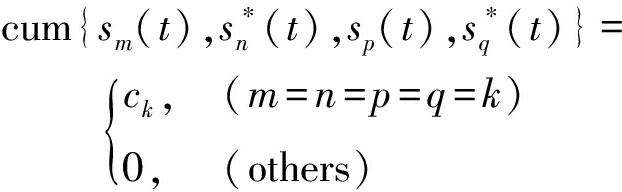
(13)
矩阵C1可以定义为
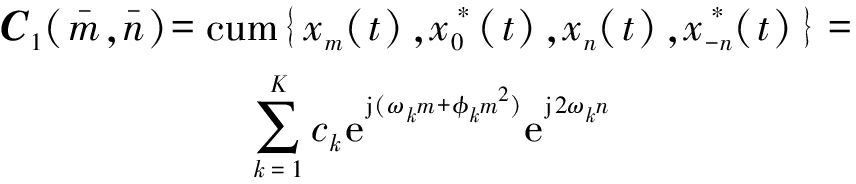
(14)
其中
那么由定义,C1可以写为
(15)
其中的C4s是K×K阶只有主对角线有值的对角矩阵,C4s=diag{c1,…,ck,…,cK},矩阵A1和A2的维度都是L×K,其第k列分别为
a1(θk)=[e-j 2ωk(-N),…,1,…,e-j 2ωkN]T
(16)
a2(θk,rk)=a(θk,rk)
(17)
其中在公式(14)定义C1时参数选为{m,0,-n,n},是因为通过{-n,n}可以得到A1(θ),从而能把角度估计与距离估计分开;而通过参数{m,0}可以得到A2(θ,r),从而可以估计近场距离。
C1奇异值分解可表示为
(18)
其中
s∈RK×K是一个由K个大的奇异值构成的对角阵,n∈R(L-K)×(L-K)是由L-K个小的奇异值组成的对角阵,K个大的奇异值对应的左奇异向量张成信号子空间Us∈CL×K,L-K个小的奇异值对应的左奇异向量张成噪声子空间Un∈CL×(L-K),K个大的奇异值对应的右奇异向量张成信号子空间Vs∈CL×K,L-K个小的奇异值对应的右奇异向量张成噪声子空间Vn∈CL×(L-K)。
接下来用类Root-MUSIC方法利用噪声子空间Vn得到近场DOA的闭式解。首先令
z1=e-j 2ωk
(19)
则a1(z1)=[z1(-N),…,1,…,z1N]T,那么可以构造如下形式的多项式
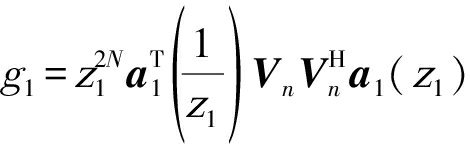
(20)
则当角度接近于近场源的角度时,g1=0。由(20)可知,g1是2N阶多项式,所以g1有N对与单位圆镜像对称的根。然而近场源的个数仅有K个,通常情况下,N>K。所以需要从N对根中挑选出满足条件的K对根。可能的挑选根的方法有两种:
1)由于z1=e-j 2ωk的模为1,所以理论上这K对根刚好落在单位圆上。
2)由于近场源的a1(θk)会与噪声空间正交,所以理论上用这K对根重构近场方向向量后,对应的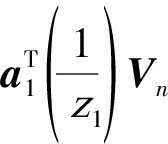
会等于0。
又由于噪声的干扰,可根据第一种办法,选取最接近单位圆的K对根z1,或者根据第二种办法,选取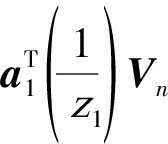最接近0的K对根。得到了这K对根之后就可以通过z1=e-j 2ωk,而
反解得到K个近场源的角度θk。
3.2 近场距离估计
把通过3.1得到的近场估计角度
依次代入a2(θk,rk),就可以用Root-MUSIC方法利用C1的L-K个小的奇异值对应的左奇异向量张成的噪声子空间Un分别得到它们对应的近场距离闭式解。首先
可以用如下形式表示
(21)
其中a(θk)=[ejωk(-N),…,1,…,ejωkN]T,Φ(rk)=diag{ejφk(-N)2,…,1,…,ejφkN2},然后令
z2=ejφk
(22)
则Φ(z2)=diag{z2(-N)2,…,1,…,z2N2},那么可以构造多项式形式如下
(23)
当r接近于对应近场源的近场距离时,g2=0。由(23)可知,g2是N2阶多项式,所以g2有N2/2对与单位圆镜像对称的根。由于近场源的角度和距离一一对应,故我们需要从N2/2对根中挑选出满足条件的1对根。
与3.1节中的角度估计挑选根的过程类似,我们选取最接近单位圆的根z2,或者选取重构方向向量并让
最接近0的根z2。然后通过
反解得到该近场源的距离rk。用这种方式还可以完成近场角度和近场距离的自动配对。
总之,本文提出的基于四阶累量矩阵估计近场源参数的算法可以总结如下:
1)构造四阶累量矩阵C1;
2)利用类Root-MUSIC方法,用C1的L-K个小的奇异值对应的右奇异向量张成的Vn估计出所有近场角度;
3)依次把步骤2)估计出的近场角度代入近场方向向量,利用类Root-MUSIC方法,用C1的L-K个小的奇异值对应的左奇异向量张成的Un估计对应的近场距离。
本文算法在构造四阶累量矩阵C1后,首先对C1进行奇异值分解,然后利用得到的右奇异向量和左奇异向量,先后用类Root-MUSIC方法分别得到近场角度估计和距离估计的闭式解。该算法不仅因为高阶累积量让其能适应不同的高斯白噪声的环境,使得分辨率和估计精度有较好的性能,而且只构造一个累量矩阵和进行一次奇异值分解,并用Root-MUSIC方法省去了谱峰搜索和参数配对的过程,大大降低了运算量。
3.3 推广至混合场源参数估计
对于远场和近场同时存在的混合场源,本文提出的算法也能快速地估计出远场角度、近场角度和近场距离。具体来说,与文献[8]不同,所提算法没有因为增加了远场源而额外构造新的矩阵,而是把远场看作是一种距离为无穷大的特殊近场,利用对累量矩阵C1奇异值分解得到的右奇异向量,用类Root-MUSIC方法同时估计出了远场和近场DOA。然后对所有估计出的角度进行简单的子空间正交性判断来区分远场和近场,对于远场源它们的距离无需估计,所以接下来按照3.2节的流程把近场估计角度依次代入a2(θk,rk)估计近场距离即可完成所有的参数估计,与文献[7]相比省去了远场源距离估计过程,几乎没有增加额外计算量。
其中远场源信源与传感器阵列之间的距离r应满足r≫2D2/λ。从公式(5)可以得知,当信号源是远场源rk=∞时,φk=0,此时第k个信源信号在被阵列接收时第l个阵元与第0个阵元之间的相位差τlk=ωkl,信源位置主要由角度参数决定。那么混合场源时,阵列接收信号x(t)可以表示为
x(t)=ANsN(t)+AFsF(t)+n(t)
(24)
其中
AF=[a(θK1+1),…,a(θK1+k),…,a(θK)]
(25)
sF(t)=[sK1+1(t),s2(t),…,sK(t)]T
(26)
其中阵列流型AF的列向量a(θk)表示远场源的导向矢量,它只与角度θ有关,具体可以表示为
a(θk)=[ejωk(-N),…,1,…,ejωkN]T
(27)
远场源的导向矢量a(θk)相当于φk=0时的近场导向矢量a2(θk,rk),即远场可以视作一种特殊的近场,此时所提算法的式(20)能得到包括远场角度在内的所有场源的角度估计。并且远场源导向矢量会与噪声空间正交,具体可以表示为
aH(θk)Un=0
(28)
利用这一正交性,能在得到所有的场源的角度后区分远近场角度。之后再把近场角度估计按照3.2节代入式(23)即得到混合场源中近场的距离。
3.4 算法复杂度
文献[8]算法的计算复杂度主要来源于一个(2N+1)×(2N+1)阶累量矩阵和一个(2N+1)×(2N+1)阶协方差矩阵的构造,分别对这两个矩阵的奇异值分解,以及一次角度谱峰搜索和K次距离谱峰搜索,计算复杂度为
,其中T是指快拍数,Δθ和Δr分别是角度估计和距离估计时谱峰搜索的步长。文献[9]算法的计算复杂度主要来源于一个(2N+1)×(2N+1)阶累量矩阵的构造,对该累量矩阵的奇异值分解,以及1次对角度的谱峰搜索和K次对距离的谱峰搜索,计算复杂度为
相比于文献[8],本文所提算法主要少构造了一个协方差矩阵以及减少了一次奇异值分解。相比于文献[9],在估计近场源的角度和距离时,本文所提算法用类Root-MUSIC方法代替了MUSIC方法的谱峰搜索。由于谱峰搜索需要对参数范围进行遍历,当搜索间隔比较大时,参数估计精度不高;当搜索间隔比较小时,算法的运算量可观。所提算法中闭式解避免了对参数范围的遍历过程,减少了计算量。所提算法的复杂度为
可以看到本文的算法比文献[8-9]中的算法具有更低的计算复杂度。
4 实验结果与分析
本节展示一些仿真结果来评估本文算法在分辨率以及准确度方面的性能,同时将文献[8-10]近场源波达方向和距离的估计算法进行了仿真对比。
实验一探究SNR对算法分辨率的影响。对比了提出的方法以及文献[8]、文献[9]以及文献[10]的估计算法分辨率。选择阵元个数为L=9的均匀对称线阵,阵元间距
近场源中有两个近场源分别位于(-3°,λ)和(3°,1.5λ)的位置,把快拍次数设置为2000拍,信噪比的范围为-20 dB到-4 dB,每个信噪比下统计100次蒙特卡罗实验。图2中展示了三种方法的近场分辨率随着信噪比的变化趋势图。可以看到文献[10]的DOA错误概率居高不下,而本文提出的算法分辨错误概率随着信噪比的增大而明显下降,且在-6 dB之前始终小于文献[8]和文献[9]的分辨错误率。因此,所提算法在阵元数很少以及低信噪比的时候也能有较高的分辨率。
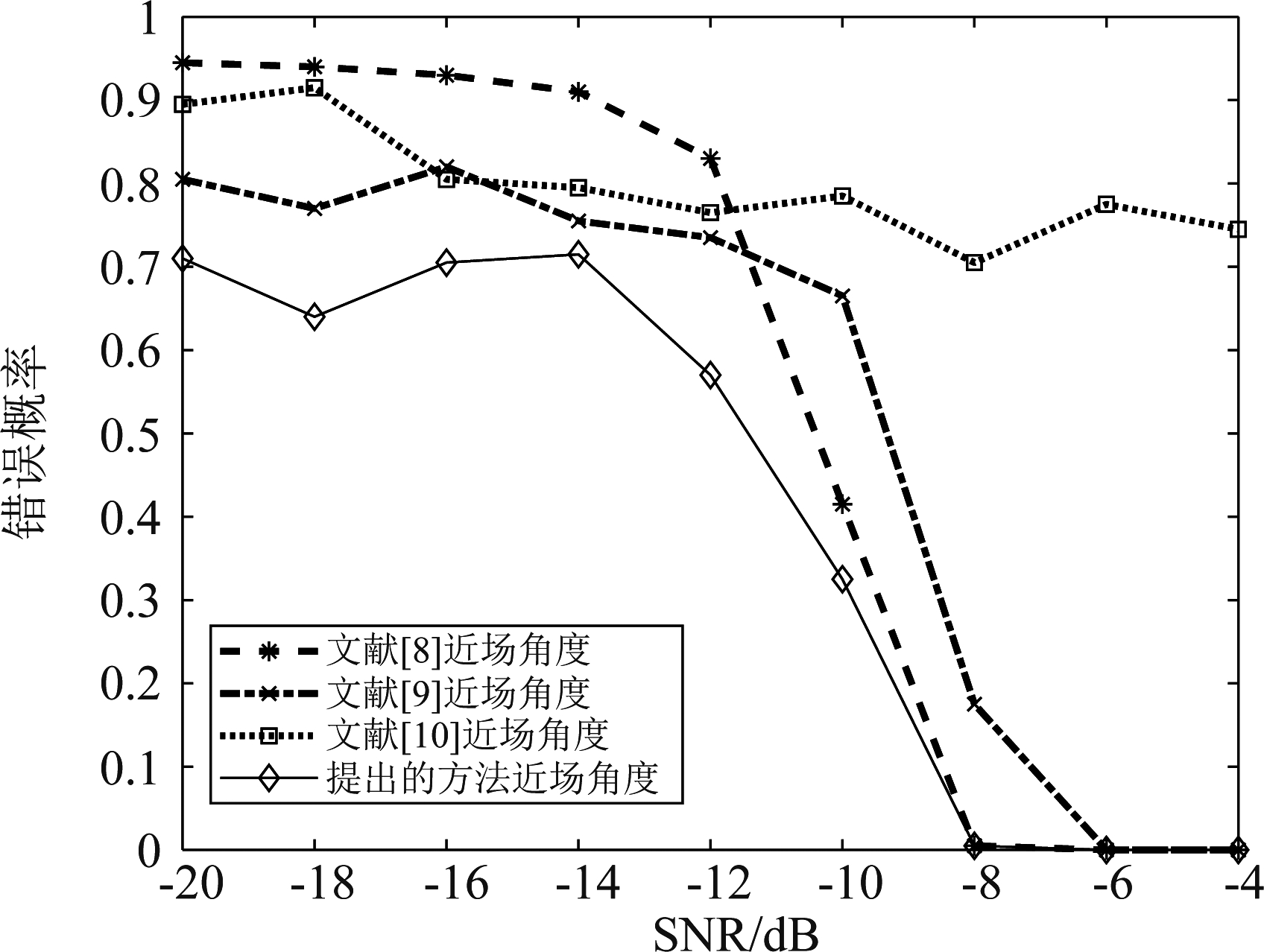
图2 近场源分辨率随SNR的变化趋势图
Fig.2 The resolutions curve versus the SNRs
实验二测试算法的最大可分辨信源数。选择阵元个数为L=7的均匀对称线阵,阵元间距有6个近场源分别位于(-25°,λ)、(-10°,1.5λ)、(10°,3λ)、(30°,2λ)、(45°,0.5λ)和(65°,2.5λ)的位置,把快拍次数设置为2000拍,SNR=20 dB。图3展示了本文算法估计的近场角度,图4展示了文献[10]的近场角度空间谱。可以看到文献[10]的近场角度谱已经无法准确估计近场DOA,而本文算法可以很好地区分开6个近场源的角度,从而达到有效DOA估计。也就是说所提算法在阵元个数为L=7时,最大可分辨信源数达到L-1=6。
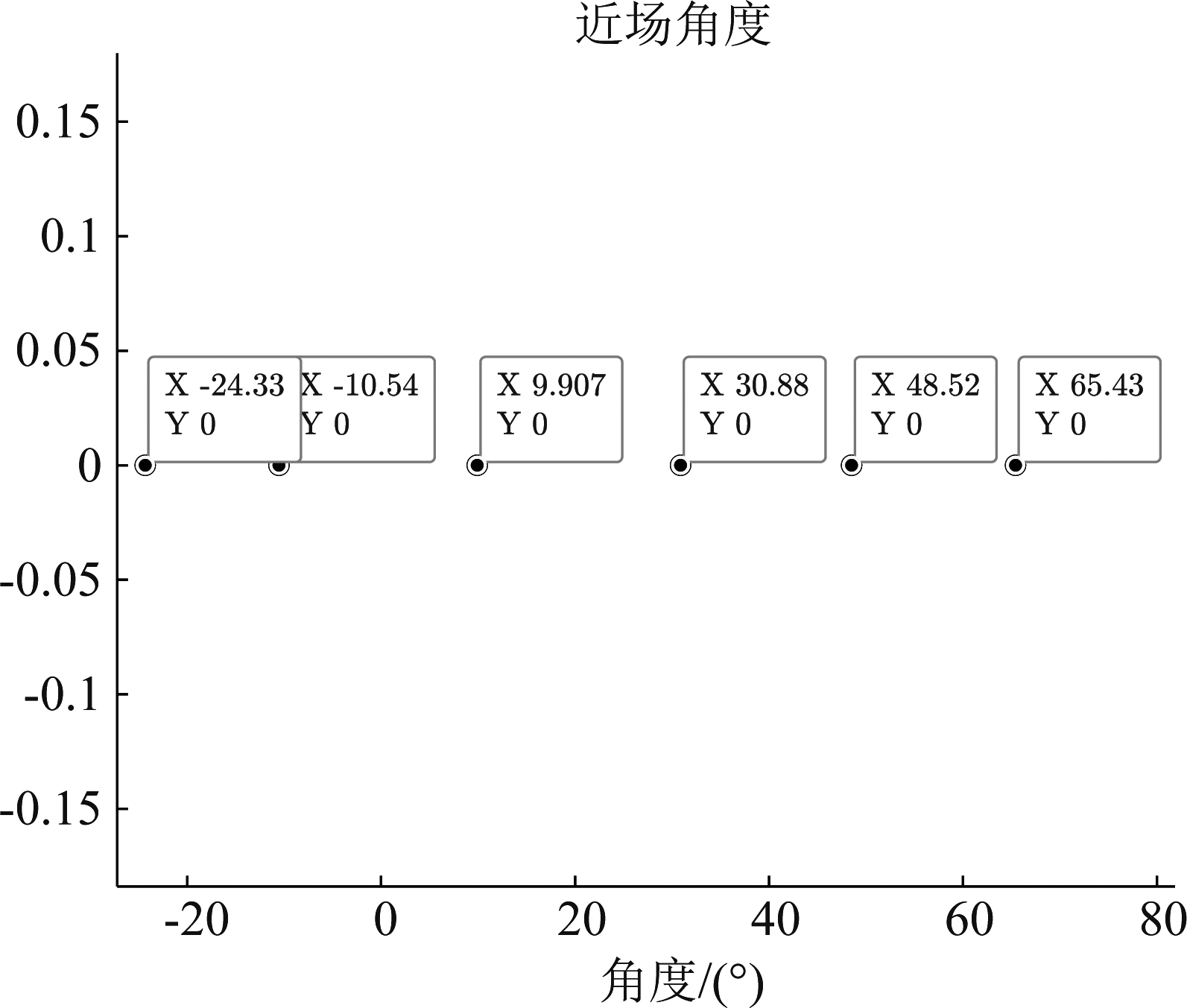
图3 提出的方法对近场源的DOA估计
Fig.3 The DOA estimation of the proposed algorithm for near-field sources
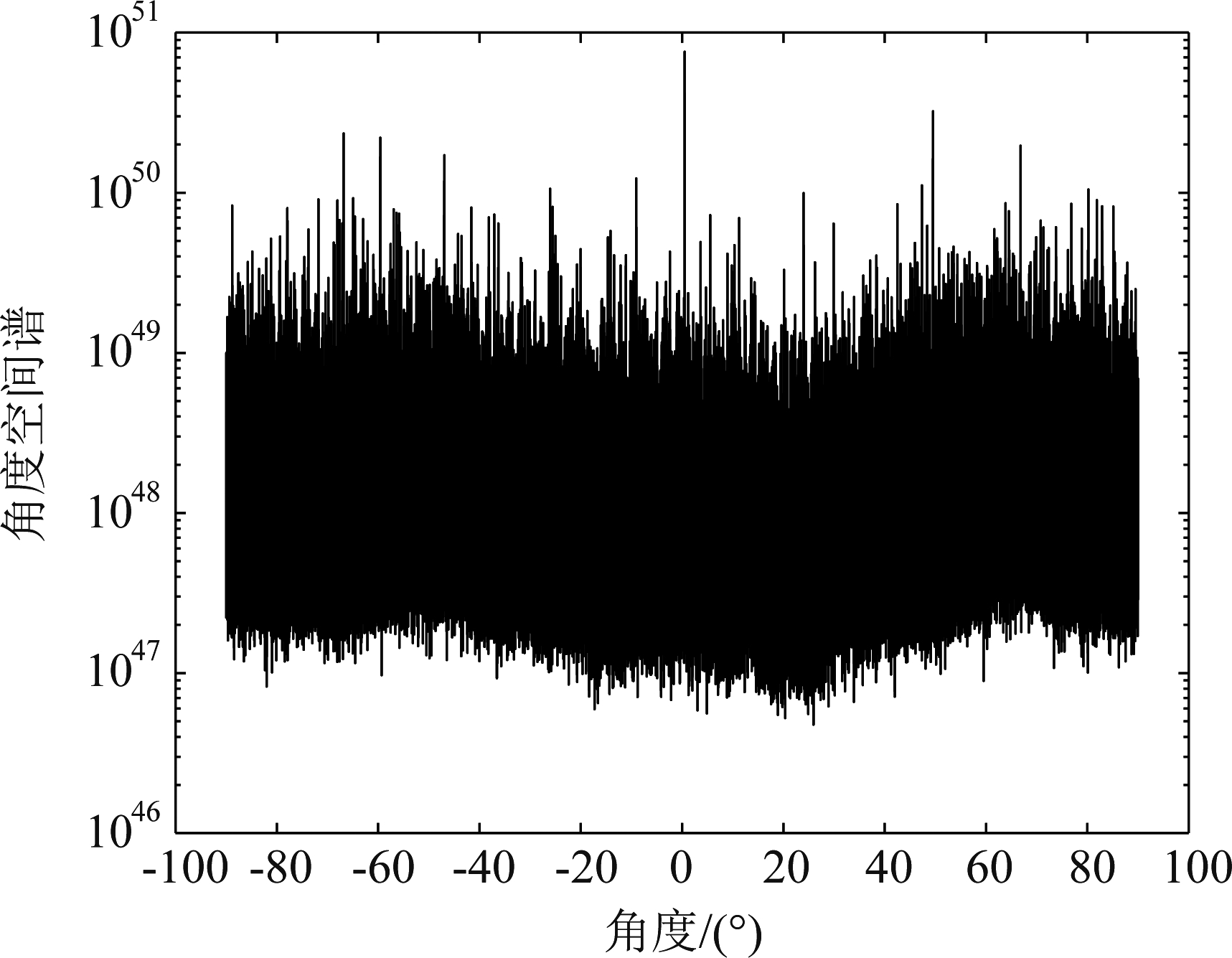
图4 文献[10]方法的近场角度空间谱
Fig.4 The angular space of method [10] for near-field sources
实验三检测信噪比的大小对提出算法的精确性能的影响。选择阵元个数为L=13的均匀对称线阵,阵元间距三个近场源分别位于(-10°,λ)、(10°,1.5λ)和(35°,2λ)的位置。通过统计100次蒙特卡罗试验结果的均方根误差(RMSE)来衡量精确性。均方根误差的定义式如下
(28)
其中||||表示Frobenius范数,x表示参数的精确值,
分别表示第i次蒙特卡罗试验中的估计值。
对文献[8]和文献[10]进行仿真对比,快拍次数设置为500拍,信噪比的范围为-14 dB到0 dB;图5给出了本文提出的方法与其他两种方法近场角度和近场距离RMSE随着信噪比的变化趋势对比图,从图中可以看出,三种方法的估计精度都随着信噪比的增加而下降。其中图5(a)显示,本文提出算法的近场角度估计精度在信噪比-12 dB以后高于文献[8]和文献[10]算法的角度估计精度,图5(b)显示近场距离估计精度在信噪比在-10 dB以后高于文献[10]算法的距离估计精度。本文提出算法的近场距离估计精度有时会低于文献[8],这是由于文献[8]不仅构造了累量矩阵估计近场角度,还额外构造了协方差矩阵估计近场距离,并且在估计距离的时候为了追求精度,用了计算量复杂度更高的MUSIC方法。虽然本文所提出的算法在近场角度方面估计精度高于文献[8],但由于本文算法仅构造了一个累量矩阵估计角度和距离,并且对参数均采用Root-MUSIC方法进行闭式解估计,有可能在距离估计精度方面不占优势。
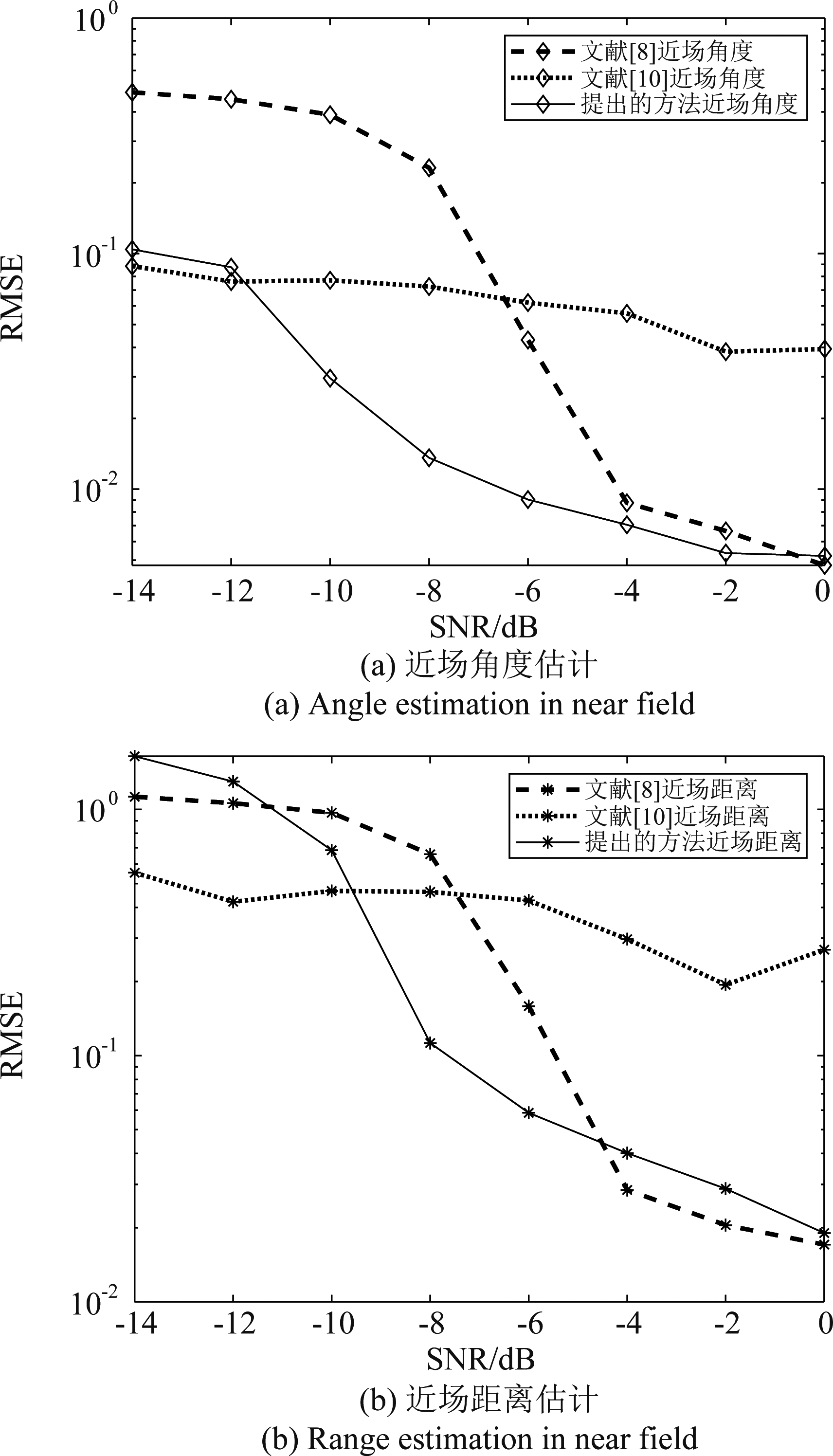
图5 提出方法和文献[8]、[10]的RMSE随信噪比变化趋势图
Fig.5 The RMSEs curve of the proposed method, method [8] and method [10] versus the SNRs
实验四检测快拍数对提出算法的性能影响。近场源和阵列的设置与实验三一致,信噪比设置为-6 dB,快拍数从500拍到2000拍变化,每个快拍下统计100次蒙特卡罗实验。图6展示了本文算法和文献[8]、文献[10]的方法下近场DOA和近场距离RMSE随着快拍数的变化情况,三种算法的估计精度都随着快拍数的增加而缓慢下降,其中本文提出的算法的角度和距离估计精度在各个快拍下始终高于文献[10]的估计精度。而文献[8]由于构造了两个矩阵,并且用了MUSIC方法谱峰搜索估计距离,所以如同实验三中不同信噪比下本文提出的算法与文献[8]估计精度的对比,在不同快拍下本文提出的算法的近场距离估计精度有时要低于文献[8]算法的距离估计精度,但是本文提出算法的角度估计精度始终要高于文献[8]的角度估计精度。
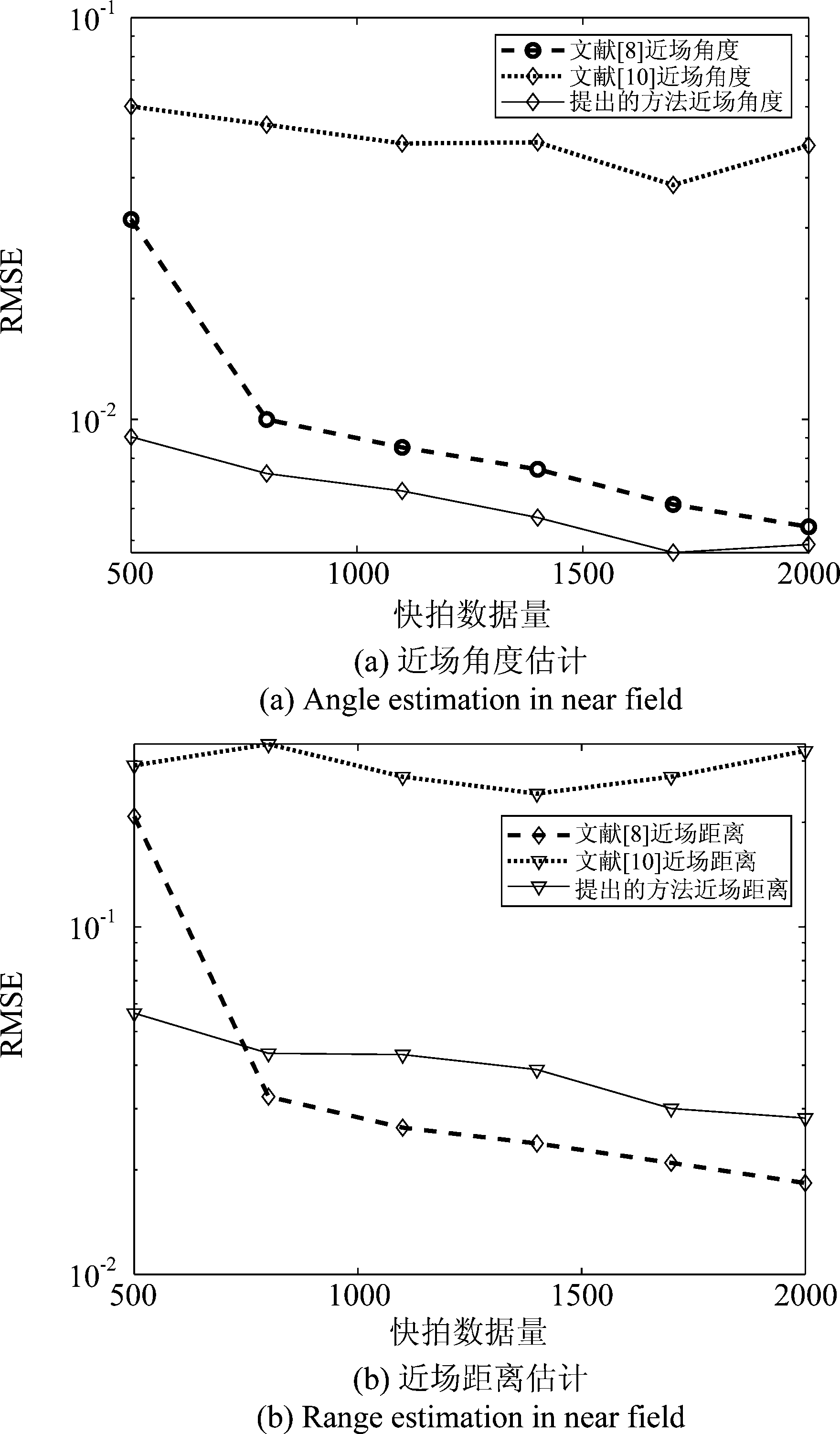
图6 提出方法和文献[8]、[10]的RMSE随快拍变化趋势图
Fig.6 The RMSEs curve of the proposed method, method [8] and method [10] versus the snapshots
实验五检测混合场源下提出的算法的估计精度。混合场源中,近场源与阵列的设置与实验三的设置一致,再添加两个分别位于空间(-2°,∞)和(2°,∞)位置的远场源。
图7 混合场源下提出的算法和文献[8]的RMSE 随信噪比变化趋势图
Fig.7 The RMSEs curve of the proposed method and method [8] versus the SNRs for mixed sources
对文献[8]进行仿真对比,图7中给出了两种方法下,远近场角度以及近场距离估计值的RMSE随着信噪比变化的趋势图。从图中可以看出,两种方法下的参数估计RMSE均随着信噪比的增大而平稳减小。其中,本文提出的算法的远场角度估计精度与本身的近场角度估计精度一致。但是由于本文算法是把远场当作距离为无穷大的特殊近场,用一次累量矩阵奇异值分解估计出所有的DOA,再通过简单的正交判断区分远场角度和近场角度。而文献[8]首先通过协方差矩阵估计远场角度,然后用混合累量矩阵减去远场的影响得到纯近场累量矩阵之后,再估计近场角度。为了减少运算量,我们没有增加额外的步骤去除远近场之间相互的影响,故所提算法中远场角度的估计精度稍差。但是所提算法中近场角度和近场距离估计的精度仍然明显高于文献[8]方法。当文献[8]中的算法减去远场影响的步骤省去,直接用混合累量矩阵估计所有角度,再与本文提出的算法比较时,二者远近场角度以及近场距离估计值的RMSE随着信噪比变化的趋势图如图8所示。从图中可以看到,在去除第一步后,文献[8]混合场源的角度和距离估计精度都要低于所提算法精度,表明本文的方法有很大的优越性。
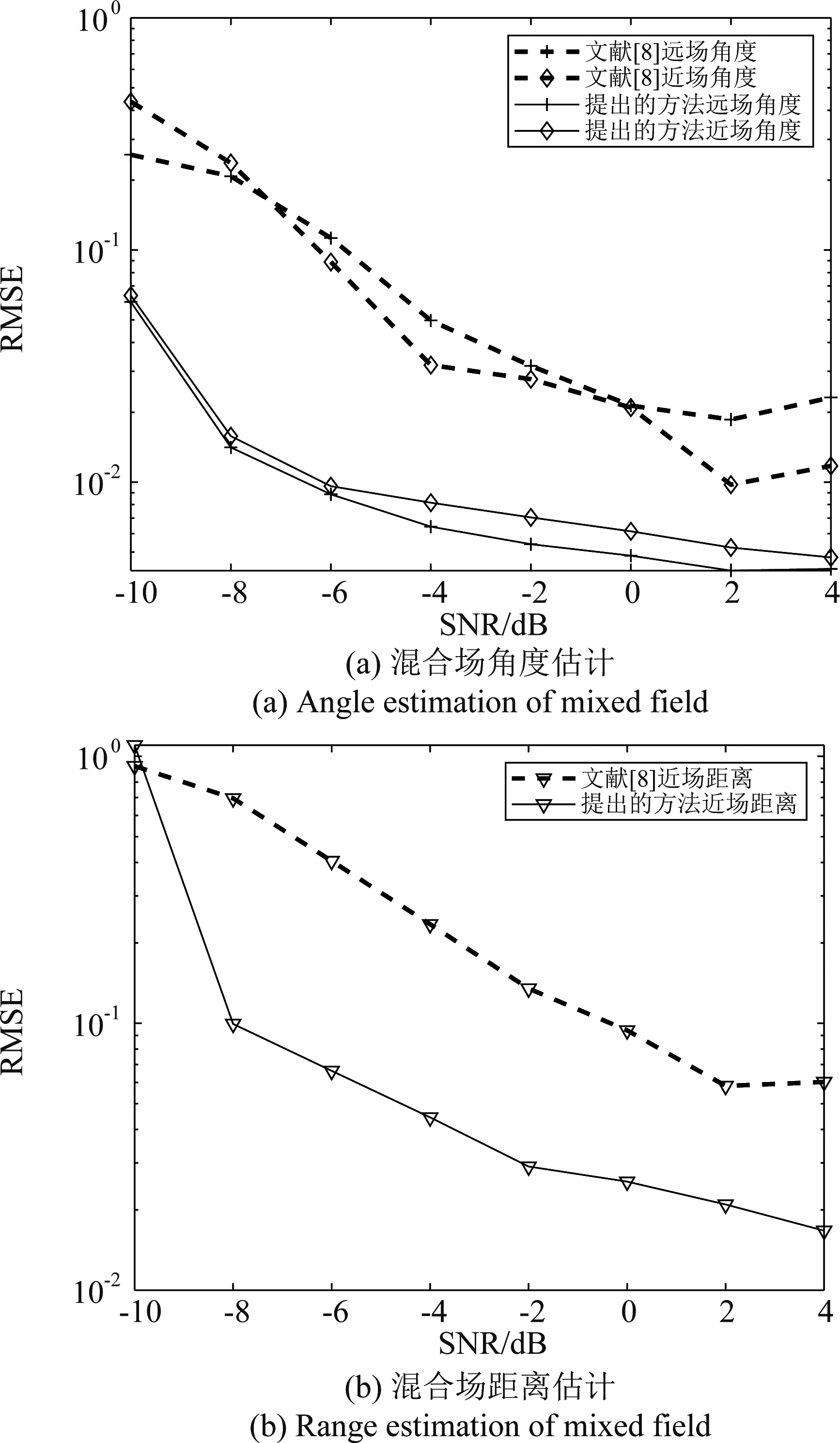
图8 混合场源下提出的算法和文献[8]处理后算法 的RMSE随信噪比变化趋势图
Fig.8 The RMSEs curve of the proposed method and processed method [8] versus the SNRs for mixed sources
5 结论
本文提出了一种基于四阶累量矩阵的快速近场源参数估计方法。本方法首先构造一个四阶累量矩阵,用类Root-MUSIC方法利用右奇异向量张成的噪声子空间得到近场源的波达方向,然后根据已经得到的近场源的波达方向对左奇异向量张成的噪声子空间再次使用类Root-MUSIC方法估计出近场源的距离。该方法在阵元数目为L时最大可分辨信源数可达到L-1,整个参数估计过程中只需要构造一个累积量和进行一次奇异值分解运算,并且类Root-MUSIC方法提供了闭式解从而省去了传统MUSIC的谱峰搜索过程。与其他基于高阶累积量的方法相比,该方法大大降低了运算量。不过本文算法的计算量与一般累量方法相比虽然大大降低但是仍然较大,本文算法与文献[8-10]算法一样适用于非实时的估计系统。仿真结果表明,本文方法的分辨率以及精度均优于文献[8]和文献[10]中的方法。此外,本文的方法可以容易地推广到混合场源的情况,使用类Root-MUSIC方法进行DOA估计时,它能同时得到混合场源中远场和近场的角度,只需添加一个简单的子空间正交性判断则可以区分出远近场角度。对于远场信号无需估计其距离,于是再利用近场角度估计近场距离即可完成所有的参数估计。本文提出的算法不仅省去了远场的距离估计过程,而且无需为远场参数的估计构造新的矩阵,相比于文献[6- 8]中的方法,该方法没有增加过多额外的计算量。
[1] JANTTI T P. The influence of extended sources on the theoretical performance of the MUSIC and ESPRIT methods: Narrow-band sources[J]. Acoustics, Speech, and Signal Processing, 1988 ICASSP- 88, 1988 International Conference on, 1992, 2: 429- 432vol.2.
[2] WU Xiaohuan, ZHU Weiping, YAN Jun. Atomic norm based localization of far-field and near-field signals with generalized symmetric arrays[C]∥ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Barcelona, Spain. IEEE, 2020: 4762- 4766.
[3] LIU Hongqing, MENG Huan, GAN Lu, et al. Subspace and sparse reconstruction based near-field sources localization in uniform linear array[J]. Digital Signal Processing, 2020, 106: 102824.
[4] SUN Jie, HAO Caiyong, ZHENG Zhi. Passive localization of near-field sources based on overlapped subarrays[J]. Circuits, Systems, and Signal Processing, 2020, 39(1): 502-512.
[5] 聂玺, 魏平. 互相关矩阵重排获取信号子空间的二维DOA估计算法[J].信号处理,2015,31(6):744-748.
NIE Xi, WEI Ping. Subspace algorithm for 2-D DOA estimation by rearranging the elements of cross-correlation matrix[J]. Journal of Signal Processing, 2015, 31(6): 744-748.(in Chinese)
[6] LIANG Junli, LIU Ding. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108-120.
[7] WANG Bo, ZHAO Yanping, LIU Juanjuan. Mixed-order MUSIC algorithm for localization of far-field and near-field sources[J]. IEEE Signal Processing Letters, 2013, 20(4): 311-314.
[8] ZHENG Zhi, FU Mingcheng, JIANG Di, et al. Localization of mixed far-field and near-field sources via cumulant matrix reconstruction[J]. IEEE Sensors Journal, 2018, 18(18): 7671-7680.
[9] LI Jianzhong, WANG Yide, LE BASTARD C, et al. Simplified high-order DOA and range estimation with linear antenna array[J]. IEEE Communications Letters, 2017, 21(1): 76-79.
[10] LIU Guohong, SUN Xiaoying. Spatial differencing method for mixed far-field and near-field sources localization[J]. IEEE Signal Processing Letters,2014,21(11):1331-1335.
[11] JIANG Jiajia, DUAN Fajie, CHEN Jin, et al. Mixed near-field and far-field sources localization using the uniform linear sensor array[J]. IEEE Sensors Journal, 2013, 13(8): 3136-3143.
[12] YAN Fenggang, JIN Ming, ZHOU Hongjuan, et al. Low-degree root-MUSIC algorithm for fast DOA estimation based on variable substitution technique[J]. Science China Information Sciences, 2019, 63(5): 1-3.
