1 引言
塔架结构大多运用三角形构造体系,具有较好的抗震与抗风性能,造价较低且经久耐用,逐步得到了广泛应用[1],如鸟巢、国家大剧院、广州新电视塔等建筑中都采用了塔架结构。塔架内部由于金属材质的散射体占比较大,遮挡严重,信号在其内部会产生大量的散射径与反射径,发生更为明显的多径效应,可视为一种特殊的通信传播环境,其信道建模比普通室内场景更具有挑战性[2]。无线传感器网络由于体积小、成本低、完成部署后无需人为操作,广泛应用于通信、航空、医疗、商业等各个领域中[3],塔架内部的传感器节点的覆盖率会直接受到整个系统性能的影响[4],因此通信性能的评估对传感器网络节点的设计和优化尤为重要。
针对室外场景的信道模型研究较多[5-7],但针对塔架结构场景的信道模型研究相对较少,考虑到塔架结构可看成是一类特殊的封闭场景,因此封闭场景的信道建模方法值得借鉴。比如,国内外专家学者对典型封闭场景的信道模型以及信道参数进行了研究,包括地铁环境[8],机舱环境[9-10],船舱环境[11],以及城际巴士环境[12]等。文献[8]基于射线追踪算法提出一种适用于地铁内部环境的混合信道模型,并通过实测数据验证了模型的有效性;文献[9]基于2.4 GHz、3.52 GHz与5.8 GHz下的实测数据,结合多种机器学习方法提出一种经验模型与机器学习相结合的路径损耗预测方案;文献[11-12]分别在船舱环境与城际巴士环境中进行了毫米波频段下的实测,其中,文献[11]研究了高金属含量环境对路径损耗的影响,文献[12]基于实测数据提出一种无线信道模型,并进一步提出一种生成功率时延谱的仿真算法,与实测数据能够较好吻合。
此外,无线传感器网络的性能很大程度上取决于网络节点的布置。如若部署大量冗余节点,不仅会提高成本,也无法保证信号覆盖质量。为了优化传感器网络节点的布置,在提高覆盖率的同时降低成本,文献[13-15]分别提出三种不同的优化算法对节点部署进行优化,从而得出节点的最佳数量与最佳位置。由于传感器网络的覆盖范围主要取决于信号强度与系统性能,因此在信道建模后对通信系统进行性能评估非常必要。系统性能评估主要包括信道容量[16]、中断概率与误码率等多个方面。K. A. Ranjan等[17]给出了衰落信道下不同调制方式的误码率表达式;文献[18]与文献[19]分别研究了衰落信道下DCSK系统与16-QAM系统的误码率性能。
本文针对复杂塔架结构通信环境,提出了一种基于射线追踪算法的三维多径簇信道模型,该模型对接收到的大量射线路径进行分簇,并根据不同路径参数计算出簇平均时延与簇平均功率等参数。此外,为保证精确度的前提下降低计算复杂度,本文忽略了功率占比较小的簇路径,进而获得简化等效后的传播模型。在此基础上,进一步分析不同位置收发节点的通信的理论误码性能,并利用仿真进行验证分析。
2 系统模型
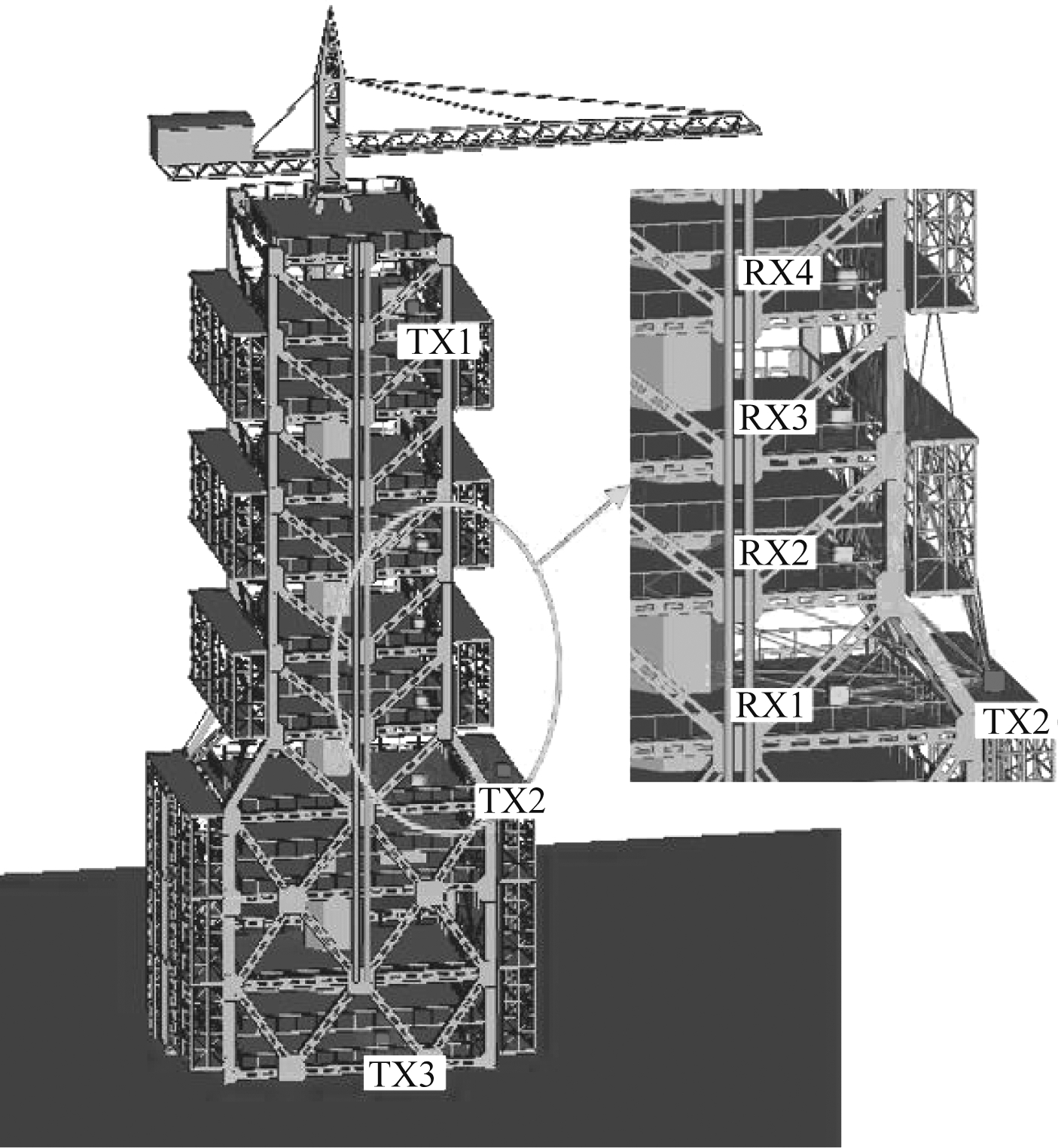
图1 复杂塔架环境传感器网络节点通信
Fig.1 Communication of sensor network nodes in complex tower environment
典型塔架结构场景如图1所示,限定的封闭空间以及结构复杂数量众多的钢架结构建筑物会对无线信号传播产生严重的影响。利用传统统计信道模型对信号传输性能分析可能会产生较大误差,因此需要建立一个更加精确且更符合具体塔架情况的信道模型。本文基于射线追踪原理,将信道建模为所有可能的传播路径叠加,对应信道单位冲击响应可表示为
(1)
其中,L表示接收端接收到的有效路径总数,Al,τl,以及ψl分别表示第l条路径的幅度,时延和均匀分布于[0,2π)的随机初始相位;Θl与Φl分别表示第l条路径下的离开角与到达角。特别的,当l=0时,表示收发端之间存在有视距路径。
考虑到传感器通信节点设备的时域分辨能力和接收灵敏度有限,而大量射线的时延差比较微小,因此多径可看做以簇的形式存在。本文采用最近邻聚类算法对接收到的多径进行分簇,使得簇内的不同射线具有相似的时延、角度等信道参数,而不同簇内的射线信道参数相差较大。每一簇内包含数量不同的射线,经由相近的散射体反射至接收端。因此,信道模型可简化为多径簇的叠加,假设接收端能够接收到的多径簇数目为N,则对应信道单位冲击响应可转换为
(2)
其中,
与
分别表示第n个簇的簇平均幅度、簇平均时延与簇平均相位。
为简化性能分析,本文假设各节点采用全向天线,且接收端利用信道均衡补偿校正经过多径衰落后的信号,故各条路径的随机相位偏移可以忽略。令发射信号为x(t),则接收信号可表示为
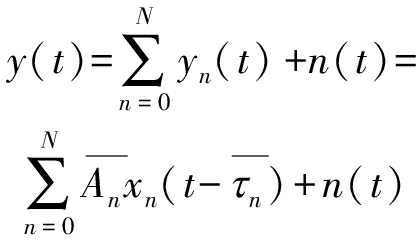
(3)
其中,yn(t)表示不同路径的达到信号,n(t)为均值为0,方差为PN/2的高斯白噪声。 此时,接收端判决器误判的概率为
Pe=P(0/1)P(1)+P(1/0)P(0)
(4)
其中,P(0/1)表示发“1”码误判成“0”码的概率,具体可表示为
P(0/1)=P(y<0)=
p(r/1)dr
(5)
同理,P(1/0)表示发“0”码误判成“1”码的概率。
3 塔架环境信道参数估计及性能分析
3.1 基于RT的多径参数估计
基于几何光学理论的射线追踪算法是一种确定性参数估计方法,考虑到塔架结构中收发端传感器节点处于固定状态,且该静态场景处于半封闭状态,内部结构复杂,散射体众多,比较适用于射线追踪的方法进行分析。
首先,我们通过几何方法来判断射线与三角面元重构所得的散射体是否有交点,从而完成对射线路径的寻迹。假设收发端位置保持不变,发射端TX坐标为PTX(xTX,yTX,zTX),射线单位方向向量为
射线长度为S,射线入射三角面元的三个顶点坐标与三角面元平面法向量分别为P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)与
则可得到射线方程与三角面元的平面方程分别表示如下
(6)
A(x-x1)+B(y-y1)+C(z-z1)=0
(7)
则,若射线与三角面元有交点,可表示为
A(xTX-x1)+B(yTX-y1)+C(zTX-z1)+ S·(aA+bB+cC)=0
(8)
经过化简后得到
(9)
通过结合式(6)可求得交点坐标。
然后,利用获得的交点位置计算不同簇的参数。假设收发端之间距离为DTX,RX,发射端与接收端到散射体的距离分别表示为DTX,s与Ds,RX。当收发端之间存在视距路径时,时延表示为
(10)
其中,c表示电磁波在自由空间的传播速度。当收发端之间不存在视距路径时,各条路径时延表示为
(11)
进而可得到簇平均时延为
(12)
同理,当收发端之间存在视距路径时,接收场强可表示为
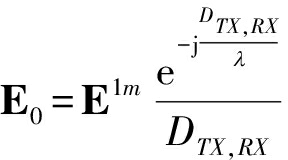
(13)
其中,E1m表示单位场强,λ表示波长。对于非视距路径,射线到达散射体时会产生反射,接收场强可表示为
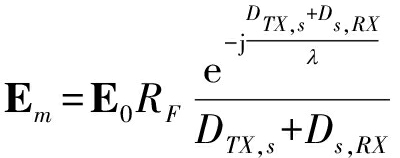
(14)
其中,RF为反射系数。当反射表面光滑时,天线采用水平极化方式与垂直极化方式的反射系数RH与RV可分别表示为
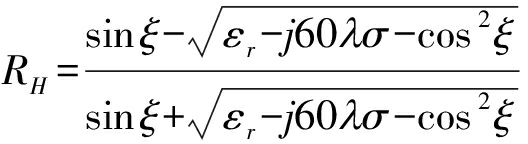
(15)
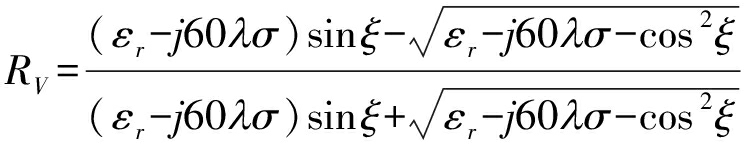
(16)
其中,ξ为信号入射角,εr与σ分别表示相对介电常数与电导率。因此,各条路径接收功率可表示为
(17)
进而可以计算得出簇平均功率,表示为
(18)
需要指出的是,由于塔架内部散射体非常复杂,利用射线追踪算法追踪每一条射线的传播过程,包括射线方向、反射与绕射等会产生巨大的计算量。因此,为保证精确度的前提下大大降低复杂度,本文将功率衰减较大和时延较大的簇信号忽略不计。
3.2 通信节点传输性能分析
误码率是衡量数字通信系统性能优劣的重要指标。要分析传感器节点无线通信的性能,需要对其误码性能进行评估。对于多进制数字相位调制系统(Multiple Phase Shift Keying, MPSK)调制系统,假设发送信号为x(t),在采样间隔t0内,接收到的判决信号可表示为
(19)
其中,第一项为期望信号,第二项为多径效应所造成的码间干扰,K表示有效的码间干扰数,第三项为高斯白噪声。
假设信道噪声方差
码间干扰项用z来表示,则系统误码率即y<0的概率可表示为
Pe(0|s1)=p(y<0)=Ez[Q(x0+z)]
(20)
其中,Ez[·]表示对随机变量z取期望,Q函数的具体表达式为
(21)
由于上式直接求解较为困难,本文采用三角函数近似式来求解存在码间干扰的MPSK系统性能。Q函数的三角函数级数近似式可表示为
(22)
式中,ci,λi,ωi为待定系数,NT为阶数且NT≥7可满足一般计算精度需求。结合式(21)与式(22)可得,
(23)
其中,Ez[e(λi+jωi)z]是随机变量z的矩生成函数。将MPSK系统中码间干扰的矩生成函数代入上式中,由于假设噪声方差
有效比特信噪比可简化为
可得多径衰落信道下MPSK系统的误码率可表示为
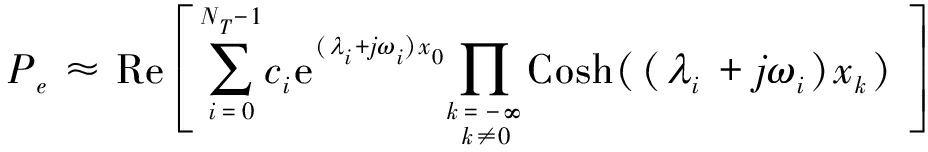
(24)
4 数值仿真与结果分析
本节将利用上述参数计算方法对塔架场景信道特性进行仿真分析。其中,塔架高度约为194.20 m,记塔架底部中心坐标为(0,0,0), 则塔顶坐标为(0,0,194.2)。将塔架分为上、中、下三部分,在每一部分放置一个发射节点,分别记为TX1、TX2和TX3,坐标分别为(10,20,145)、(30,20,53)和(5,20,5)。此外,塔架内设置了四个接收节点RX1、RX2、RX3和RX4,坐标分别为(10,20,53)、(10,20,68)、(10,20,83)和(10,20,98),如图1所示。传感器网络节点通信频率为1 GHz,最大带宽为100 MHz,其余主要仿真参数如表1所示。
表1 信道仿真参数
Tab.1 Channel simulation parameters
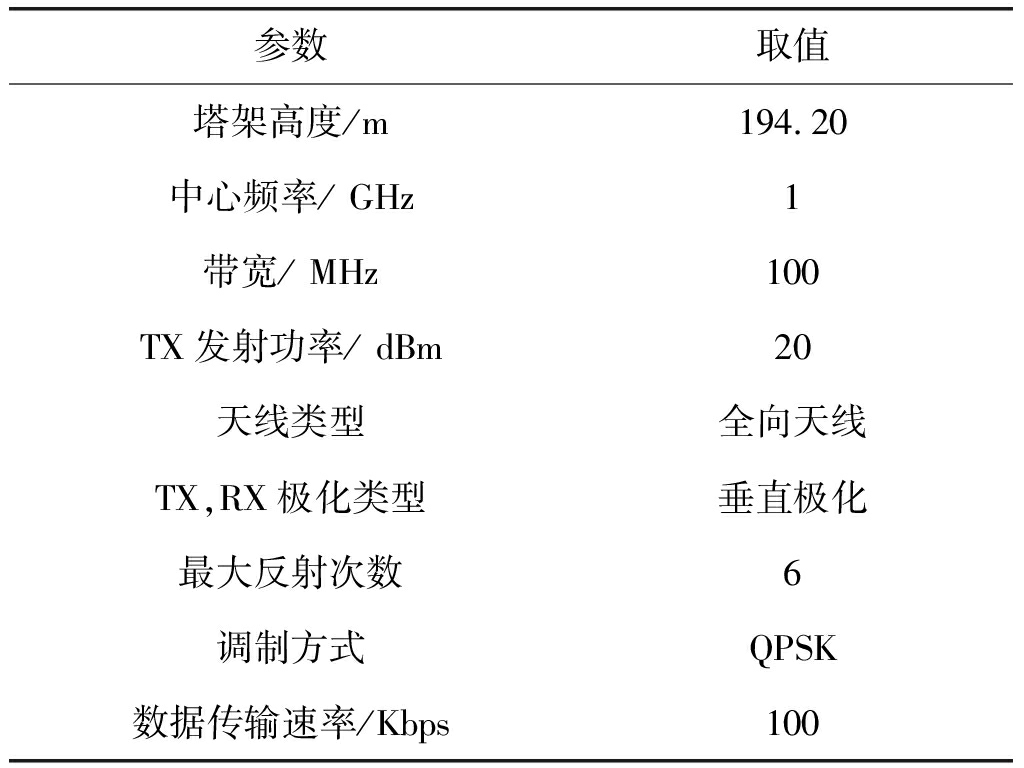
参数取值塔架高度/m194.20中心频率/ GHz1带宽/ MHz100TX发射功率/ dBm20天线类型全向天线TX,RX极化类型垂直极化最大反射次数6调制方式QPSK数据传输速率/Kbps100
图2 不同接收位置的簇平均时延分布
Fig.2 Average delay distribution of clusters at different receiving locations
多径簇的平均时延与功率对网络节点间的通信质量影响非常大,需要了解塔架信道的时延和功率的统计分布情况。以发射端TX2为例,图2和图3分别给出了四个不同接收位置的簇平均时延与功率衰减的分布情况。由图可以看出,RX1、RX2、RX3、RX4接收到的多径时延分别集中于190～210 ns、240～260 ns、260～280 ns、290～310 ns,不同的接收端位置对于信道性能影响较大,且多径时延普遍随收发端之间的距离增加而变大;各个接收端的簇平均功率衰减主要集中在5 dBm以内,说明接收端的接收功率主要集中在几个平均功率较大的簇中。此外,簇平均时延与簇平均功率衰减的分布可用指数函数y=a·exp(-b·x)进行拟合。需要指出的是,该结论与文献[20]的研究结果一致,本文拟合曲线的系数如表2所示。
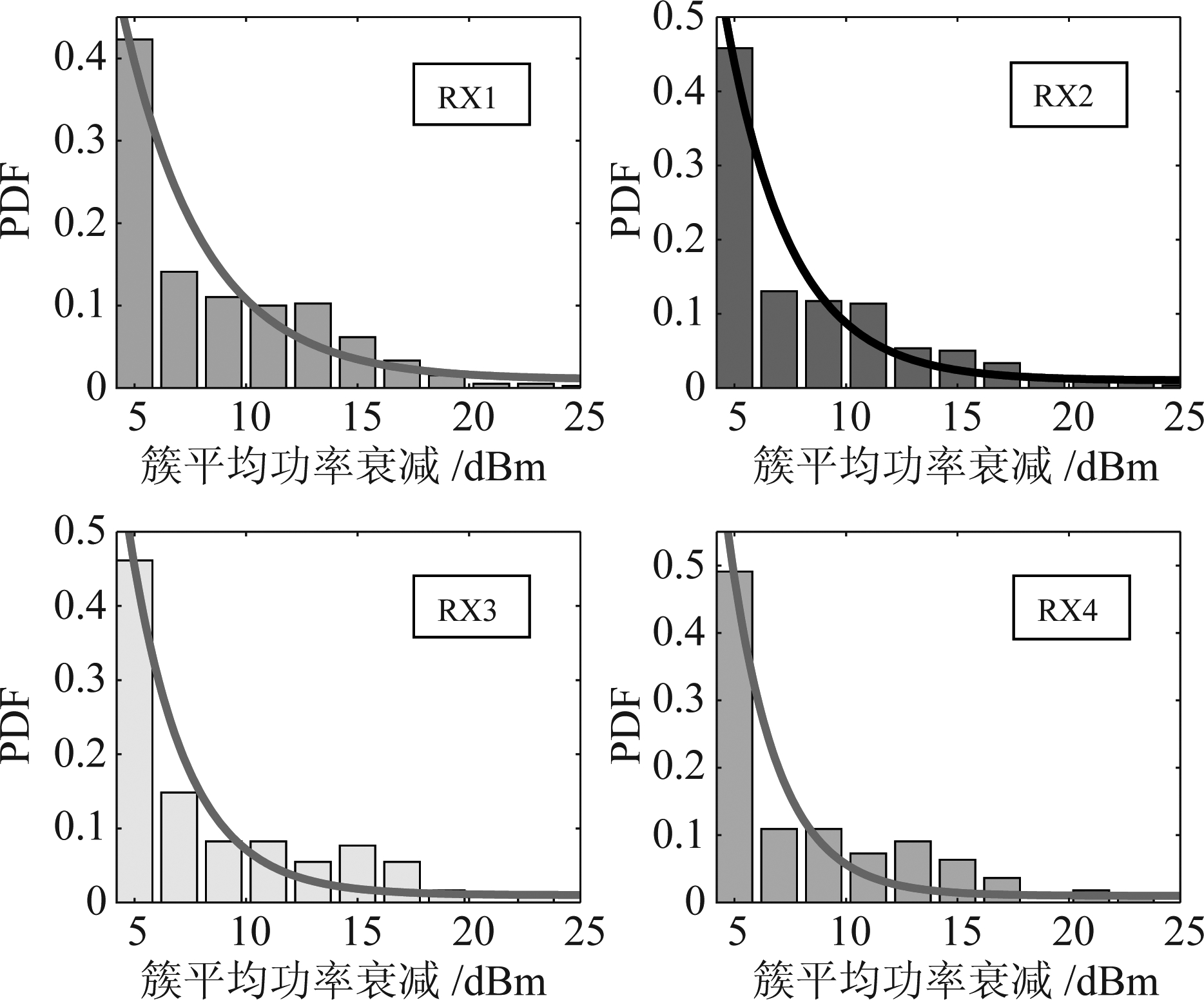
图3 不同接收位置的簇平均功率衰减分布
Fig.3 Average power attenuation distribution of clusters at different receiving locations
表2 簇平均时延与簇平均功率衰减概率密度函数拟合参数
Tab.2 Fitting parameters of cluster average delay and power attenuation probability density function
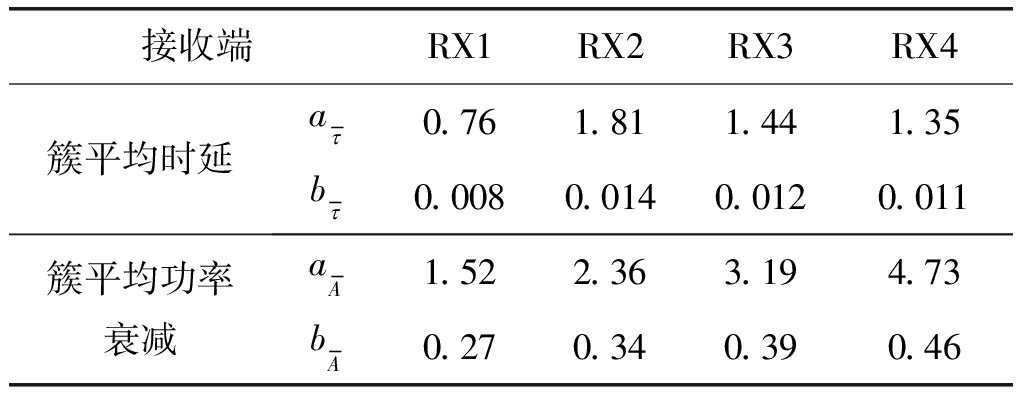
图4(a)、(b)进一步给出了不同调制方式与不同接收位置下误码率与信噪比的关系。可见,随着M的增加,误码率逐渐增大。但值得一提的是,随着M值的增加,单个符号携带的信息量也会增加,即信息速率更高。此外,随着收发端距离逐渐增加,在信噪比相同的情况下,误码率逐渐增加,即系统性能也随之恶化;当对误码率性能做出一定要求时,达到相同要求所需的信噪比也逐渐增加。
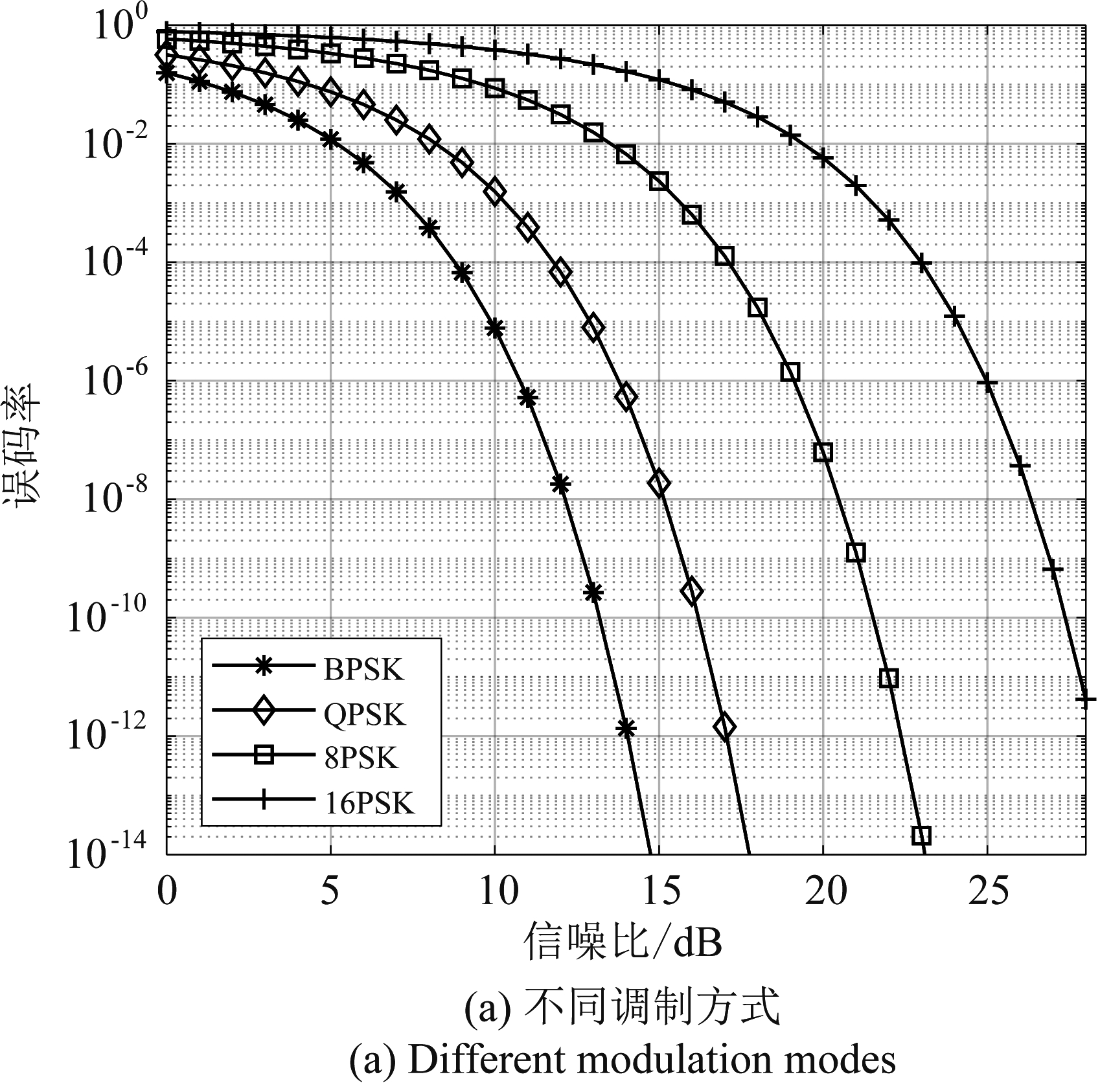
图4 系统误码性能
Fig.4 BER performance of systems
5 结论
本文提出一种针对塔架结构的三维多径簇信道模型,并推导给出对应场景下MPSK系统的误码率理论性能。仿真结果表明,簇平均时延与功率分布等信道参数与理论推导较为吻合。此外,在通信系统中,不同的接收位置会对系统性能产生影响,也从另一方面验证了误码率公式的正确性。因此,该模型可用于模拟塔架场景中的通信状况,为优化无线传感器网络布置、评估通信系统性能等提供理论基础。
[1] 童亮. 钢结构在装配式建筑中的实际运用价值研究[J]. 中国建材科技, 2020, 29(5): 101,34.
TONG Liang. Research on practical application value of steel structure in prefabricated buildings[J]. China Building Materials Science & Technology, 2020, 29(5): 101,34.(in Chinese)
[2] 朱秋明, 华博宇, 毛开, 等. 无人机毫米波信道建模进展和挑战[J]. 数据采集与处理, 2020, 35(6): 1049-1059.
ZHU Qiuming, HUA Boyu, MAO Kai, et al. Advances and challenges of UAV millimeter-wave channel modeling[J]. Journal of Data Acquisition and Processing, 2020, 35(6): 1049-1059.(in Chinese)
[3] ABBAS N, YU Fengqi, MAJEED U. Reliability and end-to-end delay evaluation of outdoor and indoor environments for wireless multimedia sensor networks[C]∥2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC). Xi’an, China. IEEE, 2018: 764-768.
[4] CHEN Qian, TAN Penghui, LIN Zhiwei, et al. Design and optimization of IEEE 802.11ad-based dense network in cabin environment[C]∥GLOBECOM 2017-2017 IEEE Global Communications Conference.Singapore.IEEE, 2017: 1- 6.
[5] JIANG Shan, ZHU Qiuming, WANG Chengxiang, et al. Map-based UAV mmWave channel model and characteristics analysis[C]∥2020 IEEE/CIC International Conference on Communications in China (ICCC Workshops). Chongqing, China. IEEE, 2020: 23-28.
[6] ZHU Qiuming, JIANG Shan, WANG Chengxiang, et al. Effects of digital map on the RT-based channel model for UAV mmWave communications[C]∥2020 International Wireless Communications and Mobile Computing (IWCMC). Limassol, Cyprus. IEEE, 2020: 1648-1653.
[7] CHENG Lele, ZHU Qiuming, WANG Chengxiang, et al. Modeling and simulation for UAV air-to-ground mmWave channels[C]∥2020 14th European Conference on Antennas and Propagation (EuCAP). Copenhagen, Denmark. IEEE, 2020: 1-5.
[8] HE Danping, GUAN Ke, GARC
A-LOYGORRI J M, et al. Channel characterization and hybrid modeling for millimeter-wave communications in metro train[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 12408-12417.
[9] WEN Jinxiao, ZHANG Yan, YANG Guanshu, et al. Path loss prediction based on machine learning methods for aircraft cabin environments[J]. IEEE Access, 2019, 7: 159251-159261.
[10] COGALAN T, VIDEV S, HAAS H. Aircraft in-cabin radio channel characterization: From measurement to model[C]∥GLOBECOM 2017-2017 IEEE Global Communications Conference. Singapore. IEEE, 2017: 1- 6.
[11] DE BEELDE B, TANGHE E, YUSUF M, et al. 60 GHz path loss modelling inside ships[C]∥2020 14th European Conference on Antennas and Propagation (EuCAP). Copenhagen, Denmark. IEEE, 2020: 1-5.
[12] CHANDRA A, RAHMAN A U, GHOSH U, et al. 60-GHz millimeter-wave propagation inside bus: Measurement, modeling, simulation, and performance analysis[J]. IEEE Access, 2019, 7: 97815-97826.
[13] XIANG Tingli, WANG H, SHI Yingchun. Hybrid WSN node deployment optimization strategy based on CS algorithm[C]∥2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC). Chengdu, China. IEEE, 2019: 621- 625.
[14] HAN Yamin, BYUN H, YANG Bo, et al. Optimization of sensor nodes deployment based on an improved differential evolution algorithm for coverage area maximization[C]∥2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). Chengdu, China. IEEE, 2019: 250-254.
[15] LIU Wei, YANG Shuai, SUN Shuang, et al. A node deployment optimization method of WSN based on ant-lion optimization algorithm[C]∥2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS). Lviv, Ukraine. IEEE, 2018: 88-92.
[16] YOO S K, COTTON S L, SOFOTASIOS P C, et al. Effective capacity analysis over generalized composite fading channels[J]. IEEE Access, 2020, 8: 123756-123764.
[17] RANJAN K A, SEHGAL A, SINGH P K, et al. BER based impact analysis of jamming signals for fading channels[C]∥2018 International Conference on Automation and Computational Engineering (ICACE). Greater Noida, India. IEEE, 2018: 224-228.
[18] DAWA M, KADDOUM G, HERCEG M. A framework for the lower bound on the BER of DCSK systems over multi-path nakagami-m fading channels[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(10): 1859-1863.
[19] HUANG Jihua, SHEN Shikai, CHEN Xingyuan. Modeling and studying of the 16-QAM based system over the fading channel[C]∥2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC). Dalian, China. IEEE, 2017: 1458-1460.
[20] 3GPP. Tech. Rep. TR 38.901 V14.1.1 Release 14. Study on Channel Model for Frequencies from 0.5 to 100 GHz[S]. 3rd Generation Partnership Project (3GPP), 2017.
