1 引言
确定脉冲重复间隔或频率是电子情报分析的一项重要工作。根据雷达脉冲重复间隔变化规律,雷达重复模式大致可分为固定、参差、组变、排定和抖动等类型[1]。每一重频类型都与雷达功能有着内在联系,比如参差重频主要应用于动目标检测(Moving Target Indicator, MTI)雷达中,用来消除盲速,而排定、抖动则更多出现在多功能先进体制雷达中[2]。固定、参差、组变等重频类型有着简单直观的脉冲重复间隔时序排列规律,在民用雷达和传统军用雷达中大量使用,本文将采用此类重频类型的雷达称为常规体制雷达。虽然目前先进体制雷达得到大量应用,信号的重频样式也趋于多样性和复杂化,但在实际雷达侦察信号中,常规体制雷达信号依然扮演着主要的角色,对此类信号进行高效自动地分析,是实现侦察大数据智能化、自动化处理的重要内容。
重频模式是指雷达发射信号在一个重频周期内的多个相邻脉冲重复间隔(Pulse Repetition Interval, PRI)的取值和时序规律[3],重频模式自动解析则是指采用自动化的处理方式提取雷达侦察脉冲列中隐藏的重频模式。与雷达侦察信号处理领域广泛研究的脉冲列分选、重频类型识别[4- 6]等问题相比,雷达重频模式解析问题在数据处理方式、输出结果形式等方面都存在显著差异,借助重频模式解析获得雷达脉冲列单个重频周期的完整模式(例如包含PRI时序信息的三参差重频模式(300 μs,400 μs,500 μs),而不是这些典型PRI值的离散集合{300 μs,400 μs,500 μs},或者仅仅只是骨架周期1200 μs),能够为脉冲列在线分选、雷达类型识别以及工作模式识别提供强有力的信息支撑。
不管是雷达脉冲列分选还是重频类型识别,国内外学者都展开了深入且富有成果的研究,这些成果对电子侦察的发展产生了深远影响。但面对如今侦察数据量、数据复杂程度都急剧增长的现状,这些方法显得有些难以应付。比如经典的分选方法[7-9]通常是利用脉冲重复间隔骨架周期等低维度重频参数分离交错脉冲列,其分选性能和适用场景相较于利用完整重频模式信息的自动机分选[10]存在差距(这里,低维度重频参数是指雷达发射信号的脉冲重复间隔,或脉冲重复间隔骨架周期的离散集合;完整重频模式信息是指雷达发射信号的脉冲重复间隔以及它们的时序关系),主要原因在于重频模式中包含的高维知识能对脉冲列时序状态进行准确描述,利用这些知识可以更好地实现脉冲列的提取分离。自动机分选是将重频模式应用到在线分选领域成功的案例,它展现了完整的重频模式(而不是重频骨架周期等非完整参数)在分选领域存在的巨大潜力[10],同时,重频模式作为辐射源参数库中的新参数,可以对雷达辐射源进行更为详细的描述,为雷达工作模式识别以及型号识别提供更完备的信息保障。
目前对重频模式的分析大多停留在人工分析的层次,在过去侦察数据量较小的时代,富有经验的情报分析人员可以从雷达侦察信号中提取出每个辐射源的重频模式,但随着侦察数据量持续增大,如果全采用人工分析这将是一项不可完成的任务,同时也会使准确率和时效性大打折扣。本文作者意识到重频模式的潜在价值,在文献[3]中提出频繁项扩展算法,利用雷达重频周期中相邻PRI共用首尾脉冲的特点,实现了对常规体制雷达信号重频模式的解析。该方法在对单个雷达脉冲列的重频解析过程中得到了较好的效果,对干扰脉冲、漏脉冲等数据噪声也体现出了较强的适应能力,但该算法迭代过程的终止准则是针对单部雷达侦察脉冲列设计的,并不能直接适用于处理多辐射源的交错脉冲列。而在实际侦察场景中,交错脉冲列经常出现,为此,本文针对常规体制雷达交错脉冲列,对频繁项扩展的雷达脉冲列重频解析方法加以改进,通过引入IS兴趣度度量[11-13],提出新的重频模式解析过程的终止准则,成功实现对交错脉冲列中各辐射源重频模式的自动解析。
2 基于频繁DTOA扩展的单部雷达重频模式解析方法
基于频繁DTOA扩展的方法是目前用于重频模式自动解析的行之有效的方法,它利用真实PRI隐藏在到达时间差分(Differential Time-of-Arrival, DTOA)信息中的性质,将聚类频次大于频繁门限的DTOA定义为频繁项,根据DTOA频繁项首尾脉冲的重叠程度依次进行扩展,从而实现了重频模式的解析[3]。解析得到的重频模式作为已知先验知识,利用有限状态自动机对其进行精细化建模,可以实现对交错脉冲列的在线、并行分选,其分选性能、适应场景都较传统分选算法有着显著提升[10],展现了重频模式在分选领域存在的较大应用价值。本文为简便表述问题,将脉宽、载频等脉冲参数设为固定值,脉冲列的状态将只取决于脉冲重复间隔及其上下文。图1展示了从雷达侦察脉冲列中解析三参差重频模式(PRI1,PRI2,PRI3)的过程(图中实线矩形代表侦察脉冲,虚线矩形代表侦察脉冲列中因各种因素漏掉的脉冲)。
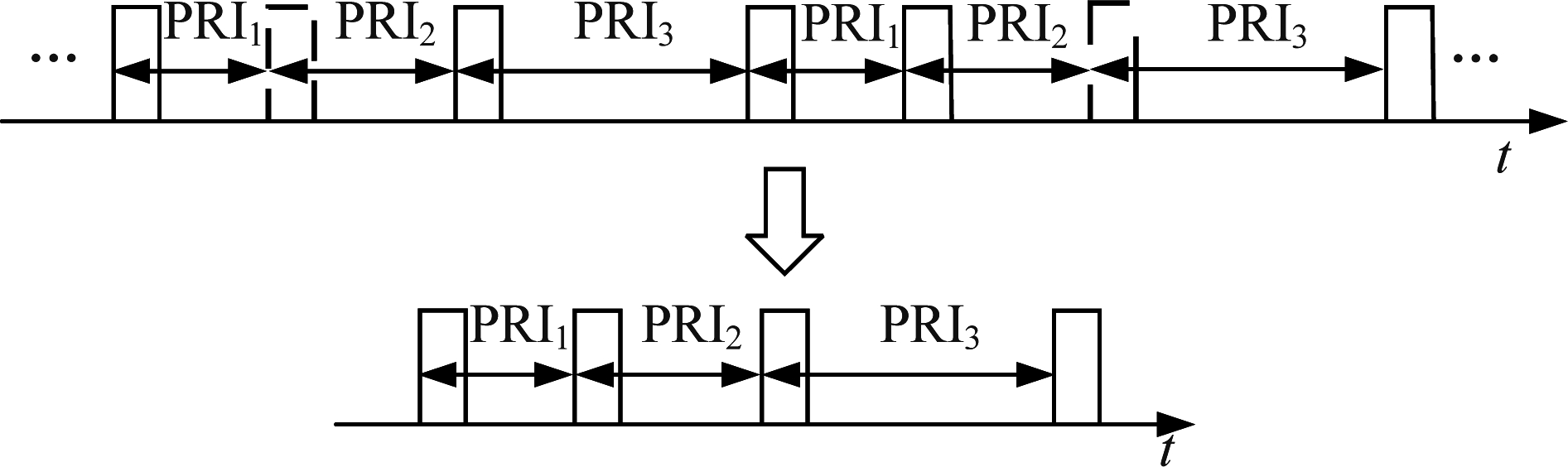
图1 雷达侦察信号重频模式解析示意图
Fig.1 Schematic diagram of pulse repetition pattern reconstruction based on radar reconnaissance signals
该算法主要分为频繁项的提取和扩展两部分。在提取部分主要利用统计分析的方法得到脉冲列中多次出现的DTOA,并定义为频繁项,由于本文将脉宽、载频等脉冲参数设为固定值,故将频繁项集简便表述为
(1)
其中I表示雷达脉冲列中出现次数超过预设门限Me的脉冲间隔数量,每个脉冲间隔对应一个频繁项;DTOAi表示第i个频繁项对应的脉冲间隔,通过数值聚类得到,在脉冲列中出现了Mi(Mi≥Me)次;频繁项DTOAi对应脉冲对的首脉冲序号构成集合![]() 尾脉冲序号构成集合
尾脉冲序号构成集合![]()
在扩展部分主要是将DTOA频繁项间首尾脉冲重叠程度最大的DTOA进行扩展。假设图2已经重建得到重频模式前两个元素(PRI1,PRI2),在此基础上扩展重频模式的原理为
(2)
其中{(PRI1,PRI2)}表示大小为(PRI1+PRI2)的重频间隔在侦察信号序列中对应的首、尾脉冲对序号,DTOAi表示以重频间隔(PRI1+PRI2)的尾脉冲集为起始时刻向后扩展的时差,函数f(·,·)是一个关于计数结果的函数,依赖于该扩展时差值处对应的脉冲数量。
图2对存在各种数据噪声情况下的重频模式解析过程进行了简单示意,其中实线、虚线矩形含义与图1相同,斜线填充矩形代表干扰脉冲,竖线填充矩形代表待扩展脉冲。紧随(PRI1,PRI2)之后的PRI3在图2第一行脉冲片段中被观测到,待扩展脉冲依重建的重频模式对齐扩展,而PRI3在图2第二、三行片段中被漏脉冲、干扰脉冲破坏,但非相邻PRI(如图2第二行片段中的(PRI2+PRI3))能够基于重频模式准确表示并扩展,干扰脉冲则由于到达时间具有随机性,其分裂产生的DTOA不会构成频繁项,不会对重频模式的扩展过程产生影响,如图2第三行片段PRI3的扩展。
与重建的重频模式相匹配的脉冲片段对应的脉冲序号构成了DTOA频繁项序号矩阵,记作E,这些脉冲片段依片段长度排列,剔除长度小的状态失配片段,当抽取的脉冲片段到达时间之间相差已提取重频模式骨架周期的整数倍时,终止重频模式的迭代扩展过程,输出此时的PRI序列作为雷达重频模式解析结果[3]。
当输入脉冲列中仅包含单部雷达脉冲列时,利用文献[3]中的终止判决准则可以有效地输出重频模式解析结果,但如果将该准则直接应用到多辐射源交错脉冲列中,则只能解析出单一重频模式,并不能确定脉冲列中辐射源的数量,也不能准确解析出所有辐射源对应的重频模式。如何在不实施分选的前提下高效且准确地解析出交错脉冲列中所有辐射源的重频模式,是实现雷达侦察数据智能化处理的重要内容。
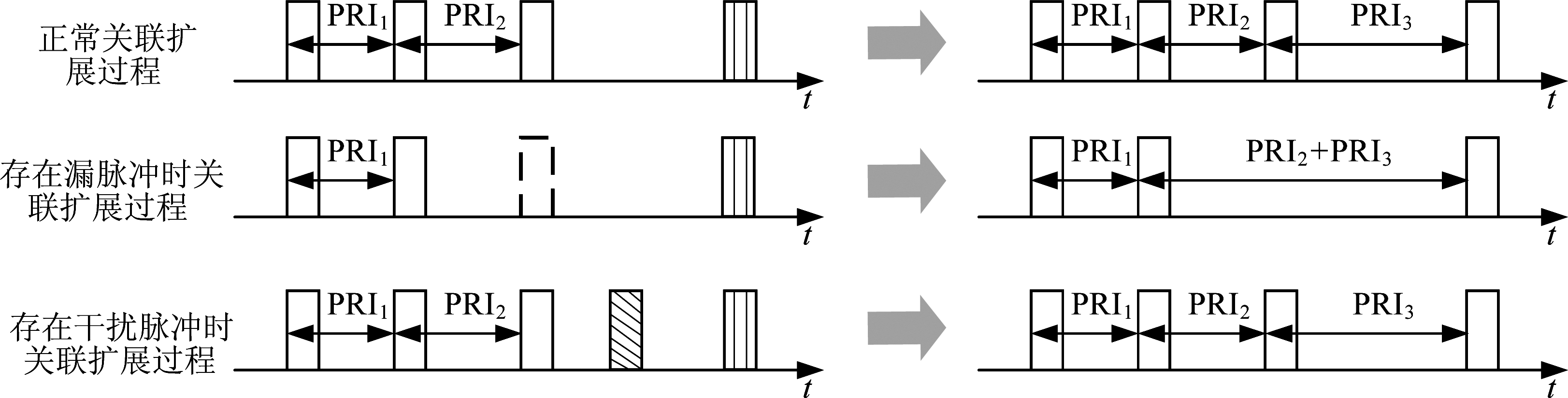
图2 通过频繁项扩展重频模式的单次迭代示意图
Fig.2 Schematic diagram of an iteration during PRI pattern reconstruction via frequent item extension
3 雷达交错脉冲列重频模式解析方法
3.1 交错脉冲列重频模式解析原理以及流程
交错脉冲列重频模式解析是要从含有多样化噪声的多辐射源交错脉冲列中提取出所有雷达的重频模式。相较于单辐射源脉冲列重频模式解析,多辐射源交错脉冲列解析过程不仅需要考虑漏脉冲、干扰脉冲的影响,更多地是要排除各辐射源侦察脉冲列之间的干扰,以及确定脉冲列中辐射源的数量。图3展现了交错脉冲列中来重频模式分别为![]() 的辐射源侦察脉冲列间互相干扰的情况。
的辐射源侦察脉冲列间互相干扰的情况。
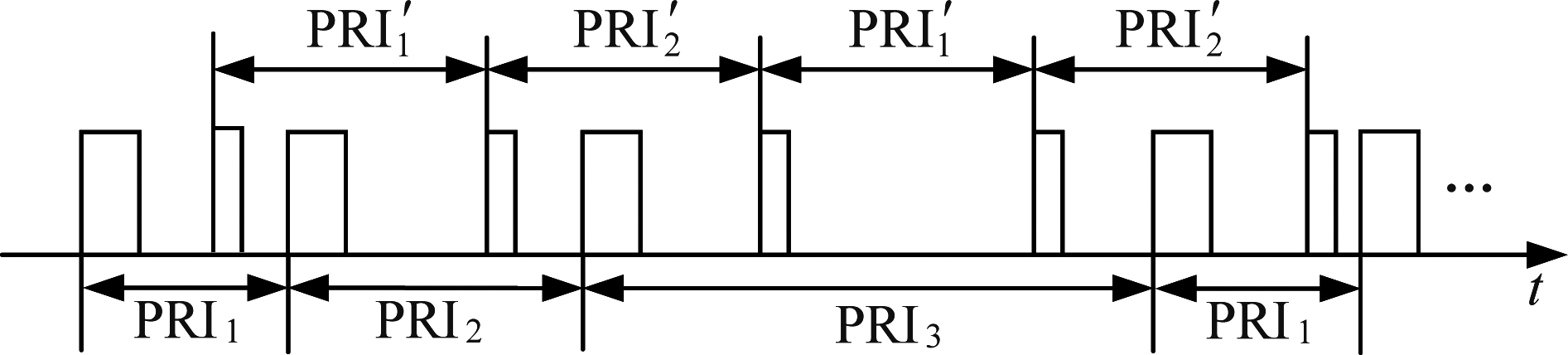
图3 交错脉冲列中不同辐射源侦察脉冲列间 互相干扰示意图
Fig.3 Schematic diagram of mutual interference among reconnaissance pulse trains of different emitters in interleaved pulse train
在多部雷达的交错脉冲列中,属于同一辐射源的脉冲之间具有时序上的关联性,不同辐射源之间的脉冲或者干扰脉冲之间不具有这一关联性。利用这一特性,本文引入关联模式的客观兴趣度度量——IS度量[11-13],它是评估关联模式关联质量高低的常用度量,关联质量反映了关联模式中二元变量间关联性的强弱。对于DTOAu频繁项和DTOAv频繁项,IS(DTOAu,DTOAv)将两频繁项间的首尾脉冲重叠程度作为观察对象,反映了DTOAu和DTOAv频繁项的关联性强弱,IS(DTOAu,DTOAv)越大关联模式的关联质量越高,两频繁项间的关联性越强。通过计算各频繁项间的IS值,依次将属于各辐射源的DTOA聚集关联在一起。
交错脉冲列重频模式解析方法的实现过程如图4所示,其处理思路为:在重频模式每轮扩展过程中,首先对重频模式中最新关联的DTOA频繁项与待关联的DTOA频繁项间进行IS度量计算;经过IS终止判决选取关联质量超过预设关联质量门限的关联模式归类为关联模式集;根据频繁项扩展算法[3]从该关联模式集中选取最合适的关联模式完成扩展;将扩展得到的重频模式实施扩展过程的终止判决[3],以判决该辐射源的重频模式是否已重建完整,如果满足终止判决准则,则认为该辐射源的重频模式重建完毕;进而实施下一辐射源重频模式的重建,直至频繁项集中各频繁项间的IS值都满足IS终止判决,即没有DTOA关联模式超过预设关联质量门限,此时终止迭代,输出各辐射源对应的重频模式解析结果。
扩展过程的终止判决[3]主要是判决单部辐射源的重频模式是否重建完成,IS终止判决主要是判决整个脉冲列的所有重频模式是否得到全部解析。
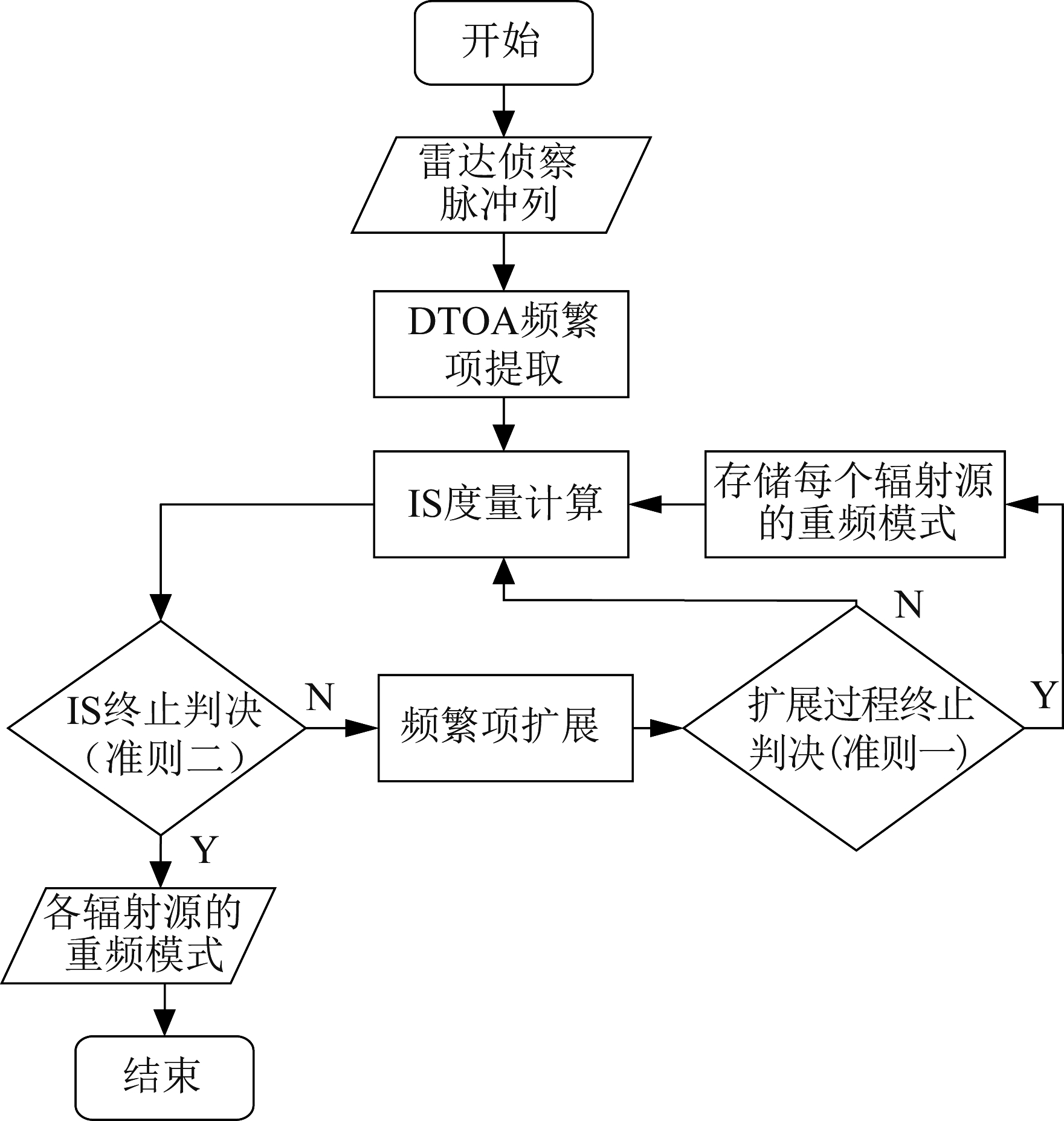
图4 雷达侦察交错脉冲列重频模式解析流程
Fig.4 Schematic diagram of PRI pattern reconstruction based on radar reconnaissance interleaved pulse train
影响本文重频模式解析算法性能的三个主要过程包括IS度量计算、用于单部雷达频繁DTOA扩展过程的终止判决准则[3]和用于交错脉冲列解析的IS终止判决准则,以下分三个小节对这几部分的原理进行阐述。第2小节主要对IS度量的计算展开论述;第3小节主要对单部雷达重频模式扩展过程终止判决准则中的状态失配脉冲片段的处理方法进行优化,提高计算效率,以适应脉冲数量较多的脉冲列处理;第4小节主要是为了保证重频模式解析进程的正常终止,对交错脉冲列解析过程的IS终止判决准则进行论述。
3.2 IS度量计算
记雷达重频模式当前重建结果为(DTOA1,…,DTOAu),其中u表示当前重频模式中包含的DTOA元素个数,当u=0时,表示该重频模式包含0个DTOA,该重建结果只显示当前重频模式的重建结果,不显示其他已重建完成的重频模式。为了更好地评估DTOA频繁项间的关联性强弱,本文将IS度量定义如下:
(3)
其中Mu表示当前重频模式的最后一个DTOAu频繁项的计数频次,当u=0时,M0=N,N表示脉冲列中脉冲的总数;Mv表示待关联DTOAv频繁项的计数频次;![]() 表示两个频繁项的首尾脉冲序号重叠数目,即
表示两个频繁项的首尾脉冲序号重叠数目,即
(4)
其中![]() 为示性函数,当
为示性函数,当![]() 时,
时,![]() 否则
否则![]()
这里,详细讨论u和v的取值情况。当u=0时,Mv对应的DTOAv将从集合B中取值,集合B数学形式为:
(5)
当u≥1时,Mv对应的DTOAv∈{DTOAi}i=1,…,I。其中集合A为已重建完成的重频模式中所有超过关联质量门限的关联模式的DTOA集合。
通过遍历式(1)中频繁项,可以得到DTOAu频繁项与各DTOAv频繁项生成的(DTOAu,DTOAv)关联模式的IS(u,v),根据各IS(u,v)值是否超过预设关联质量门限,就可以将关联模式区分开,关联质量高的关联模式被归类到一起,然后从该关联模式集合中再用频繁项扩展方法[3]选择最合适的DTOAj频繁项进行重频模式扩展,并得到单次迭代结果为(DTOA1,…,DTOAu,DTOAj)。
3.3 改进的状态失配脉冲片段处理方法
在重频模式扩展的同时,与重频模式匹配的脉冲片段序号矩阵E也同步扩展,它的每一行对应一个脉冲片段[3]。在重频模式扩展时,当重建的重频模式达到一个完整周期时,部分脉冲片段的尾脉冲与其他片段的首脉冲会重合或者相差重频模式骨架周期的整数倍,这一规律构成了重频模式终止判决准则一。但要想利用这一准则实现扩展终止,就需要保证参与终止判决的脉冲片段的状态顺序保持一致,即同时对应(PRI1,PRI2,PRI3)或(PRI2,PRI3,PRI1)或(PRI3,PRI1,PRI2)。但状态失序的脉冲片段即状态失配脉冲片段常出现在序号矩阵E中,对终止判决准则一的使用产生干扰,不利于重频模式的重建过程终止。图5展示了脉冲片段状态失配的情况,其中各矩形含义与图2相同。
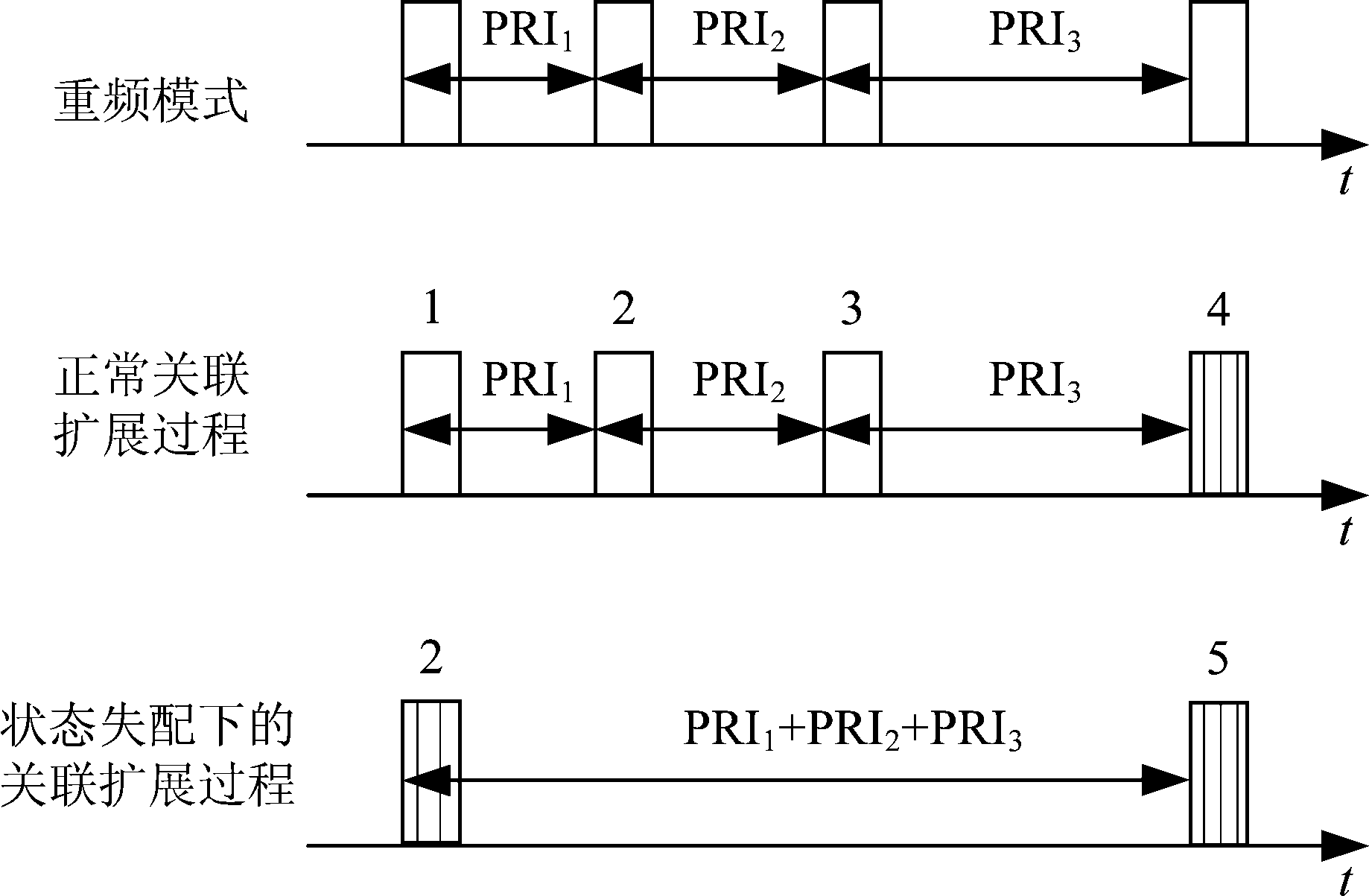
图5 脉冲片段状态失配示意图
Fig.5 Schematic diagram of pulse segments with mismatched states
文献[3]针对脉冲片段状态失配情况,提出了一个剔除状态失配脉冲片段的方法,可以很好地剔除掉序号矩阵中的状态失配片段,保证重频模式的准确重建。但该方法在算法实现时需要多次读取遍历序号矩阵E,假设序号矩阵的行数为n行,则在重频模式的一次扩展迭代中,需要读取序号矩阵![]() 次,并且随着重频模式的不断扩展,序号矩阵也在不断扩展,使得读取序号矩阵的次数呈二次方增长,计算复杂度大幅提升,尤其在交错脉冲列中脉冲数量较多时十分明显。对此本文提出一个基于置信度的脉冲片段筛选策略,策略设计原则是选尽可能少的片段做尽可能有效的判决。
次,并且随着重频模式的不断扩展,序号矩阵也在不断扩展,使得读取序号矩阵的次数呈二次方增长,计算复杂度大幅提升,尤其在交错脉冲列中脉冲数量较多时十分明显。对此本文提出一个基于置信度的脉冲片段筛选策略,策略设计原则是选尽可能少的片段做尽可能有效的判决。
序号矩阵E中首尾脉冲序号同时非0的片段序号(E的行数)集合记作T,本文置信度定义为脉冲片段中与重建中的重频模式之间匹配的脉冲数量,符号为c(比如图5中第三行脉冲片段的置信度为2),集合Pc表示为矩阵E中置信度大于等于c的片段序号集合。要想做有效的判决,则需要选取至少两个脉冲片段,因此,得到一个不等式:
|T∩Pc|≥2
(6)
其中|·| 表示集合中元素的个数,此不等式关于c的解集是一个集合{ck}k=1,…,K,K表示集合中解的数量,通过选取集合{ck}k=1,…,K中最大值即可确定参与重频模式扩展过程终止判决的脉冲片段,因此c的最优解为:
c=max{ck}k=1,…,K
(7)
由式(6)和(7),可以看到基于置信度的脉冲片段筛选方法在一次扩展迭代中,只需读取序号矩阵(c+1)次,相较于剔除方法,计算复杂度得到很大地简化,足够支持辐射源较多、脉冲数量偏多的脉冲列的重频模式解析。至于这一策略的依据是由于非相邻脉冲重复间隔频繁项在扩展时也会匹配到序号矩阵E中,使得部分脉冲片段中存在着大量漏脉冲,状态失配往往就出现在这些存在大量漏脉冲的置信度低的脉冲片段中,因此,通过策略选取合适置信度的脉冲片段可以保证重频模式重建过程的有效终止。
3.4 IS终止判决准则
当交错脉冲列中辐射源数量先验未知时,影响交错脉冲列中重频模式自动提取性能的另一问题是何时终止模式解析过程以及如何终止。按照串行提取的思想,如果不设置新的终止条件,重频模式解析的过程将一直进行下去,大量错误重频模式被提取,或者某一种重频模式被重复提取。针对这一问题,本文将上文计算得到的IS度量作为整个脉冲列终止解析的判决对象。IS度量依关联模式的关联质量高低,将DTOA频繁项完成分类关联,关联质量高的DTOA频繁项被关联到一起,并组合成一个辐射源的重频模式,随着重频模式不断地被重建,DTOA频繁项集中的关联质量高的DTOA关联模式越来越少,直到DTOA频繁项集中将不再有关联质量符合判决标准的关联模式存在,即所有辐射源的重频模式被完整重建。同时IS度量避免了脉冲列长度变化对终止条件造成不统一的影响,因此可设置重频模式串行提取的终止条件为:
∃u,∀v,IS(u,v)<ε
(8)
其中常量ε为人为设置的关联质量门限,它与真实PRI在脉冲列中出现的频次与总脉冲数的最低比例有关,关于u和v的取值上面已经讨论过,这里不再叙述。终止条件含义可以理解为对于重建中的重频模式(DTOA1,…,DTOAu)的DTOAu频繁项,如果对任意的待关联DTOAv频繁项,它们之间的IS(u,v)都小于门限ε,则说明没有DTOA关联模式的关联质量符合判决条件,没有频繁项可以支持后续扩展。因此,终止解析过程。
4 性能仿真实验
从交错脉冲列中提取重频模式,不仅要考虑漏脉冲、干扰脉冲对仿真性能的影响,而且还要考虑脉冲列中辐射源数量和重频模式阶数的影响。本部分设置了四组对照实验。
仿真过程中,假设脉冲列到达时间测量误差标准差为0.2 μs,频繁项的预设门限为10,DTOA频繁项的取值范围设为200 μs到3000 μs,存在轮换对称性的重频模式被认为是同一重频模式(比如(PRI1,PRI2,PRI3)、(PRI2,PRI3,PRI1)和(PRI3,PRI1,PRI2)),只有将脉冲列中所有辐射源的重频模式正确重建才认为解析正确,否则认为解析失败。每组仿真实验中设置三个数量不同的脉冲列做对比,侦察脉冲列中脉冲数量N分别设为2000,3000和4000。式(7)中串行提取终止条件的关联质量门限设为ε=0.1。
4.1 重频模式解析能力受漏脉冲率的影响
本仿真实验中设定不包含干扰脉冲,各脉冲随机独立丢失,漏脉冲率分别设为0、20%、40%和60%,侦察脉冲列中辐射源数量设为3,各辐射源采用参差重频,重频模式阶数统一设为5,重频参数在[300 μs,700 μs]范围内随机取值,来自每个辐射源的脉冲数相同,通过100次仿真统计得到重频模式解析正确率如图6所示。
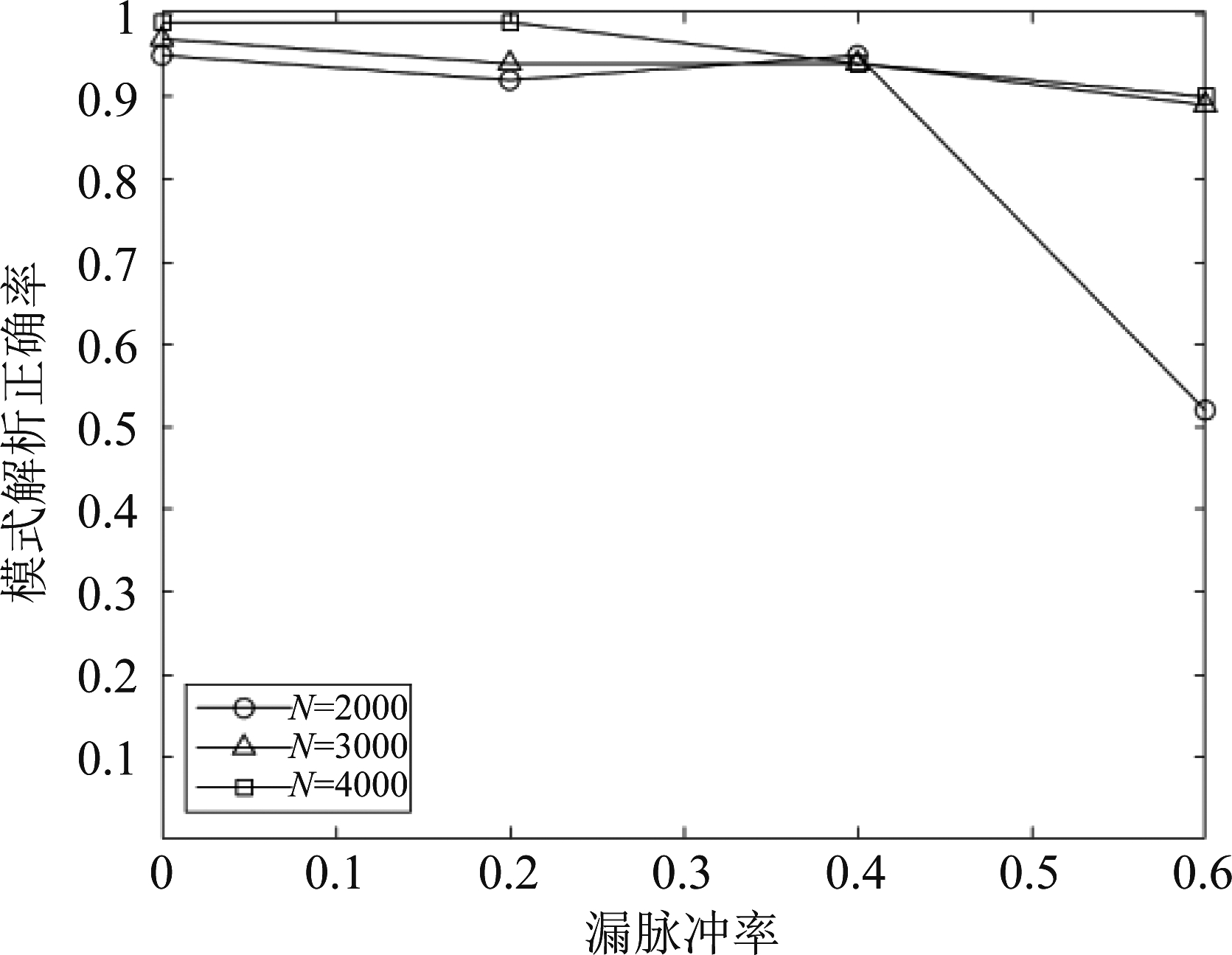
图6 重频模式解析能力受漏脉冲率的影响情况
Fig.6 Influence of pulse missing rate on PRI pattern reconstruction performance
从图中可以看出,本文给出的方法有着较强的漏脉冲适应力,当漏脉冲率不大于40%时,解析正确率在90%以上,即便漏脉冲率达到60%,则只需增加截获脉冲列中的脉冲数量至3000就可以使解析正确率维持在90%以上。
4.2 重频模式解析能力受干扰脉冲率的影响
在上一组实验的基础上,设定漏脉冲率为40%,干扰脉冲率由0逐渐增大至1,干扰脉冲到达时间随机设置。脉冲列中辐射源数量、各辐射源的重频类型、重频模式阶数以及重频参数设置与实验4.1相同,来自每个辐射源的脉冲数相同,通过100次仿真统计得到重频模式解析正确率如图7所示。
从图中可以看到随着干扰脉冲率的增加,重频模式解析正确率呈缓慢下降,当干扰脉冲率大于60%时,解析正确率大多降至90%以下,主要是因为在干扰脉冲率增加的时候,真实PRI的出现频次相较于虚假PRI将变得越来越不显著,解析过程很容易被干扰脉冲影响,此时增加侦察脉冲数量将有助于增大显著性,提高解析正确率。
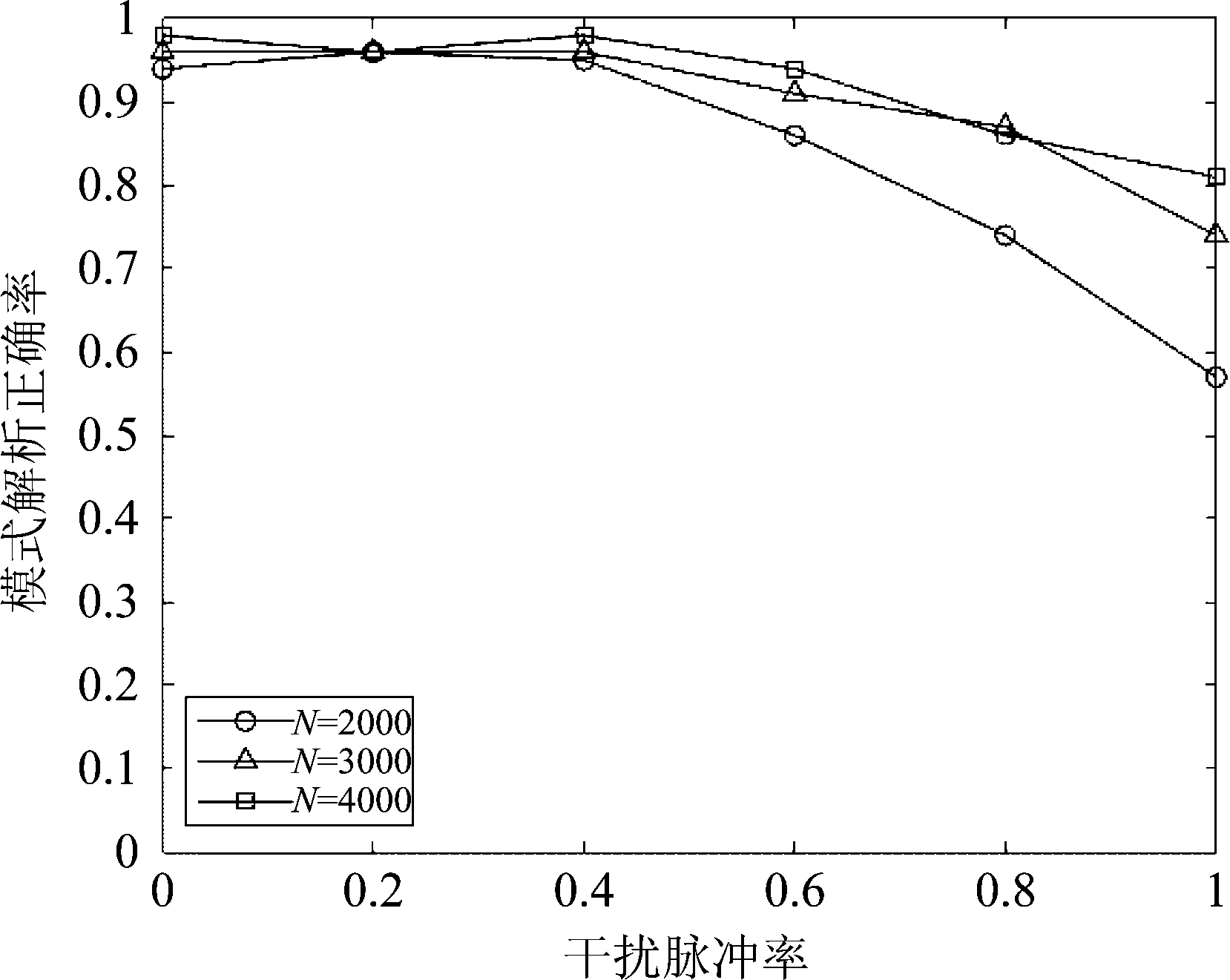
图7 重频模式解析能力受干扰脉冲率的影响情况
Fig.7 Influence of interferential pulse rate on PRI pattern reconstruction performance
4.3 重频模式解析能力受重频模式阶数的影响
在上一组实验的基础上,本仿真实验设定漏脉冲率为40%,干扰脉冲率为40%,侦察脉冲列中辐射源数量为3,各辐射源的参差重频阶数相同,且由3增加到7,重频参数在[300 μs,700 μs]范围内随机取值,来自每个辐射源的侦察脉冲数相同,通过100次仿真统计得到重频模式解析正确率如图8所示。

图8 重频模式解析能力受参差重频阶数的影响情况
Fig.8 Influence of stagger PRI order on PRI pattern reconstruction performance
从图中可以看出在重频模式阶数小于等于5时,解析正确率接近100%,之后随着阶数的增加,解析正确率逐渐变差。这是由于在总脉冲数不变,只增加重频模式阶数的条件下,每个PRI的出现频次会减少,进而缩小真实PRI与虚假PRI计数频次间的差距,使虚假PRI更容易被关联提取到。但是,即使是在雷达重频阶数达到7时,通过将侦察脉冲数积累到4000,雷达重频模式解析正确率仍然可以达到85%左右。
4.4 重频模式解析能力受辐射源数量的影响
在上一组实验的基础上,本仿真实验设定漏脉冲率为40%,干扰脉冲率为40%,辐射源数量由2增加到5,各辐射源采用参差重频,重频模式阶数统一设为5,重频参数在[300 μs,700 μs]范围内随机取值,来自每个辐射源的脉冲数相同,通过100次仿真统计得到重频模式解析正确率如图9示意。
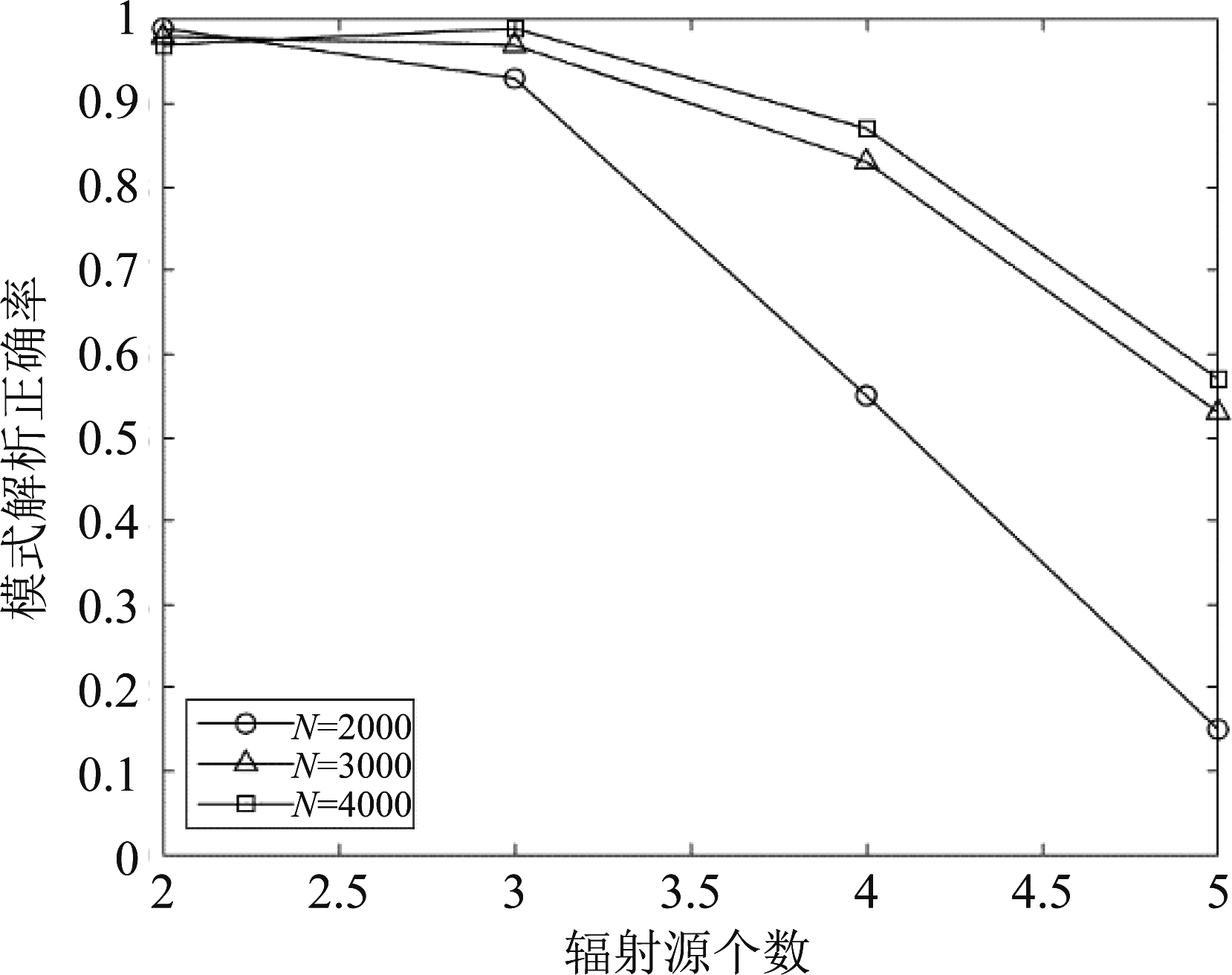
图9 重频模式解析能力受辐射源数量的影响情况
Fig.9 Influence of emitter number on PRI pattern reconstruction performance
从上图可以看出重频模式解析正确率随着辐射源个数的增加而降低,在脉冲列中脉冲数量较少时尤为明显。这是由于不同辐射源脉冲间互为干扰,增加辐射源数量,等同于在呈比例的增加干扰脉冲,并且每个真实PRI的出现频次也相应下降,双重的原因导致辐射源数量对解析性能影响较大。即便如此,当交错脉冲列中雷达辐射源数量不超过4时,通过将侦察脉冲数量积累至3000以上,仍然可以得到80%以上的重频模式解析正确率,说明增加截获脉冲数量可以显著提高新方法对中等数量辐射源交错场景的适应能力。
综合上述四组仿真实验结果可以看出,侦察脉冲列的脉冲数量是制约解析性能的关键因素,延长侦察时间、积累更多脉冲是保证新方法性能的有效手段。
5 结论
本文针对常规体制雷达侦察交错脉冲列的重频模式解析问题,遵循频繁DTOA关联扩展的基本思路,通过引入关联模式客观兴趣度IS度量,筛选兴趣度高的频繁项,实现了雷达交错脉冲列重频模式的自动、准确解析。仿真实验结果表明,该算法可以较好满足较大的漏脉冲率、干扰脉冲率等条件下的雷达重频模式解析需要,对中等重频模式阶数和辐射源数量具有较强适应性,增加截获脉冲数量可以明显提高算法性能。
[1] WILEY R G. ELINT: The interception and analysis of radar signals[M]. Boston or London:Artech House, 2006:214-215.
[2] 周一宇,安玮,郭福成,等. 电子对抗原理与技术[M]. 北京:电子工业出版社, 2014:101-103.
ZHOU Yiyu, AN Wei, GUO Fucheng, et al. Principles and Technologies of Electronic Warfare System[M]. Beijing:Publishing House of Electronics Industry, 2014:101-103.(in Chinese)
[3] LIU Zhangmeng, KANG Shiqian, CHAI Xianming. Automatic Pulse Repetition Pattern Reconstruction of Conventional Radars[J]. IET Radar Sonar and Navigation,2021,15(5):500-509.
[4] GENCOL K, AT N, KARA A. A wavelet-based feature set for recognizing pulse repetition interval modulation patterns[J]. Turkish Journal of Electrical Engineering and Computer Science, 2016, 2016(24): 3078-3090.
[5] NGUYEN HPK, NGUYEN HQ. Classification of Pulse Repetition Interval Modulations Using Neural Networks[C]∥2018 IEEE Symposium Series on Computational Intelligence(IEEE SSCI), Bengaluru,INDIA,IEEE,2018:1739-1743.
[6] LI Xueqiong, LIU Zhangmeng, HUANG Zhitao. Attention-based radar PRI modulation recogntion with recurrent neural networks[J]. IEEE Access, 2020, 8: 57426-57436.
[7] NISHIGUCHI K, KOBAYASHI M. Improved algorithm for estimating pulse repetition intervals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2):407- 421.
[8] 易波, 刘培国, 薛国义. 一种基于顺序差值直方图算法的改进雷达信号分选方法[J]. 舰船电子对抗,2012,35(1):6-10.
YI Bo, LIU Peiguo, XUE Guoyi. An improved method for radar signal sorting based on SDIF histogram algorithm[J]. Shipboard Electronic Countermeasure, 2012, 35(1) :6-10.(in Chinese)
[9] 孟祥豪, 罗景青, 马贤同. 新体制雷达信号PRI样本子图周期搜索提取方法[J]. 信号处理, 2015, 31(4): 399- 406.
MENG Xianghao, LUO Jingqing, MA Xiantong. A new system radar signal extraction method by searching PRI pulse sequence subpattern cycle[J]. Journal of Signal Processing, 2015, 31(4): 399- 406.(in Chinese)
[10] LIU Zhangmeng. Online pulse deinterleaving with finite automata[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 1139-1147.
[11] TAN Pangning, KUMAR Vipin. Interestingness measures for association patterns: A perspective[R]. Minnesota:Department of Computer Science, University of Minnesota, 2000.
[12] GENG Liqiang, HAMILTON H J. Interestingness measures for data mining: A survey[J]. ACM Computing Surveys, 2006, 38(3).
[13] TAN Pang-Ning, STEINBACH Michael, KUMAR Vipin著. 数据挖掘导论[M]. 范明, 范宏建,等,译. 北京:人民邮电出版社, 2011:228-231.
TAN Pang-Ning, STEINBACH Michael, KUMAR Vipin. Introduction to data mining[M]. FAN Ming, FAN Hongjian, et al. translation. Beijing:The People's Posts and Telecommunications Press, 2011:228-231.(in Chinese)

