1 引言
昆虫雷达是研究昆虫迁飞的有力工具。在昆虫雷达中,垂直监测昆虫雷达具有参数测量丰富,自动化程度高等特点,可以实现目标种类辨识,目前应用最为广泛[1-2]。振翅频率是昆虫迁飞的重要特征,也是实现目标种类辨识的关键参数之一。昆虫雷达对于该参数测量主要基于幅度谱和载波相位差分谱。基于幅度谱的方法主要应用于传统昆虫垂直雷达。该雷达采用圆锥扫描、旋转极化的工作模式,利用昆虫穿越雷达波束时的振翅运动对回波幅度的调制,通过傅里叶分析,实现振翅频率提取。但此方法当雷达工作于圆锥扫描模式时,无法21 Hz以下的振翅频率;2004年,Drake提出了一种在静止波束下的振翅参数提取方法,将振翅频率探测下限降低到14 Hz,但牺牲了其他参数的测量性能[3]。近年来,采用同时全极化、相参测量体制的昆虫雷达陆续出现[4]。2017年,王锐提出了基于载波相位差分的振翅频率提取方法,实测振翅频率测量精度可达1 Hz以内,但该方法成功率易受噪声影响。利用昆虫雷达对目标进行观测时,回波信号中往往会存在大量背景噪声,且昆虫体积小,翅膀振动的反射系数较小,回波信号能量弱,这些都对回波信号信噪比产生影响,降低昆虫振翅频率的提取精度。因此,研究低信噪比下昆虫振翅频率的提取方法具有重要意义。
微弱信号的信噪比提升主要分为时域平均与频域滤波两种。时域平均是一种积累平均抗干扰过程,该算法原理简单,但在实际应用中抗噪性能不佳[5]。频域滤波算法是基于有用信号与噪声频率分布不同,采用滤波形式,滤除带外噪声,实现信噪比提升[6-7]。但该算法不能区分有用信号的高频部分与由噪声引起的高频干扰,因此难以取得很好的效果。小波分析由于其良好的时频特性, 在信号处理中应用广泛[8]。小波变换对信号进行多尺度分析,能够同时在时域和频域表征信号局部特征,小波基选择灵活且计算速度快[9-10],因此在非平稳噪声环境中提升微弱信号信噪比方面得到广泛的应用[11-17]。
针对低信噪比下昆虫振翅频率提取精度低的问题,本文拟提出一种基于小波变换的低信噪比下昆虫振翅频率提取方法。首先建立昆虫精确振翅回波模型,其次采用小波变换对回波信号进行多尺度分析,通过研究各尺度下回波信号与噪声信号小波系数之间的关系,对昆虫振翅信号进行针对性降噪处理。通过仿真分析与实测数据处理,证明该算法可提高低信噪比环境下昆虫振翅频率的提取精度。
2 昆虫振翅信号分析
建立昆虫振翅的雷达精确信号模型,是研究昆虫振翅频率提取的前提。以连续波雷达为例,昆虫振翅回波信号为:
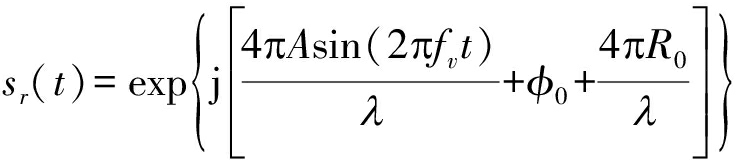
(1)
其中φ0为初始相位,R0为探测距离, fv为昆虫的振翅频率。
因此,昆虫的多普勒频率表达式为:
(2)
可以看出,昆虫引起的瞬时多普勒频率呈频率为fv的正弦变化,本文采用短时傅里叶变换的方法来分析昆虫振翅回波的微多普勒效应,昆虫振翅频率与时频分布的周期是一致的。昆虫振翅相对强度弱,回波信号信噪比低,从而导致振翅频率提取精度不高,因此改善信号信噪比是提高昆虫振翅频率提取准确性的关键因素。
3 昆虫振翅信号小波分析
3.1 小波变换
对于任意信号f(t)∈L2(R),连续小波变换WT(a,b)为f(t)与小波函数ψa,b(t)的内积:
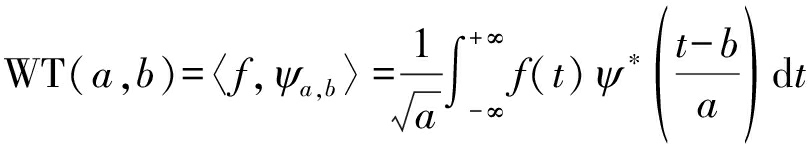
(3)
其中a是尺度因子,b是平移因子,ψ(t)是母小波,*表示复数共轭。
若将式(3)中的参数a、b离散化,取离散值:
(4)
则可得到离散小波变换,离散化后的小波变换系数求解公式为:
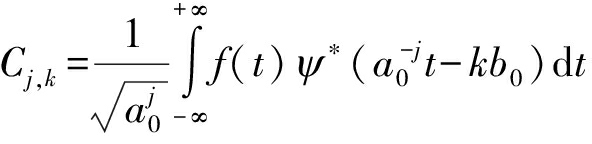
(5)
其逆变换为:
(6)
其中![]() 是一个与信号无关的常数。
是一个与信号无关的常数。
3.2 昆虫回波信号去噪与振翅频率提取
含噪声的昆虫振翅回波信号模型可以表示为:
f(t)=s(t)+n(t)
(7)
其中s(t)为昆虫振翅回波信号,n(t)为高斯白噪声。小波变换的多尺度分析特性将信号在不同尺度下进行多尺度分解,并将不同频率组成的混合信号分解成不同频段的子信号。信号小波分解如图1所示,A为信号f(t)低频系数,D为信号f(t)高频系数。
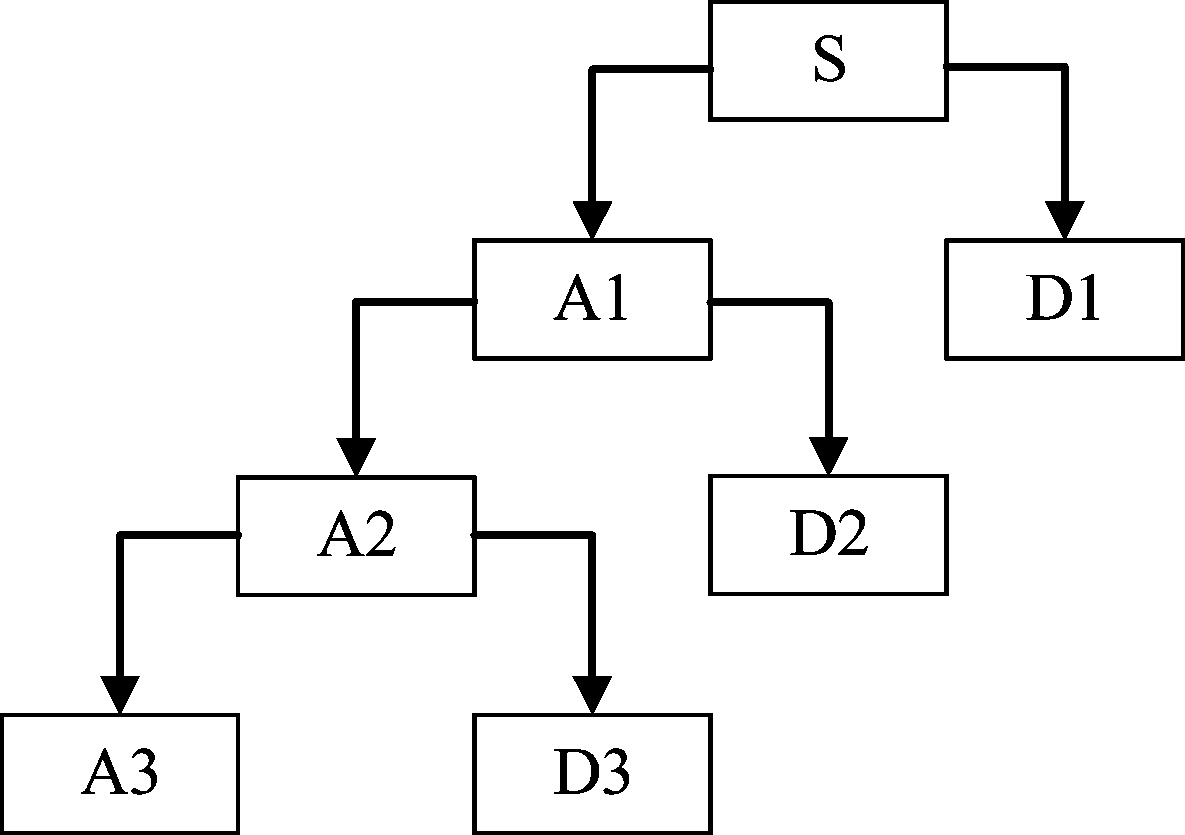
图1 小波分解示意图
Fig.1 Schematic diagram of wavelet decomposition
基于昆虫振翅信号和高斯白噪声不同的小波变换特性,在信号去噪时,将大幅值小波系数判断为昆虫振翅信号信息,小幅值小波系数判断为噪声。因此,可以根据一定的准则,设定一个阈值λ,幅值高于该阈值的小波系数保留或按照某一固定量收缩到零,幅值低于该阈值的小波系数被置为零;最后将处理的小波系数进行小波重构,恢复得到去噪信号。
综上所述,低信噪比下昆虫振翅频率提取算法的流程如图2所示。
(1) 昆虫振翅含噪信号的小波分解。选择合适的小波函数,确定小波分解的层次n,然后对含噪信号f(t)进行n层小波分解,得到个尺度小波分解系数。
(2) 小波分解后的各层系数阈值处理。对第1到第n层的小波系数,选择一个合适的阈值,对每一层的小波系数进行阈值量化处理。
(3) 昆虫振翅信号的小波重构。对阈值量化处理后的各层小波系数进行信号的小波重构,得到去噪信号。
(4) 昆虫振翅信号瞬时多普勒分析。对去噪信号采用短时傅里叶变换进行时频分析,分析其瞬时多普勒频率,进而提取昆虫振翅频率。
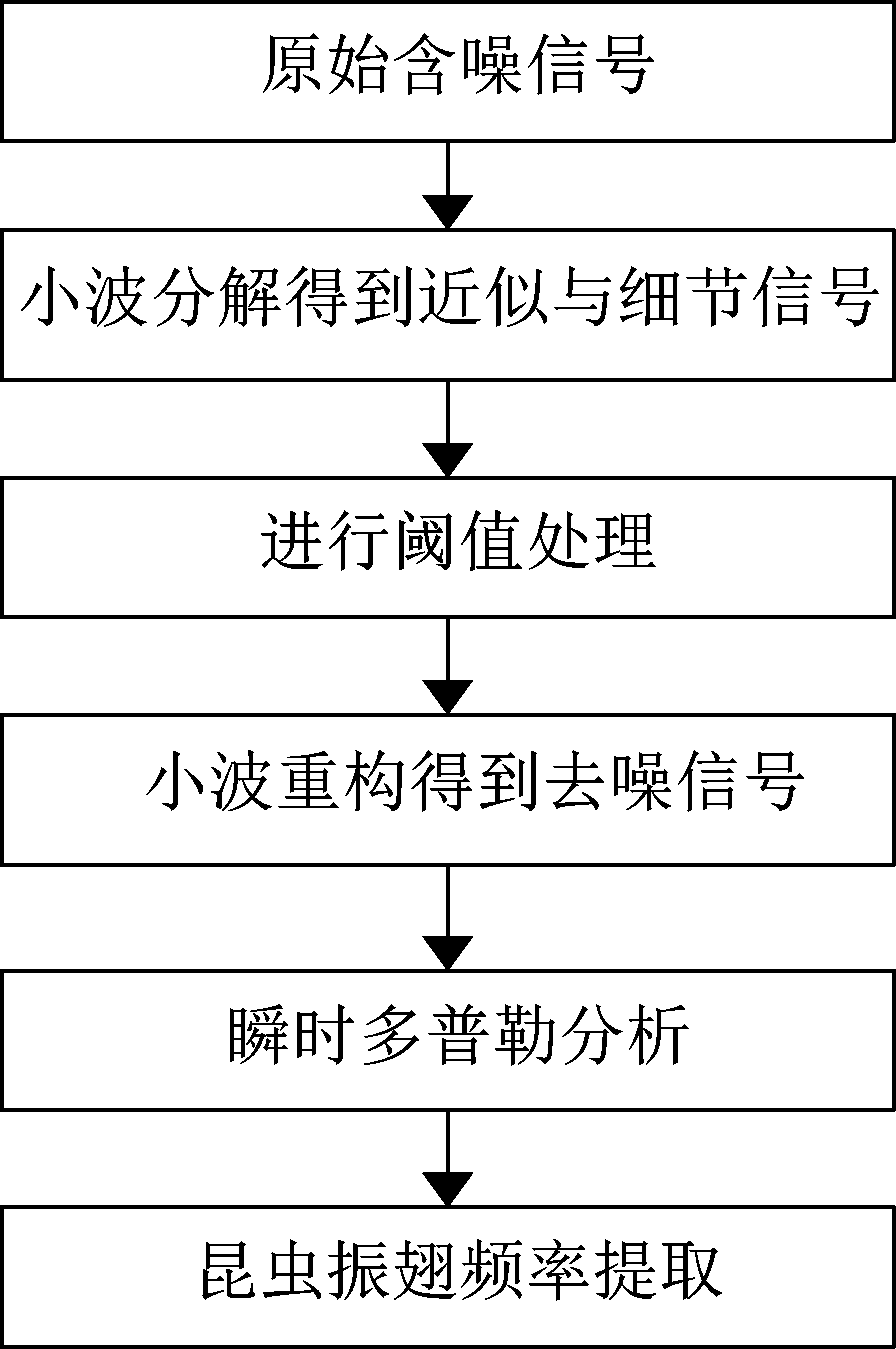
图2 低信噪比下昆虫振翅频率提取算法流程
Fig.2 The algorithm flow of insect wingbeating frequency at low SNR
3.3 参数选取
(1) 选取小波函数。不同的小波基函数的消噪结果不同。symN小波基具有紧支撑、正交性、双正交性、正则性及对称性等优点,因此,本文选用sym10小波基函数。
(2) 分解层数确定。昆虫振翅信号和噪声在不同分解的小波变换下呈现的特性不同,随着分解层数的增大,昆虫振翅回波和噪声所对应的小波变换系数分别是增大和减小,越有利于两者的分离。但若分解层数过多,昆虫振翅信号就会严重损失。不同分解层数下,去噪后的昆虫振翅信号信噪比如图3所示,可以看出,信号作2层分解效果最为理想。
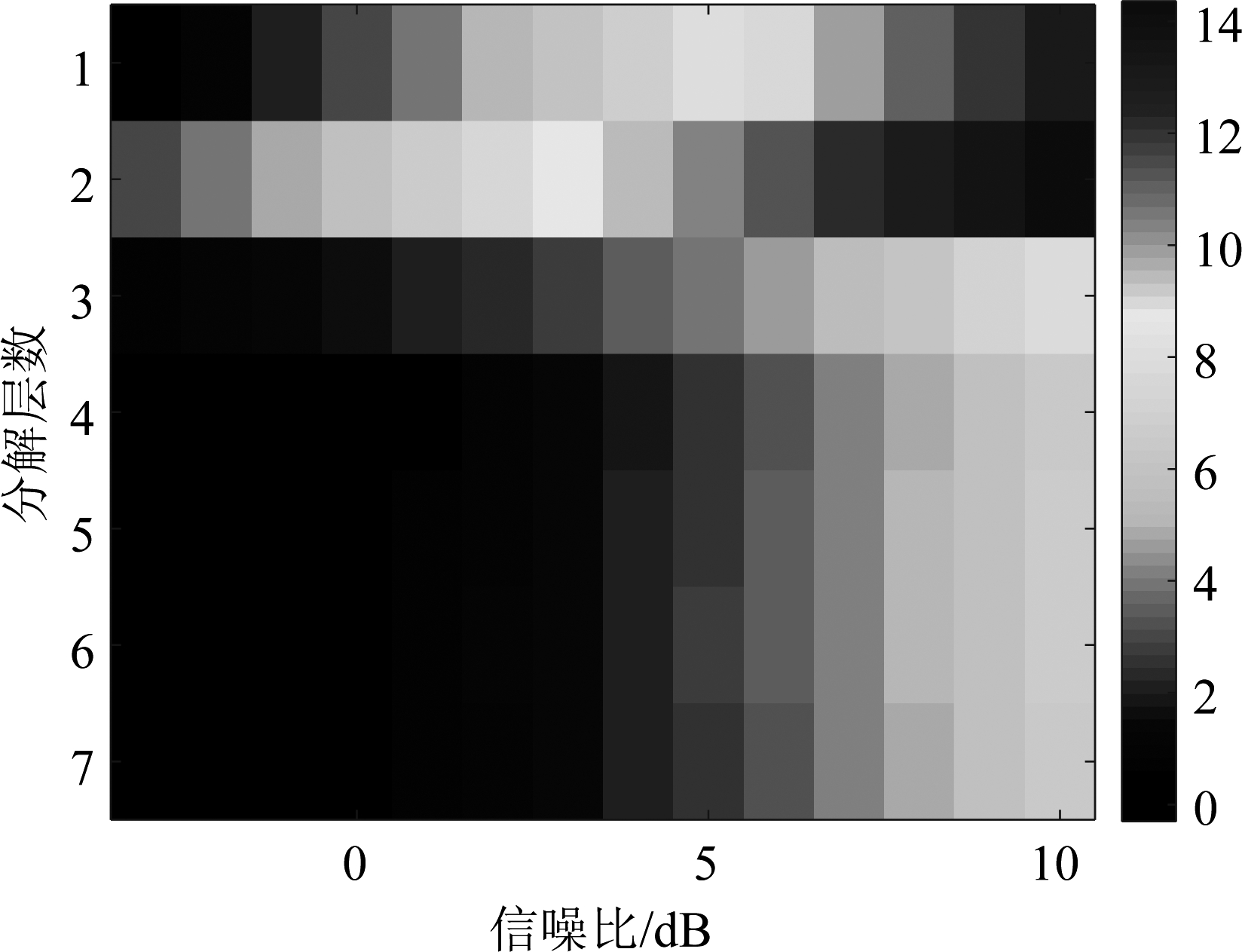
图3 不同分解层数信号去噪后信噪比
Fig.3 SNR of signals after denoising with different decomposition levels
(3) 阈值选取。在进行去噪时,阈值的选择对降噪效果起主导作用。阈值过高,会将信号当作噪声滤除,丢失部分信号信息;阈值过低,会将小波系数较大的噪声保留,不利于信号分析。本文采用启发式阈值原则,它是无偏似然估计和固定阈值估计原则的综合。无偏似然估计原理是一种基于 Stein 无偏似然估计的自适应阈值选择。对于给定的阈值λ,得到它的似然估计,再将似然λ最小化,得到阈值。信噪比很低时,采用固定阈值估计原则,固定阈值λ的计算公式为:
(8)
其中N为信号长度,σ2为噪声方差。
(4) 阈值处理。本文采用软阈值的处理方法对小波系数进行处理:将小于阈值的小波系数设置为零,将大于阈值的小波系数向零收缩。其表达式为:
(9)
4 实验结果分析
4.1 仿真分析
为验证小波分析在提高昆虫振翅频率提取精度中的有效性,首先基于式(1),构造理想昆虫振翅回波如图4(a)所示,信号参数如表1;进而对信号中加入高斯白噪声,得到-3 dB信噪比下的回波如图4(b)所示;最终通过基于sym10小波函数的小波变换进行信号去噪处理,得到结果如图4(c)所示,信号信噪比从-3 dB提升至3 dB,证明了算法的有效性。
表1 仿真参数
Tab.1 Simulation parameters

参数参数值载波频率/GHz16.2采样率/Hz500昆虫振翅幅度/mm0.45昆虫振翅频率/Hz30
图5为信噪比为-3 dB条件下昆虫振翅频率提取结果。从图5中可以看出,回波信号信噪比较低时,时频分析图中信号时频谱强度较小,提取昆虫振翅频率为22.03 Hz,与仿真设置振翅频率30 Hz相差较大。图6给出了小波变换去噪后昆虫振翅频率提取结果,可以看出,去噪后时频分析信号时频谱强度增强,能够准确提取30 Hz的昆虫振翅频率。对比图5和图6仿真结果可知,信号经过小波去噪,然后进行时频分析和振翅频率提取,提取精度得到明显提高。
为了进一步验证本文算法的有效性,通过1000次蒙特卡洛仿真,得到-3 dB~10 dB输入信噪比下的昆虫回波信号在小波去噪前后振翅频率提取仿真结果。对比图7(a)和图7(b)可发现,低信噪比下,原始回波信号直接提取昆虫振翅频率结果误差较大,小波变换去噪后振翅频率提取精度得到明显提高。
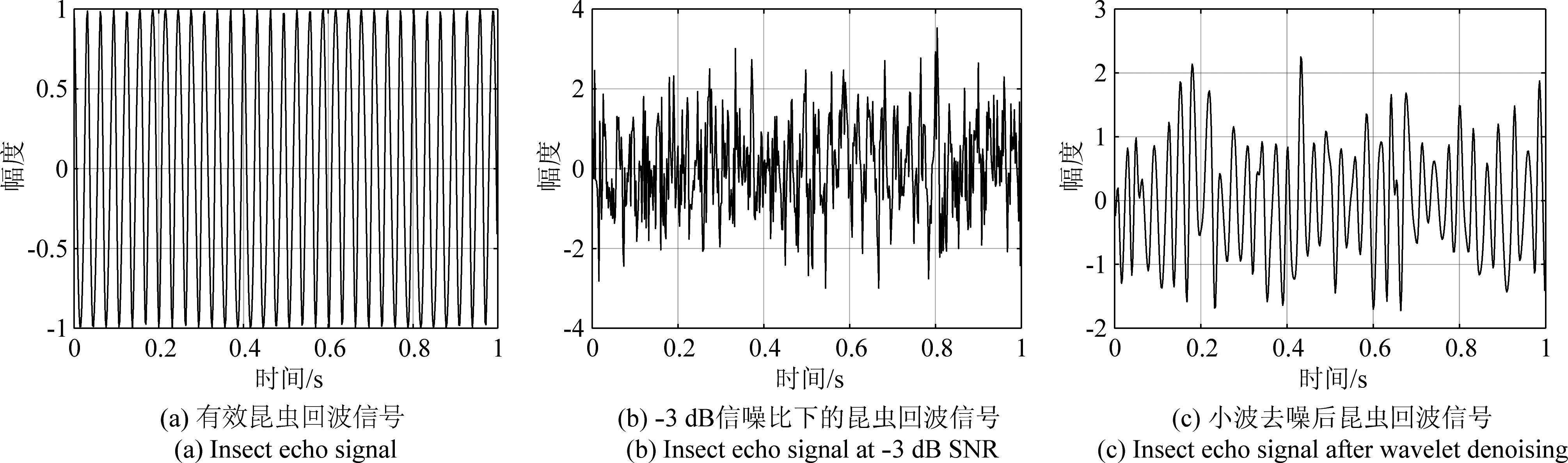
图4 小波变换去噪结果
Fig.4 Denoising results of wavelet transform

图5 -3 dB信噪比下昆虫振翅频率提取
Fig.5 Extraction of insect wingbeating frequency at -3 dB SNR
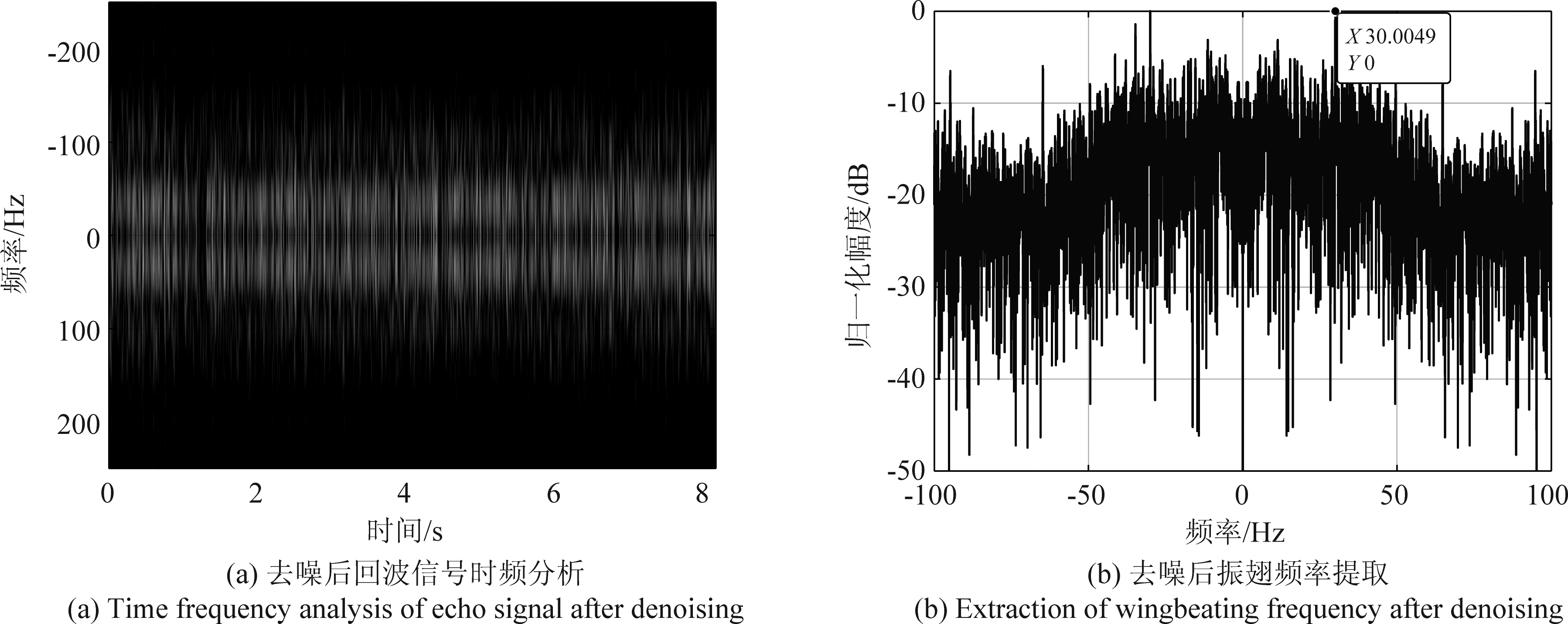
图6 小波去噪后昆虫振翅频率提取
Fig.6 Extraction of insect wingbeating frequency after wavelet denoising
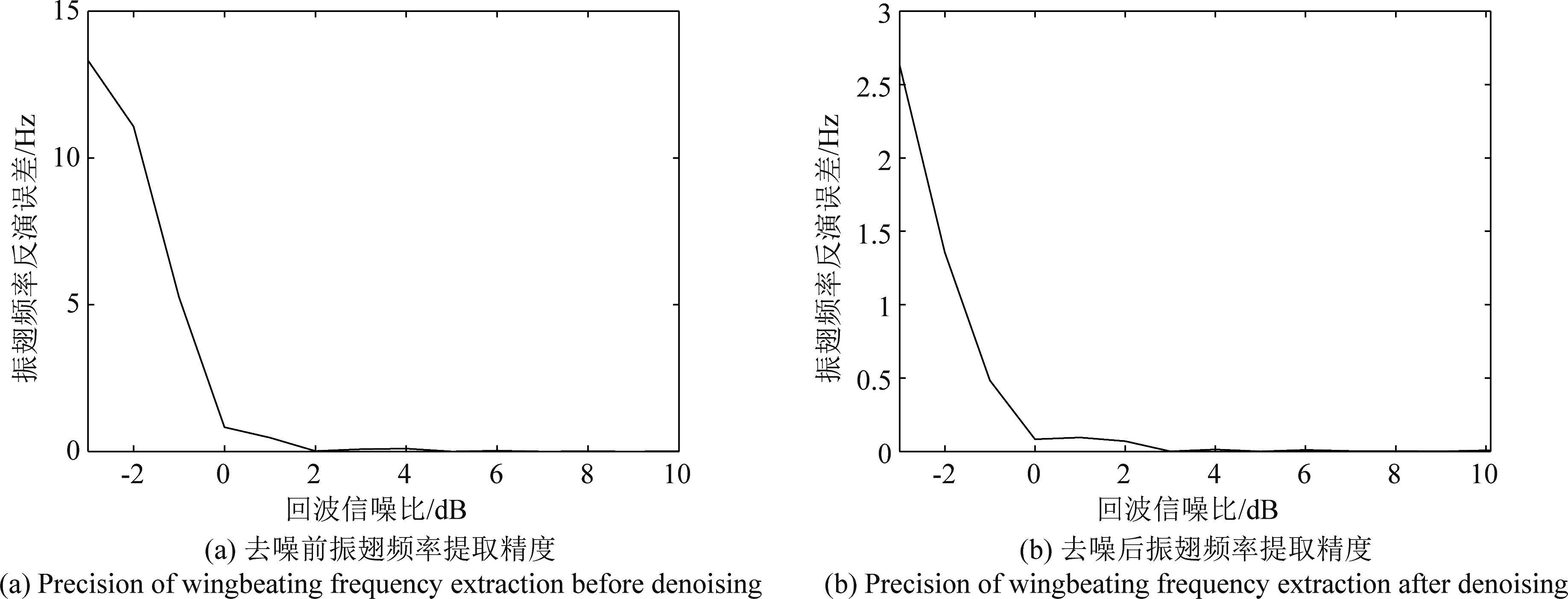
图7 各信噪比下昆虫振翅频率提取精度
Fig.7 Precision of insect wingbeating frequency extraction at different SNR
4.2 实测数据分析
为进一步说明低信噪比下本文算法的有效性,进行了相关验证性实验。由于低信噪比下昆虫振翅信号多普勒存在明显的抖动,通过现有算法无法对振翅参数准确提取,因此本文通过人肉眼分析回波信号时频分布,根据信号周期特性,确定昆虫振翅频率真值。比较去噪前后提取的振翅频率与真值误差,进而得到昆虫振翅频率提取精度改善效果。
图8为昆虫1振翅频率提取结果,根据其时频分布肉眼判断振翅频率真值为24 Hz。从图8(a)时频分析图中可以看出信号信噪比较差,直接对回波信号时频分析,得到振翅频率提取结果为10 Hz,如图8(b)所示;运用小波变换去噪后,从图8(c)可以看出信号时频分析图信噪比得到提高,其振翅频率提取结果为20.71 Hz,如图8(d)所示,与振翅频率真值误差更小。
图9为昆虫2振翅频率提取结果,根据其时频分布肉眼判断其振翅频率真值为24 Hz。去噪前,从时频分析图中可以看出信号信噪比较差,振翅频率提取结果12.14 Hz;运用小波变换去噪后,从时频分析图可以看出信号信噪比提高,振翅频率提取结果为21.86 Hz,与振翅频率真值误差更小。
根据以上两只昆虫处理结果可知, 在低信噪比情况下,直接进行瞬时多普勒分析提取振翅频率与真值相差较大,而小波变换去噪后再分析瞬时多普勒提取振翅频率,得出的结果更接近真值, 因而本文所提算法是可行和有效的。
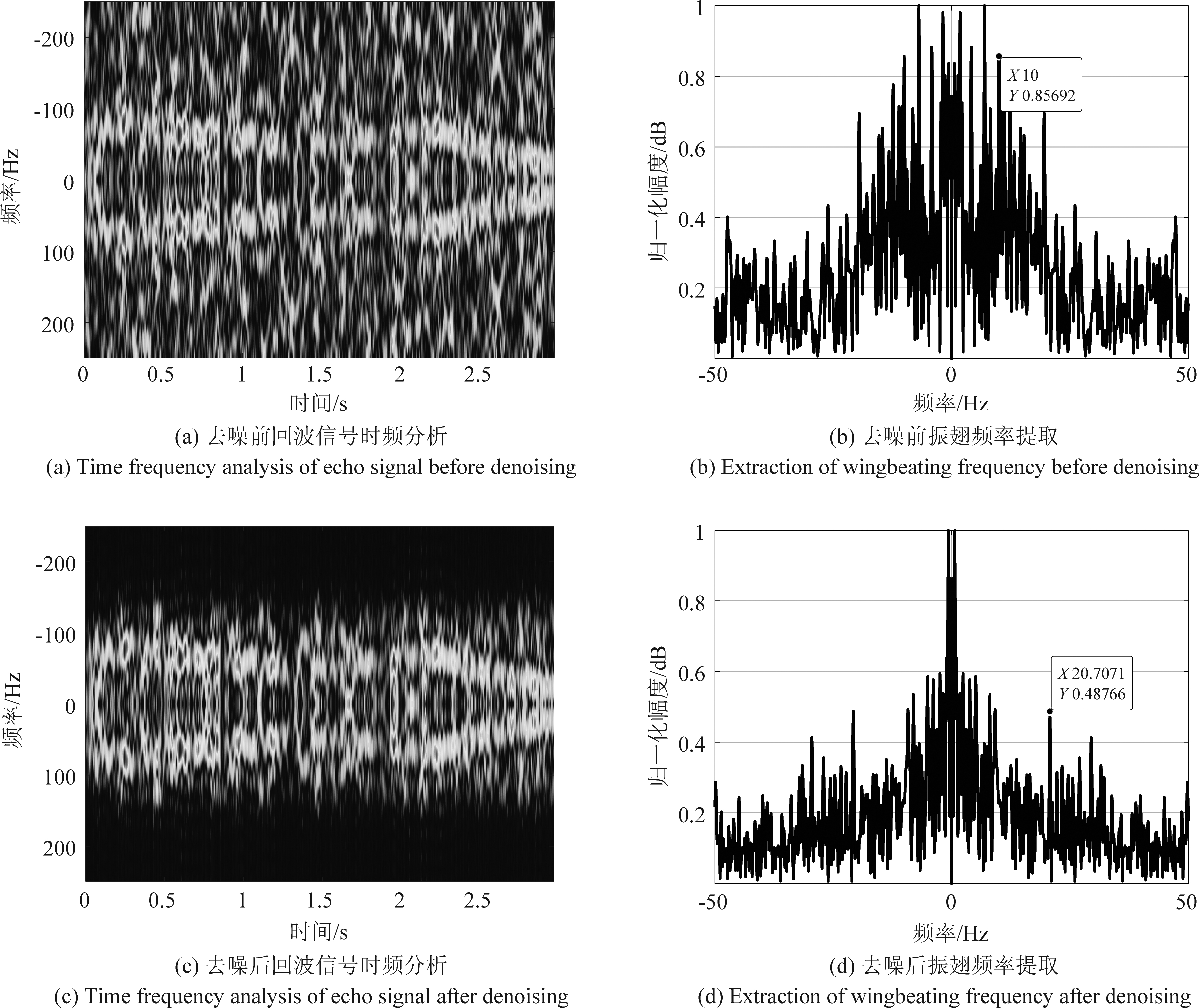
图8 昆虫1振翅频率提取
Fig.8 Extraction of insect 1 wingbeating frequency
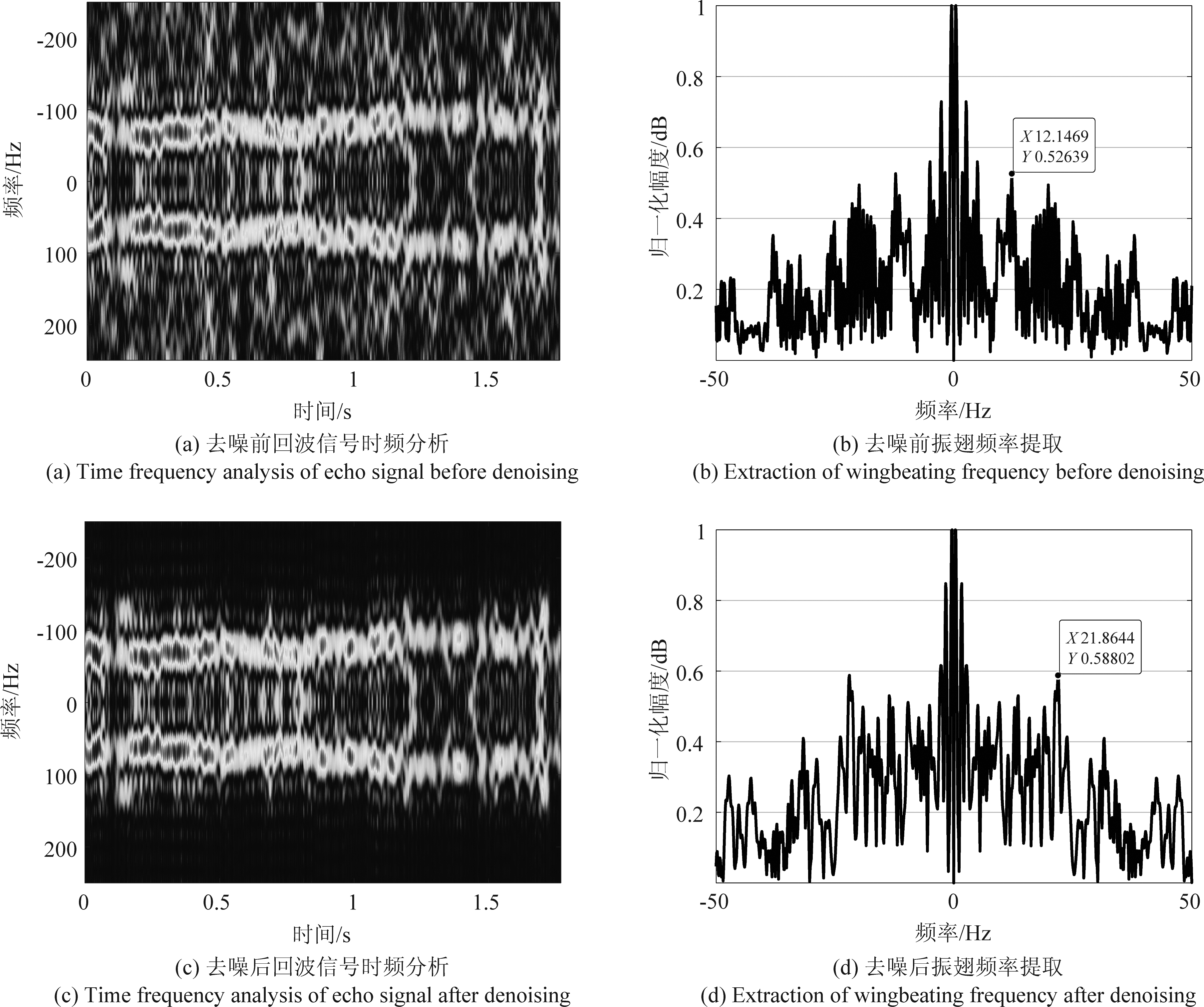
图9 昆虫2振翅频率提取
Fig.9 Extraction of insect 2 wingbeating frequency
5 结论
昆虫振翅频率提取属于微弱信号微动特征提取。本文提出了一种在低信噪比条件下的昆虫振翅频率提取方法。该方法首先对原始回波信号进行小波变换去噪处理,提高信噪比,然后利用时频分析方法提取信号瞬时频率特征,从而提高昆虫振翅频率提取的准确性。基于仿真分析和实测数据处理,成功验证了该算法的有效性。本算法在一定程度上提高了昆虫振翅特征提取的准确性,在低信噪比条件下目标微动特征提取中提供了借鉴。
[1] CHAPMAN J W, SMITH A D, WOIWOD I P, et al. Development of vertical-looking radar technology for monitoring insect migration[J]. Computers and Electronics in Agriculture, 2002, 35(2/3): 95-110.
[2] RAINEY R C. Observation of desert locust swarms by radar[J]. Nature, 1955, 175(4445): 77.
[3] WANG H K, DRAKE V A. Insect monitoring radar: Retrieval of wingbeat information from conical-scan observation data[J]. Computers and Electronics in Agriculture, 2004, 43(3): 209-222.
[4] 胡程, 李卫东, 王锐. 基于全极化的相参雷达迁飞昆虫观测[J]. 信号处理, 2019, 35(6): 951-957.
HU Cheng, LI Weidong, WANG Rui. Fully polarimetric coherent radar for migratory insect observation[J]. Journal of Signal Processing, 2019, 35(6): 951-957.(in Chinese)
[5] 陈韶华, 相敬林. 一种改进的时域平均法检测微弱信号研究[J]. 探测与控制学报, 2003, 25(4): 56-59.
CHEN Shaohua, XIANG Jinglin. A modified time averaging method in weak signal detection[J]. Journal of Detection & Control, 2003, 25(4): 56-59.(in Chinese)
[6] 谢东. 较低信噪比下信号去噪方法研究[D]. 成都: 电子科技大学, 2015.
XIE Dong. Research on the signal denoising under lower signal to noise ratio[D]. Chengdu: University of Electronic Science and Technology of China, 2015.(in Chinese)
[7] 张威, 王旭, 葛琳琳, 等. 一种强噪声背景下的微弱信号检测的新方法[J]. 计量学报, 2007(1): 70-73.
ZHANG Wei, WANG Xu, GE Linlin, et al. An algorithm for weak signal detection in strong noise environment[J]. Acta Metrologica Sinica, 2007(1): 70-73.(in Chinese)
[8] 杨秀芳, 张伟, 杨宇祥. 基于提升小波变换的雷达生命信号去噪技术[J]. 光学学报, 2014, 34(3): 300-305.
YANG Xiufang, ZHANG Wei, YANG Yuxiang. Denoising technology of radar life signal based on lifting wavelet transform[J]. Acta Optica Sinica, 2014, 34(3): 300-305.(in Chinese)
[9] MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE Transactions on Information Theory, 1992, 38(2): 617- 643.
[10] Wickerhauser M V. Adapted wavelet analysis from theory to software [M]. A.K. Peters, 2010.
[11] 洪民江. 基于小波变换的语音信号去噪算法研究[D]. 南京: 南京邮电大学, 2018.
HONG Minjiang. Speech singnal denoising research based on wavelet transformation[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2018.(in Chinese)
[12] 李晶, 张方舟. 小波变换在核磁共振测井信号去噪中的应用研究[J]. 计算机与数字工程, 2019, 47(11): 2906-2909.
LI Jing, ZHANG Fangzhou. Application research of wavelet transform in denoising of NMR logging signals[J]. Computer & Digital Engineering, 2019, 47(11): 2906-2909.(in Chinese)
[13] 徐妍琰, 孟建军, 张宇彤, 等. 基于小波分析的脉搏采集信号处理研究[J]. 工业控制计算机, 2020, 33(12): 63- 64,67.
XU Yanyan, MENG Jianjun, ZHANG Yutong, et al. Pulse acquisition signal processing method[J]. Industrial Control Computer, 2020, 33(12): 63- 64,67.(in Chinese)
[14] 胡瑞卿, 王彦春. 基于自适应Morlet小波的低信噪比微震信号初至拾取方法研究[J]. 地球物理学进展, 2019, 34(2): 561-567.
HU Ruiqing, WANG Yanchun. First arrival picking method in low SNR micro-seismic signal based on self-adaptive Morlet wavelet[J]. Progress in Geophysics, 2019, 34(2): 561-567.(in Chinese)
[15] 王超, 沈斐敏. 小波变换在探地雷达弱信号去噪中的研究[J]. 物探与化探, 2015, 39(2): 421- 424.
WANG Chao, SHEN Feimin. Study of wavelet transform in ground penetration radar weak signal denoising[J]. Geophysical and Geochemical Exploration, 2015, 39(2): 421- 424.(in Chinese)
[16] 周克良, 刘亚亚. 新阈值小波变换的心音去噪[J]. 计算机工程与设计, 2020, 41(9): 2476-2481.
ZHOU Keliang, LIU Yaya. Heart sound denoising of new threshold wavelet transform[J]. Computer Engineering and Design, 2020, 41(9): 2476-2481.(in Chinese)
[17] 胡俊文, 周国荣. 小波分析在振动信号去噪中的应用[J]. 机械工程与自动化, 2010(1): 128-130.
HU Junwen, ZHOU Guorong. Application of wavelet analysis in vibration signal denoising[J]. Mechanical Engineering & Automation, 2010(1): 128-130.(in Chinese)


