1 引言
噪声中的脉冲到达时间(time of arrival,TOA)估计是雷达侦察、电子对抗的重要研究领域之一。高精度的TOA估计是脉冲宽度(pulse width, PW)测量及脉冲重复间隔(pulse repetition interval, PRI)测量的重要前提条件,在辐射源识别、定位等领域也发挥着重要的作用[1-3]。
TOA的估计主要包括对信号到达时间的标记与提取, 可视为时延最优估计问题。传统TOA估计方法如门限法[4-5],该类方法通过设置固定或自适应门限进行判决,方法简单且易于实现。Galati等进一步提出基于差分匹配滤波的到达时间估计方法[6-7],该类方法将零点作为固定判决门限,避免由门限带来的测量误差。文献[8]和[9]提出一种相关方法,利用信号的自相关性和统计互相关检测到达时间。[10]提出一种基于时间反转的两步TOA估计方法。Chan等提出了自卷积算法[11-12],该方法先通过脉冲信号自卷积确定卷积峰值初步位置,然后使用最小二乘法进一步估计。文献[13]将最大概率准则用于基于能量检测的接收机中。然而,以上方法均依赖于高信噪比(signal to noise ratio,SNR),无法保证低信噪比条件下的估计精度。文献[14]将相关累加与小波变换相结合,低信噪比情况下,能够满足TOA的估计精度,但估计性能依赖于小波变换尺度,且同时提高了计算复杂度。
在雷达侦察系统中,信道化接收机将接收信号混频、滤波、抽取得到基带同相正交分量,进一步对包括TOA、载频、到达角(angle of arrival, AOA)等参数进行测量。本文针对低信噪比下信道化处理后的脉冲TOA估计问题,利用信号相关性和噪声随机性,对信道化输出的脉冲信号进行相关预处理以抑制噪声,然后提取信号包络判决获得TOA粗估计。由于经过抽取过程,采样间隔扩大,原始数据未得到充分利用。通过利用高采样率数据和粗估计值,通过级联窗口计算频点能量并局部滑动,根据脉冲信号频点能量的变化精炼粗估计,提高估计精度,同时可调整滑动窗口大小以及滑动步长降低运算量,便于硬件实现,仿真结果验证方法的有效性。
2 信号模型及传统方法
假定接收信号模型为
x(n)=s(n)+w(n)
(1)
其中s(n)=Aej2πfcn/fs+jφ,A为信号幅值, fc为载波频率, fs为采样率,φ为初相,w(n)为噪声。
假设x(n)的序列长度为L,对x(n)做离散傅里叶变换得X(k),有
(2)
根据式(2),以下阐述传统滑动FFT[15]估计TOA方法。如图1所示,假定x(n)中包含一个脉冲,在序列前端设置一个局部M(M=2m,m∈Ζ+)点分割窗口,且窗口长度小于脉冲持续时间长度,对其计算M点FFT并利用式(2)计算能量,记为X1,而后依次向右连续滑动,直到XL-M+1。
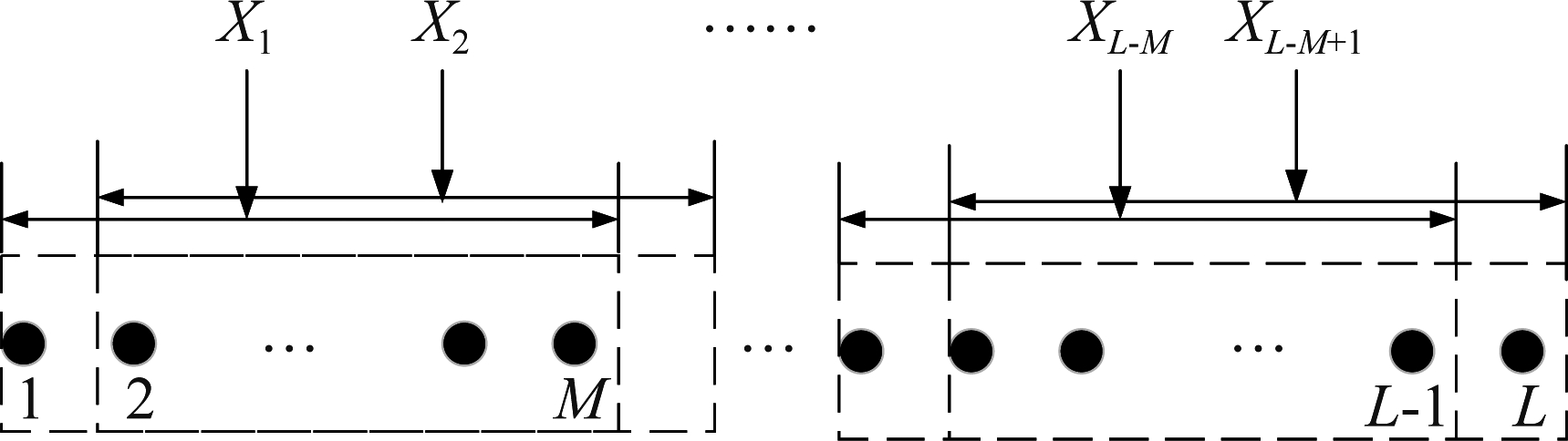
图1 滑动FFT过程
Fig.1 Sliding FFT process
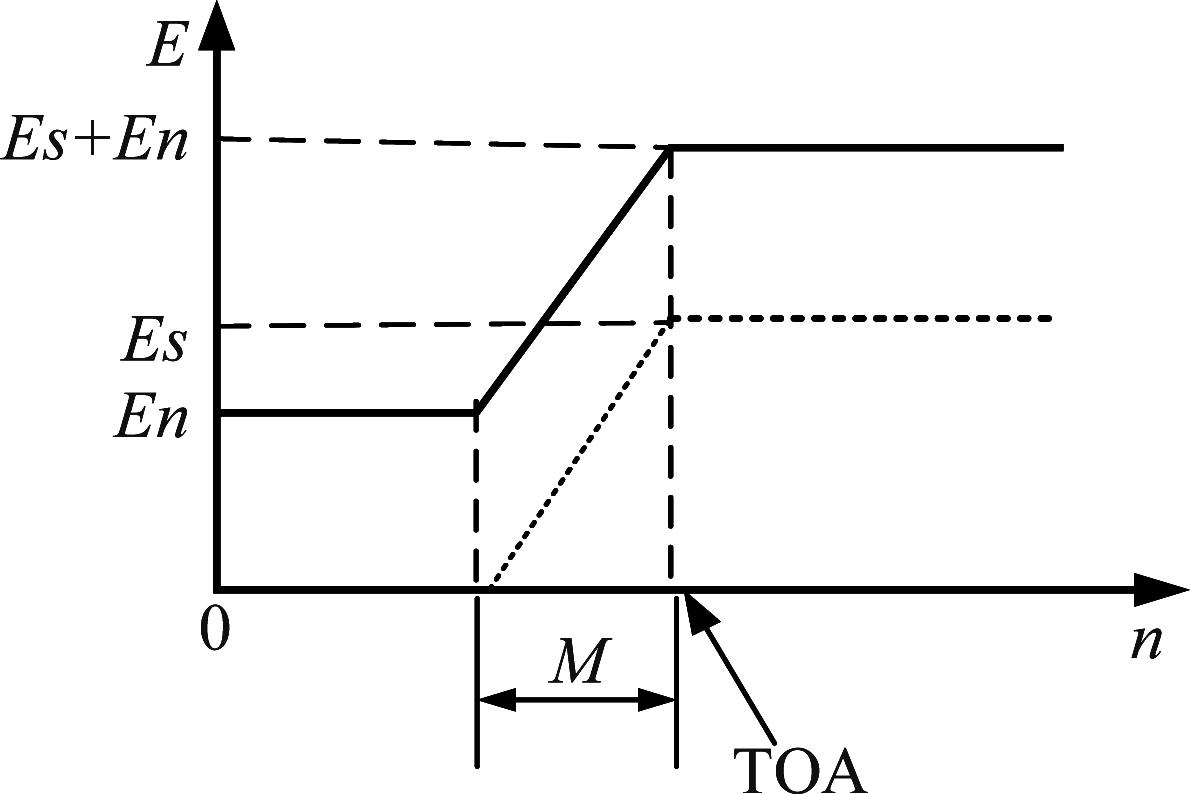
图2 能量变化过程
Fig.2 The process of energy change
设脉冲在第k个采样点到达,在滑动窗口前端(首次滑动前端为第M点)向右滑至第k点前,脉冲没有到达,所计算频域能量主要为噪声能量。窗口继续向右滑动,前端滑到第k点至第k+M-1点之间,用于滑动FFT的滑窗中脉冲不断积累,能量逐渐增大,直至滑窗全部包含脉冲。在k+M点以后和脉冲下降沿之前,窗口总是包含脉冲,能量不变。整个滑动过程中能量变化曲线如图2实线所示,其中,En为噪声能量,Es为信号能量,斜线投影的横坐标长度为滑动窗口宽度。能量达到最大值对应时刻即为TOA值,通常根据上升沿取幅度的一半为判决门限,设判决门限对应点为q,则TOA可估计为
TOA=q+M/2
(3)
3 基于级联滑窗的TOA估计
3.1 信道化
信道化旨在使用一组滤波器组,将原始宽带信号分为多个窄带子频带信号,通过子频带划分,每个子带能够滤除带外噪声,提高频带内信号信噪比,以利于进行信号检测和参数提取。基于多相滤波器组的信道化结构是一种高效实现结构,假定一FIR滤波器长度为N,其系统函数为
(4)
将滤波器冲激响应h(n)分为D组,并假设N为D的整数倍,每组长度为L=N/D,重写(4)为
H(z)=h(0)z0+h(D)z-D+…+h[(L- 1)D]z-(L-1)D+h(1)z0+h(D+1)z-(D+1)+ …+h[(L-1)D+1]z-[(L-1)D+1]+…+ h(D-1)z-(D-1)+h(2D-1)z-(2D-1)+…+ h[(L-1)D+D-1]z-[(L-1)D+D-1]= 
(5)
令
(6)
式(5)可进一步写为
(7)
式(7)为H(z)的多相表示,Ek(zD)为H(z)的多相分量。令z=ejw,则有
(8)
其中e-jwkEk(ejwD)根据k具有不同相位,H(ejw)为不同相位的和,因此,式(8)称为多相滤波结构。
信道化通过滤波器组将信道分为K个子通道,将带宽0～2π进行信道划分,各子信道输出带宽为2π/K,由于各子带信号处于过采样状态,对其D(D=K)倍抽取可降低速率且保证信号完整性。其中,第k个通道的滤波器冲激响应hk(n)与第0个子通道冲激响应h0(n)满足
(9)
其中h0(n)也称为原型低通滤波器。对(9)两边进行Z变换,得
Hk(z)=H0(zWk)
(10)
其中,
假定输入信号x(n1)经过滤波器hk(n1)输出vk(n1),由于Vk(z)=X(z)·Hk(z),其中Vk(z),X(z)分别为vk(n1),x(n1)的Z变换,将(10)代入得
Vk(z)=X(z)·H0(zWk)
(11)
根据第0通道的多相表示
(12)
可得
(13)
将(13)代入(11)得
(14)
因此
(15)
其中Up(z)=z-pX(z)Ep(zD)。
根据式(15)以及文献[16],用n1和n2分别表示抽取前和抽取后的信号,基于多相滤波器组的信道化高效实现结构可表示为图3所示。
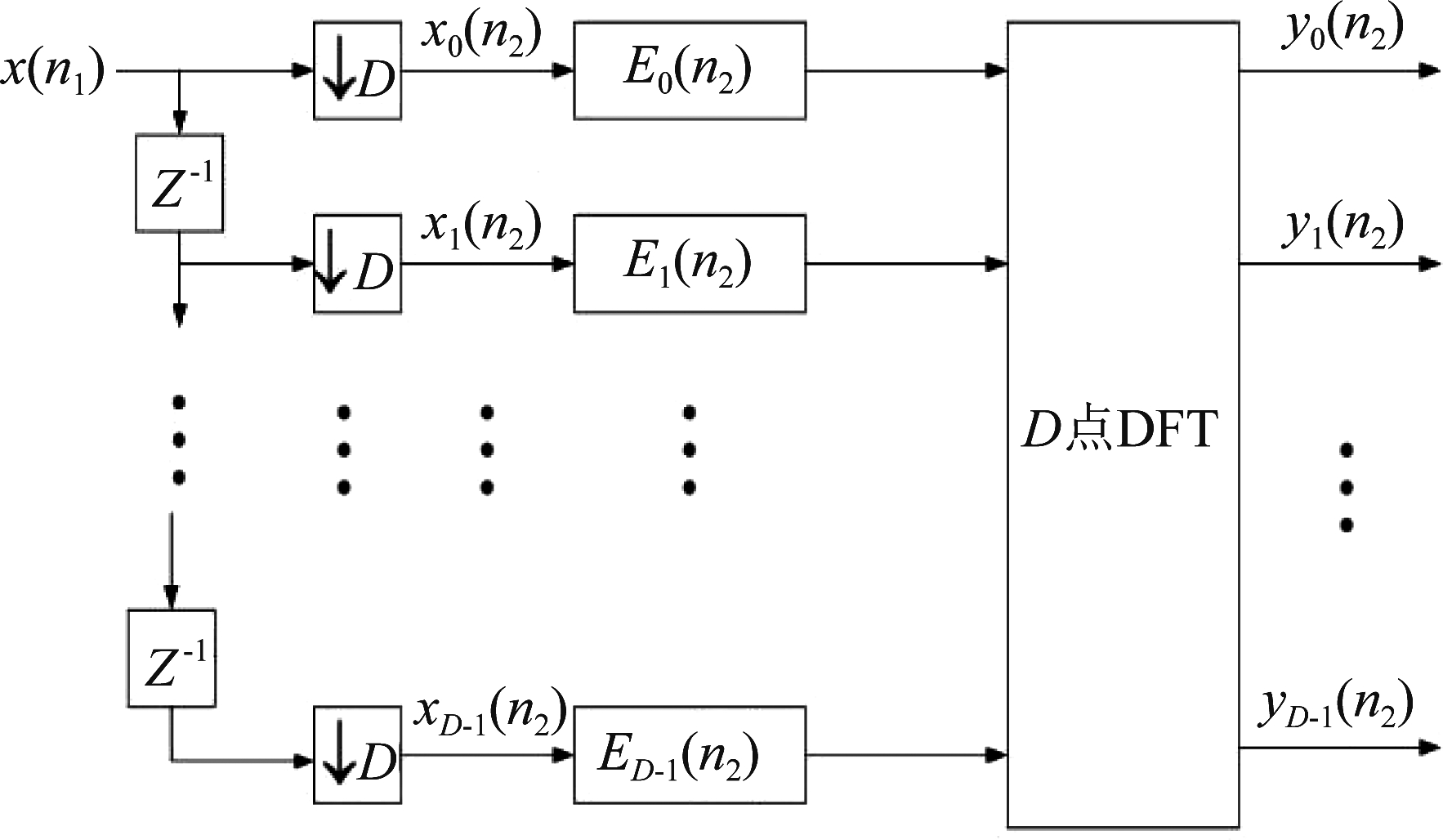
图3 基于多相滤波的信道化结构
Fig.3 Channelized structure based on polyphase filtering
3.2 粗估计
接收信号x(n1)经延迟、D倍抽取、滤波及D点DFT分D路信道输出,假定第p(p=0,…,D-1)个信道输出脉冲信号yp(n2), 其余为噪声,yp(n2)采样率为x(n1)的1/D,对其相关预处理[9]
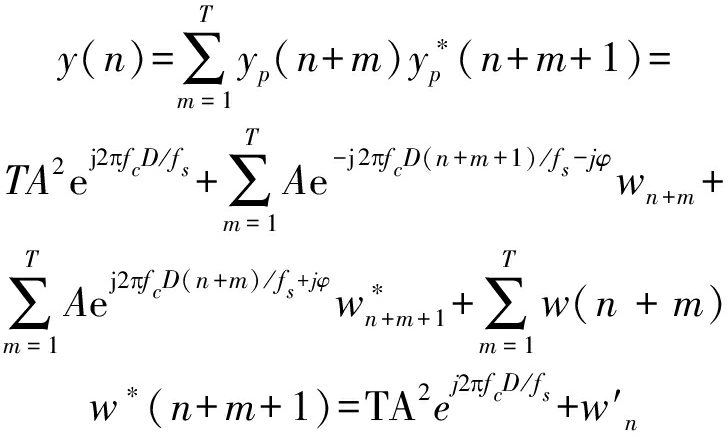
(16)
其中,信号部分为TA2ej2πfcD/fs,w′n为相关后的噪声部分。由式(16)可递归为
(17)
观察式(17)可知,每计算一个新的y(n+1)仅需一次复数乘法(其中
包含在y(n)中),适用于实时计算。由于经过相关运算,信噪比大约可提高T倍,对相关后的脉冲信号提取包络并判决,得到TOA粗估计。
3.3 精估计
由于信道化经过降采样,粗估计分辨率有限。传统滑动FFT计算的能量包含噪声能量,由于检测门限随噪声变化,低信噪比情况下能量变化情况不明显。对单脉冲信号,可略去噪声能量,只计算频点处能量,滑动结果如图2虚线所示,由图2可知,脉冲到达样点只与Es有关,判决门限不以噪声能量大小变化,提高了抗干扰能力。
据上所述,将TOA粗估计值代入原始数据并向前移一定点数确保在脉冲信号区间内,设置合适的级联窗口并计算FFT、取模,以峰值对应频率下标为信号对应频点,计算其能量并局部滑动,通过比较频点能量变化情况精炼TOA估计值。此外,由于原始数据处于过采样,可对其低倍率抽取并计算频点能量以及等步长滑动。精估计滑动范围选取是准确获得精估计的前提,由于粗估计根据脉冲包络幅度的一半作为阈值判决,真实的脉冲到达时间应比粗估计值提前,因此,只需根据粗估计向前滑动,为确定具体的滑动范围,可先粗后细的滑动,先根据粗滑动结果判断脉冲上升沿在一个大概样本区间,而后逐步缩小并最终确定滑动范围。假定依据粗估计设置局部滑动范围为[N1,N2],FFT点数设为M,滑动步长为I点,从原始数据每E点取一点做FFT,共M点,滑窗大小为ME点,以N1为起点,总共滑Q次。以图4为例,抽取倍数E=2,FFT点数M=4,滑动步长为I=3点。假定Q次滑动中根据阈值判决为第q′点,最终精估计值可表示为
(18)
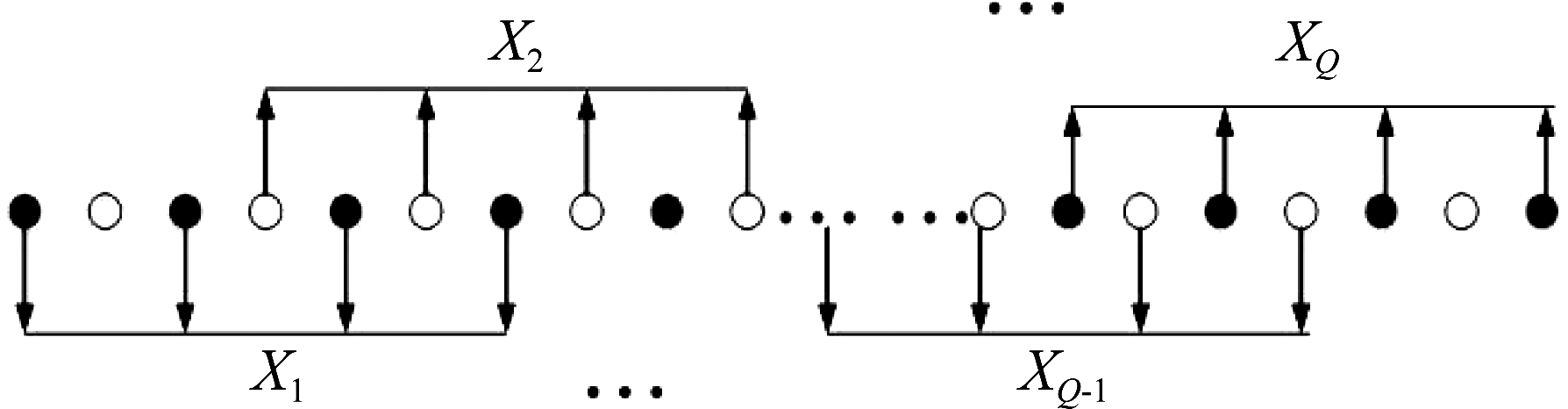
图4 间隔滑动FFT过程
Fig.4 Interval sliding FFT process
综上所述,本文提出的TOA估计方法可总结如下:
1)利用基于(15)的多相滤波结构对接收数据做信道化,检测各信道并提取脉冲信号。
2)对输出的脉冲信号利用(16)进行相关进一步提高信噪比,然后提取信号矩形包络并判决,获得粗估计。
3)基于原始数据和粗估计,设置级联窗口计算频点能量并滑动,根据滑动结果判决并利用(18)得到精估计。
4 仿真结果与性能分析
4.1 仿真结果
仿真参数设置如表1所示,同时,脉冲到达时间的均方根误差(root mean square error, RMSE)定义为
(19)
表1 仿真参数设置
Tab.1 Simulation parameter setting
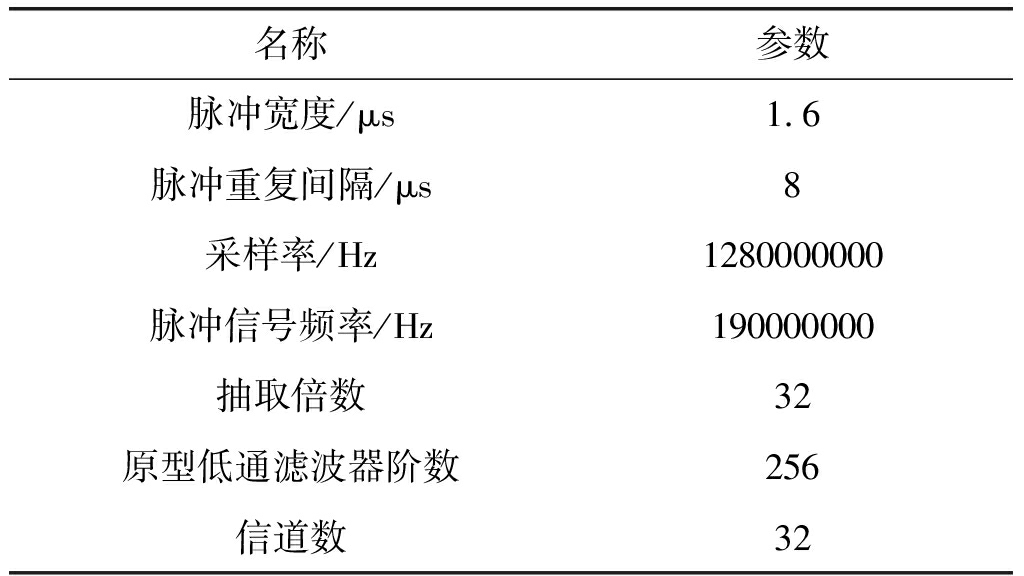
名称参数脉冲宽度/μs1.6脉冲重复间隔/μs8采样率/Hz1280000000脉冲信号频率/Hz190000000抽取倍数32原型低通滤波器阶数256信道数32
其中,G为蒙特卡洛次数,ti为估计到达时间,tr为实际到达时间。
根据设定参数,图5为在信噪比为-2 dB下的时域信号,观测时间和样本数分别为25 μs和32000点。经信道化处理后,如图6所示,通过对32路信道检测,第6信道存在脉冲信号并输出有脉冲的I、Q路信号,其余为噪声,由于滤除带外噪声,带内信噪比得到提升。第6信道包含的频率范围为(180 MHz,220 MHz),与实际脉冲频率190 MHz相验证。对信道6输出的脉冲信号相关处理并提取矩形包络,如图7所示,上、下半部分分别为未经相关处理和经处理后提取的脉冲信号包络,对比可知相关后的噪声得到抑制,据此可判决得到TOA粗估计值。
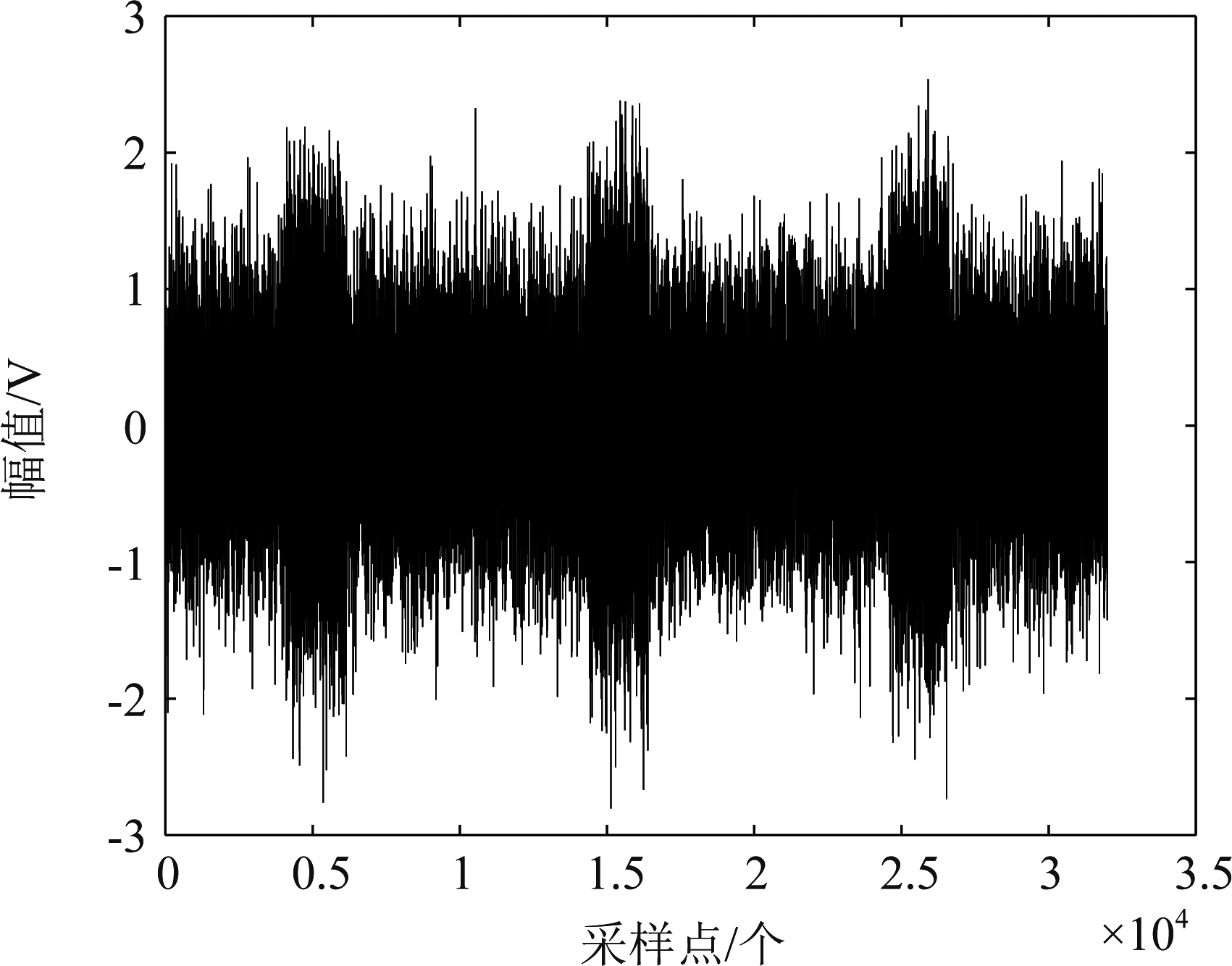
图5 采样信号时域
Fig.5 Time domain of sampling signal
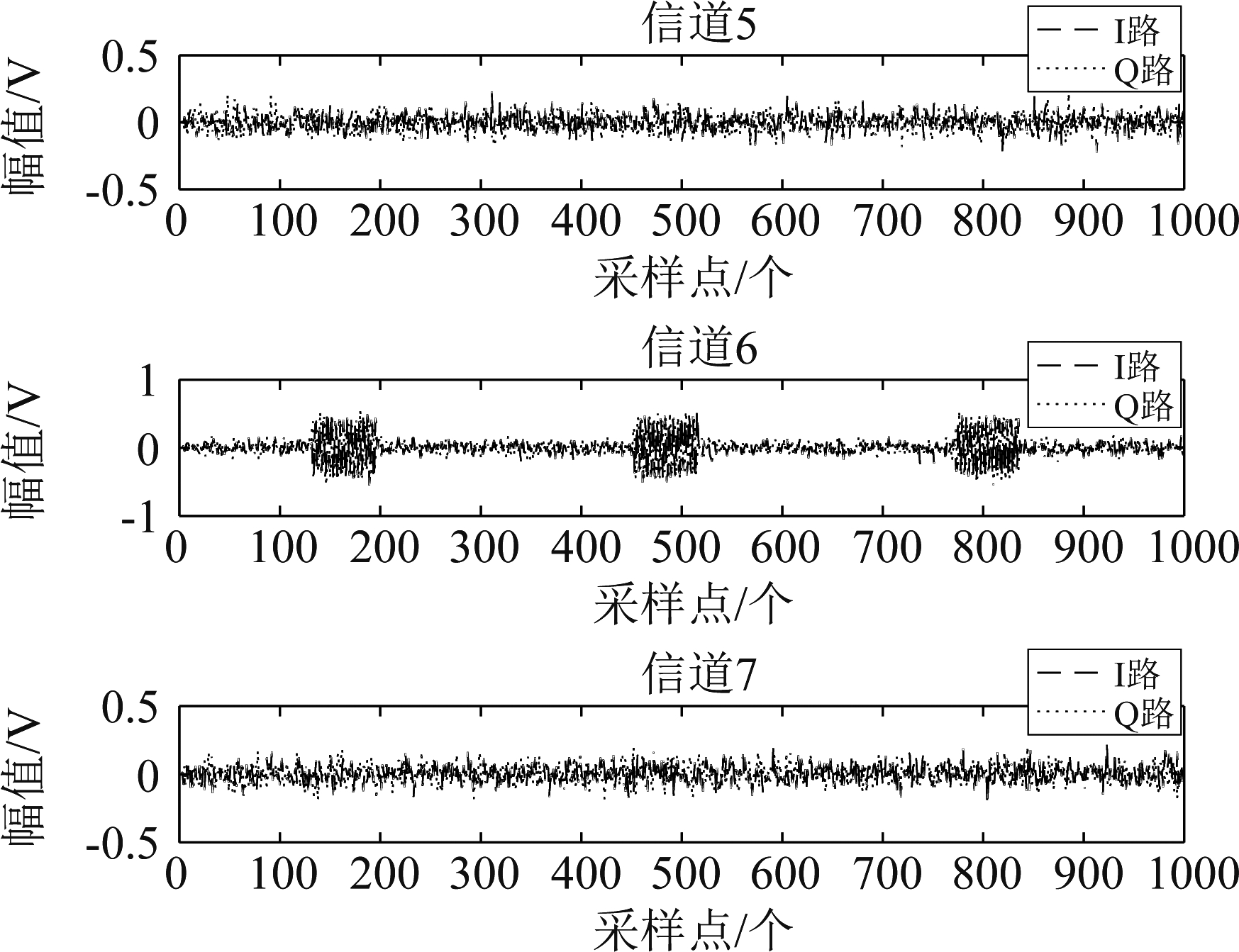
图6 信道化输出
Fig.6 Channelized output
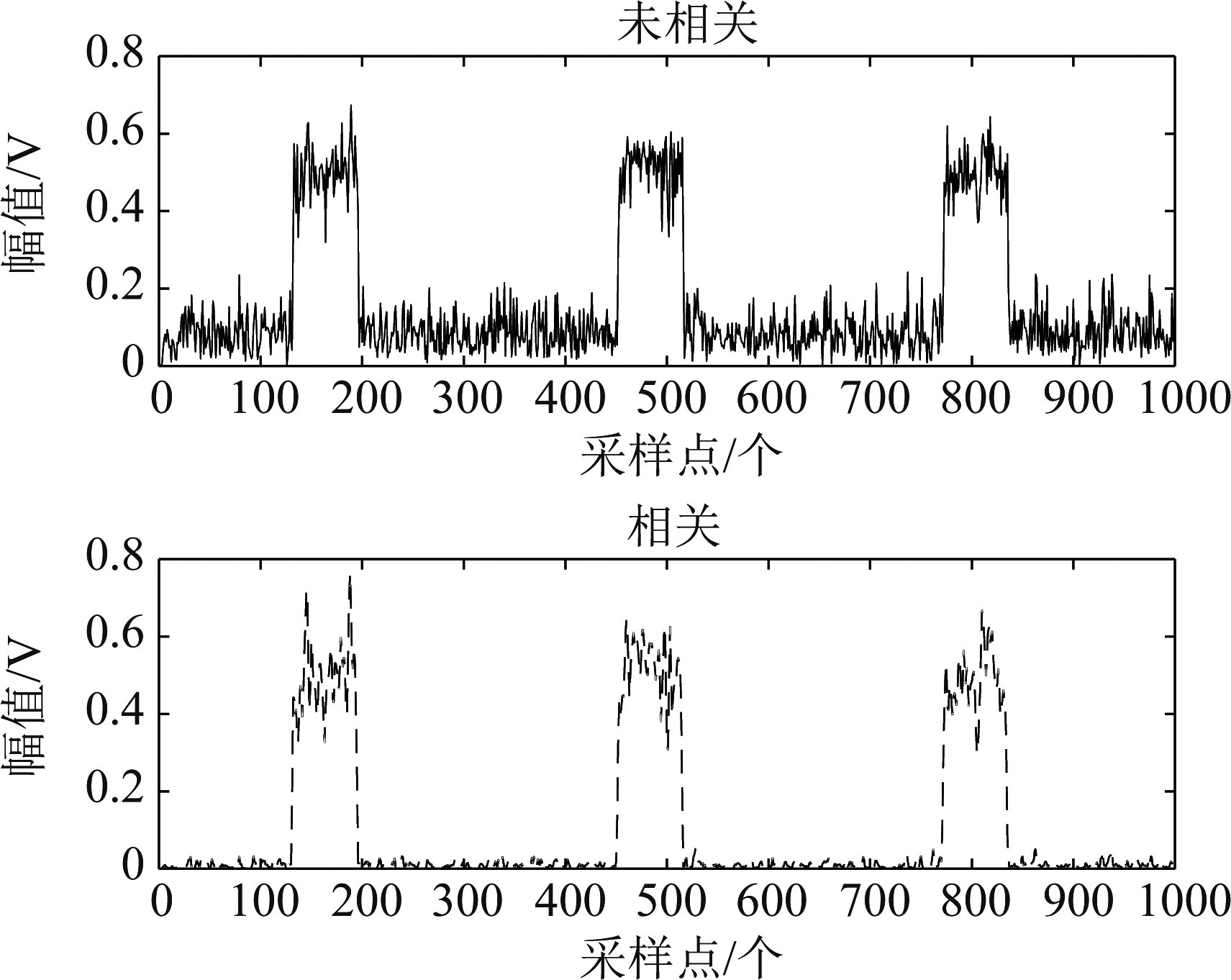
图7 相关及包络提取
Fig.7 Correlation and envelope extraction
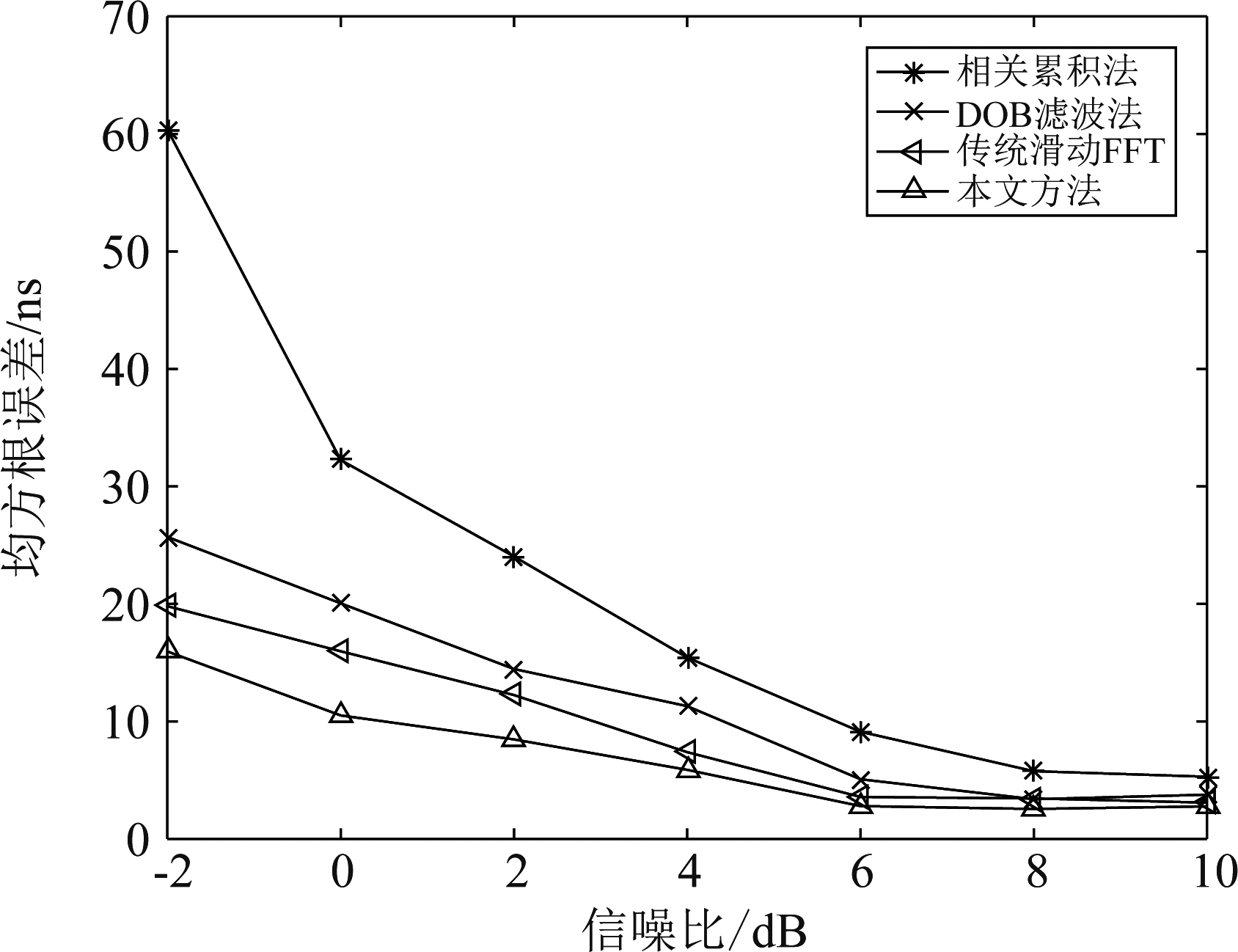
图8 均方根误差随信噪比变化曲线
Fig.8 RMSE versus SNR
由于经过32倍抽取,存在较大测时误差,为提高估计精度,根据粗估计值,利用图5数据通过设置级联窗口计算脉冲信号频点处的能量并局部滑动得到精估计。文中,每E=4取一点,共M=16点(64点中均匀取16点做FFT),滑动步长为I=25点,假定根据脉冲矩形包络判断初始到达样点为
滑动范围设为
滑动次数Q=5,蒙特卡罗次数为G=100。图8为本文方法与传统滑动FFT[16]、DOB滤波法[17]以及相关累积方法[18]的均方根误差(RMSE)随信噪比的变化曲线。由图8可知,低信噪比情况下,通过略去噪声能量,计算频点能量精炼粗估计,本文方法的估计性能优于其他三种方法。随着信噪比增加,由于传统滑动FFT方法所计算能量中频点能量占比逐渐增大,本文方法与传统滑动FFT方法性能趋于一致。图9为其他参数相同情况下,将采样率降为640 MHz的性能变化曲线,由图示可知随着采样间隔扩大,各算法的估计精度均出现不同程度下降,本文方法仍具有最高的估计性能。
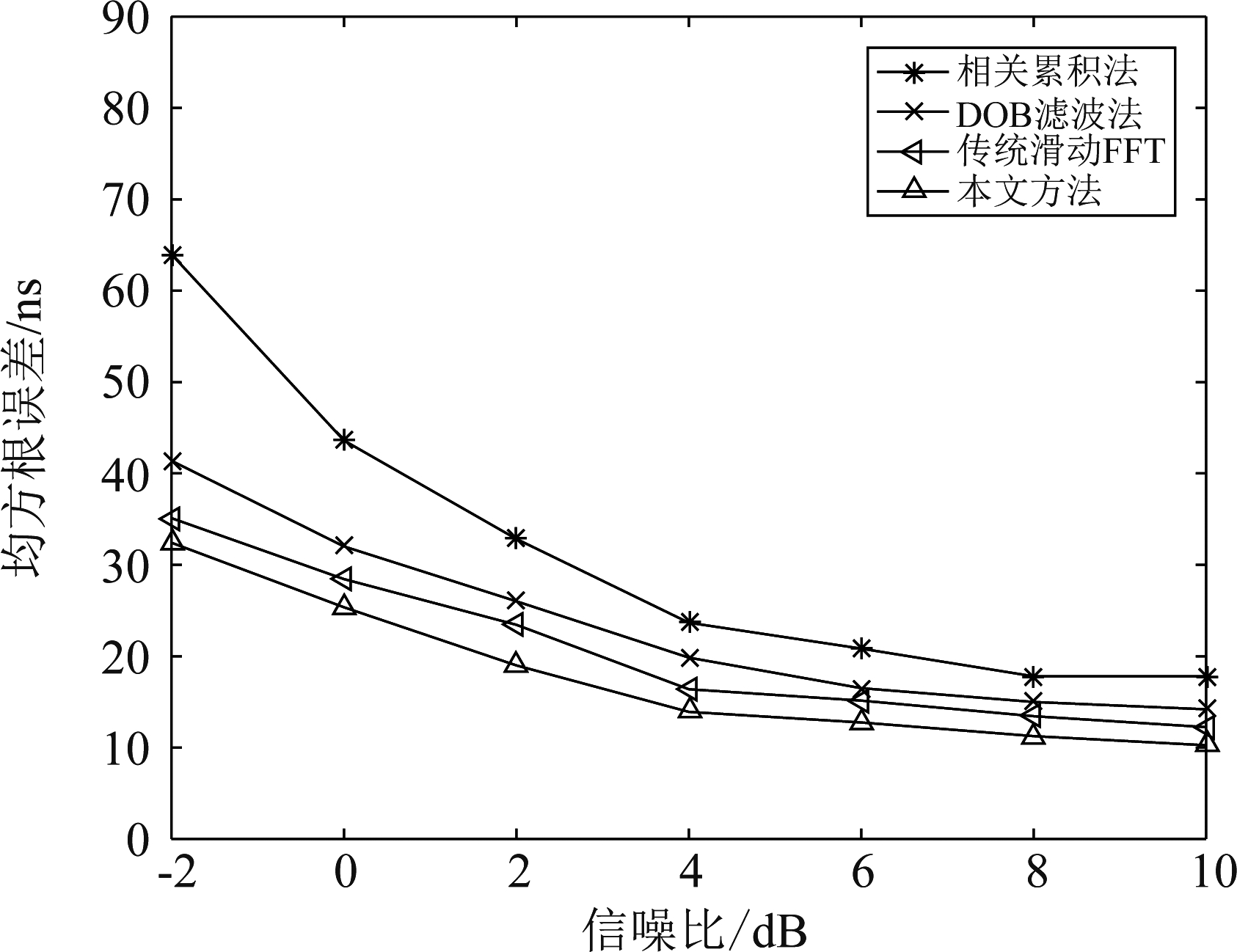
图9 均方根误差随信噪比变化曲线
Fig.9 RMSE versus SNR
考察滑窗参数对估计性能的影响,仿真条件同表1设置不变,在固定E=4,M=16点下,逐步缩小滑动步长G,由图10可知,随着滑动步长的缩小,一定滑动范围内,滑动次数增加,原始数据得到进一步利用,估计精度得到提升。同时,通过连续取样(E=1)和增加FFT 点数(M=64),估计精度在低信噪比获得较大提升,且随着滑动步长减小,性能不断得到改善。
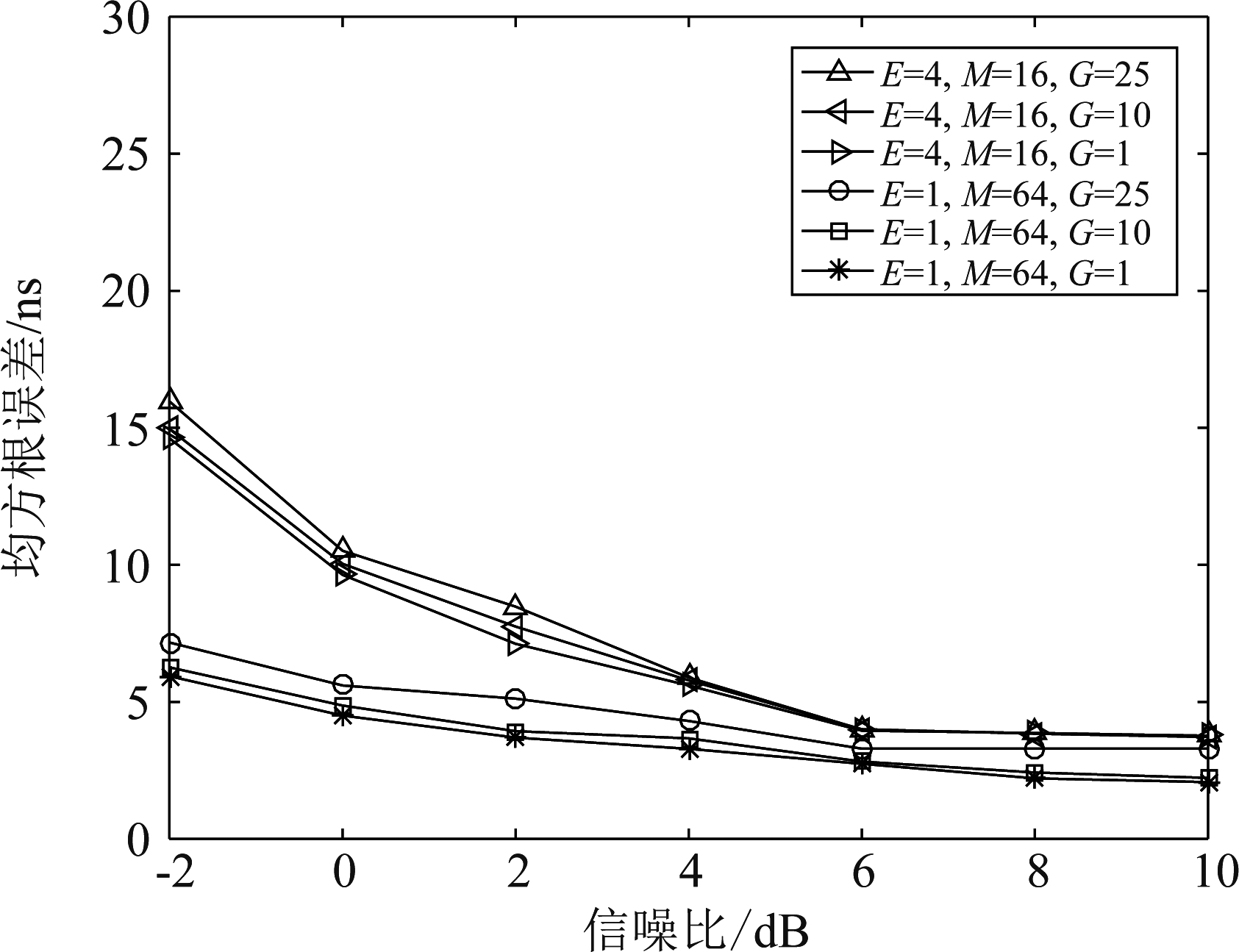
图10 均方根误差随信噪比变化曲线
Fig.10 RMSE versus SNR
4.2 复杂度分析
最后,考虑对各种算法的复杂度进行比较,复杂度由复乘次数衡量。本文计算复杂度主要包括信道化、相关和滑窗精炼粗估计,由于相关可迭代计算,每次仅需一次复乘,可忽略不计。信道化和滑窗精炼粗估计所需复数乘法分别为N+(K/2)log2K和(RQM/2)log2M,其中R为脉冲个数。传统滑动FFT[15]复杂度约5RMlog2M+N+(K/2)log2K。DOB滤波法[17]约3RN/2log2N/2,相关累积法[18]复杂度约2200R+N+(K/2)log2K。图11画出了各算法随脉冲数增加的复杂度比较,从中可知本文提出的方法具有最低的复杂度。需要指出,随着滑动步长缩小或FFT点数增加,性能得到优化的同时算法所需复杂度也会增加,实际中,在满足一定性能条件下,可适当扩大滑动步长及低倍抽取样本做FFT以降低复杂度。
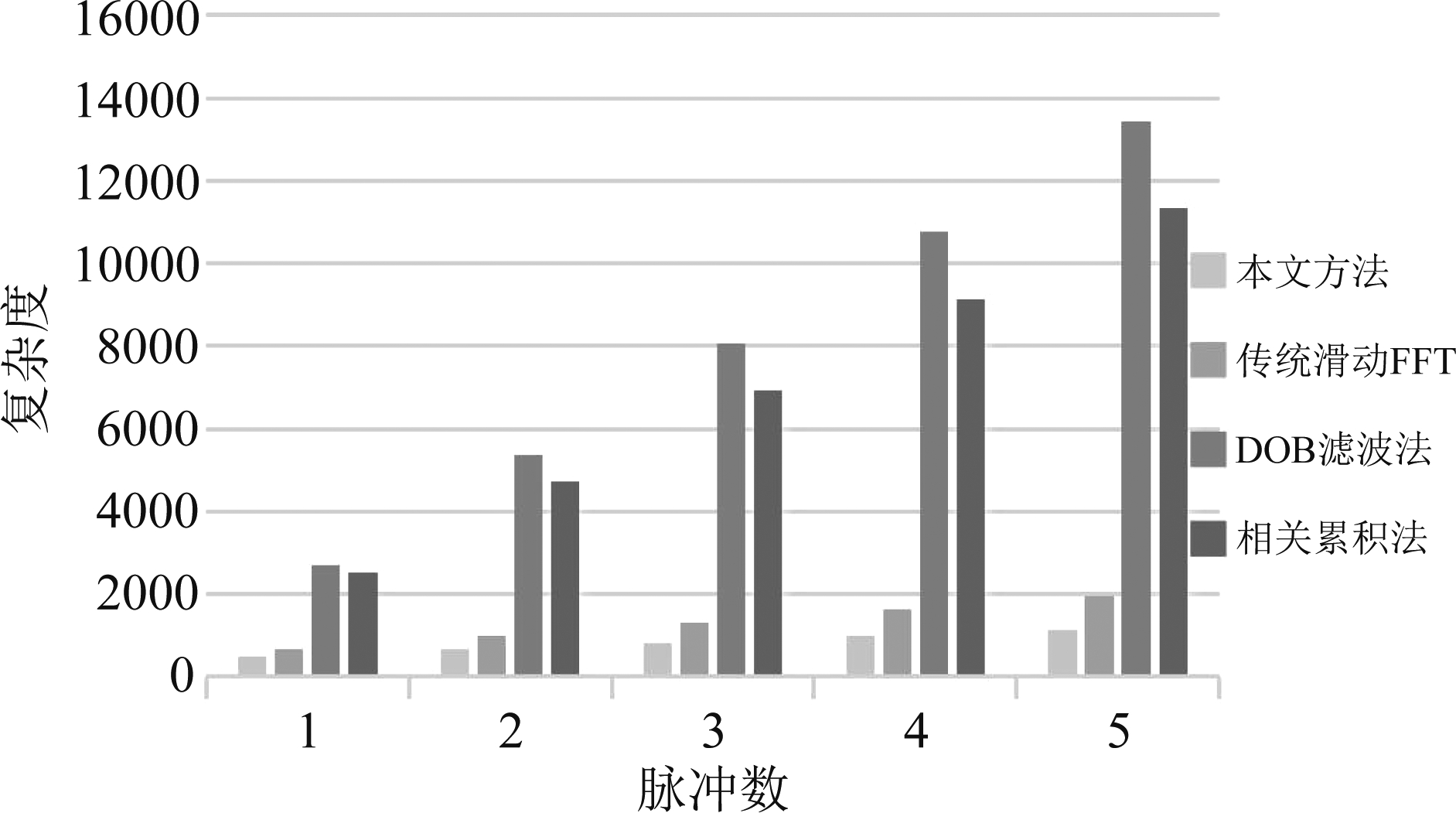
图11 不同算法复杂度比较
Fig.11 Complexity comparison of different algorithms
5 结论
本文基于信道化接收机的结构,提出了一种高效提取脉冲到达时间的方法。接收信号信道化后经过相关预处理,提取脉冲矩形包络并判决获得TOA粗估计值,再利用原始数据,通过级联滑窗计算脉冲信号频点能量并根据信号频点能量变化情况来精炼粗估计值,方法可灵活改变滑窗大小和滑动步长。仿真结果表明,低信噪比情况下该方法具有更好的估计精度,同时拥有更低的计算复杂度,工程易实现。
[1] SOBRON I, LANDA I, EIZMENDI I, et al. Adaptive TOA estimation with imperfect LOS and NLOS knowledge in UWB positioning systems[C]∥2020 IEEE SENSORS. Rotterdam, Netherlands. IEEE, 2020: 1- 4.
[2] SOBRONI I, LANDA I, EIZMENDI I, et al. Enhanced TOA estimation through tap candidate extraction for positioning in multipath channels[C]∥IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (IEEE PIMRC 2019). IEEE, 2019. 1- 6.
[3] 孙文, 高林, 魏平, 等. 多普勒耦合下的声呐系统TOA多目标跟踪[J]. 信号处理, 2018, 34(7): 757-765.
SUN Wen, GAO Lin, WEI Ping, et al. Multiple target tracking for sonar system under range-Doppler coupling[J]. Journal of Signal Processing, 2018, 34(7): 757-765.(in Chinese).
[4] HO K C. Pulse arrival time estimation based on pulse sample ratios[J]. IEEE Proceedings-Radar, Sonar and Navigation, 1995, 142(4): 153.
[5] TORRIERID J. Arrival time estimation by adaptive thresholding[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(2): 178-184.
[6] CHRABIEH R, BAGNALL P, SEZGINER S, et al. Advanced TOA estimation for multipath channels[C]∥2020 IEEE/ION Position, Location and Navigation Symposium (PLANS). Portland, OR, USA. IEEE, 2020: 1349-1357.
[7] GALATI G, GASBARRA M, LEONARDI M. Multilateration algorithms for time of arrival estimation and target location in airports[C]∥First European Radar Conference, 2004. EURAD. Amsterdam,Netherlands. IEEE, 2004: 293-296.
[8] 孙超,王世练, 朱江. 基于自相关算法的TOA估计方法研究[J].微处理机, 2014,35(4): 39- 43.
SUN Chao, WANG Shilian, ZHU Jiang. Research of TOA estimation based on auto-correlation algorithm[J]. Microprocessors, 2014, 35(4): 39- 43.(in Chinese)
[9] 席轶敏, 刘渝, 靖晟. 电子侦察信号实时检测算法及性能分析[J]. 南京航空航天大学学报, 2001, 33(3): 277-281.
XI Yimin, LIU Yu, JING Sheng. Analysis on probability of false alarm and detection[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2001, 33(3): 277-281.(in Chinese)
[10] MEI Yuxi, ZHU Zhenhai. A two-step TOA estimation algorithm based on TR technology in complex environment[C]∥2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC). Chengdu, China. IEEE, 2019: 1135-1140.
[11] CHAN Y T, LEE B H, INKOL R, et al. Estimation of pulse parameters by convolution[C]∥2006 Canadian Conference on Electrical and Computer Engineering. Ottawa, ON, Canada. IEEE, 2006: 17-20.
[12] CHAN Y T, LEE B H, INKOL R, et al. Estimation of pulse parameters by autoconvolution and least squares[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 363-374.
[13] 刘泽龙, 刘文彦, 丁宏, 等. UWB密集多径下基于检测概率差值最大的TOA估计方法[J]. 信号处理, 2012, 28(8): 1120-1126.
LIU Zelong, LIU Wenyan, DING Hong, et al. A novel probability-of-detection-difference maximum-based TOA estimation method in UWB dense multipath channels[J]. Signal Processing, 2012, 28(8): 1120-1126.(in Chinese)
[14] 胡国兵, 刘渝, 邓振淼. 基于Haar小波变换的信号到达时间估计[J]. 系统工程与电子技术, 2009, 31(7): 1615-1619.
HU Guobing, LIU Yu, DENG Zhenmiao. Arrival time estimation of signals based on Haar wavelets transform[J]. Systems Engineering and Electronics, 2009, 31(7): 1615-1619.(in Chinese)
[15] 刘刚, 植强, 吕镜清. 一种提取雷达脉冲到达时间的方法[J]. 电子对抗, 2003(4): 10-13.
LIU Gang, ZHI Qiang, LV Jingqing. Study on the new TOA calculating method for radar pulse[J]. Electronic Warfare, 2003(4): 10-13.(in Chinese)
[16] 何子述, 夏威. 现代数字信号处理及其应用[M]. 北京: 清华大学出版社, 2009.
HE Zishu, XIA Wei. Modern digital signal processing and its application[M]. Beijing: Tsinghua University Press, 2009.(in Chinese)
[17] 李程,王伟, 王雪松. 基于盒差分滤波器的脉冲检测算法[J].系统工程与电子技术,2013,35(8): 1615-1619.
LI Cheng, WANG Wei, WANG Xuesong. Pulse detection algorithm based on difference of boxes filter[J]. Systems Engineering and Electronics, 2013, 35(8): 1615-1619.(in Chinese)
[18] XU Jiacen, LIU Quanhua, CHANG Shaoqiang, et al. A novel TOA estimation method for unknown modulated pulse[C]∥2016 CIE International Conference on Radar (RADAR). Guangzhou, China. IEEE, 2016: 1- 4.
