1 引言
煤炭资源是我国能源的重要组成部分,煤矿的开采过程存在着众多风险因素,其中瓦斯突出和瓦斯爆炸在众多风险因素中占有较大比重[1],因此煤矿开采过程中的瓦斯浓度的监控和预测尤为重要。
随着开采技术的发展,我国煤矿行业在大部分煤矿巷道安装了测量瓦斯浓度的传感器,实现瓦斯浓度进行实时监控。但是这种实时监控的传感器数据难以实现瓦斯风险的预警功能[2]。为实现煤矿瓦斯风险的预警功能,同时最大限度的利用传感器采集到的数据,一些学者使用关联分析[3]等方法,将煤矿瓦斯含量的相关的因素(例如:煤层深度、地质构造、水文条件、煤的炭化程度等)结合起来,分析各种要素对瓦斯灾害的关联程度达到预测瓦斯灾害的目的[4];另一部分学者则将数据挖掘[5]、支持向量机[6]、神经网络[7- 8]等典型回归算法、动态预测方法与煤矿瓦斯采集数据结合,以实现瓦斯风险的动态预警。前者研究中需要大量的人力物力资源支撑,例如地质因素等就需要科研人员采集、实验、分析、研究得出结论,时间上也难以保证。后者则采用数据分析,最大限度地利用传感器采集数据,提高了预测的效率。本文拟采用数据分析和挖掘的方法进行瓦斯浓度的预测。
现行的由数据驱动的对煤矿开采过程中瓦斯浓度预测方法有很多,主流的研究一般是将瓦斯浓度看作时间窗下的时间序列数据进行训练模型,然后针对确定测试数据进行预测,这样不仅对时间数据没有有效利用,同时对测试数据过于肯定,以至于测试数据的微小波动会直接导致预测数据的抖动,并且难以调节预测数据对输入测试数据的敏感程度。
高斯过程回归模型是将统计学习理论和贝叶斯理论相结合的一种机器学习方法,对于处理小样本、高维度和非线性复杂关系的回归和分类问题都有较好的效果[9]。但是高斯过程处理单模态数据较有优势,对多模态、非平稳时序数据的回归拟合效果不太理想。针对这一问题,Tresp[10]在2000年从混合专家系统的角度提出了的高斯过程混合(Mixture of Gaussian Processes, 简称MGP)模型。近年来,MGP模型得到了全面的发展和广泛的应用。然而,目前利用MGP模型进行预测策略基于测试输入值是准确值,并且固定不变。但实际采煤环境中难免出现噪声的干扰,这种情形下模型的预测结果过于武断。除此之外,此模型的传统预测策略具有不可调节性,难以控制预测结果的灵敏度。为了解决这一问题,本文拟采用高斯过程混合(MGP)模型进行建模,假定测试输入数据服从真实数据的高斯分布,提出了含噪输入预测策略下的高斯过程混合回归预测方法(niMGP),并且可通过调节输入数据中噪声方差大小来实现瓦斯浓度风险的多等级预警。
本文结构安排如下:第2节简单介绍了MGP模型及其参数学习算法和传统的预测策略;第3节推导并提出了MGP模型的含噪输入预测策略;第4节给出了MGP模型含噪输入预测策略下在模拟数据上的实验结果;第5节给出了在实际煤矿瓦斯浓度数据中的实验结果; 第6节进行了简要的总结。
2 MGP模型的参数学习与传统预测
2.1 MGP模型的参数学习
MGP模型是通过混合K个独立的高斯过程(Gaussian Process, GP)分量所形成的一种线性叠加式的回归预测模型。它能够通过对时序数据的学习来建立一个随机过程或时间序列模型,对于多模态、非平稳的时序数据具有较好的预测效果。
MGP模型的基本框架可理解为输入域中的点服从混合正态分布而输出域中的点服从高斯过程。引入隐变量
表示混合模型中时间i的第k个分量出现的状态(即回归分量)指示变量,而每个回归分量都是具有特定参数的高斯过程模型。隐变量的类别概率为
针对第k个分量,输入数据
服从特定的高斯分布,其均值和方差为{μk,Sk},以为输入驱动,得到参数为θk的高斯过程(回归分量)的输出或预测值
本文采用MGP生成模型(Z->X->Y)进行回归分析和预测。实际上,它对时间序列数据有较好的预测效果,并且对输入输出之间的关系反映较清晰[11]。假设分量k中的数据集为
参数为θk={lk,fk,σk},其中参数lk和参数fk分别为第k个分量的SE核函数中的超参数,σk为第k个分量的高斯过程模型中加入的噪声项。隐变量
服从多项式分布:
(1)
在隐变量
的条件下,输入数据的概率服从高斯分布:
(2)
其中μk和Sk为模式k中的输入数据的均值和方差。
假若第k个高斯过程的数据为
即输出值
服从零均值的高斯分布:
(3)
其中
为输入数据的噪声项。
由此可以看出,需要学习的MGP模型参数为
根据模型中随机变量的关系和概率分布,当给定测试数据x*,不难得出其联合分布:
(4)
根据贝叶斯准则可得:
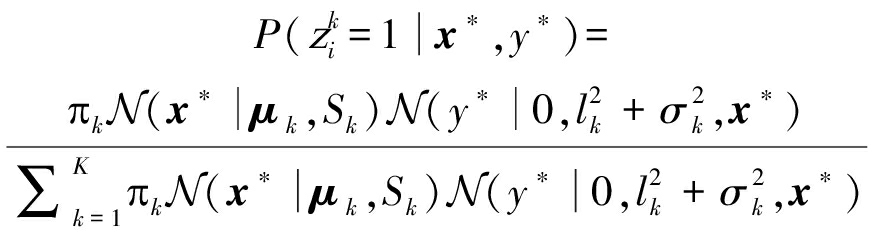
根据以上分析,将高斯过程混合模型的模型框架和参数总结如图1。
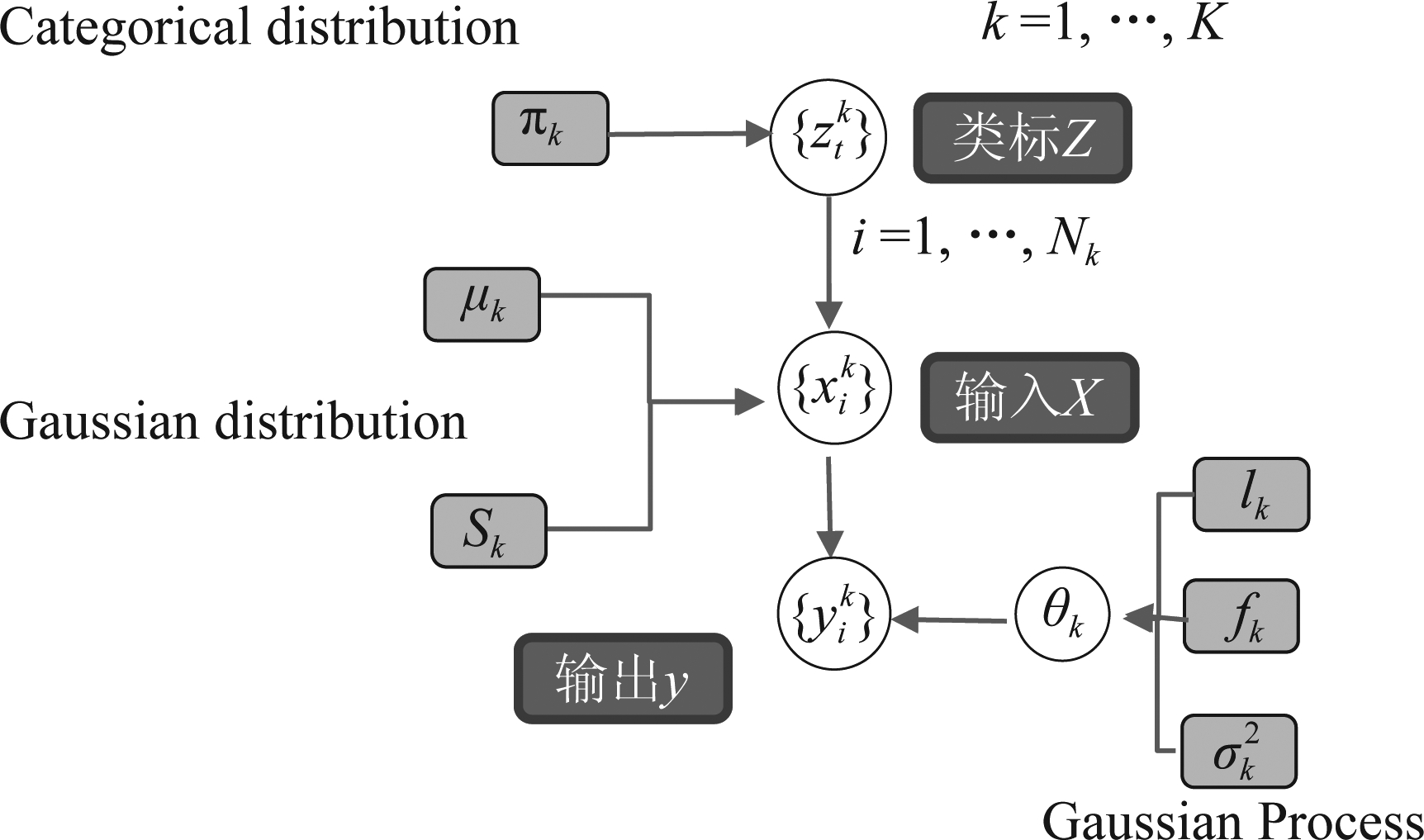
图1 高斯过程混合(MGP)模型框架及模型参数
Fig.1 Framework of Mixture of Gaussian Processes model and its parameters
由于MGP模型相较于GP模型结构更加复杂,模型参数的学习也更为困难。GP模型参数学习中的极大似然估计方法也难以求得稳定点的显式表达,因此MGP模型的参数学习多采用EM(Expectation Maximization,期望极大化)算法[12]。它具有形式简单、稳定收敛的特点。它通过引入隐变量使得对缺失数据下的训练集也有较好的表现,并且对于完全数据的似然函数(Q-函数)有单调递减的性质,因此在机器学习中有较多使用。但是EM算法也具有指数多项式求和导致计算复杂度高等问题[13]。因此本文中使用简化后的硬分类EM算法进行参数的学习。
高斯过程混合模型参数学习的硬分类EM算法主要分为两个步骤:E-步和M-步。E步计算联合分布的条件概率期望,也就是在观测点下根据不同分量模型的隐变量的条件概率的期望值;M步则是Q函数或似然函数的极大化,在MGP模型中因为有两类概率分布,所以在M步需要极大化两个似然函数,即关于输入高斯分布和输出高斯分布的似然函数,并依此获得新的参数。 算法流程见图2。
图2 高斯过程混合(MGP)模型硬分类算法
Fig.2 The hard-cut Algorithm for Mixture of Gaussian Processes
2.2 MGP模型的传统预测策略
根据硬分类EM算法所得到的参数模型MGP,对于准确的测试点x*的预测可分为两步。首先根据参数模型对测试数据x*计算其所属高斯分量k的概率,并根据每个高斯过程分量进行预测;然后对所有高斯过程分量的预测结果进行概率平均而得到MGP的回归预测结果。
假若确定测试点x*属于第k个高斯过程回归分量,下面给出其回归预测结果。为简化表示,令X={x1,x2,…,xN}表示N×p维输入矩阵,N数据个数,p为数据维数。假设在输入数据中带有方差为σ2的白噪声,由此可以得出训练数据和测试数据的联合分布为:
(5)
由多元正态分布的性质,可以得出预测点的条件分布仍然服从高斯分布[14],即
(6)
其中
μ(x*)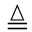
C(X,x*)[C(X,X)+σ2I]-1y
(7)
cov(x*)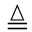C(x*,x*)- C(X,x*)T[C(X,X)+σ2I]-1C(X,x*)
(8)
MGP模型对确定测试数据的预测方法如图3。虽然模型的学习过程使用硬分类EM方法,但是在预测策略中,输出点在每个高斯分布分量都有一定的存在概率,为综合考虑各个分量对预测分布的影响,我们采用概率平均的软分类预测方法进行预测。
图3 MGP模型的传统预测策略
Fig.3 Conventional prediction strategy of the MGP model
3 MGP模型的含噪输入预测策略
虽然上述传统的预测方法能够对准确的测试数据进行合理的预测,但是在实际应用中,测试数据也会受到噪声的干扰,即测试数据本身可能会包含着噪声,这给原始测试数据带来了一定的不确定性。这时候采用上述方法则会导致预测的突变并因此产生较大的误差。实际上,在GP的预测中若能够考虑含噪输入情况,则能够有效地改善预测效果[15]。因此我们在MGP的预测中也可同样地考虑含噪输入的情况,即在测试数据的输入变量中引入噪声信号,以提高预测的鲁棒性。
对于某个高斯过程分量,我们对测试输入数据x*引入高斯噪声使其成为随机变量:
这样原预测值的条件分布的期望和方差也可看为关于u的随机变量:
(9)
σ2(u)C(u,u)- C(X,u)T[C(X,X)+σ2I]-1C(X,u)= 
(10)
其中Σ=C(X,X)+σ2I,β=Σ-1y,φi(u)=C(xi,u),Σi, j为矩阵Σ中元素σi, j的代数余子式。
为了消除噪声的干扰,对于x*的预测概率密度函数p(ν|μx*,Sx*)应为随机变量p(v|X,y,u)在μx*,Sx*下的条件期望值:
p(v|μx*,Σx*)=Eu(v|u)= 
(11)
其中条件概率分布p(v|X,y,u)为公式(9)和公式(10)所确定的均值和方差的正态分布的概率密度函数,简记为p(v|u)。因此,Ev[p(v|u)]=f(u),covv[p(v|u)]=σ2(u)。
在GP模型中,公式(11)中的被积函数是极其复杂的,很难通过积分运算求得显式表示。在实际应用中,针对这种积分的计算,出现了两大类估计方法,一类利用Monte-Carlo随机方法进行估计[16];另一类利用高斯分布近似求得积分的数值解[17]。本文将利用高斯分布近似的方法进行如下分析和推导。
我们不妨先假设含噪输入数据x*划归为第k类高斯过程(为了方便,下述表示暂时忽略标号k)。将关于测试数据x*的预测概率密度函数p(v|μx*,Sx*)近似为高斯分布,由期望迭代法则和条件方差分解公式,这个条件概率的期望和方差分别为:
m(μx*,Sx*)=Ev[p(v|μx*,Sx*)]= EvEu[p(v|u)]=EuEv[p(v|u)]=Eu(f(u))
(12)
cov(μx*,Sx*)=cov(p(v|μx*,Sx*))= Eu[covv[p(v|u)]+covu[Ev[p(v|u)]]= Eu[σ2(u)]+covu(f(u))
(13)
这样对于x*的预测概率密度函数p(v|μx*,Sx*)的期望则为:
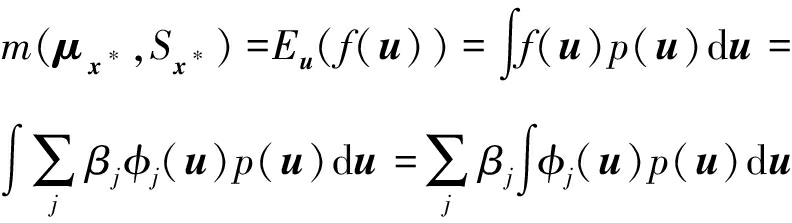
(14)
将公式(9)和p(u)的概率分布代入公式(14),化简后可得
m(μx*,Sx*)=qTβ
(15)
其中
对于测试点x*的预测概率密度函数p(v|μx*,Sx*)的方差
cov(μx*,Sx*)=Eu[σ2(u)]+covu(f(u))= Eu[σ2(u)]+Eu[f(u)]2-[Eu[f(u)]]2=
σ2I]-1C(X,u)]p(u)du+ 
C(X,u)T[C(X,X)+σ2I]-1C(X,u)]p(u)du+
(16)
同理,将公式(10)和p(u)的概率分布代入公式(16),化简后可得
cov(μx*,Sx*)= C(x*,x*)+tr[(ββT-Σ-1)Q′]-(qTβ)2
(17)
其中矩阵Q中的元素为
(Λ+2Sx*)-1(μx*-xi-xj)-xiTΛ-1xj)
(18)
详细推导过程可参考文献[18]。 基于上述推导,MGP模型对含噪输入预测策略的详细算法如图4所示。
图4 MGP的含噪输入预测策略
Fig.4 Noisy input prediction strategy of the MGP model
4 含噪输入预测策略的模拟数据实验
GP模型分别在确定和含噪输入预测策略下的预测效果对比如图5所示。对比两种方法在的单模态数据集的预测结果,对带有信噪比为10的训练数据,含噪输入预测策略更具稳定性。从图5可以看出,单个高斯过程模型采用含噪输入预测策略可在预测准确度基本不变的条件下,有效地降低了预测分布的标准差,提高预测的稳定性。左图为高斯过程的传统预测策略下的预测结果,在预测集上平均标准差为0.2220;右图为高斯过程的含噪输入预测策略下的预测结果,在预测集上的平均标准差为0.1647。这是由于在含噪输入预测策略中将输入值看作为含有高斯噪声的随机变量,比将测试数据作为确定值输入模型的预测结果有更好的鲁棒性。同时,根据含噪输入预测策略的推导过程,当数据信号存在较大波动或者震荡时,含噪输入预测策略将会适当缓和这种变化,表现为预测分布的方差相对减少。因此,当数据信号为多模态信号时,这种预测策略会有更有优势。
表1展示了单GP模型和MGP模型在不同预测策略下的实验结果。图6展示了MGP模型在两种预测策略下预测结果比较。实验结果采用均方根误差(Root Mean Square Estimate,RMSE)来衡量模型的准确程度。计算方法如公式(19)。
(19)
采用平均方差来衡量模型的预测的稳定程度。平均方差的计算方法如公式(20)。
平均方差
(20)
由表1可以看出,显然,当数据呈现多模态形式时,混合模型对数据的拟合效果优于单模型预测效果。同时对应比较MGP模型的两种预测策略下的预测效果,可以看出两种预测结果的准确程度差别不大,但是使用含噪预测策略下衡量模型预测稳定程度的平均方差远远小于传统预测策略的平均方差。
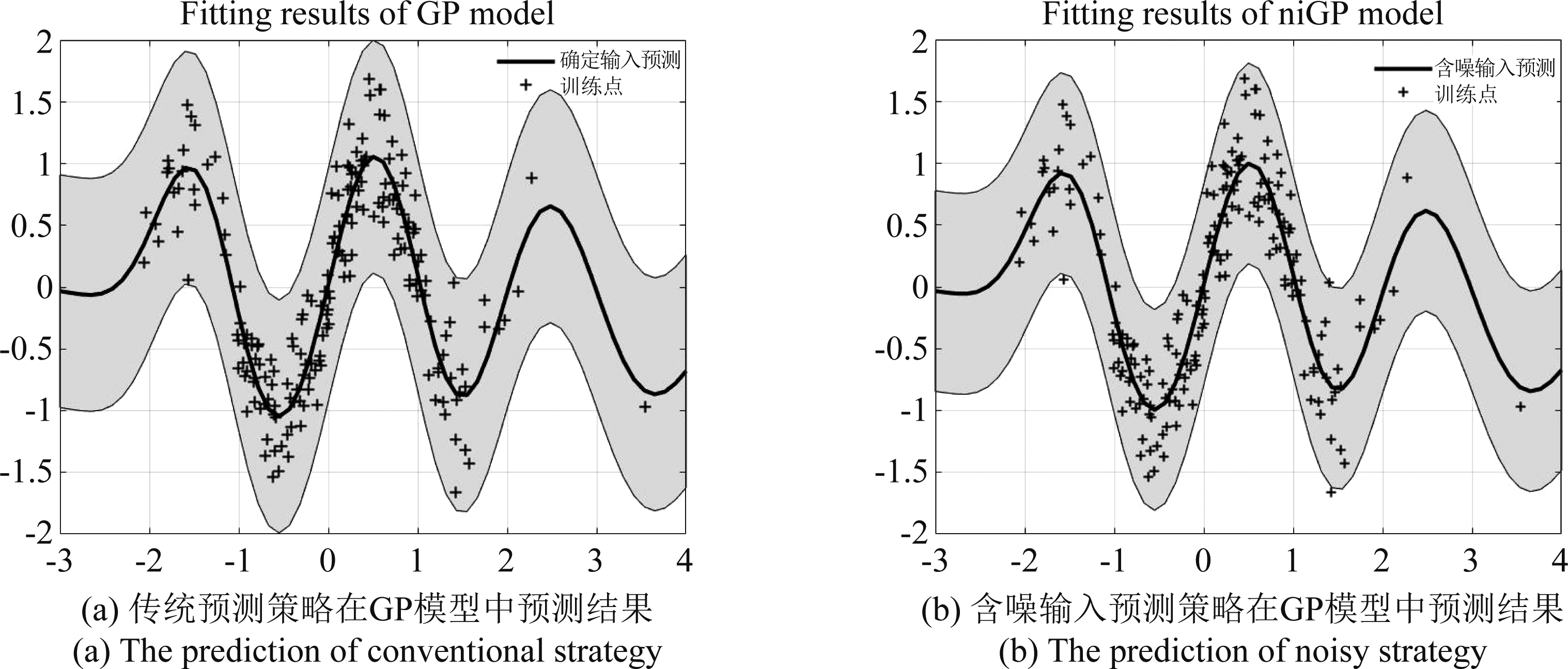
图5 含噪输入策略和传统预测策略下在高斯过程(GP)模型中结果对比
Fig.5 The comparison of predicted results using noisy input and conventional prediction strategies in the Gaussian Process (GP) model
图6 含噪预测策略和传统预测策略在MGP模型上预测结果对比
Fig.6 The comparison of predicted results using conventional and noisy input prediction strategies in the MGP model
表1 不同模型对模拟数据预测效果 Tab.1 Prediction results for certain and noisy test data strategies on synthetic data set
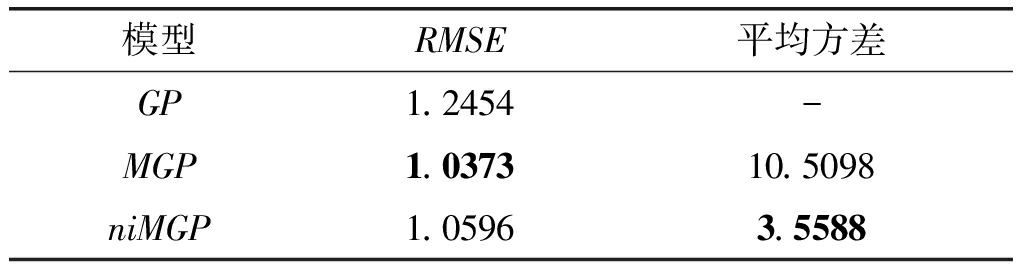
模型RMSE平均方差GP1.2454-MGP1.037310.5098niMGP1.05963.5588
在图6中,左图为人工生成的高斯过程混合数据,相同颜色代表相同参数空间下生成的高斯过程。中间和右图分别为传统预测策略和含噪预测策略下的回归预测效果。其中曲线表示预测分布的均值,我们作为该点的预测结果,阴影部分为95%的置信区间。由图6也可以看出,相比于确定输入值的传统预测策略,含噪输入预测策略在基本维持预测效果的同时,有效减小了预测分布的平均方差。因此它在多模态高斯过程的回归预测中能增加预测分布的稳定性。
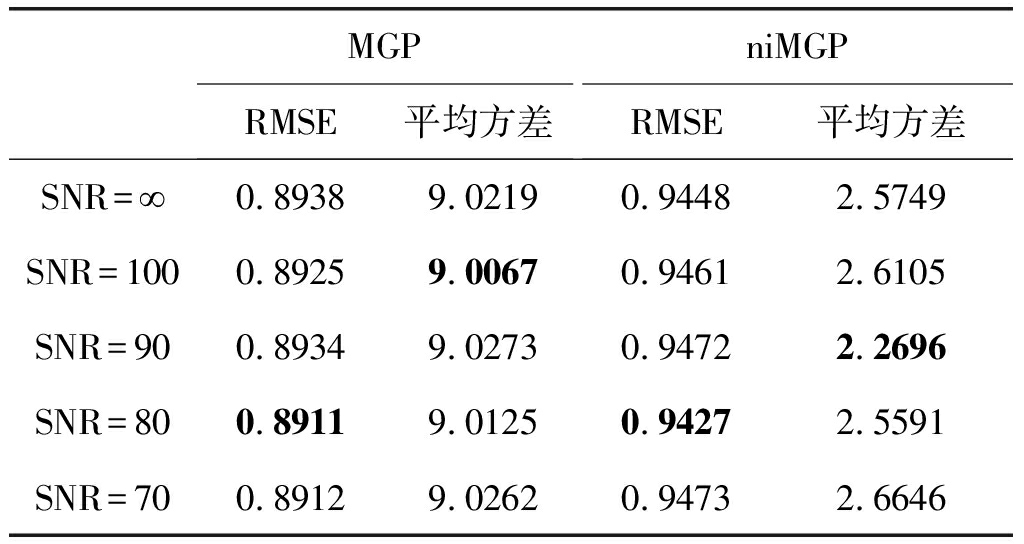
实际上,训练数据本身的含噪水平对模型的预测结果也有一定的影响。表2为在另一组高斯过程混合数据中加入不同强度噪声下两种预测策略的预测效果。SNR表示在合成数据中加入噪声的信噪比,即有用信号功率与噪声信号功率比值,计算方法如公式(21),其中SNR=∞表示未加入噪声。
(21)
显然,SNR值越大表示噪声对信号的影响越小。由表2可以看出,在训练数据中增加一定强度的噪声会所预测准确率有所提高,但含噪输入预测策略同样会在一定程度减少了模型预测的准确率,但却明显增加了预测结果的稳定性,即含噪输入预测策略总是增强了模型预测结果的鲁棒性。
表2 确定和含噪输入预测策略在不同信噪比下的预测结果
Tab.2 Prediction results for certain and noisy input test data strategies under different signal-to-noise ratios
5 瓦斯浓度的柔性预测
我们进一步采用MGP模型对于瓦斯浓度数据进行建模,并且引入含噪输入预测策略,通过调节噪声的方差大小来实现瓦斯风险的多等级柔性预 测和报警。实验数据使用松藻煤矿中打通一矿的ID为333944号传感器测得的瓦斯数据。测量时间间隔为5分钟,为保证安全性,以5分钟内瓦斯浓度最大值作为标签数据进行建模。首先,利用时间戳编码作为输入变量。实际中,时间戳是指格林威治时间1970年01月01日00时00分00秒起至记时时刻的总毫秒数。我们可对获取的时间戳归一化处理以获取合适的输入数据。由于传感器测量的瓦斯浓度为每五分钟之内的浓度最大值,因此传感器数据多为阶梯形式,并且多在浓度为0和2值处,数据随机性较小。根据在表2中的讨论,增加噪声对模型的预测结果影响不显著,因此,我们对瓦斯数据加入了信噪比为60的高斯白噪声,并对所测瓦斯浓度值取负对数后扩大十倍,以达到数据增强的目的。我们采用含噪输入预测策略来预测瓦斯浓度。假定测试输入数据值服从以该输入值为期望,方差为Sigma的高斯分布。图7展示了输入数据值服从不同方差的高斯分布时的预测结果。图中不同颜色的点代表预测点隶属不同参数空间的高斯过程。曲线表示预测分布的均值,并作为模型的预测结果。曲线的起伏的急缓表示预测的灵敏度。灰色阴影表示预测结果的主要变化区间(μ±2σ),反映预测分布的稳定性。方差越小,阴影面积越小,预测结果越稳定。对比图7(1)中展示的传统MGP模型预测策略下的回归和图7(2)中展示的含噪输入策略下的回归结果,当噪声方差Sigma较小时,两种预测策略有大致相似的预测精度,但从预测分布的稳定性上分析,含噪输入预测策略有更好的稳定性。对比图7(2)～(12),可以看出,随着Sigma变大,数据预测值随数据波动越缓和,换言之,数据波动对预测结果的影响则越小。这体现在实验结果中为当Sigma为0.001时,数据中的轻微波动就可带动预测值得变化,即预测结果对瓦斯浓度的变化非常敏感;相反的,当Sigma为6时,预测结果受短时的数据波动影响较小,换言之,较大噪声方差下的预测结果有较弱的灵敏性。这与MGP模型的含噪输入预测策略的理论结果是相符的。在考虑输入值服从高斯分布的情形下,方差越小,输入数据为高斯均值的概率越高,而高斯均值恰好为不含噪声的测试数据值,从而含噪输入预测策略下的拟合结果就越接近传统预测策略下的拟合结果。
图7 不同方差的高斯噪声下含噪输入预测策略在MGP模型中预测结果对比
Fig.7 Comparison of prediction results of the niMGP method with different variances of Gaussian noises
在实际煤矿开采工作中,瓦斯充斥在煤层之间,多为体积较小的瓦斯气体。只有煤层中瓦斯体积较大时,容易发生事故,而较大体积的瓦斯在巷道中气体渗出时间较长。传统预测对不同瓦斯气体体积均有相同的预测结果,但若采用含噪输入预测策略时,可以通过调节所测的浓度数据的噪声水平(方差)调整预测精度和灵敏度水平,使得对煤层中的不同体积的瓦斯气体进行合适的预警,因此可通过对方差的不同选择达到分级预警的目标。
6 结论
高斯过程混合模型的传统预测策略将输入数据作为确定数值做出模型预测,但实际中测得真实数据往往受到噪声的影响。为了解决这一问题,本文提出了高斯过程混合模型回归分析下的含噪输入预测策略,能够获得柔化预测结果,提高了预测稳定性。依此提出了煤矿瓦斯浓度的柔性预测方法,通过控制测试输入数据所含噪声分布方差的大小,对煤矿瓦斯浓度能够得到不同精确程度的回归预测结果,能够实现分级预警的目标。通过在合成数据和实际瓦斯浓度数据的实验结果验证了这种方法可行的和有效的,而且比传统的确定性预测方法更为稳定和可靠。
[1] 任乾. 我国煤矿瓦斯防治技术的研究进展及发展方向[J]. 当代化工研究, 2019(8): 106-107.
REN Qian. Research progress and development direction of coal mine gas prevention and control technology in China[J]. Modern Chemical Research, 2019(8): 106-107. (in Chinese)
[2] 韩磊. 基于监测技术的采煤工作面瓦斯浓度预测预警[J]. 山西焦煤科技, 2017, 41(Z1): 44- 48.
HAN Lei. Prediction of gas concentration based on monitoring technology of working face[J]. Shanxi Coking Coal Science & Technology, 2017, 41(Z1): 44- 48.(in Chinese)
[3] 孙亚杰. 灰色关联分析在煤与瓦斯突出预测中的应用[J]. 中州煤炭, 2013(4): 82- 84.
SUN Yajie. Application of grey relational analysis in coal and gas outburst prediction[J]. Zhongzhou Coal, 2013(4): 82- 84. (in Chinese)
[4] 张克树, 魏平儒, 景国勋. 瓦斯含量的灰关联分析及预测[J]. 煤矿安全, 1994, 25(10): 35-37,31.
ZHANG Keshu, WEI Pingru, JING Guoxun. Grey correlation analysis and prediction of gas content[J]. Safety in Coal Mines, 1994, 25(10): 35-37,31.(in Chinese)
[5] 彭泓. 基于数据挖掘与信息融合的瓦斯灾害预测方法研究[D]. 北京: 中国矿业大学(北京), 2013.
PENG Hong. Gas disaster prediction method research based on data mining and information fusion[D]. Beijing: China University of Mining and Technology (Beijing), 2013. (in Chinese)
[6] 付华, 丰盛成, 刘晶, 等. 基于DE-EDA-SVM的瓦斯浓度预测建模仿真研究[J]. 传感技术学报, 2016, 29(2): 285-289.
FU Hua, FENG Shengcheng, LIU Jing, et al. The modeling and simulation of gas concentration prediction based on de-eda-svm[J]. Chinese Journal of Sensors and Actuators, 2016, 29(2): 285-289.(in Chinese)
[7] 裴韶华. 基于优化的神经网络模型在矿井瓦斯涌出预测中的应用研究[D]. 太原:太原理工大学, 2014.
PEI Shaohua. Application research on optimized neural network model in mine gas emission prediction[D]. Taiyuan: Taiyuan University of Technology, 2014. (in Chinese)
[8] 姜雷. 基于BP神经网络的煤矿瓦斯浓度预测模型构建及仿真[J]. 矿业安全与环保, 2010, 37(4): 37-39.
JIANG Lei. Construction and simulation of mine gas concentration prediction model based on BP neural network[J]. Mining Safety & Environmental Protection, 2010, 37(4): 37-39.(in Chinese)
[9] 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121-1129,1137.
HE Zhikun, LIU Guangbin, ZHAO Xijing, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129,1137.(in Chinese)
[10] Tresp V. Mixtures of Gaussian processes[C]. Advances in Neural Information Processing Systems, 2001: 654- 660.
[11] CHEN Ziyi, MA Jinwen, ZHOU Yatong. A precise hard-cut EM algorithm for mixtures of Gaussian processes[M]∥Intelligent Computing Methodologies. Cham: Springer International Publishing, 2014: 68-75.
[12] 李柏椿. EM算法及其改进算法在参数估计中的应用研究[D]. 重庆: 重庆大学, 2017.
LI Baichun. Application of EM algorithm and its improved algorithm to parameter estimation[D]. Chongqing: Chong Qing University, 2017. (in Chinese)
[13] 张宏东. EM算法及其应用[D]. 济南: 山东大学, 2014.
ZHANG Hongdong. EM algorithm and applications[D]. Jinan: Shandong University, 2014. (in Chinese)
[14] RASMUSSEN C E. Gaussian processes in machine learning[M]∥Advanced Lectures on Machine Learning. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004: 63-71.
[15] GHAFFARI JADIDI M, MIRO J V, DISSANAYAKE G. Warped Gaussian processes occupancy mapping with uncertain inputs[J]. IEEE Robotics and Automation Letters, 2017, 2(2): 680- 687.
[16] BURKHART M C, HEO Y, ZAVALA V M. Measurement and verification of building systems under uncertain data: A Gaussian process modeling approach[J]. Energy and Buildings, 2014, 75: 189-198.
[17] GIRARD A, RASMUSSEN C E. Prediction at an uncertain input for Gaussian processes and relevance vector machines application to multiple-step ahead time-series forecasting[EB/OL]. 2003.http://mlg.eng.cam.ac.uk/pub/pdf/QuiGirRas03.pdf.
[18] CANDELA J Q, GIRARD A, LARSEN J, et al. Propagation of uncertainty in Bayesian kernel models-application to multiple-step ahead forecasting[C]∥2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings. (ICASSP′03). Hong Kong, China. IEEE, 2003: II-701.
