1 引言
在传统的多目标跟踪算法中,不管目标之间的间隔多小,都会假设每个目标独立地产生单个观测值。基于这一假设,数据关联处理中通常限制一个观测值(量测)最多只能分配给一个真实目标。但在实际应用中,传感器的分辨率是有限的,当两个目标在观测空间中足够接近时,传感器只能接收到一个来源于两个目标的观测值。对于此类间隔紧密目标,数据关联原来的限制条件不再适用,数据关联问题变得更加复杂。如果跟踪算法忽略传感器分辨率有限这一限制条件,可能会导致航迹过早地终结,或者关联到杂波,使得算法的跟踪性能明显下降。
Daum在文献[1]中分析了分辨率在多目标跟踪中的重要性,对未分辨量测的处理提出了明确的要求。在这之前,Chang和Bar-Shalom首先提出了处理未分辨量测的联合概率数据关联(Joint Probabilistic Data Association, JPDA)算法[2]。该算法设置了固定的距离阈值,将目标预测位置的差值与之比较来判断目标是否分辨,再结合JPDA算法和未分辨量测模型进行跟踪处理。文献[3]提出了一种新的未分辨量测概率模型,并将该模型添加到面向假设的MHT框架中来应对可能存在未分辨量测的场景。该算法中,未分辨量测概率模型被建模成一个高斯型函数,其合理且简单的描述得到了许多后续跟踪算法的认可。文献[4]在JPDA的基础上提出了耦合数据关联(Coupled Probabilistic Data Association, CPDA)算法与一种避免航迹合并的剪枝策略,这种剪枝策略提高了JPDA以及JPDA的其他改进算法的跟踪性能。文献[5]将CPDA等多种算法应用于未分辨量测的跟踪并通过仿真比较了它们的跟踪性能。Davey等人对概率多假设跟踪(Probabilistic Multiple Hypothesis Tracking, PMHT)算法进行了改进,将其用于未分辨量测的跟踪处理[6]。粒子滤波器可以应用于非线性非高斯状态空间的建模,文献[7]采用粒子滤波器以解决未分辨量测在数据关联中的“非线性”问题。
面向航迹的MHT(Track-Oriented MHT, TOMHT)[8-10]作为广泛应用的延迟决策跟踪方法,拥有较低的复杂性和良好的跟踪性能。基于TOMHT框架,文献[11]提出了随机化贪心-自适应搜索结构MHT(Greedy Randomized Adaptive Search Procedure MHT, GRASP-MHT)算法,并通过与其他跟踪算法的仿真比较,证明了GRASP-MHT的总体跟踪性能更优。该算法将数据关联问题转换为最大权重独立集问题(Maximum Weight Independent Set Problem, MWISP)并利用MWISP的近似求解方法实现最优全局假设的快速求解。
本文首先描述了GRASP-MHT和未分辨量测概率模型,然后将两者结合提出了一种改进的GRASP-MHT算法,用于可能含有未分辨量测场景的多目标跟踪处理。改进GRASP-MHT算法考虑了航迹关联未分辨量测的航迹假设,并计算了对应的航迹得分,进而将含有未分辨量测的数据关联问题建模成了MWISP,通过近似求解算法得到高质量的关联结果。仿真结果表明,改进算法相比原有算法性能明显改善,同时其计算时间没有大幅增加。
2 GRASP-MHT
2.1 TOMHT框架
TOMHT是一种 “自下而上”的MHT框架。该框架通过将上一时刻保留的航迹假设与当前时刻接收的量测进行关联,生成新的航迹假设(简称航迹),接着,根据生成的航迹枚举当前时刻所有可能的全局假设。得到的全局假设被用于若干个时刻前航迹关联结果的确认。图1给出了TOMHT算法的流程图。
航迹得分与不兼容航迹列表是全局假设生成模块的重要输入参数。航迹![]() 定义为时刻t的第i个航迹。航迹得分用于描述航迹
定义为时刻t的第i个航迹。航迹得分用于描述航迹![]() 代表真实目标的可能性,定义为航迹
代表真实目标的可能性,定义为航迹![]() 的所有量测来源于同一个真实目标与来源于杂波的对数似然比。如果不同航迹之间共用一个量测,则被认为是不兼容的。航迹的不兼容列表可以由上一时刻的不兼容航迹列表和当前时刻共用量测的航迹列表的并集表示。
的所有量测来源于同一个真实目标与来源于杂波的对数似然比。如果不同航迹之间共用一个量测,则被认为是不兼容的。航迹的不兼容列表可以由上一时刻的不兼容航迹列表和当前时刻共用量测的航迹列表的并集表示。
由航迹得分的定义可以得到航迹![]() 在时刻t的得分变化量
在时刻t的得分变化量
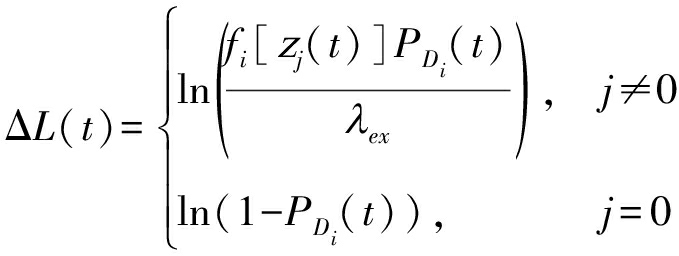
(1)
其中,λex代表杂波和新生目标的空间密度之和,在TOMHT中,所有未关联航迹的量测均用于起始新航迹,杂波量测和新生目标量测被同等对待;PDi(t)是当前时刻航迹i的检测概率;fi[zj(t)]是在航迹i一步预测值的条件下量测zj(t)的似然函数。当j≠0,zj(t)代表t时刻接收的第j个量测;当j=0,z0(t)代表航迹![]() 在当前时刻没有关联量测。
在当前时刻没有关联量测。
2.2 MWISP与GRASP生成全局假设
MWISP是一个经典的组合优化问题。定义一个无向图G=(V,E),V是图中的顶点集,E是图中的边集。如果在顶点集V中存在一个子集,这个子集内任意两个顶点之间没有属于边集E的边,则称这个子集为独立集。如果为每一个顶点赋予一个权重值,权重集W与无向图G就构成了一个有权无向图G=(V,E,W),MWISP就是在这个无向图中寻找一个权重和最大的独立集。可以用以下优化问题来表示MWISP。
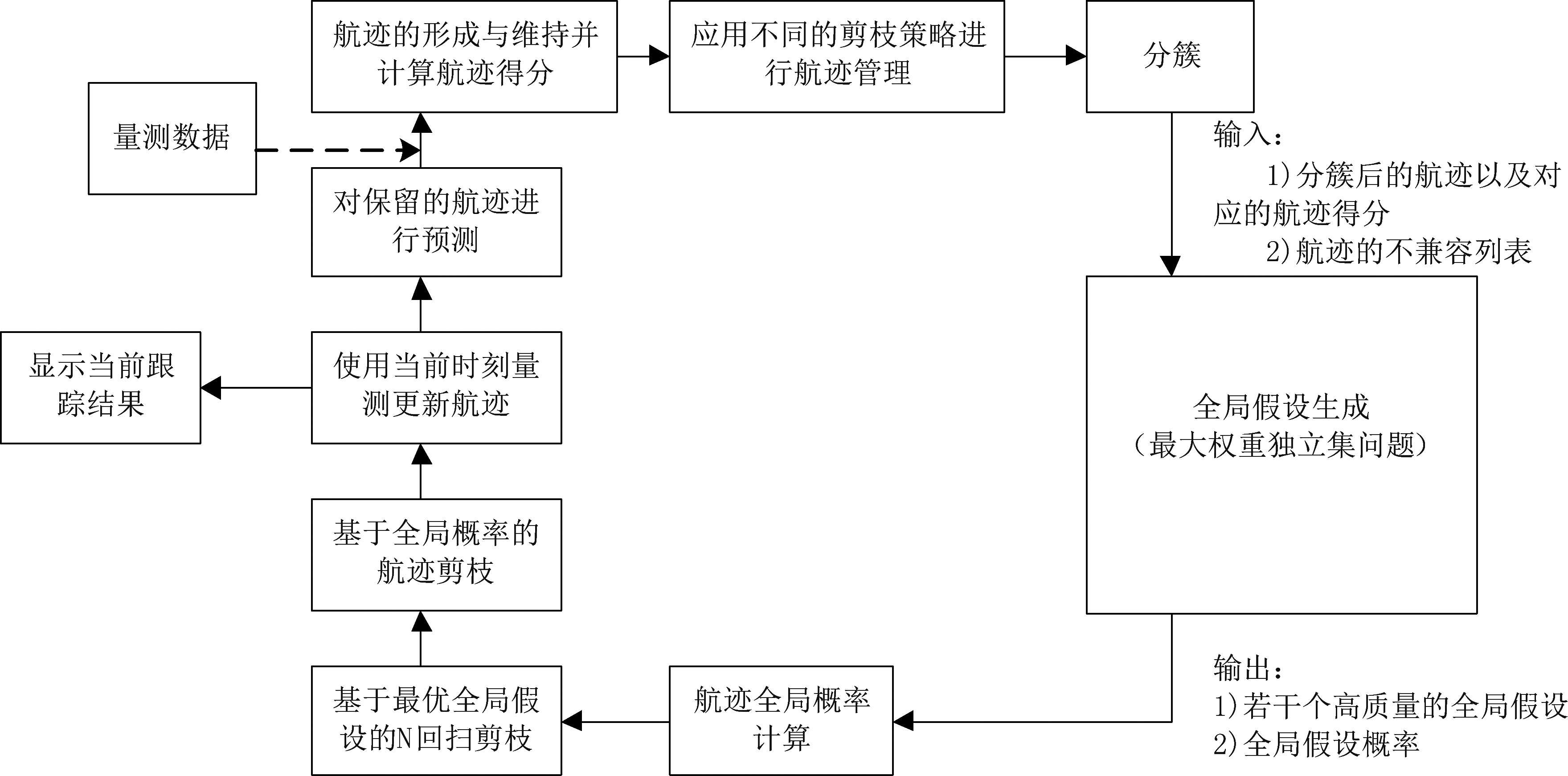
图1 TOMHT算法流程图
Fig.1 Flow chart of TOMHT algorithm
![]() s.t. xi+xj≤1,∀(vi,vj)∈E
s.t. xi+xj≤1,∀(vi,vj)∈E
(2)
其中vi∈V是顶点编号,wi∈W是每一个顶点对应的权重值,(vi,vj)∈E代表连接顶点vi和vj之间的边,二值变量xi∈{0,1}表示顶点vi是否选入独立集中。如果为每个航迹赋予一个顶点编号,航迹得分为对应的顶点权重,航迹之间的兼容关系通过顶点之间的边表示,则在当前时刻生成的航迹集合![]() 可以转换为一个有权无向图G,组合兼容的航迹生成全局假设的数据关联过程就转换为寻找无向图中最大权重独立集的过程。
可以转换为一个有权无向图G,组合兼容的航迹生成全局假设的数据关联过程就转换为寻找无向图中最大权重独立集的过程。
文献[12]论证了MWSIP问题与多维分配问题在TOMHT数据关联中的等效性。MWSIP是典型的NP难问题,但目前已有多种高效的近似求解算法,GRASP就是其中之一[13]。GRASP是一种多起点启发式算法,按照预先确定的迭代次数进行多次迭代运算。每次迭代运算主要由两个阶段组成:可行解的构造阶段和寻找局部最优解的局部搜索阶段。GRASP可以快速提供多个近似解,并通过局部搜索步骤保证这些近似解的质量。除了近似解中的最优结果,其余近似解也被保留。GRASP的这一特性与MHT在数据关联过程中枚举多个高得分全局假设的需求十分契合。因此在GRASP-MHT中,将MHT中的全局假设生成问题转换为MWSIP并通过GRASP方法求解,求得的所有近似解均可用于数据关联。
3 GRASP-MHT跟踪可能未分辨的目标
3.1 未分辨量测概率模型
两个目标是否分辨不仅仅与目标之间的距离有关,同时还与传感器的性能、信号处理的方法、信噪比等多种因素有关。两个目标未分辨的概率通常难以精确地进行描述。但直观地说,两个目标之间的距离越近,未分辨的概率越高,随着距离的增大,未分辨的概率随之降低。传感器的分辨率通常用能正确区分两个目标的最小距离来度量,距离越小,分辨率越高,两个目标未分辨的概率就越小。因此,可将两个目标未分辨的概率PM建模成与这两个因素有关的高斯概率模型[3]
PM(yk1,yk2|R)= ![]()
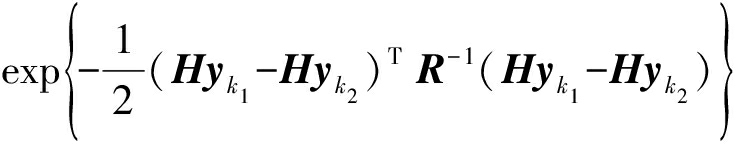
(3)
其中,d是观测状态的维数;yk1和yk2是航迹k1和k2当前时刻的状态预测值;H是观测矩阵;R是反映传感器分辨能力的矩阵,通常用雷达在不同观测维度的分辨率αd来计算![]() 选择对角阵形式的R意味着雷达在各个维度上的分辨能力是相互独立的。
选择对角阵形式的R意味着雷达在各个维度上的分辨能力是相互独立的。
3.2 关联未分辨量测的航迹得分
每当航迹与新的量测关联后,航迹得分都会有对应的变化量来描述关联的可能性大小。航迹-未分辨量测的关联假设同样会改变航迹的得分。但航迹-分辨量测与航迹-未分辨量测不完全一样,因此传统MHT航迹得分的计算公式不再适用。在推导关联未分辨量测的航迹得分前,需要先推导包含未分辨量测时的全局假设概率。Θt,h代表直至时刻t量测分配的一种可行的全局假设,由当前时刻量测分配的全局假设θh(t)与Θt-1,s构成
Θt,h={θh(t),Θt-1,s}
(4)
可以根据贝叶斯准则计算全局假设Θt,h的概率
P{Θt,h|Zt}=P{θh(t),Θt-1,s|Zt-1,Z(t)}= ![]() P{θh(t)|Θt-1,s,Zt-1}P{Θt-1,s|Zt-1}
P{θh(t)|Θt-1,s,Zt-1}P{Θt-1,s|Zt-1}
(5)
其中,c是归一化常数;Z(t)是当前时刻接收到的量测集;Zt是直至时刻t的所有量测集。等式右侧的最后一项P{Θt-1,s|Zt-1}是上一时刻全局假设的概率。
式(5)右侧第二项为考虑了时刻t航迹之间存在未分辨情况时全局假设的概率
P{θh(t)|Θt-1,s,Zt-1}= P{χh(t),κh(t)|Θt-1,s,Zt-1}= P{χh(t)|κh(t),Θt-1,s,Zt-1}P{κh(t)|Θt-1,s,Zt-1}= ![]() P{χh(t)|κh(t),Θt-1,s,Zt-1}=
P{χh(t)|κh(t),Θt-1,s,Zt-1}= ![]()
![]()
(6)
其中,M(t)是当前时刻量测的个数;θh(t)是Z(t)的一种可行的分配假设,由κh(t)和χh(t)组合形成,κh(t)将上一时刻保留的航迹划分为未分辨被检测的航迹组合、分辨被检测的航迹和未被检测的航迹,χh(t)在κh(t)的基础上将量测分配给航迹组合、单独的航迹或者杂波;m为航迹组合的编号,该航迹组合在全局假设中被认为是未分辨的,{y(t)}m是第m个航迹组合内每一个航迹的预测状态的集合;δn是指示符号,δn=1指示第n个航迹组合或者航迹被检测,δn=0则未被检测;PDn(t)是第n个航迹组合或者航迹的检测概率,未分辨的航迹组合检测概率用![]() 表示;φ是该全局假设中杂波量测的个数;V是观测区域(关联门)的体积(或面积)。
表示;φ是该全局假设中杂波量测的个数;V是观测区域(关联门)的体积(或面积)。
令![]() 其中θ(ji, jm)代表第j个量测分配给第ji条航迹或者第jm个航迹组合,若ji=jm=0,则第j个量测被认为是杂波量测。式(5)右侧第一项为考虑了存在未分辨情况时量测的似然函数,且有
其中θ(ji, jm)代表第j个量测分配给第ji条航迹或者第jm个航迹组合,若ji=jm=0,则第j个量测被认为是杂波量测。式(5)右侧第一项为考虑了存在未分辨情况时量测的似然函数,且有
p(Z(t)|Θt-1,s,θh(t){ji, jm},Zt-1)= ![]()
![]()
(7)
式中,τj和ρj均为指示符号,指示在θh(t)中第j个量测是否分配给单独的航迹或者航迹组合,一个可行的θh(t)需满足τj+ρj≤1,∀j≠0。假定杂波在观测区域内服从均匀分布,则杂波量测的概率密度函数为V-1;gjm[zj(t)]与fji[zj(t)]类似,是量测zj(t)关于航迹组合jm一步预测值的似然函数。
基于式(5)~式(7),可以写出直至时刻t的全局假设的后验概率为
P{Θt,h|Zt}= ![]()
![]() P{Θt-1,s|Zt-1}
P{Θt-1,s|Zt-1}
(8)
针对两个目标航迹的场景,可以枚举出两个航迹![]() 和
和![]() 的全局假设情况:未分辨且关联未分辨量测Θt,h1、分辨且分别关联不同量测Θt,h2、分辨但其中一个未关联量测Θt,h3、均未关联量测Θt,h4。Θt,h3包含着两种情况,这里我们假设
的全局假设情况:未分辨且关联未分辨量测Θt,h1、分辨且分别关联不同量测Θt,h2、分辨但其中一个未关联量测Θt,h3、均未关联量测Θt,h4。Θt,h3包含着两种情况,这里我们假设![]() 关联了量测但
关联了量测但![]() 未关联。不同全局假设中,可将航迹
未关联。不同全局假设中,可将航迹![]() 和
和![]() 对全局假设贡献分量的对数值作为它们的航迹得分[8,14]
对全局假设贡献分量的对数值作为它们的航迹得分[8,14]
ΔLi1i2(k)= 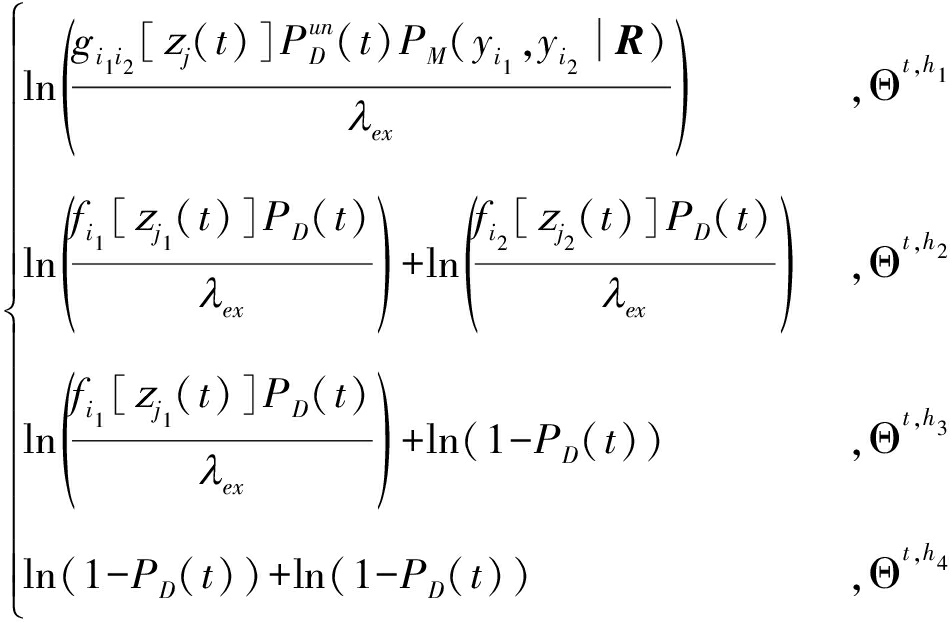
(9)
不考虑未分辨量测时,Θt,h2、Θt,h3和Θt,h4其实是单个航迹的全局假设的排列组合结果。考虑未分辨量测时,产生了新的全局假设Θt,h1并得到这种假设下的航迹得分变化量。实际跟踪中关注的是单个航迹的得分更新,在全局假设Θt,h1中,缺乏更多的先验信息来计算不同航迹对于航迹得分更新的贡献比例,因此默认单条航迹的得分变化量为![]()
3.3 含未分辨目标的MWISP
存在可能未分辨量测的跟踪场景中,一个量测最多源自一个真实目标的假设不再成立,一个量测可以同时关联多条航迹。这种情况下,无法用无向图中的最大权重独立集来表示该全局假设,全局假设生成问题无法再转换为MWISP。本节提出了一种新的思路,依旧将含未分辨量测的全局假设生成问题转换为MWISP,以便GRASP或者其他近似求解算法仍然适用。
在原来定义的无向图G中,多条航迹关联同一个量测意味着这些航迹之间是不兼容的,对应的顶点之间存在边(vi,vj)表示不兼容的关系,同时选中这些顶点意味着生成的顶点集不为独立集。GRASP与其他近似求解算法只能求得可行的独立集,无法用于含未分辨量测的全局假设的生成。另外,量测以未分辨的形式分配给多条航迹,其航迹得分,即顶点对应的权重,也会发生相应的改变,这些问题都不利于MWISP的求解。如果将多条航迹关联一个未分辨量测的情况,看作是将量测分配给了一个航迹组合,这个未分辨的航迹组合与航迹有着同等的“地位”,问题将得到简化。将每一个航迹(或航迹组合)-量测关联假设生成一个顶点vi,权重wi代表航迹(或航迹组合)得分,边(vi,vj)表示航迹(或航迹组合)之间在最近N+1个时刻中有使用共同的量测。这样生成的有权无向图G=(V,E,W)仍然可以完整描述航迹树的信息并继续适用约束条件来生成最大权重独立集。在该无向图中,约束条件xi+xj≤1,∀(vi,vj)∈E指一个量测只有一种分配情况,可以是分配给单独的某条航迹,也可以以未分辨量测的形式分配给某个航迹组合。
下面通过一个例子来说明。图2航迹树中每一个圈代表一种航迹-量测的关联假设,圈内的数字是量测在该时刻的编号,两个圈之间用虚线连接代表这两个节点共同组成了航迹组合-未分辨量测的关联假设。三个时刻的数据关联形成了两株航迹树。使用新生成的两个叶子节点表示航迹组合-未分辨量测的关联假设,原来的叶子节点仅表示航迹-分辨量测的关联假设。需要注意的是,如果确认了航迹组合-未分辨量测的关联假设,则两个叶子节点将同时保留,如果这个关联假设被剪除,则两个叶子节点将同时被删除。尽管这两个节点关联了同一个量测2,但它们是兼容的,而且是绑定的。
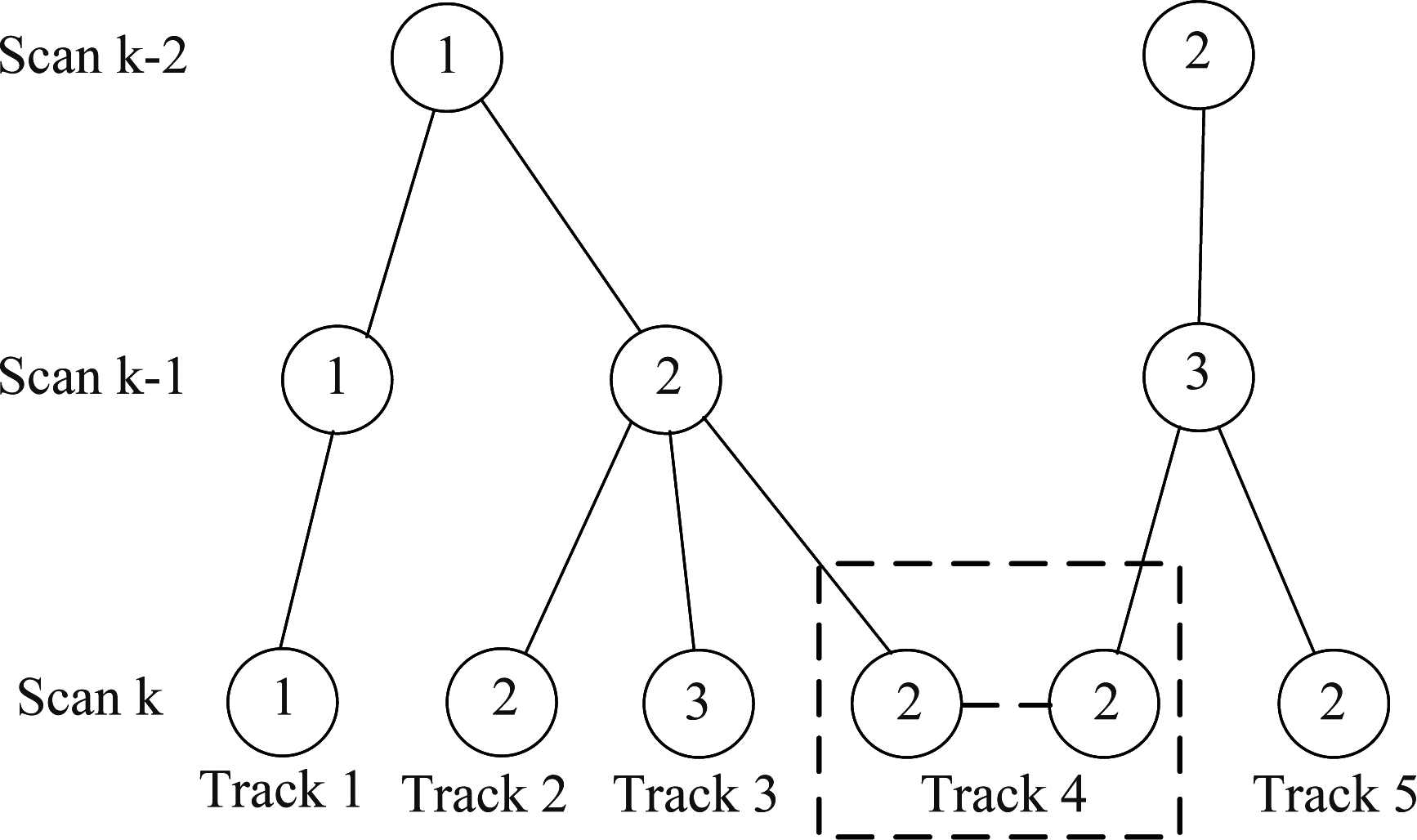
图2 考虑未分辨量测的两株航迹树
Fig.2 Two track trees considering unresolved measurements
图3是该航迹树生成的无向图。在无向图中,表示航迹组合-量测关联假设的两个叶子节点只用了一个顶点(Track4)表示。一方面是因为这两个叶子节点是“绑定”的,要同时保留或者删除,另一方面可以减少顶点集的个数,从而降低计算复杂度。无向图中,航迹1、2、3和4之间的不兼容源自于父节点的不兼容关系,航迹2、4和5之间不兼容是因为在当前时刻关联了同一个量测2,无论量测2是否未分辨。借助GRASP可以在无向图中得到最大权重独立集与对应的全局假设,如果独立集中含有航迹4顶点,则该全局假设中量测2以未分辨的形式分配给了航迹组合,解决了航迹关联未分辨量测 “多对一” 的问题。
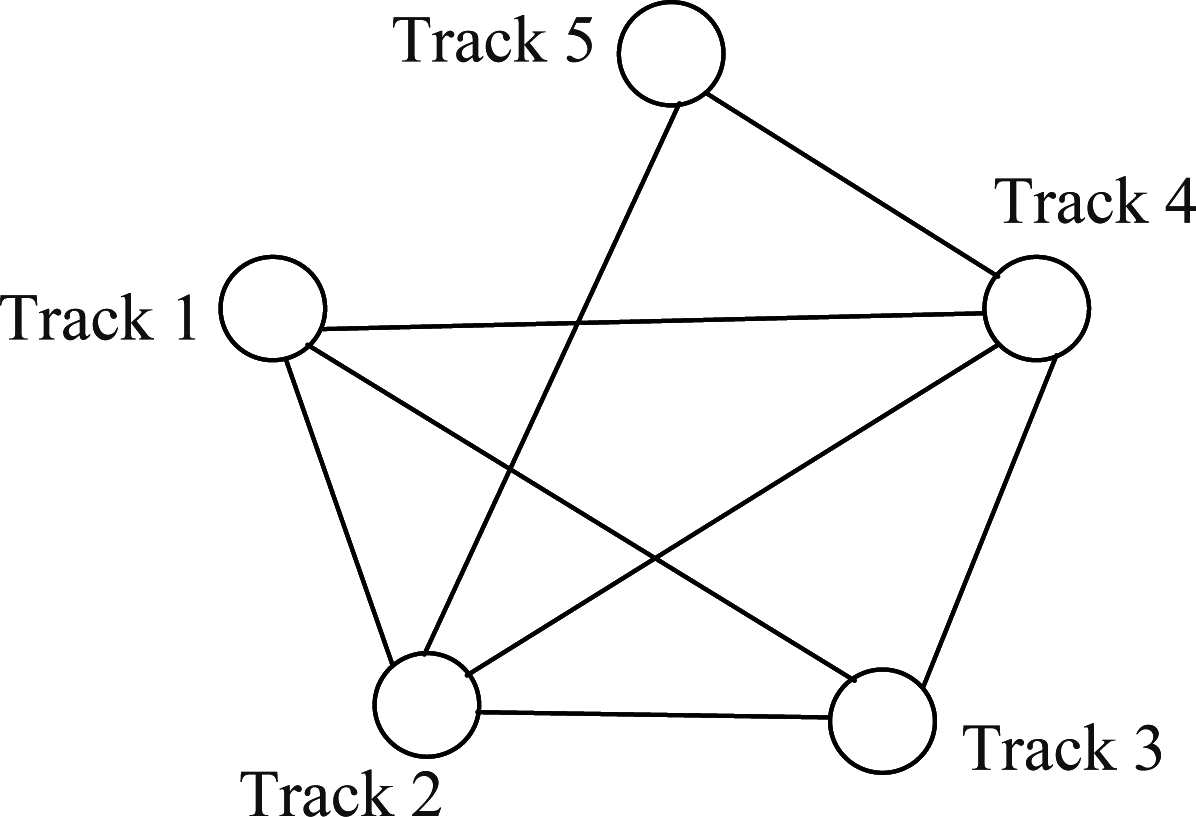
图3 对应的无向图
Fig.3 Corresponding undirected graph
4 仿真分析
为评价本文改进GRASP-MHT算法的跟踪性能,设置了两个跟踪场景,并将改进算法分别与GRASP-MHT及含合并量测模型的JPDA(JPDA with merged measurement model, JPDAM)算法进行了比较。
仿真场景A的二维航迹模型如图4(a)所示,仿真场景B的二维航迹模型如图4(b)所示。
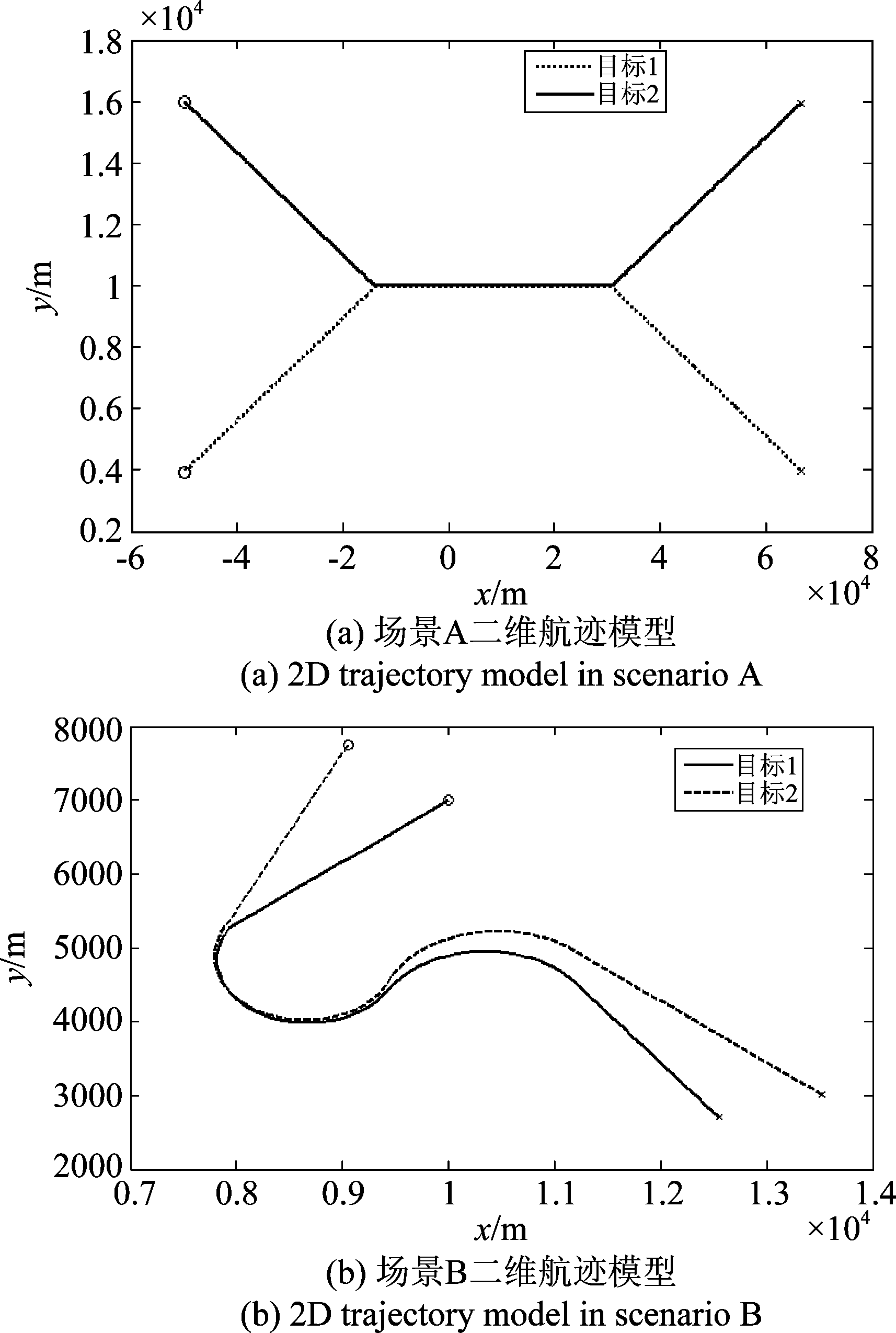
图4 二维航迹模型
Fig.4 2D trajectory model
4.1 航迹参数和跟踪性能指标
跟踪场景A中,目标1和目标2起始间隔足够大,分别以恒定的速度(vx,vy)和(vx,-vy)运动一段时间,直至两个目标之间的间隔足够小。此时两个目标的间隔为Δ。随后两个目标以恒定的速度(vx,0)运动。一段时间Tm后,目标1和目标2重新分离,以(vx,-vy)和(vx,vy)的速度继续运动直至两个目标间隔足够大。
整个航迹模型的参数设置如下:vx=300 m/s;vy=50 m/s;Δ=70 m;采样间隔T=2 s,间隔紧密运动时间Tm=150 s;总跟踪步数为195,间隔紧密运动的步数为75;传感器的分辨率α=αx=αy=200 m;杂波密度λf=10-2 km-2;检测概率![]() 轴和y轴的量测误差标准差为80 m;过程噪声标准差为10 m。跟踪采用了直角坐标系和具有高斯白噪声加速度模型的线性卡尔曼滤波器。
轴和y轴的量测误差标准差为80 m;过程噪声标准差为10 m。跟踪采用了直角坐标系和具有高斯白噪声加速度模型的线性卡尔曼滤波器。
跟踪场景B源自文献[7]。两个目标的轨迹可分为四个阶段:阶段一,两个目标分别以恒定的速度作直线运动,直至两个目标间隔足够小;阶段二,两个目标以相同的固定的转弯速率做圆周运动;阶段三,两个目标分别以不同的固定的转弯速率做圆周运动,目标之间的间隔不断增大;阶段四,两个目标分别以恒定的速度作直线运动。具体的航迹模型参数设置可见于参考文献[7]。跟踪同样采用了直角坐标系和具有高斯白噪声加速度模型的线性卡尔曼滤波器。
仿真中采用以下指标来评价跟踪性能:
1)NT:真实航迹数目。真实航迹是指由算法给出的航迹,其中至少有50%的量测来自同一个目标。
2)Nsuc:蒙特卡罗仿真中成功的次数。如果跟踪算法输出的真实航迹数量与真实目标个数相等,就认为成功完成了跟踪任务。
3)Rcc:目标量测的正确关联率。跟踪结果中真航迹的所有量测中来自真实目标的量测所占的比率。
4)Rccs:目标量测的正确或交换关联率[5,15]。在跟踪场景中,由于无法区分距离过近的两个目标,若在目标分离后,航迹关联到的量测是另外一条真实航迹的量测,则属于“交换关联”的量测。
5)TE:一次扫描数据处理所需时间,用于衡量不同算法的计算速度。
6)OSPA距离[16]:衡量多目标的真实航迹位置与多目标的估计输出结果的差异,OSPA越小输出结果越接近真实情况。
4.2 仿真结果
在跟踪场景A中,分别对改进GRASP-MHT算法和GRASP-MHT算法进行了200次蒙特卡罗仿真。表1总结了两种算法的跟踪结果。其中Rcc和Rccs这两个参数只统计成功完成跟踪任务的数据。图5给出了两种算法在仿真中的典型跟踪结果,“°”和“×”分别代表航迹的起点和终点。两种算法的OSPA距离比较如图6所示。
表1 两种算法跟踪性能对比
Tab.1 Comparing performance between two algorithms
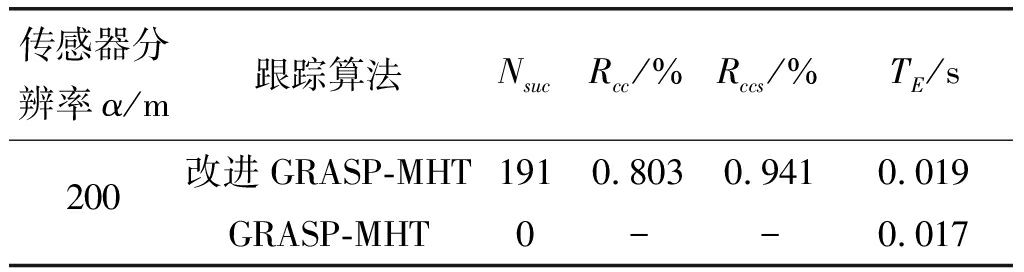
传感器分辨率α/m跟踪算法NsucRcc/%Rccs/%TE/s200改进GRASP-MHT1910.8030.9410.019GRASP-MHT0--0.017
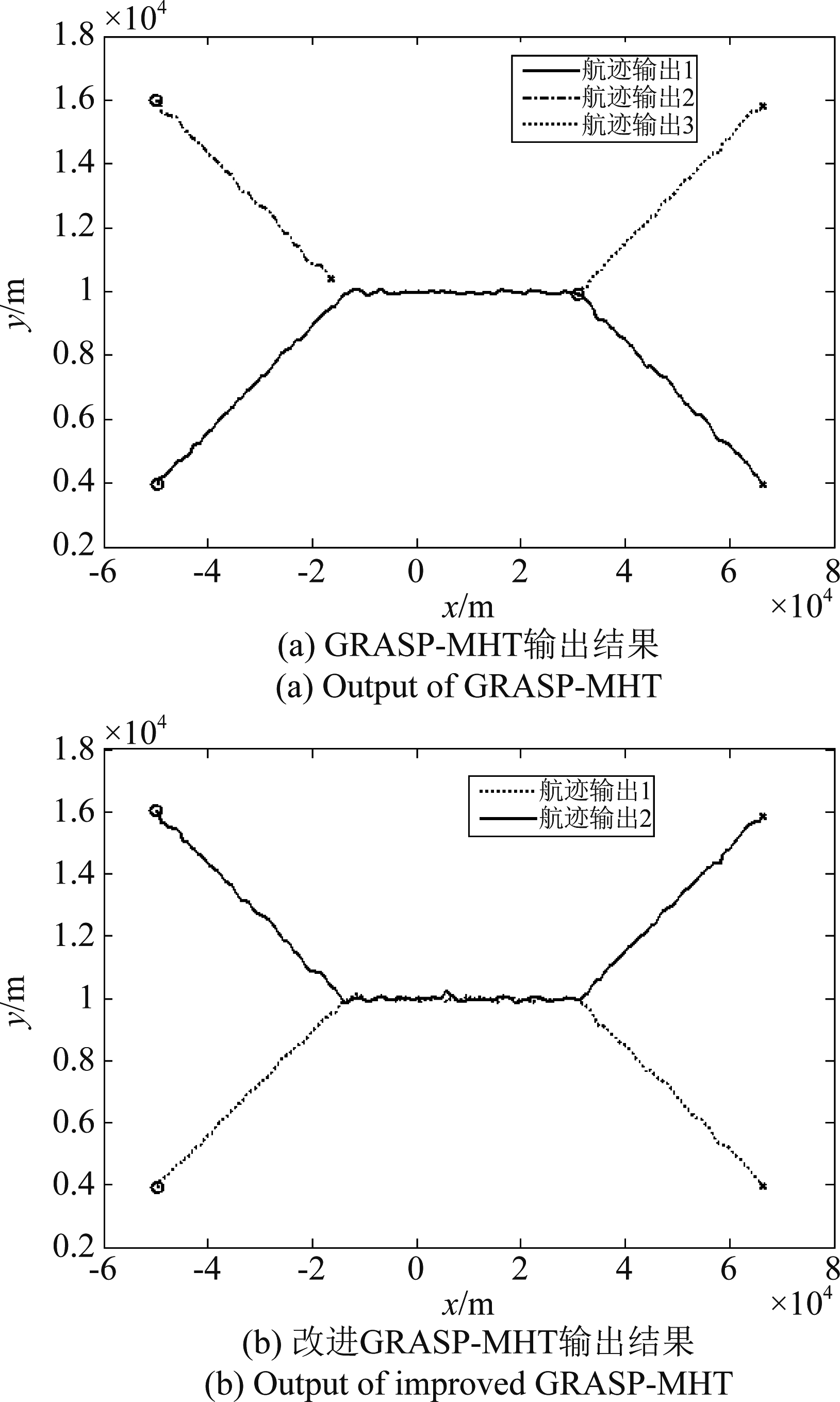
图5 两种算法在分辨率有限时的典型输出航迹图
Fig.5 Typical output of two algorithms when resolution is finite
图5(a)是GRASP-MHT的输出结果,图中有3条输出航迹。两个目标平行运动的时间段只存在一条航迹输出,过早终结的航迹输出2和后来新起始的航迹输出3实际上属于同一个目标。图5(b)是改进GRASP-MHT的输出结果,图中给出了两条真实航迹。
在分辨率有限时,GRASP-MHT没有一次能成功输出两条真实航迹,而改进的GRASP-MHT给出了191次两条真实航迹的结果,成功率为95.5%。分析可知,两个间隔紧密的目标长时间只能给出一个未分辨的量测,不考虑未分辨量测的跟踪算法会认为其中一条航迹“提前”终止了,在真实目标航迹分离后,跟踪算法会认为出现了一条新的航迹。在图6的60~135帧段,GRASP-MHT只输出了一条航迹估计,与真实目标数不同,使得它的OSPA距离远远大于改进GRASP-MHT的OSPA距离。另外,改进GRASP-MHT的跟踪的正确或交换关联率Rccs达到94.1%,这说明在不考虑航迹交换的情况下,改进GRASP-MHT既能很好地维持两个长时间未分辨目标的航迹,同时保留了GRASP-MHT的优秀跟踪性能。如果在目标分离的时刻,其中一条航迹出现漏检,改进算法可能会做出错误的判断,认为原有的两个目标沿着其中一条航迹继续做编队运动,另一条航迹为新生目标的运动轨迹。这种错判会导致目标分离后真实航迹目标个数估计出错,OSPA距离有所增大。但总的来说,改进GRASP-MHT表现出了优于GRASP-MHT的跟踪性能。
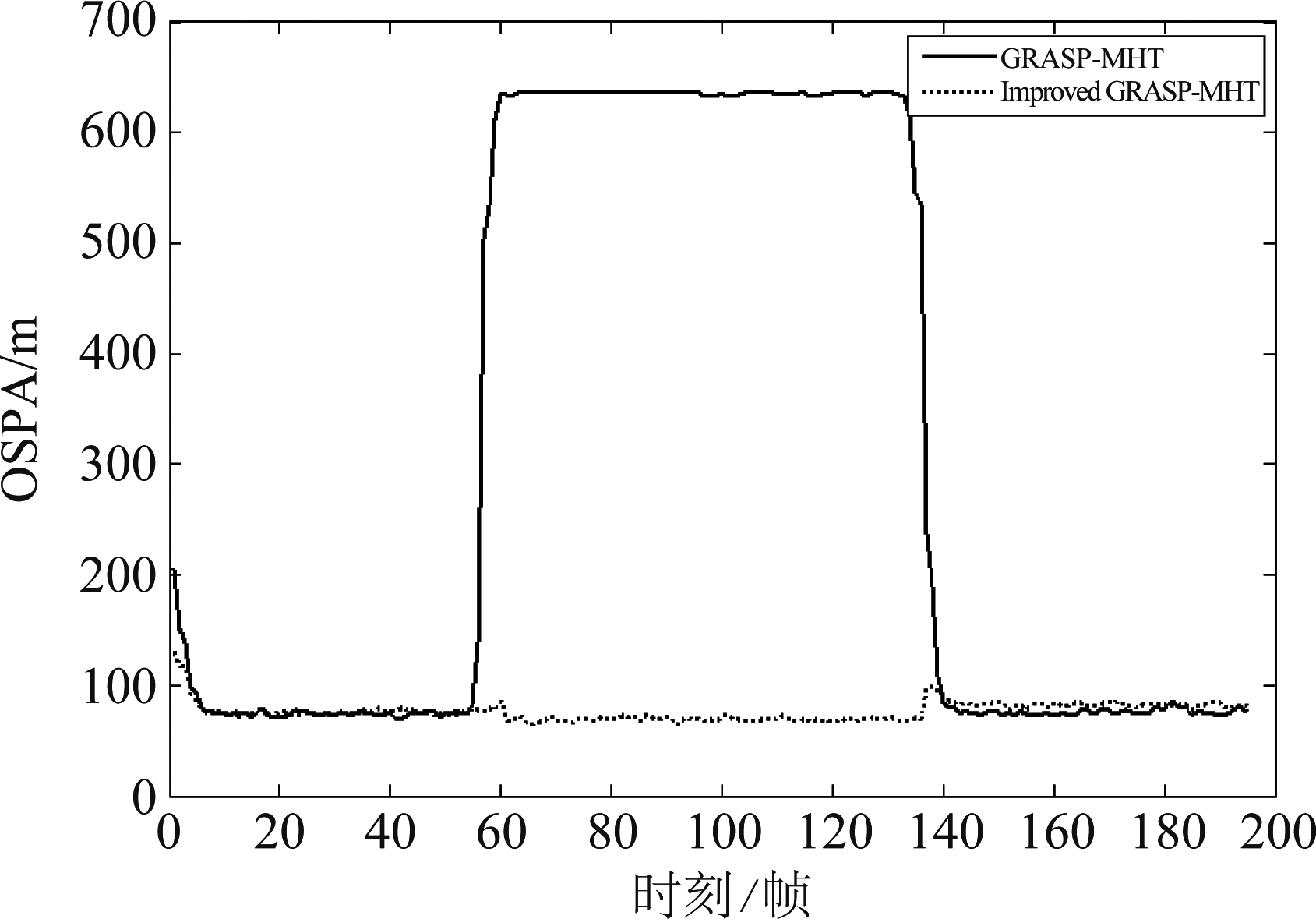
图6 OSPA距离比较
Fig.6 Comparison of OSPA distance
在计算时间上,结果显示改进GRASP-MHT的TE稍大于GRASP-MHT的TE。引入未分辨量测的模型以及航迹-未分辨量测的数据关联假设,增加了数据关联的计算复杂度。但得益于GRASP对MWISP的优秀求解能力,计算时间并没有大幅度增加。
在跟踪场景B中,分别对改进GRASP-MHT算法和GRASP-MHT算法进行了200次蒙特卡罗仿真。表2总结了两种算法的跟踪结果。其中Rcc和Rccs这两个参数只统计成功完成跟踪任务的数据。图7给出了两种算法在仿真中的典型跟踪结果。
表2 两种算法跟踪性能对比
Tab.2 Comparing performance between two algorithms

传感器分辨率α/m跟踪算法NsucRcc/%Rccs/%TE/s80改进GRASP-MHT1710.8920.9750.011GRASP-MHT0--0.010
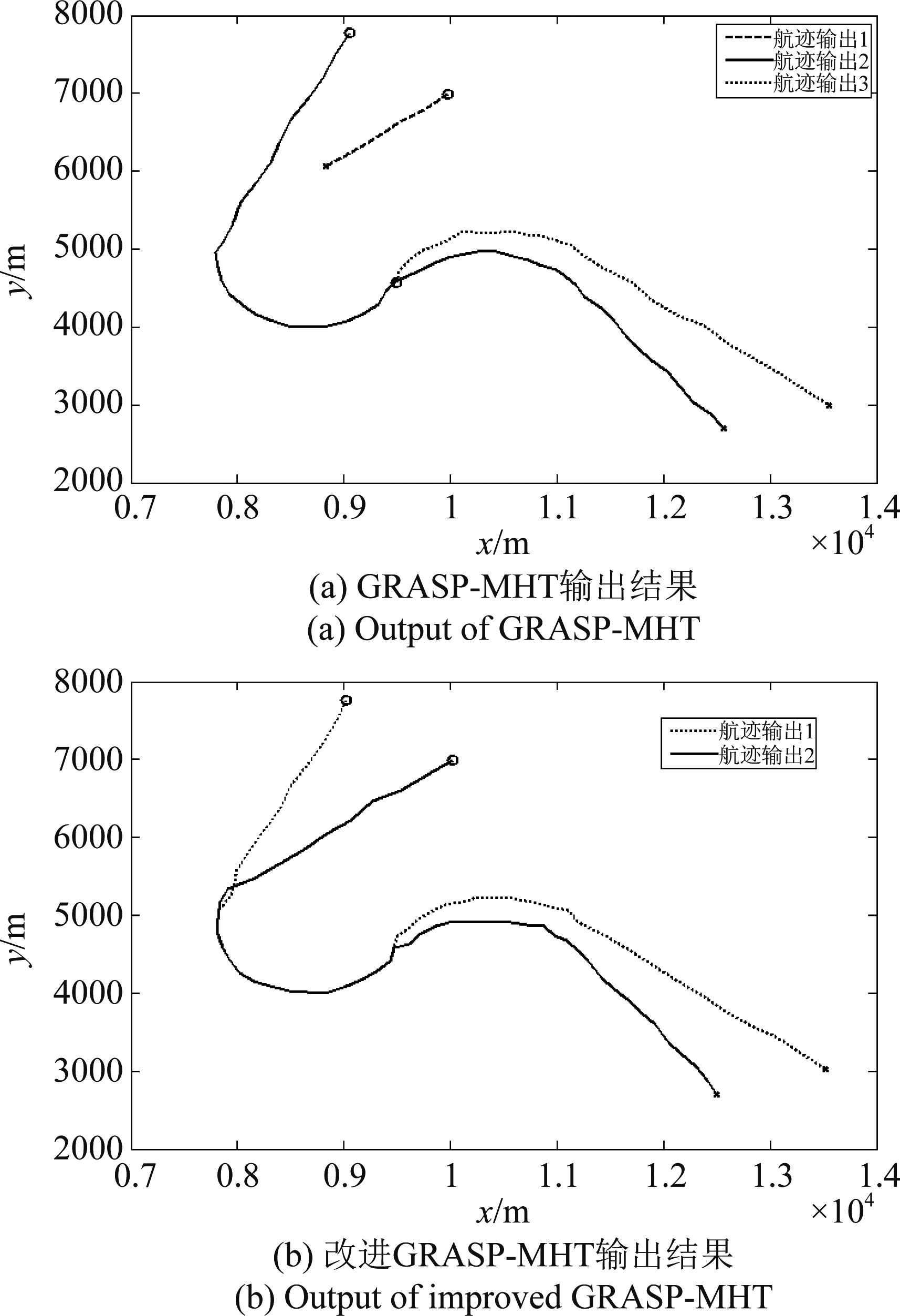
图7 两种算法在分辨率有限时的典型输出航迹图
Fig.7 Typical output of two algorithms when resolution is finite
对比表1和表2可知,两种算法的性能在场景A与场景B中表现基本一致。改进的GRASP-MHT在场景B中,成功跟踪次数稍有下降,但依旧保持了较高的成功次数Nsuc与较高的跟踪正确或交换关联率Rccs。成功跟踪次数下降的原因在于,线性卡尔曼滤波器不能很好地对机动阶段的目标运动状态进行准确的预测,从而导致了航迹的断裂,航迹目标个数估计出错。可以看出,在不同的跟踪场景中,改进的GRASP-MHT均能有效地跟踪处理未分辨目标,跟踪性能明显优于未考虑分辨率限制的GRASP-MHT。
在跟踪场景B中,分别对改进GRASP-MHT算法和JPDAM算法进行了200次蒙特卡罗仿真。两种算法的OSPA距离比较如图8所示。
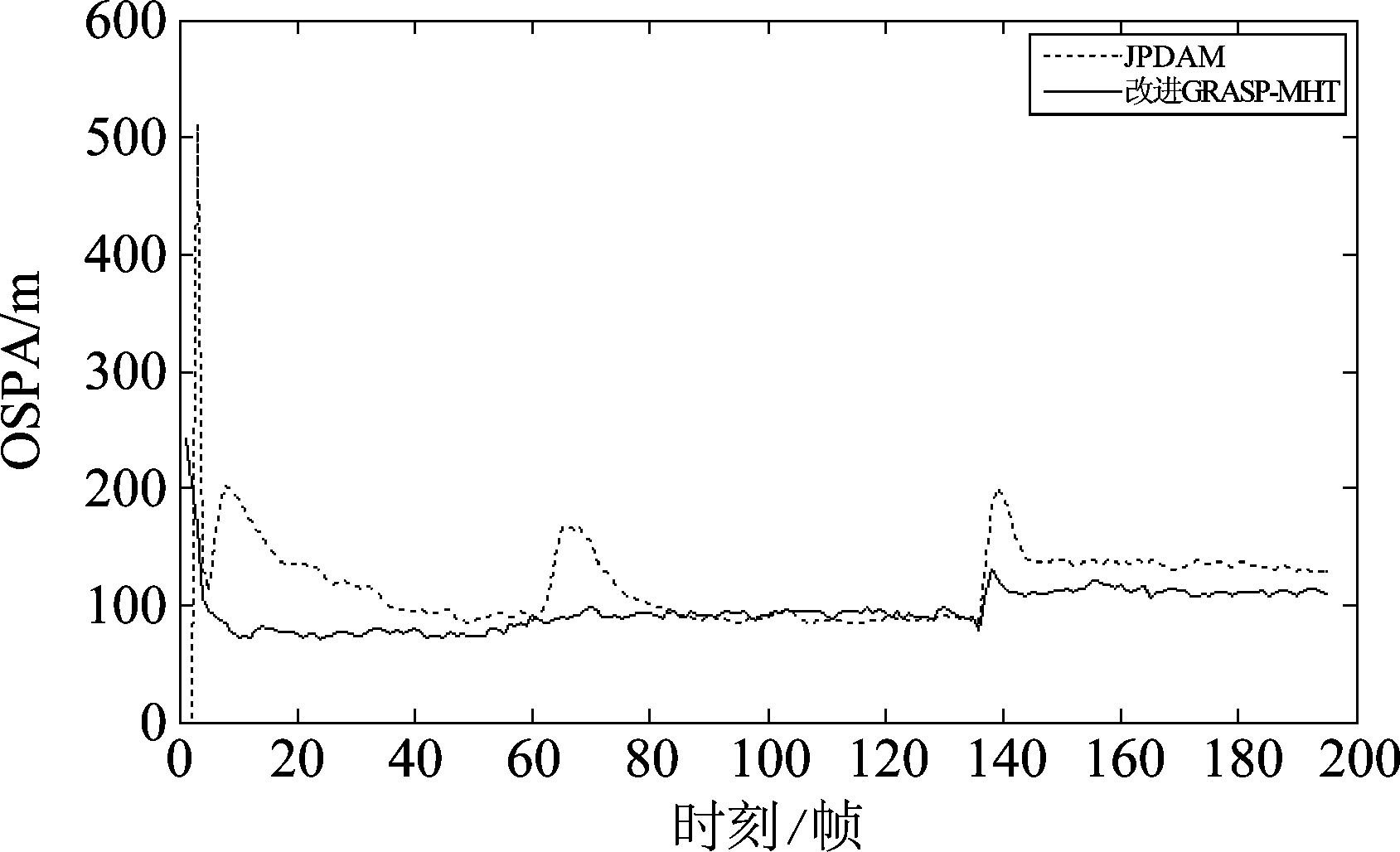
图8 OSPA对比图
Fig.8 Comparison of OSPA distance
在整个跟踪阶段中,改进GRASP-MHT的OSPA距离基本都小于JPDAM的OSPA距离。在航迹开始编队运动的时刻(65帧前后)与航迹开始分离的时刻(140帧前后),两种算法的状态估计误差都有不同程度的突增。从图中可以看出,改进GRASP-MHT算法相比JPDAM算法能提供更加准确的状态估计。另外,JPDAM算法同样面临着目标分离后真实航迹目标个数估计出错的问题,而且相比改进算法问题更加突出,表现在140帧后,JPDAM的OSPA距离相比改进算法的OSPA距离更大。总体来说,改进GRASP-MHT的跟踪性能相比JPDAM有一定的提升。
5 结论
本文基于TOMHT框架,推导了航迹关联未分辨量测的得分,将多个航迹-未分辨量测的“多对一”关联假设转化为航迹组合-量测的“一对一”关联假设,将未分辨量测概率模型与GRASP-MHT相结合,得到了改进GRASP-MHT算法。通过仿真将改进GRASP-MHT与GRASP-MHT及JPDAM的跟踪性能进行了比较。结果表明,改进GRASP-MHT在保留了GRASP-MHT优点的同时,很好地解决了两个目标长时间未分辨的跟踪问题,其计算时间相比GRASP-MHT只是略有增加。在不同场景下,改进GRASP-MHT均展现出了优于,至少是不逊色于GRASP-MHT的跟踪性能。另外,实验结果表明改进GRASP-MHT相比JPDAM算法跟踪性能更加稳定。
[1] FREDERICK E, DAUM, ROBERT J, et al. Importance of resolution in multiple-target tracking[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1994, 2235:329-338.
[2] CHANG Kuochu, BAR-SHALOM Y. Joint probabilistic data association for multitarget tracking with possibly unresolved measurements and maneuvers[J]. IEEE Transactions on Automatic Control, 1984, 29(7): 585-594.
[3] KOCH W, VAN KEUK G. Multiple hypothesis track maintenance with possibly unresolved measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 883- 892.
[4] BLOM H A P, BLOEM E A. Probabilistic data association avoiding track coalescence[J]. IEEE Transactions on Automatic Control, 2000, 45(2): 247-259.
[5] BLOM H A P, BLOEM E A. Bayesian tracking of two possibly unresolved maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 612- 627.
[6] DAVEY S J. Tracking possibly unresolved targets with PMHT[C]∥2007 Information, Decision and Control. Adelaide, SA, Australia. IEEE, 2007: 47-52.
[7] VERES G V, NORTON J P. Improved particle filter for multitarget-multisensor tracking with unresolved observations[C]∥IEE Target Tracking: Algorithms and Applications (Ref. No.2001/174). Enschede, Netherlands. IET, 2002: 12/1-12/5vol.1.
[8] BAR-SHALOM Y, BLACKMAN S S, FITZGERALD R J. Dimensionless score function for multiple hypothesis tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 392- 400.
[9] 孙进平, 付福其, 付锦斌, 等. 应用超图匹配的多假设群目标跟踪方法[J]. 信号处理, 2017, 33(11): 1497-1504.
SUN Jinping, FU Fuqi, FU Jinbin, et al. Multiple hypothesis group target tracking using hypergraph matching[J]. Journal of Signal Processing, 2017, 33(11): 1497-1504.(in Chinese)
[10] LI Qing, SUN Jinping, SUN Wei. An efficient multiple hypothesis tracker using max product belief propagation[C]∥2017 20th International Conference on Information Fusion (Fusion). Xi’an, China. IEEE, 2017: 1- 6.
[11] REN Xiaoyi, HUANG Zhipei, SUN Shuyan, et al. An efficient MHT implementation using GRASP[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 86-101.
[12] PAPAGEORGIOU D J, SALPUKAS M R. The maximum weight independent set problem for data association in multiple hypothesis tracking[C]∥Optimization and Cooperative Control Strategies, 2009: 235-255.
[13] FEO T A, RESENDE M G C, SMITH S H. A greedy randomized adaptive search procedure for maximum independent set[J]. Operations Research, 1994, 42(5): 860- 878.
[14] CORALUPPI S P, CARTHEL C A. Track-oriented MHT with unresolved measurements[C]∥2019 Sensor Data Fusion: Trends, Solutions, Applications (SDF). Bonn, Germany. IEEE, 2019: 1- 6.
[15] SCHOENECKER S, WILLETT P, BAR-SHALOM Y. Resolution limits for tracking closely spaced targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(6): 2900-2910.
[16] ZHANG Zhiguo, SUN Jinping, LI Qing, et al. A novel MS-MeMBer filter for extended targets tracking[J]. IEEE Access, 2020, 8: 37596-37607.
