1 引言
雷达目标检测常被视为一个二元假设统计检验问题，主要通过对杂波背景进行统计建模，并结合检测算法，设计相应检测器实现目标检测[1-3]。矩阵CFAR(Constant False Alarm Rate, CFAR)检测是一种新兴的雷达目标检测方法，将回波数据构建为埃米特正定(Hermitian Positive Definite, HPD)的协方差矩阵，这样的协方差矩阵集合构成了具有一定空间结构的矩阵流形，也是一种黎曼流形，进而建立黎曼流形的几何结构与目标检测的联系，将统计检验问题转化为流形上距离差异性度量问题，为研究目标检测问题和检测方法提供了一种新的技术途径[4- 6]。法国Thales Air Systems研究员Barbaresco等人在2008年提出了一种矩阵CFAR检测器，基于正定矩阵流形实现脉冲多普勒雷达的矩阵CFAR检测，避免了因回波脉冲数较少带来的多普勒谱展宽导致能量泄露问题，并验证了该检测方法相对于传统FFT-CFAR检测方法的优越性[4,7]。近年来，矩阵CFAR检测方法在国内外得到了广泛研究与应用，包括在黎曼流形上通过定义距离检测器等几何方法研究雷达目标检测，将矩阵CFAR检测技术应用到飞机尾流目标检测等[5,8-10]。国内研究人员还提出了基于信息散度的目标检测方法，对矩阵流形的各个差异性度量、矩阵流形的几何结构与检测性能之间的关系等进行了诸多研究[5,11]。研究矩阵CFAR检测方法主要有以下优势：(1)在检测需较短反应时间的目标时，能够避免一个相干处理周期(Coherent Processing Interval, CPI)内脉冲数较少导致传统CFAR检测方法处理带来的性能损失；(2)区别于传统采用算术均值估计杂波功率的方法，利用流形内在几何结构，采用几何均值来估计杂波功率受复杂杂波环境影响相对较小，具有更好的稳健性。提升复杂杂波背景下的检测性能是对目标进行有效检测的关键，降维是一种减少数据间信息冗余，提取数据特征的重要手段，本文正是基于雷达目标检测的矩阵CFAR检测方法，采用流形降维方法提取并增强目标与杂波的区分性特征，实现目标增强检测，以进一步提升检测性能。
因此，以雷达目标检测的信息几何方法为基础框架，本文重点研究流形降维的增强检测方法，主要解决复杂杂波背景下，特别是在强杂波背景下信杂比较低导致已有方法的检测性能有限，难以实现目标有效检测的问题。通过降维增强目标与杂波的区分性特征，提出一种基于黎曼流形监督降维的矩阵CFAR增强检测方法。最后采用测地线距离类和散度类作为流形的几何距离度量方式，并基于仿真和实测数据分析验证所提方法的检测性能。
2 几何检测模型与流形降维原理
2.1 矩阵CFAR检测模型
根据每个距离单元存储的雷达接收回波数据z=(z1,z2,...,zn)T，利用脉冲间的相关特性，可以将其构建为HPD协方差矩阵Rz
(1)
其中，E表示统计期望，(·)H表示共轭转置，
表示z的复共轭，ak为相关系数，由时间平均估计得
(2)
且
这样的HPD协方差矩阵集合
表示复数域)构成了一个具有一定空间结构的黎曼流形[12]。利用此黎曼流形的几何结构进行矩阵CFAR检测，基本原理如图1所示。
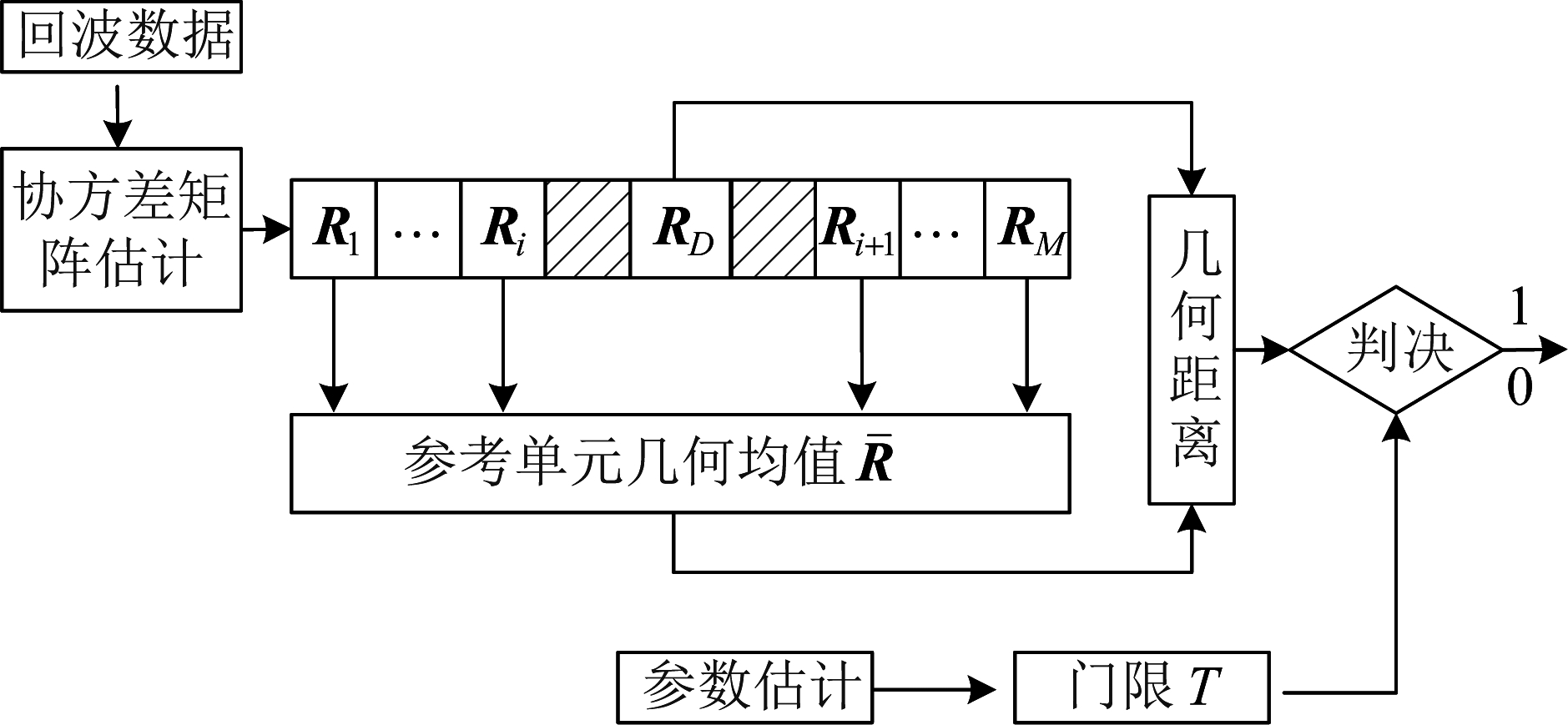
图1 矩阵CFAR检测
Fig.1 Matrix CFAR detection
因此，利用检测单元RD和参考杂波单元均值
间的几何距离与门限比较可得几何检测判决式[3,7]
(3)
其中，d(·)表示黎曼流形的几何距离。由式(3)可知，矩阵CFAR检测的问题可以看作为待检测目标单元与杂波参考单元分类问题，如何在黎曼流形上将二者进行有效区分，并增强其差异性特征是改善检测性能的关键。因此，本文旨在通过流形降维增强二者的区分性特征，实现目标的增强检测。
黎曼流形上任意一点对应于一个HPD协方差矩阵，连接两点R1，R2的最短距离称为测地线距离，其表达式为[12-13]
(4)
其中，||·||表示Frobenius范数，log(·)表示流形上的对数映射，上式也叫做黎曼距离(Riemannian Distance, RD)。同时，对数欧氏(Log-Euclidean, LE) 距离也是黎曼流形一种近似的测地线距离且易于计算，它将流形上的点通过对数映射到切空间，利用切空间内的欧氏距离作为流形的距离度量，具体的表达式为[8]
dLE(R1,R2)=||log(R1)-log(R2)||
(5)
此外，信息散度度量如KL(Kullback-Leibler, KL)散度和sKL(symmetric Kullback-Leibler, sKL) 散度等都是广泛应用几何距离度量方式，具体可分别表示为[5,11]
(6)
(7)
其中，tr(·)表示矩阵的迹，log|·|表示对数行列式。除黎曼流形的几何距离外，几何均值也是一重要概念，与欧氏空间数据的算术均值相对应，黎曼流形上点{R1,R2,…,RM}的几何均值可以表示为
(8)
上述几何距离下的几何均值可以根据式(8)计算求得[8,13]。区别于传统算术平均，几何均值利用了流形的几何结构信息，能够减少强的非均匀杂波背景对杂波功率估计的影响，具有更好的稳健性。
2.2 黎曼流形监督降维
黎曼流形降维是通过建立映射
实现[14]。即对
在映射矩阵W∈Cn×m的作用下，映射降维可以表示为
f(W,R)=WHRW
(9)
其中，W是满秩矩阵，并且具有正交约束WHW=Im。
假设集合
包含两类别信息，通过保持流形空间中同类别点间隔较近，不同类别点间隔较远，实现降维，进而增强流形上各类别的可分性。其具体过程为：首先，计算黎曼流形上每个点Ri的k个邻近点
接着，为挖掘流形各个点的几何判决信息，将
划分为类内邻近点集合
与类间邻近点集合
则
最后，构建类内权重矩阵Aw和类间权重矩阵Ab
(10)
(11)
利用黎曼流形几何结构，保持类内几何距离最小，类间几何距离最大建立优化问题
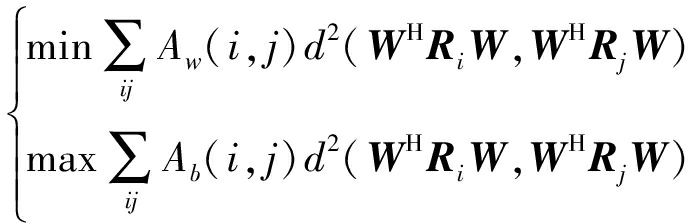
(12)
因此，根据式(12)，可以进一步建立目标函数
(13)
对映射矩阵加以正交约束，黎曼流形降维问题则转化为求解映射矩阵的优化问题
(14)
求解式(14)的优化问题可以得到最优的降维映射矩阵W*。
3 流形监督降维的增强检测方法
3.1 构建降维目标函数
基于矩阵CFAR检测原理，每个距离单元雷达回波数据可以构建为HPD协方差矩阵，则黎曼流形上HPD协方差矩阵集合
可分为两类即杂波参考单元{R1,…,Ri,…,RM}和待检测目标单元RD。根据黎曼流形监督降维原理，流形降维将保持待检测目标单元与杂波参考单元类间距离最大，各自类内距离最小。因此，可采用黎曼流形监督降维增强待检测目标单元与杂波参考单元的可分性。
本文采用LE距离作为流形降维的几何距离，此时流形映射降维可以表示为
L(W)=||log(WHRiW)-log(WHRjW)||2
(15)
将流形上的点划分为待检测目标单元RD和杂波参考单元{R1,…,RM}两类，根据式(10)、(11)可以构建流形各点的类内和类间权重矩阵Aw和Ab，相应的目标函数可以表示为
(16)
化简求解式(16)，使其满足正交集下的不变性质，即对任意
都有F(W)=F(WQ)，其中，
表示正交群，从而可使优化问题转化为Grassmann流形
上的优化问题[15]。由于LE距离本身不满足仿射不变性质，并且欧氏空间的梯度无闭式表达式[16]，因此，采用近似log(WHRW)≈WHlog(R)W，具体地，将log(I-M)在I处进行泰勒展开
(17)
则
log(WHRW)=log(I-(I-WHRW))≈ -(I-WHRW)=-WH(I-R)W≈WHlog(R)W
(18)
进而可将式(16)的目标函数化简为
||WHlog(Ri)W-WHlog(Rj)W||2
(19)
展开式(19)，令
log(Rj))WWH(log(Ri)-log(Rj))
(20)
则式(19)在正交约束下的降维优化问题可以表示为
s.t. WHW=Im
(21)
其中，目标函数F(W)=tr(WHG(W)W)，具有正交不变性，因此，式(21)的优化问题可以采用Grassmann流形上的优化方法求解。
3.2 Grassmann流形优化
Grassmann流形表示n维欧氏空间
的所有m维线性子空间的集合，0<m≤n，它是Stiefel流形
的一个商流形[17-18]，即
对任意一点
其切空间
目标函数F(W)在Grassmann流形的梯度
为
▽F=FW-WWHFW
(22)
其中，FW是F(W)的偏微分。同时，Grassmann流形上每个点具有搜索方向
并满足〈▽F,H〉W=DF(W)[H]，DF(W)[H]是目标函数F(W)在W点沿H的方向微分。对可微Grassmann流形上点W切空间内两切向量Δ1、Δ2的内积为
(23)
同时，Grassmann流形的测地线可以表示为
(24)
其中，UΣVH表示H的紧奇异值分解(Singular Value Decomposition, SVD)，t表示测地线步长，并且该测地线是连接Grassmann流形上两点的最短曲线。
为解决式(21)的优化问题，本文采用Grassmann流形的共轭梯度算法求解[15,17]，如图2所示，具体步骤描述如下:
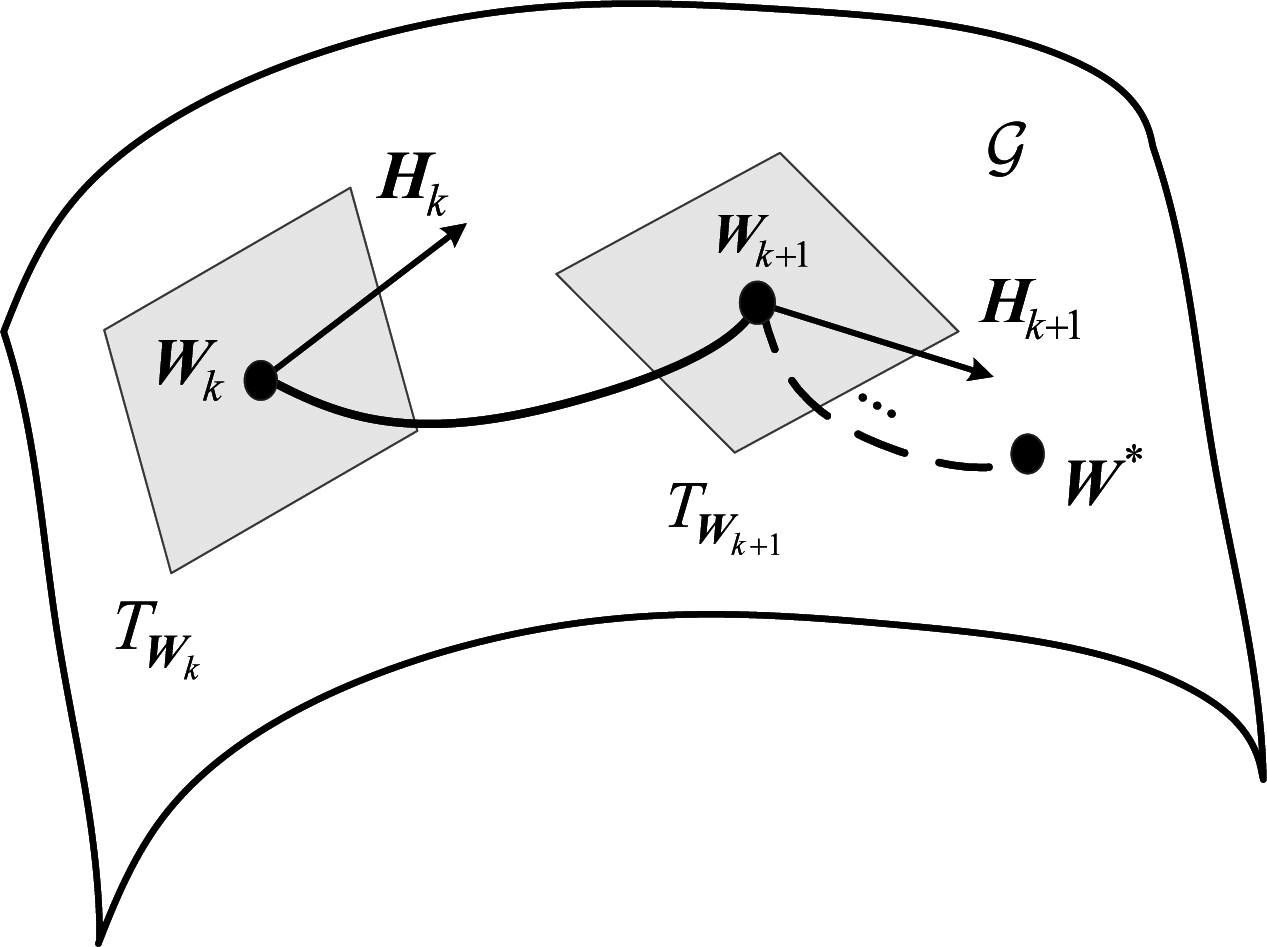
图2 Grassmann流形的共轭梯度算法优化
Fig.2 Conjugate gradient algorithm optimization on Grassmann manifold
步骤1 设置最大迭代次数p，k=0,1,…,p，在Wk点根据其搜索方向Hk沿着测地线最小化目标函数F(W)，并以步长tk进行搜索，得到下一点Wk+1；
步骤2 将Wk点的搜索方向Hk进行平行移动，如图3所示，得到下一点Wk+1的搜索方向Hk+1
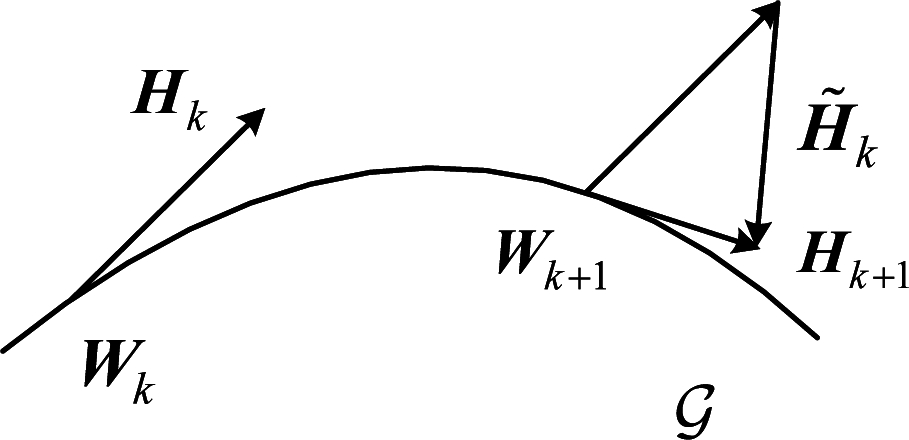
图3 Grassmann流形上的平行移动
Fig.3 Parallel transport on Grassmann manifold
(25)
其中，
为Wk点到Wk+1点的平行移动，γk为Polak Ribiére共轭性条件公式
(26)
其中，
为前一点到Wk的平行移动
U(I-cos(tkΣ ))UH▽Fk
(27)
步骤3 根据新的搜索方向Hk+1继续迭代，直到收敛或者达到最大迭代次数，最终获得最优的映射矩阵W*。
由于该优化算法的计算复杂度主要集中在每一次迭代时对H进行SVD分解，因此，优化算法的计算复杂度主要为O(kn3)。
3.3 矩阵CFAR增强检测
将上一小节在Grassmann流形上求解的最优映射矩阵W*作用到原始流形，即
表示降维符号，从而实现流形降维。在该低维流形上，待检测目标单元与杂波参考单元间的几何距离保持了最大，杂波参考单元类内的几何距离保持最小，进而目标与杂波的可分性特征得到增强。因此，本文提出基于黎曼流形监督降维的矩阵CFAR增强检测方法，相应的检测判决式为
(28)
其中，
表示流形降维后的待检测目标单元，
表示流形降维后的杂波参考单元均值，γ′为新门限。
4 实验结果与分析
4.1 仿真数据实验
假设背景杂波服从K分布，其概率密度函数为
(29)
其中，υ和μ分别表示形状参数和尺度参数，Γ(·) 和 Kυ-1(·)分别表示伽马函数和修正的贝塞尔函数。
仿真数据实验中，产生一组形状参数和尺度参数均为0.5的K分布杂波数据，包括17个距离单元，每个距离单元含有n=12个脉冲数据，利用脉冲数据间的相关特性，构建相应的HPD协方差矩阵，设置邻近点数k=8，并在第9个距离单元加入回波信号
s=αp
(30)
其中，多普勒导向矢量p=[1,ej2πfd,...,e j2π(n-1)fd]T，归一化多普勒频率fd=0.15，α是信号幅值控制系数，保护单元总数P=4，其余为参考单元数M=12，虚警率Pfa=10-3。由于杂波呈非高斯分布，检测概率和门限没有解析表达式，因此采用蒙特卡罗实验仿真检测概率和门限。
首先比较了信杂比(Signal-to-Clutter Ratio, SCR)为5 dB时，不同几何距离下，降维前、后的归一化检测统计量变化情况，如图4所示。由图4可知，随着维数降低，杂波参考单元的归一化检测统计量均逐渐降低，待检测目标单元将更加突出。结果表明通过流形监督降维能够增强目标与杂波的区分性，并且在检测中使得杂波参考单元得到有效抑制，进而将在低维获得更好的检测性能。
为探究维数变化与检测概率的关系，图5给出了当SCR为7 dB时，不同几何距离下检测概率(Pd)随维数m(m≤n)变化曲线。从图中可以看出，当维数降低时，不同几何距离下的检测概率均得到提高，这与图4中归一化检测统计量变化结果相符合，表明在映射的目标与杂波区分性增强的低维流形空间中进行目标检测，能够具有更好的检测概率，并且KL散度度量始终保持着较好的检测概率。
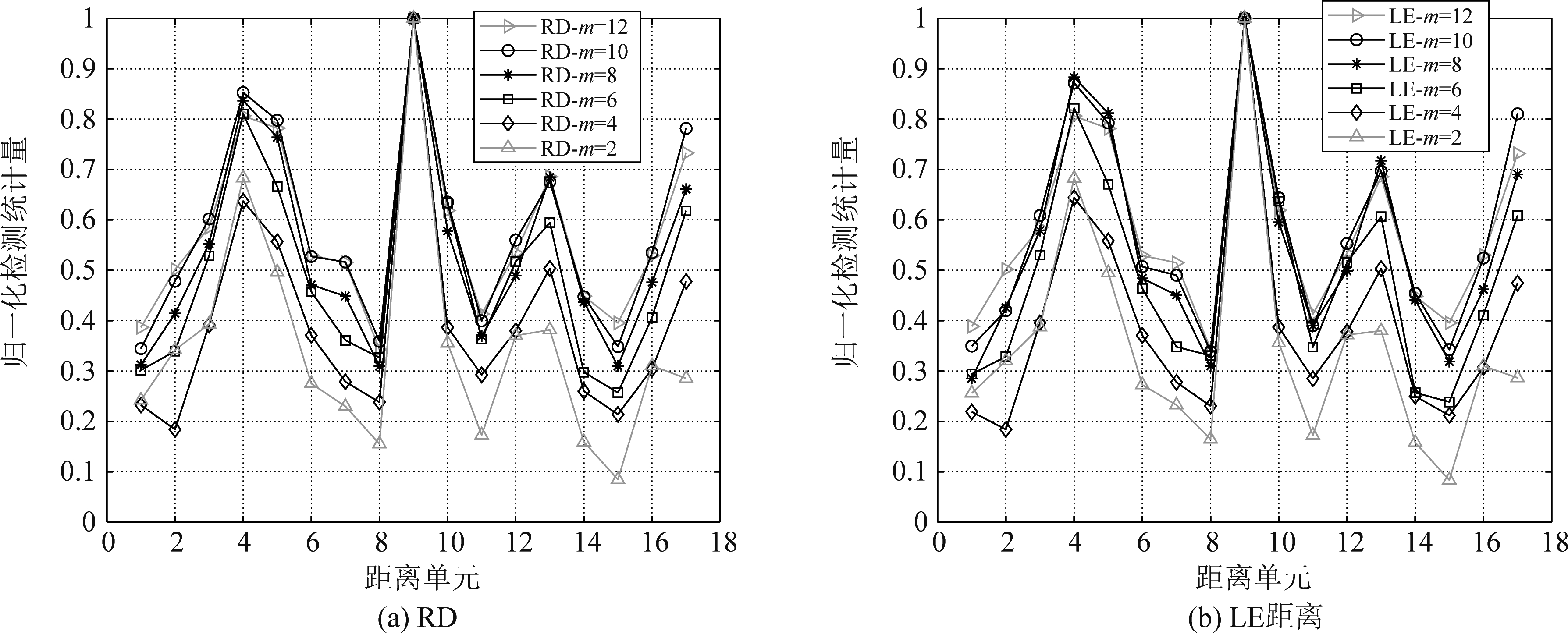
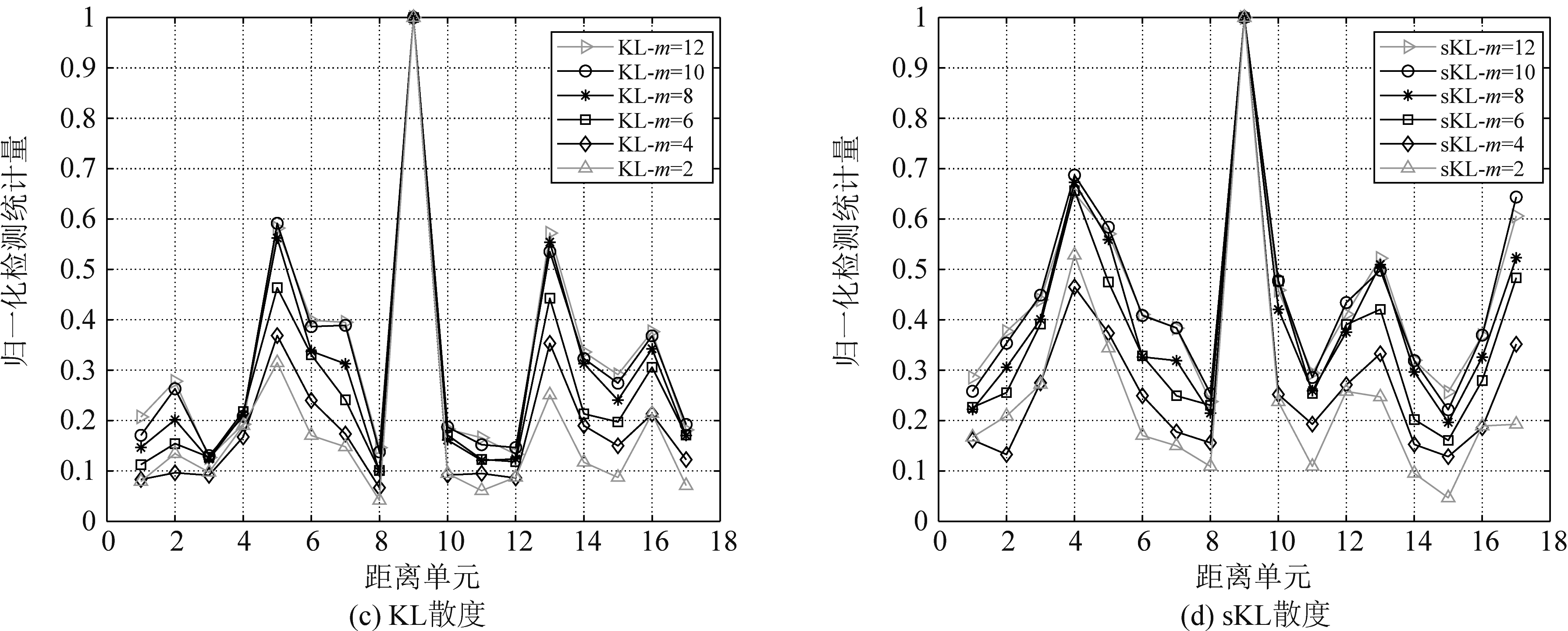
图4 不同几何距离下的归一化检测统计量
Fig.4 Normalized detection statistics of the different geometry distances
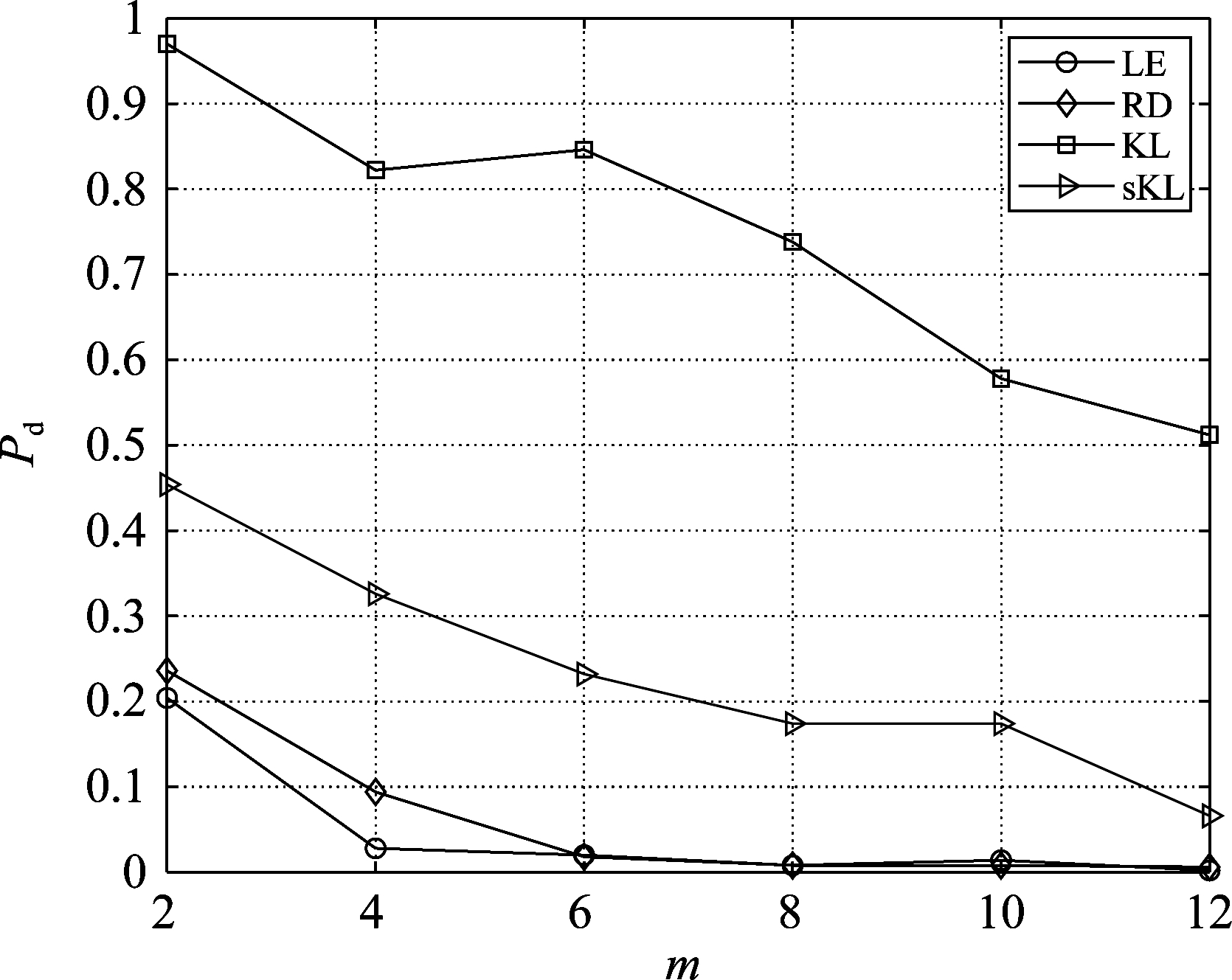
图5 检测概率随流形维数的变化
Fig.5 Detection probabilities vary with manifold dimension
接着研究了不同维数下的检测性能。假设流形监督降维后的维数分别为9、6和3，不同几何距离下检测概率随SCR变化曲线如图6所示。由图6可知，本文所提增强检测方法能够进一步提升检测性能，其中，当检测概率达到0.8时，流形的测地线距离类度量提高约4 dB，散度类度量提升约2 dB，表明了不同几何距离下的增强检测效果也会不同，并且在KL散度度量下保持着较好的检测性能。在几何检测中，不同的几何距离度量方式可以看作信号能量的不同积累方式，流形的降维映射则增强了信号的积累，因而能够带来较好的检测性能。
4.2 实测数据实验
实测数据为加拿大McMaster大学利用IPIX雷达采集的海杂波数据，本文采用该雷达采集的#202组数据，文件名为19980304_184107_ANTSTEP，其中包含28个距离单元，每个距离单元由60000个采样脉冲串组成[19]。采用蒙特卡罗仿真，仿真中取前17个距离单元，每个距离单元脉冲数n=7，利用前56000组杂波数据计算检测门限。同样在第9个距离单元加入目标s作为待检测单元，目标的归一化多普勒频率fd=0.15，待检测单元左右各设置2个保护单元。虚警概率Pfa=10-3，利用后4000组杂波数据计算检测概率。
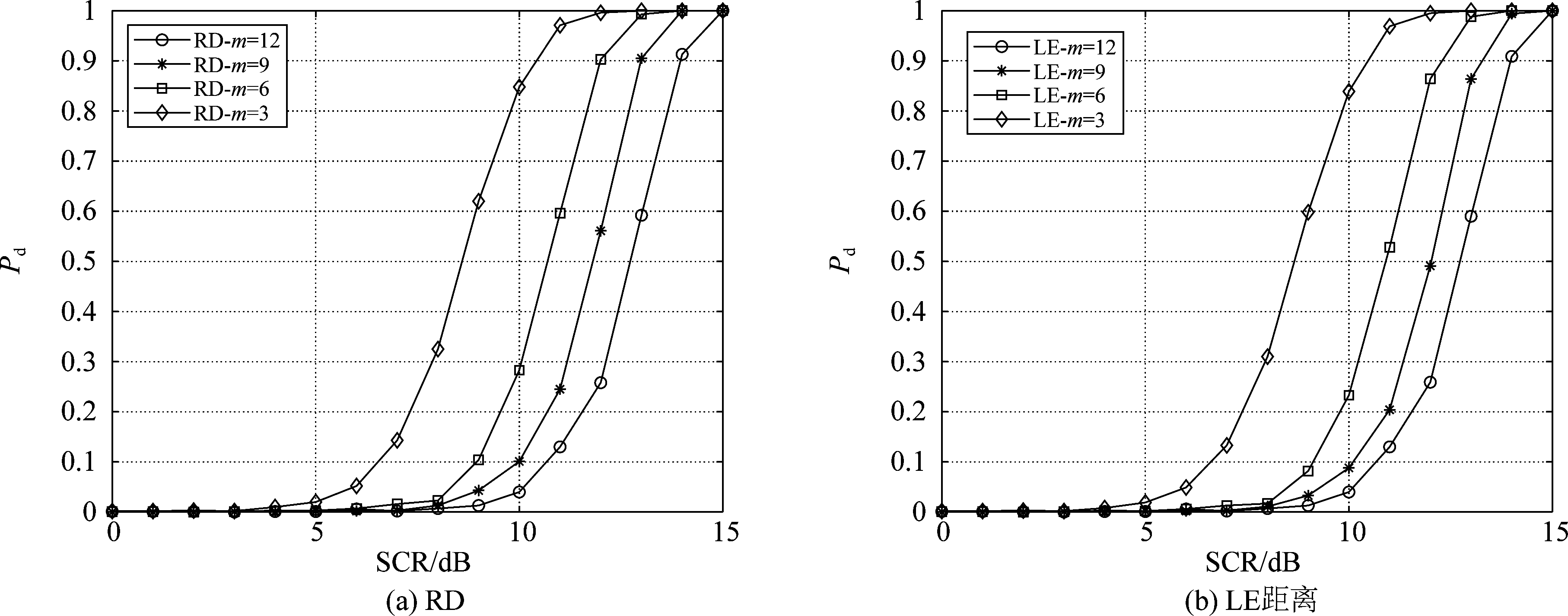
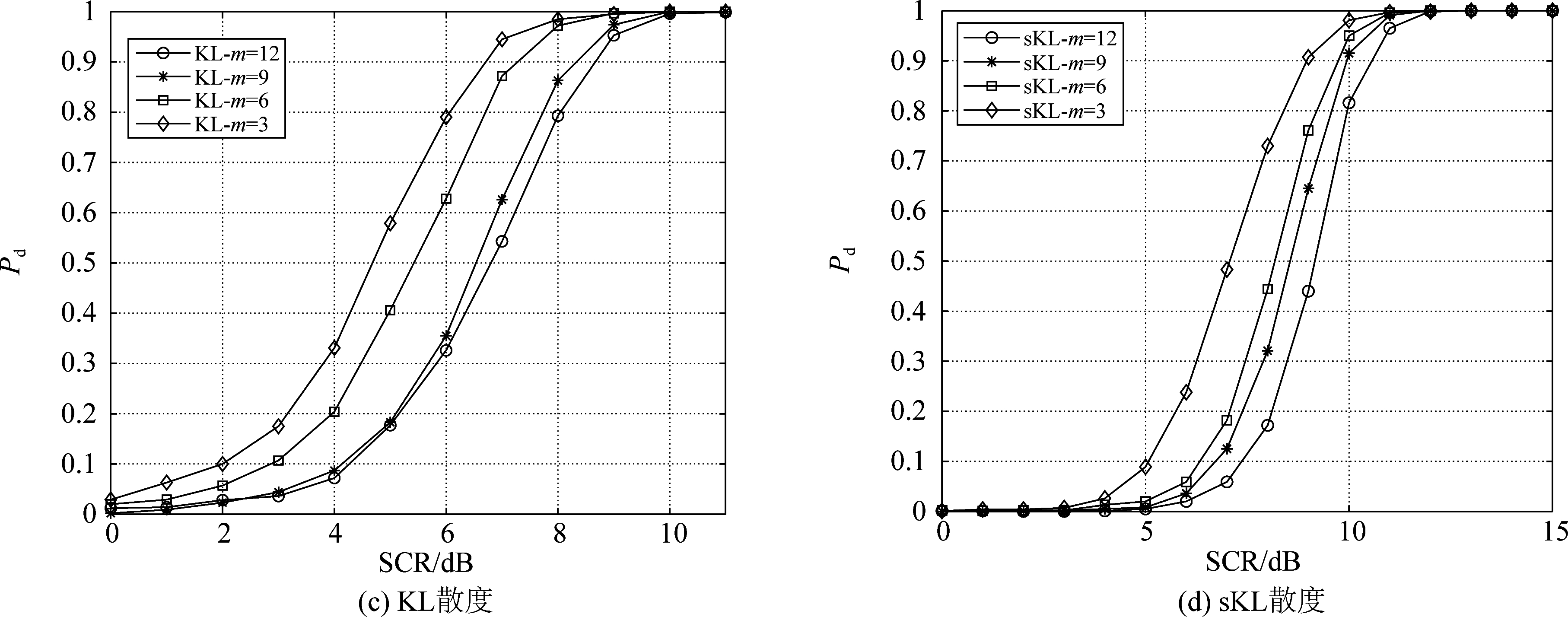
图6 基于仿真数据，不同几何距离下的检测性能
Fig.6 Detection performance of the different geometry distances based on simulated data
实测海杂波数据条件下，图7给出了不同几何距离下的检测概率Pd随流形维数m的变化曲线，SCR为8 dB。由图7可知，所提方法的检测概率随着维数降低整体依旧呈现提高的趋势，表明在低维流形能够具有更好的检测性能。同时，图8给出了所提增强检测方法与常用的自适应归一化匹配滤波器(Adaptive Normalised Matched Filter, ANMF)在实测数据下的检测性能对比。由图8可知，相比于ANMF，所提增强检测方法总体上保持着较好的检测性能。但在sKL散度下，ANMF整体优于所提方法，这说明所提方法采用不同的几何距离能够获得不同的检测性能。当降维维数m=2，检测概率Pd=0.8时，测地线距离类和散度类度量下的检测性能分别改善了约2 dB和2.5 dB，此时，KL散度下的增强检测方法相对于ANMF检测性能提升约4.5 dB。实测实验结果进一步表明，目标与杂波可区分性在映射的低维流形上得到了增强，并且目标信号获得了较强的积累，因而相比于未降维时的矩阵CFAR检测方法，所提方法能够获得更好的检测性能。
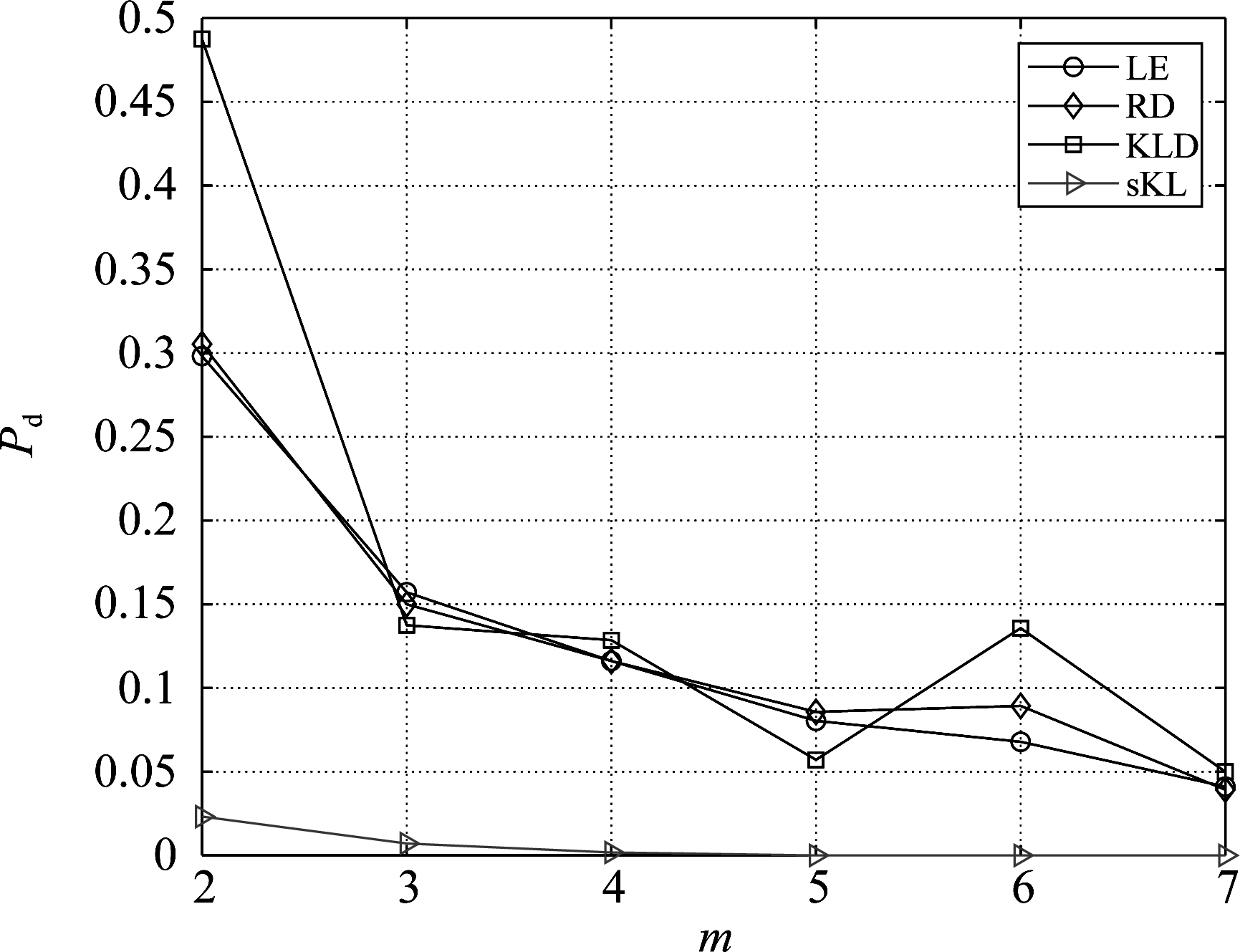
图7 实测数据条件下检测概率随维数变化曲线
Fig.7 Curves of the detection probabilities vary with dimension in real sea clutter data
图8 基于实测数据，所提方法与ANMF的检测性能对比
Fig.8 Detection performance comparison of the proposed method and ANMF in real sea clutter data
5 结论
矩阵CFAR检测是一种新兴的雷达目标几何检测技术，在一定的目标检测场景下展现着更好的检测性能。本文在前人研究基础上，进一步研究了复杂杂波背景下的目标增强检测方法，利用黎曼流形监督降维增强了目标与杂波的区分性特征，提出了一种基于流形降维的矩阵CFAR增强检测方法。采用K分布的杂波数据和实测海杂波数据进行了仿真实验分析，结果表明，本文所提增强检测方法能够进一步提升检测性能。下一步主要研究降维维数与几何检测性能的具体关系，寻找流形本征维度。此外，矩阵CFAR检测方法也有诸多问题需要开展深入研究，比如检测时最优几何距离度量方式的选择，流形几何结构与检测性能原理性关系等，解决上述问题同样能够指导增强检测方法的研究。
[1] 施赛楠, 杨静, 王杰. 基于多域多维特征融合的海面小目标检测方法[J]. 信号处理, 2020, 36(12): 2099-2106.
SHI Sainan, YANG Jing, WANG Jie. Detection of Sea-surface small target based on Multi-domain and Multi-dimensional feature fusion[J]. Journal of Signal Processing, 2020, 36(12): 2099-2106. (in Chinese)
[2] 许述文, 蒲佳. 基于四极化通道融合的海面漂浮微弱目标特征检测[J]. 信号处理, 2017, 33(3): 324-329.
XU Shuwen, PU Jia. Floating small targets detection in sea clutter based on four polarization-channels fusion[J]. Journal of Signal Processing, 2017, 33(3): 324-329. (in Chinese)
[3] LIU Weijian, LIU Jun, HAO Chengpeng, et al. Multichannel adaptive signal detection: basic theory and literature review[EB/OL]. 2021: arXiv: 2102.03474[stat.AP]. https:∥arxiv.org/abs/2102.03474.
[4] ARNAUDON M, BARBARESCO F, YANG Le. Riemannian medians and means with applications to radar signal processing[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(4): 595- 604.
[5] CHENG Yongqiang, HUA Xiaoqiang, WANG Hongqiang, et al. The geometry of signal detection with applications to radar signal processing[J]. Entropy, 2016, 18(11): 381.
[6] 黎湘, 程永强, 王宏强, 等. 信息几何理论与应用研究进展[J]. 中国科学: 信息科学, 2013, 43(6): 707-732.
LI Xiang, CHENG Yongqiang, WANG Hongqiang, et al. Progress in theory and applications of information geometry[J]. Scientia Sinica (Informationis), 2013, 43(6): 707-732. (in Chinese)
[7] BARBARESCO F. Innovative tools for radar signal processing Based on Cartan’s geometry of SPD matrices & Information Geometry[C]∥2008 IEEE Radar Conference. Rome, Italy. IEEE, 2008: 1- 6.
[8] HUA Xiaoqiang, CHENG Yongqiang, WANG Hongqiang, et al. Geometric means and medians with applications to target detection[J]. IET Signal Processing, 2017, 11(6): 711-720.
[9] 赵兴刚, 王首勇. 雷达目标检测的信息几何方法[J]. 信号处理, 2015, 31(6): 631- 637.
ZHAO Xinggang, WANG Shouyong. Information geometry method to radar target detection[J]. Journal of Signal Processing, 2015, 31(6): 631- 637. (in Chinese)
[10] 刘俊凯, 李健兵, 马梁, 等. 基于矩阵信息几何的飞机尾流目标检测方法[J]. 雷达学报, 2017, 6(6): 699-708.
LIU Junkai, LI Jianbing, MA Liang, et al. Radar target detection method of aircraft wake vortices based on matrix information geometry[J]. Journal of Radars, 2017, 6(6): 699-708. (in Chinese)
[11] HUA Xiaoqiang, CHENG Yongqiang, WANG Hongqiang, et al. Matrix CFAR detectors based on symmetrized Kullback-Leibler and total Kullback-Leibler divergences[J]. Digital Signal Processing, 2017, 69: 106-116.
[12] BHATIA R, HOLBROOK J. Riemannian geometry and matrix geometric means[J]. Linear Algebra and Its Applications, 2006, 413(2/3): 594- 618.
[13] MOAKHER M. On the averaging of symmetric positive-definite tensors[J]. Journal of Elasticity, 2006, 82(3): 273-296.
[14] HARANDI M T, SALZMANN M, HARTLEY R. From manifold to manifold: Geometry-aware dimensionality reduction for SPD matrices[C]∥Computer Vision - ECCV 2014, 2014: 17-32. DOI:10.1007/978-3-319-10605-2_2.
[15] EDELMAN A, ARIAS T A, SMITH S T. The geometry of algorithms with orthogonality constraints[J]. SIAM Journal on Matrix Analysis and Applications, 1998, 20(2): 303-353.
[16] VEMULAPALLI R, JACOBS D W. Riemannian metric learning for symmetric positive definite matrices[EB/OL]. 2015: arXiv: 1501.02393[cs.CV]. https:∥arxiv.org/abs/1501.02393.
[17] SMITH S T. Optimization Techniques on Riemannian Manifolds [J]. Mathematics, 2014, 158(2): 328-342.
[18] DONG Ganggang, KUANG Gangyao. SAR target recognition via sparse representation of monogenic signal on Grassmann manifolds[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1308-1319.
[19] IPIX radar file, IPIX radar dataset files in Grimsby on the shores of Lake Ontari, 2003. Available online: http:∥soma.mcmaster.ca/ipix.php.
