1 引言
基于相控阵的波束形成技术能够在目标方向形成高增益,并在干扰方向处形成零陷,因而被广泛应用于雷达目标探测和干扰抑制[1]。但相控阵的波束只具有角度相关性,故其不能抑制与目标角度不可分的主瓣干扰[2]。然而在日趋复杂的电磁环境中,随队支援式干扰机产生的欺骗式假目标,可与目标同处于雷达主瓣内做非线性运动,这对传统的相控阵雷达通过波束形成技术对欺骗式干扰进行实时的抑制提出了挑战。
在2006年的IEEE国际雷达会议中,Antonik首次提出频控阵(Frequency Diverce Array, FDA)概念[3],并申请了美国专利[4]。频控阵是在相控阵基础上,对各个发射阵元附加一个很小的频偏(附加频偏远远小于载频),使得雷达波束指向具有了距离角度二维相关特性,为抑制主瓣内距离维可分的干扰创造了条件,因此引起了国内外学者的广泛关注[5-9]。另一方面,认知技术赋予雷达感知环境,学习推理的能力[10],将认知雷达相关技术应用于频控阵,有望实现一种能够认知环境的新型雷达。文献[11]将认知雷达的概念与频控阵结合,并对认知频控阵雷达的特点进行了分析。文献[12]提出了一种基于认知频控阵的高效节能的自适应发射波束设计方法,能够以一种认知方式高效地探测和跟踪目标。文献[13]通过认知频控阵对运动目标距离-角度-多普勒进行多域联合估计,从而实现目标跟踪。文献[14]联合认知雷达和频控阵雷达,提出了一种自适应动目标探测和跟踪的方法。在非平稳环境中,状态估计是一项具有挑战性任务,针对运动变化的干扰源,文献[15]提出一种基于神经网络的认知频控阵动态零陷技术,通过选择合适的频偏增量使波束在干扰源预测位置产生零陷,但是该方法中需在每一周期精确调整频偏。
本文提出一种新的动态零陷形成框架,采用非均匀布阵的频控阵进行距离角度解耦合,结合认知技术利用扩展卡尔曼(Extended Kalman Filter, EKF)实现对欺骗式假目标运动轨迹的预测,最后通过距离维的波束形成技术调整权矢量,实现对主瓣中运动的假目标的实时动态抑制,而不需要在各个发射周期调整阵元的频偏增量。
接下来的内容安排是:第2节介绍频控阵的发射接收模型的基本原理并进行距离角度解耦合,第3节提出认知频控阵雷达抗主瓣欺骗式干扰框架,第4节进行仿真实验,第5节得出结论进行总结。
2 频控阵发射-接收模型
2.1 频控阵基本原理及特性
频控阵是在阵元间引入一个远小于载频f0的频偏增量Δf,从而实现波束方向图的距离角度相关性。考虑图1所示的由N(N>1)个间距相等的发射阵元构成的线性频控阵列,附加频偏线性递增。
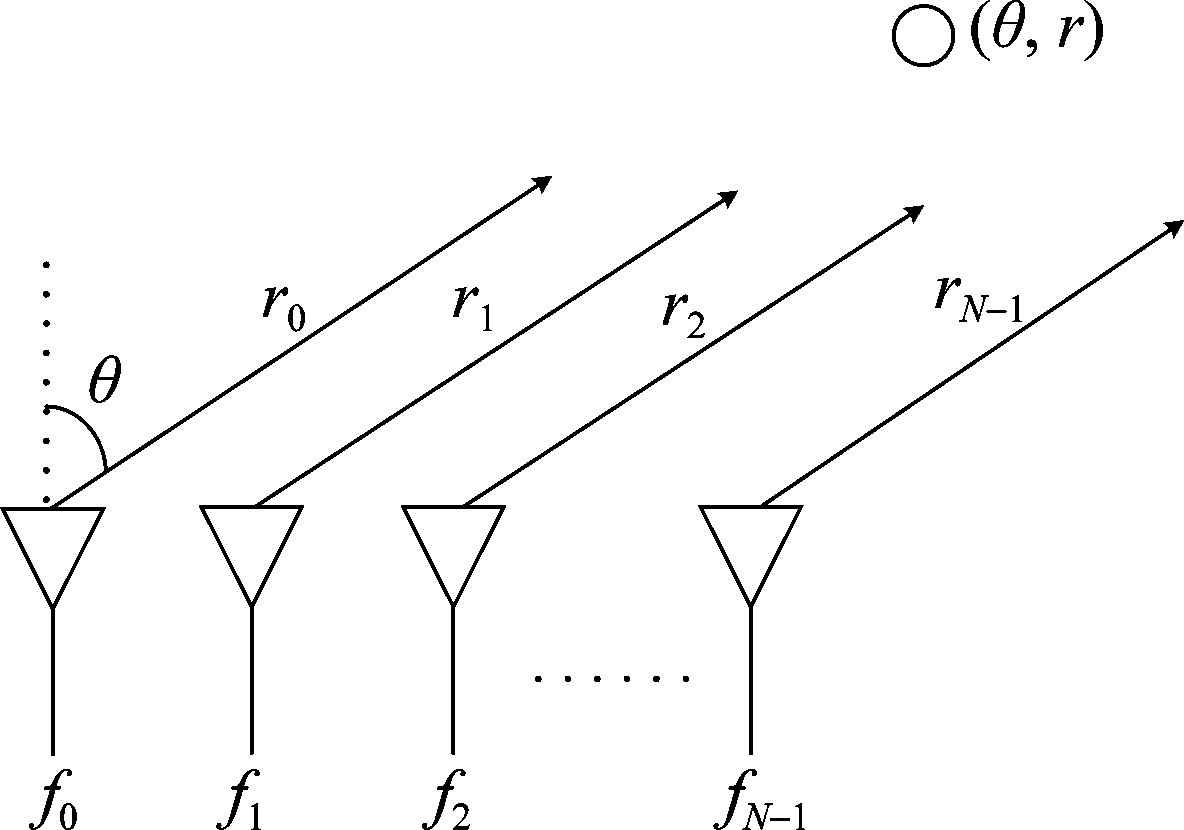
图1 线型频控阵发射阵列图
Fig.1 Transmit array diagram of ULA-FDA
为了模型简便,假设本文采用没有互耦效应的理想阵元,尽管考虑实际情况下,阵元间的互耦效应会使辐射能量受到限制导致真实的波束方向图失真。以第一个阵元为参考阵元,则阵元n到目标的距离和频率分别表示为
rn=r-dn=r-ndsin θ,n=0,1,…,N-1
(1)
fn=f0+Δfn=f0+nΔf,n=0,1,…,N-1
(2)
式中:Δfn,dn分别表示阵元n到参考阵元的频偏增量和间距,r为参考阵元到目标的距离。考虑远场窄带假设,(N-1)Δf<<f0,为防止栅瓣,阵元间隔d=c/2(f0+(N-1)Δf)远远小于目标距离,故频控阵雷达的方向矢量和阵列因子可以分别表示为[16]
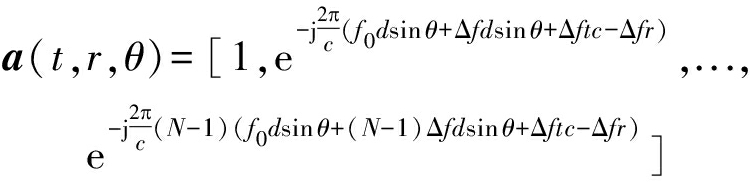
(3)
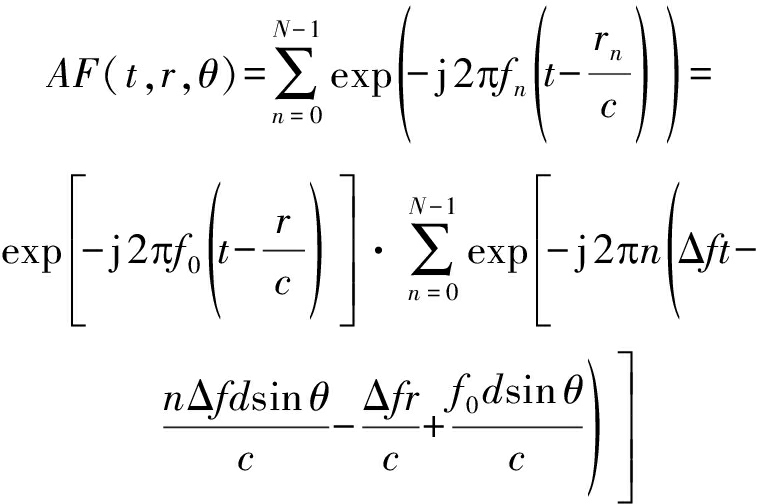
(4)
式(3)和式(4)相位中关于阵元序号n的二次项,即
在频率增量远小于信号载频时对波束方向图的影响很小,故在研究中通常被忽略。因此公式(4)可以被近似写作
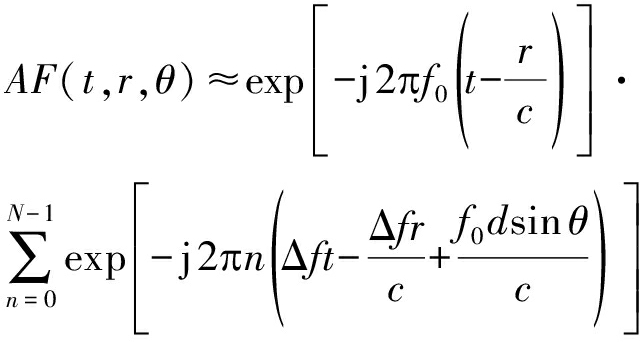
(5)
进一步,归一化的波束方向图可以表示为
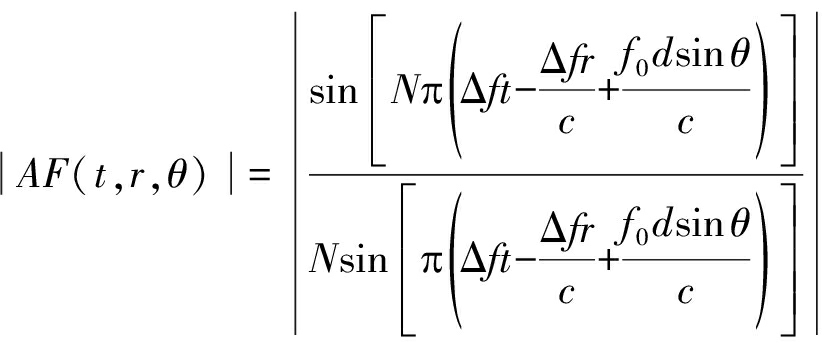
(6)
由式(6)可直观地看出频控阵波束方向图的时间-距离-角度三维依赖特性。
2.2 非均匀布阵解耦合
本文采用阵元数为N的频控阵作为发射阵列,阵元数为M的相控阵作为接收阵列,并且采用收发同置体制,频控阵雷达的收发天线位置如图2所示。
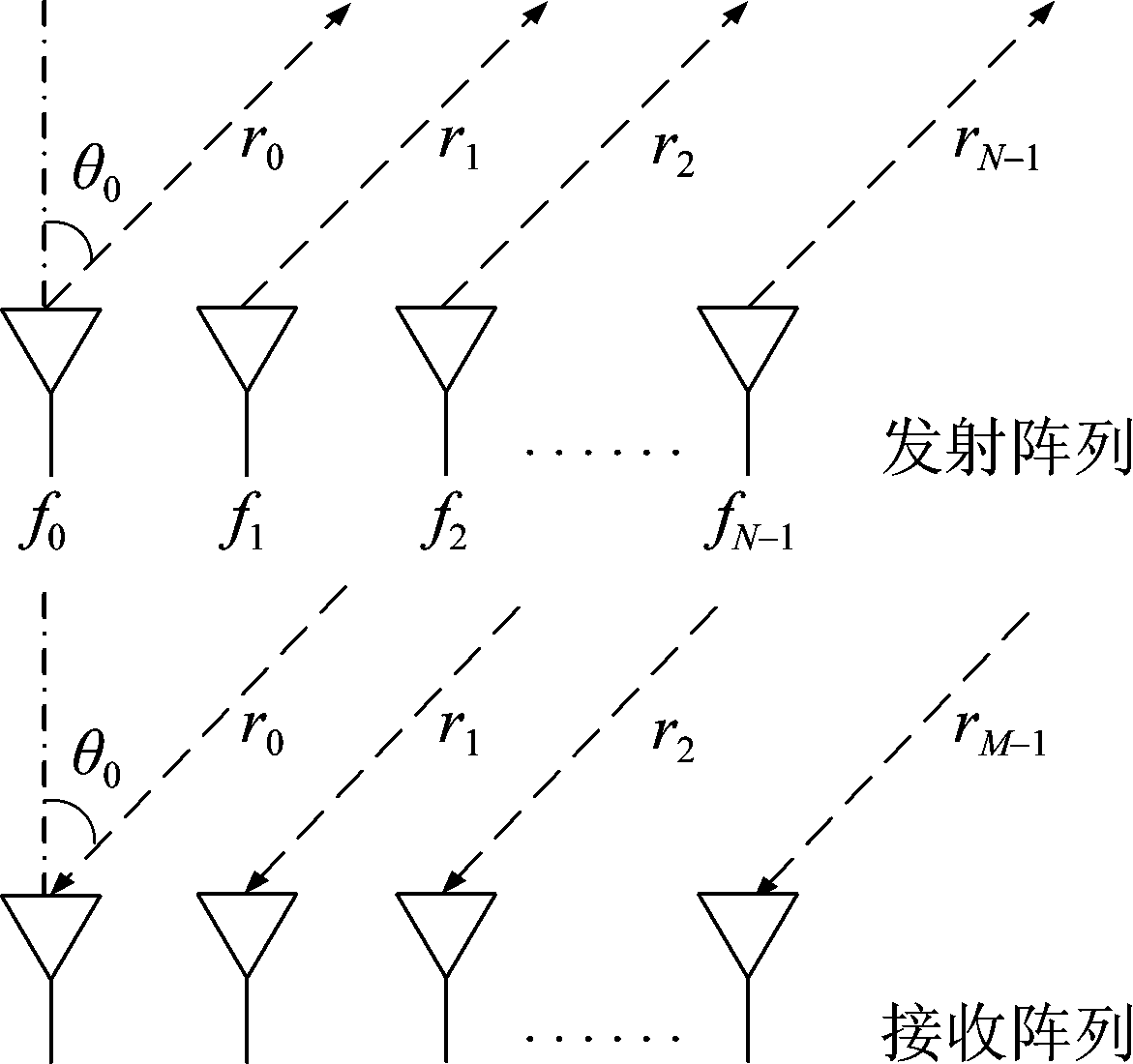
图2 FDA发射—接收阵列图
Fig.2 FDA transmit-receive array diagram
频控阵雷达可以用来实现对目标的二维定位,但是波束图具有角度和距离的耦合性,这一特点不利于主瓣能量的聚焦,也无法利用其进行无模糊的目标距离-角度联合估计,从而大大降低了其应用价值[17]。假设干扰场景中,目标和主瓣欺骗式假目标均处在雷达主瓣内,所研究的问题是在距离维度上对运动的干扰机进行动态抑制,故本文采取非均匀布阵的方式对频控阵雷达进行解耦处理,以形成完全距离依赖性的发射波束方向图。
从式(6)频控阵阵列因子表达式可以看出,如果消除表达式中所含角度项,便可以形成所需的距离依赖性波束方向图。阵元n到参考阵元之间距离重新设置为[18]
(7)
式中,L为一个经验性常数,λn=c/fn为各个阵元发射频率对应的波长。此时阵列的排列依赖于各个阵元的发射波长,相邻阵元间距差表示为
(8)
将式(7)代入式(4)中,发射阵列的波束方向图可重写为
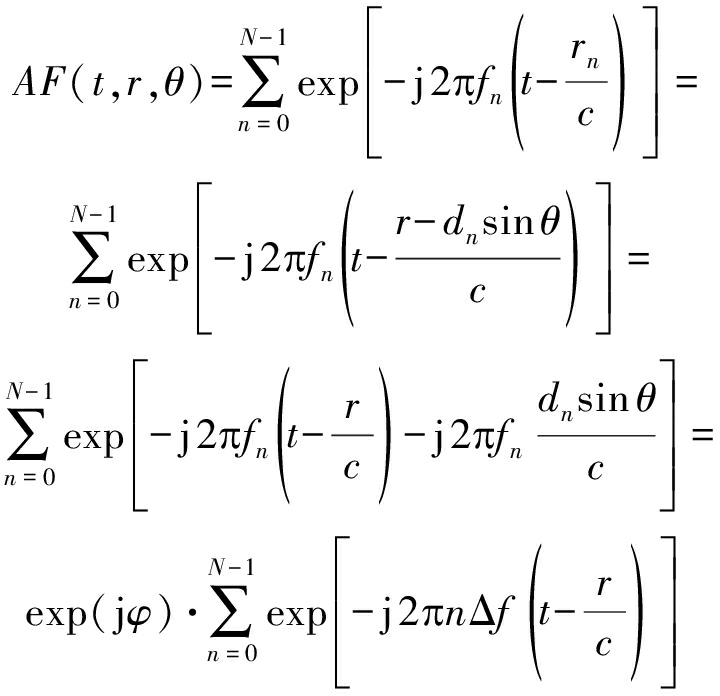
(9)
式中,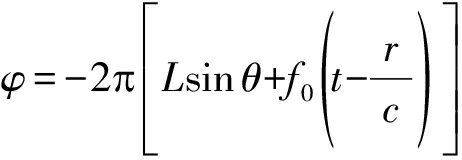
为与阵元无关的相位项,当满足阵元数N>1时恒存在。因此归一化的波束方向图可以表示为
(10)
由式(10)可知,此时频控阵的发射波束方向图仅与距离和时间有关,而阵列因子中的时间项可在雷达接收机中由特定的滤波器组消除[19],故不失一般性的认为,此时发射波束方向图仅与距离有关。因此,频控阵通过非均匀布阵的方式便得到了完全距离依赖性的发射波束方向图,结合频控阵距离维的波束控制便可对距离可分的主瓣干扰进行抑制。
3 动态零陷形成抗主瓣干扰
3.1 干扰场景
假设支援干扰作战场景如图3所示,随队支援干扰机与目标飞机始终同处于雷达照射主瓣内,并且干扰机沿着主瓣方向做着非线性运动,故其产生的延时欺骗假目标也同样在主瓣进行非线性运动,其相对雷达距离为关于时间的非线性函数。
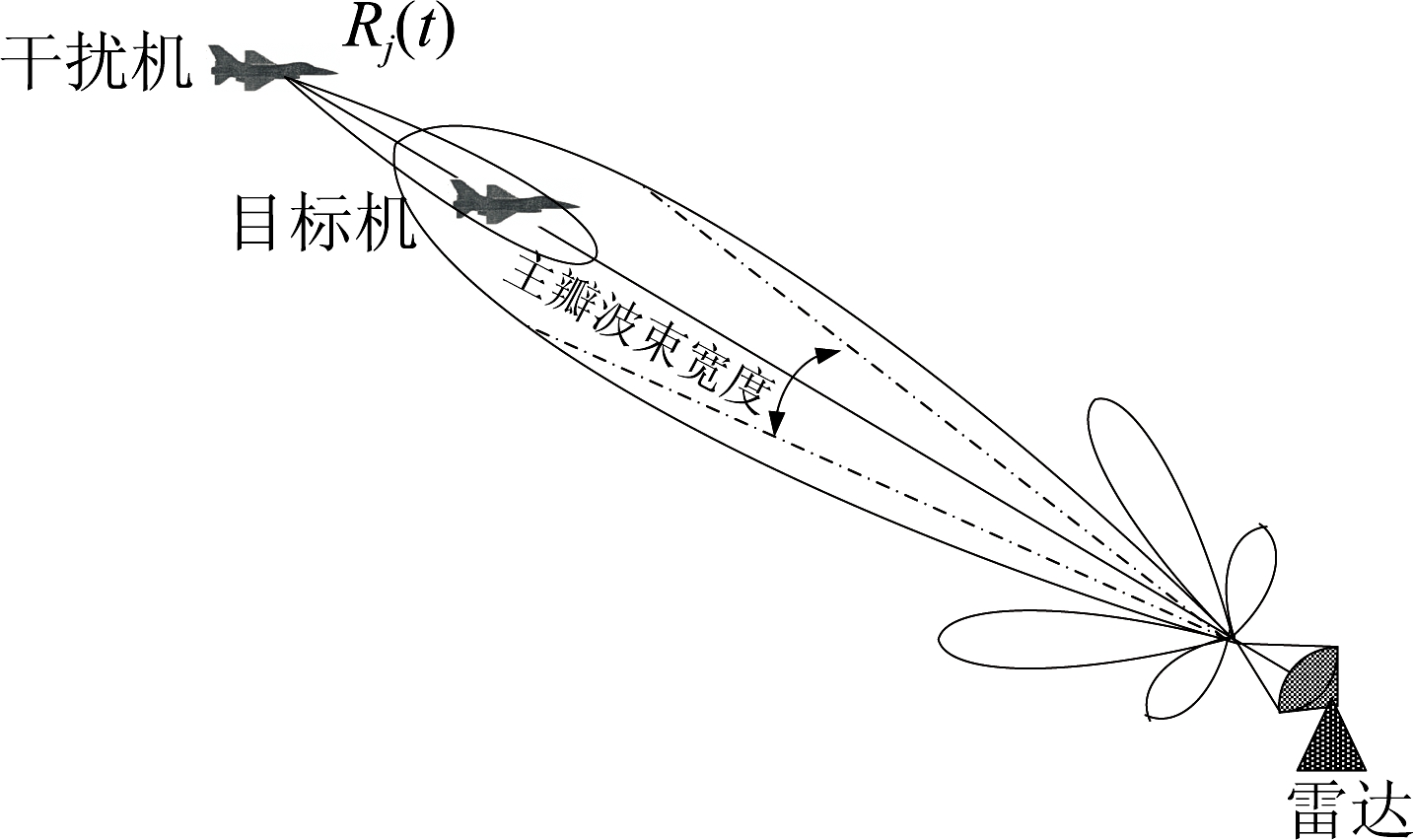
图3 随队支援干扰场景
Fig.3 Team support jamming scenario
本文研究重点为欺骗假目标相对雷达距离的估计、假目标运动轨迹的预测以及在干扰位置处实时地形成动态零陷,因此理想地认为目标与雷达的距离不变且始终与干扰机在距离维可分。
3.2 抗干扰处理框架
本文提出的抗主瓣假目标的完整流程如图4所示,所提认知频控阵雷达系统具有频控阵发射模块和相控阵接收模块,发射模块基于接收模块提供的干扰源和目标的距离预测信息通过距离维自适应波束控制得到权矢量w,通过传统的传播延迟测距技术可以分别获得干扰源和目标的距离观测值,之后通过非线性滤波方法求得干扰源在下一周期的预测值,最后将目标及干扰源的距离预测值通过反馈送回发射模块,并进行下周期的距离维波束控制,以此实现对主瓣内干扰源的动态抑制。
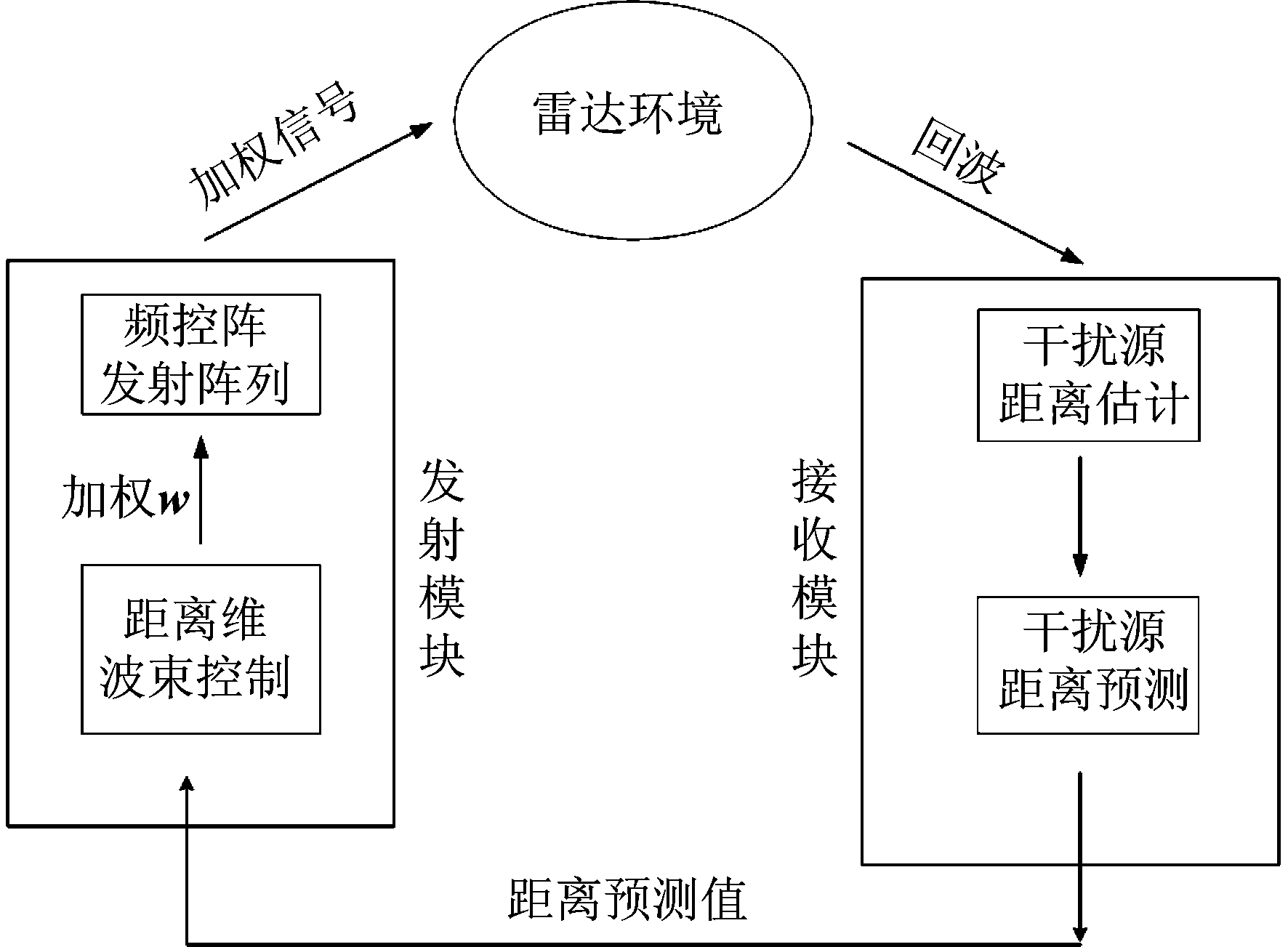
图4 认知频控阵抗主瓣假目标处理框架
Fig.4 Anti-main lobe false target processing framework of cognitive FDA
3.3 干扰源距离估计
干扰源到雷达的距离用传统的传播延迟法进行计算,对于图1所示的标准线性频控阵, 信号到达干扰机延迟时间可表示为[5]
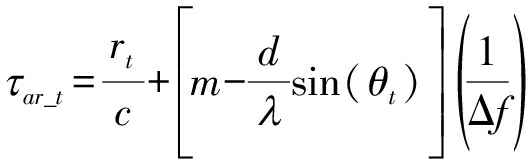
(11)
其中:rt是欺骗假目标到雷达距离,θt是干扰方向,Δf是频偏增量,m为整数代表光栅波瓣。考虑将拟议雷达的接收机和发射机配置在一起,从干扰机到达目达接收机的延迟时间可表示为
(12)
因此,总的时间延迟为
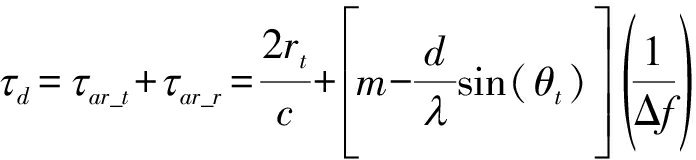
(13)
在本文所假设的主瓣干扰场景中,由于目标与欺骗假目标均位于雷达主瓣,因此干扰和目标的角度信息很容易通过空间谱估计[20]得到,这里不再赘述。因此可不失一般性地认为欺骗假目标的方位角θt始终为0°,因此,干扰源到雷达的距离可表示为
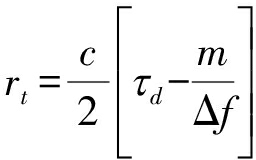
(14)
故在频率增量和时延信息已知情况下,便可得到每个周期目标的距离测量值。而距离模糊数m的确定已经得到了广泛的研究,文献[7]提出一种基于频控阵在联合发射-几首空间频率域的无模糊距离估计方法,与此同时由公式(14)显然可知,通过选择合适的Δf,可有效的增加最大无模糊距离,因此不失一般性地认为本文所获得的距离信息是无模糊的。
3.4 扩展卡尔曼滤波器预测干扰源距离
一旦干扰源被定位,下一步就是预测。预测是根据过去的值来声明函数的未来值。对于非线性系统滤波问题,常用的处理方法是利用线性化技巧将其转化为一个近似的线性滤波问题,其中应用最广泛的方法是扩展卡尔曼滤波方法[21],其核心思想是对一般的非线性系统,围绕滤波值
将非线性函数展开成Taylor级数并略去二项及以上项,得到一个近似的线性化模型,然后应用Kalman滤波完成对目标的滤波估计等处理[22]。本文研究的对象为主瓣干扰假目标,可不失一般性地认为其相对雷达主瓣的角度不变,因此只需考虑其与雷达相对距离的变化,运动状态方程可简化为一维距离标量方程,表示为
X(k)=0.9×X(k-1)+(5×X(k-1)/1+
X2(k-1))+6×cos(0.01×(k-1))+W(k)
(15)
式中,X(k)表示系统在周期k的状态值,状态噪声W(k)是均值为0方差为Q的高斯白噪声。值得说明的是,该运动方程涵盖平方关系,分式关系和三角关系为研究非线性运动的典型系统用于后续仿真验证[23],其系数的选择具有一般性。
该非线性系统的量测方程可以表示为
Y(k)=H(k)X(k)+V(k)
(16)
式中,量测矩阵H(k)为单位1,Y(k)表示在周期k的量测值,量测噪声V(k)是均值为零方差为σ2的高斯白噪声。卡尔曼滤波处理流程如下:
Step 1 初始状态X(0)、Y(0)、方差P(0);
Step 2 状态预测;
6×cos(0.01×(k-1))
(17)
Step 3 观测预测;
Y(k|k-1)=X(k|k-1)
(18)
Step 4 一阶线性化状态方程,求解状态转移矩阵Φ(k);
(19)
Step 5 求解协方差矩阵预测;
P(k|k-1)=Φ(k)P(k-1|k-1)ΦT(k)+Q
(20)
Step 6 求解Kalman滤波增益;
K(k)=P(k|k-1)HT(k)×
(H(k)P(k|k-1)HT(k)+σ2)
(21)
Step 7 状态更新;
X(k)=X(k|k-1)+K(Y(k)-Y(k|k-1))
(22)
Step 8 协方差更新。
P(k)=(In-K(k)H(k))P(k|k-1)
(23)
EKF算法的精度依赖于动态模型及之前的状态估计,在非线性系统的状态估计问题中,若状态方程线性化程度较高,则其估计精度可以达到不敏卡尔曼滤波(Unscented Kalman Filter, UKF)及粒子滤波(Particle filter, PF)算法,而前者在计算速度及工程应用上有着明显的优势[23]。
3.5 距离维自适应波束形成技术
自适应波束形成技术,其核心工作是通过调整各阵元的权矢量,使雷达波束方向图峰值指向期望的目标位置,并将波束零点置于干扰位置。在该技术中,自适应权矢量是由自适应波束形成算法计算得到的,这实际上是某一准则下的多参数最优化问题[24]。由于传统阵列的限制,相控阵波束形成技术仅针对角度维设计,能够对抗的干扰也仅是与目标角度可分的干扰。而频控阵技术提供了距离依赖性波束,因此频控阵雷达可以在距离维上对波束进行优化和设计。
在假设的雷达场景下,认为目标与雷达的距离R0固定,而干扰源相对雷达距离认为是一个时间相关的非线性函数Rj(t)。通过非线性滤波器获得干扰源的运动外推轨迹后,采用基于距离维的MVDR算法在假目标预测点处形成动态零陷,达到实时抑制主瓣干扰的效果。假设xi+n(l)为第l个干扰加噪声样本数据元素,利用EKF获得的干扰加噪声样本数据在下一周期的预测信息为
基于预测信息构造的干扰加噪声协方差矩阵可以表示为
(24)
式中,L为可利用的样本数。
解得MVDR准则下的权矢量解析表达式为[25]
(25)
式中,a(R0)为目标导向矢量表示为
a(R0)=[1,e-j2πΔfR0/c,…,e-j2(N-1)πΔfR0/c]
(26)
由式(25)获得的权矢量可以从距离维度上对距离可分的干扰进行抑制,但需要注意的是本质上该方法为MVDR算法在距离维上的应用,故当目标与干扰机距离不可分时,波束图的主瓣会发生严重畸变。
4 仿真分析
假设目标飞机相对雷达距离固定在2 km处,干扰机起始位置距离雷达3.8 km,由传统的雷达测距方法获得目标和干扰源的位置信息如图5所示。
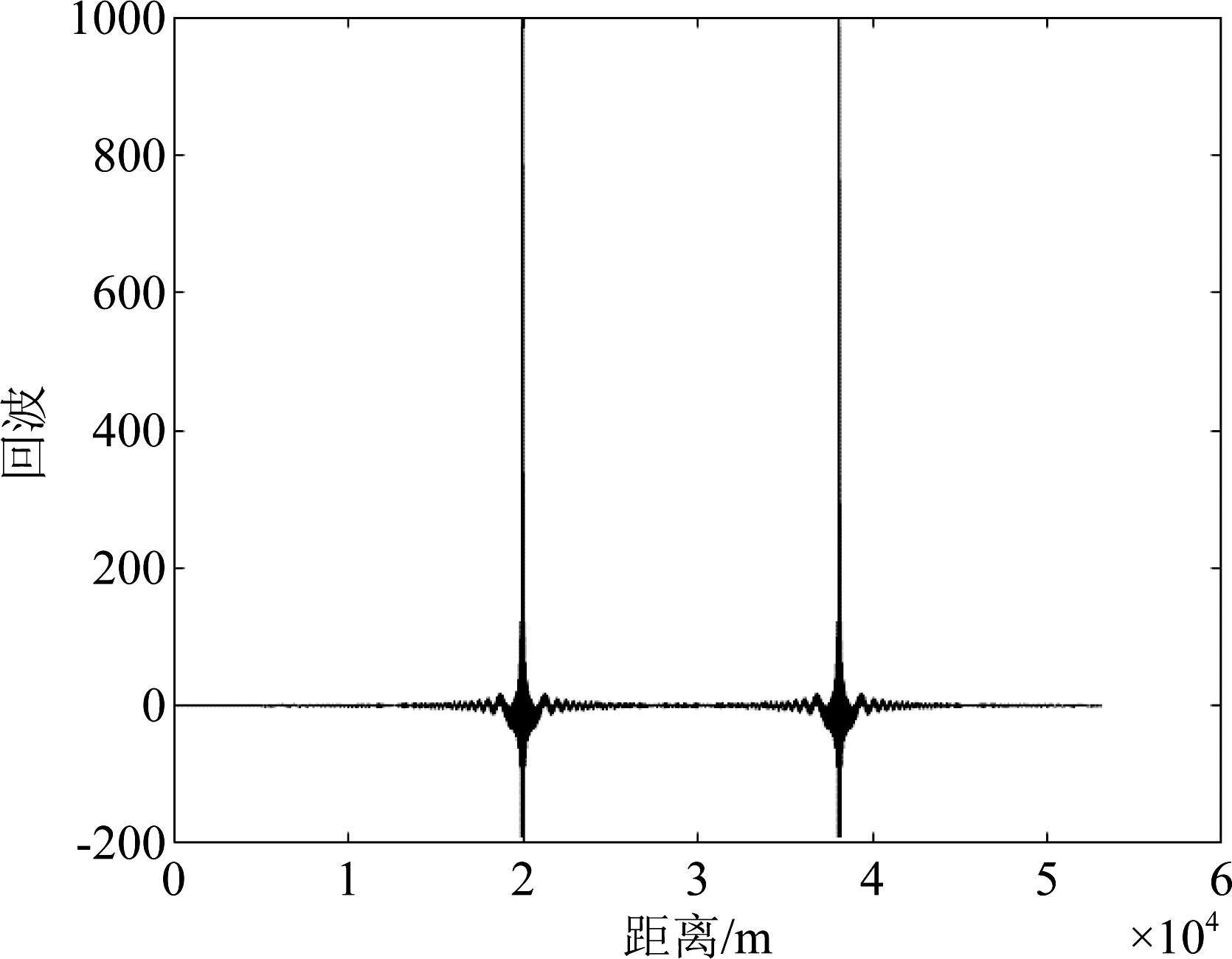
图5 雷达传播时延法测距离
Fig.5 Distance measurement by radar propagation delay method
一旦测得干扰源的距离信息,便可以通过非线性滤波器对干扰源的下一时间周期的位置进行预测,比较扩展卡尔曼滤波器、不敏卡尔曼滤波器、粒子群算法对干扰源的估计效果如图6所示。
由图6知,EKF在高斯白噪声背景下,对该非线性模型的估计精度可以达到与UKF和PF算法同样理想的精度。随后,EKF算法的95°置信区间仿真结果如图7所示。
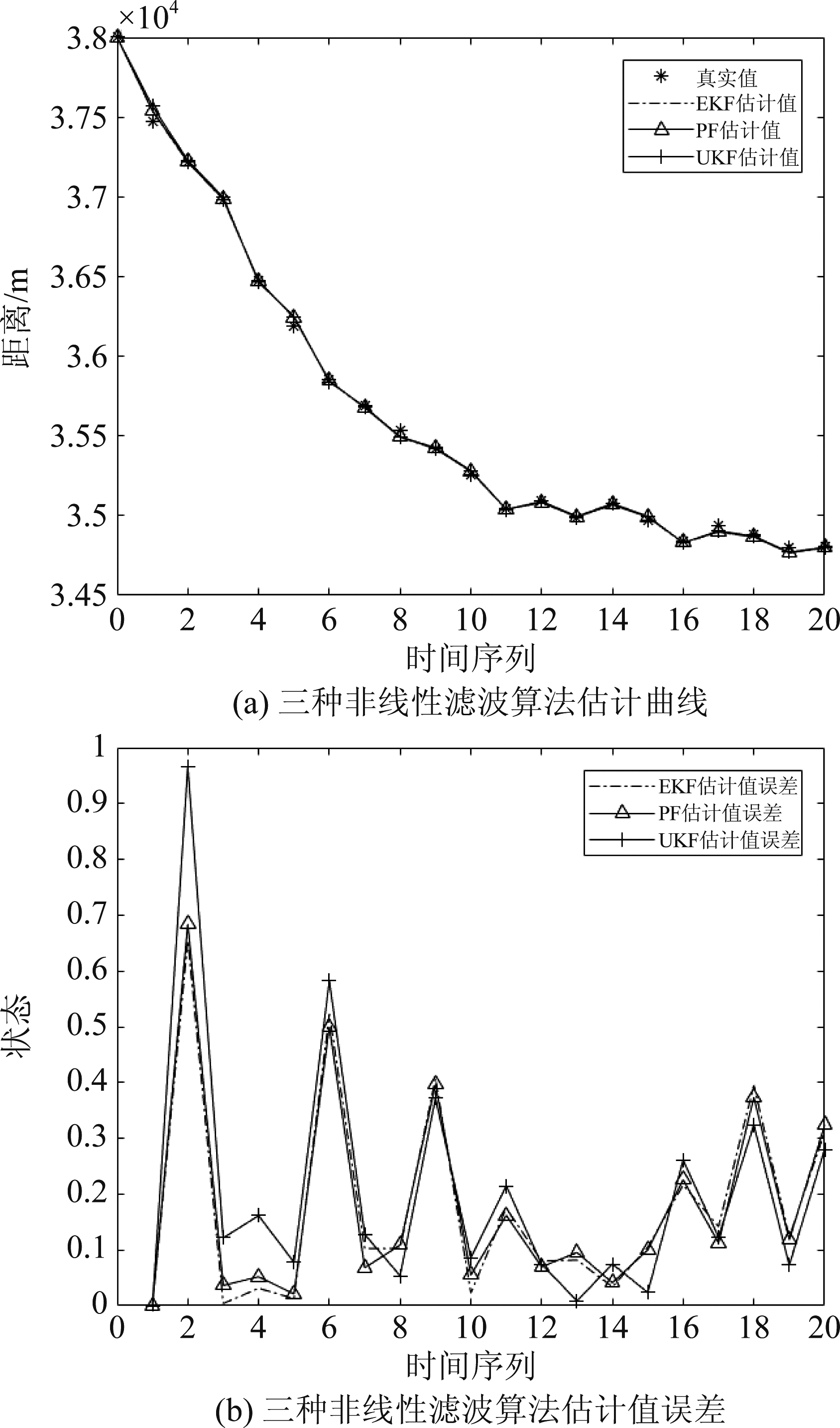
图6 三种非线性滤波算法性能对比图
Fig.6 Performance comparison of three nonlinear filtering algorithms
由图7知干扰源的距离真实值均可落在EKF估计值的95°置信区间内, 故结合雷达实时处理的需要,本文选用EKF获得的数据进行后续的处理。
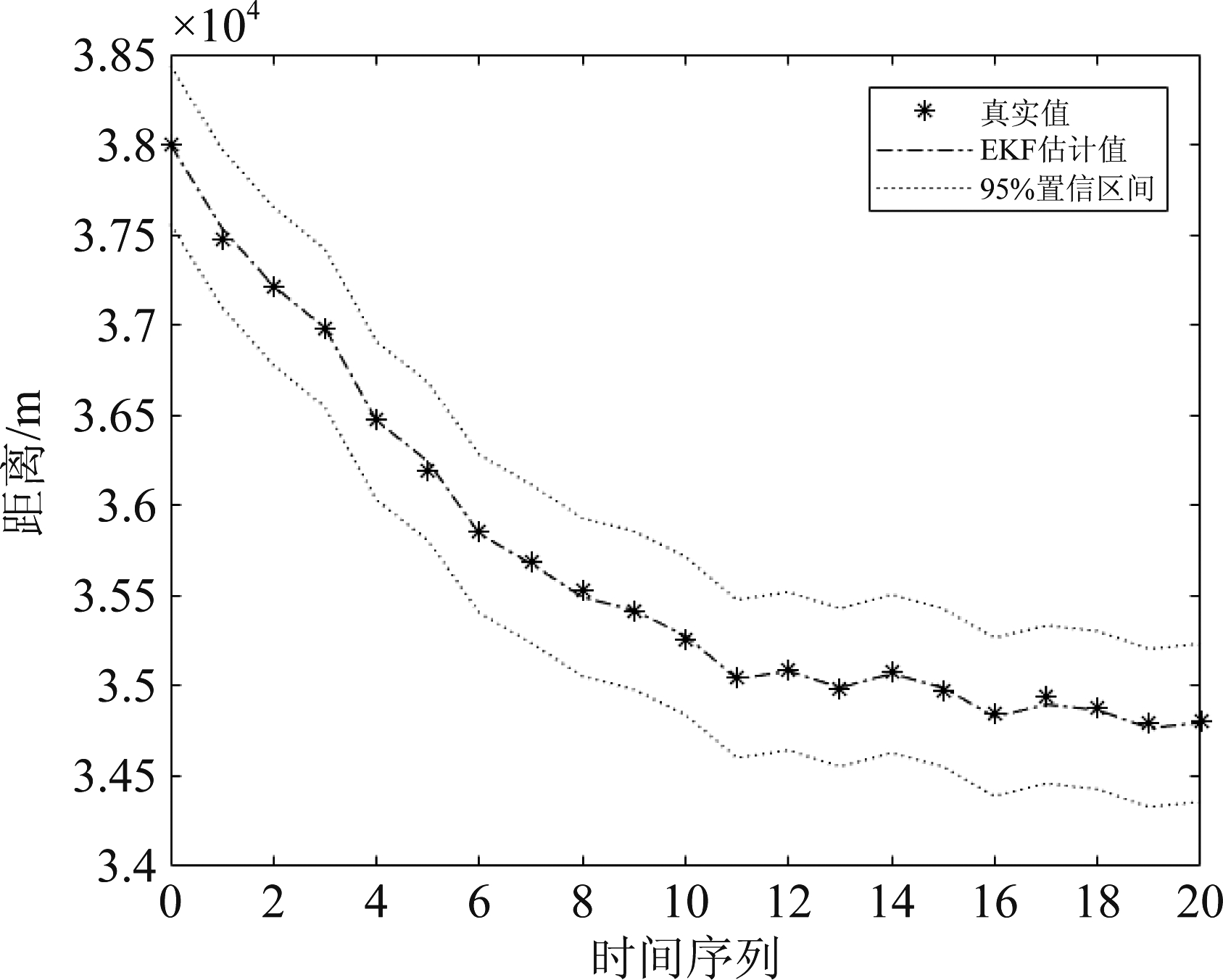
图7 EKF算法95°置信区间
Fig.7 EKF algorithm 95° confidence interval
设置参数发射阵元数N=10,天线载频f0=10 GHz,频偏增量Δf=3 kHz,固定时间t=0,经过非均匀布阵解耦合得到完全距离依赖性波束方向图如图8所示。
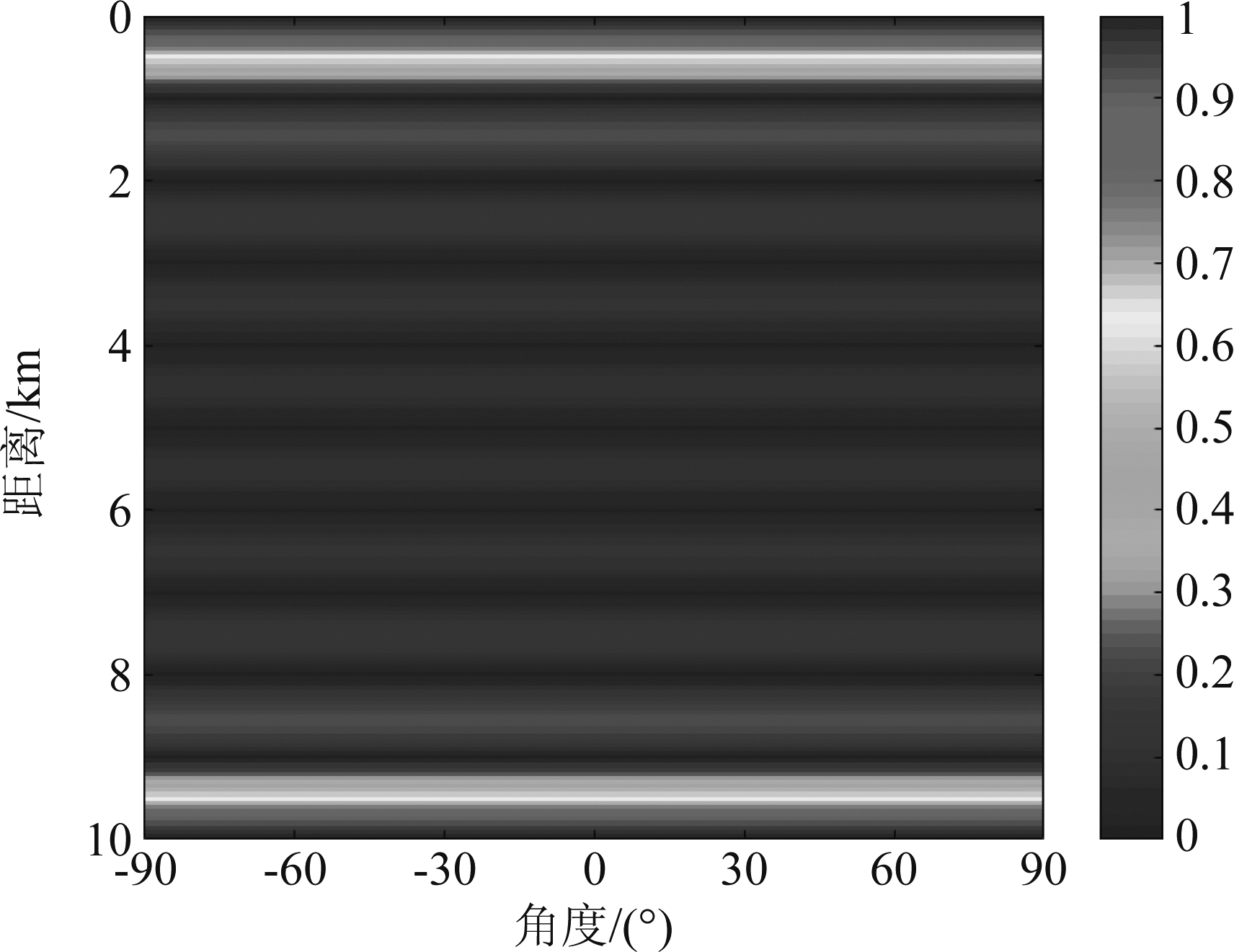
图8 完全距离依赖性波束方向图
Fig.8 Full range dependent beampattern
设第k周期雷达信号到达干扰源瞬时时刻干扰源的真实位置为Xk,所提方法利用的是上一周期的距离预测值Yk|k-1进行波束形成,而在非预测的频控阵系统,由于卡尔曼滤波对状态值的校正需要本周期的观测值Yk,故其在完成定位跟踪与波束控制后可认为干扰源移动到了下一时间序列,故认为系统对位于Xk处的干扰源处理时利用的是上周期状态值
干扰源连续6个时间序列对应的距离信息如表1所示。
表1 假目标连续6个时间序列的距离信息
Tab.1 Distance information of six consecutive time series of false target
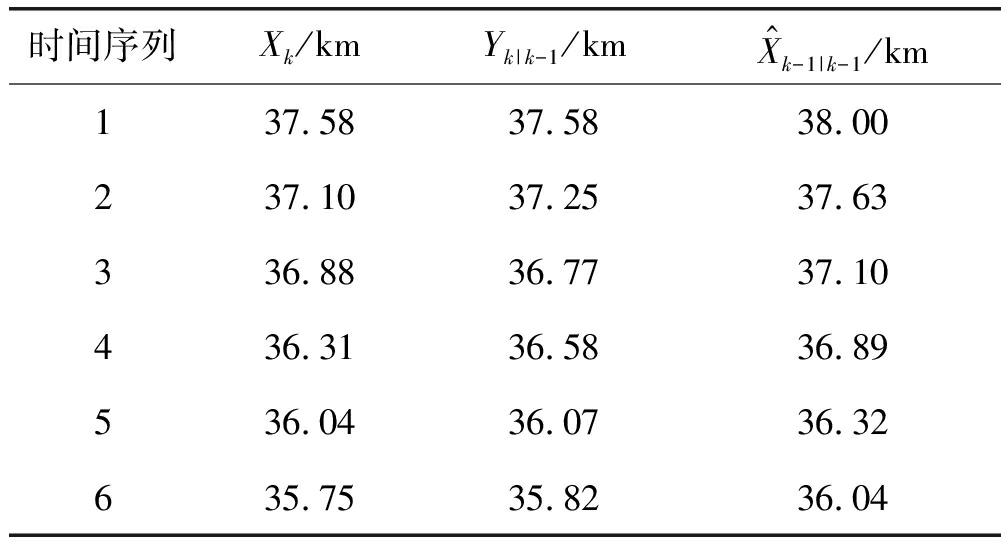
时间序列Xk/kmYk|k-1/kmX^k-1|k-1/km12345637.5837.1036.8836.3136.0435.7537.5837.2536.7736.5836.0735.8238.0037.6337.1036.8936.3236.04
基于预测的频控阵和不基于预测的频控阵的发射波束方向图在干扰目标真实位置处增益如图9所示。
由图9知,在表1所示的六个处理周期中,基于预测的频控阵可以在干扰源真实位置处产生低于目标位置20 dB以上的增益,干扰抑制效果明显优于不利用预测信息的频控阵。最后,取50个时间周期,对比频控阵、基于预测信息处理的频控阵、不基于预测信息处理的频控阵及理想频控阵在干扰目标真实位置的增益如图10所示。
图9 两种方法对干扰源抑制效果对比图
Fig.9 Comparison of interference source suppression effect of two methods
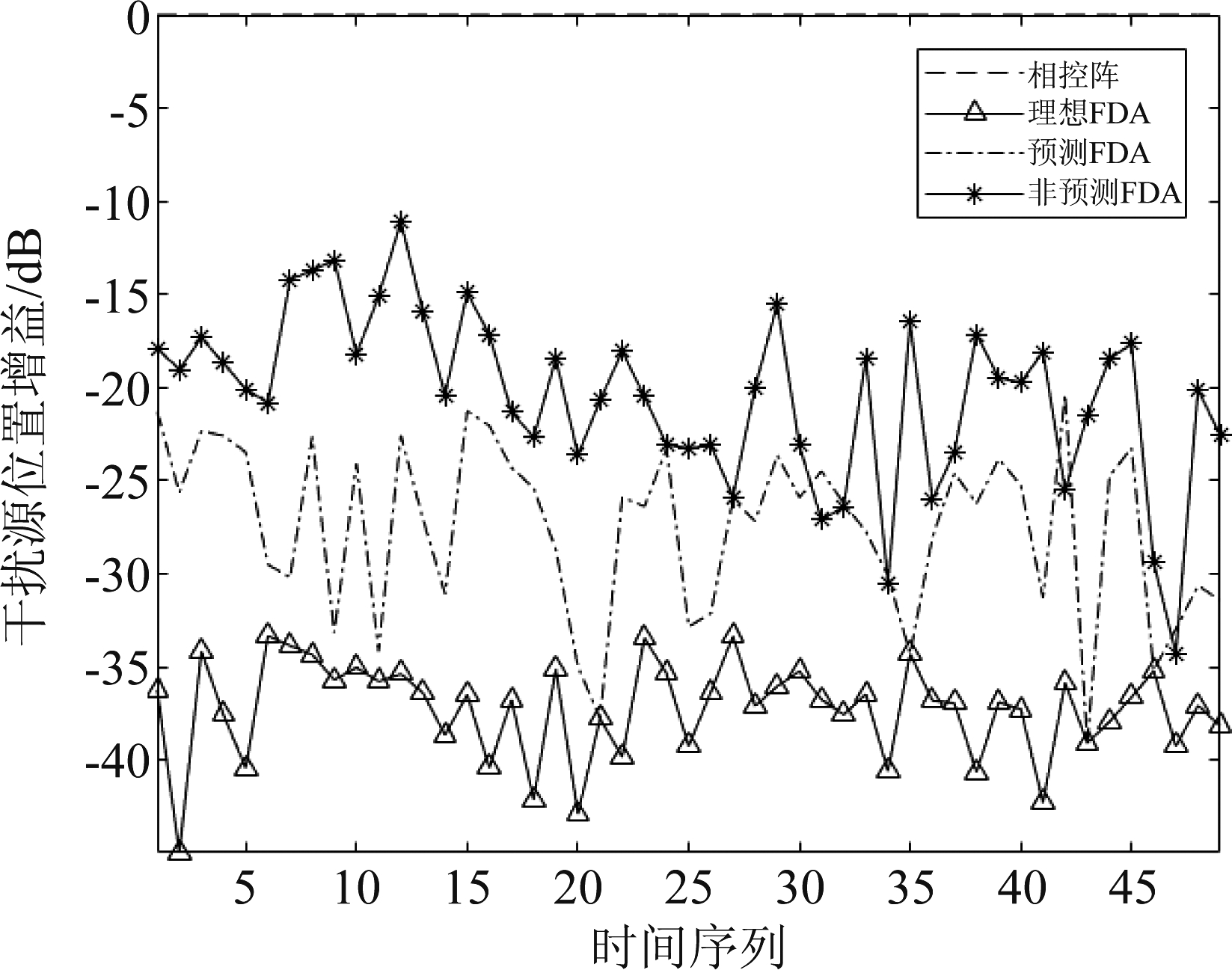
图10 跟踪周期内干扰抑制效果对比图
Fig.10 Comparison of interference suppression effect in tracking period
由图10知,所提方案能够有效对主瓣中运动的干扰机实时地进行波束抑制,且抑制效果优于不基于预测信息的频控阵干扰抑制方案。
5 结论
本文提出了一种基于认知频控阵雷达的对主瓣中运动干扰假目标形成动态零陷的方案,在该方案中,我们采用非均匀布阵方式对频控阵进行解耦产生具有完全距离依赖性发射波束图,之后通过EKF算法获得干扰源的预测位置,并以此作为先验距离信息进行距离维的波束形成。
仿真结果表明,所提方法可以有效的对主瓣中运动的干扰源进行实时的抑制,在抑制效果上比不基于预测信息的方法具有优越性。对频控阵雷达对抗主瓣欺骗式干扰研究具有一定的参考价值。
[1] MCMANAMON P F, BOS P J, ESCUTI M J, et al.A review of phased array steering for narrow-band electrooptical systems[J].Proceedings of the IEEE, 2009, 97(6): 1078-1096.
[2] LI Jian, STOICA P.The phased array is the maximum SNR active array[lecture notes][J].IEEE Signal Processing Magazine, 2010, 27(2): 143-144.
[3] ANTONIK P, WICKS M C, GRIFFITHS H D, et al.Frequency diverse array radars[C]∥2006 IEEE Conference on Radar.Verona, NY, USA, 2006: 215-217.
[4] WICKS M C, ANTONIK P.Frequency diverse array with independent modulation of frequency, amplitude, and phase: US7319427[P].2008-01-15.
[5] WANG Wenqin.Overview of frequency diverse array in radar and navigation applications[J].IET Radar, Sonar & Navigation, 2016, 10(6): 1001-1012.
[6] TAN Ming, WANG Chunyang, LI Zhihui.Correction analysis of frequency diverse array radar about time[J].IEEE Transactions on Antennas and Propagation, 2021, 69(2): 834-847.
[7] XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al.Joint range and angle estimation using MIMO radar with frequency diverse array[J].IEEE Transactions on Signal Processing, 2015, 63(13): 3396-3410.
[8] DING Zihang, XIE Junwei, WANG Bo, et al.Robust adaptive null broadening method based on FDA-MIMO radar[J].IEEE Access, 2020, 8: 177976-177983.
[9] HAYKIN S.Cognitive radar: A way of the future[J].IEEE Signal Processing Magazine, 2006, 23(1): 30-40.
[10] 兰岚,廖桂生,许京伟,等.FDA-MIMO雷达非自适应波束形成抗主瓣欺骗式干扰研究[J].信号处理,2019,35(6): 944-950.
LAN Lan, LIAO Guisheng, XU Jingwei, et al.Main-beam deceptive jamming suppression with non-adaptive beam-forming in FDA-MIMO radar[J].Journal of Signal Processing, 2019, 35(6):944-950.(in Chinese)
[11] WANG Wenqin.Cognitive frequency diverse array radar with situational awareness[J].IET Radar, Sonar & Navigation, 2016, 10(2): 359-369.
[12] BASIT A, WANG Wenqin, NUSENU S Y.Adaptive transmit beamspace design for cognitive FDA radar tracking[J].IET Radar, Sonar & Navigation, 2019, 13(12): 2083-2092.
[13] GUI Ronghua, WANG Wenqin, PAN Ye, et al.Cognitive target tracking via angle-range-Doppler estimation with transmit subaperturing FDA radar[J].IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 76-89.
[14] WANG Wenqin.Moving-target tracking by cognitive RF stealth radar using frequency diverse array antenna[J].IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 3764-3773.
[15] BASIT A, QURESHI I M, KHAN W, et al.Range-angle-dependent beamforming for cognitive antenna array radar with frequency diversity[J].Cognitive Computation, 2016, 8(2): 204-216.
[16] SAMMARTINO P F, BAKER C J, GRIFFITHS H D.Frequency diverse MIMO techniques for radar[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201-222.
[17] HIGGINS T, BLUNT S D.Analysis of range-angle coupled beamforming with frequency-diverse chirps[C]∥2009 International Waveform Diversity and Design Conference.Kissimmee, FL, USA.IEEE, 2009: 140-144.
[18] 王文钦,邵怀宗,陈慧.频控阵雷达:概念、原理与应用[J].电子与信息学报,2016, 38(4): 1000-1011.
WANG Wenqin, SHAO Huaizong, CHEN Hui.Frequency diverse array radar: Concept, principle and application[J].Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011.(in Chinese)
[19] XU Yanhong, LUK K M.Enhanced transmit-receive beamforming for frequency diverse array[J].IEEE Transactions on Antennas and Propagation, 2020, 68(7): 5344-5352.
[20] XIONG Jie, WANG Wenqin, GAO Kuandong.FDA-MIMO radar range-angle estimation: CRLB, MSE, and resolution analysis[J].IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 284-294.
[21] WAN E A, VAN DER MERWE R.The unscented Kalman filter for nonlinear estimation[C]∥Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium(Cat.No.00EX373), Lake Louise AB, Canada, IEEE, 2000: 153-158.
[22] LIU Xi, CHEN Badong, ZHAO Haiquan, et al.Maximum correntropy Kalman filter with state constraints[J].IEEE Access, 2017, 5: 25846-25853.
[23] 黄小平,王岩.卡尔曼滤波原理及应用:MATLAB仿真[M].北京: 电子工业出版社, 2015: 77-102.
HUANG Xiaoping, WANG Yan.Principle and application of Kalman filter: MATLAB simulation[M].Beijing, Publishing House of Electronics Industry, 2015: 77-102.(in Chinese)
[24] 刘聪锋,刘晓军,廖桂生.稳健自适应波束形成算法综述[J].中国电子科学研究院学报, 2009,4(6): 560-565.
LIU Congfeng, LIU Xiaojun, LIAO Guisheng.Review for robust adaptive beamforming algorithms[J].Journal of China Academy of Electronics and Information Technology, 2009, 4(6): 560-565.(in Chinese)
[25] COX H, ZESKIND R, OWEN M.Robust adaptive beamforming[J].IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(10): 1365-1376.
