1 引言
地基合成孔径雷达(GBSAR)在滑坡监测[1-2],冰川监测[3],露天矿场监测[4-5],桥梁监测[6]等领域得到了广泛应用,在保障人们生命物质财产安全方面起到重大作用。传统的基于直线轨道的GBSAR系统只能获取监测场景的二维图像,并且在对监测场景信息的表达方面,二维图像易受地形叠掩干扰,无法显示真实地貌。因此,一种具备三维成像能力的圆周扫描地基SAR系统被提出。
圆周扫描地基SAR通过雷达相位中心的旋转形成二维合成孔径,既能获得方位向信息也能获得高度向信息,从而实现三维成像[7]。圆周扫描地基SAR系统仅需通过一次旋转扫描就可以形成二维合成孔径,系统数据采集便捷迅速。
虽然近年来圆周扫描地基SAR的可行性和优势已经被验证,但是由于圆周扫描地基SAR的运动轨迹为圆周,其距离向和方位向完全耦合在一起,给三维成像增加了难度。目前时域算法可以应用于圆周扫描地基SAR系统,并得到高精度成像结果,但由于时域算法通过逐像素点相干叠加的方式进行成像,计算量巨大,成像效率较低[8]。目前已有针对机载圆迹SAR的快速算法[9-10],斜视圆迹SAR的RMA算法的基本思想是在点目标回波信号分析的基础上将经典的距离徙动算法(RMA)引入圆迹SAR,通过在极坐标域推导实现数据由空间域到空间频域的转换。机载圆迹SAR的PFA算法,将极坐标格式算法(PFA)引入圆迹SAR,该算法在方位时域进行,适用于不规则轨迹,基于平面波近似进行成像[11]。尽管这些频域算法有效扩大了成像区域并实现高效三维成像,但机载圆迹SAR与圆周扫描地基SAR的几何模型和信号收发模式存在差异(圆迹SAR通过围绕目标区域做弧线运动获取该区域SAR图像,圆周扫描地基SAR通过悬臂旋转探测前方大范围区域并获取SAR图像),因此针对机载圆迹SAR的频域成像算法不能直接应用于圆周扫描地基SAR。
目前尚无针对圆周扫描地基SAR的频域算法,因此本文将借鉴机载圆迹SAR的PFA算法原理,结合圆周扫描地基SAR的成像模型和信号特性,展开对适用于圆周扫描地基SAR的频域三维成像算法研究。本文提出了一种针对圆周扫描地基SAR的频域成像算法,信号的推导和转换在空间频域进行,由于圆周扫描地基SAR的回波信号在方位向具有沿角度维平移不变特性,即与雷达旋转中心相同距离的目标,尽管它们的方位角不同,但回波的距离徙动仅在相位上存在偏移,基于此信号特性,本文设计方位向匹配滤波器实现信号的聚焦。通过距离压缩域的重采样实现信号由斜距平面到成像平面的转换,实现三维成像问题的降维,从而实现二维成像,进而对不同距离处的平面进行层析处理,实现观测场景的三维成像,有效加快了成像效率。
本文的具体安排如下。第2节建立圆周扫描地基SAR的几何模型和信号模型。第3节对算法的原理进行论述,通过建立成像平面与斜距平面的几何关系,推导信号由斜距平面到成像平面的转换过程,在频域实现匹配滤波器的设计,并对算法进行误差分析,推导出算法的适用条件。第4节通过仿真实验验证算法成像能力,并与时域成像算法的成像质量和成像效率对比。第5节对论文进行结论总结。
2 圆周扫描地基SAR几何模型和信号模型
圆周扫描地基SAR具备一个旋转平台,天线通过悬臂作360°圆周运动,对前方大范围场景进行观测。该系统的合成孔径由天线的圆周运动形成,合成孔径的大小与天线的波束宽度成正比。天线波束宽度越大,目标被探测的时间越久,圆周扫描地基SAR的成像质量越高。具体地,圆周扫描地基SAR几何模型如图1所示。
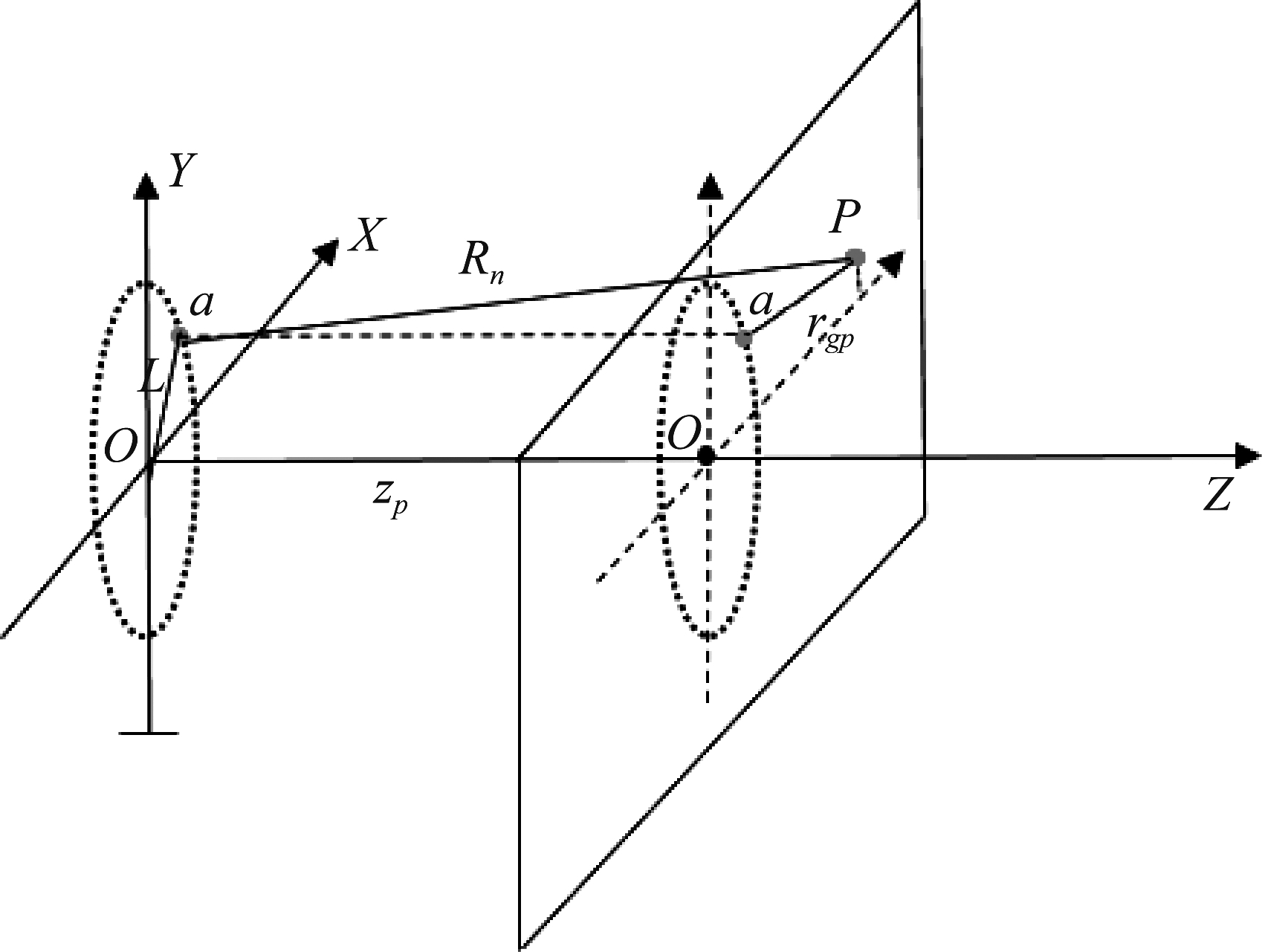
图1 GBCSAR几何模型
Fig.1 GBCSAR geometric model
a为雷达相位中心,天线通过悬臂Oa沿着水平中轴旋转,形成以O为旋转中心的圆周运动轨迹,对前方场景进行圆周扫描,悬臂长度(即轨迹半径)为L,相位中心旋转角度(即系统方位向角度)为θ。P为预设点目标,在如图1所示的平面zp上。点目标所在平面与天线运动轨迹的垂直距离为zp。点目标与相位中心的瞬时斜距为Rn,即系统的距离向。
设相位中心的空间位置坐标为(xn,yn,zn),其中
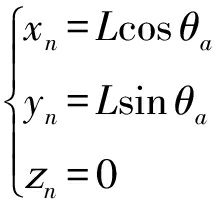
(1)
θ为相位中心旋转的角度,L为相位中心的旋转半径。点目标P的空间位置坐标为(xp,yp,zp),则点目标与相位中心的瞬时斜距Rn可以表示为
(2)
(3)
已知Rn的表达式,以天线发射信号为线性调频信号为例,可以得到经过预处理的频域信号表达式
S(θ, f)=τ·rect(f/Br)·
exp{-j4π(f+fc)Rn(r,θ)/c}
(4)
式中τ为散射系数,Br为信号带宽, f为信号频率, fc为信号中心频率,c为光速。
为了简化操作,我们定义波数K,
K=4π(f+fc)/c
(5)
代入式(4)即可得到信号的波数域表达式
(6)
3 GBCSAR频域成像算法理论
本算法将极坐标格式算法(PFA)与圆周扫描地基SAR的成像模型和信号特性结合在一起,通过距离压缩域的重采样将信号完成由斜距平面到成像平面的转换,在频域对信号进行推导,引入PFA算法,基于平面波近似设计频域匹配滤波器,实现信号在二维平面的聚焦成像,再通过层析完成场景的三维成像。
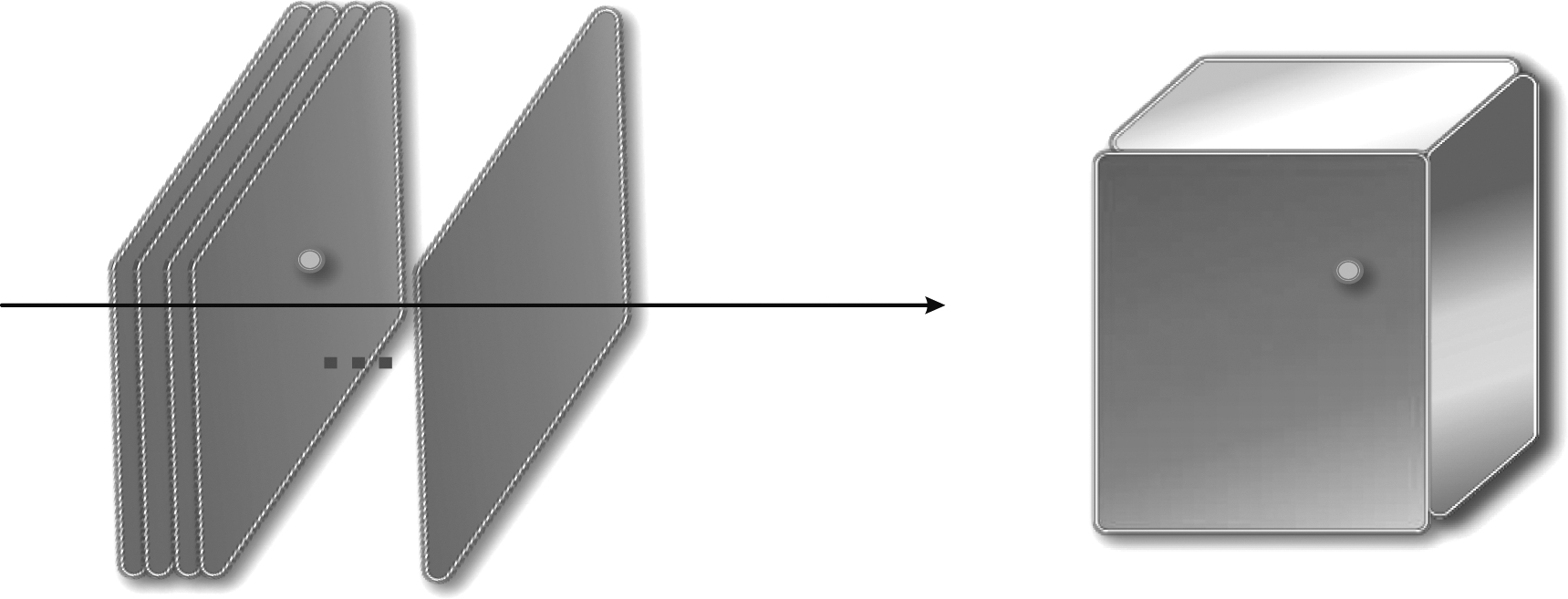
图2 圆周扫描地基SAR层析三维成像示意图
Fig.2 Schematic diagram of circular scanning ground-based SAR tomographic three-dimensional imaging
3.1 斜距平面数据到成像平面信号数据转换
如图3所示,点目标P与雷达相位中心a的斜距Rn投影到P所在成像平面即为rgp,随着雷达相位中心旋转角度θ的改变,每一个斜距Rn都对应着成像平面的一个rgp,按照这种对应关系,可以将式(6)表达的斜距回波信号转换到目标所在的成像平面,以达到将三维成像问题降维成二维成像问题的目的。具体地,将式(6)进行IFT,可以得到
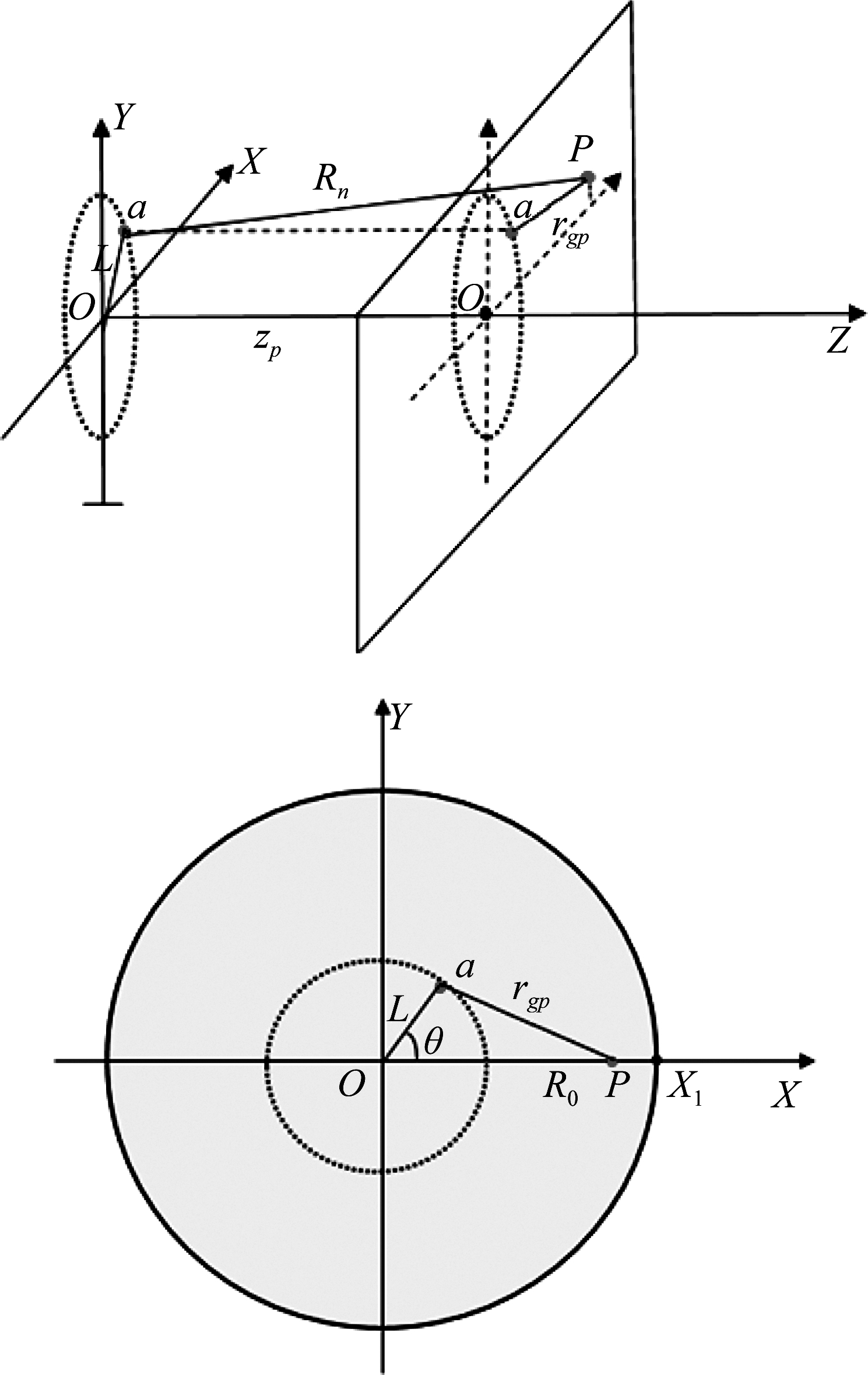
图3 信号斜距平面到成像平面转换模型
Fig.3 Signal slope to imaging plane conversion model
S(θ,r)=sin c[(c/2Br)(r-Rn)]exp(-jKcRn)
(7)
Br是信号带宽,Kc是中心波数。根据几何对应关系
(8)
式(7)通过一维插值重采样可以得到
S(θ,rg)=S(θ,r)exp(jKcRn)≈
sin c[(c/2Brg)(rg-rgp)]
(9)
其中成像平面对应的带宽为
Brg=Brsin α
(10)
波束入射角α随着相位中心的旋转而不断变化,但是由于圆周扫描地基SAR的旋转半径L远小于雷达的探测距离,相位中心在不同旋转角度引起的α的变化可以忽略不计,实际数据处理时,将α视为旋转中心O到成像区域的夹角。
定义Kg为与rg对应的成像平面的波数。重采样完成后对式(9)作距离向傅里叶变换(FT),得到成像平面距离频域-方位时域信号
S(θ,Kg)=exp(-jKgrgp)
(11)
至此,完成了斜距平面数据到成像平面数据的转换,实现了三维成像问题的降维。
3.2 方位向频域匹配滤波
接下来本小节设计频域匹配滤波器,消除信号的距离徙动,实现二维平面的聚焦。由X-O-Y平面的几何可知,
(12)
R0是点目标到雷达运动轨迹投影中心的距离,在实际的观测场景中,假设目标处于远场,因此可以将式(12)近似为
rgp≈R0-Lcos θ
(13)
那么式(11)可以重写为
S(θ,Kg)=exp(-jKg(R0-Lcos θ))=
exp(-jKgR0+jLKgcos θ)
(14)
产生距离徙动的项是jLKgcos θ,所以我们可以通过设计匹配滤波器消除此项。将式(14)进行方位向傅里叶变换(FT),定义Kθ为与θ对应的方位向波数,可得到信号的二维频域表达式
S(Kθ,Kg)=exp(-jKgR0)·S1(Kg,Kθ)
(15)
其中S1(Kg,Kθ)为exp(jLKgcos θ)项的傅里叶变换,得到该项的频域表达后,就可以针对该项设计匹配滤波函数Hg,
Hg=S1(Kg,Kθ)*
(16)
其中符号*代表共轭,将式(15)表示的二维频域信号与匹配滤波函数Hg相乘即可实现方位向的匹配滤波。
S′(Kθ,Kg)=S(Kθ,Kg)·Hg
(17)
然后,对消除了距离徙动的滤波结果进行二维傅里叶逆变换,即可得到目标所在二维平面的时域SAR图像,该图像的存储格式为极坐标格式。为了直观具体地获得目标在空间中的位置信息,最后对极坐标格式下的时域回波数据进行二维插值,得到该二维平面直角坐标格式下的时域SAR图像。
3.3 算法流程和运算量分析
对于指定距离z=zp的平面,基于3.2节的算法推导,圆周扫描地基SAR频域三维成像算法流程如图4所示,具体的操作步骤如下。同时为了对每一步操作的计算量进行分析,这里假设距离向采样点数为N,方位向采样点数为M,图像尺寸为N2,一维插值核长度为ηs。
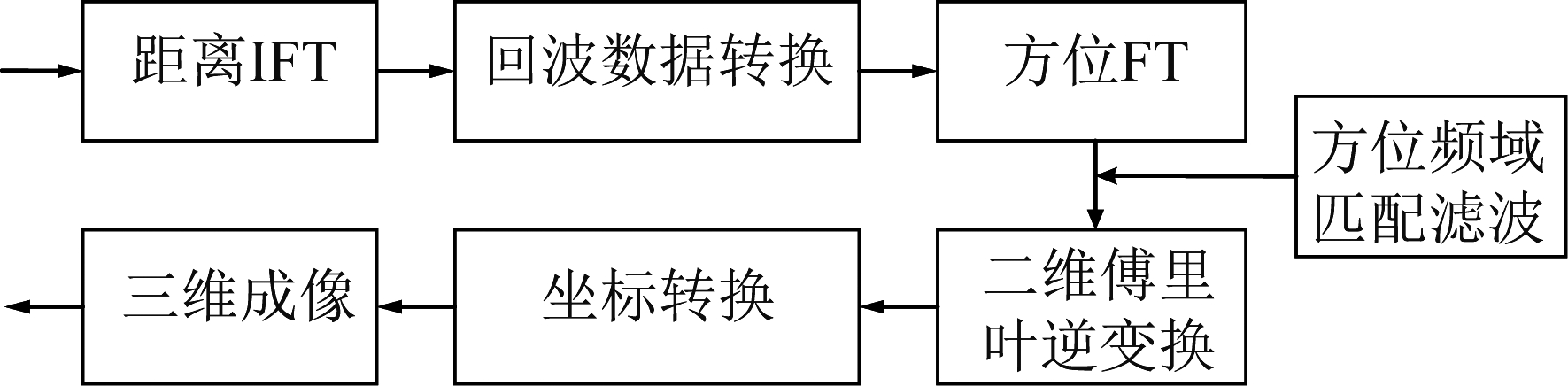
图4 圆周扫描地基SAR频域三维成像算法
Fig.4 Circumferential scanning ground-based SAR frequency domain 3D imaging algorithm
步骤1 信号S(θ,K)作距离向逆傅里叶变换(IFT),得到时域信号S(θ,r)。该步的运算量为O(Nlog2N)。
步骤2 距离压缩域重采样,实现回波数据由斜距平面到成像平面的转换,作距离向FT,得到距离压缩域信号S(θ,Kg)。该步运算量为O(ηsMN)+O(Nlog2N)。
步骤3 方位FT,得到二维频域信号S(Kθ,Kg)。该步运算量为O(Nlog2N)。
步骤4 方位频域匹配滤波,将S(Kθ,Kg)与匹配滤波函数Hg相乘。该步运算量为O(MN)。
步骤5 将步骤4得到的聚焦信号进行二维傅里叶逆变换,得到极坐标格式二维聚焦信号S(θ,rg)。该步运算量为O(N2log2N)。
步骤6 二维插值,将极坐标格式信号S(θ,rg)转化成直角坐标格式信号S(y,z)。该步运算量为![]()
步骤7 对于整个场景区域,在等间隔dz的距离平面上,重复步骤2~6,逐层实现二维成像,最后迭加在一起即可完成整个场景的三维成像。
对于BP算法,其对成像场景进行逐像素相干叠加,因此它的运算量的量级为O(ηsN2M)。因此本方法在较大范围成像区域内的成像效率更高。
4 仿真实验验证
4.1 二维成像验证
本算法在Win10,4核处理器,MATLAB2020a中运行。仿真参数如表1。以点目标P(150,0,200)为例,其回波信号为近似正弦的曲线,经过距离压缩域重采样,回波数据精准地实现了由斜距平面到成像平面的转换。目标的距离向频谱投影到了成像平面上,频谱的中心频率随着相位中心旋转角度变化,经过坐标转换,目标频谱支撑域为一个椭圆环,这与算法理论推导部分是相吻合的。
表1 GBCSAR系统仿真参数
Tab.1 GBCSAR system simulation parameters

参数参数值信号载频fmin17 GHz发射信号带宽Br1 GHz信号速率3e8 m/s距离向采样点数2048方位向采样点数1024旋转速率 8 rad/s波束角度 60°
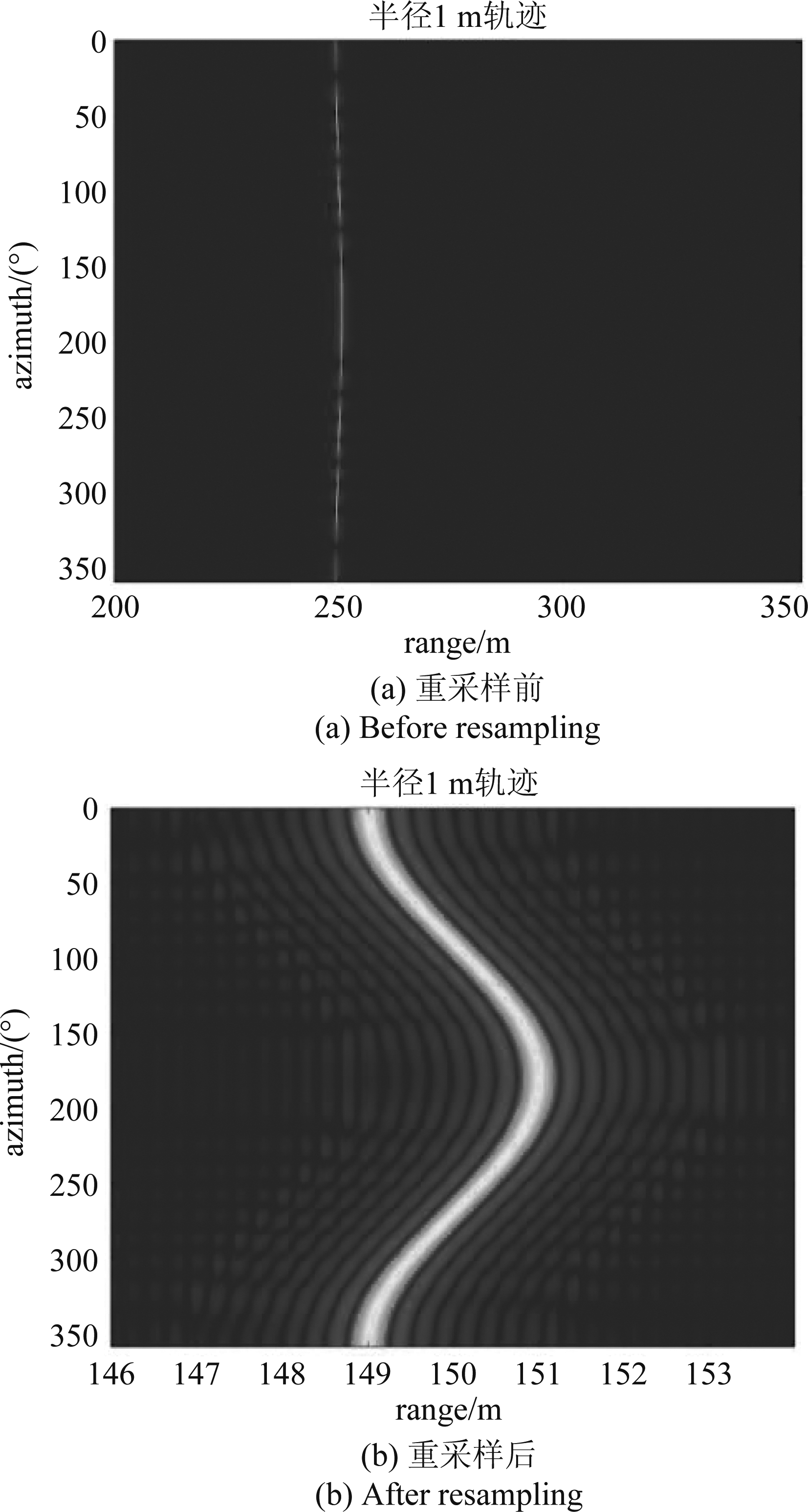
图5 信号重采样前后
Fig.5 Before and after signal resampling
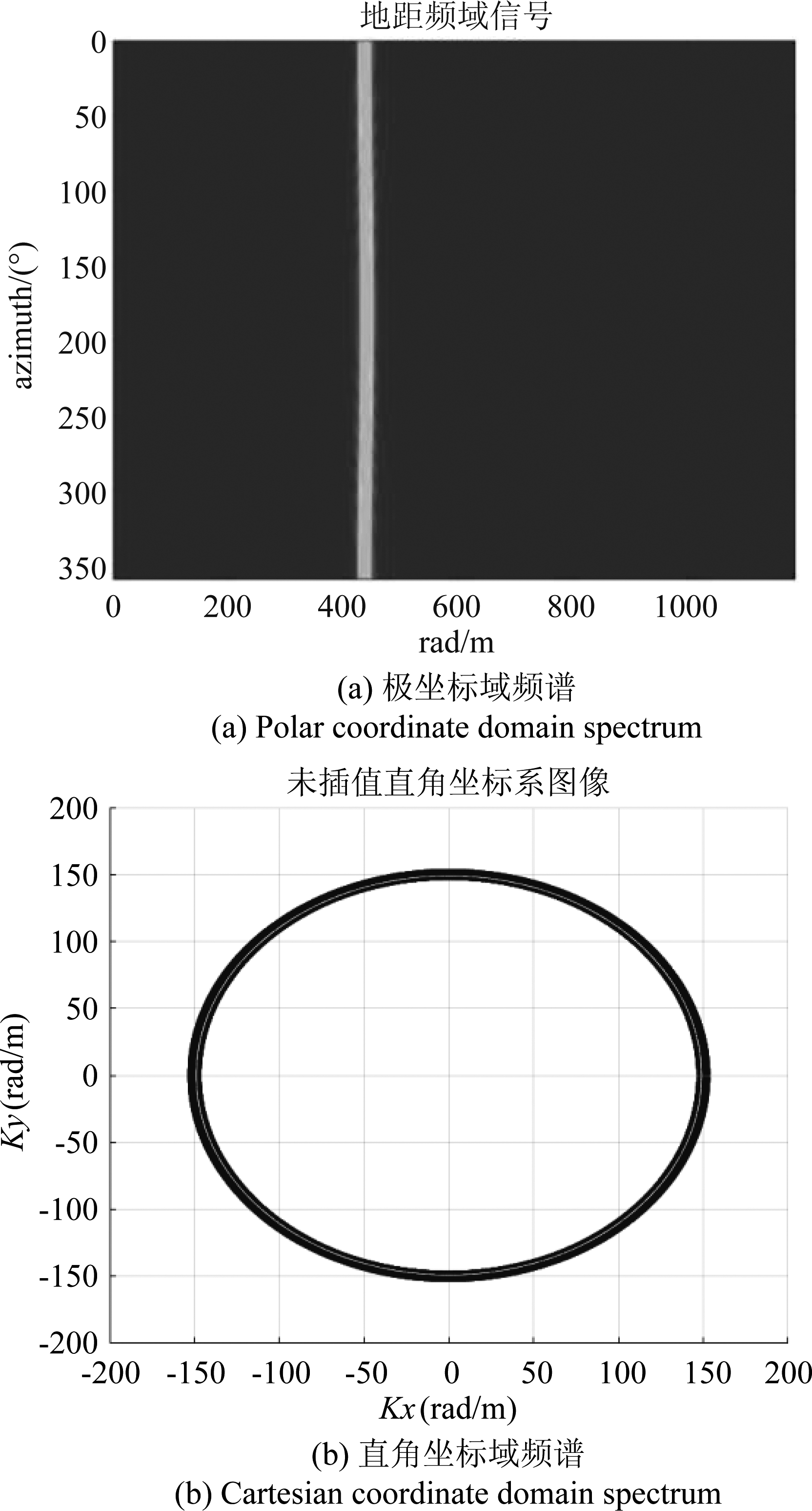
图6 坐标转换前后频谱
Fig.6 Spectrum before and after coordinate conversion
经过二维匹配滤波及二维逆傅里叶变换,目标的成像结果如下。具体的点目标仿真质量参数如表2所示。
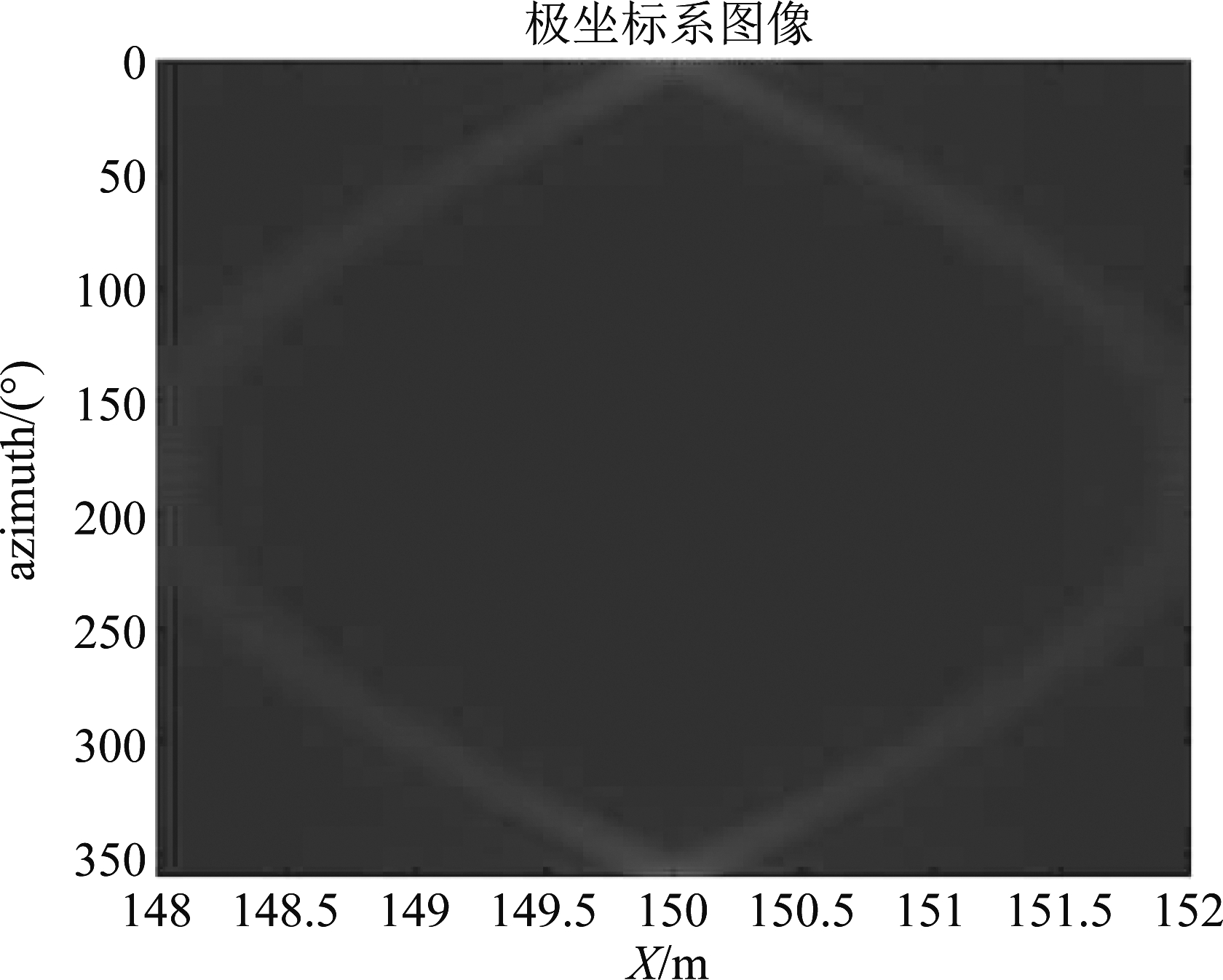
图7 点目标极坐标聚焦图像
Fig.7 Polar coordinate focused image of point target
表2 点目标仿真参数
Tab.2 Point target simulation parameters
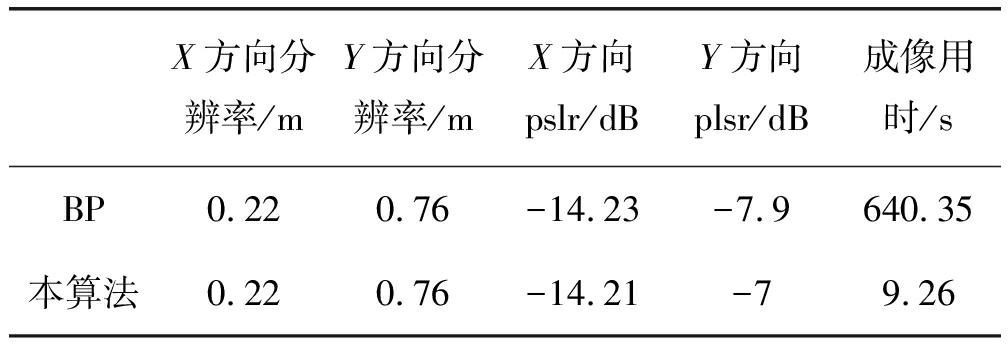
X方向分辨率/mY方向分辨率/mX方向pslr/dBY方向plsr/dB成像用时/sBP0.220.76-14.23-7.9640.35本算法0.220.76-14.21-79.26
由图4、图5及表2可知,本算法与BP算法在仿真参数相同的前提下,对同一点目标的仿真质量非常接近。由于本算法在设计匹配滤波器时采用了平面波近似,所以对PSLR产生了影响,但整体的成像质量依旧良好。BP算法成像用时640.35 s,本算法的成像用时为9.62 s,时域成像算法成像用时约为本文算法的69倍。通过对比可知,本文提出的频域成像算法成像效率更高,并且具备较为良好的成像效果。
4.2 三维成像验证
本仿真是为了验证算法三维成像能力,仿真参数同表1,图10为单目标和多目标的三维成像结果,显示的是目标的3 dB轮廓。所有目标都得到了准确的三维重建。
提取位于(150,0,200)的点目标的YOZ平面的剖面图,(动态显示-40 dB)如图11(a),并做z方向的过峰值点剖面图,如图11(b)。具体的仿真质量参数如表3所示。

图8 (a)BP二维成像结果,(b)X方向剖面,(c)Y方向剖面
Fig.8 (a)BP two-dimensional imaging results,(b)X-direction section,(c)Y-direction section
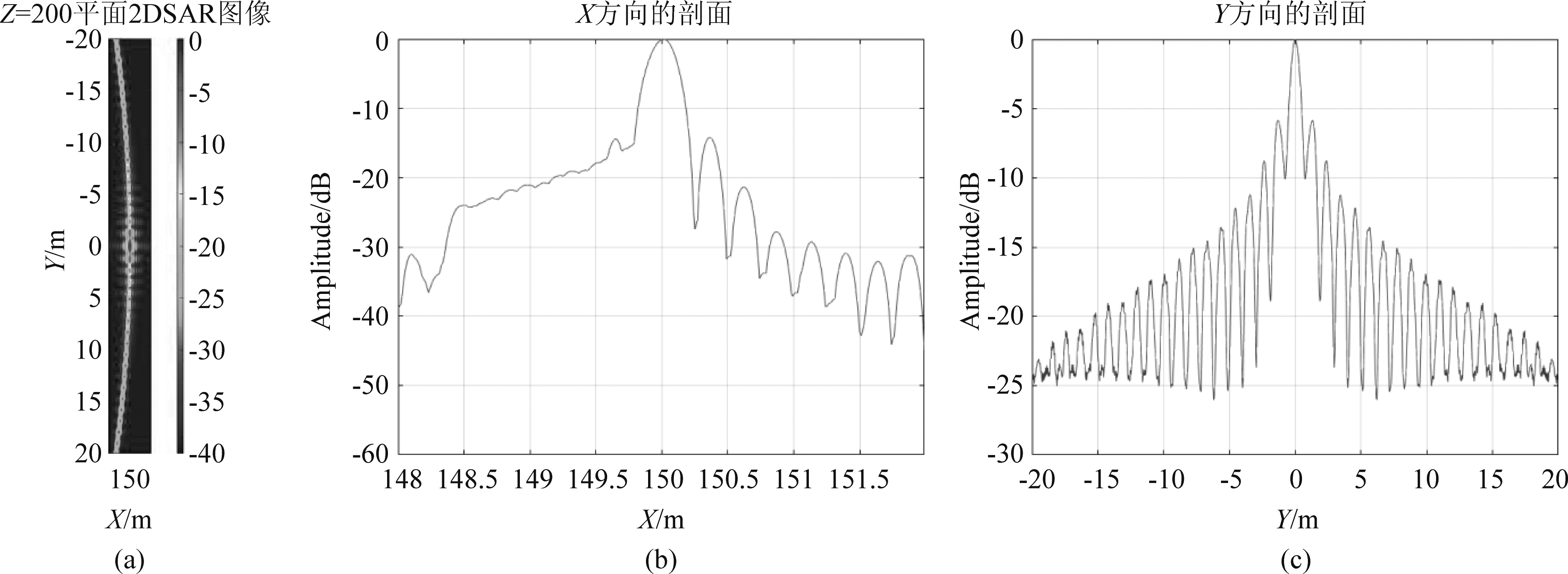
图9 (a)本算法二维成像结果,(b)X方向剖面,(c)Y方向剖面
Fig.9 (a)Two-dimensional imaging results of this algorithm,(b)X-direction section,(c)Y-direction section
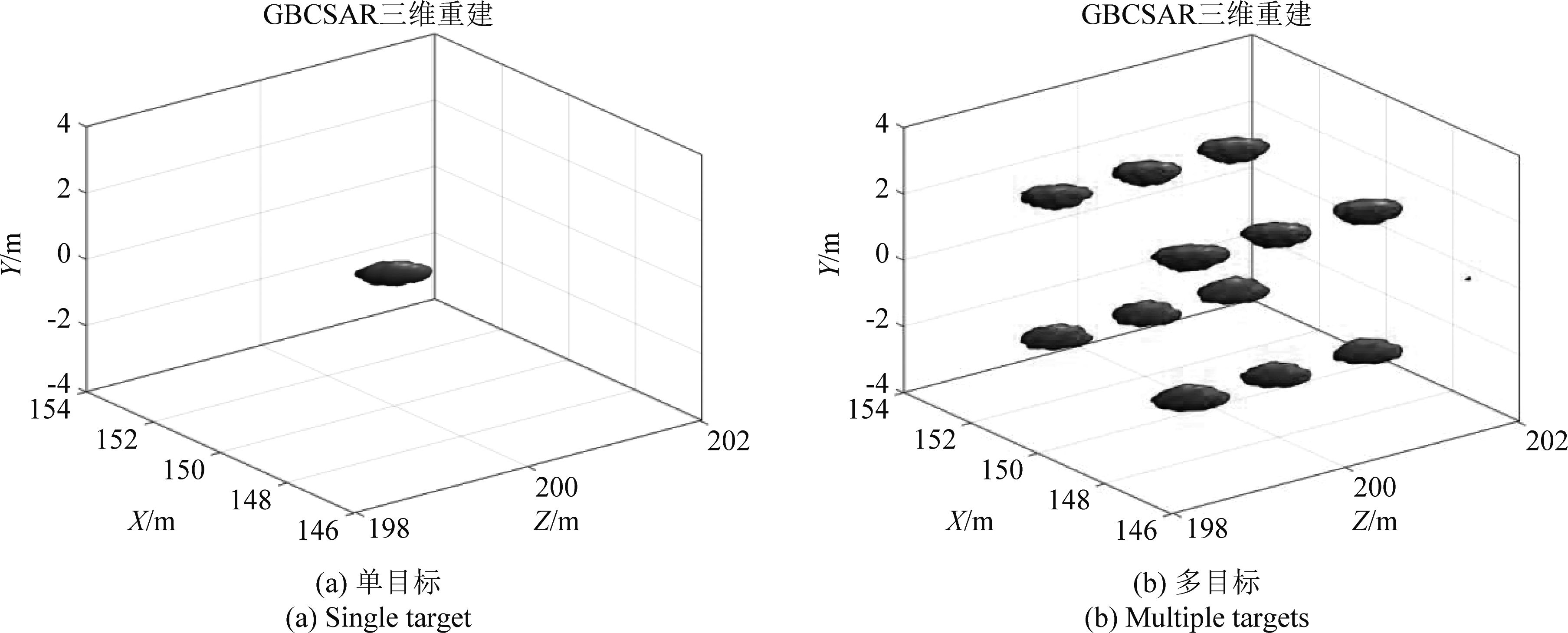
图10 点目标的三维成像结果
Fig.10 Three-dimensional imaging results of a point target

图11 点目标YOZ平面剖面图
Fig.11 Plane section view of point target YOZ
表3 仿真质量参数
Tab.3 Simulation quality parameters

Z方向分辨率/mZ方向pslr/dBBP0.16-13.53本算法0.16-13.55
根据图11、图12和表3可知,本算法和时域算法在仿真参数相同的情况下,点目标的成像质量非常接近。
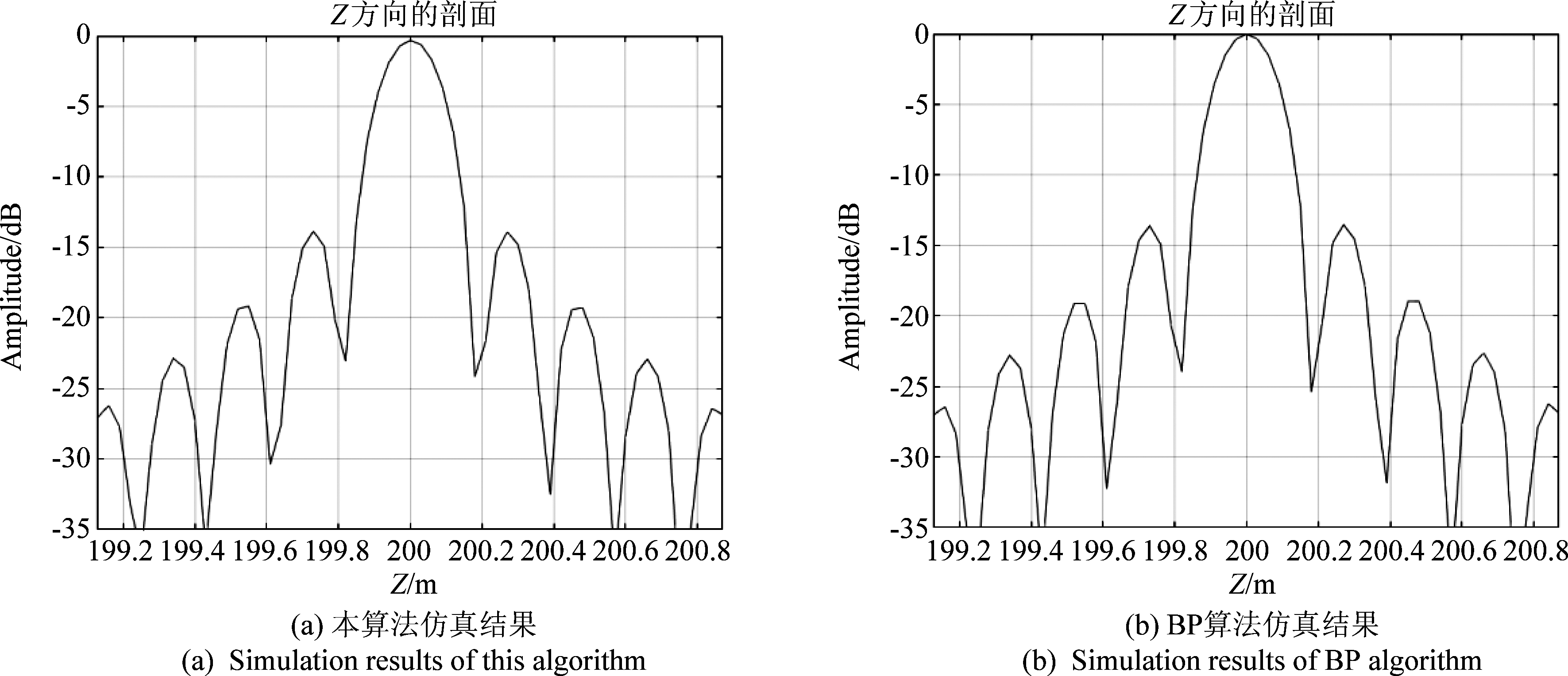
图12 Z方向剖面图
Fig.12 Z-direction section view
5 结论
本文提出了一种针对圆周扫描地基SAR的频域三维成像算法,该算法在频域对信号进行分析和推导,首先通过将回波数据进行由斜距平面到成像平面的转换,将三维成像问题降维成二维平面的成像问题,再借鉴机载圆迹SAR的PFA算法,设计二维频域匹配滤波器,实现信号在二维平面的聚焦,最后经过切片层析处理,有效实现了观测场景的三维成像。因为以上算法推导步骤在频域进行,所以成像效率优于时域算法,能够更好地适应实时监测的需求。
[1] 蒋留兵, 杨凯, 车俐.地基合成孔径雷达对目标三维形变的监测[J].测绘通报, 2020(3): 35-38,68.
JIANG Liubing, YANG Kai, CHE Li.Monitoring of 3D deformation of target by ground-based synthetic aperture radar[J].Bulletin of Surveying and Mapping, 2020(3): 35-38,68.(in Chinese)
[2] 张志春, 袁智, 王彦平.地基干涉合成孔径雷达形变监测应用综述[J].北京测绘, 2020, 34(1): 27-32.
ZHANG Zhichun, YUAN Zhi, WANG Yanping.Ground-based interferometry synthetic aperture radar and applications in deformation monitoring[J].Beijing Surveying and Mapping, 2020, 34(1): 27-32.(in Chinese)
[3] NOFERINI L, MECATTI D, MACALUSO G, et al.Monitoring of Belvedere Glacier using a wide angle GB-SAR interferometer[J].Journal of Applied Geophysics, 2009, 68(2): 289-293.
[4] MECATTI D, MACALUSO G, BARUCCI A, et al.Monitoring open-pit Quarries by interferometric radar for safety purposes[C]∥The 7th European Radar Conference.Paris, France.IEEE, 2010: 37-40.
[5] PIERACCINI M, MICCINESI L.An interferometric MIMO radar for bridge monitoring[J].IEEE Geoscience and Remote Sensing Letters, 2019, 16(9): 1383-1387.
[6] PRATESI F, NOLESINI T, BIANCHINI S, et al.Early warning GBInSAR-based method for monitoring Volterra(Tuscany, Italy)city walls[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(4): 1753-1762.
[7] PIERACCINI M, ROJHANI N, MICCINESI L.Ground based synthetic aperture radar with 3D imaging capability[C]∥2018 15th European Radar Conference(EuRAD).Madrid.IEEE, 2018.
[8] 潘丰, 王文静, 孟祥新, 等.基于SAR成像的FBP算法、FFBP算法三维快速重建[J].电子测量技术, 2020, 43(4): 153-158.
PAN Feng, WANG Wenjing, MENG Xiangxin, et al.Three-dimensional rapid reconstruction of FBP algorithm and FFBP algorithm based on SAR imaging[J].Electronic Measurement Technology, 2020, 43(4): 153-158.(in Chinese)
[9] 闵锐.机载SAR三维成像理论及关键技术研究[D].成都: 电子科技大学, 2012.
MIN Rui.Research on airborne SAR three-dimensional imaging theory and key technologies[D].Chengdu: University of Electronic Science and Technology of China, 2012.(in Chinese)
[10] 陈乐平.机载圆周合成孔径雷达成像技术研究[D].长沙:国防科技大学, 2018.
CHEN Leping.Research of airborne circular synthetic aperture radar imaging technique[D].Changsha:National University of Defense Technology,2018.(in Chinese)
[11] 李枫, 王洲, 杨文谷, 等.螺旋轨迹SAR极坐标格式算法研究[J].信号处理, 2019, 35(6): 1057-1063.
LI Feng, WANG Zhou, YANG Wengu, et al.Polar format algorithm for spiral synthetic aperture radar[J].Journal of Signal Processing, 2019, 35(6): 1057-1063.(in Chinese)




