1 引言
探地雷达是一种利用高频电磁波来探测和定位地下结构中目标和界面的物理方法[1]。它具有操作简单、快速、经济、无损检测、精度高等优点,成为浅层地球物理勘探最重要的工具之一,成功应用于土木工程[2]、环境工程[3]、考古勘探[4]、军事勘探[5]等领域。近年来,探地雷达在路面及墙体分层介质探测方面发挥出重要作用,它可以利用由层状介质分界面的电特性差异而产生的反射回波来确定分层介质的厚度和其他电性常数。目前,探地雷达在层状介质厚度和电特性参数的测量中,运用最为广泛的方法是反演法,通过使用一般原理和模型,对数据进行处理和分析来确定实测数据中有意义的介质内部结构、特性等参数分布情况。
针对一般性的层状介质参数反演方法,Chien等人利用共中点法(CMP)构建了地下多层介质滑行波模型,求取层状介质的相对介电常数和层厚信息[6];Minet等人利用Green函数建立目标函数,反演厚度和电特性参数[7];张蓓根据路面层状结构,对探地雷达时域波形进行反演,得到介质层的复介电常数和厚度[8];蔡迎春等建立了GPR路面结构介电常数的遗传反演算法,实现了路基结构层介电常数的厚度的GPR反演[9]。但这些方法都需要在时域上能够分辨出每层的反射回波。
然而在实际应用中,需要探测的场景中往往存在着薄层,甚至是超薄层介质,如冬季路面表层附着的薄冰、沥青铺路时防止沥青混合物粘在滚筒/气动轮表面而喷出的水汽层、墙体覆盖面的涂料,以及环境工程中的非水相污染(NAPL)探测等场景。这些薄层通常小于探地雷达可分辨的最小厚度,因此,近几年已展开薄层及超薄层反演方法的研究。秦瑶等人通过求取电磁波在层状介质中的传输函数,反演地层的厚度和广义反射系数,但不能求得地层的电性参数[10];黄忠来和张建中将地震波谱反演方法运用于探地雷达,提出了一种由GPR信号频谱反演地下介质介电参数的算法,能有效地识别层厚小于1/4波长的薄层,但无法反演出多层介质的结果[11];Siqi Wang等人利用梯度下降的非线性优化方法重构了薄沥青混凝土铺层的重叠面和底面反射信号,再通过重构后的反射信号幅值来计算薄层的介电常数和厚度,解决了薄层分辨的问题[12-13],但需要给定材料参数的范围。
本文提出了一种利用广义反射系数建立时域上的GPR反射信号模型,再通过遗传算法对多参数进行全局优化反演的方法。并通过分析广义反射系数频谱得到参数初值,从而提高反演计算的效率和准确性,使结果达到理想的效果,能够反演出层厚小于1/8波长的超薄层介质参数。
2 GPR估计分层介质参数
2.1 定义广义反射系数
首先,假设地下各层都是线性、均匀、各向同性的。那么,传播常数可写为[14]:
γ=α+jβ
(1)
其中,α为衰减常数,β为相位常数,且满足:
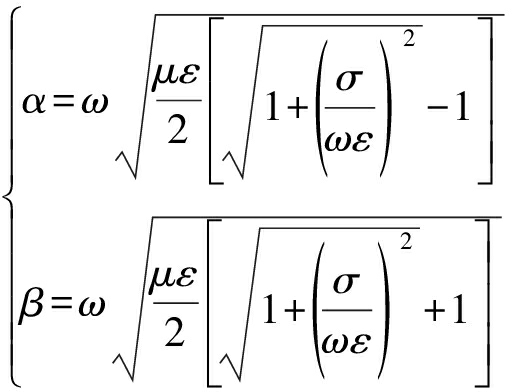
(2)
其中,ω、ε、σ、μ分别代表了角频率、介电常数、电导率、磁导率。
由分界面上反射系数和透射系数的定义可得第i层和第i+1层之间界面的反射系数ri,i+1和透射系数τi,i+1[15]:
(3)
其中,![]() 若考虑非磁性无损介质,则有:
若考虑非磁性无损介质,则有:
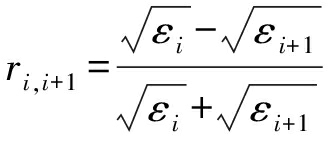
(4)
可以定义一个广义反射系数为接收到的每层分界面的反射波振幅与发射波的比值,记为Ri,i+1。由于第一层顶部上方为空气介质,因此有R01=r01。经推导可得第i个广义反射系数Ri,i+1为:
(5)
2.2 介质层间厚度和介电常数的估计
对于第一层介质的介电常数测算,国外学者Al-Qadi等人提出了一种采用振幅全反射的方法[16]。具体的测量方法为:在路面上水平放置一个尺寸较大的金属板,可以使探地雷达脉冲波到达该金属板后产生全反射效应。由此,天线所接收到的振幅Ainc则与发射信号振幅大小相同;再将金属板撤去,不改变雷达位置,发射雷达信号,使其进入分层路面并在各结构层界面产生反射。接收天线接收到的第一个反射波振幅A0即为获得的空气路面分层的反射波,最后通过式(6)来计算路面第一层的介电常数ε1。
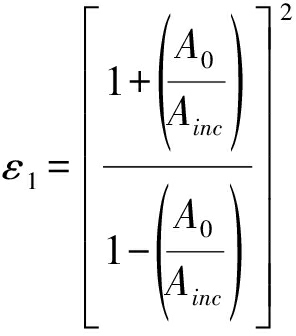
(6)
由反射系数的计算公式及传输损耗修正可得第二层介电常数为[17]:
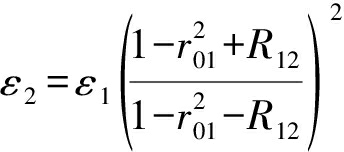
(7)
将修正公式推广至多层可得:
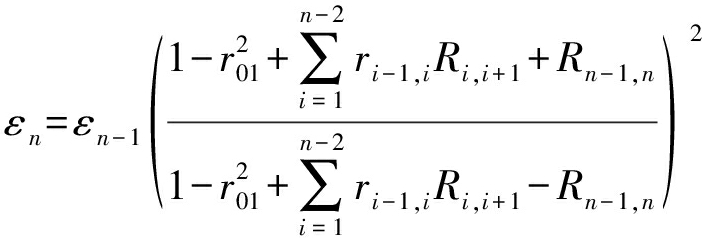
(8)
最后再根据两次反射之间的脉冲延迟是电磁波在该层中的双向传播时间这一事实,可以计算其厚度为:
(9)
上述方法采用了简化的修正计算方式,针对某材料或工程来说是有效的,但在实测中,会受探测环境影响而引起误差,且误差会随着层数的增大而增大。考虑到广义反射系数与反射系数、衰减常数、介质层厚的关系,本文将公式(2)~(5)以及厚度公式(9)结合,带入后文中所建立的代价函数中,通过优化算法对多参数进行反演,从而有效避免由修正公式引起的误差,达到改善路面雷达厚度测量精度的效果。
3 反演方法
3.1 接收回波信号的时域重构
在典型的探地雷达天线频率(200 MHz~2 GHz)范围内,路面可被视为非色散和非磁性的。因此,一些研究也将路面反射系统通常简化为线性时不变(LTI)系统[18]。令x(t)表示雷达发射信号,r(t)表示广义反射系数序列,图1展示了r(t)的模型。
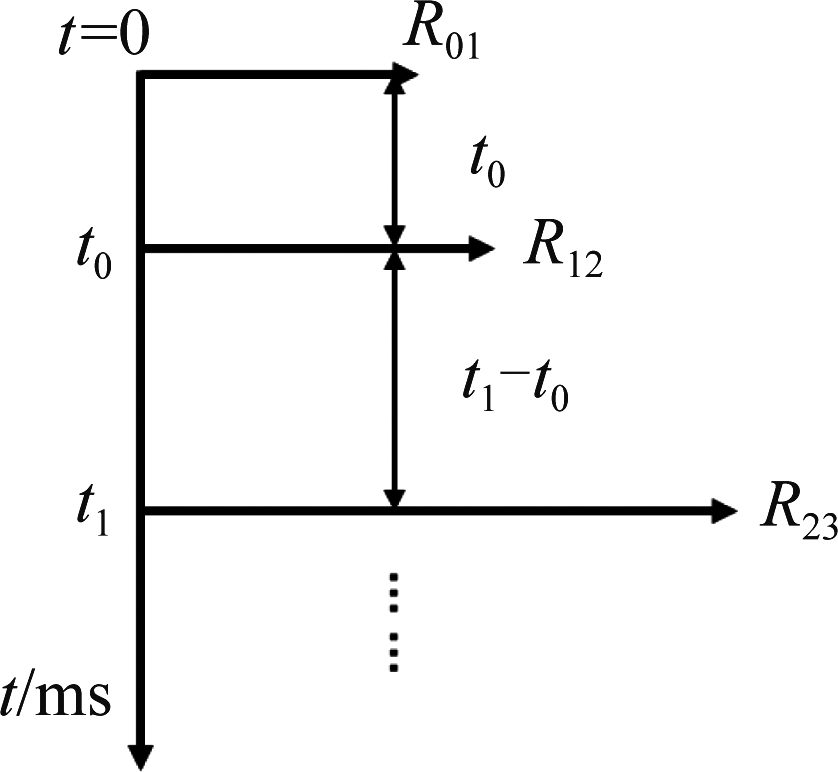
图1 广义反射系数模型
Fig.1 The model of generalized reflection coefficient
则反射系数序列可表示为:
(10)
带入LTI系统中可得接收信号yr(t)为:
(11)
其中N是界面的数量,包括空气-路面界面;Ri,i+1是比例因子,它是界面i处的反射振幅与入射信号之间的比值;ti是信号偏移时间,表示从第i层表面到第i层底部的双向传播时间,即为介质层的时间厚度。
根据广义反射系数的定义,式中的Ri,i+1比例因子即为分界面的广义反射系数,因此接收信号的表达式中不仅包含了时间参数,还包含了介质的电特性参数。
3.2 遗传优化反演算法
将代价函数定义为重构的信号yr(t)和实际接收的信号y(t)之间的误差平方,其表达式为:
(12)
其中,m为信号拟合点个数。
许多研究方法已经利用梯度下降的非线性优化算法对代价函数中的参数进行反演,然而这种算法涉及对目标函数值求导求微分的过程,还需要设置步长,且当反演参数较多时,容易陷入局部最优解,影响反演结果。遗传算法[19]是一种不依赖于梯度信息和其他辅助知识的优化搜索方法,只需要建立影响搜索方向的目标函数和相应的适应度函数。此外,遗传算法还具有群体搜索的特性,它是从一个包含多个个体的初始群体开始的,因此除了可以有效地避免搜索一些不必要的点,还能避免在对多峰分布的搜索空间进行搜索时陷入局部某个单峰的极值点,对整个参数的反演的稳定性有着较好的效果。
本研究采用遗传算法,以均方误差Oc为优化目标,将介质层双程发射时间ti与电性参数εi和σi作为优化对象,其中i代表介质层序号。具体流程如下:
1)将个体与种群的染色体编码为x=[ti,εi,σi]T、X=[x1,x2,...,xM],其中M为个体总数。将式(12)作为适应度函数,用以表征种群个体性能的优越度,驱动算法判决和寻找模型的最优解;
2)以分层介质参数的先验条件作为约束范围,按照浮点编码方式随机获取个体染色体,构成初代种群;
3)采用交叉概率为0.95的均匀交叉操作,按变异概率为0.1的基本位变异方式,根据迭代次数的变化设置变异范围设置为[-(1-t/L),1-t/L],其中t为当前迭代次数,L为总迭代次数;
4)以轮盘赌的选择方法,筛选出优良个体进入下一代;
5)经过遗传操作后得到适应度高的子代,最后通过进行种群迭代,直至达到终止条件,输出参数的最优解。
3.3 反射系数谱反演参数初值
以三层介质模型为例,分层介质第一层底面和第二层底面的反射系数序列可表示为:
r(t)=R12δ(t-t0)+R23δ(t-t1)
(13)
对反射系数系列作傅里叶变换即可得到反射系数序列谱。为实现反射系数的奇偶分解,可先将时间零点移至中间层的中点位置处,用T=t1-t0来表示第二层时间厚度,再通过傅里叶变换后得:
R(f)=R12ejπfT+R23e-jπfT
(14)
根据欧拉公式可得:
R(f)=(R12+R23)cos(πfT)+j(R12-R23)sin(πfT)
(15)
根据文献[20]分析,传统的振幅映射技术假定反射系数相等和相反,一些低于分辨率极限的重要信息不能被其捕获。将反射系数对分解成偶分量和奇分量,其中偶分量具有相等的幅度和符号,奇分量具有相等的幅度和相反的符号。由于介质层厚度接近零时偶分量相长干涉,奇数分量相消干涉,因此,随着厚度接近于零,偶数分量对噪声更稳健,从而提高分辨率。基于此,对广义反射系数进行奇偶分解,令:
(16)
再考虑时间零点为地面时,R(f)可利用奇偶分解后的广义反射系数谱表示为:
r(f)=R(f)e-2πf(t1+T/2)=
[2Recos(πfT)+j 2Rosin(πfT)]·
{cos[πf(2t0+T)]-jsin[πf(2t0+T)]}
(17)
通过分析相关参数和GPR反射系数频谱之间的联系,可以估计出待反演参数初值。首先,将整个频谱分为幅度谱和相位谱,分别观察幅频和相频特性。
对于广义反射系数幅度谱:
(18)
进行求导并令其等于0:
(19)
解得:
(20)
根据导数的定义可知, f为幅度谱极大值点和极小值点所对应的频率,且为周期性分布,即相邻的两个极大/小值的间隔为幅度谱的凹陷周期:
(21)
图2显示了当T分别取1.33 ns和4 ns,其余参数不变时的理论值与测量值的幅频特性图。当T=1.33 ns时,Δf=750 MHz,当T=4 ns时,Δf=250 MHz。利用时间厚度与幅度谱凹陷周期之间的反比关系,即可利用反射系数频谱的周期来估算出时间厚度。此外,反射系数幅度谱的理论真实值和测量值相吻合,证明了推导的无误。当层厚较小而导致幅度谱的周期超过了设定频带时,可以通过找出第一个极大值点频率fp,再利用式(20)估算T,令式中的n=2,即得到T=1/2fp。
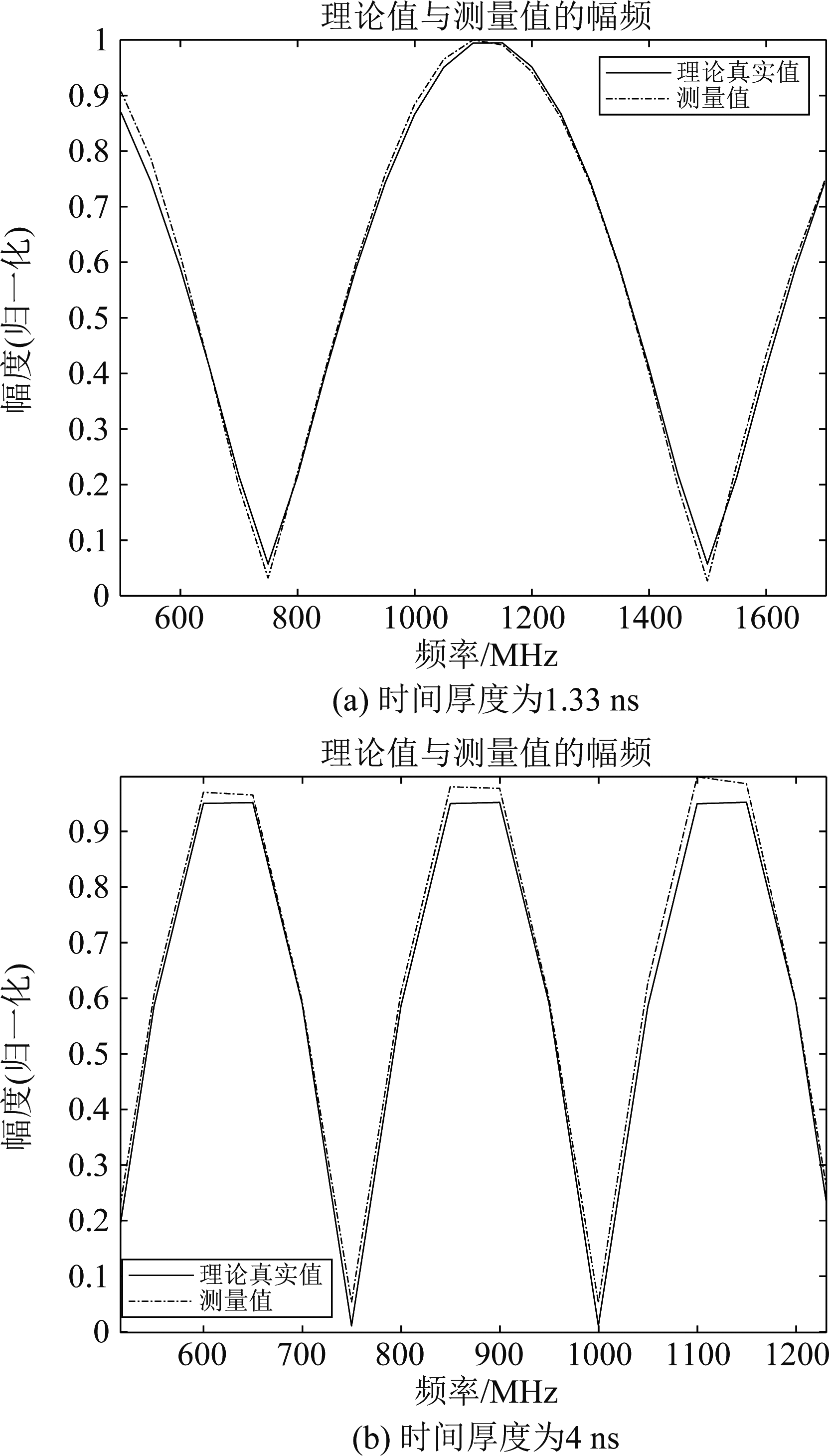
图2 幅度谱凹陷周期与时间厚度T的关系
Fig.2 Relationship between depression period of amplitude spectrum and time thickness T
接下来观察反射系数的相频谱:
θ(f)=arctan[tan(πfT)Ro/Re]-2πft0-πfT
(22)
θ(f)分为两个部分,第一部分包含参数T和反射系数奇偶分量,主要影响了相位谱的振幅大小。第二部分包含参数T和t0,主要影响了相位谱的变化速度。
不同的参数对反射系数频谱有着不同的影响。T决定了幅度谱凹陷周期大小,T和t0共同影响相位谱的变化速度,而完全确定相位谱则需要t0和各层的介电常数以及中间层的电导率。因此,确定待反演参数初值的步骤为:
1)先根据幅度谱凹陷周期确定厚度参数T;
2)再根据相位谱的变化速度反演时间位置参数t0;
3)然后根据相位谱反演三层的介电常数和中间层的电导率;
4)最后反演上层的电导率。
4 数值仿真
基于有限差分时域(FDTD)方法的数值方法已经被开发用于模拟电磁波在民用基础设施中的传播。本文利用gprMax数值模拟工具[21]建立沥青混凝土铺路时的模型,利用反射信号时域重构的方式反演铺层厚度。由于铺路时需要喷出防止滚轮粘连沥青的水汽,会导致路面铺层上方覆盖一薄层,因此模型需要考虑水汽层所带来的影响。参照常见物质的相对介电常数,如表1所示,建立三层仿真模型如图3所示。值得注意的是,水的相对介电常数为81,而在该场景下附着于铺层表面的水汽层会受温度等影响,因此,根据文献[22]建议,将其相对介电常数设置为9,电导率为0.01 S/m。
表1 常见物质的相对介电常数
Tab.1 Relative dielectric constants of common substances

物质相对介电常数εr空气1水81沥青混凝土4^7干土3湿土8^15石灰岩7^9

图3 沥青混凝土路面模型
Fig.3 Asphalt concrete pavement model
由于路面分层中的水汽层和沥青混凝土铺层都非常薄,因此本文采用了1.5 GHz中心频率的Ricker子波作为雷达发射波,以实现高轴向分辨率。发射波可以利用金属板全反射特性来进行构造。探地雷达被简化为彼此靠近的发射器和接收器,它们位于路面/金属板(PEC)表面上方0.5 m处,以模拟空气耦合天线。因此,对于两种模型,到达空气-路面/PEC界面的辐射能量相等。这里暂时先不考虑其他杂波和噪声所带来的影响。
通过gprMax对模型进行仿真我们可以得到各反射信号与发射信号的时域波形如图4所示。
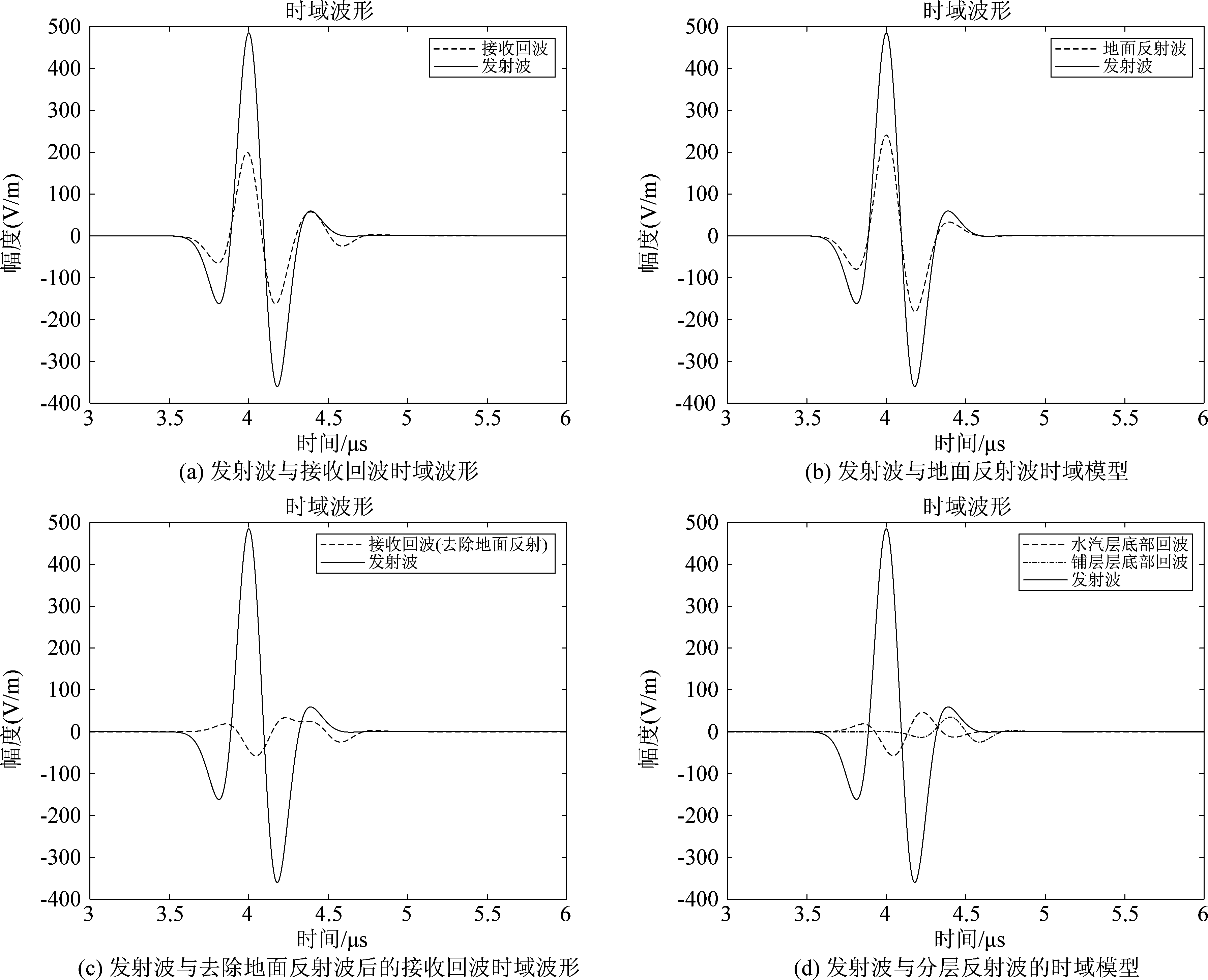
图4 各反射信号与发射信号的时域波形
Fig.4 Time domain waveforms of each reflected signal and transmitted signal
可以看出,由于第一层的水汽层和第二层的沥青混凝土层厚度均小于1/8波长,所以两层的反射波会产生叠加,导致接收回波无法区分这两层的幅度值。且由于叠加影响了地面,即水汽层顶部反射波的幅值,因此接收回波的最高幅值受三层反射回波影响而变小。
现根据本文研究方法,对接收回波进行重构:
y(t)=R01x(t)+R12x(t-t1)+R23x(t-t2)
(23)
反演参数矩阵z=[R01,R12,R23,t1,t2],利用推导公式(4)和(5),将R01和R12替换为ε1,ε2,σ1。则反演参数矩阵变为z′=[ε1,ε2,σ1,R23,t1,t2]。
根据频谱反演可以先估计出初值范围,再通过对代价函数进行遗传算法寻优后,得到的结果如表2所示。
表2 沥青混凝土模型参数反演值
Tab.2 Inversion value of asphalt concrete model parameters

参数初始范围反演结果ε1[4,10]9.0898ε2[3,6]4.7612σ1[0.008,0.012]0.0103R23[-1,1]0.0690t1/0.1 ns[5,7]0.4218t2/0.1 ns[6,9]4.0770
根据厚度计算公式(9)得到第一层厚度为2.03 mm,第二层厚度为25.2 mm。误差分别为1.5%和0.8%。利用反演值得到的重构信号时域图如图5所示。
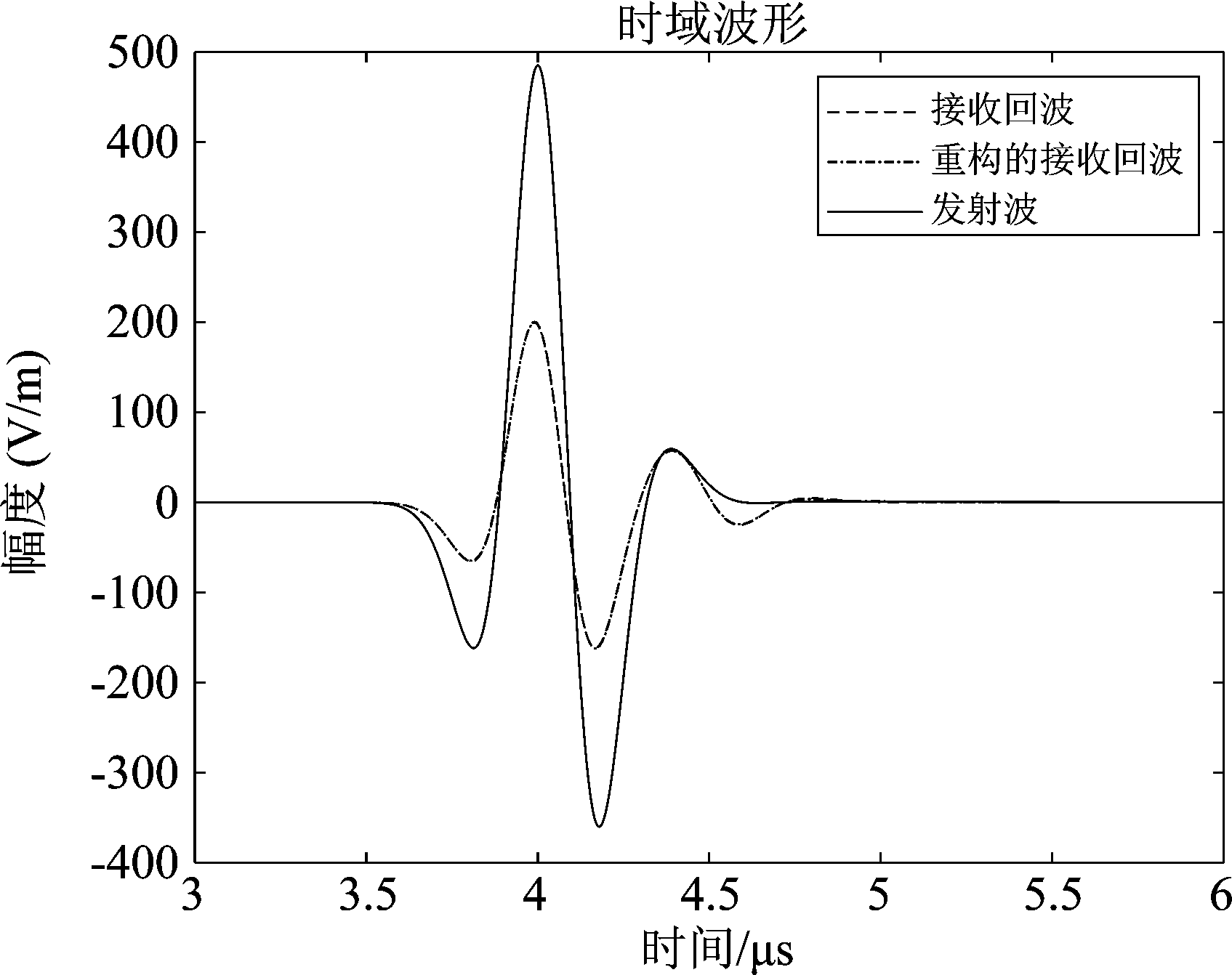
图5 接收信号、发射信号和重构信号时域图
Fig.5 Received, incident and reconstructed signals
可以看出,重构信号与接收回波重合度很高,表明了该重构方法的可行性。
若改变沥青混凝土层的厚度,可以得到的反演结果如表3所示。
表3 改变沥青混凝土层厚度的反演结果
Tab.3 Inversion results of changing asphalt concrete layer thickness
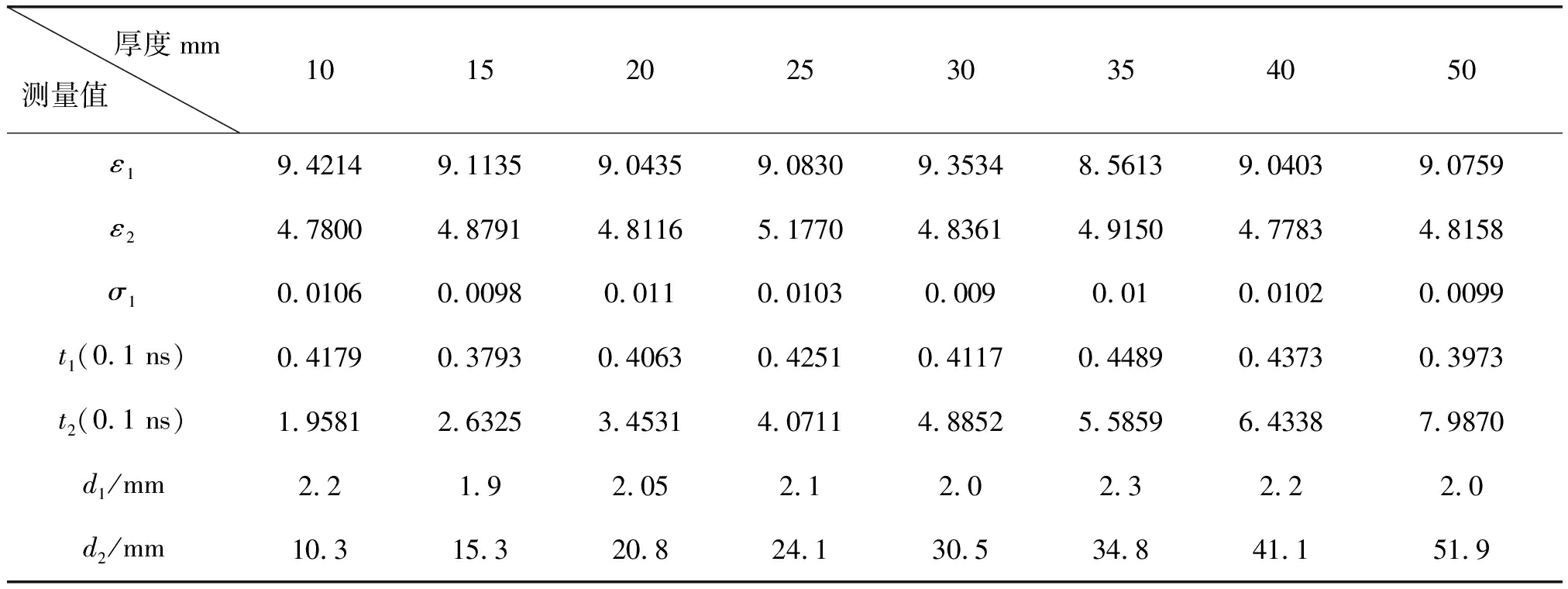
厚度mm测量值 1015202530354050ε19.42149.11359.04359.08309.35348.56139.04039.0759ε24.78004.87914.81165.17704.83614.91504.77834.8158σ10.01060.00980.0110.01030.0090.010.01020.0099t1(0.1 ns)0.41790.37930.40630.42510.41170.44890.43730.3973t2(0.1 ns)1.95812.63253.45314.07114.88525.58596.43387.9870d1/mm2.21.92.052.12.02.32.22.0d2/mm10.315.320.824.130.534.841.151.9
图6的(a)、(b)分别计算了改变沥青混凝土层厚度后的介电常数和厚度的误差值。结果显示,介电常数和厚度的均控制在5%以内。
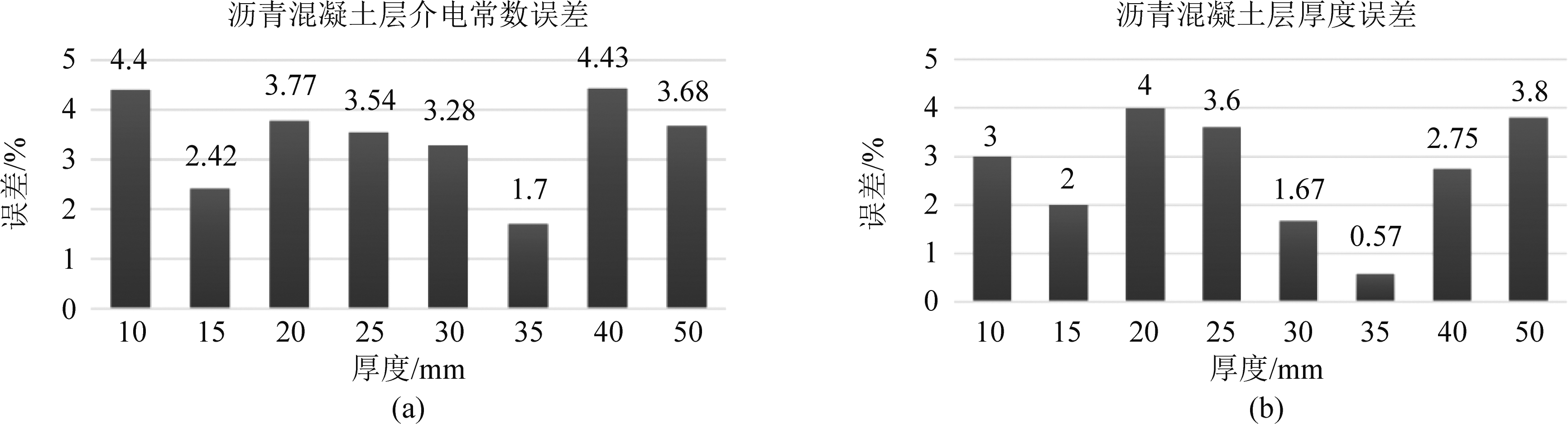
图6 沥青混凝土层参数的误差估计
Fig.6 Estimation error of thin asphalt concrete layer
为了进一步说明本文反演方法的性能,将本文方法与参考文献[13]中的反演方法进行比较。文献[13]采用了梯度下降的优化算法,反演出反射回波信号的幅值比,再利用幅值比经验公式推导出介电常数,进而计算出层厚。现将文献[13]的方法用于图3模型中,带入上文估计出的参数初值,计算沥青混凝土铺层的介电常数及厚度值。表4显示了本文方法和文献[13]方法的结果对比。
表4 两种方法反演结果对比
Tab.4 Comparison of inversion results of two methods

参数理论值本文方法结果误差文献[13]方法结果误差相对介电常数55.17703.54%4.68376.33%厚度/mm25244%278%
结果显示,本文方法在厚度测量上具有更高的准确性。并且由于梯度算法与步长设置有紧密关联,文献[13]的算法更容易陷入局部最优解。此外,修正公式的使用会随着反演层数和厚度的增加而增大结果误差,因此本文方法适合拓展到多层介质的反演中。
5 结论
本文通过对电磁波在分层介质中的传播规律进行研究,提出了一种采用非线性优化算法重构反射回波时域信号的方法来预测薄层物理参数,打破了雷达波长分辨率的限制。此外,利用反射系数频谱的特性对反演参数进行初值估算,从而使反演速度提高、结果更加准确。采用有限差分时域(FDTD)仿真软件gprMax对沥青混凝土修复路面的模型进行建模,结果表明该方法效果较好,具有较高的分辨率,可以得到厚度低于1/8波长的超薄层介质的几何和电性参数。
[1] JOL H M.Preface[M]∥Ground Penetrating Radar Theory and Applications.Amsterdam: Elsevier, 2009: xiii-xiv.
[2] LIU Tao, ZHU Yutao, SU Yi.Method for compensating signal attenuation using stepped-frequency ground penetrating radar[J].Sensors(Basel, Switzerland), 2018, 18(5): E1366.
[3] PIPAN M, FORTE E, FINETTA I.Processing and inversion of multi-offset and multi-azimuth GPR data for environmental and engineering applications[J].Proceedings of SPIE-The International Society for Optical Engineering, 2002, 4758.
[4] QIN Tan, ZHAO Yonghui, LIN Guocong, et al.Underwater archaeological investigation using ground penetrating radar: A case analysis of Shanglinhu Yue Kiln sites(China)[J].Journal of Applied Geophysics, 2018, 154: 11-19.
[5] ABUJARAD F, NADIM G, OMAR A.Clutter reduction and detection of landmine objects in ground penetrating radar data using singular value decomposition(SVD)[C]∥International Workshop on Advanced Ground Penetrating Radar.IEEE, 2005.
[6] KAO C P, LI Jing, WANG Ying, et al.Measurement of layer thickness and permittivity using a new multilayer model from GPR data[J].IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2463-2470.
[7] MINET J, LAMBOT S, SLOB E C, et al.Soil surface water content estimation by full-waveform GPR signal inversion in the presence of thin layers[J].IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1138-1150.
[8] 张蓓.路面结构层材料介电特性及其厚度反演分析的系统识别方法——路面雷达关键技术研究[D].重庆: 重庆大学, 2003.
ZHANG Bei.System identification method for backcalculating the dielectric property and thickness of pavement structures——study on applied technology of ground penetrating radar[D].Chongqing: Chongqing University, 2003.(in Chinese)
[9] 蔡迎春, 王复明, 康海贵.路面材料介电特性的遗传反演方法应用研究[J].武汉理工大学学报(交通科学与工程版), 2010, 34(3): 542-544,549.
CAI Yingchun, WANG Fuming, KANG Haigui.Research and application of backcalculation for pavement permittivity by genetic algorithm[J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2010, 34(3): 542-544,549.(in Chinese)
[10] 秦瑶, 陈洁, 方广有, 等.基于探地雷达频谱反演法的薄层识别技术研究[J].电子与信息学报, 2010, 32(11): 2760-2763.
QIN Yao, CHEN Jie, FANG Guangyou, et al.Research on thin-layer recognition technique based on the spectrum inversion method of ground penetrating radar[J].Journal of Electronics & Information Technology, 2010, 32(11): 2760-2763.(in Chinese)
[11] HUANG Zhonglai, ZHANG Jianzhong.Determination of parameters of subsurface layers using GPR spectral inversion method[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7527-7533.
[12] ZHAO Shan, AL-QADI I L, WANG Siqi.Prediction of thin asphalt concrete overlay thickness and density using nonlinear optimization of GPR data[J].NDT & E International, 2018, 100: 20-30.
[13] WANG Siqi, ZHAO Shan, AL-QADI I L.Real-time density and thickness estimation of thin asphalt pavement overlay during compaction using ground penetrating radar data[J].Surveys in Geophysics,2020,41(3):431-445.
[14] GURU B S, HIZIROGLU H R.Electromagnetic field theory fundamentals[M].China Machine Press, 2004.
[15] SPERO S.Contributors-Ground penetrating radar theory and applications[J].Tradition A Journal of Orthodox Jewish Thought, 2009, 11(2): xv-xviii.
[16] AL-QADI I L, LAHOUAR S.Measuring layer thicknesses with GPR-Theory to practice[J].Construction and Building Materials, 2005, 19(10): 763-772.
[17] 尹德, 薛冰, 范尧.基于正反演的公路厚度及介电特性的检测方法研究[C]∥第二届电子工程与计算机科学国际会议, 2017.
YIN De, XUE Bing, FAN Yao.Study on detection method of thickness and dielectric property of highway based on forward and inverse method[C]∥The Second International Conference on Electronic Engineering and Computer Science, 2017.(in Chinese)
[18] ANNAN A P.11.ground-penetrating radar[M]∥Near-Surface Geophysics.America: Society of Exploration Geophysicists, 2005: 357-438.
[19] 肖美华, 薛锦云.遗传算法机理的研究及应用[J].计算机工程, 2003, 29(20): 137-139.
XIAO Meihua, XUE Jinyun.Research and application of genetic algorithm theory[J].Computer Engineering,2003, 29(20): 137-139.(in Chinese)
[20] PURYEAR C I, CASTAGNA J P.Layer-thickness determination and stratigraphic interpretation using spectral inversion: Theory and application[J].GEOPHYSICS, 2008, 73(2): R37-R48.
[21] WARREN C, GIANNOPOULOS A, GIANNAKIS I.gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar[J].Computer Physics Communications, 2016, 209: 163-170.
[22] SHANGGUAN P, AL-QADI I L, LENG Zhen, et al.Innovative approach for asphalt pavement compaction monitoring with ground-penetrating radar[J].Transportation Research Record: Journal of the Transportation Research Board, 2013, 2347(1): 79-87.



