1 引言
目前,各种多媒体节目遍布人们的生活,但无线广播仍具有很高的覆盖率和大量的听众。作为音频广播节目播出的枢纽,无线广播发射电台有着重要的地位和作用。无线广播播出时,下级广播台常常需要转播上级广播台的一些节目。为了保证在转播时不出现错播、插播和漏播等播出事故,上级广播台需要对下级广播台播出的节目进行监测。若安排专门的工作人员实时监听接收的音频,在实际情况中难以实现,除了此项工作繁琐、枯燥外,人工监听本身也极易错报或漏报。为了提高工作效率,缓解工作人员的压力,需要智能地完成广播音频信号的监听。
由于广播音频中所包含的不仅有各种类型的语言节目,还有音乐节目,如果用识别的方法进行音频对比,所需要的训练集会非常大,而且广播具有很强的时效性,这种从音频信息中解析出其包含的语义成分的方法[1]并不太适用。在广播音频节目源信号可以利用的情况下,音频的对比可以不关心其播放的具体内容,只要音频的一些低级物理特征保持一致即可判定其相似。故音频相似度计算的关键在于音频信号物理特征的提取和特征的匹配[2]。
人们对音频信号的相似性研究已进行了一定的探索。为了提高音频相似度的鲁棒性,文献[3]和文献[4]采用梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients,MFCCs)作为音频的特征。考虑到熵可以衡量随机变量的不确定性,随机事件越不确定,所传递的信息量越大。文献[3]将两段音频提取出的MFCCs构成一个数据样本计算其Renyi二次熵,得到的熵值越小代表两信号越相似。文献[4]将两段音频的MFCCs特征距离矩阵输入卷积神经网络(Convolutional Neural Networks,CNN)进行特征匹配,实现相似程度的判断。但由于熵值和CNN的计算量太大,多点检测难以保证实时性,这两种方法并不适用于广播音频信号的相似度对比。文献[5]将音频包络的几何形态看作N维空间中的向量,再利用向量夹角余弦的值判定音频是否一样。无线信号传输带来的时延会使信号在非对齐情况下计算出的夹角余弦值错误,故首先要查找对齐点。将音频信号分帧,在音频信号窗口依次滑动对比所有连续音频帧向量的夹角余弦值,找出其最大值的位置作为对齐点之后再进行计算。现有的音频相似性检测技术多数仅以某一种物理特征作为参数进行对比,在不同噪声环境下鲁棒性不够好。文献[6]通过提取音频信号的波形、包络及过零率三种物理特征,分别计算其相关函数得到相似度,然后综合多种特征参数,从整体角度给出了适应不同信噪比的特征类型。但是,该方法在选择适合的物理特征时,需要预知接收信号的信噪比范围,这增加了其计算复杂度。倒谱可以看作是不同谱带的变化率的信息,它对功率谱中的等距离频率成分有良好的分辨能力。文献[7]针对已有算法中测量音频特征距离抗噪性能差且难以抵抗时延的问题,先对其中一音频加入短延时,然后分析两音频混合信号的功率倒谱,以得到最优时延估计值和相似度,但其预先加入短延时的大小对算法性能影响较大。
以上算法的信号模型都只考虑了传输过程中的加性白噪声和一定的时间延迟,故用于广播音频信号相似度计算均有一定局限性。与原始节目源相比,实际参与相似度计算的接收广播音频信号还存在以下影响因素:(1)向下级广播台传输信号时,为减少数据量,常采用AAC、AC-3等音频信源编解码算法;(2)下级广播台播出时,可能会使用调音台、压限器等信号设备对音频信号进行进一步处理;(3)为保证广播可控,不出现播出事故,下级广播台常会对上级广播台的信号人为加入十几毫秒~几十毫秒的延迟;(4)在下级广播台覆盖范围内接收的信号回传时,为减少数据量,也常需要用某种信源编解码算法进行压缩。此外,为在出现播出差错时能尽快采取必要措施,算法延迟、算法计算复杂度也需要兼顾考虑。
针对上述影响因素,为快速、准确地计算广播音频相似度,使之能应用于实际广播系统中,本文提出了一种新的广播音频信号相似性检测方法。由编解码器、播出设备及信道带来的非线性失真,选用自适应非线性滤波器来抵消;由各级传输带来的延时,利用相关函数与卷积的关系设计时延估计算法;为降低数据量,处理信号和计算Pearson相关系数时仅使用信号功率最大的子带;结果表明此算法在各应用场景下优于传统方法。
2 理论基础
2.1 子带分析滤波器组
子带处理[8]的基本思路是通过一个滤波器组把宽带信号按照均匀或非均匀的方式分解成若干个子频带信号,把原本对宽带信号的处理转换到子带域,而后在子带域内进行信号处理。子带处理系统基本结构如图1。
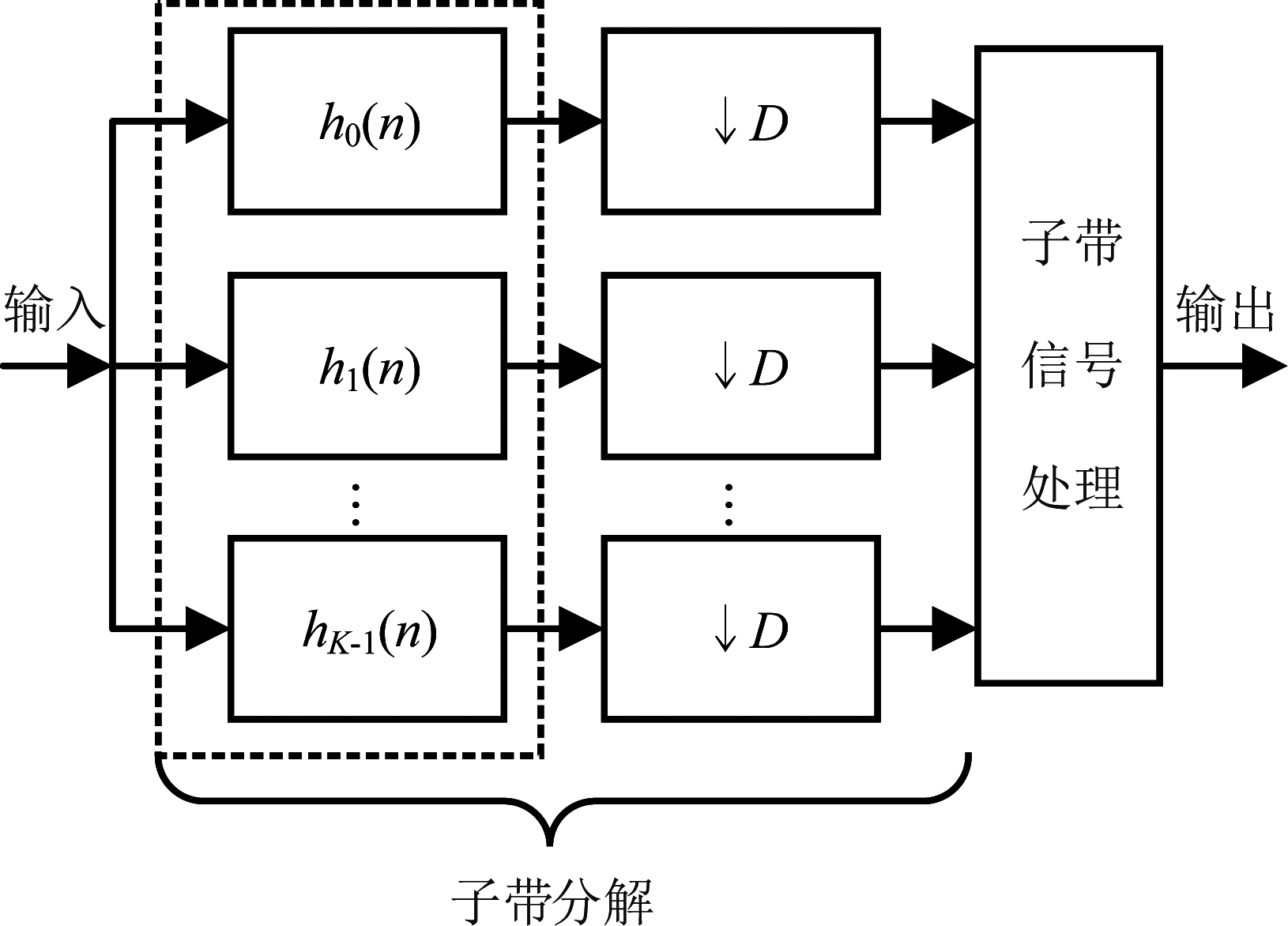
图1 子带处理系统基本结构
Fig.1 Basic structure of subband processing system
需要注意的是,在子带处理中引入了下采样模块,这意味着可以将高采样率信号转换为低采样率信号进行处理,可使计算量大大减小,处理效率得到提升。
2.2 自适应Volterra滤波器
Volterra泛函级数[9]展开是一种描述非线性系统的有效工具,因其普适性好,适用于一切可以用连续泛函描述的非线性系统而得到广泛应用。设离散、因果、非线性系统的输入为x(n),输出为d(n),其Volterra级数定义为
(1)
其中,hp(m1,m2,…,mp)称为Volterra核。在实际应用中,通常取有限项级数,其有限阶截断形式为:
(2)
其中,P为非线性阶数,M为记忆深度。Volterra级数二阶截断形式为:
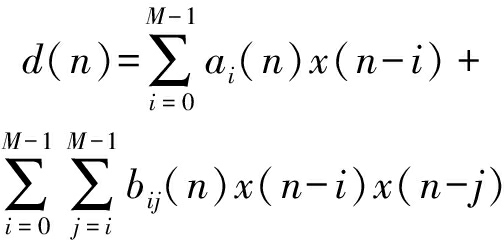
(3)
采用的学习算法是归一化最小均方算法(Normalized Least Mean Square,NLMS)[10]。令系数矩阵w(n)=[aT(n),bT(n)]T,输出d(n)=wT(n)x(n),误差估计值e(n)=y(n)-d(n),系数权重更新公式如下:
(4)
式(4)中μ为每次更新迭代的步长,a值是为了避免分母为零的一个小的增量,可以自行设置。
2.3 功率放大器模型
建立合适且准确的模型对真实场景建模有着重要意义,而功率放大器模型是无线通信链路传输仿真过程中的关键一环。由于功放的非线性和记忆特性,输出信号相较于输入信号产生的变化难以用确定的数学公式表达,需要使用记忆非线性行为模型仿真这种失真。根据实际功放获得的输入输出测试数据,在预先定义好的模型结构或算法中确定模型系数,使最终得到的模型能够尽量准确地描述功放特性。
文献[11]提出了一种记忆多项式模型如式(5),它基于Volterra级数展开的非线性模型并添加多个延迟抽头来模拟记忆特性。射频信号的频率一般较高,为满足奈奎斯特采样定理,相应的采样频率也会很高,仿真时的计算量会大大上升。而处理射频信号的通带模型和处理包络信息的基带模型是等效的,因此常将射频信号等效到基带处理。
(5)
其中复系数h的确定满足最小均方误差准则[12],使得同一离散复输入信号c(n)对应的模型复输出信号z(n)及实测复输出信号z′(n)均方差值最小。多项式阶数P和记忆深度M的选取要尽量使建模的功放特性贴近实际功放特性。
在实际情况中,功放模型的偶次幂项产生的谐波分量频率远离载频,它们会被后端的带通滤波器滤掉,所以在讨论窄带信号载频附近谐波分量时,仅考虑奇次幂项的影响,与普通Volterra级数展开式相比计算量大大减少,据此式(5)可写成式(6)形式。
(6)
2.4 信道模型
由于远距离广播多采用中波、短波通信,而中短波信道的时变特性导致其建模困难。经Watterson等[13]研究发现,在有限带宽和有限时间内可以把电离层看作平稳的信道,即可用合适的静态数学模型描述短波信道。
Watterson模型作为一种近似的中短波信道模型,用抽头延时线模仿信号的多路传播,每径时延信号用一个合适的基带增益函数调制其幅度和相位来模拟信号在信道中产生的多普勒频扩和多普勒频移现象。最后,每径时延信号与加性高斯白噪声求和得到输出信号,具体结构如图2所示。
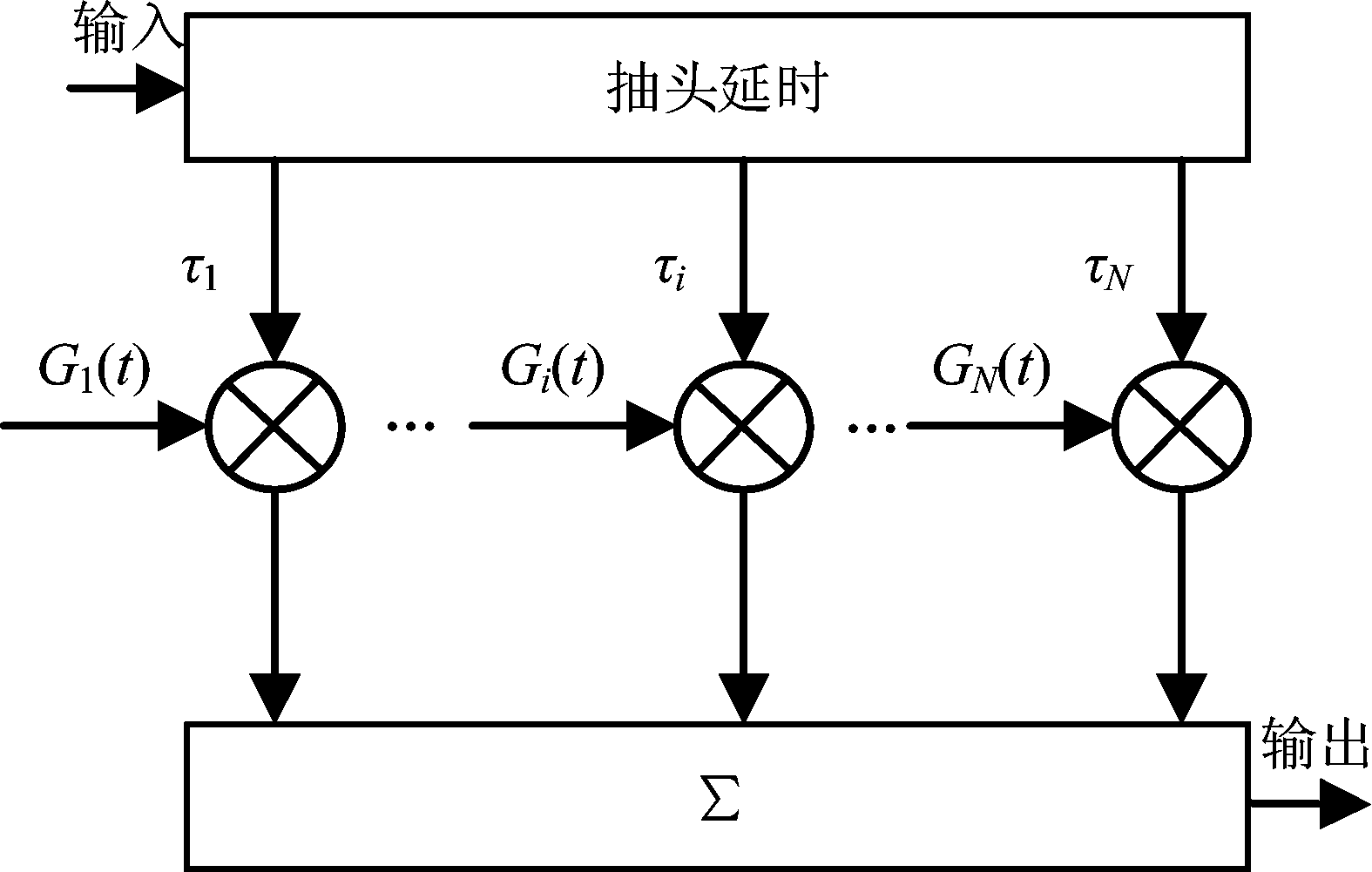
图2 Watterson信道模型结构
Fig.2 Watterson channel model structure
Watterson模型要求抽头增益函数Gi(t)是一个可产生瑞利衰落的复高斯随机过程,各个Gi(t)之间统计独立,且Gi(t)的频谱可看作两个高斯型频率函数的组合。其软件算法实现主要包括多径效应、多普勒频扩、多普勒频移、高斯白噪声四个方面的设计。
3 广播音频信号相似性检测方法
3.1 系统模型
如图3所示,本节提出了一种整合了上级监测、下级播送和下级接收三个独立处理装置的广播音频监测系统模型,用来实时监测下级广播台有无错播、插播等情况的发生。
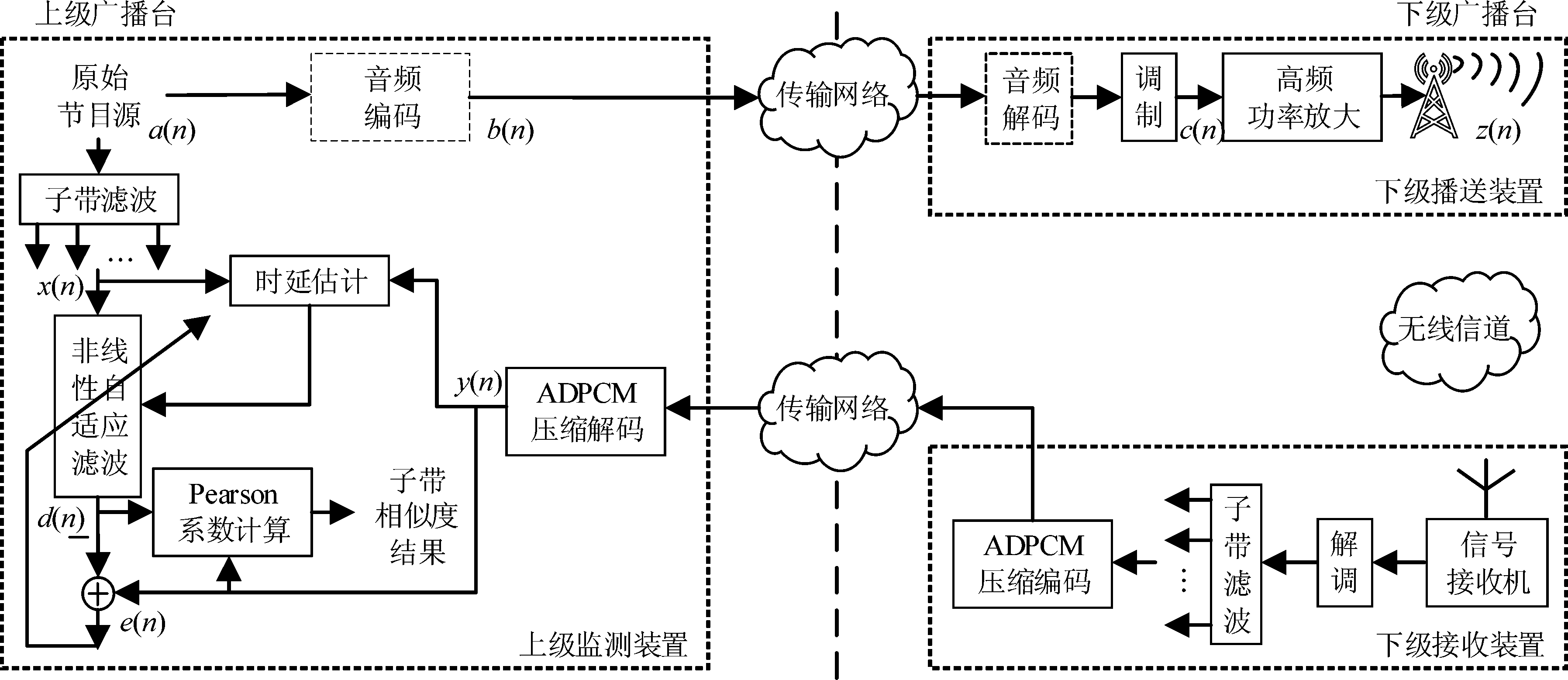
图3 广播音频监测系统框架
Fig.3 Broadcast audio monitoring system framework
上级广播台将原始广播节目信号直接(或编码后)利用有线(或无线)网络发送至下级广播台,上级广播台再对下级接收装置传来的信号进行压缩解码。在计算相似度时,为了降低计算量,考虑到用第2.1节提到的子带滤波的方式将信号分成D个子带,并降低采样率D倍再处理。另外,由于音频信号的能量大多集中在一段或一些频带中,比如,语音中的能量大多集中在低频子带,音乐中的能量大多集中在中频子带[14]。而功率较低的一些子带的信噪比较低,所以可用音频信号功率最大的子带的特征去进行后续的时延估计、自适应调整以及相似度计算。
下级播送装置负责将网络传来的原始节目源进行解码,再以无线电波的形式播送给当地的用户。
下级接收装置负责用信号接收机接收下级广播台播出的节目,之后进行解调、子带滤波等处理并以自适应差分脉冲编码调制(Adaptive Differential Pulse Code Modulation,ADPCM)[15]的形式进行压缩编码,再通过网络传送给上级监测装置。
上述的系统模型可以很好地描述真实的上级广播台对下级广播台的监测流程,充分考虑更多的实际影响因素,可更准确地判定下级广播台有无异常的播出情况。
3.2 音频相似度计算方法
在第3.1节建立的系统模型中,由于下级播送装置中射频功率放大器的非线性和记忆特性、无线信道中的多普勒频移、多普勒频扩、多径延时和加性白噪声、ADPCM压缩编解码的损失等产生的影响,上级监测装置中等待计算相似度的接收信号已产生了一系列情况复杂的失真。此时一些单纯考虑加性白噪声和路径延时的传统方法已不能使后续计算出的音频相似度保持原有的大小,如何正确计算音频相似度,并提高计算效率、保证实时性是本节讨论的问题。
Pearson相关系数是一种准确度量两个变量之间关系密切程度的统计学方法[16]。将上级监测装置中原始节目源功率最大的子带信号和经ADPCM解码后的子带信号均看作N维空间中的向量,通过计算两个向量的Pearson相关系数来衡量收发两段音频信号之间的相似度。设两向量分别为A={x1,x2,…,xn}和B={y1,y2,…,yn},它们之间的Pearson相关系数设为P,其公式描述为
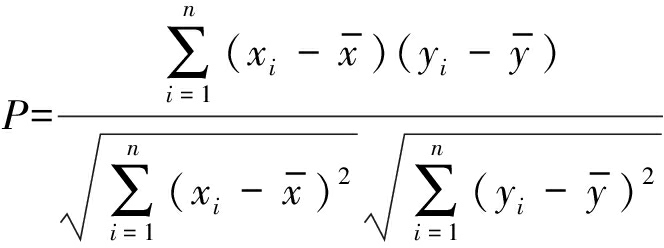
(7)
P的取值范围为[-1,1],|P|值越接近1,两向量相关度越强,|P|值越接近0,两向量相关度越弱,据此可判断两个向量是否相似。在向量方向上改变向量的模值并不影响Pearson相关系数,故音频振幅的大小不影响相似度的计算值。另外,式(7)中![]() 分别表示向量A、B的均值。音频信号的均值代表了音频的直流分量,一般情况下音频系统的输入输出不存在直流分量。如果发生了直流偏置现象,信号预处理时可简单高通滤波去除直流分量。故式(7)中
分别表示向量A、B的均值。音频信号的均值代表了音频的直流分量,一般情况下音频系统的输入输出不存在直流分量。如果发生了直流偏置现象,信号预处理时可简单高通滤波去除直流分量。故式(7)中![]() 的值均为0,实际计算中Pearson相关系数可简化为
的值均为0,实际计算中Pearson相关系数可简化为
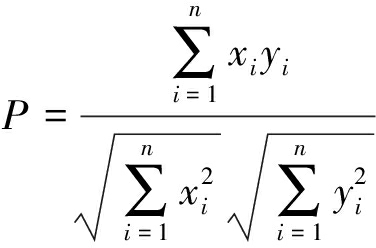
(8)
广播信号传输过程中,音频信号经过信道会带来一定的时延,而在信号非对齐情况下计算式(8)不会得到正确的结果。所以在计算Pearson相关系数时,不能只是简单地从头点对点计算,而要在音频帧内寻找两信号的对齐点,即以滑动窗口的形式找出一定延时范围内相似度最大的位置[17],作为当前帧的时延估计。设两音频功率最大的子带分别U=x(n)和V=y(n+m),n=0,1,2,…,N-1,m=0,1,2,…,M-1,其中N为音频帧长,M为预设最大的延时采样点数,式(8)中分子的计算可以改写成如下互相关的形式:
(9)
可以将音频帧滑动时每时刻的相似度值设为S,可得到式(10):
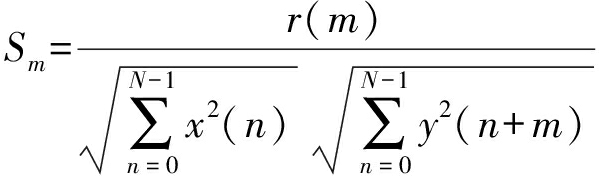
(10)
通过计算得到S0,S1,…,SM-1,共M个值,比较选取其中最大值Smax并输出其位置信息,作为当前音频帧的时延估计,这样后续计算时可以抵消时延对于相似度计算的影响。但是这种方法的计算复杂度较高,估计一帧信号时延时,M个Sm的分子的计算需要M×N次实数乘法和M×N-M次实数加法。比较式(9)关于互相关函数的定义和式(11)关于线性卷积的定义,发现它们有某些相似之处。
(11)
U和V的互相关可改写成两子带信号X=x(m)和Y=y(m),m=0,1,2,…,M-1的卷积形式,如式(12):
r(m)=x(-m)*y(m)
(12)
因为循环卷积是使用离散(快速)傅里叶变换(Discrete(Fast)Fourier Transform,DFT(FFT))[18]计算线性卷积时的衍生品,若想循环卷积等于线性卷积,取值时应使循环卷积的长度L≥2M-1,且L=2r(r为整数),以便利用快速算法来计算。根据时域循环卷积定理:序列循环卷积的离散傅里叶变换是序列离散傅里叶变换的乘积,得到式(13)、式(14):
r(m)=x(-m)○![]() L y(m)
L y(m)
(13)
R(k)=X(-k)Y(k)=X*(k)Y(k)
(14)
其中,R(k)=DFT[r(m)],X(-k)=DFT[x(-m)],Y(k)=DFT[y(m)],右上标 “*”表示取共轭;由于DFT有与之相对应的快速算法FFT,那么,X*(k)和Y(k)就可以利用FFT计算。但是相同长度的两信号用两次L点FFT计算会增大计算量,可以设计用一次L点FFT计算得到两信号的频域结果。
令h(m)=x(m)+y(m)i,H(k)=DFT[h(m)],用h(m)和h*(m)表示x(m)和y(m)得到式(15)、式(16):
(15)
(16)
由于DFT具有线性性质和奇偶虚实对称性质,可以用H(k)表示X(k)和Y(k):
(17)
(18)
式(14)展开成实部、虚部形式记为式(19),用符号Re[]表示信号实部,Im[]表示信号虚部:
R(k)=[Re[X(k)]-Im[X(k)]i][Re[Y(k)]+
Im[Y(k)]i]
(19)
Re[R(k)]=
![]()
(20)
Im[R(k)]=
![]()
(21)
最终得到的结果是用H(k)表示的R(k),H(k)可以用一次L点FFT计算得到。对结果R(k)进行IFFT,即可得到r(m)。再计算出式(10)的M个分母,选出Smax,即可得知两信号帧对齐的位置,上述操作视为信号在时间上的粗对齐。
信号粗对齐后,若直接输出两信号帧相似度则无法抵抗幅度上的一些非线性畸变,此时可以利用自适应非线性滤波器对信号进行调整,再计算Pearson相关系数,得到的相似度结果会更加准确,这个步骤称为信号的细对齐。
把原始节目源在传输、播送和接收等操作产生的变化整体看作一个非线性系统,用Volterra级数可以构成第2.2节中的自适应Volterra滤波器。由于第3.1节中建模的真实场景中功放、信道和压缩编解码误差等在实际情况下是未知的,它的逆系统不一定存在,所以把上级监测装置压缩解码后的子带信号y(n)看作监督信号,经过自适应调整使滤波器输出信号d(n)逼近y(n),即用原始节目源功率最大子带x(n)自适应地模拟传输过程中的影响得到d(n),再计算d(n)和y(n)的Pearson相关系数,即可代替x(n)与y(n)的相似度计算,达到抵抗失真的目的。
3.3 算法复杂度分析
为了进一步证明算法的有效性,对一帧信号的计算复杂度进行分析。用式(10)计算信号相似度时,由于两种方法均需要计算M个Sm的分母,故略去这部分的计算量,只统计M个Sm的分子需要的计算量,FFT时令L=4M。算法可抵抗延时的大小取决于M的值,为保证实际效果,M取值范围为N~4N。自适应滤波器细同步时设置滤波器阶数为X阶,计算需要(4X2N+3XN)次实数乘法和(2X2N+2XN)次实数加法,本文取X=32。计算一次Pearson相关系数需要N次实数乘法和N-1次实数加法。另外,将信号分解成D个子带需要[D2log2D-D2/2+4D+N/D]次实数乘法和[(5/2)D2log2D+D2+N/D-3D+1]次实数加法,本文取D=32,可以将数据量降低至原来的1/32。表1是文献[5]算法和本文算法的计算量统计,可以看出文献[5]算法的计算复杂度为O(n2),而本文算法的计算复杂度为O(nlog2n),可见本文提出的算法能够显著减少计算量。
表1 不同方法的计算量
Tab.1 The amount of computation of different algorithms
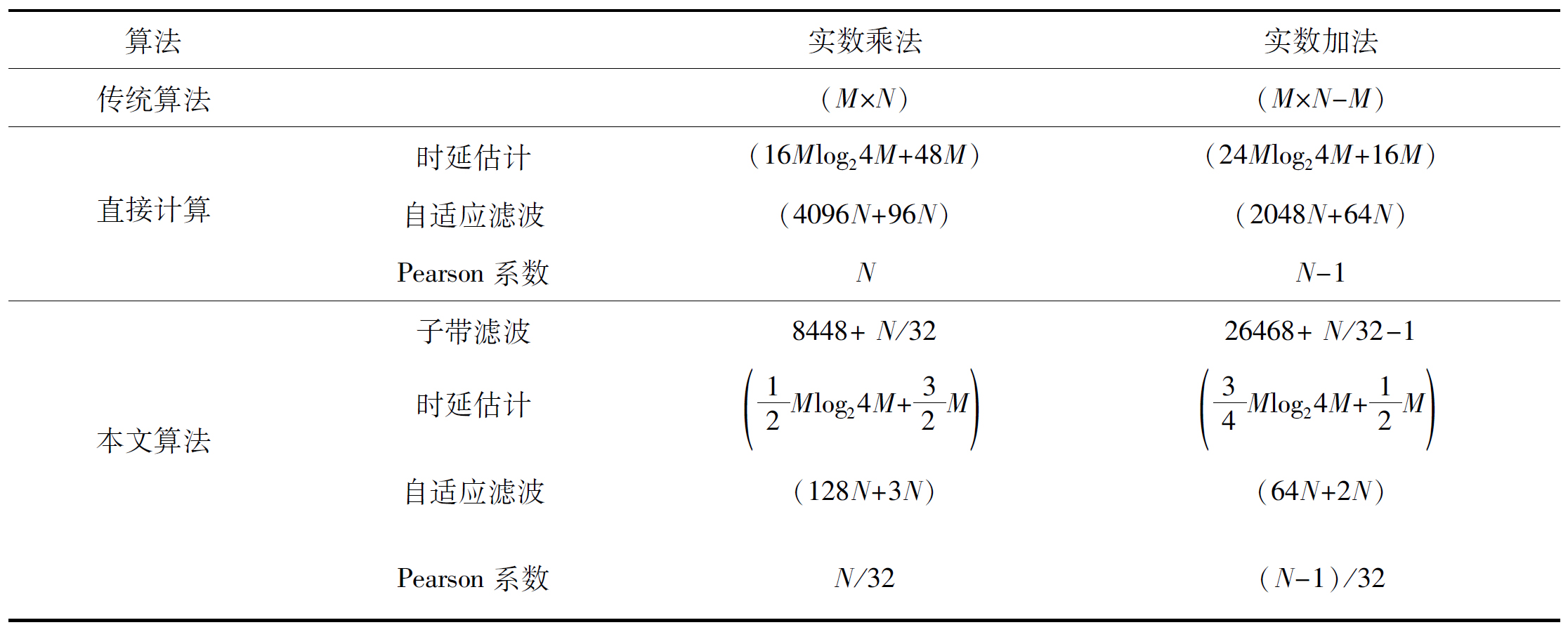
算法实数乘法实数加法传统算法(M×N)(M×N-M) 直接计算时延估计(16Mlog24M+48M)(24Mlog24M+16M)自适应滤波(4096N+96N)(2048N+64N)Pearson系数NN-1本文算法子带滤波8448+ N/3226468+ N/32-1时延估计 12Mlog24M+32M() 34Mlog24M+12M()自适应滤波(128N+3N)(64N+2N)Pearson系数N/32(N-1)/32
4 实验结果及分析
4.1 算法仿真条件
为了深入测试所提出的广播信号相似性估计算法在不同条件下的性能,进行了一系列仿真与真实数据实验。
在建立真实场景的系统模型时,调制、解调模块采用幅度调制的方式,载波频率设置为1 MHz;高频功率放大器模型采用第2.3节提到的多项式模型,取记忆深度为2,多项式阶数为7,其中模型系数见表2[11];无线信道模型采用第2.4节提到的Watterson短波信道模型;子带滤波模块将信号划分为D=32个子带进行处理;压缩编解码模块采用基于G.727协议的ADPCM方式;非线性自适应滤波器采用第2.2节提到的自适应Volterra滤波器,设置滤波器阶数X=32,迭代步长为μ=0.5。
表2 高频功率放大器模型系数
Tab.2 Model coefficient of high frequency power amplifier

hm=0m=1m=2p=11.1330+j0.0696-0.2027+j0.03380.0854-j0.0341p=3-0.2348-j0.08760.1809+j0.2447-0.0439-j0.0640p=50.2675-j0.4113-0.1376-j0.18620.0888+j0.0197p=7-0.2686+j0.26940.0273+j0.0504-0.0457+j0.0093
为了保证提出的算法可以有效地应用于实际,从中央和各省市广播电台的节目中选取了30段广播音频信号,其中包含了音乐、谈话、歌唱3种不同类型的节目以及汉语、蒙语、藏语、英语等7种不同类型的语言。参与实验的广播音频信号长度均为4分钟,划分音频帧,帧长为16384个采样点。由于不同广播台传送音频信号的采样率可能不同,在预处理时统一将音频采样率转换至8000 Hz。
4.2 仿真结果分析
将提出的算法与文献[5]的算法进行对比,仿真时信道模型参数设置为多普勒频扩8 Hz,多普勒频移0.05 Hz,3径信号,每径延时为0 ms~30 ms的随机数,接收信号的信噪比为30 dB。据此,广播节目源和经过系统模型的接收信号在下级广播台无插播、错播等情况下的相似度对比结果如图4。另取30段音频样本在相同的情况下进行测试,每段样本取所有音频帧相似度的均值作为结果,得到图5。
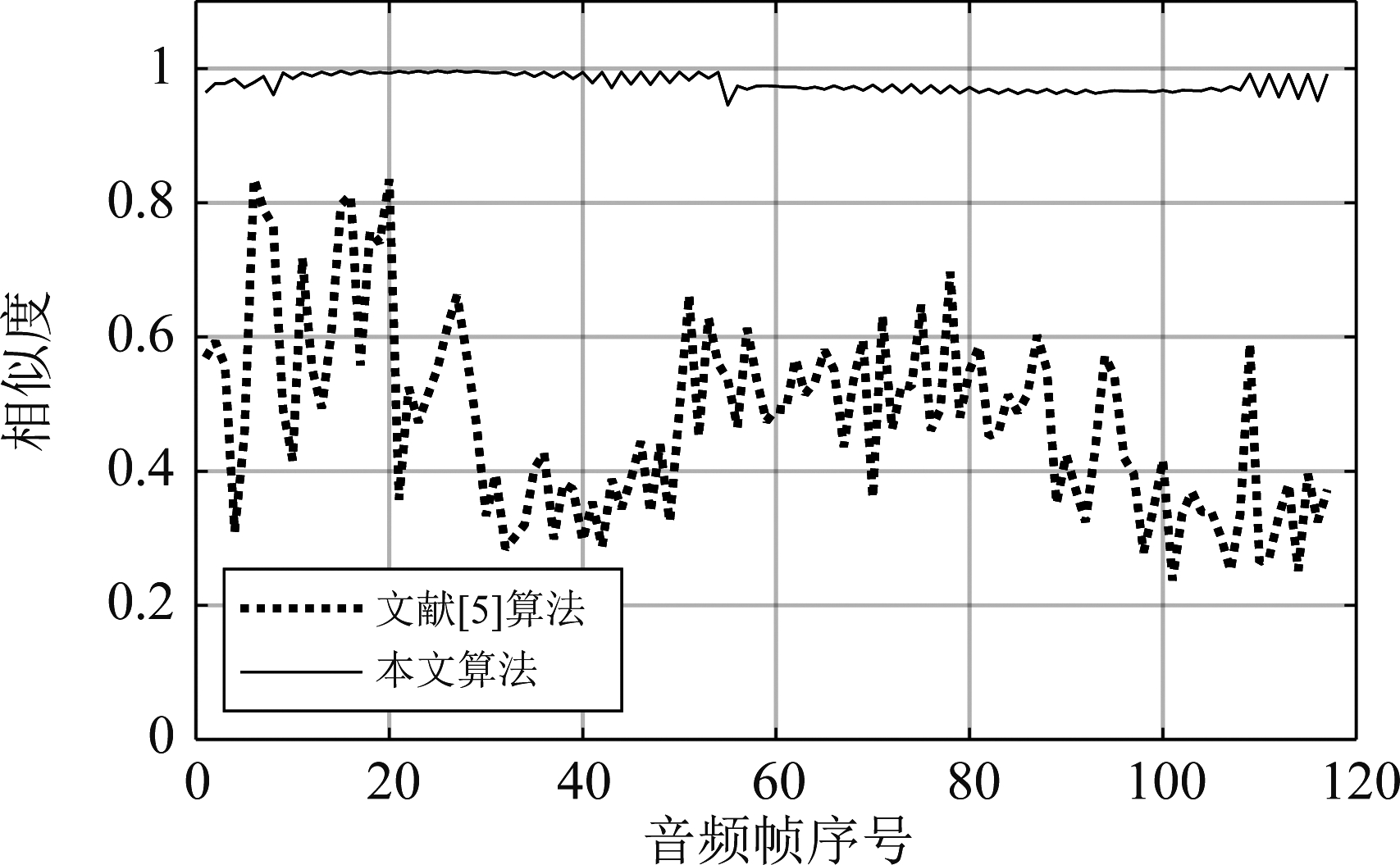
图4 音频相似度对比结果
Fig.4 Audio similarity comparison results
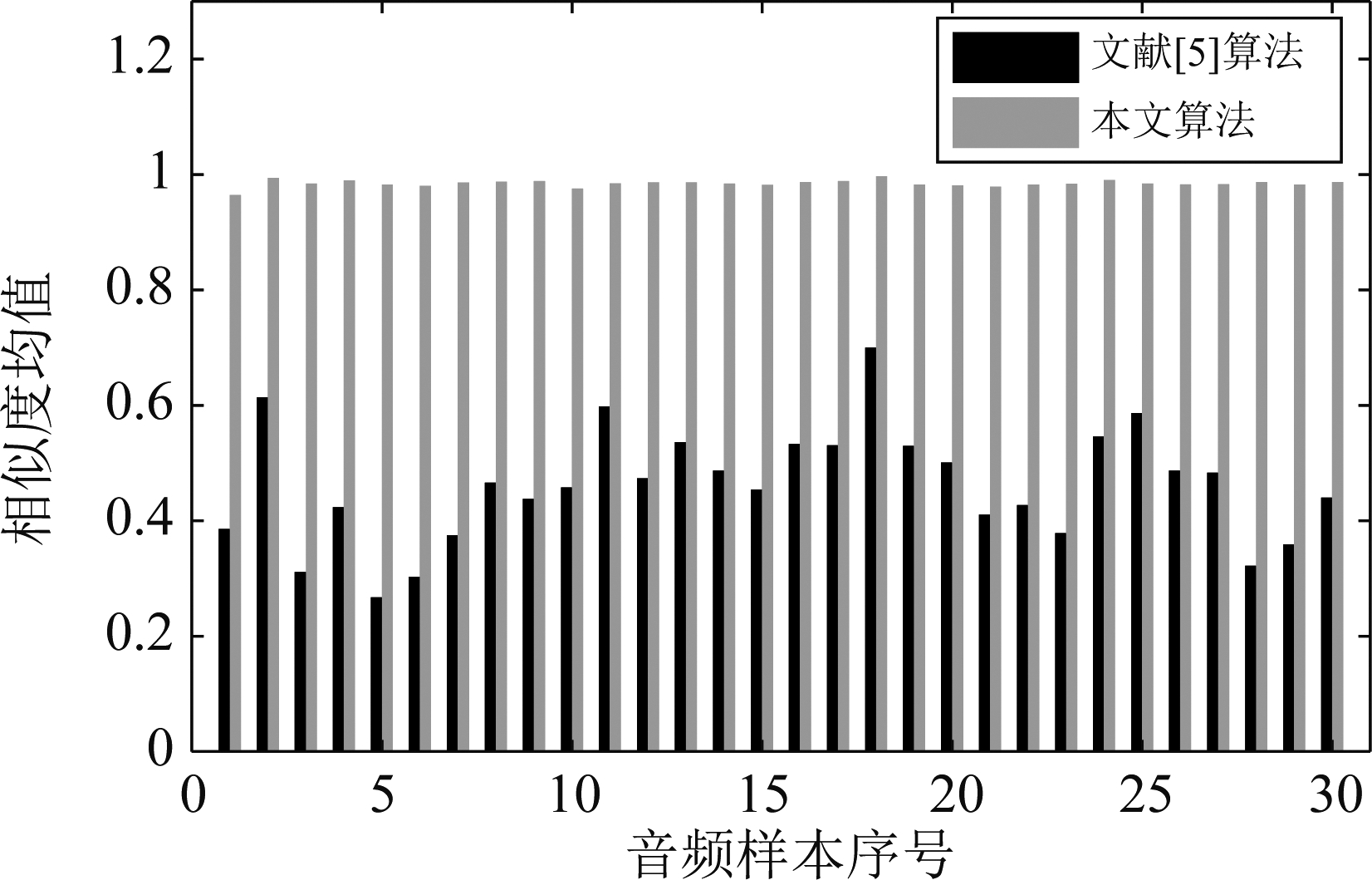
图5 多个音频样本相似度对比结果
Fig.5 Similarity comparison results of multiple audio samples
从图4和图5可以看出,在下级广播台无插播、错播等情况下,信号经过真实场景模型后,本文算法计算出的相似度结果均保持在0.95以上,更加接近真实值,明显优于文献[5]算法。
在系统模型参数设置不变的情况下,对音频样本人为地添加2 分钟的错播片段,判断算法是否能够检出错播的发生,相似度对比结果如图6。
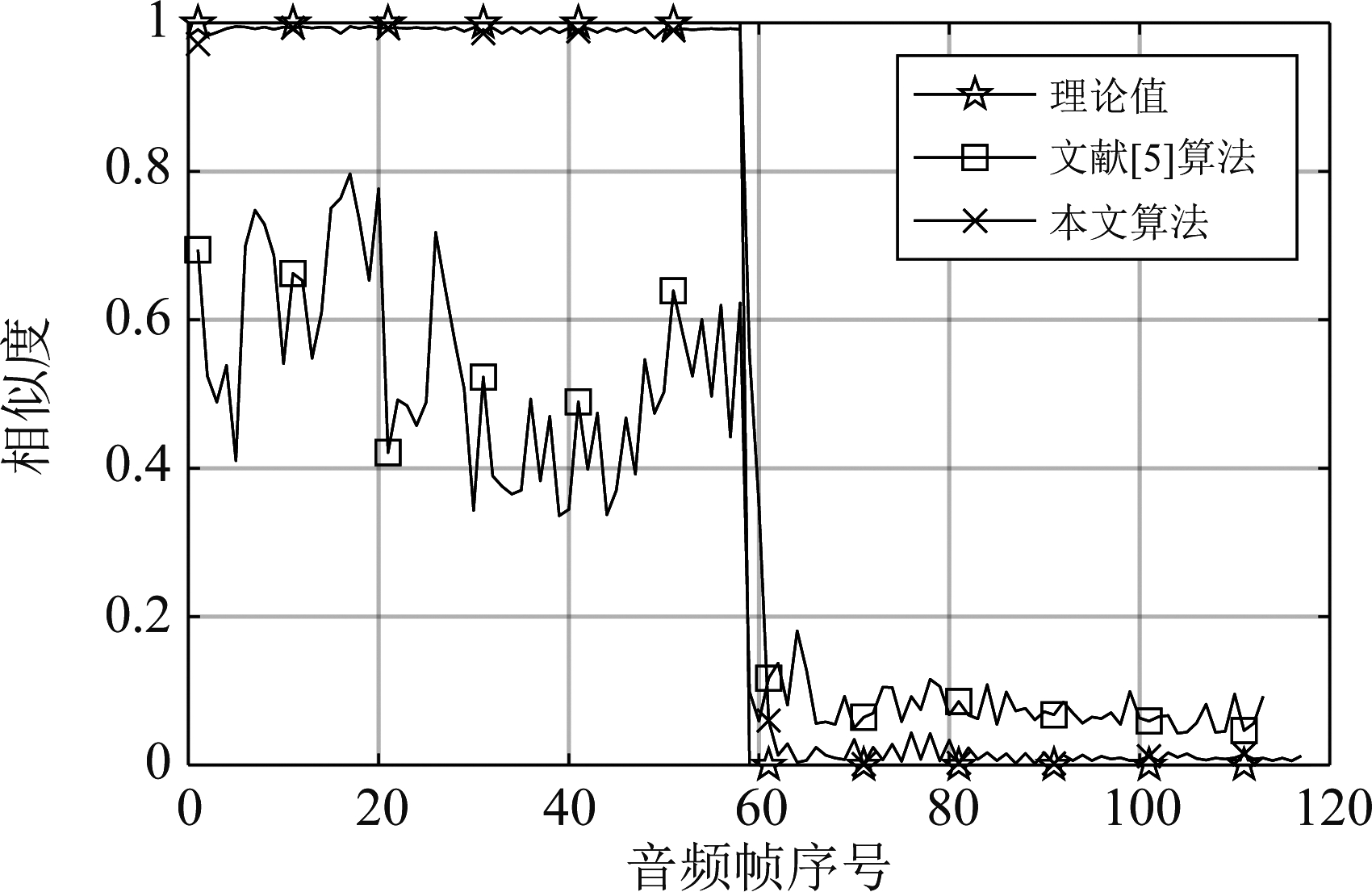
图6 存在错播片段的音频样本相似度对比结果
Fig.6 Similarity comparison results of audio samples with misbroadcast segments
由图6可以看出,在下级广播台存在错播情况下,信号经过真实场景模型后,本文算法计算出的相似度结果更加接近真实值,效果优于文献[5]算法。
为验证算法的速度,在相同平台和仿真参数情况下,统计本文算法和文献[5]算法计算上述相同音频样本相似度所用的时间,如表3所示。可知,本文算法平均每次运行时间远小于文献[5]算法。
表3 两种算法计算相似度的平均运行时间
Tab.3 Average running time of two algorithms when calculating similarity

算法平均运行时间/s文献[5]算法160本文算法6.66
为了验证在不同系统模型参数下本文算法的准确度和效果,分别比较了不同信噪比和不同多普勒频扩情况下无错播片段的相似度计算结果,如图7和图8所示。由于广播电台发送和接收音频时不会产生相对运动,实验时多普勒频移带来的影响极小,本文不再讨论。

图7 不同信噪比下音频相似度对比结果
Fig.7 Comparison results of audio similarity under different signal-to-noise ratios
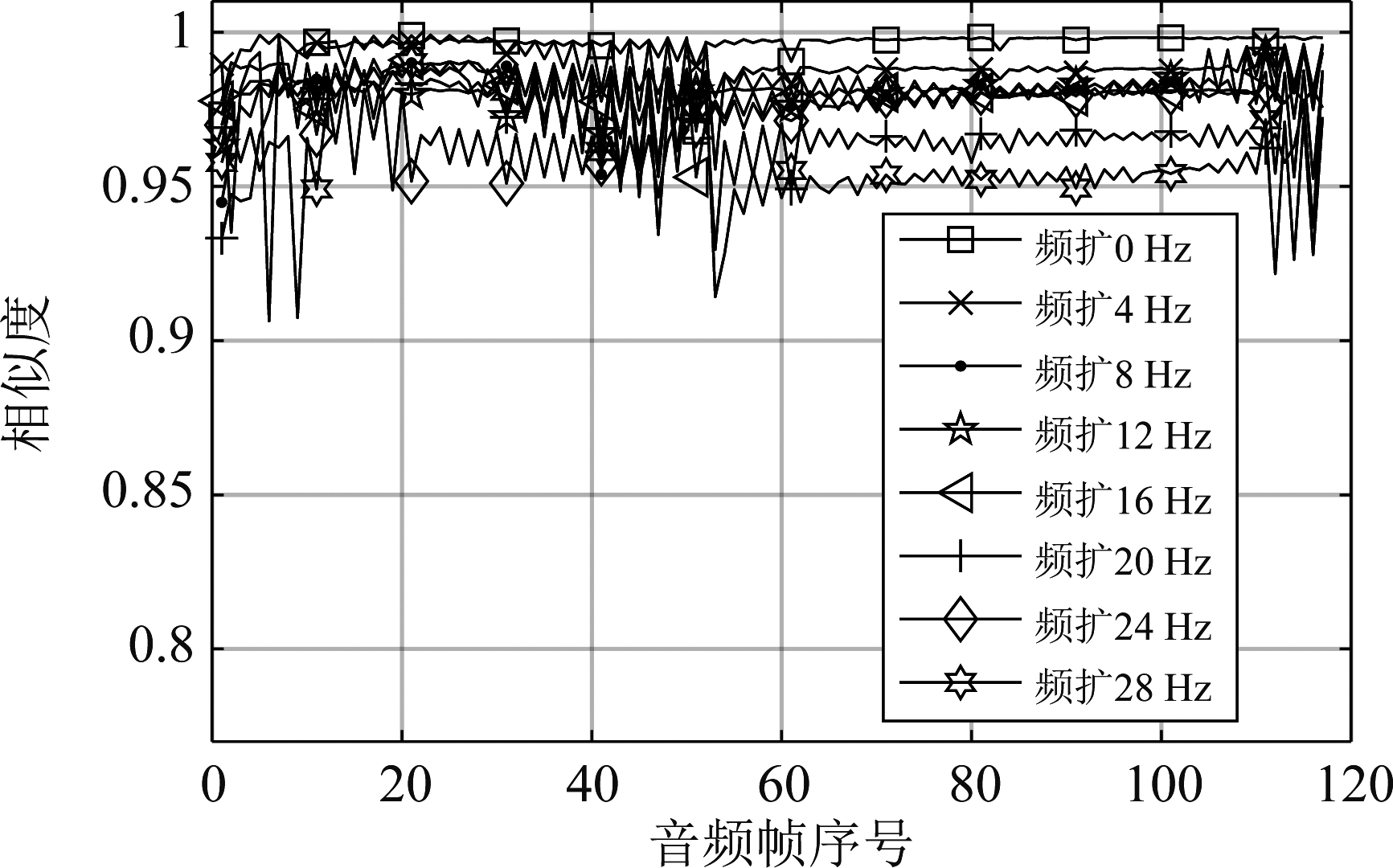
图8 不同多普勒频扩下音频相似度对比结果
Fig.8 Comparison results of audio similarity under different Doppler frequency expansions
从图7和8可知,相似度会随着音频信噪比的降低或多普勒频扩的增加而变得不准确,但在低信噪比(-3 dB)或高频扩(28 Hz)情况下,本文算法仍能计算出有效的相似度,其抗噪声性能在可接受范围内。
信道的多径效应也是影响广播信号传输的一个重要因素。为了验证算法抵抗多径效应的能力,分别比较了不同路径延时和不同多径数目情况下无错播片段的相似度计算结果,如图9和图10所示。
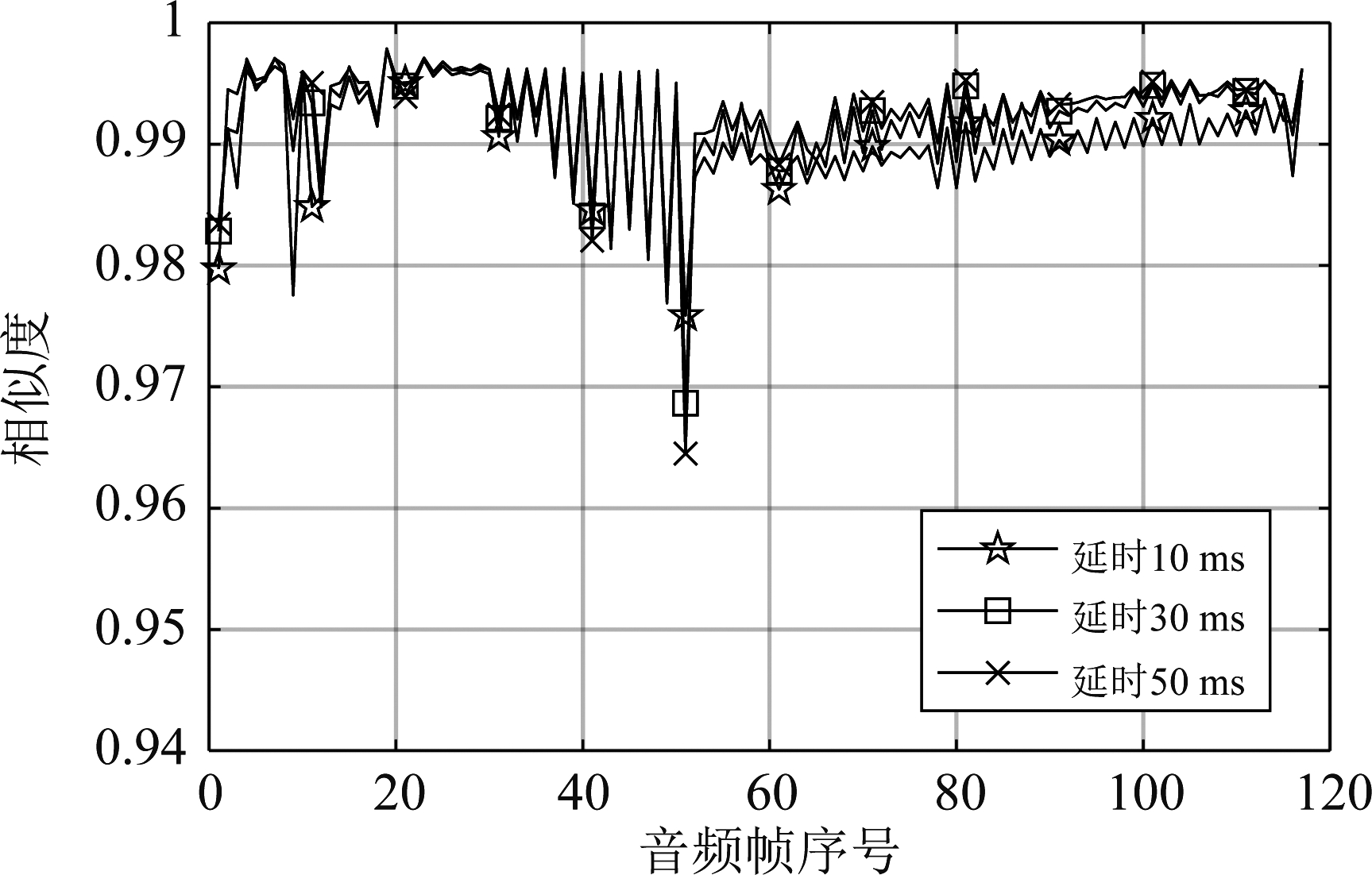
图9 不同路径延时下音频相似度对比结果
Fig.9 Comparison results of audio similarity under different path delays
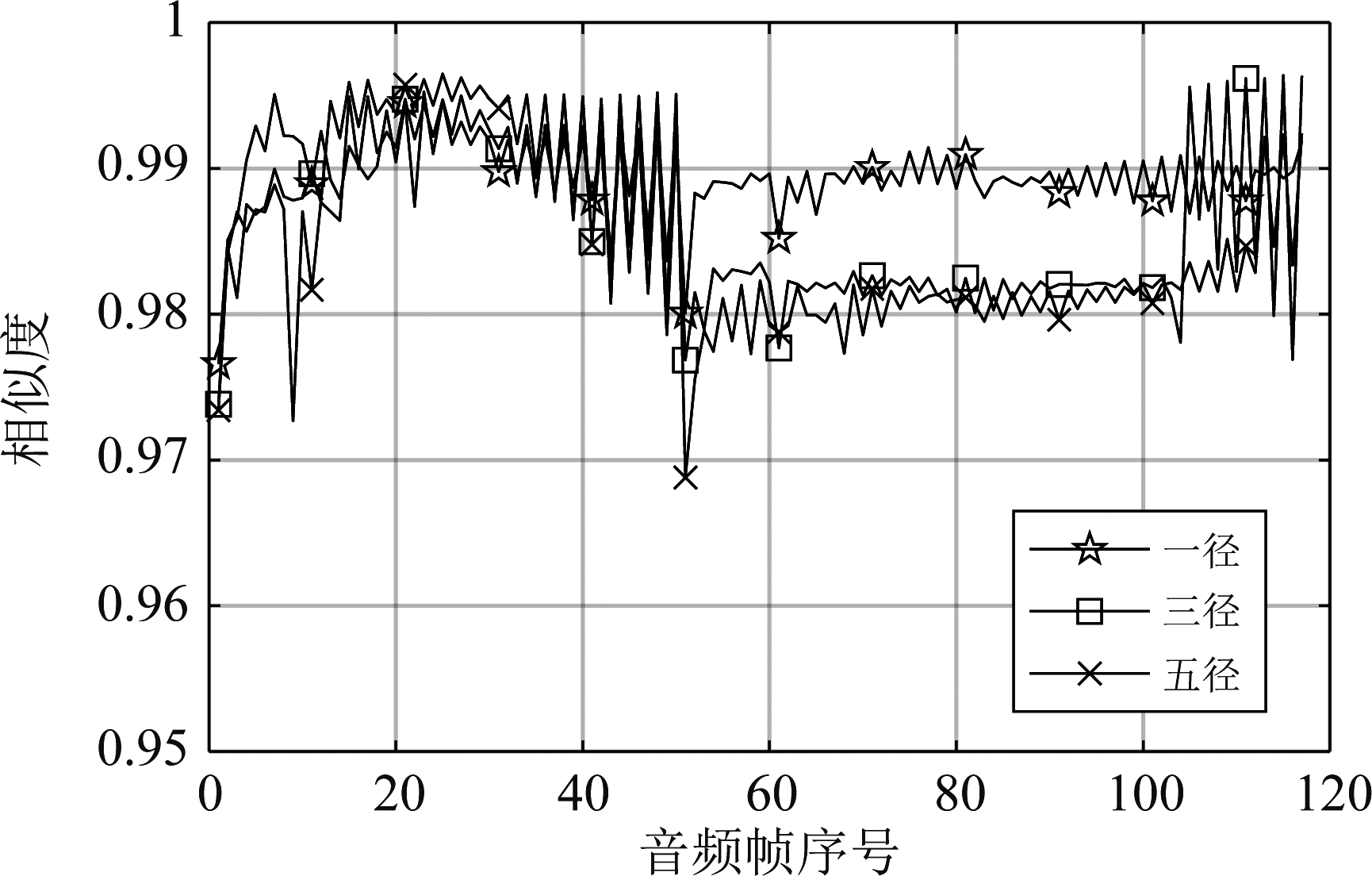
图10 不同多径数目下音频相似度对比结果
Fig.10 Comparison results of audio similarity under different multipath numbers
从图9和图10看出,相似度会随着路径延时和多径数目的增加出现波动,但在延时50 ms以内和5径以下,值均保持在0.95以上,可进一步印证本文算法的效果。
4.3 实际发送接收实验
为了进一步验证本文算法的可行性,利用实际收发设备传输广播音频信号,并对真实情况下的接收信号进行了相似度的计算。实际实验中,信号的发送模块采用了AC17CJ3912芯片,硬件实物如图11所示;接收模块采用了AD17CH9500芯片,硬件实物如图12所示。

图11 发送模块
Fig.11 Delivery module

图12 接收模块
Fig.12 Receiving module
利用本文算法与文献[5]算法分别计算实际发送信号与实际接收信号之间的相似度,在高信噪比情况下得到无错播情况的结果如图13。另取30段音频样本在同样的设置下进行测试,每段样本取所有音频帧相似度的均值作为统计结果,得到图14。对上述音频信号人为插入2分钟的错播片段再进行发送接收,得到文献[5]算法和本文算法计算所得相似度结果如图15。由这三图可知,本文算法计算所得相似度结果优于文献[5]算法,并且非常接近真实值,具有实际推广应用的潜力。
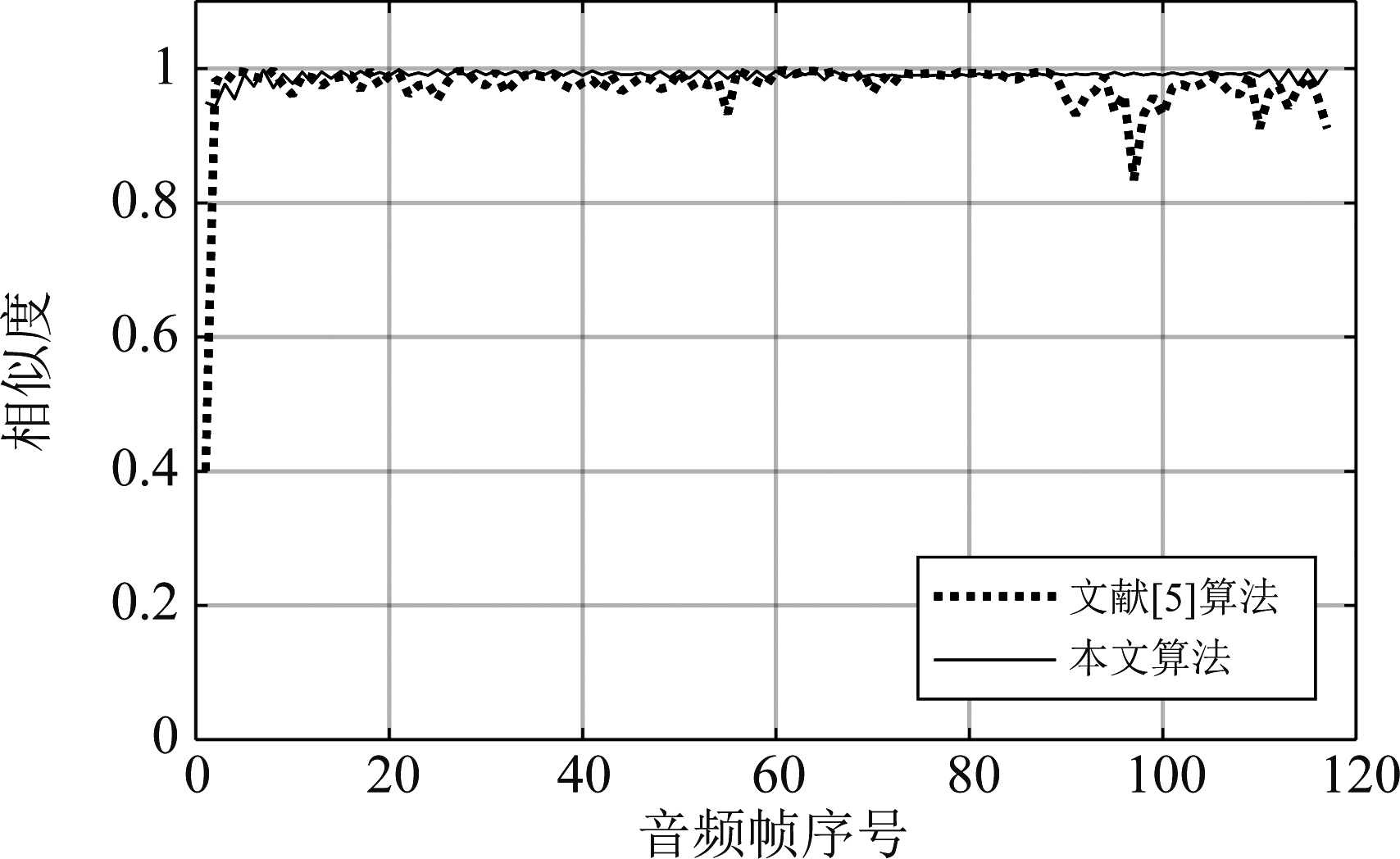
图13 实际接收音频相似度对比结果
Fig.13 The actual received audio similarity comparison results
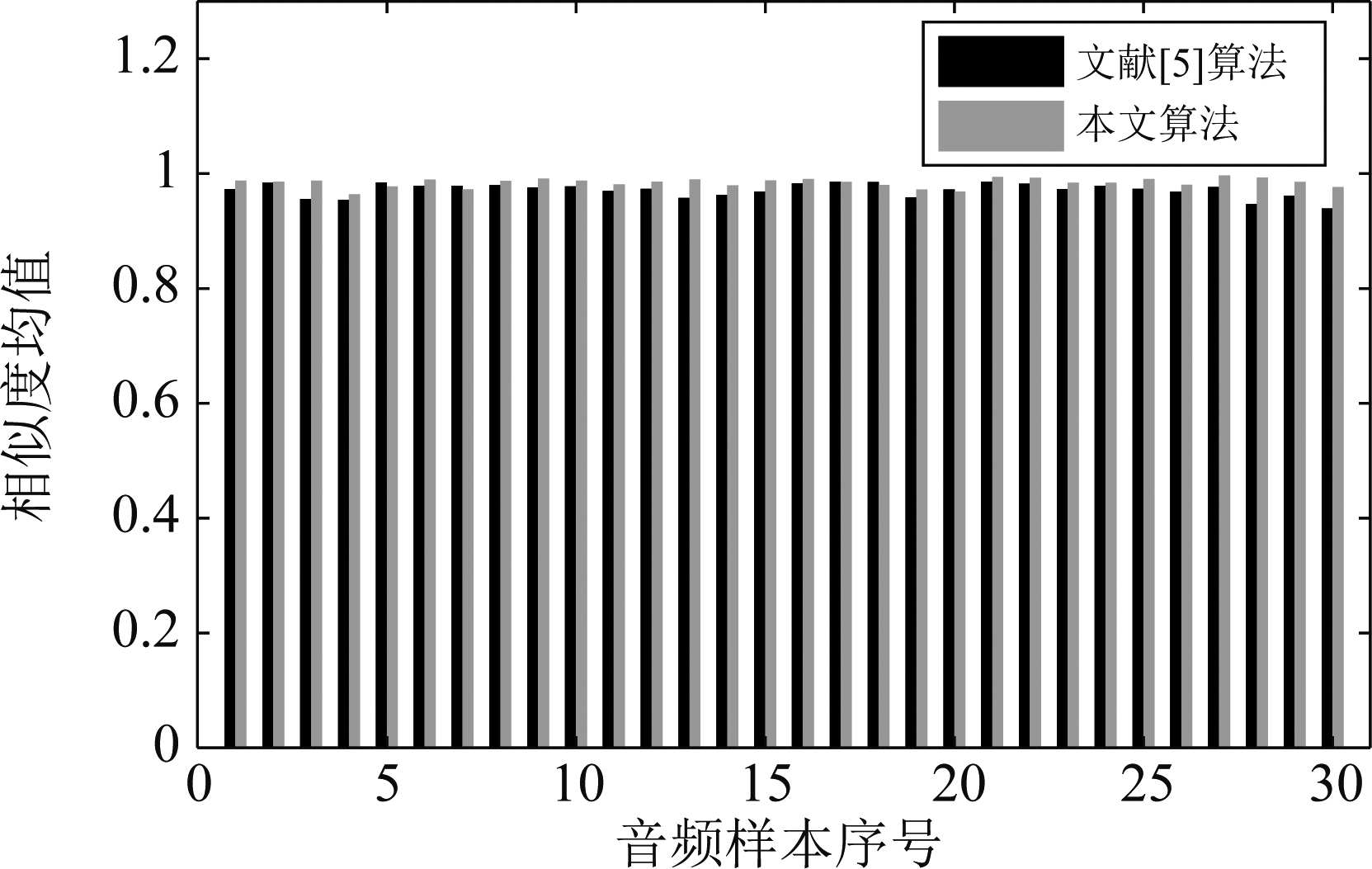
图14 实际接收多个音频样本相似度对比结果
Fig.14 Comparison results of similarity of multiple audio samples actually received
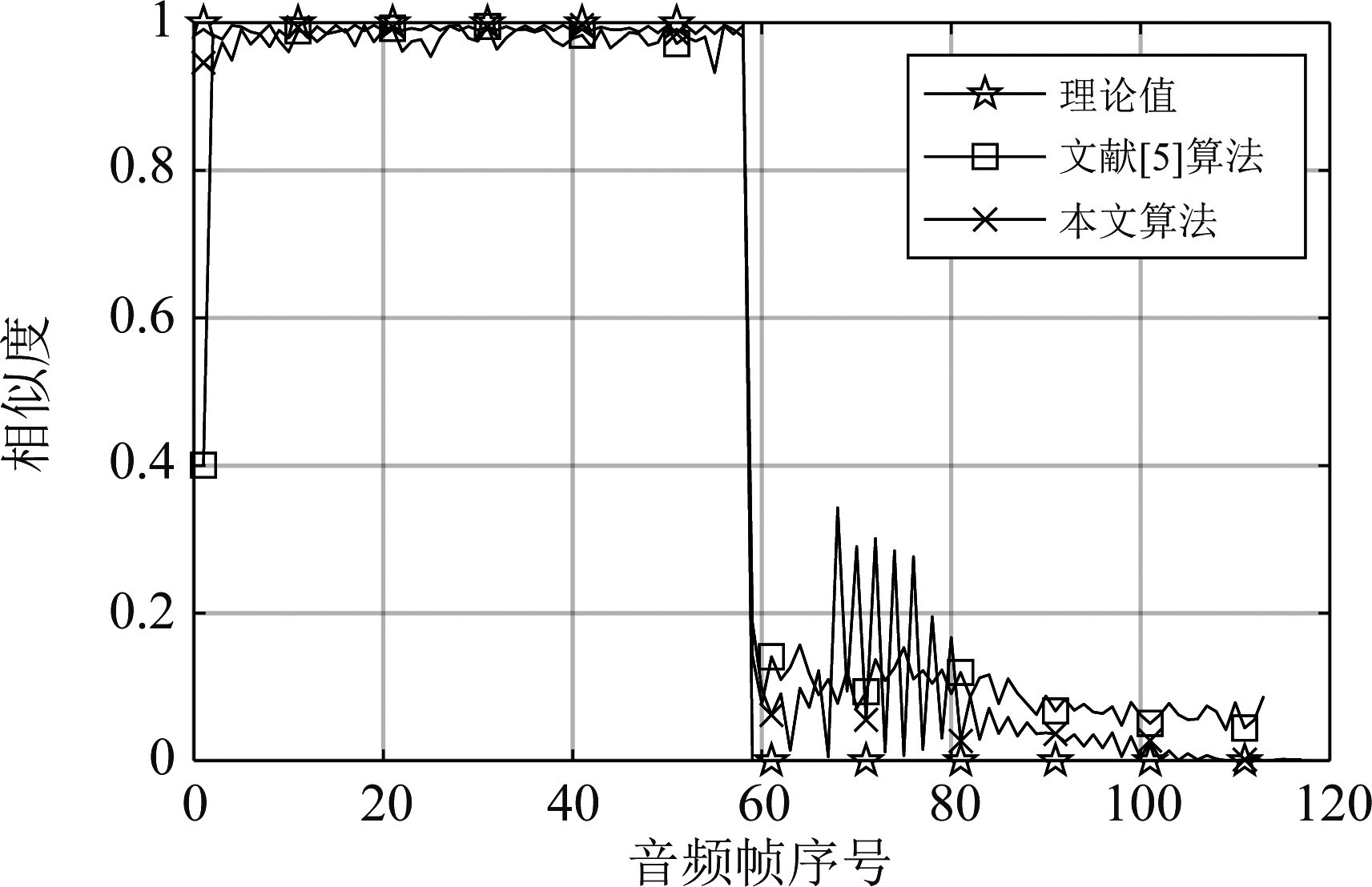
图15 存在错播片段的实际接收音频样本相似度对比结果
Fig.15 Similarity comparison results of actual received audio samples with misbroadcast segments
5 结论
音频相似性的检测对于广播信号监测工作有着重要的意义。为了得到实时的准确的监测结果,本文讨论了信号经过编解码器、功率放大器及信道后的相似性检测方法。通过对信号进行时延估计、自适应滤波来抵消收发设备和传输带来的影响,同时采用子带分解的方式降低计算量。实验表明本文提出的方法在建立的系统模型下优于传统方法,能够对不同信噪比,不同时延,不同频扩以及不同路径的信号实现相似度计算,且所得相似度较高,用时较短。同时,经过实际的收发设备接收到的音频用本文的方法计算相似度也达到了良好的效果,说明方法适用于实际信号处理。另外,所提方法虽然可以计算有延时的广播音频信号相似度,但由于系统因果性的问题,难以确认延时的正负,如何改进和优化算法得到更准确的时延估计将是未来的研究目标。
[1] SADHU S, LI Ruizhi, HERMANSKY H.M-vectors: Sub-band based energy modulation features for multi-stream automatic speech recognition[C]∥ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).Brighton, UK.IEEE, 2019: 6545-6549.
[2] BHATIA R, SRIVASTAVA S, BHATIA V, et al.Analysis of audio features for music representation[C]∥2018 7th International Conference on Reliability, Infocom Technologies and Optimization(Trends and Future Directions)(ICRITO).Noida, India.IEEE, 2018: 261-266.
[3] YU Xiaoqing, PAN Xueqian, YANG Wei, et al.Audio similarity measure based on Renyi’s quadratic entropy[C]∥2010 International Conference on Audio, Language and Image Processing.Shanghai, China.IEEE, 2010: 722-726.
[4] 聂昂, 刘树林, 杨洪柏, 等.基于MFCC和CNN的音频相似度判别研究[J].机械制造, 2019, 57(4): 7-10.
NIE Ang, LIU Shulin, YANG Hongbai, et al.Study on audio similarity discrimination based on MFCC and CNN[J].Machinery, 2019, 57(4): 7-10.(in Chinese)
[5] 齐新星.广播信号监测监听平台升级实现[J].东南传播, 2019(7): 179-182.
QI Xinxing.Upgrading and implementation of broadcast signal monitoring and listening platform[J].Southeast Communication, 2019(7): 179-182.(in Chinese)
[6] 张琳, 周韬, 杜庆治, 等.基于物理特征的音频相似度比对算法研究[J].电视技术, 2017, 41(Z4): 110-114.
ZHANG Lin, ZHOU Tao, DU Qingzhi, et al.Audio comparison algorithm based on physical characteristics[J].Video Engineering, 2017, 41(Z4): 110-114.(in Chinese)
[7] 邵玉斌, 唐传林, 赵至柔, 等.基于倒谱分析的实时广播音频相似度快速比对算法[J].工程科学与技术, 2020, 52(3): 178-185.
SHAO Yubin, TANG Chuanlin, ZHAO Zhirou, et al.Fast similarity comparison algorithm for real-time broadcast audio based on cepstrum analysis[J].Advanced Engineering Sciences, 2020, 52(3): 178-185.(in Chinese)
[8] GUO Meng, KUENZLE B.Obtaining narrow transition region in STFT domain processing using subband filters[C]∥ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).Brighton, UK.IEEE, 2019: 970-974.
[9] SHI Chuang, KAJIKAWA Y.Identification of the parametric array loudspeaker with a Volterra filter using the sparse NLMS algorithm[C]∥2015 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).South Brisbane, QLD, Australia.IEEE, 2015: 3372-3376.
[10] HUANG H C, LEE J.A new variable step-size NLMS algorithm and its performance analysis[J].IEEE Transactions on Signal Processing, 2012, 60(4): 2055-2060.
[11] RAICH R.Nonlinear system identification and analysis with applications to power amplifier modeling and power amplifier predistortion[D].Atlanta: Georgia Institute of Technology, 2004.
[12] HU Chengnan, CHANG D C.Nonlinear effects of power amplifiers on adaptive antenna systems[J].IEEE Transactions on Antennas and Propagation, 2016, 64(4): 1444-1453.
[13] LIU Ming, LI Jianqiang, JIANG Hua.Automatic classification of modulations in the flat fading HF channel based on Watterson model[C]∥2010 Second International Workshop on Education Technology and Computer Science.Wuhan, China.IEEE, 2010: 218-221.
[14] MCCALLUM M C.Foreground harmonic noise reduction for robust audio fingerprinting[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).Calgary, AB, Canada.IEEE, 2018: 3146-3150.
[15] YOSHIMURA T, HASHIMOTO K, OURA K, et al.Speaker-dependent Wavenet-based Delay-free adpcm speech coding[C]∥ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP).Brighton, UK.IEEE, 2019: 7145-7149.
[16] LIU Jing, ZHANG Yong, ZHAO Qinjun.Video stabilization algorithm based on Pearson correlation coefficient[C]∥2019 International Conference on Advanced Mechatronic Systems(ICAMechS).Kusatsu, Japan.IEEE, 2019: 289-293.
[17] SONNLEITNER R, WIDMER G.Robust quad-based audio fingerprinting[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016, 24(3): 409-421.
[18] 胡广书.数字信号处理: 理论、算法与实现[M].3版.北京: 清华大学出版社, 2012: 123-177.
HU Guangshu.Digital signal processing: theory, algorithms and implementation[M].Third edition.Beijing: Tsinghua University Press, 2012: 123-177.(in Chinese)


