1 引言
机器学习已被用于解决无线通信中的很多问题,如信息预测[1]和空-时-频资源优化[2]。与传统基于数值优化的决策方法相比,深度学习在推理阶段的计算复杂度非常低,有支持实时决策的潜力[2]。预测瞬时信道可以解决高速移动环境下信道过时导致的性能损失[3-4],预测平均信道和未来接入小区可以通过预测资源分配和主动切换等方式大幅度提升无线系统的资源利用率和用户体验[5-6]。
大部分机器学习采用集中式方法进行训练,在离线训练阶段需要从网络的不同节点搜集数据,不仅需要很大的通信开销还有泄露用户隐私的风险。联邦学习[7]是一种去中心化的训练方法,可以利用边缘节点的数据采集与计算能力,并解决用户数据的隐私问题。文献[7]提出了联邦平均算法(Federated Averaging,FedAVG),通过在各用户设备上进行多轮本地训练,在云处理中心对局部模型进行整合、并将全局模型下发给各用户,使得数据不离开用户终端也能训练机器学习模型。文献[8]讨论了联邦学习在无线通信中的应用,如边缘计算、缓存和频谱管理等。虽然提出联邦学习的主要动机是解决数据隐私问题,但很多无线通信问题中的数据(如信道)并不涉及隐私,某些用户甚至有意愿共享数据来获得更好的用户体验[9],这时采用联邦学习的主要动机是与集中式训练上传原始数据相比通信开销更低。文献[10]针对多输入多输出(Multi-input-multi-output,MIMO)信道估计问题,比较了集中式学习和联邦学习的通信开销。仿真结果表明,基站天线数为128、用户天线数为32时,联邦学习把通信开销相对于集中式学习降低了16倍。
当利用分布式随机梯度下降算法[11](Distributed Stochastic Gradient Descent,DSGD)进行分布式训练时,用户每训练完一次都需要向处理中心上传模型参数,若机器学习的模型很大,则导致很大的上行通信开销。为了降低完成联邦学习所需要传输的总数据量,现有文献提出了以下三类方法:降低通信轮次、降低单轮次传输所需的通信资源、降低单轮次训练需要传输的数据量[12]。相对于DSGD,联邦平均[7]通过用户在本地训练时进行多轮迭代降低通信轮次,是一种具有代表性的降低通信轮次方法。用户选择策略也可以降低通信轮次,例如选择各轮次训练时模型变化更明显的用户[13]。降低每轮所需通信资源的典型方法是空中计算[14],但其所需的极为严格的时间同步限制了这种思路的应用前景[12]。降低单轮次传输数据量的方法包括模型稀疏化、参数量化、低秩分解和知识蒸馏等。文献[11]提出了稀疏二元压缩算法(Sparse Binary Compression,SBC),通过残差积累、稀疏二元化和哥伦布(Golomb)编码,可将上行数据量相对于DSGD减小3531倍。文献[15]提出了结构化更新和草图更新,结构化更新限制局部更新的模型结构(如低秩结构);草图更新通过随机稀疏化、随机旋转和概率量化压缩模型,可将联邦学习的上行数据量相对于联邦平均降低100倍左右。文献[16]把草图更新用于下行数据压缩,并提出了联邦随机失活,使用户在全局模型的子集上进行训练,不但减小了上行数据量而且降低了用户端的计算量。文献[17]中提出了稀疏三元压缩,在数据集分布非独立同分布的场景下相对于SBC的性能更鲁棒。文献[18]提出了经过联邦训练的三元量化,可把上下行数据量降低16倍。文献[19]分析了采用有限精度量化时联邦平均的收敛性,并设计了上行和下行的量化方法。目前,现有考虑模型压缩的文献在评估所提出算法的压缩倍数时都没有与集中式训练所需的上行数据量进行比较,而文献[10]人为增加了集中式训练所需的数据,联邦学习所需的上行数据量是否一定比集中式学习低尚无定论。
本文旨在研究对于典型的无线任务,经过压缩后联邦学习的总通信开销是否低于集中式学习。为此,我们考虑利用机器学习(以神经网络为例)预测平均信道增益、瞬时信道和未来接入小区这三个问题,在利用联邦平均[7]降低总通信轮次的基础上,进一步通过SBC和草图更新这两种具有代表性且增益明显的压缩方法来降低单轮次上行传输的数据量,并在达到相同预测性能的前提下与集中式学习进行比较。研究结果表明,对于以上三个预测问题,引入SBC和草图更新后相对于联邦平均能把总上行数据量分别压缩60倍和20倍左右;对于平均信道增益预测,SBC相对于DSGD的压缩倍数可高达近5000倍;在预测未来接入小区和MIMO信道时联邦学习所需的上行数据量低于集中式学习;对于平均或瞬时信道增益预测问题,联邦学习所需的上行数据量是集中式学习的近两倍或六倍。
本文第2节介绍如何利用联邦学习对三种信息进行预测;第3节介绍SBC和草图更新算法;第4节分析在预测平均信道增益、瞬时信道和未来接入小区时引入SBC和草图更新后联邦平均算法的收敛速度和稳态预测性能,比较压缩后联邦学习与集中式学习在达到同样预测性能时所需要的总上行数据量。
2 基于联邦学习的信息预测
联邦学习是一种分布式训练的方法,在训练过程中多个用户参与多个回合的本地训练和模型平均。联邦学习中有两类不同的更新方法:梯度更新和模型更新,本文考虑模型更新。在每个回合的训练中,每个用户利用所记录的本地数据集对模型进行训练,而后把模型参数(或梯度)上传至处理中心,处理中心对局部模型参数进行整合后得到全局模型再下发给每一个用户,至此完成一次完整的训练回合[7]。
考虑在多小区覆盖区域内移动的多个用户,各基站通过回传链路连接到一个处理中心。用户根据过去一段时间(称为观测窗)内记录的数据、利用本地训练的神经网络模型预测未来的信息,包括用户即将接入的小区、用户的平均和瞬时信道增益。
2.1 预测未来接入小区
由于基站的位置确定,所以可通过与用户最近几个基站间的平均信道增益隐含地估计用户的位置[20]。为了预测下一个接入的小区,用户以Δr为分辨率记录To/Δr个距离最近的No个基站的平均信道增益,其中To是观测窗的长度。神经网络的输入为观测窗中的NoTo/Δr个平均信道增益,输出为用户即将接入的小区。
当利用联邦学习预测未来接入小区时,各用户记录自己的平均信道增益和所接入的小区、形成用于训练的局部数据集。
2.2 预测平均和瞬时信道
为了预测Tp秒以后用户的平均信道增益、瞬时信道增益或信道矩阵,用户记录每帧的平均信道增益、瞬时信道增益或信道矩阵。Tp为预测窗长,帧长ts为信道相干时间,预测平均信道增益时帧长为大尺度信道的相干时间(秒级),预测瞬时信道时帧长为小尺度信道的相干时间(毫秒级)。
当预测平均或瞬时信道增益时,神经网络的输入为观测窗内的To/ts个平均或瞬时信道增益,输出为用户在Tp秒后的平均或瞬时信道增益。当预测MIMO信道矩阵时,神经网络输入为观测窗内信道矩阵的实部和虚部,输出为预测窗内信道矩阵的实部和虚部。
当利用联邦学习进行预测时,各用户记录自己的平均或瞬时信道、形成用于训练的局部数据集。
3 降低每回合上行传输的数据量
3.1 稀疏二元压缩
稀疏二元压缩算法[11]的基本思想是用户每回合只上传模型更新矩阵元素中变化最大的部分值,并把未上传的部分作为残差进行积累,即在联邦平均[7]的基础上引入了以下的处理。
(1)残差积累
截止到第τ个回合,用户i在局部训练得到的未压缩和压缩后模型更新矩阵之差的累积值、即残差为:
(1)
其中▽Wτ,i为第i个用户在第τ个回合的模型更新矩阵,
为压缩后的模型更新矩阵,残差初值R0,i=0。
对于第i个用户,把此用户在第τ个回合局部训练得到的模型更新矩阵▽Wτ,i与残差矩阵Rτ,i之和进行压缩,即可得到此回合压缩后的模型更新矩阵:
(2)
其中sparse表示如下的具体压缩算法。
(2)稀疏二元化
首先,把模型更新矩阵中除最大的n个元素和最小的n个元素外的其他元素置为0,其中n=P×N,P为稀疏比例,N为矩阵中的总元素数。而后,计算最大的n个元素的平均值μ+以及最小的n个元素平均值的绝对值|μ-|。如果μ+>|μ-|,则把最小的n个元素置为0、最大的n个元素置为μ+;如果μ+<|μ-|,则把最大的n个元素置为0、最小的n个元素置为μ-。
(3)哥伦布位置编码
为了进一步降低每回合上传的数据量,对模型更新矩阵▽Wτ,i与残差矩阵Rτ,i之和进行稀疏二元化后,各用户只上传这个和矩阵中非0元素的位置和经32比特量化后的μ+或μ-。相对于上传每个非0元素的绝对位置,上传非0元素间的距离所需的比特数更少。文献[11]采用哥伦布位置编码算法对相邻非0元素之间的距离进行编码,编码所需的平均比特数为:
(3)
其中
为稀疏比例。
3.2 草图更新
草图更新[15]的基本思想是随机上传模型更新矩阵的部分元素,并对这些元素进行概率量化。在联邦平均[7]的基础上引入了以下的处理。
(1)随机稀疏化
在第τ回合中第i个用户随机选取模型更新矩阵▽Wτ,i中的n=P×N个元素进行上传。为此,用户需上传▽Wτ,i中的n个元素和用于选取这n个元素的随机种子。处理中心利用随机种子和▽Wτ,i的n个元素即可恢复▽Wτ,i,其中用户未上传的元素置为0;而后对恢复得到的各用户▽Wτ,i进行平均即可得到全局模型。
(2)概率量化
分别定义hmin,hmax为模型更新矩阵▽Wτ,i中元素的最小值和最大值,把[hmin,hmax]均匀分为2b个区间。若hj的值位于其中的某个区间[h′,h″]中,则可依概率将其量化如下:
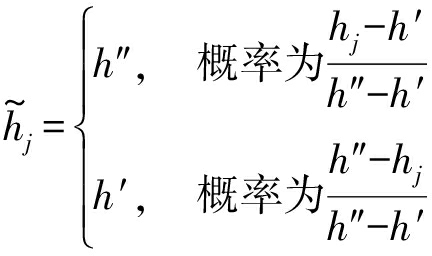
(4)
经过概率量化后,对于模型更新矩阵的每个元素只需上传b比特、而非32位浮点数。
4 联邦学习的上行通信开销分析
本节通过仿真分析利用基于稀疏二元压缩和草图更新的联邦学习对信息进行预测时每回合以及总的上行通信开销,并与联邦平均和集中式学习进行比较。
4.1 仿真场景
考虑一段长为7.5 km的道路,在距道路左端起点6 km处设置一处红绿灯,如图1所示。在道路一侧有15个半径为250 m的基站,基站距道路的最小距离为100 m。用户从道路的最左端进入道路,并开始记录信道增益。不同轨迹的平均速度服从15～25 m/s间的均匀分布,每秒的加速度为零均值、方差在0.5～1.5 m/s2间服从均匀分布的白高斯随机过程,用户的最低和最高运动速度分别为10 m/s和30 m/s。用户在红绿灯处减速和启动的加速度为2 m/s2,停车时长服从5～95 s的均匀分布。
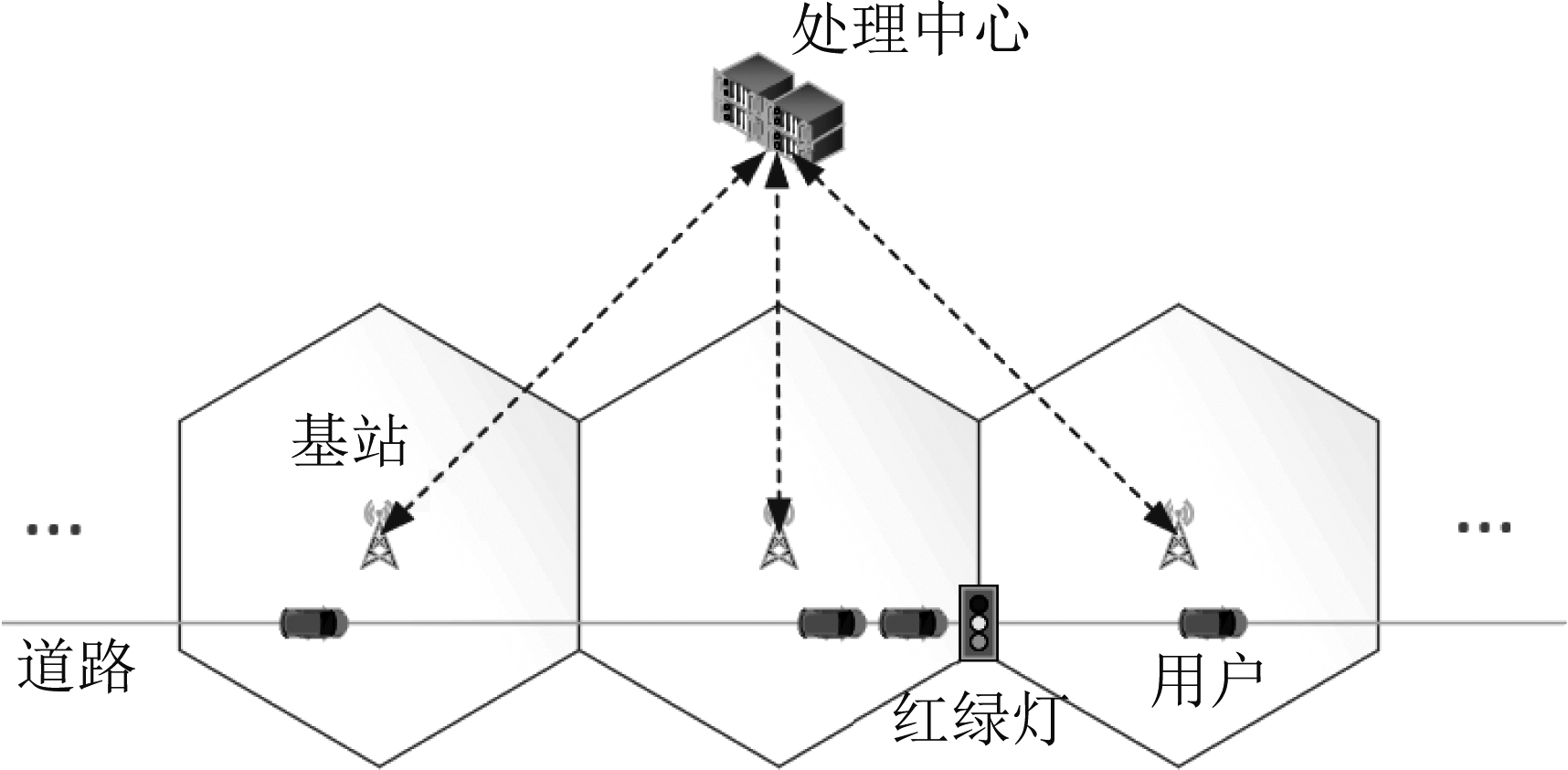
图1 仿真场景示意图
Fig.1 Simulation setups
为了根据用户的移动轨迹得到平均信道增益,按如下方式生成信道地图(即各地理位置对应的平均信道增益):路径损耗模型为α+βlog10(d),其中α=36.8,β为路径损耗因子,d为用户与所接入基站的距离,阴影衰落服从对数正态分布;每个小区的β在36.6～36.8内随机选取,阴影衰落的相关距离在40～70 m范围内随机选取、标准差在6～8 dB间随机选取,从而反映各小区传播环境的差异。对于不同的移动轨迹,在相同位置处的平均信道增益相同。
为了生成瞬时信道增益数据集,我们考虑一种改进的Jakes模型[21],对模型参数进行随机化,即可生成多条不相关的瞬时信道记录。瞬时信道系数的第k条记录可表示为:
其中
为最大车速vm对应的最大多普勒频移, fc为载频,M为参与合成瞬时信道的正弦波总数,
对所有的n和k均在[-π,π)之间服从均匀分布且相互独立。仿真中,我们选取M =8,载频fc=2 GHz。
为了比较预测MIMO信道矩阵时联邦学习和集中式学习的通信开销,我们考虑如下的信道模型[22]。k时刻信道矩阵为:H[k]=
其中N[k]为多径数,αn[k]为第n条多径的信道增益,φn,A[k]和φn,D[k]分别为到达角和发射角,ar(·)和at(·)分别为接收和发射的阵列响应向量,(·)*表示共轭转置。考虑均匀线阵,阵列响应向量为:
其中M为天线数,λ为载波波长,d=λ/2为天线间距。假设αn[k]的实部αn,R[k]和虚部αn,I[k]服从一阶马尔科夫过程:αn,i[k+1]=ραn,i[k]+ζ[k],其中i∈{R,I},ρ为相关系数,
到达角和接收角服从φn,A[k+1]=φn,A[k]+μ[k],φn,D[k+1]=φn,D[k]+γ[k],其中
仿真中选取
发射天线数Nt=64,接收天线数Nr=1,多径数N[k]=8。由于时变信道服从一阶马尔可夫过程,选取观测窗长为1。
在预测平均信道增益和瞬时信道增益时,观测窗To越长、预测窗Tp越短,则预测误差越小。在预测平均信道增益时,选取帧长ts=1 s,Tp=40 s;由于To> 60 s时,预测误差随观测窗长的变化不大,所以选取To=60 s。在预测瞬时信道增益时,选取帧长ts=1 ms,由最大多普勒频移可得到相干时间约为5 ms,我们选取Tp=5 ms;由于To> 300 ms时,预测误差随观测窗长变化不大,所以选取To=300 ms。
在预测未来接入小区时,观测窗To越长、对平均信道增益的采样分辨率越高,预测越准确。由于To> 20 s,Δr< 5 s时,预测准确率随观测窗和分辨率的变化不大,而增大观测窗长或减小分辨率时,模型复杂度增加,所以选取To=20 s,Δr=5 s。对于三个预测问题,参与联邦学习的用户数均为10,每个用户把30条信道记录作为训练集、另30条信道记录作为测试集。
我们以全连接神经网络为例,对上述信息进行预测。精调后的超参数如表1所示,其中批大小对预测性能影响不大,都选为128;用户局部训练的迭代次数(epoch数)设为不明显降低预测性能时的最大值;为了与现有文献进行比较,我们也考虑了MNIST[23]数据集,采用文献[11]的超参数。
为了理解联邦学习的上行通信开销,在表1中列出了神经网络的大小,指的是为以32位浮点数存储网络参数所需的兆字节数。以预测平均信道增益问题为例,在集中式学习中,10个用户各保存30条平均信道增益记录,每条记录包含约430帧。用户以32位浮点数上传全部平均信道增益记录所需的上行数据量为
在联邦学习中,若用户以32位浮点数上传未经任何压缩的模型更新矩阵,则每个通信回合的上行数据量为0.102 Mbytes,与集中式学习所需的上行数据量的量级相同;当联邦学习收敛所需的回合数为10或102时,相应的总上行数据量约为集中式学习的10～102倍。可见,降低联邦学习的通信开销是十分必要的。
表1 神经网络的超参数
Tab.1 DNN hyper-parameters
平均信道增益输入层隐藏层输出层网络大小/Mbytes60[30,20,10]10.0102学习率学习算法批大小用户局部训练迭代次数0.03SGD1281瞬时信道增益输入层隐藏层输出层网络大小/Mbytes300[200,100,100,50]10.364学习率学习算法批大小用户局部训练迭代次数0.3SGD1281MIMO信道Nt=64, Nr=1输入层隐藏层输出层网络大小/Mbytes128[150, 150]1280.2339学习率学习算法批大小用户局部训练迭代次数0.003Adam1281未来接入小区输入层隐藏层输出层网络大小/Mbytes60[25,25]150.0098学习率学习算法批大小用户局部训练迭代次数0.0005Adam12820
4.2 不同压缩方法的收敛速度与稳态精度
为了比较达到指定学习性能时不同方法所需的通信回合和上行数据量,首先比较无模型压缩的联邦平均(图标为“FedAVG”)、稀疏二元压缩(图标为“SBC”)和草图更新(图标为“草图更新”)的收敛速度和收敛后的稳态预测性能。由于草图更新会降低预测性能,所以我们尝试引入残差积累以提高其预测性能。
图2给出了平均和瞬时信道增益的预测误差随通信回合的变化,图3给出了未来接入小区的预测准确率随通信回合的变化。其中P表示“SBC”和“草图更新”中的稀疏比例,P=0.1意味着仅上传10%的模型参数;“有RA”意味着积累残差,“没有RA”意味着不积累残差;由于SBC算法默认积累残差,故未标出“有RA”;由于原始草图更新算法并不积累残差,故未标出“没有RA”。由式(3)可得,当P为0.01～0.2时,在SBC中哥伦布位置编码平均每元素所需的比特数约为5～9比特,所以在“草图更新”中采用5比特量化。由于在实际应用中平均信道增益的单位一般是dB,所以用平均绝对误差(Mean Absolute Error,MAE)衡量平均信道增益的预测性能,单位为dB;采用文献[24]中的归一化均方误差(Normalized Mean Square Error,NMSE)衡量瞬时信道的预测性能;用准确率(即预测的下一接入小区与标签相同的频次)衡量未来接入小区的预测性能。
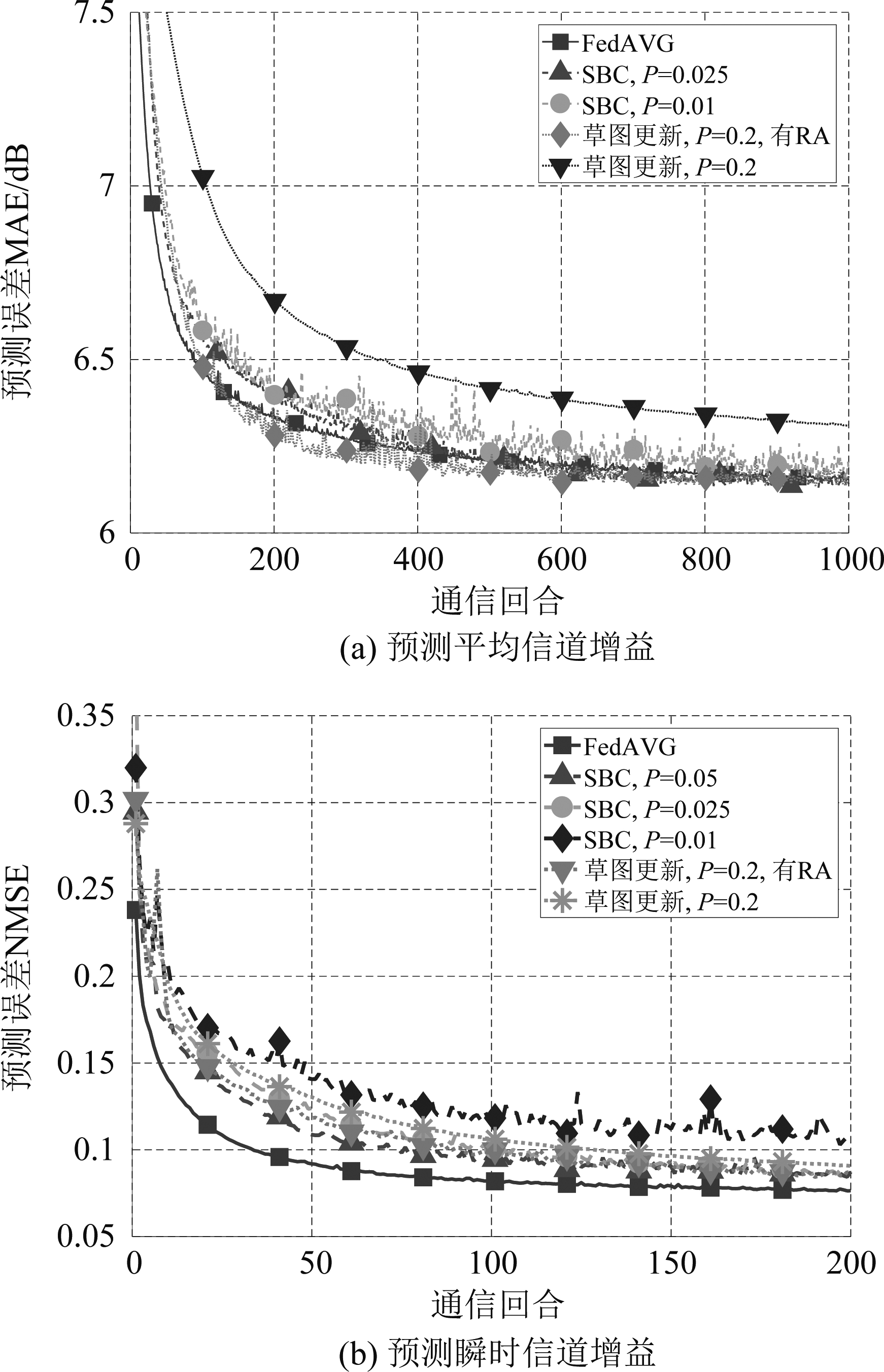
图2 不同联邦学习方法预测信道增益的性能
Fig.2 Performance of predicting channel gains with different federated learning algorithms
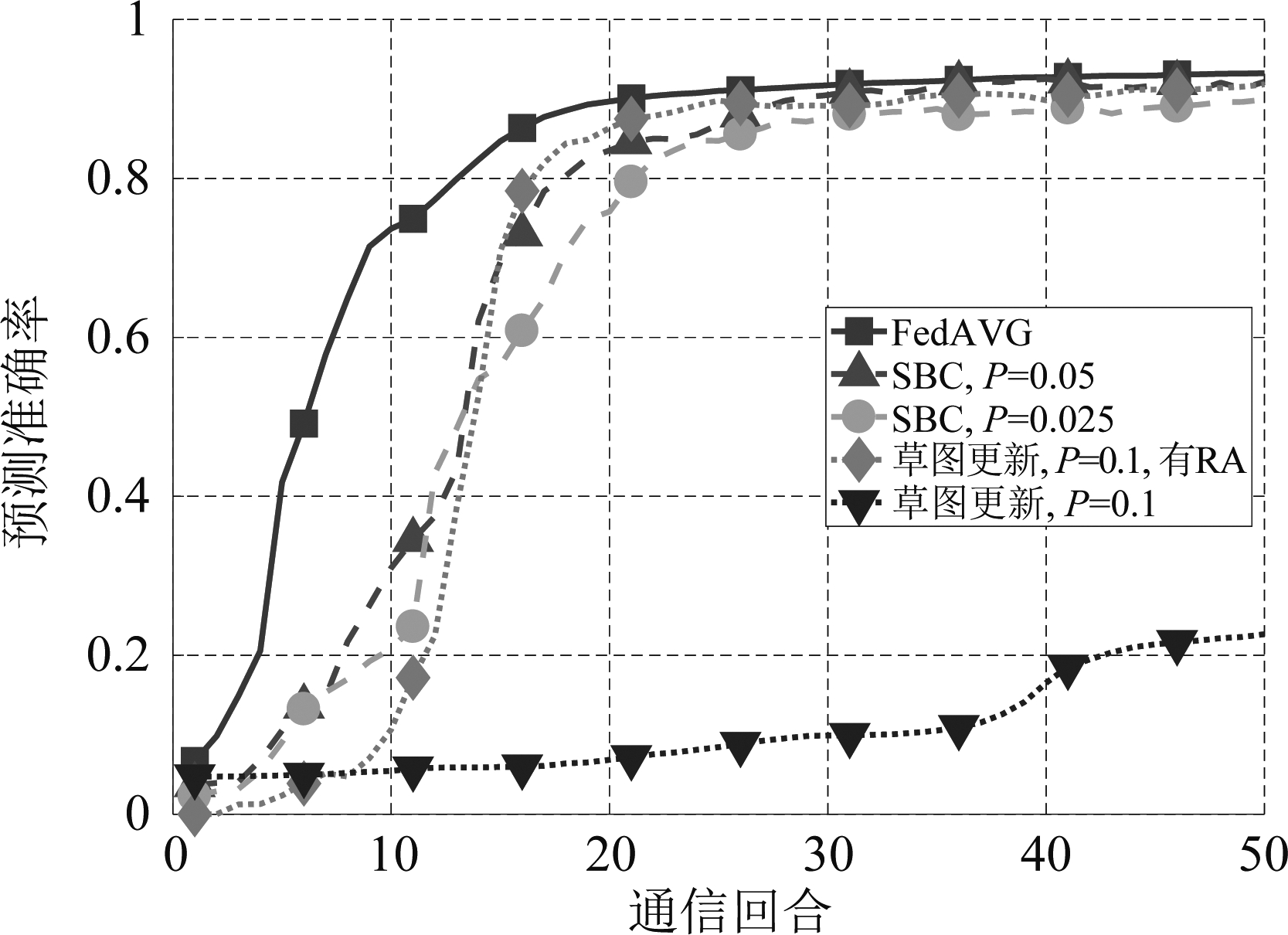
图3 不同联邦学习方法预测未来接入小区时的性能
Fig.3 Performance of predicting next cell with different federated learning algorithms
由图2(a)可见,对于预测平均信道增益,“SBC,P=0.025”的稳态预测误差几乎与联邦平均相同,P<0.025时稳态预测误差有所增加;“草图更新,P=0.2,有RA”的稳态预测误差与联邦平均非常接近。由图2(b)可见,对于预测瞬时信道增益,“SBC”在P≥0.025时稳态预测误差高于联邦平均,P<0.025时,预测误差明显增加;“草图更新,P=0.2,有RA” 的稳态预测准确率高于联邦平均。因此在后续的分析中,都在“SBC”中采用P=0.025,在“草图更新”中采用P=0.2。
由图3可见,对于预测未来接入小区,“SBC,P=0.05”的稳态预测准确率与联邦平均非常接近,P<0.05时准确率有所降低;“草图更新,P=0.1,有RA”的稳态预测准确率与联邦平均非常接近。因此后面都在“SBC”中采用P=0.05,在“草图更新”中采用P=0.1。
下面分析压缩算法中不同部分对压缩倍数的贡献。由于稀疏化、哥伦布编码和量化的贡献可直接进行计算(如对于当P=0.1时,SBC能把元素数减小10倍;由式(3)可得此时哥伦布编码所需平均比特数为5.7,相对于32位浮点数降低了5.6倍),所以只分析残差积累的贡献。图4和图5分别给出了是否积累残差时,预测三种信息时的训练收敛曲线;表2给出了不同压缩方法中是否积累残差时达到指定预测性能所需的通信回合数和上行数据量。由于当不使用残差积累时预测性能较差,故我们要求的指定预测性能较低。对于平均信道增益,指定预测性能为联邦平均预测误差的110%(MAE为6.76 dB以下);对于预测瞬时信道增益,指定预测性能为联邦平均预测误差的120%(即NMSE为9.28%以下);对于预测未来接入小区,指定预测性能为联邦平均预测准确率的90%(即准确率达到85.1%以上)。
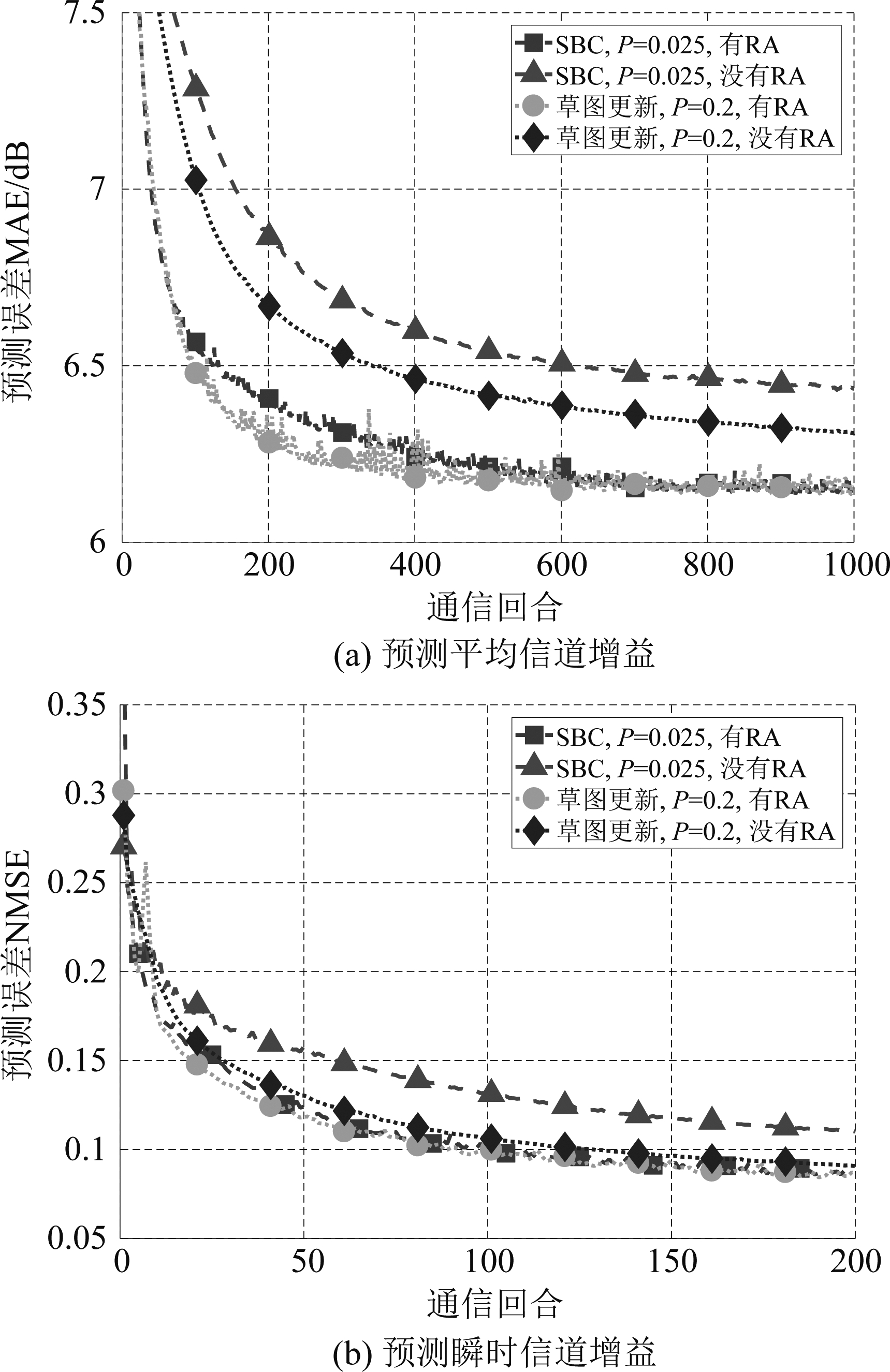
图4 残差积累对预测信道增益预测误差的影响
Fig.4 Impact of residual accumulation on predicting channel gains
由图4、图5和表2可见,残差积累对提升压缩算法性能十分重要。不论是SBC还是草图更新,使用残差积累后算法的预测性能更好,达到指定性能所需的通信回合越少,学习过程收敛所需的上行数据量越小。在预测平均信道增益时,残差积累可把SBC上行数据量降低4.2倍,把草图更新上行数据量降低2.6倍;在预测未来接入小区时,残差积累可把SBC上行数据量降低10倍,把草图更新上行数据量降低7倍;在预测瞬时信道增益时,不使用残差积累时,SBC无法达到指定性能。可见,与草图更新相比,积累残差后SBC预测性能提升更明显、压缩倍数更大。
表2 是否使用残差积累时所需的通信回合和总上行数据量
Tab.2 Impact of residual accumulation on communication rounds and uplink data
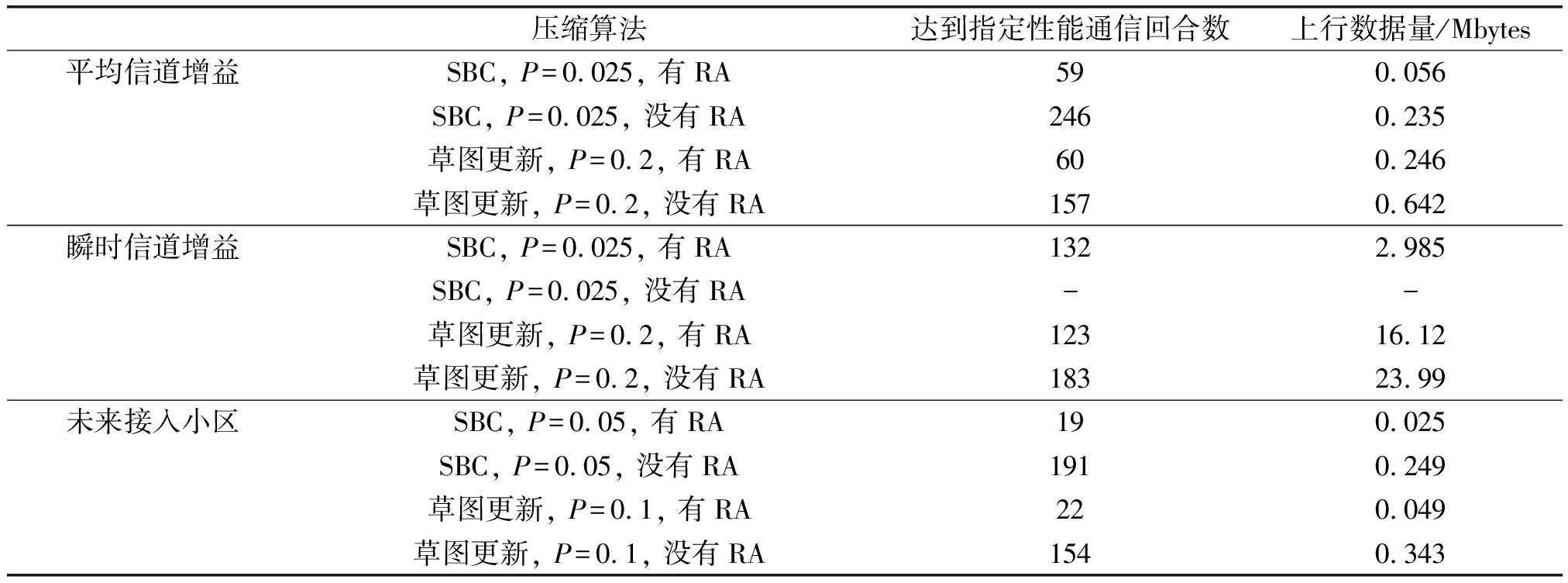
压缩算法达到指定性能通信回合数上行数据量/Mbytes平均信道增益SBC, P=0.025, 有RA590.056SBC, P=0.025, 没有RA2460.235草图更新, P=0.2, 有RA600.246草图更新, P=0.2, 没有RA1570.642瞬时信道增益SBC, P=0.025, 有RA1322.985SBC, P=0.025, 没有RA--草图更新, P=0.2, 有RA12316.12草图更新, P=0.2, 没有RA18323.99未来接入小区SBC, P=0.05, 有RA190.025SBC, P=0.05, 没有RA1910.249草图更新, P=0.1, 有RA220.049草图更新, P=0.1, 没有RA1540.343
注:-表示此方法无法达到指定性能。
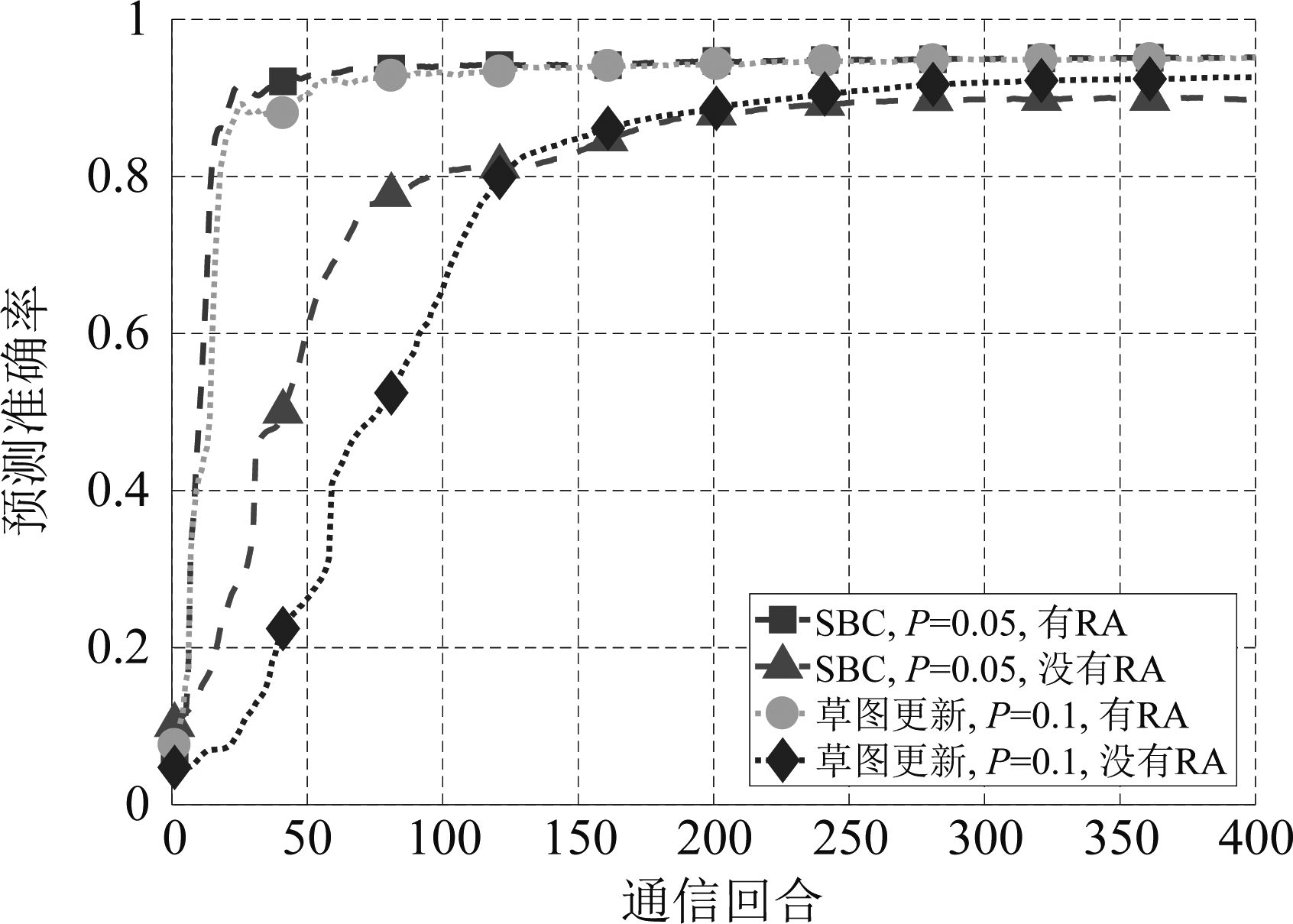
图5 残差积累对预测未来接入小区预测准确率的影响
Fig.5 Impact of residual accumulation on predicting the next cell
然而,由于移动用户参与训练的总时间较短且不一定能持续参与训练,因此可能无法一直积累残差。图6给出了预测平均信道增益时每回合随机选择部分用户参与联邦学习上传局部模型用户时的性能,其中C表示每回合参与训练的用户的比例。此时由于各用户不能每回合均与处理中心通信并进行残差积累,此前积累的残差可能过时。由图中可见,SBC的预测性能明显下降,训练过程中误差方差很大,且残差积累带来的性能增益减少。这意味着对于移动用户如果需要采用比草图更新压缩倍数更高的SBC,必须解决残差过时的问题。
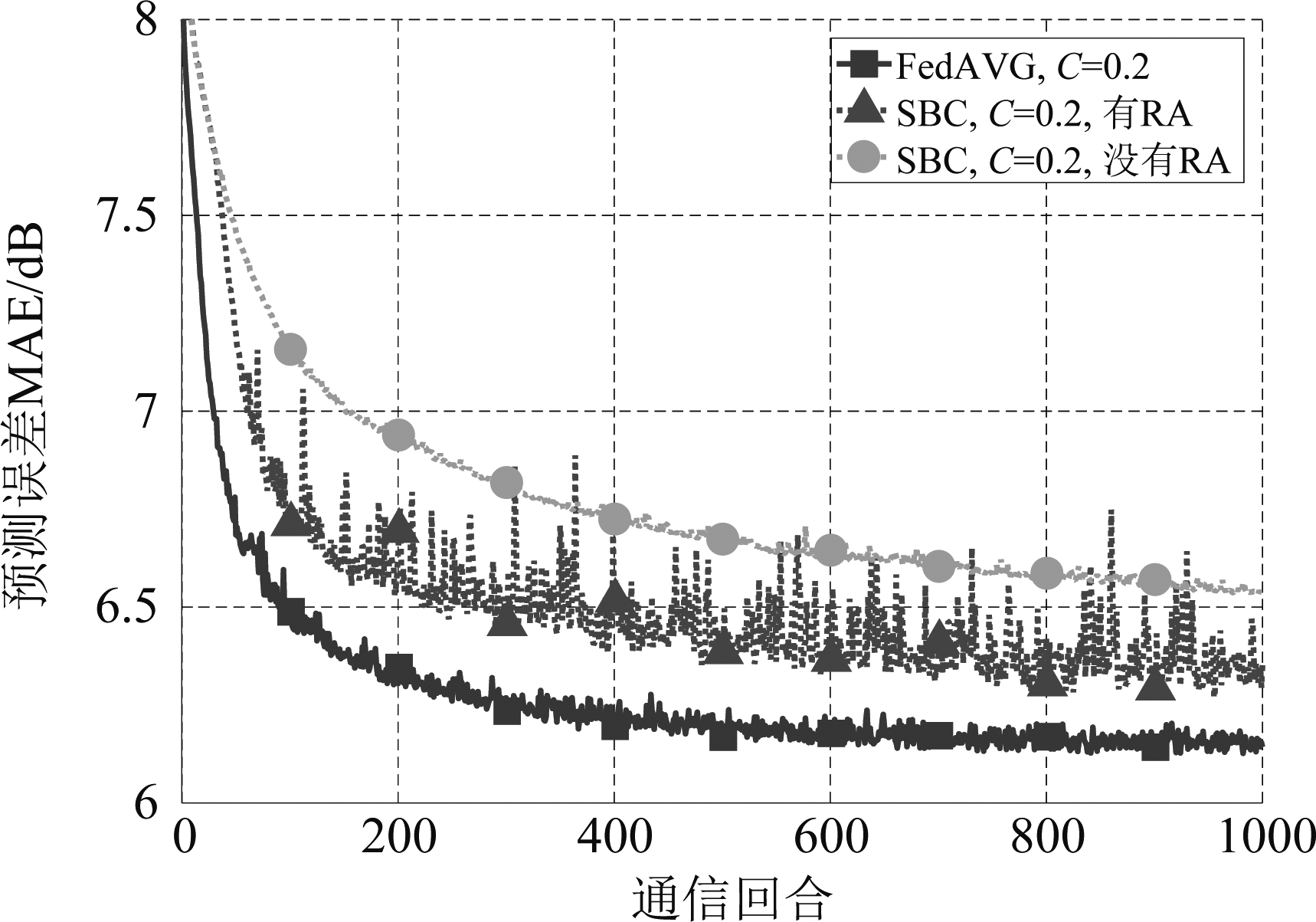
图6 用户随机部分接入时平均信道增益预测误差
Fig.6 MAE of predicting average channel gain when partial users participate federated learning
4.3 联邦学习与集中式学习上行数据量
为了降低集中式学习的上行数据量,我们对训练所用的数据集进行量化,因此压缩倍数指的是不同量化比特数相对于32位浮点数时的压缩倍数。
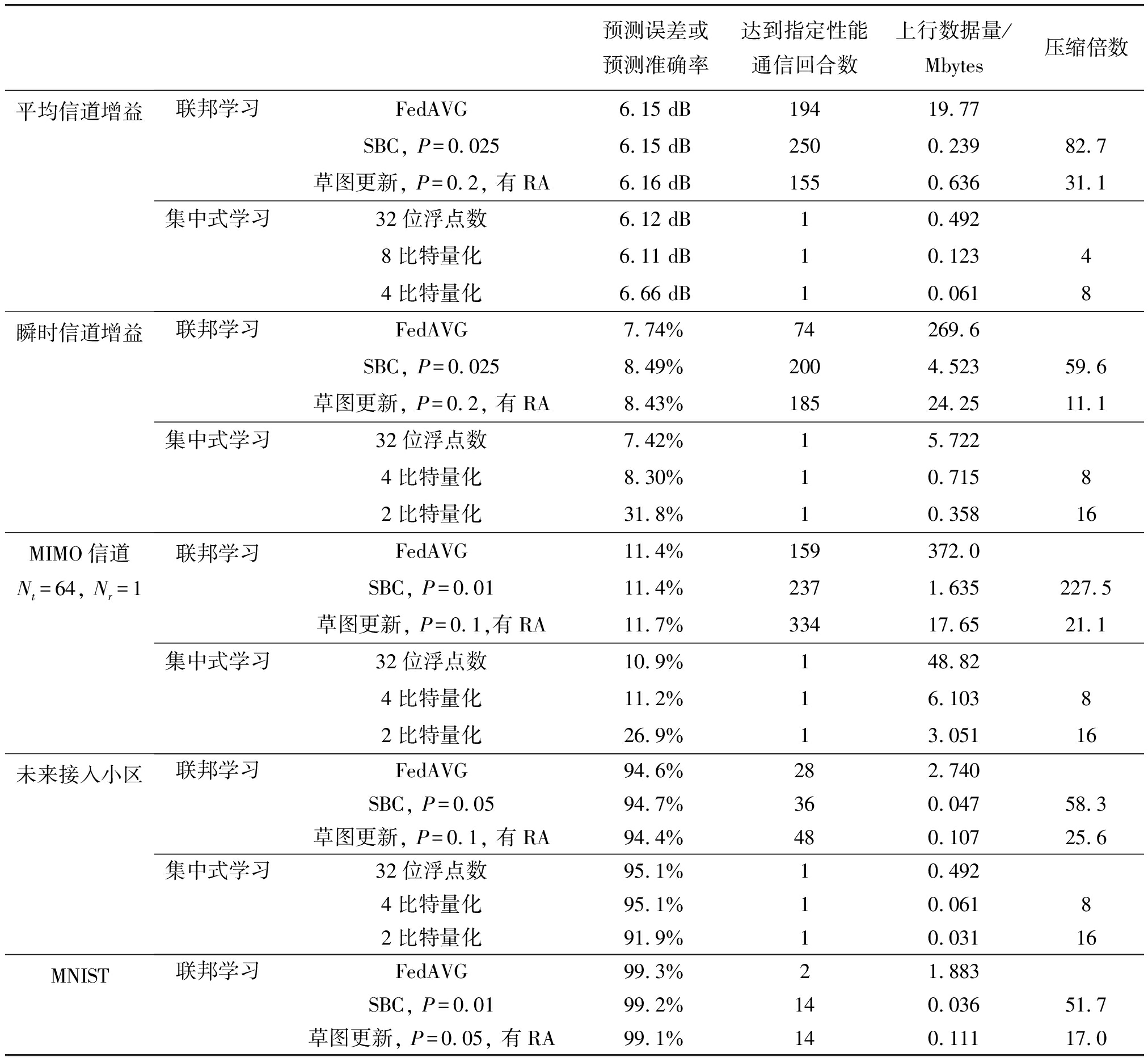
表3比较了不同方法在达到相同指定预测性能时所需的通信回合数和总上行数据量,其中对于联邦学习,压缩倍数指的是不同压缩方法相对于联邦平均的压缩倍数。为了观察对于无线通信任务不同算法的压缩倍数是否与经典机器学习问题有明显区别,我们也考虑一个公开的图像分类数据集MNIST。由于压缩方法对模型精度有一定影响,我们把指定预测性能规定为所有压缩方法都能达到的性能。在所列出的预测任务中,预测平均和瞬时信道是回归问题,采用预测误差来衡量预测性能;预测未来接入小区和MNIST手写数字识别为分类问题,采用预测准确率来衡量预测性能。对于平均信道增益预测和MIMO信道预测,指定预测误差为联邦平均性能的103%;对于未来接入小区预测和MNIST手写识别,指定预测准确率为联邦平均性能的97%(即未来接入小区预测准确率达到91.8%以上,MNIST预测准确率达到96.3%以上);由于瞬时信道增益预测时压缩后模型性能的降低较大,指定预测性能为联邦平均预测误差的110%(即预测误差达到8.51%以下)。
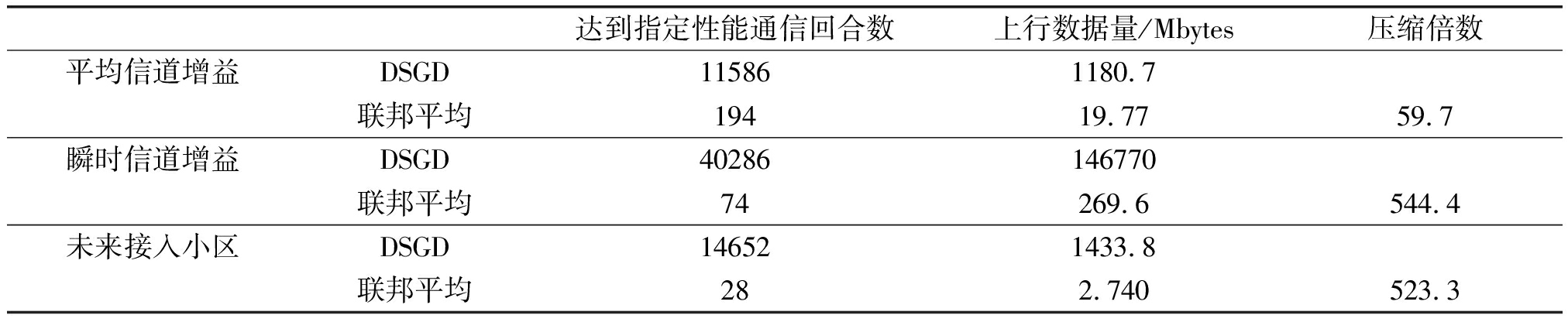
为了与现有文献中给出的压缩倍数相比较,表4给出了达到上述指定预测性能时,DSGD所需的通信回合数和上行数据量,以及联邦平均相对于DSGD的压缩倍数。把不同压缩方法相对于联邦平均的压缩倍数与联邦平均相对于DSGD的压缩倍数相乘,即可得到不同压缩方法相对于DSGD的压缩倍数。
由表3可见,无论是平均信道增益、瞬时信道增益、未来接入小区还是MNIST数据集,相对于联邦平均,SBC都能把总上行数据量压缩60倍左右,而草图更新压缩倍数仅为20倍左右。可见保留绝对值最大的模型更新矩阵元素的稀疏算法优于随机保留模型更新矩阵元素的稀疏算法。另外,相对于DSGD,SBC的压缩比更高,例如,对于平均信道增益预测问题,从表3和表4可见,SBC的压缩倍数可以高达近5000倍！然而,当与集中式学习相比时,联邦学习的通信开销却不容乐观。
表3 不同方法所需的通信回合数和总上行数据量
Tab.3 Communication round and uplink data of different compression algorithms
预测误差或预测准确率达到指定性能通信回合数上行数据量/Mbytes压缩倍数平均信道增益联邦学习FedAVG6.15 dB19419.77SBC, P=0.0256.15 dB2500.23982.7草图更新, P=0.2, 有RA6.16 dB1550.63631.1集中式学习32位浮点数6.12 dB10.4928比特量化6.11 dB10.12344比特量化6.66 dB10.0618瞬时信道增益联邦学习FedAVG7.74%74269.6SBC, P=0.0258.49%2004.52359.6草图更新, P=0.2, 有RA8.43%18524.2511.1集中式学习32位浮点数7.42%15.7224比特量化8.30%10.71582比特量化31.8%10.35816MIMO信道Nt=64, Nr=1联邦学习FedAVG11.4%159372.0SBC, P=0.0111.4%2371.635227.5草图更新, P=0.1,有RA11.7%33417.6521.1集中式学习32位浮点数10.9%148.824比特量化11.2%16.10382比特量化26.9%13.05116未来接入小区联邦学习FedAVG94.6%282.740SBC, P=0.0594.7%360.04758.3草图更新, P=0.1, 有RA94.4%480.10725.6集中式学习32位浮点数95.1%10.4924比特量化95.1%10.06182比特量化91.9%10.03116MNIST联邦学习FedAVG99.3%21.883SBC, P=0.0199.2%140.03651.7草图更新, P=0.05, 有RA99.1%140.11117.0
表4 DSGD所需的通信回合数和总上行数据量
Tab.4 Communication round and uplink data of DSGD
达到指定性能通信回合数上行数据量/Mbytes压缩倍数平均信道增益DSGD115861180.7联邦平均19419.7759.7瞬时信道增益DSGD40286146770联邦平均74269.6544.4未来接入小区DSGD146521433.8联邦平均282.740523.3
对于平均信道增益的预测,8比特量化时集中式学习的预测误差与32位量化时基本相同,当量化比特数低于8比特时预测误差明显增加。当对集中式学习所用的数据进行8比特量化时,上传训练数据的总数据量为0.123 Mbytes(预测误差6.11 dB);而采用SBC,P=0.025的联邦学习所需的总上行数据量为0.239 Mbytes(预测误差6.15 dB),为集中式学习的1.9倍。
对于瞬时信道增益的预测,4比特量化时集中式学习的预测误差与32位量化时的预测误差略有上升,当量化比特数低于4比特时预测误差明显增加。当对集中式学习所用的数据进行4比特量化时,上传训练数据的总数据量为0.715 Mbytes(预测误差8.30%);而采用SBC,P=0.025的联邦学习所需的总上行数据量为4.523 Mbytes(预测误差8.49%),是集中式学习的6.3倍。
对于MIMO信道的预测,当量化比特数低于4比特时集中式学习的预测误差明显增加。对集中式学习所用的数据进行4比特量化时,上传训练数据的总数据量为6.103 Mbytes(预测误差11.2%);而采用SBC,P=0.01的联邦学习所需的总上行数据量为1.635 Mbytes(预测误差11.4%),是集中式学习的26.8%。这是因为,仿真中所考虑的时变信道模型服从一阶马尔科夫过程,所以进行预测所需的神经网络规模不大。
对于未来接入小区的预测,4比特量化时集中式学习的预测误差与32位量化时基本相同。当对集中式学习所用的数据进行4比特量化时,上传训练数据的总数据量为0.061 Mbytes(预测准确率95.1%);而采用SBC,P=0.05的联邦学习所需的总上行数据量为0.047 Mbytes(预测准确率94.7%),是集中式学习的77%。
可见,对于所考虑的几个无线任务,虽然联邦学习经过SBC压缩后所需的上行数据量已经降低了很多,但仍然可能高于集中式学习。
5 结论
本文针对无线信道预测任务,研究了联邦学习的通信效率是否高于集中式学习的问题。我们考虑平均信道增益预测、瞬时信道增益预测、信道矩阵预测和下一个接入小区预测的问题,把采用典型压缩算法后联邦学习在达到期望预测性能时所需的总上行数据量与集中式学习进行了比较。分析结果表明,尽管稀疏二元压缩等算法能把上行数据量相对于DSGD降低将近5000倍,压缩后联邦学习的上行数据量仍可能大于集中式学习;对于信道预测问题,比较的结果与信道模型有关。另外,残差积累对压缩算法的性能影响很大,而由于移动用户难以保证每个轮次都参加分布式训练,存在残差过时的问题,导致稀疏二元压缩算法的性能下降。如果进一步考虑集中式训练所需的数据集本身也可以进行比量化更高效的压缩(例如估计或预测信道向量,信道本身由于具有空间相关性而可被压缩),则联邦学习的上行总通信开销更会高于集中式学习。可见,如何有效地融合几类降低联邦学习所需要总数据量的方法从而进一步大幅度降低联邦学习的通信开销依然是亟待解决的问题。
[1] JIANG Wei, SCHOTTEN H D.A deep learning method to predict fading channel in multi-antenna systems[C]∥2020 IEEE 91st Vehicular Technology Conference(VTC2020-Spring).Antwerp, Belgium.IEEE, 2020: 1-5.
[2] SUN Haoran, CHEN Xiangyi, SHI Qingjiang, et al.Learning to optimize: Training deep neural networks for wireless resource management[C]∥2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications(SPAWC).Sapporo, Japan.IEEE, 2017: 1-6.
[3] LIU Yan, JIANG Zhiyuan, ZHANG Shunqing, et al.Deep reinforcement learning-based beam tracking for low-latency services in vehicular networks[C]∥ICC 2020-2020 IEEE International Conference on Communications(ICC).Dublin, Ireland.IEEE, 2020: 1-7.
[4] YIN Haifan, WANG Haiquan, LIU Yingzhuang, et al.Addressing the curse of mobility in massive MIMO with prony-based angular-delay domain channel predictions[J].IEEE Journal on Selected Areas in Communications, 2020, 38(12): 2903-2917.
[5] YAO Chuting, YANG Chenyang, XIONG Zixiang.Energy-saving predictive resource planning and allocation[J].IEEE Transactions on Communications, 2016, 64(12): 5078-5095.
[6] LEE C, CHO H, SONG S, et al.Prediction-based conditional handover for 5G mm-wave networks: A deep-learning approach[J].IEEE Vehicular Technology Magazine, 2020, 15(1): 54-62.
[7] MCMAHAN H B, MOORE E, RAMAGE D, et al.Communication-efficient learning of deep networks from decentralized data[C]∥International Conference on Artificial Intelligence and Statistics, 2017.
[8] NIKNAM S, DHILLON H S, REED J H.Federated learning for wireless communications: Motivation, opportunities, and challenges[J].IEEE Communications Magazine, 2020, 58(6): 46-51.
[9] HOSSEINALIPOUR S, BRINTON C G, AGGARWAL V, et al.From federated to fog learning: Distributed machine learning over heterogeneous wireless networks[J].IEEE Communications Magazine, 2020, 58(12): 41-47.
[10] ELBIR A M, COLERI S.Federated learning for channel estimation in conventional and IRS-assisted massive MIMO[EB/OL].2020.https:∥arxiv.org/pdf/2008.10846.pdf.
[11] SATTLER F, WIEDEMANN S, MÜLLER K R, et al.Sparse binary compression: Towards distributed deep learning with minimal communication[C]∥2019 International Joint Conference on Neural Networks(IJCNN).Budapest, Hungary.IEEE, 2019: 1-8.
[12] 刘婷婷, 杨晨阳, 索士强, 等.无线通信中的边缘智能[J].信号处理, 2020, 36(11): 1789-1803.
LIU Tingting, YANG Chenyang, SUO Shiqiang, et al.Edge intelligence for wireless communication[J].Journal of Signal Processing, 2020, 36(11): 1789-1803.(in Chinese)
[13] RIBERO M, VIKALO H.Communication-Efficient Federated Learning via Optimal Client Sampling[EB/OL].2020.https:∥arxiv.org/pdf/2007.15197.pdf.
[14] ZHU Guangxu, WANG Yong, HUANG Kaibin.Broadband analog aggregation for low-latency federated edge learning[J].IEEE Transactions on Wireless Communications, 2020, 19(1): 491-506.
[15] 
J, MCMAHAN H B, YU F X, et al.Federated learning: Strategies for improving communication efficiency[EB/OL].2016.https:∥arxiv.org/pdf/1610.05492.pdf.
[16] CALDAS S, 
J, MCMAHAN H B, et al.Expanding the reach of federated learning by reducing client resource requirements[EB/OL].2018.https:∥arxiv.org/pdf/1812.07210.pdf.
[17] SATTLER F, WIEDEMANN S, MÜLLER K R, et al.Robust and communication-efficient federated learning from non-i.i.d.data[J].IEEE Transactions on Neural Networks and Learning Systems,2019,31(9):3400-3413.
[18] XU Jinjin, DU Wenli, JIN Yaochu, et al.Ternary compression for communication-efficient federated learning[J].IEEE Transactions on Neural Networks and Learning Systems, 2020, PP(99): 1-15.
[19] ZHENG Sihui, SHEN Cong, CHEN Xiang.Design and analysis of uplink and downlink communications for federated learning[J].IEEE Journal on Selected Areas in Communications, 2020, PP(99): 1.
[20] GUO Jia, YANG Chenyang, CHIH-LIN I.Exploiting future radio resources with end-to-end prediction by deep learning[J].IEEE Access, 2018, 6: 75729-75747.
[21] ZHENG Y R, XIAO Chengshan.Improved models for the generation of multiple uncorrelated Rayleigh fading waveforms[J].IEEE Communications Letters, 2002, 6(6): 256-258.
[22] VA V, VIKALO H, HEATH R W.Beam tracking for mobile millimeter wave communication systems[C]∥2016 IEEE Global Conference on Signal and Information Processing(GlobalSIP).Washington, DC, USA.IEEE, 2016: 743-747.
[23] LECUN Y.The MNIST database of handwritten digits[EB/OL].http:∥yann.lecun.com/exdb/mnist/, 1998.
[24] SUN Dechun, LIU Zujun, MA Shuai, et al.Channel prediction using IAA-based spectral estimation in precoded TDD-MIMO systems[J].IEEE Communications Letters, 2013, 17(4): 701-704.
