1 引言
组网雷达指由多个被统一控制的雷达节点组成的雷达系统。由于其观测构型的特殊性,组网雷达可以充分利用目标多角度回波的空间分集,借此提升系统整体的检测与跟踪性能[1-2]。另一方面,组网雷达远超单基地雷达孔径的基线长度为干扰抑制提供了更多的可能[3]。当压制式干扰源和目标位于单基地雷达的相同波瓣时,自适应波束会同时抑制目标和干扰能量,进而导致目标无法被有效检测。一些文献[4-6]利用组网雷达多角度观测中目标散射系数的差异实现干扰信号与目标回波的分离,但其未考虑干扰源与目标的运动,也未能充分利用目标回波的稀疏特性。
为了更好地解决组网雷达对运动辐射源的抑制问题,本文提出了一种基于干扰延时、多普勒二维对齐的自适应干扰抑制算法。该算法充分利用了目标回波在距离多普勒平面内的稀疏特性,实现了对辐射源信号的有效抑制。本文剩余内容结构如下:第2小节主要给出了单脉冲与多脉冲场景下的信号模型。其后,于第3小节详细介绍了所提抑制算法的处理流程。第4小节对一典型观测场景进行了仿真分析,验证了所提算法的有效性。最后,第5小节对全文进行总结。
2 信号模型
2.1 单脉冲信号模型
不失一般性的,本文仅对一发多收(Single Input Multiple Outputs, SIMO)构型下的组网雷达进行建模(多发多收网络可以用多个SIMO网络等效)。如图1所示,假设组网雷达包含K个分别位于Rk,k=1,…,K的接收节点,以及一个位于T的发射节点。考虑到大基线导致的多角度目标回波起伏,本文假设一个散射特性服从Swelling I模型的复杂目标位于各收发节点波束的共同照射区域。该目标散射相位在[0，2π)内服从均匀分布，其位置记为X。经过推导,各个节点接收到的目标回波可以用下式表示:
图1 单脉冲场景下组网雷达观测构型示意图
Fig.1 Topology diagram of radar network interfered by a single point radiation source with one pulse
(1)
其中τk(X)=τt(X)+τrk(X)表示接收节点k采集的回波对应的传播延迟。fc代表了整个系统的载频。ηk为目标在对应通道内的散射系数,其服从圆周对称的零均值复高斯分布[1]。
假设波束覆盖区域内包含一辐射源,坐标记为Y。该辐射源全向发射伪随机噪声信号。为确保干扰信号的相关特性,各个接收节点前端特性以及传播通道特性的差异均被忽略。在该假设的基础上,采集到的干扰信号即:
gk(t)=|βk|g(t-τrk(Y))exp(-j2πfcτrk(Y))
(2)
上式中g(t)表示干扰信号的复包络,|βk|表示干扰信号的幅度。τrk(Y)表示辐射源和接收节点k之间的单程传播延迟。
基于先前的分析,各通道内的接收信号包含了目标回波,辐射源干扰以及接收机噪声,即:
ek(t)=sk(t)+gk(t)+nk(t)
(3)
为了简化分析，上式中目标回波分量sk(t)与干扰分量gk(t)均按噪声分量nk(t)的功率进行归一化。
2.2 多脉冲信号模型
本小节将上一小节建立的单脉冲信号模型推广到多脉冲场景。如图2所示,多脉冲模型和单脉冲模型的核心区别在于对目标与辐射源运动的建模。假设各脉冲内目标与辐射源的运动均可以用“走停模型”近似,且一个相参积累周期内发射节点共发射M个脉冲,则可定义目标与辐射源的位置矢量为:
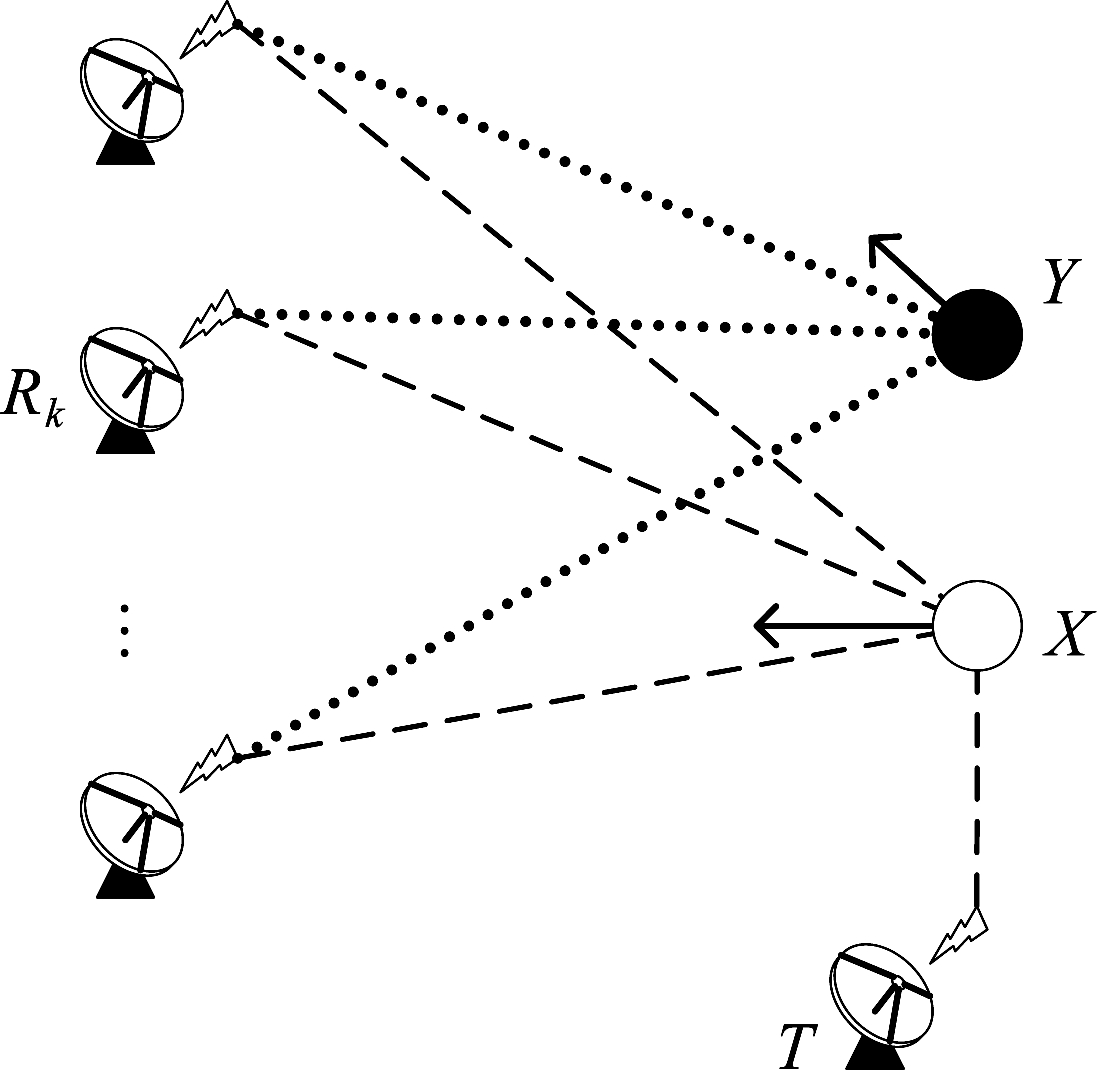
图2 多脉冲场景下组网雷达观测构型示意图
Fig.2 Topology diagram of radar network interfered by a single point radiation source with multiple pulses
(4)
本文假设目标起伏特性满足Swelling-I模型,即同一个接收通道内目标散射特性在各脉冲中均保持一致。另一方面,由于相参积累时间内辐射源与各接收节点的相对构型变化较小,其导致的干扰信号相对功率变化可以忽略。此时,多脉冲场景下的组网雷达回波模型如下:
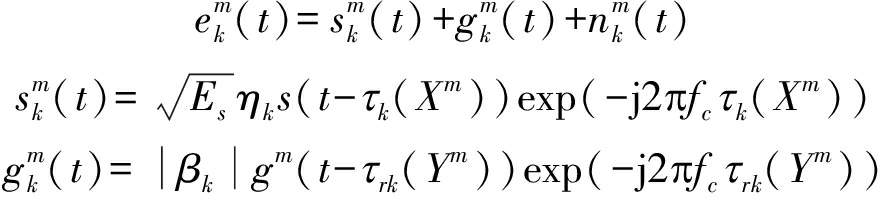
(5)
上式中，上标m代表了脉冲编号。值得注意的是，各脉冲内干扰信号的复包络gm(t)也存在差异。
3 基于延时多普勒对齐的抑制算法
当目标与辐射源位于单基地雷达不同波瓣时,传统自适应波束形成方法可以在辐射源方向构造一个波束零陷,以抑制干扰能量,进而带来显著的信干噪比(Signal to Interference and Noise Ratio, SINR)改善。但当辐射源位于目标所在波瓣时,由于目标信号和干扰会被同时抑制,该处理方法无法有效改善SINR,并会导致旁瓣抬升,波束形状畸变以及波峰位置偏移等问题[7-10]。这些问题对后续的信号处理造成了严重的影响。
在本文中,组网雷达的每个接收节点都被视作传统单基地相控阵雷达的一个阵元。由于辐射源信号自身的强相关特性,各节点接收到的干扰信号可以通过相参对消实现抑制。不同于传统相参分布式雷达利用长基线带来的角度高分辨实现干扰抑制,本文利用组网雷达中目标多角度回波在延迟、多普勒乃至散射特性上的差异上实现目标与干扰的分离。
本文所提算法主要包含以下步骤,各项处理将在后续进行详细介绍:
(1)干扰包络延迟对齐;
(2)干扰多普勒历程对齐;
(3)多脉冲积累(Moving Target Detection, MTD);
(4)基于修正加权平均的干扰抑制;
(5)对齐复原。
3.1 干扰包络延迟对齐
为了实现干扰信号的相参相消,不同通道内干扰信号包络延迟必须被消除。为此各通道的回波信号需要进行时域平移以对齐干扰包络。将接收通道1作为参考通道,则各通道所需延迟对齐矢量即:
(6)
则对齐后各通道的回波信号形如下式:
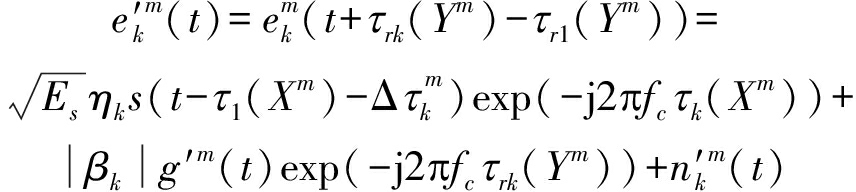
(7)
上式中，
即第m个脉冲内，目标回波在对齐后的残余延迟偏差，其表达式为：
(8)
干扰包络对齐所需的时域平移量可以通过对各通道内接收信号的互相关得到。为了实现高效的高精度相对延迟估计,本文使用一种延迟整数、小数部分分别估计的两步估计方法:首先通过FFT对离散互相关进行快速计算,得到整数采样偏移,接着利用Chirp-Z变换对峰值附近的互相关函数进行局部升采样,进而得到精确的相对延迟估计。为了提高估计精度,可以对各组互相关进行冗余求解,并利用最小二乘法得到最终的估计结果。
3.2 干扰多普勒历程对齐
多普勒历程对齐是保证多脉冲积累后各个多普勒通道内干扰信号相关的关键步骤。为了确保不同节点采集的干扰信号在MTD处理后具备相同的复包络,各通道内干扰信号脉冲间的相位变化历程必须被统一。和延迟对齐类似,以通道1为参考通道,则各个通道所需的多普勒对齐矢量即:
φm=-2πfcτm
(9)
图3 局部升采样示意图
Fig.3 Diagram of local over sampling
对齐后的信号为:
(10)
可以发现,经过两维对齐后,各通道内的干扰分量具有统一的形式,仅幅度存在差异。和时域对齐类似,各个通道内的相位调整量也可以通过互相关峰值处相位得到,其精度通过局部升采样保证。
3.3 多脉冲MTD处理
和文献[6]不同的是,本文将多脉冲回波积累提前至干扰抑制前,以充分利用目标回波多普勒的空间分集。可以发现,式(10)中各通道内目标延迟的残余对齐偏差
在不同脉冲内存在差异。该差异可以等效为单基地雷达中的距离走动。将系统有效带宽记为B，则当积累时间内
成立时，包络走动对多普勒处理的影响可以忽略:
(11)
当积累时间较短时,目标与辐射源的高次运动同样可以忽略。此时,目标与干扰源的传播延迟可以使用如下式子近似:
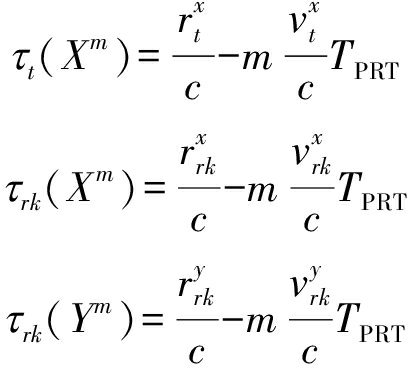
(12)
上式中TPRT即脉冲重复周期,进而有:
(13)
故而,在干扰延迟-多普勒均被对齐后,目标的多普勒频率即:
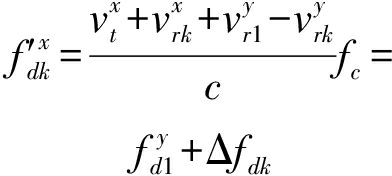
(14)
上式中，
即目标与辐射源在各个接收通道内对应的多普勒频差，
即对齐基准通道内干扰分量的多普勒频率。为了简化分析,本文使用单位冲击函数近似脉冲压缩与多脉冲MTD处理后目标回波信号的2维包络,即:
(15)
其中，αk包含了目标回波的初始多普勒相位，g″(t, f)即经过脉冲压缩和多脉冲积累的干扰二维包络，
即处理后的干扰分量。
3.4 干扰复包络估计与抑制
为了实现干扰信号的有效抑制,本文将干扰空间内的回波信号直接去除。由于先前的多普勒对齐处理,可以认为各个通道内的干扰分量只存在幅度差异。此时,各多普勒通道内的干扰复包络可以按干扰分量的相对幅度进行加权平均得到。该复包络估计可用于重构各通道内的干扰分量,进而实现干扰对消。与文献[6]类似,该处理会导致目标能量泄露,并在其余通道内生成虚假目标。
基于直接加权求和的干扰分量复包络的估计结果可以用下式表示:
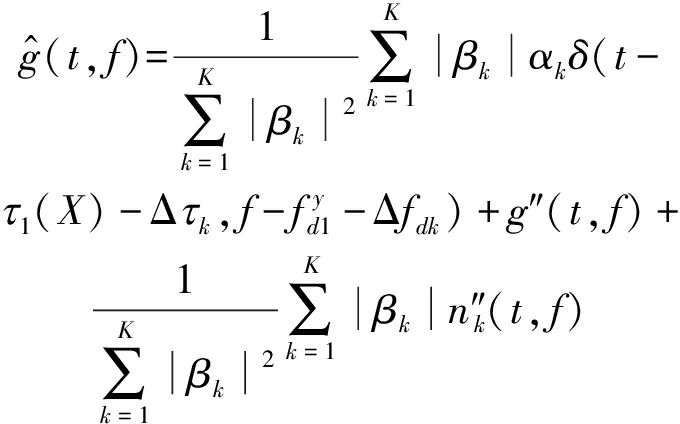
(16)
上式中使用的幅度加权因子可以通过第一步中局部升采样后各互相关函数的峰值点幅度获得。将上述估计直接应用于干扰消除,可以发现,在忽略干扰分量的对齐误差以及相对幅度估计误差的情况下,各通道内的干扰分量被完全去除。残余的噪声与目标回波分别为:
(17)
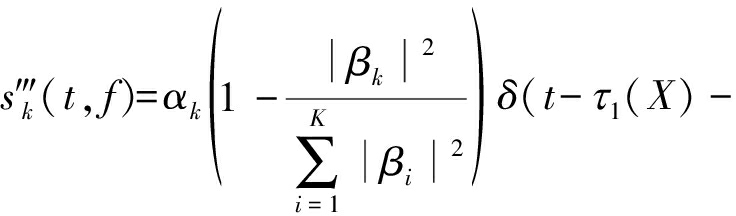
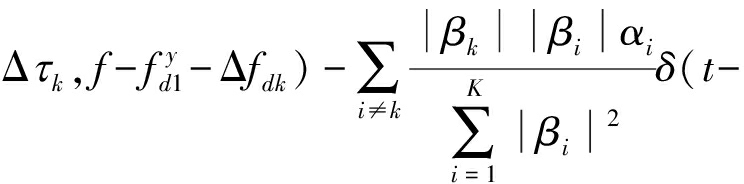
(18)
(18)中的目标回波内包含总共K个冲击函数分量，当MTPRT|Δfdi-Δfdj|≪1,且B|Δτi-Δτj|≪1时，各冲击函数位置近似重合，此时目标回波分量可以进一步简化为:
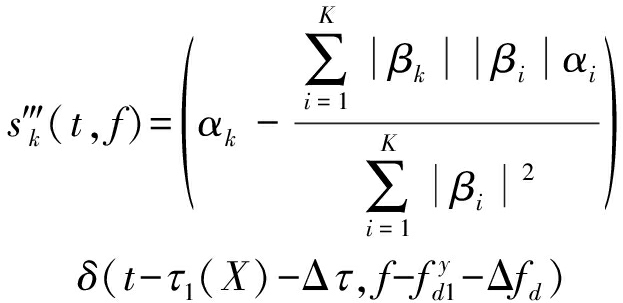
(19)
当积累时间内目标和辐射源具有一致航迹时，上式严格成立。此时目标散射特性的空间分集导致各通道内αk的相位随机分布，故而上式中目标分量不会相消，其能量被有效保留。而当目标和辐射源的航迹不完全重叠时，其相对运动的多角度投影差异导致各通道内的延迟偏差Δτk和多普勒偏差Δfdk并不相同。此时，各通道对应的目标分量在距离多普勒平面内相互分离，其中距离维和多普勒维内的回波分离程度分别由目标和辐射源的相对位置矢量以及相对速度矢量决定。当任意维度的分离程度超过对应的分辨率时，式(19)中的近似不再成立，目标回波在各通道内位于不同的距离多普勒单元，相参相消被有效避免，目标能量得以保留。但由于能量泄露的存在，此时处理后的回波中包含虚假目标。式(18)中的第一、第二项，分别对应真实目标分量以及虚假目标分量。
为了减少目标能量泄露以抑制虚假目标，本文对干扰复包络的估计进行修正。不难发现，基于加权求和的复包络估计仅在高斯误差下最优，当某通道内数据存在目标时，误差分布不再满足高斯模型。当总接收通道数K>2时，本文通过将通道κ排除的方式解决目标能量泄露问题。其中κ通过下式求出：
(20)
上式以单通道干扰复包络估计以及多通道融合估计的偏差为判决依据,将偏差最大的通道直接去除。该处理充分利用了脉冲压缩和多脉冲积累后目标回波较高的SNR以及其在距离多普勒平面内良好的稀疏特性。后续仿真对该修正的有效性进行了验证。
3.5 对齐复原
观察式(15)可以发现,对齐后目标时域延迟与多普勒频率均发生变化。对于后续的数据融合过程,这些变化会导致目标拓扑失配,进而导致检测失效。因此处理中需要恢复目标原始的延迟多普勒特性。
由于MTD处理与干扰抑制均未引入额外的时频域平移,仅需在处理中存储二维对齐使用的参数,并对距离多普勒平面的坐标原点进行修正即可完成对齐复原。如需要抑制后的原始信号,也可将对消后信号还原为逐脉冲形式,并使用共轭系数恢复对齐造成的平移。
4 算法仿真验证
本小节对所提算法进行仿真验证。假设场景中存在一个由5个雷达节点组成的线状雷达网络,各个节点等间距均匀部署。系统总基线长度为200 km,基线方向如图中虚线所示。中央节点为收发节点,其余节点仅负责接收。如图4所示,场景中放置4个目标和1个辐射源。不同目标分别对应一种2维对齐偏差残余情况,各目标的散射截面积(Radar Cross Section, RCS)均为1 m2。该四个目标的初始位置构成一个正方形(目标1,3连线与组网雷达基线平行),辐射源位于正方形中央。各目标与辐射源的初始距离均为5 km。辐射源位于中央节点正前方300 km处。
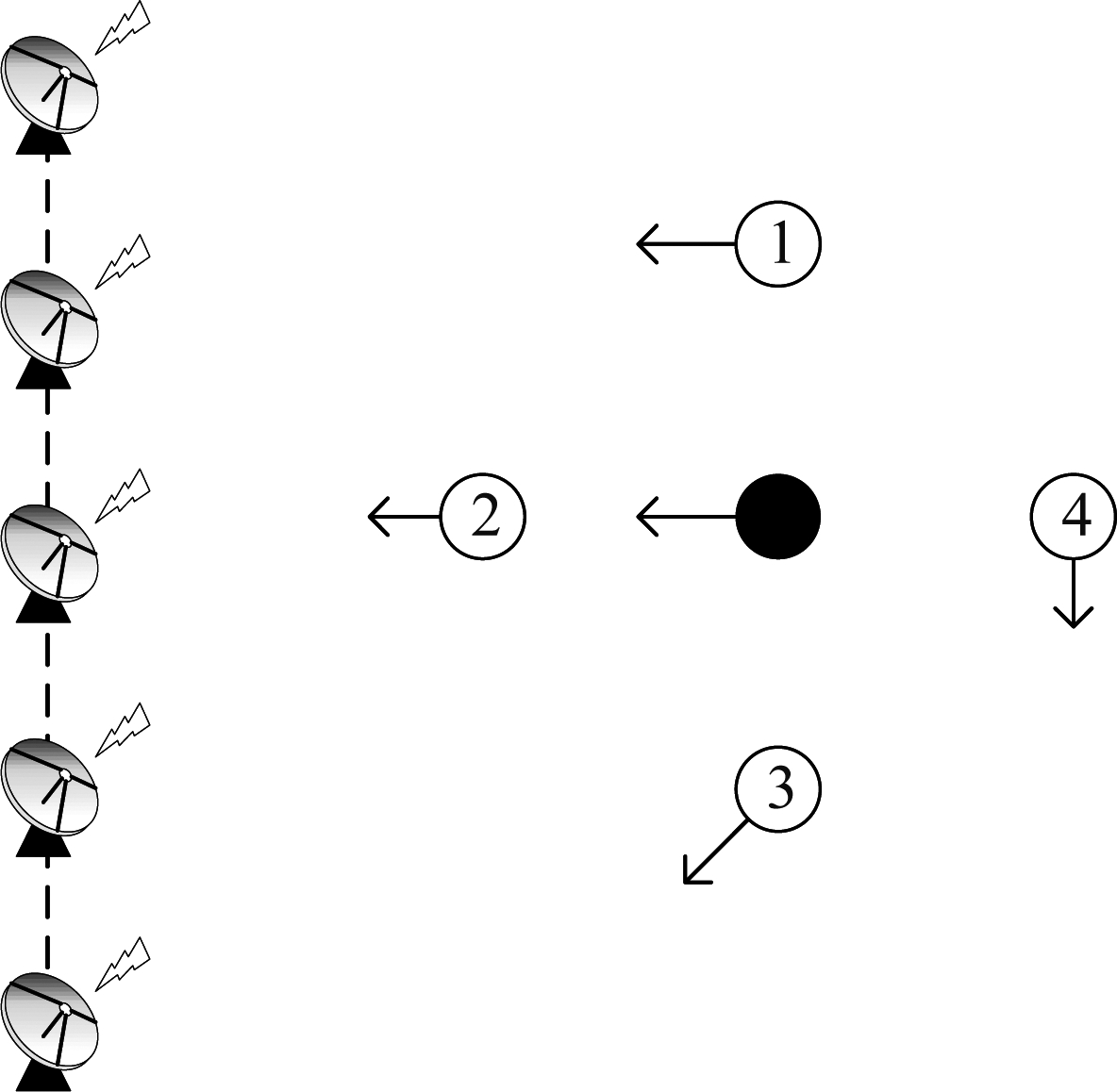
图4 仿真场景示意图
Fig.4 Topology diagram of simulation
辐射源与4个目标的速度均为100 km/h,其速度矢量与基线的夹角如表1所示。
表1 运动方向与基线夹角
Tab.1 The angle between the baseline and the movement direction
运动物体夹角/(°)目标190目标290目标345目标40辐射源90
仿真中其余参数如表2所示。
表2 仿真参数
Tab.2 Simulation parameter
参数参数值载频/MHz440信号带宽/MHz1采样率/MHz2平均信噪比/dB19平均信干比/dB-30
图5即使用加权平均完成干扰抑制后各接收通道内MTD的输出结果。其中,由于目标1、2和辐射源的速度矢量完全一致,其回波在干扰对齐后满足MTPRT|Δfdi-Δfdj|≪1,即多普勒重叠。此外,由于在仿真构型下,目标和辐射源之间平行基线方向的位置偏差更容易导致目标包络的延迟分离,目标1在对消后存在虚假目标,且各个虚假目标沿着距离维分布,而目标2满足式(19)的假设,不存在虚假目标。相比之下,由于目标3、4和辐射源之间存在速度矢量差异,其回波的多普勒分离不可忽略,两者在对消后均产生虚假目标,其中目标4的虚假目标沿着多普勒维分布。图5中各目标对消后的能量分布已经使用不同颜色的椭圆标出,其中椭圆的长轴方向即虚假目标的分布方向。
图5 抑制后各通道MTD输出(加权平均)
Fig.5 The outputs of adaptive suppression with weighted mean
为了验证式(20)中的筛选方法对虚假目标抑制的效果,采用修正加权平均对相同的仿真数据进行处理,结果如图6所示。在进行数据筛选以及通道排除后,目标1、3、4附近的虚假目标被有效抑制,而目标2在各通道内的回波分析虽然和图5存在差异,但其能量仍被有效保留。
图6 抑制后各通道MTD输出(修正加权平均)
Fig.6 The outputs of adaptive suppression with weighted mean after outlier detection
5 结论
为了实现组网雷达对运动单点源干扰的有效抑制,本文提出了一种基于干扰延迟、多普勒二维对齐的自适应抑制算法,并通过对典型场景的仿真分析验证了其有效性。从仿真结果可以看出,对于干扰对齐后包络相互分离的目标,所提算法利用其延迟多普勒差异实现目标与干扰的分离;对于干扰对齐后包络重叠的目标,所提算法也可以利用目标散射特性的空间分集实现有效的SINR改善。该算法主要问题为无法直接应用于多辐射源的场景,以及对干扰信号的传输特性的一致性有较高要求,这些需要进一步的研究。
[1] HAIMOVICH A M, BLUM R S, CIMINI L J.MIMO radar with widely separated antennas[J].IEEE Signal Processing Magazine, 2008, 25(1): 116-129
[2] NIU Ruixin, BLUM R S, VARSHNEY P K, et al.Target localization and tracking in noncoherent multiple-input multiple-output radar systems[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1466-1489.
[3] DELIGIANNIS A, ROSSETTI G, PANOUI A, et al.Power allocation game between a radar network and multiple jammers[C]∥2016 IEEE Radar Conference(RadarConf).Philadelphia, PA, USA.IEEE, 2016: 1-5.
[4] YANG Yang, SU Hongtao, HUANG Junsheng, et al.Duplicate false targets discrimination for mainlobe jamming cancellation in multistatic radar[C]∥2017 IEEE International Conference on Signal Processing, Communications and Computing(ICSPCC).Xiamen,China.IEEE,2017: 1-5.
[5] 宁立跃, 杨小鹏.多基地极化雷达主瓣干扰抑制算法[J].信号处理, 2017, 33(12): 1571-1577.
NING Liyue, YANG Xiaopeng.Multi-base polarization radar main-lobe interference suppression algorithm[J].Journal of Signal Processing, 2017, 33(12): 1571-1577.(in Chinese)
[6] MIAO Yingjie, LIU Feifeng, TIAN Lun, et al.Adaptive signal suppression based on modified PCA for a single-point radiation source in radar networks[J].The Journal of Engineering, 2019, 2019(21): 7538-7541.
[7] 张宗傲.阵列雷达自适应主瓣干扰抑制算法研究[D].北京: 北京理工大学, 2015.
ZHANG Zong’ao.Research on adaptive mainlobe interference suppression algorithm of array radar[D].Beijing: Beijing Institute of Technology, 2015.(in Chinese)
[8] HOROWITZ L L, BLATT H, BRODSKY W G, et al.Controlling adaptive antenna arrays with the sample matrix inversion algorithm[J].IEEE Transactions on Aerospace and Electronic Systems, 1979, AES-15(6): 840-848.
[9] LORENZ R G, BOYD S P.Robust minimum variance beamforming[J].IEEE Transactions on Signal Processing, 2005, 53(5): 1684-1696.
[10] HASSANIEN A, VOROBYOV S A, WONG K M.Robust adaptive beamforming using sequential quadratic programming: An iterative solution to the mismatch problem[J].IEEE Signal Processing Letters, 2008, 15: 733-736.
