1 引言
多声源分离是一种从麦克风录制信号中获取场景中的各声源信息[1-2]的技术,目前广泛用于虚拟现实、增强现实等领域,是近年来音频信号处理领域最热门研究课题之一。
根据麦克风数与声源数的比值(记作r),多声源分离可分为: 超定分离(r>1)、确定分离(r=1)和欠定分离(r<1)三种。早期的独立成分分析(Independent Component Analysis, ICA)[3-4] 方法,被广泛应用于确定分离和超定分离场景下的声源信号获取。该方法通过结合最大似然估计[5]、最小化互信息[6]等算法求得分离矩阵,以使估计得到的声源信号具有最大的非高斯性,从而实现多声源分离。然而,该方法无法有效解决欠定场景下的多声源分离问题。
近年来,随着麦克风阵列技术的发展,有研究者将语音信号稀疏特性引入多声源分离领域,典型的有基于稀疏成分分析(Sparse Component Analysis, SCA)[7-8]、时频掩蔽(Time Frequency Masking)[9]估计的欠定分离方法。文献[7]提出的利用SCA的声源分离方法,首先利用各时频点处方位角估计值实现稀疏成分的分离,其次以稀疏成分为指导实现非稀疏成分的分离,最终联合得到各声源信号。该方法恢复出的非稀疏成分与稀疏成分的能量不匹配,影响了最终的分离质量。基于时频掩蔽的多声源分离方法,通过估计每个时频点中各声源的贡献概率,求得分离掩蔽值来恢复各声源信号。按照计算方式的不同,可将其分为二值掩蔽(Ideal Binary Mask, IBM)[10]和理想比率掩蔽(Ideal Ratio Mask, IRM)[11-13]。其中,IBM估计的主要思想是根据某种准则,判断每一个时频点的成分是否属于某个目标声源,若属于,分离系数取值为1,否则为0。在声源数量较少的情况下,基于IBM估计的方法能够取得较好的分离效果,但随着场景中声源数逐渐增多,声源间混叠严重,分离质量逐渐下降。针对此问题,研究者提出了基于IRM估计的多声源分离方法,该方法能够将发生混叠的时频成分按照一定比例划分给各个声源信号,更符合实际场景中多声源分离的本质。于是,文献[12]提出利用时频点处的方位信息构建概率模型,实现理想比率掩蔽的估计。然而,该方法需要预估各声源的方位用于模型参数的求解。随着相邻声源间隔减小,时频谱混叠愈加严重,文献[12]所采用的声源定位方法将存在无法获得全部声源方位角的问题,进而导致后续多声源分离效果急剧下降。针对此问题,文献[13]提出利用归一化声压梯度信号向量为特征构建高斯混合概率密度模型,获得各声源的理想掩蔽估计。然而,归一化声压梯度信号向量的分布具有峰值尖锐、尾部平坦的特性,更适合使用拉普拉斯分布进行拟合。
为解决上述问题,本文提出了一种基于概率混合模型的理想比率掩蔽多声源分离方法。首先利用柯尔莫可洛夫-斯米洛夫(Kolmogorov-Smirnov,K-S)检验[14]对单个声源场景下归一化声压梯度信号向量进行分析,发现拉普拉斯模型比高斯模型更能准确其分布特性;随后,为提高理想比率掩蔽估计结果的可靠性与准确度,本文采用冯·米塞斯模型和拉普拉斯模型分别对时频点处的方位角估计和归一化声压梯度信号向量联合建模;最终,通过对模型参数求解,实现多声源的分离。
2 声源分离信号模型
考虑到声场麦克风具有记录场景内声压信息以及声压梯度信息的特点,本文选用该麦克风进行信号采集。假设一个声场麦克风位于房间中央,与其同一水平高度的C个声源信号来自不同方位角。于是,对时域上的麦克风录制信号{po(t),gx(t),gy(t),gz(t)}做短时傅里叶变换(Short Time Fourier Transform, STFT),可得到时频域上声场麦克风的录制信号模型如下:
(1)
其中,n和k分别为帧索引和频率索引。Si(n,k)为第i个声源信号的时频系数。X(n,k)=[Po(n,k),Gx(n,k),Gy(n,k),Gz(n,k)]T为声场麦克风B-格式信号的时频表达,其中声压信号Po(n,k)可认为由全指向型麦克风记录得到,声压梯度信号Gx(n,k)、Gy(n,k)、Gz(n,k)可等价为由空间直角坐标系下分别沿x、y、z轴方向上的三个8字型指向性麦克风记录得到。为了便于描述,本文仅考虑水平面的声源分离。
表示第i个声源信号与B-格式声场麦克风四路信号之间的导向向量。本文从压力信号Po(n,k)中提取各个声源信号,而声压梯度信号用于估计时频掩蔽。
基于时频掩蔽的多声源分离算法通过估计目标声源对混合信号中每个时频点成分的贡献比例,即掩蔽值,进而提取出各个声源信号。假设第i个声源在每一个时频点的掩蔽值为Mi(n,k),那么该声源信号通过下列公式计算得到:
(2)
最终通过逆短时傅里叶变换即可得到估计的声源信号,完成声源分离过程。因此从麦克风录制信号中估计得到每个声源对应的时频掩蔽Mi(n,k)是实现多声源分离的关键。
3 基于理想比率掩蔽的多声源分离
考虑到相同声源能量占主导的时频点所对应归一化声压梯度信号向量的方向一致,故本文提出的基于概率混合模型的时频掩蔽多声源分离方法,以时频点处的方位角估计和归一化声压梯度信号向量为特征分别建立相应的概率密度模型,其原理框图如图1所示。本文首先对B-格式麦克风录制信号进行短时傅里叶变换;随后,对时频点处的方位角估计和归一化声压梯度信号建立概率混合模型。模型参数则通过期望最大化算法(Expectation-Maximization algorithm,EM)估计获得;最终,以各个声源信号在每一个时频点的贡献概率为该声源的理想比率掩蔽,进而实现多声源的分离。
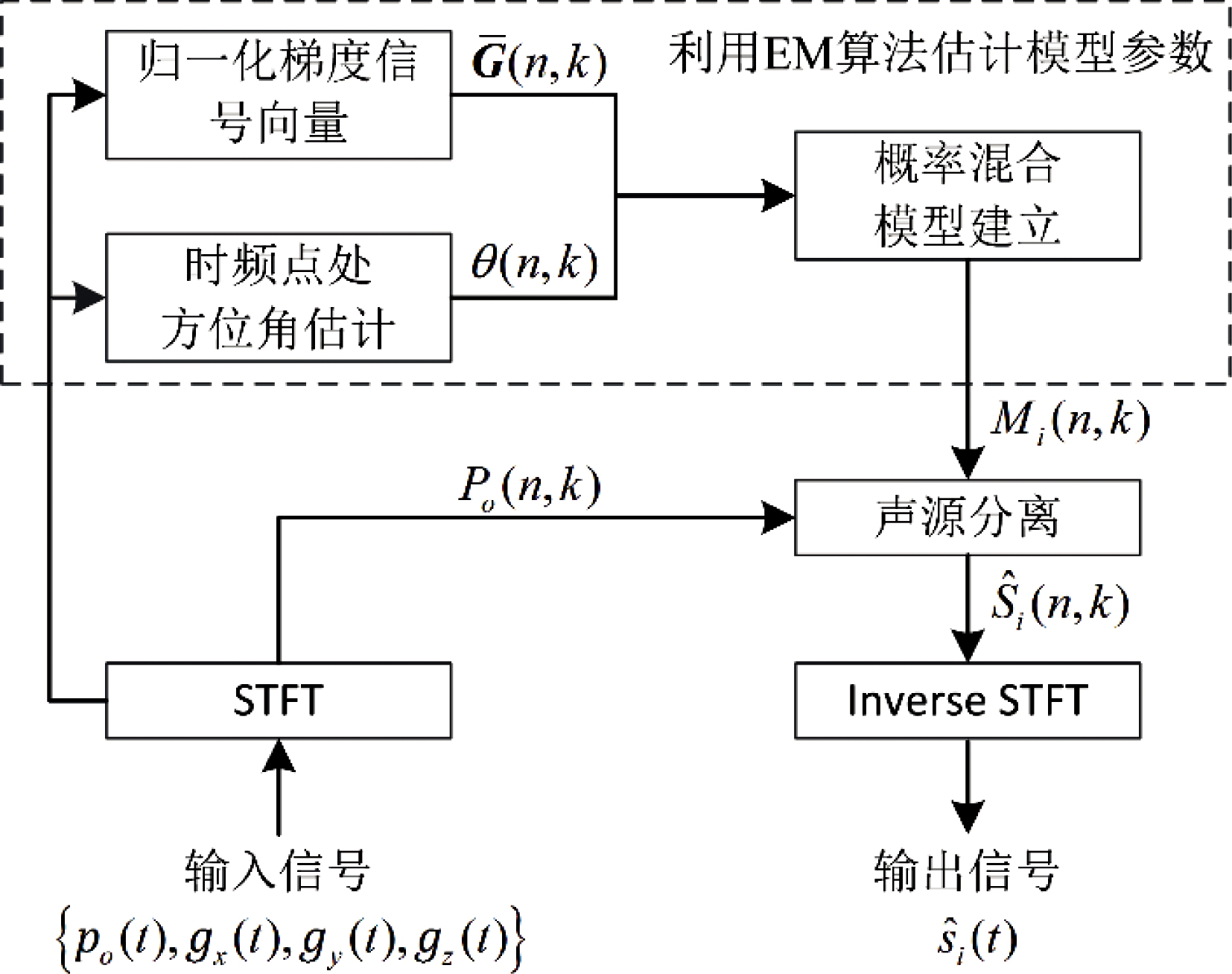
图1 本文所提多声源分离方法框图
Fig.1 System block diagram of the proposed multiple sound source separation method
3.1 归一化声压梯度信号向量的分布特性分析
假设在时频点(n,k)是第i个声源能量占主导,则在该点的麦克风信号可近似表示为:
X(n,k)≈Hi(k)Si(n,k)
(3)
其中,Si(n,k)为第i个声源信号,Hi(k)为B-格式下声场麦克风对应第i个声源信号在频率k处的导向向量。
为了去除声源信号能量对拟合的影响,需要对声压梯度信号G(n,k)=[Gx(n,k),Gy(n,k)]T进行归一化,得到归一化声压梯度信号向量
即:
(4)
其中,
表示第i个声源信号与B-格式下沿x、y轴方向上两路声压梯度信号之间的导向向量。向量
其中
和
是B-格式下声场麦克风沿x、y轴方向上的归一化声压梯度信号。由同一声源能量占主导的时频点所对应归一化声压梯度信号向量的方向相同,反之则不同。因此可以利用归一化声压梯度信号向量
为特征估计每个声源的时频掩蔽。有研究者利用高斯分布对进行描述[13],但通过实验发现的分布具有峰值尖锐、尾部平坦的特性,适合使用拉普拉斯模型进行拟合。为此,本文利用K-S检验比较高斯模型和拉普拉斯模型分别对的拟合程度,进而选出该向量的最佳拟合模型。
本文通过计算单个声源场景下归一化声压梯度信号向量的经验分布函数FH与参考分布的概率密度函数F(本文选择拉普拉斯分布和高斯分布作为参考分布),在垂直方向上的最大距离DH,得到用于评估拟合程度的K-S统计量,计算公式如下:
DH=max|FH-F|
(5)
其中,经验分布函数FH是通过对实验数据提取归一化声压梯度信号向量为观测样本估计得到。实验数据为静音环境下单个声源的麦克风录制信号。本文利用ROOMSIM[15]软件模拟一个长、宽、高分别为6 m、4 m、3 m的房间。声场麦克风处在房间的中心位置,而声源位于和麦克风同一水平高度直线距离为1 m的0°方位角上。录制场景内的声源信号均选自NTT数据库,其采样率均为16 kHz,语音长度约为8 s。
选取上述实验数据中B-格式下声场麦克风沿x、y轴方向上的归一化声压梯度信号
和
作为两个独立样本进行K-S检验。图3给出了不同样点数的时频变换下,单个声源场景中高斯模型和拉普拉斯模型分别与归一化声压梯度信号之间的平均K-S统计量,其中置信区间为95%。实验数据为3名男生说话者(M1、M2、M3)和3名女生说话者(F1、F2、F3)各20段时长为2 s的语音数据作为单个声源信号时利用ROOMSIM 软件模拟生成的仿真数据,高斯模型和拉普拉斯模型对应的均值和方差由样本数据计算得到。
图2的统计结果表明,利用拉普拉斯模型作为理想分布计算得到的K-S统计量均小于高斯模型对应的K-S统计量。这也就意味着,拉普拉斯模型比高斯模型更能准确描述单个声源场景下归一化声压梯度信号
的分布特性。
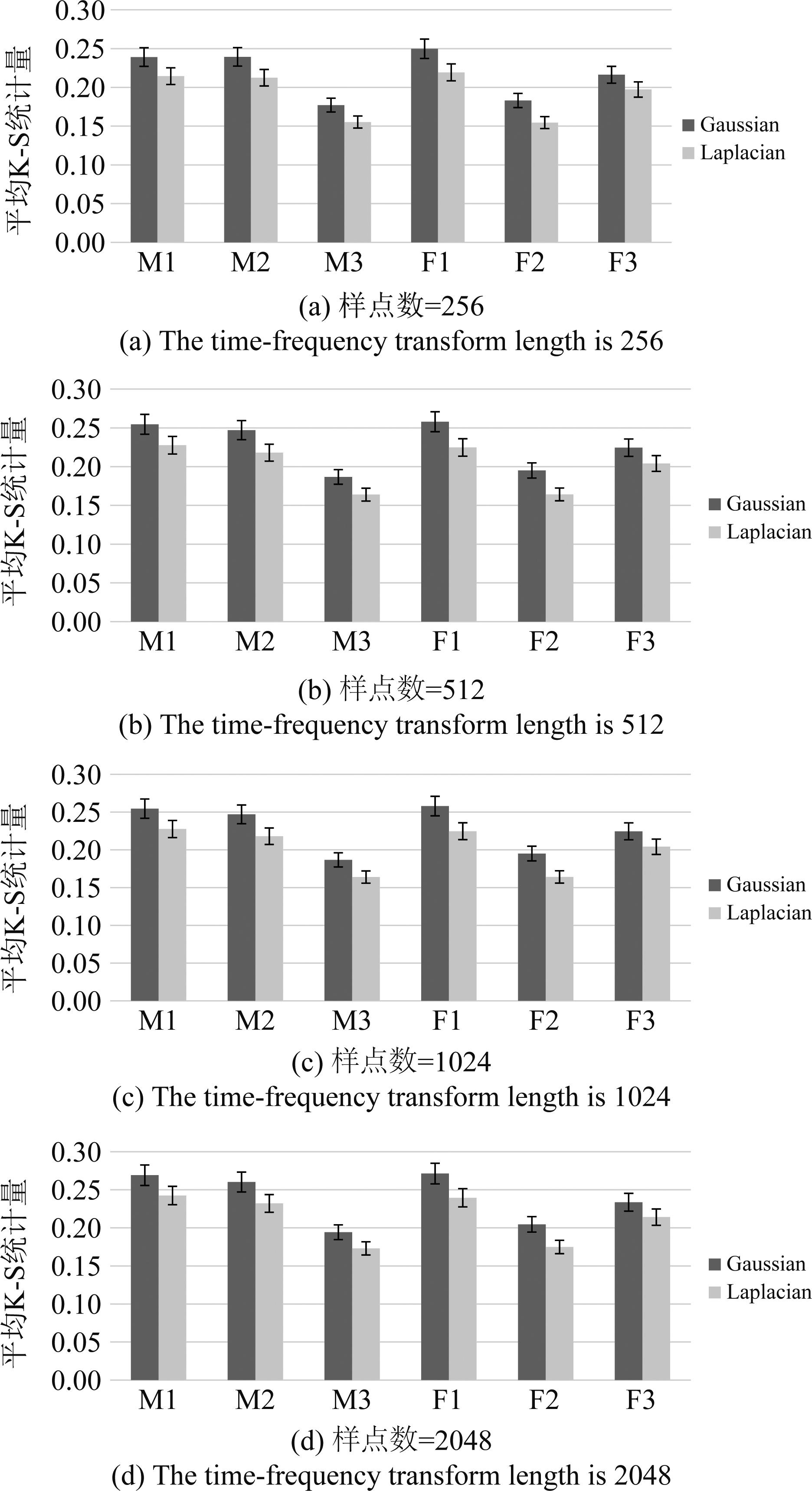
图2 不同样点数的时频变换下,6个不同说话者的平均K-S统计量
Fig.2 The average K-S statistics of six speakers under the different length of STFT
为了进一步直观展示时频变换的样点数对拟合优度检测值的影响,图3给出了上述实验数据所对应K-S统计量的总平均值。从此折线图中可以发现,K-S统计量都随着时频变换样点数的减小而减小。这也就意味着时频变换的样点数越小,模型对单个声源场景下归一化声压梯度信号的拟合程度越好。但以高计算复杂度为代价,折中考虑本文将时频变换样点数选取512。
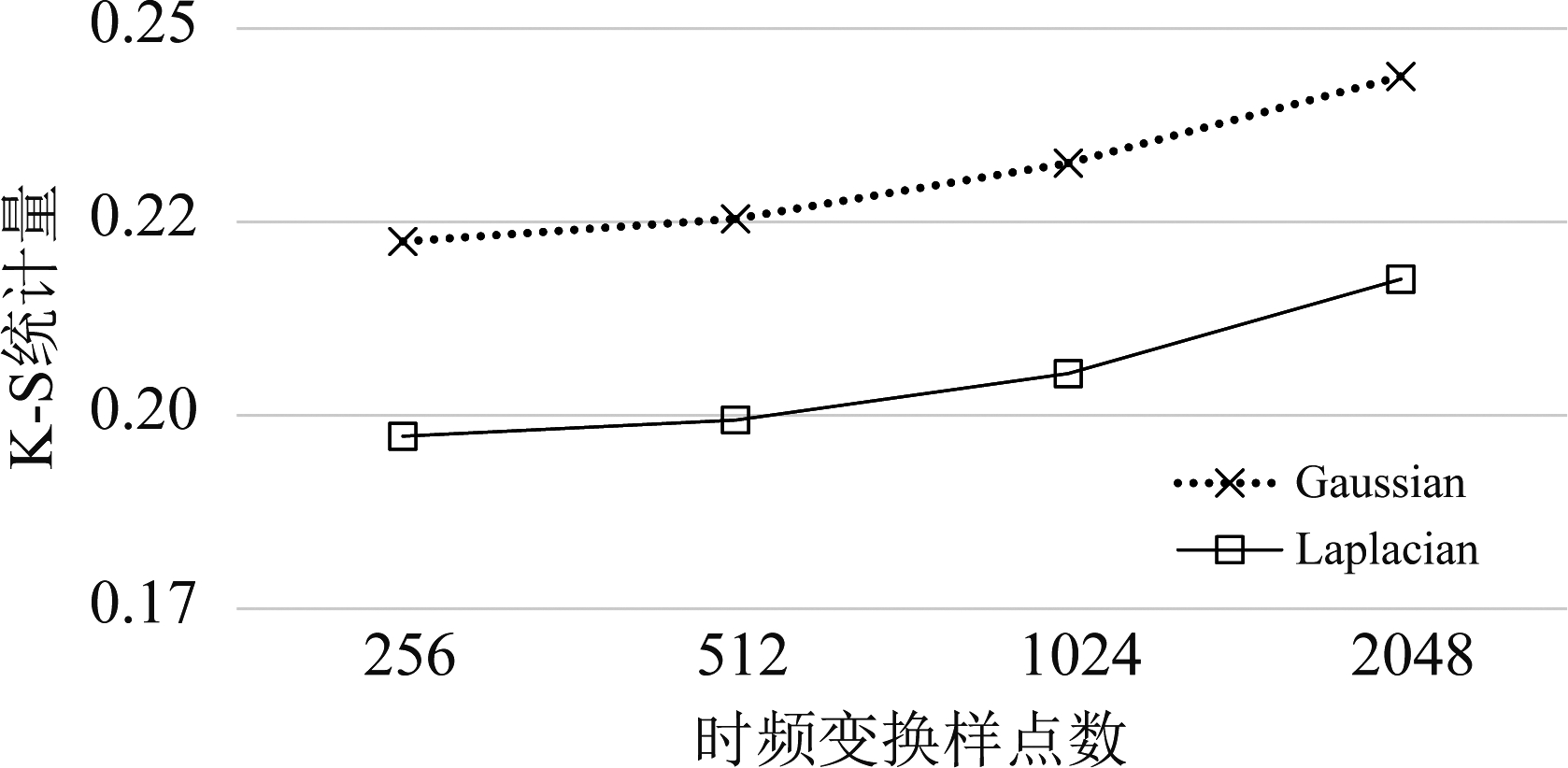
图3 不同样点数的时频变换下,拉普拉斯模型和高斯模型分别作为理想分布时K-S统计量的总平均值
Fig.3 The average K-S statistics of the Laplacian model and the Gaussian model which are used as the ideal distribution under the different length of the time-frequency transform
3.2 利用概率混合模型的理想比率掩蔽估计
本文通过对时频点处的方位角估计和归一化声压梯度信号向量分别利用冯·米塞斯分布和拉普拉斯分布建立概率混合模型的方法,来对多声源分离的理想比率掩蔽进行估计。
首先,采用冯·米塞斯分布对时频点处的方位角估计进行建模,由此得到概率密度模型为:
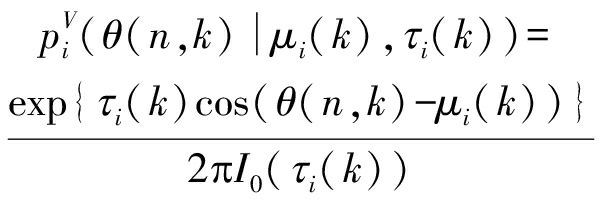
(6)
其中,θ(n,k)是利用声场麦克风录制信号的复声强信息得到的方位角估计值[16],μi(k)和τi(k)分别为第i个声源的方位和集中度,I0(·)为零阶的修正贝塞尔函数。其次,利用在一维线性子空间上以向量的方向为特征进行聚类,得到归一化声压梯度信号向量的概率密度模型如下:
(7)
其中,*表示共轭转置操作,ai(k)代表第i个声源信号对应归一化声压梯度信号向量的中心,其模值为1,即‖ai(k)‖=1。γi(k)反应了的集中程度。根据向量数量积的定义,可知
为向量
在中心向量ai(k)上的矢投影。
代表的是向量到中心向量ai(k)的垂直距离,反映了归一化声压梯度信号向量和中心向量间的相似程度。
根据公式(6)和(7),得到方位角估计和归一化声压梯度信号向量的联合概率密度函数为:
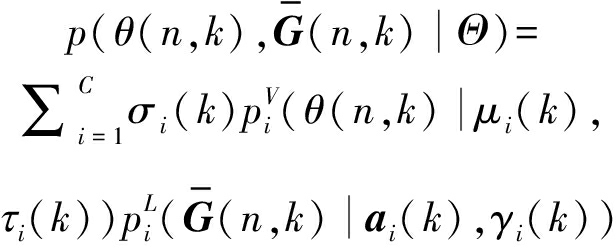
(8)
其中,σi(k)代表第i个声源信号的权重,并且满足
模型参数集为Θ={σi(k),μi(k),τi(k),ai(k),γi(k)}1≤i≤C。按照最大似然法的思想,参数估计具体是指寻找一组模型参数,最大程度拟合观测值
其中,对数似然函数为:
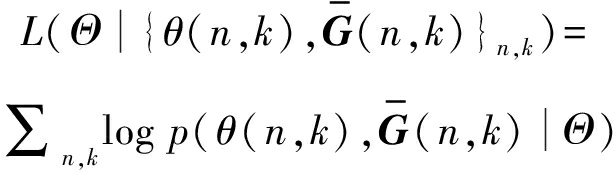
(9)
对于模型参数的估计,将采用EM算法通过迭代逐步接近似然函数最大值的方式实现。
3.3 利用EM算法的模型参数估计
EM算法是一种针对含有隐变量的概率模型的最大似然估计方法。通常包含以下步骤:首先对模型参数进行初始化,接着重复计算期望的E步骤和将似然函数最大化的M步骤,直到满足收敛条件,最终实现模型参数的估计。
将本文提出的概率混合模型所包含隐变量记作Z(n,k)。该隐变量的后验概率
代表一个时频点属于第i个声源信号的概率,其中Θi={σi(k),μi(k),τi(k),ai(k),γi(k)}。在利用EM算法进行迭代之前,需要对模型参数初始化。首先设置每一个声源信号的权重{σi(k)}1≤i≤C均为1/C。针对时频点方位信息的模型参数{μi(k)}1≤i≤C则通过对时频点处方位角所构成的统计直方图进行后处理估计得到。考虑到归一化声压梯度信号向量的先验知识难以得到,本文将公式(8)中的
初始化为1。
接着,在E步骤中根据模型参数的初值,可得到隐变量后验概率的迭代公式:
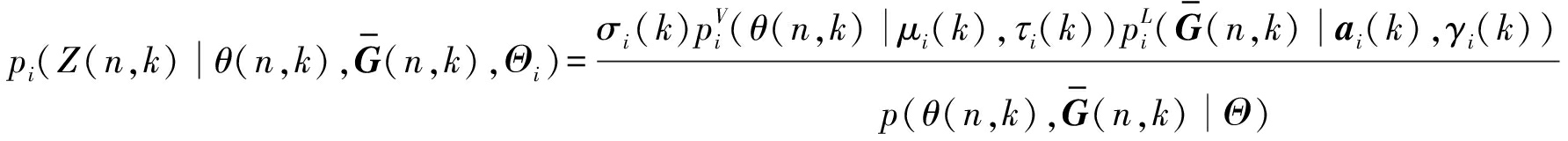
(10)
在M步骤中,利用拉格朗日乘子法将似然函数最大化,可得到各个参数的迭代公式。由于归一化声压梯度信号向量和中心向量ai(k)的长度均为1,因此ai(k)可通过计算下列矩阵最大特征值对应的特征向量得到:
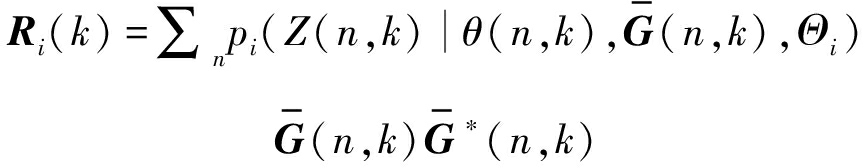
(11)
反映归一化声压梯度信号向量的集中程度的γi(k)通过下列公式迭代更新:
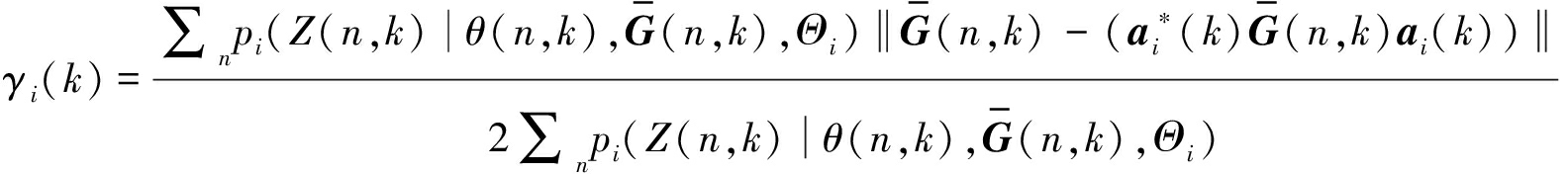
(12)
最后,按照下列公式得到时频点方位信息对应的模型参数和独立声源信号的权重:
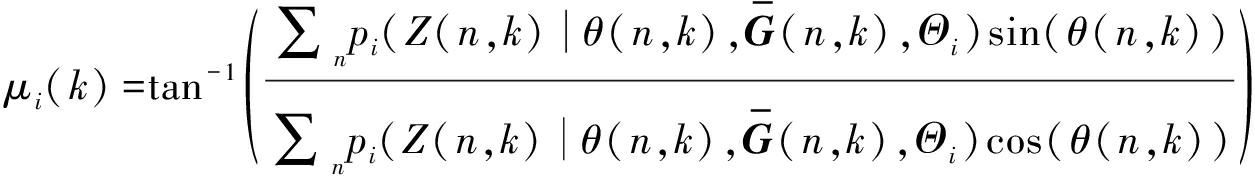
(13)
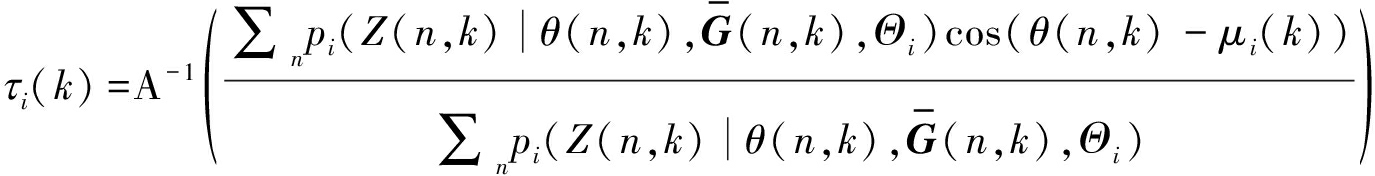
(14)
(15)
通过重复E、M步骤,直到达到预设的最大迭代次数,获得概率混合模型的参数估计值。于是,第i个声源的理想比率掩蔽值,可通过下式得到:
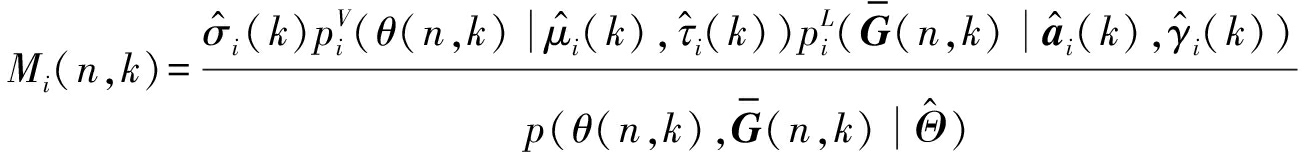
(16)
第i个声源声源分离信号的时频系数为:
(17)
最后对该时频系数进行逆短时傅里叶变换,得到时域分离声源信号。
4 实验结果与分析
本节将利用仿真数据和实录数据对所提方法的分离性能进行实验测评。为了表明所提分离方法的有效性,本文选择两种参考方法作为对照,分别是联合稀疏与非稀疏成分分离(Sparse and Non-sparse Components Separation, SNCS)[7]的多声源分离方法和基于理想二值掩蔽估计(Ideal Binary Mask Estimation, IBME)[10]的多声源分离方法。其中,基于SNCS的分离方法与本文同样是对理想比率掩蔽进行估计实现多声源分离,而基于IBME的分离方法所使用的分离掩蔽是通过利用设置固定的时频点方位角阈值估计得到(在本文的实验测评中设置该阈值为8°)。同时,本文以B-格式中的声压信号po(t)为分离前的混合信号,加入实验测评作为参考基准。需要注意的是,虽然声场麦克风由四个声学传感器构成,但是在实验环境中声源和麦克风位于同一水平面,所以本文仅使用了B-格式下的声压信号和空间直角坐标系沿x、y轴方向的声压梯度信号。因此,对四个及以上声源混合信号的分离,即是本文所提方法的欠定分离场景。
本文分别使用语音感知质量(Perceptual Evaluation of Speech Quality, PESQ)和信号失真比(Signal-to-Distortion Ratio, SDR)对不同声源数量和声源间隔角度下分离声源信号的质量进行评估。其中,PESQ得分越低则感知质量越差;SDR得分越低则表明分离声源信号失真越严重。本文在不同声源数量和声源间隔角度所对应的每一组实验条件下,均进行36次试验。每次试验相对上次试验,声源方位整体偏移10°,同时保持声源数量和间隔角度不改变。
4.1 实验条件
对于仿真数据的测评,本文选用NTT数据库中采样率为16 kHz的语音段随机组合作为声源信号。测评语音中包含6名男性说话者和6名女性说话者,讲话时长均为8 s。本文使用ROOMSIM软件模拟一个长宽高分别为6 m、4 m、3 m的房间。声场麦克风处在房间的中心位置,而声源位于和麦克风同一水平高度直线距离为1 m的不同方位上。依据第3.1节的实验分析,本文设置时频变换的样点数为512,在减少计算复杂度的同时保证声源分离质量。
本文所使用的实录环境是一个长度为4.5 m、宽度为3.5 m、高度为2.8 m的测听室。经测量此房间内的混响时间约为400 ms,平均信噪比约为20 dB。声场麦克风Sennheiser Ambeo VR Mic被放置在的房间中央,同时使用扬声器播放从NTT数据库中随机选取的信号作为声源。除此之外,扬声器被均匀放置在于声场麦克风同一水平面,距离1.5 m远的圆上。
4.2 仿真环境中的声源分离质量评测
首先,本文利用PESQ对所提方法和参考方法的声源分离质量进行评估。通过将分离得到的声源信号和干净语音信号进行对比评估分离声源信号的感知质量。PESQ的分值在-0.5至4.5之间,其中4.5分表示声源信号的感知质量最佳,而-0.5分表示声源信号的感知质量最差。如图4给出了不同声源数量的测评条件下,本文所提多声源分离方法和参考分离方法的平均PESQ值。其中Mixture为分离前的混合信号(B-格式下的声压信号)的感知质量。
图4(a)～(d)给出了声源间隔角度分别为{40°,50°,60°,70°}时的测评结果。从图中可以看出,本文所提多声源分离方法与基于SNCS的方法和基于IBME的方法相比表现出最好的分离效果。随着场景内声源数量的增加,所有方法的分离质量均有所下降,特别是基于IBME的方法在声源数量为5时,几乎和混合信号的平均PESQ值相同。这是因为声源之间的混叠随着声源数的增多而愈加严重,混合信号中声源的稀疏特性也随之减弱,导致基于IBME的方法分离性能急剧下降。而基于SNCS的方法和本文所提方法是通过估计声源信号的理想比率掩蔽实现分离的,即便在声源混叠严重的场景下,仍能得到较好的分离质量。然而,在所有测评场景中,本文所提方法的分离性能始终优于基于SNCS的分离方法。原因在于基于SNCS的分离方法仅利用时频点处的方位角估计为特征,而本文所提方法还加入了归一化声压梯度信号向量联合进行理想比率掩蔽的估计。随着场景内各声源间隔角度减小,能反映真实声源方位角的时频点数量随之减少,这势必导致基于SNCS的分离方法性能下降,而本文所提方法因为结合了归一化声压梯度信号向量和时频点处方位估计两种声源特征,即便在较小角度间隔下仍能取得优于对比方法的分离效果。
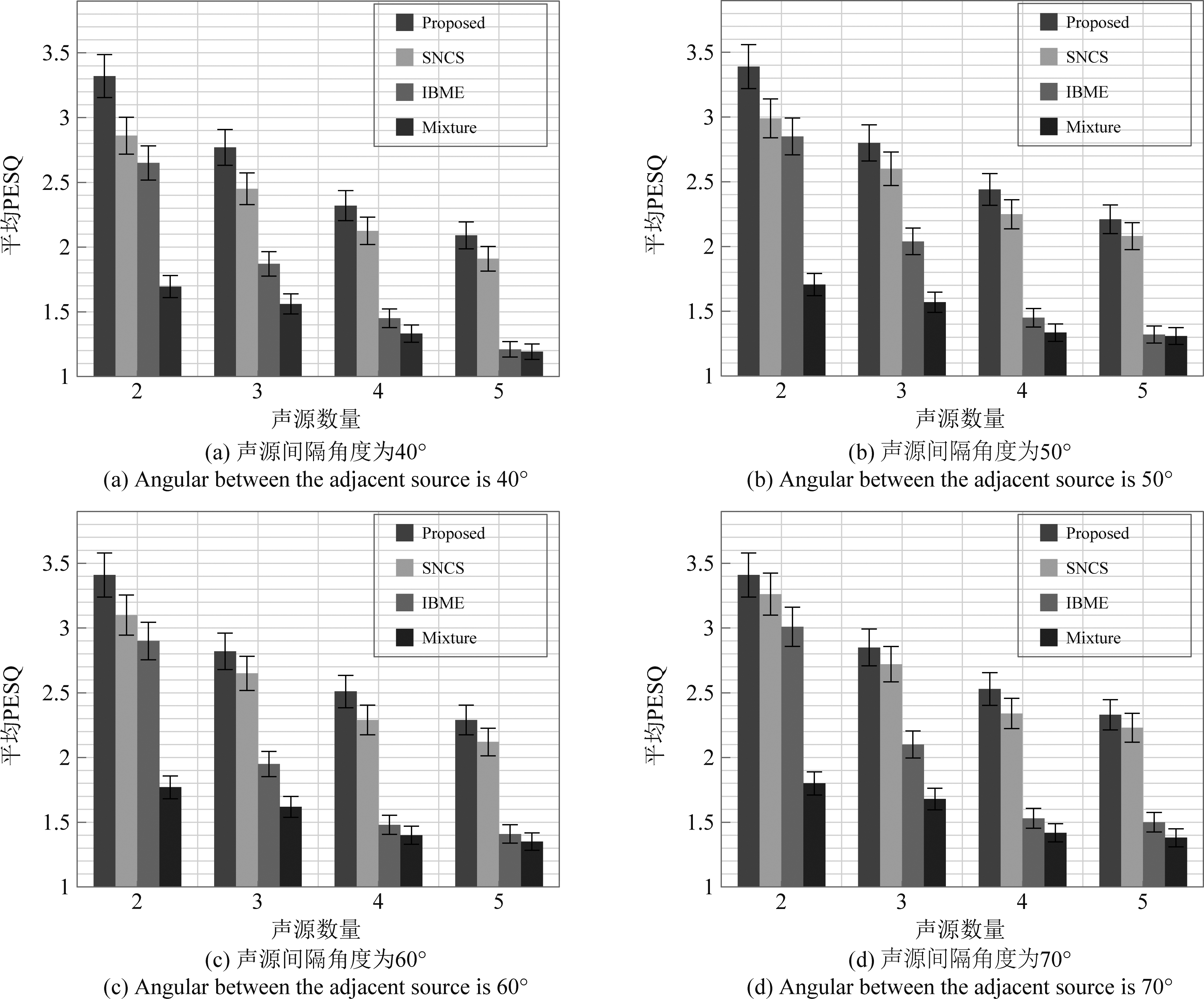
图4 PESQ评测结果
Fig.4 PESQ results
随后,本文利用SDR对分离声源信号的质量进行评估。通过计算目标声源的干扰信号与原始声源信号的能量比值可得到SDR分数。在不同声源数量和声源间隔下,使用本文所提方法和参考方法分离得到声源信号的平均SDR结果如图5所示,其中(a)～(d)分别表示声源间隔角度为{40°,50°,60°,70°}。从图中可以发现平均SDR的变化趋势和平均PESQ相同。本文所提方法的分离质量在所有测评条件下均优于基于 IBME的分离方法和基于SNCS的分离方法。
图5 SDR评测结果
Fig.5 SDR results
4.3 实录环境中的声源分离质量评测
为了测评所提方法在实际环境中的分离效果,本文利用实录数据计算各方法的平均PESQ值。需要注意的是,实录数据是在混响时间约400 ms的测听室中采集得到,其背景噪声约为20 dB。图6为不同声源角度间隔下,利用本文所提方法和参考方法得到的分离声源信号的平均PESQ值,图6中(a)、(b)分别代表声源数量为2和3的测评结果。
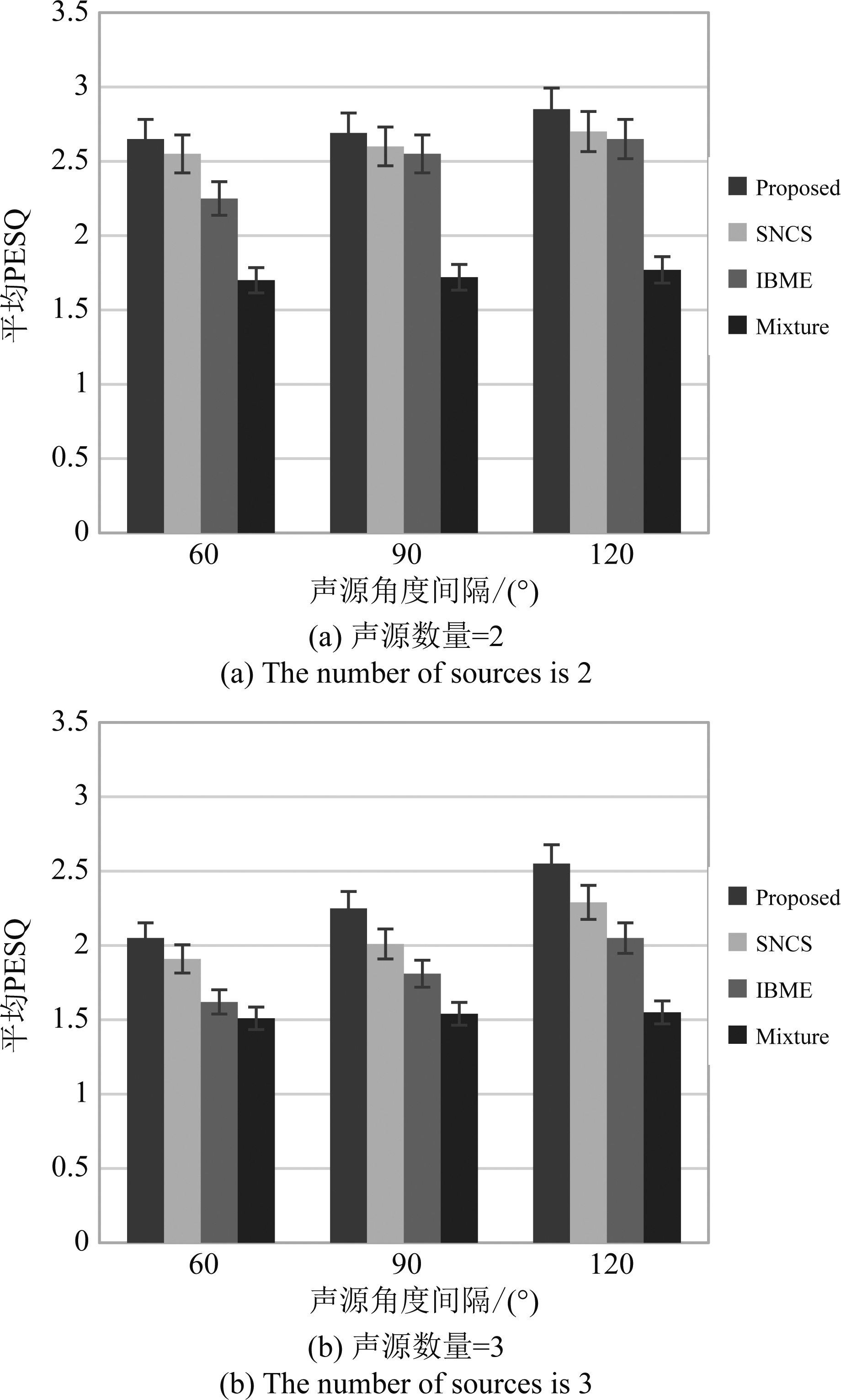
图6 不同声源数量下的PESQ测评结果
Fig.6 PESQ results under different number of sources
从图中可以发现,在声源间隔为120°时,所有方法均取得较为理想的分离效果,然而当声源间隔减小为60°时,分离效果有所下降,其中基于IBME的方法性能下降最为明显。这是当相邻声源角度间隔减小时,各声源间时频谱混叠严重,这会导致以时频点处方位角估计为唯一分离准则的IBME方法受到严重影响。本文所提方法通过联合归一化声压梯度信号向量,进行更为准确的分离掩蔽估计,从而展现出最佳的分离效果。因此可以得出结论,利用本文所提分离方法得到各声源信号质量优于基于SNCS的分离方法和基于IBME的分离方法。
5 结论
本文提出一种基于概率混合模型的理想比率掩蔽多声源分离方法,该方法采用冯·米塞斯分布和拉普拉斯分布分别对时频点处方位角估计和归一化声压梯度信号向量进行拟合,并结合EM算法实现概率混合模型的建立与求解,最终实现多声源的分离。实验结果表明,与传统方法比较,所提多声源分离方法具有更为出色的性能。
[1] SGOUROS T, MITIANOUDIS N.A novel directional framework for source counting and source separation in instantaneous underdetermined audio mixtures[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 2025-2035.
[2] DUONG T T H, DUONG N Q K, NGUYEN P C, et al.Gaussian modeling-based multichannel audio source separation exploiting generic source spectral model[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(1): 32-43.
[3] COMON P, JUTTEN C.Handbook of blind source separation, independent component analysis and applications[EB/OL].2010.https:∥ieeexplore.ieee.org/document/6461612.
[4] WANG Lin, CAVALLARO A.Pseudo-determined blind source separation for ad-hoc microphone networks[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(5): 981-994.
[5] HYV
RINEN A, OJA E.Independent component analysis: Algorithms and applications[J].Neural Networks, 2000, 13(4/5): 411-430.
[6] 季策, 孙梦雪, 张君.基于EMD改进算法的欠定混合盲分离[J].东北大学学报(自然科学版), 2018, 39(8): 1108-1113.
JI Ce, SUN Mengxue, ZHANG Jun.Underdetermined blind separation based on improved EMD algorithm[J].Journal of Northeastern University(Natural Science), 2018, 39(8): 1108-1113.(in Chinese)
[7] JIA Maoshen, SUN Jundai, BAO Changchun, et al.Separation of multiple speech sources by recovering sparse and non-sparse components from B-format microphone recordings[J].Speech Communication, 2018, 96: 184-196.
[8] FENG Fangchen, KOWALSKI M.Underdetermined reverberant blind source separation: Sparse approaches for multiplicative and convolutive narrowband approximation[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(2): 442-456.
[9] TOGAMI M.Deep multi-channel speech source separation with time-frequency masking for spatially filtered microphone input signal[C]∥2020 28th European Signal Processing Conference(EUSIPCO).Amsterdam, Netherlands.IEEE, 2021: 266-270.
[10] SHUJAU M, RITZ C H, BURNETT I S.Separation of speech sources using an Acoustic Vector Sensor[C]∥2011 IEEE 13th International Workshop on Multimedia Signal Processing.Hangzhou, China.IEEE, 2011: 1-6.
[11] LUO Yi, MESGARANI N.Conv-TasNet: Surpassing ideal time-frequency magnitude masking for speech separation[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(8): 1256-1266.
[12] HUNG W L, CHANG-CHIEN S J, YANG M S.Self-updating clustering algorithm for estimating the parameters in mixtures of von Mises distributions[J].Journal of Applied Statistics, 2012, 39(10): 2259-2274.
[13] SAWADA H, ARAKI S, MAKINO S.A two-stage frequency-domain blind source separation method for underdetermined convolutive mixtures[C]∥2007 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics.New Paltz, NY, USA.IEEE, 2007: 139-142.
[14] GLEN A G, LEEMIS L M, BARR D R.Order statistics in goodness-of-fit testing[J].IEEE Transactions on Reliability, 2001, 50(2): 209-213.
[15] CAMPBELL D R, PALOMAKI K J, BROWN G.A MATLAB simulation of “shoebox” room acoustics for use in research and teaching[J].Computing and Information Systems J, 2005, 9: 48-51.
[16] GUNEL B, HACIHABIBOGLU H, KONDOZ A M.Intensity vector direction exploitation for exhaustive blind source separation of convolutive mixtures[C]∥2009 IEEE International Conference on Acoustics, Speech and Signal Processing.Taipei, Taiwan, China.IEEE, 2009: 41-44.
