1 引言
通信安全不只局限于通信内容的安全还包含通信行为的安全[1],即通信行为隐蔽。通信行为安全受到监控方检测准则的宽松和严格程度的影响。如果通信双方面对宽松的监控方(例如执法人员,在执法过程中,执法人员往往只有在证据确凿的情况下,才能进行执法行动),则较容易实现隐蔽通信。但是如果通信双方面对的是严格的监控方(例如残暴的犯罪分子,为了逃避法律制裁,犯罪分子往往采用最严格的检测准则和最严厉的处罚手段对付潜伏其中的卧底),则很难实现隐蔽通信。对于潜伏于犯罪组织内部的卧底警察而言,身份暴露意味着灭顶之灾,此类场景中的隐蔽通信对于保护卧底警察安全至关重要。
虽然扩频通信技术被广泛应用于隐蔽通信[2-3],但是直到Bash[4]等人将隐写术的思想引入无线通信,才将无线隐蔽通信问题理论化。实际工作环境中,诸多自然或者人为因素(如气温、风霜雨雪、机械运动)导致背景噪声在一定范围内变化。Tandra[5]在噪声功率存在不确定性的模型中,研究了弱信号的鲁棒检测问题,并将实现鲁棒检测的最小信噪比(SNR,signal to noise ratio)称为信噪比墙(SNR wall)。随后,Baxley[6]等人据此研究了监控方只有在能够鲁棒检测通信行为的条件下,才能判定存在信息传递的隐蔽通信问题,并求解了对应的隐蔽通信速率。
在上述研究中,对于通信双方面对的监控方的假设过于理想[7]。对于严格的监控方,Baxley等人的隐蔽通信方案可能不足以保证其安全。因此,为保证卧底安全,应当在对监控方检测最有利条件下设计隐蔽通信方案。文献[7]在噪声不确定场景中，分析了对于监控方最有利条件下的隐蔽通信速率。在此基础上，文献[8]分析了信道预编码方法的隐蔽吞吐量。通过上述分析可知，当前研究通常关注隐蔽通信中的理论问题。本文结合工程实际，引入合理约束，关注隐蔽通信的应用问题。
在隐蔽通信的理论研究过程中，通常假设监控方检测阈值的设定不受限制。而在现实世界中，由于材料和制造工艺的制约，实际接收机往往存在检测能力极限，进而限制了监控方检测阈值的设定。同时,功率计[9](radiometer)易于工程实现、对瞬时干扰具有一定的抵消作用、不受通信体制制约且广泛应用于信号检测。因此,本文研究接收机利用功率计进行通信行为检测时的隐蔽通信问题。对于采用功率检测的接收机,其检测极限(或者称为检测阈值)可以采用最小可检测信号(MDS,minimum detectable signal)[10]表示。由于MDS是相对于背景噪声定义的检测阈值,且在本文研究的噪声具有不确定性的场景中,功率计无法将接收信号总功率中的信号功率和噪声功率区分开。因此,本文采用“有信号发送”时接收信号总功率与“没有信号发送”时接收信号总功率的比值表示MDS和检测指标。根据该定义,本文中对于监控方检测最有利的条件指的是监控方的检测指标达到取值范围的最大值。从对抗的角度看,通信双方与监测方是相对立的,对监控方检测最有利条件就是对于从发送方到接收方隐蔽通信最不利条件。类似地,本文中对于监控方检测最不利的条件指的是监控方的检测指标达到取值范围的最小值,此时最有利于隐蔽通信。
本文关注对于监控方检测最有利条件下的单向隐蔽通信问题。具体而言,若在对于接收方检测最不利条件下,接收方的检测指标超过其检测阈值;并且在对于监控方检测最有利条件下,监控方的检测指标低于其检测阈值,则可以实现隐蔽通信。若接收方检测能力优于监控方,则容易实现隐蔽通信。为了进一步保证隐蔽性能,本文研究监控方具有检测能力优势时的隐蔽通信问题。
一种可行的隐蔽通信思路是发送信号在接收方处同相叠加,而在监控方处异相抵消。一个广泛应用的方案是扩频通信,但是其隐蔽性能来源于扩频码。一旦扩频码泄漏,其隐蔽性能急速下降。而物理层安全技术[11](如预编码技术[12])提供了一种免扩频码分发、且与扩频通信具有同样效果的解决方案。当前基于信道预编码技术的隐蔽通信,通常通过引入人工噪声[13-14]或者干扰节点[15-16]的方式实现。但是人工噪声或者干扰的引入,导致监控方检测到的背景噪声功率增加,有可能增加监控方通过功率计检测到通信行为的成功概率。
为了在对于监控方检测最有利的条件下实现隐蔽通信。首先,基于任一实际接收机存在检测极限的事实,利用信道预编码实现基于信道差异的隐蔽通信。其次,利用双门限法分析隐蔽通信的约束条件,并推导平均遍历隐蔽通信速率,为隐蔽通信方案的设计提供参考。再次,通过仿真实验,分析发送天线数和发送功率对于隐蔽通信速率的影响。最后,总结全文并根据理论分析和仿真实验结果,为实现隐蔽通信提供建议。
2 系统模型
如图1所示,系统中存在一个发送方,一个接收方和一个监控方,分别记作Alice,Bob和Willie。其中,Alice配置M根天线,Bob和Willie均配置单天线。本文研究Bob和Willie采用功率计检测时,Alice到Bob的单向隐蔽通信问题。例如,Bob伪装成公开的广播基站或者流动广播站。在其功率覆盖范围内,Alice和Willie可以通过信号处理手段(如过采样方式)还原广播信号,并以此为导频,恢复出Bob到Alice和Willie的信道状态信息。为了保证Bob正确还原信息,需要保证Bob始终能够检测到通信行为。同时,为了保证Alice向Bob发送信号的通信行为对Willie隐蔽,需要防止Willie通过功率检测发现Alice到Bob的通信行为,继而阻断Alice到Bob的通信行为。Alice和Bob希望通过控制发送策略,假设在Willie采用最优检测情况下,依然能够实现Alice到Bob的隐蔽通信。本文假设Alice,Bob和Willie在时间上同步,且Bob和Willie以发送符号持续时间为基本检测单元,始终进行功率检测。
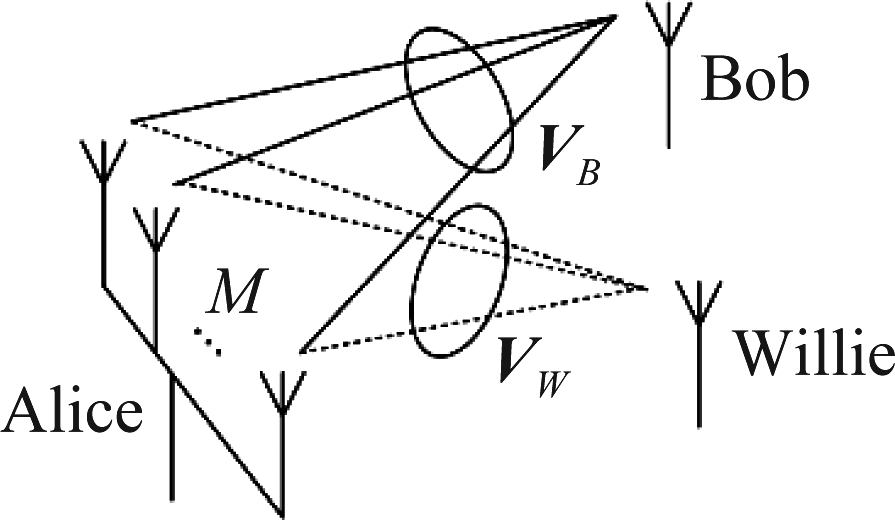
图1 系统模型
Fig.1 System model
由无线信道的互易性可知,在信道相干时间内,从Alice到Bob(Willie)的信道与从Bob(Willie)到Alice的无线信道近似相同。因此,在系统模型中,Alice到Bob和Willie的信道分别记作VB=[VB(1),VB(2),…,VB(M)]和VW=[VW(1),VW(2),…,VW(M)]。本文假设VB和VW中的元素相互独立;无线信道VB和无线信道VW中的元素服从均值为零、方差分别为
和
的复高斯分布,即
和
其中i=1, 2, …, M。
设系统中存在均值为零的加性高斯白噪声,Alice,Bob和Willie处噪声及其方差分别记作
和
由于环境中温度、湿度、风霜雨雪等气候条件影响,背景噪声方差在一定范围内波动。本文沿用文献[5]中的几何对称模型描述噪声不确定性。假设存在一个噪声方差名义值(nominal noise variance)PN和一个不确定性衡量因子ρ≥1,则系统中背景噪声方差PNA,PNB和PNW按照某种分布在闭区间[PN/ρ,ρPN]内变化,其中分布函数随着环境的变化而变化。
3 隐蔽通信方案以及平均遍历隐蔽通信速率
本节在噪声存在不确定性的场景中,利用信道预编码技术实现隐蔽通信。首先,介绍信道预编码技术。随后,研究实现Alice到Bob的隐蔽通信时,功率和天线数需要满足的约束条件。最后,推导所提方案的平均遍历隐蔽通信速率。为了简化表述,在不失一般性的前提下,本文以Alice发送单个符号时的隐蔽通信过程为例,分析隐蔽通信的约束条件,以及单符号隐蔽通信速率。事实上,通过假设连续两个发送符号之间存在时间间隔,且该时间间隔超过信道相干时间,则可以将本文研究的单符号隐蔽通信结果推广到多符号隐蔽通信场景。
3.1 信道预编码
为了实现信号能量在Bob处汇聚,而在Willie处弥散的差异化传输。本文假设Alice能够准确获取Bob与Alice之间的信道信息VB(例如,Alice利用Bob发送的大功率广播信号进行信道估计。根据无线信道的互易性,在信道相干时间内,Alice估计出的Bob到Alice的信道信息与Alice到Bob的无线信道信息近似相等)。为了保证接收信号在Bob处同相叠加、而在Willie处异相相消,并且保证预编码之后的发送信号的功率保持不变。本文中Alice按照式(1)生成预编码向量U。
(1)
Alice利用U对发送信息X进行预编码,得到Alice端待发送符号UX。设发送信号X服从均值为零、方差为PX的复高斯分布,即X～CN(0,PX)。由于无线信道的上下行信道之间具有互易性,当Alice在信道相干时间内发送UX时,Bob和Willie接收到的信号YB和YW分别为
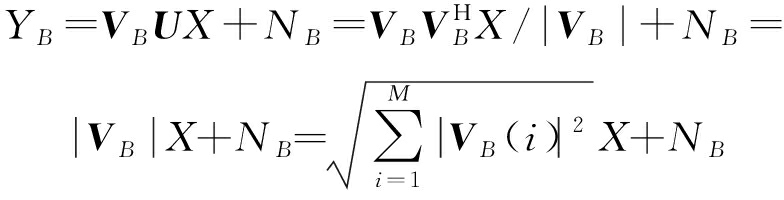
(2)
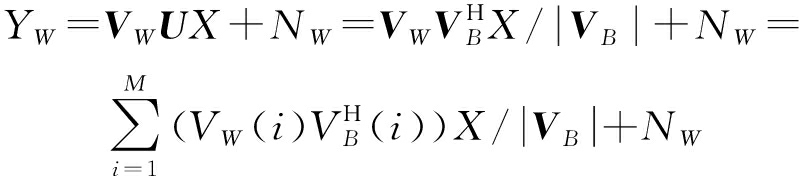
(3)
3.2 隐蔽通信约束条件
隐蔽通信包含“通信”和“隐蔽”两种约束条件,其中“通信”约束要求Bob能够准确还原Alice发送的信息;“隐蔽”约束要求通信过程不被Willie检测。而在无线通信中,接收机准确检测通信行为是信息还原的基础,若不能检测到通信行为,则接收机通常会将该次接收到的样本视为噪声,而不对其进行信息还原操作。本小节首先介绍通信行为检测指标。其次,分析Bob完成通信行为检测的约束条件,得到发送功率下界。最后,分别在对于Willie检测最有利和最不利条件下,分析隐蔽约束,得到发送功率上界。
3.2.1 通信行为检测指标
本文中Bob和Willie采用功率计检测通信行为,Bob和Willie将“有信号发送”时接收信号总功率与“没有信号发送”时接收信号总功率的比值作为通信行为检测指标,通过比较该比值与检测阈值的关系,确定Alice是否发送信息。Bob和Willie的检测阈值以及检测指标分别记作γB,γW,ηB和ηW。当噪声功率确定时,若ηB>γB,则Bob可以判断出Alice确实发送了信号。同理,若ηW>γW,则Willie也可以判断出Alice确实发送了信号。
由于Bob和Willie始终利用功率计进行功率检测。因此,在Alice发送UX的前一个时隙,Bob和Willie通过功率计测量的接收信号功率中只包含噪声功率。在Alice发送UX的时隙,Bob和Willie通过功率计测量得到的接收信号功率中既包含信号功率又包含噪声功率。为了便于理解,在不引起歧义的前提下,将发送UX之前的一个“没有信号发送”的时隙称之为“背景噪声测量阶段”;而将发送UX的时隙称之为“通信行为检测阶段”。
由于背景噪声的方差在[PN/ρ,ρPN]内变化,且背景噪声测量阶段和通信行为检测阶段不能同时进行。因此,两个阶段的噪声功率可能不同。在Bob(Willie)背景噪声测量阶段和通信行为检测阶段,背景噪声及其功率分别记作
和
和
结合式(2)和式(3),则ηB和ηW分别为
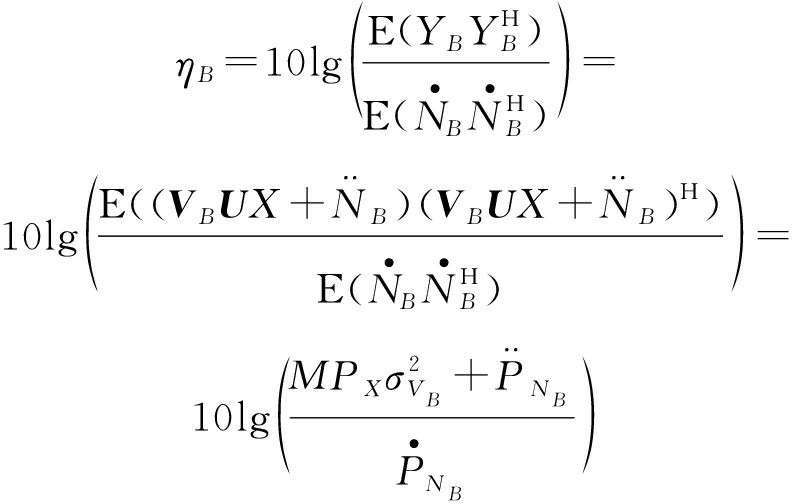
(4)
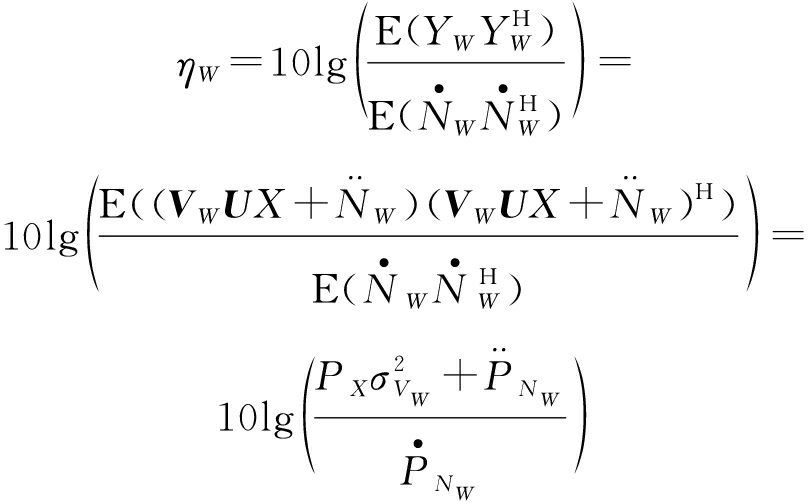
(5)
由于
因此,ηB和ηW的取值范围分别为
(6)
(7)
3.2.2 Bob检测约束
为了保证Bob能够准确还原Alice发送的数据,通信策略需要首先保证Bob能够准确判断Alice是否发送信息。为此,需要保证Bob在最不利于其检测的条件下能够准确检测到通信行为。在噪声存在不确定性的场景中,最不利于Bob检测的条件指的是在背景噪声测量阶段,Bob处的噪声功率达到最大值,而在通信行为检测阶段,Bob处的噪声功率达到最小值。此时,ηB达到最小值,该数值最可能小于其检测阈值γB,即最不利于Bob进行通信行为检测。为了保证Bob始终能够正确检测到通信行为,需要保证检测指标ηB的最小值min(ηB)大于Bob的检测阈值γB,即若发送功率和天线数满足式(8)的约束,则可以保证采用功率计检测通信行为的Bob始终能够检测到通信行为。
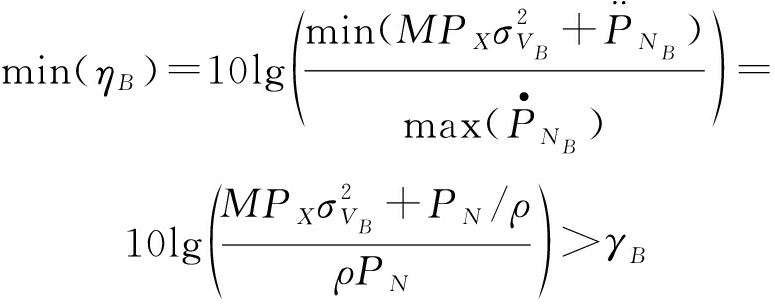
(8)
3.2.3 隐蔽约束
Willie检测成功率受到ηW与γW之间关系的影响。具体而言,若γW
本文关注对于Willie检测最有利条件下的Alice到Bob的隐蔽通信问题。其中,对于Willie检测最有利条件指的是在背景噪声测量阶段,Willie处的噪声功率达到最小值,而在通信行为检测阶段,Willie处的噪声功率达到最大值。此时,ηW达到最大值,该数值最可能超过其检测阈值γW,即最有利于Willie进行通信行为检测。本文称该条件下的Willie为最严格的监控方,并称该条件为对于Alice到Bob隐蔽通信最不利的条件。为了保证Alice到Bob的通信行为不被最严格的Willie检测到,需要保证检测指标ηW的最大值max(ηW)小于Willie的检测阈值γW,即若Allice端的发送功率和天线数满足式(9),则可以保证采用功率计检测通信行为的最严格的Willie始终检测不到通信行为。
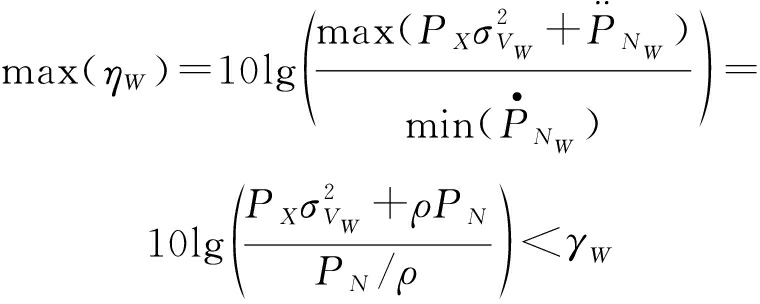
(9)
结合式(8)和式(9)可知,若发送功率PX满足式(10)的约束,则可以在对于Willie检测最有利的场景中,保证Bob能够通过功率计检测到通信行为,而最严格的Willie无法通过功率计检测到通信行为。在上述对于Alice到Bob隐蔽通信最不利的场景中,PX的取值范围的集合记作AWC。
(10)
作为对比,下边计算对于Willie检测最不利条件下,实现Alice到Bob单向隐蔽通信的功率约束。其中,对于Willie检测最不利条件指的是在背景噪声测量阶段Willie处的背景噪声功率达到最大值,而在通信行为检测阶段其噪声功率达到最小值。此时,ηW达到最小值,最不利于Willie进行通信行为检测。本文称该条件下的Willie为最宽松的监控方,并称该条件为对于Alice到Bob隐蔽通信最有利的条件。为了保证Alice到Bob的通信行为不被最宽松的Willie检测到,只需要保证检测指标的最小值min(ηW)小于Willie的检测阈值γW,即若Allice端的发送功率和天线数满足式(11),则可以保证采用功率计检测通信行为的最宽松的Willie无法无误地检测到通信行为。
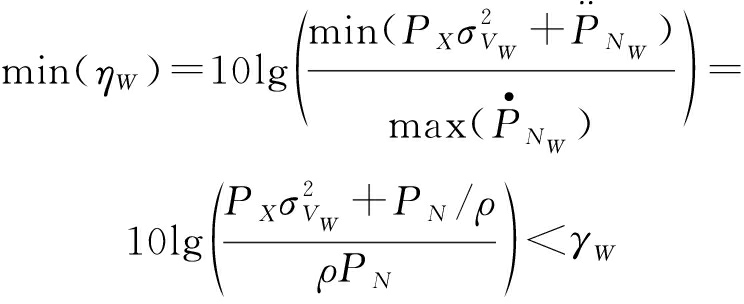
(11)
由式(8)和式(11)可知,若发送功率PX满足式(12)的约束,则可以在对于Willie检测最不利的场景中,保证Bob能够通过功率计检测到通信行为,而最宽松的Willie无法通过功率计无误地检测到通信行为。在上述对于Alice到Bob通信最有利的场景中,PX的取值范围的集合记作ABC
(12)
综合式(10)和式(12)可知,若PX大于式(12)中的PX上界,则Willie能够利用功率计始终无误地检测到通信行为;若PX小于式(10)中PX的上界,则Willie始终无法通过功率计检测到通信行为;若PX介于二者之间,则Willie能够利用功率计以一定的成功概率检测到通信行为。对比式(10)和式(12)可知,最宽松Willie条件下的功率范围比最严格Willie条件下的功率范围大。据此可知,面对最宽松的监控方Willie时,实现Alice到Bob的隐蔽通信对功率限制更加宽松;而面对最严格的监控方Willie时,实现Alice到Bob的隐蔽通信对功率限制更加严格。
3.3 平均遍历隐蔽通信速率
在无线通信中,检测是信息还原的基础,若不能检测到通信行为,接收机通常丢弃本次观测样本符号,不进行后续信息还原操作。当通过控制功率和天线数使得Bob能够准确检测,而采用特定检测准则(严格或者宽松)的Willie无法检测到隐蔽通信时,隐蔽通信速率为Alice向Bob传输的通信速率。
由于隐蔽通信速率的闭式解难以求解。因此,本小节借鉴平均遍历保密容量[12]的定义,引入平均遍历隐蔽通信速率,记作RCC,用于进一步分析隐蔽通信的影响因素以及变化规律。注意到,信道信息VB的分布信息是公开的。因此,通过对信道信息VB求期望,可以计算平均遍历隐蔽通信速率。具体而言,在最有利于和最不利于Alice到Bob隐蔽通信的条件下,PX分别属于集合ABC和集合AWC。这两种情况下的平均遍历隐蔽通信速率可以通过式(13)计算。
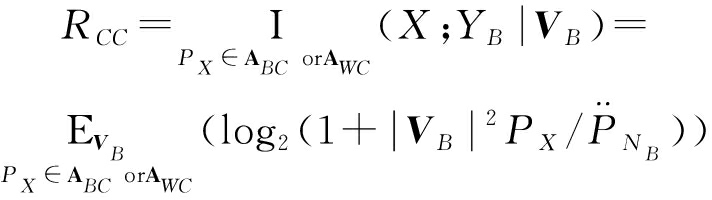
(13)
为了计算式(13),首先计算|VB|2的分布。当高斯随机变量Z的均值为0、方差为0.5,即Z～CN(0,0.5)时,Z2服从伽马分布,即Z2～Γ(0.5,1)。设随机变量
则S～Γ(M,1),且S的分布函数为
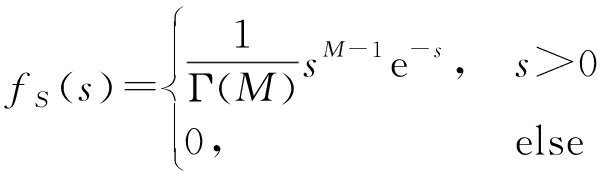
(14)
将式(14)代入式(13)可得在对于Willie隐蔽条件下,Alice向Bob传递信息的平均遍历隐蔽通信速率为
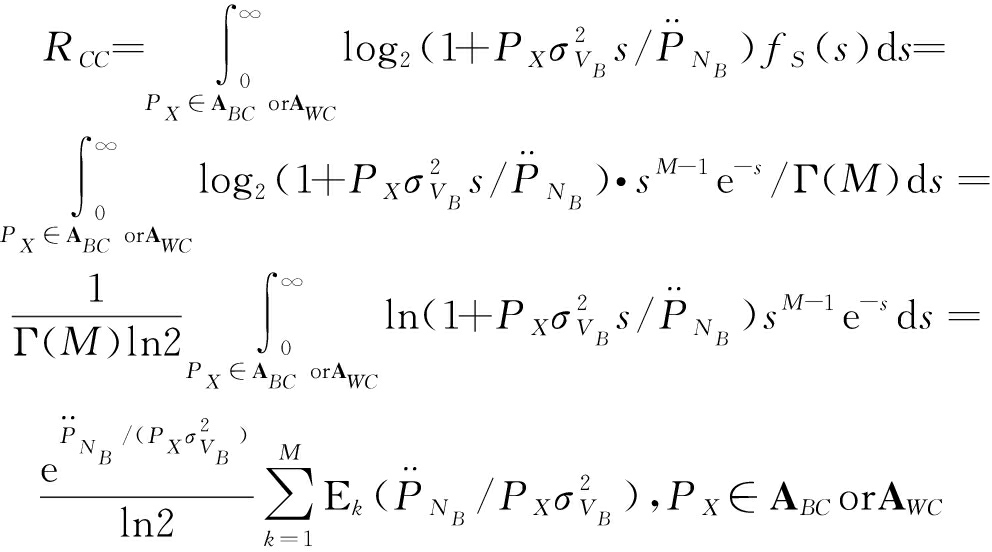
(15)
式(15)中运用的积分公式为
(16)
其中,En(z)表示指数积分(exponential integral),表达式为
En(z)=
e-ztt-ndt, (n=0,1,…,Re z>0)
(17)
由于
因此Alice与Bob之间的平均遍历隐蔽通信速率的取值集合ACC为
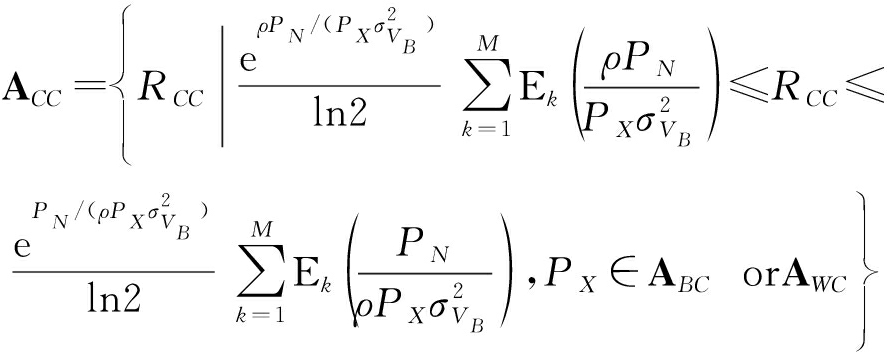
(18)
根据式(18)可知,RCC的影响因素包括天线数M,噪声不确定因子ρ,PX/PN,噪声方差
以及Alice和Bob所处场景(本文涉及对于Alice到Bob隐蔽通信最有利和最不利两种场景)。当环境给定时,和PN随之确定。因此,下文通过仿真实验分析M,PX,ρ,以及Alice和Bob所处场景对隐蔽通信的影响。
4 仿真分析
根据接收机检测能力存在极限的客观事实,在背景噪声存在不确定性且Willie检测能力优于Bob的条件下,本小节通过仿真实验,验证利用信道预编码技术能够实现正的隐蔽通信速率。仿真条件列举如下:
(1)设Bob和Willie均只有一根天线,Alice的天线数目M=10, 20, 30。
(2)无线信道VB和VW中的元素均服从均值为零、方差为1的复高斯随机分布,即
(3)设噪声方差名义值PN=1,信号功率PX与PN的比值PX/PN∈[0,1.5],噪声不确定因子ρ=1.05, 1.1, 1.15。
(4)假设Willie检测能力优于Bob。具体而言,本文假设γB=6 dB,γW=3dB。
(5)Alice和Bob所处场景设定为对Alice到Bob隐蔽通信最有利和最不利两种场景。
仿真步骤如下:
(1)按照仿真条件设定天线数,信道的分布,PN=1,PX/PN∈[0,1.5],ρ,γB=6 dB,和γW=3 dB。
(2)将仿真条件代入式(10)和式(12),得到对于Alice到Bob隐蔽通信最有利和最不利条件下的功率约束。
(3)在背景噪声测量阶段,根据Alice和Bob所处场景确定
和
在通信行为检测阶段,根据Alice和Bob所处场景确定
和
并依据PX/PN的取值确定PX。
(4)在通信行为检测阶段,按照CN(0,1)生成无线信道VB和VW的元素。重复该步骤106次,得到106组VB和VW的观测值。将观测数据代入Monte Carlo仿真,得到满足式(10)和式(12)约束的平均遍历隐蔽通信速率上下界的仿真估计值。
(5)将仿真条件代入式(18),得到满足式(10)和式(12)约束的平均遍历隐蔽通信速率上下界的理论值。
(6)改变仿真步骤(1)中参数设定,重复步骤(2)至步骤(5),得到平均遍历隐蔽通信速率随着Alice天线数M,PX/PN,以及ρ变化而变化的仿真估计值和理论计算值,据此得到系统中遍历隐蔽通信速率的仿真结果图,即图2～图4。其中,RCC表示依照式(18)计算的平均遍历隐蔽通信速率理论值,RCCsim表示Monte Carlo仿真实验估计出的平均隐蔽通信速率,“worst”表示式(10)约束条件下的隐蔽通信速率,“best”表示式(12)约束条件下的隐蔽通信速率,“up”表示速率上界,“down”表示速率下界。纵坐标表示信息速率,单位为比特每符号,表示Alice的M根天线发送一个UX符号后,能够向Bob传输的信息比特数。
观察图2～图4可以得出如下结论:
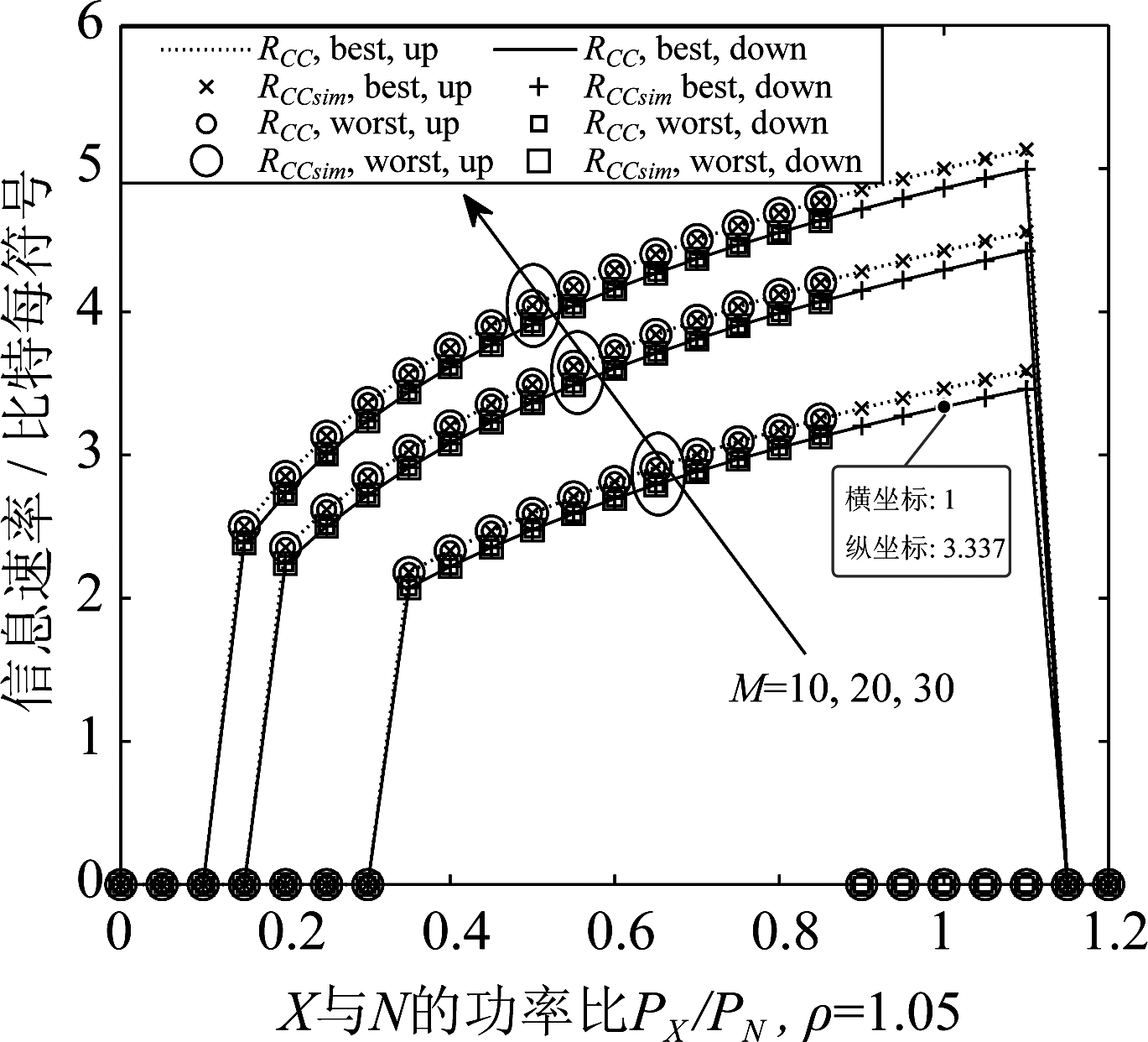
图2 平均遍历隐蔽通信速率随着PX/PN 的变化曲线,ρ=1.05
Fig.2 The curves of the average ergodic covert communication rate with PX/PN, ρ=1.05
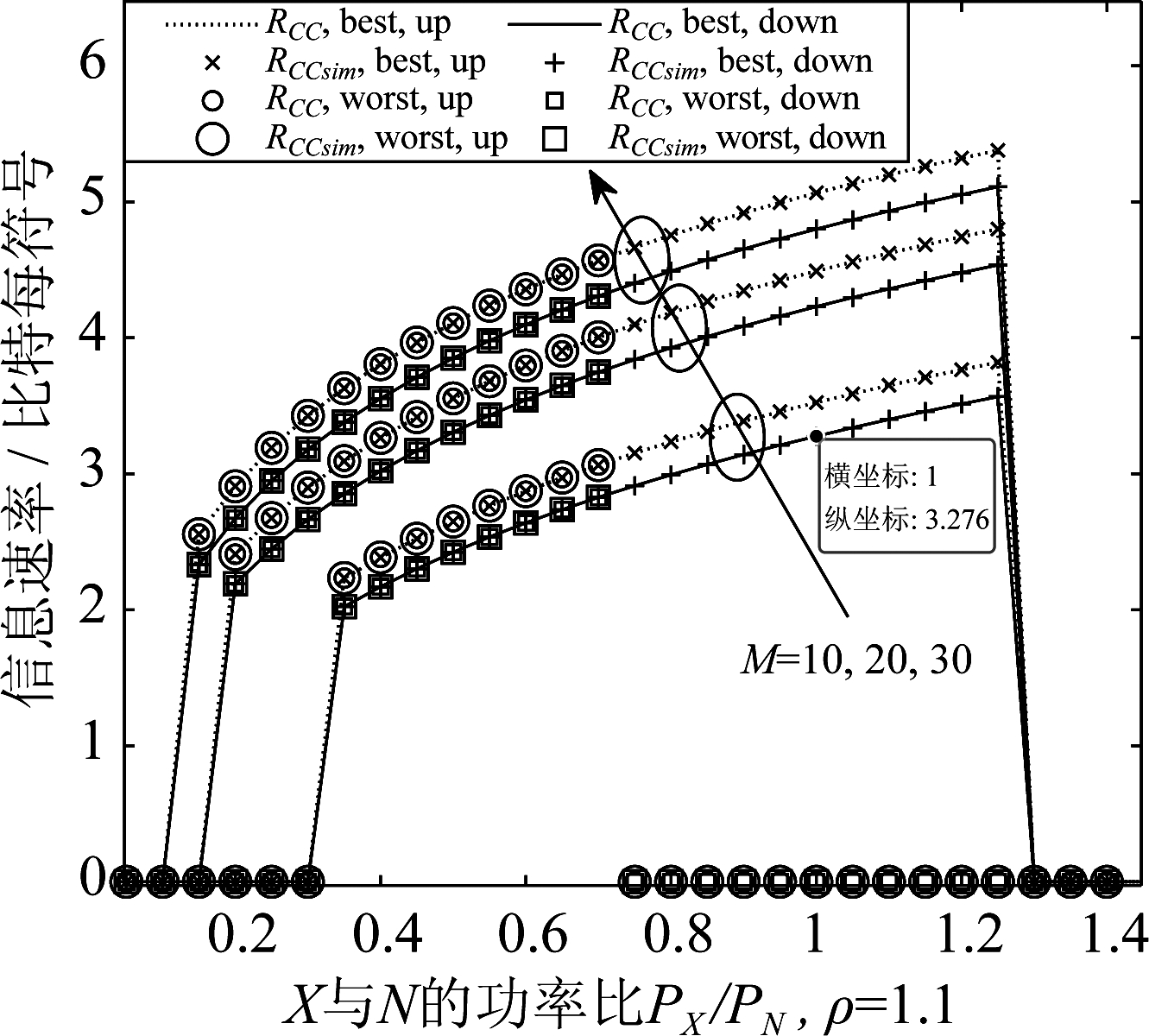
图3 平均遍历隐蔽通信速率随着PX/PN 的变化曲线,ρ=1.1
Fig.3 The curves of the average ergodic covert communication rate with PX/PN, ρ=1.1
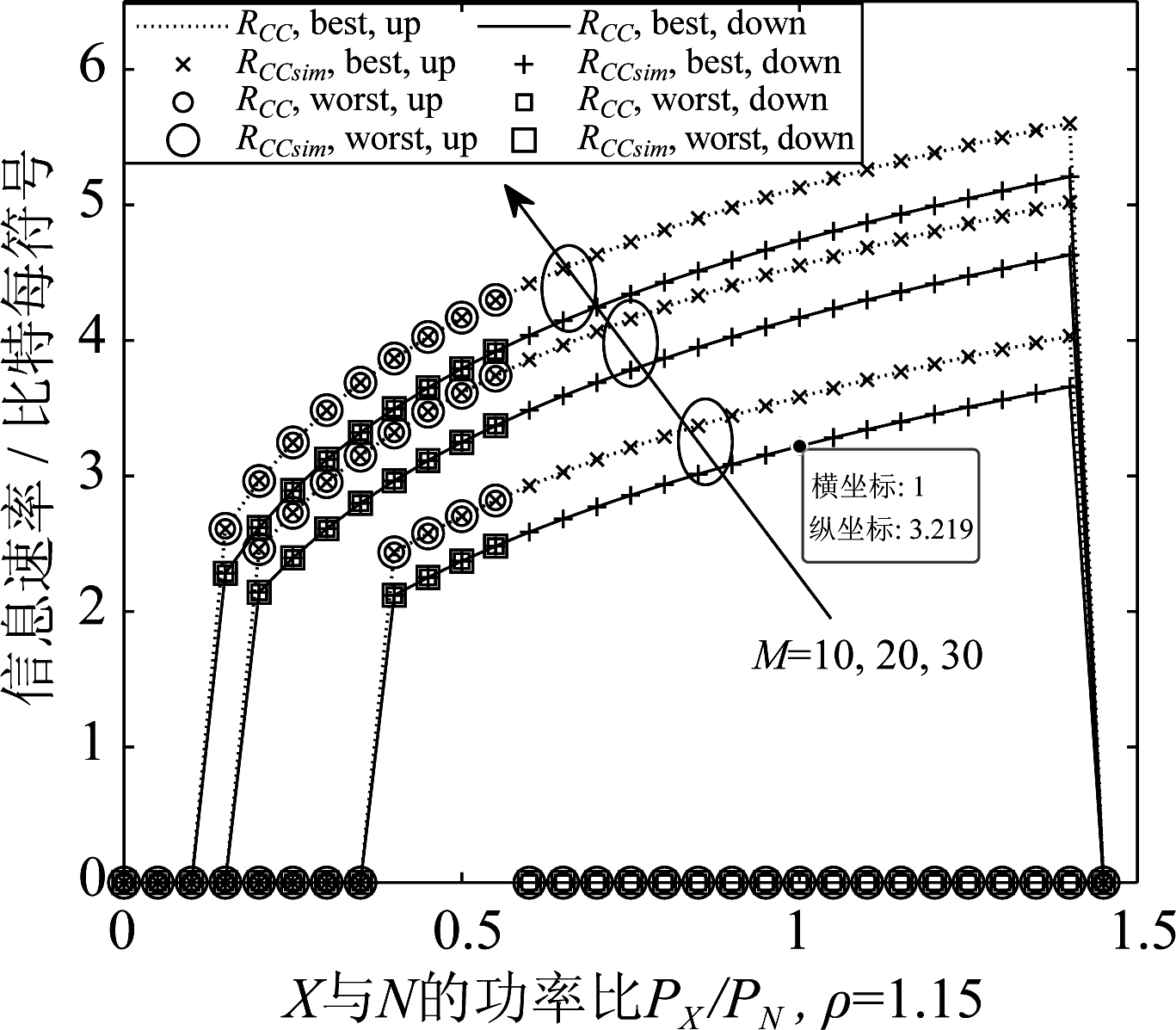
图4 平均遍历隐蔽通信速率随着PX/PN 的变化曲线,ρ=1.15
Fig.4 The curves of the average ergodic covert communication rate with PX/PN, ρ=1.15
(1)当ρ,M,以及Alice和Bob所处的场景给定时,利用信道预编码技术进行隐蔽通信时,通过控制发送天线数和发送功率,能够达到正的隐蔽通信速率,即所提方案能够实现隐蔽通信。且Monte Carlo仿真值与利用式(18)计算的理论值相吻合,从而验证推导结果的正确性。
(2)当ρ以及Alice和Bob所处的场景给定时,RCC随着M的增加而增加,且使得RCC>0的PX/PN的下界随着M的增加而减小。由此可知,通过增加M可以增加隐蔽通信速率和功率的取值空间,此时对于功率精确控制要求下降。
(3)隐蔽通信速率的上下界之间的距离随着ρ的增加而增加。通过对比图2～图4中,M=10且PX/PN=1时RCC下界的数值可知,隐蔽通信速率的下界随着ρ的增加而减小。
(4)通过对比图3和图4可知,当M给定时,实现正的隐蔽通信速率的功率取值范围的下界随着ρ的增加而增加。但是通信功率取值范围的上界随着Alice和Bob所处场景的不同而变化。在对于Alice到Bob隐蔽通信最不利的场景中,功率取值范围的上界随着ρ的增加而减小;在对于Alice到Bob隐蔽通信最有利的场景中,功率取值范围的上界随着ρ的增加而增加。相应地,在对于Alice到Bob隐蔽通信最不利的场景中,RCC的最大值随着ρ的增加而减小;在对于Alice到Bob隐蔽通信最有利的场景中,RCC的最大值随着ρ的增加而增加。
仿真结果表明,在对于Alice到Bob隐蔽通信最有利的场景中,噪声不确定性有助于提升隐蔽性能,该结论说明了当前研究中利用噪声不确定性实现隐蔽通信的合理性。但是在Alice到Bob隐蔽通信最不利的场景中,噪声不确定性恶化了隐蔽性能。因此,对于卧底警察而言,假设Willie采用宽松的检测准则过于乐观,不足以保证其安全。虽然在Alice到Bob隐蔽通信最不利的场景中,噪声不确定性导致隐蔽性能恶化,但是通过控制天线数和发送功率,依旧可以实现正的隐蔽通信速率。将M个子信道类比于文献[4]中的N次信道使用,结合图2～图4中仿真数值可知,式(18)得到的平均遍历隐蔽通信速率符合
律的要求。此外,由于噪声不确定性由环境决定,通过人为干预方式进行控制较难长期维持或者需要引入大量额外开销,因此,建议采用可控因素(如天线数和发送功率)来实现隐蔽通信。
最后需要说明的是,虽然在噪声功率确定的场景中,功率检测是最优的检测手段[6],但是在噪声功率存在不确定性的场景中,功率检测可能并不是最优的检测手段。因此,本文结论没有律适用范围广泛。但是本文利用任一接收机都存在检测极限的客观事实,为检测能力处于劣势的通信双方提供了一种实现隐蔽通信候选方案。在实际中,工业制造水平往往是公开的,因此接收机检测能力极限通常可以获知。除此之外,通过假设Willie的检测能力超过当前工艺水平条件下的接收机最强检测能力,能够实现存在代差优势的单向隐蔽通信。
5 结论
本文在具有噪声不确定性的场景中,研究对于监控方检测最有利条件下的单向隐蔽通信问题。此时,具有检测能力优势的监控方采用最严格的监控准则。首先,采用信道预编码技术保证接收信号在接收机处同相叠加,而在监控方处异相相消,进而实现基于信道差异的单向隐蔽通信。其次,在对于监控方检测最有利和最不利场景中,分析了单向隐蔽通信的约束条件,并推导了满足不同隐蔽约束的平均遍历隐蔽通信速率的闭式解。理论分析和仿真结果表明,在对于监控方检测最有利的场景中,噪声不确定性对隐蔽通信有负面作用。此时,隐蔽通信对于功率控制要求更高,且最大隐蔽通信速率下降。尽管如此,仍然可以通过增加天线数量的方式消除噪声不确定性对隐蔽通信的负面作用,并且实现正的隐蔽通信速率。除此之外,通过设定监控方检测能力具有代差优势,能够实现存在代差优势的单向隐蔽通信。后续将研究收发双方以及监控方均配备多天线条件下的隐蔽通信问题。
[1] YAN Shihao, ZHOU Xiangyun, HU Jinsong, et al. Low probability of detection communication: opportunities and challenges[J]. IEEE Wireless Communications, 2019, 26(5): 19-25.
[2] GOLDSMITH A. Wireless communications[M]. Cambridge, UK: Cambridge University Press, 2005: 337-342.
[3] PICKHOLTZ R L, SCHILLING D L, MILSTEIN L B. Theory of spread-spectrum communications-a tutorial[J]. IEEE Transactions on Communications, 1982, 30(5): 855- 884.
[4] BASH B A, GOECKEL D, TOWSLEY D. Limits of reliable communication with low probability of detection on awgn channels[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 1921-1930.
[5] TANDRA R, SAHAI A. SNR walls for signal detection[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 4-17.
[6] LEE S, BAXLEY R J, WEITNAUER M A, et al. Achieving undetectable communication[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(7): 1195-1205.
[7] HE Biao, YAN Shihao, ZHOU Xiangyun, et al. On covert communication with noise uncertainty[J]. IEEE Communications Letters, 2017, 21(4): 941- 944.
[8] 林钰达, 金梁, 周游, 等. 噪声不确定时基于波束成形的隐蔽无线通信性能分析[J]. 通信学报, 2020, 41(7): 49-58.
LIN Yuda, JIN Liang, ZHOU You, et al. Performance analysis of covert wireless communication based on beam forming with noise uncertainty[J]. Journal on Communications, 2020, 41(7): 49-58. (in Chinese)
[9] SOBERS T V, BASH B A, GUHA S, et al. Covert communication in the presence of an uninformed jammer[J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 6193-6206.
[10] JENN D C. Radar and laser cross section engineering[M]. Second Edition. Reston, Virginia: American Institute of Aeronautics and Astronautics Inc., 2005: 1-11.
[11] POOR H V, SCHAEFER R F. Wireless physical layer security[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(1): 1- 8.
[12] ZHOU Xiangyun, MCKAY M R. Secure transmission with artificial noise over fading channels: achievable rate and optimal power allocation[J]. IEEE Transactions on Vehicular Technology, 2010, 59(8): 3831- 3842.
[13] ZHENG Tongxing, WANG Huiming, NG D W K, et al. Multi-antenna covert communications in random wireless networks[J]. IEEE Transactions on Wireless Communications, 2019, 18(3): 1974- 1987.
[14] SOLTANI R, GOECKEL D, TOWSLEY D, et al. Covert wireless communication with artificial noise generation[J]. IEEE Transactions on Wireless Communications, 2018, 17(11): 7252- 7267.
[15] SOBERS T V, BASH B A, GUHA S, et al. Covert communications on continuous-time channels in the presence of jamming[C]∥Proceedings of the 51st Asilomar Conference on Signals, Systems, and Computers. Pacific Grove: IEEE, 2017: 1697-1701.
[16] SHMUEL O, COHEN A, GUREWITZ O, et al. Jamming strategies in covert communication[C]∥Proceedings of the 3rd International Symposium Cyber Security, Cryptography, and Machine Learning. Beer-Sheva, Israel: Springer, 2019: 1-15.
