1 引言
双基合成孔径雷达(Bistatic Synthetic Aperture Radar,BiSAR)作为一种遥感微波有源成像系统,具有全天时、全天候和高分辨率成像等工作特点[1-2]。由于发射平台和接收平台分置工作,与单基SAR相比,在运用上有更大的灵活性,能够获取更丰富的信息,作用距离更远,基于这些优势,BiSAR在军事侦察、资源勘测等方面具有广阔的应用前景[3]。机载BiSAR受到大气湍流或其他外界因素影响时,其运动轨迹不再是匀速直线运动,会不可避免的引入加速度从而使得雷达平台偏离理想航线,这会增加距离-方位向的耦合以及多普勒调频率的空间移变性,从而影响成像质量,因此其成像轨迹中必须考虑加速度的影响[4-5]。方位回波信号为非线性调频信号,不能再通过理想匀速直线运动的多普勒中心和多普勒调频率来生成方位压缩函数处理回波信号,否则会降低聚焦效果引起图像畸变。因此,有必要提出新的算法来处理具有加速度的BiSAR数据。
BiSAR收发平台分置的结构导致斜距函数为两个双曲线之和,即斜距历程由发射平台与目标之间距离与接收平台与目标之间距离共同决定[6- 8],而加速度的存在,使双基SAR的斜距模型更趋复杂,这给二维频谱解析式的求解带来了困难。双基SAR回波信号中,距离徙动包含线性距离走动(Linear Range Cell Migration,LRCM)[9]和剩余RCM,LRCM中包含大部分的距离多普勒耦合,不利于MSR的应用[10],应将它们去除进而提高算法的运算效率。频谱相位中存在距离和方位的耦合项,这个耦合项不能直接补偿,一般是通过Stolt插值[11]处理来解除此耦合,但是这种做法的缺点是效率较低。针对双基SAR算法问题,已研究出多种理论和算法。Loffeld利用Taylor展开和驻留相位原理,推导出了一种二维频谱求解方法[12]；级数反演法(Method of Series reversion,MSR)[13]理论上也可以得到精确的二维频谱,其精度取决于展开项的级数。文献[15]利用级数反演法推导出二维频谱,考虑了平台高速度和加速度问题,在适当近似斜距基础上,解决了斜距中高阶误差问题。文献[14]提出了一种全孔径频域算法,对非线性斜距进行多项式拟合,再利用扩展的NLCS算法对目标聚焦,解决了具有非线性路径和非平坦地形双基前视SAR的成像问题。文献[14]和文献[15]都是在频域考虑了距离和方位向耦合问题,但算法中没有考虑方位向的空变性,降低了算法的适用性。文献[16]是针对双基SAR的NLCS算法,但只考虑了平台的三维速度,忽略了因大气湍流等引起的三维加速度带来的误差影响。文献[17]将KT(keystone transform)变换应用于NLCS算法中,修正了双基SAR静止场景中运动目标的LRCM,但忽略了剩余RCM,使得聚焦效果在方位和距离向有比较大的衰减。文献[18]采用逆映射插值操作解决了空间相位误差和图像畸变问题,实现了运动误差、几何畸变的局部补偿,得到了无畸变的SAR地面图像,但该方法实现效率较低。文献[19]提出了一种自适应NLCS技术,校正了高阶RCM并平衡了多普勒参数的空变性,但是该方法只适用于前视SAR的运动目标模式,适用范围受限。文献[20]是将斜距采用Taylor级数展开,方位向通过NLCS算法均衡了不同点目标的调频率,但对合成孔径时间有约束,大的合成孔径时间下会发生频谱混叠现象。
本文在前人研究的基础上,针对加速度影响下BiSAR系统成像的要求,首先对斜距函数进行Chebyshev正交分解,然后近似为幂级数形式,提高了斜距的近似精度。有效补偿了LRCM和多普勒线性相位,便于利用MSR得到精确的二维频谱。其次,为了提高处理精度和效率,提出了一种二维频谱的正交解耦合方法,即利用Chebyshev正交多项式对二维谱的耦合相位进行三阶近似,以构造精确的相位补偿函数,从而解除距离和方位的耦合,代替了传统的Stolt插值处理方法,在二维频域进行距离向的剩余相位补偿。最后在距离多普勒域完成方位补偿及成像。
2 双基SAR信号模型
2.1 信号模型
图1所示为加速度作用下双基SAR的几何空间模型,地面设置了25个静态点目标,场景中心点为P13(X0,Y0,0),T和R分别表示发射平台和接收平台,发射平台和接收平台分别沿不同路径,以不同速度VT和VR在不同高度飞行,且具有不同的加速度aT和aR。
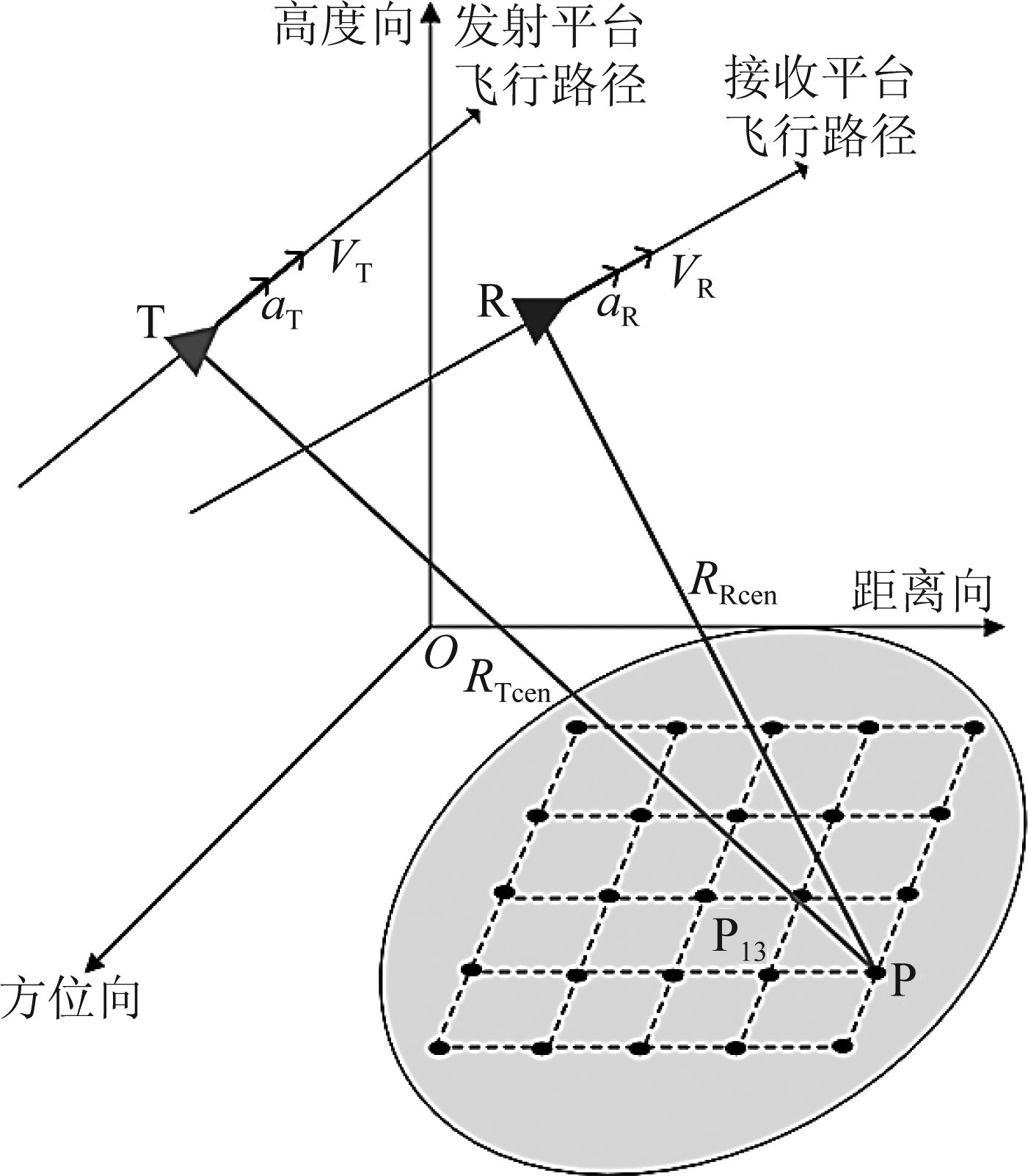
图1 具有加速度的BiSAR几何空间模型
Fig.1 Geometric space model of BiSAR with acceleration
假设t=0时,P13处于波束中心。当t=t0时,波束中心照射到点目标P,此时其斜距分别为RTcen和RRcen；θT和θR分别为发射平台和接收平台的斜视角。点目标P的瞬时斜距总历程为
R(t)=RT(t)+RR(t)
(1)
其中,
(i为T或R,表示收发平台)。
场景区域点目标的回波信号可以表示为式(2)。
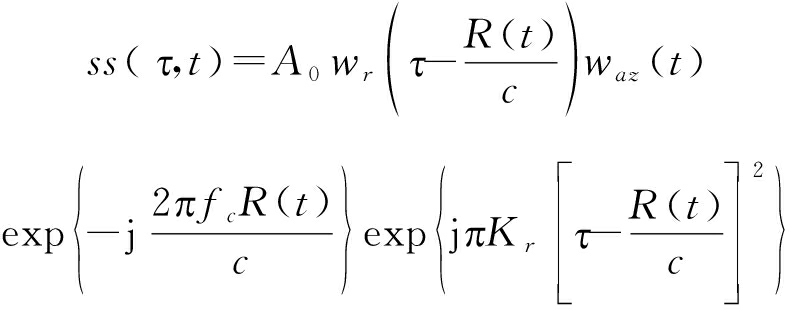
(2)
其中,A0是点目标的后向散射系数,τ和t∈[-Tsar/2,Tsar/2]分别为距离向快时间和方位向慢时间,Tsar是合成孔径时间；wr(·)和waz(·)分别为距离窗函数和方位窗函数；c为光速； fc为载波频率；Kr为发射信号的调频率。
2.2 斜距近似处理
由于双基SAR斜距函数的双根号形式,不便于相位频谱函数的解析式求解,文献[15]对斜距历程在t=0处展开为Taylor级数形式,而由Taylor级数的数学模型的特性可知,在阶数一定的情况下,近似误差会随着远离展开点而单调增加,斜距误差增加会导致方位向补偿不完全,甚至产生散焦,聚焦深度不完全的情况。针对这一情况,本文提出了一种采用Chebyshev正交多项式来近似斜距函数R(t)的方法,有效减小了斜距误差,提高了斜距精度,具体过程见附录A。
经整理合并得到加速度作用下双基SAR斜距的Chebyshev分解式为
R(t)=p0+p1(t-t0)+p2(t-t0)2+
p3(t-t0)3+p4(t-t0)4
(3)
其中,
是初始斜距,p1是线性距离走动项系数,p2是距离弯曲项系数,p3和p4是高阶项系数。
图2是基于Chebyshev和Taylor的四阶斜距误差对比,系统参数如表1所示,中心点目标距离和方位向坐标为(3700 m,1250 m),各点之间间隔200 m。图2(a)是无加速度时的四阶斜距误差对比,当Tsar=12 s时,实验测得此时斜距近似产生的多普勒相位误差为
故Tsar=12 s为斜距误差临界时间,而
此时的斜距误差分别为ΔRTay=71.02 m、ΔRChe=5.51 m,随着时间积累Tsar>12 s后,基于Taylor分解的斜距逐渐偏离真实斜距,其误差逐渐增大,不可忽略,基于Chebyshev分解的斜距基本与真实斜距重合,其斜距误差可忽略。图2(b)是当加速度aT=10 m/s2,aR=15 m/s2时基于Chebyshev和Taylor分解的四阶斜距误差对比,同上述分析,当Tsar=9 s时,
此时的斜距误差分别为ΔRTay=339.56 m,ΔRChe=23.22 m,随着时间积累Tsar>9 s后,基于Taylor分解的斜距误差逐渐增大,基于Chebyshev分解的斜距误差仍然很小。综上所述,基于Chebyshev多项式分解的斜距函数误差较小、精度高,且可弱化因加速度增大而带来的误差。
表1 系统参数
Tab.1 System parameter
系统参数发射平台接收平台载波频率13 GHz信号带宽脉冲重复频率190 MHz900 Hz飞行速度300 m/s400 m/s初始斜距10 km8 km
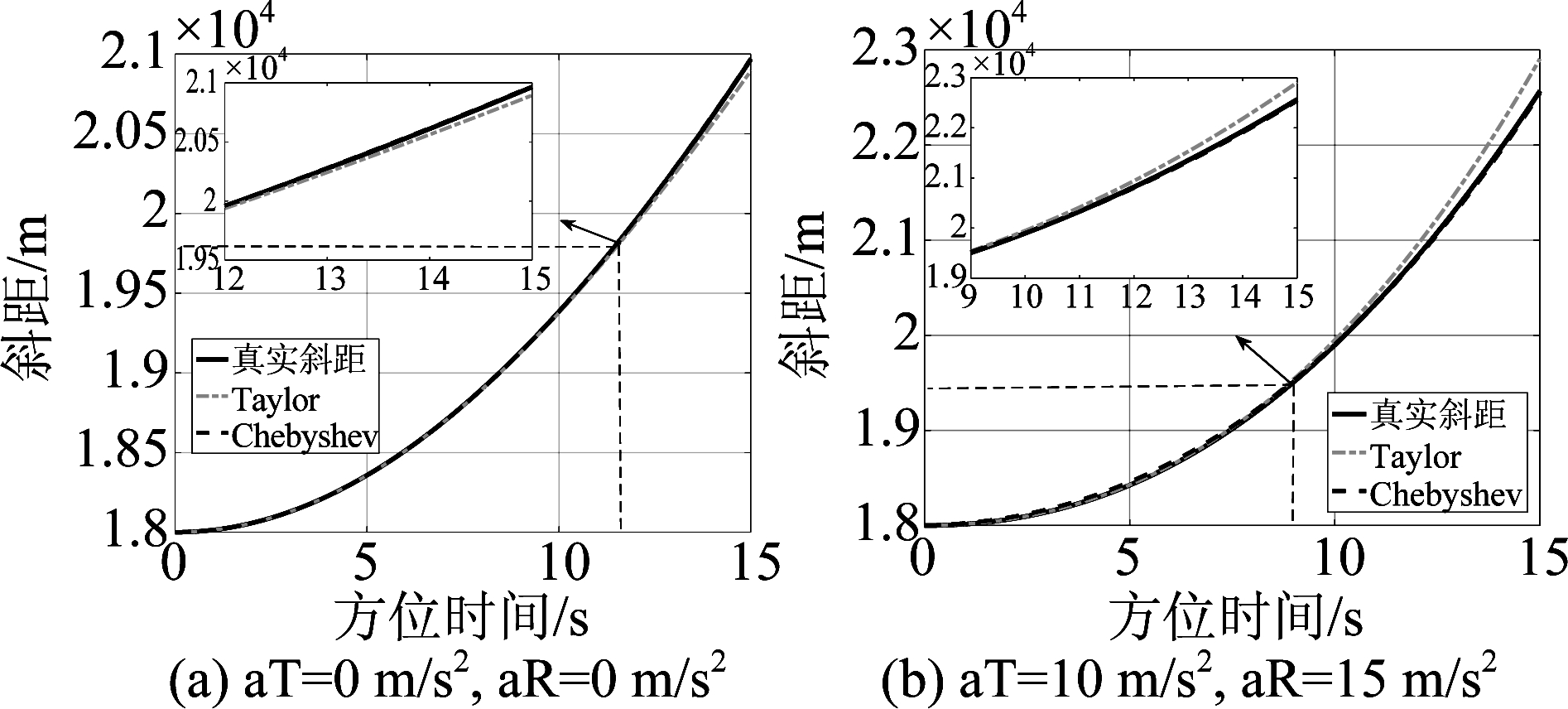
图2 两种斜距近似方法对比
Fig.2 Comparison of two slant range approximation methods
3 成像处理
3.1 LRCM校正和线性相位去除
点目标的斜距轨迹一般包含LRCM分量和非线性RCM分量,而大部分的距离多普勒耦合都来自LRCM,因此需要通过LRCMC操作去除此LRCM分量,将目标轨迹与方位轴对齐,以便于利用MSR求得二维频谱进而进行方位补偿。计算出相对参考点(中心点处t0=0)的双向的距离偏移量为:
(4)
对式(1)作距离向Fourier变换得:
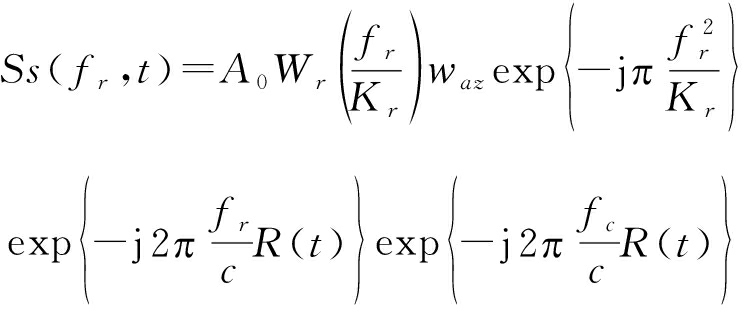
(5)
在距离频域-方位时域进行距离压缩和LRCMC,补偿函数为
(6)
场景中心点经过LRCMC后的斜距函数为
R1(t)=p0+p2(t-t0)2+p3(t-t0)3+p4(t-t0)4+…
(7)
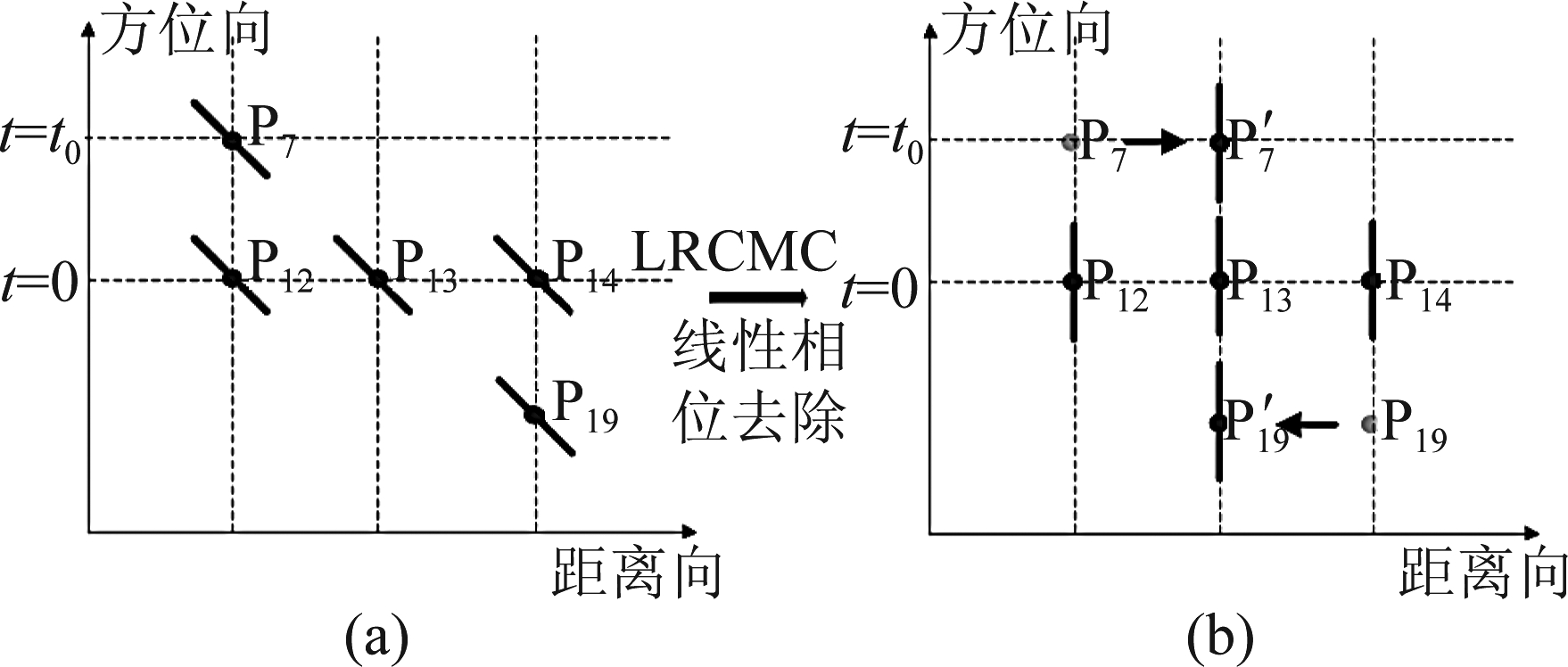
图3 LRCMC操作示意图
Fig.3 LRCMC operation diagram
如图3(a)所示场景区域有五个点目标,P13为参考点,P13、P12与P14具有相同的波束中心时刻；P12与P7、P14与P19有相同的最近斜距,在同一个距离单元内。经过LRCMC操作后,P7、P19点时移
变为
如图3(b)所示与P1位于相同的距离单元内。
虽然LRCMC去除了斜距历程的线性平移分量,但没有消除多普勒频移引起的线性相位项,为了便于应用MSR,应将此线性相位去除,进而消除距离和方位的线性耦合。对式(5)经过LRCMC和距离压缩的回波信号在距离频域-方位时域进行线性相位去除,相应的匹配滤波函数为
(8)
经过LRCMC和线性相位去除后的点目标回波信号表示为
(9)
3.2 二维频谱
对经过预处理的回波信号式(9)作方位向Fourier变换,得到点目标的二维频谱:
exp(-j 2πfat)dt
(10)
要得到式(10)的精确解析表达式,可采用驻留相位原理,但由于双基SAR斜距的复杂性,直接用驻留相位原理很难求得其准确解析式。
利用驻留相位原理和MSR求得驻留相位点如式(11)
3p3(t-t0)2+4p4(t-t0)3
(11)
其中,
为了得到原始回波信号ss(τ,t)的点目标二维频谱,利用Fourier变换的频移性质
(12)
联立式(10)～(12),并保留fa的四阶以下相位,得到恒加速度作用下双基SAR的点目标回波
(13)
其中二维频谱相位为
(14)
同样,由于式(14)中存在fr与fa的耦合,所以对式(14)中的
和
采用Chebyshev多项式展开为fr幂级数形式,由于fr∈[-Br/2,Br/2],Br为LFM信号带宽,首先进行归一化处理,即令
最后整理为关于fr的三阶幂级数形式,如式(15)。
(15)
利用附录A中的Chebyshev递推式可以得出
通过机载条件下仿真得到三阶展开的最大相位误差,如图4所示,故将相位展开到三阶即可满足算法的误差极限要求。
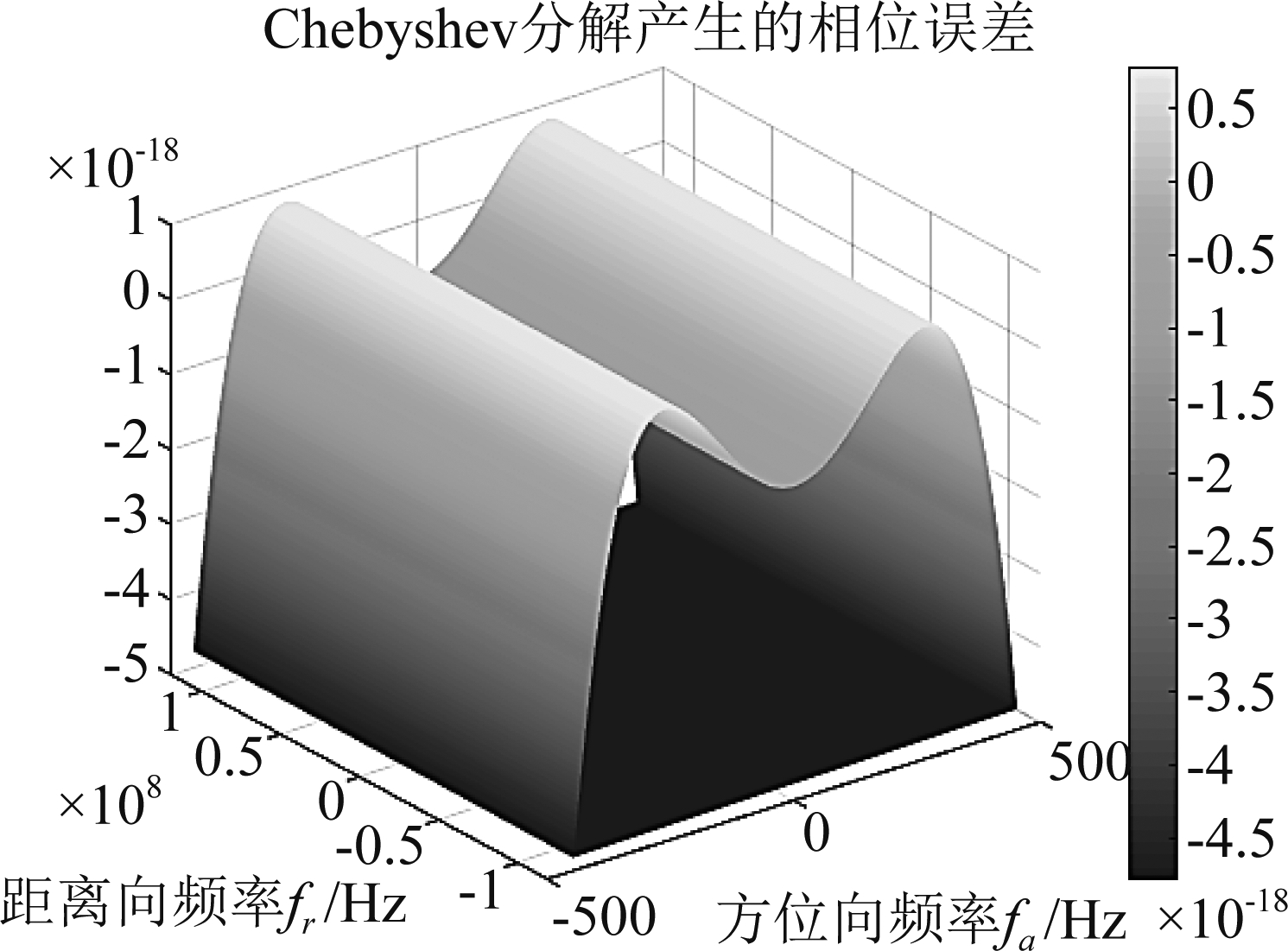
图4 三阶相位误差
Fig.4 Third order phase error
将式(15)代入式(14)整理合并,二维频谱相位表示为
ψ(fr, fa)=φ0(fc)+φ1(fa)fr+
(16)
其中φ0(fc),φ1(fa),φ2(fa),φ3(fa),φ4(fa)详见附录B。
考察式(16)中各个相位项,φ0(fc)与fr和fa都无关,对应常数相位项；φ1(fa)fr是fr的一次函数,还与fa有关,对应剩余距离徙动
是fr的二次函数,对应二次距离压缩
是fr的三次函数,还与fa有关,对应高次耦合项；φ4(fa)只与fa有关,是方位调制项,对应方位压缩。
3.3 距离向和方位向处理
经过上述分析可知:虽然加速度使双基SAR的斜距方程更复杂,从而增加了回波信号距离和方位的耦合。但通过对二维频谱的正交分解,能有效解除该耦合,成像处理流程图如图5所示。首先通过预处理,完成LRCMC和线性相位去除,将不同距离单元的点目标校正在同一个距离单元内。然后利用MSR得到基于Chebyshev多项式近似的点目标二维频谱精确解析式。再利用Chebyshev多项式对二维频谱相位中fr和fa的耦合项进行正交分解,从而解除距离和方位向的耦合,以便构造精确的相位补偿函数。这取代了经典波数域算法中的Stolt插值处理,该方法较Stolt插值运算效率更高。下面将详细推导出各相位补偿函数。
图5 算法流程图
Fig.5 Algorithm flow chart
将完成预处理后的信号变换到二维频域先进行距离向处理,其中常数相位补偿函数为
H1=exp{-jφ0(fc)}
(17)
然后进行剩余距离徙动校正,补偿函数为
H2=exp{-jφ1(fa)fr}
(18)
在二维频域进行二次距离压缩,补偿函数为
(19)
在二维频域进行fr的高阶相位补偿,补偿函数为
(20)
距离向相位处理完成后,作距离向IFFT,在距离-多普勒域进行方位向补偿,补偿函数为
Hac=exp{-jφ4(fa)}
(21)
最后经方位IFFT,得到点目标的聚焦图像。该算法忽略了四阶及更高阶的耦合相位项,本文第4节通过仿真实验证明该算法的有效性。
算法运算复杂度的分析可以用算法的计算量来描述,在信号处理中,一般情况下,N点的FFT或IFFT运算的计算量是5Nlog2N次浮点运算,一次复数乘法的计算量是6N次浮点运算。由图5算法流程图可知,本文算法的运算量包括距离向一次FFT和一次IFFT,方位向一次FFT和一次IFFT,以及四次复数乘法运算,距离向和方位向的采样点数分别用Nr和Na表示,则本文算法的计算量为CC,文献[20]算法的计算量为CT,如式(22)。比较CC和CT后可知,本文算法的计算量更小,故运算复杂度更小。
CC=10NaNrlog2Nr+10NaNrlog2Na+24NaNr
CT=10NaNrlog2Nr+20NaNrlog2Na+42NaNr
(22)
4 实验仿真及误差分析
为了验证二维频谱正交去耦合方法的有效性和可行性,采用表2中的机载SAR参数进行仿真。
表2 仿真参数
Tab.2 Simulation parameter
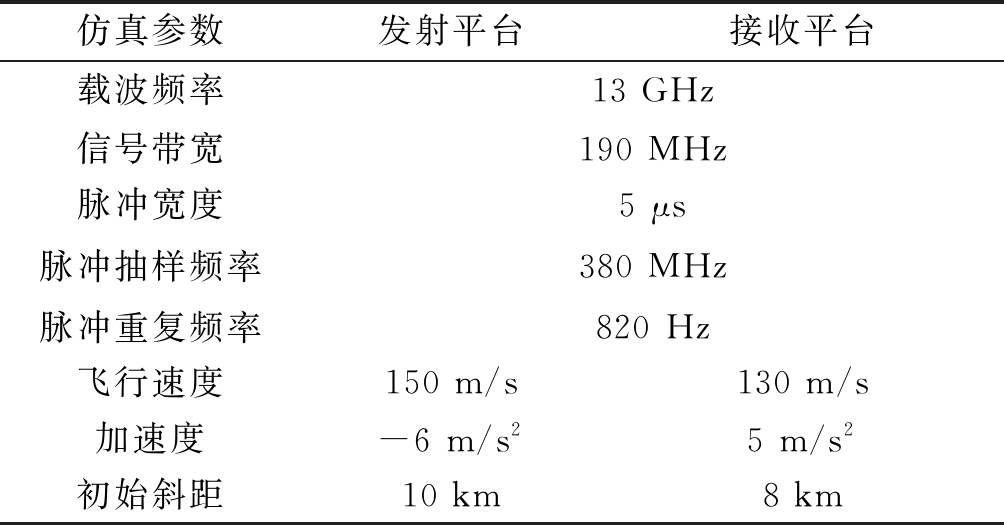
仿真参数发射平台接收平台载波频率13 GHz信号带宽190 MHz脉冲宽度脉冲抽样频率脉冲重复频率5 μs380 MHz820 Hz飞行速度150 m/s130 m/s加速度-6 m/s25 m/s2初始斜距10 km8 km
通过实验仿真,得出本文算法模型适用的正向加速度范围为[0 m/s2,23 m/s2],负向加速度范围为[-13 m/s2,0 m/s2],选取此范围内的任意加速度进行三种算法的仿真对比。仿真使用了25个点目标阵列,它们排列在2000 m×8000 m的成像区域内,如图6所示。
图6 场景区域25点目标分布示意图
Fig.6 Diagram of target distribution of 25 points in scene area
图7(a)、(b)分别不同加速度下基于Chebyshev多项式的改进算法的多点目标等高线图对比。可以看出,无加速度作用和有恒定加速度作用下的点目标在成像区域内均匀分布,各个点目标在距离向和方位向均得到良好聚焦,验证了本文算法能补偿加速度的运动误差,从而对点目标进行有效成像。
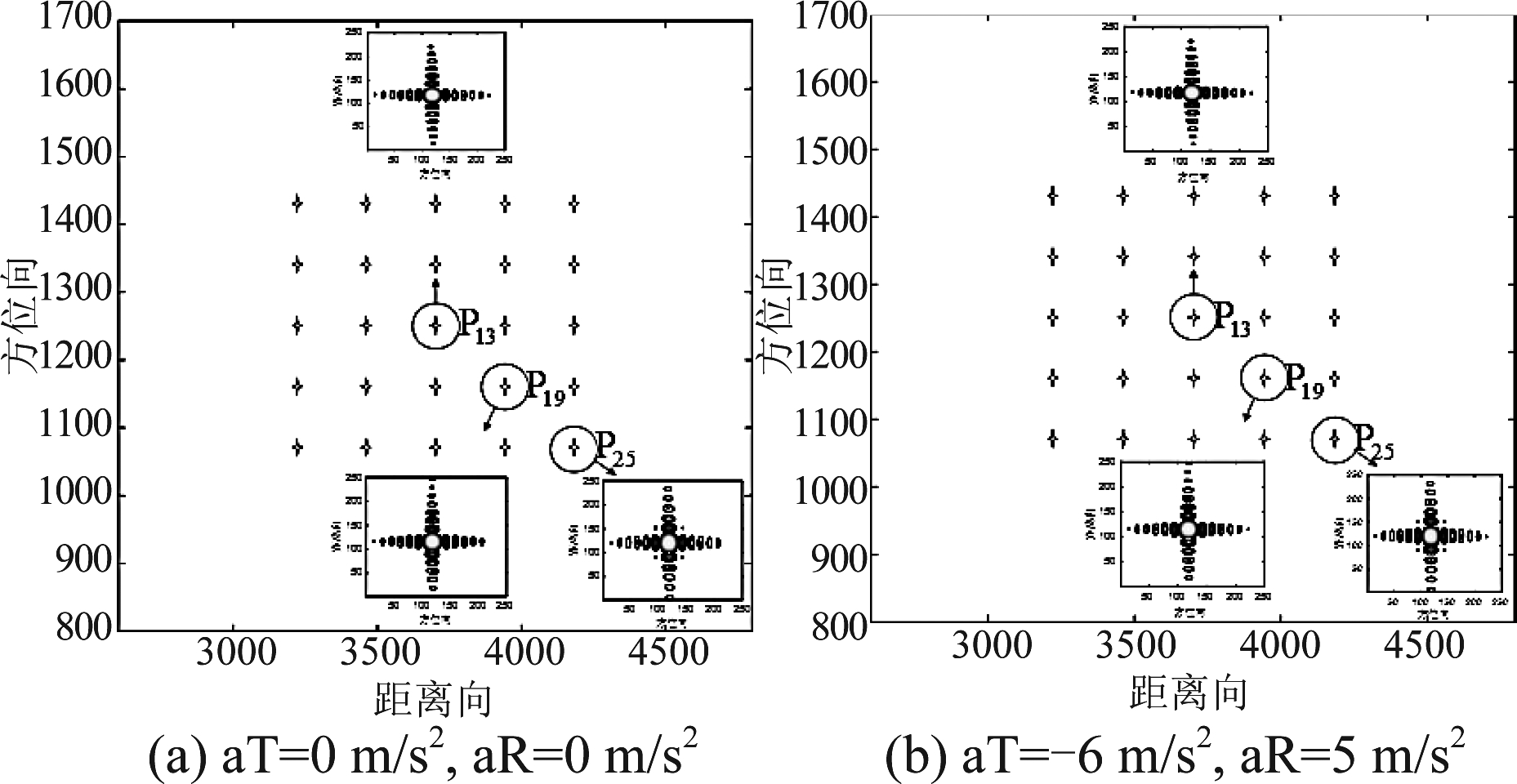
图7 不同加速度下基于Chebyshev多项式的改进算法的多点目标等高线图对比
Fig.7 Comparison of multi-point target contour map with improved Algorithm based on Chebyshev decoupling at different accelerations
图8是加速度作用时本文算法与传统的直线运动BiSAR处理算法任意点目标等高线图的对比。可以看出,传统的直线运动BiSAR处理算法对点目标方位像成像质量很差,且方位向分辨率也较低。而本文的改进算法能够很好的补偿加速度带来的运动误差,对点目标良好成像,且积分旁瓣比和峰值旁瓣比都接近理想数值。
图8 aT=-6 m/s2,aR=5 m/s2时两种算法等高线图对比
Fig.8 Comparison of contour map between the two algorithms when aT=-6 m/s2,aR=5 m/s2
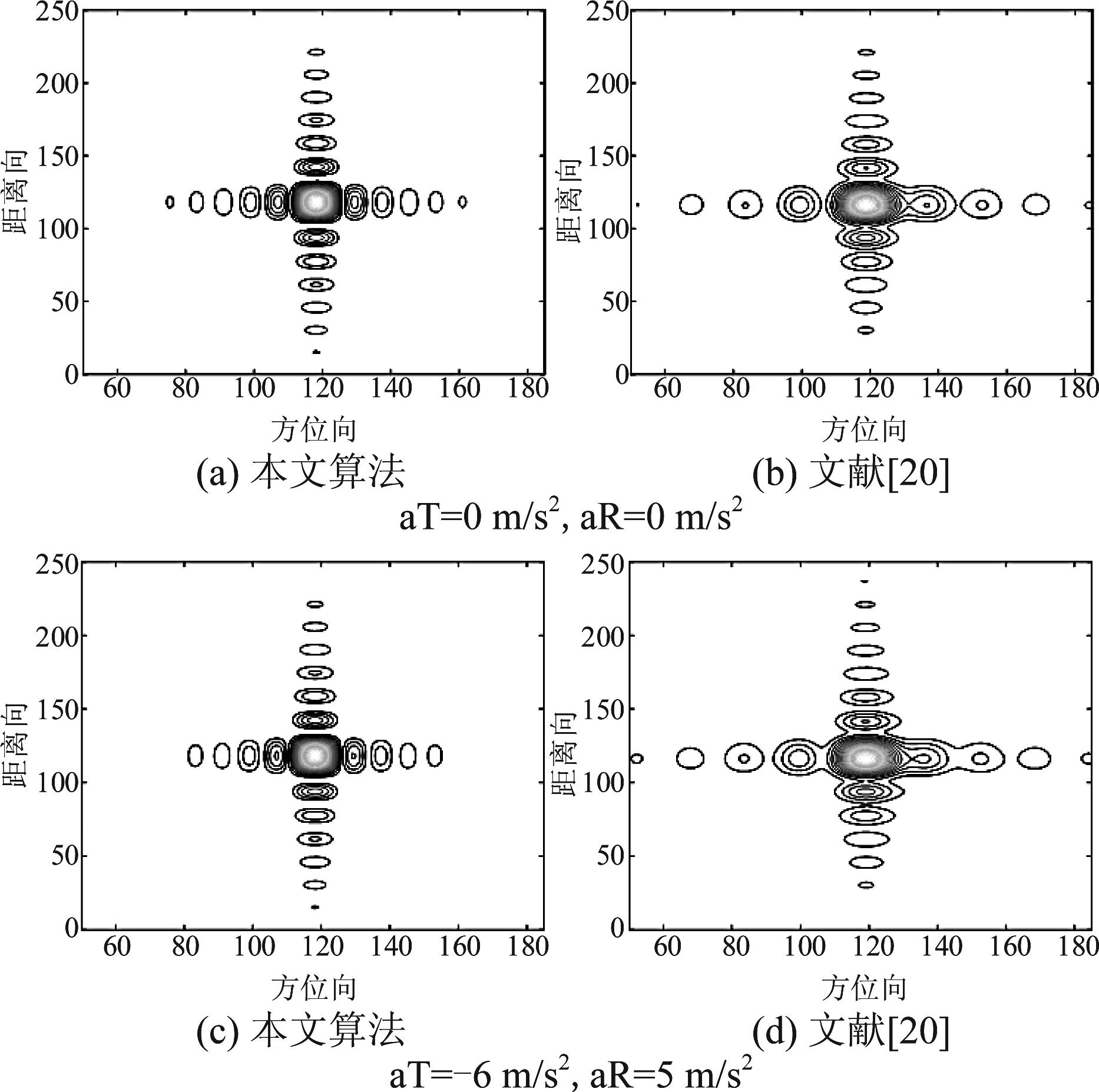
图9 两种算法的中心点P13等高线图对比
Fig.9 Comparison of the contour chart of the point P13 of the two algorithms
图9～图12是有无加速度作用时基于Chebyshev解耦合的改进算法与文献[20]的ENLCS算法的中心点P13和边缘点P25的等高线图和脉冲响应剖面图对比。为了评估不同算法的成像性能,表3分别计算了不同加速度作用下中心点和边缘点的方位和距离向的ISLR和PSLR,以及分辨率。对于中心点P13,在有无加速度作用下,本文算法都可以实现高分辨率成像,且从表3可知,其PSLR和ISLR都接近理想值；在大的合成孔径时间积累下,文献[20]算法成像存在频谱混叠现象,出现虚假目标,如图13所示,这种现象在SAR成像中是不允许的,由图10和图11的(b)、(d)可以看出,方位向脉冲响应的主瓣较宽,旁瓣升高,且不对称性较明显,表2的数据表明了该算法的分辨率也较低。
图10 两种算法的边缘点P25等高线图对比
Fig.10 Comparison of the contour chart of the point P25 of the two algorithms
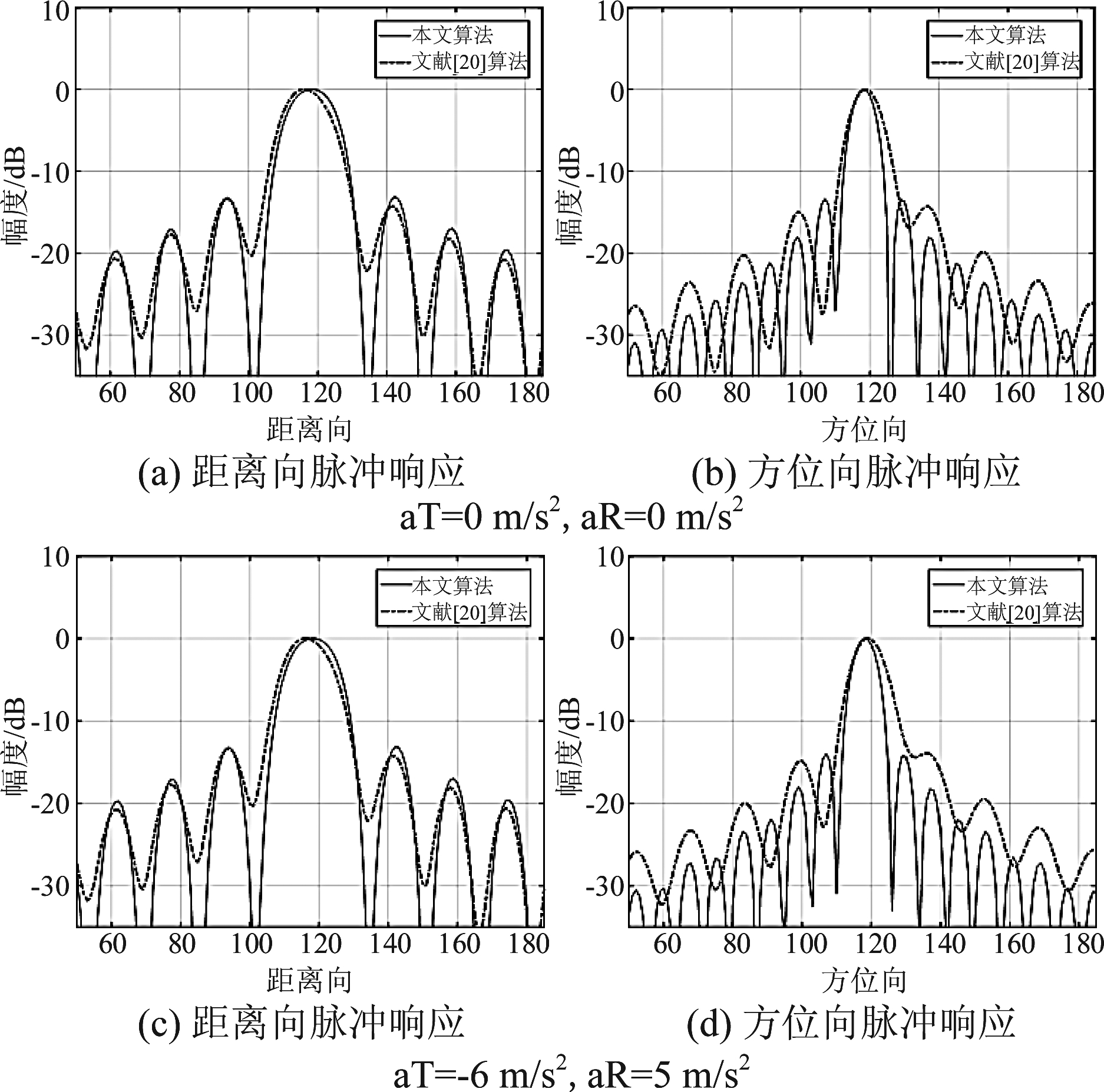
图11 两种算法的中心点P13脉冲响应对比
Fig.11 Comparison of impulse response between point P13 of the two algorithms
图12 两种算法的边缘点P25脉冲响应对比
Fig.12 Comparison of impulse response between point P25 of the two algorithms
表3 BiSAR成像质量评估
Tab.3 BiSAR imaging quality assessment
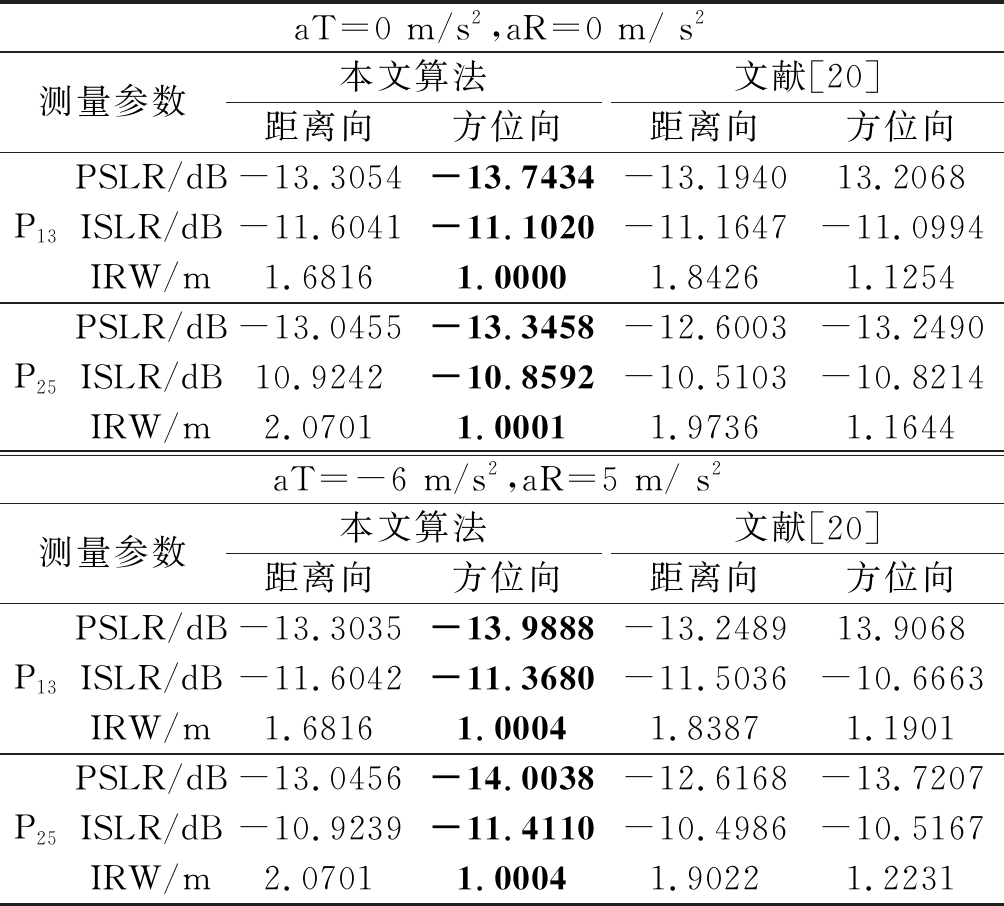
aT=0 m/s2,aR=0 m/ s2测量参数本文算法距离向方位向文献[20]距离向方位向P13PSLR/dB-13.3054-13.7434-13.194013.2068ISLR/dB-11.6041-11.1020-11.1647-11.0994IRW/m1.68161.00001.84261.1254P25PSLR/dB-13.0455-13.3458-12.6003-13.2490ISLR/dB10.9242-10.8592-10.5103-10.8214IRW/m2.07011.00011.97361.1644aT=-6 m/s2,aR=5 m/ s2测量参数本文算法距离向方位向文献[20]距离向方位向P13PSLR/dB-13.3035-13.9888-13.248913.9068ISLR/dB-11.6042-11.3680-11.5036-10.6663IRW/m1.6816 1.00041.83871.1901P25PSLR/dB-13.0456-14.0038-12.6168-13.7207ISLR/dB-10.9239-11.4110-10.4986-10.5167IRW/m2.07011.00041.90221.2231
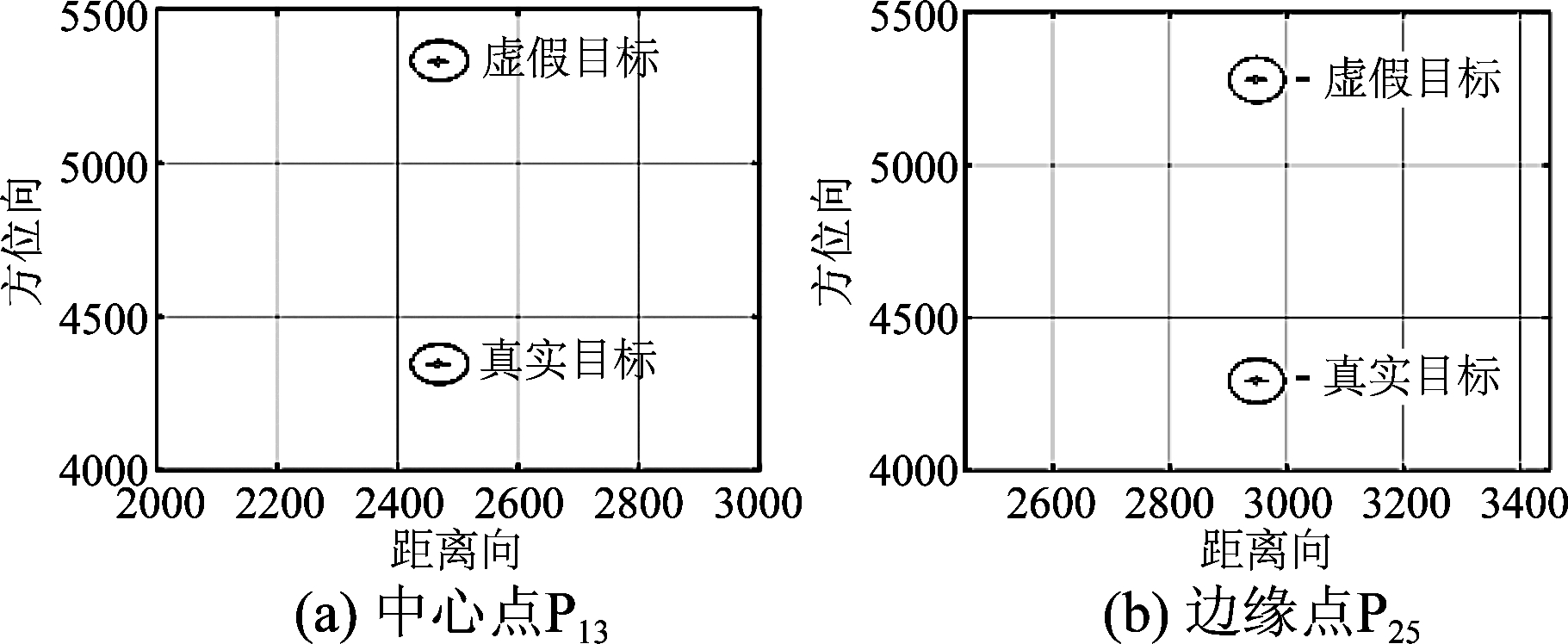
图13 文献[20]成像虚假目标图
Fig.13 Literature [20] imaging false target map
综合图9～图12以及表3的数据可知,本文基于Chebyshev解耦合的改进算法不管是在有无加速度作用下,都可以有效补偿加速度带来的运动误差,对中心点和边缘点实现高分辨率成像。
基于Chebyshev解耦合的改进算法对频谱耦合相位采用Chebyshev多项式近似,文献[20]算法则采用Taylor级数近似,所产生的二维耦合相位误差如式ΔψC(fr, fa)和ΔψT(fr, fa)。当加速度aT=14 m/s2,aR=15 m/s2,从图14(a)(b)可以看出,
可以忽略,
相位误差较大不可忽略。综上所述,基于Chebyshev解耦合的改进算法所产生的耦合相位误差较小,可以得到良好的成像效果。
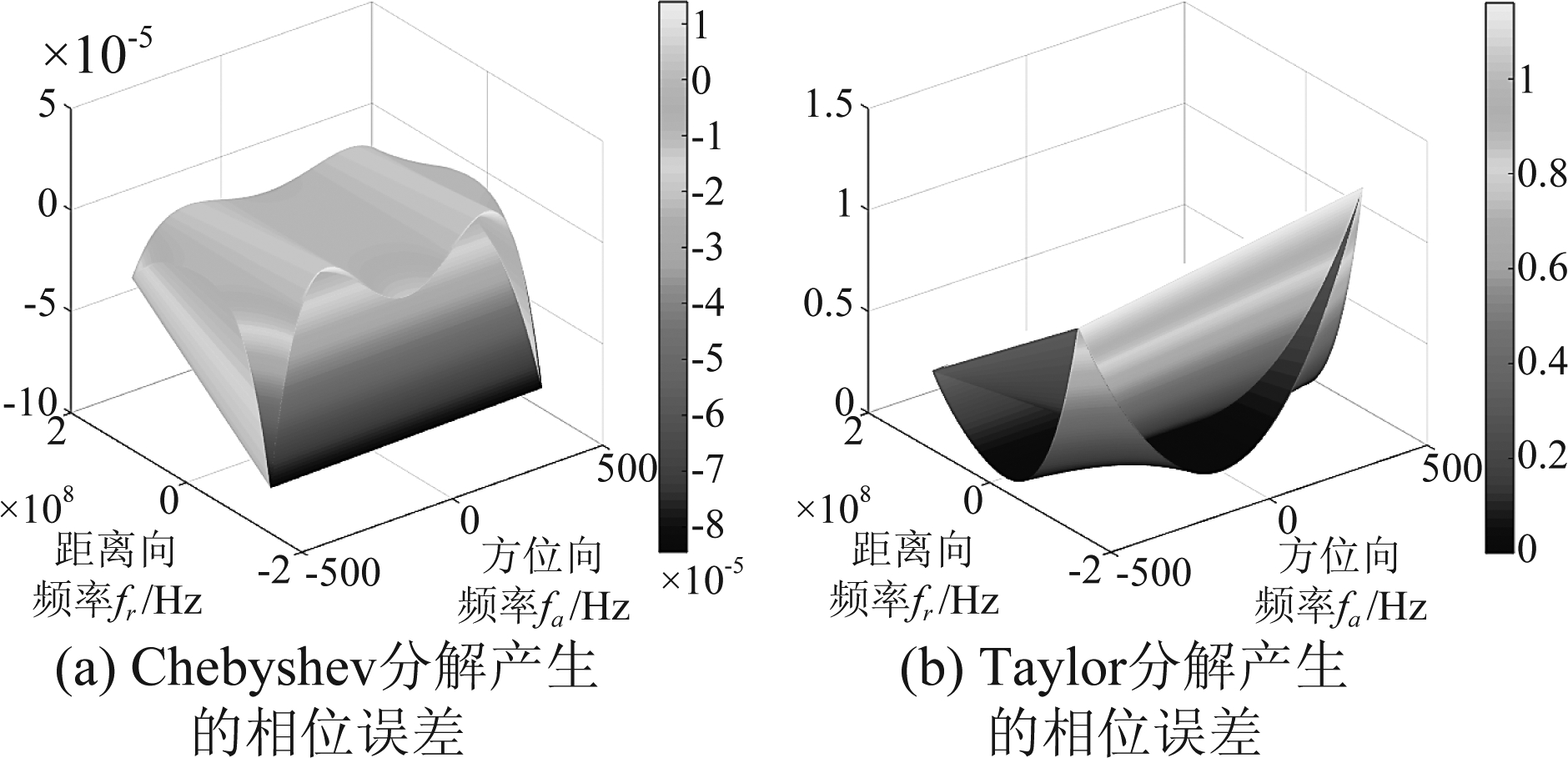
图14 耦合相位近似产生的相位误差
Fig.14 Phase errors generated by coupling phase approximation
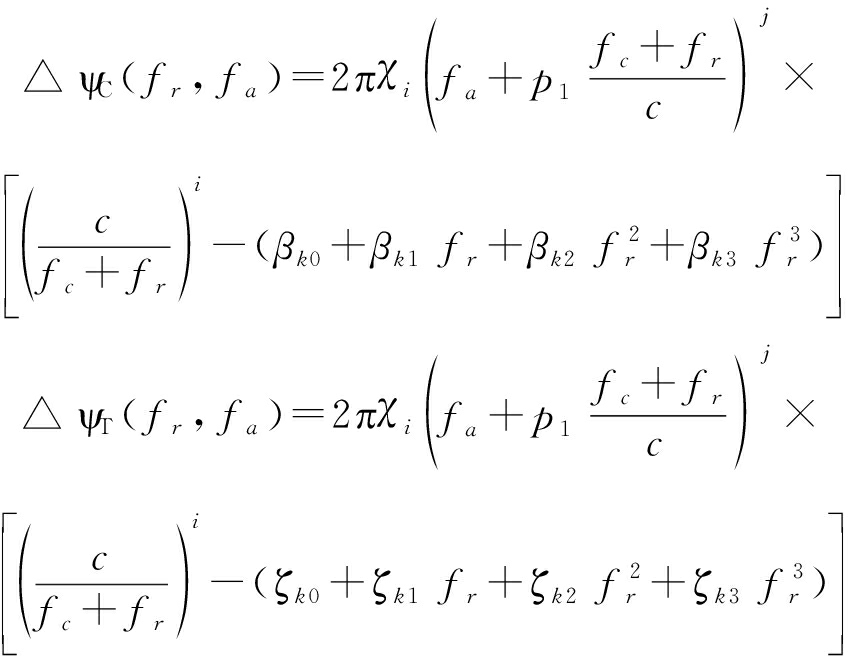
(23)
其中
为耦合相位Taylor分解系数,参见文献[20]。
5 结论
应用场景的复杂性及应用需求的多样性,使平台不能保持理想的匀速运动,加速度不可避免,这增加了双基SAR斜距历程的复杂性,使回波信号距离和方位的耦合更为严重。本文提出了一种二维正交解耦合方法,利用Chebyshev多项式对二维频谱进行正交分解,能有效解除距离和方位的耦合,从而减小加速度对成像的影响。该算法考虑了LRCM和多普勒线性相位带来的影响,并进行了有效补偿,以便于MSR的应用,对斜距和耦合相位进行了Chebyshev多项式近似,从而提高了斜距和频谱相位的近似精度,减小了误差。仿真结果表明,该方法对点目标有较好的聚焦性能和成像质量。下一步将研究不同点目标方位向调频率均衡的问题,讨论双基SAR的ENLCS成像算法。
附录A:
对于式(3)斜距的Chebyshev分解式求解具体如下:
首先对方位向时间t作归一化处理,即令
斜距函数表示为:
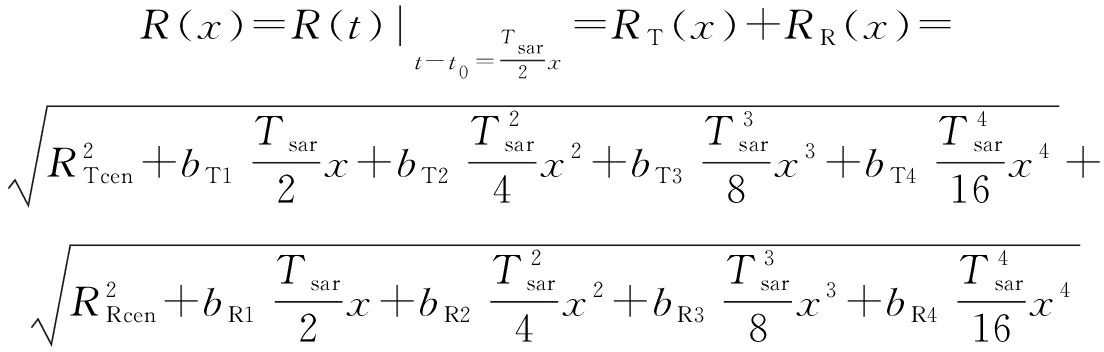
然后分别对RT(x)和RR(x)进行Chebyshev正交分解,并按x的幂级数整理为:
RT(x)=αT0+αT1x+αT2x2+αT3x3+αT4x4
RR(x)=αR0+αR1x+αR2x2+αR3x3+αR4x4
其中,Chebyshev分解系数
式中Cij是Chebyshev系数, j=0,1,2,3,4,i指T或R),且有
其中,Tj(x)是Chebyshev多项式递推式,且有
为变量节点,n=4是展开阶数,
将x=2(t-t0)/Tsar代入Ri(xk),并按t的四阶幂级数整理,得到加速度作用下双基SAR斜距的Chebyshev分解式为
R(t)=p0+p1(t-t0)+p2(t-t0)2+
p3(t-t0)3+p4(t-t0)4+…
其中,pj=(2/Tsar)j(αTj+αRj),p0是初始斜距,p1是线性距离走动项系数,p2是距离弯曲项系数,p3和p4是高阶项系数。
附录B:
正文中式(16)中二维频谱相位ψ(fr, fa)中的φ0(fc),φ1(fa),φ2(fa),φ3(fa),φ4(fa)表示为:
[1] FENG Dong, AN Daoxiang, HUANG Xiaotao. Spatial Resolution Analysis for Ultrawideband Bistatic Forward-Looking SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(6): 974-978.
[2] MEI Haiwen, LI Yachao, XING Mengdao, et al. A Frequency-Domain Imaging Algorithm for Translational Variant Bistatic Forward-Looking SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 1502-1515.
[3] AN Hongyang, WU Junjie, SUN Zhichao, et al. A Two-Step Nonlinear Chirp Scaling Method for Multichannel GEO Spaceborne-Airborne Bistatic SAR Spectrum Reconstructing and Focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3713-3728.
[4] WANG Zhigui, LIU Mei, AI Gengting, et al. Focusing of Bistatic SAR With Curved Trajectory Based on Extended Azimuth Nonlinear Chirp Scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4160- 4179.
[5] WU Junjie, AN Hongyang, ZHANG Qianghui, et al. Two-dimensional frequency decoupling method for curved trajectory synthetic aperture radar imaging[J]. IET Radar, Sonar and Navigation, 2018, 12(7): 766-773.
[6] LI Tingting, CHEN Kunshan, MING Jin. Imaging Performance of Backward and Forward Bistatic SAR[C]∥2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, 2018.
[7] SHIN H S, LIM J T. Omega-k Algorithm for Airborne Forward-Looking Bistatic Spotlight SAR Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 312-316.
[8] WU Junjie, LI Zhongyu, YANG Jianyu, et al. Focusing translational variant bistatic forward-looking SAR using extended nonlinear Chirp Scaling algorithm[C]∥Radar Conference. IEEE, 2013.
[9] 肖忠源, 徐华平, 李春升. 基于俯冲模型的频域距离走动校正NLCS-SAR成像算法[J]. 电子与信息学报, 2013, 11(5): 78- 84.
XIAO Zhongyuan, XU Huaping, LI Chunsheng. NLCS-SAR Imaging Algorithm with Range-walk Correction in Frequency Domain Based on Dive Model[J]. Journal of Electronics & Information Technology, 2013, 11(5): 78- 84.(in Chinese)
[10] WONG F H, CUMMING I G, NEO Y L. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(9): 2493-2505.
[11] WU Junjie, LI Zhongyu, HUANG Yulin, et al. An Omega-K Algorithm for Translational Invariant Bistatic SAR Based on Generalized Loffeld’s Bistatic Formula[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(10): 6699- 6714.
[12] LOFFELD O, NIES H, PETERS V, et al. Models and useful relations for bistatic SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2031-2038.
[13] NEO Y L, WONG F, CUMMING I G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 93-96.
[14] MENG Ziqiang, LI Yachao, XING Mengdao, et al. Imaging of missile-borne bistatic forward-looking SAR[C]∥2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP). IEEE, 2014.
[15] ZHANG Qianghui, WU Junjie, YANG Jianyu, et al. Extended nonlinear chirp scaling algorithm with topography compensation for maneuvering-platform bistatic forward-looking SAR[C]∥IGARSS 2017-2017 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2017.
[16] HAI Yu, WANG Jingjing, LI Zhongyu, et al. Bistatic forward-looking SAR imaging processing based on optimized NLCS algorithm[C]∥2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 2019.
[17] WU Junjie, LI Zhongyu, HUANG Yulin, et al. Focusing Bistatic Forward-Looking SAR With Stationary Transmitter Based on Keystone Transform and Nonlinear Chirp Scaling[J]. IEEE Geoscience & Remote Sensing Letters, 2014, 11(1): 148-152.
[18] DENG Huan, LI Yachao, LIU Mengqi, et al. A Space-Variant Phase Filtering Imaging Algorithm for Missile-Borne BiSAR With Arbitrary Configuration and Curved Track[J]. IEEE Sensors Journal, 2018, 18(8): 3311-3326.
[19] LI Zhongyu, WU Junjie, SUN Zhichao, et al. An adaptive NLCS technique for large-size moving target imaging with bistatic forward-looking SAR[C]∥IGARSS 2017-2017 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2017.
[20] LI Yu, DUAN Chongdi, WANG Weiwei, et al. Improvement of non-linear chirp-scaling algorithm for highly squint bistatic SAR data focusing[J]. The Journal of Engineering, 2019, 20(10): 6712- 6717.
