1 引言
随着民航事业的快速发展,空中交通量也不断增大。短期4D航迹预测技术可以增加空中交通需求预测的准确性,对于保障空中交通的安全和高效运行具有重要意义。
目前有关短期航迹预测的方法已经有很多,这些方法可以分为三类:基于粒子运动、基于混合估计和基于机器学习。基于粒子运动是传统的预测方法,它主要将飞行器视为一个质点,对其进行受力分析,并结合飞行器性能模型建立运动学和动力学模型,实现对飞行器的四维轨迹预测[1-3]。基于混合估计主要是使用混合估计模型来对未来将要出现的航迹点位置进行估计,包括单模估计和多模估计。单模估计包括卡尔曼滤波算法、改进卡尔曼滤波算法和改进的基于“当前”统计模型的自适应滤波算法[4- 6]。因为飞机不仅要考虑飞行过程中的外部运动,还要考虑自身的状态,即水平和垂直的三维状态。因此,在复杂的航空环境下单模估计会受到很多限制,为此汤新民等提出了交互式多模型(Interactive Multiple Model,IMM)算法估计 [7-11]。
随着大数据相关理论的发展,机器学习成为了一种很重要的短期4D航迹预测方法。机器学习通常从大量的数据中挖掘出隐藏的特征信息,将这些信息进行融合来寻找内在的联系。为了解决传统气动模型在预测四维飞行轨迹时误差较大的问题,吴鹍和潘薇[12]等提出了一种基于数据挖掘的预测模型。通过对历史数据进行挖掘来预测下一次飞行的完整飞行时间,然后对历史位置数据进行分析,得到飞机在每个采样周期开始时的位置,从而实现完整的4D航迹预测。Tastamberkov 和Hong [13-14]等将航迹预测问题看作一个函数回归问题,分别利用小波分解和建立多元logistic回归模型并结合机器学习来实现航班轨迹的预测。钱奎和权波[15-17]等提出了基于神经网络的机载目标预测模型,通过建立神经网络的预测模型来对目标实现轨迹的预测。石庆研和岳聚财等[18]提出了一种以LSTM为主,差分自回归移动平均模型(Autoregressive Integrated Moving Average,ARIMA)为辅的组合短期航迹预测模型。该算法先利用LSTM作为主预测模型对经纬度和高度进行预测,随后再与辅助模型ARIMA的预测值进行数据融合处理从而提升航迹预测的准确性。但是该算法利用普通的基于历史航迹建立的预测模型对当前正在飞行的航班进行航迹预测,没有考虑到当前实时飞行过程中不同的驾驶员和前方变化的天气等因素对当前正在飞行线路的影响,这些因素可能会产生一些只适用于当前正在飞行航班的航迹特征信息。
为考虑航班实时飞行过程中相关因素对飞行航迹的影响,提出了一种基于在线更新LSTM神经网络的短期4D航迹预测算法,在传统的LSTM预测模型基础上,通过在线更新模型参数,有效引入当前航班的航迹特征信息,从而提高航迹预测性能。
2 LSTM神经网络的相关理论
本节简要介绍循环神经网络[19](Recurrent Neural Network, RNN)、LSTM[20]神经网络模型的基本结构和Adam梯度下降参数优化算法。
RNN最初是用来处理时间序列数据的神经网络。时间序列是指在不同时间点上收集的数据,这类数据是用来体现某些物体、现象随着时间而变化的状态规律或者程度。由于飞机的航迹点也属于时间序列数据,因此可以使用RNN来分析。
虽然RNN是用来处理时间序列的神经网络,但其对于较长延迟的时间序列会产生梯度消失或者梯度爆炸的问题。LSTM就是为了解决这个问题而产生的,LSTM神经网络的结构模型为图1所示,比RNN多出了三个控制器,分别为输入门it、输出门Ot、遗忘门ft。输入门和输出门控制输入和输出的信息,而遗忘门主要负责保留和丢弃部分信息,使得LSTM可以克服梯度消失和梯度爆炸这个问题,具有长期记忆的能力。前向传递算法如公式(1)~(6)所示。
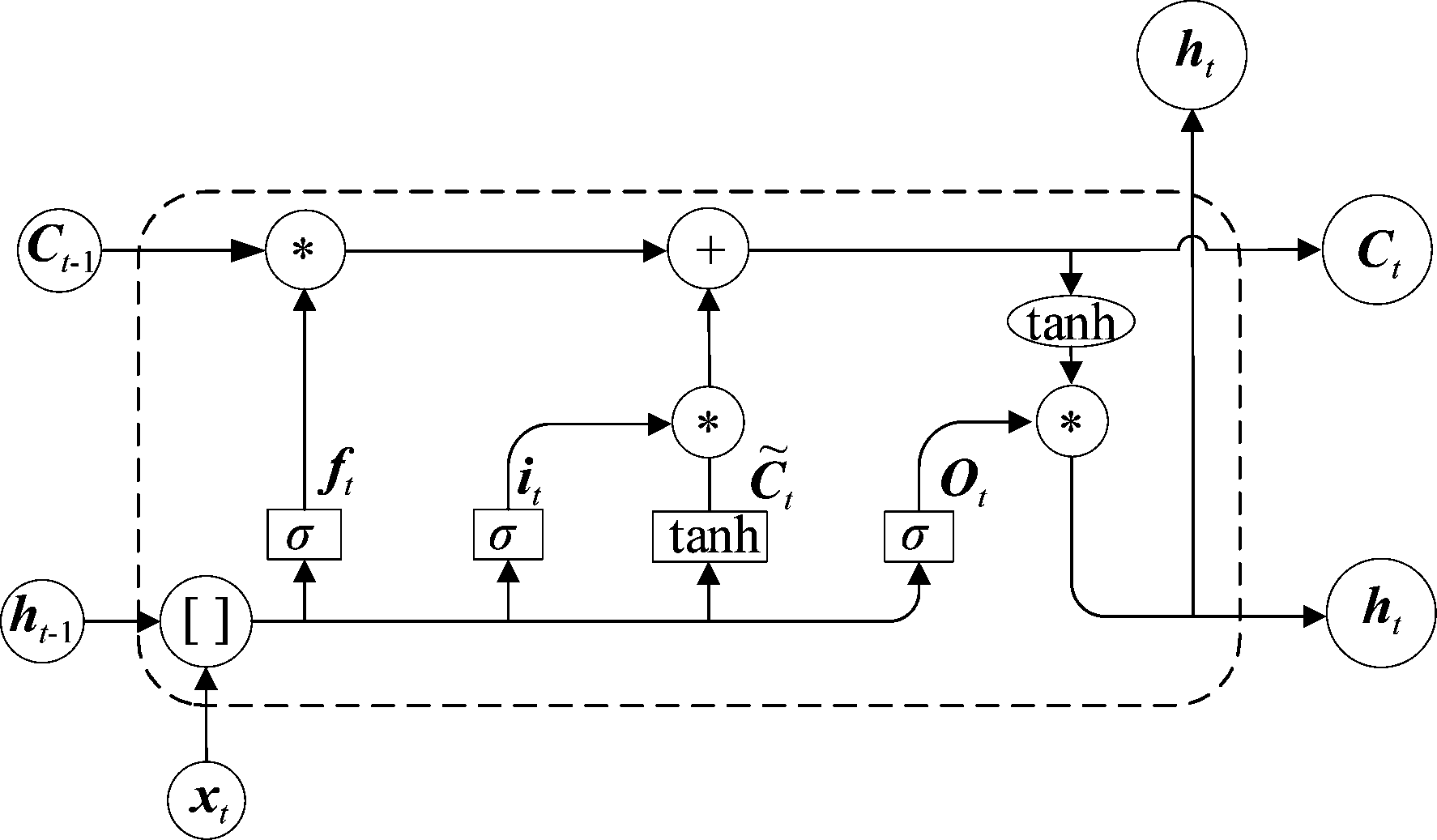
图1 LSTM隐藏层细胞结构
Fig.1 LSTM hidden layer cell structure
ft=σ(Wf·[ht-1,xt]+bf)
(1)
it=σ(Wi·[ht-1,xt]+bi)
(2)
(3)
(4)
Ot=σ(WO·[ht-1,xt]+bO)
(5)
ht=Ot*tanh(Ct)
(6)
其中[]表示两个向量相连接,·表示矩阵乘法,*表示矩阵中的每个元素对应相乘,σ为sigmoid函数,Ct为细胞状态,![]() 是临时状态,W代表权重系数,b代表偏置,h代表网络的输出。
是临时状态,W代表权重系数,b代表偏置,h代表网络的输出。
本文LSTM神经网络采用的减小误差的寻优方法是适应性动量估计(Adaptive Moment Estimation,Adam)算法[21]。Adam算法的优势在于为不同的参数设计独立的自适应性学习率,所占用的内存较少,适合解决含大规模数据和参数的优化问题,可适用于非稳态(Non-stationary)目标,因此使用Adam算法是比较合适的。
3 基于在线更新LSTM网络的短期4D航迹预测算法
依据航迹数据的特点,结合前一节介绍的LSTM模型,本文提出了基于在线更新LSTM网络的短期4D航迹预测算法,主要解决的问题就在于给出当前L个航迹点![]() 来预测未来L′个的航迹点
来预测未来L′个的航迹点![]()
基于在线更新LSTM网络的短期4D航迹预测算法是在使用历史航迹数据训练结束后,使用实时航迹飞行数据对历史航迹预测模型进行在线学习,实现模型参数的实时更新,将参数微调成更适合预测当前正在飞行航班轨迹的预测模型,最后完成对当前正在飞行航班航迹的实时预测。该过程主要分为2个阶段:
第一阶段是历史预测模型的初始化训练。将历史航迹数据用作训练集,将数据传入基于LSTM神经网络的历史预测模型,训练其中的参数,并将已训练好的历史预测模型参数作为下一阶段LSTM神经网络的初始参数输入到在线更新预测模型。
第二阶段是航迹的实时预测阶段。第一阶段训练的LSTM神经网络参数被用作在线更新预测模型中参数的初始值。利用接收到的实时航迹数据在线更新LSTM神经网络的参数,实现预测模型中参数值的微调,并实时预测飞行点。具体流程如图2所示。
3.1 数据的预处理
进行训练前,首先对整体数据进行去空值和去异常值的操作,然后定义某架飞机第r个航迹点特征![]()
(7)
其中![]() 分别表示该航迹点的经度、纬度、高度和时间四个维度的特征。随后对导入原始数据
分别表示该航迹点的经度、纬度、高度和时间四个维度的特征。随后对导入原始数据![]() 的经度、纬度和高度数据进行归一化处理。归一化处理可以消除因量纲和类别不同而造成不同数据取值范围所带来的影响。归一化使用的方法是离差标准化(Min-Max Normalization),转化式为:
的经度、纬度和高度数据进行归一化处理。归一化处理可以消除因量纲和类别不同而造成不同数据取值范围所带来的影响。归一化使用的方法是离差标准化(Min-Max Normalization),转化式为:
(8)
其中,Xmax为样本数据的最大值,Xmin为样本数据的最小值,X为原始训练数据,X*为归一化数据。接着将归一化后的原始数据Fo拆分开,前A天的飞行数据集Fhistory:
(9)
其中![]() 表示A天历史航迹数据中的第a天航迹数据。
表示A天历史航迹数据中的第a天航迹数据。
随后对历史航迹数据集进行数据分割处理。设置一个长度为L的滑动窗,对每天的航迹数据利用滑动窗截取数据,并且对航迹数据的下标进行重排。因此截取后的历史模型训练集的输入数据形式为:

图2 基于在线更新LSTM网络的短期4D航迹预测算法流程图
Fig.2 Flow chart of online-updating short-term 4D trajectory prediction algorithm based on LSTM
![]()
(10)
其中![]() 且r∈[1,n-(L+L′-1)];r,L,L′∈N;n为第a天的数据长度。
且r∈[1,n-(L+L′-1)];r,L,L′∈N;n为第a天的数据长度。
其对应的L′个理论预测值为:
(11)
其中![]()
下一步是在线更新预测模型的数据集划分,主要是通过第A+1天的飞行数据来模拟接收到的实时航迹数据,并且对其做出预测。首先对实时接收到的第A+1天飞行数据进行预处理,并将这些数据动态划分为在线更新训练集和在线更新测试集。在线更新预测模型部分也利用滑动窗对的训练集和测试集进行数据分割,这部分与历史飞行数据分割相同,就不再进一步赘述。然后使用在线更新训练集对已经训练好的历史预测模型中的参数进行再次训练和微调,在线更新测试集用来预测未来将要飞过的三维航迹点坐标和时间。将处理好的航迹数据代入模型中进行训练和预测。
3.2 模型的训练与预测
神经网络训练主要分为两个部分。第一部分是历史航迹预测模型的训练,将归一化后的历史数据集X输入神经网络的隐藏层。隐藏层为b个相互连接的同结构LSTM细胞,X经过隐藏层后的输出可以表示为:
D=[D1,D2,...,Dr,...,Dn-(L+L′-1)]
(12)
(13)
其中C和H分别为LSTM细胞的状态和输出;Dr表示数据经过LSTM和全连接层计算后的输出结果。
第二部分是对历史预测模型的参数进行在线更新并实现航迹预测。当算法接收到第r个实时飞行航迹数据点后,将第r及其前(L+L′-1)个实时飞行航迹数据点作为在线更新训练集代入历史预测模型进行再次训练和微调预测模型中参数,用在线更新后的实时训练模型来得到后面L′个预测点。随后,重复上述操作直到接收到该飞行任务的所有飞行数据为止,同时,获得实时预测的飞行轨迹P。其中
P=[P1,P2,...,Pr,...,Pm]
(14)
其中![]() 且r∈[1,m];r,L,L′∈N;m表示一次飞行过程中进行预测的实时航迹点次数。
且r∈[1,m];r,L,L′∈N;m表示一次飞行过程中进行预测的实时航迹点次数。
4 仿真实验与性能对比
4.1 实验数据与参数
本文使用ADS-B和二次雷达融合后的数据,对提出的基于在线更新LSTM网络的4D航迹预测算法进行验证。使用的航班飞行数据量共有十二天,包含7209个航迹点,这些航迹点的信息包括经度、纬度、高度和时间。算法参数具体数值是通过网格化参数选优试验比较航迹预测结果的均方根误差(Root Mean Square Error, RMSE)以及以往的实验经验进行选定的,如表1和表2所示。
表1 算法在不同参数情况下的预测误差
Tab.1 The prediction errors of the algorithm under different parameters
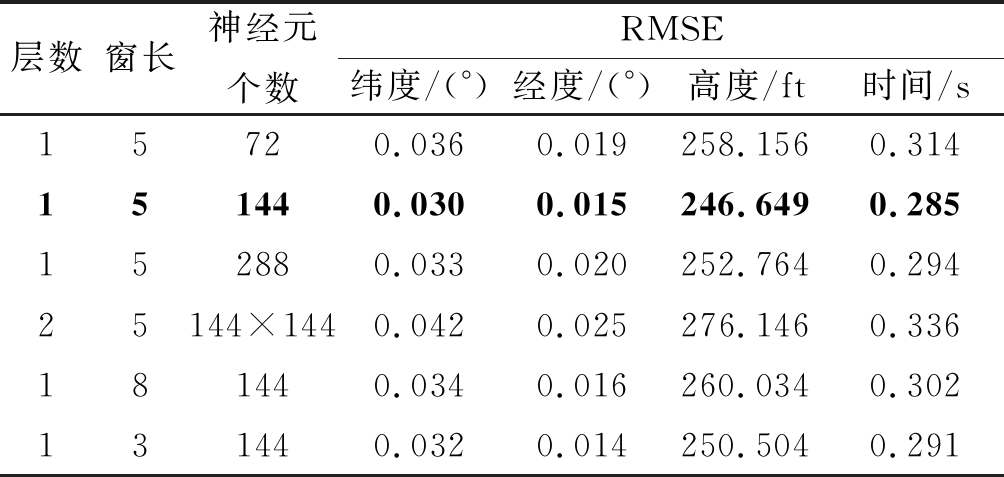
层数窗长神经元个数RMSE纬度/(°)经度/(°)高度/ft时间/s15720.0360.019258.1560.314151440.0300.015246.6490.285152880.0330.020252.7640.29425144×1440.0420.025276.1460.336181440.0340.016260.0340.302131440.0320.014250.5040.291
表2 基于LSTM的在线更新4D航迹预测算法中的参数选择
Tab.2 The values of parameters in online-updating short-term 4D trajectory prediction algorithm based on LSTM

参数值原始航迹点的个数7209历史航迹点的个数6584滑动窗的长度5一次预测的航迹点个数1隐藏层1学习率0.001一次训练所选取的样本数10隐藏层的神经元的个数144
飞机能否安全的起飞、巡航、着陆主要取决于风向和风力、能见度、云高和跑道的条件,出于安全因素的考虑航班改航通常会绕过影响飞行安全的区域[22]。因此天气的不同也会使航迹数据产生差异,表3将这十二天的航迹数据所在机场当天的天气情况列举出来。通过表3可以看出来,这十二天的航迹数据是不同的天气条件下产生的,因此能够间接地验证算法的普适性。
表3 2018年5月10号~21号北京机场的天气情况
Tab.3 The weather at Beijing Airport from May 10th to 21st, 2018

日期最高温最低温天气风向风力2018-05-1026℃18℃多云东南风1级2018-05-1123℃15℃小雨东风2级2018-05-1228℃16℃雷阵雨西南风2级2018-05-1330℃17℃晴南风2级2018-05-1434℃22℃多云西南风2级2018-05-1530℃22℃小雨北风2级2018-05-1628℃21℃多云东南风2级2018-05-1725℃19℃小雨西风1级2018-05-1828℃16℃晴南风2级2018-05-1928℃16℃多云西风1级2018-05-2020℃16℃小雨东风2级2018-05-2118℃14℃小雨西风1级
由于实验模拟的场景是对航班实时飞行过程中的航迹点进行预测,因此将飞行数据分为历史飞行数据(前十一天)和实时飞行数据(第十二天)。利用局部异常因子(Local Outlier Factor,LOF)检测算法来检测历史数据中的异常点,并将其删除[23]。随后,将数据输入到建立好的基于在线更新LSTM网络的4D航迹预测模型进行预测,对预测值进行反归一化处理,输出航迹预测结果。
4.2 预测结果与比较
图3、图4分别为基于在线更新LSTM网络航迹预测算法、普通LSTM航迹预测算法得到的整体航迹预测值和真实航迹值的比较。
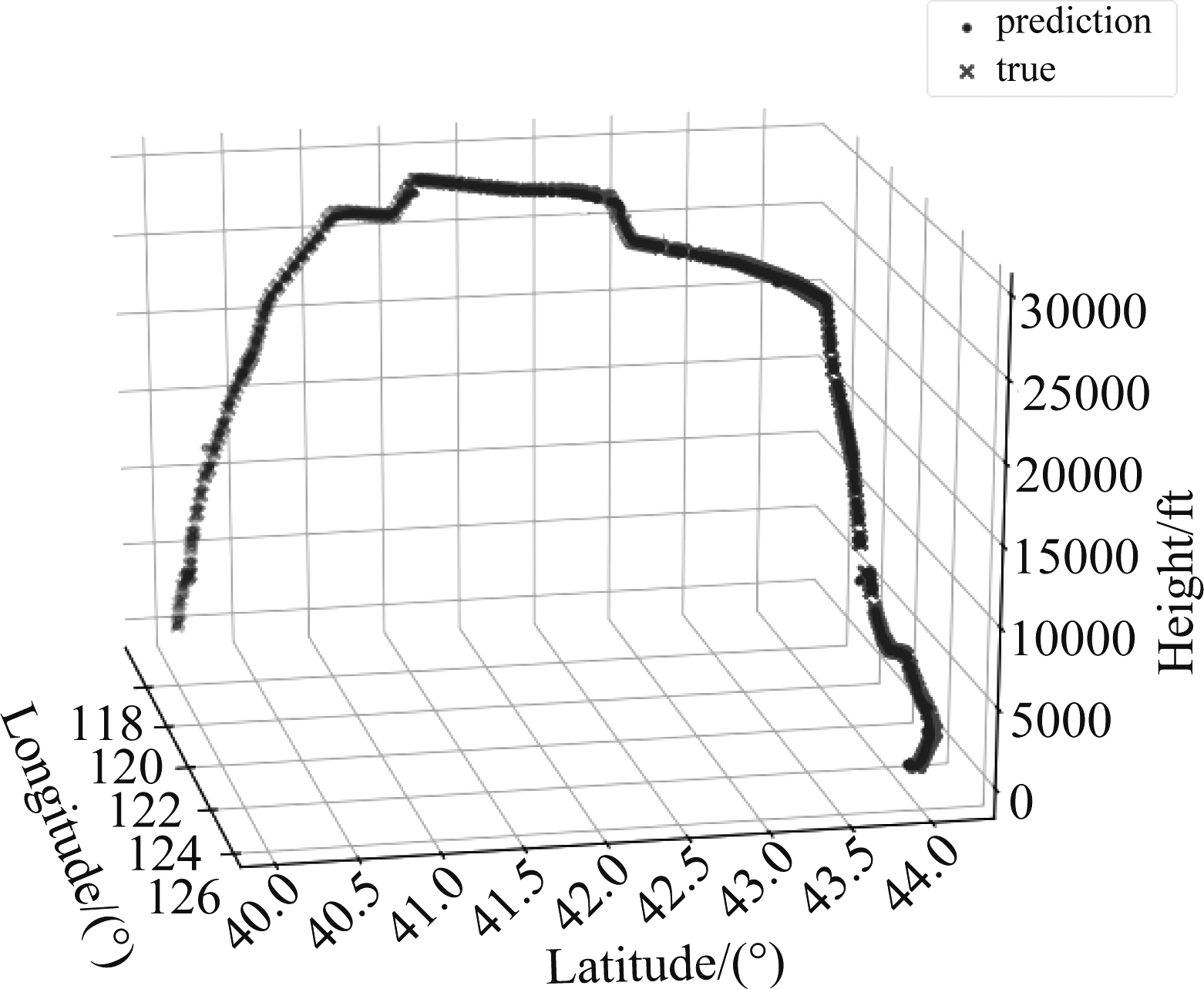
图3 在线更新LSTM算法的航迹预测结果
Fig.3 Trajectory prediction result based on online-updating LSTM algorithm
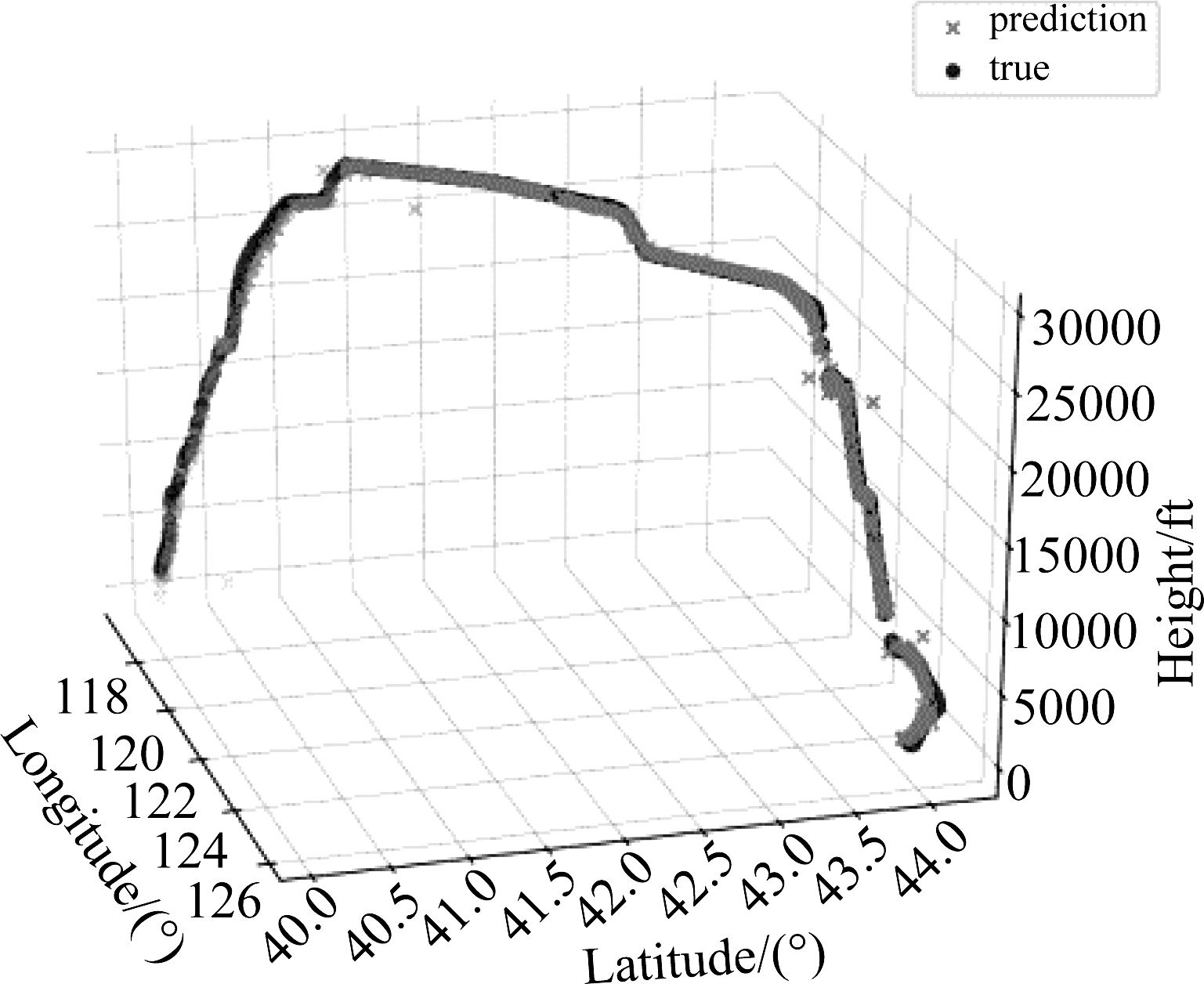
图4 普通LSTM算法的航迹预测结果
Fig.4 Trajectory predication result based on normal LSTM algorithm
图3、图4对比可以看出,图4有部分预测值与真实值的重合度较低,预测值与真实值之间误差较大。分别计算在线更新、普通LSTM两个预测模型在经度、纬度、高度和时间上的预测值与真实值的RMSE值,结果如表4所示。
表4 两种航迹预测算法预测误差对比
Tab.4 Comparison of prediction errors of two kinds of prediction algorithms
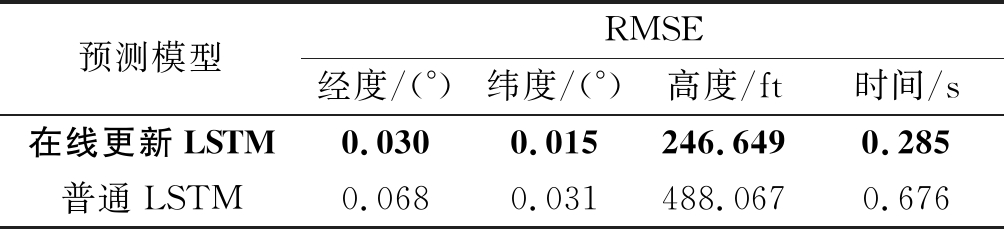
预测模型RMSE经度/(°)纬度/(°)高度/ft时间/s在线更新LSTM0.0300.015246.6490.285普通LSTM0.0680.031488.0670.676
对比表4中各项预测误差可以得出,本文提出来的基于在线更新LSTM网络的4D航迹预测模型在时间、经度、纬度和高度四个维度上的预测结果均要优于常规的LSTM神经网络预测模型,而且有一个较大的提升。表4中的普通LSTM神经网络预测模型的预测结果也是优选参数后得到的。
通常期望由训练集训练出来的预测模型具有很强的泛化能力,即对新输入的数据能够输出较好的预测结果。因此本文在表5中分别列举出使用训练集中的第十一天的航迹数据与测试集即第十二天的航迹数据来对模型进行验证的预测误差结果。
表5 不同数据集下在线更新LSTM网络的预测误差
Tab.5 The prediction errors on online-updating LSTM network under different data sets
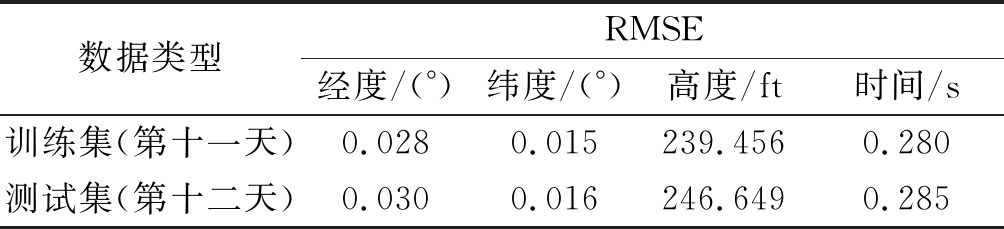
数据类型RMSE经度/(°)纬度/(°)高度/ft时间/s训练集(第十一天)0.0280.015239.4560.280测试集(第十二天)0.0300.016246.6490.285
对比表5中的预测误差可以看出,基于在线更新LSTM网络的短期4D航迹预测模型在测试集上的预测误差并没有明显地升高,表明该模型具有良好的泛化能力。
为了验证不同大小训练数据集对预测结果的影响,分别使用了前5天、前7天、前9天和前11天的航迹数据作为训练数据集,第12天的数据作为测试集,采用基于在线更新LSTM网络的4D航迹预测算法进行航迹预测,计算预测航迹和真实航迹之间的误差,结果如表6所示。
表6可以得出,基于在线更新LSTM网络的短期4D航迹预测模型的预测准确度和训练集大小密切相关,随着训练集的增大,预测误差逐渐减小,预测的准确度有所提升,因此本文用前11天的历史航迹数据对模型进行训练。图5为在线更新LSTM网络、普通LSTM网络分别在经度、纬度和高度上的预测值与真实值之间的误差对比,可以看出,新算法预测误差波动较小。用基于在线更新LSTM网络的短期4D航迹预测模型预测下一个航迹点所需要的时间大约是0.0645 s,远远小于相邻航迹点的平均时间间隔9.11 s,(CPU: Intel Core i5- 8500CPU@3.00GHz,RAM:16GB),所以本文提出来的预测算法具有较好的实时性。
表6 不同大小训练集时的预测误差
Tab.6 The prediction errors with different sizes of training sets
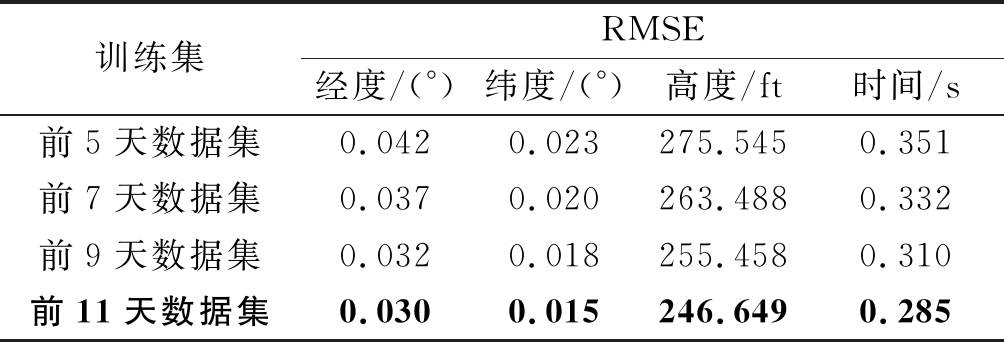
训练集RMSE经度/(°)纬度/(°)高度/ft时间/s前5天数据集0.0420.023275.5450.351前7天数据集0.0370.020263.4880.332前9天数据集0.0320.018255.4580.310前11天数据集0.0300.015246.6490.285
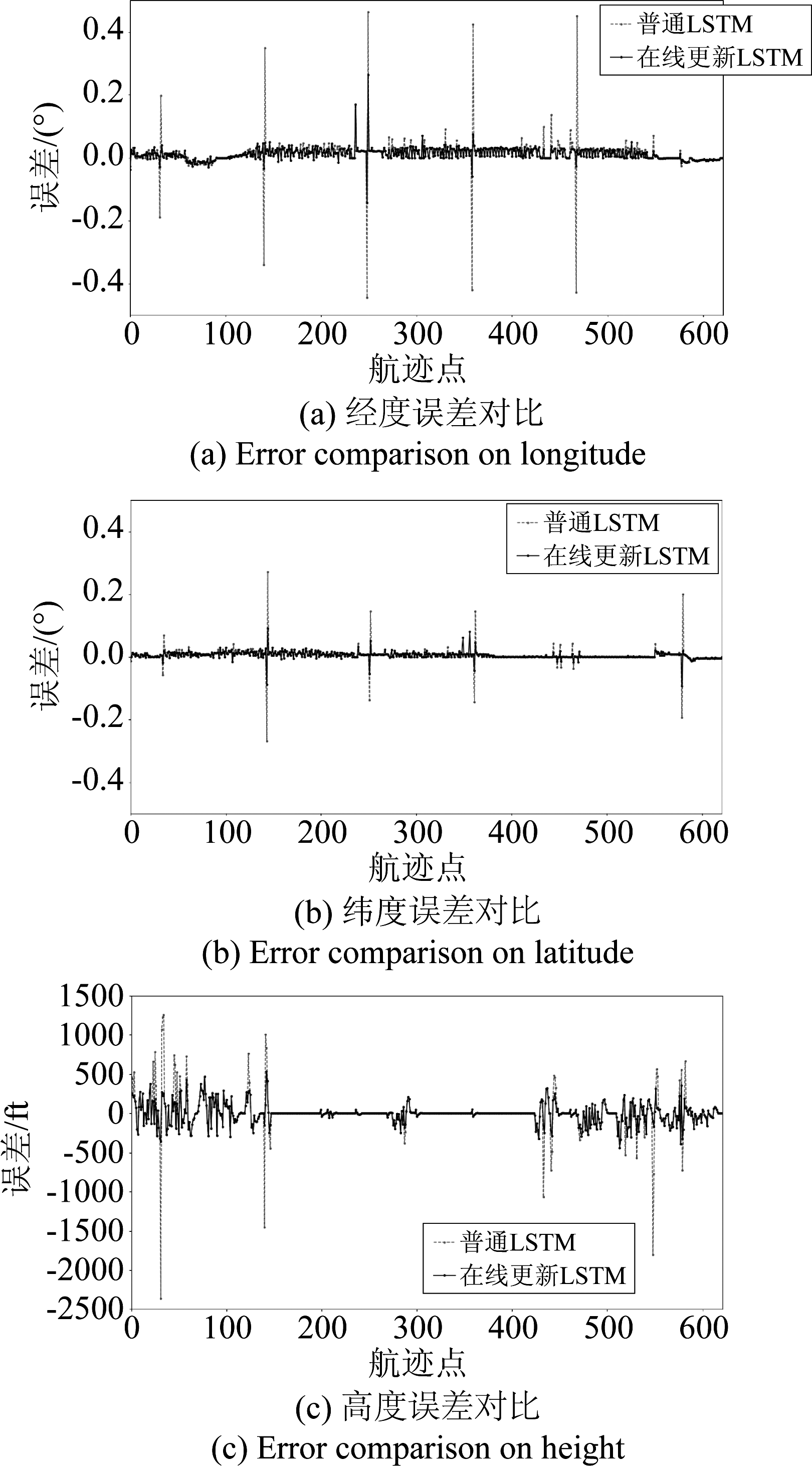
图5 两种算法预测误差对比
Fig.5 Comparison of prediction errors of two algorithms
除了和普通LSTM预测算法相比较,本文还使用了其他传统的时间序列预测算法,例如Holt-Winter[24]模型和ARIMA[25]模型,与基于LSTM的在线更新4D航迹预测算法来进行对比,结果如表7所示。
表7 多种4D航迹预测算法预测误差比较
Tab.7 Comparison of prediction errors of various 4D trajectory prediction algorithms
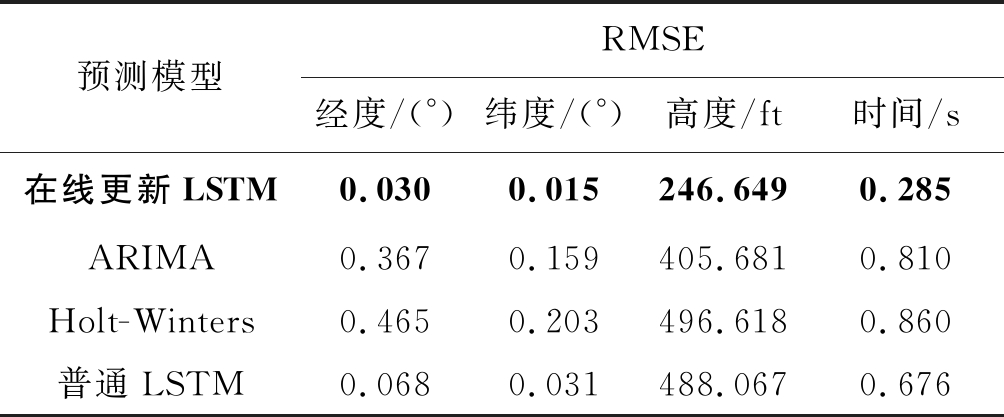
预测模型RMSE经度/(°)纬度/(°)高度/ft时间/s在线更新LSTM0.0300.015246.6490.285ARIMA0.3670.159405.6810.810Holt-Winters0.4650.203496.6180.860普通LSTM0.0680.031488.0670.676
从表7可以看出,本文提出的预测模型比其他传统预测算法结果更加准确。分析以上结果,可能的原因是本文提出来的在线更新LSTM航迹预测算法,可以根据实时飞行航迹来微调模型中的参数,使得预测模型与当前飞行过程更加匹配,而其他传统的预测模型只是挖掘历史航迹数据特征,因此新算法预测误差较其他算法更小。
5 结论
本文提出的基于在线更新LSTM网络的短期4D航迹预测算法,首先用历史航迹数据来训练历史预测模型,当接收到实时飞行航迹数据后,对已经训练好的历史预测模型进行再次训练来微调其中的参数,以实现模型参数的自适应更新。随后与普通LSTM、传统预测模型的预测能力进行了对比,实验对比表明新算法可以提高算法预测的准确度。
基于在线更新LSTM网络的短期4D航迹预测算法具有良好的适用性以及良好的泛化能力,下一步计划从引入新的数据特征和进一步优化参数入手,继续探究该航迹预测算法。
[1] ACCARDO D, MOCCIA A, FIORILLO L, et al. A Trajectory Prediction Tool to Support Air Traffic Management[C]∥Aiaa InfoTech at Aerospace Conference & Exhibit & Aiaa Unmanned Unlimited Conference. Seattle: American Institute of Aeronautics and Astronautics, 2009: 1-10.
[2] PORRETTA M, DUPUY M. D, SCHUSTER W, et al. Performance Evaluation of a Novel 4D Trajectory Prediction Model for Civil Aircraft[J]. The Journal of Navigation, 2008, 61(3): 393- 420.
[3] 王超, 郭九霞, 沈志鹏. 基于基本飞行模型的4D航迹预测方法[J]. 西南交通大学学报, 2009, 44(2): 295-300.
WANG Chao, GUO Jiuxia, SHEN Zhipeng. Prediction of 4D Trajectory Based on Basic Flight Models[J]. Journal of Southwest Jiaotong University, 2009, 44(2): 295-300.(in Chinese)
[4] LIU T, BAHL P, CHLAMTAC I. Mobility Modeling, Location Tracking, and Trajectory Prediction in Wireless ATM Networks[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(6): 922-936.
[5] 王涛波, 黄宝军. 基于改进卡尔曼滤波的四维飞行航迹预测模型[J]. 计算机应用, 2014, 34(6): 1812-1815.
WANG Taobo, HUANG Baojun. 4D Flight Trajectory Prediction Model Based on Improved Kalman Filter[J]. Journal of Computer Applications, 2014, 34(6): 1812-1815.(in Chinese)
[6] 欧阳超, 杨霄鹏, 贾航川, 等. 改进的基于"当前"统计模型自适应滤波算法及其在航迹预测中的应用[J]. 科学技术与工程, 2013, 13(26): 7656-7661.
OUYANG Chao, YANG Xiaopeng, JIA Hangchuan, et al. A Fuzzy Adaptive Algorithm Based on Current Statistical Model for Track Prediction[J]. Science Technology and Engineering, 2013, 13(26): 7656-7661.(in Chinese)
[7] 汤新民, 李腾, 陈强超, 等. 基于交互式多模型的短期4D航迹预测[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(1): 39- 45.
TANG Xinmin, LI Teng, CHEN Qiangchao, et al. Short-term 4D Trajectory Prediction Based on Interactive Multi-models[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2020, 44(1): 39- 45.(in Chinese)
[8] HWANG I, SEAH C E. An Estimation Algorithm for Stochastic Linear Hybrid Systems with Continuous-State-Dependent Mode Transitions[C]∥IEEE Conference on Decision & Control. San Diego: IEEE, 2006: 131-136.
[9] YEPES J L, HWANG I, ROTEA M. New Algorithms for Aircraft Intent Inference and Trajectory Prediction[J]. Journal of Guidance Control & Dynamics, 2007, 30(2): 370-382.
[10] WEIYI Liu, INSEOK. Probabilistic Trajectory Prediction and Conflict Detection for Air Traffic Control[J]. Journal of Guidance Control & Dynamics, 2011, 34(6): 1779-1789.
[11] ZHANG Junfeng, WU Xiaoguang, WANG Fei. Aircraft Trajectory Prediction Based on Modified Interacting Multiple Model Algorithm[J]. Journal of Donghua University (English Edition), 2015,32(2): 180-184.
[12] 吴鹍, 潘薇. 基于数据挖掘的四维飞行轨迹预测模型[J]. 计算机应用, 2007, 27(11): 2637-2639.
WU Kun, PAN Wei. 4D Trajectory Prediction Model Based on Data Mining[J]. Computer Applications, 2007, 27(11): 2637-2639.(in Chinese)
[13] TASTAMBEKOV K, PUECHMOREL S, DELAHAYE D, et al. Aircraft Trajectory Forecasting Using Local Functional Regression in Sobolev Space[J]. Transportation Research Part C Emerging Technologies, 2014, 39: 1-22.
[14] HONG S, LEE K. Trajectory Prediction for Vectored Area Navigation Arrivals[J]. Journal of Aerospace Information Systems, 2015, 12(7): 490-502.
[15] 钱夔, 周颖, 杨柳静, 等. 基于BP神经网络的空中目标航迹预测模型[J]. 指挥信息系统与技术, 2017, 8(3): 54-58.
QIAN Kui, ZHOU Ying, YANG Liujing, et al. Aircraft Target Track Prediction Model Based on BP Neural Network[J]. Command Information System and Technology, 2017, 8(3): 54-58.(in Chinese)
[16] 权波,杨博辰,胡可奇,等. 基于LSTM的船舶航迹预测模型[J]. 计算机科学, 2018, 45(11A): 126-131.
QUAN Bo, YANG Bochen, HU Keqi, et al. Ship Trajectory Prediction Model Based on LSTM[J]. Computer Science, 2018, 45(11A): 126-131.(in Chinese)
[17] 胡玉可, 夏维, 胡笑旋, 等. 基于循环神经网络的船舶航迹预测[J]. 系统工程与电子技术, 2020, 42(4): 871- 877.
HU Yuke, XIA Wei, HU Xiaoxuan, et al. Vessel Trajectory Prediction Based on Recurrent Neural Network[J]. Systems Engineering and Electronics, 2020, 42(4): 871- 877.(in Chinese)
[18] 石庆研, 岳聚财, 韩萍, 等. 基于LSTM-ARIMA模型的短期航班飞行轨迹预测[J]. 信号处理, 2019, 35(12): 2000-2009.
SHI Qingyan, YUE Jucai, HAN Ping, et al. Short-term Flight Trajectory Prediction Based on LSTM-ARIMA Model[J]. Journal of Signal Processing, 2019, 35(12): 2000-2009.(in Chinese)
[19] CHO K, VAN Merrienboer B, GULCEHRE C, et al. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation[C]∥2014 Conference on Empirical Methods in Natural Language Processing. Doha City Center Hotel in Doha: EMNLP 2014-2014 Conference on Empirical Methods in Natural Language Processing, 2014: 1724-1734.
[20] HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[21] AMARI S I. Backpropagation and Stochastic Gradient Descent Method[J]. Neurocomputing, 1993, 5(4-5): 185-196.
[22] 李雄. 飞行危险天气下的航班改航路径规划研究[D]. 南京:南京航空航天大学, 2009.
LI Xiong. Flight Rerouting Path Planning in Severe Weather[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2009. (in Chinese)
[23] 王莉莉, 彭勃. 基于LOFC时间窗分割算法的航迹聚类研究[J]. 南京航空航天大学学报, 2018, 50(5): 89-93.
WANG Lili, PENG Bo. Track Clustering Based on LOFC Time Window Segmentation Algorithm[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2018, 50(5): 89-93.(in Chinese)
[24] CHATFIELD C. The Holt-Winters Forecasting Procedure[J]. Journal of the Royal Statistical Society. Series C(Applied Statistics), 1978, 27(3): 264-279.
[25] BARTHOLOMEW D. Time Series Analysis Forecasting and Control[J]. Journal of the Operational Research Society, 1971, 22(2): 199-201.


