1 引言
目标跟踪一直以来都是计算机行业的热门课题,尤其在视频监控、无人驾驶、无人飞行器、医学图像分析、空中预警等诸多领域。由于跟踪时存在遮挡,尺度变化,光照变换等影响因素,所以如何在复杂场景下实现准确跟踪仍然是目标跟踪领域的重要课题[1]。
目前的目标跟踪算法可分为生成式算法[2-4]和判别式算法[5- 6],其中以相关滤波为代表的判别式算法备受学者青睐。Henriques等人提出了核相关滤波器跟踪算法(KCF)[7],其具有高鲁棒性、高精确度、速度快等特点。但是,核相关滤波器仅仅使用了单一的HOG(Histogram of Oriented Gradient)特征,并且不能应对尺度变化。Danelljan M等人在KCF算法的基础上提出DSST(Discriminatiive Scale Space Tracker)算法[8],增加了尺度滤波器以应对尺度变化,但是位置与尺度是利用两个滤波器单独处理,因此结果只是尺度最优的,位置却不一定是最优的。Li Y 等人将CN(Color Names)和FHOG(Fast Histogram of Oriented Gradient)特征融合,提出了尺度自适应滤波器SAMF(Scale Adaptive Multiple Feature)[9],其尺度估计的准确性依赖于定位器的准确性。Bertinetto L等人提出了尺度滤波器Staple[10],先用CN提取目标特征,再对CN特征降维处理,然后线性加权CN和FHOG特征。Martin Danelljan等人提出了C-COT(Continuous Convolution Operators)算法[13],把传统手工特征换成了VGG特征,提出了一个通用框架来学习连续空间域中的区分卷积算子,但是,跟踪速度大大下降。之后,Martin Danelljan等人在目标特征提取上做了简化,把目标特征通过插值转换到连续的空间域,提出了ECO(Efficient Convolution Operators)算法[14],改进了C-COT速度上的不足,但是沿用了DSST中的尺度估计策略,仍然未对尺度变化进行深入研究。胡正平[15]等人在KCF算法的基础上将HOG、CN和灰度特征构成特征池,并采用相位相关算法计算目标尺度。胡云层[16]等人融合DSST和KCF算法采用最小二乘法获取位置滤波器,在目标位置应用DSST算法中的尺度滤波器估算目标尺度。喻露[17]等人基于KCF算法提出了一种全局块与局部块协作的跟踪算法,对跟踪目标水平或垂直分成两块,并同时训练两个局部滤波器和全局滤波器,跟据局部滤波器的跟踪结果对全局滤波器进行修正。
尺度变换一直是跟踪领域的一大挑战,因此,本文在KCF算法的基础上提出一种多特征融合的尺度自适应跟踪算法。在特征提取阶段,首先使用帧差法得到连续两帧图像之间的差值,并对差值图像进行HOG特征提取,再将之与待测图像目标提取的ULBP(Uniform Local Binary Pattern)特征和CN特征进行线性融合,从而增强核相关滤波算法对目标的识别度,其次,在目标定位阶段加入了尺度估计策略,将尺度滤波器与分块算法结合求得目标的尺度与位置,提高算法的跟踪性能。
2 改进的KCF算法
2.1 KCF算法
相关滤波器的核心是通过当前帧和前序帧训练的滤波器预测目标的位置。KCF算法首先在首帧中获取跟踪目标在图片帧中的实际位置及HOG特征信息用以初始化训练跟踪器,在目标定位阶段,计算滤波器预测的位置以及其周围采样点位置的响应值,取最高响应值的位置为跟踪的目标所在位置,并对跟踪器进行更新。
为了检测出跟踪的目标,通常使用回归函数f(x)去估算目标位置。针对回归函数f(x)=wTz,训练目的是利用xi使得回归目标yi的误差最小,
(1)
其中λ是正则化参数,根据文献[7]可知,基本样本与训练样本之间的滤波响应图的极大响应值即为预测的目标位置:
(2)
其中·表示点乘,^表示傅里叶变化;x为基本样本,z为训练样本;kxz为基本样本与训练样本之间的核关系;α为向量系数。
KCF算法只使用了单一的HOG特征,HOG特征是一个局部的特征,不能很好的表述较大区域的特征,因此,本文融入了CN特征来处理目标的整体特征,并且加入了ULBP特征对目标的纹理进行描述,用以提高跟踪的准确率。KCF算法跟踪框的大小是固定不变的,而当目标尺度发生变化时,KCF没有尺度估计的弊端就会导致无法准确提取目标的特征,从而造成跟踪的失败,因此,本文在KCF的基础上加入了尺度估计策略,并将构造的一维尺度滤波器与分块算法的结果相融合,得出目标最终的尺度因子和位置。
2.2 特征提取融合
本文多特征融合算法采用HOG、CN和ULBP三种特征。KCF算法只使用了单一的HOG特征,HOG特征对处理局部信息效果较好,当目标较小时,直方图对于该目标的特征表述非常鲜明,而当目标较大时,当前图片帧中的不同区域也可能产生相似的HOG特征,所以目标容易出现漂移现象,因此,我们需要一种全局的特征去抑制这种情况。而CN和ULBP对整体的处理效果比较好,对光照变换、运动模糊等跟踪效果较好,能较好地区分目标和背景信息。所以本文在HOG的基础上加入CN和ULBP特征,利用特征的互补性有效提高跟踪的稳定性。
2.2.1 HOG特征提取
HOG算法是利用边缘梯度方向的分布来描述被跟踪目标的外形特征。首先对当前图像帧进行灰度化,再进行gamma压缩和归一化操作,然后统计每个cell里的梯度方向直方图。将4*4个cell合成一个block,作为这个block的hog的特征,并对这个特征进行归一化处理,最后得到一个M*N*31梯度直方图。由文献[7]可知
Gx(x,y)=I(x+1,y)-I(x-1,y)
Gy(x,y)=I(x,y+1)-I(x,y-1)
(3)
θ(x,y)=arctan(Gy(x,y)/Gx(x,y))
(4)
式中,I(x,y)为像素点;Gx(x,y)、Gy(x,y)为x, y方向梯度值;θ(x,y)为梯度方向。
2.2.2 帧差法特征提取
对图像序列相邻两帧采用基于像素的时间差分,通过闭值化来提取出图像中的运动区域。如图1所示,首先将后一帧图像减去前一帧图像的对应像素值得到差分图像,再对差分图像进行HOG特征提取,得到一个M*N*31梯度直方图。
图1 差分图
Fig.1 Difference map
2.2.3 ULBP特征提取
本文使用均一局部二值模式ULBP算法提取的特征来加强HOG提取的特征。ULBP算法是对LBP(Local Binary Pattern)算法的一种改进,是单维度的特征表述,LBP描述的是图像局部纹理特征。LBP算子是对样本中的每个像素点,选取其为中心的3*3邻域,在该邻域内,将其周围的8个像素值与之比较,大于该像素点的值置1,否则置0,然后按照顺时针方向组合即可产生8位二进制数,即28种模式,如图2所示。
图2 LBP示意图
Fig.2 Schematic diagram of LBP
但是,过多的二进制模式不利于纹理的表达,且对于特征提取的速度也有一定的影响,所以我们需要的是尽可能少且具有代表性的一些目标特征。Ojala提出了LBP算法的一种等价模式(uniform Pattern)[18],其核心思想是对该方法进行降维,绝大多数LBP模式只包含两次从1到0或者从0到1 的跳变,并将最多有两次跳变的归为一个等价模式类,其余的归为混合模式类,通过这样改进,3*3的邻域的二进制模式就由28模式减少为58种,并且不会丢失任何信息,也能减少高频噪声的影响。因此本文采取了ULBP算法,使用更少的数据来最好地表示图像的信息,如图3所示。
图3 ULBP特征图
Fig.3 ULBP feature map
2.2.4 CN特征提取融合
CN算法是将RGB颜色细化分为11种颜色去提取特征,然而CN的11个通道颜色并非均有意义,其中代表主要颜色的只有2维,因此对提取的特征用PCA进行降维,降至2维,去除其中的冗余信息,更好地区分背景信息,增强算法的鲁棒性,如图4所示。
图4 CN特征图
Fig.4 CN feature map
2.2.5 多特征融合
首先对差分图像进行HOG特征提取,得到一个M1*N1*31的HOG梯度直方图MD,与原图像HOG提取得到的M*N*31梯度直方图MH线性加权融合得到特征图M1。经过多次实验,λ取0.3。
M1=MD+MH*λ
(5)
再用ULBP算法提取的特征去加强HOG特征的每个通道,并将ULBP特征独立构成第32通道得到特征图M3,其中ω=0.05。
M2=M1+MULBP*ω
M3=(M2,MULBP*ω)
(6)
最后与CN算法降维后提取的两个维度特征MCN加入第33、34通道,得到目标的融合特征M。
M=(M3,MCN)
(7)
2.3 尺度估计
传统的KCF算法采用固定大小的窗口来训练滤波器模型,对目标运动过程中出现的尺度变化问题难以处理,导致滤波器模型对误差的累计越来越大,最终使跟踪目标出现漂移。针对此问题,本文在KCF算法上加入了尺度估计策略,首先,引入了DSST算法中[8]的尺度金字塔模型来估算目标尺度,但是DSST算法中采用的是固定范围的尺度池,因此当目标尺度变化较大时会产生偏差,所以,本文融合了分块算法的尺度估计值对尺度滤波器的估计值进行修正。
2.3.1 尺度滤波器
本文采用了DSST算法中的尺度估计策略,构建了一个一维的尺度滤波器,建立金字塔模型来估算目标尺度。由文献[8]可知,训练样本f从目标中心抠取。假设当前样本块的大小为M*N,尺度为S,我们抠取目标中心大小为anM*anN的窗口标记为Jn,尺度等级为n的训练样本f是Jn的特征描述。其中a表示一个尺度因子,n的取值范围如下:
(8)
以样本块为中心,截取m个尺度的样本,这样就能得到m个不同尺度的图像Patch,计算每个图像Patch的响应值,最大响应值对应的尺度即为当前目标的尺度因子,其中m=33。
2.3.2 分块跟踪
分块跟踪算法是将样本分成若干个目标块,每个跟踪目标块都有不同的特征信息,连续的跟踪过程中,随着整体目标尺度发生变化,每个分块的尺度也会随之变化,那么特征距离中心点的距离也会发生变化,因此,只需求得相对位置的变化量即可求得尺度的变化量。每个分块的中心点位置可以通过当前帧的中心点位置计算得出,由于跟踪实时性的要求,本文算法先将目标等分为9份,如图5所示,取最中间的1份与其邻接的4份分别串联得到4个新的特征分块,对新的4个特征块分别进行位置跟踪,并将每块跟踪得到的位置进行融合计算,最终得到分块融合的位置和尺度:
pos1=(pos2+pos3+pos4+pos5)/4
(9)
t=|pos2-pos5|*|pos3-pos4|
scale1=ti/ti-1
(10)
其中,pos2、 pos3、pos4和pos5是4个分块的中心点坐标位置,pos1为融合后的目标位置;ti为第i帧分块目标跟踪得到的目标尺度;scale1为第i帧分块目标跟踪得到的尺度因子。
图5 目标分块
Fig.5 Target block
2.3.3 尺度融合
用分块算法尺度因子与尺度滤波器得到的尺度因子先进行加权融合,得到当前帧的尺度因子:
pos=(1-μ)*pos2+μ*pos1
(11)
scale=(1-θ)*scale2+θ*scale1
(12)
其中,pos2是核滤波器得到的位置,scale2为尺度滤波器计算求得的尺度因子,scale为最终求得的当前帧的尺度因子,μ,θ为系数,μ=0.1,θ=0.08。
2.4 流程图
本文算法在特征提取阶段融合了HOG,CN,ULBP三种特征,之后在目标定位阶段,将尺度滤波器求得的尺度因子与分块算法求得的尺度因子融合得出当前帧的尺度因子,并将KCF预测的目标位置与分块算法预测的位置融合得出当前帧目标的中心点位置,见图6。
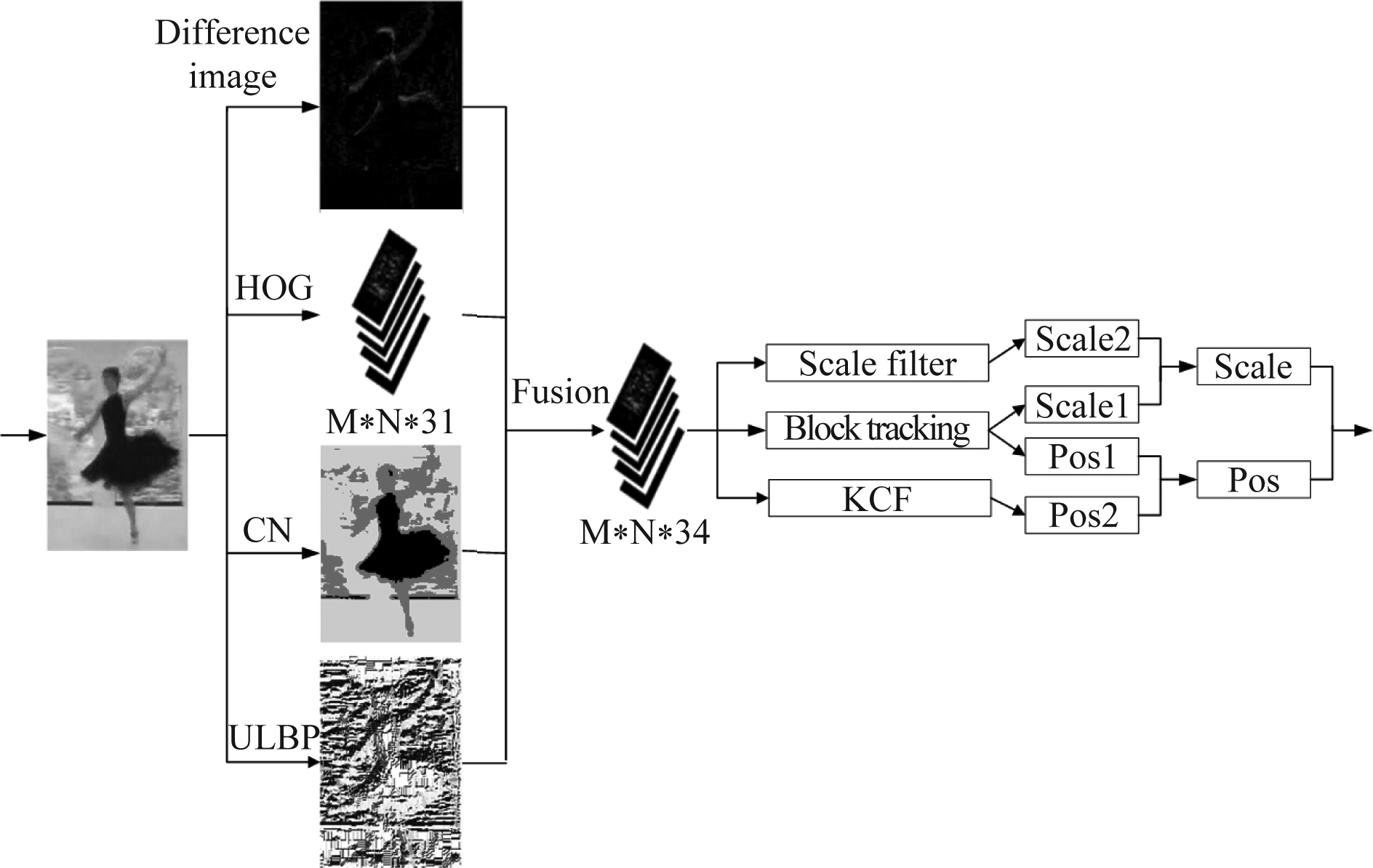
图6 改进算法的流程图
Fig.6 Flow chart of our method
3 实验结果分析
3.1 实验环境与参数
本文实验环境的处理器为Intel(R) i5- 84002.8 GHz,内存为8GB,采用Matlab2018b的作为编程语言。本算法的基本参数:高斯核的标准差σ为0.5,学习因子η为0.02,正则化系数 λ为0.0001。为了验证本文MFKCF算法的有效性,本文在16个包含尺度变化的不同背景条件的视频序列上进行测试,如表1所示。除了与KCF进行对比之外,本文还选取了DSST,ECO,LADCF,LDES和SAMF进行比较。本文分别从距离精确度,中心误差和速度对算法进行分析。本文采用的评价标准，距离精确度DP=m/N(Distance Precision,DP),中心误差
(Center Location Error,CLE)、速度V=N/toc。其中,m为中心点位置小于等于20个像素点的次数,N是当前视频序列的总帧数。(xt,yt)是第t帧预测的目标中心点坐标,(xt0,yt0)是目标在第t帧的中心点实际坐标。toc为运行该视频序列的总时长。
表1 实验中测试视频
Tab.1 Test video in the experiment
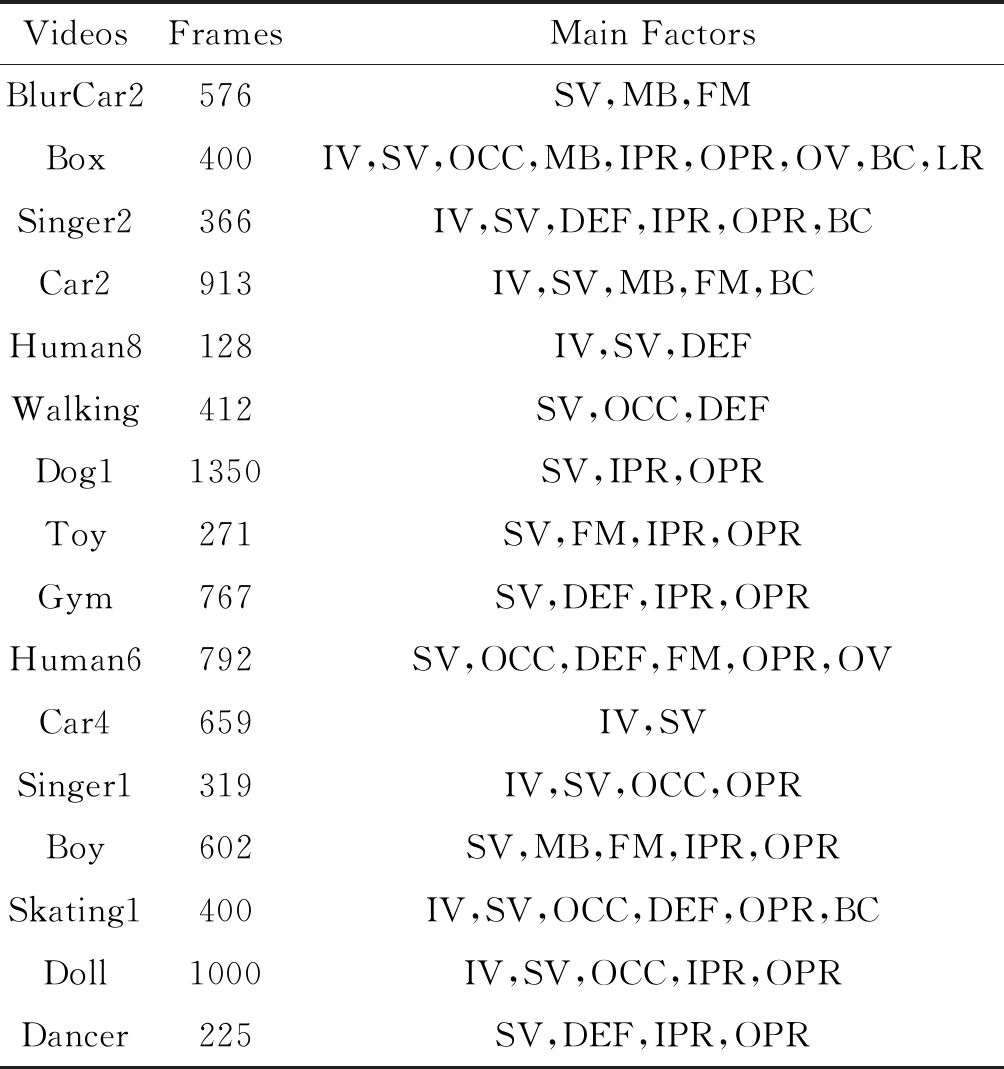
VideosFramesMain FactorsBlurCar2576SV,MB,FMBox400IV,SV,OCC,MB,IPR,OPR,OV,BC,LRSinger2366IV,SV,DEF,IPR,OPR,BCCar2913IV,SV,MB,FM,BCHuman8128IV,SV,DEFWalking412SV,OCC,DEFDog11350SV,IPR,OPRToy271SV,FM,IPR,OPRGym767SV,DEF,IPR,OPRHuman6792SV,OCC,DEF,FM,OPR,OVCar4659IV,SVSinger1319IV,SV,OCC,OPRBoy602SV,MB,FM,IPR,OPRSkating1400IV,SV,OCC,DEF,OPR,BCDoll1000IV,SV,OCC,IPR,OPRDancer225SV,DEF,IPR,OPR
3.2 融合系数λ阈值的选定
本文通过将差分图像与HOG梯度直方图提取的特征线性加权从而增强目标特征,提高跟踪的稳定性。因此,融合系数λ阈值的选择至关重要。为取得更好的跟踪效果,本文基于16组测试视频,对不同阈值下的改进算法进行测评,以获取最佳阈值。图7中可以看出,当阈值取0.3时,在DP评价曲线上表现良好。阈值由0.1逐渐增至0.5的过程中,本文算法在CLE评价曲线上效果先升高再降低,在λ=0.3时,平均中心误差值最小。因此,本文选择0.3作为式(5)中融合系数λ的阈值。
3.3 消融实验
本文也在这16个视频序列上进行消融实验来验证本算法每个特征的有效性。如表2所示,当只采用HOG特征时,跟踪效果在精确度下降了4个百分点。然后从本算法中移除ULBP特征后,本算法的表现力在精确度上下降了1.9个百分点,由此可见ULBP特征对目标纹理的处理在后续的跟踪上有较好的效果。最后,移除了CN特征,算法在精确度上下降了1.6个百分点,证明了CN特征对于全局信息的处理是有效的。
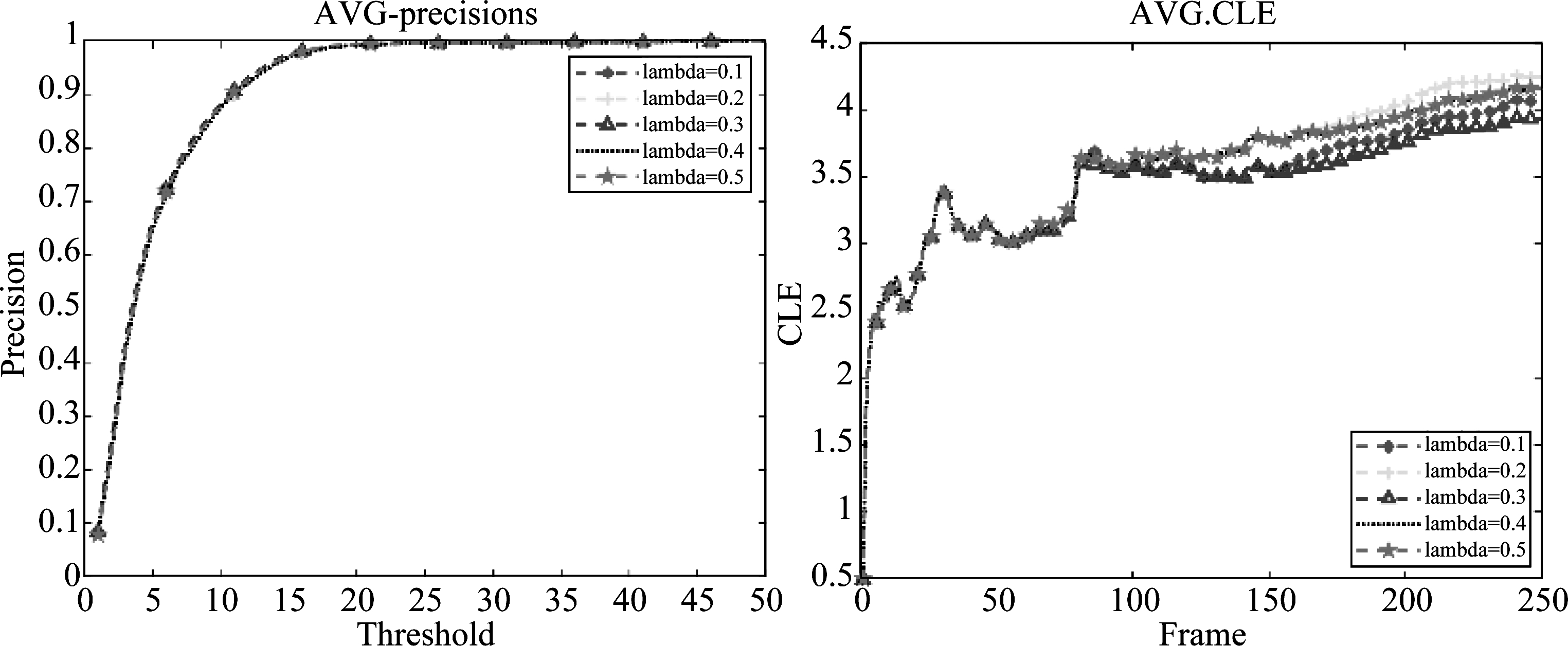
图7 λ取不同阈值的测评结果
Fig.7 Evaluation results of our method when λ takes different thresholds
表2 消融实验
Tab.2 Ablation experiment
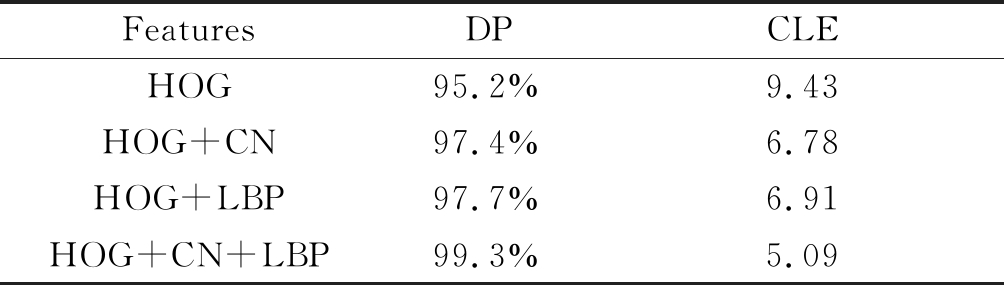
FeaturesDPCLEHOG95.2%9.43HOG+CN97.4%6.78HOG+LBP97.7%6.91HOG+CN+LBP99.3%5.09
3.4 MFKCF与KCF跟踪效果对比
本文选择两个视频作为示例来对比分析MFKCF与KCF的跟踪效果。图8显示了MFKCF和KCF在视频集Gym第670,680,690,700帧上的跟踪效果。可以看出,KCF不含尺度变化,因此跟踪框大小是固定不变的,但是MFKCF的跟踪框随着目标尺度的改变而改变。该组视频序列中,背景颜色与跟踪目标的颜色相近,跟踪过程中背景容易对目标造成干扰,特别是背景的地板颜色。传统的KCF目标跟踪算法在这个背景颜色与跟踪目标颜色相接近时极易跟丢目标,但是本文改进的尺度估计和多特征融合目标跟踪算法能很好地跟踪目标。
图9显示了MFKCF与KCF在视频集Gym上CLE和DP评价曲线。虽然在前600帧MFKCF的CLE比KCF要差一点,但是在650帧之后,KCF的中心误差变大,导致在680帧左右KCF丢失目标,之后MFKCF效果好于KCF。在平均精度上,MFKCF明显好于KCF。
图8 MFKCF,KCF跟踪效果(红色是MFKCF,黄色是KCF)
Fig.8 MFKCF, KCF tracking effect (red is MFKCF, yellow is KCF)
图9 MFKCF,KCF在CLE,DP上的曲线
Fig.9 MFKCF, KCF curve on CLE, DP
图10 MFKCF,KCF跟踪效果(红色是MFKCF,黄色是KCF)
Fig.10 MFKCF, KCF tracking effect (red is MFKCF, yellow is KCF)
图10显示了MFKCF和KCF在视频集Human6第222,224,226,228帧上的跟踪效果。该组视频序列在220帧左右时,背景信息与目标特征框内部分信息一致,很容易使KCF跟丢目标。且KCF的跟踪框与目标初始大小一致,在目标变大后,其跟踪框远小于目标大小,因此提取的特征也会产生偏差,造成跟踪偏移,但MFKCF加入尺度估计策略后,跟踪框随着目标的变化而变化,相较KCF增加了算法的鲁棒性,能实现对目标尺度变化的稳定跟踪。
表3显示MFKCF算法与原KCF算法精度对比结果。由表3可以看出,在视频Dancer,Dog1和Toy上,本算法的中心误差稍高于KCF算法,在精确度上只在视频Toy上稍逊于KCF算法,但是在其他视频上的精确度和中心误差,本文算法都比KCF表现的要好。在这16个视频上,本文算法与KCF相比,在精确度上从0.936提升到0.993,提高了5.7%。中心误差从12.69降到5.09,降低了7.6%。因此,本文方法总体上比KCF有较强的鲁棒性。
表3 本文算法与KCF精确度、中心误差对比表
Tab.3 Comparison of algorithm and KCF accuracy, center error
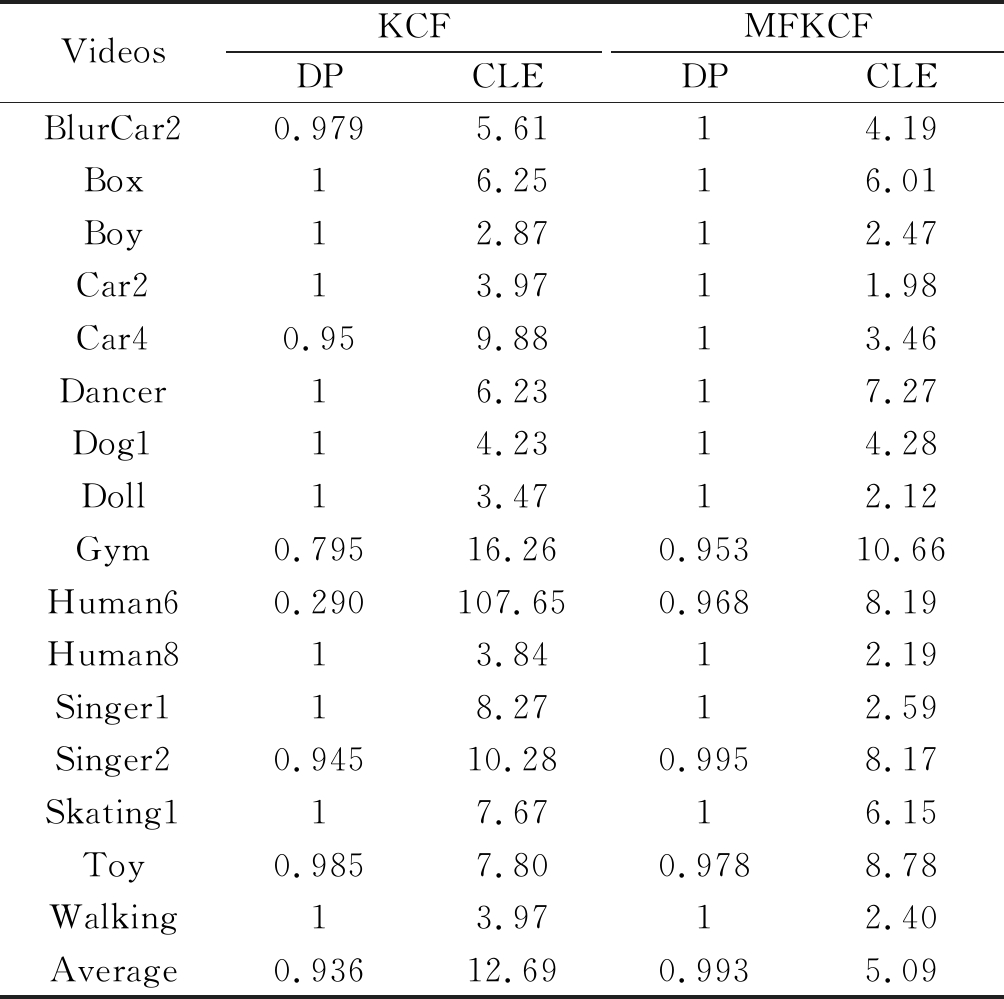
VideosKCFDPCLEMFKCFDPCLEBlurCar20.9795.6114.19Box16.2516.01Boy12.8712.47Car213.9711.98Car40.959.8813.46Dancer16.2317.27Dog114.2314.28Doll13.4712.12Gym0.79516.260.95310.66Human60.290107.650.9688.19Human813.8412.19Singer118.2712.59Singer20.94510.280.9958.17Skating117.6716.15Toy0.9857.800.9788.78Walking13.9712.40Average0.93612.690.9935.09
图11显示了MFKCF与KCF在视频集Human6上CLE和DP评价曲线。MFKCF在CLE和DP上的跟踪效果明显好于KCF。
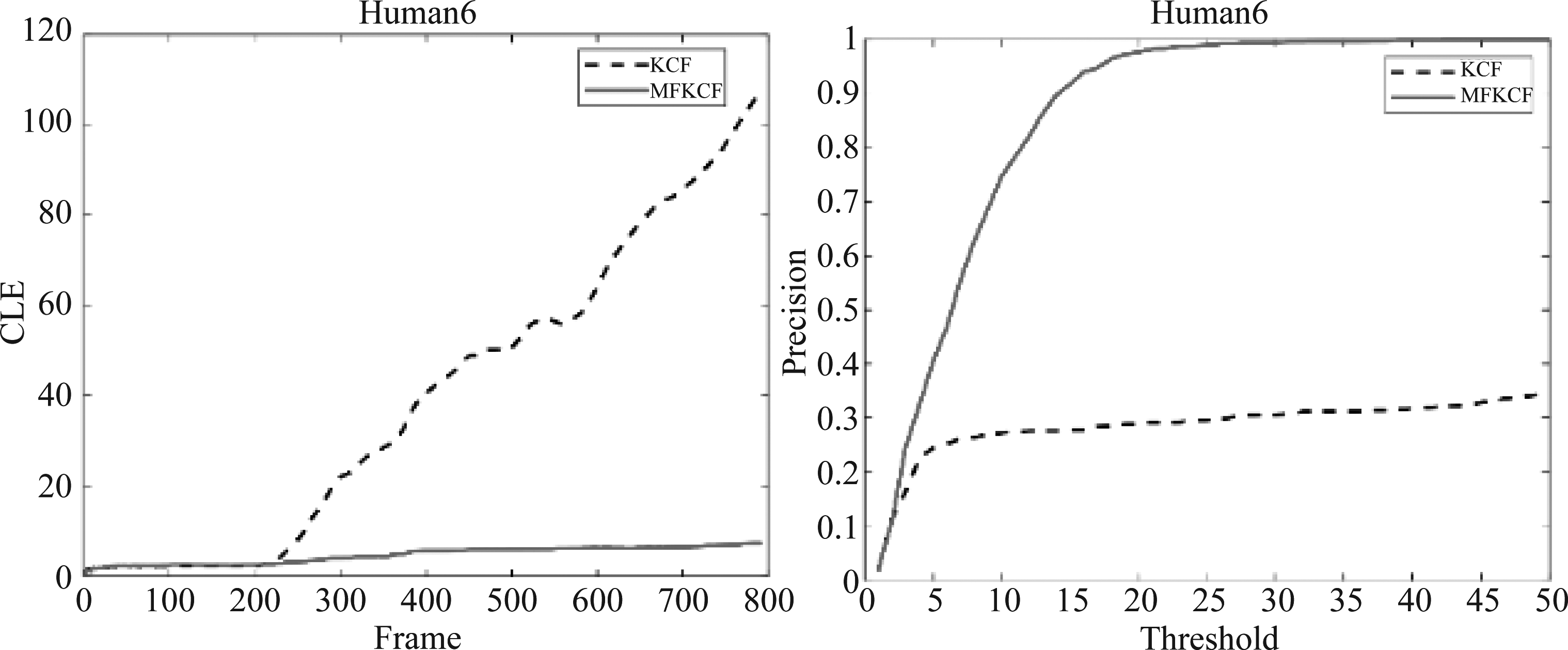
图11 MFKCF,KCF在CLE,DP上的曲线
Fig.11 MFKCF, KCF curve on CLE, DP
图12显示了MFKCF与KCF在视频集Human8、Car4、Dog1和Toy上的跟踪效果图,可以看出MFKCF算法的跟踪框随着目标尺度变化而变化,能较准确地估计出跟踪目标的尺度,而KCF算法的跟踪框的大小是不变的。
3.5 MFKCF与其他算法跟踪效果对比
表4列出了MFKCF算法与其他几种算法在16个视频上评价指标的均值,其在距离精确度,中心误差上性能均有所提升,虽然相较KCF算法速度有所下降,但也达到了实时的标准(实时性以24帧/s为阈值)。
与其他几种算法相比,ECO、LADCF和LDES算法在部分视频集上出现跟踪丢失的情况,导致整体在DP和CLE评价上表现不佳,且在CLE上都超过了15。DSST在DP上达到95.2%,CLE达到了15.0。SAMF在DP上达到93.0%,在CLE是15.7。在速度方面,LADCF、LDES和SAMF都没有达到实时性的要求。图13显示了算法在测试视频Human8的最后一帧以及其他15个测试视频上第200帧的表现情况。
表4 距离精确度、中心误差和速度的均值比较
Tab.4 Mean value comparison of distance precision, center location error and velocity
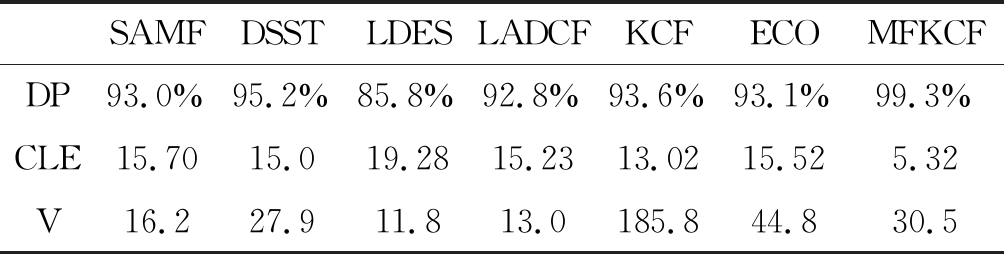
SAMFDSSTLDESLADCFKCFECOMFKCFDP93.0%95.2%85.8%92.8%93.6%93.1%99.3%CLE15.7015.019.2815.2313.0215.525.32V16.227.911.813.0185.844.830.5
例如在视频Singer2上,由于受到背景因素的干扰,导致ECO,LADCF,LDES和SAMF在跟踪过程中产生不同程度的漂移,而本文的算法却很好的完成跟踪,见图14。
为了更好地显示本文算法与其他算法对比效果,本文对测试视频绘制了CLE,重叠和DP评价曲线。从图15上显示,MFKCF有明显优势,对KCF算法有着很好改进。
图12 尺度变化效果图.(a)Human8;(b)Car4;(c)Dog1;(d)Toy (红色是MFKCF,黄色是KCF)
Fig.12 Effect picture of scale variety. (a) Human8;(b) Car4;(c) Dog1;(d) Toy (red is MFKCF, yellow is KCF)
图13 部分跟踪效果
Fig.13 Partial tracking effect
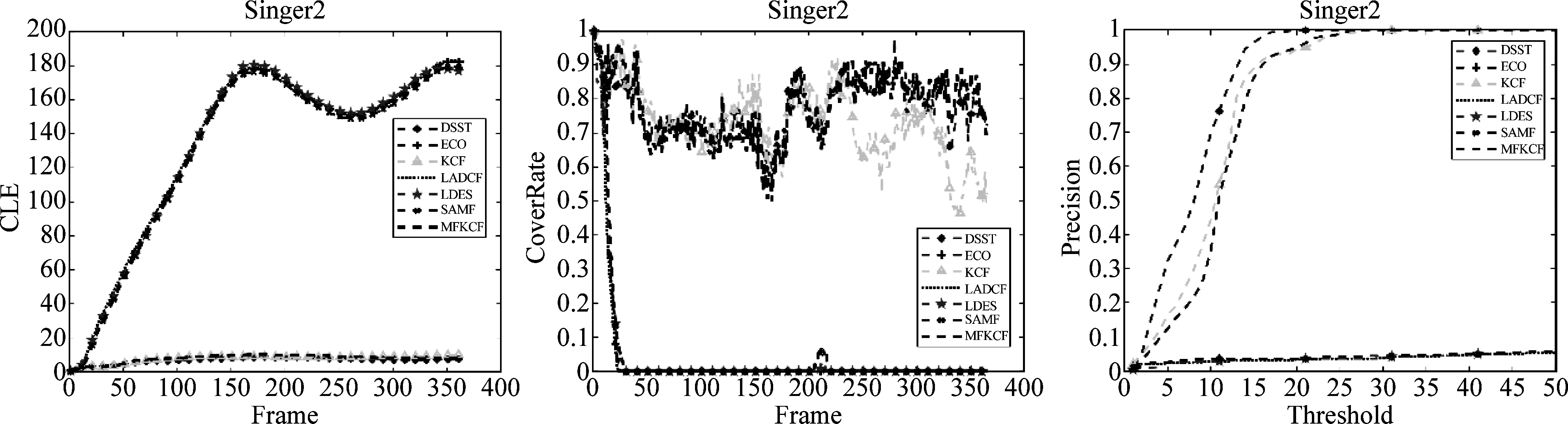
图14 视频Singer2上的跟踪结果
Fig.14 Tracking results on video Singer2
图15 CLE,重叠和DP上的曲线
Fig.15 curve on CLE,Overlap and DP
4 结论
本文基于KCF算法,针对目标跟踪算法面临的尺度变化的问题,提出了改进算法MFKCF。首先,针对目标的整体和局部处理分别采用了HOG,CN与ULBP特征;其次,采用帧差法对图像进行处理,并将三种特征进行融合;最后,引入了尺度估计策略,将尺度滤波器与分块算法得到的估计值融合得出目标最终的位置与尺度。MFKCF算法通过加强对目标的识别,增强了目标模板的准确性,提高了算法的跟踪性能。本文算法虽然提高了跟踪的准确率,但是速度却受到了较大影响,这个问题将是下一步研究的方向。
[1] 吴小俊, 徐天阳, 须文波. 基于相关滤波的视频目标跟踪算法综述[J]. 指挥信息系统与技术, 2017, 8(3): 1-5.
WU X J, XU T Y, XU W B. Review of target tracking algorithm in video based on correlation filtering[J]. Command Information System and Technology, 2017, 8(3): 1-5.(in Chinese)
[2] 朱文青, 刘艳, 卞乐, 等. 基于生成式模型的目标跟踪方法综述[J]. 微处理机, 2017, 38(1): 41- 47.
ZHU W Q, LIU Y, BIAN L, et al. Survey on object tracking method based on generative model[J]. Microprocessor, 2017, 38(1): 41- 47.(in Chinese)
[3] NGUYEN H T, SMEULDERS A W M. Fast occluded object tracking by a robust appearance filter[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(8): 1099-1104.
[4] COMANICIU D, RAMESH V, MEER P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564-577.
[5] HARE S, GOLODETZ S, SAFFARI A, et al. Struck: Structured output tracking with kernels[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 38(10): 2096-2109.
[6] KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-Learning-Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409-1422.
[7] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.
[8] DANELLJAN M, H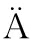
GER G, KHAN F, et al. Accurate scale estimation for robust visual tracking[C]∥British Machine Vision Conference, Nottingham, September 1-5, 2014. BMVA Press, 2014.
[9] LI Y, ZHU J. A scale adaptive kernel correlation filter tracker with feature integration[C]∥European Conference on Computer Vision. Springer, Cham, 2014: 254-265.
[10] BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: Complementary learners for real-time tracking[C]∥Proceedings of The IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1401-1409.
[11] DANELLJAN M, HAGER G, SHAHBAZ KHAN F, et al. Learning spatially regularized correlation filters for visual tracking[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2015: 4310- 4318.
[12] CHOI J, JIN CHANG H, YUN S, et al. Attentional correlation filter network for adaptive visual tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4807- 4816.
[13] DANELLJAN M, ROBINSON A, KHAN F S, et al. Beyond correlation filters: Learning continuous convolution operators for visual tracking[C]∥European Conference on Computer Vision. Springer, Cham, 2016: 472- 488.
[14] DANELLJAN M, BHAT G, SHAHBAZ KHAN F, et al. Eco: Efficient convolution operators for tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 6638- 6646.
[15] 胡正平, 尹艳华, 顾健新. 位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法[J]. 信号处理, 2019, 35(12): 1979-1989.
HU Z P, YIN Y H, GU J X. Multi-feature Selection Correlated Filtering Target Tracking Algorithms Based on Location-Scale Different Space Coordination[J]. Journal of Signal Processing, 2019, 35(12): 1979-1989.(in Chinese)
[16] 胡云层, 路红, 杨晨, 等. 融合DSST和KCF的尺度自适应跟踪算法[J]. 计算机工程与设计, 2019, 40(12): 3563-3568.
HU Y C, LU H, YANG C, et al. Scale adaptive tracking algorithm combining DSST and KCF[J]. Computer Engineering and Design, 2019, 40(12): 3563-3568.(in Chinese)
[17] 喻露, 胡剑锋, 姚磊岳. 全局块与局部块协作的相关滤波目标跟踪算法[J]. 计算机科学, 2020, 47(6): 157-163.
YU L, HU J F, YAO L Y. Correlation Filter Object Tracking Algorithms Based on Global and Local Block Cooperation[J]. Computer Science, 2020, 47(6): 157-163.(in Chinese)
[18] KART U, LUKEZIC A, KRISTAN M, et al. Object tracking by reconstruction with view-specific discriminative correlation filters[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019: 1339-1348.
[19] ZHANG M, WANG Q, XING J, et al. Visual tracking via spatially aligned correlation filters network[C]∥Proceedings of the European Conference on Computer Vision (ECCV), 2018: 469- 485.
[20] WANG N, SONG Y, MA C, et al. Unsupervised Deep Tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019: 1308-1317.
[21] OJALA T, PIETIKAINEN M, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987.
[22] WANG Q, ZHANG L, BERTINETTO L, et al. Fast online object tracking and segmentation: A unifying approach[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019: 1328-1338.
[23] BHAT G, DANELLJAN M, GOOL L V, et al. Learning discriminative model prediction for tracking[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2019: 6182- 6191.
