1 引言
目标跟踪是计算机视觉中的一个重要研究方向,在视频监控、人机交互、无人驾驶等方面有着广泛的应用[1]。但跟踪器的跟踪效果容易受到尺度变化、遮挡和形变等复杂环境因素的影响,因此提高目标跟踪算法在复杂环境下的跟踪准确性和鲁棒性仍然是一个研究热点和难点。
传统的目标跟踪算法主要分成生成式模型和判别式模型。基于判别式模型的相关滤波跟踪算法通过分析目标模块间的相似度,将目标跟踪转换为区分目标模块和背景模块的二分类问题,根据不同候选目标的置信度值确定预测目标的位置。相比于基于生成式模型的跟踪算法,基于判别式模型的相关滤波跟踪算法更能充分利用背景信息。得益于其强大的计算能力,判别式相关滤波器(DCF)已被广泛应用于视觉跟踪领域[1-5]。但边界效应的存在使得DCF跟踪器的鲁棒性和跟踪准确性受到很大限制。空间正则化判别相关滤波(Spatially Regularized Discriminative Correlation Filters, SDRCF)[6]和时空正则化相关滤波(Learning Spatial-Temporal Regularized Correlation Filters, STRCF)[7]利用空间正则来改善边界效应,虽然提高了目标跟踪的准确度,但扩大了的搜索区域大大增加了计算负担。背景感知相关滤波器(Background-Aware Correlation Filter,BACF)[8]使用裁剪矩阵从背景集中提取补丁,以较低的计算成本扩展了搜索区域,但引入了过多背景噪声容易发生数据异常,使得判别式滤波器更容易偏向从背景环境中学习,而非从目标区域学习。虽然在检测出现异常后采取修复措施可以抑制异常的影响,但效果有限[9-10]。异常抑制相关滤波器(Aberrance Repressed Correlation Filter,ARCF)[11]通过限制在检测阶段的响应图变化率实现异常的有效抑制。但是,ARCF模型没有充分利用滤波器响应图中隐含的时间相关信息,在形变或遮挡等环境条件下,当前帧的跟踪目标很难与前一帧的目标相匹配,跟踪容易发生偏移,甚至发生目标跟踪失败的情况。虽然采用多特征选择的跟踪算法能够在目标发生形变、遮挡等情况下保持较好的跟踪有效性[12],但复杂的特征选择和置信度计算同样加大了模型计算复杂度。
为了更好地应对复杂环境下的目标跟踪问题,本文提出了一种时间驱动的异常学习相关滤波器(Aberrance Learning via Time-driven Correlation Filter, ALTCF),ALTCF模型将时间正则化和异常学习在检测过程中相结合,在时域中提供了更具鲁棒性的外观模型。在某种程度上,ALTCF不仅可以看作是学习过程中ARCF损失函数的合理近似,还可以抑制滤波器学习过程中的异常。但引入时间信息的模型都会受到时间滤波器退化的影响,一些跟踪算法[13,7]采用模板匹配的方法来缓解时间退化问题,提高跟踪运动目标的准确性。而我们的ALTCF利用Online Passive-Aggressive(PA)算法[14]引入时间正则项,以确保相关滤波器在更新过程中保持与前一帧的相似度,从而提高了分类精度,使模型具有鲁棒性。不仅如此,由于PA算法一般用来在线学习分类器,尤其在分类样本不均衡时能够实现有效的分类学习[15],利用在线PA算法的ALTCF能够在外观发生较大变化时依赖主动学习,确保正负样本的分类,以获得更为准确的预测目标。另外,考虑到现实生活中的数据常带有噪声,数据容易发生异常,则会导致样本标识错误。而根据在线PA学习,一个标识错误的实例可能就会在一个错误的方向上大幅度改变了权值向量,进而出现过拟合的现象。因此,本文引入的时间正则项利用时间域上的特征来确保目标跟踪模型保持时间上的相似性,可以抑制过拟合现象,提高跟踪模型的精度和鲁棒性。
我们的ALTCF模型与13种先进的跟踪器在OTB数据集上进行了对比实验,通过对跟踪的精确度和成功率的分析来展示ALTCF在复杂环境条件下的跟踪性能。另外我们还进行了与STRCF跟踪器的对比实验来讨论ALTCF的时域鲁棒性,主要通过滤波器在每帧图像中的估计目标框与初始目标框的重叠率来体现。
2 时间驱动的异常学习相关滤波器(ALTCF)
我们通过在线PA算法[14]对一般跟踪模型引入时间正则项,再结合ARCF的异常学习构造出ALTCF的损失函数。在目标跟踪的过程中,时间正则项可以确保相关滤波器在更新过程中保持与前一帧图像的相似度,可以防止模型学习过程中的过拟合现象,保证跟踪模型在遇到遮挡等复杂情况依旧能保持良好的鲁棒性。图1为ALTCF的流程框图。相似度信息和异常学习相结合，通过模型迭代得到当前帧的目标位置信息，并将该信息用于下一帧的学习和迭代，不断反复，最终得到整个视频序列中目标图像的位置。接下来我们将详细介绍损失函数的求解过程来获得每帧图像的目标跟踪位置。
2.1 ALTCF的损失函数
给出图像在D个通道的矢量化样本z,即zd∈RN(d=1,2,…,D)和滤波器的矢量化理想响应m∈RN,构建ALTCF的损失函数如下:
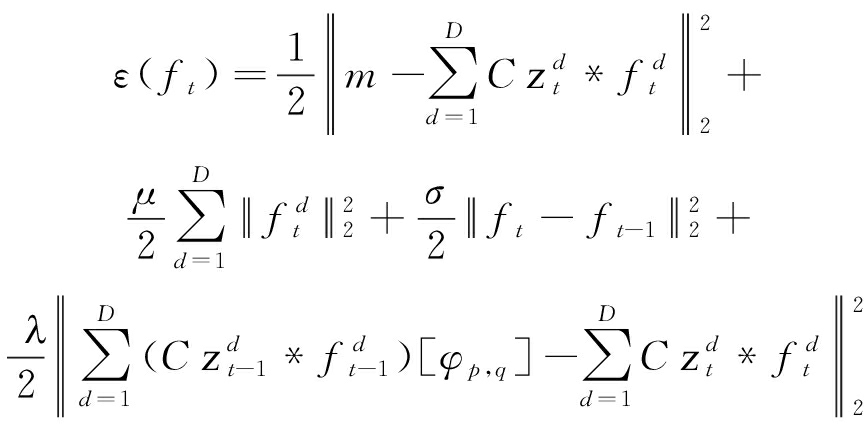
(1)
其中,C∈RM×N是用于选择每个通道内输入矢量化样本zd的M个中心元素的裁剪矩阵,
是模型在第d个通道中对第t帧图像学习得到的相关滤波器,σ表示时间参数。另外,将运算符*定义为相关运算符。损失函数的第三项为时间正则项,第四项为抑制异常的正则化项,参数λ为惩罚因子。我们将式(1)以矩阵形式表示,方便目标函数转换到频域,如下所示:
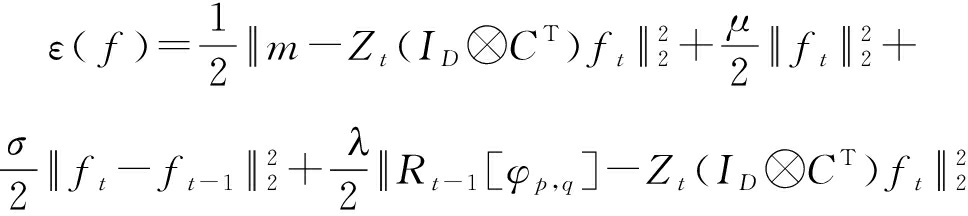
(2)
其中Zt是输入样本zt的矩阵形式。ID是一个大小为D×D的单位矩阵。运算符⊗和上标T分别表示Kronecker乘积和共轭转置运算[16]。Rt-1表示前一帧的响应图,其值为Zt-1(ID⊗CT)ft-1,而[φp,q]表示两个峰的移位操作,p和q表示二维空间中两个响应图中两个峰的位置差。
2.2 模型的频域转换
根据Parseval定理,将式(2)转换到频域形式,以确保足够的计算效率,转换后的公式如下:
(3)
其中上标 ^ 表示已执行离散傅里叶变换(DFT)的信号,即
其中, ft表示第t帧图像的相关滤波器,
为用于优化过程的辅助变量。
表示移位信号Rt-1[φp,q]的离散傅里叶变换。 由于前一帧中的响应映射已经计算,因此在优化计算过程中可以将视为第t帧中的恒定信号。
2.3 基于ADMM的优化过程
由于式(3)中的函数是凸函数的,我们选择交替乘子算法(ADMM)来计算目标函数的全局最优解。首先,我们引入拉格朗日乘子
得到式(3)的增广拉格朗日形式。
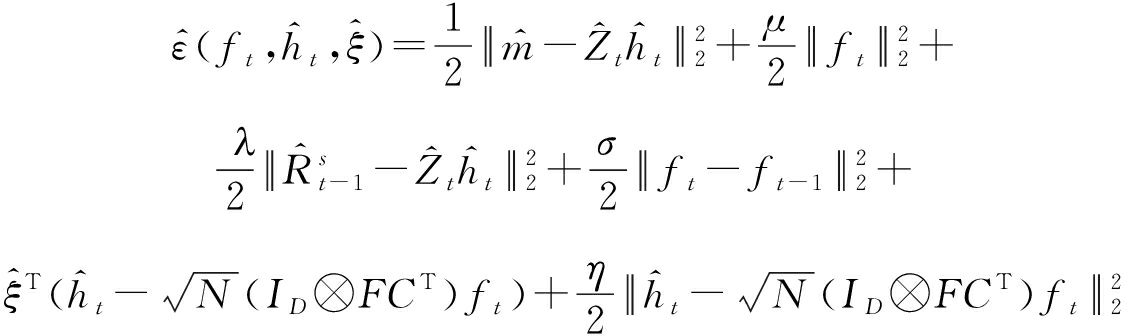
(4)
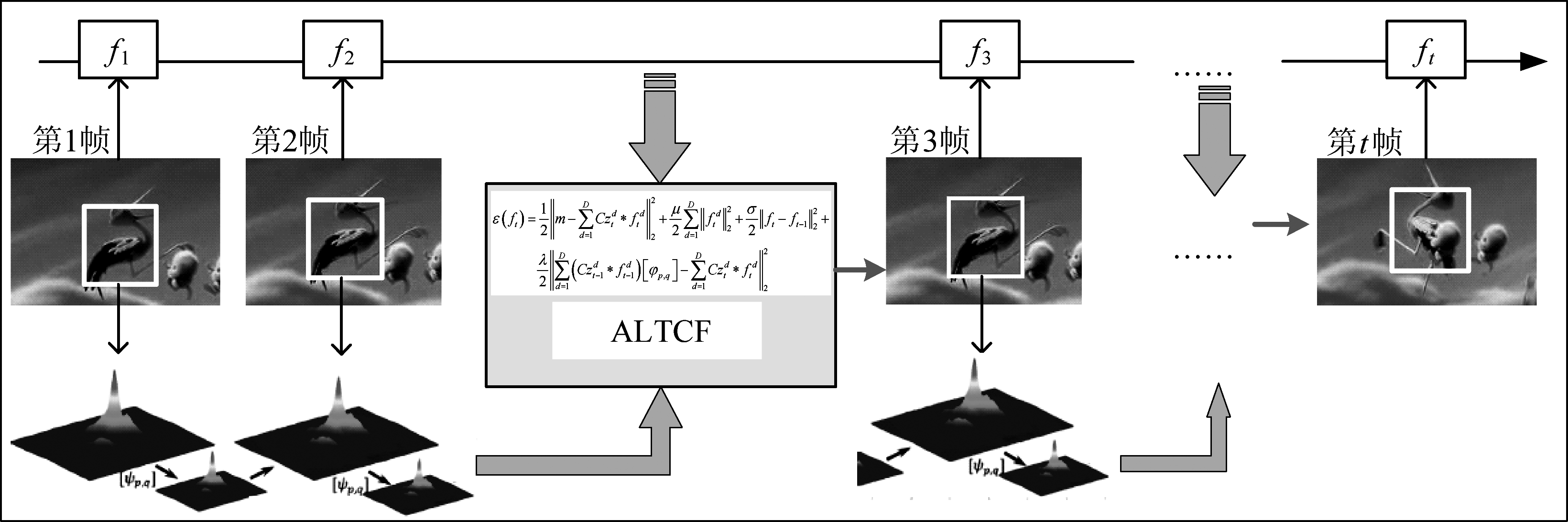
图1 ALTCF模型的流程框架图
Fig.1 The process framework diagram of the ALTCF model
其中η是惩罚因子,拉格朗日矢量
的大小为DN×1。然后,利用ADMM算法将第t帧的增广拉格朗日函数划分为两个子问题来解决损失函数的优化问题,具体表达形式如下:
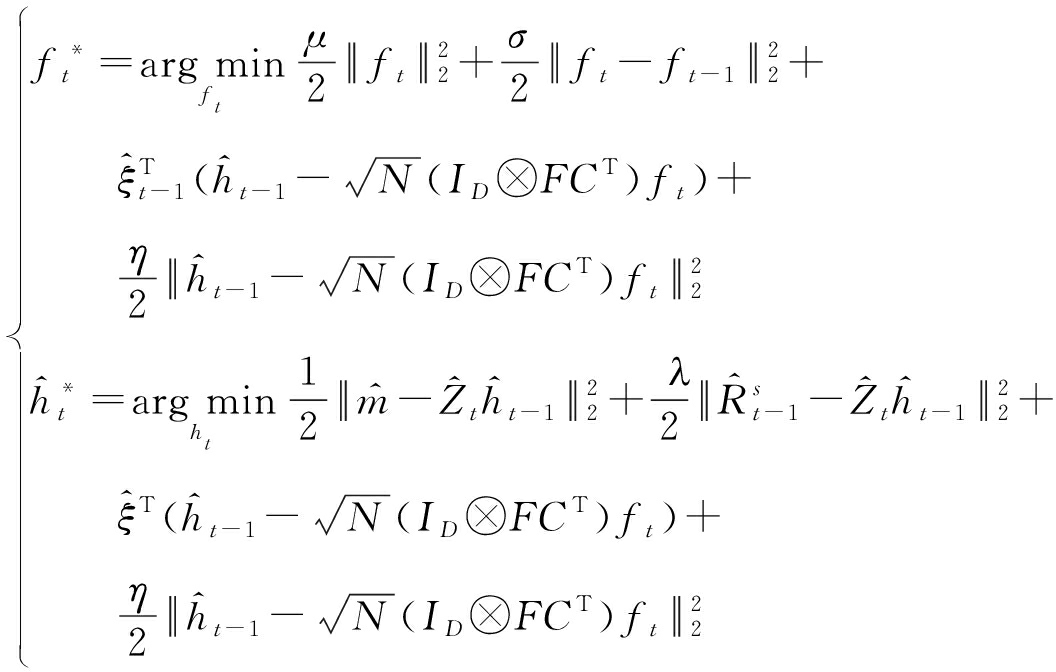
(5)
2.3.1 求解子问题
通过对公式(5)的第一个等式求导得到
的更新表达:
(μ+σ+ηN)-1(σft-1+Nξt-1+ηNht-1)
(6)
其中ht和ξ可以通过快速傅里叶逆变换(IFFT)求得:
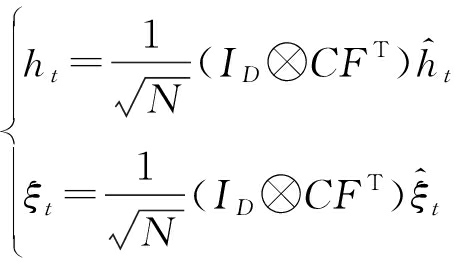
(7)
2.3.2 求解子问题
由于子问题
的求解计算中包含
其求解计算过程要比求解要复杂得多。为了降低在每次ADMM迭代中的计算复杂度,我们利用了
的稀疏特征。考虑到
的每个元素,即
都可由每个
和
联合确定,其中运算符conj(·)表示复共轭运算。因此,我们将子问题
进一步划分为N个更小的问题,分别在n=1,2,…,N的情况下进行计算。
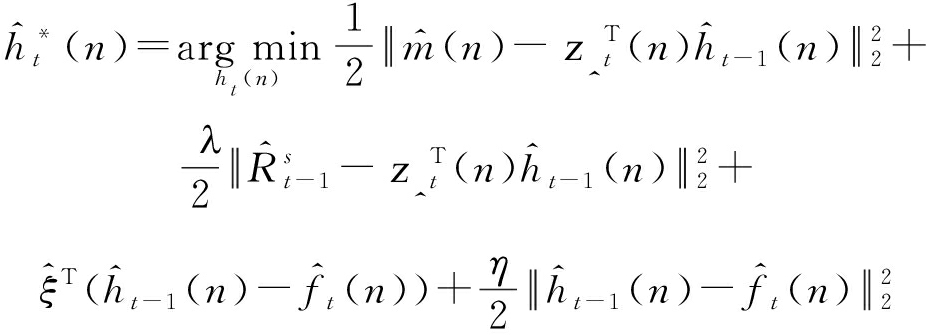
(8)
其中
是
的DFT变换,即
则式(8)的解为:
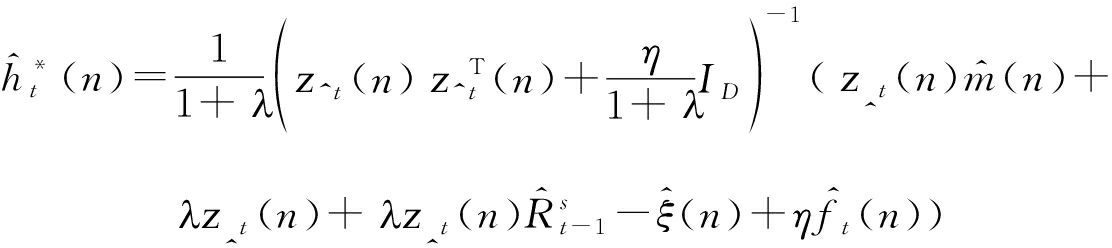
(9)
利用Sherman-Morrison公式,即(A+uνT)-1=A-1-A-1u(Im+νTA-1u)-1νTA-1,其中A,u和ν矩阵的大小分别为a×a,a×m和m×a。代入到式(9)中,则有
那么式(9)可以转化为:
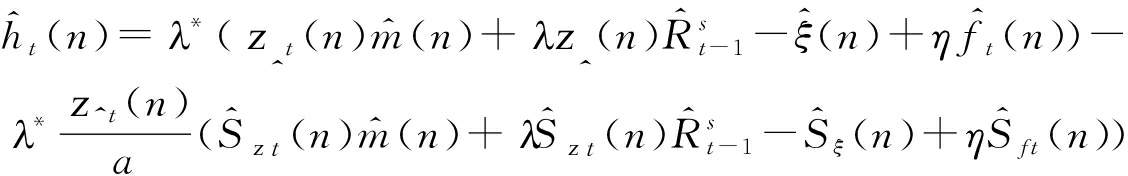
(10)
其中,
以及
2.3.3 拉格朗日参数的更新
为了提高计算的精确度,往往要经过多次迭代以获得目标函数的最优解。则拉格朗日参数的迭代更新结果如下:
(11)
其中下标j和j+1分别表示第j次和第j+1次迭代。
2.3.4 外观模型的更新
外观模型更新对视觉跟踪具有重要影响。在目标物体形状,尺度,遮挡和旋转的影响下,目标物体的外观在跟踪过程中经常发生变化。 因此,我们应用在线更新策略来更新外观模型以提高我们所提出的跟踪算法的鲁棒性。在第t帧时,外观模型的更新公式如下:
(12)
其中τ是外观模型的学习率。需要注意的是,前面计算中所涉及的
均为
2.3.5 计算复杂度分析
在不采用任何优化算法时,公式(2)的模型计算复杂度接近于Ο(D3N2M)。但本文采用了ADMM算法,将增广拉格朗日函数划拆解成两个子问题来计算,减少计算量。公式(6)的计算量主要集中在对ht和ξ的求解,将ht和ξ的Kronecker乘积转换成D个快速傅里叶逆变换计算
和
因此式(6)的计算复杂度为Ο(DMNlog(MN))。而在子问题的求解中,我们利用
的稀疏特征包含来降低在每次ADMM迭代中的计算复杂度,最终转化为D个通道内的N个子问题的线性解,因此式(10)的计算复杂度为Ο(DN)。最终整个模型的计算复杂度的数量级为Ο(DMNlog(MN))。尽管ALTCF模型的优化过程通过ADMM算法简化实现,但由于增加了时间正则项和滤波器响应图的在线学习,相比于deepSTRCF的5.3,ALTCF的跟踪速度(Average frame per second, FPS)在深度特征条件下只达到了1.2106。因此,本文所提出的ALTCF是以牺牲模型效率来获得更高的跟踪鲁棒性。
3 实验和结果
与ALTCF跟踪器进行对比实验的13个最先进的跟踪器分别为ECO[16]、CCOT[17]、STRCF[7]、ECO-HC[16]、SRDCFdecon[18]、BACF[8]、Staple+CA[19]、SRDCF[6]、SAMF+AT[20]、SAMF[21]、MEEM[22]、DSST[4]和ASRCF[23],所有方法均采用方向梯度直方图(HOG)特征。另外,我们着重比较分析ALTCF、ASRCF和STRCF的跟踪结果,以突出ALTCF的优越性。实验结果的衡量指标为精确度(precision plot)和成功率(success plot)。精度主要指的是预测位置中心点与人工标注的中心位置间的欧式距离小于给定阈值的视频帧数的百分比,是以像素为单位进行的计算,阈值设定为20个像素点。成功率则是表明预测目标与标注目标范围的重合程度。另外实验还考虑了在11个属性下的跟踪情况来展示跟踪算法的鲁棒性。
我们的对比实验主要在OTB数据集上进行,具体的数据集包括OTB50[24]、CVPR2013[25]、OTB100[25]和Temple-Color[26]数据集。实验中的参数设置如下:μ=0.01、λ=0.71、σ=1、τ=0.0192和η=1。在所有实验过程采用Matlab 2014a软件实现,在配备Inteli7700CPU、32GB RAM和单个NVIDIA GTX1070GPU的PC机上运行。为了确保实验数据的真实性和比较结果的公平性,我们使用作者提供的公共代码或结果。
3.1 基于OTB50的实验分析
OTB50数据集只有50个视频序列,属于短期目标跟踪,因此对跟踪器的计时要求较低。图2显示了ALTCF跟踪器和其他跟踪器的跟踪对比结果。从图中可以看到,ALTCF跟踪器的精确度为0.829,在所有跟踪器中排名第三,成功率为0.627,排名第二。 显然,我们的方法经过改进,跟踪效果比STRCF和ASRCF都要好。具体来说,ALTCF在精确度和成功率上分别比STRCF[7]高0.36%和3.47%。同样地,相比于ASRCF[24]的精确度0.824和成功率0.615,我们的ALTCF分别提升了0.61%和1.95%。虽然与排名第一的ECO还有一定的差距,但我们的ALTCF在所有跟踪方法中表现依旧相当不错。
图2 基于HOG特征的OTB50数据集上各跟踪器的跟踪精确度和成功率
Fig.2 The precision and success plots of all trackers on the OTB50 dataset with HOG features
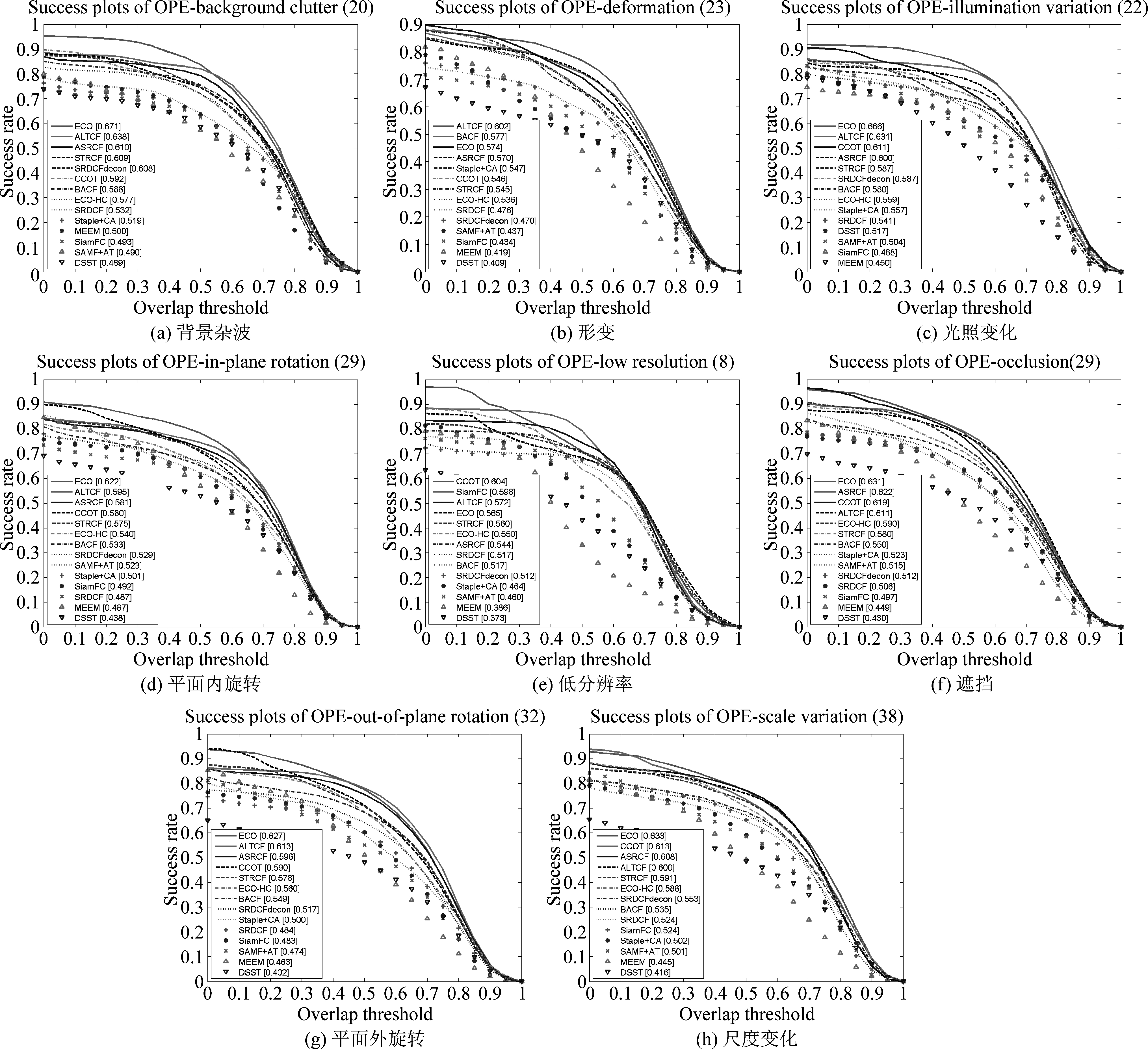
图3 基于OTB50数据库的8个属性条件下的跟踪成功率比较
Fig.3 The comparison of success plots on OTB50 for the subsets of 8 challenging attributes
我们挑选展示了与鲁棒性相关的8个属性,基于不同属性下的跟踪器的目标跟踪成功率如图3所示。在图3(b)的形变条件下,ALTCF模型的跟踪性能最佳,成功率比排名第二的BACF高4.33%。 我们的ALTCF跟踪器在四个属性(包括背景杂波(a)、光照变化(c)、平面内旋转(d)和平面外旋转(g)上均具有良好的性能,成功率分别为0.638、0.631、0.595和0.613。由于缺少移动目标的时间正则化模型,其他跟踪器在这种情况下的效果不佳。
3.2 基于CVPR2013的实验分析
CVPR2013数据集的视频序列比OTB50数据集多了一帧,其他特征相似,因此我们放在相邻位置进行讨论比较。一方面,与13个最新的跟踪器相比,我们的ALTCF在成功率上表现最佳,如图4(b)所示。 ALTCF的成功率为0.700,比ECO[16]高出0.14%。与ASRCF和STRCF相比,我们的ALTCF在成功率上也分别增长了2.49%和4.63%。另一方面,ALTCF的精确度为0.901,仅次于ECO,但优于ASRCF的0.886,而STRCF的精确度仅为0.873。因此,ALTCF在精确度上比ASRCF和STRCF分别提高了1.69%和3.21%。 总体而言,ALTCF的性能在CVPR2013数据集上是相当出色的。
3.3 基于OTB100数据集的实验分析
OTB100数据集是检验目标跟踪算法性能的最常用的基准数据库。它具有100个完全注释的视频序列,远远超过了OTB50数据集。在图5展示的形变(a),光照变化(b),平面外旋转(c)和尺度变化(d)四种属性中,ALTCF跟踪器展现出更好的跟踪性能。形变属性下的成功率中,我们的ALTCF在所有跟踪器中排名第一,具有最佳性能,比排名第二的ASRCF高6.11%,比ECO高6.75%,比STRCF高11.42%。在光照变化和,平面外旋转下,ALTCF的性能表现排名第二,分别比ASRCF高2.6%和1.1%。与STRCF相比,进步更为明显,分别增长了5.9%和4.5%。主要原因是我们的ALTCF使用了时序信息并通过滤波器的响应图来缓解异常数据的不利影响,而STRCF无法抑制异常,因此在某些视频上的跟踪效果并不理想。
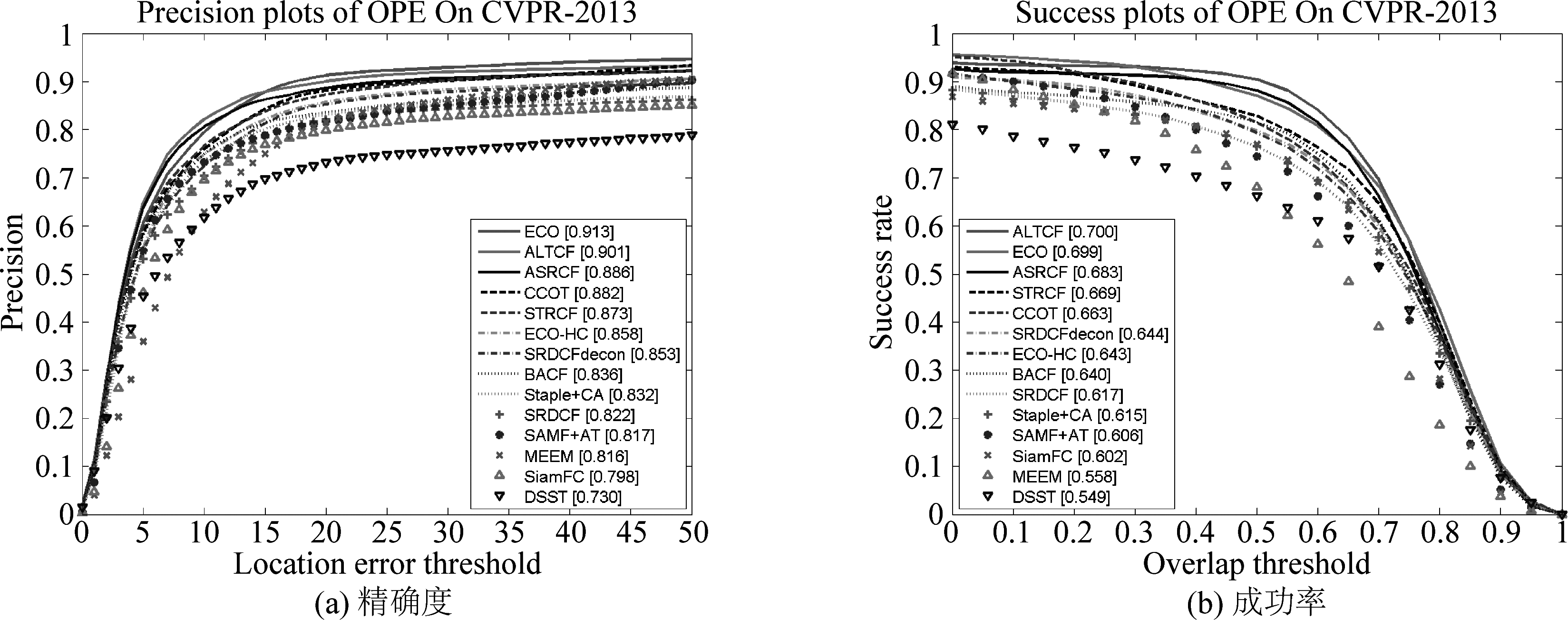
图4 在CVPR2013数据集上各跟踪器的跟踪结果比较
Fig.4 A comparison of the tracking results with the trackers on CVPR2013
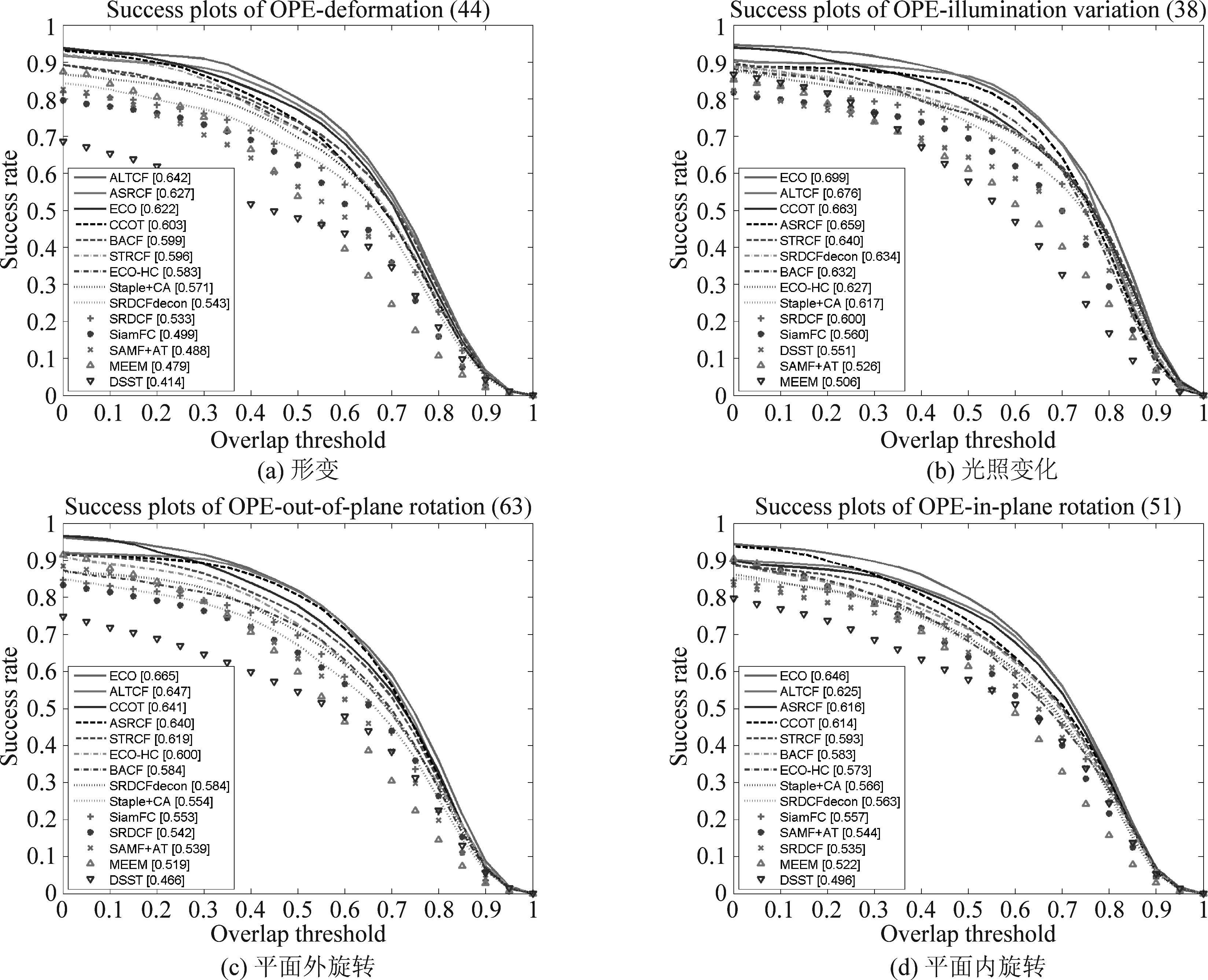
图5 在OTB100数据集不同属性上各跟踪器的成功率。属性分别为(a)形变、(b)光照变化、(c)平面外旋转和(d)平面内旋转
Fig.5 The success plots of the trackers on the OTB100 dataset for the different attributes: deformation, illumination variation, out-of-plane rotation and in-plane rotation
图6 在OTB100数据集上各跟踪器的精确度和成功率
Fig.6 The precision plots and success plots of all trackers on OTB100 dataset
图6展示了跟踪器在OTB100数据集上的整体性能,ALTCF的精确度为0.877,成功率为0.670。就精确度而言,ALTCF比STRCF高了2.45%,比ASRCF高0.92%,而成功率则比STRCF高3.08%,比ASRCF高1.51%。基于OTB100数据集的实验结果比基于OTB50的实验结果更有参考价值,主要原因是OTB100的视频序列的数量更大,视频类型更丰富。
3.4 基于Temple-Color数据集的实验分析
Temple-Color数据集包含129个颜色序列,与OTB50和OTB100有很大不同。 我们主要比较了前面提到的八个最先进的跟踪器,分别是ARCF[12],STRCF(HOG),STRCF(HOGCN),DeepSTRCF[7],ECO[16],ECO-HC[16],DSST[4]和CCOT[17]。 图7展示了所有跟踪器的关于跟踪成功率的比较。尽管ALTCF的性能略逊于ECO和CCOT,但它优于STRCF和STRCF(HOGCN)。 ALTCF的成功率比STRCF高13.26%。
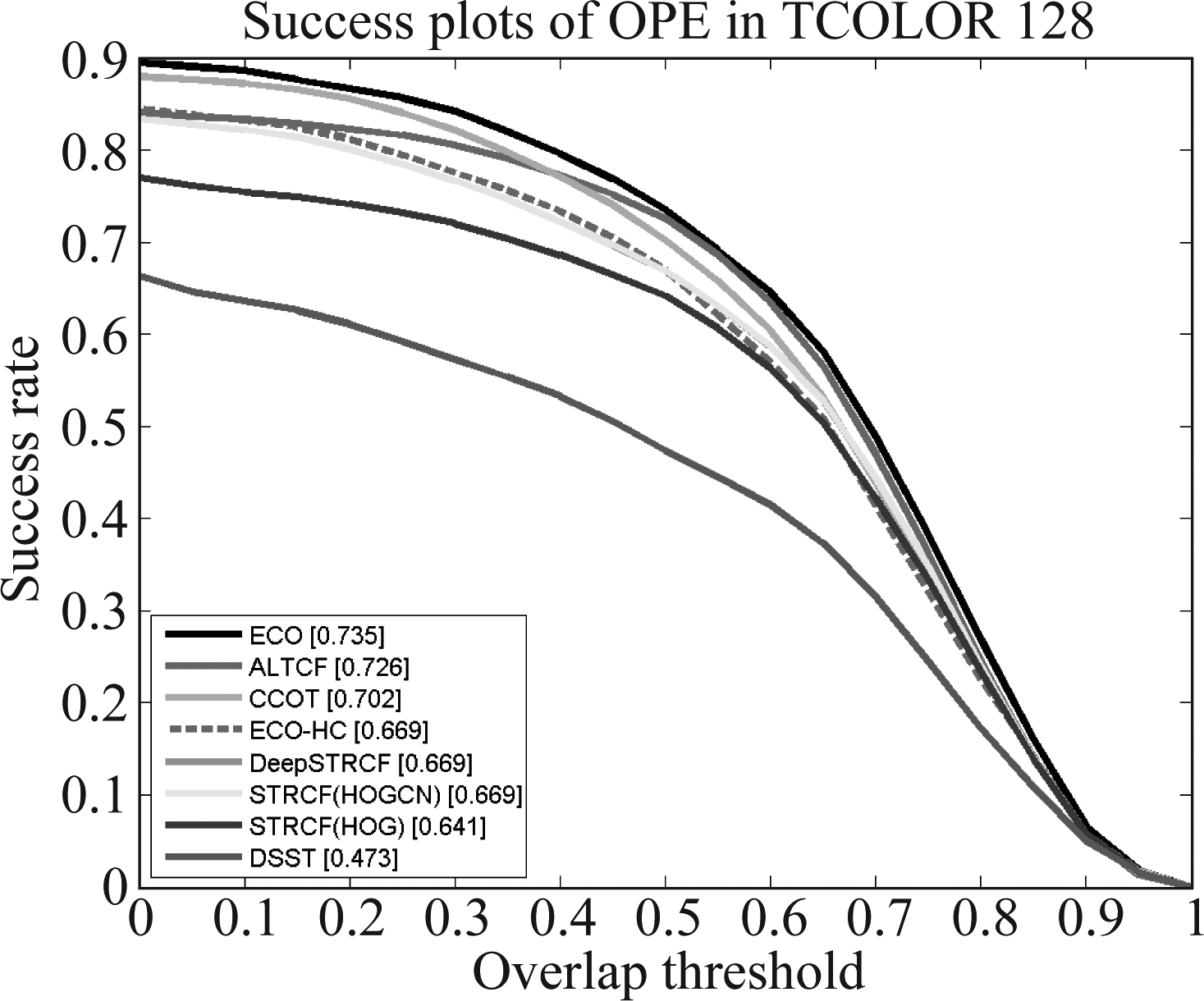
图7 在Temple-Color数据集上关于成功率的比较.
这里,ALTCF主要与7个跟踪器进行了比较
Fig.7 The comparison of success plots on Temple-Color dataset. Here we compared 7 trackers
图8展示了形变,平面外旋转,光照变化和遮挡这4个属性的结果图,我们的ALTCF在形变下的跟踪成功率排名第一,比ASRCF提高1.14%。ALTCF在光照变化和平面外旋转方面均排名第二,在遮挡方面排名第三。尽管ALTCF的结果不是最好的,但是与ASRCF和STRCF相比,跟踪性能仍有很大的提高。
3.5 腐蚀性分析
在许多实验中,我们发现损失函数的参数对性能也有重要影响。我们通过将现有跟踪器与ALTCF依赖不同参数下的变体进行比较。在实验中,我们以0.5的增量将式(8)中λ值在0.5～2.5区间逐渐增加来获得ALTCF的变体。我们基于包括OTB50,OTB100和CVPR2013在内的数据集进行实验以进行验证,最终ALTCF变体和ASRCF[23],ECO[15],STRCF[4],SRDCF[9]在三个数据集上的成功率对比情况如图9所示。随着λ值的增加,成功率在0.5～1之间逐渐降低,在1～1.5之间增加,然后又在1.5～2.5之间呈下降趋势,则ALTCF实现最佳跟踪性能时的λ值为1.5。 而在CVPR2013和OTB100数据集上,λ的最佳取值为2。考虑到OTB100和CVPR2013数据集的视频数量更加丰富,我们在其他对比实验中的λ值设置为2。
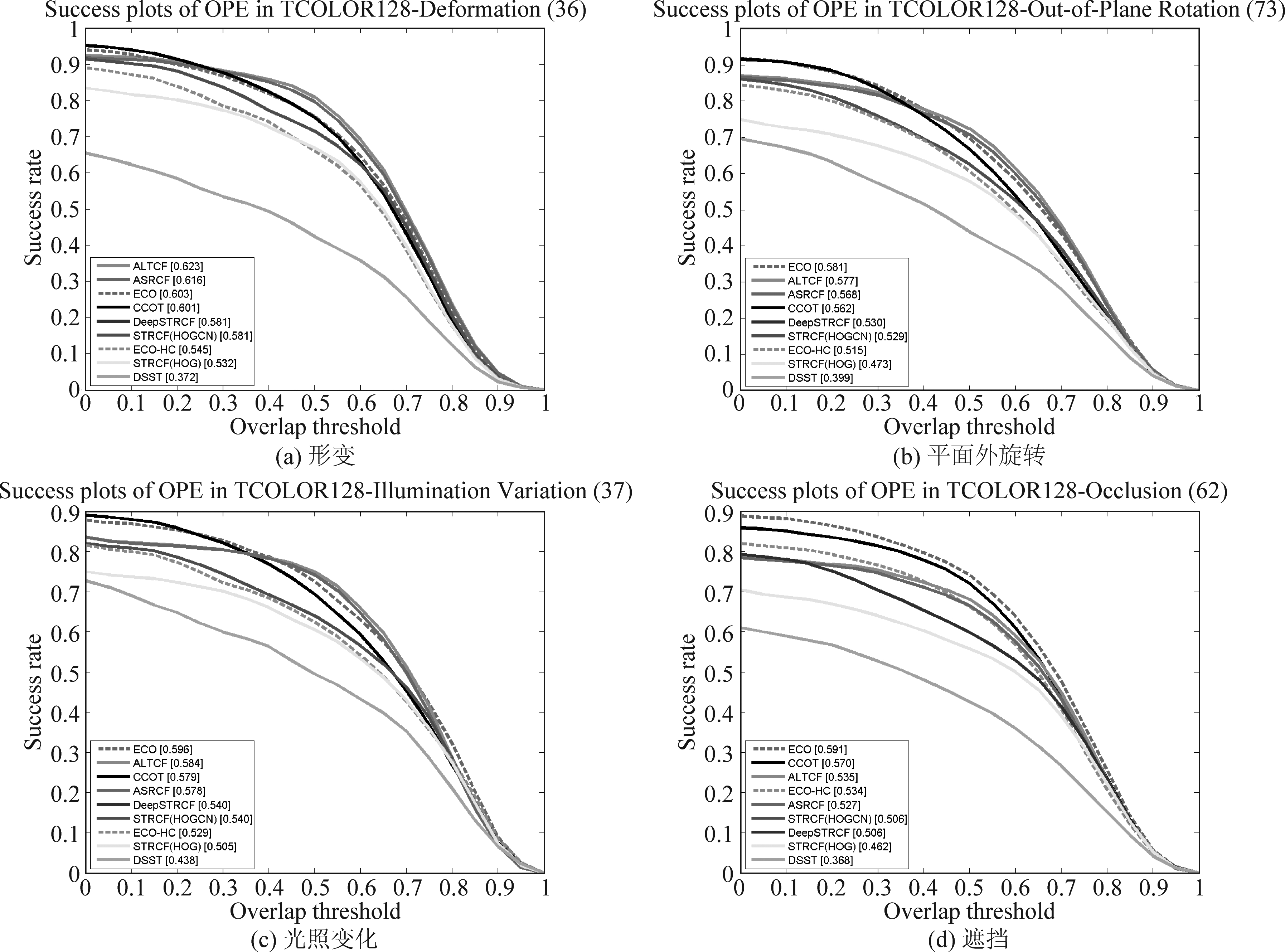
图8 在Temple-Color数据集不同属性下的成功率,属性包括:形变、平面外旋转、光照变化和遮挡
Fig.8 The success plots of the competing trackers on the Temple-Color dataset for the challenging attributes: deformation, out-of-plane rotation, illumination variation and occlusion
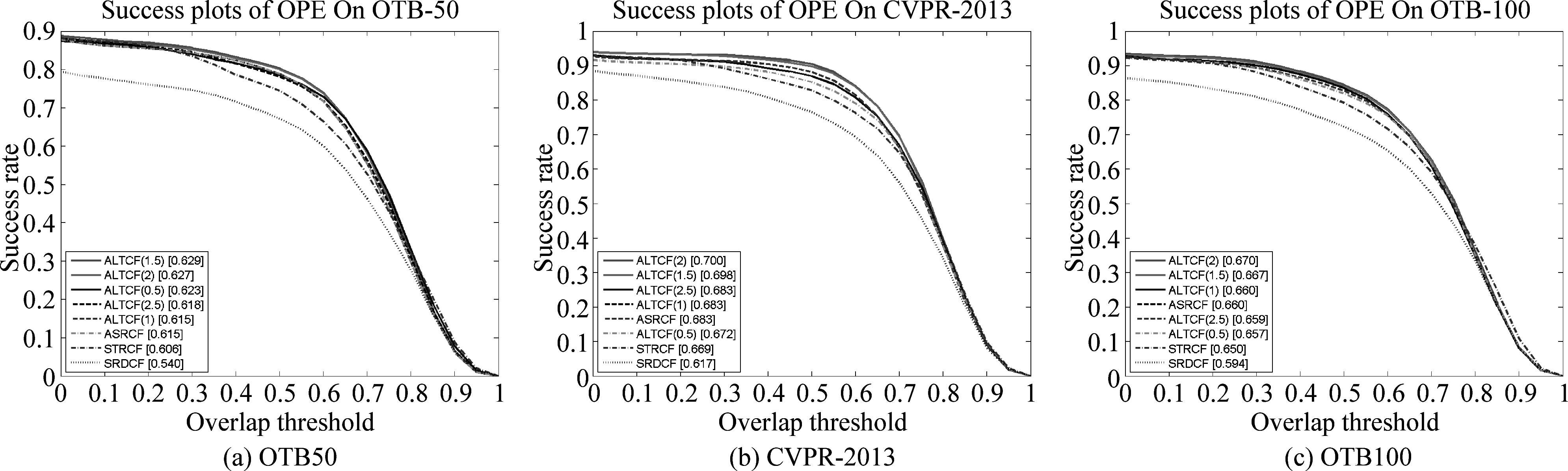
图9 ALTCF变体在OTB50、CVPR-2013和OTB100数据集上的成功率
Fig.9 The success plots of ALTCF variants on OTB50, CVPR2013 and OTB100
3.6 定性分析
为了更加直观地展示ALTCF的跟踪性能,我们通过逐帧对比对ALTCF与STRCF[7],SRDCF[6],BACF[8]和DSST[4]的跟踪结果进行分析。 从图9可以看出,ALTCF在所有展示帧中都成功捕获了目标,其跟踪精度高于其他跟踪器。当遇到旋转,遮挡,低对比度,跟踪对象快速变化或形变等复杂变化时,我们的方法仍然可以正确跟踪对象,并且性能受环境影响较小。结果表明,ALTCF在具有挑战性的视频序列中的跟踪性能具有更好的跟踪性能。
3.7 时域鲁棒性分析
我们基于birds视频序列上进行了ALTCF和STRCF的对比数据分析来讨论时域鲁棒性。如图所示,折线图表示不同帧中模型估计出的目标框与初始目标框的重叠率。红色线条表示ALTCF模型,绿色线条表示STRCF模型。从图中可以看到,目标图像“大鸟”在40至50帧图像中与“小鸟群”发生重叠,同时目标图像还发生了旋转和形变,此时两种模型的重叠率都发生严重下降,但ALTCF的值经过突然下降后保持较为稳定的值,甚至在后期逐渐恢复了对目标的跟踪效果。而STRCF面对这种变化,跟踪效果损失严重,甚至发生跟踪失败。由此得出,ALTCF在面对遮挡,旋转形变等复杂情况是依旧能保持良好的鲁棒性,保证高质量的目标跟踪。
图10 跟踪器在6个视频序列上的定性分析
Fig.10 Qualitative evaluation of trackers on 6 video sequences
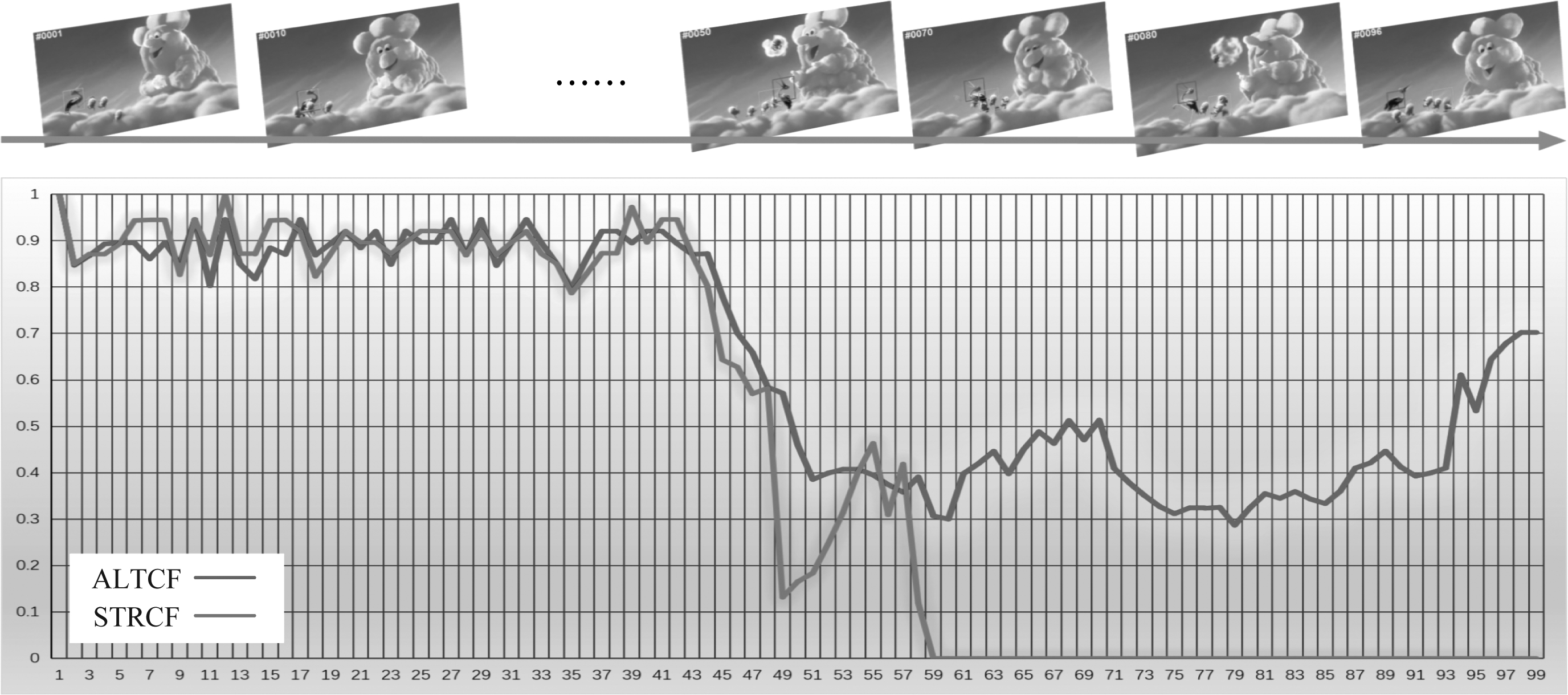
图11 ALTCF和STRCF跟踪器在视频序列上的重叠率
Fig.11 Overlap rate of ALTCF and STRCF trackers on video sequences
4 结论
本文所提出的时间驱动的异常学习相关滤波器(ALTCF)能够获得更好的跟踪性能。ALTCF引入时间正则化项,利用时序相关信息,同时在检测过程中有效抑制异常,并利用时域信息获得更具鲁棒性的外观模型。模型采用的ADMM算法能够很好地实现目标函数的优化和更新问题,并大大减少计算复杂度。最后,充足且有效的对比实验充分验证了ALTCF跟踪算法的性能优越性。
[1] 卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76.
LU Huchuan, LI Peixia, WANG Dong. Visual Object Tracking: A Survey[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61-76.(in Chinese)
[2] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.
[3] LIN Z, YUAN C. Robust Visual Tracking in Low-Resolution Sequence[C]∥IEEE International Conference on Image Processing (ICIP), Athens, 2018: 4103- 4107.
[4] ZHAO H, YANG G, WANG D, et al. Lightweight Deep Neural Network for Real-Time Visual Tracking with Mutual Learning[C]∥IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 2019: 3063-3067.
[5] 张能波, 苏振斌, 谢维信．Lasso约束下融合光流信息的DCF目标跟踪算法[J]. 信号处理, 2019, 35(5): 911-918.
ZHANG Nengbo, SU Zhenbin, XIE Weixin. DCF Visual Object Tracking Algorithm with Lasso Constraints and Fusion Optical Flow[J]. Journal of Signal Processing, 2019, 35(5): 911-918.(in Chinese)
[6] DANELLJAN M, HGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]∥IEEE International Conference on Computer Vision, Santiago, 2015: 4310- 4318.
[7] LI Feng, TIAN Cheng, ZUO Wangmeng. Learning spatial-temporal regularized correlation filters for visual tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2018: 4904- 4913.
[8] GALOOGAHI H K, FAGG A, LUCEY S. Learning background-aware correlation filters for visual tracking[C]∥IEEE International Conference on Computer Vision, 2017: 1135-1143.
[9] WANG Mengmeng, LIU Yong, HUANG Zeyi. Large Margin Object Tracking with Circulant Feature Maps[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4800- 4808.
[10] CHOI J, CHANG H J, YUN S, et al. Attentional Correlation Filter Network for Adaptive Visual Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4828- 4837.
[11] HUANG Ziyuan, FU Changhong, LI Yiming. Learning Aberrance Repressed Correlation Filters for Real-Time UAV Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Seoul, Korea (South), 2019: 2891-2900.
[12] 胡正平, 尹艳华, 顾剑新. 位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法[J]. 信号处理, 2019, 35(12): 1979-1989.
HU Zhengping, YIN Yanhua, GU Jianxin. Multi-feature Selection Correlated Filtering Target Tracking Algorithms Based on Location-Scale Different Space Coordination[J]. Journal of Signal Processing, 2019, 35(12): 1979-1989.(in Chinese)
[13] XU Cheng, ZHANG Yifeng, CUI Jinshi, et al. Object Tracking via Temporal Consistency Dictionary Learning[J]. IEEE Transactions on Systems Man and Cybernetics Systems, 2017, 47(4): 628- 638.
[14] CRAMMER K, DEKEL O, KESHET J, et al. Online Passive-Aggressive Algorithms[J]. Journal of Machine Learning Research, 2006, 7(3): 551-585.
[15] HAN Chao, TAN Yunkun, ZHU Jinhui. Online Feature Selection of Class Imbalance via PA Algorithm[J]. Journal of Computer Science and Technology, 2016, 31(4): 673- 682.
[16] DANELLJAN M, BHAT G, KHAN F S, et al. ECO: Efficient Convolution Operators for Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2017: 6931- 6939.
[17] DANELLJAN M, ROBINSON A, KHAN F S, et al. Beyond Correlation Filters: Learning Continuous Convolution Operators for Visual Tracking[C]∥European Conference on Computer Vision, 2016: 472- 488.
[18] DANELLJAN M, HäGER G, KHAN F S, et al. Adaptive Decontamination of the Training Set: A Unified Formulation for Discriminative Visual Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1430-1438.
[19] MUELLER M, SMITH N, GHANEM B. Context-aware correlation filter tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, 2017: 1387-1395.
[20] BIBI A, MUELLER M, GHANEM B. Target Response Adaptation for Correlation Filter Tracking[M]. Computer Vision-ECCV 2016, Springer International Publishing, 2016.
[21] LI Yang, ZHU Jianke. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration[C]∥European Conference on Computer Vision. Springer, Cham, 2014: 254-265.
[22] ZHANG Jianming, MA Shugao, SCLAROFF S. MEEM: Robust Tracking via Multiple Experts Using Entropy Minimization[C]∥European Conference on Computer Vision. Springer, Cham, 2014: 188-203.
[23] DAI Kenan, WANG Dong, LU Huchuan, et al. Visual Tracking via Adaptive Spatially-Regularized Correlation Filters[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, CA, USA, 2019: 4665- 4674.
[24] WU Yi, LIM Jongwoo, YANG Ming-Hsuan. Online Object Tracking: A Benchmark[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, 2013: 2411-2418.
[25] WU Yi, LIM Jongwoo, YANG Ming-Hsuan. Object Tracking Benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
[26] LIANG Pengpeng, BLASCH Erik, LING Haibin. Encoding color information for visual tracking: Algorithms and benchmark[J]. IEEE Transactions on Image Processing, 2015, 24(12): 5630-5644.
