1 引言
MIMO系统以其对空间资源的有效利用,成为了无线电通信领域的一项重要技术,尤其是在电子战、无线电侦查和频谱监测等军用领域[1- 4]。其中,空时分组码作为一种利用MIMO系统的编码方式,其识别问题受到了越来越多的关注。目前,现有的STBC识别算法以传统方法为主,主要包括基于二阶统计量的算法[5- 6]、基于循环统计量的方法[7]和基于高阶统计量的方法[8]。这些方法往往需要已知信道和噪声的先验信息,但在无线电侦查等军用的非协作通信下,这些先验信息常常难以获得。此外,传统算法需要人为设计特征参数和检验阈值,且每次对信号进行识别时都需要采集大量数据,并重复计算其统计特征,而深度学习算法虽然在训练时需要较多数据,但训练完成后可直接对STBC码进行识别,避免了人为设计参数和特征反复计算的问题,具有更强的适应性。以上算法[5- 8]均在多接收天线下讨论,没有考虑在单根接收天线下的串行序列空时分组码识别问题。单在实际应用中,接收天线数量的增加会使通信系统消耗的成本和资源大大增加,因此,单接收天线下的STBC码识别问题仍是研究重点[9-12]。
近年来随着深度学习算法与计算机硬件的快速发展,在通信信号处理领域的研究人员已经开始将人工神经网络算法运用到信号识别的问题当中[13-19]。文献[13]结合通信信号的时频特性提出了一种基于卷积神经网络的调制识别算法,文献[14]构建了基于卷积神经网络的水声通信信号调制识别系统,利用卷积神经网络对信号的特征进行学习,实现水声通信信号的调制识别,文献[15]提出一种基于时频图和深度卷积神经网络的识别算法,将实测信号通过短时傅里叶变换转换成时频图输入网络进行训练和学习,鲁华超等[16]将利用多个节点的I/Q路数据计算得到的协方差矩阵作为特征,使用卷积神经网络对信号进行频谱感知,Byeoungdo Kim等[17]利用深度神经网络提取21种信号的特征参数,对BPSK、QPSK、8PSK、16QAM、64QAM 五种调制信号进行了识别。以上算法[13-16]主要使用了卷积神经网络提取信号的空间特征,并未考虑使用循环神经网络对信号时序特征进行提取。循环神经网络对时间序列数据有强大的处理和预测能力,是深度学习领域中一类非常重要的模型,其在语言识别、文本分类、信息检索和机器翻译等各领域均得到了应用,各种尤其是当数据与时间有着较强的依赖性时。文献[18]采用两层卷积层后级联一层长短期记忆层结构对11种调制方式进行识别,翁建新等[19]利用卷积层和循环层的并联提取信号特征,完成了对BPSK、QPSK、8PSK、16QAM、32QAM、16APSK、32APSK 等 7 种信号的调制样式识别。文献[18-19]对信号调制方式识别的成功实现,说明了卷积-循环神经网络的并联和串联形式在信号识别领域应用的可能性。基于此,本文提出了一种利用卷积-循环神经网络的串行序列空时分组码识别方法,将串行STBC码信号的实部和虚部输入网络,利用CNN对信号的空间特征进行提取后,经过LSTM提取信号的时序特征,最后经全连接层输出网络。该算法能够对单接收天线下的串行序列STBC码进行识别,并且训练后的网络模型可直接用于识别,不需要重复计算信号的统计特征,在低信噪比情况下有较好的识别性能。
2 信号模型与假设条件
对于nt个发射天线,单个接收天线的无线电通信系统,每组STBC码传输的符号数为n,具体表示为S=[s1,s2,…,sn]T。对于长度为L的STBC码矩阵,其具体表示为[12]:
(1)
其中,Ai(i=1,2,…,L)为nt×2n维的编码矩阵,编码方式由发射端决定,
由传输符号S的实部和虚部按行拼接组成,维度为2n×1。
本文对最常用的空间复用(Special Multiplexing, SM)信号和Alamouti空时分组码进行识别,其具体表示为:
(1)空间复用(SM)信号
发射天线数为nt=2,编码矩阵长度为L=1,码矩阵中的符号数n=2,信号的具体编码方式为:
G=[s1 s2]T
(2)
(2)Alamouti STBC信号(AL信号)
发射天线数为nt=2,编码矩阵长度为L=2,码矩阵中的符号数n=2,信号的具体编码方式为:
(3)
由于接收端为单接收天线,故接收的信号均为串行序列(即接收信号按时间排列成一维信号)。接收端天线在t时刻接收到的信号为:
yt=HGt+bt
(4)
其中,
为t时刻发送端nt个发射天线的发射信号,
对应发射端传输的第ν组符号Sν的实部和虚部,Au为第ν个STBC码组的编码矩阵的第u列,下标ν、u、t满足u=tmodL,ν=「t/L⎤,「·⎤为向上取整,H=[h1,h2,…,hnt]为平坦衰落信道系数,bt为加性噪声。
本文在以下的条件下产生空时分组码仿真数据集:
假设1 传输的信道为频率平坦的Nakagami-3衰落信道,该信道是进行STBC码仿真的常用信道,且更接近真实的信道环境[11-12];
假设2 传输过程中的加性噪声bt为高斯白噪声;
假设3 传输信号与噪声不相关,即E[sibk]=0;
假设4 传输符号之间独立同分布,即E[sisk]=0。
3 卷积-循环神经网络模型及训练过程
3.1 卷积-循环神经网络模型
将接收的串行序列STBC码分为实部和虚部两行,组成2×N维矩阵输入卷积-循环神经网络,网络的结构如图1所示,主要包括卷积层、池化层、循环层和全连接层四部分,除最后一层只有2个节点的全连接层使用归一化指数函数(Soft-max函数)作为激活函数外,其余网络均采用线性整流函数(ReLU),网络的输出为1×2维的独热(One-Hot)编码形式,对应待识别的2类STBC码。
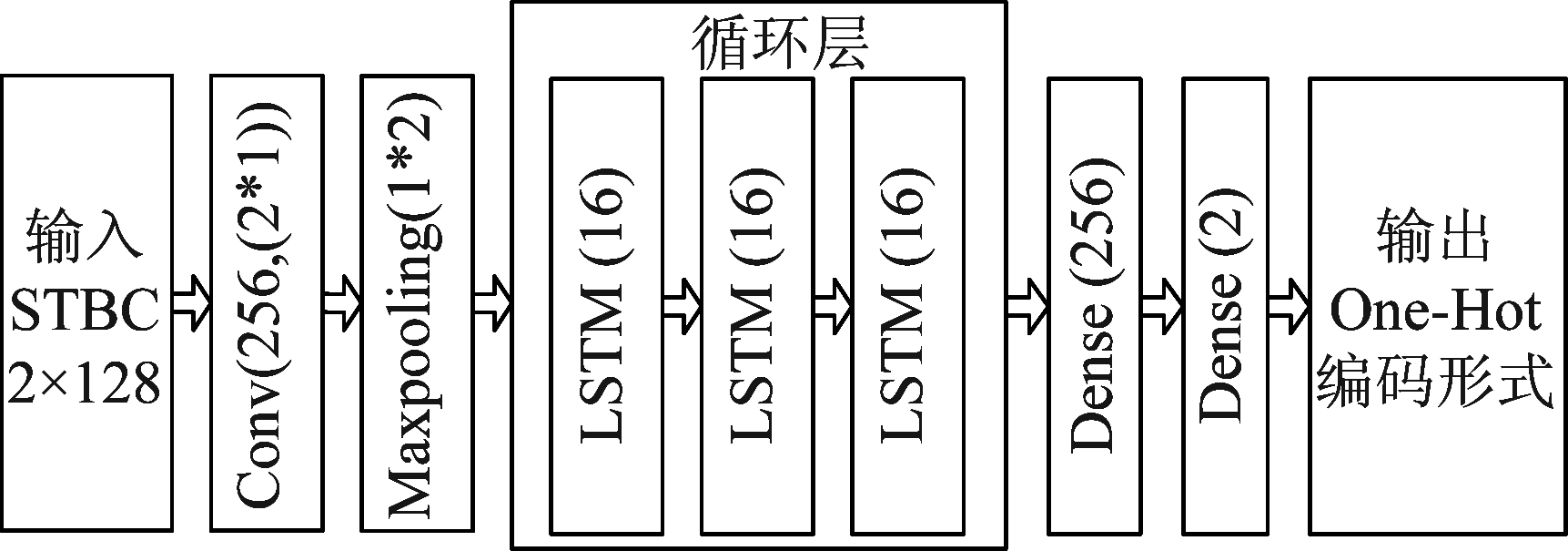
图1 卷积-循环神经网络模型
Fig.1 Convolution-recurrent neural network model
卷积层对输入的空时分组码进行特征提取,并将大小为2×128的输入样本合并成一维(1×128)。卷积层采用256个2*1的卷积核对信号进行卷积,得到256个大小为1×128的特征图,其输出特征图与输入之间的关系满足:
(5)
其中,
为第l个卷积层的第j个特征图,
为上一个卷积层的第i个特征图,对应本文网络的输入层(将大小为2×128的输入样本作为一个特征图),
为特征图与特征图之间的卷积核,
为第l个卷积层的第j个特征图的偏置, f(·)为第l个卷积层的激活函数。
池化层对卷积层的输出进行降维处理,缩小特征图尺寸。将合并后大小为1×128的一维时间序列降为1×64,其过程可表示为:
(6)
其中,
为第l-1层中的第j个特征图,p(·)为池化方法,本文使用最大池化法, f(·)为第l个卷积层的激活函数,
和为第l层中的第j个特征图的权重和偏执单元。
循环层包括三层长短期记忆网络(LSTM,Long Short-Term Memory),用于处理卷积后的一维时间序列,以挖掘接收信号的时序信息,而长短期记忆网络的特点在于其携带了跨越多个时间步的信息,从而防止较早期的信息在处理的过程中逐渐消失。LSTM网络的基本结构如图2所示。
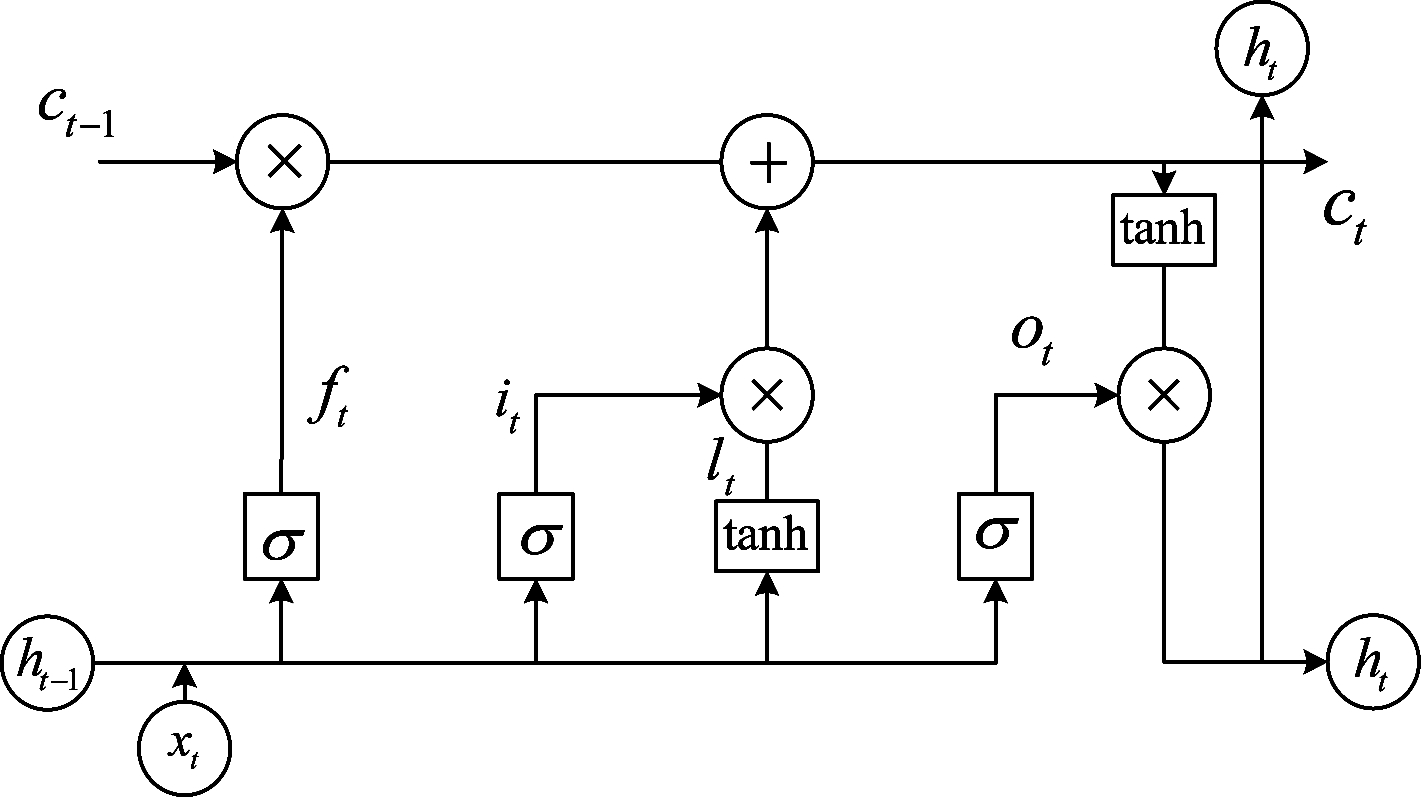
图2 LSTM网络基本结构
Fig.2 Basic structure of LSTM network
LSTM网络的基本结构包括一个记忆单元和三个控制单元组成,即输入门、输出门和遗忘门。输入门控制当前接收信息对记忆单元的影响程度,输出门决定是否输出记忆单元信息,遗忘门决定是否保留记忆单元之前的信息[16]。图2中遗忘门的输出为:
ft=σ(Wf[ht-1,xt]+bf)
(7)
其中,ht-1为t-1时刻LSTM网络的输出,xt为网络在当前时刻的接收信号,Wf为遗忘门的权重矩阵,σ为sigmoid激活函数。遗忘门的输出是[0,1]之间的数,其值为0时,不保留历史信息,值为1时,保留所有历史信息。
输入门和候选向量的状态更新如下:
it=σ(Wi[ht-1,xt]+bi)
(8)
lt=tanh(Wl[ht-1,xt]+bl)
(9)
ct=ft·ct-1+it·lt
(10)
其中,Wi与Wf为输入门it和候选向量lt的权重矩阵,bi和bl为对应的偏置,tanh为产生候选向量的激活函数,ct为更新后记忆单元的状态。式(10)表明,记忆单元的状态由遗忘门控制的历史信息和输入门控制的候选向量共同决定。LSTM网络更新记忆单元后,其输出状态的具体表达式为:
ot=σ(Wo[ht-1,xt]+bo)
(11)
ht=ot·tanh(ct)
(12)
其中,Wo为输出门ot的权重矩阵,bo为对应偏置。该表达式说明LSTM网络的输出由输出门控制的记忆单元决定,并由输出门决定其对结果的影响程度。
全连接层指的是当前层与前一层网络的所有特征图进行全连接,将提取的高维特征进行降维。该层一般位于网络的末端,最后一层的单元数与分类个数相同,并且常与Soft-max激活函数配合使用,以实现对输出特征的分类。
3.2 网络训练过程1
将公式(5)、(6)、(7)、(8)、(9)和(10)中的参数
与
统一用权值W和偏置b表示,考虑样本大小为m的训练数据{(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))},其中x(i)(i=1,…,m)为输入的STBC码数据,y(i)(i=1,…,m)为STBC码对应的类型标签。网络的训练过程包括前向传播和反向传播两个阶段,前向传播得到的输出结果与目标值形成误差,当误差不满足停止条件时反向传回网络,根据梯度下降法对权值W和偏置b进行更新[20]:
(13)
(14)
其中,α为学习率,J(W,b;x,y)为损失函数。在网络训练过程中,选取Adam优化器对参数进行调整,采用交叉熵作为损失函数:
λ∑||W||2
(15)
其中, f(W,b;x(i))表示输入样本为x(i)时网络的输出值,y(i)为对应样本x(i)的实际标签值,λ∑||W||2为网络权值的正则化,λ为正则化系数,对网络进行正则化可有效地避免过拟合现象。
4 算法仿真与性能分析
4.1 STBC码数据集的产生及仿真环境
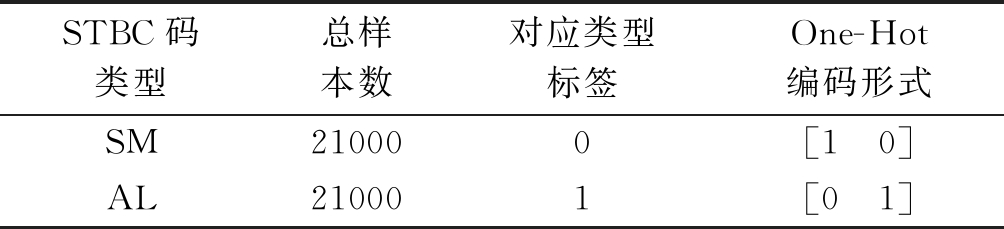
将接收到的128个STBC信号作为一组数据,则提取实部和虚部后的输入样本的维度为2×128。根据待识别信号的类型设置对应的标签,并将数据转化成One-Hot编码形式,如表1所示。仿真采用QPSK调制,信道为Nakagami-3衰落信道,噪声为高斯白噪声。信噪比设置为[-10 dB～10 dB]之间的整数,每种信噪比下产生1000个输入样本,故每种STBC码的总样本数为21000个。在训练过程中,随机选取42000个输入样本中的50%作为训练样本,其余50%作为测试样本。
表1 STBC码仿真数据集
Tab.1 STBC code simulation datasets
STBC码类型总样本数对应类型标签One-Hot编码形式SM210000[1 0]AL210001[0 1]
本文使用Matlab软件产生STBC码数据集,利用python完成数据的预处理,并在基于TensorFlow后端的keras深度学习框架下进行模型的搭建、训练和测试,安装CUDA等运算平台以搭建GPU加速环境。硬件仿真环境为Intel(R) core(TM) i7-9750H CPU,运行内存大小为16GB,使用GeForce GTX 1650 GPU对训练过程进行加速,显存大小为8G。
4.2 算法性能测试与分析
实验1 卷积核大小对网络性能的影响
卷积核大小决定了提取输入信号特征的维度和方式,对STBC码的识别准确率和收敛性能有着较大的影响,过大的尺寸会使特征的细节信息丢失,而过小的尺寸又无法很好地提取特征信息,故选取适当的卷积核尺寸将有效地提高网络识别的性能。为了分析卷积核大小对STBC码识别性能的影响,固定其他网络结构和维度不变,这里选取池化窗大小为1*2的最大池化层和两层循环单元为32个的LSTM层。输入信号维度为2*128,因将一维数据输入LSTM层有利于提取其时序特征,设置卷积核尺寸为2*1、2*2、2*3和2*4,对比不同情况下的网络识别性能,如图3所示。
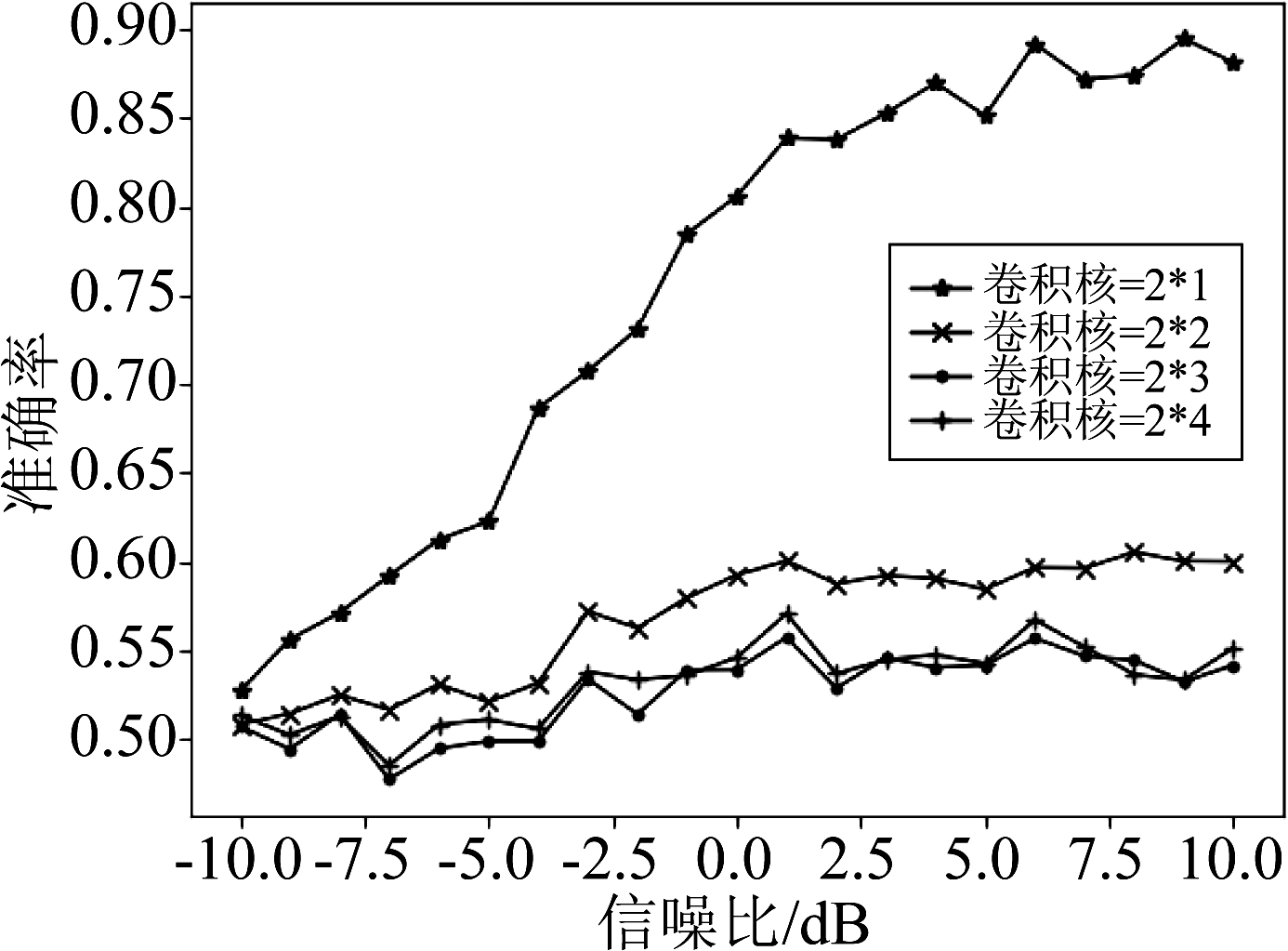
图3 卷积核大小对网络识别性能的影响
Fig.3 Influence of convolution kernel size on network recognition performance
从图3中可以明显的看出,卷积核尺寸为2*2、2*3和2*4时网络的识别性能较差,在其他网络结构不变的情况下,卷积核大小为2*1时网络对STBC码的识别准确率达到了较好的性能,且在低信噪比下能够对信号进行有效地识别,因此本文选用大小为2*1的卷积核参数。
实验2 池化层对网络性能的影响
考虑到LSTM层对识别性能的影响,为了对池化层的参数设置进行分析,本节在固定LSTM层参数的情况下,分析了循环单元个数分别为16、32和64时池化层参数对网络性能的影响,其结果如图4、图5和图6所示。
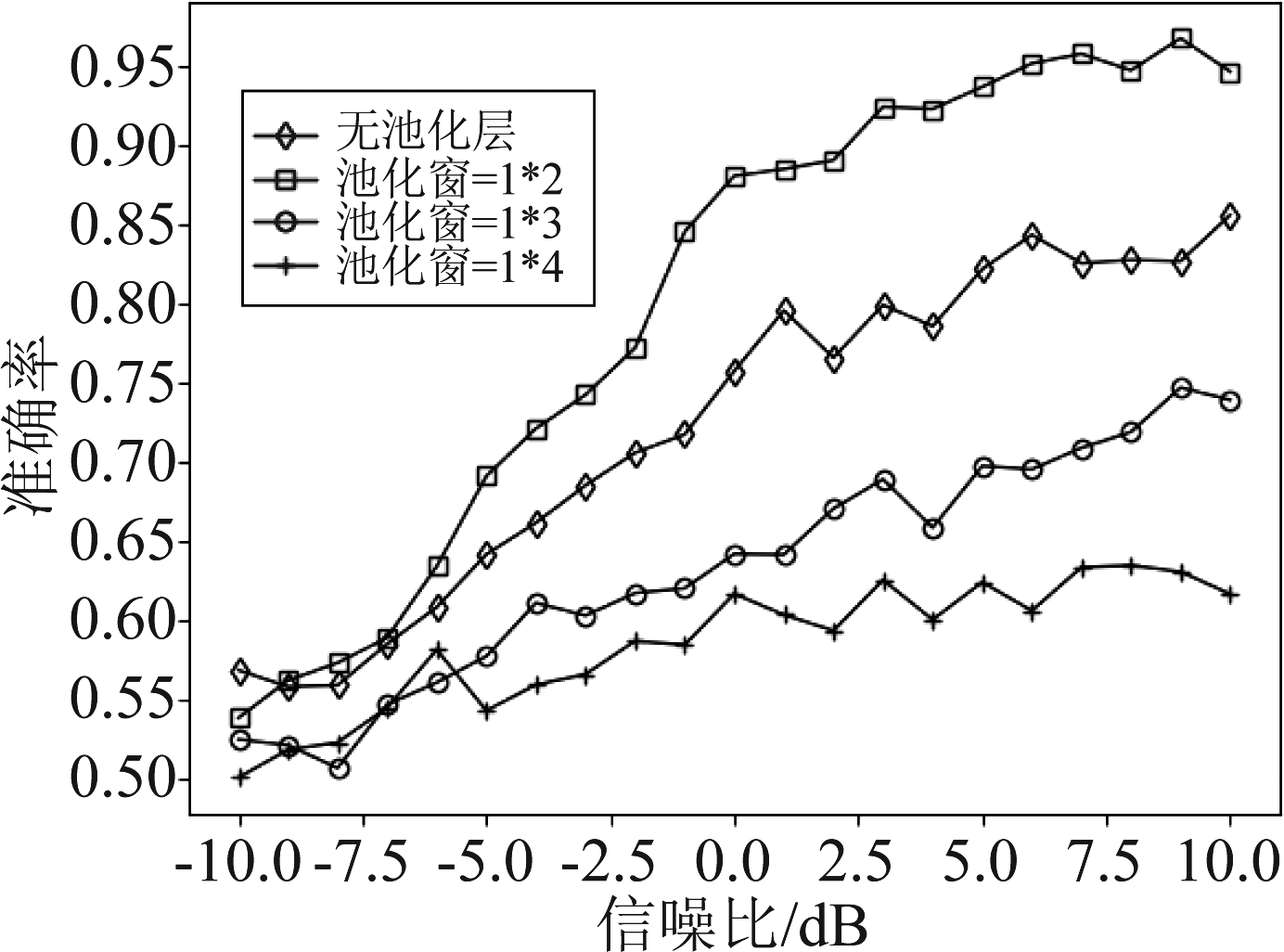
图4 循环单元数为16时池化层对网络性能的影响
Fig.4 Influence of pooling layer on network performance when the number of recurrent units is 16
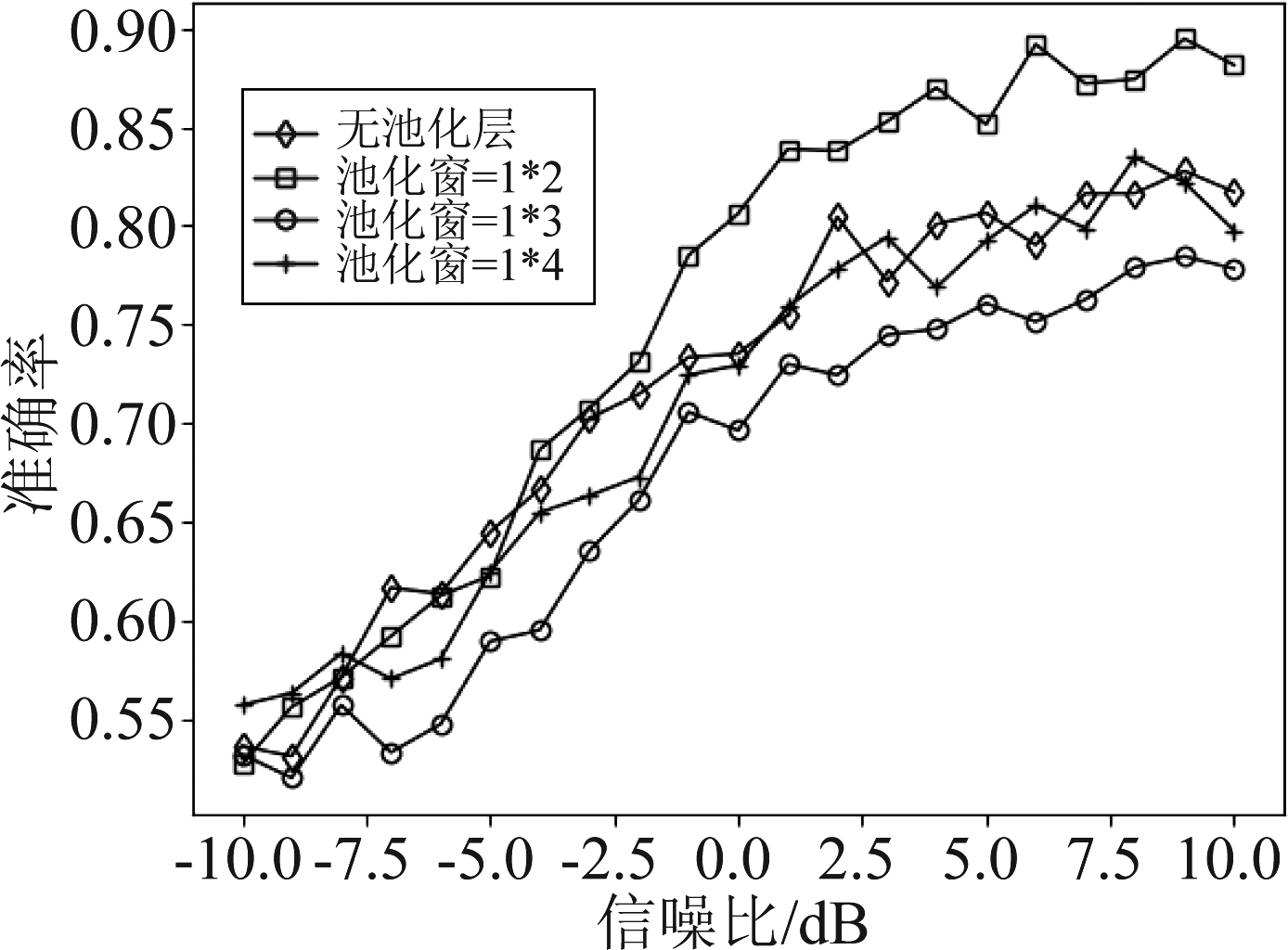
图5 循环单元数为32时池化层对网络性能的影响
Fig.5 Influence of pooling layer on network performance when the number of recurrent units is 32
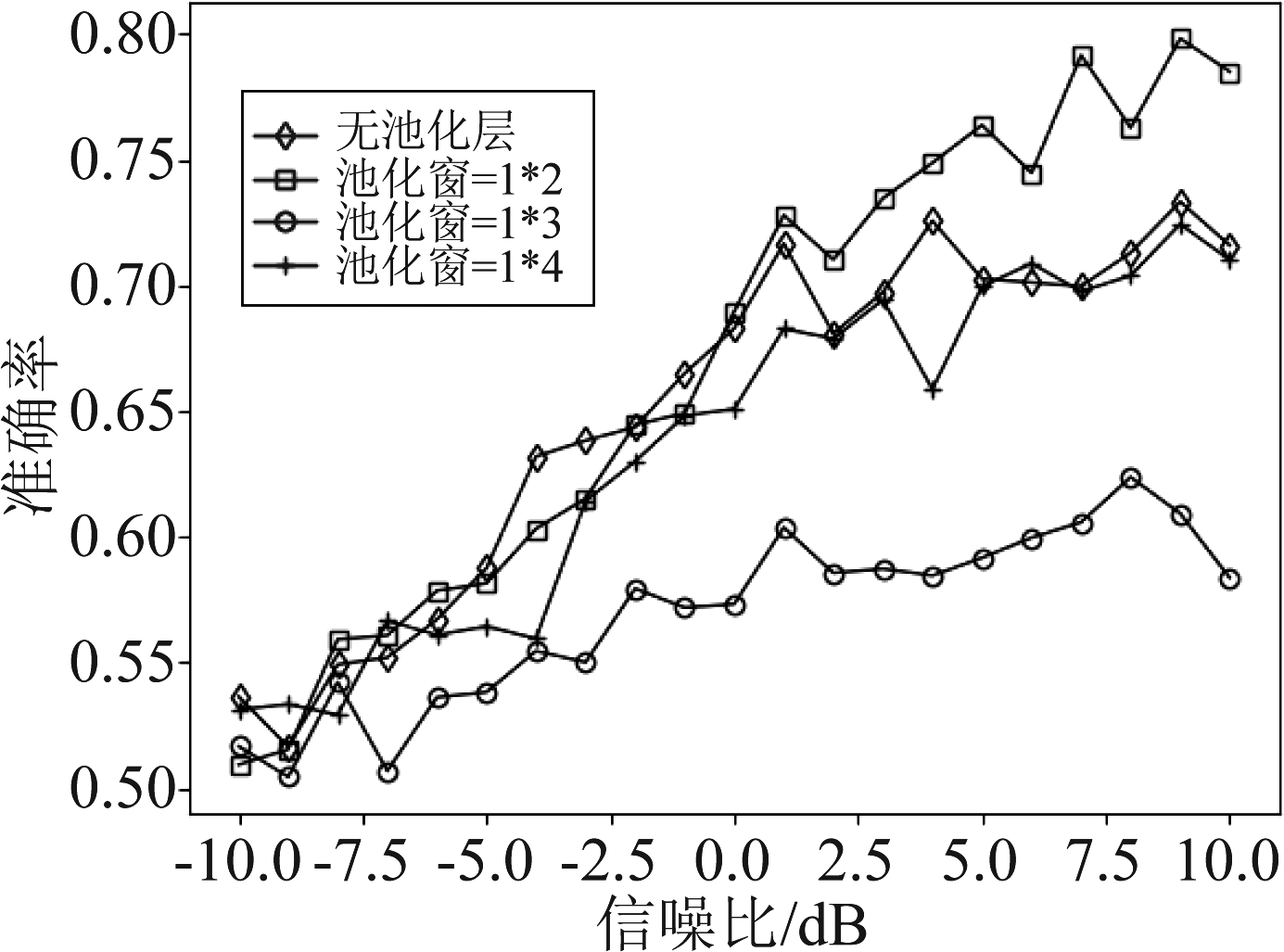
图6 循环单元数为64时池化层对网络性能的影响
Fig.6 Influence of pooling layer on network performance when the number of recurrent units is 64
从图6中可以看出,使用大小为1*2的池化窗的识别性能优于其余3种情况。这是由于池化窗长度过大时,输出特征的部分细节信息被丢失,使得网络识别性能下降;但不加池化层时网络的冗余信息过多,也不利于网络对特征的有效提取,从图4和图5中也可以得到相同的结论。因此,本文选用大小为1*2的池化窗对卷积层的输出特征进行池化。
实验3 循环层层数对网络性能的影响
在给定循环单元个数的情况下,LSTM层数对网络性能有着较大的影响。为得到最优的网络结构,本文对循环单元数分别为16、32和64时不同LSTM层数的识别性能进行了仿真,其结果如图7、图8和图9所示。
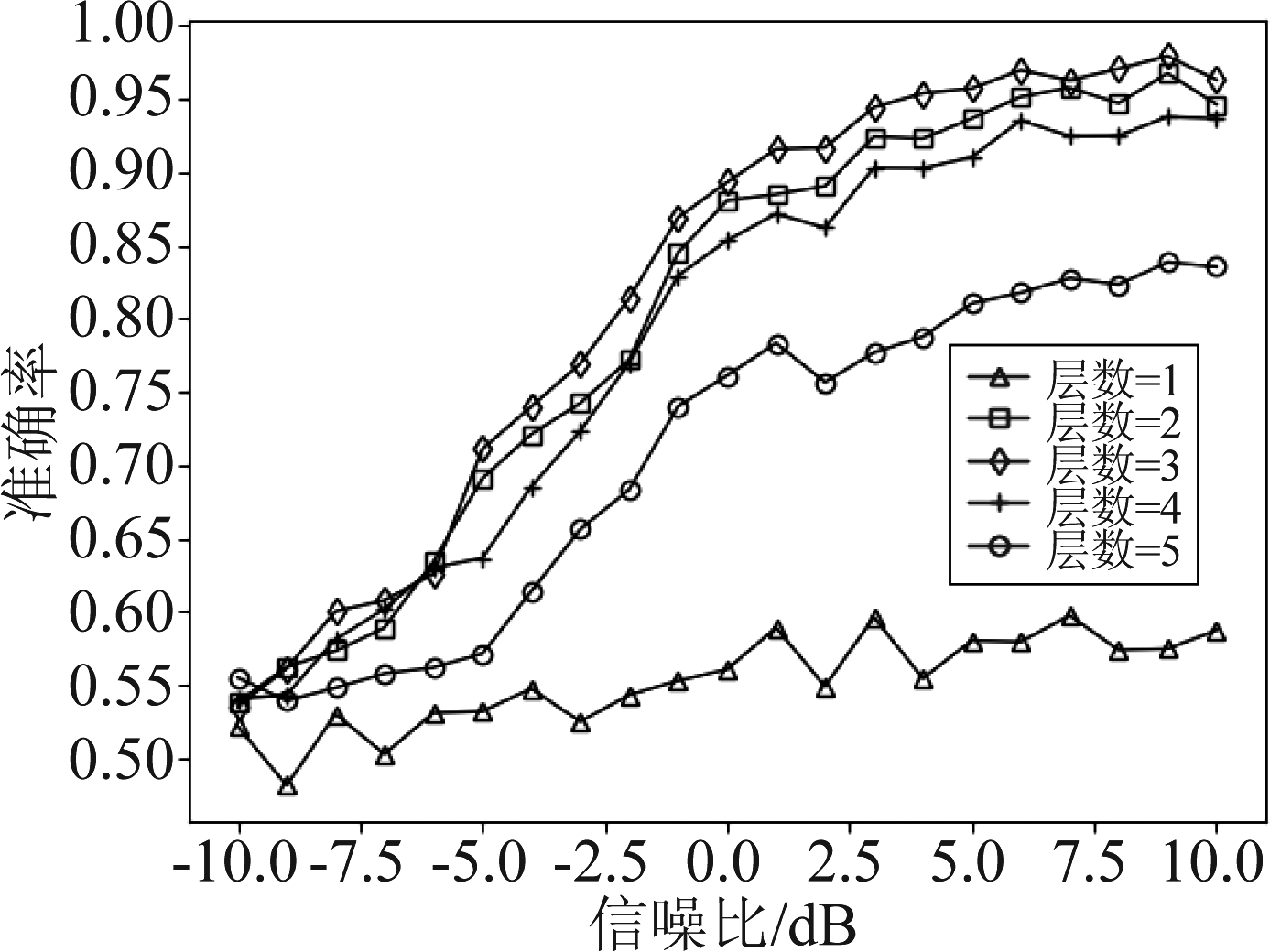
图7 循环单元数为16时LSTM层数对网络性能的影响
Fig.7 Influence of the number of LSTM layers on network performance when the number of recurrent units is 16
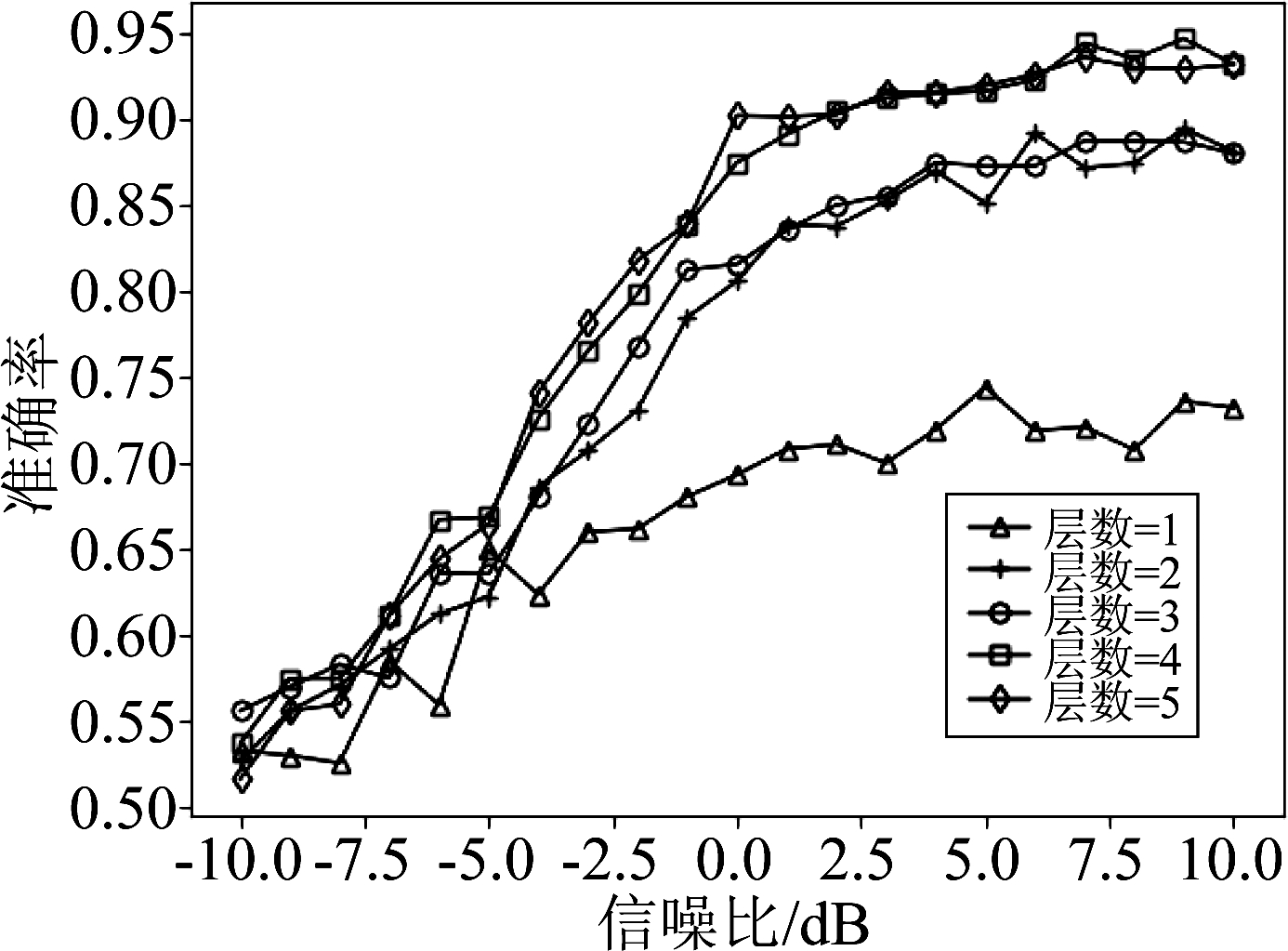
图8 循环单元数为32时LSTM层数对网络性能的影响
Fig.8 Influence of the number of LSTM layers on network performance when the number of recurrent units is 32
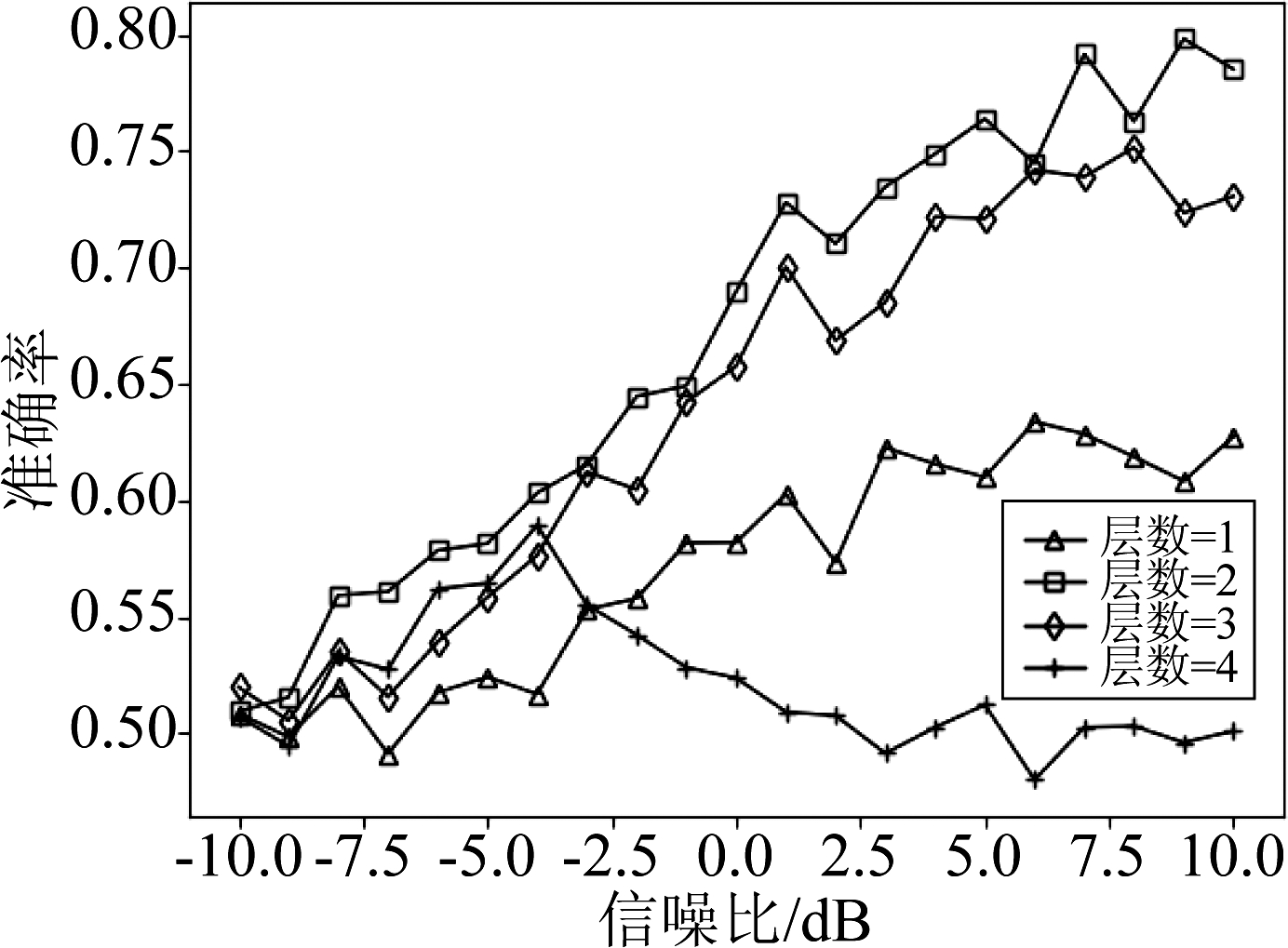
图9 循环单元数为64时LSTM层数对网络性能的影响
Fig.9 Influence of the number of LSTM layers on network performance when the number of recurrent units is 64
从图7中可以看出,当循环单元数为16时,3层LSTM的网络识别性能最优。层数过少的网络无法充分提取信号的时序特征,因而识别性能并不理想;但过深的网络则容易导致过拟合,使得识别准确率反而发生了下降。从图8和图9中同样可以看出这一规律,当循环单元数为32和64时,性能最优的网络层数分别为4层和2层,过深或过浅的网络均不能带来更好的识别性能。图9中的识别准确率随信噪比变化的波动较大,这是由于循环单元数过多而导致训练参数量过大,使得网络的性能不稳定,在图6中也存在这样的现象,而循环单元数较少时网络的识别性能则较为稳定,在图3～5和图7～8中可以看出这一趋势。
实验4 不同循环层单元个数的网络性能分析
本实验分析对比在LSTM层数最优情况下,循环层单元数分别为16、32和64时的网络性能,每种条件进行20次仿真,其结果如图10所示。从图中可以看出,循环层单元数为64时,在信噪比达到9 dB的识别准确率也只有78.3%,其性能不如其他两种情况;随着信噪比的增大,单元数为16、32和64的网络识别准确率分别稳定在95%、93%和75%左右,单元数为16的网络在总体上比其他两个更优,故本文选择循环层单元数为16的网络作为最终的网络模型。
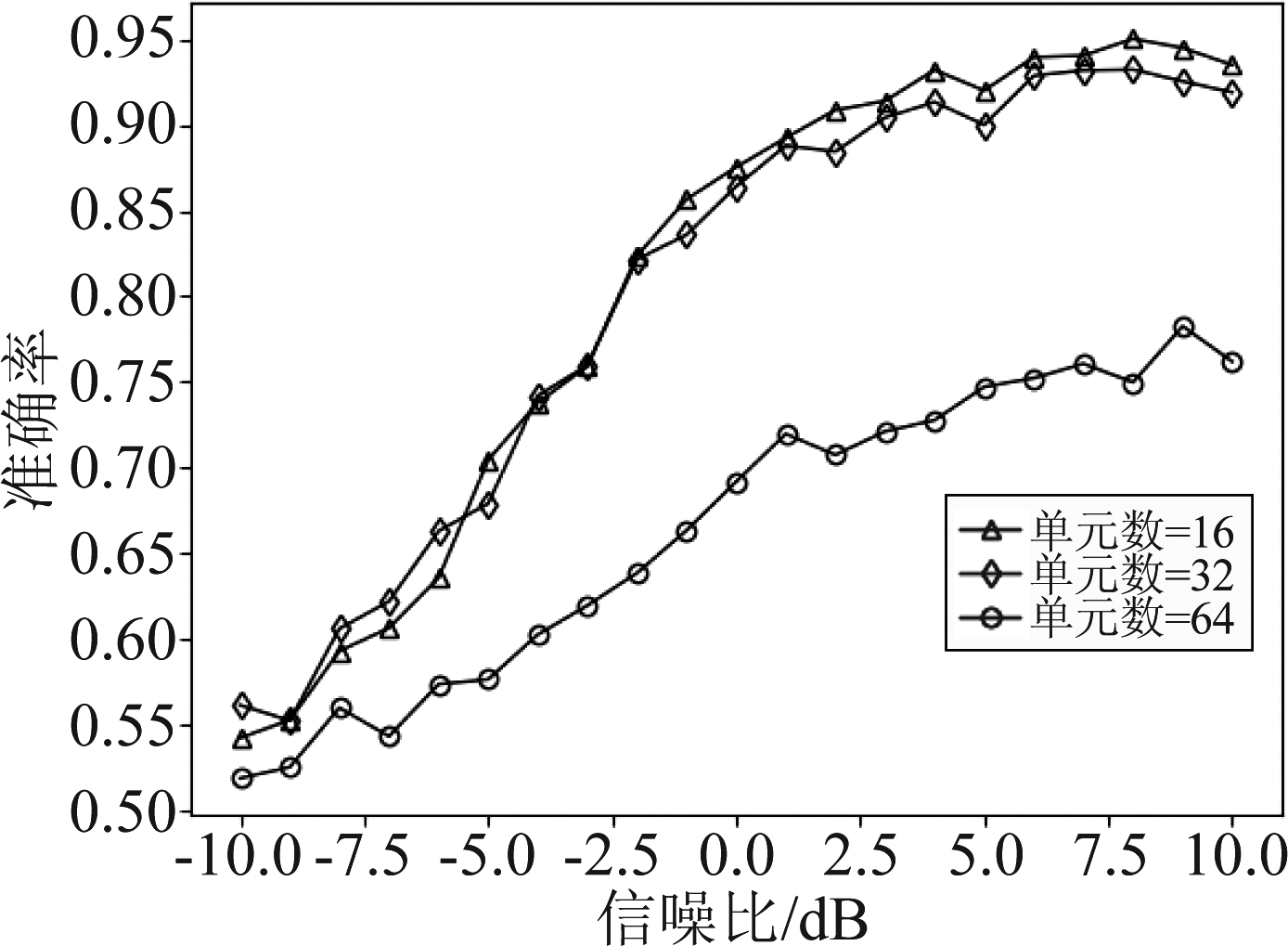
图10 循环层单元个数对网络性能的影响
Fig.10 The influence of the number of recurrent layer units on network performance
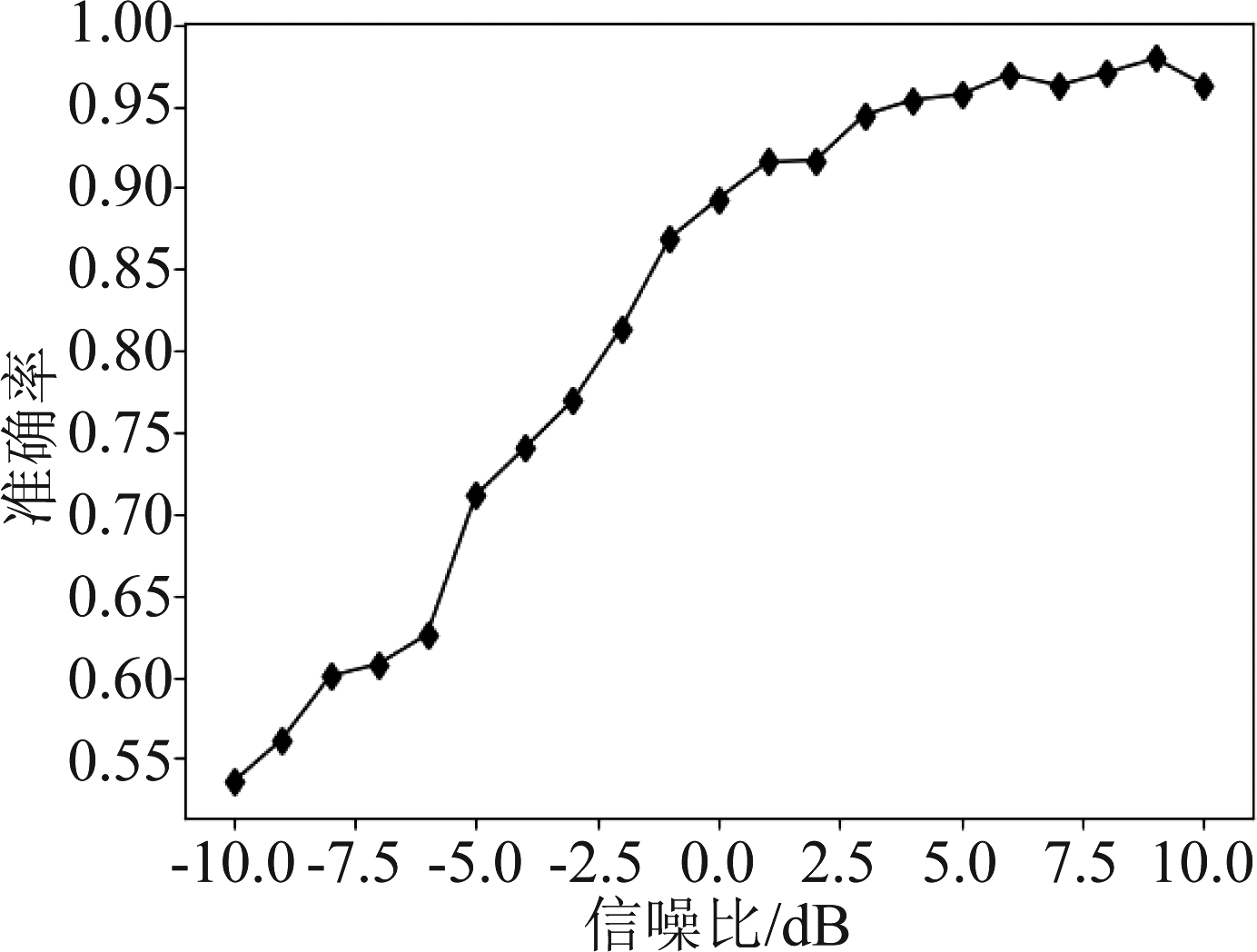
图11 卷积-循环层神经网络模型性能
Fig.11 Performance of convolutional-recurrent layer neural network model
实验5 卷积-循环神经网络识别性能分析
本实验分析了得到的最优CNN-RNN网络性能,其识别准确率随信噪比变化图像如图11所示。从图中可以看出,当STBC码信噪比大于1 dB时,CNN-RNN网络识别准确率达到了90%以上,并最终稳定在了97%左右,网络性能随信噪比稳定增加,在低信噪比下识别性能较好。
信噪比为-1 dB时的混淆矩阵如图12所示,从图中可以看出,SM信号和AL信号的颜色区分较为明显,预测标签与真实标签一致。该实验验证了即使在低信噪比下,CNN-RNN网络也具有优异的识别性能,这对无线电侦查情况下的空时分组码识别具有重要意义。
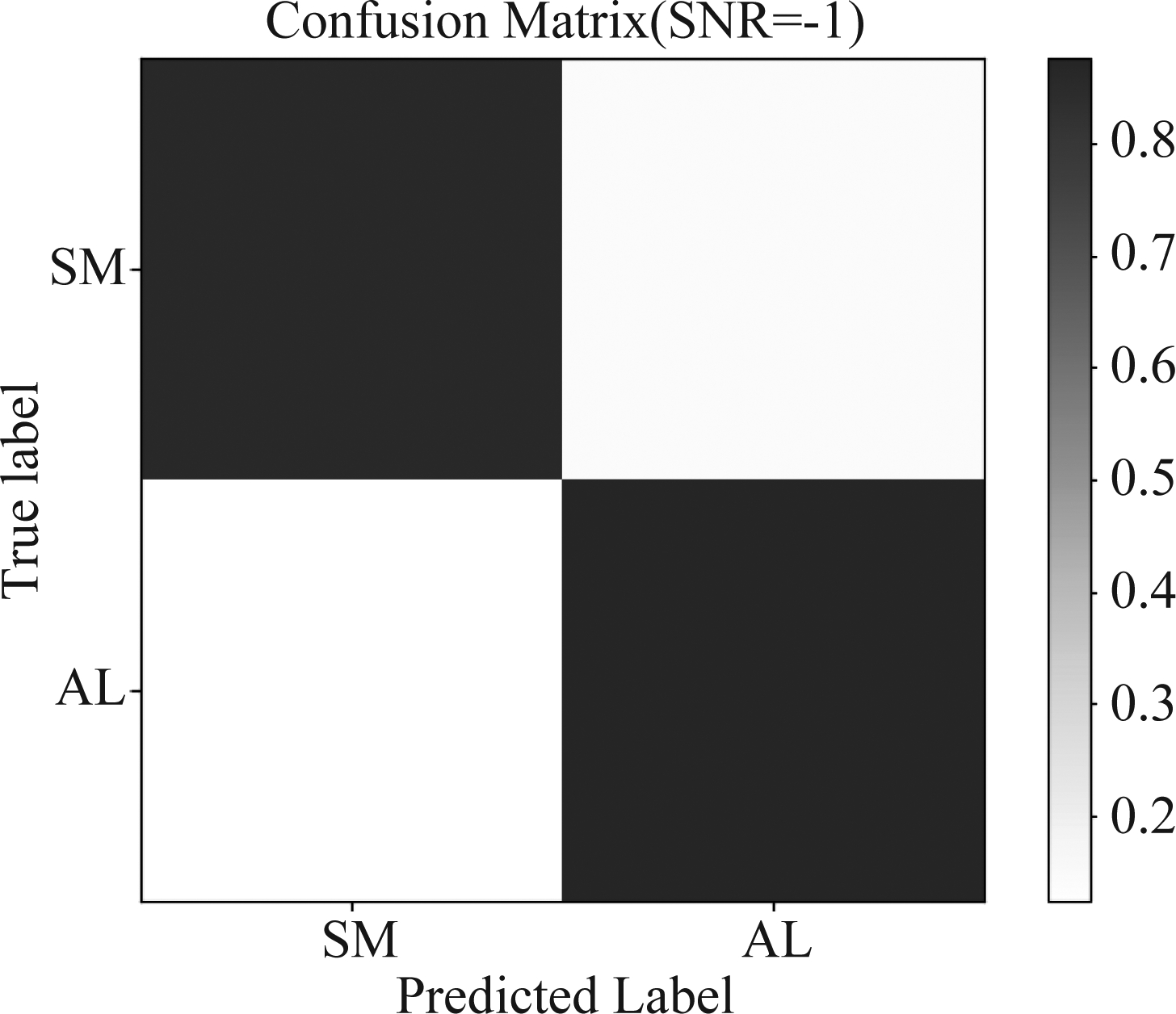
图12 信噪比为-1 dB时模型的混淆矩阵
Fig.12 The confusion matrix of the model when the SNR is -1 dB
实验6 不同算法识别性能分析
本实验分析了本文CNN-RNN网络与文献[21]和文献[22]两种典型的传统算法的识别性能。文献[21]利用接收信号的四阶统计特征并对其进行离散傅里叶变换,通过将变换后得到的参数与设定的阈值进行比较,以实现对空时分组码进行识别。文献[22]利用了STBC码的空时冗余,并将信号的四阶矩作为判别特征以实现似然比检测。以上两种算法[21-22] 均利用了信号的四阶统计特征,是较为典型的利用STBC码信号相关特性和统计特征对其进行盲识别的传统算法,并且针对的也是SM和AL码的识别问题。此外,文献[21]和文献[22]也是在Nakagami-3衰落信道、单接收天线、QPSK调制和SM、AL两类STBC码情况下进行仿真,三种算法的识别准确率如图13所示。在低信噪比下(-5 dB),本文算法、文献[21]算法和文献[22]算法的识别准确率分别为71%、51%和56%,本文算法明显优于传统算法。实际上,在识别准确率达到稳定之前(即信噪比小于6 dB时),本文算法均优于其他两种传统算法。
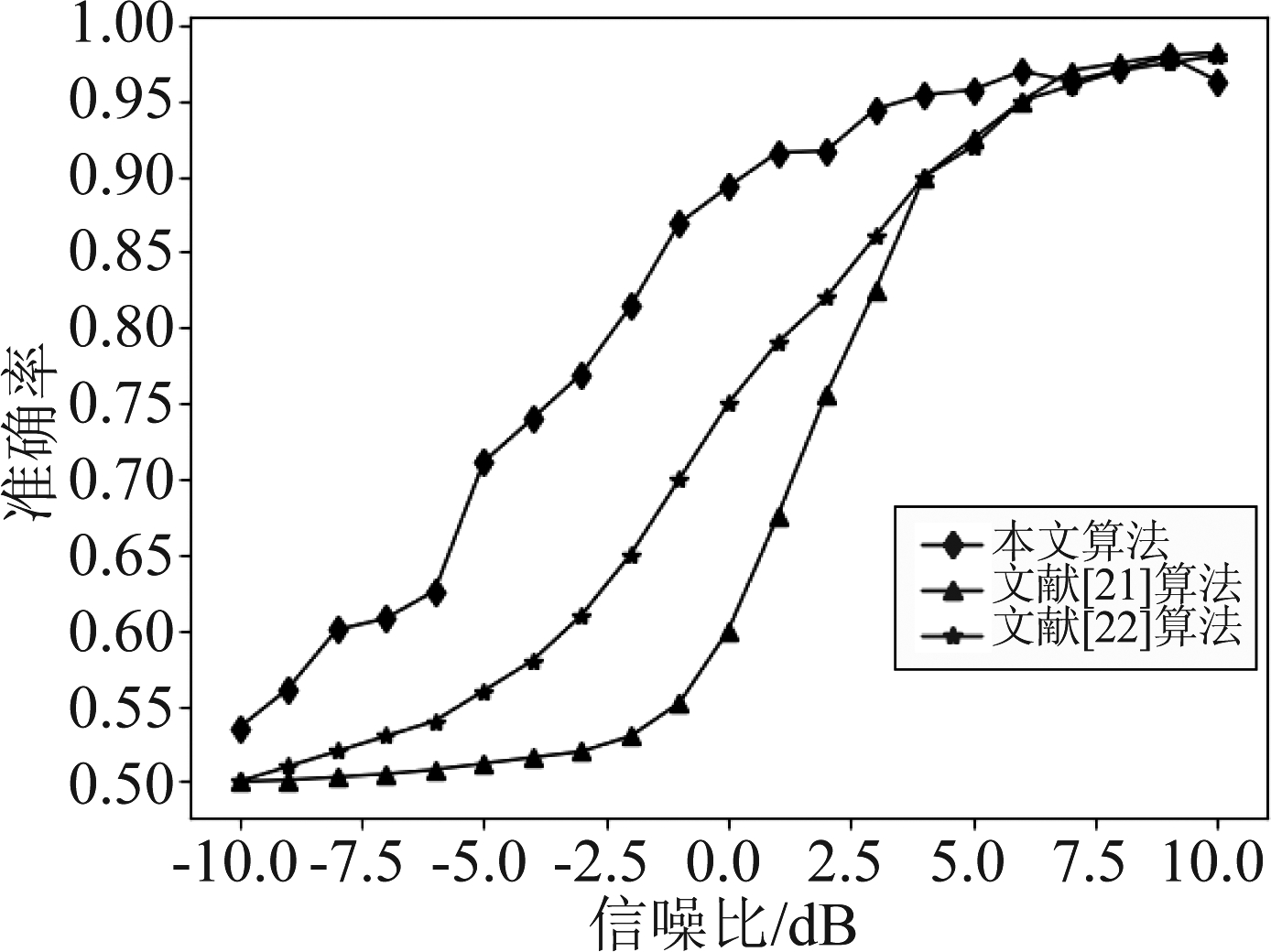
图13 不同算法识别性能对比
Fig.13 Comparison of different algorithm on identification performance
实验7 样本维度对模型性能的影响
本实验分析了样本维度对CNN-RNN网络性能的影响。在计算机视觉领域(Computer Vision, CV),输入样本的维度大小会对网络的性能造成影响,同样,信号样本的长度也会影响CNN-RNN模型的识别性能。考虑到神经网络的输入维度常采用2的整数倍,为探究适合于STBC识别的样本长度,本实验分析了符号数量为64、128和256情况下CNN-RNN模型的识别性能,结果如图14所示。从图中可以看出,选取的符号数量为128时网络的识别性能最好,减少或增加符号数时网络的性能均有所下降,故本文选取符号数量为128。
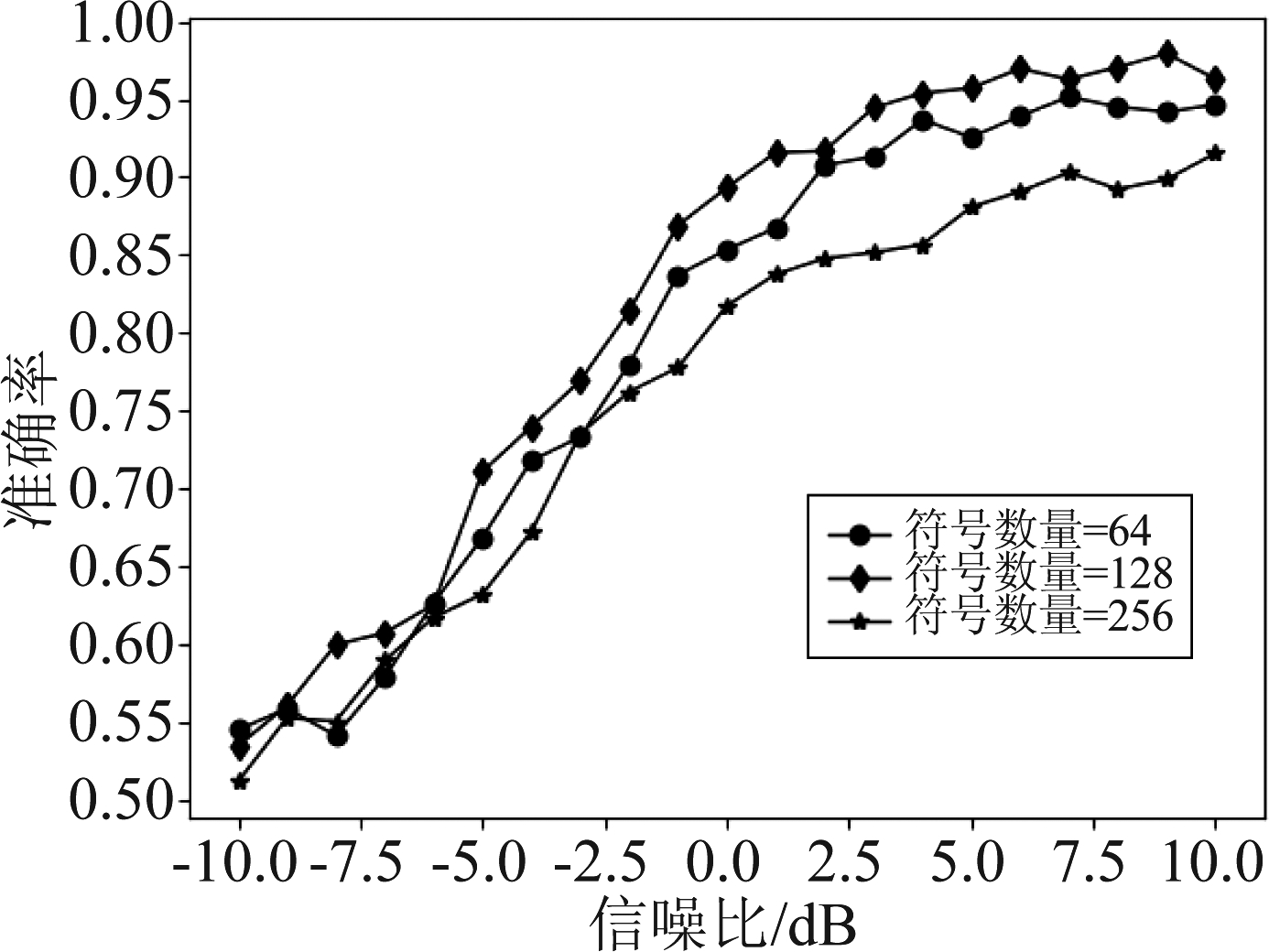
图14 不同样本长度下的识别性能对比
Fig.14 Comparison of different length of samples on identification performance
5 结论
深度学习作为新兴的研究热点,正逐步应用于信号识别的各领域。本文针对非协作通信条件下的串行序列空时分组码识别问题,提出了一种利用卷积-循环神经网络的深度学习识别算法。将接收端的一维时间序列提取出实部和虚部信息,利用卷积层提取信号的空间特征后,再输入循环层深度提取信号的时序特征,经全连接层输出后,实现对STBC信号的识别。该方法克服了传统方法对先验信息依赖强问题,不需要知道信道和噪声的先验信息,适用于无线电侦查等非协作通信情况。CNN-RNN网络不需要反复计算信号累积特征量,避免了人为设定参数与检验阈值的不足,对不同通信环境有更强的适应性。实验的仿真结果表明,该算法能够对单接收条件下的串行序列空时分组码进行有效的识别,且在低信噪比下有较好的识别性能,具有较好的工程应用前景。
[1] 甘天江, 傅友华, 王海荣. 毫米波大规模MIMO系统中基于机器学习的自适应连接混合预编码[J]. 信号处理, 2020, 36(5): 677- 685.
GAN Tianjiang, FU Youhua, WANG Hairong. Machine Learning-based Adaptive Connection Hybrid Precoding for mmWave Massive MIMO Systems[J]. Journal of Signal Processing, 2020, 36(5): 677- 685.(in Chinese)
[2] LU Z L, ZHANG Y L, ZHANG J Y. Quantized hybrid precoding design for millimeter-wave large-scale MIMO systems[J]. China Communications, 2019, 16(4): 130-138.
[3] 林洋, 张顺生, 王文钦. FDA-MIMO雷达主瓣距离模糊杂波抑制方法[J]. 信号处理, 2020, 36(1): 84-92.
LIN Yang, ZHANG Shunsheng, WANG Wenqin. Main-beam Range-ambiguous Clutter Suppression Method with FDA-MIMO Radar[J]. Journal of Signal Processing, 2020, 36(1): 84-92.(in Chinese)
[4] WANG Z, LI M, LIU Q, et al. Hybrid Precoder and Combiner Design With Low-Resolution Phase Shifters in mmWave MIMO Systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(2): 256-269.
[5] MAREY M, DOBRE O A. Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J]. IEEE Signal Processing Letters, 2014, 21(9): 1098-1102.
[6] ELDEMERDASH Y A, DOBRE O A, LIAO B J. Blind identification of SM and Alamouti STBC-OFDM signals[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 972-982.
[7] KARAMI E, DOBRE O A. Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity[J]. IEEE Transactions on Vehicular Technology, 2015, 64(3): 942-953.
[8] 赵知劲, 谢少萍, 王海泉. OSTBC信号累积量的特征分析[J]. 电路与系统学报, 2013, 18(1): 150-155.
ZHAO Zhijin, XIE Shaoping, WANG Haiquan. The characteristic analysis of cumulants of the OSTBC signals[J]. Journal of Ciruits and Systems, 2013, 18(1): 150-155.(in Chinese)
[9] 闫文君, 张立民, 凌青, 等. 基于高阶统计特征的空时分组码盲识别方法[J]. 电子与信息学报, 2016, 38(3): 668- 673.
YAN Wenjun, ZHANG Limin, LING Qing, et al. An algorithm for blind classification of space-time block code based on higher-order statistics[J]. Journal of Electronics & Information Technology, 2016, 38(3): 668- 673.(in Chinese)
[10] ELDEMERDASH Y A, DOBRE O A, MAREY M, et al. An efficient algorithm for space-time block code classification[C]∥IEEE Global Communications Conference, Atlanta, USA, 2013: 3329-3334.
[11] 闫文君, 张立民, 凌青. 基于FOLP的STBC-OFDM信号盲识别方法[J]. 电子学报, 2017, 45(9): 2233-2240.
YAN Wenjun, ZHANG Limin, LING Qing. A method for blind recognition of STBC-OFDM signals based on FOLP[J]. Acta Electronica Sinica, 2017, 45(9): 2233-2240.(in Chinese)
[12] 张立民, 闫文君, 凌青, 等. 一种单接收天线下的空时分组码识别方法[J]. 电子与信息学报, 2015, 37(11): 2621-2627.
ZHANG Limin, YAN Wenjun, LING Qing, et al. A method for blind recognition of space-time block coding using single receive antenna[J]. Journal of Electronics & Information Technology, 2015, 37(11): 2621-2627.(in Chinese)
[13] 徐茂, 侯进, 吴佩军, 等. 基于通信信号时频特性的卷积神经网络调制识别[J]. 计算机科学, 2020, 47(2): 175-179.
XU Mao, HOU Jin, WU Peijun, et al. Modulation recognition of convolutional neural networks based on time-frequency characteristics of communication signals[J]. Computer Science, 2020, 47(2): 175-179.(in Chinese)
[14] 姚晓辉, 杨宏晖, 李益青. 基于卷积神经网络的水声通信调制识别[J]. 无人系统技术, 2018, 1(4): 68-74.
YAO Xiaohui, YANG Honghui, LI Yiqing. Modulation recognition of underwater acoustic communication based on convolutional neural network[J]. Unmanned Systems Technology, 2018, 1(4): 68-74.(in Chinese)
[15] 吴佩军, 侯进, 吕志良, 等. 基于卷积神经网络的多进制相位调制信号识别算法[J]. 计算机应用与软件, 2019, 36(11): 202-209.
WU Peijun, HOU Jin, LV Zhiliang, et al. Recognition algorithm of multi-base phase modulation based on convolutional neural network[J]. Computer Applications and Software, 2019, 36(11): 202-209.(in Chinese)
[16] 鲁华超, 赵知劲, 尚俊娜, 等. 利用卷积神经网络和协方差的协作频谱感知算法[J]. 信号处理, 2019, 35(10): 1700-1707.
LU Huachao, ZHAO Zhijin, SHANG Junna, et al. Cooperative spectrum sensing algorithm using convolutional neural networks and covariance[J]. Journal of Signal Processing, 2019, 35(10): 1700-1707.(in Chinese)
[17] BYEOUNGDO Kim, JAEKYUM Kim, HYUNMIN Chae, et al．Deep neural network-based automatic modulation classification technique[C]∥2016 International Conference on Information and Communication Technology Convergence (ICTC). IEEE, 2016.
[18] WU Y, LI X, FANG J. A Deep learning approach for modulation recognition via exploiting temporal correlations[C]∥2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). IEEE, 2018.
[19] 翁建新, 赵知劲, 占锦敏. 利用并联CNN-LSTM的调制样式识别算法[J]. 信号处理, 2019, 35(5): 870- 876.
WENG Jianxin, ZHAO Zhijin, ZHAN Jinmin. Modulation recognition algorithm by using parallel CNN-LSTM[J]. Journal of Signal Processing, 2019, 35(5): 870- 876.(in Chinese)
[20] 周龙梅. 基于深度学习的通信信号识别技术研究[D]. 北京: 北京邮电大学, 2018.
ZHOU Longmei. Research on Communication Signal Recognition Technology Based on Deep Learning[D]. Beijing: Beijing University of Posts and Telecommunications, 2018.(in Chinese)
[21] YAHIA A. Eldemerdash, MOHAMED Marey, OCTAVIA A. Dobre, et al. Blind identification of SM and alamouti STBC signals based on fourth-order statistics[C]∥2013 Signal Processing for Communications Symposium (SPCS). IEEE, 2013.
[22] YAHIA A. Eldemerdash, MOHAMED Marey, OCTAVIA A. Dobre, et al. Fourth-order statistics for blind classification of spatial multiplexing and Alamouti space-time block code signals[J]. IEEE Transactions on Communications, 2013, 61(6): 2420-2431.
