1 引言
被动定位在雷达、声纳和电子战等领域都有着广泛的应用。被动定位是指探测系统不往外辐射信号,而是通过被动接收目标的辐射信号或者目标反射的第三方辐射源信号来完成对目标的定位[1-2]。被动定位具有隐蔽性好、定位精度高的优势特征,促使其在理论与实践中被广泛关注。目标辐射源一般分为窄带辐射源和宽带辐射源。对于窄带信号而言,由于相对运动导致接收信号相比发射信号产生了多普勒频移和时间延迟。因此,窄带辐射源往往是通过窄带互模糊函数估计出两路接收信号之间的时差和多普勒频差来定位未知的辐射源[3]。而宽带辐射信号在空间传输中,由于接收机和辐射源存在相对运动,接收机所接收到的信号波形相比于发射信号表现出被拉伸或者压缩的特性,即信号到达两个独立的接收机上存在到达时差(TDOA)和尺度差(SDOA)。对于宽带辐射源目前研究的重点在于尺度差/时差的精确估计[4]。
宽带互模糊函数(WBCAF)是估计信号尺度差/时差的常用工具之一,目前,这一课题已经引起众多研究者的关注[5- 6]。宽带互模糊函数对尺度差/时差进行估计的原理是在时间域和尺度域进行二维相关,通过全局搜索宽带互模糊函数的最大值来得到信号的尺度差/时差估计,而尺度差/时差则刻画了目标的位置信息和运动参数。针对尺度差/时差估计的算法研究,不同学者基于不同视角提出了不同的估计方法。如Zhang等人提出了一种基于期望最大化的估计方法来估计被动雷达中运动目标的时延和多普勒展宽[7];Qu等人提出了一种基于宽带互模糊函数的宽带信号时延和多普勒展宽估计方法[8];Niu等人提出了一种基于小波变换的宽带交叉模糊函数(WB-WBCAF)方法来估计两个受噪声污染的接收信号之间的时延和多普勒展宽[9]。由于小波变换需要对信号进行变采样率处理,从而产生较大的时间成本和计算复杂度,Niu等人基于互小波理论估计尺度差/时差,提出了对离散信号进行尺度变换的快速算法[10],并给出估计的克劳美罗下限,此方法不需要进行变采样率处理,但是这一算法仍需要对宽带互模糊函数进行二维搜索。在此基础上,郭付阳等根据线性调频信号的信号特性,利用分数阶傅里叶变换(FRFT)的尺度性质,通过将时域信号变换到分数阶傅里叶域并采用三级搜索算法求出尺度差[4]。由于分数阶傅里叶变换具有较好的抗噪性,能处理时频域耦合噪声,在一定程度上降低了运算量,提高了估计精度。但其中的三级搜索算法仍然是传统的网格搜索法。Alieva等基于准极坐标系中表示的模糊函数与分数阶功率谱之间的关系,引入分数阶傅里叶变换矩,推导了整体二阶分数阶傅里叶变换矩的重要等式,建立了局部矩和分数次幂谱的角导数之间的联系,并讨论了其在信号分析中的应用[11]。
综合上述研究进展的分析,本文研究了基于分数阶傅里叶四阶中心矩的尺度差/时差估计算法。本文分为四部分,第一部分回顾了宽带信号尺度差/时差估计算法研究历程。第二部分简述了宽带信号模型以及宽带互模糊函数的定义,分析了信噪比对宽带互模糊函数的影响。第三部分针对目前基于分数阶傅里叶变换的尺度差/时差估计算法在搜索效率和在低信噪比下估计精度上的不足,根据模糊函数(AF)、魏格纳分布(WVD)和分数阶傅里叶变换(FRFT)之间的关系,理论推导出分数阶傅里叶四阶中心矩算法,并从信噪比改善角度推导分数阶傅里叶四阶中心矩的抗噪性与信噪比的关系。第四部分,针对理论推导,利用MATLAB对两种算法的性能进行仿真。
2 宽带信号模型
设两个独立接收机接收到的信号模型如下所示[4]:
x1(t)=a1f[s1(t-τ1)]+b1n1(t)
(1)
x2(t)=a2f[s2(t-τ2)]+b2n2(t)
(2)
式中, f(t)表示未知辐射源的发射信号,即
(3)
T为信号持续时间, f0为源信号初始频率,μ为源信号调频率;τ1为源信号到第一路接收机时差,s1表示源信号由于多普勒效应到第一路接收机的时间尺度因子(尺度差),τ2为源信号到第二路接收机时差,s2表示源信号由于多普勒效应到第二路接收机的时间尺度因子。a1,a2,b1,b2分别表示传输过程中源信号到两路接收机的路径增益系数,路径增益系数根据功率衰减系数来刻画,n1(t)和n2(t)是相互独立的广义复高斯白噪声。
尺度差/时差估计的常用方法是对接收信号的宽带互模糊函数进行峰值的二维搜索。其原理是宽带互模糊函数最大值对应的时延τ和尺度差s即为两路接收机信号到达尺度差/时差估计。以x1(t)为参考基准,可将式(1)和式(2)改写为[13]:
x1(t)=a1f(t)+b1n1(t)
x2(t)=a2f[s0(t-τ0)]+b2n2(t)
(4)
式中,s0和τ0分别表示两路接收信号的实际尺度差和时差。定义宽带互模糊函数如下[14]
(5)
式中,s表示两路接收信号尺度差,τ表示两路接收信号时差,![]() 表示两路信号由于多普勒效应产生的信号路径增益系数差。可将式(4)代入式(5)中得到:
表示两路信号由于多普勒效应产生的信号路径增益系数差。可将式(4)代入式(5)中得到:
χx1,x2(τ,s)=χf, f(τ,s)+χf,n1(τ,s)+χn2, f(τ,s)+
χn2,n1(τ,s)=χf, f(τ,s)+Δχ(τ,s)
(6)
式(6)中,Δχ(τ,s)表示由于噪声引起的偏移,从式(4)~(6)可以看出,当![]() 时,宽带互模糊函数会出现峰值,因此,可通过峰值搜索来得到尺度差/时差的估计值。当信噪比较高时,偏移量Δχ(τ,s)对尺度差/时差估计的影响可以忽略不记[15]。
时,宽带互模糊函数会出现峰值,因此,可通过峰值搜索来得到尺度差/时差的估计值。当信噪比较高时,偏移量Δχ(τ,s)对尺度差/时差估计的影响可以忽略不记[15]。
3 基于分数阶傅里叶四阶中心矩的尺度差/时差估计算法
3.1 基于分数阶傅里叶四阶中心矩的尺度差估计
宽带线性调频信号在传输过程中,由于接收机和运动目标存在相对运动而呈现出信号被扩展或者压缩的特性。准确估计出接收信号由于多普勒效应所产生的尺度差对获取目标运动参数尤为重要。利用分数阶傅里叶变换可以通过估计两路独立接收信号的调频率比值来获得信号的尺度差。当式(4)中不考虑噪声扰动时,x(t)的分数阶傅里叶变换为:
(7)
其中,α表示转换角度,Kα(t,u)表示分数阶傅里叶变换核函数,其定义式为:
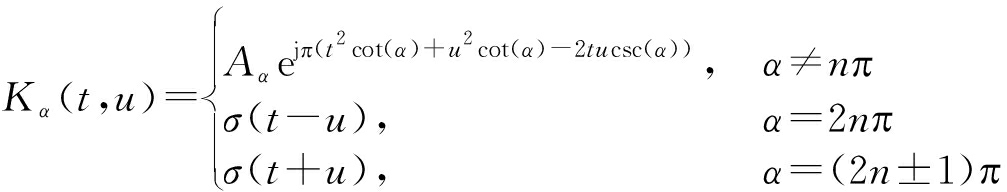
(8)
式中,![]() 分数阶傅里叶变换是傅里叶变换的广义形式,当α=2nπ+π/2分数阶傅里叶变换变为传统的傅里叶变换。分数阶傅里叶变换根据信号调频率旋转坐标轴,使线性调频信号可在某最优分数阶傅里叶域表现为冲击函数形式。通过对x1(t)和x2(t)两路接收信号进行分数阶傅里叶域最优变换角度估计得到[16]:
分数阶傅里叶变换是傅里叶变换的广义形式,当α=2nπ+π/2分数阶傅里叶变换变为传统的傅里叶变换。分数阶傅里叶变换根据信号调频率旋转坐标轴,使线性调频信号可在某最优分数阶傅里叶域表现为冲击函数形式。通过对x1(t)和x2(t)两路接收信号进行分数阶傅里叶域最优变换角度估计得到[16]:
(9)
其中,![]() 和
和![]() 分别表示两路信号的分数阶傅里叶变换最优角度估计值,
分别表示两路信号的分数阶傅里叶变换最优角度估计值,![]() 和
和![]() 分别表示两路信号的调频率估计值。可知s>0,由此可得基于分数阶傅里叶变换的尺度差估计式如下[4]:
分别表示两路信号的调频率估计值。可知s>0,由此可得基于分数阶傅里叶变换的尺度差估计式如下[4]:
(10)
3.1.1 估计算法
郭付阳等提出分数阶傅里叶尺度差估计算法,其出发点是利用两路信号调频率的比值对尺度差进行估计,提出的峰值分级搜索算法在一定程度上能降低运算量[4],但对于低信噪比情况下,其峰值搜索精度将降低。信号的分数阶傅里叶域带宽可以由信号的分数阶傅里叶二阶中心矩估计[11],但是这一算法对噪声非常敏感,估计效果较差。而分数阶傅里叶四阶中心矩是分数阶傅里叶二阶中心矩的推广,已被广泛应用于多分量分离以及相位检索等信号处理领域[11]。本节根据模糊函数(AF)和分数阶傅里叶变换的关系,利用RadonWVD(RWD)的模平方,以及时频面旋转对分数阶傅里叶四阶中心矩应用于两路线性调频信号的尺度差估计进行了推导。
已知AF表达式如下:
(11)
分数阶傅里叶变换作为一种时频面上的旋转算子,它与传统时频分布之间存在着紧密的联系,RWT与相应分数阶傅里叶变换的模值平方相等的关系是其中一个非常有用的重要结论。容易知道WVD的时间和频率边缘积分分别与信号在频域和时域的模值平方相等,即有关系:
|X(ω)|2=![]() W(t,ω)dt
W(t,ω)dt
|x(t)|2=![]() W(t,ω)dω
W(t,ω)dω
(12)
RWT作为WVD的广义边缘积分,也可以推导出相似的结论,即,在时频面上倾角为α的直线积分投影与旋转角度相同的FRFT的功率谱相等:
RWTα(u)=![]() W(ucos α-νsin α,usin α+νcos α)dν=
W(ucos α-νsin α,usin α+νcos α)dν=
|Xα(u)|2
(13)
WVD和AF都是瞬时相关函数的傅里叶变换。前者是时间频率的函数,表示能量分布,称之为能量域;而后者是时延频偏的函数,表示相关,称为相关域。两者之间存在简单的二维傅里叶关系如下:
(14)
考察分布在φ倾角直线上的模糊函数切片,令
τ=ρcos φ,ξ=ρsin φ
(15)
若用α-π/2=φ代换式(15)中倾角φ,则有τ=ρcos α,ξ=-ρsin α,那么式(14)可以进一步写为
![]()
exp[jρ(-tcos α+ωsin α)]dωdt
(16)
再次做变量替换t=ucos α-νsin α,ω=usin α+νcos α,则式(16)可以写成
![]()
usin α+νcos α)dνexp(jρu)du
(17)
利用式(12),得到:
AF(ρcos α,ρsin α)=![]() |Xα(u)|2exp(jρu)du
|Xα(u)|2exp(jρu)du
(18)
根据矩和模糊函数的关系,可得信号的分数阶傅里叶域一阶矩mα为[18]:
(19)
式(19)中,分数阶傅里叶一阶矩与分数功率谱的能量重心有关,由AF在方向φ上的一阶偏导数确定。通过求mα在ρ上的极大值可得到分数功率谱的能量重心。
接下来求信号的分数阶傅里叶二阶矩wα为:
![]()
-![]() |Xα(u)|2u2exp(jρu)du
|Xα(u)|2u2exp(jρu)du
(20)
式(20)表示信号的有效带宽由AF在方向φ上的切片二阶偏导数确定。由于高斯白噪声在分数阶傅里叶域中能量是均匀分布的,一般认为其能量重心在u域是相对固定的,而信号由于能量聚集性,在最优分数阶傅里叶上实现能量聚集,其能量重心受噪声影响而偏移。通过分数阶傅里叶二阶中心矩可求出线性调频信号的最小有效带宽。因此,接下来求信号的分数阶傅里叶二阶中心矩Rα为:
Rα=-![]() |Xα(u)|2(u-mα)2exp(jρu)du
|Xα(u)|2(u-mα)2exp(jρu)du
(21)
当噪声和信号能量重心在u域偏移量的差别很小时,二阶中心矩抗噪性将降低。通过式(21)我们可建立起分数阶傅里叶四阶中心矩Pα和分数阶傅里叶二阶中心矩Rα之间的关系如下所示:
![]()
|Xα(u2)|2(u1-mα)2(u2-mα)2δ[ρ(u1-u2)]![]()
(22)
通过式(22)可知分数阶傅里叶四阶中心矩等于其分数阶傅里叶域二阶中心矩的平方沿方向ρ积分而得,即,分数阶傅里叶四阶中心矩在α∈[0,π]的分数阶傅里叶域中存在最大延伸或者最小带宽[12]。而最小带宽则对应于最优分数阶傅里叶变换角度。也就是说,最优分数阶傅里叶变换角度可通过峰值搜索来估计,因此,可得到基于分数阶傅里叶四阶中心距的尺度差估计值![]() 如下:
如下:
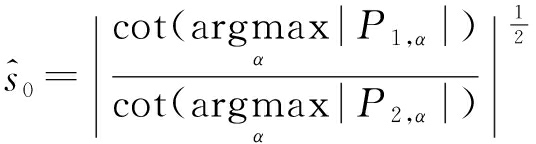
(23)
式中,α表示分数阶傅里叶变换角度的搜索范围,P1,α和P2,α分别表示两路接收信号的α角度分数阶傅里叶四阶中心矩。
3.1.2 分数傅里域四阶中心矩的抗噪性分析
在3.1.1节通过二阶中心矩,推导出四阶中心矩之间的联系,根据文献[13]中建立二阶中心矩的思维,在本节假设ρ=0,对信号抗噪性进行证明,假设接收信号模型如下所示:
(24)
其中f(t)如式(3)所示,n(t)是零均值复高斯白噪声,且方差![]()
利用式(24)和式(8),式(19)可以改写为:
(25)
将式(24)代入,则式(25)可以改写为
(26)
令
(27)
则可将式(25)改写成:
![]()
[f*(ν)+n*(ν)]udtdνdu
(28)
式中,E[n(t)]=0,E[n*(ν)]=0,E[n(t)n*(ν)]=N0δ(t-ν)。进一步可得到:
(29)
式(29)中,前一项积分是信号项,后一项积分是噪声项。将式(29)代入(22)中可得:
(30)
其中
E[|Xα(u)|4]=|Fα(u)|4+
2|Fα(u)|2TN0cscα+(TN0cscα)2
(31)
将式(31)代入(30)可得:
![]()
(TN0cscα)2)(u-mα)4du
(32)
令
(33)
式中,SNRi表示分数阶傅里叶域中传统信噪比定义,由理论峰值点的信号和噪声平均功率比计算得到。将式(32)改写如下:
(34)
因此,含噪信号x(t)的分数阶傅里叶四阶中心矩中有用信号f(t)所占比例为:
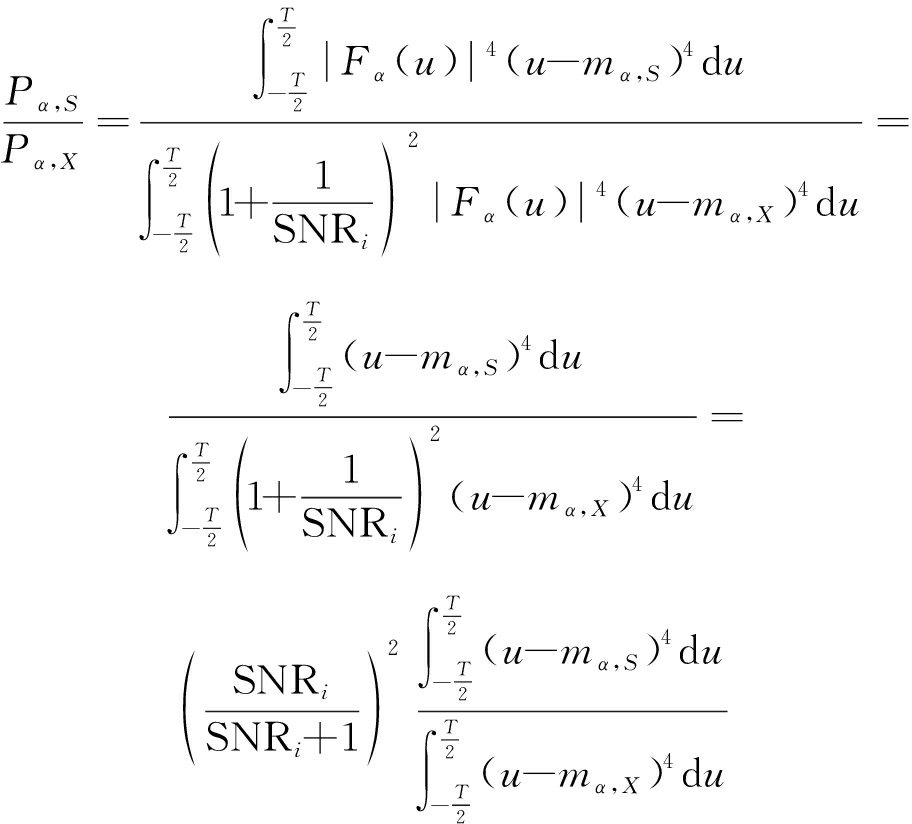
(35)
其中,Pα,S表示有用信号f(t)的分数阶傅里叶四阶中心矩,Pα,X表示含噪信号x(t)的分数阶傅里叶四阶中心矩,mα,S表示有用信号f(t)的分数阶傅里叶域一阶原点矩,mα,X表示含噪信号x(t)的分数阶傅里叶域一阶原点矩。定义
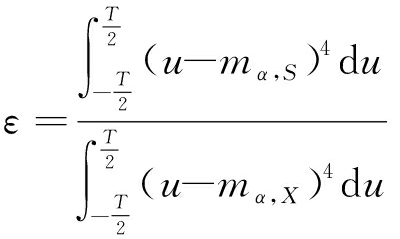
(36)
可见,在信号截获时间内ε≥1。
由于背景噪声的影响下,含噪信号的分数阶傅里叶域峰值位置相较理论峰值点会出现偏移,因此,以理论峰值点的功率比来定义信噪比(如SNRi所示)已经不再适合[17],而考虑噪声影响修正后的分数阶傅里叶域信噪比与分数阶傅里叶域理论峰值点功率定义的信噪比之间关系为[18]
(37)
联合式(33)、式(35)、式(36)和式(37)可得:
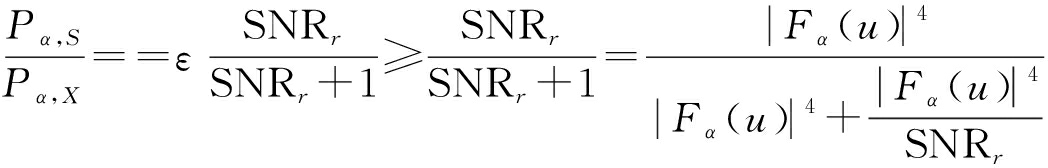
(38)
式中,SNRr表示修正后的分数阶傅里叶域信噪比,![]() 表示分数阶傅里叶域有用信号f(t)在含噪信号x(t)中所占的比例。对式(38)进行改写,得到分数阶傅里叶四阶中心距的信噪比为:
表示分数阶傅里叶域有用信号f(t)在含噪信号x(t)中所占的比例。对式(38)进行改写,得到分数阶傅里叶四阶中心距的信噪比为:
(39)
式中,SNRr>0,ε≥1。式(39)可改写为:
![]() ≥εSNRr≥SNRr
≥εSNRr≥SNRr
(40)
将式(40)写成dB形式,有
![]()
10log10SNRr≥10log10SNRr
(41)
通过分析有用信号分量在含噪信号分量中所占的比重可建立其与信噪比之间的关系,因此,从式(41)可发现:基于分数阶傅里叶四阶中心矩的算法抑制噪声的能力优于文献[4]中所提算法的噪声抑制能力。
3.1.3 分数阶傅里叶四阶中心矩的分级搜索
通过计算分数阶傅里叶四阶中心矩,找到分数阶傅里叶四阶中心矩极大值的对应变换角度就是最优分数阶傅里叶变换角度。为了满足精度要求,传统单步长全局搜索算法,其产生额外的数据点将导致搜索时间成本增加。本文通过设置变步长算法实现步长的调整,以达到精度要求,步长的选取根据实际情况的精度需要进行选择。本文选取步长缩放因子为10。其算法步骤如下:
(1)设置初始步长r,以初始步长对角度区间![]() 递进搜索
递进搜索![]() 和
和![]()
(2)更新递进步长为![]() 更新搜索角度区间[a1-r,a1+r]和[a2-r,a2+r],通过更新步长进行递进搜索得到最优角度
更新搜索角度区间[a1-r,a1+r]和[a2-r,a2+r],通过更新步长进行递进搜索得到最优角度![]() 和
和![]()
(3)更新递进步长为![]() 更新搜索角度区间[a1-r1,a1+r1]和[a2-r1,a2+r1],通过更新步长进行递进搜索得到最优角度
更新搜索角度区间[a1-r1,a1+r1]和[a2-r1,a2+r1],通过更新步长进行递进搜索得到最优角度![]() 和
和![]()
3.2 时差估计算法
估计出尺度差![]() 后,代入式(5)得到:
后,代入式(5)得到:
(42)
通过对式(42)所示的宽带互模糊函数进行一维峰值搜索,可得到时差估计![]()
(43)
式中,χx1,x2(τ,s)是已知尺度差后x2(t)和x1(t)的时域相关函数。
3.3 运算量分析
上述通过接收信号的变换域峰值搜索来估计出尺度差/时差的运算量由两部分组成,一部分表征变换运算的复杂度,另一部分则表征峰值搜索复杂度。分数阶傅里叶变换尺度差/时差估计算法[4]中的变换运算量为6MNlog2N+6MN+5N+7MNlog2N(M表示分级搜索的分数阶傅里叶变换角度个数,N表示信号点数),但是该算法对每个变换角度的分数阶傅里叶域都需要进行比对来求得极大值,则进行一次估计共需要进行2MN-2次比对。本文所提算法的尺度差估计结合采用FrFT和分数阶傅里叶四阶中心矩,其中,对两路信号进行一次FrFT所需的复乘次数为6MNlog2N+6MN,进行一次分数阶傅里叶四阶中心矩运算所需要复乘次数为9MN,所以,本文算法进行一次尺度差估计所需复乘次数为6MN+6MNlog2N+9MN。而对于时差的估计,两种方法所需的复乘次数一致,则本文算法完成一次尺度差/时差估计所需复乘次数6MNlog2N+5N+15MN+7MNlog2N,但本文只需要进行2M-2次一维比对求极大值就能得到最优分数阶傅里叶变换角度。这两种方法的运算量比较如表1所示,通过CPU占用时间的仿真对比可以发现:由于峰值搜索复杂度的降低,从而提升了本文算法在高估计精度条件下的运算效率。
表1 运算复杂度比较
Tab.1 Computational complexity comparison

方法变换运算的复杂度峰值搜索复杂度分数阶傅里叶变换尺度差/时差估计算法6MNlog2N+6MN+7MNlog2N+5N2MN-2本文算法6MNlog2N+15MN+7MNlog2N+5N2M-2
4 仿真分析
本文设置在不同信噪比环境下对基于分数阶傅里叶变换的尺度差/时差估计算法和本文所提算法进行仿真分析。
4.1 尺度差/时差估计算法
假设式(3)中源信号参数为;信号持续时间T=2.5 μs,信号带宽为B=400 MHz,信号采样率为fs=1 GHz,式(4)中两接收机信号到达时间差τ0=1.43 μs,尺度差s=1.00001,对两路信号进行仿真得到图1所示。
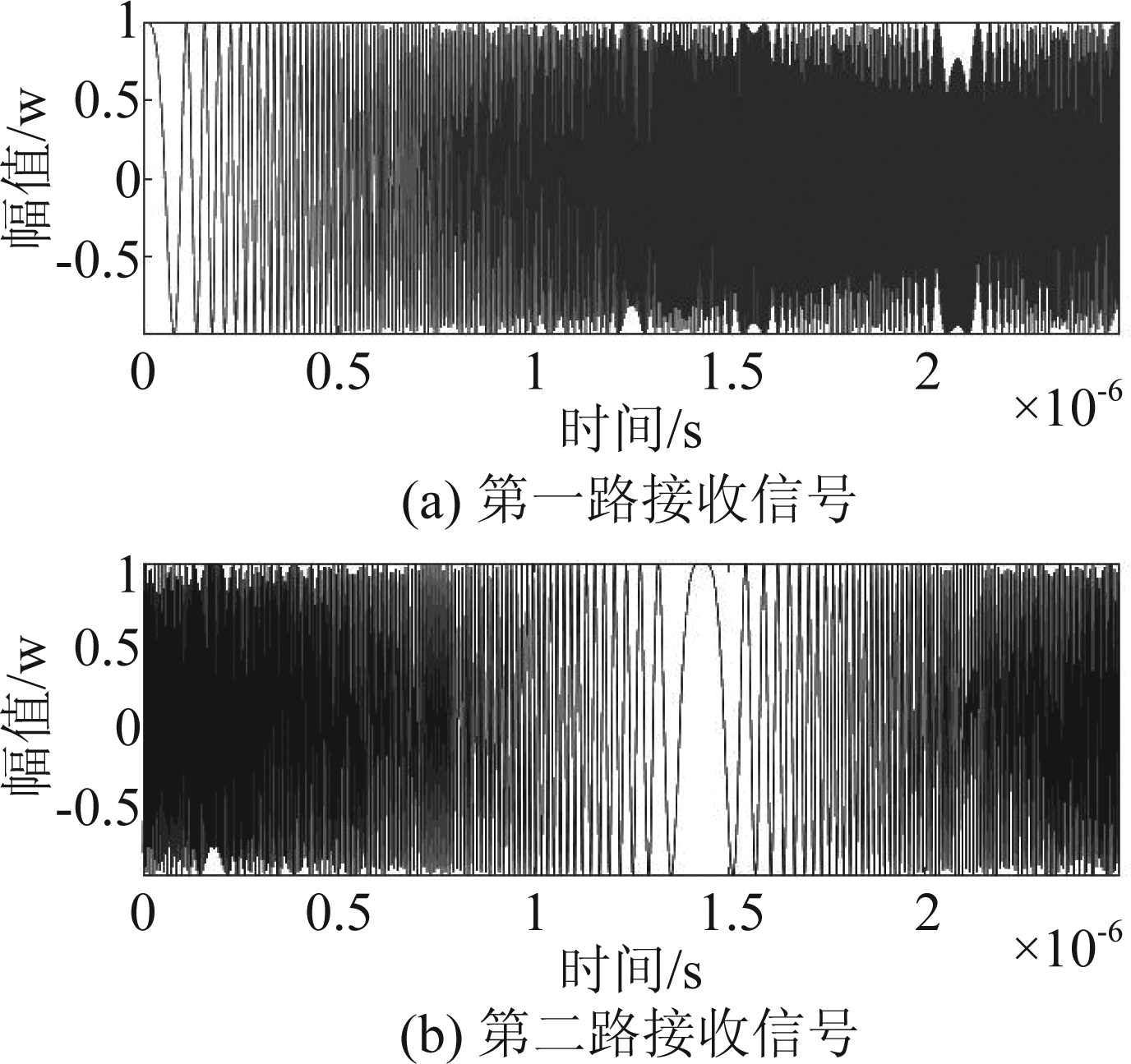
图1 两路源信号
Fig.1 Two source signals
通过图1所示,(b)图中信号相对于(a)图中信号发生延时。设置信噪比为-10 dB时,利用MATLAB中AWGN函数对图1中信号叠加高斯白噪声,将两路信号展示在图2的分数阶傅里叶变换三维图上。
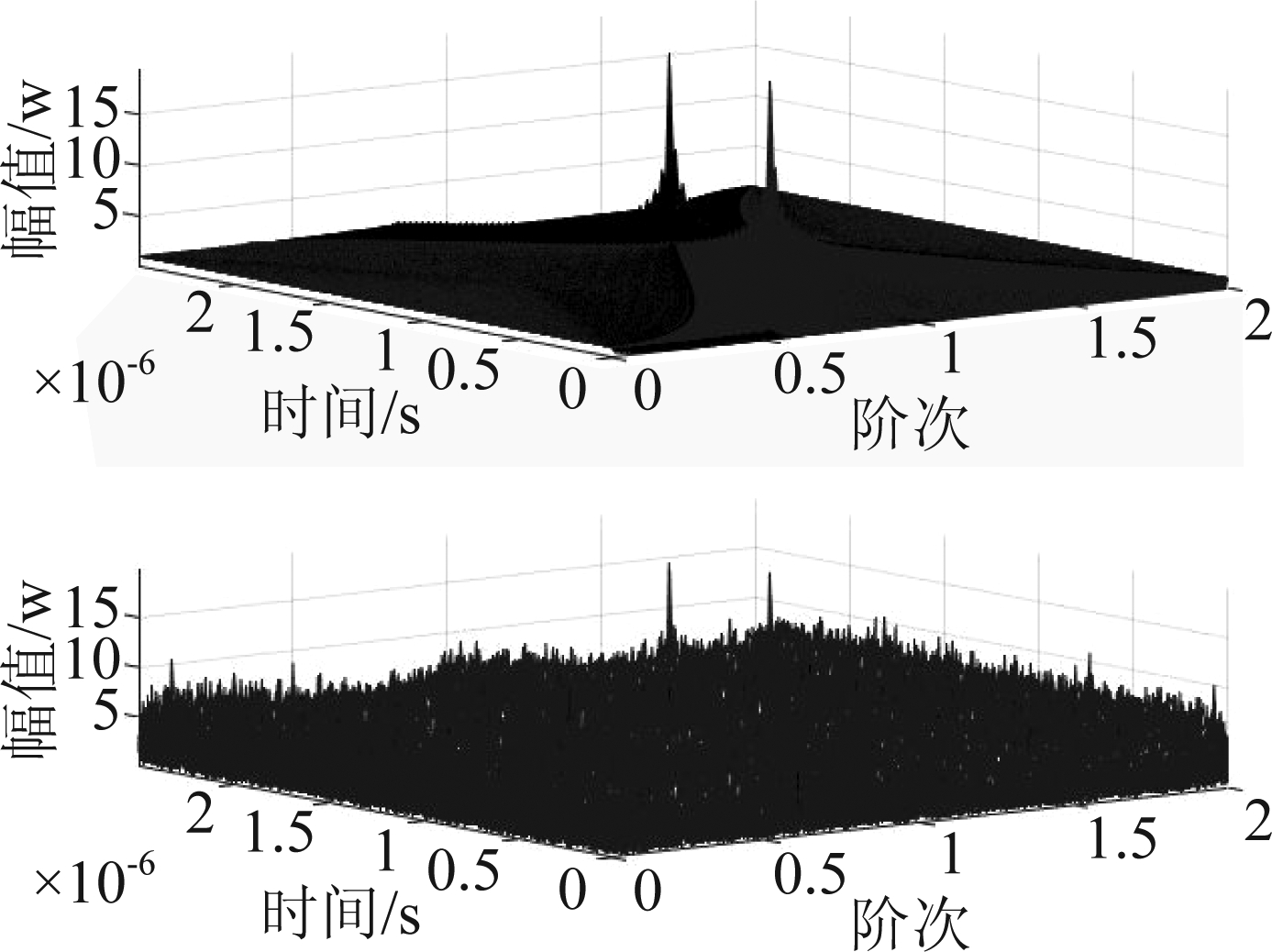
图2 -10 dB下两路信号的峰值分数阶傅里叶域幅度谱图
Fig.2 Peak graph of two signals at -10 dB
根据图2所示,当信噪比为-10 dB时,分数阶傅里叶变换对线性调频信号具有较强的抗噪性[19-20]。接下来,利用本文算法和分数阶傅里叶变换尺度差/时差估计算法在-20 dB~20dB范围内对上述信号进行仿真。通过对每个信噪比进行200次蒙特卡罗仿真,得到误差曲线如下。
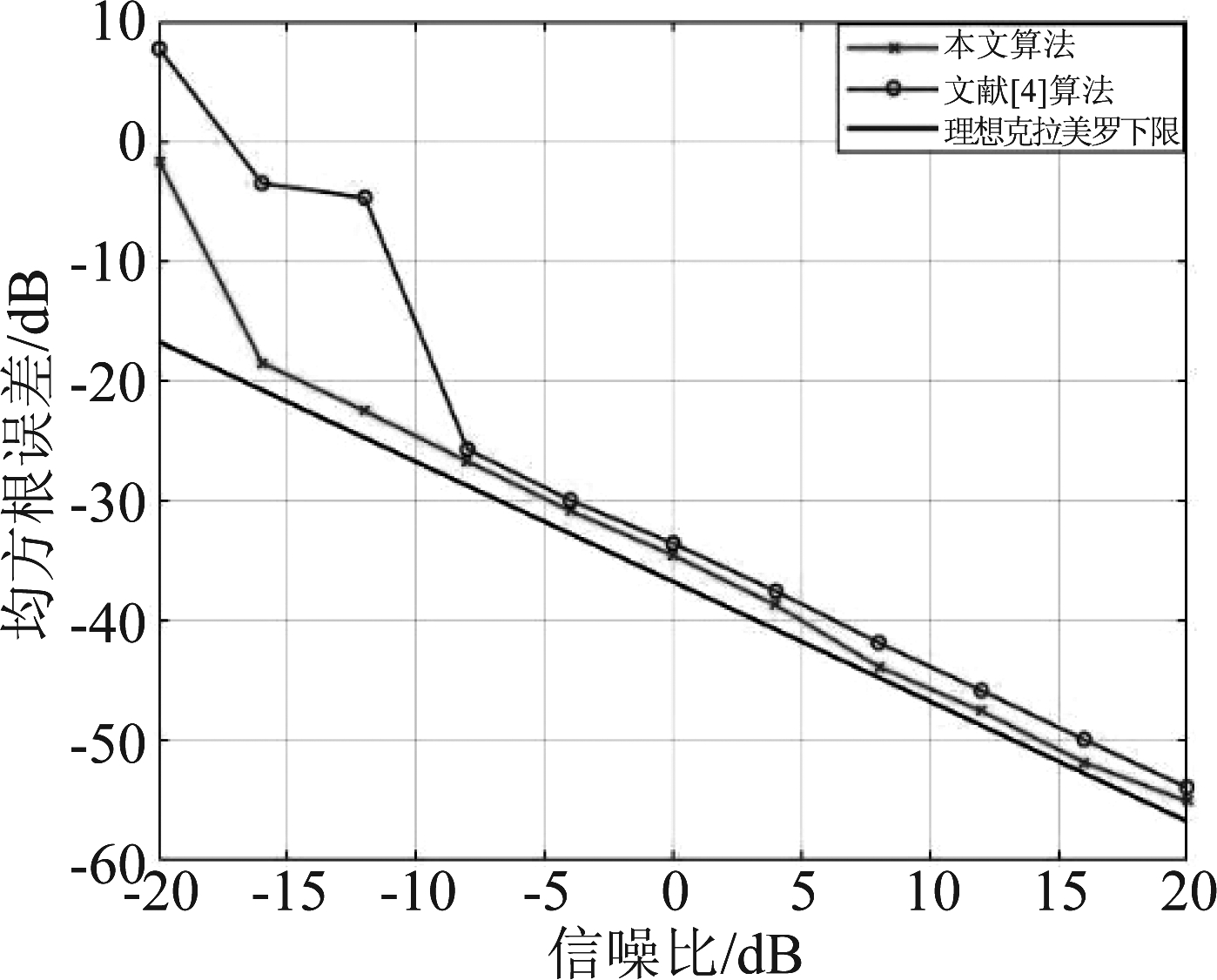
图3 尺度差估计均方根误差仿真
Fig.3 Root mean square error simulation of SDOA
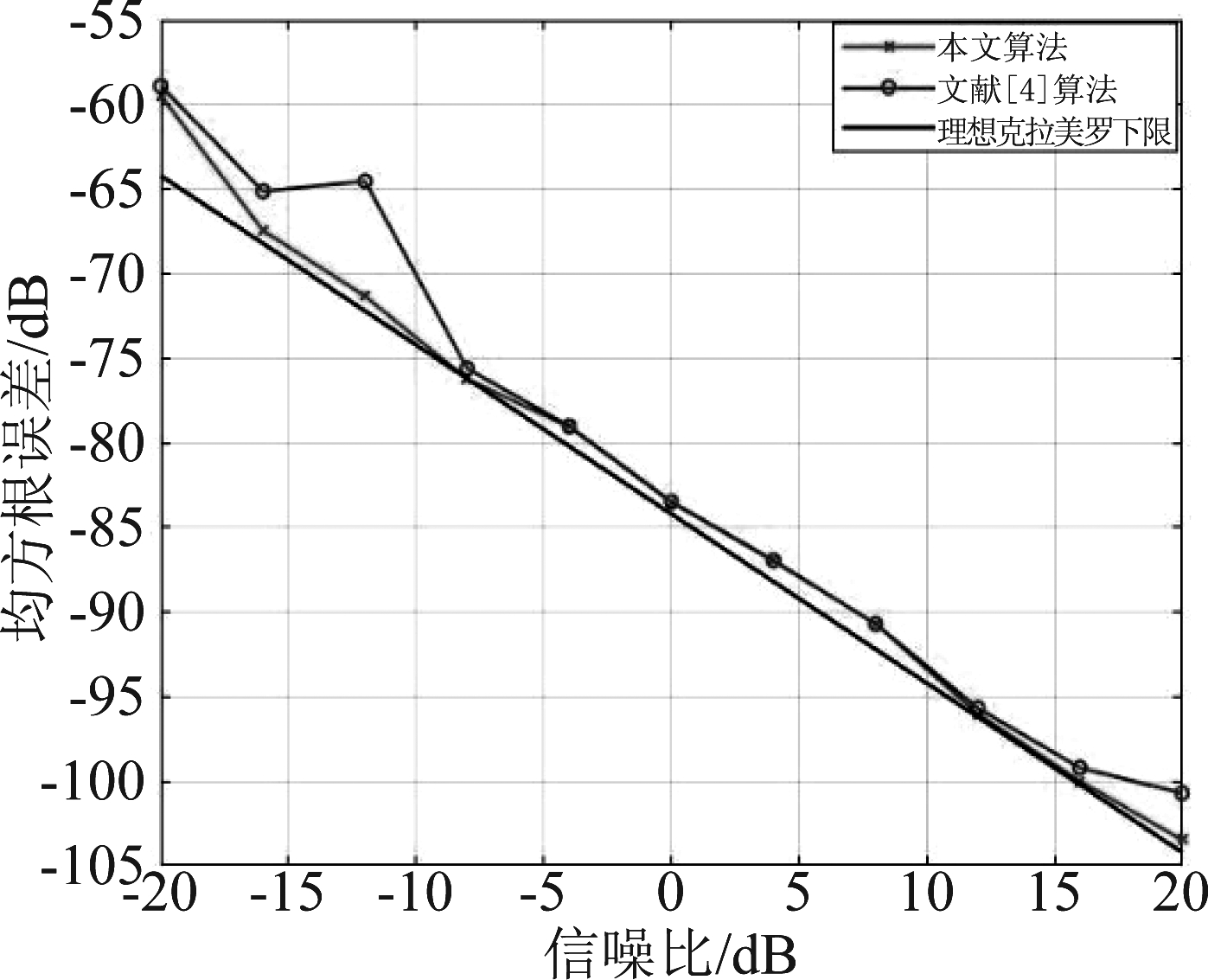
图4 时差估计均方根误差仿真
Fig.4 Root mean square error simulation of TDOA
通过上述仿真结果可以发现,本文算法在低信噪比下对尺度差/时差估计能进行准确估计,在精度上比文献[4]所提方法更高。
4.2 分数阶傅里叶四阶中心矩抗噪性仿真分析
从4.1节的仿真可以发现本文算法在噪声背景下的估计精度上优于文献[4]。3.1.2节对分数阶傅里叶四阶中心矩抗噪性能进行了理论分析,推导得到式(38)。在此基础上,本小节将以第一路接收信号x1(t)为例,通过有用信号分量f1(t)在带噪信号x1(t)中所占的比例(简称有用信号比)来对比分析两种方法的抗噪性。
如图5所示,分数阶傅里叶四阶中心矩的有用信号比明显大于文献[4]的分数阶傅里叶域有用信号比。当在最优变换角度的时候,有用信号比出现尖峰且抗噪性能最好。
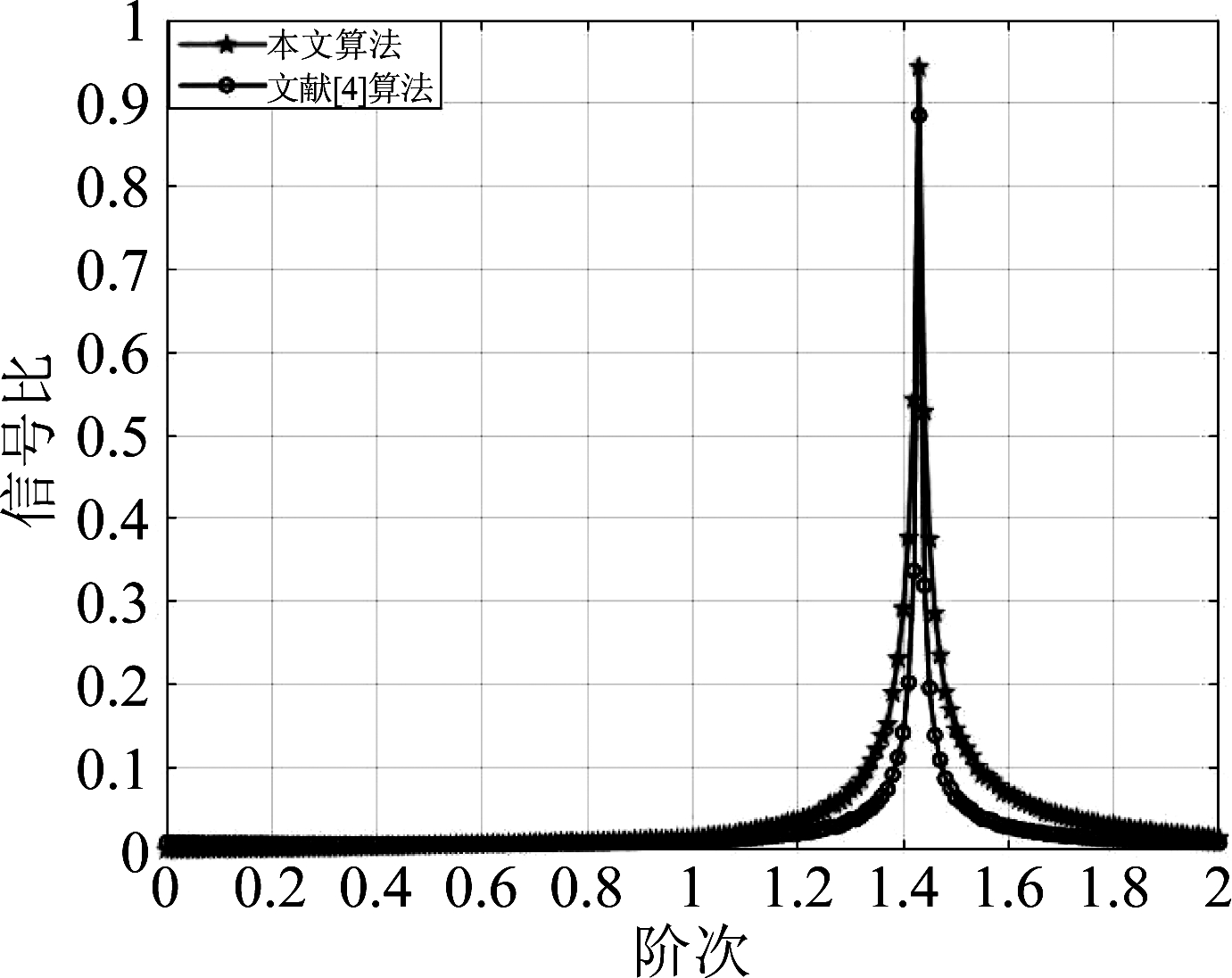
图5 -10 dB下第一路信号比值
Fig.5 The first signal ratio at -10 dB
接下来通过对比两种算法对信噪比的影响来反映分数阶傅里叶四阶中心矩抗噪性。根据图6所示,分数阶傅里叶四阶中心矩抗噪性明显好于文献[4]算法,进而验证了式(41),说明噪声背景下本文算法的尺度差/时差估计较文献[4]算法得到较大提高。
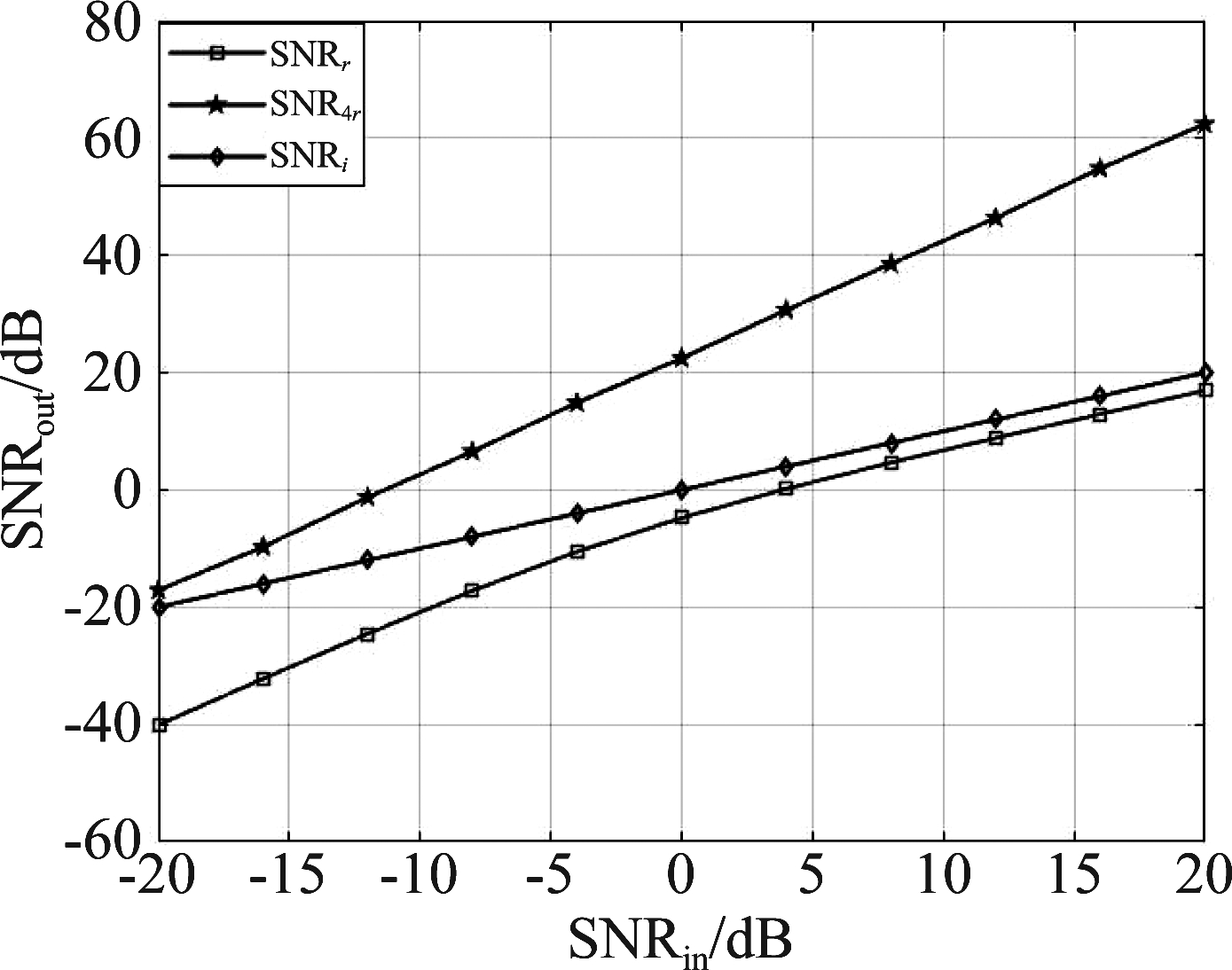
图6 输入和输出信噪比仿真图
Fig.6 Input and output signal to noise ratio simulation diagram
4.3 估计时间
3.3节对运算量进行了分析,考虑到两种方法的时差估计复杂度相同,因此,接下来利用两种算法进行尺度差估计的CPU占用时间来对两者的运算复杂度进行仿真对比。我们知道,同理于频域估计,延长采样时间同样有利于提高分数阶傅里叶域峰值位置的估计精度,而延长采样时间则必然导致样本数据点的增多。此外,缩小分数阶傅里叶变换角度步长,增大搜索角度个数,也会有利于提高分数阶傅里叶域最优角度的估计精度。即,大样本点数和多搜索角度直接关系到尺度差估计精度的提高。因此,本小节对比分析了不同采样点数和不同搜索角度个数条件下,进行一次尺度差估计两种算法所占用的CPU时间。从表2可以发现,本文算法较文献[4]算法在大采样点数和多搜索角度时候,CPU运行时间更短,也就是说,本文算法较文献[4]算法在估计的时效性上更有优势。
表2 CPU时间
Tab.2 CPU time
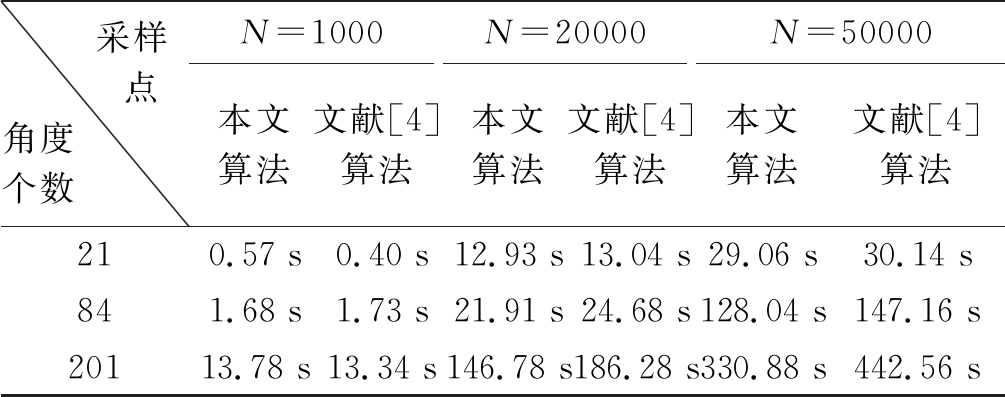
采样 点角度 个数 N=1000本文算法文献[4]算法N=20000本文算法文献[4]算法N=50000本文算法文献[4]算法210.57 s0.40 s12.93 s13.04 s29.06 s30.14 s841.68 s1.73 s21.91 s24.68 s128.04 s147.16 s20113.78 s13.34 s146.78 s186.28 s330.88 s442.56 s
5 结论
本文提出了基于分数阶傅里叶四阶中心矩的尺度差/时差估计算法,并从理论上分析了分数阶傅里叶四阶中心矩的抗噪性,可以发现其优于分数阶傅里叶变换的抗噪性,有利于提高低信噪比条件下的尺度差/时差估计精度。同时,所提算法通过将二维搜索变为一维搜索,降低了传统二维网格搜索算法带来的时间成本;并在算法实现上提出了分级搜索方式,进一步减少了一维搜索的复杂度。最后,通过仿真对比验证了上述结论。本文成果为下一步的多分量宽带线性调频信号尺度差/时差算法研究奠定了基础。
[1] RICHARD A. Electronic warfare target location methods[M]. Artech House, 2012.
[2] MACLEOD, MALCOLM D. Electronic Warfare Target Location Methods-Second edition[J]. Aeronautical Journal, 2014, 118(1202): 453.
[3] YU Wanting, YU Hongyi, DU Jianping, et al. Direct position determination for digital modulation signals based on improved particle swarm optimization algorithm[C]∥Ninth International Conference on Graphic & Image Processing, 2018.
[4] 杨林森, 张子敬, 郭付阳. 线性调频信号时/频差快速联合估计方法[J]. 信号处理, 2017, 33(6): 872- 879.
YANG Linsen, ZHANG Zijing, GUO Fuyang. Fast Algorithm for Joint TDOA/FDOA Estimation of Chirp Signals[J]. Journal of Signal Processing, 2017, 33(6): 872- 879.(in Chinese)
[5] 郭付阳, 张子敬, 杨林森. 基于尺度变换的宽带线性调频信号时差尺度差估计算法[J]. 电波科学学报, 2017, 32(4): 441- 448.
GUO Fuyang, ZHANG Zijing, YANG linsen. Scaling-based TDOA/SDOA estimation algorithm for wideband chirp signals[J]. Chinese Journal of Ratio Science, 2017, 32(4): 441- 448.(in Chinese)
[6] NAPOLITANO A. A New Signal-Selective Wide-Band Ambiguity Function[J]. European Signal Processing Conference, 2019, 18: 1-5.
[7] NAPOLITANO A. An Interference-Tolerant Algorithm for Wide-Band Moving Source Passive Localization[J]. in IEEE Transactions on Signal Processing, 2020, 68: 3471-3485.
[8] ZHANG Xin, LI Hongbin, LIU Jun, et al. Joint delay and Doppler estimation for passive sensing with Direct-Path interference[J]. IEEE Transactions on Signal Processing, 2016, 64(1): 630- 640.
[9] QIU T, WANG H, ZHANG Y, et al. Non-linear transform-based robust adaptive latency change estimation of evoked potentials[J]. Methods of Information in Medicine, 2002, 41(4): 331-336.
[10] NIU X X, CHING P C, CHAN Y T. Wavelet based approach for joint time delay and Doppler stretch measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 1111-1119.
[11] ALIEVA T, BASTIAANS M J. On fractional Fourier transform moments[J]. IEEE Signal Processing Letters, 2000, 7(11): 320-323.
[12] 臧义林, 于凤芹. 利用短时分数阶实现多分量信号分离[J]. 计算机工程与应用, 2014, 50(4): 211-214.
ZANG Yilin, YU Fengqin. Multi-component Chirp signal separation using pseudo Wigner-Ville distribution in short-time fractional Fourier domain[J]. Computer Engineering and Applications, 2014, 50(4): 211-214.(in Chinese)
[13] 吴宪岭, 朱伟强. 基于宽带模糊函数的时差时间尺度联合估计[J]. 航天电子对抗, 2011, 27(4): 50-53.
WU Xianling, ZHU Weiqiang. Joint estimation of TDOA and time-scale based on WBAF[J]. Aerospace Electronic Warfare, 2011, 27(4): 50-53.(in Chinese)
[14] 郭付阳. 无源定位中的时差、频差和尺度差估计[D]. 西安: 西安电子科技大学, 2017.
GUO Fuyang. TDOA/FDOA and SDOA estimation in passive localization[D]. Xi’an: Xidian University, 2017.(in Chinese)
[15] ALDIMASHKI O, SERBES A. Performance of Chirp parameter estimation in the fractional Fourier domains and an algorithm for fast Chirp-Rate estimation[J]. in IEEE Transactions on Aerospace and Electronic Systems, 2020, 5(56): 3685-3700.
[16] CAO Fan, WANG Shuxun, WANG Fei. A New Time-Frequency Analysis Method of Multi-Component Chirp Signal[C]∥International Conference on Signal Processing. IEEE, 2006.
[17] 刘建成, 刘忠, 王雪松, 等. 高斯白噪声背景下的LFM信号的分数Fourier阶域信噪比分析[J]. 电子与信息学报, 2007, 29(10): 2337-2340.
LIU Jiancheng, LIU Zhong, WANG Xuesong, et al. SNR analysis of LFM signal with Gaussian white noise in fractional[J]. Journal of Electronics and Information Technology, 2007, 29(10): 2337-2340.(in Chinese)
[18] BARBAROSSA S. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1511-1515.
[19] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 297-300.
TAO Ran, DENG Bing, WANG Yue. Fractional Fourier transform and its application[M]. Beijing: Tsinghua university Press, 2009: 297-300.(in Chinese)
[20] HAN Jun, WANG Qian, QIN Kaiyu. The Non-stationary Signal of Time-Frequency Analysis Based on Fractional Fourier Transform and Wigner-Hough Transform[J]. Mechatronics and Automatic Control Systems, 2014, 237: 1047-1054.

