1 引言
变换域通信系统(Transform Domain Communication System, TDCS)是二十世纪末提出并发展的一种新型抗干扰通信,具有隐蔽性和保密性强的优点,能抵抗多种形式的干扰,能够应用在频段拥挤的通信场合,特别是在保密通信和军事通信中具有很大的应用潜力。
TDCS在频域进行通信波形设计,通过频谱空洞感知、伪随机相位生成等过程,构造出具有类噪声性的时域通信波形——基函数。其中,伪随机相位生成是一个重要环节,很大程度决定了基函数的隐蔽性、保密性以及多址通信等方面的性能。伪随机相位是在PN序列的基础上产生的,将其通过移位寄存器输出,进而映射成一串伪随机相位序列,以此赋予了基函数类噪声性。传统基函数生成方法中,其伪随机相位通常由m序列、gold序列等PN序列产生[1-2],但由于其正交序列集数量有限,使得传统基函数复杂度低,容易被破译。混沌序列因其伪随机性能好、抗破译能力强的特点,在保密通信中已有深入的研究[3- 4]。但是在混沌的数字化实现时,其时间和空间上都被离散化,使得任何数字混沌系统都将陷入一个周期,与真实轨道完全不同,即混沌系统不再混沌[5]。这种混沌退化现象造成序列复杂度降低,并且退化现象越严重,序列复杂度越低,保密系统越容易被入侵。如何减小数字混沌系统(Digital chaotic systems, DCSs)的退化是一个难题,通常的方法是使用更高的计算精度[6]、多个DCSs级联[7]、DCSs扰动[8]、DCSs切换[9]、误差补偿[10]等。其中,前两种方法只能增加循环周期,并未对DCSs退化问题产生较大改进;第三种方法能改善DCSs退化,但和扰动源密切相关;第四种方法能延长循环周期,且在一定切换规则下能降低序列互相关性。上述方法都只是对序列的统计规律产生了改进,并未对混沌系统数字化过程中的退化问题提出较为有效的解决方案。第五种方案则能使补偿后的DCSs较大程度恢复原始混沌系统的属性,从而改善DCSs的退化,但由于参数空间较小,且补偿DCSs性能难以达到理想状态,因此应用到TDCS中时,基函数仍然难以达到遍历和高复杂度。反馈控制方法则是上述方法的综合,通过适当的反馈控制方案设计,能较大程度改善DCSs退化,并使DCSs序列具备良好的伪随机性。
在上述研究基础上,本文将反馈控制方法引入混沌基函数生成。在传统混沌序列基础上,使用模值计算提高系统复杂度;加入随机切换因子,改善基函数伪随机相位的遍历性;并从相关性,遍历性、近似熵(Approximate Entropy, APEN)等角度对基函数的安全通信方面进行分析。仿真结果表明,该方案能较大程度改善混沌基函数数字化形成过程中的退化问题,提高了TDCS通信的安全性。
2 改进型反馈控制混沌序列原理
混沌是指确定系统中出现的类似随机的行为,目前在离散系统中,关于混沌现象的描述有多种理解,其中Devaney混沌定义被普遍认可[11],概括起来离散混沌特点可描述为对初值敏感依赖、具备拓扑传递性和周期点稠密。
由于系统的确定性和不确定性并存,对于系统演化难以预测,所以通常使用Lyapunov指数描述系统的敛散性。在一个离散系统中,当Lyapunov指数出现正值时混沌现象出现,系统具备上述三个特点。
混沌系统在数字化过程中,计算机的运算精度和取值精度是有限的,因此,DCSs系统的迭代方程可表示为式(1)
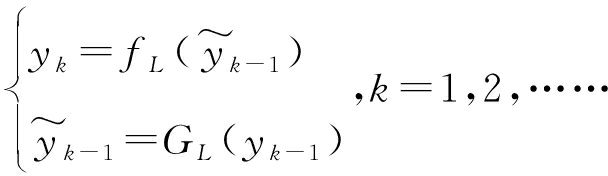
(1)
式中, fL为运算精度为L bits时的f映射;
为yk的L bits精度取值。在该系统中,运算精度和取值精度相等,由于混沌系统最高次幂n通常大于1,这使得迭代结果的精确度受限,且系统性能发生改变,加剧混沌退化。
对于非线性系统,文献[12]提出引入控制因子和模1运算,调节系统运行,提高其混沌性能,如式(2)
(2)
式中,g为迭代系统映射函数;uk为控制因子;常数c、β满足:
控制因子的引入,使系统取值范围向外扩散,而模值操作则将系统取值向内回缩。这样所引起的伸缩效应和折叠效应,使得Lyapunov指数严格为正,即实现Devaney混沌。
对于Devaney混沌系统f=g+u,在进行有限精度取值的数字化实现时,若能完全保持其系统特性,则不会影响其混沌效应[13],即:若序列xk为Devaney混沌序列,则
也为Devaney混沌序列,如式(3)
(3)
式中,GL(·)为L bits精度取值运算。
根据式(3)可得,DCSs可表示为
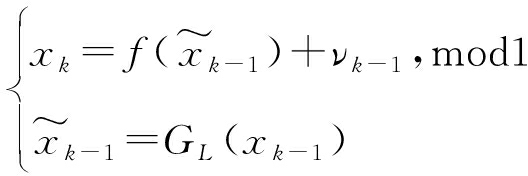
(4)
式中,νk为反馈因子,使得混沌系统数字化时,特性保持不变。同时,若混沌系统的最高次幂为n,取值精度为L bits,则最小运算精度需为nL bits才不影响序列的精确度。
除去不连续点,结合式(3)、式(4)可得
(5)
式中, f ′(·)为f函数的一阶导数。
在xk与相差不大时,引入随机数s∈(0,1),对轨道产生随机切换,对系统性能影响较小,如式(6)
(6)
结合式(2)、式(4)、式(6)可得,在nL bits运算精度下,L bits精度的系统输出可表示为
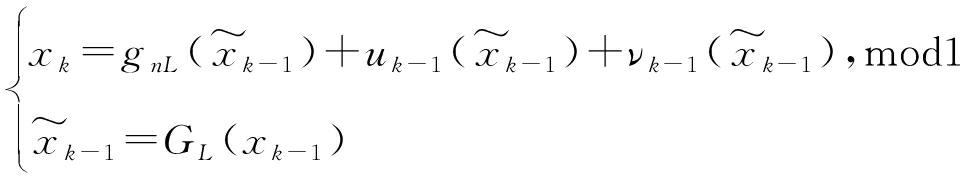
(7)
式中,xk为中间变量;gnL(·)为nL bits的g映射;uk(·)、νk(·)的运算精度都为nL bits。可以看出,该系统中当uk(·)较小时,反馈因子对系统性质起主导作用,使得其性质更接近于g映射;反之,则控制因子对系统性质起主导作用,使系统更加发散。
下面以Logistic序列作为基底,生成改进型反馈控制混沌序列,分析其运算量。Logistic序列迭代公式为g(x)=μx(1-x),其中μ∈(3.5699456,4]时,系统为混沌状态。若产生长度为N的改进型反馈控制Logistic序列,一共需3N次乘法,3N+1次加法运算;而Logistic序列则需2N次乘法,N次加法。两者相比,改进型反馈控制Logistic序列的运算量稍大,但仍与Logistic序列处于相同数量级。因而在N较小的情况下,仍能满足时效性需求。
3 TDCS概述
TDCS综合了频谱认知技术和扩频通信技术的特点,通过寻找频谱空洞避开干扰频段,同时用伪随机相位为可用频段编码,生成具有类噪声性的通信波形—基函数。TDCS具备良好的抗干扰、隐蔽和保密等潜能,最早出现在军事通信领域[14],而近年来,其在民用领域的可靠信令传输,多址通信等方面也发挥着越来越重要的作用[15-16]。
3.1 TDCS原理
TDCS原理框图如图1所示,假设通信双方处于相同的电磁环境下,则通过相同的规则生成相互匹配的基函数进行通信。其生成过程主要包括幅度谱和伪随机相位生成,功率控制以及反傅里叶变换。
幅度谱生成部分,如果收发双方处于相同的频谱环境,则通过频谱感知可获取相差不大的环境频谱密度分布。对环境频谱进行N点采样,与预先设定的门限值比较,划分出可用频点和不可用频点,并用1或0进行标记。其中,低于门限值的频段可用,标记为1;高于门限值的频段不可用,标记为0。通过N点频谱标记,获取幅度谱A(n)。
获取幅度谱后,还需要为每一个幅度谱采样点分配一个相位值才能形成完整的信号波形,该相位值即是伪随机相位ejθ(n)。伪随机相位是由伪随机序列经过线性映射产生的,其具体形成过程将在3.2节详细描述。
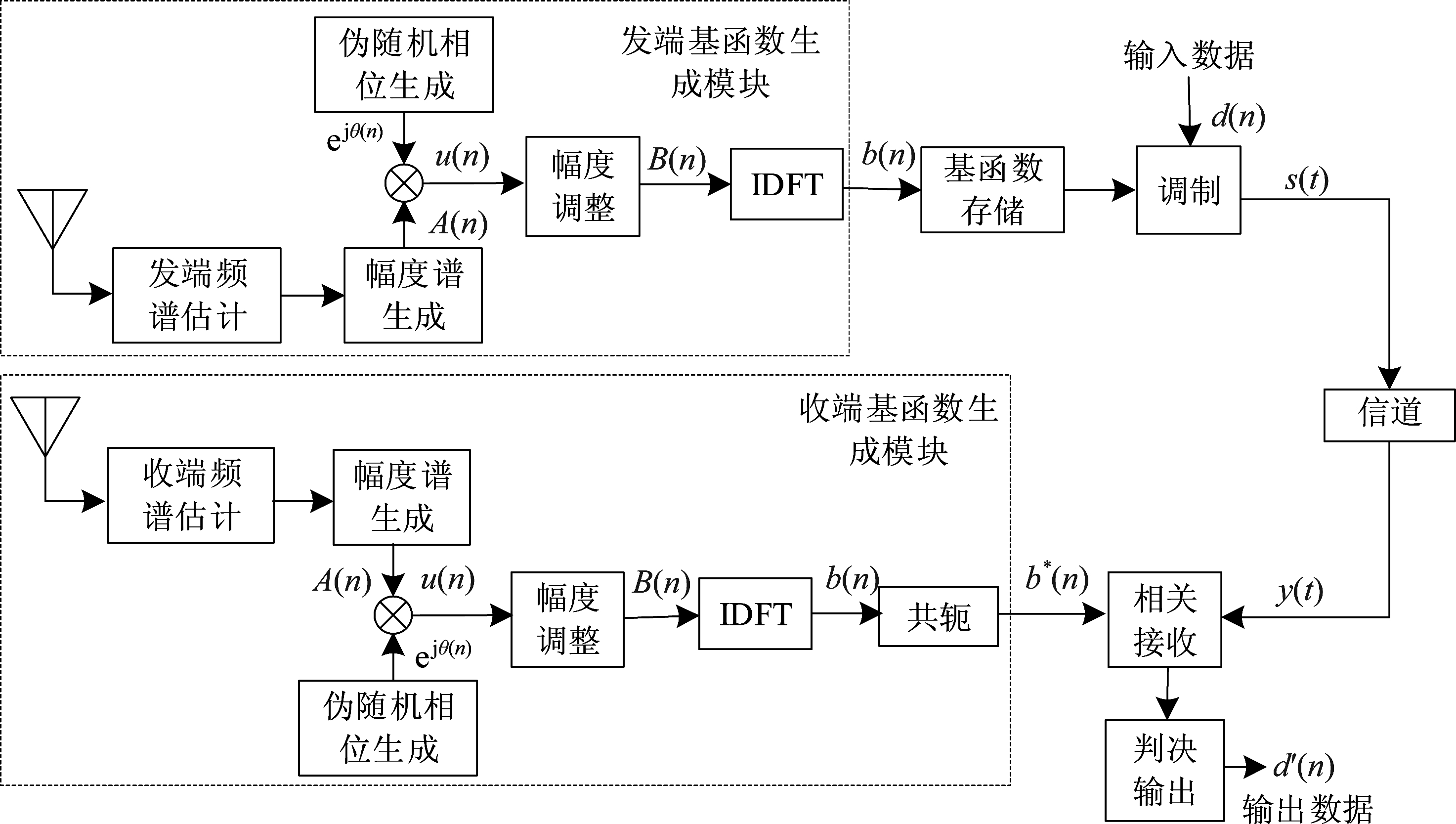
图1 TDCS原理框图
Fig.1 Functional block diagram of the TDCS
TDCS所处的频谱环境通常是随时间不断变化的,这种变化将导致幅度谱码重变化,从而使得信号功率不稳定。因此,为了保证TDCS在不同时间能以稳定功率发送信号,需要对其进行功率控制。功率控制因子为
其中NC为幅度谱中标记为1的频点数。
在完成幅度谱生成、伪随机相位分配、功率控制等一系列过程以后,将信号进行反傅里叶变换,返回到时域,便得到基函数波形b(n)。此时,b(n)同时具备了抗干扰、类噪声性、码分多址等方面的性能特点。
与传统通信系统不同的是,TDCS的调制没有使用载波,而是以设计好的基函数为基本调制单元对数据进行调制。在发送端,对基函数进行功率控制,使信号功率达到稳定;然后,采用CCSK或PSK调制方式对基函数调制发送。在接收端使用与发送端匹配的基函数进行相关接收。
基函数具有天然的隐蔽和保密通信潜能。一方面,基函数的类噪声性使得通信难以察觉,具有良好的隐蔽效果;同时,非目标台站在不知道发送端的基函数生成规则时,无法实现数据拦截,因此具有较强的保密效果。下面介绍混沌伪随机相位生成原理。
3.2 混沌伪随机相位生成
伪随机相位是根据取值为0和1的伪随机序列生成的。由于混沌序列在数值上连续,在进行相位映射前,首先要将其转化为取值为0和1的PN序列。通常根据混沌序列取值范围的中值,将取值空间划分为两个区域,其中一个区域的点可统一表示为0,则另一个区域统一表示为1,从而获取PN序列bn。
使bn通过移位寄存器,在移位寄存器上的r个抽头将通过的数值输出,并线性映射得到一个相位值ejθ;随后,bn移位l bits,用相同映射方式生成下一个相位值;经过N次移位后,得到伪随机相位序列a(n)=ejθ(n),如图2。
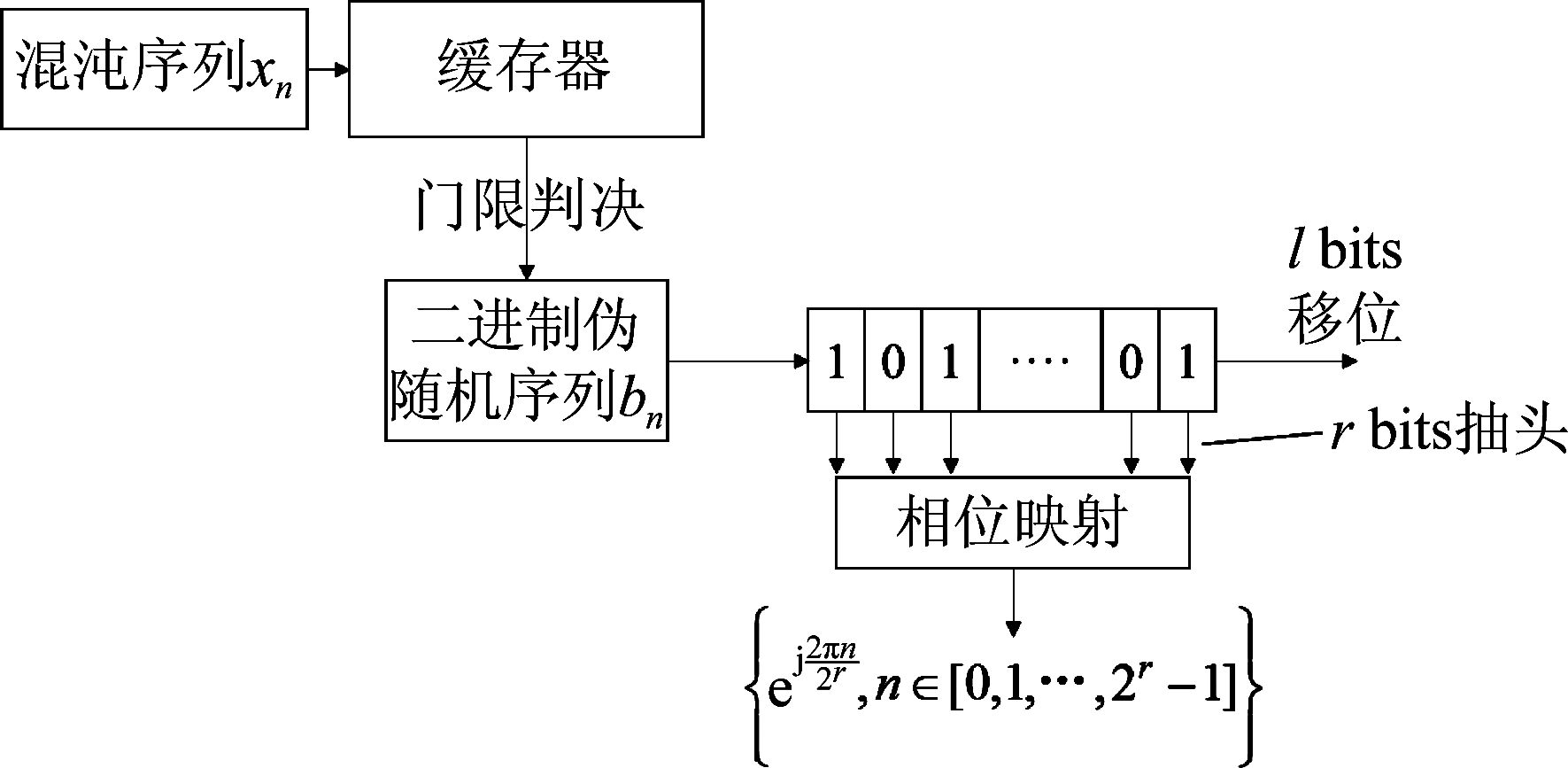
图2 混沌伪随机相位生成原理框图
Fig.2 Block diagram of chaotic pseudo-random phase generation principle
b(n)是将a(n)与A(n)逐位相乘并取反傅里叶变换得到的时域波形,如式(8)
b(n)=IDFT(A×ejθ)=
(8)
传统方法利用m序列、gold序列生成伪随机相位,但序列集数量有限,因而容易被破译。而混沌序列因其对初始值敏感依赖,可形成大量随机序列集,因此形成的基函数在抗破译性方面比传统方法具有更大的优势。下节将在基于第2节中的改进型反馈控制混沌序列生成基函数的基础上,对其相关性、复杂度等方面性质进行讨论。
4 改进基函数性能分析
本节将从隐蔽性及保密性等方面,对改进基函数性能进行讨论分析。
4.1 延时自相关
信号一般具有较强的自相关性,从信号检测角度,相关检测法常用来检测未知信号是否存在。通过延时采样信号与初始采样信号相关卷积,计算出能量值,若能量值高于判定阈值,则认为存在信号,反之,认为不存在信号。因此,延时自相关能量越低,信号被检测到的可能性就越小,隐蔽性越高[17]。
为定量描述基函数的隐蔽性,定义延时自相关C为基函数部分采样信号与其延时采样信号做相关卷积的能量平均值,如式(9)
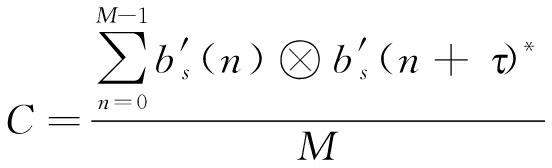
(9)
式中, τ为延时;⊗为卷积运算;
为长度为N基函数中,取前M(M<N)个采样点的初始采样信号;
为一定时延后,再对基函数取相同长度采样,得到的延时采样信号。
4.2 遍历性
遍历性是伪随机序列的必要条件,同样对于伪随机相位,当序列长度足够大时,序列元素应该能够覆盖整个相角空间。由3.2节可知,理想状态下,采用r个抽头对二进制伪随机序列进行相位映射时,将产生2r种相位,并均匀分布在整个相角区间
但DCSs混沌退化使得相位的覆盖范围收缩,序列无法遍历相角空间中各个元素。如图3所示,相位生成中的相位种类数小于2r种,是整个相角空间的子集。
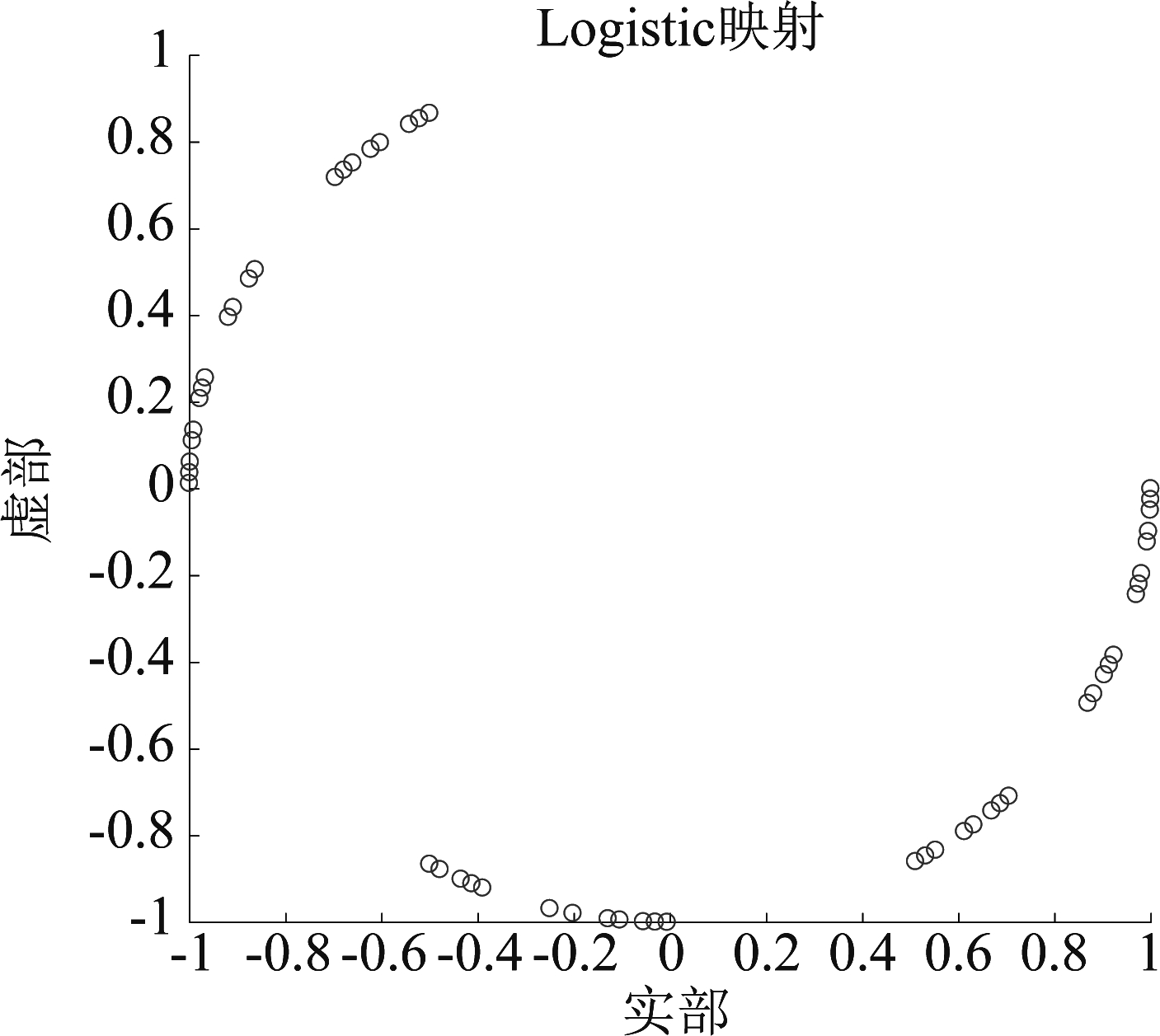
图3 Logistic基函数相角分布(系数μ=3.8,运算精度16位)
Fig.3 Logistic basis function phase angle distribution (coefficient μ=3.8, operation precision 16 bits)
引入相位覆盖率η表示基函数相位在整个相位空间的覆盖程度,如式(10)
(10)
式中,r为抽头数;p为伪随机序列足够长时,通过相位映射所形成的相位种类数。
η介于0和1之间,数值越大,表明伪随机相位在整个相角空间的覆盖程度越高,相位跳变规则通常越复杂。理想条件下,基函数相位覆盖率可达到1,遍历相角空间的所有元素。
4.3 近似熵(Approximate Entropy, APEN)
高相位覆盖率只是表明基函数复杂度高的一个必要条件,为更精确描述基函数的复杂度,还需进一步考察其跳变规则。APEN是一种在少量样本数据中估计系统复杂度的量化指标,可区分低维确定性系统、周期和多重周期系统、高维混沌系统、超混沌系统和混合系统等。参考文献[18],基函数近似熵计算方法如下:
1)根据3.2节所述原理,生成基函数序列b(n),n=0,1,…,N-1;
2)将序列b(n)以m位为一组,分成N-m+1组序列集{B(1),…,B(N-m+1)},其中B(i)=[b(i),…,b(i+m-1)]T,i=1,2,…,N-m+1;
3)定义组距d[B(i),B(j)]=max(|b(i+h)-b(j+h)|),h=0,1,…,m-1;设定阈值r,对于每组数据,统计d[B(i),B(j)]<r的个数,将其与总组数之比记为
其中j=1,2,…,N-m+1且j≠i;
4)定义
计算φm(r)与φm+1(r),则基函数近似熵为
根据统计规律,一般取m=2,r=0.1～0.2σ,其中σ为基函数标准差。符合近似熵的一般性质,基函数近似熵为非负数,是对基函数复杂度的度量。由于其绝对值没有明显的含义,因此可使用基函数近似熵对比考察不同基函数的复杂度,复杂度越高,近似熵则越大。
5 仿真分析
对比分析Logistic基函数及改进型反馈控制Logistic基函数,从基函数的延时自相关、相位覆盖率和近似熵等角度模拟仿真,分析其隐蔽性和安全性。
由于幅度谱对基函数安全通信方面影响较小,不妨令频谱带宽为1 kHz的幅度谱A(n),采样点数N=1024,且采样点全为1。为方便仿真,设置计算机的运算精度为16 bits,序列取值精度L=8 bits。混沌序列转化为PN序列的判决门限为0.5。移位寄存器抽头数r=8,每次相位生成移位数k=1。
仿真1 延时自相关仿真
对于logistics映射,选取μ=4时,系统的混沌特性最好,在该条件下,分析两种基函数的延时自相关特性。在(0,1)之间随机取1000个数作为初始值x0,分别产生长度为N的伪随机相位序列,计算延时自相关的平均值,如图4。
据图可知,改进型基函数的延时自相关曲线接近于0,而传统方法接近135,低延时自相关使得信号更难被敌军检测,因此在隐蔽通信方面,改进型方法具有更大优势。
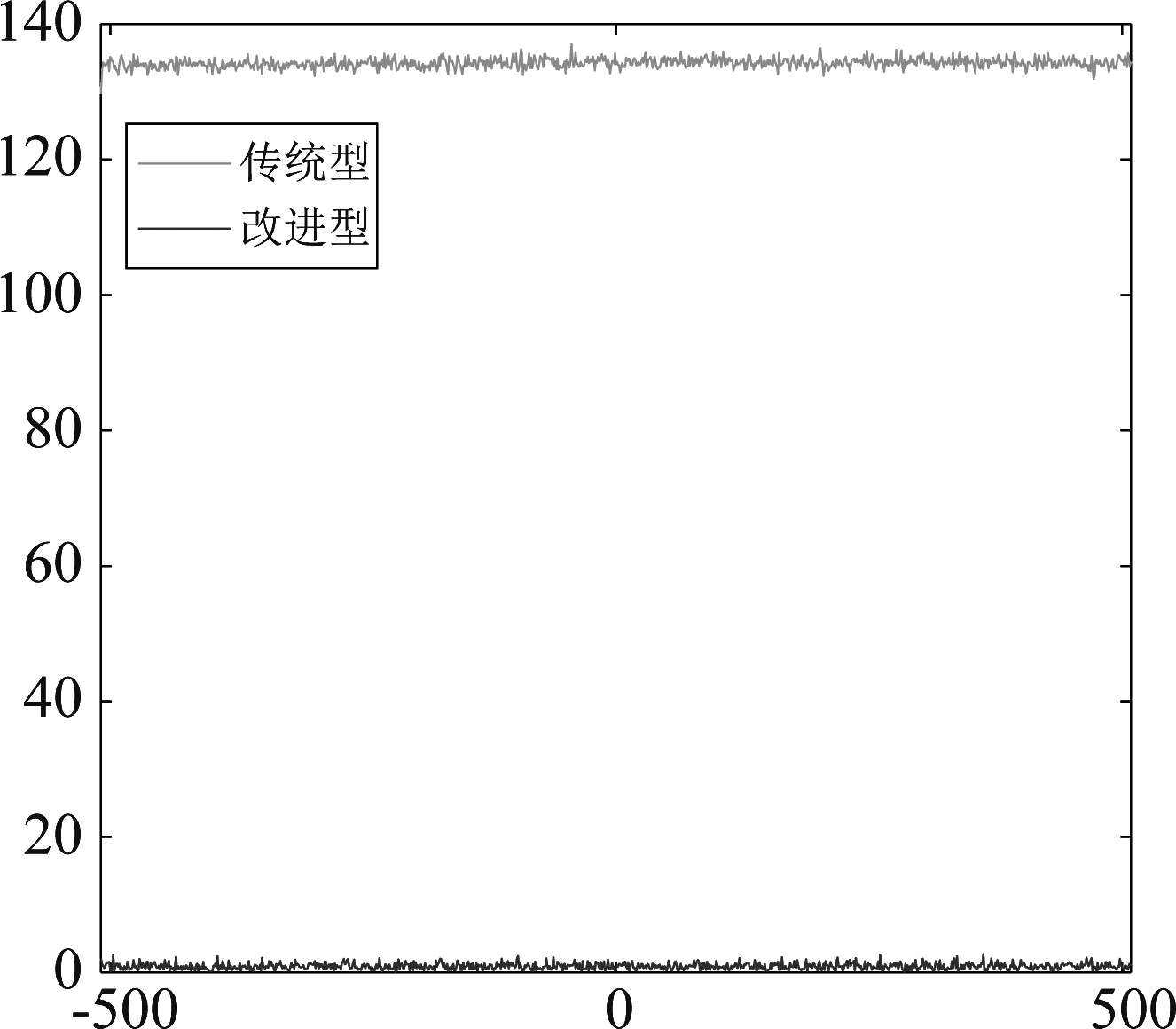
图4 基函数延时自相关的变化规律
Fig.4 The variation rule of delay autocorrelation of basis function
计算量方面,传统型方法需0.018965 s,而改进型方法则需0.023343 s,改进型方法所用时长略大于传统型方法,但两种方法用时都较短,能较好的满足TDCS应用的实时性需求。
仿真2 基函数复杂度仿真
为了和3.2节的Logistic基函数对比,本仿真选取参数μ=3.8,得到改进型反馈控制Logistic基函数相角分布,如图5。
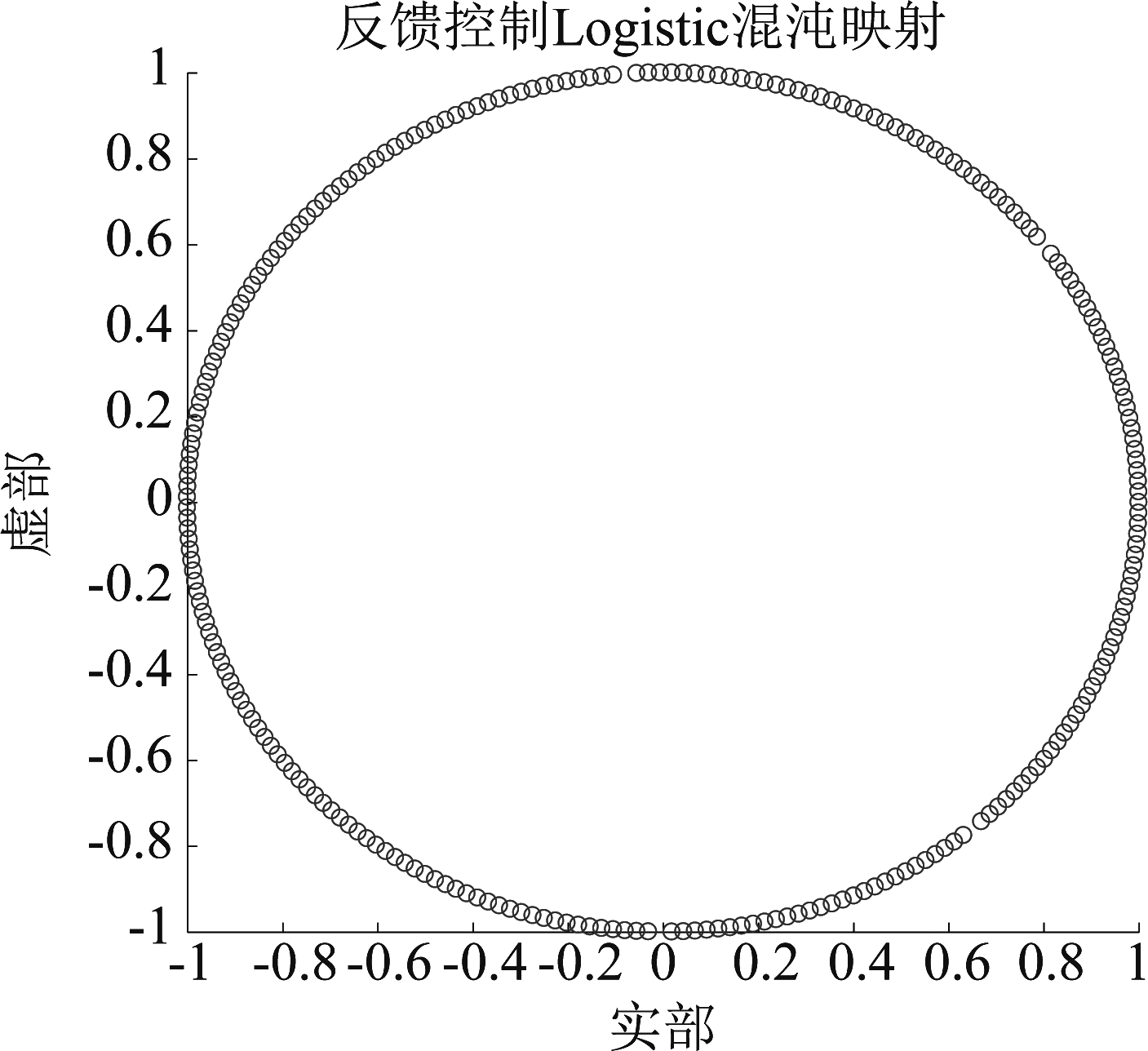
图5 改进型反馈控制Logistic基函数相角分布
(系数μ=3.8,运算精度16位)
Fig.5 Phase angle distribution of Improved feedback control Logistic basis function (coefficient μ=3.8, operation precision 16 bits)
对比分析图3和图5,在运算精度和基函数生成方式相同时,改进型方法比传统方法相位覆盖率有较大提升,基本上实现了相位全覆盖。
下面在参数μ选取不同值时,分别在初始值x0∈(0,1)之间随机取1000个数,进行1000次仿真,统计两种方法的相位覆盖率平均值,如表1。
表1 基函数相位覆盖率(%)
Tab.1 Basis function phase coverage(%)
μ3.63.653.73.753.83.853.93.954传统型3.15.112.518.420.735.941.855.998.4改进型98.197.398.198.197.398.898.898.498.4
从统计结果可知,传统型基函数的相位覆盖率随着参数μ的增大而增大,在μ=4时达到最大,接近于1;而改进型反馈控制混沌基函数的相位覆盖率一直稳定保持较高水平,且接近于1。由此可知,改进型方法相比于传统型方法,在保持较大相位覆盖率方面具有更大优势,且稳定性更强,码字种类更多。
在参数μ接近于4时,两种方法的相位覆盖率都能稳定保持较高水平,因此在相位覆盖率达到相同水平时,分析两种方法的近似熵。保持其他条件不变,在μ∈[3.95,4]时,计算不同参数下的基函数近似熵,并做归一化处理,如图6。
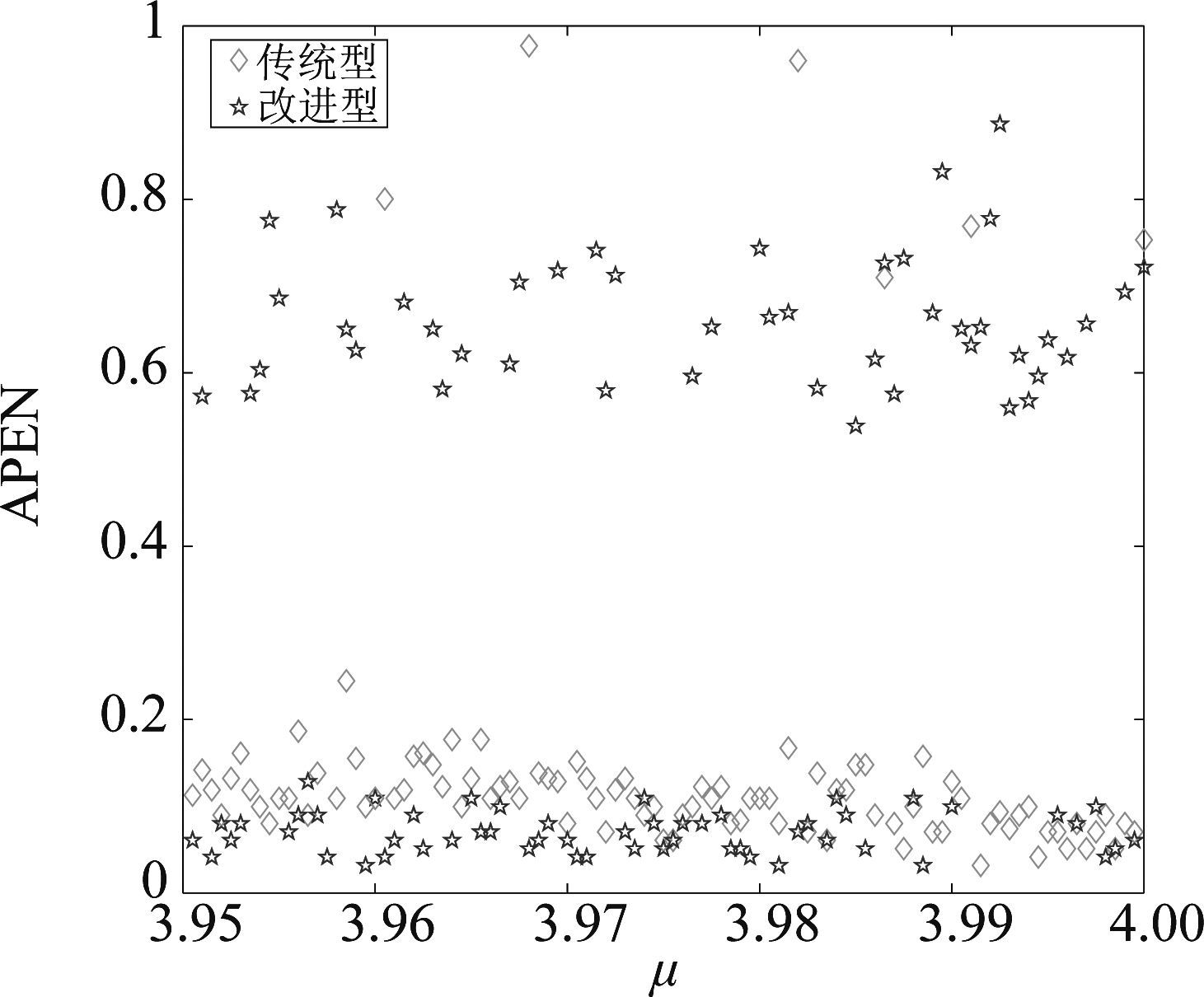
图6 基函数近似熵
Fig.6 Approximate entropy of the basis function
由图6可知,在改进型方法和传统方法的相位覆盖率相差不大的情况下,其复杂度仍存在较大差异。传统方法APEN大部分分布在0到0.2之间,而在0.6到1之间存在极少的野点;而改进型方法则有着两极分化的趋势,几乎一半的点分布在0到0.2之间,而另一半的点则分布在0.6到0.9附近。由此可以看出,改进型方法比传统方法有更多的点分布在0.6到1之间,因此改进型方法更容易产生高复杂度码组。
6 结论
本文提出了改进型反馈控制混沌基函数的生成方法,缓解在混沌系统数字化实现时出现的混沌退化问题,提高基函数的安全性;采用基函数延时自相关、相位覆盖率、近似熵等指标对基函数的相关性及复杂度等方面进行评价,定量分析TDCS通信的隐蔽性和安全性。仿真结果表明,本文所提出的改进型基函数延时自相关较低、复杂度较高。但是,改进型方法并未使所有点的近似熵都处于较高水平,因此在使用基函数前,还需对其复杂度进行考察。下一步可对随机数s的选取进行改进,使得所有点的近似熵都处于较高水平。
[1] SWACKHAMMER P J, TEMPLE M A, RAINES R A. Performance simulation of a transform domain communication system for multiple access applications[C]∥IEEE Military Communications Conference Proceedings. IEEE, 1999: 1055-1059.
[2] 徐兵政, 任清华, 孟庆微, 等. 变换域通信系统最优误码率多元幅度谱编码算法[J]. 信号处理, 2019, 35(1): 8-15.
XU B Z, REN Q H, MENG Q W, et al. Optimal bit error rate multiple amplitude spectrum coding algorithm for transform domain communication system[J]. Journal of Signal Processing, 2019, 35(1): 8-15.(in Chinese)
[3] LING G, LI S. Chaotic spreading sequences with multiple access performance better than random sequences[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(3): 394-397.
[4] 陈尚春. 现代信息安全与混沌保密通信应用研究的进展[J]. 信息记录材料, 2018, 19(9): 2- 4.
CHEN S C. Research progress of modern information security and chaotic secure communication[J]. Information Recording Materials, 2018, 19(9): 2- 4.(in Chinese)
[5] CHIRIKOV B V, VIVALDI F. An algorithmic view of pseudochaos[J]. Physica D Nonlinear Phenom, 1999, 129(3- 4): 223-235.
[6] WHEELER, DANIEL D, MATTHEWS R, et al. Supercomputer investigations of a chaotic encryption algorithm[J]. Cryptologia, 1991, 15(2): 140-151.
[7] 陈紫强, 舒亮, 谢跃雷. 一种高安全性的级联型混沌扩频序列[J]. 电讯技术, 2016, 56(5): 476- 482.
CHEN Z Q, SHU L, XIE Y L. A cascade chaotic spread spectrum sequence with high security[J]. Telecommunication Engineering, 2016, 56(5): 476- 482.(in Chinese)
[8] LI C, CHEN Y, CHANG T, et al. Period extension and randomness enhancement using high-throughput reseeding-mixing PRNG[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2012, 20(3): 385-389.
[9] 王忠林, 刘树堂. 一个切换Lorenz混沌系统的特性分析[J]. 重庆邮电大学学报, 2017, 29(1): 68-74.
WANG Z L, LIU S T. Characteristic analysis of a switched Lorenz chaotic system[J]. Journal of Chongqing University of Posts and Telecommunications, 2017, 29(1): 68-74.(in Chinese)
[10] HU H, XU Y, ZHU Z. A method of improving the properties of digital chaotic system, Chaos Soliton[J]. Chaos Solitons & Fractals, 2008, 38(2): 439- 446.
[11] DEVANEY R L. An Introduction to Chaotic Dynamical Systems[M]. New York, Addison-Wesley Press, 1989: 48-50.
[12] CHEN G, LAI D. Feedback anticontrol of discrete chaos[J]. Int J Bifurcat Chaos, 1998, 8(7): 1585-1590.
[13] DENG Y, HU H, XIONG W, et al. Analysis and Design of Digital Chaotic Systems With Desirable Performance via Feedback Control[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(8): 1187-1200.
[14] ANDREN A F. Low probability of intercept communication system[P]. U.S.: 5029184, 1991．
[15] HU S. TDCS-IDMA System for Cognitive Radio Networks With Cloud[J]. IEEE Access, 2018, 6: 20520-20530.
[16] MA S, HU S, ZHU X, et al. A Hybrid Clustering Strategy for Transform Domain Communication System[J]. IEEE Access, 2019, 7: 92561-92571.
[17] ZENG Y, LIANG Y. Covariance Based Signal Detections for Cognitive Radio[C]∥2007 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2007: 202-207.
[18] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences of the United States of America, 1991, 88(6): 2297-2301.
