1 引言
波达方向(DOA: direction of arrival)估计是阵列信号处理领域的关键技术,其广泛应用于雷达,声纳和无线通信等领域。传统的DOA估计方法特指一类基于线性模型的方法[1-3],这类方法利用已知的阵列采样数据,通过建立波达方向和阵列输出之间的线性映射模型来恢复信号的入射角度。然而,由于非理想情况下实际的阵列模型存在误差,例如通道相位不一致,阵元位置误差以及阵元之间的耦合,基于线性模型的方法的估计性能会严重退化[4]。为了克服模型误差引起的估计性能下降,一些基于非线性模型的方法被提出,其中包括最大似然估计方法[5],压缩感知方法[6]和稀疏贝叶斯学习(sparse Bayesian learning:SBL)[7]等方法。稀疏贝叶斯学习方法利用信号在空域是稀疏的这一先验知识,将非线性参数估计问题转化为线性模型下的稀疏信号恢复问题求解。由于基于非线性模型的方法需要迭代求解最优解,因此这类方法的计算复杂度高。另外,稀疏贝叶斯学习方法还涉及超参数的选取,而超参数的选择与信噪比相关。
最近,随着深度学习的快速发展,深度卷积神经网络(DCNN: deep convolution neural network)被用于DOA估计[8-11]。其思想是将DOA估计问题看作分类问题,通过把参数空间均匀离散为不同的类别,然后利用DCNN分类器学习阵列采样数据到参数空间的逆映射[12-13]。因此,DCNN分类器用于DOA估计有以下几个优点:一是由于DCNN分类器是离线训练的,因此一旦训练完成能够实现DOA的实时估计;二是DCNN分类器对阵列模型误差不敏感,其可以通过训练集增广的方式学习和适应阵列误差;三是相比于稀疏贝叶斯学习等方法,不涉及超参数的选取。文献[10]和文献[11]基于信号在空域是稀疏的这一先验知识,利用DCNN分类器去学习稀疏信号恢复的过程。然而,由于采用了标签为one-hot编码的分类器,当分类器的类别数增大时,网络的参数量会急剧增加,因而需要占用巨大的计算资源来训练网络,进一步导致训练网络的难度大大增加甚至现有的计算平台无法实现网络的训练。文献[9]提出了一种两级DCNN分类器框架。该框架的第一级采用一个自编码网络用于整个参数空间粗划分,相当于一个空域滤波器组。第二级为多个类别个数较小的相同的DCNN分类器,每个分类器分别级联在自编码网络的每个输出,从而进一步对每个子空域进一步精细的划分类别。虽然相对于大规模分类问题这种分类框架可以大大降低分类器网络的复杂度并且并行独立地训练每个小分类器能够大大降低了网络训练所需的计算资源,但是由于空域滤波器组是无交叠的且其中的每个子滤波器的幅度响应不理想,因此两个子滤波器之间存在盲区或间隙。当信号入射到盲区时,分类器无法完成DOA估计。
本文基于大规模分类网络难以训练这一事实,将one-hot标签的分解成多个长度为质数的小标签,对应每个小标签设计一个小的分类器。然后利用多个类别互质的小分类器通过离线训练学习从阵列采样到参数空间的逆映射。最后,联合使用多个互质的小分类器的输出重构原始one-hot标签。另外,本文提出的互质分类器满足两个很好的性质:一是类别的高可分性;二是分类器的独立性。仿真表明,相比于one-hot分类器,互质分类器具有更少的参数量并且更易训练。互质分类器比one-hot分类器以及稀疏贝叶斯学习方法的估计精度更高。
2 问题描述
2.1 阵列模型
考虑一个具有M个阵元的理想均匀线阵(uniform linear array,ULA),阵元之间的间距为半波长。假设有K个远场窄带信号分别从角度θ1,...,θK入射,则L个快拍的阵列采样输出可以表示为:
Y=AX+E
(1)
其中Y∈CM×L和E∈CM×L分别表示阵列输出矩阵和加性高斯白噪声矩阵。X∈CK×L表示信号幅度矩阵,A=[a(θ1),a(θ2),...,a(θK)]表示阵列流型矩阵。其中,a(θk)=[1,ejπsin(θk),...,ejπ(M-1)sin(θk)]T表示第k个信号的导向矢量。根据公式(1),已知阵列输出矩阵Y和阵列的几何结构,需要恢复出信号的波达方向,θ1,...,θK。稀疏重构理论表明,假设信号在空域是稀疏的并将空域参数空间(-90°,90°]离散划分成N个栅格
通过构造过完备字典
估计问题可以转化为过完备字典
下的稀疏信号重构问题。已有理论表明,深度卷积神经网络能够学习阵列输出到稀疏信号的逆映射。然而,在低信噪比条件下,Y受到严重的噪声污染,并且由于实际中每次用于DOA估计的快拍数可能不同,因此Y不能直接用于网络训练。考虑到阵列采样输出Y中不同采样快拍之间具有联合稀疏性,需要根据已知稀疏先验进行特征提取。
2.2 特征提取
首先,对Y实施奇异值分解(singular value decomposition, SVD)可以得到:
(2)
其中,Dr=diag{σ1,...,σr}和DM-r=diag{σr+1,...,σM}表示奇异值矩阵,r表示协方差矩阵
的秩并且奇异值的大小满足:σ1≥...≥σr≥σr+1=...=σM=σ。矩阵U∈CM×M和矩阵V∈CL×L的列向量分别表示左奇异向量和右奇异向量。向量ui∈CM,i=1,...,M,又称为矩阵Y的特征向量并且有以下定理:
定理1 令K个远场窄带信号入射到包含M个阵元的阵列,与之相关的阵列流型矩阵的秩为K并且协方差矩阵的秩为r,r≤K。假设是加性高斯白噪声,那么对于相干与非相干信号源都有:
(3)
其中αr(k)表示线性组合因子。定理1的证明参考文献[14],本文在此忽略。定理1表明,较大奇异值对应的特征向量包含所有信号的波达方向信息。因此,考虑构造如下向量:
(4)
显然,向量
中包含所有信号的波达方向信息。由于是信号子空间的线性组合,因此与噪声子空间正交。与文献[10]直接将协方差矩阵矢量化作为训练数据不同的是,本文将作为训练数据完成了去噪,实现了特征增强。虽然文献[11]也通过提取信号子空间实现特征增强,但是其训练数据的维度为r,相比本文训练数据的维度为1,会增加分类器网络的复杂度。
2.3 构造训练集
为了构造训练集,需要对每个训练样本添加对应的one-hot标签。假设将空域参数空间按间隔Δθ均匀划分成N个类别,那么标签h的长度为N。当
时,h对应位置处的元素取值为1,否则为0。考虑空域范围[θstart,θend],则
(5)
如果信号的入射角度为θk,h中取值为1的位置个数为
(6)
one-hot标签表示为
(7)
将训练数据和标签一一对应,可以构造训练集
其中,
和
分别表示训练数据的实部和虚部。由于N≫M,所以随着N的增加网络的复杂度会超线性增加,训练集中的标签也需要占用大量的存储资源。因此,本文考虑将标签分解为多个类别数为质数的小标签,使用多个互质的小分类器替代one-hot分类器解决大规模分类问题。互质分类器的设计在下节中。
3 互质分类器
根据信息论理论,如果使用分类数为q的分类器完成N分类问题,q<N,那么至少需要「logqN⎤个q分类器。例如,对于一个N=120类的分类问题,至少需要两个类别数为13的小分类器。本文考虑将n 个小分类器的类别设置为互质的数,但是qi,i=1,...,n,设置为质数并不是必要的,本文后面将会证明设置为质数会使得互质分类器满足两个良好的性质。
3.1 标签分解
首先定义一组标签分解函数fi:ΩN→Ωqi,i=1,2,...,n,n≥「logqN⎤。其中集合ΩN={0,1,...,N-1}表示one-hot分类器的标签类别集合,集合Ωqi={0,1,...,qi-1}表示第i个互质分类器的标签类别集合。对于集合ΩN中的任意一个类w,可以分解为n个
fi(w)=w mod qi
fi(w)∈Ωqi
(8)
通过式(8)中的标签分解,一个N类的标签能够被分解为多个互质的小标签。下面我们结合定理2给出qi的选择准则。
定理2 (质数定理) 小于整数a的质数的密度近似为
对于整数N,考虑区间
区间的长度由κ和ε确定。其中κ是取值为2或3等一个较小的正整数,ε是一个取值在(0,1]区间的一个较小的正数。根据定理2,在区间
中的质数个数为
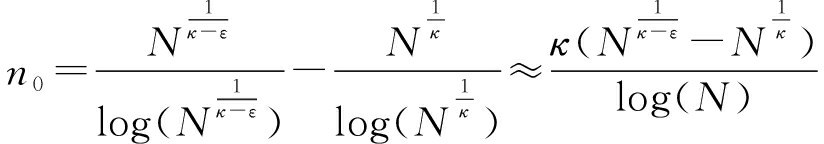
(9)
因此,通过微调κ和ε,可以得到n个互质的质数q1,q2,...,qn。下面证明质数q1,q2,...,qn使得互质分类器满足两个良好的性质:
1)类别的高可分性:对于两个不同的类别w,ν∈ΩN,且w≠ν,存在尽可能多的fi使得fi(w)≠fi(ν)。
2)分类器相互独立性:对于w∈ΩN且i≠j, fi(w)与fj(w)之间的互耦信息近似为0。
首先,对于性质1,有以下定理。
定理3 考虑任意两个类别w,ν∈ΩN且w≠ν,则fi(w)=fi(ν)时i的取值至多为n-1。
证明 假设w≠ν并且有n个不同的i使得fi(w)=fi(ν),即:
fi(w)=fi(ν),i=1,...,n
(10)
那么,对于所有的i=1,...,n,都有
w≡ν mod qi
(11)
由于{qi}是一组互质的数,必有
(12)
又因为集合
所以假设w≠ν不成立,得证。
对于性质2,有以下定理。
定理4 考虑类别w∈ΩN,对于任意i≠j, fi(w)与fj(w)之间的互耦信息I[fi(w), fj(w)]≈0。
在证明定理4之前,我们先给出引理5。
引理5 考虑类别w∈ΩN,对于一个正整数q定义变量
取得集合Ωq中的每个类别值的概率为
或
证明 基于映射:
(13)
集合Ωq中的每个类别值在集合ΩN中的原像是一个元素个数为
或
的集合。下面给出定理4的证明。
证明 考虑变量
和
根据引理5, fi(w)在集合Ωqi中每个类别取得的概率为
或
在集合Ωqi×Ωqj中取得的概率为
或
和gj=fj(w)之间的互耦信息为:
(14)
当κ=2时,有qiqj>N且
因此,pi, j(gi,gj)在集合Ωqi×Ωqj中的N个类别上的取值为
其他类别上的取值为0。互耦信息
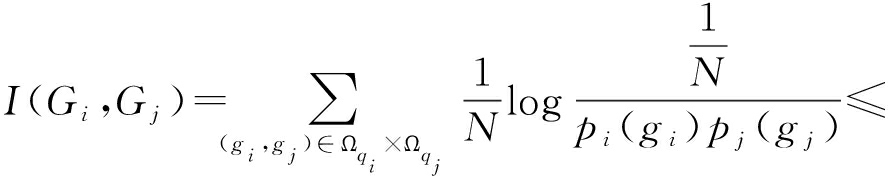
log(N)-log(ri-1)-log(rj-1)<
(N→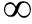
)
(15)
当κ≥3时,有
则
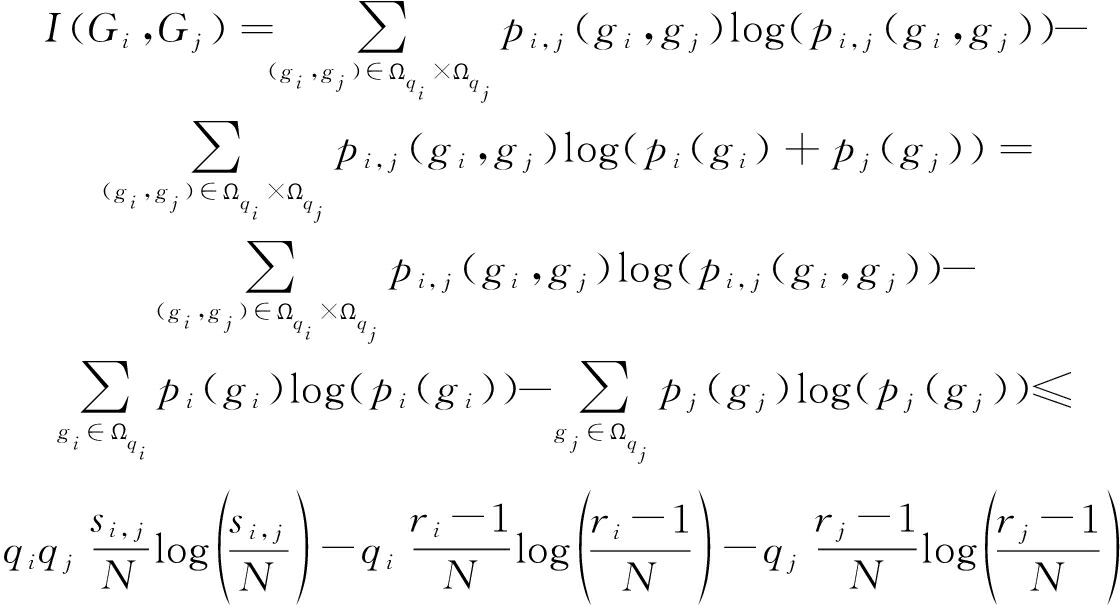
(16)
考虑有下面不等式关系
(si, j-1)qiqj<N≤si, jqiqj
(ri-1)qi<N≤riqi
(rj-1)qj<N≤rjqj
(17)
可以得到
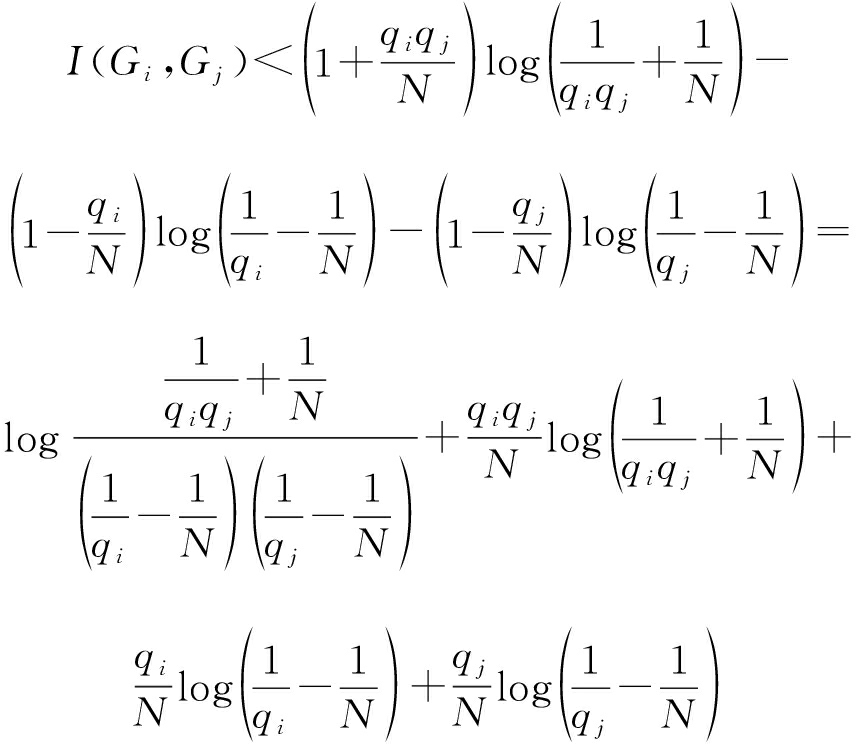
(18)
又因为
以及
可以进一步得到
(N→)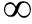
(19)
因此,当N足够大时,不同分类器对于同一个w的互耦信息近似为0,得证。
3.2 网络模型
定理3和定理4表明互质分类器能够替代one-hot分类器解决大规模分类问题。如图1所示,互质分类器与one-hot分类器具有相同的网络输入,不同的网络输出。由于N≫M时,one-hot分类器的参数量取决于类别数N,当类别数N很大时,one-hot分类器的参数和标签会占用大量的内存,甚至可能超出内存容量,另外计算成本也会急剧增长甚至无法实现。而互质分类器通过标签分解,将长度为N的one-hot标签分别映射为长度为q1,...,qn的小标签,降低了存储标签占用的内存。同时,由于每个互质分类器的分类规模较小,网络的参数量也大大降低。另外,如图1(b)所示,互质分类器是并行部署的,彼此之间相互独立,因此互质分类器网络的训练可以部署在多个分立的计算平台实现,且不需要相互通信,从而降低了大规模分类问题的网络训练难度和训练时间。
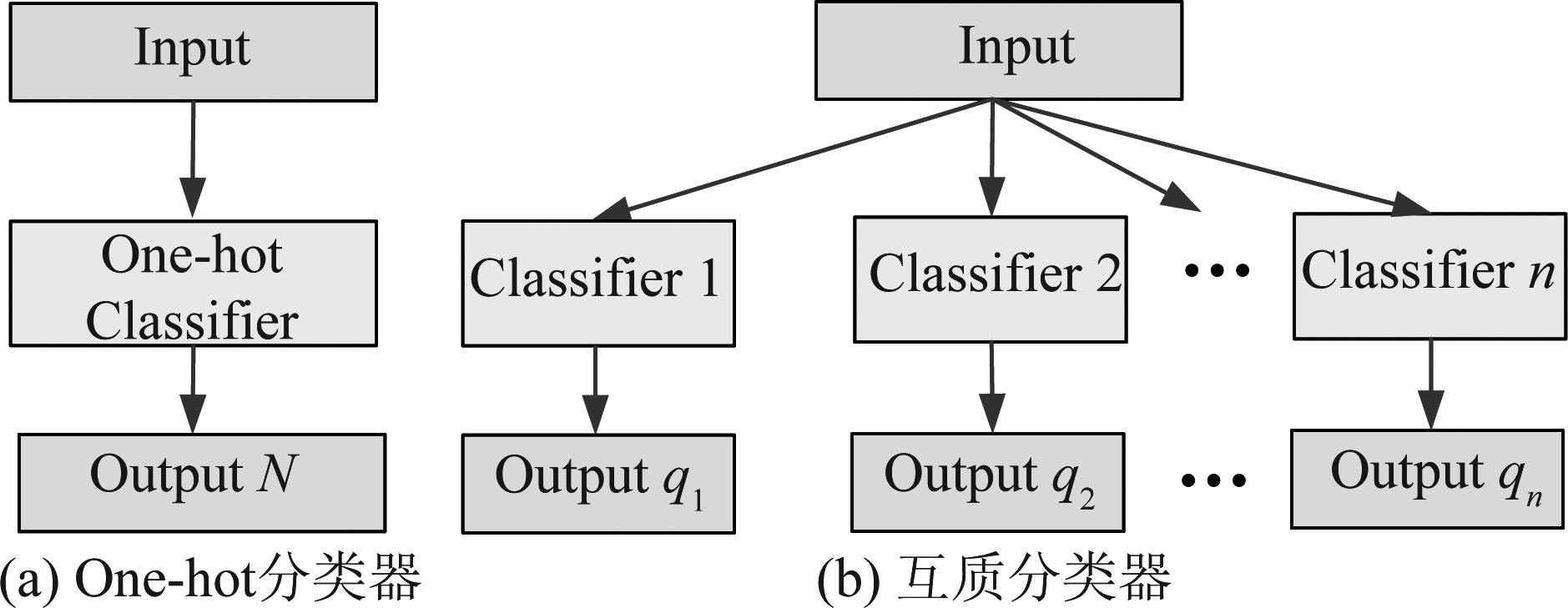
图1 One-hot分类器和互质分类器示意图
Fig.1 The schematic diagram of one-hot classifier and co-prime classifiers
3.3 标签重建
互质分类器训练完成后,根据式(8),需要通过互质分类器的计算结果重建标签
进一步确定特征数据对应的类别。根据统计理论,分类器的计算结果可以作为特征数据在该类别取得的概率,即
(20)
通过应用互质分类器相互独立的性质,P(w)可以表达为
(21)
对上式两边取对数可得
(22)
显然标签
可以看作空间谱的估计结果,谱峰处对应的角度类别即为DOA的估计值。
4 仿真实验与分析
本文通过仿真比较了one-hot分类器和互质分类器的网络的复杂度和网络的训练时间。通过仿真SBL方法,进一步比较了one-hot分类器,互质分类器与SBL方法估计DOA的平均耗时。另外,还通过循环实验,得到了三种方法估计DOA的MSE(mean square error)随信噪比(signal to noise ratio: SNR)的变化关系。本文中涉及到用于训练的阵列观测数据的信噪比设置为0 dB,快拍数设置为500。仿真实验平台为一台Intel 志强E3-1535M v6 CPU和英伟达Quadro M2200 GPU的笔记本电脑。
4.1 实验1
本实验中,考虑空域范围[-60°,59°]并且按Δθ=1°均匀划分类别,因此对应one-hot分类器的标签长度N=120,根据式(9)选择为q1=13,q2=17和q3=19的分别作为互质分类器的类别。one-hot分类器和互质分类器的网络结构分别如图2(a)和图2(b)所示。分类类别数N=120时,one-hot分类器的可由4个卷积层,1个全连接层(dense)以及1个softmax层组成,其中dropout层为正则化层,用于防止网络过拟合且不包含任何参数。每个互质分类器由2个卷积层,1个全连接层以及1个softmax层组成。one-hot分类器和互质分类器的总层数分别为6层和4层。
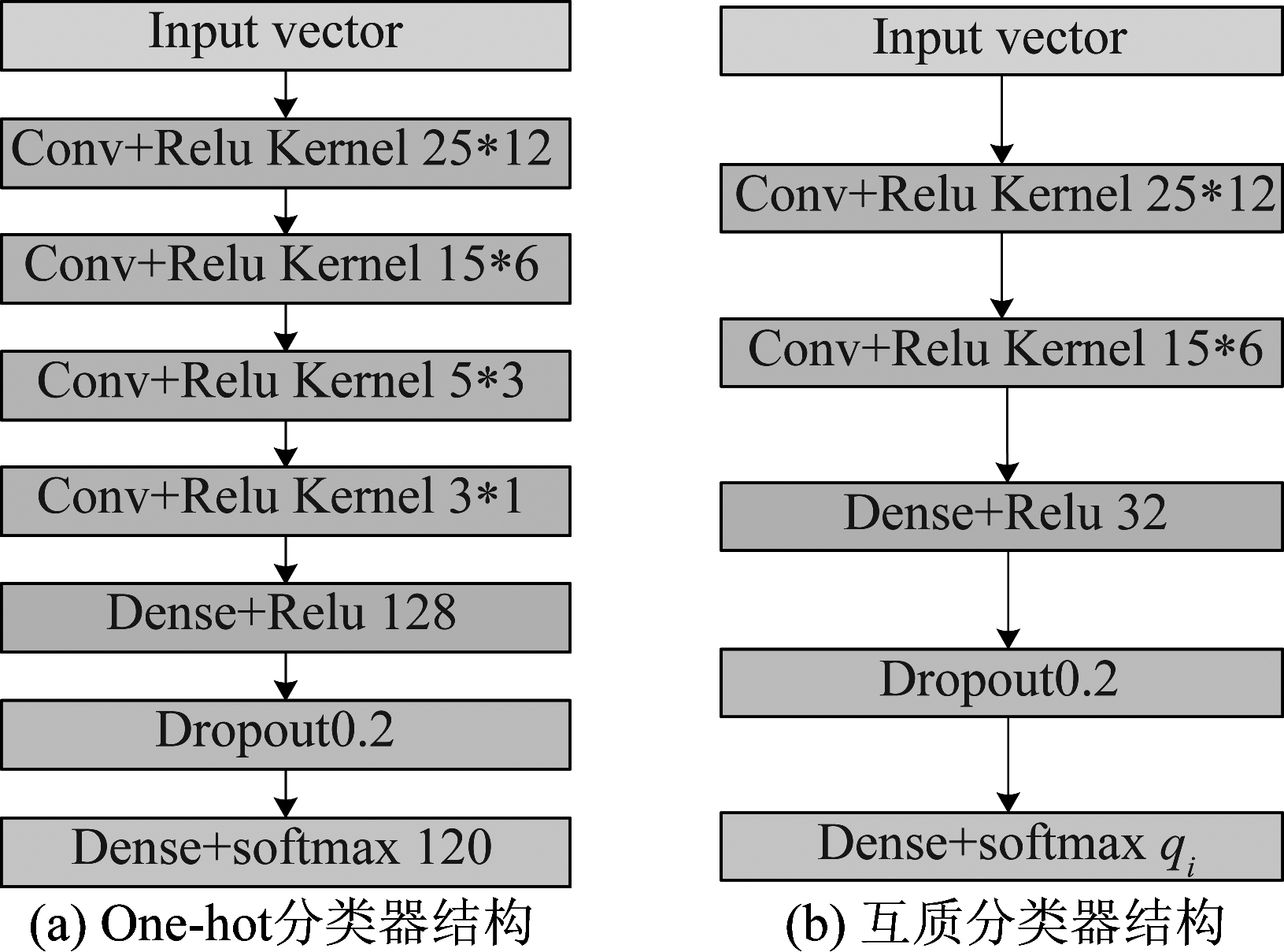
图2 One-hot分类器和互质分类器的网络结构
Fig.2 The network structure of one-hot classifier and co-prime classifiers
分类器网络的训练过程如图3所示,在训练过程中,学习率的初始值设置为0.001,为了提高网络的收敛速度,每20个迭代轮回学习率减小为原来的一半。在图3(a)中,one-hot分类器的测试准确率在100次轮回迭代后收敛到0.99,图3(b)～(d)中,每个互质分类的测试准确率在100次迭代轮回后也能收敛到0.99。
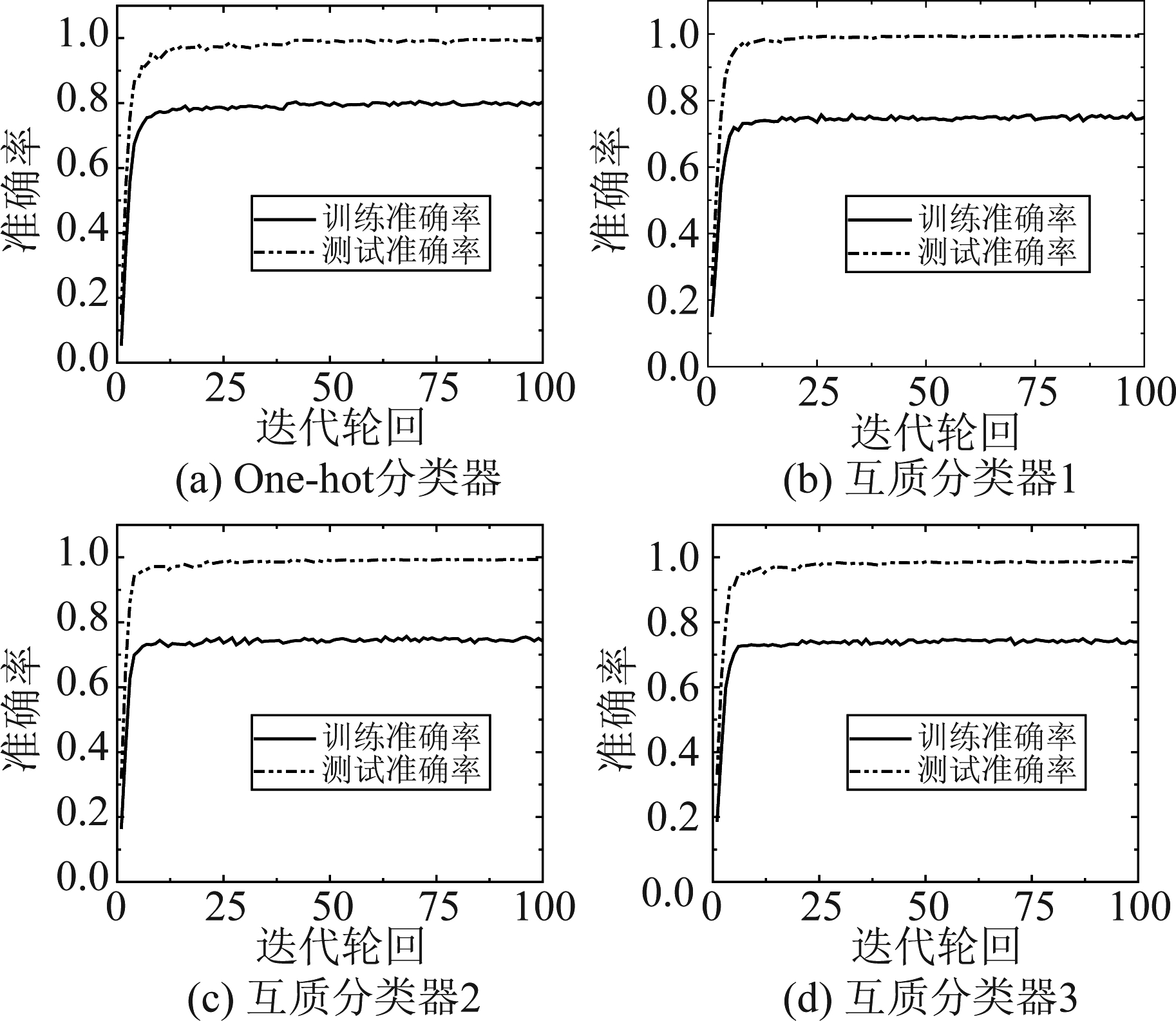
图3 分类器网络的分类准确率与训练迭代轮回的关系
Fig.3 Relationship between classification accuracy of classifier network and training epoch
表1 三种方法的总参数量、网络训练时间及运行时间
Tab.1 The total number of parameters, network training time and running time of the three methods
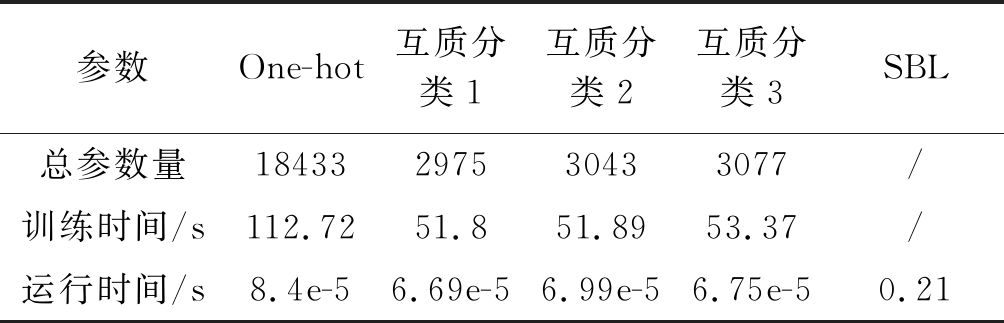
参数One-hot互质分类1互质分类2互质分类3SBL总参数量18433297530433077/训练时间/s112.7251.851.8953.37/运行时间/s8.4e-56.69e-56.99e-56.75e-50.21
网络的总参数量,训练时间和运行时间如表1所示。另外,与分类器类别划分间隔相同,本实验中SBL方法选择1°间隔用于划分栅格。由表1可以看出,完成相同类别的分类任务互质分类器所包含的参数远少于one-hot分类器包含的参数,并且互质分类器网络的训练用时大概是one-hot分类器训练用时的一半。在运行时间方面,由于互质分类器是独立并行计算的,互质分类器的运行时间由运行时间最长的分类器决定,互质分类器比one-hot分类器的运行时间缩短了大概17%。SBL方法的运行时间是one-hot分类器的2500倍,是互质分类器的3000倍。因此,相对于SBL方法,基于DCNN分类器的DOA估计方法具有实时估计的特点。
4.2 实验2
为了验证大类别条件下分类器的性能,考虑空域范围[-60.0°,59.8°]并且按Δθ=0.2°均匀划分类别,因此对应one-hot分类器的标签长度N=600。根据式(9)选择为q1=29、q2=31、q3=37、q4=41、q5=43、q6=47和q7=53分别作为互质分类器的类别。one-hot分类器和互质分类器的网络结构分别如图4(a)和图4(b)所示,分类类别数N=600时,one-hot分类器的可由4个卷积层,3个全连接层(dense)以及1个softmax层组成,每个互质分类器由3个卷积层,3个全连接层以及1个softmax层组成。one-hot分类器和互质分类器的总层数分别为8层和7层。
分类器网络的训练过程如图5所示，在训练过程中,学习率的初始值设置为0.001,为了提高网络的收敛精度,每20个迭代轮回学习率减小为原来的一半。在图5(a)中,one-hot分类器的测试准确率在200次轮回迭代后收敛到0.52,图3(b)～(h)中,每个互质分类的测试准确率在100次迭代轮回后能收敛到0.58,在类别数较大的情况下,互质分类器的准确率收敛精度更高。另外比较图5(a)和图5(b)～(h)的准确率曲线可以发现,由于互质分类器的网络复杂度较小,在相同容量的训练样本下分类器更容易训练,可以在较短时间内收敛到较高的准确率。
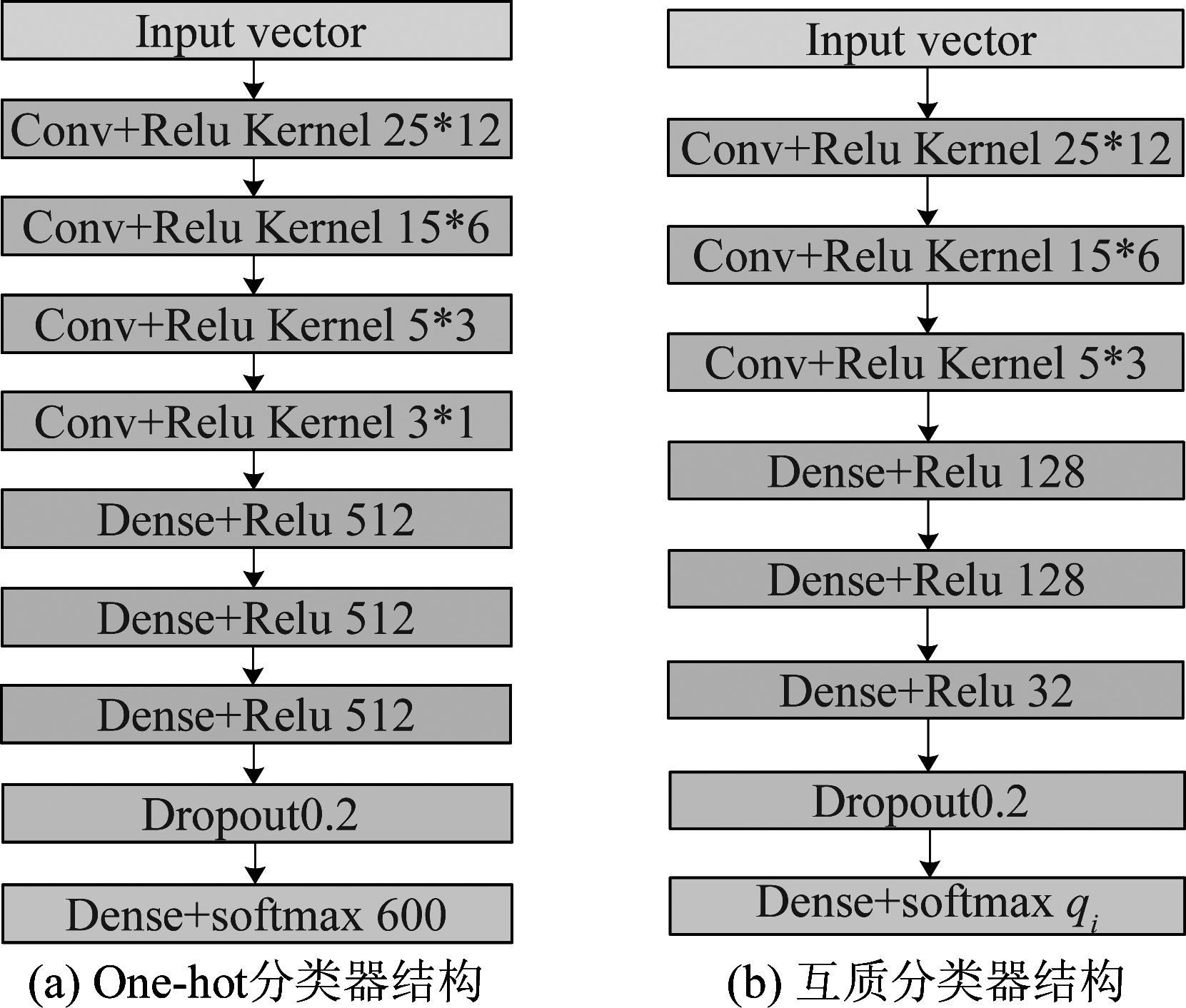
图4 One-hot分类器和互质分类器的网络结构
Fig.4 The network structure of one-hot classifier and co-prime classifiers
网络的总参数量、训练时间和运行时间如表2所示,本实验中SBL方法选择0.2°间隔用于划分栅格。由表2可以看出,完成类别N=600分类任务互质分类器所包含的参数远少于one-hot分类器包含的参数,并且互质分类器网络的训练用时大概是one-hot分类器训练用时的一半。在运行时间方面,互质分类器的最高运行时间比one-hot分类器的运行时间缩短了大概9%,并且SBL方法的运行时间是one-hot分类器的185600倍,是互质分类器的225000倍。因此,相对于SBL方法,类别数增加对分类器运行时间的影响较小。
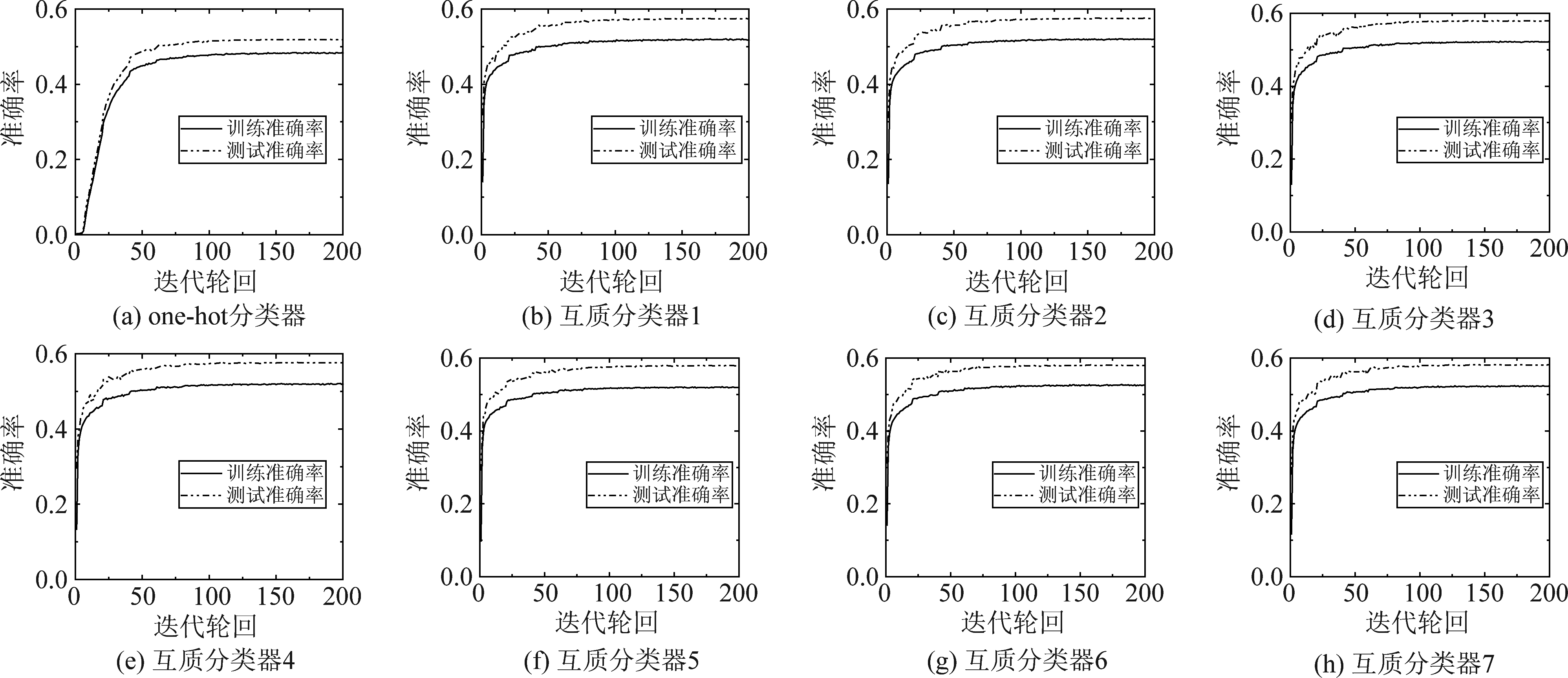
图5 分类器网络的分类准确率与训练迭代轮回的关系
Fig.5 Relationship between classification accuracy of classifier network and training epoch
表2 三种方法的总参数量、网络训练时间及运行时间
Tab.2 The total number of parameters, network training time and running time of the three methods
参数One-hot互质分类1互质分类2互质分类3互质分类4互质分类5互质分类6互质分类7SBL总参数量83952130113301793037730509305753070730905/训练时间/s583.05238.65225.55234.91236.08235.63240.51248.29/运行时间/s9.81e-55.98e-57.69e-58.1e-57.69e-58.1e-57.69e-58.4e-518.19
4.3 实验3
考虑一个远场窄带信号从角度20.33°入射到阵列,本实验分别仿真产生不同信噪比条件下的阵列采样数据,信噪比由-10 dB按照2 dB步进增加至10 dB。每个信噪比条件下产生1000次阵列采样数据,分别使用三种方法从阵列采样数据中恢复信号的DOA。如图6所示,通过统计1000次的估计误差并做平均处理,得到了均方根误差随信噪比变化的关系。
从图6(a)可以看到,当类别数N=120时,互质分类器的估计误差小于one-hot分类器和SBL方法,信噪比低于-6 dB的条件下,one-hot分类器的估计误差急剧增大,而互质分类器和SBL方法的估计误差变化相对较小。在信噪比高于-6 dB的条件下,one-hot分类器的估计误差随信噪比增加逐渐减小到和互质分类器的估计误差相同的水平,并且两者的估计误差明显小于SBL方法。从图6(b)可以看到,当类别数N=600时,已知训练数据的信噪比为0dB,one-hot分类器的估计性能对噪声较敏感,信噪比小于-2 dB条件下有较大的估计误差。而互质分类器在低信噪比条件下的估计误差明显小于SBL方法,同时计算耗时约为SBL方法的二十万分之一。
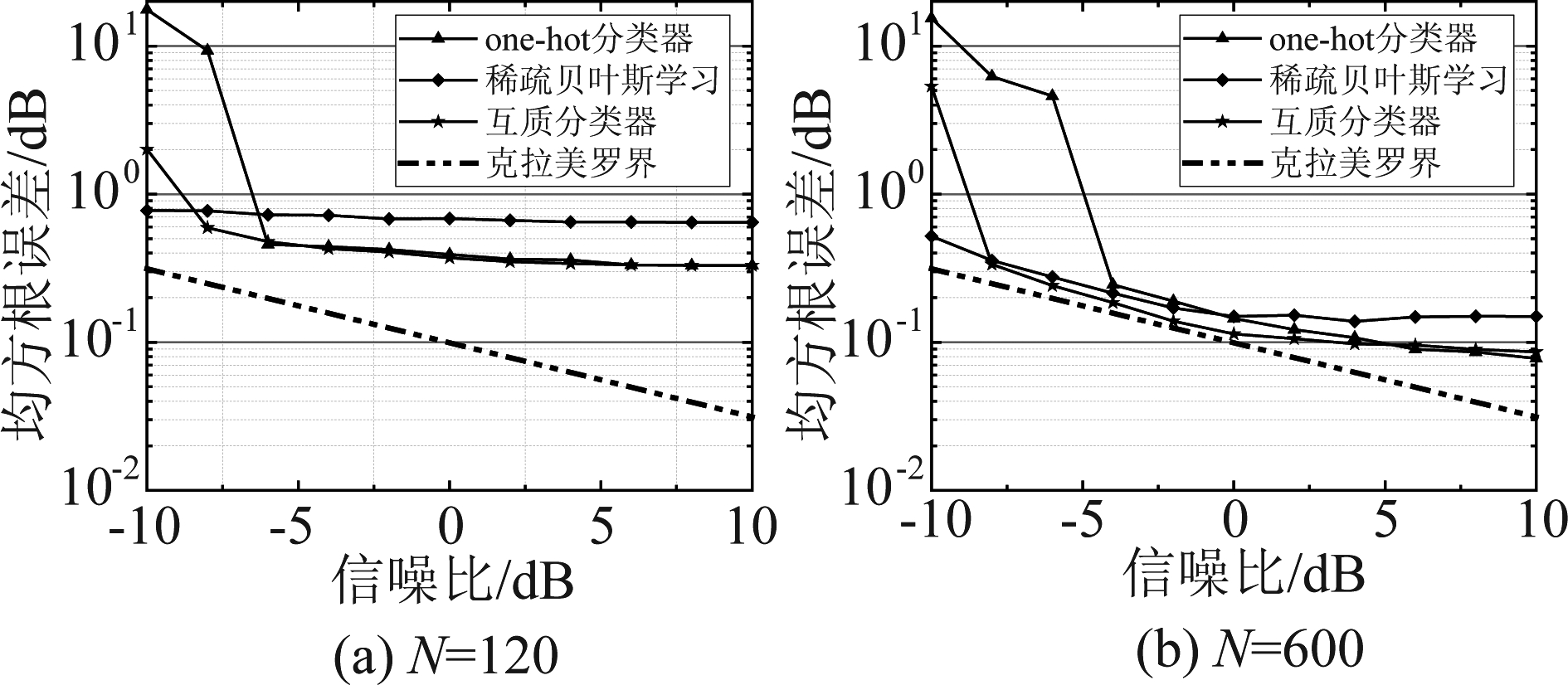
图6 DOA估计的均方根误差与信噪比的关系
Fig.6 Relationship between the root mean square error of DOA estimation and SNR
4.4 实验4
在这一部分,我们仿真了不同方法对两个信号的空间谱估计的对比实验。考虑两个角度分别由{-1.1°,1.9°},{50.1°,55.9°}以及{10.1°,30.9°}入射的情况,信噪比设置为10 dB。如图7(a)～(c)所示,当两个信号的之间的间隔为3°且分别位于均匀线阵的法线两侧时,MUSIC方法无法分辨出两个角度。虽然SBL方法和本文所提方法能够分辨出两个角度,但是显然SBL方法的估计偏差大于所提方法。进一步考虑两个信号位于线阵法线的一侧,并且两个角度间隔为5.8°。如图(c)～( f )所示,由于MUSIC方法在该空域分辨率较低,增加角度间隔仍然无法分辨出两个角度。同样,SBL方法虽然能够分辨出两个角度,但是其估计偏差明显较大。最后,我们进一步增加两个角度的间隔为20.8°,如图(g)～(i)所示,三种方法均取得了很好的估计效果,但是所提方法具有实时估计的特点。上述实验结果表明,与MUSIC方法和SBL方法相比,所提方法的估计精度和分辨率在角度间隔较小时均优于上述两种方法。
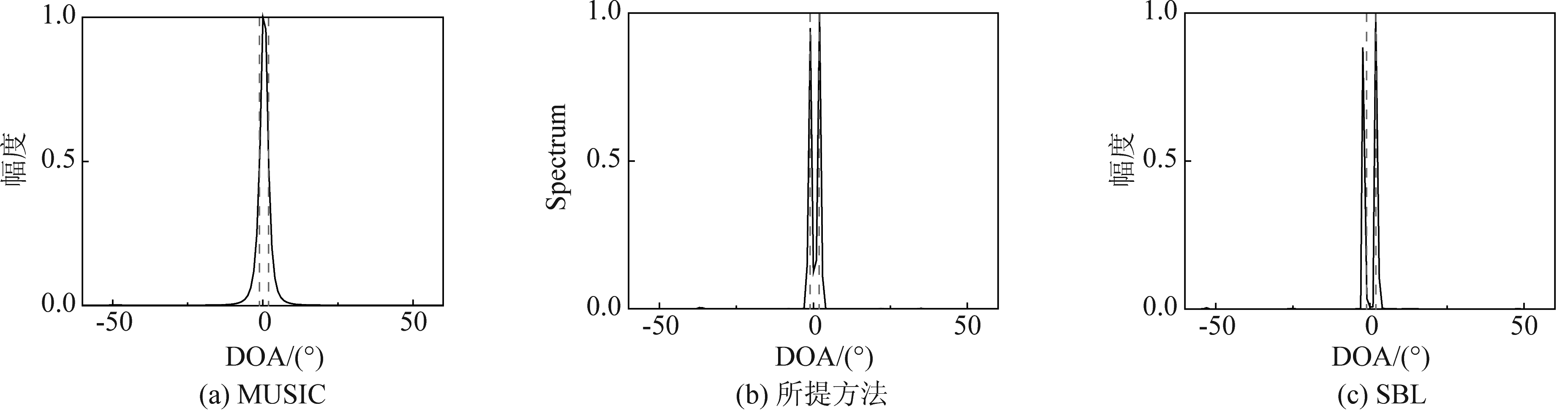
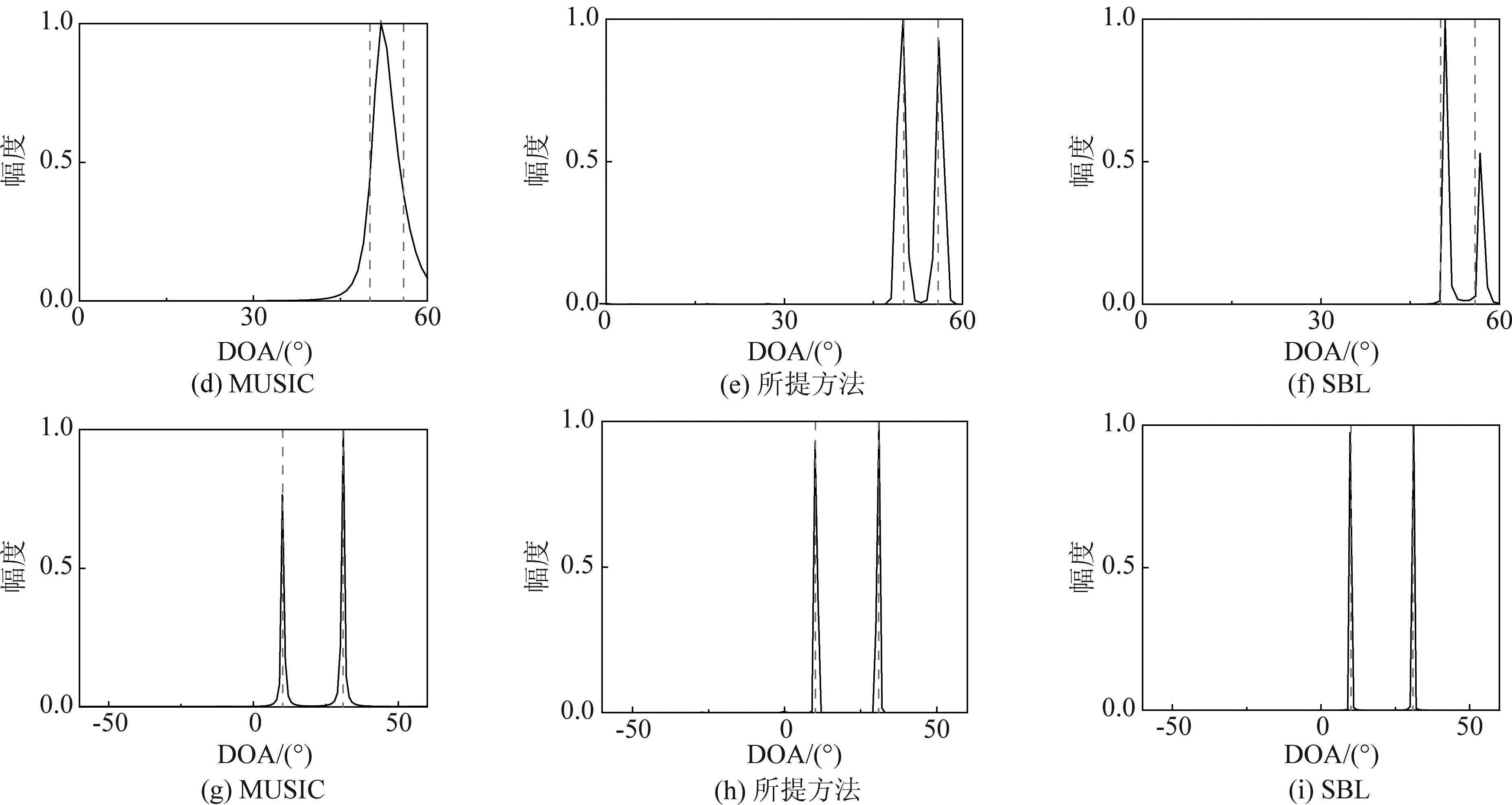
图7 不同方法估计的空间谱,第1行为-1.1°和1.9°;第2行为50.1°和55.9°;第3行为10.1°和30.9°
Fig.7 Spatial spectra of different methods. The first row are -1.1° and 1.9°. The second row are 50.1° and 55.9°. The third row are 10.1° and 30.9°
5 结论
本文使用标签分解,将大规模分类问题转换成多个较小的互质类别数的分类问题,并成功应用于DOA估计。首先本文提出了一种新的特征提取技术,不仅将特征数据维度减小至一维减小了分类网络的复杂度,而且还实现了特征增强。其次,为了降低大规模one-hot分类器的复杂度和训练难度,提出了用于解决大规模分类问题的互质分类器。与one-hot分类器和SBL方法相比,互质分类器具有计算资源少、训练时间短、估计精度高的优点。此外,互质分类器的DOA估计速度也明显快于one-hot分类器,与SBL方法相比具有实时估计的特点。仿真和实验也验证了本文所提方法的优越性。
[1] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276- 280.
[2] ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995.
[3] KRIM H, VIBERG M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Process Magazine, 1996, 13(4): 67-94.
[4] DAI J, HU N, XU W, et al. Sparse Bayesian learning for DOA estimation with mutual coupling[J]. Sensors (Basel), 2015, 15(10): 267- 280.
[5] 杨靖雯, 王金龙, 徐以涛. 用于最大似然2-DOA估计的裂变粒子群算法[J]. 信号处理, 2010(8): 1181-1186.
YANG J W, WANG J L, XU Y T. Fission particle swarm optimization for maximum likelihood 2-DOA estimation[J]. Signal Processing, 2010(8): 1181-1186.(in Chinese)
[6] MALIOUTOV D, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transaction on Signal Processing, 2005, 53(8): 3010-3022.
[7] YANG Z, XIE L, ZHANG C. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38- 43.
[8] HUANG H, GUI G, SARI H, et al. Deep Learning for Super-Resolution DOA Estimation in Massive MIMO Systems[C]∥ 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 2018: 1-5.
[9] LIU Z, ZHANG C, YU P S. Direction-of-Arrival Estimation Based on Deep Neural Networks With Robustness to Array Imperfections[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(12): 7315-7327.
[10] WU L, LIU Z, HUANG Z. Deep Convolution Network for Direction of Arrival Estimation With Sparse Prior[J]. IEEE Signal Processing Letters, 2019, 26(11): 1688-1692.
[11] 葛晓凯, 胡显智, 戴旭初. 利用深度学习方法的相干源DOA估计[J]. 信号处理, 2019, 35(8): 1376-1384.
GE X K, HU X Z, DAI X C. Coherent Source DOA estimation using deep learning method[J]. Journal of Signal Processing, 2019, 35(8): 1376-1384.(in Chinese)
[12] MOUSAVI A, PATEL A B, BARANIUK R G. A deep learning approach to structured signal recovery[C]∥2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, 2015:1336-1343.
[13] MOUSAVI A, BARANIUK R G. Learning to invert: Signal recovery via Deep Convolutional Networks[C]∥2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, 2017:2272-2276.
[14] CADZOW J A, KIM Y S. General direction-of-arrival estimation-A signal subspace approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(1): 31- 47.
[15] NILSSON M. Introduction to analytic number theory[M]. Springer-Verlag, 1976.
