1 引言
图像超分辨率重建是计算机视觉领域的重要任务,目的在于将低分辨率(Low-Resolution,LR)图像重建得到高分辨率(High-Resolution, HR)图像。由于一幅LR图像往往有多种形态的HR图像映射,因此,该重建过程是一种不适定性问题。为了获得更加符合视觉任务的HR图像,许多超分辨重建方法已被提出来。这些方法主要分为三类,分别为:基于插值的方法[1]、基于模型的方法[2]和基于学习的方法[3]。
以双线性插值和双三次插值为代表的早期的插值方法简单方便,但是其重建得到的图像质量已经无法满足日益发展的应用需求。为了适应更加灵活、更高质量的重建需求,基于模型的方法应运而生。具有代表性的方法包括全变分模型[4]、非局部先验模型[5]和稀疏表示模型[6]。相较于插值的方法,基于模型的方法更加灵活且能够获得更加高质量的图像。但这些方法依然存在较大的缺陷:(1)这些算法在优化和重建过程中需要耗费大量的时间,不利于其在应用领域的推广;(2)过度依赖于先验信息,在没有先验条件的情况下,图像的重建质量急剧降低。
卷积神经网络强大的非线性表达能力在计算机领域取得了前所未有的成功,并且其端到端的训练模式与图像超分辨率重建思想完美契合。Dong等人[7]第一次将深度学习引入到超分辨领域中,他们设计了一个简单的包含三个卷积层的超分辨率重建方法,命名为SRCNN,该方法在亮度通道上对图像进行修复,相比于之前的基于插值和基于模型的方法,SRCNN无论在重建质量还是在性能上都获得了巨大的提升。为了进一步提升网络的性能,Kim等人将方法VDSR[8]和DRCN[9]的网络层数增加到了20层,在重建质量上,相比于SRCNN取得了显著的提升。值得一提的是,He等人[10]的残差网络(ResNet)提出以后,在一定程度上改善了网络加深后的梯度爆炸或消失现象,使得深度网络更加易于加深和训练。随后,残差网络几乎被运用于所有的深度学习网络中,在超分辨领域中也同样得到广泛的运用。Lim等人[11]通过移除传统残差网络中批归一化层构建了一种增强的深度超分辨率网络(EDSR),该网络主要通过扩大模型的尺寸来提高网络的性能,其重建出来的效果又进一步得到提升。由于这种模式在重建图像质量上取得了较大的进步,使得更宽更深网络变得越来越流行。随后,Zhang等人[12]利用通道注意力机制设计了RCAN网络,该网络的层数达到了400+层。而Dai等人[13]的SAN网络在RCAN的基础上提出二阶注意力机制,但网络的参数依然巨大。在如此深的网络情况下,毫无疑问他们的网络能够取得更好的指标。但是,随着网络宽度和深度的增加,不可避免地带来了庞大的网络参数,比如EDSR的参数到达了惊人的44M,RCAN也高达15M。庞大的网络参数占用了过多的计算资源,这给其在应用领域的推广带来了阻碍,并且过于巨大的网络也容易造成网络的过拟合等问题。
为了减少网络参数,Hui等人[14]设计出了蒸馏神经网络来充分利用网络的浅层信息。Li等人[15]构建了一种循环神经网络,利用循环结构将深层信息通过循环网络回传到初始层并且将其编码映射到浅层信息中。Yang等人[16]利用多尺度、多级别的U型网络结构来进行优化,以减少网络参数。尽管这些网络在控制网络参数和保证图像重建质量上都取得了较好的效果,但在控制参数和提升图像质量上还有进一步的提升空间。
基于上述分析,本文在网络参数的减少和重建图像细节的增强方面,提出了一种渐进式特征增强网络的超分辨率重建方法。主流的基于深度学习的图像超分辨方法大多都是利用3×3的卷积核提取特征,受到感受野大小的限制,提取到的局部特征不明显。因此,往往会通过改变特征图的大小或者改变卷积核的大小来增加网络感受野进行图像特征的提取。由于改变特征图的大小不可避免地会丢失掉图像的部分特征信息,而采用不同的卷积核提取特征则会增加网络的参数且不易于训练。针对这一问题,我们在不改变卷积核及特征图大小的前提下,利用扩张卷积的方法增加感受野来提取多个尺度的特征。基于人眼视觉观察机制中不同特征引起人眼的关注度不同的这一原理,本文在多个尺度特征提取之后引入注意力机制,实现对多尺度的特征进行分配权重参数,起到特征信息增强的作用。基于上述两个思想,本文构建了一个多尺度注意力模块来实现浅特征层信息和深层特征信息的增强。本文所提出的超分辨率重建网络的主要贡献如下:
(1)我们设计了一个端到端的渐进式特征增强网络的图像超分辨率重建算法。在公共数据集上的实验结果表明,相比于其他的方法,我们的网络取得了更好的效果。
(2)我们设计了一个多尺度注意力机制模块,模块中利用扩张卷积的方式来提取不同尺度的特征信息,并引入注意力机制对不同尺度的特征图分配权重,来实现图像特征信息的增强。其中,扩张卷积的方式在不增加网络参数及不丢失特征信息的同时扩大了卷积核的感受野,且使网络更容易训练。
(3)在整个网络结构中,我们设计了两种信息增强模块,即浅层特征信息增强模块和深层特征信息增强模块。这两个模块中都采用了多尺度注意力机制模块,并针对提取的浅层信息和深层信息来实现不同尺度的特征提取和增强。
2 相关工作
在本节中,我们将介绍与本文工作相关的一些工作,包含基于深度学习的单幅图像超分辨率重建、图像重建的多尺度结构以及注意力机制等。
2.1 基于深度学习的单幅图像超分辨重建
深度学习的基本思想是以数据为驱动,通过一系列的隐藏层来实现输入到输出的映射,而单幅图像超分辨率的目的在于通过输入LR图像来得到符合人眼视觉的HR图像。因此比较容易将深度学习引入到单幅图像超分辨领域中。基于深度学习的单幅图像超分辨率重建的一般过程如下:首先,通过对数据进行处理得到包含LR和HR图像对的数据集,通常数据集样本数量要求比较大且包含的信息越丰富越好;然后设计算法的网络框架,一般网络结构越深,提取到的细节信息越丰富,得到的结果越好;最后通过训练得到最终的从LR图像到超分辨率图像的映射模型。在Dong等人[7]的推动下,深度学习被广泛应用于单幅图像超分辨率重建过程中。相比于之前的方法,无论在主观视觉感知上还是在客观指标上都获得了质的提升。但是目前的主流的深度学习超分辨率方法热衷于提升客观指标,不断地将网络加大加深,忽视了网络模型的大小对于其在应用领域推广带来的影响。为解决这一问题,本文提出了渐进式特征增强的图像超分辨率算法,在控制网络参数的同时取得了较好的重建效果。
2.2 图像重建的多尺度结构
多尺度的本质是对信号进行不同粒度的采样,即在不同的尺度下能够观测到不同的特征。源于多尺度这一特性,该结构已成为计算机视觉研究的热点之一。一些学者也在探索多尺度在图像复原任务中的作用,Han等人[17]提出了双态递归网络(DSRN),通过联合低分辨率和高分辨率尺度上的信息来实现图像超分辨率。具体来说,DSRN中的递归信号通过延迟反馈的方式来进行两个尺度间的信息交换。多尺度残差网络(MSRN)[18]通过使用不同尺度的卷积核来提取图像在不同尺度下的特征。Yang等人[16]提出多级多尺度图像超分辨率网络(M2SR),利用残差U型网络和注意力U型网络提取图像的多尺度特征,增强网络的表达能力。本文在上述思想的基础上,设计出多尺度注意力块来进一步增强网络提取多尺度特征的能力。
2.3 注意力机制
注意力机制来源于人的感知理论,指的是人类的视觉系统会在感兴趣的区域上投入更多的关注[19]。近些年来,许多视觉任务利用注意力机制来提升卷积神经网络的性能。比如在图像和视频分类任务中[20-21]。Wang等人[20]通过引入非局部空间注意力构建了非局部神经网络。与之相对应的,Hu等人[21]提出了通道注意力机制模块(SENet)来处理通道域的关系并且取得了显著的效果。
最近,注意力机制也被引用到图像超分辨率领域并且使得图像重建质量获得显著提高。然而。这些网络不论是引用通道注意力机制还是空间注意力机制都是在单一尺度下,忽略了多尺度在图像重建中的作用。因此,为了强化多尺度结构提取特征效率,我们将通道注意力与多尺度相结合,进一步增强多尺度结构提取图像特征。
3 本文方法
为了更好地重建出HR图像的细节信息,本文提出一种基于渐进式特征增强网络的超分辨率重建方法。该网络整体结构如图1所示,主要包含两个模块:浅层信息增强模块和深层信息增强模块。该方法重建HR图像的过程描述如下。首先,我们对数据集进行预处理来增强网络的表达能力;然后,LR图像先通过一个卷积层获得图像的浅层信息,再利用一个多尺度注意力模块提取图像的浅层多尺度特征并对其进行增强;接着,增强后的特征信息再通过一个残差学习模块获得图像的深层特征,同样经过一个多尺度注意力模块达到特征信息增强的目的;最后,利用一个跳转连接将图像初始的浅层特征与深层多尺度特征进行像素级相加并通过一个上采样操作得到最终的HR图像。
3.1 数据预处理
为了增强网络的泛化能力,防止过拟合,我们对数据集进行了预处理。首先我们将训练集图像大小比例分别调整为1,0.9,0.8,0.7,0.6,并且对得到的五组图像进行180°翻转,由此得到样本量为原数据十倍的训练数据集。这些操作可以增加数据集包含的信息量,丰富数据特征,可增强网络的鲁棒性和泛化能力,在一定程度上也强化了网络的学习能力。
3.2 网络结构描述
超分辨率重建过程主要体现在对图像纹理特征的重建,因此本文通过构建一种渐进式的增强网络来实现图像纹理特征的重构和增强。该网络如图1所示,主要由两大模块组成,其中浅层特征增强模块是由一个卷积层和一个多尺度注意力块构成,深层信息增强模块是由一个残差学习块和一个多尺度注意力块构成。下面主要对网络中的浅层信息增强模块、深层信息增强模块、及最后图像重建过程进行详细描述。
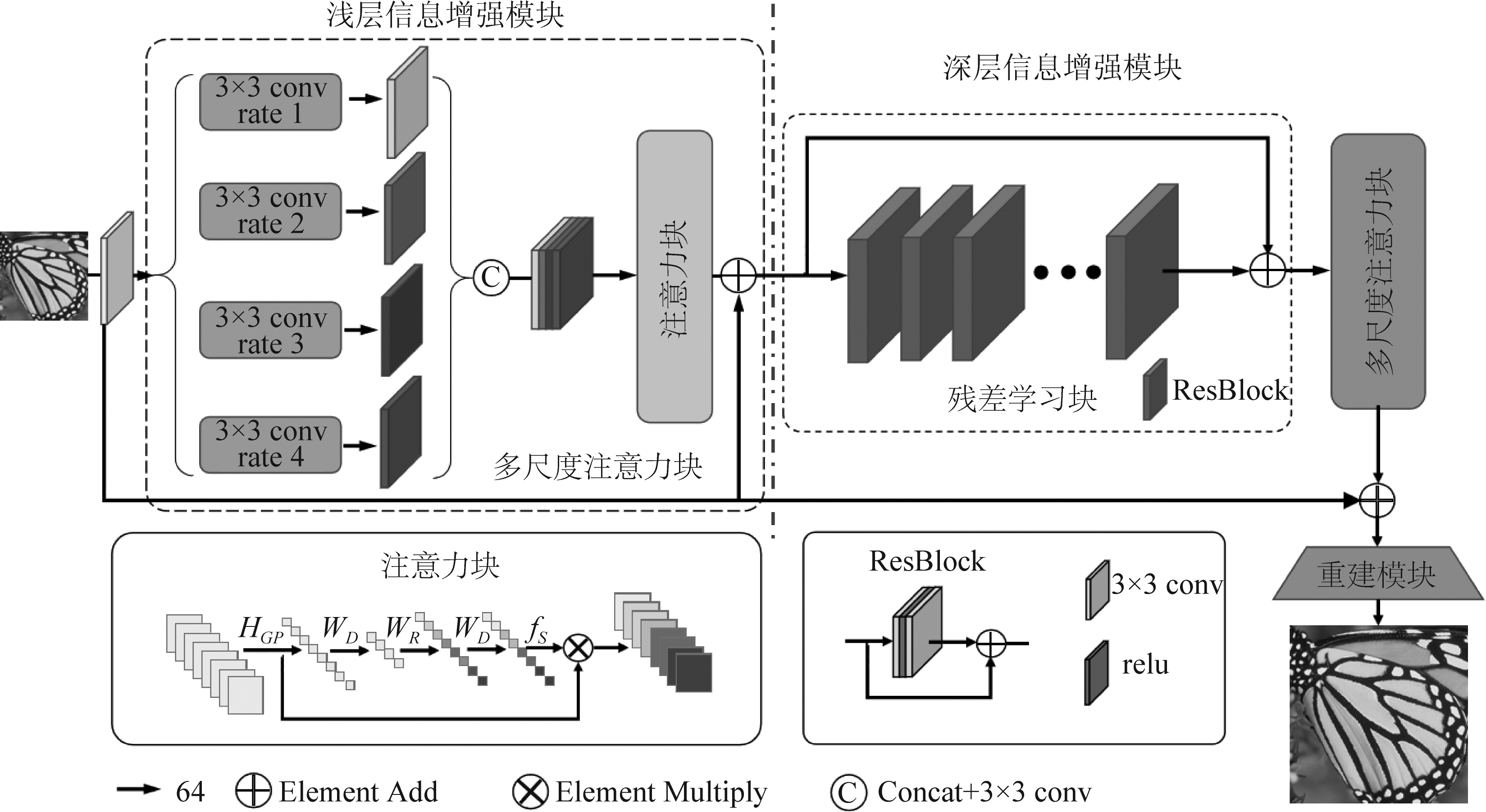
图1 网络框架流程图
Fig.1 Flow chart of the proposed network
3.2.1 浅层信息增强模块
首先将接收到的红、绿、蓝三个通道的LR图像,通过一个卷积层获得初始的浅层特征图。该卷积层利用大小为3的卷积核获得64个特征图,其操作如下:
F0=Con1(ILR)
(1)
其中ILR代表输入的LR图像,Con1(·)表示第一层卷积层的卷积操作,F0是提取到的初始浅层特征。
然后,将获得的初始浅层特征通过一个多尺度注意力块实现浅层信息的增强,该模块主要由多尺度特征提取部分和注意力机制部分组成。其中多尺度特征的提取结构不同于传统的多尺度结构,我们的结构既不改变特征图的大小也无需改变卷积核的大小。我们采用大小相同的3×3的卷积核利用扩张卷积的方式来提取图像四个尺度的特征,即卷积核大小为3×3,膨胀率分别为1、2、3、4。其中,每个尺度的卷积块组成方式为conv+ReLU+conv,即在两个卷积层之间加一层激活函数。该结构能够更加充分地提取多尺度特征、参数更少且易于训练。其结构表示公式如下:
Fi=Coni(relu(Coni(F0)))
(2)
FMF=HC(F1,F2,F3,F4)
(3)
式中,Coni(·)表示膨胀率为i的3×3卷积核,relu(·)代表ReLU激活函数,Fi是提取到的不同尺度特征。Hc(·)表示对多尺度特征的融合,包含Concat操作和一层卷积操作。FMF表示融合得到的图像多尺度特征。
对于提取到的图像多尺度局部与非局部特征,我们希望能够更加有效地利用这些不同的特征,而不是对于每个尺度特征以同等方式对待。因此,本文将通道注意力加入到多尺度结构之后来有选择性地增强网络提取的特征,通道注意力结构块如图1中左下方的方框所示。具体操作如下:首先,利用全局平均池化函数将输入的特征图压缩成与通道数相对应的一维向量;然后对向量进行一个全连接的编解码,即将向量维度降低到原输入维度的1/16,再经过一个ReLU激活函数之后再扩张到输入的维度。这一过程的主要目的在于构建通道之间的相关性。相比于直接使用一个全连接层,其优点在于:(1)拉大通道间的距离,具有更多的非线性,能够更好地拟合通道之间的复杂关系;(2)相比于全连接操作,在计算量和参数量上有巨大的降低。最后,将得到的权重参数运用Sigmoid函数归一化映射到0~1区间再加权到最初输入的每个通道特征图中,这样就完成了对多尺度特征图权重参数的分配。
对于经过多尺度结构和注意力机制结构获得的多尺度特征,我们利用跳转连接将初始浅层特征与其进行像素级相加,这种局部残差的方式能够加快训练的收敛速度,同时在一定程度上改善网络的性能,获得浅层信息的增强。浅层信息增强模块的公式表示如下:
FMSAB=HAB(FMB)+F0
(4)
式中的FMB表示公式(3)得到的浅层多尺度特征,HAB(·)表示为通道注意力结构的操作, FMSAB是经过浅层信息增强模块得到的图像特征。
3.2.2 深度信息增强模块网络
网络的浅层和深层学习获得的特征所体现的图像信息是不同的,因此,我们针对浅层信息增强模块得到的图像特征信息,进一步使用残差学习模块来学习不同尺度特征图之间的关联性以及深层的特征信息,并利用多尺度注意力模块来实现深层信息的增强。其中,残差学习模块如图1中所示,该残差结构包含32个残差单元组成,每个残差单元有两个3×3卷积层,在两个卷积层中间接入一层激活函数ReLU。整个残差单元的输入和输出通道数均为64。
接着,将残差学习模块得到的特征信息输入到一个多尺度注意力块,通过四层卷积来获得不同尺度的特征信息,并利用通道注意力块获得不同特征图的权重系数,来自适应地增强或抑制不同尺度的结构特征,获得增强后的深度特征信息。
3.2.3 图像重建
在上述两个模块学习到的特征信息基础上,我们利用跳转连接将初始的浅层特征与深层增强模块学习到的特征进行像素级相加,构建全局残差网络,输出重建后的特征图。然后,将重建后的特征图经过一个上采样模块来获取最终的HR图像。上采样模块包含一个3×3卷积层、一个激活函数ReLU和PixeShuffle函数,卷积层的输入通道数为64,输出通道数为3。整个网络结构可以表示为:
ISR=(HDFEB(HSFEB(ILR))+F0)↑
(5)
其中ISR表示为重建得到的HR图像,ILR代表LR图像,HSFEB(·)和HDFEB(·)分别代表了浅层信息增强模块和深层信息增强模块的操作。↑是对图像进行上采样操作。
4 实验设置及结果分析
4.1 实验数据集
在实验过程中,我们选用了DIV2K[22]作为我们网络的训练集。该数据集由800张训练集图片和100张验证集图片组成。为了充分利用数据集,增强网络的表达能力,我们对训练数据集进行了预处理。关于测试集,我们选用5个标准数据集,分别为:Set5[23],Set14[24],BSD100[25],Urban100[26],Manga109[27]。其中测试集BSD100包含有多种风格类型的图片,Urban100为各种类型的建筑物图片,Manga109为各种类型的卡通图片。这5个测试集具有丰富多样的信息,能够很好地验证超分辨率方法的有效性。
4.2 客观评价指标
为了客观评价方法的性能,实验中我们采用PSNR和SSIM[28]作为客观评价指标。PSNR与均方差(Mean Square Error, MSE)有一定的相关性。PSNR值越大时,网络的输出与真实图像之间的均方差越小,这就代表了重建出的图像质量越高。PSNR定义如下所示:
(6)
(7)
其中,y表示原始的真实图像,![]() 表示网络重建得到的HR图像,s表示了最大的可能像素值(s取值为255)。
表示网络重建得到的HR图像,s表示了最大的可能像素值(s取值为255)。
人眼视觉感知结构相似指数(Structural Similarity Index,SSIM)评价指标通常用来衡量两幅图像之间的相似度,被用来弥补在相同的PSNR情况下呈现的不同质量感知问题。SSIM的取值范围在0~1之间,数值越接近于1表示图像失真越小,算法性能越好。公式为:
(8)
其中uy和![]() 和
和![]() 分别表示原图像y和超分图像
分别表示原图像y和超分图像![]() 的均值和标准差,而
的均值和标准差,而![]() 则表示交叉协方差,c1和c2为常数,通常c1=(0.01s)2,c2=(0.03s)2,s的含义同公式(7)。
则表示交叉协方差,c1和c2为常数,通常c1=(0.01s)2,c2=(0.03s)2,s的含义同公式(7)。
4.3 损失函数
我们采用L1损失函数来优化提出的网络。对于给出的训练集![]() 包含了N个LR和HR图像对。我们的网络目标是训练图像对并利用L1损失函数来进行优化,公式如下所示:
包含了N个LR和HR图像对。我们的网络目标是训练图像对并利用L1损失函数来进行优化,公式如下所示:
(9)
HPFEN(·)表示网络重建结果。||·||1定义为L1范数,而θ表示了网络中的参数。
4.4 训练配置
本文的模型采用ADAM优化函数来优化网络,网络的初始学习率为设置为3×10-4,并且每迭代2×105次学习率减半。本文所提出的方法实现测试的硬件环境搭配Intel(R)Xenon(R)CPU(2.6GHz)、内存32GB、配置NVIDIA GeForce GTX 1080 Ti GPU的计算机。软件环境为64位Win10操作系统,PyTorch框架和Matlab R2014a。
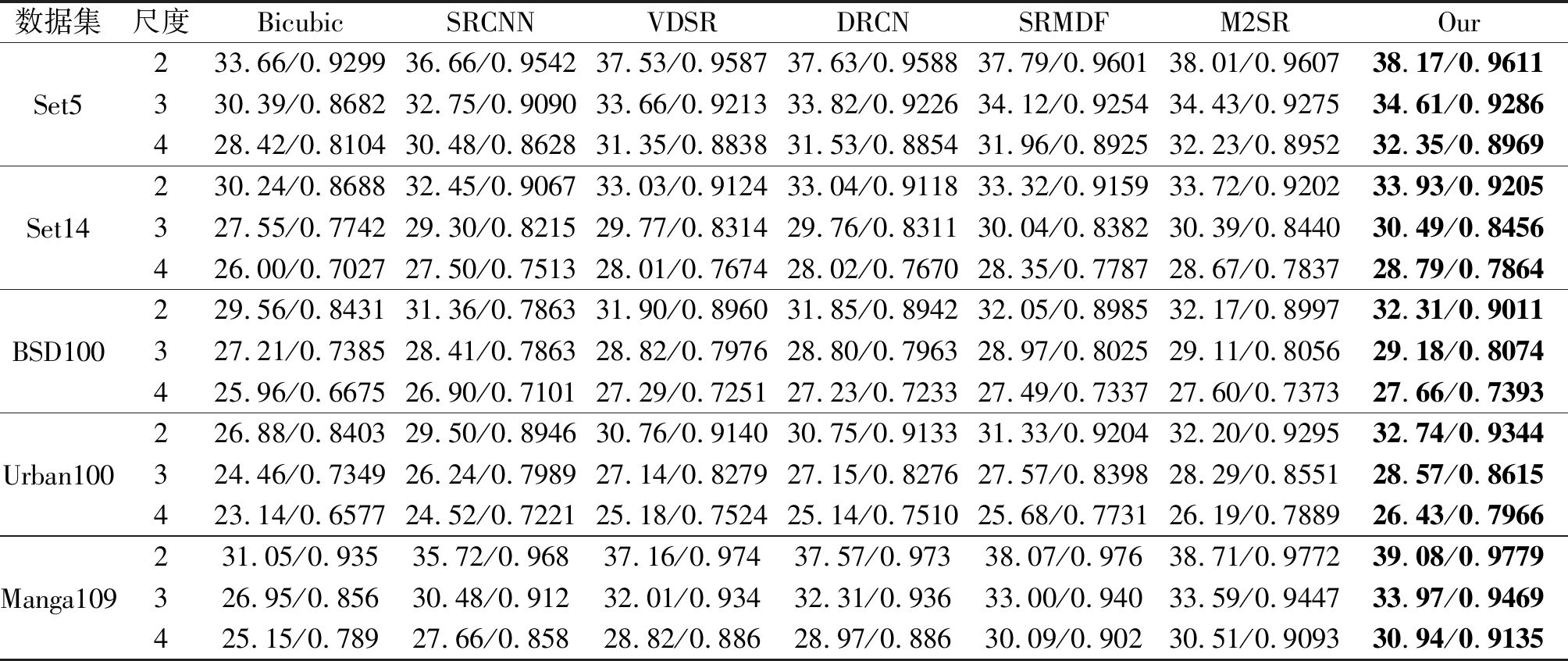
表1 在数据集Set5、Set14、BSD100、Urban100、Manga109上放大倍数分别为2、3、4的平均PSNR(dB)和SSIM的结果比较
Tab.1 The average results of PSNR/SSIM with scale factor ×2, ×3 and ×4 on datasets Set5, Set14, BSD100, Urban100 and Manga109
数据集尺度BicubicSRCNNVDSRDRCNSRMDFM2SROurSet5233.66/0.929936.66/0.954237.53/0.958737.63/0.958837.79/0.960138.01/0.960738.17/0.9611330.39/0.868232.75/0.909033.66/0.921333.82/0.922634.12/0.925434.43/0.927534.61/0.9286428.42/0.810430.48/0.862831.35/0.883831.53/0.885431.96/0.892532.23/0.895232.35/0.8969Set14230.24/0.868832.45/0.906733.03/0.912433.04/0.911833.32/0.915933.72/0.920233.93/0.9205327.55/0.774229.30/0.821529.77/0.831429.76/0.831130.04/0.838230.39/0.844030.49/0.8456426.00/0.702727.50/0.751328.01/0.767428.02/0.767028.35/0.778728.67/0.783728.79/0.7864BSD100229.56/0.843131.36/0.786331.90/0.896031.85/0.894232.05/0.898532.17/0.899732.31/0.9011327.21/0.738528.41/0.786328.82/0.797628.80/0.796328.97/0.802529.11/0.805629.18/0.8074425.96/0.667526.90/0.710127.29/0.725127.23/0.723327.49/0.733727.60/0.737327.66/0.7393Urban100226.88/0.840329.50/0.894630.76/0.914030.75/0.913331.33/0.920432.20/0.929532.74/0.9344324.46/0.734926.24/0.798927.14/0.827927.15/0.827627.57/0.839828.29/0.855128.57/0.8615423.14/0.657724.52/0.722125.18/0.752425.14/0.751025.68/0.773126.19/0.788926.43/0.7966Manga109231.05/0.93535.72/0.96837.16/0.97437.57/0.97338.07/0.97638.71/0.977239.08/0.9779326.95/0.85630.48/0.91232.01/0.93432.31/0.93633.00/0.94033.59/0.944733.97/0.9469425.15/0.78927.66/0.85828.82/0.88628.97/0.88630.09/0.90230.51/0.909330.94/0.9135
4.5 实验结果与分析
实验中,我们将本文方法与现阶段一些具有代表性的方法作对比,其中包含Bicubic、SRCNN[7]、VDSR[8]、DRCN[9]、MS-LapSRN[29]和M2SR[16]。为了公平比较,我们将所有的方法在公共测试集Set5、Set14、BSD100、Urban100和Manga109上进行实验测试,然后对于不同测试集上得到的PSNR和SSIM指标值分别取平均值。获得的结果列于表1中,表中红色加粗字体表示在指标上取得的最好结果。从表中可以看出我们的方法获得的PSNR和SSIM值都高于其他的对比方法获得的结果值,比如在数据集Set5上放大2倍的情况下我们的模型重建图像的PSNR和SSIM值相比于排序第二的M2SR方法分别提高了0.16(dB)和0.004,相比于其他方法我们的指标提升得更加明显。表1中的客观指标的实验对比结果证明了我们方法的有效性。
在主观表现方面,将我们的方法也与上述主流方法进行了对比,其中GT(Ground Truth)代表原始HR图像。图2、图3、图4展现了各种方法的在不同测试图像中对比效果。为了突出对比效果,我们选取了图像的局部区域使用双三次插值的方法放大了4倍。通过观察对比图可以看出,我们的方法重建的图像拥有更丰富的细节,更清晰的边缘且更加符合人眼视觉,结果看起来也更清晰。尤其在图3的局部放大部分可以清晰地观察到,其他的方法重建出的图像细节很模糊,甚至无法重建出图像的边缘信息,而我们的方法重建出的细节更加清晰,具有较好的识别度。这些结果也表明了,我们的方法在主观表现上也取得了更优的效果。

图2 图像Urban_010和图像Set5_head在4倍下的效果对比图
Fig.2 The SR results of Urban_010 and Set5_head with scale factor ×4
4.6 消融实验
对于残差学习模块和多尺度注意力模块的有效性,我们在测试集Set5中对图像放大4倍的情况下进行了剥离实验来验证本文模型的优越性。表2给出了网络包含多尺度注意力模块和残差学习模块

图3 图像78004(BSD100)在放大4倍下的效果图
Fig.3 The SR results of 78004(BSD100) with scale factor ×4

图4 图像image_039(Urban100)和image_048(Urban100) 在放大4倍情况下的效果对比图
Fig.4 The SR results of image_039 (Urban100) and image_048(Urban100) with scale factor ×4
中一种或者两种的情况下的实验结果。从表中可以看出,当我们的网络同时包含多尺度注意力模块和残差学习模块时PSNR值相比于只包含多尺度注意力模块和只包含残差学习模块的情况下分别提高了0.83 dB和0.05 dB, 而在SSIM上也获得了最大值。
为了更好的展示网络中两个增强模块的功能,我们对两个模块学习到的特征图进行了可视化,其结果如图5所示。其中图(a)表示网络在第一层卷积输出的结果,图(b)和图(c)分别代表浅层特征增强模块的输出结果和深层残差的特征图,图(d)为整个模型的最终输出结果。从图(b)和(c)可以看出,浅层特征增强模块学习到了图像的结构信息,而深层特征增强模块学习到了更多的图像纹理细节。实验结果表明了本文网络中的两个增强模块起到了很好的纹理细节补充的作用。
表2 多尺度注意力模块和残差学习模块在 数据集Set5放大4倍下结果比较
Tab.2 The results of multi-scale attention block and residual learning block with scale factor ×4 on Set5

多尺度注意力块√×√残差学习块×√√PSNR31.5232.3032.35SSIM0.88510.89650.8969
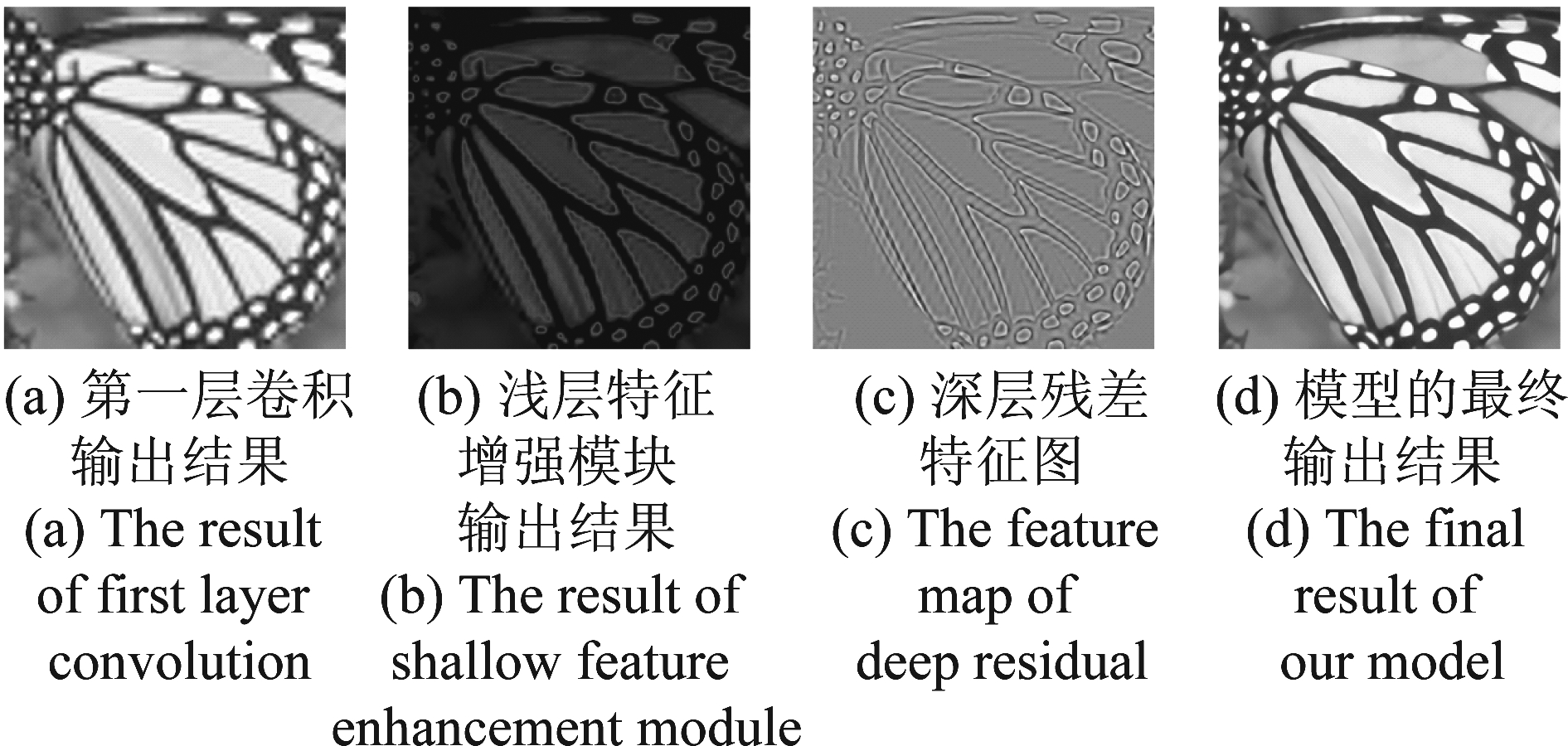
图5 网络的不同深度输出结果
Fig.5 Results of the network at different depths
4.7 参数分析
为了进一步验证本文提出模型的有效性,我们在参数的数量方面和图像重建质量方面将本文方法与当前公认取得效果最好的一些深度学习的超分辨率方法进行了比较,这些方法包括EDSR[11],DBPN[30],RDN[31],RCAN[12]和SAN[13],参数结果如表3所示。从表中可以看出我们的方法在取得了较好的客观指标的同时,大幅缩减了网络的参数量。由此可以证明,我们的网络在图像重建质量和模型压缩上取得了更好的平衡,即我们的模型在参数较少时也能获得较好的PSNR和SSIM结果。虽然本文的模型与RCAN均是利用SEblock[21]来对通道域进行增强,但RCAN模型是在单一尺度下对通道域赋予权值,而我们的网络考虑了多尺度信息在通道域上的差异性,利用注意力机制来增强多尺度信息的表达。在主观视觉效果上,如图6所示,我们的方法与目前客观指标上最优的RCAN[12]和SAN[13]方法进行比较,取得了相近的重建质量,但我们的模型参数仅约是上述两种模型参数的1/5。
表3 模型大小在数据集Set5放大2倍情况下的效果比较
Tab.3 Model size and performance comparison on Set5(×2)
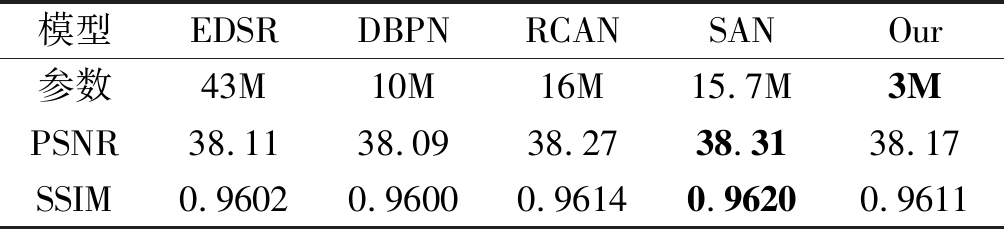
模型EDSRDBPNRCANSANOur参数43M10M16M15.7M3MPSNR38.1138.0938.2738.3138.17SSIM0.96020.96000.96140.96200.9611

图6 图像image_051(Urban100)在放大4倍 情况下的效果对比图
Fig.6 The SR results of image_051 (Urban100) with scale factor ×4
5 结论
本文提出了一种基于渐进式特征增强网络的超分辨率重建方法。该方法着重于对浅层信息和深层信息的特征增强,其增强的过程是基于设计的一种多尺度注意块,利用扩张卷积的方式来高效地获取图像多尺度下的结构信息并利用通道注意力机制来增强提取的特征。不同于以往的专注于加深和加宽网络的深度学习超分辨率方法,该网络的构建既考虑到了图像细节的重建也考虑了模型参数量问题。实验结果表明,本文提出的方法无论在客观指标还是在主观表现下都取得了较好的效果。本文方法的不足之处在于,当放大倍数较大时在纹理丰富的区域会出现平滑现象。未来,我们的工作目标是在较少参数的前提下,设计出更加高效合理的多尺度结构提取更丰富的特征来消除平滑现象,从而获得更好的客观指标和主观效果。
[1] Zhang L, Wu X. An Edge-guided Image Interpolation Algorithm via Directional Filtering and Data Fusion[J]. IEEE Transactions on Image Processing, 2006, 15(8): 2226-2238.
[2] 汪雪林, 文伟, 彭思龙. 基于小波域局部高斯模型的图像超分辨率[J]. 中国图象图形学报, 2004, 9(8): 941-946.
Wang Xuelin, Wen Wei, Peng Silong. Image Super Resolution Based on Wavelet-domain Local Gaussian Model[J]. Journal of Image and Graphics, 2004, 9(8): 941-946.(in Chinese)
[3] Wang S, Zhang L, Liang Y, et al. Semi-coupled Dictionary Learning with Applications to Image Super-Resolution and Photo-sketch Synthesis[C]∥2012 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2012: 2216-2223.
[4] 班晓征, 李志华, 李贝贝, 等. 基于改进广义全变分的稀疏图像重建算法[J]. 激光与光电子学进展, 2018, 55(11): 245-255.
Ban Xiaozheng, Li Zhihua, Li Beibei, et al. Sparse Image Reconstruction Based on Improved Total Generalized Variation[J]. Laser & Optoelectronics Progress, 2018, 55(11): 245-255.(in Chinese)
[5] Zhang K, Gao X, Tao D, et al. Single Image Super-Resolution with Non-Local Means and Steering Kernel Regression[J]. IEEE Transactions on Image Processing, 2012, 21(11): 4544- 4556.
[6] 林格平, 马晓川, 鄢社锋, 等. 无字典的超分辨率多径稀疏信道估计方法[J]. 信号处理, 2017, 33(9): 1239-1247.
Lin Geping, Ma Xiaochuan, Yan Shefeng, et al. Super-Resolution Multipath Sparse Channel Estimation With No Dictionary[J]. Journal of Signal Processing, 2017, 33(9): 1239-1247.(in Chinese)
[7] Dong C, Loy C C, Tang X. Accelerating the Super-Resolution Convolutional Neural Network[C]∥2016 European Conference on Computer Vision. ECCV, 2016: 391- 407.
[8] Kim J, Lee J K, Lee K M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2016: 1646-1654.
[9] Kim J, Lee J K, Lee K M. Deeply-Recursive Convolutional Network for Image Super-Resolution[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2016: 1637-1645.
[10]He K, Zhang X, Ren S et al. Deep Residual Learning for Image Recognition[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2016: 770-778.
[11]Lim B, Son S, Kim H, et al. Enhanced Deep Residual Networks for Single Image Super-Resolution[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. CVPRW, 2017: 1132-1140.
[12]Zhang Y, Li K, Li K, et al. Image Super-Resolution Using Very Deep Residual Channel Attention Networks[C]∥2018 European Conference on Computer Vision. ECCV, 2018: 294-310.
[13]Dai T, Cai J, Zhang Y, et al. Second-Order Attention Network for Single Image Super-Resolution[C]∥2019 IEEE Computer Vision and Pattern Recognition. CVPR, 2019: 11065-11074.
[14]Hui Z, Gao X, Yang Y, et al. Lightweight Image Super-Resolution with Information Multi-distillation Network[C]∥2019 ACM Multimedia. ACMM, 2019: 2024-2032.
[15]Li Z, Yang J, Liu Z, et al. Feedback Network for Image Super-Resolution[C]∥2019 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2019: 3862-3871.
[16]Yang Y, Zhang D, Huang S, et al. Multilevel and Multiscale Network for Single-Image Super-Resolution[J]. IEEE Signal Processing Letters, 2019, 26(12): 1877-1881.
[17]Han W, Chang S, Liu D, et al. Image Super-Resolution via Dual-State Recurrent Networks[C]∥2018 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2018: 1654-1663.
[18]Li J, Fang F, Mei K, et al. Multi-scale Residual Network for Image Super-Resolution[C]∥2018 European Conference on Computer Vision. ECCV, 2018: 527-542.
[19]Itti L, Koch C, Niebur E, et al. A Model of Saliency-based Visual Attention for Rapid Scene Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(11): 1254-1259.
[20]Wang X, Girshick R, Gupta A, et al. Non-local Neural Networks[C]∥2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR, 2018: 7794-7803.
[21]Hu J, Shen L, Sun G. Squeeze-and-Excitation Networks[C]∥2018 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2018: 7132-7141.
[22]Timofte R, Agustsson E, Van Gool L, et al. Ntire 2017 Challenge on Single Image Super-Resolution: Methods and Results[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. CVPRW, 2017: 114-125.
[23]Bevilacqua M, Roumy A, Guillemot C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]∥Proc. Brit. Mach. Vis. Conf. BMVC, 2012:1-10.
[24]Zeyde R, Elad M, Protter M. On Single Image Scale-Up Using Sparse-Representations[C]∥2010 IEEE International Conference on Curves and Surfaces. ICCS, 2010: 711-730.
[25]Martin D, Fowlkes C, Tal D, et al. A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics[C]∥2001 IEEE International Conference on Computer Vision and Pattern Recognition. CVPR, 2001, 2: 416- 423.
[26]Huang J B, Singh A, Ahuja N. Single Image Super-Resolution From Transformed Self-exemplars[C]∥2015 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2015: 5197-5206.
[27]Matsui Y, Ito K, Aramaki Y, et al. Sketch-based Manga Retrieval Using Manga109 Dataset[J]. Multimedia Tools and Applications, 2017, 76(20): 21811-21838.
[28]Wang Z, Bovik A C, Sheikh H R, et al. Image Quality Assessment: From Error Visibility to Structural Similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600- 612.
[29]Lai W, Huang J, Ahuja N, et al. Fast and Accurate Image Supe-Resolution with Deep Laplacian Pyramid Networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 41(11): 2599-2613.
[30]Haris M, Shakhnarovich G, Ukita N, et al. Deep Back-Projection Networks for Super-Resolution[C]∥2018 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2018: 1664-1673.
[31]Zhang Y, Tian Y, Kong Y, et al. Residual Dense Network for Image Super-Resolution[C]∥2018 IEEE Conference on Computer Vision and Pattern Recognition. CVPR, 2018: 2472-2481.



