1 引言
图像分割是目标检测和图像理解等众多图像分析应用中至关重要的预处理环节,需要精确、稳定和高效的算法。然而,由于图像中存在的不确定性和复杂性,使得图像分割仍然是一项具有挑战性的任务。目前国内外被广泛使用的图像分割算法有阈值分割法[1]、边缘分割法[2]、聚类分割法[3]、区域分割法[4]和基于人工神经网络的分割算法[5]等。模糊C-均值聚类(Fuzzy C-Means clustering, FCM)算法[6]是一种经典的模糊聚类算法,它假设图像中的每个像素以不同的隶属程度属于多个类,通过模糊隶属度函数和聚类中心的交替迭代实现每个像素的归属,能够有效地处理图像中的模糊性。FCM算法效率高、稳定性好,在图像分割领域获得了成功的应用[7-8]。
基于直觉模糊集理论[9-11],Xu和Wu[12]提出了直觉模糊C-均值聚类(Intuitionistic Fuzzy C-Means clustering, IFCM)算法。作为FCM的一种有效拓展算法,IFCM算法在隶属度和非隶属度的基础上,引入了犹豫度的概念,试图更好刻画客观事物的模糊本质。与FCM算法相比,IFCM算法能够更好地处理图像中的不确定信息。
需指出,无论是IFCM算法还是FCM算法应用于图像分割时,都只单一地使用了图像的像素信息,而没有根据图像本身的几何特性、空间特性或区域特性考虑更多的图像信息。现实世界中的许多自然物体、人工建筑和交通工具等在不同程度上都具有一定的几何对称性。由于对称的普遍性,使得对称特性成为了图像分割的有用特征之一。近年来,很多学者已经通过研究证明,对称信息有助于图像分割[13-15]。一些将对称信息与FCM相结合的工作[16-17]也证明了对称性能够有助于提高模糊聚类算法的图像分割性能。为了有效利用图像的空间特性,学者们后续提出了具有空间约束的模糊聚类方法,如引入邻域空间限制项的FCM算法(FCM with Spatial constraints, FCM_S)算法[18],模糊局部信息C-均值(Fuzzy Local Information C-Means, FLICM)聚类算法[19],结合局部信息的直觉模糊核聚类(Intuitionistic Kernel-based Fuzzy C-Means clustering with Local information, IKFCM_L)算法[20]等。这些方法大多使用了固定窗口内的近邻像素来获取局部空间信息,提高了模糊聚类算法对于图像噪声的鲁棒性。此外,一般的聚类算法应用于图像分割时,往往是在像素层面上进行聚类,导致算法计算时间长,且忽略了图像的区域信息。因此,学者们尝试将区域信息引入到模糊聚类算法中,通过将图像分为若干个小区域,再提取出各个区域的特征,以各个区域特征作为基本处理单元来进行聚类,已有研究工作证明[21-23],引入区域信息的模糊聚类算法能够有效保持图像的区域特性且提高了算法的运行效率。
经典的FCM和IFCM算法都是无监督聚类方法,在进行图像分割时未使用图像中的任何先验信息。因此,对于背景复杂的图像分割性能较差。此外,如果聚类中心初始化不当,搜素聚类最优解的过程也具有一定的盲目性,使得聚类算法易陷入局部最优。在实际分割场景中,我们有时可以利用原始数据获得一部分先验信息,例如:成对约束,类别标签,监督隶属度等。近年来,学者们研究了使用少量监督信息来指导聚类过程,提出了一系列半监督模糊聚类方法[24-25]。例如,Yasunori等人[26]将监督隶属度分别引入到标准模糊C-均值聚类和熵正则化模糊C-均值聚类算法中,构建了半监督标准模糊C-均值聚类算法(Semi-supervised standard Fuzzy C-Means clustering, sSFCM)和半监督熵正则化模糊C-均值聚类(Semi-supervised entropy regularized Fuzzy C-Means clustering, eSFCM)。Son等人[27]提出将空间约束引入到半监督模糊聚类中,提出了一种具有空间约束的半监督模糊聚类算法(Semi-Supervised Fuzzy Clustering algorithm with Spatial Constraints, SSFC-SC)。
为了进一步提升IFCM算法在图像分割这一应用场景下的性能,本文提出了一种融合对称特性的混合标签传递半监督直觉模糊C-均值聚类算法(Hybrid Label Propagation Semi-supervised Intuitionistic Fuzzy C-Means clustering incorporated Symmetric property, HLPS-SIFCM)。HLPS-SIFCM算法的要点归纳如下:1)考虑了图像的对称特性,通过对称轴检测算法获得图像的对称性信息;2)考虑了图像的区域信息,利用超像素策略获取图像的区域信息;3)利用图像的对称特性进行对称像素的标签传递并改进像素对聚类中心的直觉模糊距离测度,设计了一种混合标签传递半监督策略,使得监督信息得到充分利用;4)将对称信息、区域信息和监督信息引入进来,构造了构建融合对称特性的混合标签传递半监督直觉模糊聚类目标函数,获得最终的分割结果。在两个彩色图像库上进行实验,结果表明HLPS-SIFCM算法能够将目标从复杂背景中较好地分割出来,分割效果优于FCM[6]、IFCM[12]、symFCM[16]、sSFCM[26]、SSFC-SC[27]和eSFCM[26]算法。
2 相关算法
2.1 直觉模糊C-均值聚类算法
1986年,Atanassov[9]提出了直觉模糊集理论,在隶属度和非隶属度概念的基础上,引入了犹豫度的概念,能够进一步描述客观世界的模糊性和不确定性,它是模糊集理论的有效扩展。设X为一已知数据集,将X上的直觉模糊集A定义为:
A={〈x,μA(x),vA(x)〉|∀x∈X,0≤μA(x), vA(x)≤1,0≤μA(x)+vA(x)≤1}
(1)
其中,μA(x)和vA(x)分别表示数据x对应的隶属度函数和非隶属度函数。
通常,直觉模糊集的非隶属度函数vA(x)可以由Sugeno函数[28]生成,其表达式如下:
![]() (-1<δ<
(-1<δ< )
)
(2)
其中,δ一般取值为2.5。
此外,直觉模糊集引入了犹豫度函数![]() A(x),使得在处理模糊性和不确定性等方面更具灵活性和实用性[29]。基于隶属度和非隶属度,
A(x),使得在处理模糊性和不确定性等方面更具灵活性和实用性[29]。基于隶属度和非隶属度,![]() A(x)可定义为:
A(x)可定义为:
![]() A(x)=1-μA(x)-vA(x),0≤
A(x)=1-μA(x)-vA(x),0≤![]() A(x)≤1
A(x)≤1
(3)
在模糊C-均值算法中引入直觉模糊集的概念,Xu和Wu[12]提出了直觉模糊C-均值算法(IFCM)。IFCM算法的目标函数如下:
(4)
其中,![]() 是一个具有N个数据点的直觉模糊数据集,并且每一个数据点
是一个具有N个数据点的直觉模糊数据集,并且每一个数据点![]() 都以直觉模糊集
都以直觉模糊集![]()
![]() (xj))的形式表示,k为聚类数目。uij表示第j个数据点
(xj))的形式表示,k为聚类数目。uij表示第j个数据点![]() 对于第i类的隶属度,满足
对于第i类的隶属度,满足![]() 为模糊指数,一般取
为模糊指数,一般取![]() 表示第i类的聚类中心,定义为
表示第i类的聚类中心,定义为![]() 是
是![]() 和
和![]() 之间的直觉欧式距离,定义为:
之间的直觉欧式距离,定义为:
![]() (v(xj)-v(ci))2+(
(v(xj)-v(ci))2+(![]() (xj)-
(xj)-![]() (ci))2]1/2
(ci))2]1/2
(5)
2.2 熵正则化半监督模糊聚类算法
Yasunori等人[26]通过将监督隶属度引入熵正则化模糊C-均值聚类算法中,提出半监督熵正则化模糊C-均值聚类算法(eSFCM),其目标函数如下:
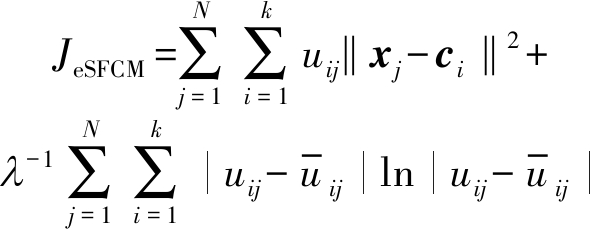
(6)
其中,X={x1,x2,…,xj,…,xN}表示一个具有N个数据点的数据集,k是聚类数目。uij表示第j个数据点xj对于第i类的隶属度,满足![]() 表示第i类的聚类中心,λ表示监督项的权重指数,
表示第i类的聚类中心,λ表示监督项的权重指数,![]() 表示第j个标记数据点xj对于第i类的监督隶属度,当标记数据点xj属于第i类时,
表示第j个标记数据点xj对于第i类的监督隶属度,当标记数据点xj属于第i类时,![]() 否则
否则![]() 此外,未标记数据点的监督隶属度也为0,因此
此外,未标记数据点的监督隶属度也为0,因此![]()
通过拉格朗日乘子法来最小化目标函数,可求得uij和ci的更新公式分别为:
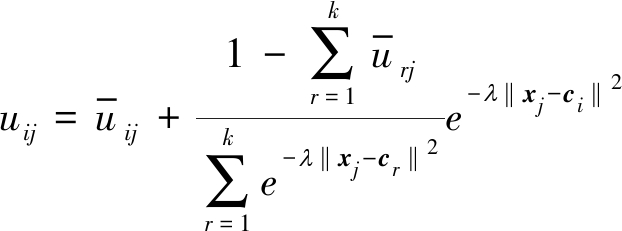
(7)
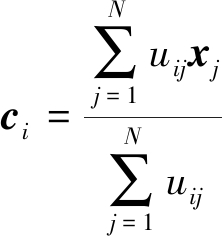
(8)
3 融合对称特性的混合标签传递半监督直觉模糊聚类算法
3.1 图像的直觉模糊化
直觉模糊聚类方法用于图像分割时,首先需要将图像进行直觉模糊化[30]。设X={x1,x2,…,xN}为一幅具有N个像素的彩色图像,其中,xj表示第j个像素的3维RGB值。那么,图像X的直觉模糊集可以表示为:
XIFS={〈xj,μ(xj),v(xj),![]() (xj)〉|j=1,2,…,N}
(xj)〉|j=1,2,…,N}
(9)
上式中,μ(xj)表示像素j的隶属度,在彩色图像中,需要分别计算出RGB三个分量下的隶属度,以R分量为例,可以通过以下函数计算得到:
(10)
其中,![]() 和
和![]() 分别代表图像X在R分量下的最小值和最大值。同理,可以计算出G和B分量下的μG(xj)和μB(xj),即得到了像素j的隶属度:
分别代表图像X在R分量下的最小值和最大值。同理,可以计算出G和B分量下的μG(xj)和μB(xj),即得到了像素j的隶属度:
μ(xj)=(μR(xj),μG(xj),μB(xj))
(11)
然后,通过式(2)和式(3)计算得到第j个像素的非隶属度v(xj)和犹豫度![]() (xj)。通过这种方式实现了图像的直觉模糊集表示的获取。
(xj)。通过这种方式实现了图像的直觉模糊集表示的获取。
3.2 图像对称特性的利用
自然界中很多事物具有天然的对称特性。在一幅具有对称特性的图像中,位于对称位置的像素往往具有一定的相似性[16],这意味着它们属于同一类的可能性较大。因此,将对称特性引入到图像分割算法中有助于提高图像分割性能。为了获得图像的对称性信息,本文采用基于配准的对称轴检测方法[31]来获得图像的对称轴,通过对称轴来确定像素的对称像素,以此作为图像的对称性信息。
利用原像素与对称像素相似的特点,将对称特性引入到已知标签像素的标签传递和像素与聚类中心的距离测度中,具体来说:
一方面,利用对称特性对用户给定标签的像素进行对称传递。由于相对称的两个像素它们属于同一类的可能性较大,因此假设关于对称轴对称的像素具有相同的类别标签,从而利用对称轴将标签进行对称传递。实现方法为:首先,对有标签的像素求解其关于对称轴的对称像素。需要注意的是,对于不同的图像检测到的对称轴并不一定位于图像中央,这样可能导致求得的对称像素并不一定位于图像内部,因此,需要将超出图像边界的对称像素丢弃。然后,对未超出图像边界的对称像素赋予与原像素相同的类别标签。
另一方面,在像素与聚类中心的直觉模糊距离测度中引入对称特性。当像素在结构上具有一定程度的对称性时,由局部颜色不均匀引起聚类错误的像素可以得到校正。因此在距离测度中考虑对称特性是有效的。融合对称特性的像素与聚类中心之间的直觉模糊距离函数表示为:
(12)
其中,![]() 是
是![]() 的对称像素的直觉模糊表示,α是用来调节对称信息贡献的加权因子。
的对称像素的直觉模糊表示,α是用来调节对称信息贡献的加权因子。
3.3 基于混合标签传递的半监督策略
为了将半监督学习方法引入到直觉模糊聚类算法中,本文提出一种混合标签传递的半监督策略,其本质是通过引入监督隶属度来指导整个直觉模糊聚类过程。混合标签传递策略共分为两部分,一是假设关于对称轴对称的像素具有相同的类别标签,通过对称轴进行一次标签传递,那么对称像素的隶属度与原像素的隶属度也相等;二是通过度量有标签像素与其余无标签像素之间的距离得到无标签像素的估计隶属度。此外,还利用混合标签传递后的监督隶属度进行初始聚类中心的计算,从而代替传统的随机初始化聚类中心,这样可以更加快速地找到最优解,也提高了聚类准确率。具体做法如下:
首先,根据用户可以获得的先验知识对部分像素做类别标记,预先得到部分像素对于某些类的先验隶属度![]() 表示为:
表示为:
(13)
通常,对于像素xj,如果它是一个没有标记的像素,那么![]() 如果它是一个有标记的像素,且属于第i类,那么
如果它是一个有标记的像素,且属于第i类,那么![]() 否则,
否则,![]()
其次,利用对称特性对用户给定标签的像素进行对称标签传递,使得对称像素获得与原像素相同的类别标签和隶属度。然后,将对称像素的隶属度与先验隶属度![]() 合并,作为对称标签传递后的隶属度,称其为对称传递隶属度
合并,作为对称标签传递后的隶属度,称其为对称传递隶属度![]()
为了更好的发挥标记像素的作用,考虑利用标记像素xl与未标记像素xu的距离关系来对未标记像素的隶属度进行估计,定义为估计隶属度![]() 计算公式如下:
计算公式如下:
(14)
其中,![]() 表示标记的像素集合,dlu表示xl与xu之间的欧式距离,显然,xl与xu之间距离越近,得到的未标记像素的估计隶属度就越接近标记像素的隶属度。
表示标记的像素集合,dlu表示xl与xu之间的欧式距离,显然,xl与xu之间距离越近,得到的未标记像素的估计隶属度就越接近标记像素的隶属度。
将未标记像素的估计隶属度![]() 与有标记像素的对称传递隶属度
与有标记像素的对称传递隶属度![]() 合并,得到最终混合标签传递后的隶属度矩阵
合并,得到最终混合标签传递后的隶属度矩阵![]() 把
把![]() 作为指导聚类整个过程的监督隶属度。
作为指导聚类整个过程的监督隶属度。
最后,利用最终得到的监督隶属度![]() 求得初始聚类中心
求得初始聚类中心![]() 计算公式如下:
计算公式如下:
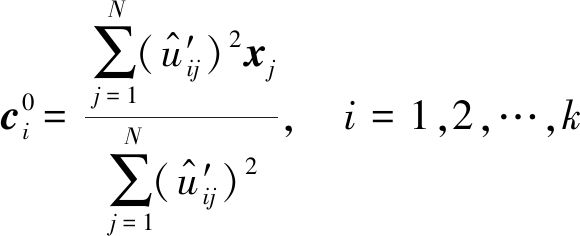
(15)
混合标签传递半监督策略的具体流程如下:
步骤1 用户利用可以获得的先验信息对图像部分像素进行类别标记,并求出它的先验隶属度![]()
步骤2 对用户标记的像素求其关于对称轴的对称像素,并判断是否位于图像内部,将超出图像边界的对称像素丢弃;
步骤3 对未超出图像边界的对称像素赋予与原像素相同的类别标签和隶属度,将对称像素的隶属度与先验隶属度![]() 合并,得到对称传递隶属度
合并,得到对称传递隶属度![]()
步骤4 根据标记像素与未标记像素的距离关系,通过式(14)求出未标记像素的估计隶属度![]()
步骤5 将估计隶属度![]() 与对称传递隶属度
与对称传递隶属度![]() 合并,得到整幅图的监督隶属度
合并,得到整幅图的监督隶属度![]()
步骤6 将监督隶属度![]() 代入式(15)中,求出初始聚类中心
代入式(15)中,求出初始聚类中心![]()
3.4 融合对称特性的混合标签传递半监督直觉模糊聚类目标函数的设计
通常情况下,图像并不是严格对称的,所以仅使用图像的对称信息对图像分割进行指导是不够充分的。传统的直觉模糊聚类算法应用于图像分割时,往往还忽略了图像的区域信息。鉴于此,本文利用简单线性迭代聚类(Simple Linear Iterative Cluster, SLIC)算法[32]将图像分割成许多大小和形状不同的区域,然后获取每个区域的代表性特征,以此作为该区域内像素点的区域特征信息。因此将图像像素的区域特征信息、对称信息及监督隶属度![]() 同时引入到直觉模糊聚类的目标函数中,构造了融合对称特性的混合标签传递的半监督直觉模糊聚类目标函数,定义如下:
同时引入到直觉模糊聚类的目标函数中,构造了融合对称特性的混合标签传递的半监督直觉模糊聚类目标函数,定义如下:
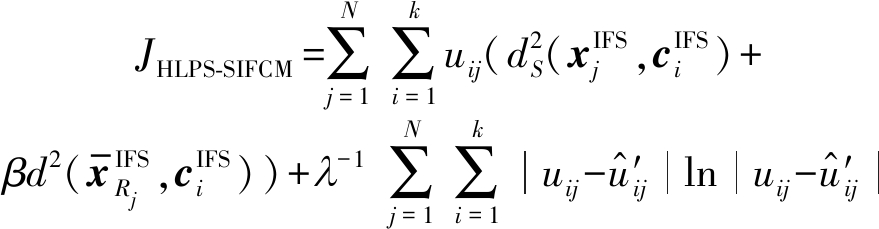
(16)
其中,![]() 表示一个具有N个像素点的彩色图像,每个像素点都定义为
表示一个具有N个像素点的彩色图像,每个像素点都定义为![]()
![]() (xj)),k是聚类数目,uij表示第j个像素点对于第i类的隶属度,满足
(xj)),k是聚类数目,uij表示第j个像素点对于第i类的隶属度,满足![]()
![]() (ci))表示第i类的聚类中心。如公式(12)所示,
(ci))表示第i类的聚类中心。如公式(12)所示,![]() 是融合对称特性的像素与聚类中心之间的直觉模糊距离的平方,其中,α是调节对称信息贡献的加权因子,
是融合对称特性的像素与聚类中心之间的直觉模糊距离的平方,其中,α是调节对称信息贡献的加权因子,![]() 是
是![]() 的对称像素。β是调节区域信息贡献的加权因子,Rj表示第j个像素点所属的区域,
的对称像素。β是调节区域信息贡献的加权因子,Rj表示第j个像素点所属的区域,![]() 表示区域Rj内像素特征的平均值的直觉模糊表示。λ表示监督项的权重指数,
表示区域Rj内像素特征的平均值的直觉模糊表示。λ表示监督项的权重指数,![]() 表示第j个像素点对于第i类的监督隶属度。
表示第j个像素点对于第i类的监督隶属度。
由于每个形状和大小不同的区域在一定程度上都是由相似特性的像素组成,同一区域的像素之间的关系要比不同区域的像素之间关系更为密切,使得提取的区域信息会比传统的基于固定窗口形状的方法更加有效。此外,区域信息与混合标签传递监督隶属度的引入也能够在对称特性不好的情况下,对分割结果进行补充修正,从而进一步提高直觉模糊聚类图像分割的性能。
利用拉格朗日乘子γ构造一个新函数L,用来求解使得目标函数最小化的最优解![]() 将其定义为:
将其定义为:
![]()
![]()
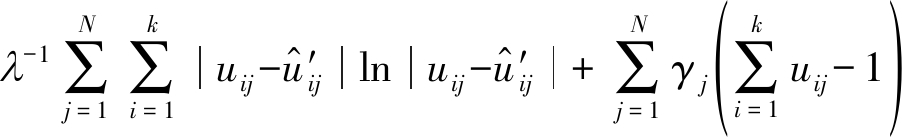
(17)
对函数L分别求关于μ(ci)、v(ci)和![]() (ci)的偏导数并设置为0。
(ci)的偏导数并设置为0。
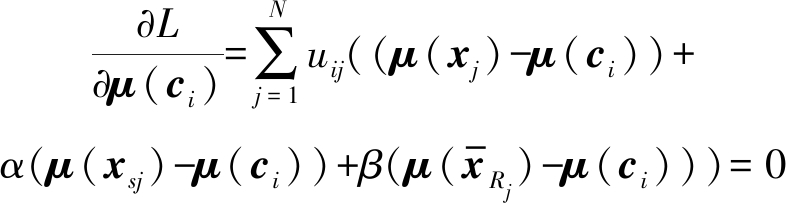
(18)
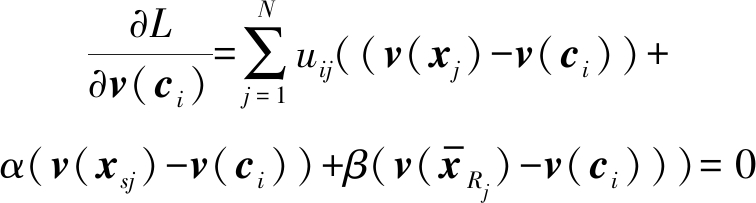
(19)
![]()
![]() (xj)-
(xj)-![]() (ci))+ α(
(ci))+ α(![]() (xsj)-
(xsj)-![]() (ci))+β(
(ci))+β(![]()
![]()
![]() (ci)))=0
(ci)))=0
(20)
通过求解公式(18)~(20),可以求得聚类中心![]() 的更新公式为:
的更新公式为:

(21)
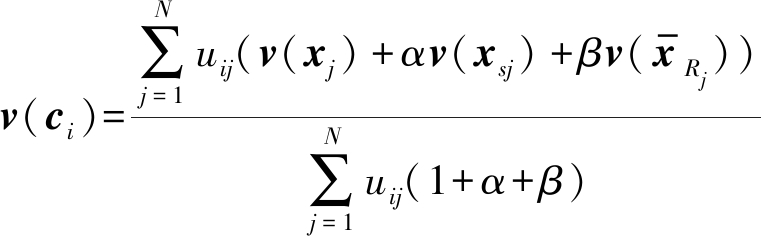
(22)
![]()
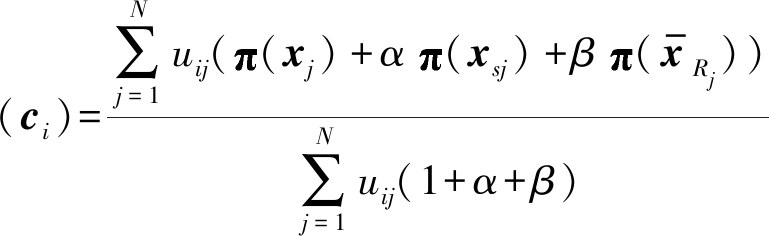
(23)
然后,为了求解使目标函数最小化的最优解uij,考虑以下没有绝对值的目标函数:

(24)
同样的,引入拉格朗日乘子γ构造一个新函数L′,用来求解使得目标函数最小化的最优解uij。
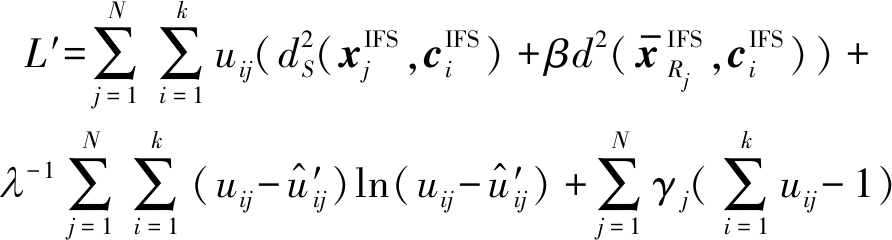
(25)
对函数L′分别求关于uij和γj的偏导数并使其等于0,可得
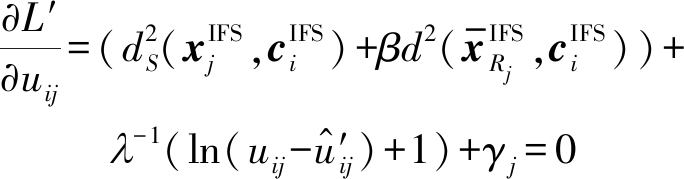
(26)
(27)
由公式(26)可得
(28)
将公式(28)代入公式(27)中,得到
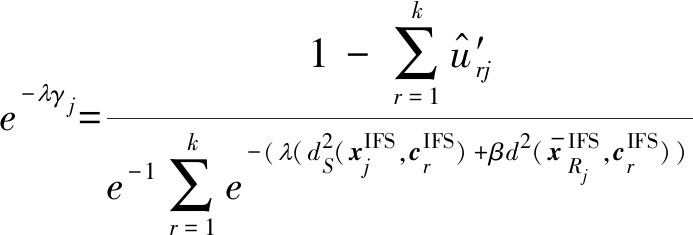
(29)
根据公式(28)和公式(29),可得
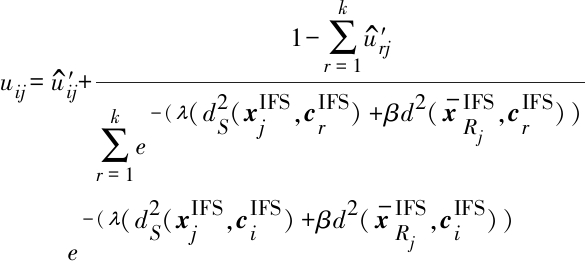
(30)
3.5 算法流程
融合对称特性的混合标签传递半监督直觉模糊聚类图像分割算法的步骤如下:
输入 图像X,用户标记信息,聚类数目k,最大迭代次数T,终止阈值ε,加权因子α和β,监督项权重指数λ。
输出 图像X的分割结果。
步骤1 根据式(11),(2)和(3)对图像X进行直觉模糊化处理;
步骤2 获得图像的对称信息和区域信息;
步骤3 由用户标记信息构造先验隶属度![]() 再通过标签混合传递策略得到监督隶属度
再通过标签混合传递策略得到监督隶属度![]() 由公式(15)求得初始聚类中心
由公式(15)求得初始聚类中心![]() 并对其进行直觉模糊化;
并对其进行直觉模糊化;
步骤4 初始化迭代次数t=0;
步骤5 根据公式(30)更新隶属度U;
步骤6 根据公式(21)~(23)更新直觉模糊聚类中心![]()
![]() (ci));
(ci));
步骤7 判断迭代终止条件。若![]() 或算法迭代次数t>T,则获得隶属度矩阵U和直觉模糊聚类中心
或算法迭代次数t>T,则获得隶属度矩阵U和直觉模糊聚类中心![]()
![]() (ci)),执行步骤8;否则,t=t+1,返回步骤5。
(ci)),执行步骤8;否则,t=t+1,返回步骤5。
步骤8 根据获得的隶属度矩阵U中像素对聚类中心的隶属度值,获得图像像素的聚类标签,输出图像X的分割结果。
4 实验结果及分析
4.1 实验设置
为了验证HLPS-SIFCM算法的优越性和有效性,本实验选用了FCM[6]、IFCM[12]、symFCM[16]、sSFCM[26]、SSFC-SC[27]和eSFCM[26]等6种算法作为对比算法,用聚类准确率(CA)[33]作为分割性能的评价指标,使用Berkeley[34]和Weizmann[35]两个图像库上的图像进行实验验证。对于各个算法所涉及到的参数设置如下:FCM、IFCM、symFCM、sSFCM和SSFC-SC的模糊指数m设置为2;所有算法的聚类数目按照人工分割的标准图给定,最大迭代次数设置为100,终止阈值设置为10-5;sSFCM、SSFC-SC、eSFCM和本文算法都使用相同的标记信息;eSFCM 和本文算法监督项权重指数λ设置为2;SSFC-SC算法中参数![]() 取值为0.9;本文算法中对称特性和区域信息的加权因子α和β取经验值0.5,超像素块数目设置为300。
取值为0.9;本文算法中对称特性和区域信息的加权因子α和β取经验值0.5,超像素块数目设置为300。
4.2 Weizmann图像对比实验
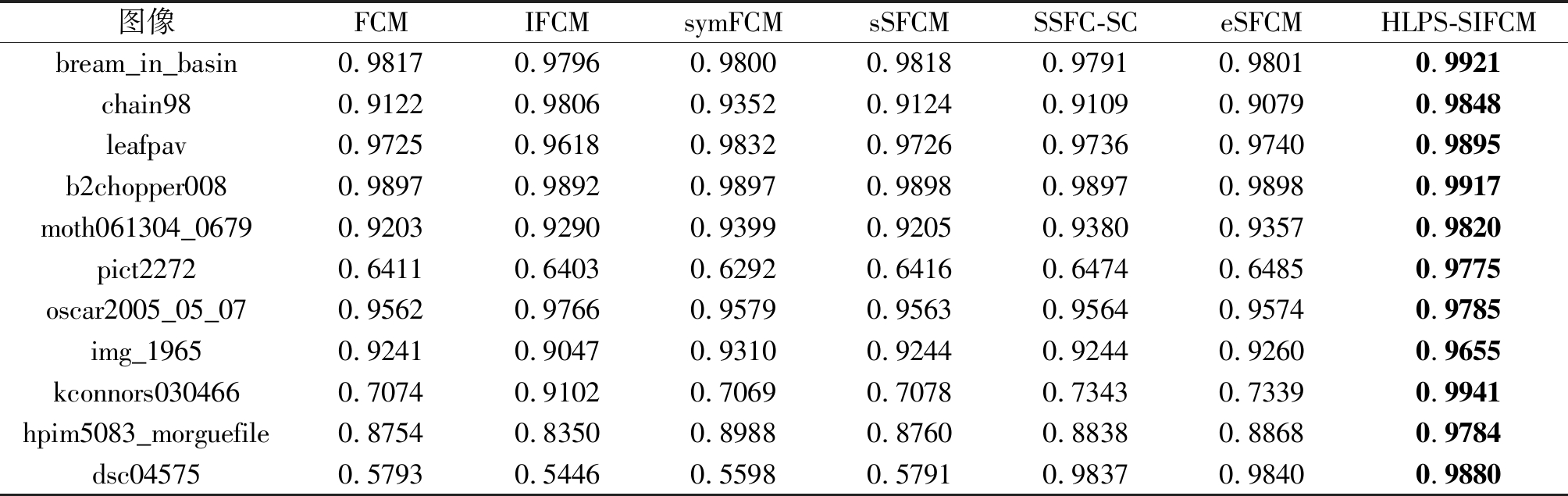
本节采用了多幅来自于Weizmann图像库中的彩色图像来验证HLPS-SIFCM算法和对比算法的分割性能。表1给出了各个算法在不同图像上获得的聚类准确率。对比sSFCM、SSFC-SC、eSFCM和HLPS-SIFCM算法的准确率结果可以看出,虽然它们作为半监督聚类算法都使用了相同的标签信息,但HLPS-SIFCM算法在多数情况下聚类准确率都优于其他算法,这是由于sSFCM、SSFC-SC、eSFCM这三种算法仅使用了人工标记的标签数据,并未对监督信息进行充分的利用。本文方法设计的混合标签传递策略不仅使用了人工标记的标签数据,而且还对无标签数据进行了预测,使得监督信息得到了有效的扩充,可以更好的指导聚类。例如,以图像pict2272、kconnors030466、hpim5083_morguefile的准确率结果来看,半监督方法与无监督方法相比,准确率并没有得到很大的提升,而本文的HLPS-SIFCM分割准确率较为突出,由此表明,本文采用的混合标签传递策略可以为聚类图像分割提供更为有效的引导作用。
为了展示视觉分割效果,图1~图6展示了所有算法在6幅Weizmann图像上的分割结果图。图1表明,在背景相对比较杂乱的情况下,只有IFCM算法和HLPS-SIFCM算法能将目标与背景完全分割出来,由此可以体现本文采用的基础算法IFCM用于图像分割时具有一定优越性。可以看出图1(a)具有良好的对称性,通过图1(f)与(h)对比发现,添加对称特性后分割结果得到了一定程度的改善,这也验证了在模糊聚类图像分割算法中引入对称特性具有一定的可行性。从图2可以看出,所有算法都能对目标区域进行大致的提取,但是对比算法对背景区域误分现象比较严重,无论是添加对称特性的symFCM算法,还是半监督聚类算法sSFCM以及添加区域信息的半监督聚类算法SSFC-SC都未取得理想的分割结果,而本文的HLPS-SIFCM算法由于引入了混合标签传递策略,其分割结果有了明显的改善。图3结果显示,与对比算法相比,由于本文算法融合了图像的对称特性和区域信息,对于目标细节的分割更为完整。从图4、图5和图6的(j)与(i)结果对比可以看出,虽然SSFC-SC算法和sSFCM算法使用了相同的标签信息,但是SSFC-SC算法在sSFCM算法基础上考虑了区域信息,因此对分割结果有明显的提升,这也验证了在半监督模糊聚类中添加区域信息的可行性。对于图5,虽然对称轴确定的不是十分理想,本文的HLPS-SIFCM算法仍取得了较好的分割效果,这是由于算法中的区域信息与监督信息可在聚类过程中将对称性不好的像素进行修正。
表1 Weizmann图像上的聚类准确率对比
Tab.1 Comparison of clustering accuracy on Weizmann images
图像FCMIFCMsymFCMsSFCMSSFC-SCeSFCMHLPS-SIFCMbream_in_basin0.98170.97960.98000.98180.97910.98010.9921chain980.91220.98060.93520.91240.91090.90790.9848leafpav0.97250.96180.98320.97260.97360.97400.9895b2chopper0080.98970.98920.98970.98980.98970.98980.9917moth061304_06790.92030.92900.93990.92050.93800.93570.9820pict22720.64110.64030.62920.64160.64740.64850.9775oscar2005_05_070.95620.97660.95790.95630.95640.95740.9785img_19650.92410.90470.93100.92440.92440.92600.9655kconnors0304660.70740.91020.70690.70780.73430.73390.9941hpim5083_morguefile0.87540.83500.89880.87600.88380.88680.9784dsc045750.57930.54460.55980.57910.98370.98400.9880
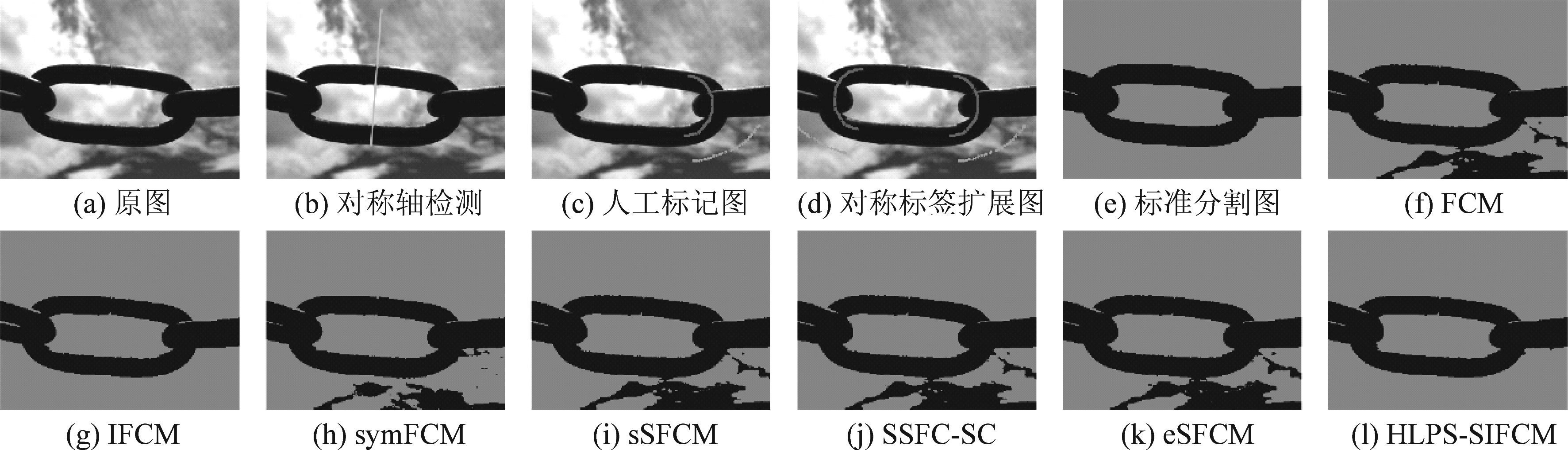
图1 chain98分割结果图
Fig.1 chain98 Segmentation results

图2 pict2272分割结果图
Fig.2 pict2272 Segmentation results

图3 oscar2005_05_07分割结果图
Fig.3 oscar2005_05_07 Segmentation results


图4 kconnors030466分割结果图
Fig.4 kconnors030466 Segmentation results
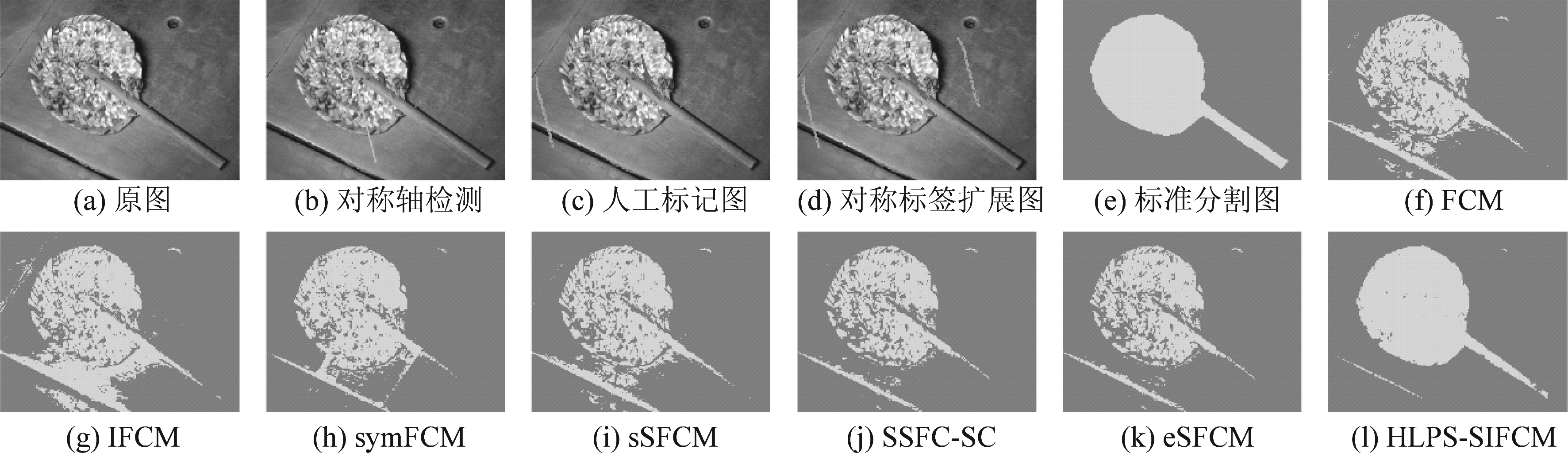
图5 hpim5083_morguefile分割结果图
Fig.5 hpim5083_morguefile Segmentation results

图6 dsc04575分割结果图
Fig.6 dsc04575 Segmentation results
4.3 Berkeley图像对比实验
为了进一步测试HLPS-SIFCM算法的分割性能,本节采用来自于Berkeley图像库的多幅图像来测试所提算法的有效性。表2展示了所有方法在这些图像上获得的聚类准确率。可以看出,HLPS-SIFCM算法由于引入了对称特性、区域信息和混合标签传递半监督策略,这些信息在分割过程中相互补充,使得本文算法的分割性能明显优于其他方法。
图7~图12展示了所有方法在6幅Berkeley图像上的视觉分割结果。图7(a)的两朵花具有良好的对称特性,从图7( f )与(h)的对比可以看出,添加对称特性的模糊聚类算法其分割效果有明显的改善,说明对称特性对良好的分割是有帮助的,而且在sSFCM算法基础上添加区域信息的SSFC-SC算法分割结果图7(j)也相较于sSFCM算法的图7(i)结果有相应的提升,这说明区域信息也对分割性能有一定的提升,HLPS-SIFCM算法的分割结果是理想的。观察图8、图9以及图10,我们发现对比方法的分割结果都对背景区域的误判较多,分割效果并不理想,特别是从各个图像的(g)、(h)、(i)、(j)、(k)的对比可以看出,采用直觉模糊聚类、添加对称特性、区域信息以及引入半监督学习都未能将目标与背景分离开来,而HLPS-SIFCM算法由于采用了混合标签传递策略使得分割结果更为理想。从图11可以看出,由于花瓶上下颜色不一致,对比算法都错误地将花瓶与墙面分为一类,而HLPS-SIFCM算法更加接近标准分割图,表明本文算法的良好分割性能。从图12中的分割结果可以发现,大多数对比方法对沙漠的错分比较明显,由于这幅图像对称性较好,HLPS-SIFCM结果最优,其次为symFCM算法,其余算法分割效果差异很小,说明对称特性与混合标签传递策略对于这幅图的分割提供了积极的引导作用。
表2 Berkeley图像上的聚类准确率对比
Tab.2 Comparison of clustering accuracy on Berkeley images
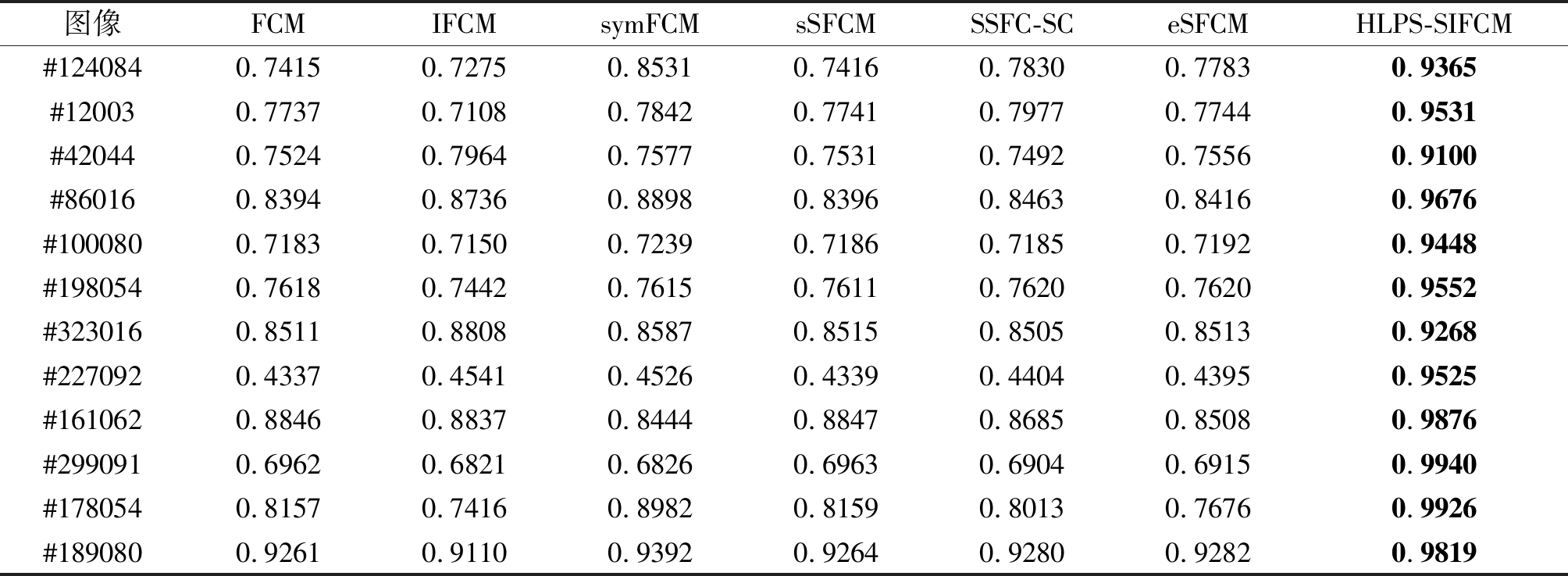
图像FCMIFCMsymFCMsSFCMSSFC-SCeSFCMHLPS-SIFCM#1240840.74150.72750.85310.74160.78300.77830.9365#120030.77370.71080.78420.77410.79770.77440.9531#420440.75240.79640.75770.75310.74920.75560.9100#860160.83940.87360.88980.83960.84630.84160.9676#1000800.71830.71500.72390.71860.71850.71920.9448#1980540.76180.74420.76150.76110.76200.76200.9552#3230160.85110.88080.85870.85150.85050.85130.9268#2270920.43370.45410.45260.43390.44040.43950.9525#1610620.88460.88370.84440.88470.86850.85080.9876#2990910.69620.68210.68260.69630.69040.69150.9940#1780540.81570.74160.89820.81590.80130.76760.9926#1890800.92610.91100.93920.92640.92800.92820.9819

图7 #124084分割结果图
Fig.7 #124084 Segmentation results

图8 #12003分割结果图
Fig.8 #12003 Segmentation results

图9 #86016分割结果图
Fig.9 #86016 Segmentation results

图10 #100080分割结果图
Fig.10 #100080 Segmentation results

图11 #227092分割结果图
Fig.11 #227092 Segmentation results

图12 #178054分割结果图
Fig.12 #178054 Segmentation results
5 结论
为了改善直觉模糊聚类算法对于复杂彩色图像的分割性能,本文提出了一种融合对称特性的混合标签传递半监督直觉模糊聚类图像分割算法,该算法首先挖掘了图像的对称信息,然后将对称信息分别用于对称像素的标签传递和融合对称特性的直觉模糊距离测度的构造中,接着设计了一种新的混合标签传递策略,该策略使用用户获得的先验信息来估计出所有数据的监督隶属度和初始聚类中心,更大程度地发挥了先验信息的作用,最后将对称信息、区域信息以及监督隶属度结合构建了融合对称特性的混合标签传递半监督直觉模糊聚类目标函数,利用直觉模糊聚类获得最终的分割结果。实验结果证明了,HLPS-SIFCM算法可以有效地分割复杂彩色图像,而且分割性能也优于对比算法。
需要指出的是,HLPS-SIFCM算法中控制对称信息和区域信息贡献的加权因子α和β,在实验中都使用了经验值0.5。如果能够通过衡量图像的对称性和同一区域内像素的相似性,自适应的确定α和β将是一个有意义的研究内容,将在未来的工作中展开进一步研究。
[1] 罗钧, 杨永松, 侍宝玉. 基于改进的自适应差分演化算法的二维Otsu多阈值图像分割[J]. 电子与信息学报, 2019, 41(8): 2017-2024.
Luo Jun, Yang Yongsong, Shi Baoyu. Multi-threshold Image Segmentation of 2D Otsu Based on Improved Adaptive Differential Evolution Algorithm[J]. Journal of Electronics & Information Technology, 2019, 41(8): 2017-2024.(in Chinese)
[2] Akter L A, Kwon G. Integration of Contourlet Transform and Canny Edge Detector for Brain Image Segmentation[C]∥Tenth International Conference on Ubiquitous and Future Networks (ICUFN). Prague, Czech Republic: IEEE, 2018: 798- 800.
[3] 李玉, 胡海峰, 赵雪梅, 等. 遥感图像扫描聚类分割算法[J]. 信号处理, 2018, 34(9): 1130-1141.
Li Yu, Hu Haifeng, Zhao Xuemei, et al. The Remote Sensing Image Scan Clustering Segmentation Algorithm[J]. Journal of Signal Processing, 2018, 34(9): 1130-1141.(in Chinese)
[4] Fan Huaiyu, Meng Fanbin, Liu Yutang, et al. A novel breast ultrasound image automated segmentation algorithm based on seeded region growing integrating gradual equipartition threshold[J]. Multimedia Tools and Applications, 2019, 78(19): 27915-27932.
[5] 邹亚君, 李翌昕, 马尽文. 基于深度学习的酒标分割研究[J]. 信号处理, 2019, 35(4): 623- 630.
Zou Yajun, Li Yixin, Ma Jinwen. Research on Deep Learning Based Wine Label Segmentation[J]. Journal of Signal Processing, 2019, 35(4): 623- 630.(in Chinese)
[6] Bezdek J C, Ehrlich R, Full W. FCM: The fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191-203.
[7] Bai Xiangzhi, Zhang Yuxuan, Liu Haonan, et al. Intuitionistic Center-Free FCM Clustering for MR Brain Image Segmentation[J]. IEEE Journal of Biomedical and Health Informatics, 2019, 23(5): 2039-2051.
[8] Xiao Leyi, Qi Han, Fan Chaodong, et al. Energy Noise Detection FCM for Breast Tumor Image Segmentation[J]. IEEE Access, 2020, 8: 62895- 62904.
[9] Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.
[10]Xu Zeshui, Chen Jian, Wu Junjie. Clustering algorithm for intuitionistic fuzzy sets[J]. Information Sciences, 2008, 178(19): 3775-3790.
[11]Szmidt E, Kacprzyk J. Distances between intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 2000, 114(3): 505-518.
[12]Xu Zeshui, Wu Junjie. Intuitionistic fuzzy C-means clustering algorithms[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 580-590.
[13]Cao Jiale, Pang Yanwei, Li Xuelong. Pedestrian Detection Inspired by Appearance Constancy and Shape Symmetry[J]. IEEE Transactions on Image Processing, 2016, 25(12): 5538-5551.
[14]Sun Y, Bhanu B. Symmetry integrated region-based image segmentation[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Miami, USA: IEEE, 2009: 826- 831.
[15]Sun Y, Bhanu B. Reflection Symmetry-Integrated Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 24(9): 1827-1841.
[16]Jayasuriya S A, Liew A W. Symmetry incorporated fuzzy c-means method for image segmentation[C]∥IEEE International Conference on Fuzzy Systems (FUZZ-IEEE). Hyderabad, India: IEEE, 2013: 1-7.
[17]Bai Xiangzhi, Wang Yingfan, Liu Haonan, et al. Symmetry Information Based Fuzzy Clustering for Infrared Pedestrian Segmentation[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(4): 1946-1959.
[18]Ahmed M N, Yamany S M, Mohamed N, et al. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3): 193-199.
[19]Krinidis S, Chatzis V. A robust fuzzy local information C-means clustering algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328-1337.
[20]湛西羊, 李良群, 张富有. 融入局部信息的直觉模糊核聚类图像分割算法[J]. 信号处理, 2017, 33(3): 397- 405.
Zhan Xiyang, Li Liangqun, Zhang Fuyou. An intuitionistic Kernel-based Fuzzy C-means Clustering Algorithm with Local Information for Image Segmentation[J]. Journal of Signal Processing, 2017, 33(3): 397- 405.(in Chinese)
[21]赵凤, 张咪咪, 刘汉强. 区域信息驱动的多目标进化半监督模糊聚类图像分割算法[J]. 电子信息学报, 2019, 41(5): 1106-1113.
Zhao Feng, Zhang Mimi, Liu Hanqiang. Multi-objective Evolutionary Semi-supervised Fuzzy Clustering Image Segmentation Motivated by Region Information[J]. Journal of Electronics & Information Technology, 2019, 41(5): 1106-1113.(in Chinese)
[22]Liu Guoying, Zhao Zhe, Zhang Yun. Image Fuzzy Clustering Based on the Region-Level Markov Random Field Model[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1770-1774.
[23]Fakouri R, Zamani B, Fathy M, et al. Region-Based Image Clustering and Retrieval Using Fuzzy Similarity and Relevance Feedback[C]∥International Conference on Computer and Electrical Engineering. Phuket, Thailand: IEEE, 2008: 383-387.
[24]Mei Jianping, Lv Huajiang. Semi-supervised fuzzy c-means regularized with pairwise constraints[C]∥Fourteenth International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). Huangshan, China: IEEE, 2018: 781-786.
[25]Arshad A, Riaz A, Jiao L. Semi-Supervised Deep Fuzzy C-Mean Clustering for Imbalanced Multi-Class Classification[J]. IEEE Access, 2019, 7: 28100-28112.
[26]Yasunori E, Yukihiro H, Makito Y, et al. On semi-supervised fuzzy c-means clustering[C]∥IEEE International Conference on Fuzzy Systems. Jeju Island, South Korea: IEEE, 2009: 1119-1124.
[27]Son L H, Tuan T M. Dental segmentation from X-ray images using semi-supervised fuzzy clustering with spatial constraints[J]. Engineering Applications of Artificial Intelligence, 2017, 59: 186-195.
[28]Sugeno M. Fuzzy Sets for Intelligent Systems[M]. San Mateo, CA, USA: Morgan Kaufmann, 1993: 251-257.
[29]徐泽水. 直觉模糊信息集成理论及应用[M]. 北京: 科学出版社, 2008: 1-5.
Xu Zeshui. Theory and Application of Intuitionistic Fuzzy Information Integration[M]. Beijing: Science Press, 2008: 1-5.(in Chinese)
[30]Vlachos I K, Sergiadis G D. Towards Intuitionistic Fuzzy Image Processing[C]∥International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC′06). Vienna, Austria: IEEE, 2005: 2-7.
[31]Cicconet M, Hildebrand D G C, Elliott H. Finding Mirror Symmetry via Registration and Optimal Symmetric Pairwise Assignment of Curves: Algorithm and Results[C]∥IEEE International Conference on Computer Vision Workshops (ICCVW). Vienna, Austria: IEEE, 2017: 1759-1763.
[32]Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.
[33]Wu Mingrui, Schölkopf B. A Local Learning Approach for Clustering[C]∥Advances in Neural Information Processing Systems 19, Proceedings of the Twentieth Annual Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada: MIT, 2006: 1529-1536.
[34]Arbel ez P, Maire M, Fowlkes C, et al. Contour Detection and Hierarchical Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916.
ez P, Maire M, Fowlkes C, et al. Contour Detection and Hierarchical Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916.
[35]Alpert S, Galun M, Brandt A, et al. Image Segmentation by Probabilistic Bottom-Up Aggregation and Cue Integration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2): 315-327.


