1 引言
图像修复[1]的目标是对图像中缺失或损坏的部分进行重建。近二十年来,数字图像修复领域取得了巨大的进步,方法主要包括基于扩散方程[1-3]、基于图像片(patch)[4-5]等传统方法和基于深度学习的新型方法[6-15]。传统方法的核心思想是通过在源图像已知区域或在其他图像中找到相似信息,通过扩散或粘贴方式来填补破损图像中缺失的信息,而基于深度学习的方法通过对数据学习图像特征,从而为缺失区域填补合理的结构和纹理,取得了不俗的视觉效果。此外,深度学习方法不仅可以填补图像内部区域的缺失部分,还可以对图像外围像素进行推断[16]。通常采用基于端到端的卷积神经网络(Convolutional Neural Networks, CNN)结构或生成对抗网络(Generative Adversarial Networks, GAN)结构实现深度图像修复,在生成对抗网络结构中,生成器(generator)通常采用基于像素的重构损失函数,利用输入图像的已知信息为缺失区域预测合理的填补部分,同时结合采用对抗损失的鉴别器(discriminator)提升修复图像的视觉质量。
Pathak等人[7]首次提出应用于图像修复的端到端“编码器—解码器”深度网络。该网络中的编码器网络以具有缺失区域的图像作为输入,产生图像的潜特征,解码器网络利用潜特征预测缺失部分的像素,并采用重构损失和对抗损失保证预测的像素逼近真实像素。Iizuka等人[8]提出了一种结构,通过考虑全局和局部的视觉一致性,引入全局鉴别器和局部鉴别器提供对抗损失,使整体视觉效果和纹理细节得到改善提升。针对人脸图像修复,Li等人[9]在重构损失和对抗损失的基础上引入了语义解析损失,提高图像的语义信息一致性。
充分利用破损图像中的线索可用于一些复杂的修复情况。Yu等人[10]提出了一个上下文注意力层,从已知的背景信息中学习兼容的特征,从而修复缺失的区域。文献[11]中的局部卷积(Partial Convolutions)和文献[12]中的门控卷积(Gated Convolutions)可以利用退化区域附近的有效像素为条件学习特征。Nazeri等人[13]提出了一种两阶段生成网络,第一阶段用边缘生成网络预测缺失区域的边缘轮廓,第二阶段利用生成的边缘作为先验重构细节。在文献[14]中也利用了类似的思想,先执行缺失结构推断,然后完成内容填补。文献[15]提出了移位网络(Shift-Net),通过假设缺失部分是已知部分信息的空间重排来处理深层特征。深度学习技术使得数字图像修复能力得到了极大的提升,然而,一些研究人员也注意到深度图像修复算法中存在的一些问题。如Xiong等人[14]注意到,在一些修复图像中,在修复前景和真实背景的边界处存在伪影。因此,他们提出关注修复前景轮廓的解决方案。Iizuka等人[8]指出,修复区域可能与周围真实区域存在颜色不一致,因此修复后图像需要进行泊松混合的后处理操作。
深度图像修复方法可以产生不错的视觉效果,但他们不能确保修复图像与真实图像在统计特性上的一致性。具体而言,深度修复的图像会留下修复痕迹,这些痕迹容易被图像取证方法检测。例如,Wang等人[17]采用了Faster R-CNN模型[17]来获得由算法[7,10]生成图像的不一致证据。Li等人[18]发现算法[8]生成的修复图像与真实图像在其高通滤波残差中存在差异,并以此设计端到端深度取证网络,以高精度定位修复区域。深度修复图像中修复前景和真实图像背景的差异源于他们不同的处理过程,真实图像背景可能会经历一系列常见的图像处理操作,而修复的区域则是由卷积神经网络操作获得,因此它们之间统计特性可能存在不一致。
针对上述问题,本文提出了一种用于改善深度修复图像统计特性一致性的方法,从机器感知的角度使深度修复的图像更接近自然图像。首先,本文提出了固有身份信号(intrinsic identity signal, IIS)的概念,并分别采用非线性高通滤波残差和深度神经网络提取IIS,称为NIIS和DIIS,其中NIIS是文献[19]所述提取的基于小波去噪的非线性信号,DIIS是拟合NIIS提取过程的深度神经网络(DIIS提取网络)的输出信号,两者在空域数值和特征空间上的距离都相近。本文分析表明,深度修复图像与真实图像在IIS(NIIS和DIIS)上存在差异,且对于不同的图像来源[20-21]以及不同的深度修复算法[8,10,13],在修复区域和真实区域之间普遍存在IIS统计不一致性。然后,本文设计了一个基于U-net结构[22]的卷积神经网络作为后处理生成器来处理深度修复区域,使其DIIS逼近对应内容的真实区域DIIS,因此生成区域在DIIS统计特性方面与真实区域保持一致,并且不会对视觉质量造成较大改变,同时NIIS统计特性也能达到一致。为了达到DIIS统计一致性的目的,除了DIIS提取网络,本文还设计了另外一个辅助的神经网络进行特征提取及监督学习,保证修复区域DIIS与图像已知真实区域DIIS的统计一致性。最后,考虑到真实图像的来源可能不同,分布也各不相同,本文采用随机策略,在合理的范围内对已训练好的部分网络参数进行随机扰动,使得采用同一网络也能产生具有多样性的图像,即使在白盒场景,即网络结构和某一时刻输出的生成图像被检测者所获下,也能有效降低生成图像被识别来源的概率。
2 固有身份信号
2.1 定义
数码相机的采集过程和各种后处理操作在图像上会留下内在痕迹,可用于检验图像的完整性。例如,传感器模式噪声是成像传感器的固有属性,可用于相机源识别[23]。图像压缩或图像增强操作,如插值,对比度增强,中值滤波等,也留下可用于取证检测的痕迹[24-25]。此外,GAN模型也具有类似相机的稳定模式可以进行识别[26]。
本文将固有身份信号(intrinsic identity signal,IIS)定义为能够便于辨识其来源的信号。由于修复前景和真实背景具有不同的处理过程,因此它们可能具有不同的IIS模式。深度修复算法生成的区域与真实区域之间的IIS统计区别可以反映它们的不一致性。
2.2 基于噪声的固有身份信号
本文提取了一种基于小波去噪的IIS,称为基于噪声的固有身份信号(noise-based IIS, NIIS)。它遵循文献[19]所述的去除图像内容和保留噪声痕迹的方法。提取NIIS的具体步骤如下:
步骤1 用DB-8(Daubechies 8-tap)小波基对输入图像进行4级的二维离散小波变换,每一级里的小波系数子带记为ωl,s,其中l∈{1,2,3,4},s∈{H,V,D},H,V,D分别表示水平子带、垂直子带和对角子带。最后的图像内容低频子带记为ω4,L。
步骤2 用(i, j)表示各小波系数子带里的系数坐标,通过W×W的方形邻域
去估计每个子带的无噪小波系数
的方差:
(1)
其中
(2)
按文献[19]设置,
步骤3 估计的无噪小波系数:
(3)
(4)
步骤4 对
和
进行小波逆变换,得到的结果就是NIIS。
在相机识别任务中,从同一设备的不同图像中提取的NIIS累加后平均形成该设备的指纹信号。由于修复区域的来源与真实区域不一致,因此修复图像中修复区域的NIIS统计特性与真实区域的NIIS统计特性可能存在不一致。
2.3 基于深度学习的固有身份信号
NIIS依赖于输入信号,并且以非线性的方式获得。本文提出了一种用于模拟提取NIIS过程的深度神经网络,使其能够更好地与深度修复框架相兼容。定义一幅图像为I,提取它的NIIS过程记为
提出的深度神经网络模拟NIIS提取过程记为
合成的
信号称为基于深度学习的固有身份信号(deep-learning based intrinsic identity signal (DIIS))。
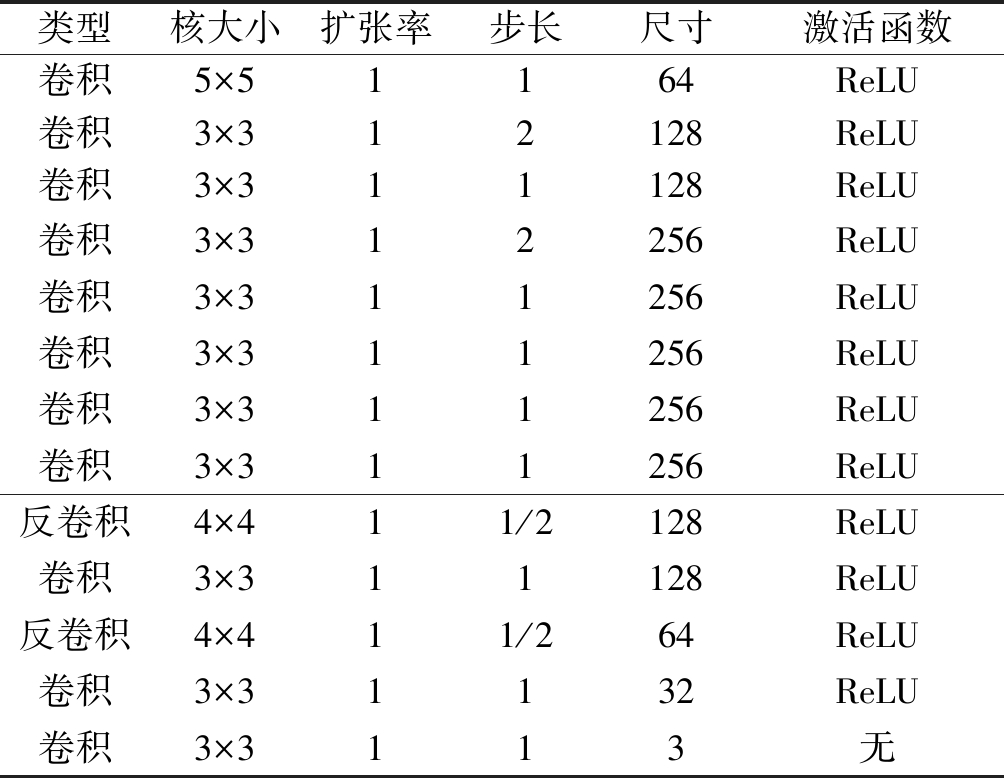
DIIS提取网络采用全卷积神经网络结构[27],它是基于“编码器—解码器”结构去提取输入图像的信息。网络设置细节如表1示。在编码器端,有两个步长为2的卷积层用于降低空间分辨率,而在解码器端,有两个反卷积层用于恢复原始分辨率。除最后一层外,所有卷积/反卷积层均采用“卷积/反卷积—批量归一化(batch normalization)—ReLU激活函数”,因为网络是全卷积结构,因此网络输入可以是任意图像尺寸,输出
的尺寸与输入I相同。损失函数表示如下:
表1 DIIS提取网络结构
Tab.1 Architecture of the DIIS extraction network
类型核大小扩张率步长尺寸激活函数卷积5×51164ReLU卷积3×312128ReLU卷积3×311128ReLU卷积卷积3×33×31121256256ReLUReLU卷积3×311256ReLU卷积3×311256ReLU卷积3×311256ReLU反卷积4×411/2128ReLU卷积3×311128ReLU反卷积4×411/264ReLU卷积卷积3×33×31111323ReLU无
(5)
DIIS是依赖于训练数据的,这意味着不同的训练数据可能会导致DIIS提取网络的不同权值。为了训练DIIS提取网络,本文使用真实图像和修复图像两种数据混合训练网络。具体而言,从公开的CelebA人脸数据集[21]中随机选择了25000幅真实图像,将其大小缩小为160×160,并使用算法[8]进行修复。修复区域在图像内随机选取,宽度和高度在[24,48]范围内。通过此方法,获得了25000幅真实图像相应的25000幅修复图像,从而可获得了它们的NIIS。网络的批次大小(batch size)为32,优化器选择ADAM优化器[28]。初始学习率为5×10-3,每轮(epoch)训练完成后会降低 1%。使用Xavier初始化[29]网络参数。训练时,训练数据会被打乱,形成不同的批次组合。网络总共训练了750轮。三个示例图像的NIIS和DIIS结果如图1所示。可以看出,当网络收敛时,所提取的DIIS和NIIS比较接近。值得注意的是,即使DIIS提取网络是在人脸数据集上训练的,它对于自然图像(图1(c))提取的DIIS也接近于相应的NIIS。除了在视觉上DIIS和NIIS比较接近,本文同时计算了两者的均方根误差 (Root Mean Squared Error, RMSE),具体过程为使用50000幅真实图像和50000幅修复图像,提取 DIIS和NIIS,然后将所有数据放于一起,归一化到[-1,1], 再计算每张DIIS和NIIS的RMSE,最后计算平均值。对修复图像的计算过程也是如此,其中,修复图像包含修复像素和真实像素,因此本文分开两个区域计算结果和整张图像计算结果,而真实图像只有真实像素,因此只计算整张图像结果,如表2所示,从表中看出,本文网络所拟合的DIIS和NIIS在均方根误差数值误差上也比较小。
图1 三个示例图像的NIIS和DIIS,其中(a) 和(c)为真实图像,(b)为修复图像
Fig.1 NIIS and DIIS of three example images,where (a) and (c) are the pristine images and (b) is the deep inpainted image
表2 DIIS与NIIS的均方根误差
Tab.2 The RMSE (Root Mean Squared Error) between DIIS and NIIS
图像类型区域类型RMSE修复图像修复区域1.305×10-4真实区域1.149×10-4整张图像1.158×10-4真实图像整张图像1.471×10-4
2.4 仿真分析
如图2所示,分别定义Io、Im、Ic为真实图像、含缺失区域的破损图像、修复图像。掩摸M用来指示缺失区域的位置,其中白色区域(数值1)代表缺失区域,其他黑色区域(数值0)代表已知真实区域。Rm是缺失区域的真实内容,Rc是修复算法的生成内容。Rp是真实图像中与Rc相同尺寸的随机真实区域块,Rp′是修复图像中与Rp对应的区域块。本文对真实区域和深度修复区域进行以下的实验,来分析NIIS和DIIS的统计。
图2 用于分析NIIS和DIIS的图像和区域
Fig.2 Images and regions for analyzing NIIS and DIIS
给定一对真实图像Io和修复图像Ic:
1)提取
和
然后计算Rp,Rm,Rp′,Rc对应区域的标准差,记为
2)提取
和
然后计算Rp,Rm,Rp′,Rc对应区域的标准差,记为
给定一组图像集(真实图像或修复图像)。
3)统计标准差频率直方图,记为Ha(x)。其中
是直方图,bin是索引。
4)计算两个直方图的卡方距离dχ2(Hp,Hq):
(6)
本文主要针对3种深度图像修复方法(Globally and Locally算法[8](GL)、Contextual Attention算法[10](CA)、EdgeConnect算法[13](EC))和两个图像数据集(Places2[20]、CelebA[21])进行直方图统计,每个直方图对应2000幅图像,统计的区域大小为32×32。直方图结果如图3所示。可以观察出,对于真实图像的NIIS统计,卡方距离非常小,表示两个真实区域Rm和Rp的NIIS统计特性一致。类似的现象也在真实图像的DIIS统计观察到。另一方面,对于修复区域Rc和真实区域Rp′存在明显的统计特性不一致性。
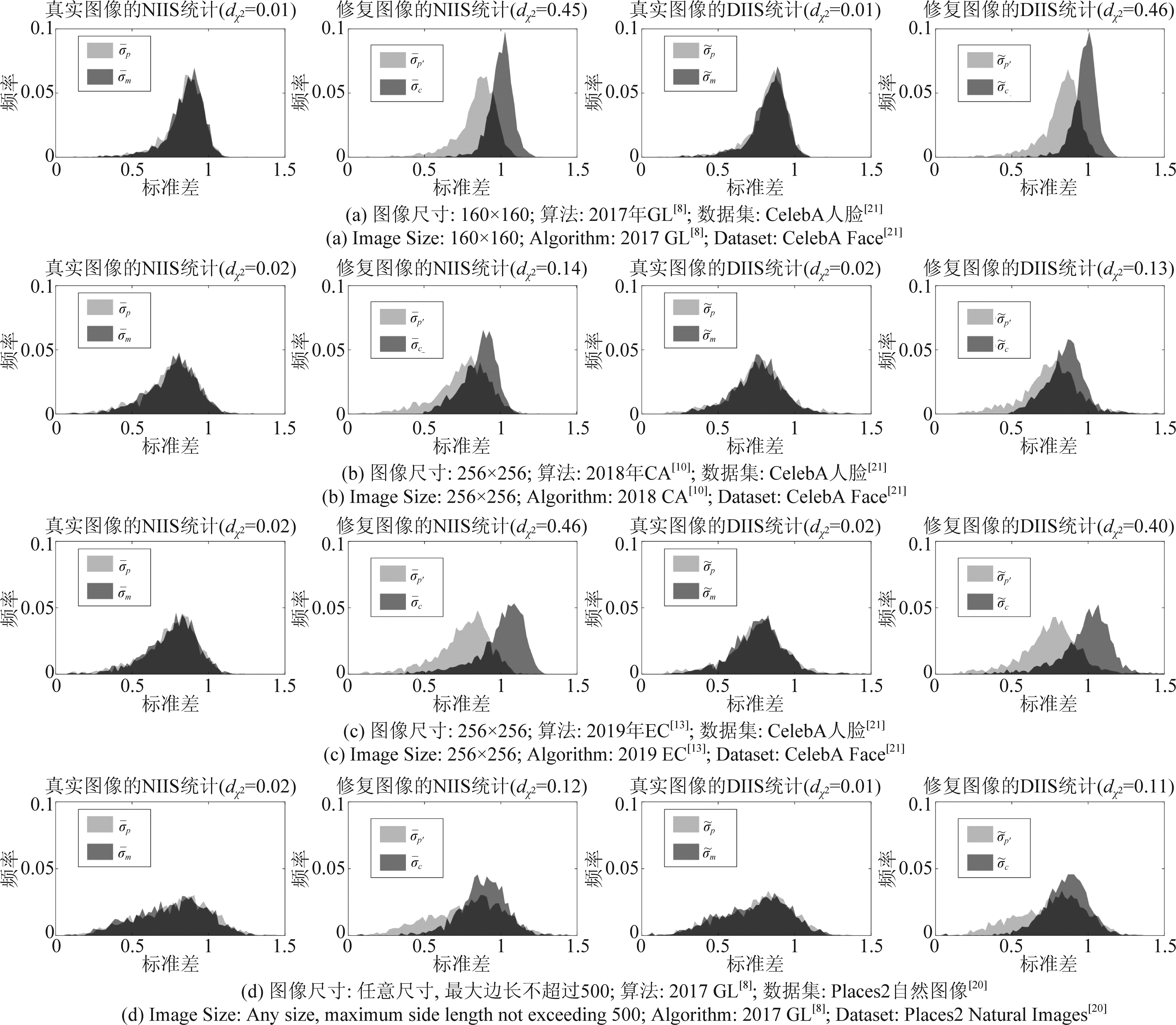
图3 对于不同数据来源和不同深度图像修复算法中,修复图像与真实图像之间NIIS和DIIS的不一致现象
Fig.3 The NIIS and DIIS inconsistency phenomenon between the deep inpainted images and the pristine images for different datasets and different deep inpainting algorithms
或
通常大于
或
这种现象存在于不同的数据集和不同的深度修复方法中。为了理解这一现象,本文对提取NIIS过程的公式(3)进行分析,图像小波系数的局部方差
位于分母,即它的值越大,结果NIIS信号的方差也就越小。这说明修复区域小波系数的局部方差小于真实区域的局部方差,说明修复区域缺乏高频细节。这启发我们在设计图像修复算法应考虑引入更多高频细节到修复区域中,以保持统计特性的一致性。
3 面向统计特性一致的处理方法
3.1 方法概述
基于上述对NIIS和DIIS的分析,可知修复区域与真实区域之间的IIS统计特性不一致性现象在修复图像中普遍存在。现有的深度修复算法并未考虑IIS这一统计特性。因此,本文方法的目标是通过一个由深度卷积神经网络实现后处理操作来弥补这一缺陷,实现修复区域与真实区域在DIIS及NIIS的统计一致性。为此,本文提出了一个应用于修复区域后处理的生成网络。在损失函数中,不仅采用了传统的内容损失(content loss),而且还引入了两种新的损失,即DIIS保真损失(DIIS fidelity loss)和DIIS一致性损失(DIIS consistency loss)。一个预训练好的DIIS提取网络(定义为
和另外一个预训练好的三元组损失网络(Triplet-loss network)分别计算这两个损失。生成网络通过学习策略进行训练,它输出图像具有良好的视觉质量并且至少在DIIS方面具有统计特性一致,为了防止生成的图像遵循为一个固定分布,本文在生成网络中设置了随机策略。因此,不同的输出图像可以等同看作从不同版本的生成网络中生成,扩大了图像来源的多样性。图4展示了该方法网络的总体框架。
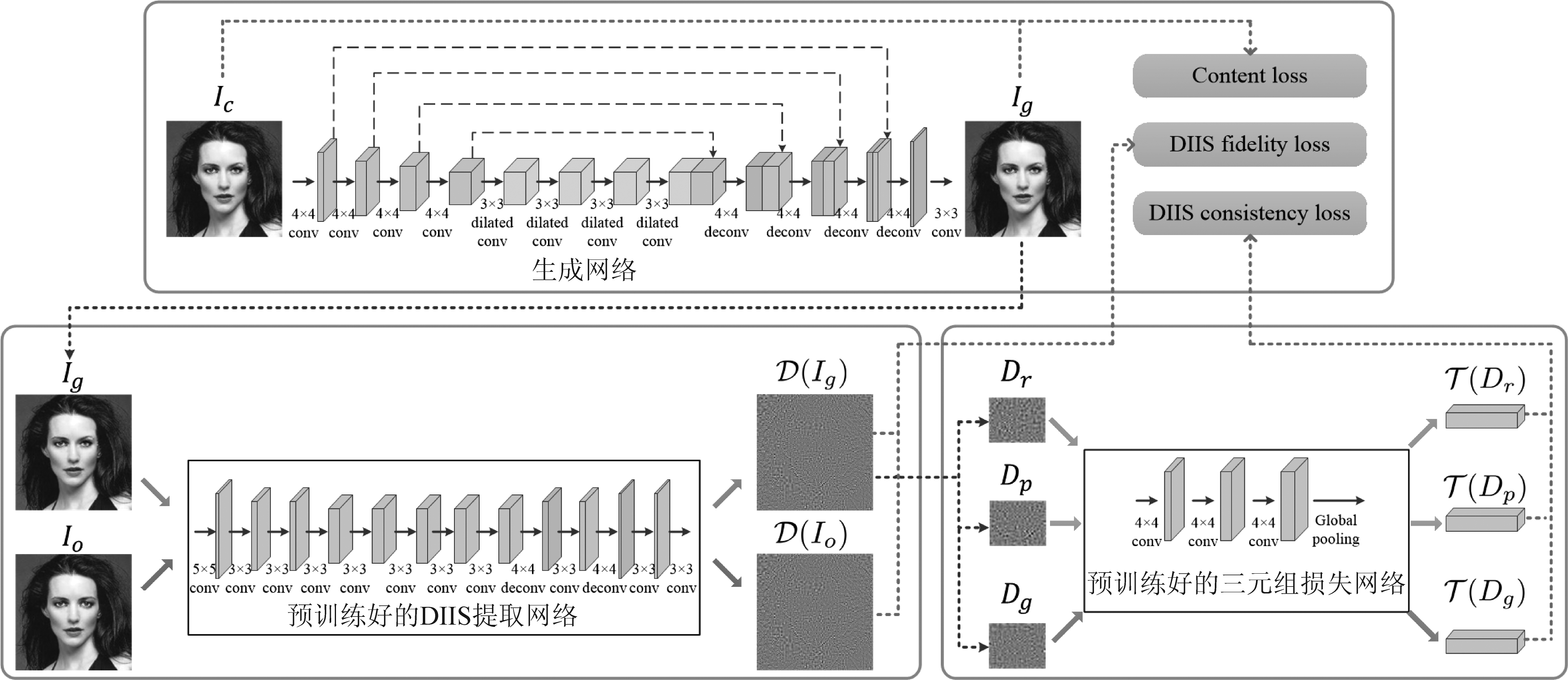
图4 提出的网络总体框架
Fig.4 Overview of the proposed network architecture
3.2 生成网络
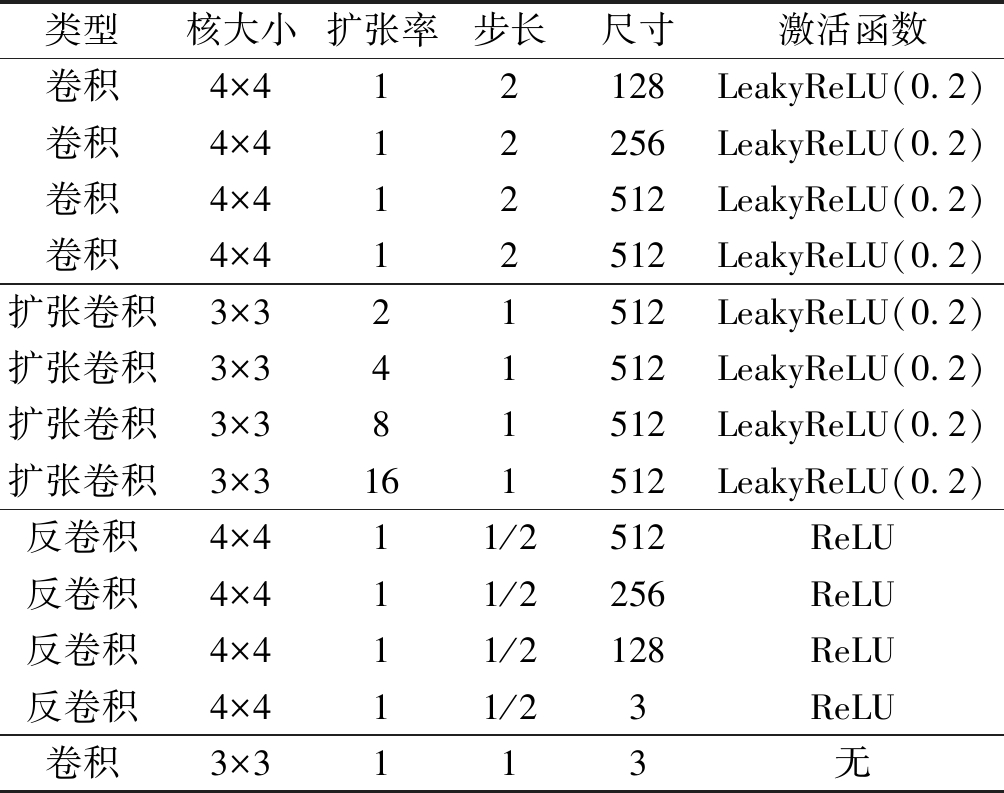
给定一张修复图像Ic,采用提出的生成网络作为后处理模块来生成DIIS统计特性一致的生成图像Ig。本文网络是一个基于U-net的结构,它的详细结构参数如表3所示。除最后一层外,所有卷积/反卷积层均采用“卷积/反卷积—批量归一化(batch normalization)—非线性激活函数”的组合。使用零填充使输出图像具有与输入图像相同的大小。
1)损失函数的定义
生成网络总的损失函数为:
lG=lC+λ1lDF+λ2lDC
(7)
其中,lC,lDF,lDC分别是内容损失(content loss),DIIS保真损失(DIIS fidelity loss)和DIIS一致性损失(DIIS consistency loss)。λ1和λ2的值由后文第4.2节实验得到。
内容损失定义为:
(8)
表3 生成网络结构
Tab.3 Architecture of the Generation Network
类型核大小扩张率步长尺寸激活函数卷积4×412128LeakyReLU(0.2)卷积4×412256LeakyReLU(0.2)卷积4×412512LeakyReLU(0.2)卷积4×412512LeakyReLU(0.2)扩张卷积3×321512LeakyReLU(0.2)扩张卷积3×341512LeakyReLU(0.2)扩张卷积3×381512LeakyReLU(0.2)扩张卷积3×3161512LeakyReLU(0.2)反卷积4×411/2512ReLU反卷积4×411/2256ReLU反卷积4×411/2128ReLU反卷积4×411/23ReLU卷积3×3113无
其中,⊙为像素乘积,M是如图2所示的掩摸,S是修复区域的像素个数。这样的损失是用来确保生成图像和修复图像具有相同的视觉质量。
保真损失定义为:
(9)
其中,
是已训练好的DIIS提取网络。由于
中修复区域的DIIS与其他区域没有统计特性上的一致性,所以本文方法没有使用作为优化目标,而使用真实图像的DIIS,即
作为优化模板。这个损失函数被用来确保生成图像的DIIS逼近真实图像的DIIS。除此之外,还可通过这种方式获得更多的高频细节。
DIIS一致性损失定义为:
(10)
其中,
是一个已训练好的提取DIIS特征的三元组损失网络,将在后文描述。Dg,Dr和Dp分别是修复区域的DIIS,参考区域的DIIS和真实区域的DIIS,这些区域是直接从
中提取的,即预先训练好的DIIS提取网络输出的DIIS。Dp和Dr都来自真实区域,因此它们在DIIS特征空间上应当是相近的。当修复区域与真实区域统计特性一致时,则Dg与Dr之间的距离将近似于Dp与Dr之间的距离。
2)三元组损失网络
为了确保修复区域的DIIS统计特性与图像内任何真实区域的DIIS统计特性无法区分,本文使用了一个三元组损失网络
它在预训练阶段的作用在于使真实区域的DIIS与修复区域的DIIS在网络特征空间中尽量远离,而在联合训练时,生成网络利用三元组损失网络来减小修复区域的DIIS与真实区域的DIIS在特征空间的距离。网络结构如表4所示,三元组损失网络可接收任意尺寸的DIIS区域块作为输入,输出一个512维的向量。使用三种区域Dc、Dp′和Dr′,分别对应于修复图像Ic中的一个修复区域和两个随机选择的真实区域的DIIS,如图5所示。在本文实验中,对于一幅160×160的输入图像,它的修复区域块的宽度和高度在[24, 48]之间。在预训练阶段的损失函数为:
图5 DIIS区域块,用于分析lT(公式(11))
Fig.5 DIIS patches for analyzing lT(Formula(11))
lT=max {0,dn-dn+m}
(11)
其中,
是间隔参数,在实验中设置其值为0.04。当三元组损失网络训练完成,它就被用作生成网络中的一个固定模块来提供DIIS一致性损失。
表4 三元组损失网络结构
Tab.4 Architecture of the Triplet-loss Network
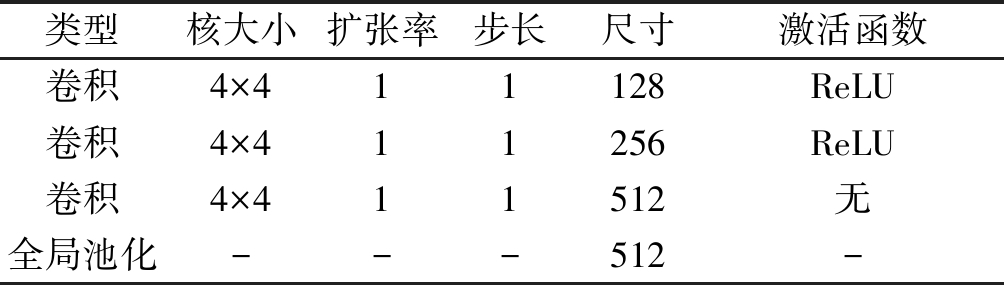
类型核大小扩张率步长尺寸激活函数卷积4×411128ReLU卷积4×411256ReLU卷积4×411512无全局池化---512-
3.3 网络参数的随机策略
一个特定的GAN网络有其固有的“模型指纹”[26]。当图像是由同一个修复网络生成的时候,相似的内在痕迹可能会出现在这些图像中。为了避免有相同的“模型指纹”,本文提出了一种应用于深度神经网络的随机策略,使得模型产生模式多样化的图像。不同的网络参数(如卷积权重和偏置)会导致不同的生成模型。因此,本文提出轻微扰动一些已经训练好的网络参数,使其处于一个合理的范围内,以获得不同的模型,但不会对生成网络的性能造成太大的影响。用户密钥用于保护随机策略,以便不同的用户会生成不同的模型。这样,即使一个检测器有一些图像用于训练,但在测试的图像分布可能会不同于训练图像的分布,因此即使在一个生成算法已知的白盒场景时,密钥是未知的,可以减少信息泄露的风险。具体策略如下。
设
为给定一幅图像时的卷积网络权值的L×1维向量,序列索引为n,与用户k相关联。它是由公式(12)决定。
(12)
其中,w(0)是已经训练好的参数向量;
是一个L×1维的随机向量,里面只有1个元素为1,其他元素都为
是一组随机数。
的随机性由密钥k决定。它们的具体实现如下。
定义离散均匀分布的概率密度函数为:
(13)
对于
从离散均匀分布中随机采集一个样本x(j),并令的第x(j)个元素为1,其余为0。由于在本文生成网络中,最后一层(即输出层)的权重参数与输出图像直接相关,且不带任何激活函数,因此比较容易得到控制参数变化范围而不引起图像质量等方面的损失,若在其他网络层,一方面可能会由于激活函数的影响使得权重参数改变后的特征值被减弱或消除,另一方面,也可能由于累积效应,导致输出变化太大而引起图像质量的下降,因此在本文实验中,被扰动的卷积权值是生成网络的最后一层权值,其输入的特征图和输出的特征图的数量都是3,卷积核大小是3×3,因此L=81。伪随机数
是由均匀分布、Gamma分布和Beta分布共同决定的。首先,设a,b,c,d为均匀分布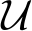
(slow,shigh)中采集的随机样本,取值范围为[slow,shigh]。在本文实验中,slow=0,shigh=5。其次,设u,ν分别为不同参数的Gamma分布中抽取的随机样本,即Γ(a,b)和Γ(c,d)。对于一个伽玛分布概率密度函数定义为:
表5 k1曲线与其他曲线(k2到k10)的平均l1距离
Tab.5 The average l1 distance between k1 curve and other curves (k2 to k10)
ek2k3k4k5k6k7k8k9k100.0010.00480.00510.00530.00600.00710.01020.00920.00630.00500.010.16080.26060.10450.11690.07340.36830.23730.10900.09260.10.91311.06800.50310.66830.38250.49900.55301.18190.5721
(14)
其中,Γ(α)=
tα-1e-tdt。Gamma分布是最大熵概率分布,其期望是α/β。这样,E(u)=a/b,E(ν)=c/b。然后,由Beta分布Β(u,ν)产生了n个随机样本,每个样本设为z(j)。对于一个Beta分布的概率密度函数定义为:
(15)
其中,Β(α,β)=
tα-1(1-t)β-1dt。Beta分布的输出值在[0,1]之间,它的均值是α/(α+β)。最后,用z(j)去随机乘以-e或e,得到
在本实验中,设e=0.01。这样,就可以得到
其中随机数
的均值和方差由用户密钥决定,并且较为多样化。
在图6中,展示了10种不同密钥对一个参数的扰动情况。具体地,本文给出e取值幅度为0.001,0.01和0.1的实验结果。每个幅度基于上述方法产生10种不同的密钥(在每个密钥包含
和
然后每个密钥根据公式(12)去扰动最后一层网络的权值,每个密钥的和
都是不同的。被扰动的权值包含81个参数,而本文以其中一个权值为例绘制它的值的变化,如图6所示。在这个实验中,n=50000。从图中可以到看,的取值区间越小,曲线的波动越不明显。为了探究这一趋势,以k1曲线为参考,计算其他曲线(k2到k10)与它的平均l1距离,如表5所示。可以看出,当
时,距离值的波动非常接近,而
或(-0.1,0.1)时,距离值的波动范围比较大。
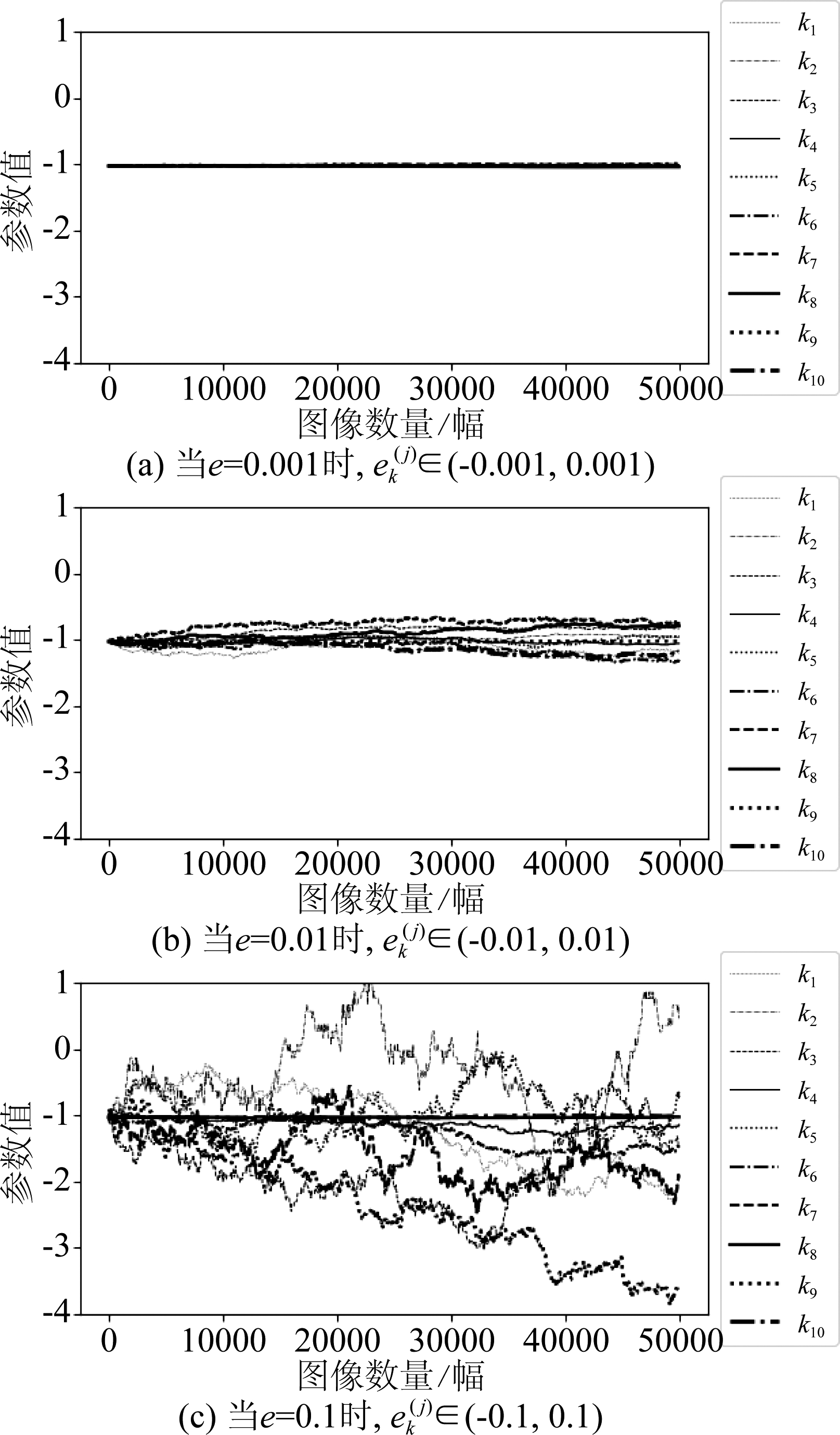
图6 最后一层权值的随机性情况。该权值在训练后的值为 -1.0291516,它被10种不同的密钥根据公式(12)扰动
Fig.6 The randomness of the weights in the last layer. The weight’s value after training is -1.0291516 and it is perturbed according to Eq.(12) using 10 different keys
4 实验结果及分析
4.1 实验设置
1)数据集
本文实验主要在CelebA人脸图像数据集[21]上进行,图像尺寸缩小为160×160。选择Iizuka等人提出的修复算法[8],记为GL。修复区域在图像中随机选取,宽度和高度在[24,48]之间。图像以无损PNG格式存储,以避免有损压缩痕迹的影响。随机选择50000幅用于训练,2000幅用于模型验证,50000幅用于测试。
2)评估标准
NIIS一致性:选择图3(a)中的2000幅修复图像数据和第2.4节介绍NIIS统计方法,获得生成图像Ig并验证NIIS一致性,即比较
的
和
图像质量:选择峰值信噪比(PSNR)评估生成图像Ig质量,计算修复图像和生成图像的PSNR。
对抗性能:选择四种常见的像素级分类指标来衡量对抗取证检测器性能:Recall, Precision, IoU(Intersection over Union)和F1-score,计算公式如下:
(16)
(17)
(18)
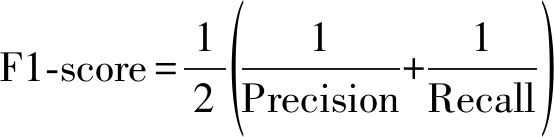
(19)
其中,TP表示生成区域中被正确定位的像素个数,FP表示真实区域中被错误定位的个数,FN表示生成区域中被错误定位的像素个数。Recall越高,说明检测器对生成区域的识别能力越强,IoU功能与之相似;Precision高,说明检测器对真实区域的误判少;F1-score是两者的综合,越高,说明检测器越稳健。
3)三元组损失网络训练
三元组损失网络的训练使用修复图像Ic的DIIS数据。因为修复区域块Dc的尺寸不确定,因此网络设置批次大小为1。真实区域块Dp′和参考区域块Dr′会在每轮训练后重新随机选择。网络参数设置由Xavier[29]初始化,更新优化采用ADAM算法[28],初始设定学习率为5×10-3,训练完每轮后会被降低1%,网络训练了20轮。
4)生成网络训练
在第2.3节所述DIIS提取网络和第4.1节所述三元组损失网络训练完成之后,训练生成网络。通过数据(Ic, Io, M)向设定的目标公式(7)进行训练,其中λ1=4和λ2=1/512,在后文将展示λ1和λ2取值的消融实验结果。网络参数由Xavier[29]初始化,更新优化采用ADAM算法[28],初始设定学习率为5×10-3,训练完每轮后会被降低1%,批次大小为32。由于每幅图像之间的DIIS区块块大小不相等,而三元组损失网络无法接收一批次尺寸不定的输入,因此,对于DIIS一致性损失函数(公式(10)),实验中是对一批次里每幅图像的DIIS区域块逐一进行计算损失,之后累计一批次损失总和并求出平均值。采用与三元组损失网络相同的训练技巧,真实区域块Dp和参考区域块Dr会在每轮后重新随机选择。生成网络总共训练200轮,根据验证集来选择最佳的模型。在验证时,以真实图像作为参考,计算修复图像和生成图像各2000个PSNR值,之后分别计算出两类图像对应PSNR平均值。选择两个PSNR平均值相差的绝对值最小的轮数对应的模型作为最佳的模型。在本实验中,最佳模型在第137 轮获得。
4.2 不采用随机策略的生成网络的实验
1)λ1和λ2取值的消融实验
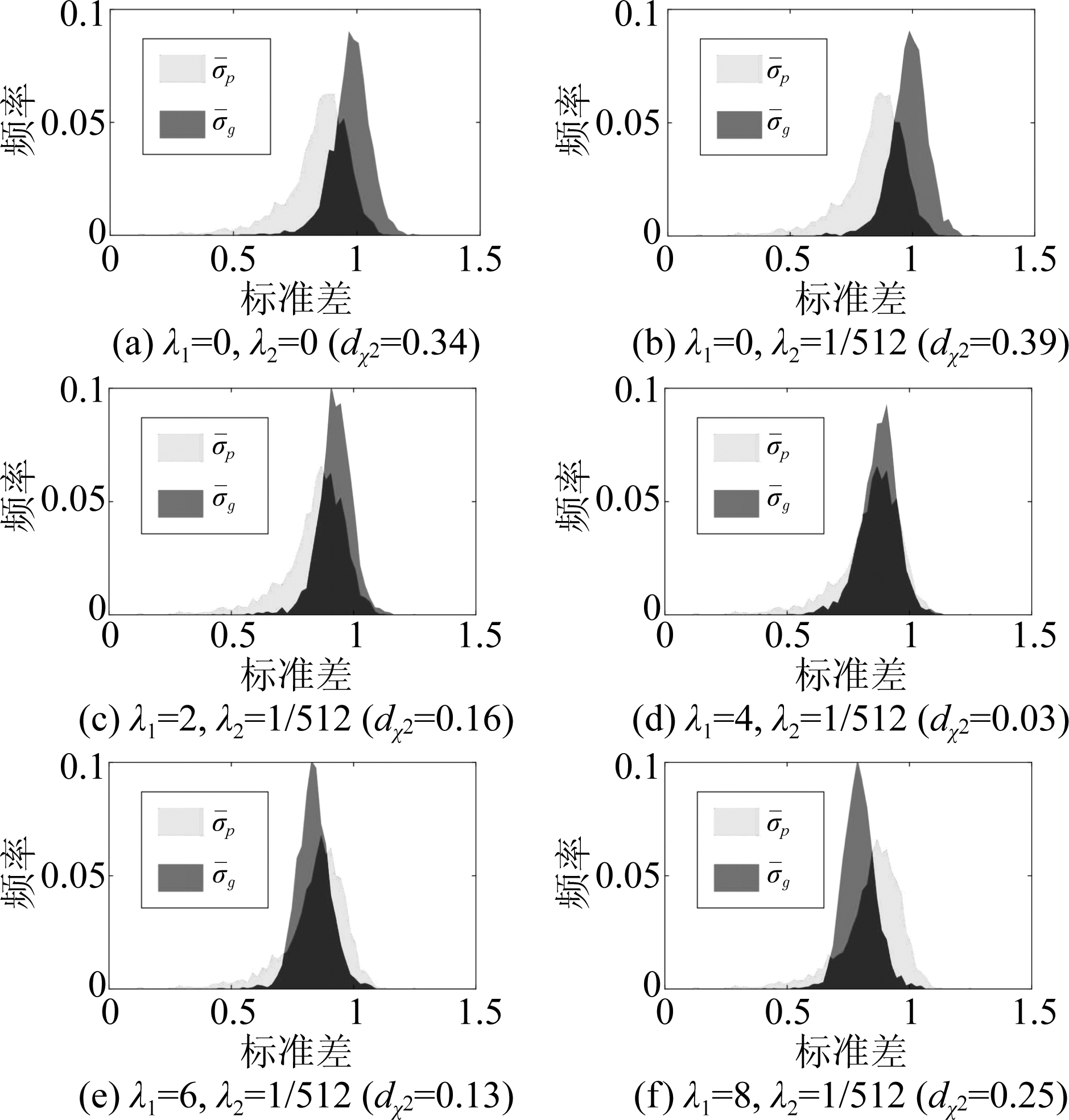
图7 针对GL算法[8]和CelebA数据集[21],λ1和λ2取值 对实现生成图像的NIIS一致性的影响。 其中,生成网络未采用随机策略
Fig.7 For GL algorithms[8] and CelebA data set[21], impact of λ1 and λ2 on achieving NIIS consistency for generated images. Stochastic strategy is not used in the generation network
本实验通过探究λ1和λ2的不同取值对实现生成图像的NIIS一致性的影响,从而确定最佳的λ1和λ2的取值。具体地,根据几组不同λ1和λ2的取值设置训练多个生成网络,λ1的取值是[0,8]之间,步长为2;λ2的取值是0或1/512,训练细节如4.1节(4)所述。接着,生成网络采用图3(a)的GL算法修复的2000幅修复图像数据去获取生成图像Ig,然后根据第2.4节方法统计它们的NIIS一致性和卡方距离,如图7所示。与对应的修复图像NIIS统计直方图(图3(a))情况相比较,λ1和λ2的不同取值会影响到生成图像NIIS的统计特性一致性,并且最好的统计情况是图(d),因此本文选择λ1=4,λ2=1/512作为4.1节生成网络的最佳选择。
2)生成图像Ig的视觉质量
本实验探究测试集50000幅修复图像与对应的生成图像质量对比。如图8所示,修复图像PSNR曲线(虚线)和生成图像PSNR曲线(实线)没有明显差异,并且平均值也相近,说明本文的处理操作对修复图像的质量影响不大。
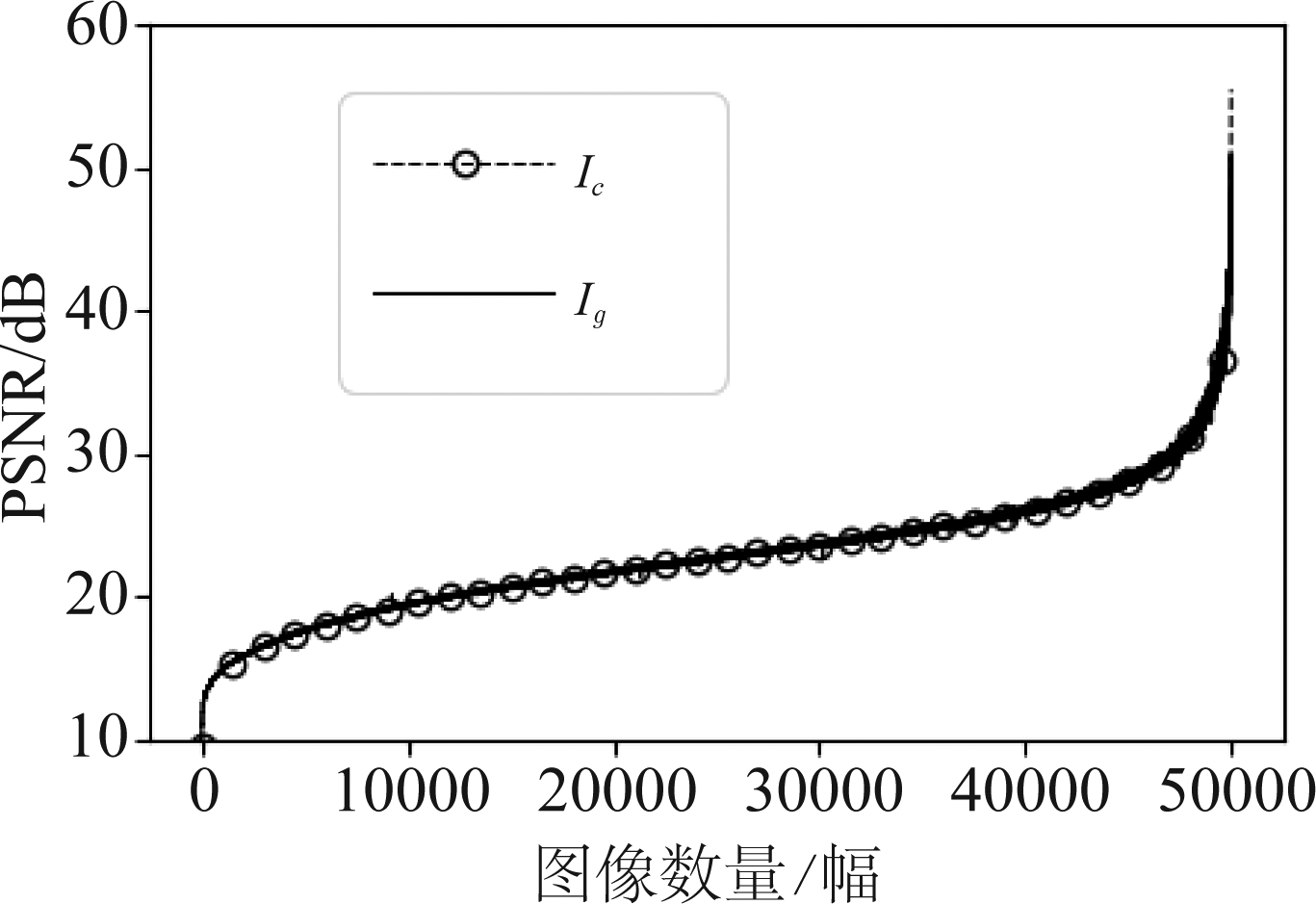
图8 生成图像Ig的图像质量。生成网络未采用随机策略。 虚线平均值为22.88 dB,实线平均值为22.90 dB
Fig.8 The image quality ofIg. Stochastic strategy is not used in the generation network. The average of the dotted line is 22.88 dB and solid line is 22.90 dB
3)生成图像Ig的对抗性能
本实验使用两个CNN取证检测器,即High-Pass Fully Convolutional Network (HPFCN)算法[18]和Multi-Task Fully Convolutional Network(MFCN)算法[30]。其中,MFCN算法[30]是用于定位拼接的生成图像,此实验用50000幅图像(Ic和M)训练它们用于定位深度修复图像,在测试阶段,使用50000幅测试图像(Ic, Ig和M)计算Recall, Precision, IoU和F1-score,性能如表6所示。在定位生成图像Ig时,两个检测器的取证性能在所有指标上都显著下降。特别是MFCN算法,已经完全无法正确定位出生成图像Ig的修复区域。对于HPFCN算法,生成图像Ig在F1-score方面能够实现攻击的取证性能为0.0772,实际对抗效果如图9所示。通过观察,可以发现检测器无法确定修复区域的位置。
4)检测器对生成图像Ig的重训练情况
本实验研究两个CNN取证检测器对生成图像Ig的重训练的情况,即检测器是用生成图像Ig数据重新进行训练,这属于白盒攻击,结果如表7所示。可以发现重训练后检测器能够重新识别生成图像Ig的修复区域,并且生成图像Ig和修复图像Ic存在一定的差异,如对于HPFCN算法,对匹配的生成图像数据的F1-score是96.96%,而不匹配的修复图像数据的F1-score是69.48%。
表6 当用修复图像Ic训练检测器时,生成图像Ig的对抗性能
Tab.6 When the detectors are trained with Ic, the counter-performance of Ig
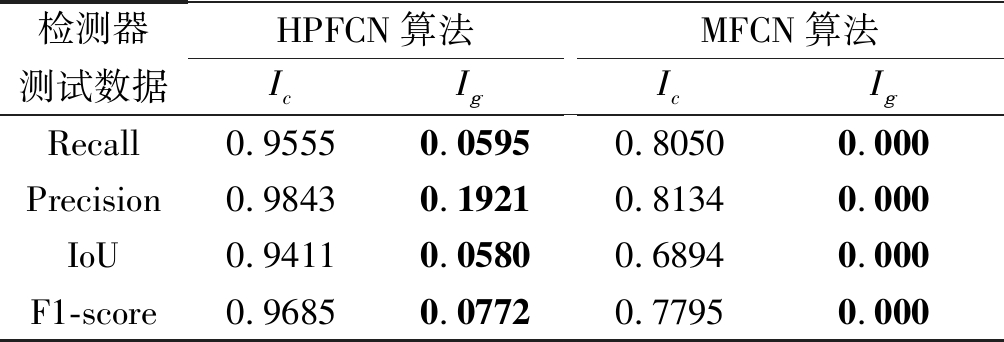
检测器测试数据HPFCN算法IcIgMFCN算法IcIgRecall0.95550.05950.80500.000Precision0.98430.19210.81340.000IoU0.94110.05800.68940.000F1-score0.96850.07720.77950.000
图9 生成图像Ig的对抗HPFCN算法的效果
Fig.9 The effect of Ig against HPFCN algorithm
表7 当用生成图像Ig训练检测器,对生成图像Ig的 重训练情况
Tab.7 When the detectors are trained with Ig, the retraining situation of Ig
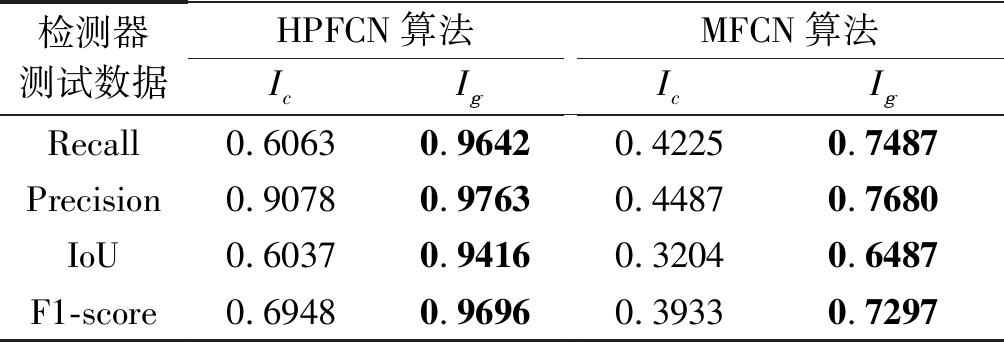
检测器测试数据HPFCN算法IcIgMFCN算法IcIgRecall0.60630.96420.42250.7487Precision0.90780.97630.44870.7680IoU0.60370.94160.32040.6487F1-score0.69480.96960.39330.7297
4.3 采用随机策略的生成网络的实验
通过以上第4.2节实验的结果,可知生成图像Ig可以通过重新训练的取证检测器进行重新识别,采用第3.3节所述应用于深度神经网络的随机策略来产生模式多样的图像。生成网络的初始参数固定在第137轮的模型。
的合适扰动区间
从4.2节可知,HPFCN算法[18]的取证检测器有着较强的识别能力,因此本实验以该检测器为例。观察图6中范围[-0.001, 0.001]和[-0.01, 0.01],可知网络参数值有较明显的变化,因此选择这两个区间进行以下的对抗实验。在训练阶段,根据随机策略方法产生一组随机数
和一个随机向量
然后根据公式(12)去扰动生成网络的最后一层参数,并使用训练集数据产生50000幅生成图像Ig去训练检测器。在测试阶段,一方面,使用训练阶段的密钥
和测试集数据去产生50000幅生成图像,验证检测器对由同样密钥扰动产生的数据分布识别的能力;另一方面,重新产生
和
去产生50000幅生成图像,验证检测器对测试数据分布识别的能力,结果如表8所示。可以看出,当
时,由于扰动强度小,随机策略无法对抗重训练的检测器。然而,可以清楚地看到, 当扰动能力达到一定强度时,如
随机策略即使在白盒情景下,即网络结构和某一时刻输出的生成图像被检测者所获得,也会对重训练的检测器产生影响,检测器只能对由同样密钥
扰动产生的数据有着较强的检测能力,而对由测试阶段不同的密钥
扰动产生的数据识别能力降低,如对于F1-score指标,检测器对训练数据分布的识别性能是95.94%,而对测试数据分布的识别性能是79.72%。这意味着本文提出的随机策略方法能够使网络产生多样化的图像。
表8 用随机策略的生成图像Ig训练检测器时, HPFCN算法对生成图像Ig的识别性能
Tab.8 The recognition performance of HPFCN algorithm when training with Ig generated with stochastic strategy
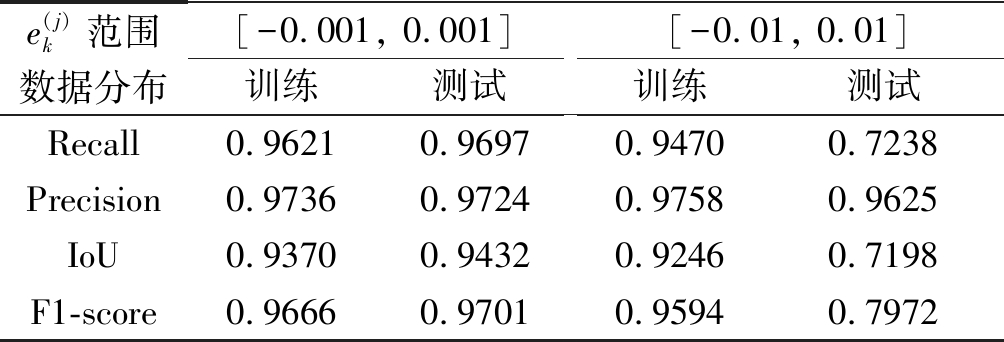
e(j)k范围数据分布[-0.001, 0.001]训练测试[-0.01, 0.01]训练测试Recall0.96210.96970.94700.7238Precision0.97360.97240.97580.9625IoU0.93700.94320.92460.7198F1-score0.96660.97010.95940.7972
接着,本文进一步探究在同一个
的条件下,不同
对结果的波动影响。具体地,选择上述产生测试图像的随机数
然后按第3.3节的均匀分布随机方法重新产生8组随机向量
之后产生多组测试图像,然后HPFCN算法[18]检测器进行检测,性能如表9所示。可以看出,同一个
的条件下,不同对结果有波动影响,此时检测器的性能主要由决定。同时本文计算了每组测试图像的PSNR平均值,与图8原先数值22.88 dB对比,结果表明采用随机策略后,生成图像视觉质量仍保持良好。
2)生成图像Ig的NIIS一致性
实验使用和图7(d)同样的修复图像Ic,配合随机策略去获得生成图像Ig。其中,
对生成图像Ig的NIIS的生成区域和真实区域进行统计直方图结果如图10所示。可以看出,随机策略并不影响实现NIIS的一致性。
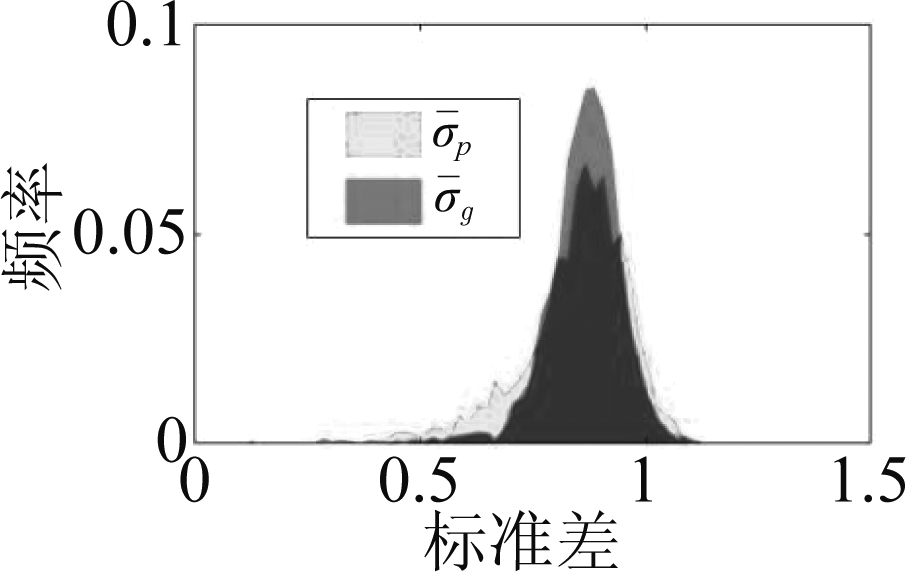
图10 针对GL算法[8]和CelebA数据集[21],随机 策略对实现生成图像的NIIS一致性的影响。(dχ2=0.05)
Fig.10 For GL algorithms[8] and CelebA data set[21], impact of stochastic strategy on achieving NIIS consistency for generated images
4.4 与对抗样本方法的比较实验
对抗样本方法Fast Gradient Sign Method[31] (FGSM快速梯度下降法)是一种向原有样本添加微小扰动,达到攻击检测器的算法,因此,本文进行了与FGSM算法在实现修复图像的对抗性能、NIIS统计特性和重训练方面的对比。具体地,本文对修复图像Ic的修复区域添加对抗样本噪声,使之成为对抗样本,然后测试其对HPFCN算法[18]的对抗性能。
表9 当
时,不同
取值对HPFCN算法检测器的对抗性能的影响
Tab.9 The counter-performance of different 
[-0.01, 0.01]
实验12345678PSNR average/dB22.8922.8622.9022.8822.8422.9122.8822.90Recall0.81330.44420.67010.65790.62520.82190.58540.4951Precision0.96370.75550.90270.86480.94760.94490.88210.8483IoU0.79910.44040.66140.64930.62290.81080.58240.4932F1-score0.86190.51640.73520.71330.71470.85770.66270.5797
对抗样本噪声强度为:4/255, 5/255和6/255。其中,4/255表示在8位修复图像中的修复区域,每个像素将被改动4个像素值,而像素改动的方向 (加/减)由检测器的梯度决定。对抗样本对检测器[18]的对抗性能和相应PSNR变化如表10所示,当扰动强度越大,图像质量损失越严重,而对抗性能却没有提升。此外,表10表明了FGSM对检测器的对抗结果,而对比表6中HPFCN算法实验表明的是本文生成图像对检测器的对抗结果,两者对比可知本文方法实现的生成图像Ig对HPFCN算法[18]检测器的对抗性能优于对抗样本FGSM[31]方法。另一方面,本文研究了FGSM[31]方法对实现NIIS一致性的能力,如图11所示。因为修复图像NIIS不一致的根本原因是修复区域高频成分的不足,因此对修复区域添加对抗噪声等同于为其提高高频成分,因此NIIS统计特性一致可以得到一定程度的改善。然而,从图10和图11的卡方距离看出,对抗样本实现的NIIS一致性比本文方法差,同时,对修复区域添加噪声还会破坏图像质量。最后,本文还研究了检测器对对抗样本重训练的识别情况,如表11 所示,FGSM[31]方法会给CNN检测器带来许多可区分痕迹,以至于重训练的检测器性能显著提高。综上所示,本文提出的方法对修复图像的NIIS一致性,图像质量,对抗性能方面都优于FGSM[31]对抗样本方法。
表10 对抗样本图像的对抗性能和PSNR变化。用修复 图像Ic训练HPFCN算法的检测器[18]
Tab.10 The counter-performance and PSNR change of adversarial samples. The detectors with HPFCN algorithm are trained with Ic
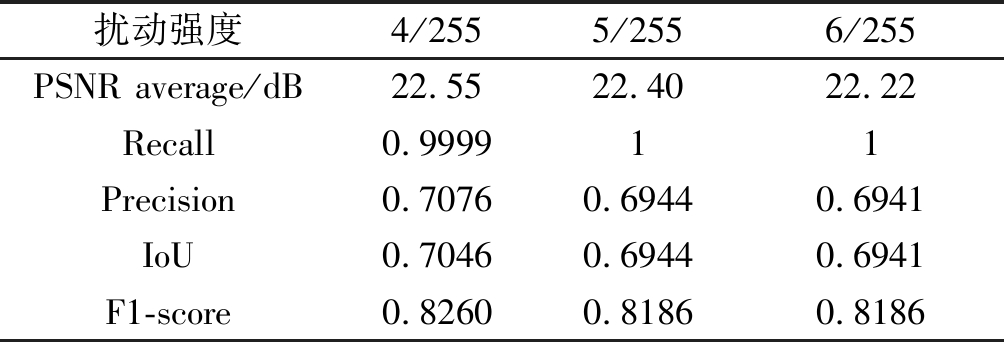
扰动强度4/2555/2556/255PSNR average/dB22.5522.4022.22Recall0.999911Precision0.70760.69440.6941IoU0.70460.69440.6941F1-score0.82600.81860.8186
4.5 在其他算法和数据集的实验
本实验展示使用提出的生成网络方法实现其他算法[13]和数据集[20]的NIIS统计特性一致性。实验直接使用前文已训练好的DIIS提取网络和三元组损失网络去重新训练两个新的生成网络,以实现图3中(c)“EC算法[13]和CelebA数据集[21]”、(d)“GL算法[8]和Places2数据集[20]”的NIIS统计特性一致性。具体实现如下:
表11 HPFCN算法对对抗样本的重训练情况, 即用对抗样本图像训练检测器
Tab.11 The retraining situation of adversarial samples by HPFCN algorithm, and the detectors of HPFCN algorithm are trained with adversarial samples
扰动强度4/2555/2556/255Recall0.99930.99940.9990Precision0.99950.99970.9994IoU0.99890.99910.9984F1-score0.99940.99950.9992
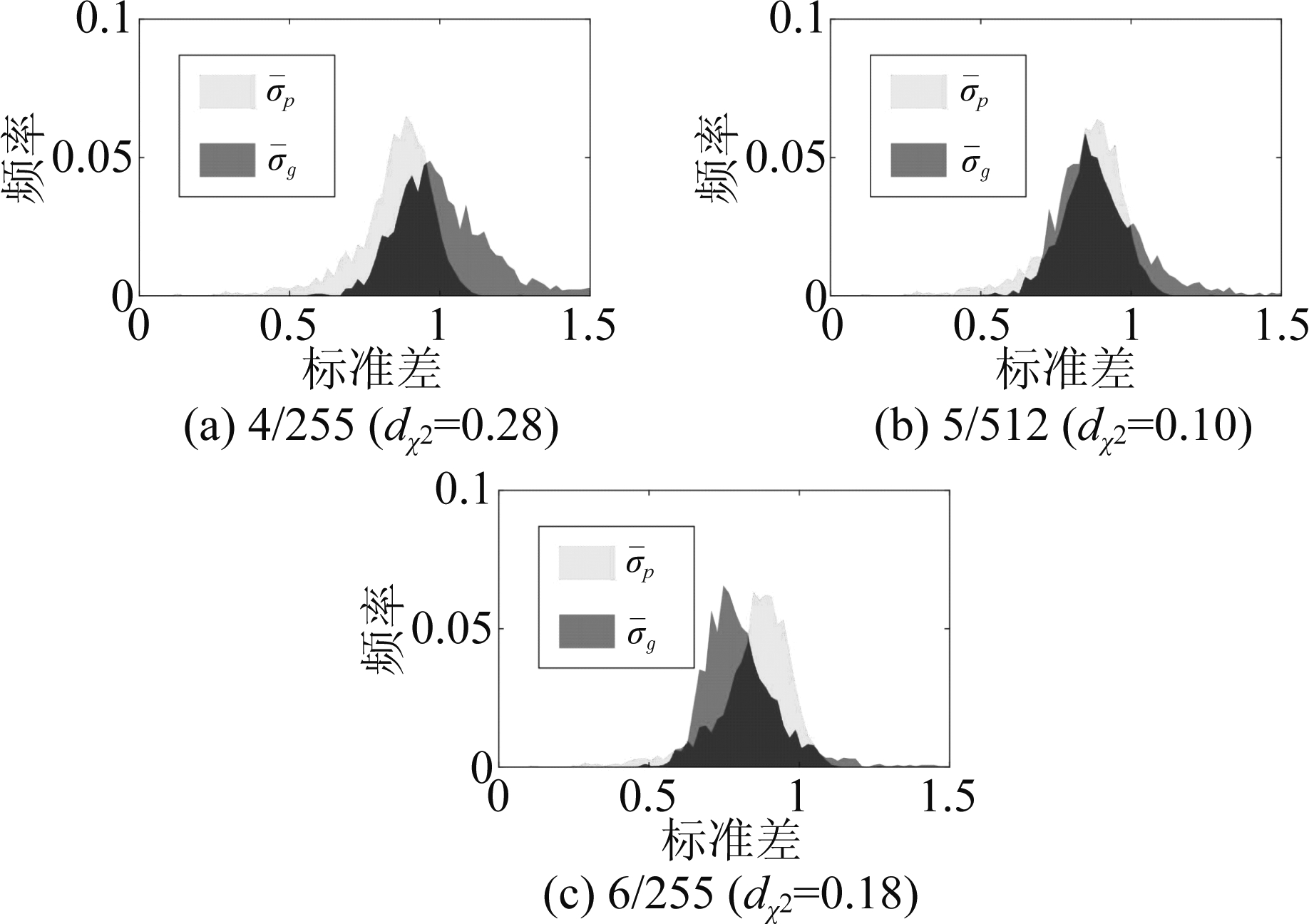
图11 For GL algorithms[8] and CelebA data set[21], 对抗样本方法FGSM实现的NIIS一致性
Fig.11 For GL algorithms[8] and CelebA data set[21], adversarial sample method FGSM on achieving NIIS consistency
1)从CelebA数据集随机挑选50000幅图像,然后使用EC算法[13]修复,图像尺寸会被扩大为256×256,修复区域在图像内随机选择,其长度和宽度在[32, 128]之间。生成网络训练的参数λ1=4,λ2=1/512,批次大小为32,其他超参数和第4.3节所述一样。
2)从Places2数据集中随机挑选了50000幅图像,然后使用GL算法[8]进行修复,图像尺寸不确定,其中最大边长度不超过500,另一边长会等比例缩小,修复区域在图像内随机选择,其长度和宽度在[32, 128]之间。生成网络训练的参数λ1=4,λ2=1/512,批次大小为1,其他超参数和第4.3节所述一样。
接着,两个生成网络各训练了200轮,分别采用图3中(c)和(d)的修复图像数据去获取生成图像Ig,同时为生成图像使用随机策略
然后统计它们的NIIS直方图和卡方距离情况,如图12所示。对比图3中(c)和(d)中修复图像的NIIS统计直方图,本文提出的方法依旧能实现其他算法和数据集的NIIS统计特性一致性。
图12 对于(a)EC算法[13]和CelebA数据集[21]、(b)GL 算法[8]和Places2数据集[20],本文方法实现的NIIS一致性
Fig.12 For EC algorithms[13] and CelebA data set[21], GL algorithms[8] and Places2 data set[20], the proposed method on achieving NIIS consistency
5 结论
本文分别采用非线性高通滤波残差和深度神经网络提取固有身份信号(intrinsic identity signal,IIS),称为NIIS和DIIS,研究发现深度修复图像普遍存在IIS统计特性不一致性,针对此问题,设计了一种基于卷积神经网络的图像修复后处理方法改善修复图像,使得其保持IIS统计特性一致性。本文提出了生成网络、DIIS提取网络和三元组损失网络联合优化深度修复图像。其中,主网络,即生成网络,在保持修复图像质量的同时,优化了修复区域DIIS与真实区域DIIS的统计特性不一致问题。作为监督网络,DIIS提取网络使得修复区域DIIS逼近对应内容的真实区域DIIS,三元组损失网络保证修复区域DIIS与图像已知真实区域DIIS的统计一致,同时优化后的生成图像能在NIIS统计特性方面达到了一致。实验结果表明,本文方法改善后的深度修复图像能够保持良好图像质量的前提下达到IIS统计特性一致。同时,本文还设计了一个应用于深度神经网络的随机策略,在合理范围内对生成网络部分参数进行扰动,从而生成具有模式多样的图像,该策略有效降低了白盒场景下生成图像被识别来源的概率,还保持了图像高质量。
由于本文提出的随机策略扰动网络参数的方式是有时序性的,而实际中更多时候还是需要独立的扰动方式。因此,今后工作将探究更加完善的随机策略。本文提出的方法目前只作为深度修复图像的后处理过程,今后将考虑在修复算法上注重统计一致性和高频细节的引入,以端到端的方式使图像修复在机器感知方面更加自然。
[1] Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting[C]∥Proceedings of the 27th annual conference on Computer Graphics and Interactive Techniques, 2000: 417- 424.
[2] 翟东海, 段维夏, 鱼江, 等. 局部特征分类的自适应扩散模型[J]. 信号处理, 2014, 30(9): 1039-1047.
Zhai Donghai, Duan Weixia, Yu Jiang, et al. Adaptive diffusion model based on Local Feature Classification[J]. Journal of Signal Processing, 2014, 30(9): 1039-1047.(in Chinese)
[3] 阮秋琦, 仵冀颖. 数字图像处理中的偏微分方程方法[J]. 信号处理, 2012, 28(3): 301-314.
Ruan Qiuqi, Wu Jiying. Partial Differential Equation (PDE) Method on Digital Image Processing[J]. Journal of Signal Processing, 2012, 28(3): 301-314.(in Chinese)
[4] Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: A randomized correspondence algorithm for structural image editing[C]∥ACM Transactions on Graphics (ToG). ACM, 2009, 28(3): 24.
[5] Criminisi A, Perez P, Toyama K. Region Filling and Object Removal by Exemplar-Based Image Inpainting[J]. IEEE Transactions on Image Processing, 2004, 13(9): 1200-1212.
[6] 范春奇, 任坤, 孟丽莎, 等. 基于深度学习的数字图像修复算法最新进展[J]. 信号处理, 2020, 36(1): 102-109.
Fan Chunqi, Ren Kun, Meng Lisha, et al. Advances in Digital Image Inpainting Algorithms Based on Deep Learning[J]. Journal of Signal Processing, 2020, 36(1): 102-109.(in Chinese)
[7] Pathak D, Krahenbuhl P, Donahue J, et al. Context encoders: Feature learning by inpainting[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 2536-2544.
[8] Iizuka S, Simo-Serra E, Ishikawa H. Globally and locally consistent image completion[J]. ACM Transactions on Graphics, 2017, 36(4): 1-14.
[9] Li Y, Liu S, Yang J, et al. Generative Face Completion[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2017: 3911-3919.
[10]Yu J, Lin Z, Yang J, et al. Generative image inpainting with contextual attention[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 5505-5514.
[11]Liu G, Reda F A, Shih K J, et al. Image Inpainting for Irregular Holes Using Partial Convolutions[C]∥European Conference on Computer Vision, 2018: 89-105.
[12]Yu J, Lin Z, Yang J, et al. Free-form image inpainting with gated convolution[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2019: 4471- 4480.
[13]Nazeri K, Ng E, Joseph T, et al. “Edge-connect: Generative image inpainting with adversarial edge learning.” arXiv: Computer Vision and Pattern Recognition, 2019.
[14]Xiong W, Yu J, Lin Z, et al. Foreground-aware image inpainting[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019: 5840-5848.
[15]Yan Z, Li X, Li M, et al. Shift-net: Image inpainting via deep feature rearrangement[C]∥Proceedings of the European Conference on Computer Vision (ECCV), 2018: 1-17.
[16]Sabini M, Rusak G. Painting outside the box: Image outpainting with GANs[J]. arXiv preprint arXiv: 1808.08483, 2018.
[17]Wang X, Wang H, Niu S. An Image Forensic Method for AI Inpainting Using Faster R-CNN[M]. Artificial Intelligence and Security, 2019.
[18]Li H, Huang J. Localization of Deep Inpainting Using High-Pass Fully Convolutional Network[C]∥International Conference on Computer Vision, 2019: 8301-8310.
[19]Lukas J, Fridrich J, Goljan M. Digital camera identification from sensor pattern noise[J]. IEEE Transactions on Information Forensics and Security, 2006, 1(2): 205-214.
[20]Zhou B, Lapedriza A, Khosla A, et al. Places: A 10 million image database for scene recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 40(6): 1452-1464.
[21]Liu Z, Luo P, Wang X, et al. Deep learning face attributes in the wild[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2015: 3730-3738.
[22]Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]∥International Conference on Medical Image Computing and Computer-assisted Intervention. Springer, Cham, 2015: 234-241.
[23]Lukas J, Fridrich J, Goljan M. Detecting digital image forgeries using sensor pattern noise[C]∥Security, Steganography, and Watermarking of Multimedia Contents VIII. International Society for Optics and Photonics, 2006, 6072: 362-372.
[24]Stamm M C, Liu K J R. Forensic detection of image manipulation using statistical intrinsic fingerprints[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(3): 492-506.
[25]Cao G, Zhao Y, Ni R, et al. Contrast Enhancement-Based Forensics in Digital Images[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(3): 515-525.
[26]Marra F, Gragnaniello D, Verdoliva L, et al. Do gans leave artificial fingerprints?[C]∥2019 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR). IEEE, 2019: 506-511.
[27]Long J, Shelhamer E, Darrell T. Fully Convolutional Networks for Semantic Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(4): 640- 651.
[28]Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[J]. Computer Science, 2014.
[29]Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]∥Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010, 9: 249-256.
[30]Salloum R, Ren Y, Kuo C C J. Image Splicing Localization using a Multi-task Fully Convolutional Network (MFCN)[J]. Journal of Visual Communication & Image Representation, 2018, 51(feb.): 201-209.
[31]Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples[C]∥ICML, 2015.
