1 引言
从图像中准确地估计深度是许多场景理解任务的基本问题,如场景分割、场景对象检索及视觉跟踪等。深度估计可以分为单目深度估计、双目深度估计以及多目深度估计。单目深度估计就是从单张图像中恢复出场景的深度信息,而双目深度估计和多目深度估计就是从两张或多张图片中求取深度。双目深度估计和多目深度估计可以通过输入图像的视角变化得到视差信息,从而得到深度。对人类来说,单目深度估计和双目深度估计一样并不困难,因为人类可以利用透视、相对于已知物体的比例以及视觉经验等线索获取深度信息。然而,在计算机视觉领域,由于一幅二维图像可能对应无限个三维场景,单目深度估计是一项比双目深度估计和多目深度估计更加困难的任务。
单目深度估计的研究由来已久,早期的工作通过几何约束和手工特征从图像中推断深度信息。Saxena等[1]提出了Make3D模型,该模型将输入图像分割成超像素,然后通过马尔可夫随机场推断每个超像素三维表面的三维位置和方向。
近年来,基于深度学习的方法在单目深度估计方面取得了令人瞩目的成绩。Eigen等[2-3]首先提出了一种多尺度深度神经网络(DNN),该方法利用额外的网络对原始网络的预测结果进行细化,它证明了基于深度神经网络的深度估计方法可以有效地提取局部和全局信息。基于该方法提出的改进方案包括:深度卷积神经场模型[4-5];将深度估计视为像素级别的分类任务而非回归问题[6];采用鲁棒性更强的损失函数如Huber损失[7]。Kendall等[8]通过构造匹配代价卷来分析几何特征并采用3D卷积合并上下文信息。Chang等[9]提出使用金字塔池化模块来捕捉更多的全局信息。虽然这些基于有监督学习的方法取得了很好的效果,但是需要对数据集进行大量的真实深度值标记,对于深度估计任务而言,深度值的标记工作是比较困难的。另外,由于有监督学习方法比较依赖真实的深度值数据,所以模型在新场景中的泛化能力很差。因此,近年来出现了一些用于单目深度估计的无监督框架。基于无监督学习的深度估计方法不需要对数据集进行真实深度值的标记,且对新场景的泛化能力更好。Garg等[10]提出的网络从左图像中预测出一张视差图,然后利用该视差图和原始右图重建出合成左图,通过最小化原始左图和合成左图的光度误差训练网络。Godard等[11]提出了左右视差一致性损失,从而保持单目深度估计的几何一致性。Pilzer等[12-13]首先提出将循环网络结构应用于深度估计。
本文提出了一种新的单目深度估计算法——基于自注意力机制的多阶段网络。该方法是完全无监督的,即训练过程中无需标记出真实深度值。该方法将双目图像对中的左图作为网络输入进行训练和测试。Godard等[11]提出的左右视差一致性损失函数有效地提升了深度图预测效果,因此网络也输出两张视差图用于计算左右视差一致性损失函数来加强两张预测视差图之间的一致性。利用两张预测视差图对双目图像对进行采样可以得到重建的左右两张图,用于计算左右两张图的重建损失函数以及对应的平滑度损失函数。值得注意的是,卷积网络的输入仅为单独的左图,而只有训练过程中需要使用右侧图像。整个网络结构由两个子网络构成,形成循环。正向子网络预测了两张视差图,重建的右图输入到反向子网络中预测两张新的视差图,重建出新的左右图像对,通过最小化新的重建图像对和原始图像的误差训练反向子网络。此外,该模型采用了自注意力机制,通过计算图像中任意两个位置之间的相互作用来捕获更多图像信息。网络利用左右视差一致性损失、平滑度损失以及掩模加权重建损失进行优化。综上所述,本文提出了以下几点创新:1)多阶段网络结构为单目深度估计提供了更强的约束和监督;2)自注意力特征提取器有利于提取更多的上下文信息;3)本文所提出的方法在KITTI数据集上获得了令人满意的预测效果。
2 主要方法
本文方法的详细架构如图1所示。立体图像对中的左图 Il 输入到正向子网络中预测两个视差图{dr,dl}。值得注意的是,同时估计两个视差图是为了计算左右视差一致性损失作为网络的约束。因此,尽管训练过程中需要使用立体图像对来计算左右两个视角的损失函数,测试时仅需要输入单张图像就可以估计出深度。原始图像对{Il,Ir}基于预测视差图{dr,dl}采样后重建出新的图像对![]() 重建图像对被用于计算左右两个视角的重建损失等损失函数。重建右图
重建图像对被用于计算左右两个视角的重建损失等损失函数。重建右图![]() 输入到反向子网络中预测出新的视差图
输入到反向子网络中预测出新的视差图![]() 正向子网络得到的重建图像对
正向子网络得到的重建图像对![]() 基于
基于![]() 采样后得到了新的重建图像对
采样后得到了新的重建图像对![]() 反向子网络通过最小化新的重建图像对
反向子网络通过最小化新的重建图像对![]() 和原始输入图像对{Il,Ir}的误差而得到优化。
和原始输入图像对{Il,Ir}的误差而得到优化。
如图1所示,整个网络经过了多阶段的训练。首先对正向子网络进行单独训练,直到正向子网络收敛,然后固定正向子网络的参数,再训练反向子网络。最后,联合训练整个网络直到收敛。测试时只使用正向子网络来估计单个图像的视差图。
下文分别介绍网络结构的细节,自注意力模块以及损失函数。
2.1 网络结构
如前所述,本文提出的网络结构包括正向子网络和反向子网络。正向子网络 Gf 从输入左图 Il 中预测两个视差图{dr,dl}:
{dr,dl}=Gf(Il)
(1)
其中 dr 和 dl 分别表示从左到右和从右到左的视差。原始输入图像对{Il,Ir}基于预测视差{dr,dl}采样(fw)后合成新的图像对![]()
(2)
(3)
合成图像对中的右图![]() 输入到反向子网络 Gb 中预测新的视差图
输入到反向子网络 Gb 中预测新的视差图![]()
(4)
接下来用新的视差图![]() 和合成图像对
和合成图像对![]() 重建出新的图像对
重建出新的图像对![]()
(5)
(6)
新的合成图像对![]() 和原始图像对{Il,Ir}之间的差异被用来优化反向子网络。
和原始图像对{Il,Ir}之间的差异被用来优化反向子网络。
测试时不需要反向子网络。单张图像输入到正向子网络中可以直接预测出视差图。两个子网络均采用编码器-解码器结构。如图1所示,本文采用Densenet169[14]作为编码器结构,包括一个卷积层、一个池化层以及四个下采样模块,每个下采样模块由多个DenseBlock(DB)和一个卷积层组成。解码器网络结构由一系列上采样层组成,每个上采样层后面连接一个卷积层。在上采样过程中,网络会预测出四个不同尺度的视差图。此外,编码器和解码器对应尺度之间的跳跃连接可以一定程度上保留图像的高分辨率细节。
在训练过程中,正向子网络从原始输入图像中学习视差,而反向子网络从合成图像中学习视差。

图1 本文方法的详细框架(参见2)。Warp是用来合成左右视图图像的重建函数(参见2.1)。自注意力模块是2.2中 介绍的自注意力特征提取器。掩膜生成解码器用于产生多尺度掩模,并计算掩模加权重建损失,详见2.3
Fig.1 Framework overview of proposed method (see Sec 2). Warp is the warping operation to synthesize left and right view images (see Sec 2.1). Self-attention denotes the self-attention feature extractor introduced in Sec 2.2. Mask decoder is used to produce multi-scale masks and compute mask weighted reconstruction loss detailed in Sec 2.3
训练反向子网络时,为了最小化重新合成的图像与原始输入图像之间的差异,反向子网络的输入应当是准确的图像对。因此,反向子网络对正向子网络的深度估计结果有很强的约束。与文献[12]中提出的用于双目深度估计的网络结构不同,本文方法用于单目深度估计,即两个子网络的输入都是单幅图像。
2.2 自注意力特征提取器
近年来,深度学习与注意力机制相结合的研究工作在很多领域得到了广泛应用[15]。在计算机视觉领域,注意力机制可以在提取特征的过程中获取更多的全局信息。本文方法中两个子网络都采用了自注意力特征提取器。自注意力机制[16-17]的作用是通过保证相似像素具有相似的深度特征来提高弱纹理区域的效果。自注意力模块被连接到编码器结构的最后一层,生成自注意力特征图,并将其与之前的特征图连接起来。
本方法所采用的自注意力模块的细节如图2所示。首先,将给定的特征图![]() 输入两个1×1卷积层中,得到两个新的特征图
输入两个1×1卷积层中,得到两个新的特征图![]() 其中C表示图像通道数,N=H×W表示特征图的大小。然后在矩阵Q与KT之间进行矩阵乘法运算,再对上述结果的每一行进行Softmax激活,得到注意力图S:
其中C表示图像通道数,N=H×W表示特征图的大小。然后在矩阵Q与KT之间进行矩阵乘法运算,再对上述结果的每一行进行Softmax激活,得到注意力图S:
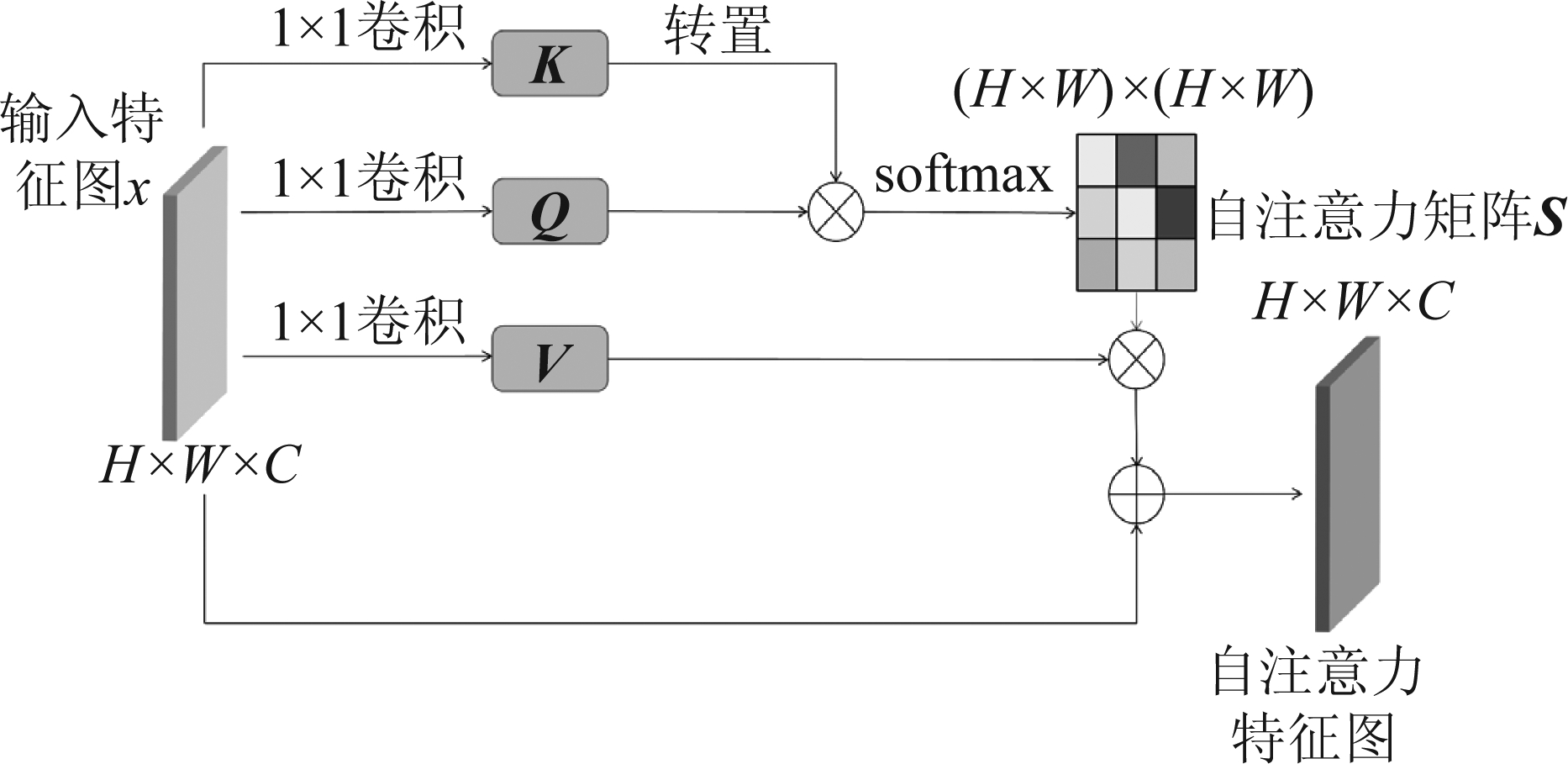
图2 自注意力模块实现细节
Fig.2 Details of the self-attention module
![]()
(7)
βj,i 代表位置i对位置j的影响。其中,相关性更强的两个位置的特征表示的相似性更高。
与此同时,将特征图x输入另一个1×1卷积层,生成新的特征图![]() 然后对S与V做矩阵乘法运算。最后得到的自注意力模块的输出如下:
然后对S与V做矩阵乘法运算。最后得到的自注意力模块的输出如下:
(8)
尺度参数 α 初始化为0,在训练过程中逐渐分配更多的权重。如公式(8)所示,输出的特征图是自注意力特征图和之前的特征图的叠加。
自注意力模块通过计算每个位置与其他所有位置之间的相似度,并将具有相似特征或外观的像素聚合在一起,保证了相似像素具有相似的深度特征,从而提高了弱纹理区域的预测效果。值得注意的是,自注意力模块被连接到编码器的最后一层,因此它在增强了特征表示的基础上并没有大幅提升计算复杂度。
2.3 损失函数
本文的方法不使用任何真实深度值数据,因此主要由重建损失进行监督。本文的单目深度估计框架所作的假设是:场景中没有运动的物体;左右视图之间没有遮挡关系。然而,在真实场景中,这些假设并不成立,因此训练过程可能会受到一些负面的影响。受到文献[18]的启发,本文采用一个额外的网络来估计掩模,作为重建损失的权重。如图1所示,掩模估计网络与每个子网络共享部分编码器权重,其解码器部分包含与主网络结构的编码器类似的四个上采样层和卷积层。掩膜生成网络预测出四个不同尺度的像素级别的掩膜![]() 作为重建损失函数的权重来提高网络的鲁棒性。
作为重建损失函数的权重来提高网络的鲁棒性。
掩模加权重构损失采用了L1和SSIM组合的形式。对于正向子网络,该重建损失最小化![]() 和{Il,Ir}之间的差异,而对于反向子网络,该重建损失最小化
和{Il,Ir}之间的差异,而对于反向子网络,该重建损失最小化![]() 和{Il,Ir}之间的差异。网络估计了四种不同尺度下的视差和掩模,四种尺度下的损失之和为最终损失,掩膜加权重建损失的计算方法如下:
和{Il,Ir}之间的差异。网络估计了四种不同尺度下的视差和掩模,四种尺度下的损失之和为最终损失,掩膜加权重建损失的计算方法如下:
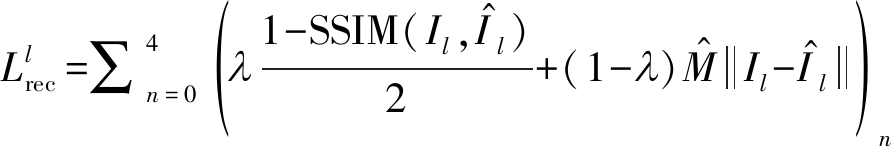
(9)
设置 λ为0.85。
此外,该方法引入平滑度损失,平滑度损失通过参考输入图像的梯度使视差图更加平滑,平滑度损失的计算方法如下:
(10)
本文还采用了左右视差一致性损失[11],该损失加强了两张视差图之间的一致性,有利于无监督网络的收敛:
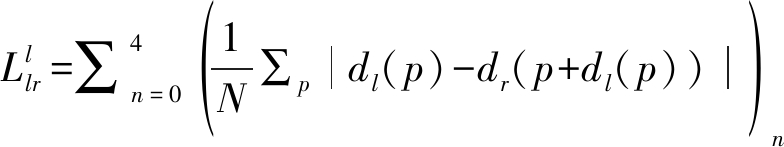
(11)
其中p表示视差图中的像素位置。公式(10)和公式(11)中,dl 和dr用于训练正向子网络,而对于反向子网络,这些损失函数中应使用![]() 和
和![]()
完整的训练损失函数包括掩模加权重建损失、平滑度损失和左右视差一致性损失的组合。所有的损失函数均包含左视角和右视角两项:
(12)
3 实验过程及结果
KITTI数据集[19]是一个用于深度估计的大规模公开数据集,本文算法主要在该数据集上进行评估。另外,Cityscapes数据集[20]用于泛化能力的评估。
3.1 实验设置
3.1.1 数据集
本文算法在KITTI数据集上进行训练和测试,使用Eigen等[3]提出的数据集分割方式。测试集包括697对分辨率为1242×375的图像对,共覆盖29个场景。其余23488对图像用于训练和交叉验证,其中22600对用于训练,剩余的用于验证。由于KITTI原始数据集的真实视差图非常稀疏,本文另外在包含200组图像对的KITTI 2015的训练集上进行了测试。
为了评估该单目深度估计模型的泛化能力,本文将KITTI数据集上训练的模型直接对Cityscapes数据集进行测试。Cityscapes测试集包括1525对分辨率较高的图像对。
3.1.2 训练细节
本文提出的网络结构使用Pytorch框架实现。训练时将输入图像大小调整为512×256。网络由Adam[21]优化器进行优化,优化器参数设置为 β1=0.9, β2=0.999。初始学习率设置为0.0001,mini-batch尺寸设置为8。损失函数各个部分的权重设置如下:αrec=1, αsmooth=0.1,αlr=1。
整个网络的训练过程分为多个阶段。首先,对正向子网络训练25次迭代,然后固定正向子网络的参数,再对反向子网络训练20次迭代。最后,对整个网络训练10次迭代,得到最终的模型。
3.1.3 评价指标
基于先前工作[3,11],本文采用如下客观评价指标来评估深度估计模型:
平均相对误差![]()
相对均方误差![]()
均方根误差![]()
均方根对数误差 (RMSE log):
准确率——满足如下条件的![]() 的百分比:
的百分比:
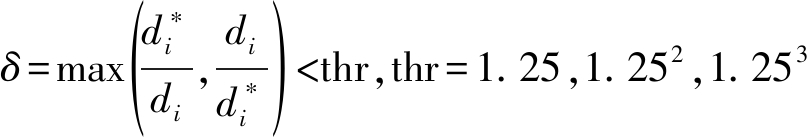
其中,![]() 和 di分别为像素i的预测深度和真实深度,T为图像的像素总数。
和 di分别为像素i的预测深度和真实深度,T为图像的像素总数。
3.2 实验结果与分析
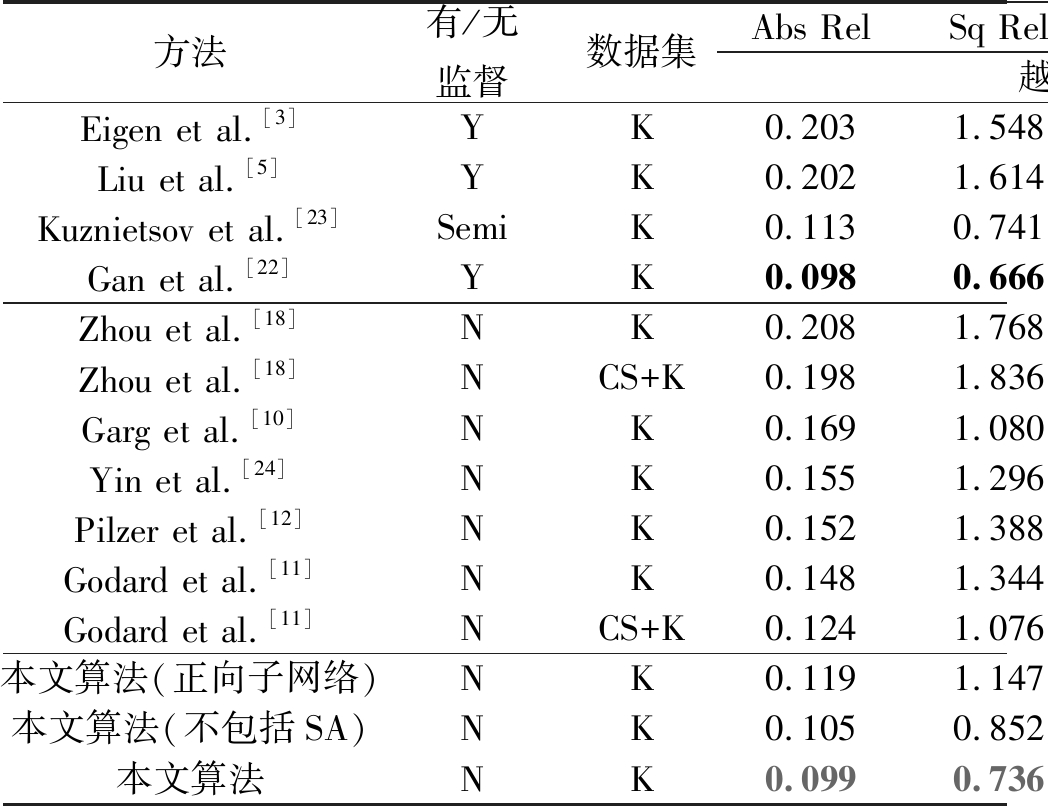
表1所示为本文方法与几个先进的基于有监督学习(Eigen et al.[3], Liu et al.[5],Gan et al.[22])、基于半监督学习(Kuznietsov et al.[23])以及基于无监督学习(Zhou et al.[18], Garg et al.[10], Yin et al.[24], Pilzer et al.[12], Godard et al.[11])的方法的对比结果。结果表明,本文算法的深度估计效果明显优于其他无监督学习方法的效果,同时也达到甚至超过了有监督学习方法的效果。为了证明该算法各部分的有效性,表1提供了在KITTI数据集上的消融实验结果。仅对正向子网络进行训练的客观指标证明了多阶段网络结构的有效性。另外,通过对比有无自注意力机制的实验结果,验证了自注意力特征提取器的有效性。
图3展示了KITTI数据集上的深度估计效果图。与其他方法相比,该模型在具有挑战性区域的预测效果更好,如细小物体、运动的车辆以及遮挡区域等。本文算法得到的深度图整体上看起来更加平滑,同时细节的预测效果也更好,特别是前景边缘部分的深度图预测得更加锐利清晰。
为了评估本文方法的泛化能力,该模型直接被用于测试Cityscapes 数据集,并将结果同其他基于无监督学习的方法进行对比,如图4所示。该模型只在KITTI数据集上进行训练,而没有用到Cityscapes数据集。尽管两个数据集在摄像机参数和场景特征上存在一定差异,该模型仍然可以产生视觉上令人信服的深度图像。
表1 KITTI数据集上的测试结果。K 代表 KITTI[19],CS代表Cityscapes[20]。深度的最大值是80米
Tab.1 Results on KITTI dataset. K represents KITTI[19] and CS is Cityscapes[20]. Depth predictions are capped at 80 meters
方法有/无监督数据集Abs RelSq RelRMSERMSE log越小越好δ<1.25δ<1.252δ<1.253越大越好Eigen et al.[3]YK0.2031.5486.3070.2820.7020.8900.958Liu et al.[5]YK0.2021.6146.5230.2750.6780.8950.965Kuznietsov et al.[23]SemiK0.1130.7414.6210.1890.8620.9600.986Gan et al.[22]YK0.0980.6663.9330.1730.8900.9640.985Zhou et al.[18]NK0.2081.7686.8560.2830.6780.8850.957Zhou et al.[18]NCS+K0.1981.8366.5650.2750.7180.9010.960Garg et al.[10]NK0.1691.0805.1040.2730.7400.9040.962Yin et al.[24]NK0.1551.2965.8570.2330.7930.9310.973Pilzer et al.[12]NK0.1521.3886.0160.2470.7890.9180.965Godard et al.[11]NK0.1481.3445.9270.2470.8030.9220.964Godard et al.[11]NCS+K0.1241.0765.3110.2190.8470.9420.973本文算法(正向子网络)NK0.1191.1475.0080.2130.8610.9470.975本文算法(不包括SA)NK0.1050.8524.4410.1830.8970.9620.982本文算法NK0.0990.7364.4350.1800.8970.9620.982

图3 本文方法在KITTI 2015上的深度预测结果示例
Fig.3 Results on the KITTI 2015 training set containing 200 images

图4 本文方法在Cityscapes上的深度预测结果示例。该模型仅在KITTI数据集上进行训练,直接在Cityscapes上测试
Fig.4 Our example depth predictions on the Cityscapes. Our model is trained on KITTI only, and directly tested on Cityscapes
4 结论
本文提出了一种基于自注意力机制的多阶段单目深度估计网络。网络结构由两个子网络构成,形成一个循环,为深度估计提供更强的约束和监督。此外,本文采用了掩模加权重建损失和左右一致性损失等损失函数,提高了深度估计的准确性。该方法在KITTI数据集上获得了较为满意的深度估计结果。但是,该方法对弱纹理区域预测结果的改进并没有达到理想的效果,天空等远景部分仍存在一定程度的伪影,这也是今后工作需要重点解决的问题。另外,今后的工作将会由图像深度估计扩展到视频深度估计领域进行更加深入和系统的研究。
[1] Saxena A, Sun M, Ng A Y. Make3d: Learning 3-d scene structure from a single still image[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5): 824- 840.
[2] Eigen D, Fergus R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture[C]∥ICCV, 2015: 2650-2658.
[3] Eigen D, Puhrsch C, Fergus R. Depth map prediction from a single image using a multi-scale deep network[C]∥NIPS, 2014: 2366-2374.
[4] Liu Fayao, Shen Chunhua, Lin Guosheng. Deep convolutional neural fields for depth estimation from a single image[C]∥CVPR, 2015: 5162-5170.
[5] Liu Fayao, Shen Chunhua, Lin Guosheng, et al. Learning depth from single monocular images using deep convolutional neural fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(10): 2024-2039.
[6] Cao Yuanzhouhan, Wu Zifeng, Shen Chunhua. Estimating depth from monocular images as classification using deep fully convolutional residual networks[J]. arXiv preprint arXiv: 1605.02305, 2016.
[7] Laina I, Rupprecht C, Belagiannis V, et al. Deeper depth prediction with fully convolutional residual networks[C]∥3DV, 2016: 239-248.
[8] Kendall A, Martirosyan H, Dasgupta S, et al. End-to-end learning of geometry and context for deep stereo regression[C]∥ICCV, 2017: 66-75.
[9] Chang Jiaren, Chen Yongsheng. Pyramid stereo matching network[C]∥CVPR, 2018: 5410-5418.
[10]Garg R, Kumar BG V, Carneiro G, et al. Unsupervised CNN for single view depth estimation: Geometry to the rescue[C]∥ECCV, 2016: 740-756.
[11]Godard C, Mac Aodha O, Brostow G J. Unsupervised monocular depth estimation with left-right consistency[C]∥CVPR, 2017: 270-279.
[12]Pilzer A, Xu Dan, Puscas M, et al. Unsupervised adversarial depth estimation using cycled generative networks[J]. arXiv preprint arXiv: 1807.10915, 2018.
[13]Pilzer A, Lathuiliere S, Sebe N, et al. Refine and distill: Exploiting cycle-inconsistency and knowledge distillation for unsupervised monocular depth estimation[C]∥CVPR, 2019: 9768-9777.
[14]Huang Gao, Liu Zhuang, Weinberger K Q, et al. Densely connected convolutional networks[C]∥CVPR, 2017: 4700- 4708.
[15]肖易明, 张海剑, 孙洪, 等. 引入注意力机制的视频声源定位[J]. 信号处理, 2019, 35(12): 1969-1978.
Xiao Yiming, Zhang Haijian, Sun Hong, et al. Video Sound Source Localization with Attention Mechanism[J]. Journal of Signal Processing, 2019, 35(12): 1969-1978.(in Chinese)
[16]Wang Xiaolong, Girshick R, Gupta A, et al. Non-local neural networks[C]∥CVPR, 2018: 7794-7803.
[17]Zhang Han, Goodfellow I, Metaxas D, et al. Self-attention generative adversarial networks[J]. arXiv preprint arXiv: 1805.08318, 2018.
[18]Zhou Tinghui, Brown M, Snavely N, et al. Unsupervised learning of depth and ego-motion from video[C]∥CVPR, 2017: 1851-1858.
[19]Geiger A, Lenz P, Urtasun R. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]∥CVPR, 2012: 3354-3361.
[20]Cordts M, Omran M, Ramos S, et al. The cityscapes dataset for semantic urban scene understanding[C]∥CVPR, 2016: 3213-3223.
[21]Kingma D, Ba Adam J. A method for stochastic optimization[J]. arXiv preprint arXiv: 1412.6980, 2014.
[22]Gan Yukang, Xu Xiangyu, Sun Wenxiu, et al. Monocular depth estimation with affinity, vertical pooling, and label enhancement[C]∥ECCV, 2018: 224-239.
[23]Kuznietsov Y, Stuckler J, Leibe B. Semi-Supervised Deep Learning for Monocular Depth Map Prediction[C]∥CVPR, 2017: 6647- 6655.
[24]Yin Zhichao, Shi Jianping. GeoNet: Unsupervised learning of dense depth, optical flow and camera pose[C]∥CVPR, 2018: 1983-1992.


