1 引言
随着计算机硬件技术和数值模拟技术的发展,基于流体动力学模型的烟雾仿真研究已成为计算机图形学和仿真领域的重要分支。烟雾作为一种特殊的流体,运动过程中容易产生涡环等复杂结构,具有丰富的细节。烟雾仿真算法需要对细节进行实现和保持以得到高真实度的仿真结果。在游戏、动画制作等实际应用中烟雾常与其他物体或场景进行交互,需要实现高效实时的烟雾仿真。综上烟雾仿真算法需要实现高真实度与高算法效率两方面的要求。
传统的流体仿真算法(如稳定流体方法等)一般需要通过大量连续的迭代计算对偏微分方程(如N-S方程,泊松方程等)进行求解。这一类仿真算法难以实现并行化以提高计算速度,在实现三维烟雾仿真等复杂度较高计算量较大的仿真问题时计算耗时较长,难以实现高效实时的仿真。
格子玻尔兹曼方法是20世纪80年代建立和发展起来的一种流体模拟计算方法,这是一种基于介观模拟尺度的计算流体力学方法。基于离散和统计的思想通过网格对计算区域进行离散化,利用分布函数来刻画流体,通过分布函数项在格点之间的移动模拟流体的流动过程,通过添加外力项和碰撞项来仿真流体粒子受的外力和流体粒子之间的相互作用。格子玻尔兹曼方法设置的格点之间耦合性较低,因此其可并行性较强,在图形处理器(Graphic Processing Unit, GPU)上进行编程可以有效地提高计算的效率,成为高效求解流体问题的有效方法。
格子玻尔兹曼方法在实现烟雾仿真方面存在一定的局限性。格子玻尔兹曼方法一般基于速度传输方程进行求解,只针对动量分布函数进行处理,因此只能保证仿真过程中流体的质量守恒,而对于涡量等物理量没有进行针对性修正。烟雾仿真的效果容易受涡量损失的影响。若仿真过程中缺少有效的涡量的修正步骤,可能导致生成仿真图像细节缺失,真实性较低。
本文提出基于亥姆霍兹方程追踪涡量的大小和方向,依据追踪的涡量信息计算并添加涡量修正力实现涡量补偿的格子玻尔兹曼算法实现高效真实的三维烟雾仿真。本文提出的算法针对烟雾仿真得到较好的涡量保持效果,可以生成具有丰富细节和高真实度的烟雾仿真图像。
本文的主要研究贡献可总结为如下三点:
(1)设计基于纳维-斯托克斯方程和亥姆霍兹方程对烟雾仿真过程中涡量的大小和方向进行追踪的算法,解决了传统涡量修正方法中涡量信息缺失的问题,不需要添加额外的无物理意义的参数进行涡量修正。
(2)提出利用追踪的涡量大小和方向计算涡量修正力对格子玻尔兹曼方法进行涡量修正的烟雾仿真算法,实现具有丰富细节和高真实度的烟雾仿真。
(3)结合统一计算设备架构(Compute Unified Device Architecture, CUDA)并行编程实现本文提出的烟雾仿真算法,利用GPU进行加速在可得到合理烟雾仿真效果的时间与空间分辨率下实现烟雾的实时仿真。
本文余下部分的组织结构如下:第2节介绍计算机仿真与计算机图形学领域内流体与烟雾仿真的相关工作;第3节介绍本文提出的涡量追踪和基于追踪的涡量信息计算涡量修正力进行涡量修正的格子玻尔兹曼算法;第4节介绍算法的编程实现细节并展示算法实验结果;第5节对全文内容进行总结。
2 相关工作
2.1 烟雾仿真算法
烟雾仿真研究是计算机图形学和流体仿真领域的重要分支。烟雾的运动具有丰富的细节,烟雾流场的涡量成分较大,涡量的损失对烟雾仿真效果会产生严重影响,缺乏有效的涡量修正步骤容易导致烟雾仿真过程中的误差不断积累,仿真稳定性降低,涡环扩散等细节缺失,因此难以得到具有较高真实度的仿真结果。Fedkiw[1]等人提出经典的针对气体仿真的涡量修正方法,通过人为添加一个无物理意义的参数对整个烟雾场的涡量进行相同幅度的修正,得到了基于稳定流体算法的经典烟雾仿真算法。BFECC[2-3]等算法从稳定流体方法出发通过反复的迭代提高计算精度。Ding[4]基于稳定流体算法将烟雾仿真模型分为对流项,扩散项,外力项和投影项,基于粒子系统并添加涡量限制实现二维空间中的烟雾仿真。Wu[5]利用离散正弦变换保留烟雾细节,在粗网格上求解修正的泊松方程以替代原有的投影步骤实现算法简化,提升算法效率。
基于稳定流体的算法在计算效率方面有所受限,格子玻尔兹曼方法与稳定流体算法相比具有较高并行性,可以实现高效的仿真计算,在计算力学和计算机仿真领域得到广泛应用。格子玻尔兹曼方法[6-7] 将整个空间用网格进行离散化,采用概率的思想使用分布函数进行离散化来刻画流体的分布,离散化的模式用“DnQm”进行表示,n代表仿真问题的维度,m代表分布函数项可以沿m个速度方向进行转移,常用的模式如“D1Q3”,“D2Q9”,“D3Q15”等等。Li[8]提出热格子玻尔兹曼模型(Thermal Lattice Boltzmann Method)在格子玻尔兹曼模型中实现了温度场的更新,进一步提升了格子玻尔兹曼方法应用于烟雾仿真的真实性。
除以上介绍的基于流体动力学方程的仿真方法外,近年来还有其他的烟雾仿真方法被提出。Hua[9]提出基于物理模型的算法实现红外烟雾仿真。Jeremy[10]使用时间逆向仿真指导烟雾动画生成,给定最终的流体配置,反向迭代生成序列再将该序列正向播放完成图像生成以实现与明确的艺术导向相匹配的仿真。Liu[11]通过小波分解进行频域分析增强流体的小尺度细节提升仿真效果。文献[12-13]采用谐波分析与主成分分析,二进制聚类树等方法从其他角度定义烟雾和烟雾粒子的运动过程进行仿真,可在某些场景下得到具有良好视觉效果的仿真结果。近年来机器学习算法和计算机硬件计算能力的进步也为更多流体仿真算法的出现创造了可能,如Xiao[14]使用适应性学习的方法取代传统仿真算法中的投影过程以提高仿真效率,Deng[15]则基于可编程GPU实现实时性的高效烟雾仿真算法,Shi[16]使用多特征判别的机器学习方法利用视频对复杂环境下的烟雾进行检测,Wiewel[17]使用神经网络提取烟雾运动的特征并基于LSTM网络实现烟雾仿真的时序预测。
2.2 烟雾仿真的涡量修正
涡量修正是烟雾仿真中的重要步骤,合适的涡量修正步骤是得到具有高真实度烟雾仿真结果的必要条件。Fedkiw[1]的方法通过添加额外的无物理意义的参数计算并施加涡量修正力对全场的涡量进行相同幅度的修正,无法针对烟雾场的局部情况进行对应的涡量修正,仿真结果受参数影响明显。Michael[18]在Fedkiw[1]方法的基础上添加了流场的密度场信息,根据烟雾的分布进行适应性的涡量修正,但仍需要通过参数调节涡量信息。Xu[19]提出一种自适应的两尺度涡量约束方法,可自适应的确定涡量细节丰富的区域并在选定区域内通过设定的阈值进行涡量修正,该算法只对涡量细节丰富的区域进行修正,但仍然需要添加无物理意义的阈值。Tang[20]根据涡量的强度计算自适应涡量修正力进行涡量修正,并将上采样的速度场和涡量修正项混合消除噪声并得到高分辨率的结果,提高计算效率。Masato[21]通过计算低分辨率网格中每个单元的能量级联比并与描述空间中湍流能量分布的Kolmogorov的五分之三定律进行比较找到正确的物理位置适当添加噪声和外力对湍流实现外观自然的涡量修正和细节填充效果。Chen[22]基于涡流丝对烟雾进行仿真,并且引入了涡流环,通过对涡流丝模型进行谐波分析避免涡流丝拉伸过程中采样不足,可以更好地控制烟雾,得到更快的渲染速度和更好的时间稳定性。Zhu[23]利用可高效计算的高阶数值方法实现烟雾仿真中的细节保持,获得良好的细节保持仿真结果。Zhang[24-25]提出了使用均匀网格动态连接涡流细丝和烟雾颗粒,通过求解泊松方程得到速度场,涡量场和质量场均通过速度场进行迭代更新的仿真方法。该方法从涡量场角度出发进行求解可以有效减少涡量的耗散,实现具有涡旋扩散效果的稳定烟雾模拟。
以上的涡量修正算法实现或基于稳定流体算法或直接从涡量场出发进行计算,难以直接应用到格子玻尔兹曼方法中。Wen[26]提出VPLBM(Vorticity preserving lattice Boltzmann method)算法针对格子玻尔兹曼算法进行涡量修正,在仿真过程中对涡量的大小进行追踪并基于追踪的信息计算涡量修正力实现涡量修正,不需要添加其他参数,得到较好的涡量修正效果,但忽视涡量方向随时间的变化,因此在较长时间步的仿真中可能由于忽视涡量方向产生的误差积累导致仿真结果失真。本文提出的算法是VPLBM算法的扩展,在VPLBM算法的基础上增加对涡量方向的追踪并进一步改进涡量修正力项,使烟雾仿真算法可以更好地实现涡量修正,在较多时间步迭代的计算中得到更真实的烟雾仿真结果。
3 涡量修正的格子玻尔兹曼算法
3.1 基于亥姆霍兹方程的涡量追踪
对N-S(Navier-Stokes)方程的左右两侧同时取旋度可以得到描述涡量变化的亥姆霍兹方程(公式(1))。
![]() =-(u·
=-(u· )ω+(ω·
)ω+(ω· )u+νΔω+
)u+νΔω+ ×F
×F
(1)
公式(1)中的ω代表涡量场,u代表速度场,ν代表运动粘性系数,F代表流体所受外力,t代表时间。
Wen[26]的研究中给出了基于亥姆霍兹方程追踪涡量大小的方法,将公式(2)代入到亥姆霍兹方程中可以得到追踪涡量大小的公式(3),其中sω代表涡量源项。
(2)
![]() =-(u·
=-(u· )ω+νΔω+sω
)ω+νΔω+sω
(3)
sω的具体表达式如下(x,y,z代表三维坐标):
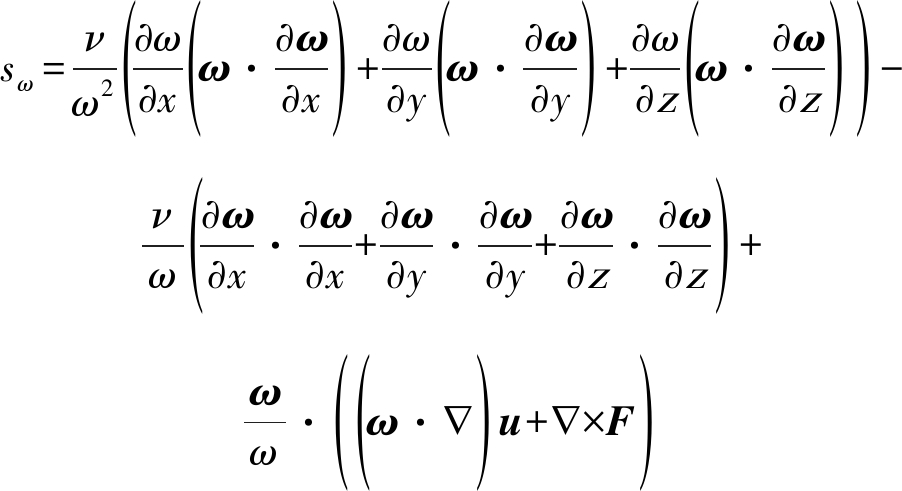
(4)
本文设计算法在完成对涡量的大小追踪的基础上利用亥姆霍兹方程对涡量的方向进行追踪。首先将涡量向量分解为涡量的绝对值和涡量方向向量的乘积,之后再计算对时间的偏导数。
ω=ωe
(5)
(6)
由公式(6)可以推导得到涡量的方向向量对时间的导数的计算公式(公式(7))。
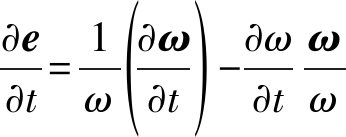
(7)
将涡量及其对时间的导数写成分量形式代入到方程中进行计算可以得到如下的分量形式的涡量方向向量对时间的导数的计算公式(公式(8))。
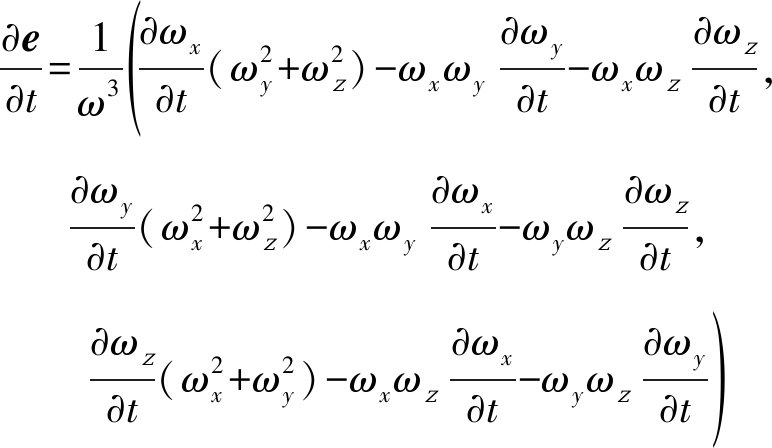
(8)
公式(8)中涡量分量对时间的导数可通过亥姆霍兹方程并利用速度场、涡量场、外力信息进行计算得到。根据涡量方向向量对时间的导数通过公式(9)迭代更新可计算下一时刻的涡量方向向量。

(9)
考虑到数值误差的影响每次更新迭代方向向量可能导致方向向量的模不为1,因此在每次更新后需要再对方向向量进行归一化操作。
3.2 涡量修正格子玻尔兹曼算法推导
格子玻尔兹曼方法使用离散化的分布函数对流体进行建模,涡量修正格子玻尔兹曼算法模型是热格子玻尔兹曼模型[8]和VPLBM[26]模型的扩展,对速度,温度和涡量的绝对值的分布函数以及涡量方向场进行迭代更新实现烟雾仿真。算法仿真过程中涡量的修正通过施加利用追踪的涡量信息计算的涡量修正力实现。
3.2.1 格子玻尔兹曼算法更新方程推导
速度(公式(11)),温度(公式(12))和涡量的绝对值(公式(13))均符合一般的流动扩散方程(公式(10)的形式,α为扩散系数,s为源项)。
![]() =-(u·
=-(u· )φ+αΔφ+s
)φ+αΔφ+s
(10)
![]() =-(u·
=-(u·
![]()
 p+F
p+F
(11)
![]() =-(u·
=-(u· )T+αΔT+sT
)T+αΔT+sT
(12)
![]() =-(u·
=-(u· )ω+νΔω+sω
)ω+νΔω+sω
(13)
对于流动扩散方程可利用Chapman-Enskog展开计算平衡态分布函数(ωi为离散格子的权重系数,cs为归一化系数)。
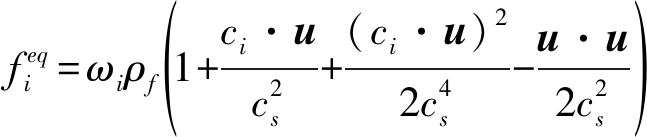
(14)
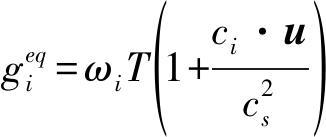
(15)

(16)
对应引入BGK碰撞算子可以得到动量分布函数fi(公式(17)),温度分布函数gi(公式(18)),和涡量的绝对值分布函数hi(公式(19))的更新方程。
(17)
(18)
(19)
上式中的系数τν,τα由扩散方程中的系数决定
通过分布函数项的叠加可以完成宏观量(密度,动量(速度)和温度)的计算。
(20)
(21)
(22)
3.2.2 涡量修正力的计算
格子玻尔兹曼方法通过对散度的约束实现质量守恒,但这一过程中对速度场进行约束可能导致涡量的不守恒,因此需要添加涡量修正力进行涡量补偿。涡量修正格子玻尔兹曼模型使用公式(23)(N定义见公式(24))定义的涡量修正力项,利用追踪的涡量大小和方向与当前时刻速度场的旋度作差进行计算实现涡量的修正。
Fref=|ω-
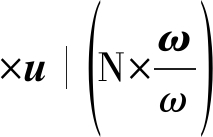
(23)
![]()
 |ω|)
|ω|)
(24)
这一涡量修正力项与Wen[26]提出的VPLBM算法相比利用了基于亥姆霍兹方程追踪得到的涡量方向信息,避免了忽视涡量方向导致的误差累积,对于涡量场和速度的旋度场较接近的情况产生较小的噪声,可以在较多的仿真迭代步数下得到更好的涡量修正效果。
3.3 涡量修正格子玻尔兹曼算法流程
涡量修正格子玻尔兹曼算法的仿真过程由三个分布函数的更新以及涡量方向向量场的更新迭代组成。在每一帧的计算中重复如下循环实现完整的烟雾仿真过程。
算法1 涡量修正格子玻尔兹曼算法
Algorithm.1 Vorticity refinement lattice Boltzmann method

涡量修正格子玻尔兹曼算法开始循环1.计算外力,包括涡量修正力和浮力2.基于亥姆霍兹方程对涡量方向场进行更新3.计算涡量源项4.计算涡量分布函数和动量分布函数的碰撞过程更新5.计算涡量分布函数和动量分布函数的迁移过程更新6.处理涡量分布函数和动量分布函数的边界条件7.计算宏观物理量(动量和涡量)的数值并更新8.计算温度分布函数的碰撞过程更新9.计算温度分布函数的流动过程更新10.处理温度分布函数的边界条件11.计算宏观物理量(温度)的数值并更新12.计算速度场的旋度结束循环
通过亥姆霍兹方程更新得到的涡量方向向量场代表下一时刻的涡量方向,因此涡量场的迭代实际上比速度场的迭代快一个时间步,因此需要在更新速度场前更新涡量的方向场以得到合理的涡量修正力实现涡量修正。
4 算法实现与结果展示
4.1 算法实现简述
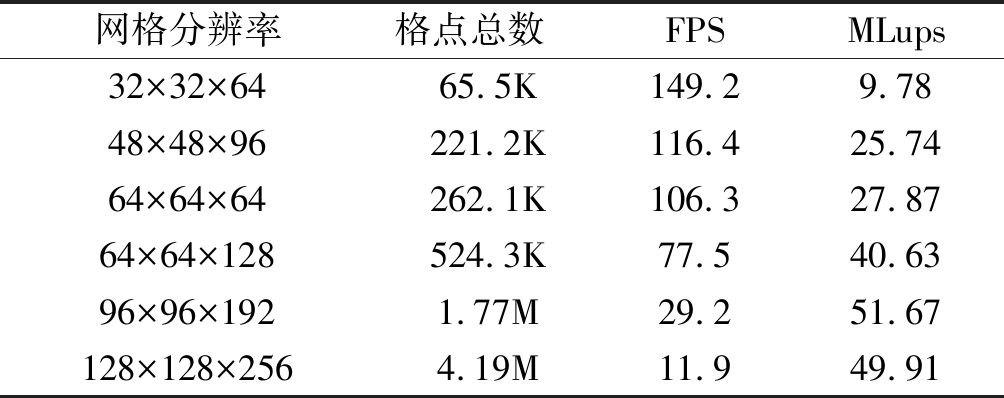
本文的涡量修正格子玻尔兹曼算法利用C++语言进行编程实现。为利用格子玻尔兹曼方法的可并行性以提高仿真的计算效率,算法程序在NVIDIA公司推出的通用并行计算框架CUDA下实现。烟雾仿真结果通过基于OpenGL(Open Graphics Library)编写的渲染模型实现可视化。为格子玻尔兹曼模型中的每一个离散单元分配一个线程进行计算,不同的线程对不同的数据执行相同的算法流程以获得更高的算法实现效率。利用单GPU(NVIDIA RTX 2060)进行加速,使用离散格式为“D3Q15”的格子玻尔兹曼格式进行仿真。表1给出不同分辨率下的算法仿真效率测试结果。算法实现中利用涡量修正格子玻尔兹曼方法的并行性在单GPU加速的条件下对于空间分辨率64×64×128,时间步长为0.02 s的烟雾仿真模型计算帧率超过50,可以实现高效实时的烟雾仿真,对更高分辨率的网格也可实现快速的计算。在空间分辨率超过96×96×192以后百万格子更新每秒出现下降代表此分辨率下GPU的应用已达到最大化。
表1 不同分辨率网格下的单GPU加速烟雾仿真效率, 性能指标为帧率(FPS)和百万格子更新每秒(MLups)
Tab.1 Smoke simulation performance with single GPU acceleration with different grid resolutions, performance indexes include FPS(frames per second) and MLups (million lattice updates per second)
网格分辨率格点总数 FPSMLups32×32×6465.5K149.29.7848×48×96221.2K116.425.7464×64×64262.1K106.327.8764×64×128524.3K77.540.6396×96×1921.77M29.251.67128×128×2564.19M11.949.91
4.2 涡量修正格子玻尔兹曼算法结果
烟雾仿真实验环境设置为一个长方体的密闭空间,长方体的长和宽相等,高为长和宽的两倍。网格分辨率设置为64×64×128,时间步长为0.02 s,粘性系数υ为0.05,热扩散系数α为1.0。仿真过程中将烟雾源置于底面模拟烟雾上升过程。在不同环境下进行多组烟雾仿真实验(单一烟雾源与多烟雾源,不同障碍物设置等),本小节对仿真算法计算结果进行展示和讨论。
图1~图4分别展示了单烟雾源单障碍物,多烟雾源单障碍物,单烟雾源多障碍物和多烟雾源多障碍物的仿真计算结果。固定障碍物采用half-way反弹边界条件[27]进行处理。实验中烟雾从底部的烟雾源产生,受浮力的作用向上运动。烟雾在遇到障碍物后均可绕开障碍物继续上升,在上升过程中烟雾粒子之间的作用以及烟雾与障碍物之间的作用形成涡环,通过涡量修正格子玻尔兹曼算法实现烟雾运动过程中的涡量修正,可以在烟雾运动过程中保持涡环的完整结构,生成具有丰富细节和高真实度的烟雾仿真图像。
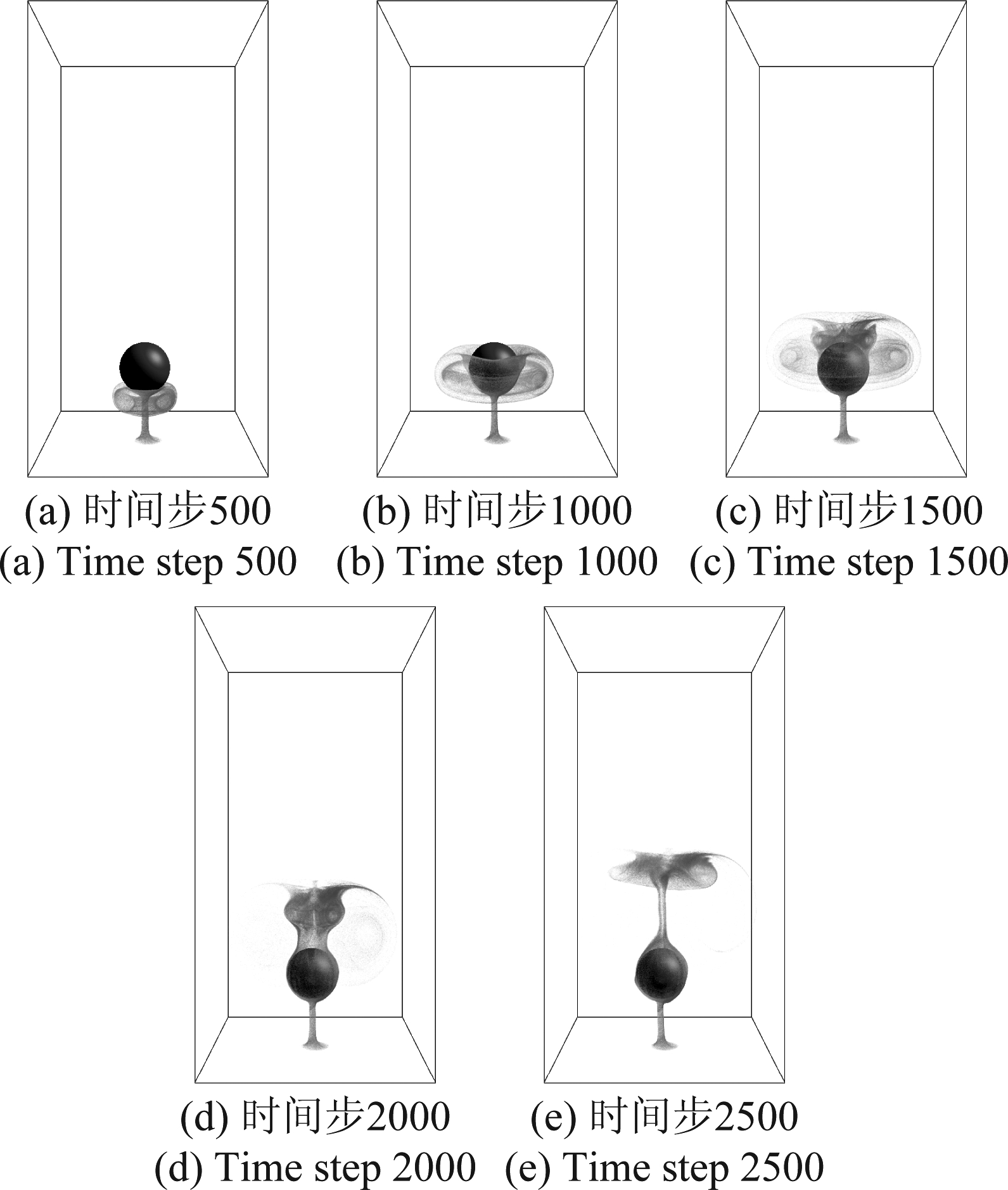
图1 单烟雾源单障碍物仿真结果示例
Fig.1 Smoke simulation example with single smoke source and single obstacle
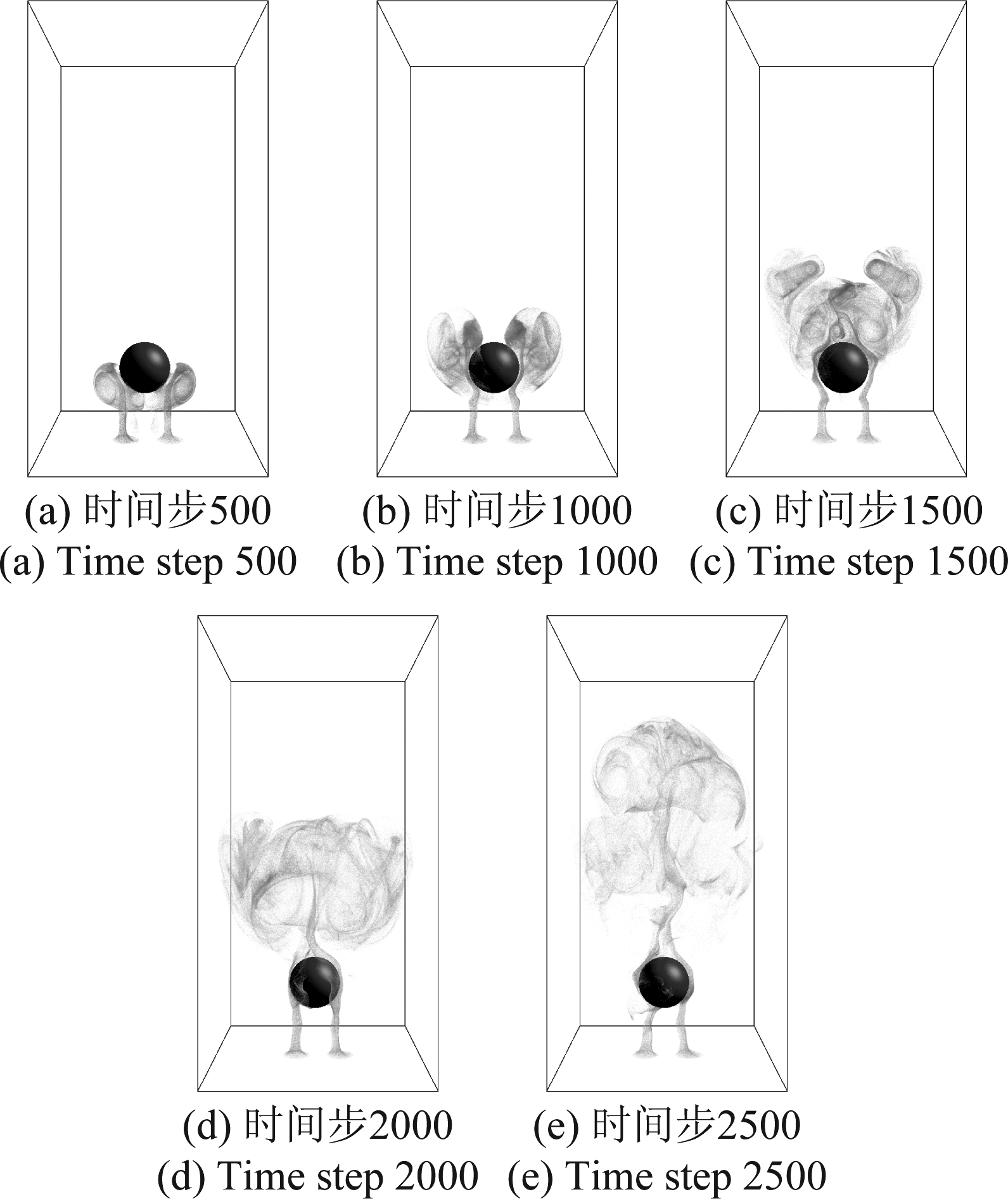
图2 多烟雾源单障碍物仿真结果示例
Fig.2 Smoke simulation example with double smoke sources and single obstacle
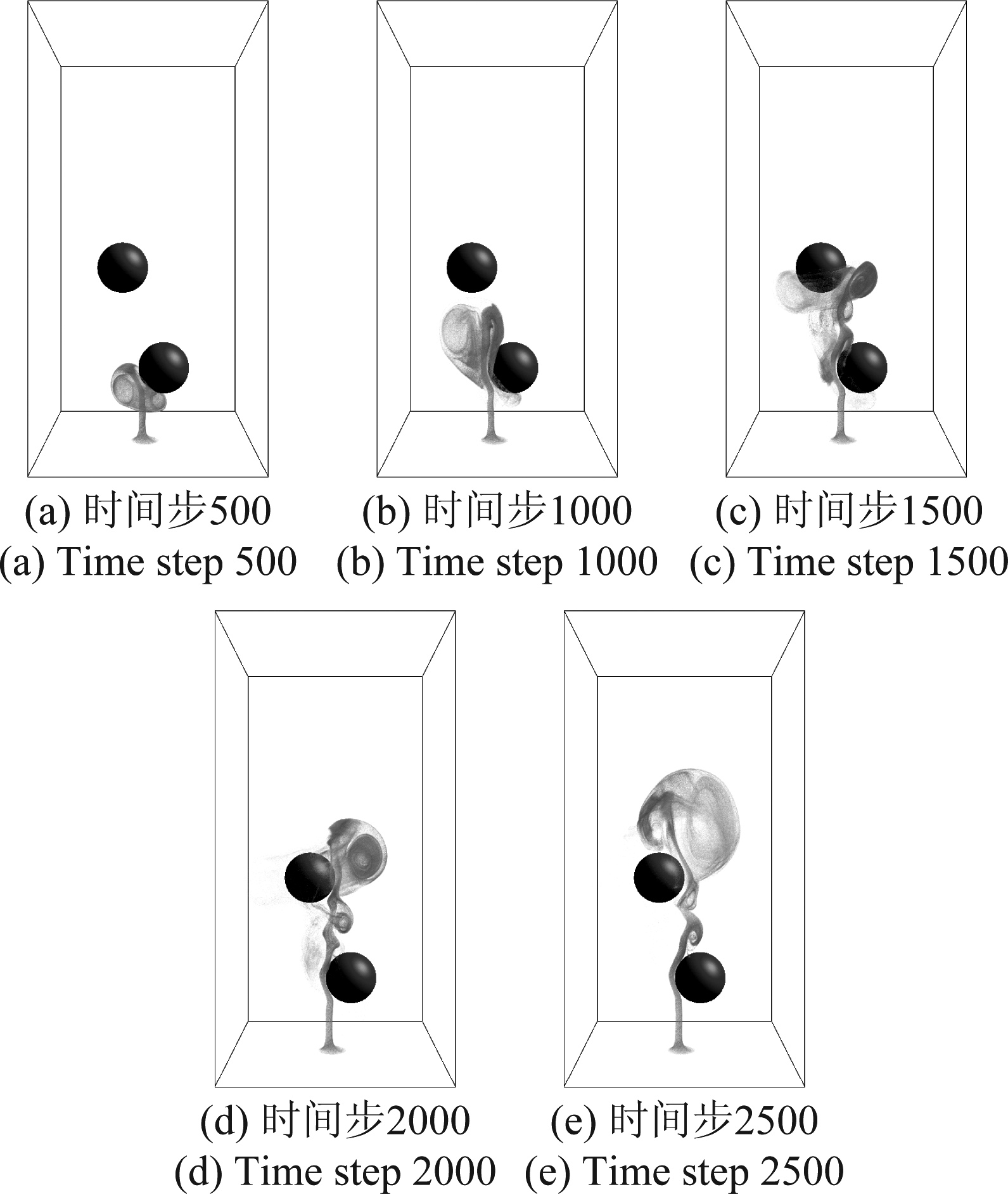
图3 单烟雾源多障碍物仿真结果示例
Fig.3 Smoke simulation example with single smoke source and double obstacles
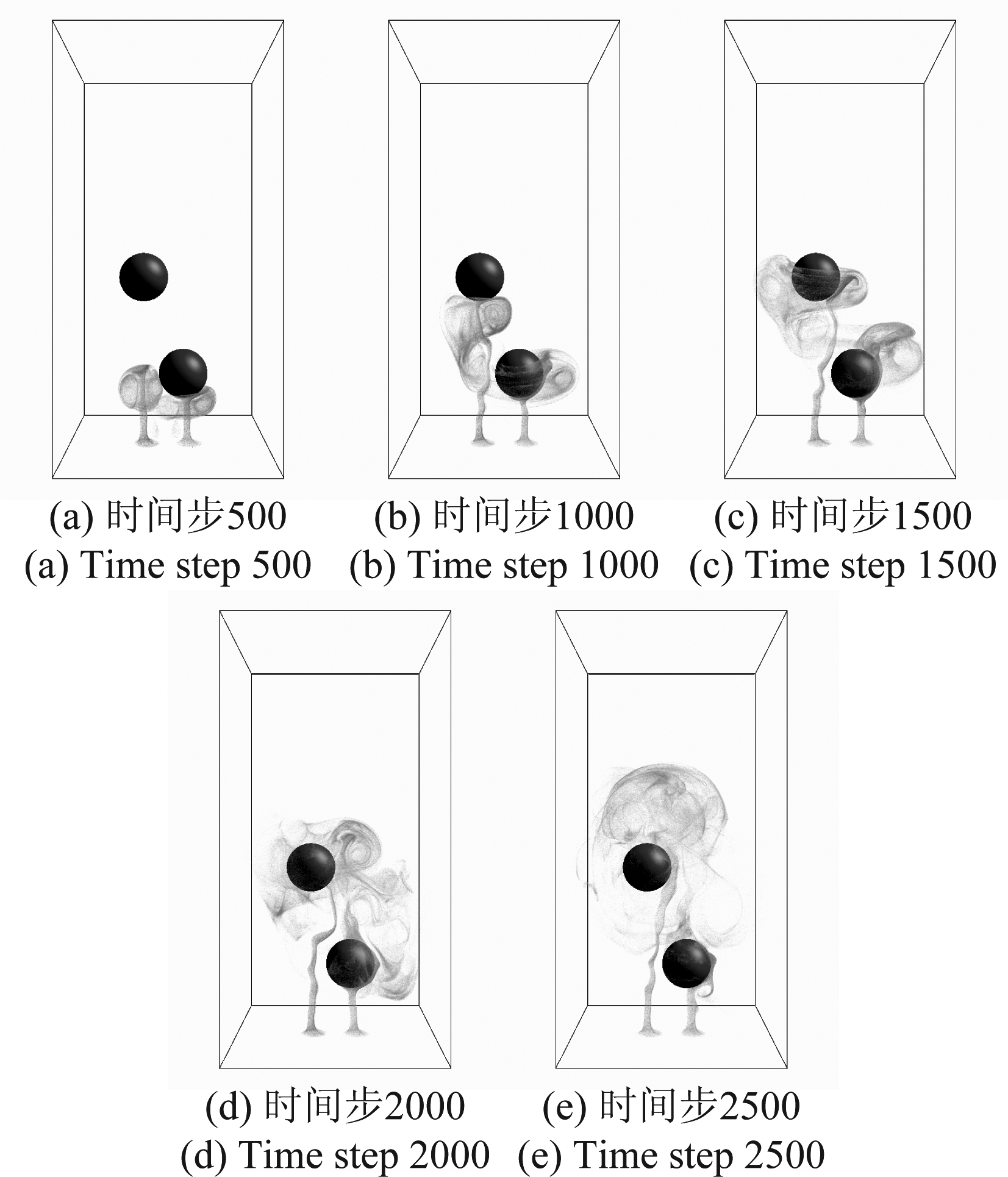
图4 多烟雾源多障碍物仿真结果示例
Fig.4 Smoke simulation example with double smoke sources and double obstacles
图5在相同实验条件下对比不添加涡量修正力的格子玻尔兹曼算法与涡量修正格子玻尔兹曼算法的结果对比,两种算法生成的图像具有明显的差异。不添加涡量修正力的格子玻尔兹曼算法涡量损失严重,涡环在烟雾上升过程中容易破碎,难以保持完整的涡环结构,烟雾仿真的细节缺失,生成的仿真图像真实度较低。涡量修正格子玻尔兹曼算法可以很好的实现涡量的修正,获得更平稳的烟雾上升和扩散效果,生成细节丰富且具有高真实度的烟雾仿真图像。
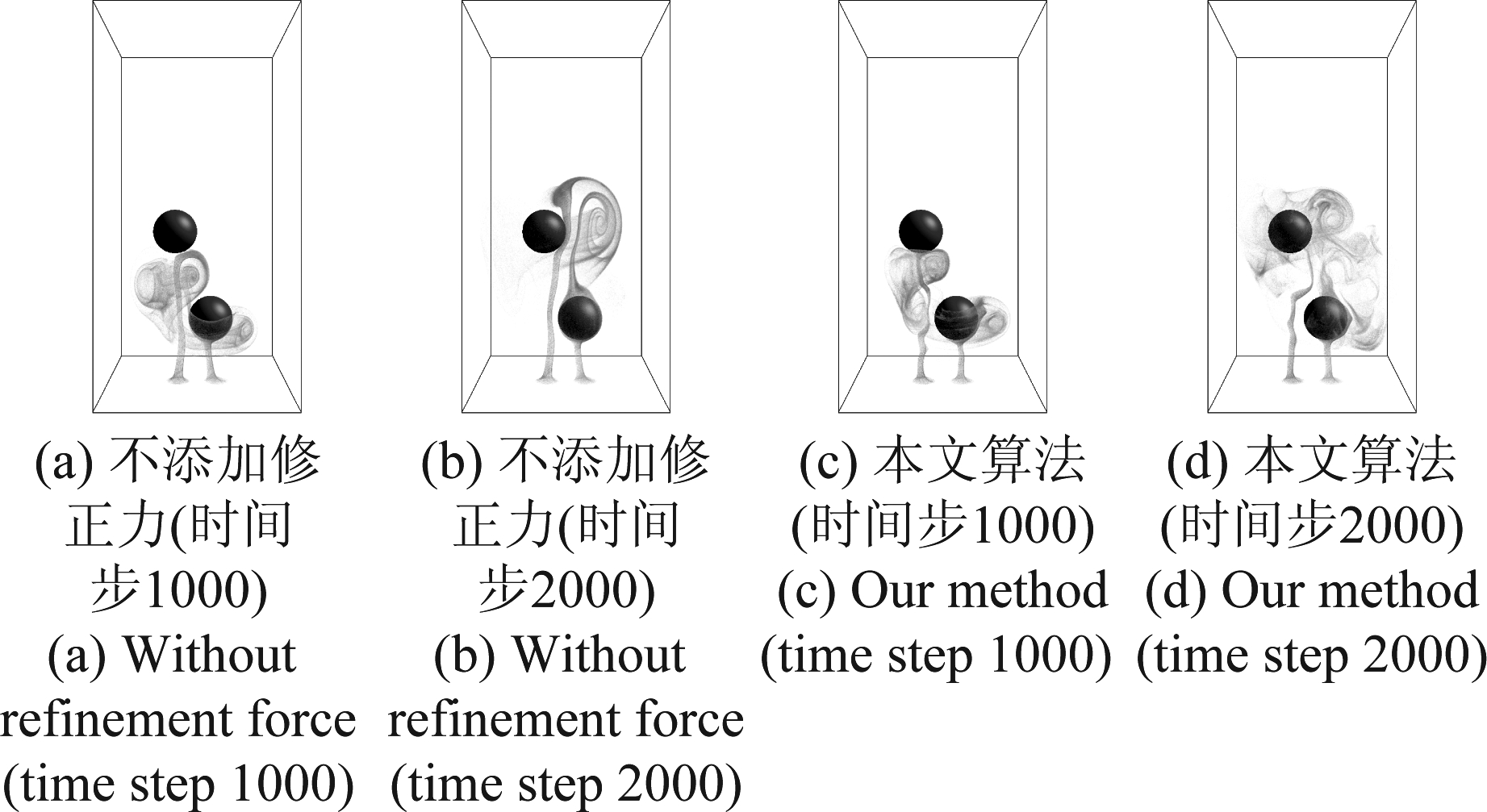
图5 不添加涡量修正力的格子玻尔兹曼算法与 涡量修正格子玻尔兹曼算法的仿真结果对比
Fig.5 Smoke simulation results comparison between lattice Boltzmann method without refinement force and vorticity refinement lattice Boltzmann method
图6在相同实验条件下对比同一时刻采用不同涡量修正方法进行烟雾仿真的实验结果。Fedkiw[1]和Michael[18]的仿真算法需要引入无物理意义的参数进行修正,仿真结果受参数影响明显,稳定性不佳,难以得到真实的烟雾仿真效果。相比之下Wen[26]提出的VPLBM算法与本文算法生成的图像中烟雾可自然地绕过障碍物上升并扩散,得到更加合理真实的烟雾仿真效果。
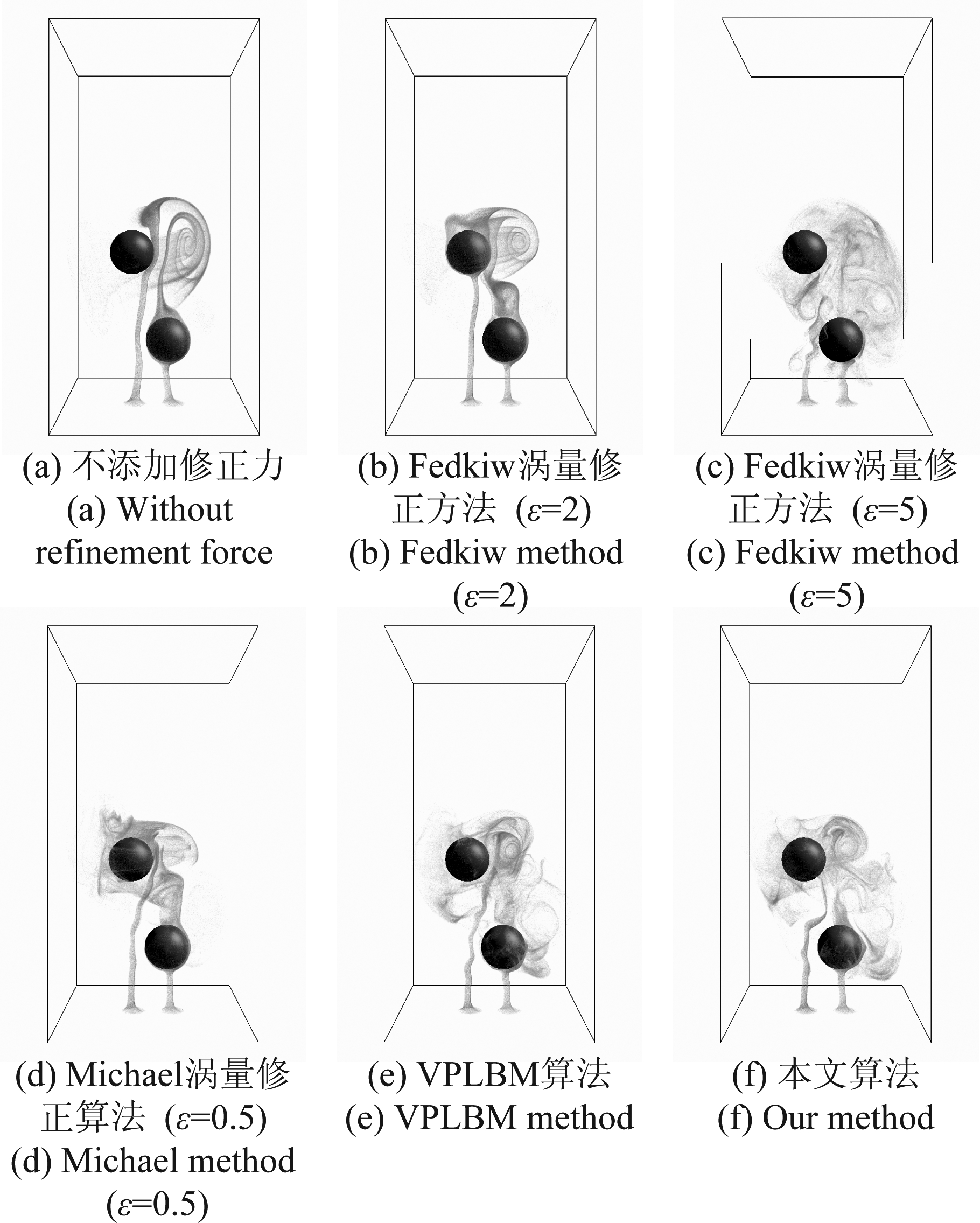
图6 采取不同涡量修正方法的烟雾 仿真算法结果(时间步2000)对比
Fig.6 Smoke simulation results comparison among different vorticity refinement methods (time step 2000)
图7在相同实验条件下对比Wen[26]提出的VPLBM算法和涡量修正格子玻尔兹曼算法的实验结果。本文的算法在VPLBM算法的基础上增加了涡量方向场的追踪并进一步改进了涡量修正力的计算方式,避免了由于忽略涡量方向导致的误差随时间积累影响仿真效果。从图7的对比实验结果可以看出在较短的仿真步数内两种算法仿真结果基本一致,随时间步的增加两种算法的仿真结果出现明显差异。涡量修正烟雾仿真算法在烟雾上升实验中可

图7 VPLBM算法与涡量修正格子 玻尔兹曼算法仿真结果对比
Fig.7 Smoke simulation results comparison between VPLBM method and vorticity refinement lattice Boltzmann method
以得到更平稳的烟雾上升效果,在烟雾运动过程中更好地保持涡环的完整性,在较长仿真步数内得到更加均匀真实的烟雾扩散效果,更好的实现了基于格子玻尔兹曼方法的烟雾仿真中的涡量修正。
5 结论
本文提出了基于涡量追踪的涡量修正格子玻尔兹曼算法实现烟雾的仿真。从N-S方程和亥姆霍兹方程出发对涡量的大小和方向分别进行追踪,利用追踪的涡量信息与对应时刻的速度场信息计算涡量修正力,通过添加涡量修正力实现烟雾仿真的涡量修正。这一算法可以有效对烟雾仿真的涡量进行保持和修正,得到更加真实的烟雾仿真图像。相比之前的只追踪涡量大小的涡量修正算法本文的算法能够避免因忽视涡量方向导致的误差随迭代过程积累,在较多仿真步数下针对烟雾得到更好的涡量保持效果。未来的工作希望将本文的算法扩展到非均匀网格上,尝试处理更加复杂的边界条件问题。此外还希望尝试利用多GPU进行加速进一步提高仿真算法的计算效率,在更高分辨率的网格下实现实时仿真。
[1] Fedkiw R, Stam J, Jensen H W. Visual simulation of smoke[C]∥Proceedings of the 28th annual conference on Computer graphics and interactive techniques. [S.l.]: ACM, 2001: 15-22.
[2] Li X, Liu L, Wu W, et al. Erratum to: Dynamic BFECC Characteristic Mapping Method for Fluid Simulations[J]. Visual Computer, 2014, 30(6- 8): 963-966.
[3] Dupont T F, Liu Y. Back and Forth Error Compensation and Correction Methods for Semi-Lagrangian Schemes with Application to Level Set Interface Computations[J]. Mathematics of Computation, 2007: 647- 668.
[4] Ding Wanning, Jia Limin, Jiao Hongqiang. A New Method of Smoke Simulation[C]∥2010 International Conference on Educational and Network Technology, Qinhuangdao, 2010: 267-270.
[5] Wu X, Yang X, Yang Y. A Novel Projection Technique with Detail Capture and Shape Correction for Smoke Simulation[J]. Computer Graphics Forum, 2013, 32(2pt4): 389-397.
[6] Chen S, Doolen G D. Lattice Boltzmann Method for Fluid Flows[J]. Ann. Rev. fluid Mech, 1998, 30(1): 329-364.
[7] He X, Luo L S. Theory of the Lattice Boltzmann Method: from the Boltzmann Equation to the Lattice Boltzmann Equation[J]. Physical Review E, 1997, 56(6): 6811- 6817.
[8] Li Weizhong, Zhou Xun, Dong Bo, et al. A Thermal LBM Model for Studying Complex Flow and Heat Transfer Problems in Body-fitted Coordinates[J]. International Journal of Thermal Sciences, 2015, 98: 266-276.
[9] Hua A C, Liao B S Y, Zhang C Z Y, et al. Simulation of IR Smoke Screen Based on Physical Model[C]∥2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 2018: 1- 6.
[10]Oborn J, Flynn S, Egbert P, et al. Time-Reversed Art Directable Smoke Simulation[C]∥Proceedings of the 39th Annual European Association for Computer Graphics Conference: Short Papers, 2018: 1- 4.
[11]Liu S, Xu Y, Noh J, et al. Visual Fluid Animation via Lifting Wavelet Transform[J]. Computer Animation and Virtual Worlds, 2014, 25(3- 4): 475- 485.
[12]Angelidis A, Neyret F, Singh K, et al. A Controllable, Fast and Stable Basis for Vortex Based Smoke Simulation[C]∥Symposium on Computer Animation (SCA 06), ACM-SIGGRAPH/EG, 2006: 25-32.
[13]Zhuo Nengwen, Rao Yunbo. Real Time Dense Smoke Simulation Based Particle System[C]∥International Symposium on Intelligent Information Technology Application Workshops. IEEE Computer Society, 2008: 809- 813.
[14]Xiao Xiangyun, Yang Cheng, Yang Xubo. Adaptive Learning-based Projection Method for Smoke Simulation[J]. Computer Animation and Virtual Worlds, 2018, 29(3- 4): e1837.
[15]邓定胜. 一种基于可编程GPU的实时烟雾模拟算法研究[J]. 计算机科学. 2019(S2): 604- 608.
Deng Dingsheng. Study on Real-time Smoke Simulation Algorithm Based on Programmable GPU[J]. Computer Science, 2019(S2): 604- 608.(in Chinese)
[16]史玉坤, 仲贞, 张德馨, 等. 利用多特征判别的烟雾检测方法研究[J]. 信号处理, 2015, 31(10): 1336-1341.
Shi Yukun, Zhong Zhen, Zhang Dexin, et al. A Study on Smoke Detection Based on Multi-feature[J]. Journal of Signal Processing, 2015, 31(10): 1336-1341.(in Chinese)
[17]Wiewel S, Becher M, Thuerey N. Latent-space Physics: Towards Learning the Temporal Evolution of Fluid Flow[J]. Computer Graphics Forum, 2019, 38(2): 71- 82.
[18]Robinson, Michael A. Application of Vorticity Confinement to Inviscid Missile Force and Moment Prediction[C]∥Aiaa Aerospace Sciences Meeting & Exhibit, 2004, 717: 5- 8.
[19]Xu Y X, Liu S G, Wu L Q. Smoke Simulation with Two-Scale Vorticity Confinement[J]. Communications in Computer & Information Science, 2012, 346: 467- 474.
[20]唐勇, 吴娱, 吕梦雅, 等. 一种改进的自适应漩涡限制实时烟雾模拟[J]. 小型微型计算机系统, 2012, 33(12): 2676-2679.
Tang Yong, Wu Yu, Lv Mengya, et al. Real-time Smoke Simulation Using the Improved Adaptive Vorticity Confinement[J]. Journal of Chinese Computer Systems, 2012, 33(12): 2676-2679.(in Chinese)
[21]Ishimuroya M, Kanai T. Adding Turbulence Based on Low-Resolution Cascade Ratios[C]∥International Symposium on Visual Computing, ISCV 2016: Advances in Visual Computing, 2016: 67-76.
[22]陈国栋, 苏志鹏, 王娜. 基于涡丝模型的烟雾仿真研究[J]. 贵州大学学报: 自然科学版, 2018, 35(1): 57- 62.
Chen Guodong, Su Zhipeng, Wang Na. The Research of Smoke Simulation Based on Vortex Filament Method[J]. Journal of Guizhou University: Natural Science, 2018, 35(1): 57- 62.(in Chinese)
[23]Zhu J, Yang Z, Sun H, et al. Detail-preserving Smoke Simulation Using an Efficient High-order Numercial Scheme[J]. Science China Information Sciences, 2020, 63(6): 1-3.
[24]Zhang M, Liu S, Sun H, et al. Hybrid Vortex Model for Efficiently Simulating Turbulent Smoke[C]∥Proceedings of the 13th ACM SIGGRAPH International Conference on Virtual-Reality Continuum and its Applications in Industry, 2014: 71-79.
[25]Zhang Meng, Si Weixin, Qian Yinling, et al. Vortex Filaments in Grids for Scalable, Fine Smoke Simulation[J]. IEEE Computer Graphics and Applications, 2015, 35(6): 60- 68.
[26]Wen Jinghuan, Ma Huimin. Real-time Smoke Simulation Based on Vorticity Preserving Lattice Boltzmann Method[J]. Visual Computer, 2019, 35(9): 1279-1292.
[27]Wan Rongzheng, Fang Haiping. Test of the Possible Application of the Half-way Bounce-Back Boundary Condition for Lattice Boltzmann Methods in Complex Geometry[J]. Communications in Theoretical Physics, 2001, 35(5): 593-596.


