1 引言
定位技术由20世纪的90年代就渐渐开始受到关注,历经几十年至今,人们从简单的“得到某时刻某人的位置”开始不断拓展,由点逐渐变为面、再发展到如今的三维定位,定位技术不断发展,在我们的生活中也变得越来越活跃。在室外,全球卫星导航系统(Global Positioning System,GPS)能全天候的对海、陆、空进行全方位实时的三维定位。但是在室内,GPS信号无法很好地穿透建筑,也就无法对室内目标进行定位。为此,许多科学研究者都在寻找适用于室内定位的方法,如视频图像分析,可见光定位,超宽带定位[1]等。如今,WiFi的普及和部署变得越来越普遍,并且WiFi协议的物理层能够提供检测到的信道状态信息(Channel State Information,CSI),是否能利用CSI对室内信号覆盖范围内的人物运动进行定位,变成一个十分热门的研究方向。
近年来,很多高校、机构和个人都对基于WiFi的室内定位进行了大量的研究。室内定位技术主要分为两个分支,一为有源定位,二为无源定位。有源定位方式,即运动的人需携带某些无线传感器设备来帮助系统获取信息用于定位。此方式在非视距线(Non-Line-of-Sight,NLoS)上的高精度定位已经达到了厘米级[2-3]。无源方式,即人无需携带任何设备,利用人体对无线传输的影响来对人进行定位。无源定位的研究进行的十分火热,主要是依赖构建指纹库对室内人物进行定位[4-5];随着研究的深入,也有了利用软件无线电(Universal Software Radio Peripheral,USRP)设备来更好的控制无线信号,从而获得想要的信息来进行手势识别等定位[6-7],但这些需要专用的设备,并不具有普遍适用性。近年,渐渐有了通过CSI信息来获得多普勒频移(Doppler Shift,DFS)、到达角度(Angle of Arrival,AoA)等参数来进行定位的算法[8-9],但是他们通常是只对单个参数进行评估,且大多数只能进行二维平面定位。为了解决三维立体问题,有研究者通过分析分别部署在不同高度的设备接受到的信号来判别目标的高度[10-11]。
针对如今的高开销、甚至要求专用通信设备去构建无线传感器网络来进行室内无源平面定位的现状,本文提出一种基于商用无线传感器网络,少链路,多参数结合的三维轨迹跟踪方法,以减小开销,增加普遍适用性,并且能够对做多维运动的人物进行定位。本算法的主要思想是利用频谱分析得到DFS用以计算运动速度,使用最大似然法得到AoA和飞行时间(Time of Flight,ToF)。将三维空间映射为垂直平面和水平平面,通过分别对两个平面上的运动进行轨迹跟踪,再使用融合算法得到三维空间中人的运动轨迹。
2 基本原理
2.1 信道状态信息(CSI)
现代数字无线通信多使用了正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术,通过在不同频率的相互正交的子载波来传送信息[12-13]。每个传送的符号X( f )都会被调制到子载波f上,接收到的符号Y( f )由无线传输信道H( f )来决定:
Y( f )=H( f )×X( f )
(1)
无线传输信道H={H( f )}f=1,2,…,K被称为信道状态信息,其中K是子载波编号。
2.2 多普勒频移(DFS)
发送端和接收端之间的相对运动会导致多普勒频移现象,发送出的波频与接收到的波频存在着频率差,这个差被称为DFS。室内环境由于四周摆放物品等影响,发送端发出的信号到达接收端有多种路径,当目标在环境内走动时,目标反射信号路径长度的变化,将会引起多普勒频移现象[14],如图1所示。人体的反射信号多普勒频移可表示为:
(2)
其中f,τ(t),νpath,c分别为子载波频率、ToF、反射路径长度变化速度和光速。
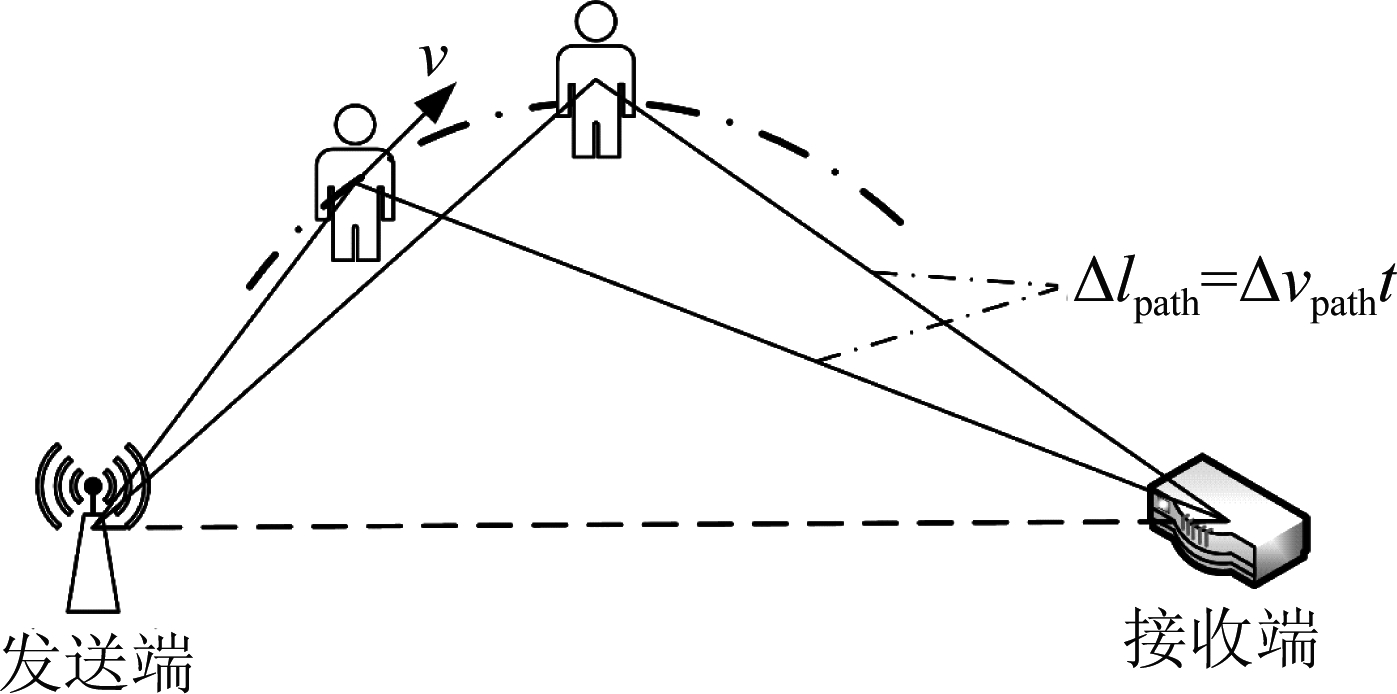
图1 多普勒频移与反射路径长度变化
Fig.1 Doppler shift and reflect path length change
鉴于以上现象,可以利用DFS来推算运动速度。
2.3 到达角度(AoA)与飞行时间(ToF)
传感器网络的定位方式问题主要是利用已知位置节点(锚节点)来测算被定位人的位置,主要分为基于测距的定位算法和非测距的定位算法两类。其中,基于AoA和ToF的算法则为非测距定位方式。AoA是指经由被测物体反射到接收端时估算出的夹角,可用于估算人体方向;ToF指的是电磁波信号从发送端出发于接收端接收到信号之间的时间差,可用于估算信号经过的距离。如图2所示,发射端发出信号经目标反射到达接收端的ToF可以用来估计目标反射信号路径的长度,反射信号到达接收端的AoA可以用来确定目标的方位。
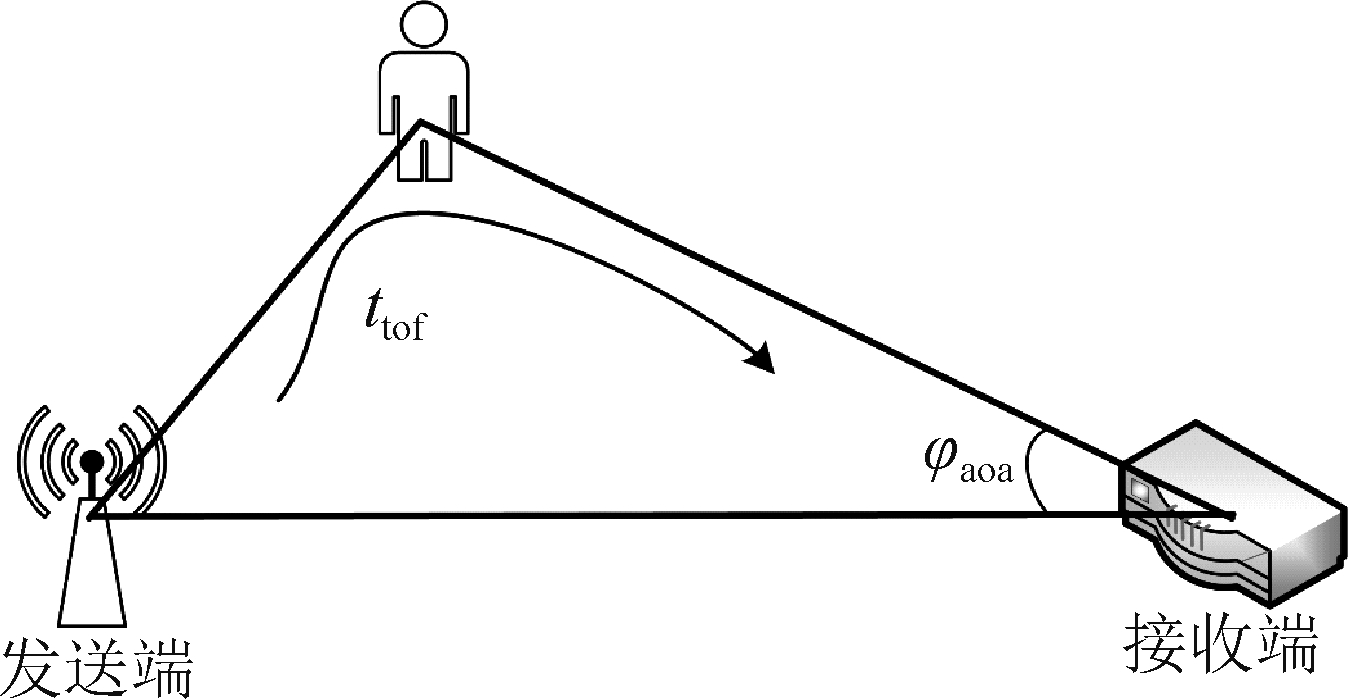
图2 AoA和ToF模型
Fig.2 The model of AoA and ToF
3 基于CSI的多参数估计算法的三维轨迹跟踪
本文所提出的三维轨迹跟踪算法包括DFS提取,AoA和ToF估计,三维定位三个部分。首先提取DFS,用于垂直平面的定位和后面的AoA和ToF估计;然后利用ToF和DFS计算反射路径长度,结合AoA对目标水平位置进行定位。系统算法流程如图3所示。
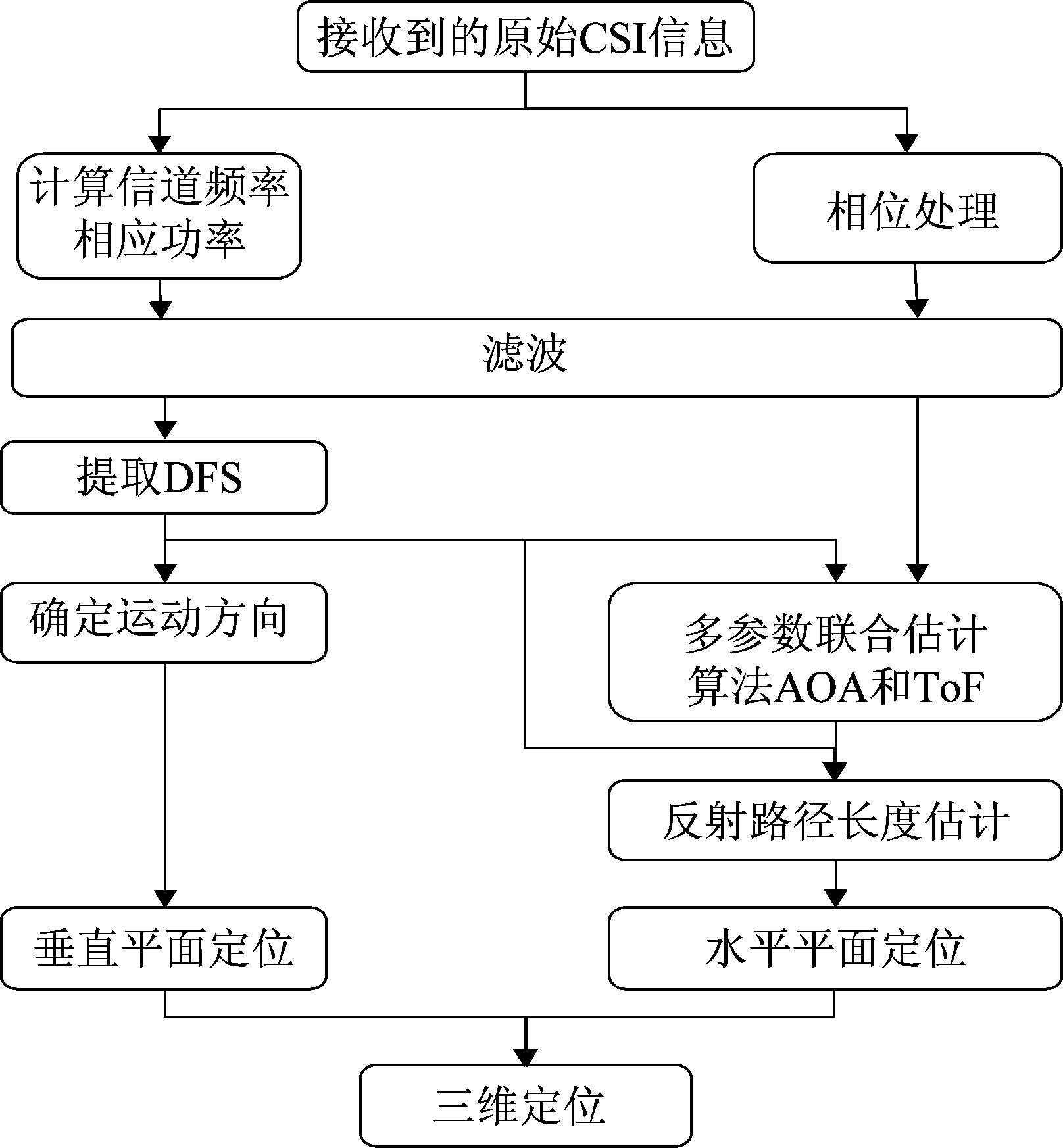
图3 系统框图
Fig.3 System diagram
3.1 通过频谱分析估算DFS
在实际传输过程中,由于多径效应的原因,CSI信号应表示为多条反射路径的信号的和[14]:
H( f,t)=e-j 2πΔf·t∑l∈plal( f,t)e-j 2πfτl(t)
(3)
其中Δf为发射端发射的信号与接收端接收到的信号的频率差,即DFS;Pl为多条信号反射路径;al( f,t)为第l条路径的信号幅值;τl(t)为第l条路径的路径延迟。
由于室内环境存在墙壁或者基础物品,多径信号并不全是由目标身体反射的,但是由于墙壁或者基础物品是固定不动的,他们反射回的信号并不会因为目标移动而变化;同时,由于目标在不停的运动,位置会发生变化,所以目标反射回的多径信号会随着时间变化。于是可以将CSI信号分成两个部分,如下式所示：
H( f,t)=(Hs( f )+HD( f ))e-j 2πΔft=
(4)
其中Hs( f )为环境反射信号(静态路径信号)部分;HD( f )为目标反射信号(动态路径信号)部分;Pd为动态路径;dl(t)为第l条路径的路径长度。
为了对目标进行定位,需要对由目标身体反射回的信号即动态路径信号进行处理,提取出用于定位的参数。首先我们分析了CSI的功率特性。由于在很短的时间内,可以视目标移动速度一定,则动态路径中dl(t)=dl(0)+νlt,其中的dl(0)和νl均为常数,则CSI信号功率为:
|H( f,t)|2= 
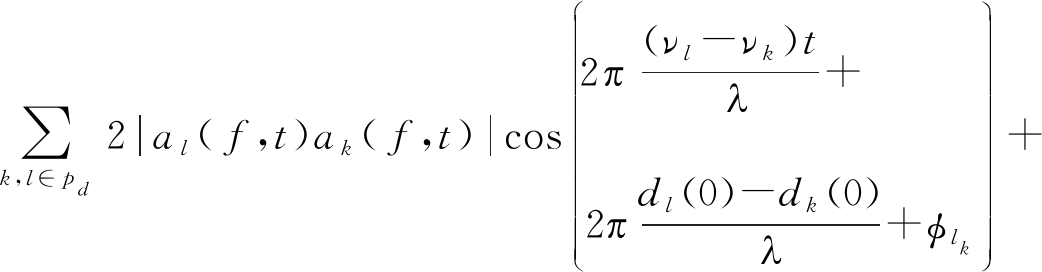|Hs( f )|2+∑l∈pd|al( f,t)|2
(5)
其中2π
+φsl和2π
+φsk均为常数。
由此可见,CSI功率信号只包含了一个频移常数和包含了DFS的正弦信号,将数据分段对其进行傅里叶变换频谱分析即可提取出这个正弦信号的频率即DFS。为了得到更好的频谱,我们采用高斯窗来平滑频谱并加入零序列来将频谱分辨率提高到1 Hz。
在进行频谱分析之前,还需要对信号进行滤波以去除环境噪声。由于目标移动造成的反射路径变化相对平稳,与噪声和脉冲信号的突变频率进行比较,可以发现噪声信号的频率更高,同时,由视距线传输的信号与无人时传输过程中已存在的环境多径信号(静态信号)的频率比较低。因此,很容易设想到,使用一个带通滤波器来滤除这些“噪声”信号。
本系统会对每一个子载波的功率信号|H( f,t)|2分别进行滤波处理。由于人的行走速度一般小于2 m/s,当WiFi设定在5.8 GHz频段时,DFS约为:
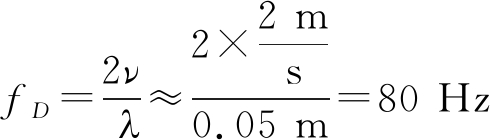
(6)
则滤波器上限设为80 Hz。考虑到DFS的低频分量和其他干扰,将下限设为2 Hz。
由于人体躯干相比身体其他部分能反射更多信号,这些信号是频谱图中的主要成分,所以我们选择频谱中能量最高的部分视为人体移动时造成的DFS,并采用移动窗的提取方法,去除数据中依旧可能存在的因环境等噪声而导致频谱图出现异常波动。
由于人的正常行走速度在一定范围内,即可以利用时域来限制频域变化速度,相邻两时间段内的频率变化应在一定值内。所以在选定最高能量的频率时,并不是选择这一时刻能量最高的频率,而是随时间,选出整体能量最高的频率带,即利用移动窗:
s.t.|fi-fi-1|<=1; i=2,…,T
(7)
通过傅里叶变换分析,可以得到一个如图4的WT×F时频图,F为其频率块的个数,T为时间块的个数。
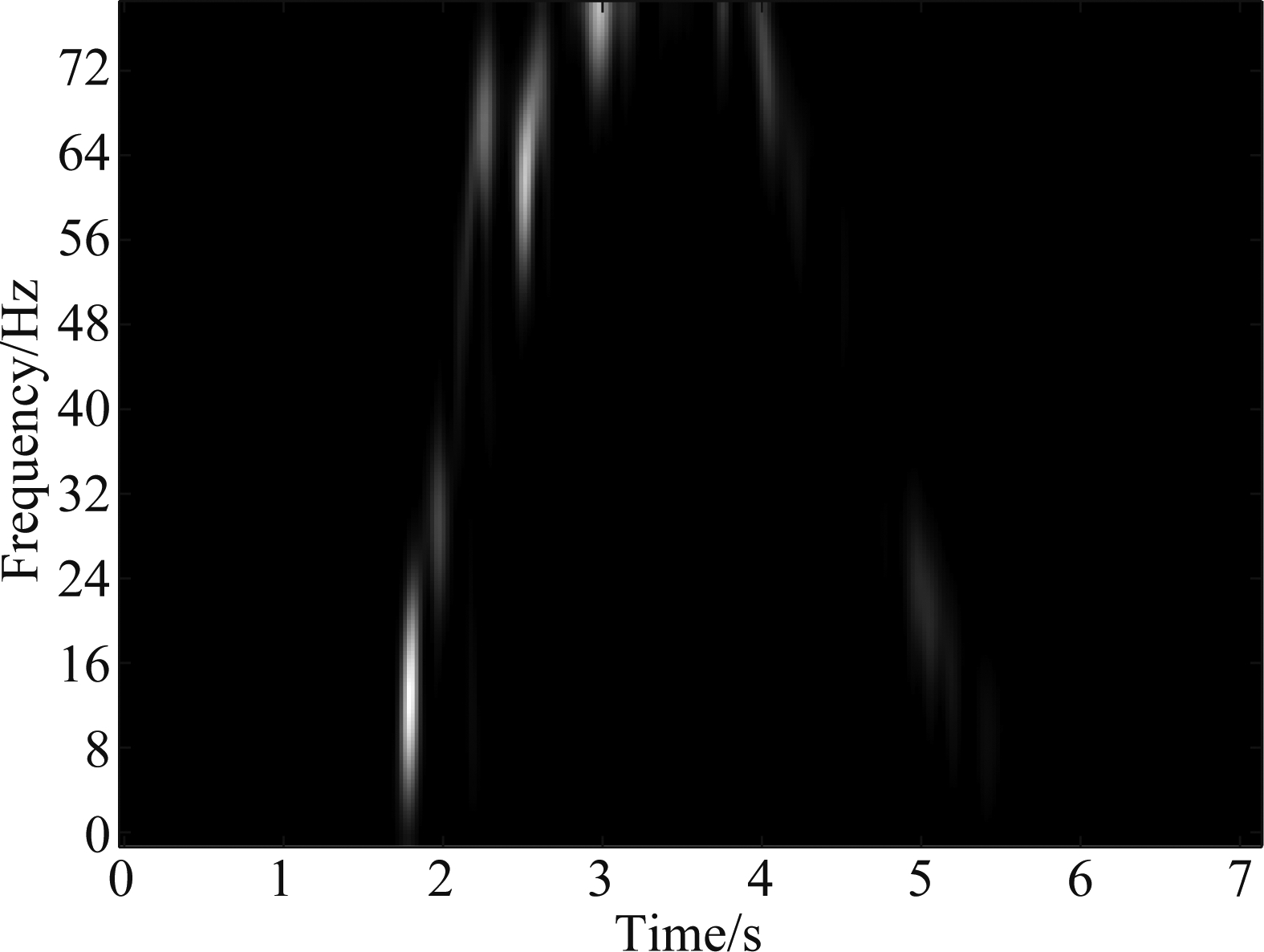
图4 CSI信号频谱分析结果
Fig.4 CSI Spectrogram Analyze
同时,因为人体运动加速度a(t)和多普勒频移fD满足如下关系,利用提出的DFS可以得到:
(8)
其中λ为载波波长,当WiFi运行在2.4 G频段的情况时:
(9)
而当WiFi运行在5.8 GHz频段的情况时:
(10)
则同样路径变化率情况下, fD2.4 G<fD5.8 G,即多普勒分辨率更低。
鉴于以上情况,我们选择将运行在5.8 G频段的WiFi来进行实验,因为它有更高的分辨率,能够减小误差。
3.2 运动方向检测
通过得到的DFS后,还有一个重要的问题,就是如何知道其方向,利用确定了的运动方向对位置估计进行修正。我们知道,多普勒频移的反映来自于目标移动导致的路径长度变化,远离链路会使反射路径变长;相反,走向链路则会使反射路径长度变短。具体地说,当目标向链路移动时,波长较大的子载波比波长较小的子载波更早地变化;而当目标远离链路时,波长较短的子载波变化更早[15]。为了防止方向估计产生突变,本系统采用一种计算子载波在相邻时间块上的相关性的算法。定义s(t,T)作为一个以时间t为中心时间,T为时间长度的时间块。对于子载波s1,s2,则他们之间的互相关函数R(τ)为:
R(τ)= 
(11)
其中F是傅里叶变换,w(t)为一个在
之间时为1,其余情况为0的窗;而
是为了将两子载波信号相关函数归一化而引入的。
计算两个波长不同的子载波s1,s2在一个时间段内的互相关函数,其自相关函数最大的时间点若靠前,则判断目标为离开链路;相反,若其自相关函数最大的时间点若靠后,则判断目标为接近链路。
同时,当人运动方向发生改变时,其反射路径长度变化率νpath一定会有一个穿越0线的过程,也会有一个明显的下降过程,而如果一直以一个速度或加速度运动时,其方向不会发生改变。通过相关性的符号可以映射运动方向的变化。
3.3 利用最大似然函数估计AoA和ToF
无线信道具有多径特征,WiFi无线网卡可以对第s个传感器接收到的在f频率上,t时刻的信道状态进行测量,得到CSI为[16]:
(12)
其中αl和τl分别为此多径上的衰减因子和传播延迟;N则为背景高斯噪声。为了更好地量化参数,分析一段时间内子载波信号成分关系,定义m=(i, j,k),其中i=0,…,T-1; j=0,…,F-1;k=0,…,S-1,为一个CSI信息的联合信息,其中T,F,S分代表时间,子载波,接收天线数量;则第k个接收端在时间i接收到的第j个子载波信号为H(i, j,k)=H(m),当选择H(0,0,0)作为参考信号时,H(i, j,k)的第l条路径的信号除以2π相位后的可表示为:
fcτl+Δfjτl+fcΔsk·φl- fDlΔti
(13)
其中fc为信道中心频率;Δti,Δfj,Δsk则分别为H(i, j,k)与参考信号H(0,0,0)之间的时间差,频率差和传感器空间位置差异;τl,φl, fDl则分别为第l条多径信号的ToF,AoA以及
为目标移动导致的ToF变化;Δsk·φl为不同接收端之间的ToF差。
之所以可以这么简化是因为在一个短暂的时间内窄带宽信号的衰减因子αl可视为一个常数, fc≈Δfj,而
很小。
为了对复数个参数进行同时估计本文利用了最大似然函数。首先计算观察函数h(m)和多维度、多径信号的参数ϑ
的最大似然函数[17]:
Λ(ϑ
(14)
它的最大似然估计则是其最大值:
ϑ;h)}
(15)
为了更好的解决这个问题,本文采用了Space-Alternating Gneralized Expection-Maximization Algorithm(SAGE)[18]算法,对AoA和ToF进行估计。利用前节所述频谱分析提取出单链路DFS对剩余两个参数进行校准,可以使AoA和ToF的估计变得更精确。对多条路径中的第l条路径,分解CSI,计算信号Pl:
(16)
其中
为上一次迭代中得到的估计参数。βl为一个非负的参数用以控制融合率,初始值为1。
则最大化如下:
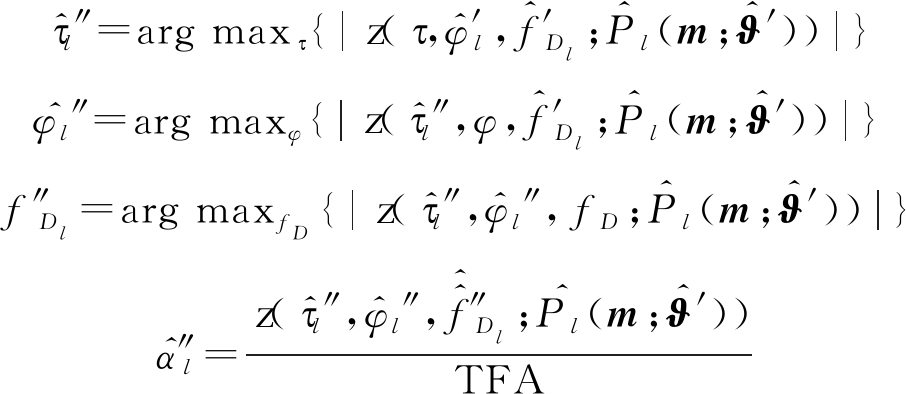
(17)
其中:
则分别为第l条多径信号的ToF,AoA以及DFS的最大似然估计。
在最开始,将ϑ设为0,对每条路径都进行公式(16)、公式(17)的运算,然后计算相邻两次运算后ϑ的差,当其小于一个既定的阈值,则迭代算法结束,得到l条路径的参数AoA和ToF的估计值,再通过匈牙利算法对l条路径的参数进行最佳分配,通过参数变化的平滑性来分辨出l条路径,由于这并不是本文的主要研究内容,故不详述,最后对估计值进行线性拟合和平滑处理,得到最终结果,如图5所示。
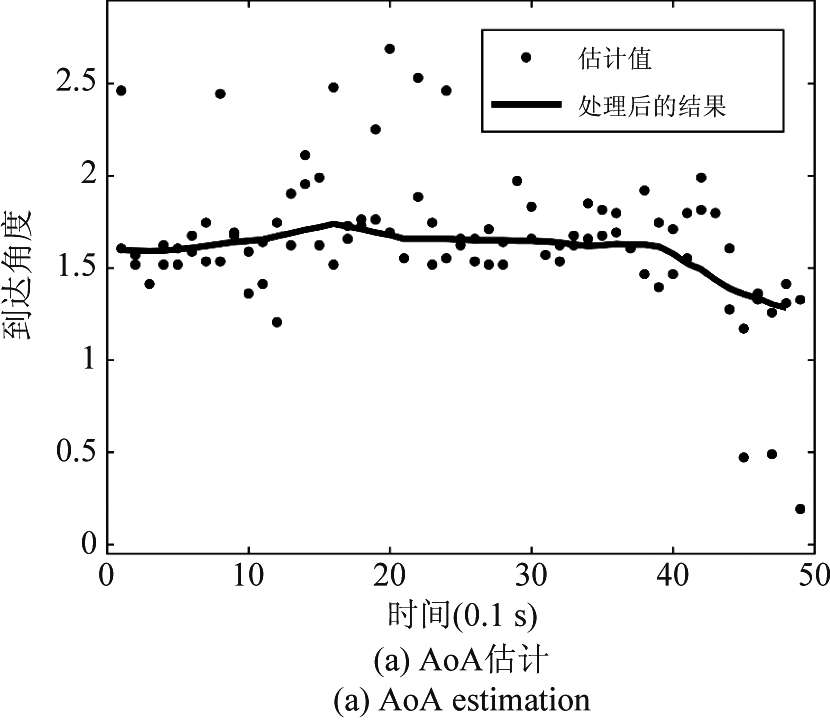
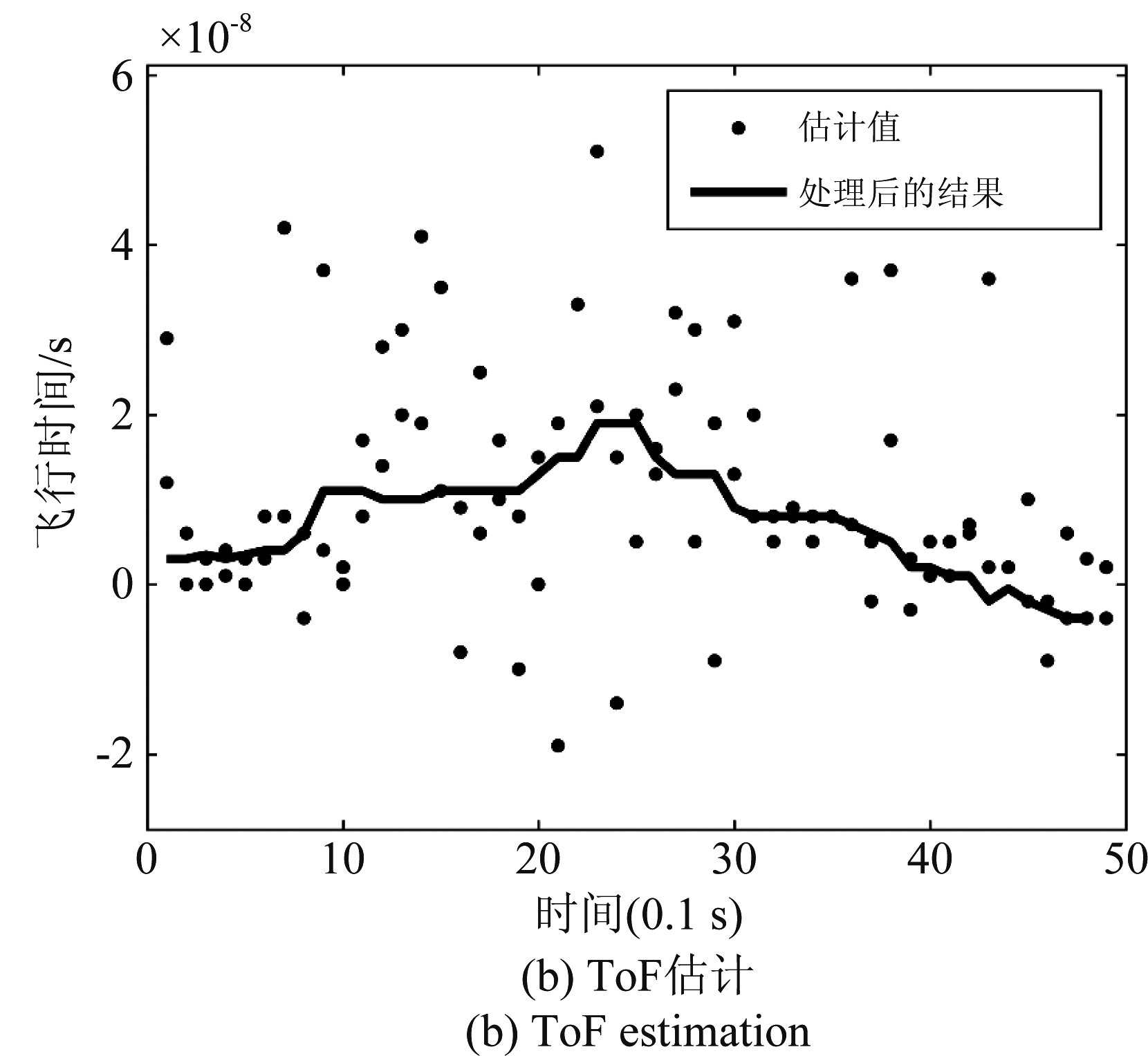
图5 ToF和AoA估计
Fig.5 Example of AoA and ToF estimation
4 定位系统及位置估计
考虑到通信系统布置开销和定位精度,本系统采用的是一发两收定位系统。系统和采集数据通过算法计算得到用于计算位置的多参数后,为了进行三维轨迹计算,将三维空间投影成两个面,对两个面的轨迹分别进行估计,得到两个平面轨迹;其中X-Z平面称为高度平面,X-Y平面称为水平平面,分别对投影在这两个面的位置进行估计,最后融合成三维轨迹,系统示意图与位置轨迹效果示意如图6所示,由于接收端放置在测量区域的边缘,所以得到的AoA范围为[0,180°)。
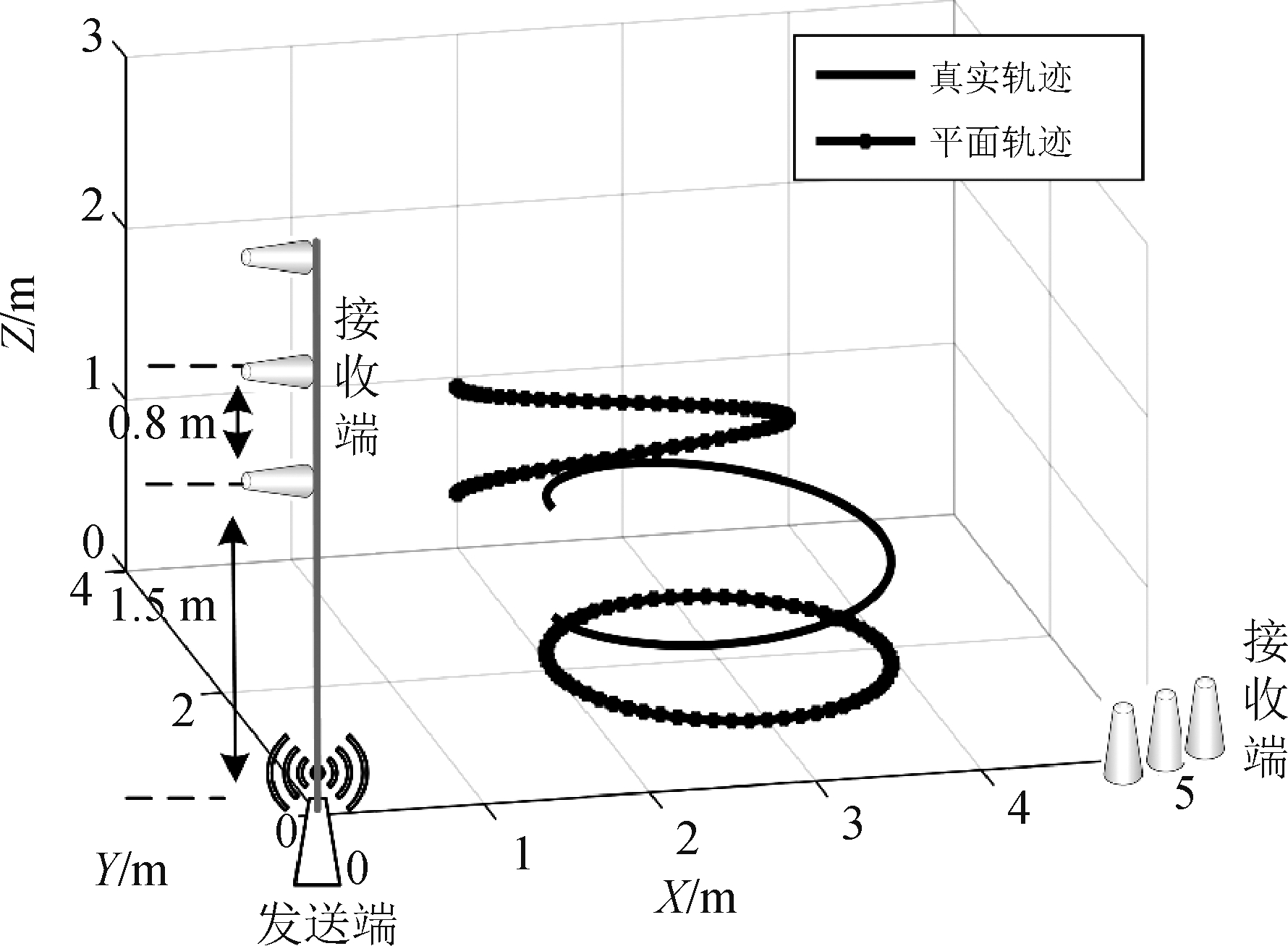
图6 系统模型及效果示意图
Fig.6 System model and Tracking result illustration
4.1 水平平面(X-Y平面)定位模型
水平平面上,为了减小开销,采用一发一收的系统,接收端通过SAGE算法估计出所需的ToF和AoA,再结合通过频谱分析得到的DFS,对人此时所在位置进行估计。
首先需要估计反射路径长度。理论上,可以使用前面参数估计得到的ToF来直接得到反射路径长度,如式(18):
L=τ·c
(18)
但是由于噪声和ToF的估计误差,只使用ToF可能会导致定位产生很大的误差。为了得到更准确的反射路径长度,我们将DFS和ToF相结合。本系统利用DFS进行卡尔曼滤波,在通过参数估计此时路径长度的同时,利用前面的测量值对此时的值来进行预测,以减小误差造成的影响,由卡尔曼滤波原理:
xk+1=Øxk+Buk+wk
(19)
Yk=Hxk+νk
(20)
其中k为时间,在k时刻的距离为x(k)∈Rn,Y(k)∈Rm为k时刻对应的观测变量,u(k)为控制向量,而本系统利用DFS作为控制向量,wk∈Rr为系统噪声,νk∈Rm为观测噪声,Ø,B,H分别为状态转移矩阵、激励噪声矩阵和观测矩阵。式(19)称为状态方程,式(20)则称为观测方程。
通过卡尔曼滤波,不断地更新误差矩阵,我们将观测值和估计值一起使用得到了更准确的反射路径长度,图7为是否采用DFS对反射路径长度进行卡尔曼滤波器的反射路径长度估计结果比较。
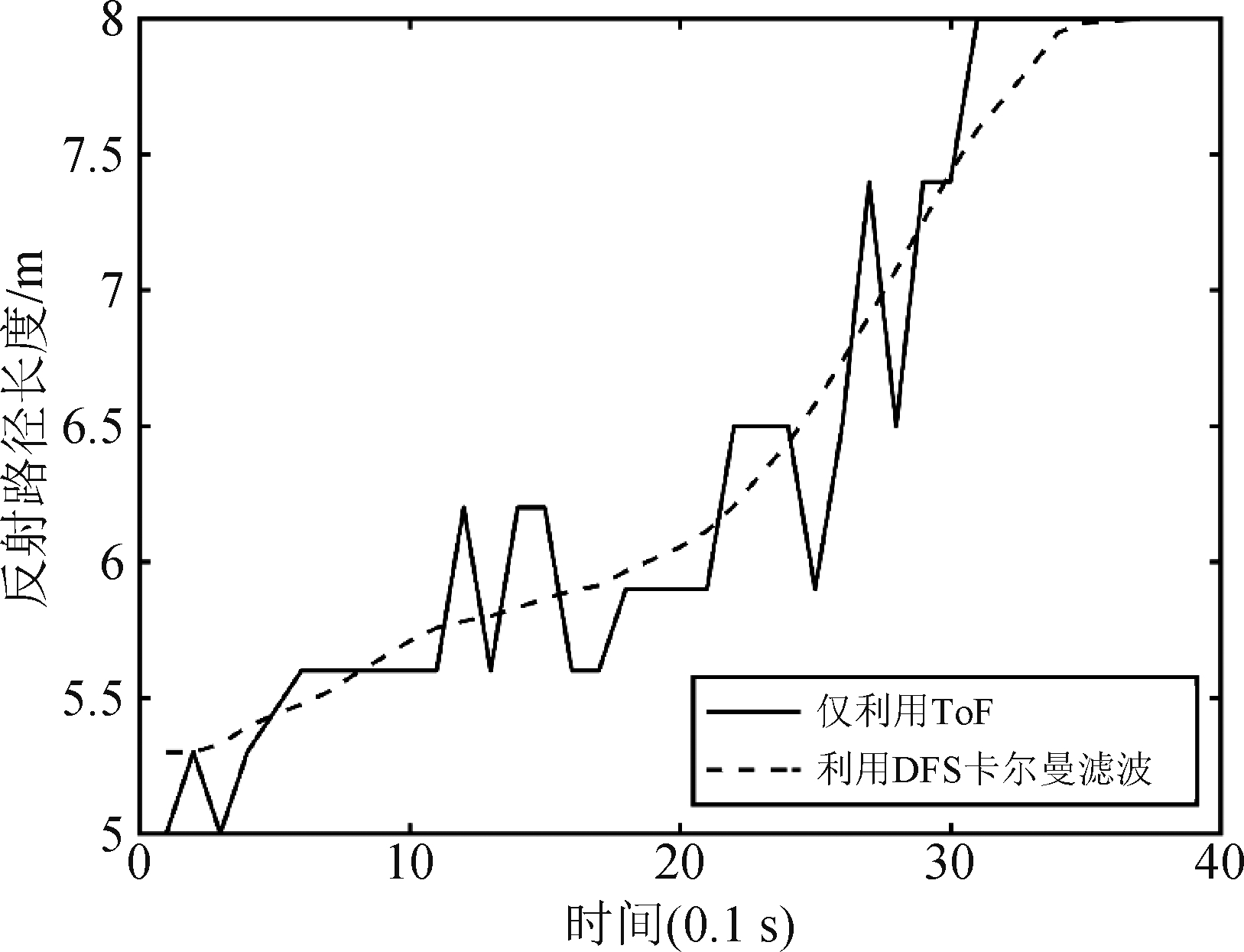
图7 DFS卡尔曼滤波前后的反射路径长度
Fig.7 Reflected signal path length calculated by ToF and DFS Kalman filter
如图8所示,构建几何模型,可以得到以下关系:
(21)
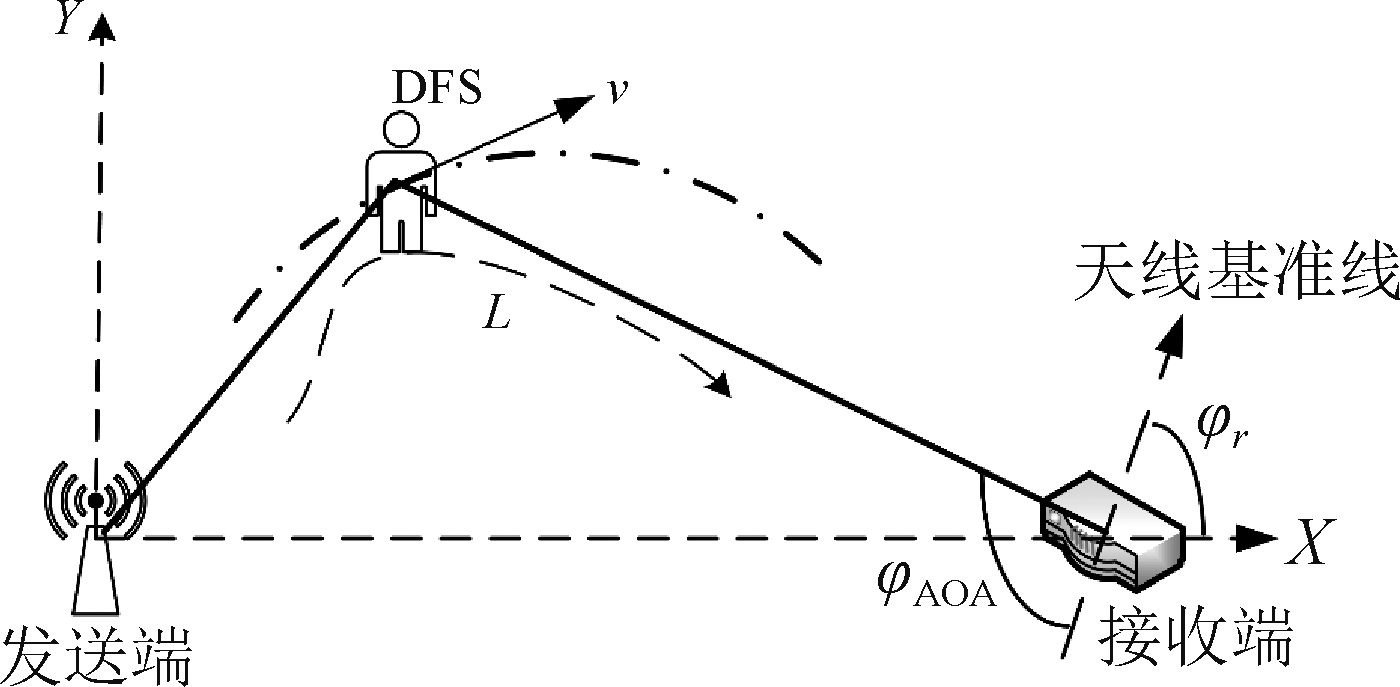
图8 水平平面定位模型
Fig.8 Location model of Horizontal plane
其中天线基准角是指利用静态无人状态下采集的数据估计出的AoA。解方程即可得到此时位置(x,y)。
4.2 高度平面(X-Z平面)定位模型
高度平面上,为了更高的准确度,采用一发两收的系统,利用DFS估计运动速度,对目标进行定位。如图9所示,目标运动速度
是由相对于两条链路的法线方向速度
的和。已知发送端坐标为
接收端1坐标为
接收端2坐标为
假设目标此时位置为
两组接收端通过提取DFS分别对相对于X轴和Z轴的运动方向和速度做估计。
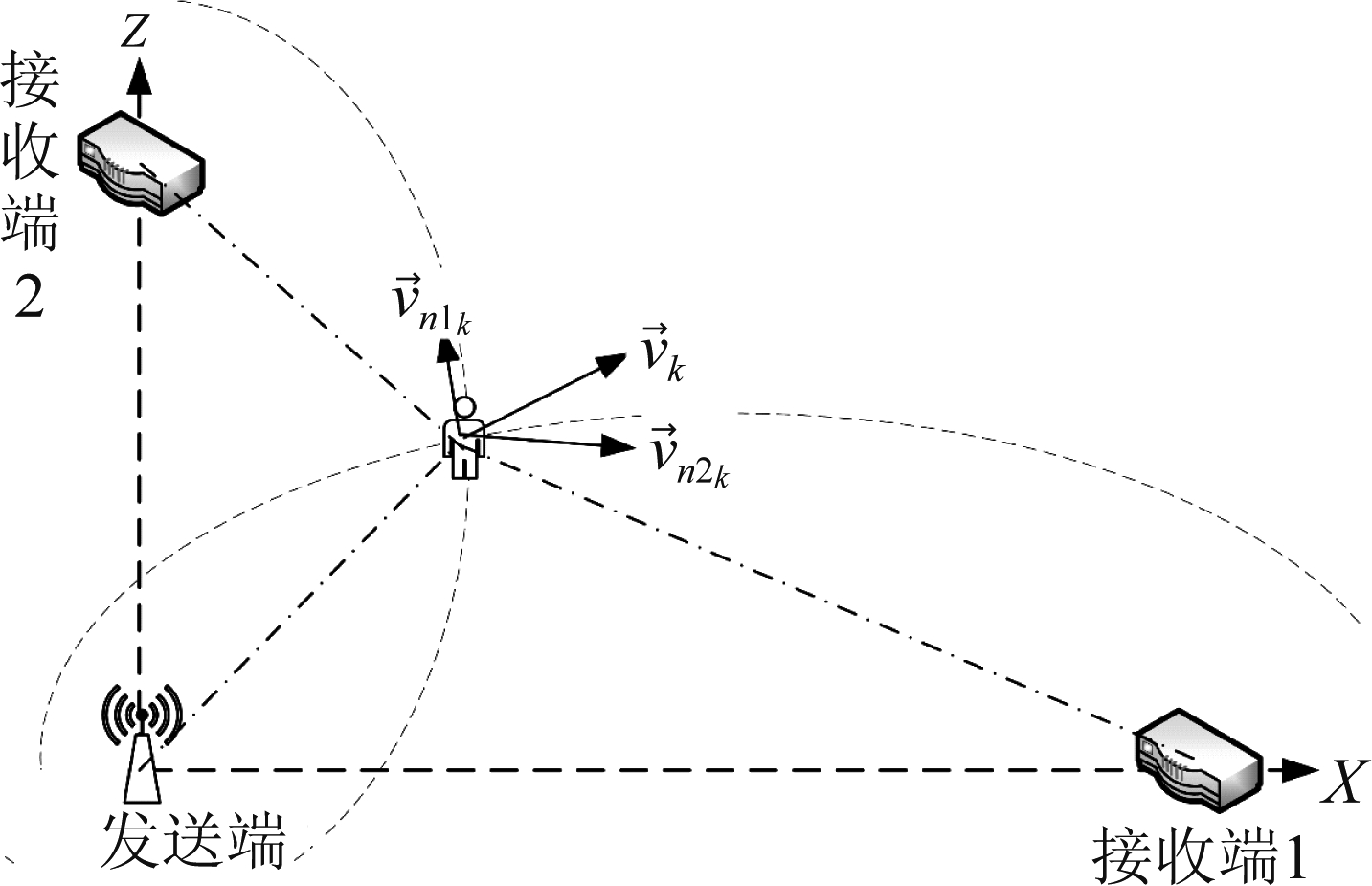
图9 运动速度模型
Fig.9 Velocity model
对于其中任一链路,如图10所示,可以建立模型:
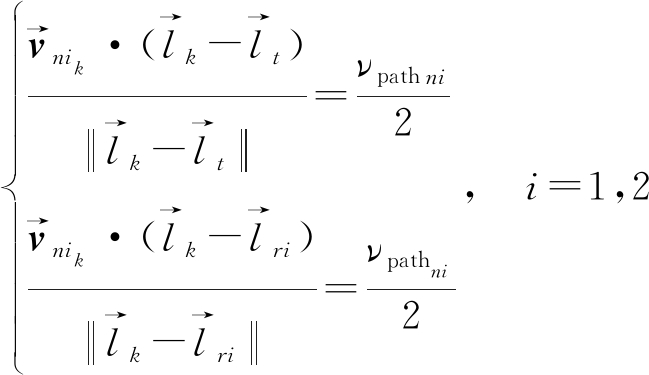
(22)
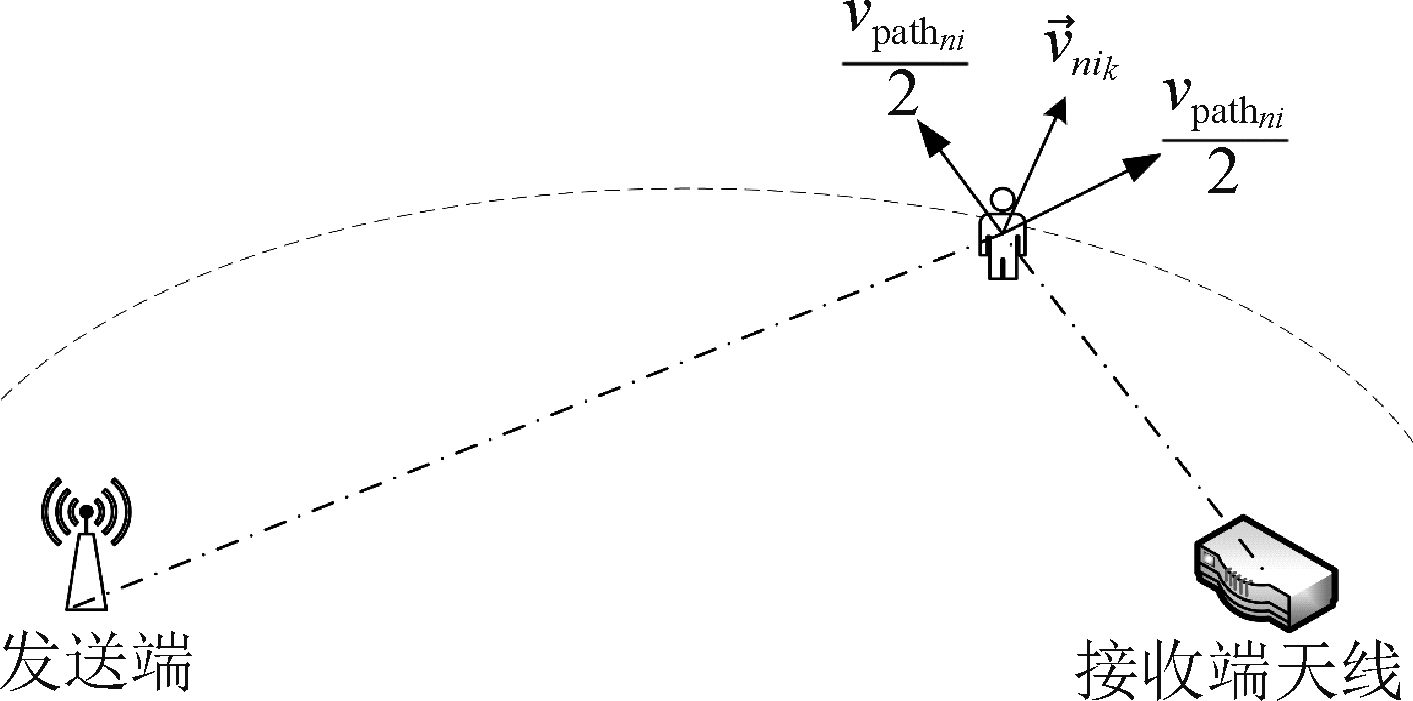
图10 多普勒频移与运动速度
Fig.10 Doppler shift and velocity
由此我们可以分别解出
和
而
在知道k时刻运动速度
后,结合上一时刻的位置
和时间差Δt则可得出下一刻的位置(x,z):
(23)
5 实验结果及分析
5.1 实验环境
现在,为了获取CSI信息,主要使用Intel 5300或Atheros 9380两种无线网卡,本文使用基于Intel 5300网卡的Linux 802.11n CSI Tool[16]来收集CSI信息。将发送端发送频段定为5.825 GHz,以1024 Hz的频率发送数据包。接收端使用两台CPU型号为Intel E8400,操作系统是Ubuntu11.04的台式电脑,每台电脑连接3根接收天线。测试场地为5 m×4 m的区域,中间放置了一个长1.8 m,高约1.2 m的楼梯,如图11所示。
图11 实验场景
Fig.11 Experience environment
5.2 实验结果及性能分析5.2.1 实验结果
本文主要的实验场景是人上下楼梯的情况,分别作了两类实验,一类为垂直于X轴上下楼梯,另一类则是斜着上下楼梯,忽略人在上下楼梯时的重心抖动等问题,将上下楼梯的真实轨迹简单地估计为一条直线用于比对。测试结果如图12、图13所示。
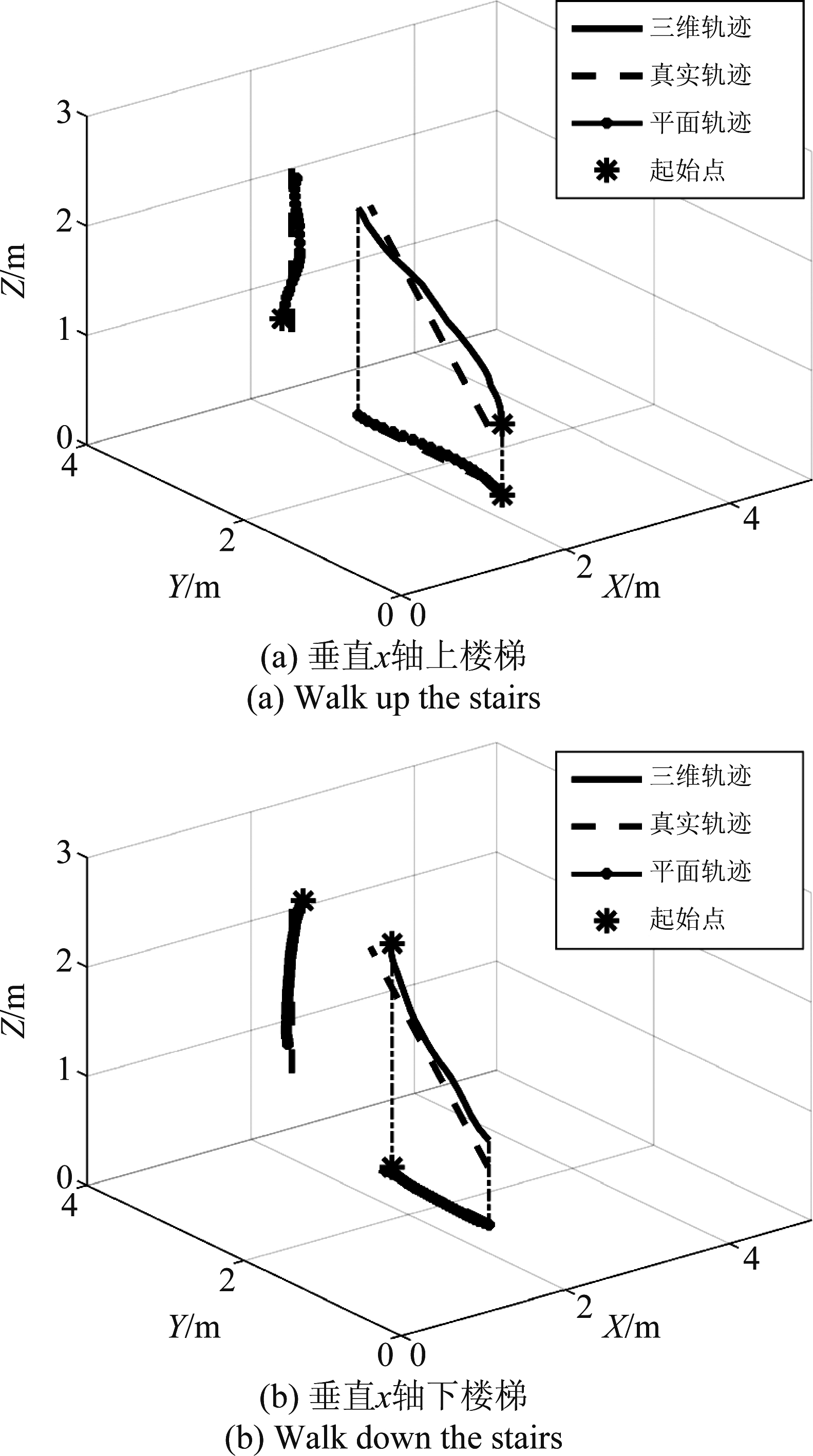
图12 垂直X轴上、下楼梯结果
Fig.12 The tracking result of walking up and down the stairs which was set perpendicular to the X axis
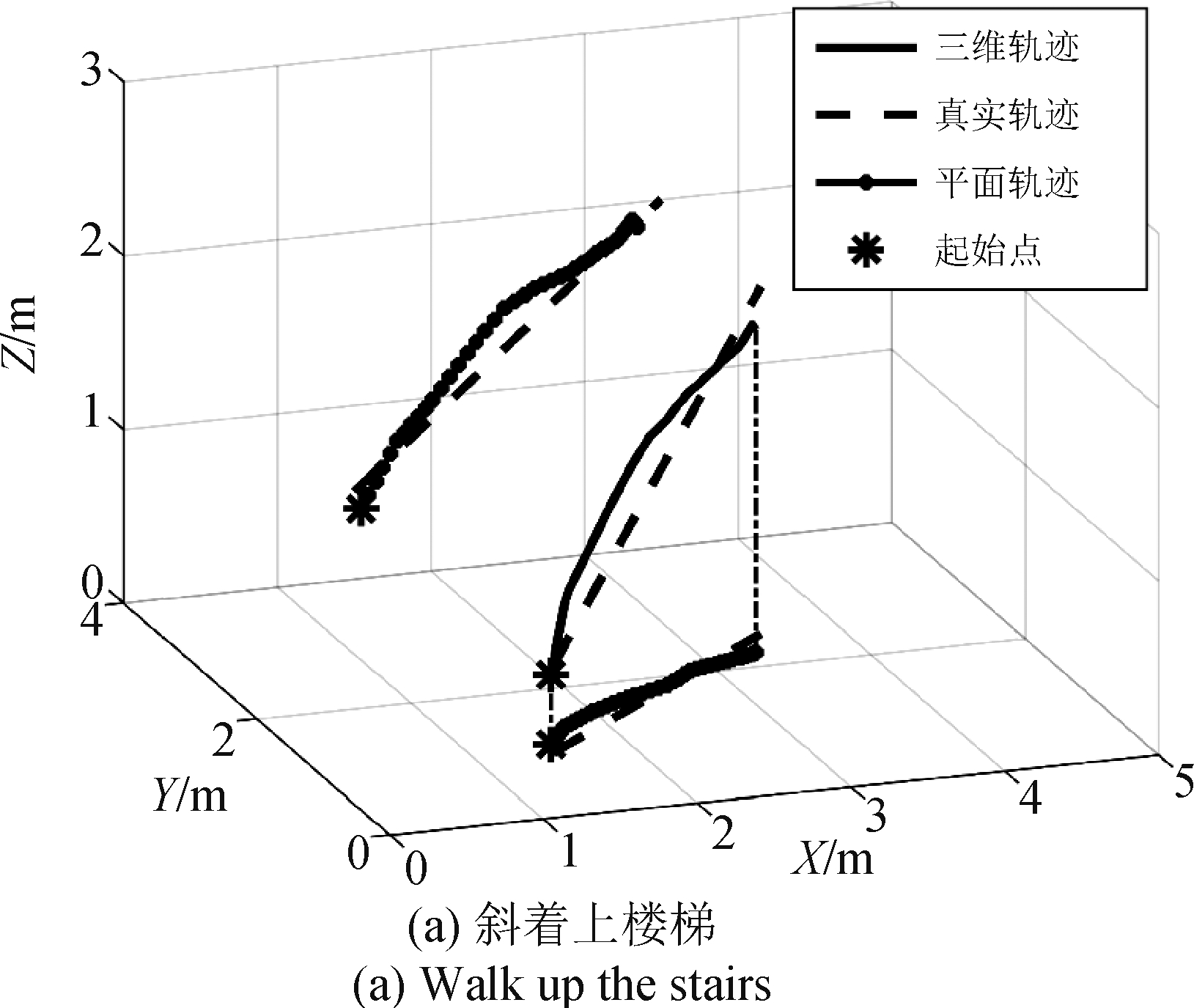
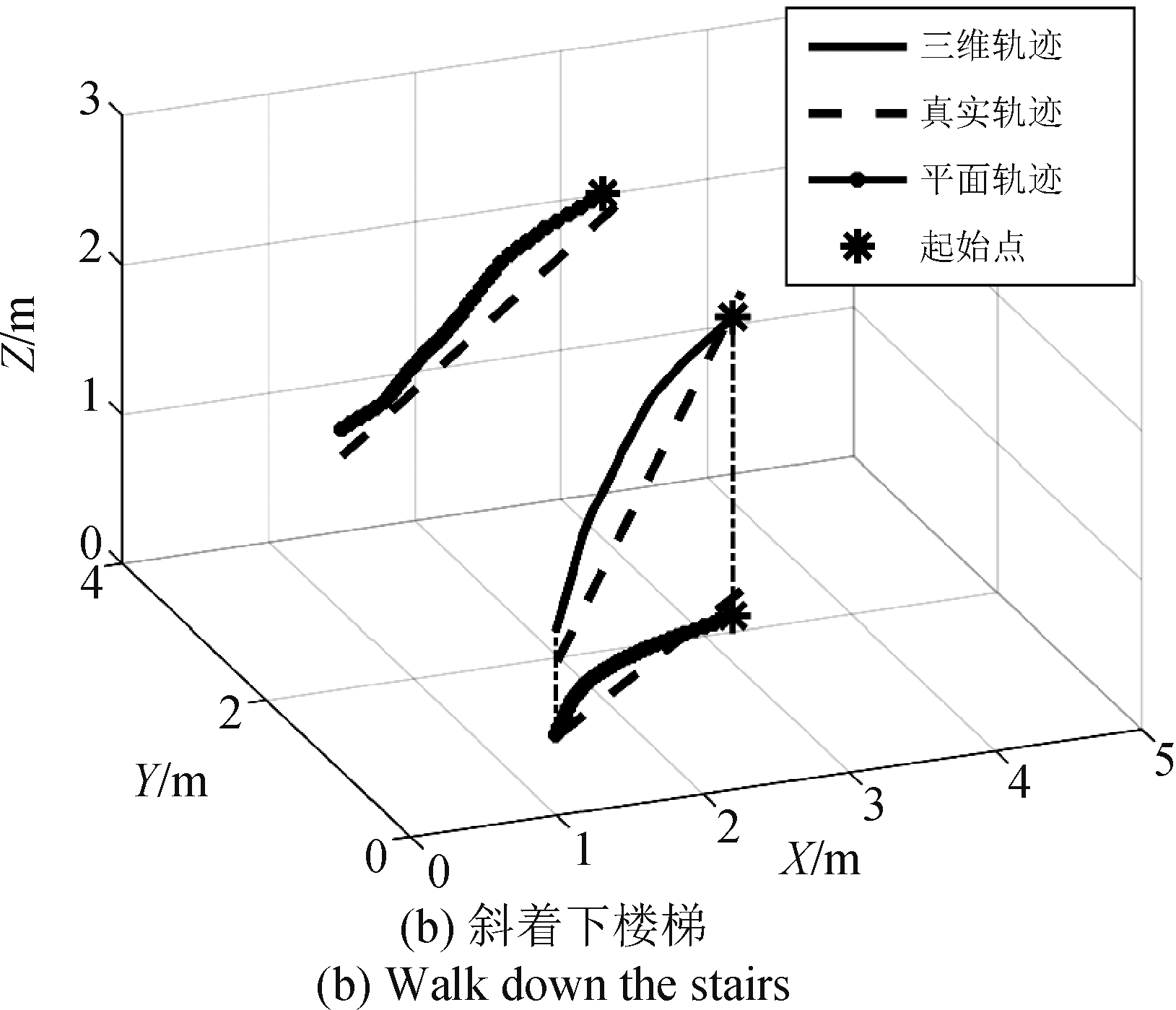
图13 斜着上、下楼梯结果
Fig.13 The tracking result of walking up and down the stairs which was set with some off-axis angle
可以看出,本系统能很好地对运动的方向和位置进行估计。当运动比较简单,方向垂直于某个轴时,定位精度十分高;当运动方向变得“复杂”时,精度虽有所下降,但仍能不错地对运动轨迹进行估计。这说明本文提出的算法通过对信号的处理,能够滤掉多数静态多径信号,从而保留由目标反射回的多径信号,以提取参数对目标进行定位。
5.2.2 定位精确度分析
本文的三维轨迹跟踪算法,采用的是一发两收系统,对两个面的运动进行轨迹跟踪;其中,X-Y平面为一发一收系统,估算多参数进行位置估计,较之单纯利用DFS这一个参数来估计,有更小的错误率;X-Z平面则利用了一发两收系统,双链路虽有高消耗,但能对DFS进行更精准的估计来计算位置,有很小的错误率,如图14所示;在考虑了系统开支和准确度的平衡后,选择了一发两收系统。
本系统位置误差为0.7 m。作为对比,选取了Dynamic-Music[19]]和IndoTrack[20]两种算法。图15显示了这些算法的表现。Dynamic-Music算法采用了JADE来计算人体反射的AoA,只用AoA进行位置计算,误差较大;IndoTrack则同时利用了DFS和AoA信息来做位置估计,在短距离内有很好的表现,但是却没有评估DFS的突变性,导致长距离运算时的异常值会对整个估计造成影响。相比之下,本系统利用了多种参数,在估计DFS时也考虑了前后关联性来选择合适的值,所以在整体上都有更好的表现。
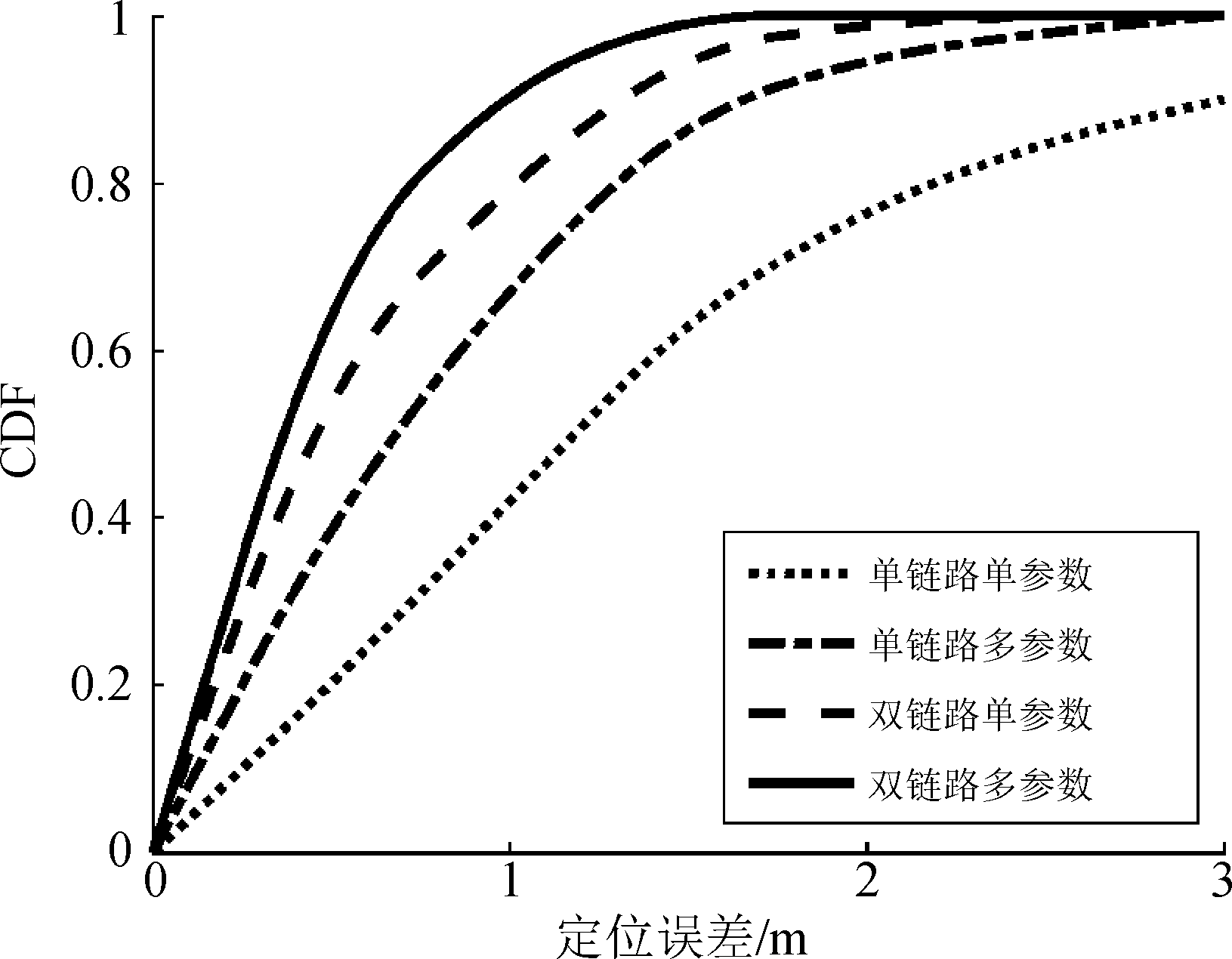
图14 多种定位方案的比较
Fig.14 Compare the various localization methods
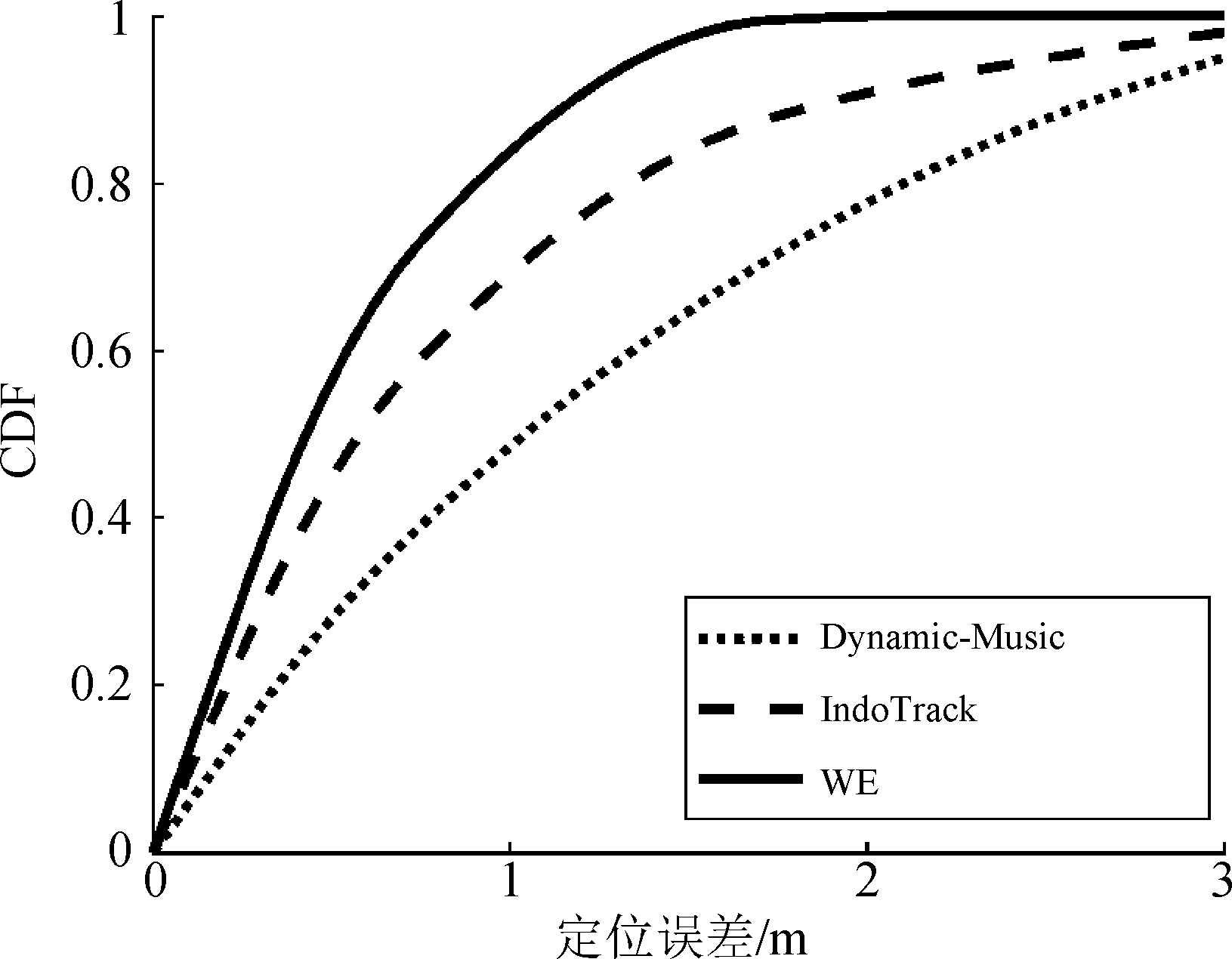
图15 多种定位算法的比较
Fig.15 Compare the various localization algorisms
5.2.3 运动速度对算法的影响
人的走动速度一般低于4 m/s,我们对不同运动速度下的位置估计结果进行了比较,图16是不同运动速度情况下多次实验结果的误差分布图。可以看出,即使是在各种速度情况下,都基本稳定在0.7 m左右,说明此算法能很好的评估DFS,对AoA、ToF、速度进行修正,以得到准确的位置。
5.2.4 不同发包率对算法的影响
将发包率分别设为1024 Hz、512 Hz、256 Hz进行了实验,图17为各发包率多次实验结果的误差分布图。可以看出,发包率的改变几乎不会大幅度地改变算法的准确度,而这个范围与真实WiFi传输的速率也相近。理论上,降低发包率会同时改变进行频谱分析时的采样率,这样可能会导致频谱中高频部分与目标频率部分混杂,但低采样率下的实验结果只有微小下降,这说明在CSI估计过程中的主要频率部分集中在频谱下部,而本系统采用的高频谱提取算法可以很好地避免这个问题。
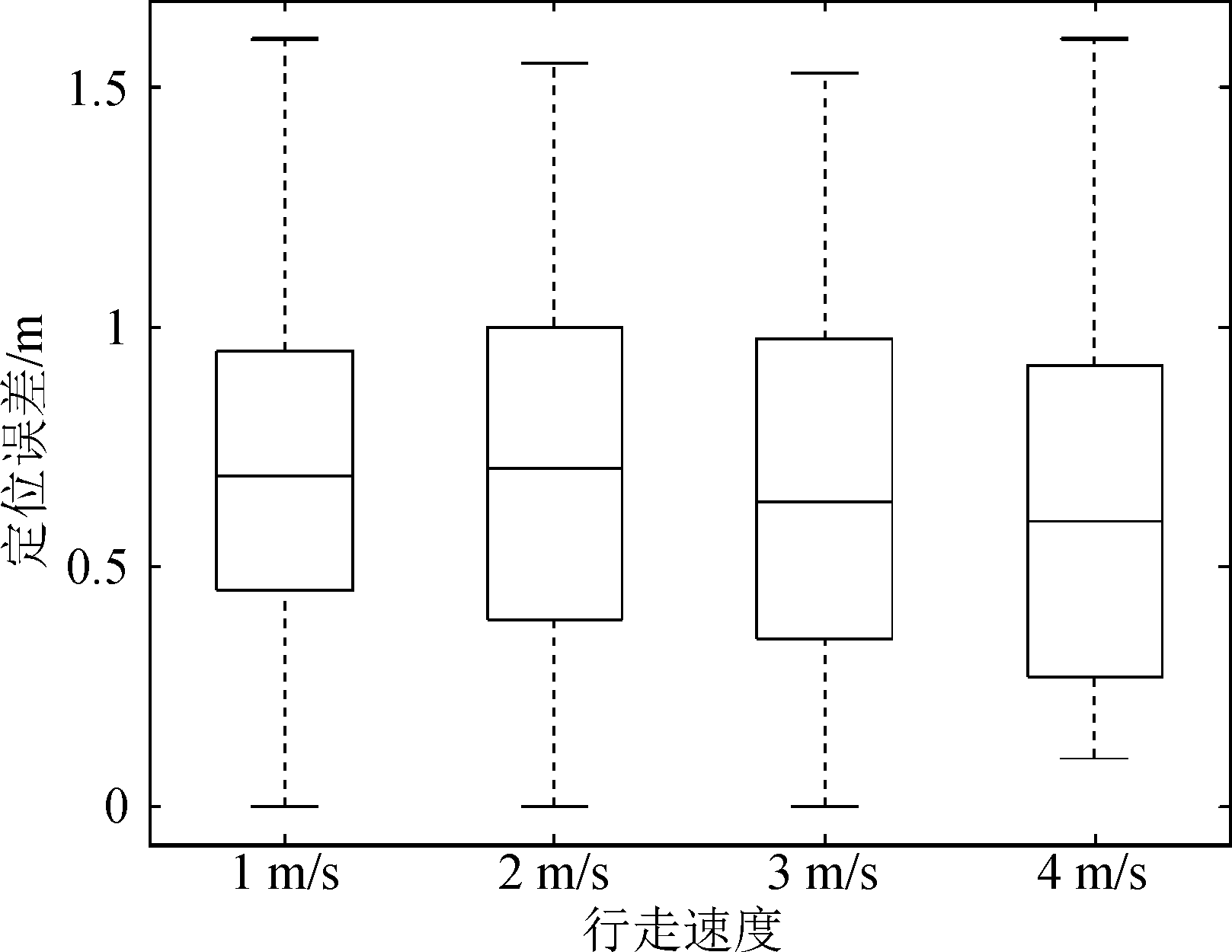
图16 不同运动速度时的定位误差
Fig.16 Different location error of various walking speed
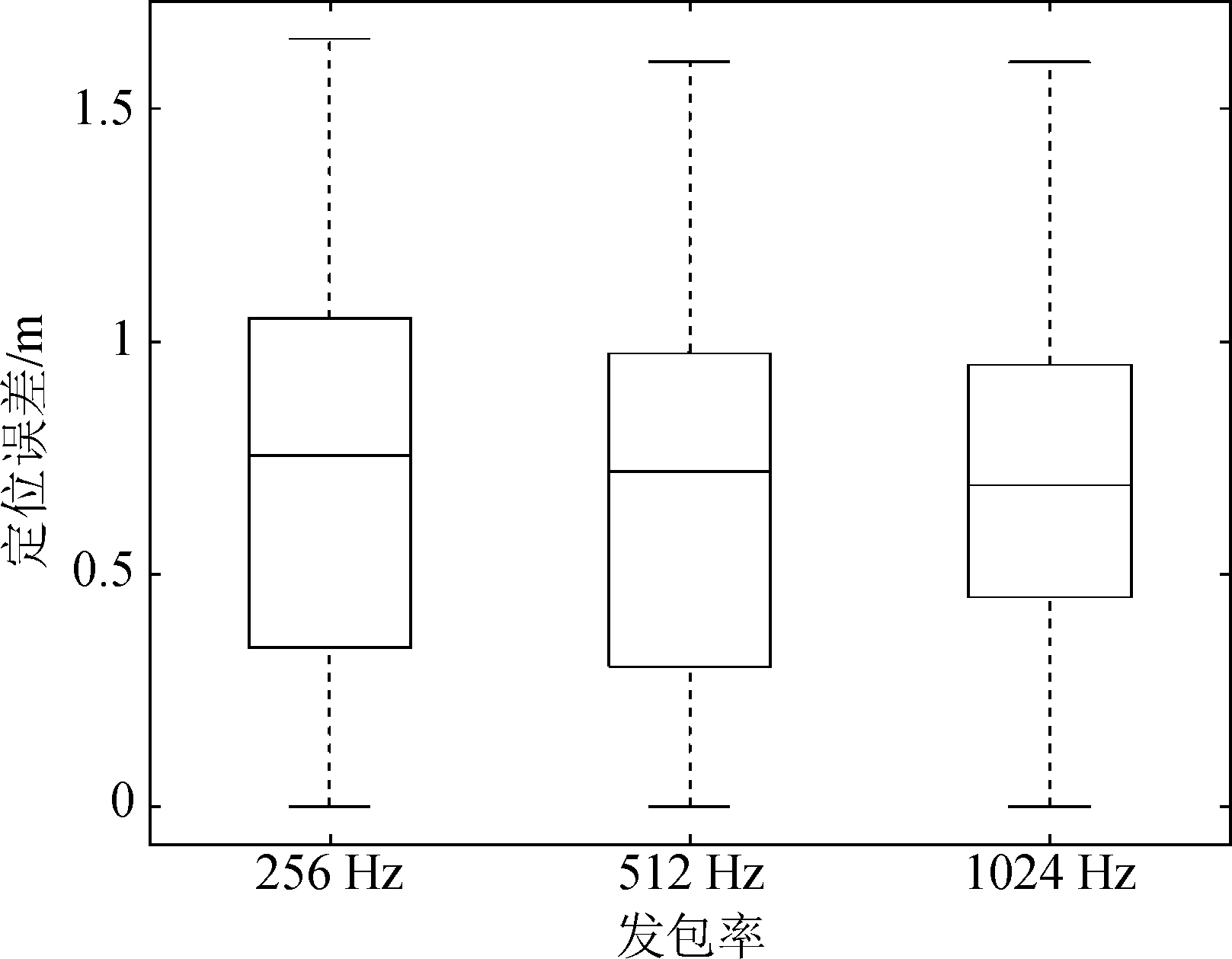
图17 不同发包率情况下的定位误差
Fig.17 Different location error of various sampling speed
综上,本文提出的三维轨迹跟踪算法在有着不错的误差的情况下,同时能够减少链路数量,对不同运动速度的人进行轨迹估计,在不同发包率的情况下也有很好的效果。
6 结论
本文在回顾了现有室内定位现状和需求后,针对性地提出了一种基于商用WiFi的无源三维轨迹跟踪系统,在尽量减少链路的情况下实现三维轨迹跟踪,达到了厘米级的精度。这个系统不需要提前布置任何设施、做大量实验,也不需要人携带任何设备。通过分离出由人体反射回的信号并进行处理,成功的提取出了多普勒频移、信号飞行时间、到达角度多维参数,依相应模型,利用多维参数对人的三维运动进行跟踪。实验结果显示本文提出的算法的误差达到了0.7 m,说明了其可行性和可靠性。
[1] 毛永毅, 阴颖. 面向室内定位的DHOHF-Elman神经网络算法[J]. 信号处理, 2019, 35(8): 1358-1365.
Mao Yongyi, Yin Ying. DHOHF-Elman neural network algorithm for indoor localization[J]. Journal of Signal Processing, 2019, 35(8): 1358-1365.(in Chinese)
[2] Kotaru M, Joshi K, Bharadia D, et al. SpotFi: Decimeter Level Localization Using WiFi[J]. ACM Sigcomm Computer Communication Review, 2015, 45(4): 269-282.
[3] Qian Kun, Wu Chenshu, Zhang Yang, et al, Detecting radio frequency interference for CSI measurements on COTS WiFi devices[C]∥2017 IEEE International Conference on Communications (ICC). IEEE, 2017.
[4] 左泽谦, 潘军, 蒋立军, 等. 基于WIFI的位置指纹参考节点密度与定位精度关系研究[J]. 世界地质, 2019(2): 532-538.
Zuo Zeqian, Pan Jun, Jiang Lijun, et al. Research on the relationship between density of reference nodes of location fingerprint and positioning accuracy based on WIFI[J]. Global Geology, 2019(2): 532-538.(in Chinese)
[5] 杜留锋, 田熙燕. 基于细粒度指纹的室内定位系统[J]. 应用科学学报, 2019, 37(3): 313-326.
Du Liufeng, Tian Xiyan. Indoor location system based on fine-grained fingerprint[J]. Journal of Applied Sciences, 2019, 37(3): 313-326.(in Chinese)
[6] Pu Qifan, Gupta S, Gollakota S, et al. Whole-Home Gesture Recognition Using Wireless Signals[C]∥Proceedings of the ACM SIGCOMM 2013 Conference on SIGCOMM. ACM, 2013: 27-38.
[7] Wang Wei, Liu Alex X, Sun Ke. Device-free gesture tracking using acoustic signals[C]∥International Conference on Mobile Computing & Networking. ACM, 2016.
[8] Qian Kun, Wu Chenshu, Zhang Yang, et al, Widar: Decimeter-Level Passive Tracking via Velocity Monitoring with Commodity Wi-Fi[C]∥Mobihoc ′17 Proceedings of the 18th ACM International Symposium on Mobile Ad Hoc Networking and Computing. ACM, 2017.
[9] Qian Kun, Wu Chenshu, Zhang Yang, et al, Widar2.0: Passive Human Tracking with a Single Wi-Fi Link[C]∥MobiSys ′18 Proceedings of the 16th Annual International Conference on Mobile Systems, Applications, and Services. ACM, 2018: 350-361.
[10]Zhang Lingyan, Wang Hongyu. 3D-WiFi: 3D Localization with Commodity WiFi[J]. IEEE Sensors Journal, 2019: 5141-5152.
[11]Aly H, Agrawala A. Hapi: A Robust Pseudo-3D Calibration-Free WiFi-based Indoor Localization System[C]∥MobiQuitous ′18 Proceedings of the 15th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services. ACM, 2018: 166-175.
[12]Nee R V, House A. OFDM for Wireless Multimedia Communications[M]. Britain: London, 2000: 21-23.
[13]Shen Weiliang, Lin C, Gollakota S, et al. Rate Adaptation for 802.11 Multiuser MIMO Networks[J]. IEEE Transactions on Mobile Computing, 2014, 13(1): 35- 47.
[14]Wang Wei, Liu Alex X, Shahzad M, et al. Understanding and Modeling of WiFi Signal Based Human Activity Recognition[C]∥MobiCom ′15 Proceedings of the 21st Annual International Conference on Mobile Computing and Networking. ACM, 2015: 65-76.
[15]Wu Dan, Zhang Daqing, Xu Chenren, et al. WiDir: walking direction estimation using wireless signals[C]∥Acm International Joint Conference. ACM, 2016: 351-362.
[16]Halperin D, Hu Wenjun, Sheth A, et al. Predictable 802.11 packet delivery from wireless channel measurements[C]∥SIGCOMM ′10 Proceedings of the ACM SIGCOMM 2010 Conference. ACM, 2010: 159.
[17]Vincent Poor H. An Introduction to Signal Detection and Estimation[M]. 2nd Ed. Springer-Verlag, 1994: 173-180.
[18]Fessler J A, Hero A O. Space-alternating generalized expectation-maximization algorithm[J]. IEEE Transactions on Signal Processing, 1994, 42(10): 2664-2677.
[19]Li Xiang, Zhang Daqing, Lu Qin, et al. Dynamic-MUSIC: accurate device-free indoor localization[C]∥UbiComp′16 Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing. ACM, 2016.
[20]Li Xiang, Zhang Daqing, Lu Qin, et al. IndoTrack: Device-Free Indoor Human Tracking with Commodity Wi-Fi[C]∥Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies. ACM, 2017.
