1 引言
基于随机有限集理论的概率假设密度(Probability hypothesis density,PHD)滤波器[1]通过联合估计监测区域中的所有目标,可以避免复杂的数据关联问题,是目前对于复杂条件下的未知、时变多目标进行跟踪的主要方法之一[2-5]。分布式传感器网络中每个节点仅处理本地及其邻近节点的信息,它不需要像集中式结构那样将所有节点的多目标后验信息送到融合中心处理,因此能够将信息的传输和运算压力分散到各本地节点,从而很大程度上降低了对系统运算处理能力的需求,为多目标跟踪的应用提供了一个理想的平台。
在分布式多传感器网络中,每个传感器节点具有独立的传感和运算能力,应用PHD滤波进行跟踪时,需要将PHD滤波器进行分布式扩展,即在每个传感器运行一个本地PHD滤波器,并与相邻传感器交换相关信息[6]。本地PHD滤波器通常采用高斯混合或粒子滤波方法实现。目前,分布式多目标跟踪通常采用广义协方差交集(Generalized Covariance Intersection, GCI)准则进行PHD融合[7],也称为几何平均或指数混合密度方法,它通过求解相对于本地后验分布的Kullback-Leibler散度加权和最小的融合后验分布实现,该方法符合最小信息差异准则。如文献[8]利用 GCI 融合准则实现了基于 PHD 滤波器的分布式跟踪融合。文献[9]结合网络一致性理论和GCI融合准则实现了基于势概率假设密度滤波器的分布式跟踪融合。但是,GCI融合方法需要在由所有广义协方差组成的传感器之间传递整个PHD,从而在整个网络范围内达成其状态的一致性并在每个节点上获得估计,这将造成巨大通信成本,同时具有对目标漏检比较敏感、容易低估目标数量等缺陷[10-12]。
然而,大多数现有的分布式RFS滤波器通常都假定所有传感器具有相同的视野,即监测区域内所有传感器都能够得到目标的测量,这在很多情况下是不符合实际的,因为实际传感器通常只有有限的感测范围。在传感器网络中,每个传感器的视野范围通常是部分重叠,有时候甚至是不重叠的。目前对于视野有限传感器网络中的多目标跟踪已有若干相关研究,但基本都是在集中式网络中进行讨论的,在分布式网络中的相关研究目前尚比较少。如文献[13]提出协作PHD滤波器,通过将PHD滤波器推广到非重叠视野中实现移动车辆的协同跟踪。文献[14]研究了传感器节点视野不重叠的网络中的集中式广义标签多伯努利多目标跟踪。文献[15]提出了一种在GCI融合背景下处理不同传感器视野的标签多伯努利多目标跟踪方法,可用于集中式和分布式传感器网络。
本文主要研究视野有限的分布式传感器网络基于粒子PHD滤波的多目标跟踪问题。由于每个节点的感测范围都是有限的,因此,某一时刻监测区域中的目标仅能由网络中所有节点的某个子集看到,当目标随时间运动时,该子集会随之发生变化。因此,在每个时间步都可将传感器网络中的节点划分为活动和非活动两部分。在整个监测区域中,传感器网络是以分布和协作的方式检测和观察目标,而不是在整个网络范围内达成其状态的一致性。针对上述传感器有限感测范围的特点,本文提出一种在后验PHD的粒子集上进行混合式融合的分布式粒子PHD算法,可适用于在感测范围有限的传感器网络中的多目标跟踪。
2 传感器网络及目标模型
2.1 传感器网络模型
考虑一个由有向图表示的分布式传感器网络
其中
为所有传感器节点集合,
表示所有网络中相邻传感器之间的双向通信链路。分布式传感器网络的基本结构如图1所示,图中传感器网络包含5个节点,节点之间的双向箭头表示通信链路,每个传感器节点只与其相邻节点交换信息。若用
表示网络中任一节点
及其相邻节点集合,则图1网络中节点1与三个节点相邻,即S1={1,2,3,4}。假设节点的感测半径为Rs,则其视野范围可认为是一个以节点位置为圆心,以Rs为半径的圆形区域。因此,传感器网络的视野范围并不是整个区域,而是网络中所有传感器视野的并集。图1中标出了每个节点的感测范围,即该传感器网络在监测区域内的视野为五个圆域的并集,则在某一时刻,目标T1能够同时被节点2和节点4测量,但所有节点都无法直接得到目标T2的测量。
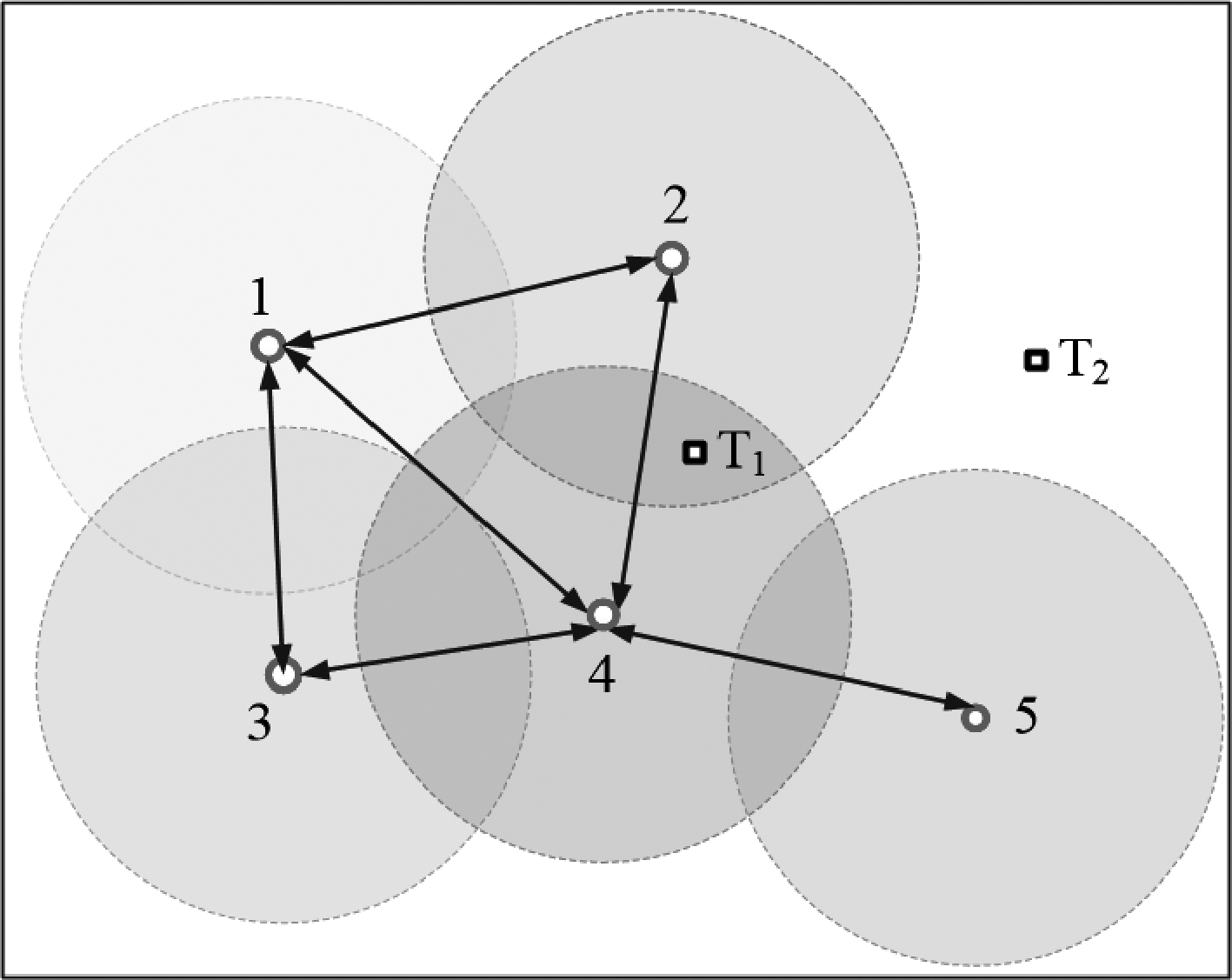
图1 传感器网络的分布式结构及其视野范围
Fig.1 The distributed structure of sensor network and its field of view
2.2 目标状态及测量模型
本文采用二维线性模型描述目标的运动。假设目标在k时刻的状态为xk=[pk,vk]T,pk和vk分别表示目标的位置和速度,则目标的状态方程和测量方程分别为:
xk=Fk,k-1xk-1+uk-1
(1)
zk=Hkxk+wk
(2)
式中Fk,k-1为状态转移矩阵;uk-1和wk分别为状态转移和测量过程噪声,两者同为零均值的高斯噪声,协方差矩阵分别用Qk-1和Rk表示。zk表示k时刻传感器的测量值,Hk为测量矩阵。
若节点感测半径为Rs,则测量方程(2)可写为:
zk(i)=Hkxk+wk, i∈M
(3)
式中zk(i)表示传感器节点i在k时刻的测量值;M={m∈V|pk(m)-pk2≤Rs},表示与目标位置pk间的欧氏距离不超过感测半径Rs的节点集合,pk(m)表示节点m的位置。
3 随机有限集下的PHD滤波器
随机有限集(Random Finite Set,RFS)是一种无序的有限集合,它所包含元素的个数和取值都是随机的[16]。在多目标跟踪过程中,由于多个目标可能出现消亡和新生等变化,因此目标的数目可能是随着时间不断变化的,利用RFS可以更准确地描述多目标的状态、测量及数目情况。假设k时刻目标数目为Nk,建立k时刻多目标状态的RFS为Xk={xk,1,xk,2,…,xk,Nk},且有:
Xk=Sk|k-1(Xk-1)∪Bk
(4)
式中Sk|k-1(Xk-1)是由k-1时刻已存在,且k时刻仍然存活在传感器网络覆盖范围内的目标状态集合;Bk表示k时刻出现的新生目标状态。用Zk={zk,1,zk,2,…,zk,Mk}表示k时刻的多目标测量的RFS,其中Mk为k时刻得到目标测量的节点数目,则有:
Zk=Θk(Xk)∪Ck
(5)
式中Θk(Xk)为由目标状态Xk产生的测量,Ck表示由杂波或虚警产生的虚假测量。
于是多目标后验密度可由多目标贝叶斯滤波器以递归方式传播,其预测方程和更新方程分别为:
pk|k-1(Xk|Z1:k-1)= 
(6)
pk|k(Xk|Z1:k)=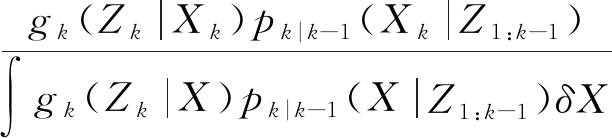 
(7)
式中pk|k-1(Xk|Z1:k-1)表示预测后验概率密度,pk|k(Xk|Z1:k)表示更新后验概率密度,Z1:k=(Z1,Z2,…,Zk)表示到时刻k的历史测量集合, fk|k-1(Xk|Xk-1)表示RFS下的多目标转移密度,gk(Zk|Xk)表示RFS下多目标似然概率密度。
由于最优贝叶斯滤波器包含复杂的集合积分,难以直接计算,需要找到一组统计数据来对后验密度进行近似和传播。概率假设密度PHD滤波器通过传播多目标后验密度的一阶矩实现多目标状态估计,是多目标后验在Kullback-Leibler信息准则下的最优近似。它避免了后验密度的直接计算以及传统跟踪方法中的数据关联问题,从而在很大程度上降低了计算复杂度。
多目标预测密度pk|k-1(Xk|Z1:k-1)的PHD为Dk|k-1(xk)=Dk|k-1(xk|Z1:k-1),多目标后验密度pk|k(Xk|Z1:k)的PHD为Dk|k(xk)=Dk|k(xk|Z1:k),它的积分即为目标数目的估计[1]:
(8)
PHD滤波的预测和更新方程分别为:
Dk|k-1(xk)=bk(xk)+ 
(9)
Dk|k(xk)=Dk|k-1(xk)[1-PD,k(xk)]+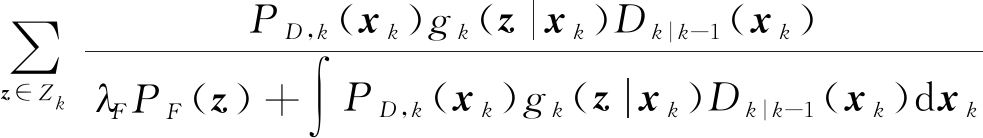 
(10)
式中bk(xk)为k时刻新生目标随机有限集的PHD;PS,k|k-1(xk-1)为目标由k-1时刻存活到k时刻的存活概率;PD,k(xk)目标的检测概率,它相对于时间和节点的视野是不变的;λFpF(z)表示由杂波引起的泊松分布虚警,其中λF为虚警参数,pF(z)为其空间分布。
上述PHD滤波器可以通过序贯蒙特卡罗方法实现,称为粒子PHD滤波器[17]。
4 提出的分布式粒子PHD滤波算法
常规的分布式粒子PHD滤波算法[8]不考虑传感器的视野问题,即认为监测区域内所有节点都能够同时得到目标的测量,且每个节点只利用自己的测量值运行本地PHD滤波器,最后通过GCI准则进行后验PHD的融合。但是在感测范围有限的传感器网络中,并非所有的节点都能获得目标的测量,即当目标存在时,网络可分为活动和非活动两个部分,只有活动部分内的传感器节点才能够获得目标的测量。本文提出的分布式粒子PHD滤波算法通过本地节点与相邻节点的粒子集与测量集的传递和处理,可以使得每个节点都能获得其视野范围之外目标的后验信息,实现后验PHD的混合式融合。
4.1 提出算法的流程
(1)初始化
传感器网络活动部分中的每个节点i基于其相邻节点的测量值可获得当前目标的PHD,其当前粒子集和对应的权值用
表示,其中Ni,p(k)表示k时刻网络中节点i对应的粒子数目。也就是说,每个活动节点通过访问其相邻节点的测量值执行一个独立的粒子PHD滤波过程。
(2)粒子集合并
通过合并粒子集的方式将来自于每个活动节点及其相邻节点的估计量进行合并,得到联合估计。在粒子PHD滤波中,由于粒子集及其权值代表了目标的PHD,合并粒子集实际上相当于累加相应的PHD。即将节点i的当前粒子集与其所有相邻节点的粒子集进行合并,得到节点i的联合粒子集
其中Ni,pn(k)表示k时刻节点i及其所有相邻节点的粒子总数。
若将k-1时刻传感器节点i的新生粒子集表示为
则该新生粒子集和k-1时刻的上述联合粒子集合并,可以得到节点i在k时刻的总粒子集:
Li,total(k)=Li,new(k-1)∪Li,np(k-1)
(11)
式中Ni,new(k-1)表示k-1时刻的新生粒子数目,总粒子集的数目为:
Ni,total(k)=Ni,new(k-1)+Ni,pn(k-1)
(12)
(3)状态预测
式(11)的总粒子集中的每个粒子通过式(1)的系统模型进行传播,由于过程噪声可以通过粒子的扩散来体现,因此可以从模型中去掉噪声项,从而得出k时刻的当前粒子集为:
(13)
粒子的权值相应地通过乘以目标的存活概率PS,k|k-1进行调整:
(14)
(4)权值更新
网络活动部分范围内的传感器节点获得目标的测量,并将测量值通过节点间的通信链路传递给相邻节点,这一传递过程可以使得非活动部分的节点也能够获得当前目标的测量值。然后根据每个节点获得的测量值集合进行粒子权值的更新,于是节点i对应粒子集的权值可根据公式(10)递推得到:
(15)
式中
表示由节点l获得的测量集合,且有:
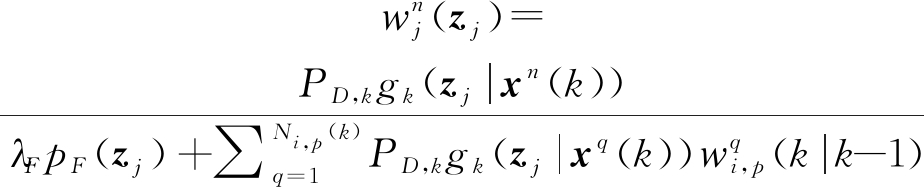
(16)
(5)目标数目估计
将每个节点i的总粒子集对应的权值相加,可得到每个节点对目标数目的估计值:
(17)
假设每个目标对应的粒子数为Np,则更新后节点i的当前粒子数为:
(18)
(6)重采样
粒子滤波实现过程需要进行重采样以防止粒子退化,重采样Ni,p(k)个粒子对节点i的粒子集进行替换。由于权值和(即目标数目)没有进行归一化处理,因此第n个粒子的概率为
将粒子的权值在重采样后统一设置为:
(19)
于是,重采样后的节点i粒子集为
并将其传递给它的相邻节点。
(7)目标状态估计
将节点i及其所有相邻节点的粒子集合并起来构成节点i的联合粒子集:
(20)
其中粒子数目等于与i相邻节点对应的粒子数之和:
(21)
目标状态的估计可通过对联合粒子集进行聚类操作得到。由于每个相邻节点的目标数目期望可能是不同的,本文选择采用单链型的层次聚类方法进行,将相邻节点的目标数目期望之和作为聚类数目的上限。
接下来该联合粒子集再与k时刻的新生粒子集合并,得到节点i的总粒子集,返回步骤(2)中的粒子合并步骤,进入下一时刻的预测和更新过程。如果一个目标被多个相邻节点检测到,那么它们的PHD可能不是互相独立的。但这对算法不会造成影响,因为合并粒子集的结果只是用更多的粒子来表示各个目标,从而使节点i能够得到目标位置更精确的估计。
4.2 改进的自适应新生目标模型
由上述步骤可以看到,在每一个时间步都要考虑新生目标的出现,因此新生目标的预测对整个算法有重要的影响[18]。PHD滤波器在实现过程中,通常假设新生目标集合Bk及其PHD是已知的,但这一假设多数情况下并不符合实际。文献[19]提出了测量驱动的自适应新生目标模型,通过在每个目标测量值的周围随机放置NP个新粒子来近似新生目标的PHD,其中NP为每个目标对应的粒子数。本文在该方法的基础上提出一种改进的自适应新生目标模型。
通过分析可知,新生目标和当前目标都会产生测量值,但理论上新生目标的测量值不会影响当前已有的目标,即不会对当前粒子集的最大权值产生贡献。所以在进行新生目标预测时,不必考虑所有的目标测量值,而只需要考虑对现有粒子权值没有明显影响的那些目标测量值,因为这些测量值能够更准确地预示新目标的出现。这样的操作不仅可以减少新生目标的粒子数目,而且能够有效避免当前目标和新生目标的PHD之间可能出现的重叠。在时间过渡到下一时刻k+1后,新生目标粒子继续存在,成为下一时刻的当前粒子。权值更新后,从节点i的所有测量值集合中去掉对当前粒子权值产生影响的测量值,即可得到一个由新生目标产生的测量值集合:
(22)
根据上述分析,该测量集中的测量值极有可能是由新生目标产生的,可以用来进行新生目标的自适应估计。在每个测量值
周围随机放置Np个粒子,于是节点i的新生粒子数目为
每个新生粒子的权值为:
(23)
式中PB是目标出生概率,取决于时间以及各个粒子的位置。为方便起见,假设新目标进入监测区域的概率对区域中所有位置都是相等的。上述目标新生的过程对应于式(9)中的第一项。
在整个算法的每次迭代结束时执行上述新生目标自适应模型进行新生目标预测和新生目标粒子集的产生,并且仅在预测、加权和重采样步骤中考虑表示当前PHD的粒子。上述改进的自适应新生目标模型能够将新生粒子更准确地放置在新生目标的周围,因此具有更高的效率。此外,由于第一个进入的目标会触发新生粒子围绕相应测量值的出现,所以在该模型下不需要明确的初始化步骤。
提出的算法完整流程伪代码如表1所示。
表1 提出的分布式粒子PHD算法
Tab.1 The proposed distributed particle PHD algorithm
初始化:Li,new(0)=Li,np(0)=⌀while k≤T (T为跟踪结束时刻)for i=1, …, N 合并粒子集:Li,total(k)=Li,new(k-1)∪Li,np(k-1) for n=1, …, Nk,total(k) 状态预测:xni,p(k)=Fk,k-1xni,total(k) 权值调整:wni,p(kk-1)=PS,k|k-1wni,total(k) 权值更新:wni,p(k)=∏l∈Si[1-PD,k+∑zj∈Zlkwnj(zj)]wni,p(kk-1) end for 目标数目估计:N^i(k)=∑Ni,total(k)n=1wni,p(k) 粒子数更新:Ni,p(k)=N^i(k)·Np 重采样:wni,p(k)=N^i(k)/Ni,p(k) 目标状态估计:Li,np(k)=∪l∈SiLi,p(k) 新生目标测量集:Zik,new=Zik-{zmm=argmaxjwnj(zj)} 新生目标粒子集:Li,new(k)end fork=k+1end whilereturn
5 仿真实验与分析
在一个感测范围有限的分布式传感器网络中对本文提出的算法性能进行分析,仿真实验及数据处理均在matlab 2016b环境下完成。考虑一个包含10个节点的传感器网络,运动目标总数目为4个,传感器网络结构及多目标跟踪场景如图2所示。监测区域范围设定为[-100 m,100 m]×[-100 m,100 m]。图中红色圆圈表示传感器节点,虚线为传感器间的通信链路,通信半径为80 m,目标1、目标2、目标3和目标4分别在时刻k=0, 10, 16, 22进入监测区域,又分别在时刻k=18, 54, 47, 60消失,目标运动轨迹的起点和终点在图2中分别用‘□’和‘△’表示。传感器节点的视野由感测半径Rs决定,例如图2中,当Rs=50 m时,传感器网络中的一个节点S的视野范围为图中较小的圆域,该节点只能得到目标4的测量;当Rs=100 m时,节点S的视野范围为图中较大的圆域,可以同时得到目标3和目标4的测量。
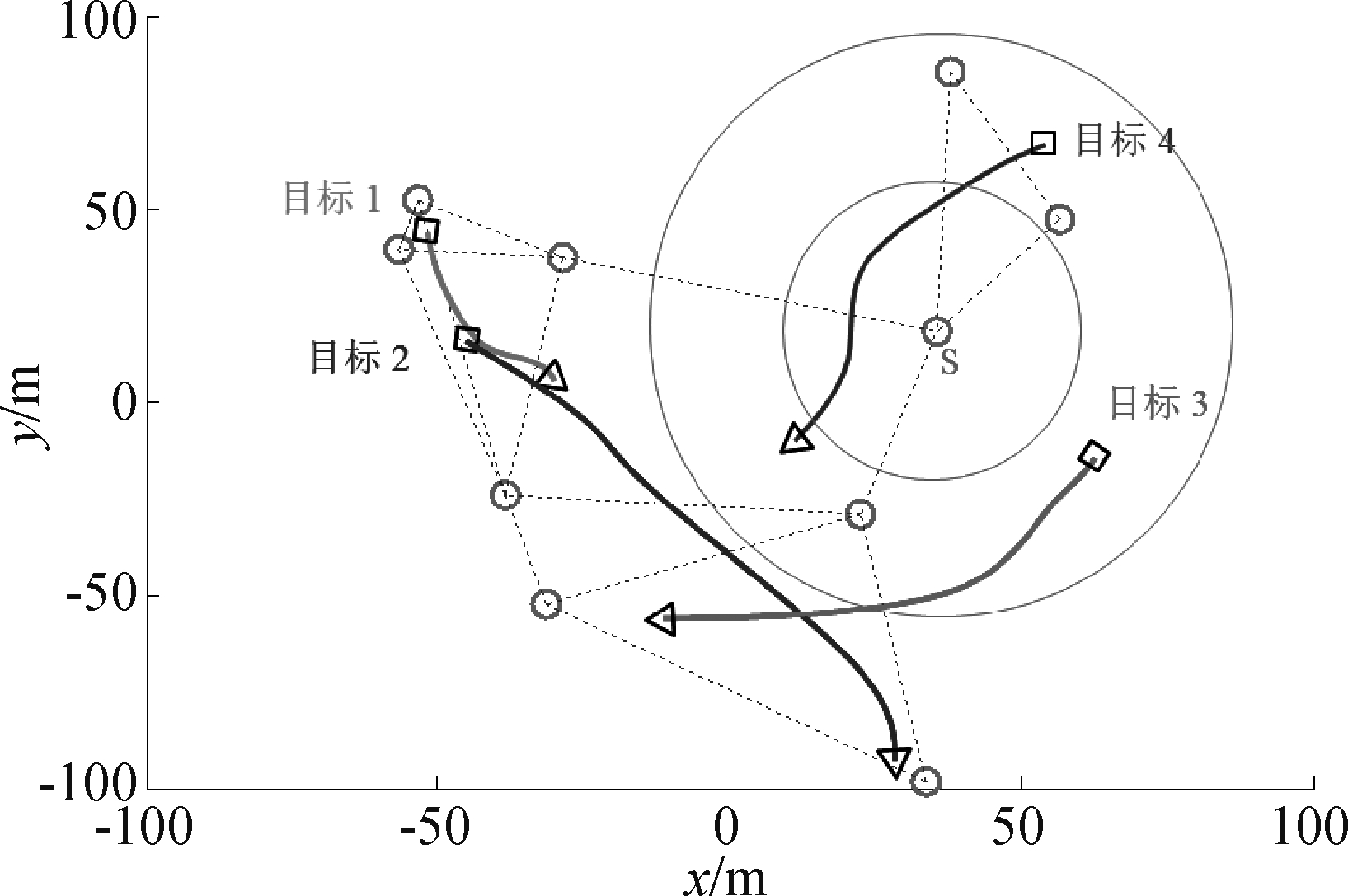
图2 传感器网络中的多目标跟踪场景 Fig.2 Multi-target tracking scenario in sensor network
根据式(1)和(2)定义的目标状态及测量模型,目标状态包含二维位置和二维速度,即:
模型参数设定如下:
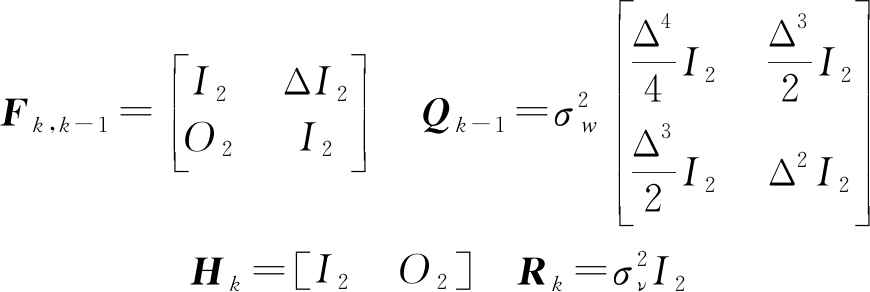
式中I2为2阶单位阵,O2为2阶零矩阵,Δ=1 s为采样周期,σw、σν分别为过程和测量噪声标准差。
设定目标存活概率PS,k|k-1=0.98,目标出生概率PB=0.8,传感器检测率PD,k=0.95,在此基础上建立两个仿真场景对图2所示传感器网络中4个目标进行跟踪。每个场景中分别在不同的感测半径下对本文提出的分布式粒子PHD算法进行性能仿真,并将其与常规分布式粒子PHD算法(常规DPHD)进行对比。每个目标采样粒子数目为200,蒙特卡罗仿真次数为100次,持续时间60 s,采用最优子模式分配误差(OSPA)进行跟踪性能的评估。
5.1 场景1:低杂波
在该场景下,测量噪声为零均值的高斯噪声,方差
杂波为泊松形式,均匀分布在每个节点的感知范围内,平均杂波率设定为λF=0.1。该场景中常规DPHD算法与本文提出算法的仿真分析结果如图3和图4所示,其中图3为OSPA误差,图4为目标数目估计。由于常规DPHD算法假定监测区域内所有节点都能得到目标的测量,所以常规算法下不考虑感测半径。
由图3可以看出,常规DPHD算法和本文算法的OSPA误差具有相似的变化趋势,即在有新目标出现的时刻会升高,在曲线上表现为一个尖峰。这是由于算法需要在新目标出现的下一时刻才能更新目标数目,造成该时刻的误差升高,这在多目标跟踪算法中是普遍现象。此外,还可以观察到,在k=40附近OSPA误差曲线出现了升高现象,这是由于目标2和目标3在该时刻轨迹发生了交叉,而滤波器采用的聚类算法难以分离高度重叠的测量集,因此只要两个目标接近到一定程度,跟踪算法会将其合并为一个目标,从而造成误差增大。而随着时间推移,两目标逐渐分离之后,算法又重新识别为两个目标,曲线开始下降并趋于稳定。
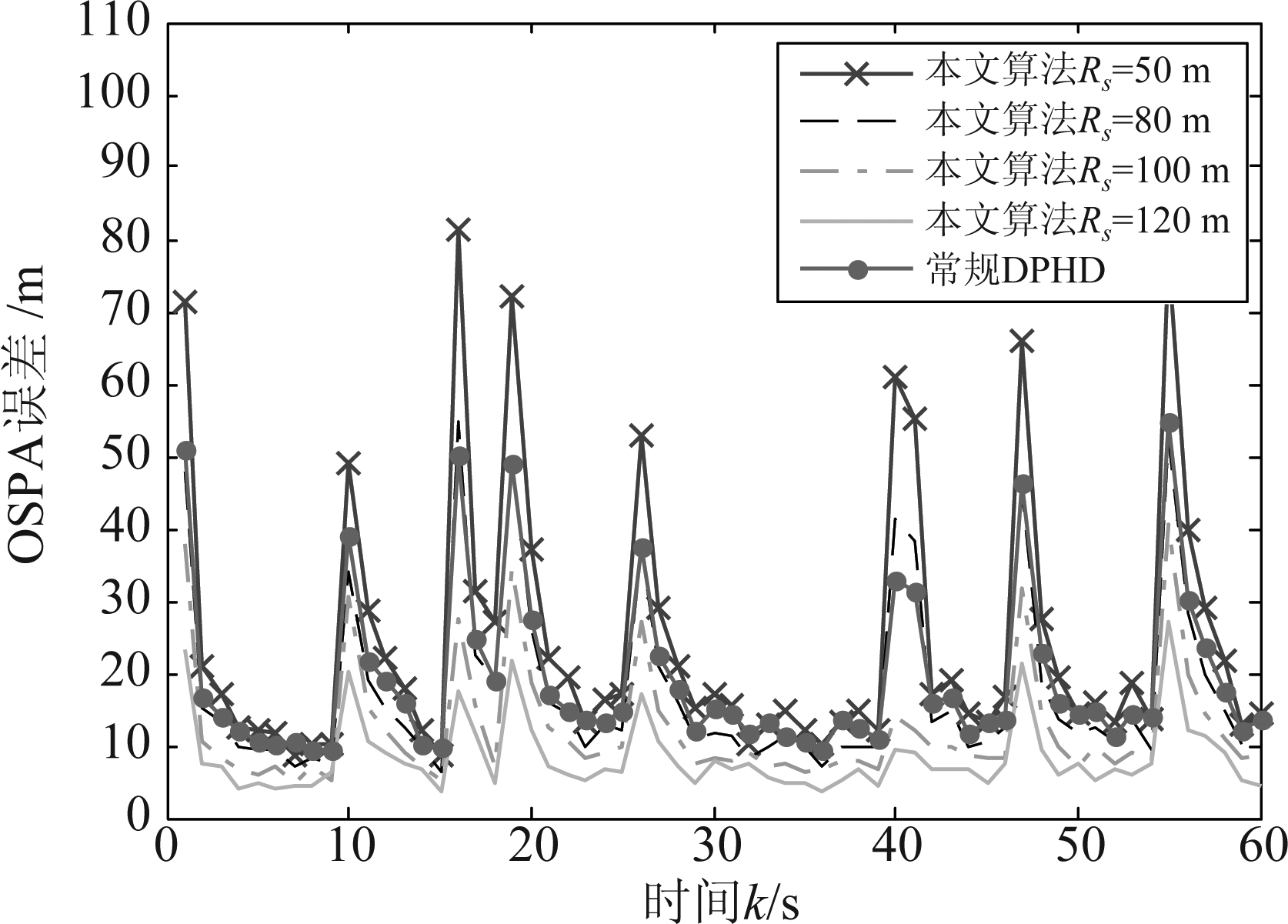
图3 低杂波场景(场景1)下的OSPA误差
Fig.3 OSPA error in low clutter scenario (scenario 1)
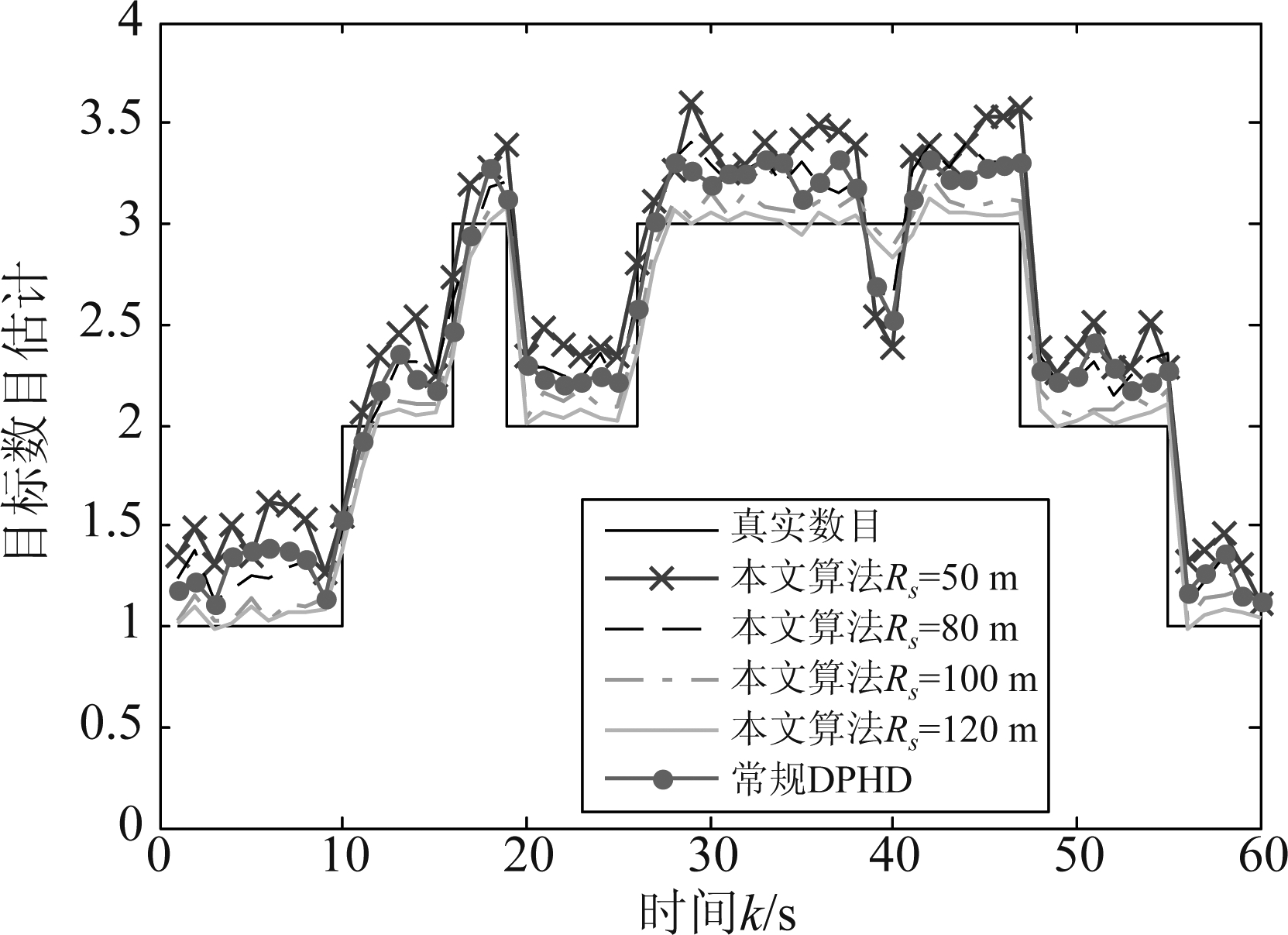
图4 低杂波场景(场景1)下的目标数目估计
Fig.4 Target number estimation in low clutter scenario (scenario 1)
此外,由图3还可以看出,当检测半径较小(如Rs=50 m)时,由于传感器网络的活动节点数目太少,得到目标的测量信息有限,因此比常规DPHD算法性能稍差。但当Rs扩大到80 m时,即可达到与常规DPHD相当的性能,当Rs大于100 m之后,本文算法与常规DPHD算法相比明显具有更好的性能。可见,本文算法的OSPA误差呈现出随传感器检测半径增大而减小的趋势。
由图4可以看到,两种算法都能实现对目标数目基本准确的估计。虽然本文算法在感测半径为50 m时的数目估计性能不如常规DPHD算法,但随着传感器视野范围的扩大,对目标数目的估计逐渐优于常规算法。此外,由于上述的目标轨迹交叉现象,相应地在图4中k=40附近的位置出现了目标数目估计的突然下降,这一点在感测半径为50 m时最为明显。
5.2 场景2:较高杂波
在该场景下,测量噪声方差与场景1相同,泊松杂波比场景1高,设定为λF=0.3。图5为该场景下OSPA距离误差,图6为目标数目的估计。
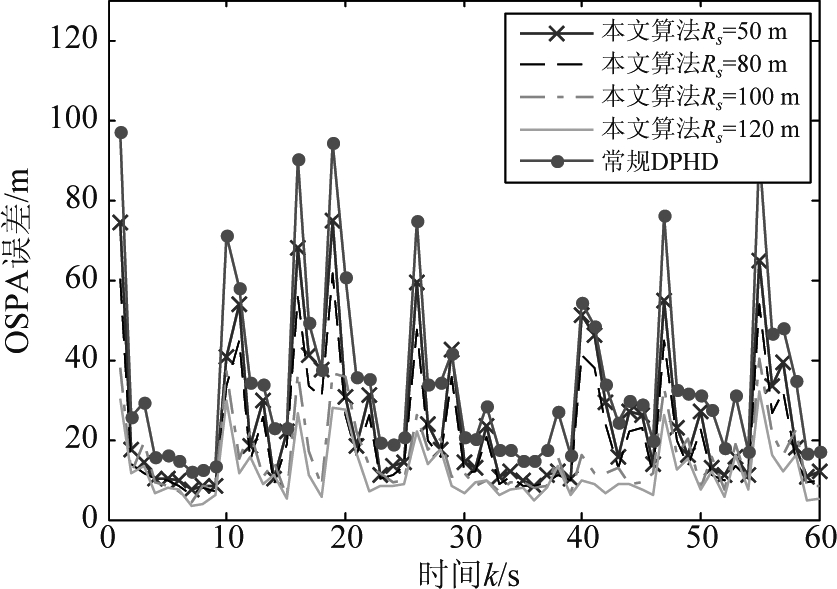
图5 较高杂波场景(场景2)下的OSPA误差
Fig.5 OSPA error in high clutter scenario (scenario 2)
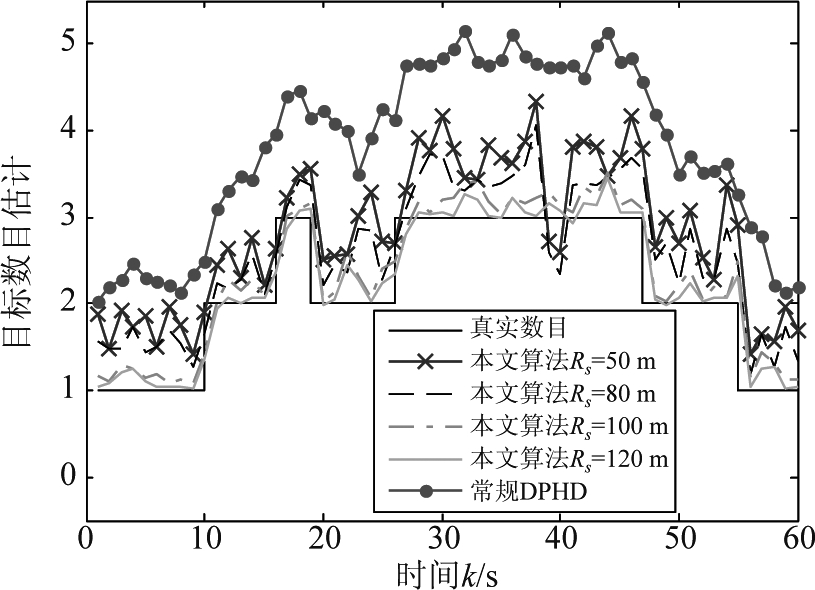
图6 较高杂波场景(场景2)下的目标数目估计
Fig.6 Target number estimation in high clutter scenario (scenario 2)
由图5和图6可以看出,虽然较高的杂波率会导致所有算法的OSPA误差和目标数目估计误差增大,但本文的算法仍然能够得到目标数目较为正确的估计,没有过大偏差,OSPA曲线也仅仅比场景1情况下略高,但常规DPHD算法的性能下降较为严重,已经难以得到目标数目的准确估计。这是由于常规算法只利用本地节点的测量值运行本地PHD滤波器,而本文算法在每个节点处采用相邻节点信息进行估计的方案能够一定程度上抑制杂波对跟踪过程的影响,提高跟踪算法整体的稳定性。
由以上跟踪试验可以看出,本文提出的分布式粒子PHD算法在感测范围有限的传感器网络中可以实现有效的跟踪,且跟踪性能随传感器网络视野范围的扩大呈升高趋势。当感测半径较小时,本文算法的性能虽有一定程度下降但仍能够保证有效的跟踪本文算法的性能。此外,本文算法还具有较好的杂波抑制作用,在杂波率升高的情况下能够基本保持算法整体的稳定性。
6 结论
本文研究了视野范围有限的分布式传感器网络中多目标跟踪问题,提出了一种能够在感测范围有限的传感器网络中实现多目标跟踪的分布式粒子PHD滤波算法,并对算法中涉及的新生目标自适应预测模型进行了改进。提出的算法通过融合传感器网络视野范围内的后验概率假设密度粒子集来克服传感器节点视野范围的局限,能够在感测范围有限的分布式传感器网络中情况下实现多目标状态和数目的有效跟踪,并且在感测半径较小的情况下仍然能够保证跟踪性能,同时对杂波有一定的抑制作用,具有较好的稳定性。
[1] Mahler R P. Multitarget bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.
[2] 杨峰, 王永齐, 梁彦, 等. 基于概率假设密度滤波方法的多目标跟踪技术综述[J]. 自动化学报, 2013, 39(11): 1944-1956.
Yang Feng, Wang Yongqi, Liang Yan, et al. A survey of PHD filter based multi-target tracking[J]. Acta Automatica Sinica, 2013, 39(11): 1944-1956.(in Chinese)
[3] 彭华甫, 黄高明, 田威. 随机有限集理论及其在多目标跟踪中的应用和实现[J]. 控制与决策, 2019, 34(2): 225-232.
Peng Huafu, Huang Gaoming, Tian Wei. Random finite set: theory, application and implementation for multi-target tracking[J]. Control and Decision, 2019, 34(2): 225-232.(in Chinese)
[4] 熊志刚, 黄树彩, 赵炜, 等. 嵌入式容积粒子PHD多目标跟踪算法[J]. 信号处理, 2016, 32(6): 676- 683.
Xiong Zhigang, Huang Shucai, Zhao Wei, et al. Imbedded Cubature Particle PHD Filter Multi-target Tracking Algorithm[J]. Journal of Signal Processing, 2016, 32(6): 676- 683.(in Chinese)
[5] 曹倬, 冯新喜, 蒲磊. 基于高斯混合概率假设密度滤波器的扩展目标跟踪算法[J]. 系统工程与电子技术, 2017, 39(3): 494- 499.
Cao Z, Feng X X, Pu L. Extended targets tracking algorithm based on Gaussian mixture probability hypothesis density filter[J]. Systems Engineering and Electronics, 2017, 39(3): 494- 499.(in Chinese)
[6] Dong P, Jing Z L, Leung H, et al. Robust Consensus Nonlinear Information Filter for Distributed Sensor Networks With Measurement Outliers[J]. IEEE Transactions on Cybernetics, 2019, 49(10): 3731-3743.
[7] Mahler R P. Optimal/robust distributed data fusion: a unified approach[C]∥Proc. of the SPIE Defense and Security Symposium, United States, 2000: 128-138
[8] Üney M, Clark E, Julier S. Distributed fusion of PHD filters via exponential mixture densities[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 521-531.
[9] Battistelli G, Chisci L, Fantacci C, et al. Consensus CPHD filter for distributed multi-target tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 508-520.
[10]Wang B, Yi W, Hoseinnezhad R, et al. Distributed fusion with multi-Bernoulli filter based on generalized covariance intersection[J]. Transactions on Signal Processing, 2017, 65(1): 242-255.
[11]Yu J Y, Coates M, Rabbat M. Distributed multi-sensor CPHD filter using pairwise gossiping[C]∥Proc. of IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 2016: 3176-3180.
[12]Li T, Corchado J, Sun S. On generalized covariance intersection for distributed PHD filtering and a simple but better alternative[C]∥Proc. of the International Conference on Information Fusion, Xi’an, China, 2017: 808- 815.
[13]Gan J, Vasic M, Martinoli A. Cooperative multiple dynamic object tracking on moving vehicles based on sequential Monte Carlo probability hypothesis density filter[C]∥Proc. of IEEE 19th International Conference on Intelligent Transportation Systems, Rio de Janeiro, Brazil, 2016: 2163-2170.
[14]Liu W, Chen Y, Cui H, et al. Multi-sensor tracking with non over-lapping field for the GLMB filter[C]∥Proc. of the International Conference on Control, Automation and Information Sciences, Chiang Mai, Thailand, 2017: 197-202.
[15]Li S, Battistelli G, Chisci L, et al. Multisensor multi-object tracking with different fields-of-view using the LMB filter[C]∥Proc. of the International Conference on Information Fusion, UK, 2018: 1201-1208.
[16]Mahler R P. Advances in statistical multisource multitarget information fusion[M]. Artech House, 2014.
[17]Vo B N, Singh S, Doucet A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.
[18]Ristic B, Clark D E, Vo B N. Improved SMC implementation of the PHD filter[C]∥Proc. of the 13th International Conference on Information Fusion, Edinburgh, UK, 2010: 1- 8.
[19]Ristic B, Clark D, Vo B N, et al. Adaptive target birth intensity for PHD and CPHD filters[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1656-1668.
