1 引言
随着卫星业务需求的不断升级,卫星频谱资源短缺问题日益凸显。认知无线电(Cognitive Radio,CR)作为一种高效利用频谱资源的手段,成为卫星通信网络中的一个研究热点[1-3]。在无线认知网络中,认知用户(Secondary User,SU)利用授权用户(Primary User,PU)信道的“频谱空穴”进行接入,以提高频谱利用率。而可以高效利用频谱资源的关键前提是SU是否能准确检测到PU的信道状态[4]。能量检测算法作为经典频谱检测方法,由于其在计算量及实现程度上有着较好的表现,被广泛应用在认知通信网络中[5-7]。但是在卫星通信网络中,由于信道的低信噪比特性,能量检测算法性能会迅速降低[8]。并且卫星信道存在通信时延,当前的感知结果未必是当前PU信道的真实状态,SU贸然接入会造成与PU的频谱冲突。因此,在卫星通信网络中,要判断PU的信道状态,不仅需要准确的频谱检测手段,还需要有效的频谱预测手段。
近年来,人工神经网络(Artificial Neural Network,ANN)被人们应用于频谱感知预测领域中,通过感知预测PU信道状态,以更高效地利用空闲频谱[9]。胡翩翩等人[10]针对BP(Back Propagation)网络易陷入局部最优的问题,通过和声搜索算法对BP网络的初始权重和阈值进行优化,结果表明,优化的网络有良好的频谱感知性能;Zhang S等人[11]提出基于K均值聚类算法的RBF(Radial Basis Function)神经网络算法对频谱进行感知预测,对比传统RBF网络,感知误差减少2/3;Hou X等人[12]利用模糊小波神经网络(Fuzzy Wavelet Neural Network,FWNN)进行频谱预测感知,其算法吞吐量较一般预测算法增加了15.3%;Lee G等人[13]提出一种基于卷积神经网络的频谱检测算法,在低信噪比条件下,其算法性能优于传统的能量检测算法;Ghasemi A等人[14]通过深度时间卷积网络直接感知数据,结果表明,该方法比需要构造特征值的算法性能更优。
目前,许多学者将神经网络应用于频谱感知中,而对于卫星认知通信场景的研究却很少。主要由于卫星网络中具有较大通信时延,难以实时获取数据,无法对信道状态做出准确评估。针对处理时间序列问题,长短期记忆(Long Short-Term Memory,LSTM)网络有着独特的性能。LSTM网络将时间的概念融入到网络中,挖掘深层次特征,解决了循环神经网络(Recurrent Neural Network,RNN)梯度消失及长时依赖时问题,更好地处理时序数据。利用LSTM网络对时序数据进行预测[15],可较好地解决卫星信号的时延问题;另一方面,LSTM网络在处理低信噪比信号时,有着较好的分辨性能[16]。综上,LSTM网络适合应用于卫星认知通信场景中。
本文针对卫星认知通信网络特点,提出了一种基于LSTM网络的多门限值优化感知预测算法,从分析卫星业务开始,结合排队论对卫星网络中PU链路的信道状态进行建模,由SU接收端对感知到的卫星信号进行处理,经处理后的数据送入LSTM网络进行训练,选用SGDM算法更新梯度,对输出数据进行多门限值优化,最后与其他神经网络及未采用多门限值优化的LSTM网络作性能对比。仿真结果表明,在卫星信道条件下,本文提出的算法性能要优于其他网络算法性能。
2 卫星频谱感知模型建模
在卫星认知通信网络中,PU与SU共同使用通信卫星的信道资源。SU通过感知PU信道的“频谱空穴”,与PU共享卫星信道资源,以达到卫星频谱资源高效利用。本文采用的卫星认知通信网络模型如图1所示。

图1 卫星认知通信网络模型
Fig.1 Network model of satellite cognitive communication
假设PU与SU在同一卫星认知通信网络中,通信卫星为同步轨道(Geostationary Orbit,GEO)卫星,采用透明转发模式进行通信,多址方式为频分多址(Frequency Division Multiple Access,FDMA)。多个个体用户汇聚为一个PU,在卫星网络中进行通信。针对一条完整的PU通信链路,SU可以通过接收感知其链路的下行信道(卫星接收端到PU链路接收端)状态以判断该通信的上行信道(PU链路发送端到卫星接收端)状态,从而确定该通信链路是否被占用。
2.1 PU信道状态建模
假设多个个体用户汇聚为一个PU,在其分配的固定信道上进行通信。根据排队理论,本文采用M/M/1模型。模型中,第一个M表示个体用户的到达时间服从参数为λ的泊松分布,第二个M表示每个个体用户的服务时间服从参数为μ的负指数分布,1表示服务信道为单信道。其中,参数λ代表单位时间个体用户到达数,参数μ代表单位时间个体用户服务数。泊松分布和几何分布的表达式如式(1)、(2)所示。
(1)
P(Tserve≤t)=1-e-μt
(2)
PU信道状态模型如图2所示。

图2 PU信道状态示意图
Fig.2 Sketch map of PU channel status
在M/M/1模型中,信道的主要通信参数为通信强度ρ,其可以表示为:
(3)
在本文卫星认知通信场景中,对于参数μ一般是不变的,即个体用户的服务时长期望不变。可以通过改变参数λ来产生不同通信强度的PU信道状态,以此来对比不同通信强度下的算法性能。
2.2 SU感知数据建模
在传统的认知无线网络中,SU可实时感知PU的信道状态。而在卫星认知通信网络中,经过卫星通信时延后,SU端才能感知到当前时刻PU的信道状态,并且当SU利用PU信道的“频谱空穴”进行频谱接入,则还需要将SU发送到卫星端的时延考虑进去,具体场景如图3。
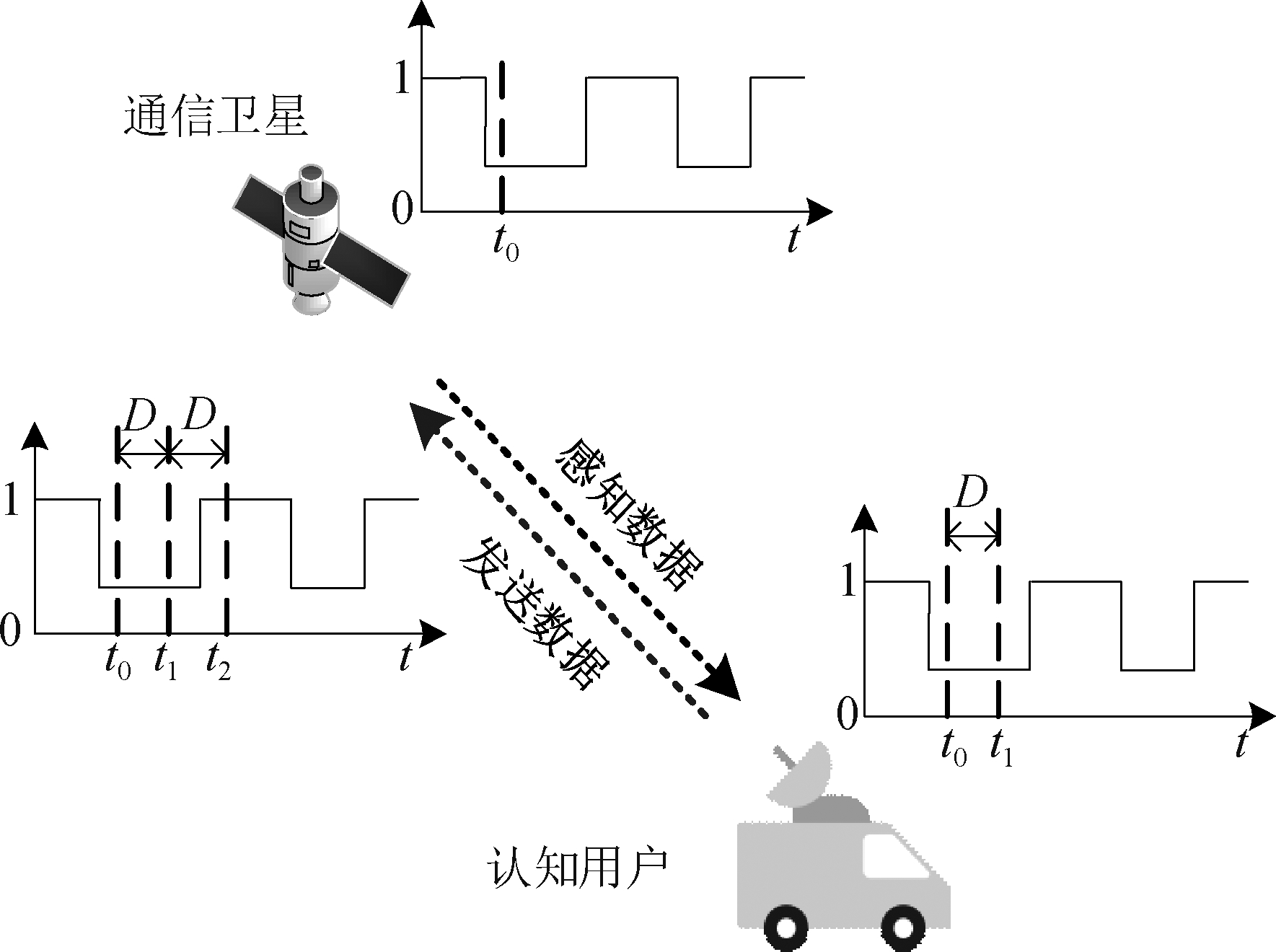
图3 SU频谱感知示意图
Fig.3 Sketch map of SU spectrum sensing
卫星通信时延定义为D,假设当前 PU下行链路的信道状态为t0时刻的信道状态,SU在t1时刻感知到t0时刻的PU信道状态,当SU检测到PU信道的“频谱空穴”而进行接入时,发送数据将会经过时延D在t2时刻到达卫星端,即SU要根据t0时刻的信道状态,来预测时延为2D后的PU信道状态。
根据卫星信道特性,设SU接收的信号功率为PR,EIRP为PU链路发送端的全向辐射功率,Gsat为卫星端增益,GR为SU接收端增益,则PR以dB形式可表示为:
PR(dBW)=EIRP+Gsat+GR-Lup-Ldowm
(4)
式中,Lup为PU链路发送端到卫星接收端的路径损耗,Ldowm为卫星发送端到SU接收端的路径损耗,Lup和Ldowm可表示为:
Lup=20lg(dup)+20lg(fup)+32.4
(5)
Ldowm=20lg(ddowm)+20lg(fdowm)+32.4
(6)
式中,dup为PU发送端到卫星端的距离,ddowm为SU到卫星端的距离,fup和fdowm分别为PU通信链路的出境中心频率和入境中心频率。对于SU接收端,其感知的数学模型可表示为:
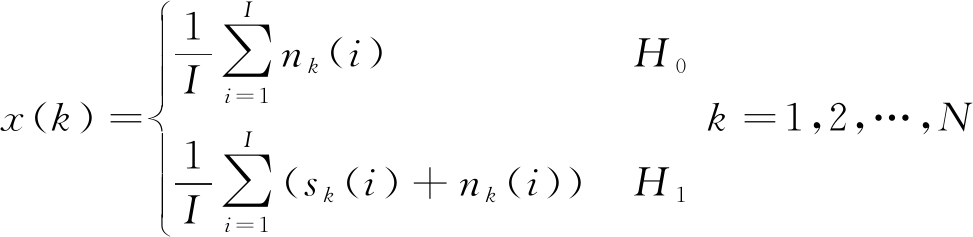
(7)
式中,x(k)为在感知时隙为k时,SU采用能量检测算法取得的统计量,采样点数I取10,采样频率为20 MHz,H0表示PU信道空闲的状态,H1表示PU信道占用的状态,sk为SU接收的PU卫星信号,nk为噪声信号,其功率表示为:
PN=KTB
(8)
式中,K为玻尔兹曼常数,数值为1.38×10-23 J/K,T为SU工作时的绝对温度,单位为K,B为SU的单信道接收带宽,单位为Hz,SU的接收信号的信噪比可表示为:
(9)
在实验中可通过改变EIRP值以调整SNR值,从而对比不同算法间的性能差异,本文采用卫星信道仿真参数如下表。
表1 卫星信道仿真参数
Tab.1 Simulation parameters of satellite channel

参数参数值卫星端增益/dB32SU接收增益/dB34出境中心频率/MHz14253入境中心频率/MHz12028PU链路发送端到卫星距离/km40000SU到卫星距离/km37000PU信道带宽/MHz10单跳卫星时延/ms250调制方式QPSK
对于SU的感知数据集X可表示为:
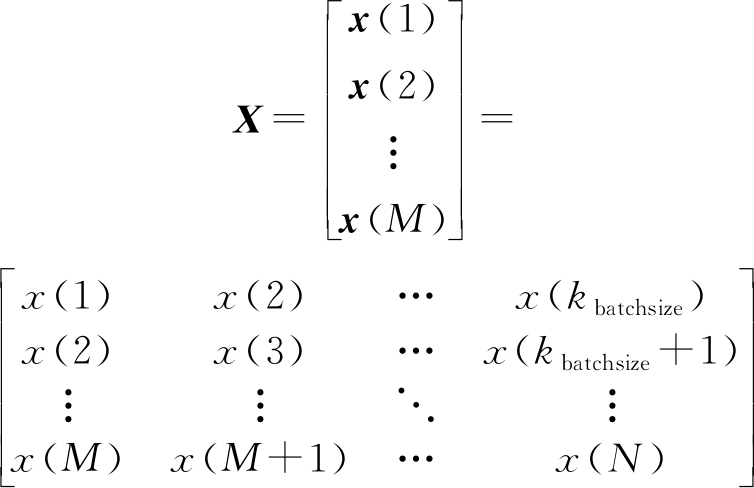
(10)
其中,kbatchsize为每次序列送入网络训练的分块长度,本文将x(k)分为M个长度为kbatchsize的数据块,再将X=[x(1), x(2),..., x(M)]T按9∶1分为训练集和测试集,与其对应的信道状态Y=[y(1), y(2),..., y(M)]T作为目标输出集,投入网络进行训练。
3 频谱预测感知算法
3.1 LSTM神经网络
传统的神经网络算法在处理时间序列时,不能很好地解决其延续性问题,即前一时间段的输入无法对后一时间端的结果造成影响。在20世纪80末,Fernando J. Pineda等人针对此类问题设计了一种处理时间序列数据的神经网络结构——循环神经网络(Recurrent Neural Network,RNN)[17],其具体结构如图4。
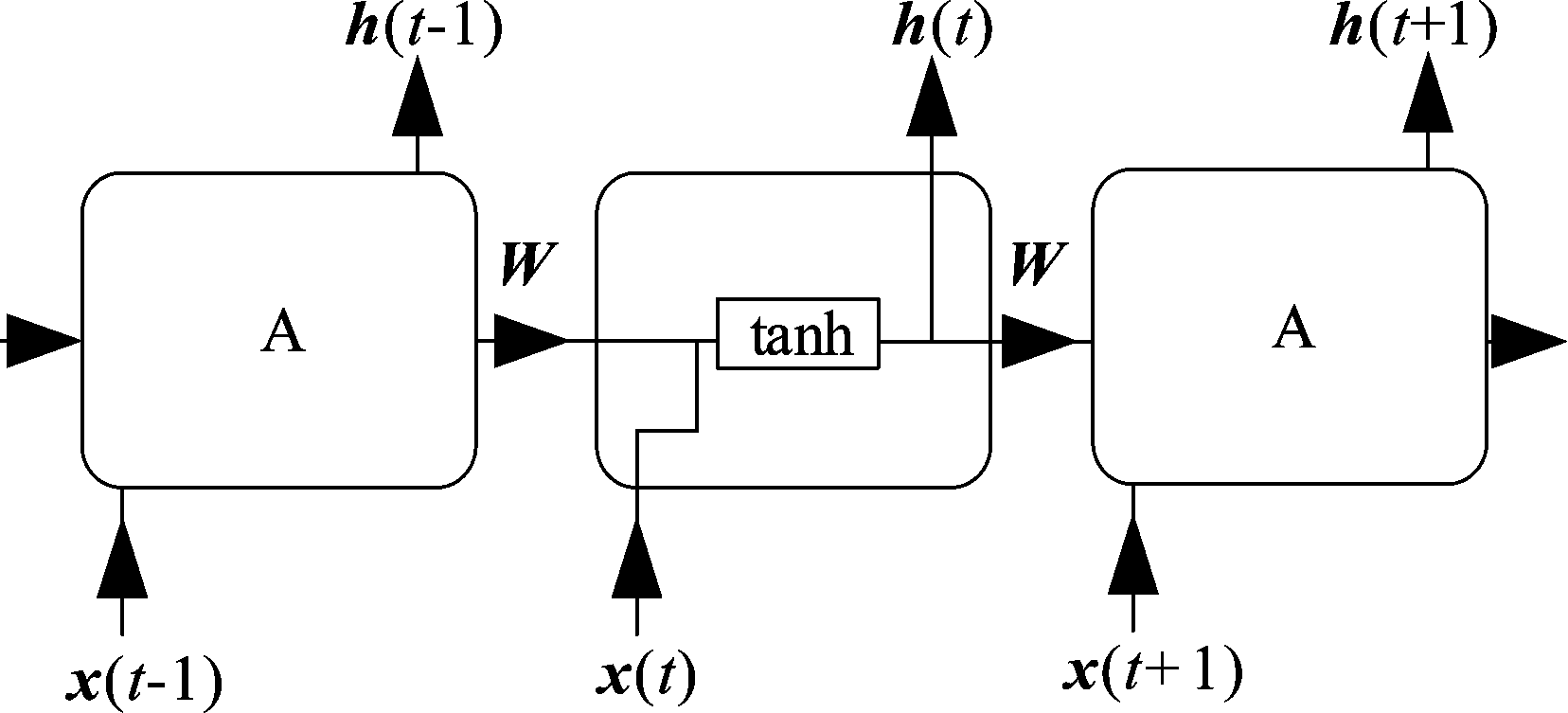
图4 循环神经网络示意图
Fig.4 Sketch map of RNN
当时刻为t时,其输出h(t)不仅输入x(t)有关,还与上一时刻输出h(t-1)有关。RNN的隐藏层单元A可以将上一时刻输出状态h(t-1)传输给下一时刻,由上一时刻状态h(t-1)和当前输入x(t)共同决定当前输出状态h(t),并且由于RNN的循环结构,使得每个时刻的状态信息都与之前所有时刻的状态信息有关,即RNN在处理数据上具有了延续性。然而,RNN有一个主要缺陷,即当输入数据与所求输出的时间跨度较大时,信息的时间相关度会降低,之前较长时间的信息无法对之后输出造成影响,造成历史信息的流失以导致判断不准确,产生长期依赖时的问题。
针对此问题,Hochreiter S在1997年提出了LSTM网络[18]。其在RNN结构的基础上,改变了神经网络的隐藏层单元,具体结构如图5所示。
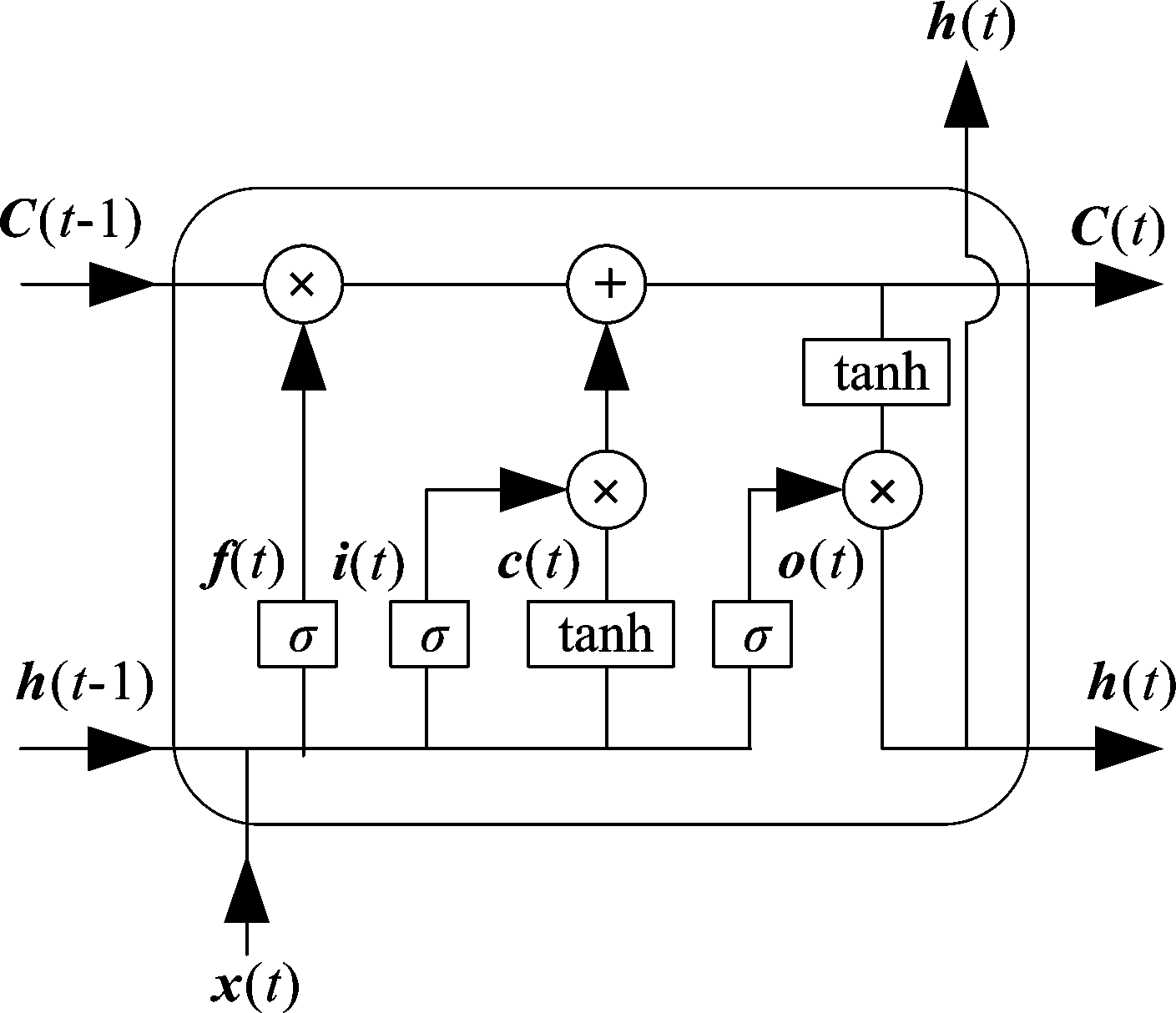
图5 LSTM隐藏层单元结构
Fig.5 The structure of LSTM hidden layer cell
LSTM网络在隐藏层单元增添了三个信息控制单元,以保留有用信息并去除无用信息,分别为输入门i(t)、遗忘门f(t)、输出门o(t),表达式如下:
i(t)=σ(Wix(t)x(t)+Wih(t)h(t-1)+bi(t))
(11)
f(t)=σ(Wfx(t)x(t)+Wfh(t)h(t-1)+bf(t))
(12)
o(t)=σ(Wox(t)x(t)+Woh(t)h(t-1)+bo(t))
(13)
式中,W(t)为权重系数矩阵(i(t)的权重系数矩阵为Wix(t),依次同理),b(t)为偏置矩阵(i(t)的偏置矩阵为bi(t),依次同理),σ为sigmoid函数,tanh为双曲正切函数,而状态信息C(t)、隐藏层输出h(t)和网络输出y(t)可表达为:
C(t)=f(t)C(t-1)+i(t)tanh(Wcx(t)x(t)+ Wch(t)h(t-1)+bc(t))
(14)
h(t)=o(t)tanh(C(t))
(15)
y(t)=Wyh(t)h(t)+by(t)
(16)
LSTM网络通过控制门从而控制历史信息流向,使得网络具有利用长时间历史数据的能力,解决了RNN的长期依赖时问题。本文采用LSTM网络模型,根据当前SU感知数据统计量及历史数据统计量预测下一时刻PU信道状态,如图6所示。
图6 预测PU信道状态示意图
Fig.6 Sketch map of predicted PU channel status
本文采用基于时间的反向传播算法(Back Propagation Trough Time,BPTT)训练LSTM网络模型,其原理与反向传播(Back Propagation,BP)算法相同,LSTM网络训练流程如下表。
表2 LSTM网络训练算法流程
Tab.2 Algorithm flow of LSTM neural network training

算法1 LSTM网络训练算法流程1.输入训练集数据,根据式(11)~(16)计算LSTM网络的输出参数。2.根据输出数据集和目标输出集,反向计算LSTM网络中各参数的误差项。3.根据各参数相应的误差项,计算参数误差。4.利用合适的梯度更新算法更新梯度。5.当迭代次数达到最大值或误差达到最小误差时,停止网络更新,否则转向步骤1。6.输入测试集数据,得到频谱感知预测结果。
3.2 SGDM更新算法
对于神经网络更新,随机梯度下降算法(Stochastic Gradient Descent,SGD)是较为基本的梯度更新算法。其基本思想是利用小批量数据更新参数,以权重系数矩阵W(t)为例,更新方式如下:
W(t)=W(t-1)+ΔW(t)
(17)
ΔW(t)=-η▽E(W(t))
(18)
式中,ΔW(t)为t时刻更新W的梯度算子,即梯度更新部分,η为神经网络的学习率,▽E(W(t))为t时刻W损失函数的一阶梯度,记为gW(t)。
SGD算法的主要缺陷为更新方向不稳定,容易陷入局部最优点。1999年,Qian N将动量(Momentum)的概念引入到SGD算法中,即带动量的随机梯度下降算法(Stochastic Gradient Descent with Momentum,SGDM)[19]。其原理为在保留原先梯度更新方向的基础上,加入当前数据损失函数的一阶梯度进行调整,表达式为:
ΔW(t)=βΔW(t-1)-ηgW(t)
(19)
SGDM算法在式(18)的基础上引入了动量项,其中β为动量因子,取值在0至1之间。当参数在局部最优点附近震荡时,gW趋向于0,动量项就会增大,使其跳出局部最优点。简单理解就是使更新参数获得“惯性”,在坡度大的地方,参数改变快,反之,则参数改变小。当PU信道状态发生变化时,SGDM算法可使网络参数更快地变化,以确保预测结果的准确性。
3.3 多门限优化算法
在PU信道状态变化的情况下,SGDM算法可以使LSTM网络做出快速的调整,以避免误判。但尽管SGDM算法可针对数据作出快速调整,其还有一个累计动量过程。设LSTM网络输出的感知预测序列的取值范围为(0,ymax],其中ymax为网络输出序列的最大值,通常不超过2,PU信道状态为0的预测平均值为ymeanOFF,状态为0的预测平均值为ymeanON,判决门限可表示为:
(20)
在本文场景中,单门限判决有两个缺点:
①对于低信噪比信道,假设当前PU信道状态为1,输出序列值有几率会低于νth,判决为0,造成误判,即输出结果产生“毛刺”。
②假设PU信道状态由0变为1,在爬升初始阶段,由于“惯性”造成网络参数改变量较少,会使输出序列值不足νth,使得结果判决为0,影响感知预测性能。
针对单门限判决的不足,有学者提出了双门限判决算法,算法流程如表3。
表3 双门限判决算法
Tab.3 Algorithm of dual-threshold decision

算法2 双门限判决算法输入:ν0,ν1,y,t,tmax输出:yorg1. 数据初始化,令y(0)=0。2. 输入y(t),若y(t)>ν1,则yorg(t)=1;若y(t)<ν0,则yorg(t)=0,转向步骤4,若都不符合转向步骤3。3. 若yorg(t-1)=1,则yorg(t)=1;若yorg(t-1)=0,则yorg(t)=0。4. 若t ≤ tmax,则t=t+1,转向步骤2,否则,输出yorg。
上表中,ν0和ν1分别为当输入值被判决为0和1的门限值,y为神经网络输出序列,yorg为判决后输出序列。双门限判决算法可较好地解决“毛刺”问题,而对于“惯性”问题,其步骤3会使输出序列后滞,以致感知预测性能下降。本文在传统的双门限判决算法基础上,针对“惯性”问题,提出了一种针对神经网络感知预测条件下的多门限优化算法,其流程如表4。
表4 优化的多门限判决算法
Tab.4 Optimization algorithm of multi-threshold decision

算法3 优化的多门限判决算法输入:ν0,ν1,ν10,ν01,y,t,tmax输出:yopt1. 数据初始化,令y(0)=0。2. 输入y(t),若y(t)>ν1,则yopt(t)=1;若y(t)<ν1,则yopt(t)=0,转向步骤8,若都不符合转向步骤3。3. 若yopt(t-1)=1,转向步骤4;若yopt(t-1)=0,转向步骤6。4. 若y(t)>ν10,则yopt(t)=1,转向步骤8;反之,则转向步骤5。5. 若y(t)>y(t-1),则yopt(t)=1;反之,则yopt(t)=0,转向步骤8。6. 若y(t)<ν01,则yopt(t)=0,转向步骤8;反之,则转向步骤7。7. 若y(t)
表中,ν10和ν01为次级门限,其作用为快速检测数据变化过程,几种算法工作原理如图7。
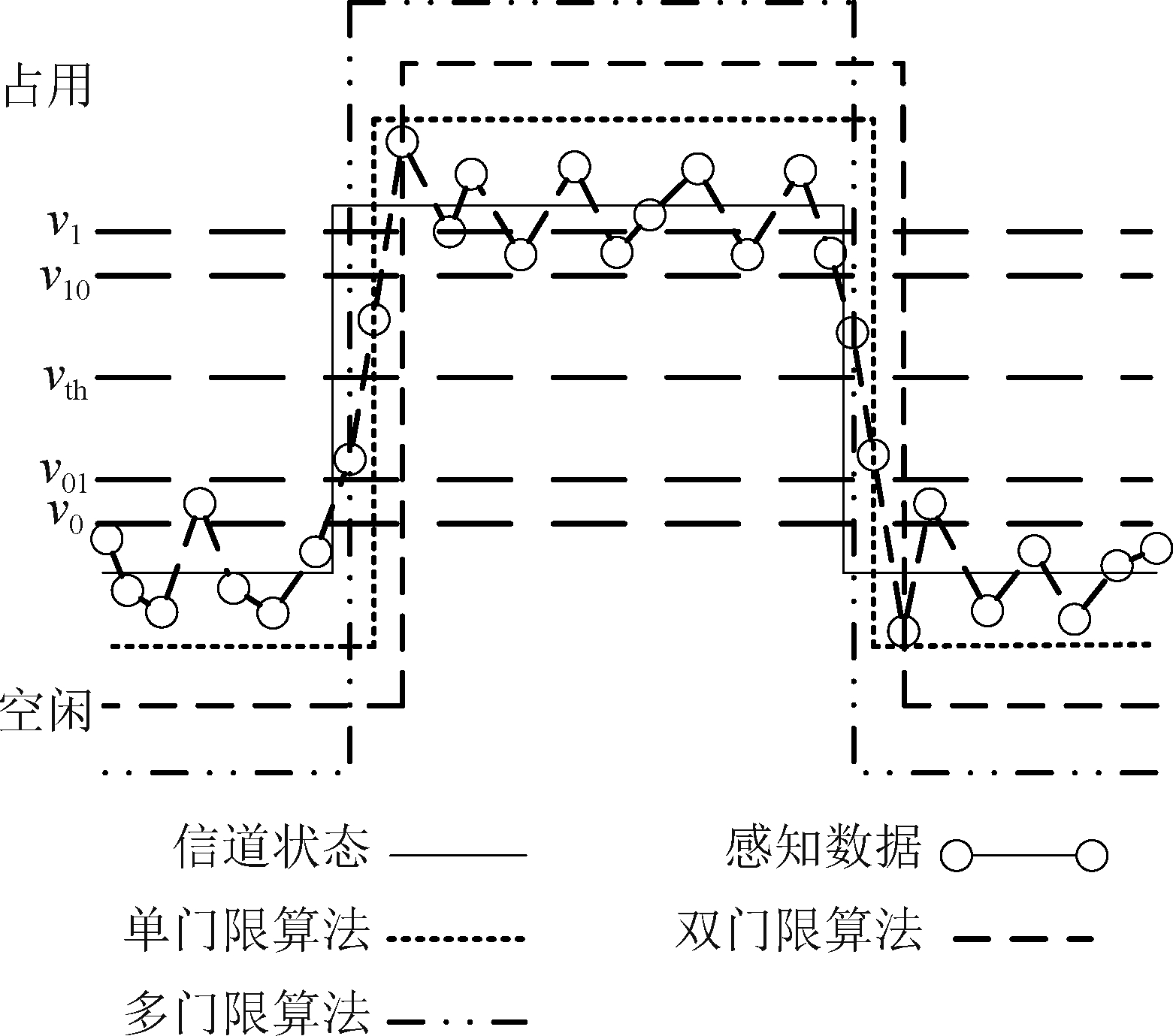
图7 算法性能对比示意图 Fig.7 Sketch map of algorithm performance comparison
通过后期实验多次矫正,ν0、ν1、ν01和ν10分别设置为0.2、0.8、0.3和0.7。本文提出的多门限算法在单独解决“毛刺”问题上能力有限,但在认知通信场景中及时发现PU的存在更为重要,并且在实验期间我们发现,LSTM网络输出的预测结果区分较为明显,很大程度上解决了“毛刺”问题,形成算法性能互补。
4 实验结果与分析
本文主要目的为在卫星认知通信场景下,SU感知PU信道信息,通过选取不同类型的神经网络进行性能对比,并对改变参数时对算法性能造成的影响作出分析评价。
4.1 实验数据集
本文实验数据根据第2节介绍的卫星感知信道模型,通过Matlab实验平台产生,具体参数参考表1,根据卫星通信时延,将感知间隔设置为500 ms,将SU感知数据统计量分长度为kbatchsize(本文取128)的数据块,再按照9∶1的比例分为训练集和测试集,投入网络进行训练。仿真模型可通过改变参数λ产生不同ρ的PU信道状态,以此来对比不同通信强度下各网络的感知性能,图8为六分钟内ρ为0.5时经归一化处理的SU感知数据统计量。
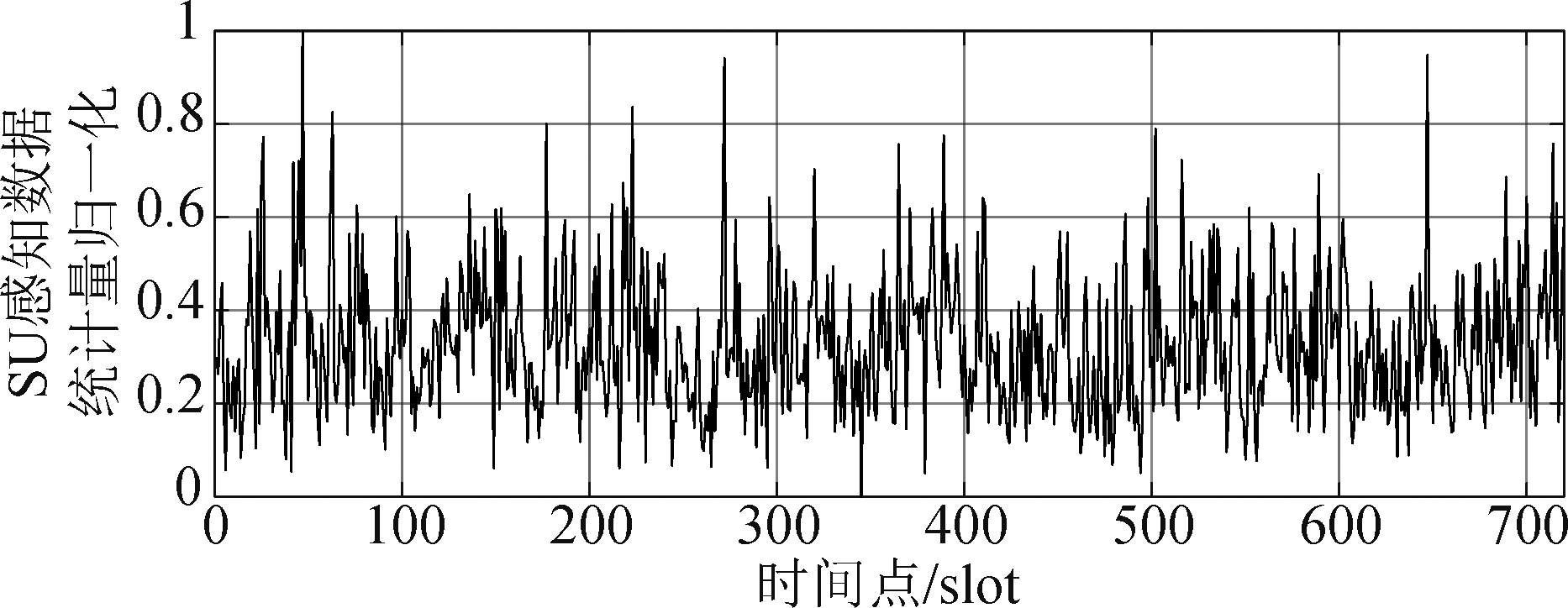
图8 归一化SU感知数据统计量
Fig.8 Normalization of SU sensing data statistics
4.2 网络模型
本文采用在时序预测方面应用较多的BP网络,非线性自回归(Nonlinear Autoregression,NAR)网络和LSTM网络,并在LSTM网络条件下将目前应用较广的适应性动量估计(Adaptive Moment Estimation,ADAM)更新算法与本文算法作对比。
4.2.1 反向传播网络
BP网络是一种经典的神经网络,在解决频谱预测感知问题上性能较为突出,其网络模型原理简单,易于训练,被国内外学者广泛研究。本文BP网络具体参数参考文献[9]。
4.2.2 非线性自回归网络
NAR网络是一种动态的神经网络,适合处理时序数据,因其网络在输入层与隐藏层间有延时结构,具有很强的非线性学习能力,本文NAR网络为三层结构,输入层神经元设为128,隐藏层神经元设为64(设置过多训练时间较长),输出层神经元设为1,时延环节设为10∶1。
4.2.3 基于ADAM算法的长短期记忆网络
ADAM算法是一种高效的梯度更新算法,其融合自适应步长(Adaptive Gradient,AdaGrad)和梯度平方根(Root Mean Square Prop,RMSProp)算法的主要思想[20]。ADAM算法会自动调节学习率,并且有较高的计算效率,可应用于各种网络参数更新中。在本文中,基于ADAM算法的LSTM网络为三层结构,其中隐藏层神经元设为128,其余与NAR网络相同。
4.3 性能标准
本文根据改变通信强度、网络迭代次数、接收信噪比对不同类型网络的性能作对比分析;本文采用预测准确率Ap(Prediction accuracy)、误警概率Pfa(False Alarm Probability)和漏检概率Pla(Loss Alarm Probability)作为不同网络在卫星认知通信场景下预测感知性能的评价标准。
4.4 实验结果4.4.1 通信强度对频谱感知算法的性能影响
为表述各网络在不同通信强度下的性能,本文产生通信强度0.1至0.9的9条信道状态信息(间隔为0.1),通过训练计算网络性能指标,其对比如图9,对于图(a),LSTM网络性能较为平稳,BP网络的预测准确率相对较低,而NAR网络的预测曲线波动较大;对于图(b),LSTM网络同样处于平稳的水平,BP网络的误警概率曲线波动较大;对于图(c),各网络的漏检概率都处于上升趋势,这是因为随着ρ的增加,信道的空闲状态逐渐减少,只要出现感知出现错误,漏检概率就会有较大幅度上升,而在ρ较高时,相较于其他算法,本文算法的漏检概率依然可以维持在相对稳定的水平。

图9 不同通信强度下的各神经网络性能对比
Fig.9 Performance comparison of ANN under different ρ
由图9可知,LSTM网络较BP网络和NAR网络性能更优,这是因为BP网络和NAR网络虽然有着较好的预测性能,但由于卫星通信时延决定的感知间隔较大,致使数据时间关联性降低,网络预测性能下降。而对于LSTM网络,其性能较为稳定,这是由于LSTM网络更适合处理时序信息。与ADAM算法相比,SGDM算法在卫星信道条件下性能有所提升,但提升较小。相对于其他算法,本文算法性能提升较为明显。
4.4.2 迭代次数对频谱感知算法的性能影响
为了表述迭代次数对网络性能影响,选取迭代次数5至100(间隔为5)进行性能对比,由于各网络在Ap、Pfa和Pla上变化类似,本文选取只选取Ap作性能对比,对比图如图10。

图10 不同迭代次数下的各神经网络性能对比
Fig.10 Performance comparison of ANN under different Iteration
由图10可知,相较其他两种网络,LSTM网络可更快收敛。在LSTM网络条件下,当迭代次数为25时,本文算法和SGDM算法的Ap就趋于平稳,而ADAM算法在迭代次数为85时才收敛,这是由于SGDM算法具有“惯性”,使其在网络更新上有着更大的跨度,以便快速找到全局最优点。
4.4.3 接收信噪比对频谱感知算法的性能影响
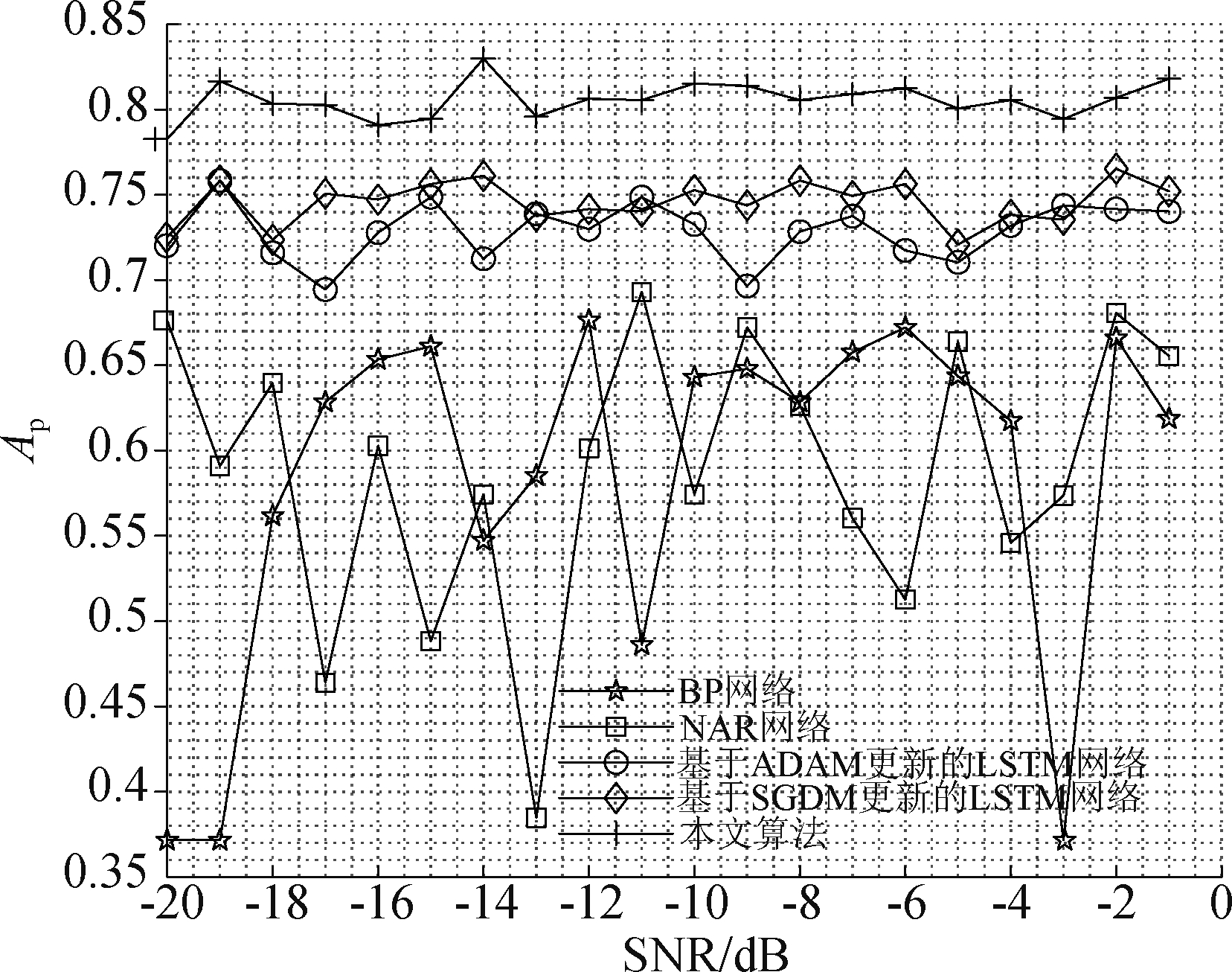
图11 不同接收信噪比下的各神经网络性能对比
Fig.11 Performance comparison of ANN under different SNR
在卫星认知通信场景中,通信信道参数的变化在大多数情况可以等效为SU接收功率的增益或衰减,最终体现为SU接收信噪比的增减。本文针对低接收信噪比情况,选取SNR范围为-20 dB~0 dB(间隔1 dB),图11为迭代次数为85,通信强度为0.5时各网络在不同接收信噪比情况下的对比图,在图中,我们发现所有网络的感知性能都有所下降,相比于BP网络和NAR网络,LSTM网络的预测准确率保持在0.75至0.7之间,而本文算法的预测准确率稳定在0.8左右,有着较好的表现。
4.4.4 网络结构对离线训练时长的影响
本文利用仿真模型模拟两小时内的SU感知统计量数据,产生14400条SU感知统计量数据,实验采用GPU训练,型号为NVIDIA GeForce GTX 1050。表5为不同网络的离线训练时长对比,由表可知,相对于BP网络和NAR网络,LSTM网络的离线训练时长较长,这是由于LSTM网络的隐藏层单元结构较为复杂,需要较长时间来计算更新,以计算复杂度来换取性能优势。
表5 不同网络的离线训练时长对比
Tab.5 Comparison of off-line training time with different neural networks
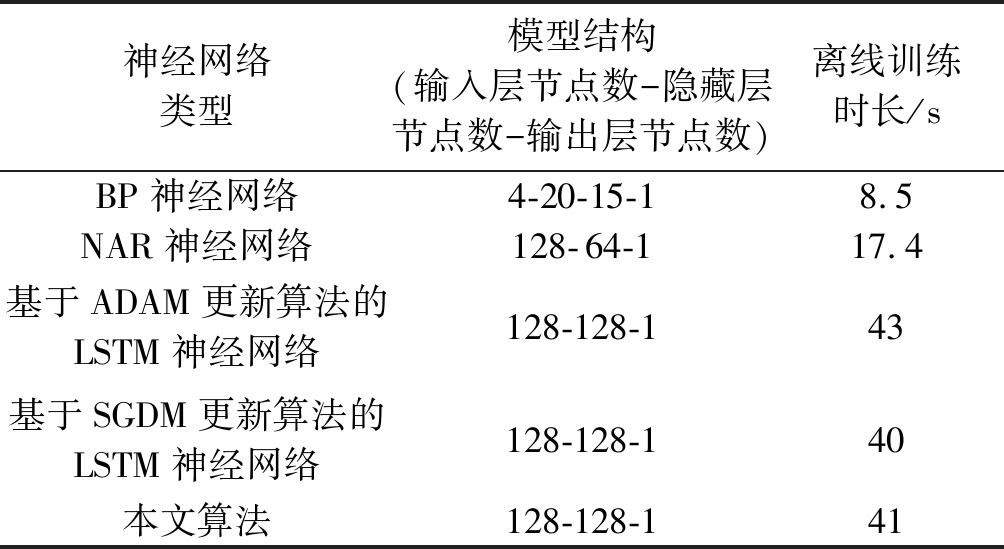
神经网络类型模型结构(输入层节点数-隐藏层节点数-输出层节点数)离线训练时长/sBP神经网络4-20-15-18.5NAR神经网络128-64-117.4基于ADAM更新算法的LSTM神经网络128-128-143基于SGDM更新算法的LSTM神经网络128-128-140本文算法128-128-141
5 结论
文中针对卫星认知通信场景中频谱感知所存在的问题,通过卫星认知通信场景进行建模仿真,采用LSTM网络对接收数据进行预测感知处理,根据卫星认知通信场景频谱感知特点,采用SGDM算法更新网络,并采用多门限算法对感知结果进行优化。实验结果表明:在相同条件下,本文算法较其他对比算法有着更好的预测感知性能。当面对低网络迭代次数和接收信噪比时,本文算法性能依然可以维持在较高水平。
[1] Lagunas E, Sharma S K, Maleki S, et al. Resource Allocation for Cognitive Satellite Communications With Incumbent Terrestrial Networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2015, 1(3): 305-317.
[2] Maleki S, Chatzinotas S, Evans B, et al. Cognitive spectrum utilization in Ka band multibeam satellite communications[J]. IEEE Communications Magazine, 2015, 3(53): 24-29.
[3] Liang T, An K, Shi S. Statistical Modeling-Based Deployment Issue in Cognitive Satellite Terrestrial Networks[J]. IEEE Wireless Communications Letters, 2018, 2(7): 202-205.
[4] Yucek T, Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 116-130.
[5] Liang Y C, Zeng Y, Peh E C Y, et al. Sensing-Throughput Tradeoff for Cognitive Radio Networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(4): 1326-1337.
[6] Shinde K V, Deshmukh M M. Energy detection: Efficient utilization of electromagnetic radio spectrum in CR network[C]∥2015 International Conference on Pervasive Computing (ICPC), Pune, India: IEEE, 2015: 1- 4.
[7] Gupta I, Har A, Sahu O P. Hardware Implementation of Energy Detection Scheme in Cognitive Radio Networks[C]∥2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, Uttar Pradesh, India: IEEE, 2018: 575-577.
[8] Lee G F, Barbe K, Vanmoer W, et al. Cognitive radios: discriminate analysis finds the free space[J]. IEEE Transactionson Communication, 2013, 32(4): 2012-2019.
[9] Singh R, Kansal S. Performance evaluation of neural network based spectrum sensing in cognitive radio[C]∥2016 International Conference on Internet of Things and Applications (IOTA), Pune, India: IEEE, 2016: 368-372.
[10]胡翩翩, 曾碧卿. 基于HS-BP神经网络的认知无线电频谱预测技术[J]. 计算机工程, 2017, 43(7): 146-150, 155.
Hu Pianpian, Zeng Biqing. Cognitive Radio Spectrum Prediction Technology Based on HS-BP Neural Network[J]. Computer Engineering, 2017, 43(7): 146-150, 155.(in Chinese)
[11]Zhang S, Hu J, Bao Z, et al. Prediction of spectrum based on improved rbf neural network in cognitive radio[C]∥International Conference on Wireless Information Networks & Systems, Reykjavik, Iceland: IEEE, 2013: 1-5.
[12]Hou X, Sobabe G C, Zhang C, et al. Spectrum prediction based on fuzzy system and wavelet network[C]∥International Congress on Image & Signal Processing, Shanghai, China: IEEE, 2017: 1- 6.
[13]Lee G, Lee Y, Koo I. Convolution Neural Network-Based Spectrum Sensing for Cognitive Radio Systems Using USRP with GNU Radio[C]∥2018 Tenth International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic: IEEE, 2018: 862- 864.
[14]Ghasemi A, Parekh C, Guinand P. Spectrum Sensing for Modulated Radio Signals Using Deep Temporal Convolutional Networks[C]∥2019 IEEE Wireless Communications and Networking Conference Workshop (WCNCW), Marrakech, Morocco: IEEE, 2019: 1-5.
[15]Ling Y, Jin C, Guoru D, et al. Spectrum Prediction Based on Taguchi Method in Deep Learning with Long Short-Term Memory[J]. IEEE Access, 2018, 6(1): 45923- 45933.
[16]Balwani N, Patel D K, Soni B, et al. Long Short-Term Memory based Spectrum Sensing Scheme for Cognitive Radio[C]∥2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy: IEEE, 2019: 1- 6.
[17]Pineda F J. Generalization of Back-Propagation to Recurrent Neural Networks[J]. Physical Review Letters, 1987, 59(19): 602- 611.
[18]Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[19]Qian N. On the momentum term in gradient descent learning algorithms[J]. Neural Networks the Official Journal of the International Neural Network Society, 1999, 12(1): 145.
[20]Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[C]∥2015 International Conference on Learning Representations (ICLR), San Diego, America: Ithaca, 2015: 69- 80.



