1 引言
随着物联网及移动互联网的蓬勃发展,5G/B5G无线通信网络面临着爆炸性的流量增长和成倍的设备接入问题。这使得传统异构网络技术的利用从简单的语音和数据转变为资源匮乏的多媒体信息娱乐应用。在这些高数据需求的驱动下,5G/B5G网络必须以更灵活的方式利用频谱资源[1]。
为满足日益增长的高数据需求,现有的蜂窝网络向小区密集化和以用户为中心部署的小基站(Small Base Station,SBS)演进。在密集部署的小小区网络中,传统的宏基站被大规模部署的低功耗SBS所覆盖,这使得更多的用户设备(User Equipment,UE)可以被服务,并使UE更接近于基站(Base Station,BS)。SBS共同形成小小区,并与传统的高功率宏基站共存,从而产生了异构网络(Heterogeneous Networks,HetNets)[2]。小小区的密集化部署在提高网络性能的同时也带来了严重的系统干扰管理问题[3- 4]。针对这一问题,文献[5-9]研究了部分频率复用(Fractional Frequency Reuse,FFR)技术。在FFR中,小区中心UE与小区边缘UE不共享任何频谱,可以减少小区中心和小区边缘UE的干扰。文献[10-12]研究了软频率复用(Soft Frequency Reuse,SFR)技术。与FFR不同,SFR则允许在每个小区中复用一个完整的频带。虽然,上述研究表明FFR和SFR优于传统网络。但是,在未来5G/B5G HetNets中,由于UE的随机性,网络在形状和大小上具有不规则性和随机性,导致难以实现符合FFR和SFR要求的子信道分配。为解决这一问题, 文献[13]提出了一种共享频谱分配(Shared Spectrum Allocation, SSA)方法,该方法由无线电频谱的正交共享和共信道共享方案组成。文献[14]通过对比分析验证了SSA方法可以有效提高频谱效率和网络容量。受上述文献的启示,本文针对三层异构网络模型,提出了一种改进的SSA方法。
在多层5G/B5G HetNets中,由于BS部署的不规则性,随机几何空间成为异构网络精确建模和分析的主要工具。在这种方法中,大规模无线网络被抽象为方便的点过程。文献[5-12]利用随机几何模型对FFR和SFR蜂窝网络的性能进行了研究。文献[14]利用随机几何空间,导出了基于SSA的HetNets覆盖性能。然而,这些工作都只是将每一层中BS和UE位置建模为独立的泊松点过程(Poisson Point Process,PPP)。在基于5G/B5G HetNets的热点区域中,BS和UE之间的独立假设不是非常的准确,它们之间存在相关性。此时,则需要部署小小区来为UE簇提供服务。文献[15]利用泊松簇过程(Poisson Cluster Process,PCP),研究了用户分类的异构网络性能。利用了UE簇和BS之间的相关性。然而,在现实场景中,热点区域业务的密集化,导致数据速率在短时间内激增,造成簇中心BS过载。此时需要以簇中心部署模式为UE部署更多低功耗的FBS。这些簇中心FBS,可以为过载的中心BS提供流量分流。实际上,对于高密集HetNets,一个通用的模型是从热点中抽象出簇中心并建模为PPP。UE和所有SBS均匀分布在热点中心周围,并建模为PCP。然而,在基于SSA干扰管理的异构网络中这种建模是不可实现的。在SSA中,为进行干扰管理,将UE和FBS分为小区中心和小区边缘两类,导致小区中心和小区边缘用户的位置空间分离。对于活动节点的位置呈现空间分离的场景,单独的PCP和PPP模型不可实现。在这种情况下,更合适的模型是泊松洞过程(Poisson Hole Process,PHP)。如文献[16-18]所述,PHP是通过从PPP基线执行洞而形成的,其中洞的中心假定遵循独立的PPP。PPP边界线基线剩余点形成一个PHP。
综上所述,本文构建了一个由MBS、PBS和FBS组成的三层异构网络模型。利用PPP、PCP和PHP方法,将MBS和PBS位置建模为独立的PPP,将簇中心和簇边缘FBS和UE位置建模为PCP和PHP。为解决干扰问题,提出了改进的SSA方法,基于用户簇的分类为SSA的实现提供了可能性。在SSA中,总可用带宽被划分为两个正交子带,分别通过SSA中的正交共享分配给簇中心毫微微用户(Femto User Equipment, FUE)和簇边缘FUE。同时,为了提高频谱效率,采用共信道共享方法,两个子带分别由微微用户(Pico User Equipment, PUE)和宏用户(Macro User Equipment, MUE)共享。通过PHP和PCP方法,推导出了簇中心和簇边缘FBS的干扰统计特性,考虑了有序FBS和无序FBS两种情况,计算了FUE下行链路覆盖概率,对比分析了网络参数对覆盖概率的影响。
2 系统模型及假设
2.1 系统模型
如图1所示,基于用户簇分布的三层异构网络由宏小区层(M层, microcell tier),微微小区层(P层, picocell tier)和毫微微小区(F层, femtocell tier)层构成。其中,M层由MBS组成、P层由PBS组成,F层由FBS组成。每一层具有不同的发射功率、覆盖范围和空间密度。一般情况下,同一层中的BS具有相同的发射功率。PM、PP和PF分别表示MBS、PBS和FBS的发射功率,且遵循功率约束PM>PP>PF。MBS和PBS密集部署在MBS的覆盖范围之内,减轻MBS负载。MBS配备有NM个大规模多输入多输出(Multiple Input Multiple Output,MIMO)发射天线,可与SM个用户同时通信。PBS配备有NP个传统的MIMO发射天线,可与SP个用户同时通信。而FBS和UE均配备单天线,每层的每一个BS至少级联一个UE。MBS和PBS的位置建模为独立PPP ΦM和ΦP,密度分别是λM和λP。在5G/B5G HetNets中为解决热点区域盲点覆盖以及MBS负载过重问题,密集化部署PBS和FBS成为重要解决方法。由于FBS的密集部署,导致PBS的位置与UE和FBS之间存在相关性。因此,对于簇边缘位置的点采用PHP 辅助建模更符合实际。将PBS和UE位置建模为托马斯簇过程(Thomas Cluster Process,TCP) ΘF和ΘU,密度分别是λF和λU。ΘF父点过程服从ΦP,即点过程ΘF是由分散在父点过程ΦP周围的簇成员(FBS)按照方差为
的对称正态分布形成的[19-21]。每个簇中的平均点数为
为描述UE和PBS位置的相关性,UE根据平均数为
的TCP独立地散布在父点过程ΦP周围。同时,为提高小区边缘UE的性能,采用PHP对簇边缘的点进行建模。给定父点过程ΦP中PBS的覆盖半径为R2,在PBS的覆盖区域内的点ΘF称为簇中心FBS被建模为 
余下的FBS点称为簇边缘FBS建模为PHP 
在PBS的覆盖区域内的点ΘU称为簇中心UE被建模为 
剩余的UE点称为簇边缘UE建模为PHP 
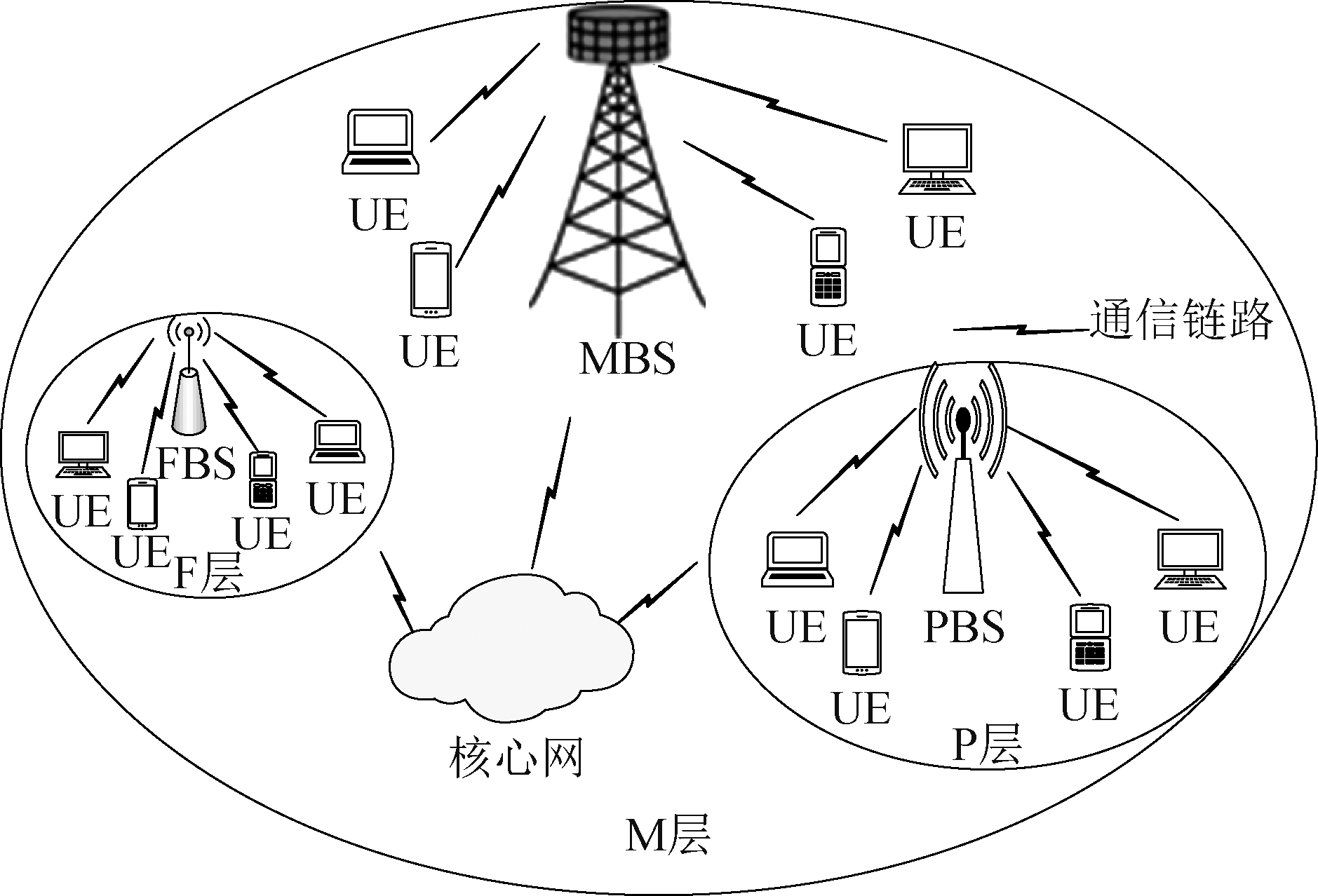
图1 三层异构网络系统模型
Fig.1 Three-tier heterogeneous network system model
假设忽略簇和洞的重叠影响,随机选择簇中任一用户为目标UE,该簇称代表簇。服务于目标UE的BS称为标记基站。根据著名的Slivnyak-Moche定理,在Borel空间上,当且仅当Palm分布几乎与原分布定理一致时,点的过程是PPP。因此,对以xP0∈ΦP为代表簇中位于原点的目标UE进行分析。由于MBS的位置被建模为ΦM,则目标UE到最近MBS的距离表示为xM,xM的PDF由f‖xM‖(x)=2πλMxexp(-πλMx2)给出,其中λM表示MBS的密度。目标UE到簇中心PBS的距离表示为xP,xP的PDF由
给出,其中σ2表示围绕簇中心的散射距离。
由于簇中FBS的数量是固定的,本文分别考虑了有序FBS和无序FBS两种情况。所谓有序FBS是指簇中FBS按照一定规律有序分布,此时,允许目标UE访问代表簇中最近的FBS。而无序FBS是指簇中FBS的分布是随机的,同时允许目标UE在代表簇中随机选择FBS。将目标UE到代表簇中FBS的距离记为xF。有序FBS情况下,距离
由离目标UE最近的FBS的距离来表示,
由
给出。此方法下产生的路径损耗相对较小。无序FBS情况下,允许目标UE在簇中随机选择访问FBS,则目标UE到FBS的距离表示为
由
给出。此时每个UE接入FBS的机会均等,网络不需要额外的瞬时信道状态信息。为方便描述,后续
和
的上标索引统一删除,用xF表示UE到FBSs的距离。
2.2 共享频谱接入
为限制严重的干扰,本文采用了SSA干扰管理策略,频谱分配如图2所示。根据带宽分配因子ξ将可用总带宽W划分为两个正交子带W1和W2,即W1=ξW、W2=(1-ξ)W。假设子带W1分配给为簇中心UE提供服务的PBS,子带W2分配给为簇边缘UE提供服务的MBS。由于采用了正交频谱共享,有效地抑制了MBS与PBS之间的干扰。除正交频谱共享外,还使用了共信道频谱共享。簇中心FBS与MBS共享子带W2,簇边缘FBS与PBS共享子带W1。显而易见,由于PBS(MBS)和FBS之间的反向频谱分配,所考虑的共信道共享方案能够有效抑制层间干扰以及簇内FUEs和PUEs之间的干扰。此外,簇中心和簇边缘FBS采用正交频谱,从而抑制了同层干扰。
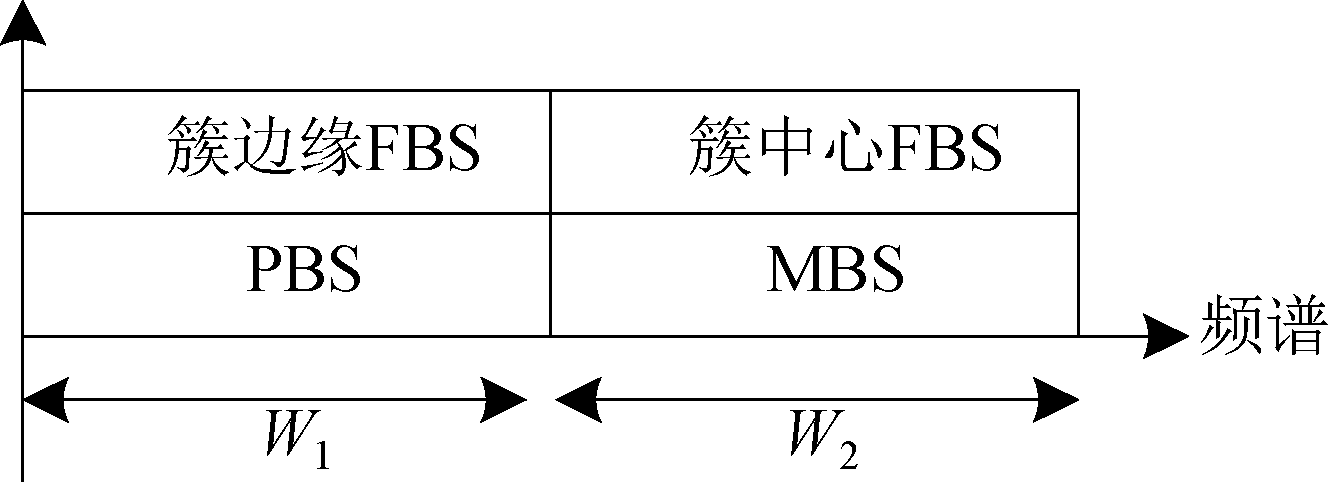
图2 频谱分配策略
Fig.2 Spectrum allocation scheme
3 FBS网络干扰统计描述
根据上述三层异构网络模型,给出目标UE干扰的拉普拉斯变换。现有研究大多基于两层网络模型给出M层和P层的干扰统计(如文献[13-15]),很少去考虑三层模型下,部署及性能接近于UE的F层干扰特性。故此本节主要研究F层网络的干扰统计特性。考虑到信号的传播损耗,仅分析实际在目标UE处有贡献的主导干扰。根据目标UE在簇中位置,给出簇中心FUE和簇边缘FUE两类干扰统计描述。
3.1 簇中心FUE干扰统计描述
首先, 考虑目标UE与来自ΘF的FBS级联的情况。ΘF中的FBS在PBS的覆盖区域内的点建模为
而其余点建模为
从图2可以看出,由于簇中心FBS和MBS共享子带W2,因此,FBS级联的簇中心UE ΦCFU到
的目标簇中心FUE的干扰公式如下:
(1)
其中,
是目标簇中心FUE接收到的簇中心FBS的干扰,
是来自MBS的干扰。考虑到目标UE位于PBS的覆盖范围内,假设FBSs的覆盖半径为R3,则可能的簇中心位于
区域。因此,目标簇中心FUE与其服务FBS之间的级联距离为
则目标簇中心FUE受到位于
内所有FBS的干扰。因此,式(1)簇中心干扰写为:
(2)
目标簇中心FUE接收到MBS的干扰为:
(3)
其中,gxm是遵循伽马分布的小尺度衰落干扰信道功率增益。得命题1,其证明见附录A。
命题1 目标簇中心FUE受到总干扰
的拉氏变换写为
式中
计算为:
(4)
为:
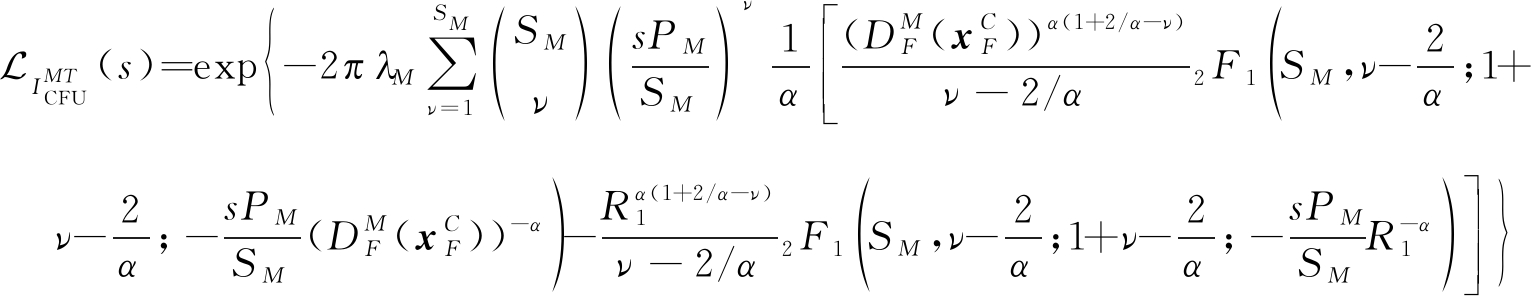
(5)
其中,
级联距离由有序FBS情况下
和无序FBS情况下
给出。
3.2 簇边缘FUE干扰统计描述
当FBS位于簇外时,簇边缘FBS与所有PBS共享子带W1。由于目标簇边缘FUE总是落在PBS的覆盖范围之外,且只考虑主干扰,则目标簇边缘FUE的干扰IEFU写为:
(6)
其中,
表示落入半径为
和R3环内的一组簇边缘FBS干扰,而位于的服务FBS除外。由于使用了SSA,目标簇边缘UE所经历的干扰被有效地抑制了。因此,得到命题2,证明见附录B。
命题2 干扰IEFU的拉氏变换为:
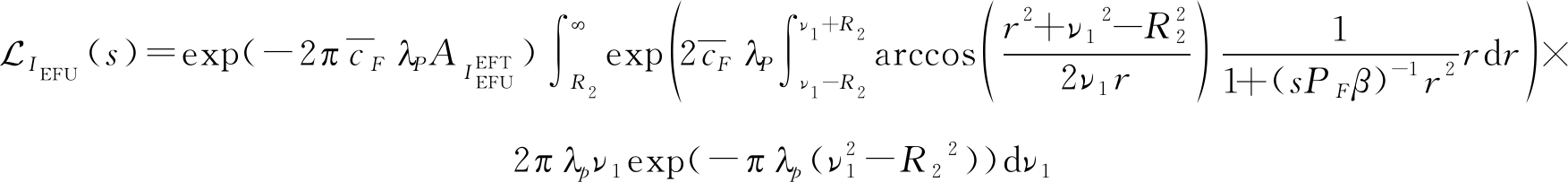
(7)
(8)
其中是目标簇边缘FUE到其服务FBS的级联距离,由有序FBS下
和无序FBS下
给出。
4 SINR覆盖性能
上文构建了基于用户簇分布的异构网络模型,描述了FBS网络干扰统计特性,本节将研究该模型下的SINR覆盖概率。考虑到UE可以和三种类型发射机(MBS、PBS和FBS)中的一种级联,并且可能位于簇中心或簇边缘,故将目标UE接收到的SINR建模为:
(9)
其中,
为热噪声功率,
表示目标UE从位于
且级联距离为
的服务BS接收的瞬时信号功率,I{V}{U}U为目标U∈{F,P,M}UE受到的干扰。则SINR覆盖概率的一般形式为:
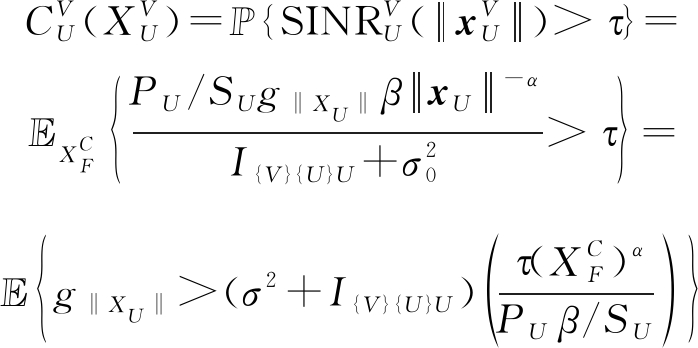
(10)
其中,τ表示SINR阈值由目标速率确定。本小节主要研究UE和FBS级联的FUE下行链路覆盖概率。
4.1 FBS下行链路覆盖概率
当目标簇中心(或簇边缘)FUE与位于
且级联距离为
的FBS级联时,目标FUE接收到的下行链路SINR写为:
(11)
在小尺度衰落信道增益为
的情况下,级联距离
表示为
干扰IC(E)FU表示为
即FUE来自FBS和MBS的干扰。IEFU通过命题2得到。利用小尺度衰落信道增益
很容易得到定理1给出的条件SINR的覆盖概率
定理1 当目标簇中心(簇边缘)UE与FBS级联时,SINR覆盖概率
写为:
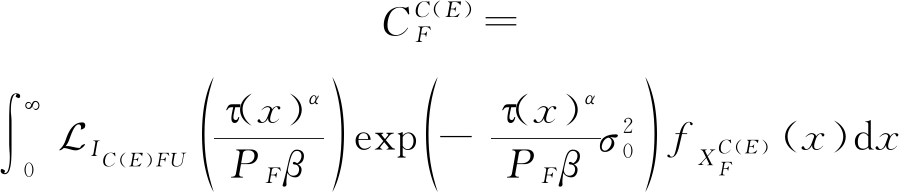
(12)
其中,
分别由命题1和命题2给出。有序和无序FBS的级联距离
的PDF分别为:
(13)
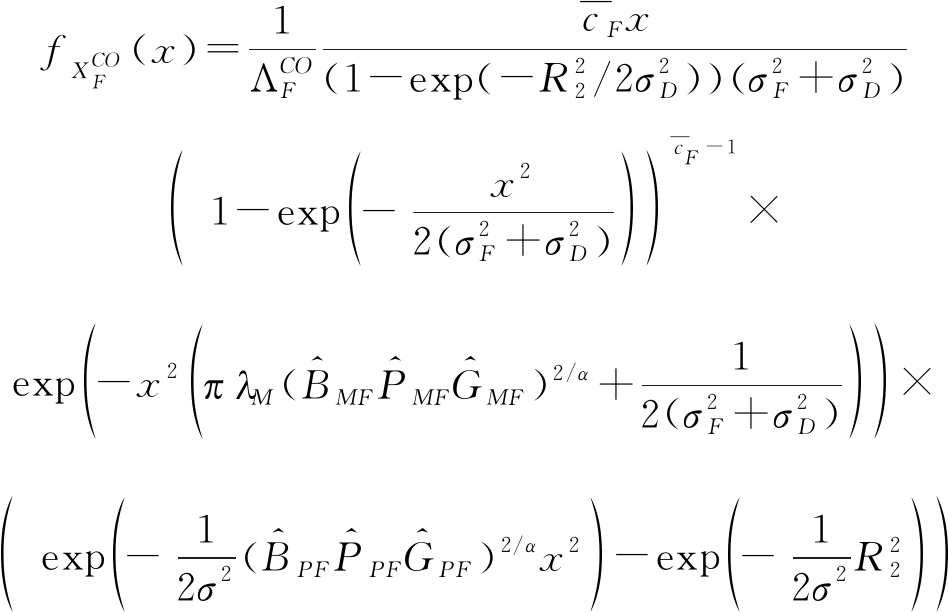
(14)
(15)
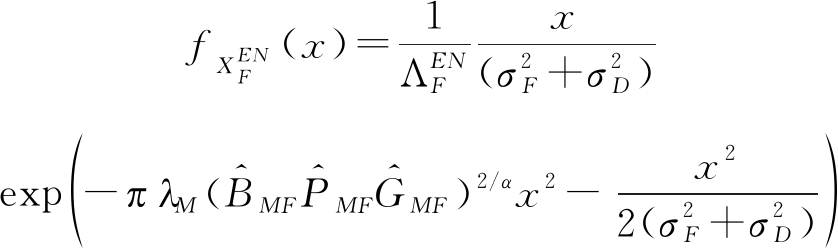
(16)
其中,
表示最强平均偏置接收功率准则下UE和FBS级联的级联概率。
5 仿真与分析
本节对前面得到的覆盖概率进行了数值分析与仿真。若无特别说明,数值分析与仿真将用下述参数值。假设网络中路径损耗指数为α=2,MBS和PBS的密度为λM=(1～10)MBSs/(π×Km2)和λP=10λM。ΘF和ΘU以方差
和
分布在父点周围。活动FBS和UE的平均数目为
和
和MBS的发射功率分别为PF=30 dBm、PP=20～45 dBm、PM=20～46 dBm,覆盖半径分别为R1=1000 m、R2=70～800 m、R3=50～150 m。MBS天线阵列数NM=80,SM=6,PBS天线阵列数NP=10,SP=2。SINR阈值τ=1.5。网络的总可用带宽B=20 MHz,整个网络工作在低于6 GHz的频带上。
图3研究了FUE下行链路覆盖概率与FBS关键参数
和
的关系。该图表明,随着FBS参数的增大,簇边缘FUE的覆盖概率增大。这是由于平均FBS分布越多,其覆盖范围越大,则其覆盖概率自然也就变大了,与实际相符。同时,还给出了有序FBS和无序FBS两种情况下参数和
对FBS覆盖概率的影响。从图中可以观察到对无序FBS的覆盖概率影响较小,对有序FBS的覆盖概率影响较大,而且有序FBS的性能增益随平均数的增大而增大。这是由于随着的增加,更多FBS远离其簇中心,使目标簇边缘FUE受到的干扰减小。
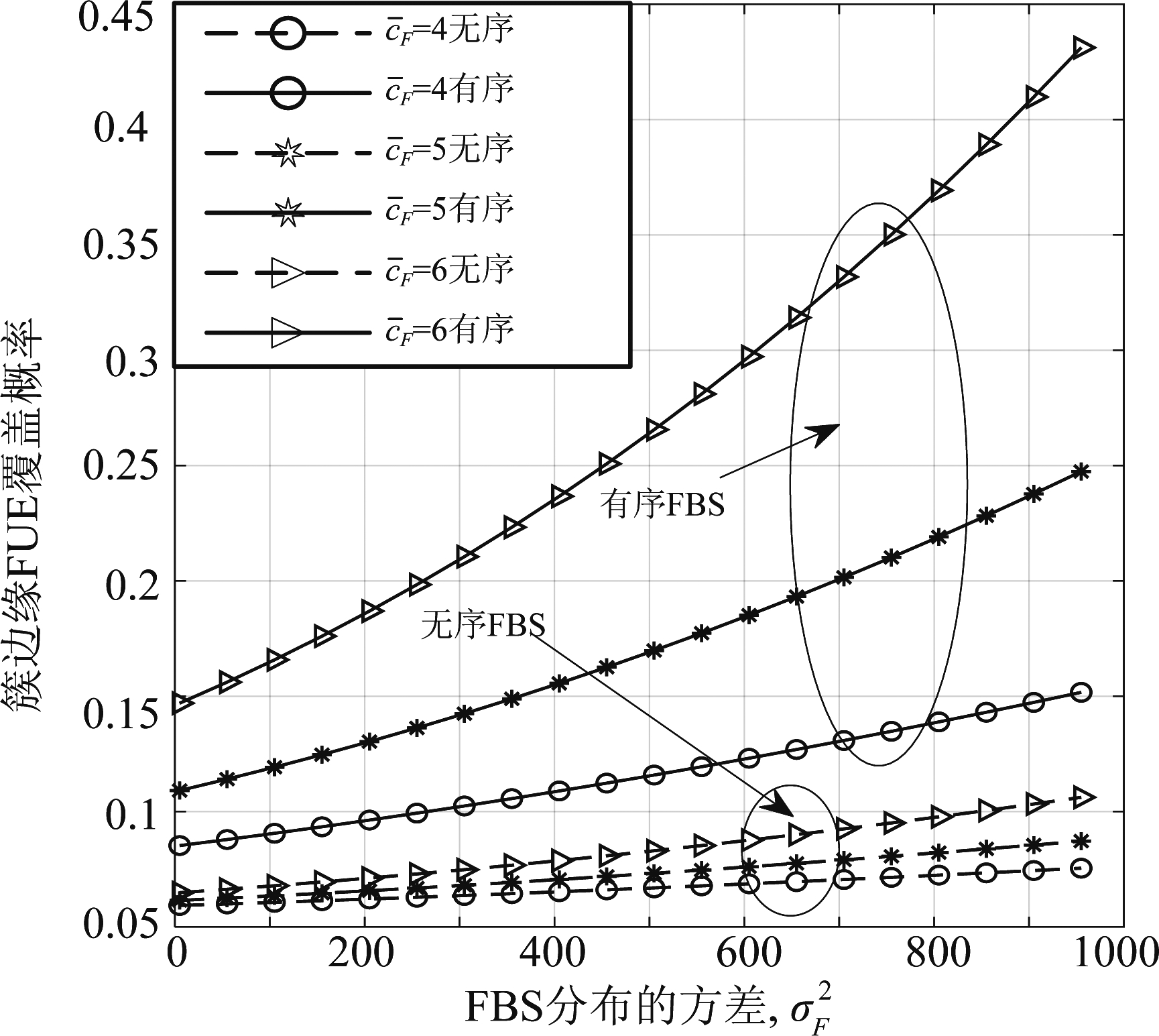
图3 FUE覆盖概率与
和
的关系
Fig.3 Relationship between coverage probability 
图4给出了FUE的覆盖概率与MBS密度λM之间的关系。由于MBS和簇中心FBS共享子带W2,目标簇中心FUE的覆盖概率随着MBS密度λM的增加而降低。同时,该图表明有序FBS方案可达性能增益与BS的半径有关。此外,在相同的系统参数下,有序FBS方案下簇中心和簇边缘FUE的覆盖概率小于无序FBS方案下的两类覆盖概率。而且,覆盖概率的差距随着密度λM的增大而增大。
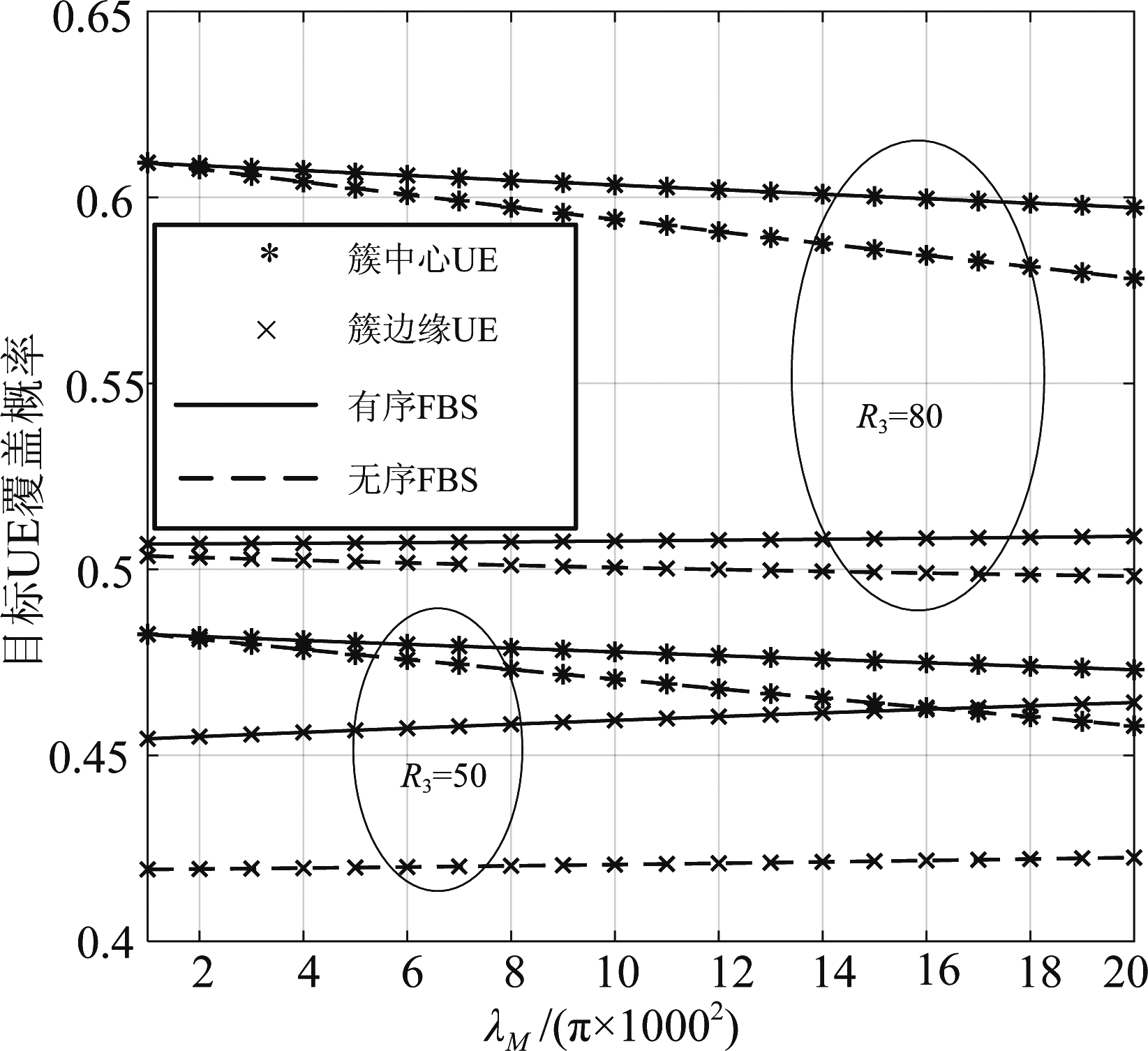
图4 FUE覆盖概率和λM的关系,R2=90 m
Fig.4 Relation between coverage probability of FUE and λM,R2=90 m
图5进一步研究了覆盖概率与覆盖半径R2和R3之间的关系。通过观察可得,在有序FBS和无序FBS下,簇中心和簇边缘FUE的覆盖概率都随着PBS半径R2的增大而减小。然而,在给定簇中,活动FBS的数量
恒定,目标簇中心FUE受到的干扰主要由MBS控制。因此,覆盖半径R2和R3对簇边缘FUE的影响较大,对簇中心FUE影响较小。比较图5中(a)、(b)、(c)可得,对于簇边缘FUE,有序FBS方案是否优于无序FBS方案很大程度上由R2和R3共同决定。不难看出,只有在覆盖半径R3较小的情况下,较大的覆盖范围内,有序FBS方案在簇边缘FUE的覆盖概率优于无序FBS方案。另外,当覆盖半径R2很小时,有序FBS方案的性能并不优于无序FBS方案。只有当覆盖半径R2较大时,有序FBS方案才具有优越性。这是因为R2的增加表示簇边缘FBS的增加,使得簇边缘FUE的干扰减小。另一方面,随着半径R3的增大,增加的FBS落入给定FBS的覆盖范围内。
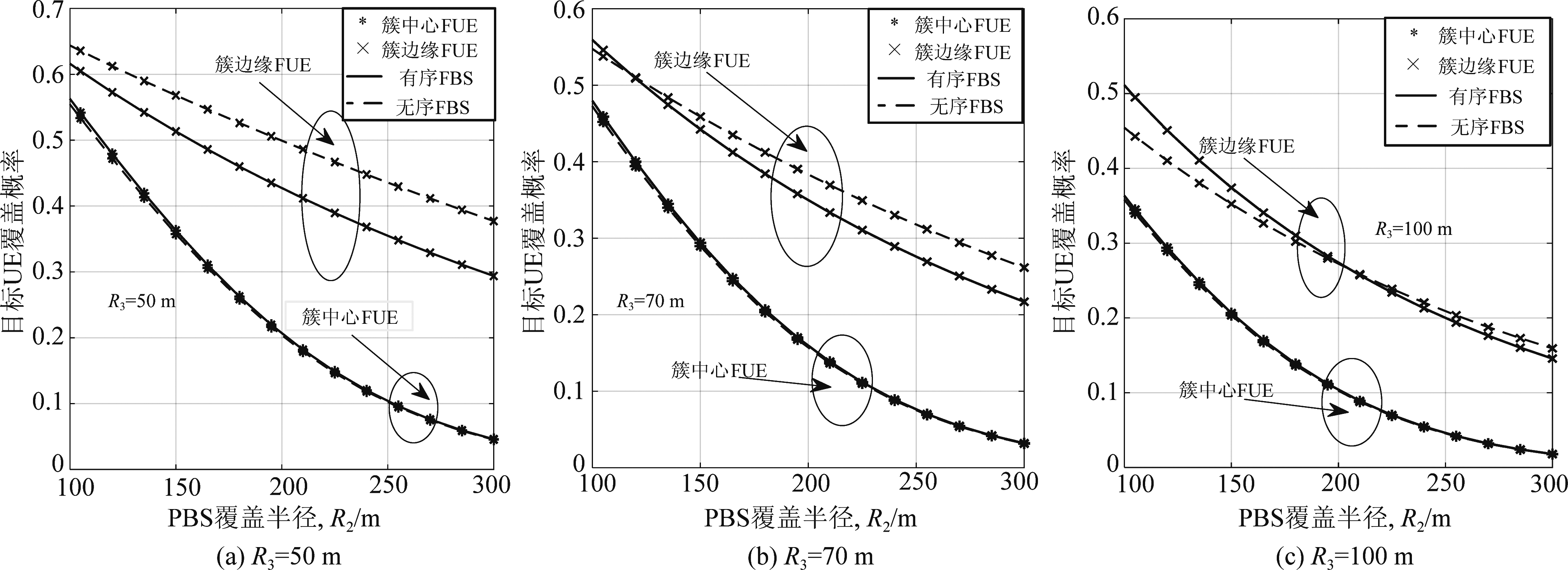
图5 覆盖半径R2和R3对FUE覆盖概率的影响
Fig.5 Impact of the coverage radii R2 and R3 on the coverage probabilities of FUE
6 结论
针对热点区域小基站密集部署问题,本文提出了一种基于用户簇分布的三层异构网络模型。为抑制层内和层间干扰,提出了SSA干扰管理方案。采用PPP、PCP和PHP对网络进行建模,给出毫微微基站层网络干扰统计特性,分析了FBS下行链路的覆盖概率,并分析了参数对系统性能的影响。为进一步发掘其潜能,讨论了有序FBS和无序FBS两种情况。仿真结果表明,有序FBS方案在覆盖概率方面优于无序FBS方案。下一步将进一步研究网络整体的覆盖概率。
附录
附录A:命题1的证明
证明 首先计算干扰
的拉氏变换,表示为:
(17)
其中,(a)由所有干扰的独立假设得到,(b)为瑞丽衰落假设hyc～exp(1),(c)为通过将概率生成函数(PGFL)应用于TCP中密度为
的单个簇,即
然后,通过将子点(FBSs)的分布应用于极坐标,子点在TCP和笛卡尔坐标系中围绕父点(PBS)分布,则
进一步计算为:
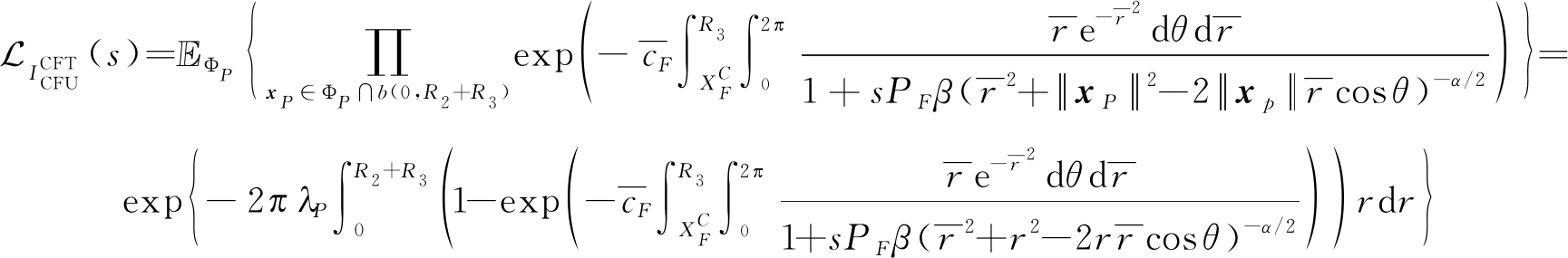
(18)
为计算干扰
的拉氏变换。首先考虑,当目标簇中心UE和FBS级联时,根据所使用的UE级联准则
xM∈ΦM。则干扰MBS的最近距离为
注意,对于有序FBS,级联距离xF由
给出,对于无序FBS,级联距离xF由
给出。因此,目标FUE受到MBS的干扰为
其中,gxm是遵循伽马分布的小尺度衰落干扰信道功率增益。因为假设每个MBS配备有NM天线,并与SMUE同时通信,所以gxm的
给出[12,24]。因此,干扰的拉氏变换计算为:
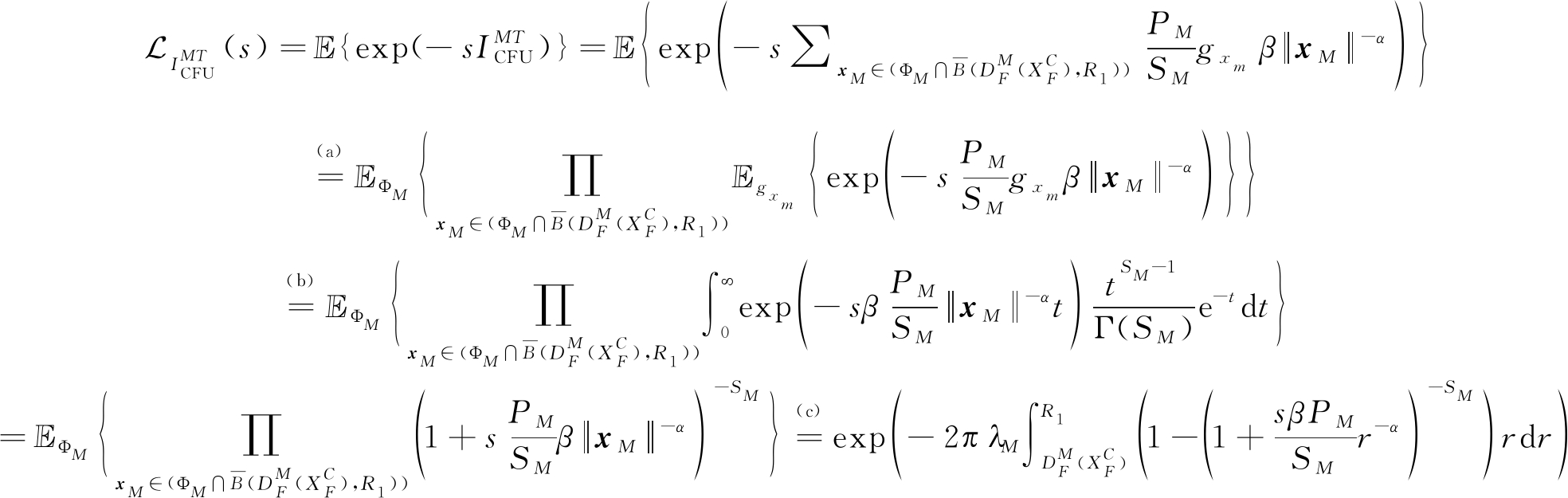
(19)
其中(a)服从ΦM和ΘF中点的独立假设,(b)通过使用文献[16]中的(3.351.3)获得,(c)通过应用TCP中单个簇的概率生成函数(PGFL)获得,即
为进一步推导出
的简易形式,(19)的积分重新写为:
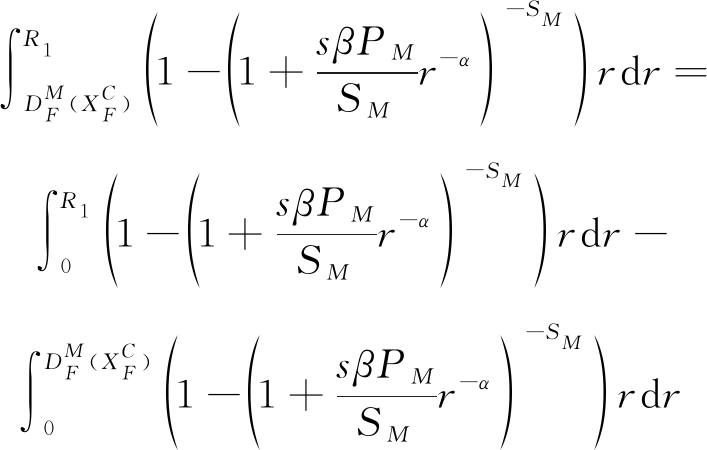
(20)
使用[25]中的(3.191.6),式(20)的第一部分计算为
(21)
因此,结合(21)、(20)和(19),得到如式(5)。得证命题1。
附录B:命题2证明
证明 簇边缘FBS受到的干扰
的拉氏变换为:
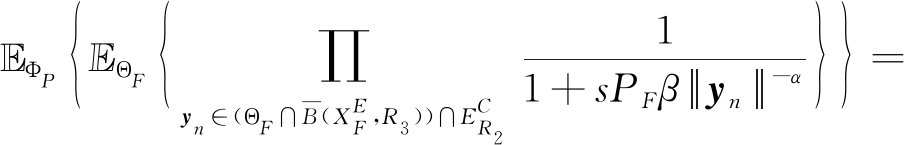
(22)
其中,
是从目标簇边缘FUE到其服务FBS的级联距离。对于有序
由给定。对于无序由给定。在式(22)中,使用文献[25]中的(3.191.6),则第一部分写为
(23)
受文献[16]、[17]的启发,通过利用
忽略洞重叠的影响,则(22)的第二部分为:
(24)
对于给定的洞过程b(xP,R2),有xP-R2≤yn≤xP+R2。然后,利用余弦定律
和r=yn,上述表达式进一步计算为:
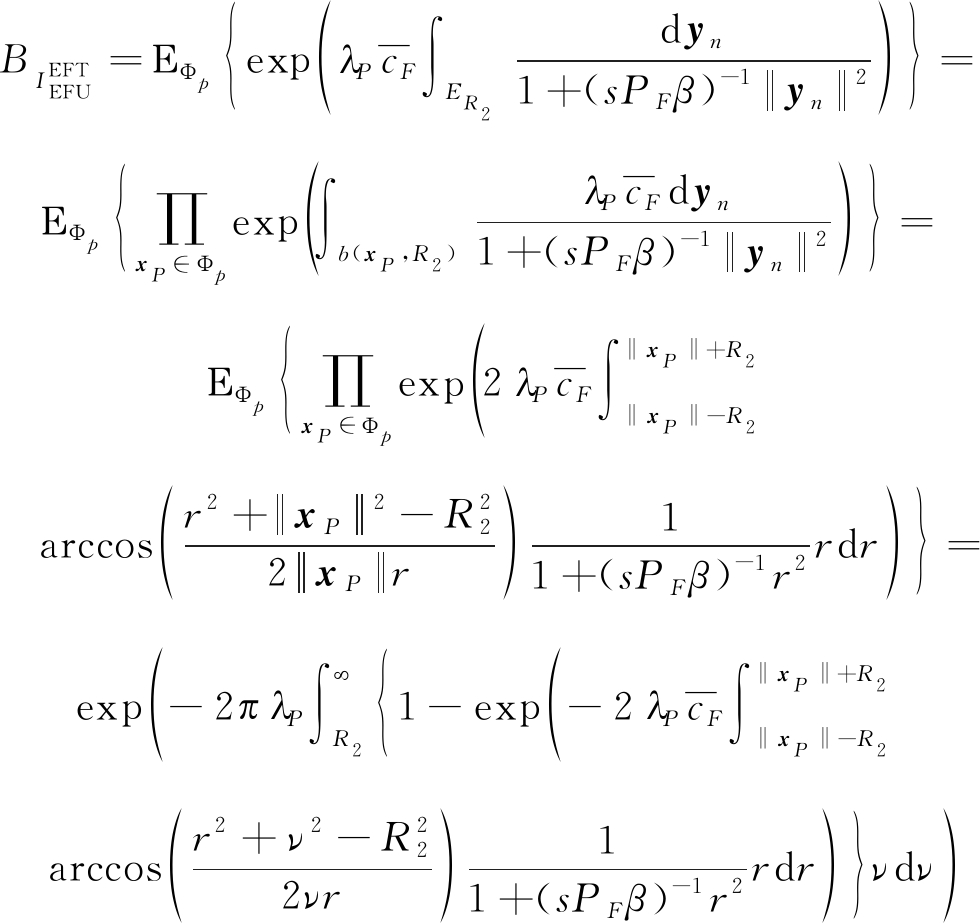
(25)
同时,与距离较远的洞相比,靠近簇边缘的洞FUE影响要显著得多。因此,为了实现易于使用的推导,本文只考虑一个洞,即最靠近簇边缘的洞FUE,而忽略其他洞。由于目标簇边缘FUE总是位于相关半径为R2的洞外,其最接近ΦP的点位于距其距离为R2的位置。基于上述分析,通过假设最近点的距离为ν1=xP,且xP∈ΦP,得出ν1的PDF为:
(26)
然后,对关于fV1(ν1)分布的表达式(25)。进行解条件,得到:
(27)
结合(27)、(22)和 (23),得出:
(28)
其中,
由(23)给出。注意,从(23)得到的是从目标簇边缘FUE到其服务FBS的访问距离XF的拉式变换
得证命题2。
[1] Agiwal M, Roy A, Saxena N. Next generation 5G wireless networks: A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1617-1655.
[2] Kamel M, Hamouda W, Youssef A. Ultra-dense networks: A survey[J]. IEEE Communications Surveys & Tutorials, 2016, 18(4): 2522-2545.
[3] 徐文娟, 贾向东, 杨小蓉, 等. 多层异构网络第m阶用户级联方案[J]. 信号处理, 2019, 35(2): 275-284.
Xu Wenjuan, Jia Xiangdong, Yang Xiaorong, et al. A novel m-th best user association scheme for multi-tier heterogeneous networks[J]. Journal of Signal Processing, 2019, 35(2): 275-284.(in Chinese)
[4] 江玉函, 邹玉龙, 郑宝玉. 新一代超密集异构蜂窝无线网络研究[J]. 信号处理, 2020, 36(2): 159-167.
Jiang Yuhan, Zou Yulong, Zheng Baoyu. Research on New Generation of Ultra-Dense Heterogeneous Cellular Wireless Networks[J]. Journal of Signal Processing, 2020, 36(2): 159-167.(in Chinese)
[5] Chang S H, Park H G, Kim S H, et al. Study on Coverage of Full Frequency Reuse in FFR Systems Based on Outage Probability[J]. IEEE Transactions on Communications, 2018, 66(11): 5828-5843.
[6] García-Morales J, Femenias G, Riera-Palou F. On the design of OFDMA-based FFR-aided irregular cellular networks with shadowing[J]. IEEE Access, 2018, 6: 7641-7653.
[7] Huawei. Soft frequency reuse scheme for UTRAN LTE[C]∥3GPP TSG RAN WG1 Meeting 41, Athens, Greece, May, 2005.
[8] Li J, Shroff N, Chong E. A reduced-power channel reuse scheme for wireless packet cellular networks[J]. IEEE/ACM Transaction on Networking, 1999, 7(6): 818- 832.
[9] Doppler K, Wijting C, Valkealahti K. Interference aware scheduling for soft frequency reuse[C]∥IEEE Vehicular Technology Conference, 2009: 1-5.
[10]Peng M, Zhang K, Jiang J, et al. Energy-Efficient Resource Assignment and Power Allocation in Heterogeneous Cloud Radio Access Networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(11): 5275-5287.
[11]He A, Wang L, Chen Y, et al. Throughput and Energy Efficiency for S-FFR in Massive MIMO Enabled Heterogeneous C-RAN[C]∥IEEE Global Communications Conference (GLOBECOM), 2016: 1- 6.
[12]Wang L, Wong K, Elkashlan M, et al. Secrecy and Energy Efficiency in Massive MIMO Aided Heterogeneous C-RAN: A New Look at Interference[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(8): 1375-1389.
[13]Kim Y, Kwon T, Hong D. Area spectral efficiency of shared spectrum hierarchical cell structure networks[J]. IEEE Transactions on Vehicular Technology, 2010, 59(8): 4145- 4151.
[14]Mankar P D, Das G, Pathak S, et al. Load-aware performance analysis of cell center/edge users in random HetNets[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2476-2490.
[15]路艺, 贾向东, 吕亚平, 等. 用户设备分类的毫米波异构网络性能研究[J]. 信号处理, 2020, 36(3): 407- 414．
Lu Yi, Jia Xiangdong, Lv Yaping, et al. Research on Performance of Millimeter-Wave Heterogeneous Networks Based on User Equipment Classification[J]. Journal of Signal Processing, 2020, 36(3): 407- 414.(in Chinese)
[16]Kishk M A, Dhillon H S. Tight Lower Bounds on the Contact Distance Distribution in Poisson Hole Process[J]. IEEE Wireless Communications Letters, 2017, 6(4): 454- 457.
[17]Afshang M, Dhillon H S. Spatial modeling of device-to-device networks: Poisson cluster process meets Poisson Hole Process[C]∥Asilomar Conference on Signals, Systems and Computers, 2015: 317-321.
[18]Yazdanshenasan Z, Dhillon H S, Afshang M, et al. Poisson Hole Process: Theory and Applications to Wireless Networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7531-7546.
[19]Chun Y J, Hasna M O, Ghrayeb A, et al. Modeling heterogeneous cellular networks interference using poisson cluster processes[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(10): 2182-2195.
[20]Afshang M, Dhillon H S. Poisson cluster process based analysis of HetNets with correlated user and base station locations[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2417-2431.
[21]Tabassum H, Hossain E, Hossain J. Modeling and analysis of uplink non-orthogonal multiple access in large-scale cellular networks using poisson cluster processes[J]. IEEE Transactions on Communications, 2017, 65(8): 3555-3570.
[22]Chiu S, Stoyan D, Kendall W, et al. Stochastic Geometry and its Applications[M]. Third Education, United Kingdom: John Wiley & Sons, 2013.
[23]Ganti R K, Haenggi M. Interference and Outage in Clustered Wireless Ad Hoc Networks[J]. IEEE Transactions on Information Theory, 2009, 55(9): 4067- 4086.
[24]He A, Wang L, Elkashlan M, et al. Spectrum and energy efficiency in massive MIMO enabled HetNets: A stochastic geometry approach[J]. IEEE Communications Letters, 2015, 19(12): 2294-2297.
[25]Gradshteyn I, Ryzhik I, Geronimus Yu, et al. Table of Integrals, Series, and Products[M]. Seventh Education, San Diego, Academic Press, 2007.
