communication
1 引言
正交频分复用(OFDM)技术是一种正交的多载波传输技术,由于其具有良好的抗频率选择性衰落和多径传输引起的码间干扰而得到广泛的应用。在OFDM系统设计中通常采用循环前缀、前导序列、内插导频等方式使得接收方能够准确进行定时、频率偏差和信道估计[1-3]。线性调频(Linear Frequency Modulated, LFM)信号具有高处理增益、低发射功率、抗多普勒频移等优点,在雷达、扩频通信、水声通信等领域中应用广泛[4-7]。在一些卫星移动通信同步应用中,采用双Chirp同步头进行时延和多普勒频偏估计[6-7];在一些水声通信系统中,以LFM信号作为前导序列用于解决水声信道传输中的多径时延和多普勒效应[8-10];在一些多径传输和多普勒效应明显的通信系统中,将OFDM信号与LFM信号相结合使用,如大疆的OcuSync无线图传系统采用内插LFM的方式用于信道探测和多普勒频移估计。为了保证系统结构的一致性,对LFM信号也加入循环前缀保护间隔,形成了循环前缀线性调频信号(Cyclic Prefix Linear Frequency Modulated, CP-LFM)。
对于非合作接收方,频谱侦察中需要在大频率范围下搜索目标信号并确定其准确中心频率,因此准确检测目标信号并精确估计其频率是非合作接收处理中的重要环节。文献[10-13]等提出了很多针对LFM信号的参数估计方法,包括DTFT变换、分数阶傅里叶变换(Fractional Fourier Transform, FRFT)等,其中FRFT是应用最为广泛的一种方法,能够对LFM信号的斜率、起始频率等参数进行估计,但离散分数阶傅里叶变换计算复杂度高,更适用于调频斜率未知或斜率发生变化的场合。对于CP-LFM信号的频率估计,由于其具有循环前缀结构,可以采用CP-OFDM频率估计中的基于循环前缀的最大似然估计[3],但该方法频偏估计范围只有子载波带宽的一半,而非合作接收往往需要大的频率估计范围。
针对上述问题,本文针对特殊结构的CP-LFM信号,提出了一种基于循环前缀和线性调频信号特性的频率估计方法,可满足非合作通信中宽范围高精度的频率估计需求。该方法利用循环前缀相关确定符号周期起点,从而实现对LFM信号时延和频偏的解耦合;然后推导了基于时延差的频偏粗估计,并通过缩短线性调频信号的相关匹配长度来扩大频偏估计的范围;最后对部分匹配相关后的残余频偏使用高精度单频估计方法提高频率估计精度,从而得到了宽范围高精度的频率估计值。
2 系统和信号模型
OFDM系统是一种正交多载波传输系统,它将串行高速数据流变换成若干个并行低速数据流,并通过彼此相互正交的多个子载波进行调制。与传统单载波系统相比,OFDM系统具有更高的频谱利用率。为了克服多径效应的影响,通常在OFDM符号之间插入循环前缀保护间隔,即将OFDM符号尾部的若干个样点复制到OFDM符号的前面。在高速移动环境下,为了更好地实现大范围频率偏差估计和信道状态估计,通过在OFDM系统中插入LFM信号,发射系统模型如图1所示。
由该模型生成的CP-LFM是由一个线性调频信号和其尾部的循环复制组合而成的,其时频分布如图2所示。
图2中起始频率为fl,带宽为B的连续时间LFM复信号可以表示为
图1 信号发射系统模型
Fig.1 Signal transmitting system model
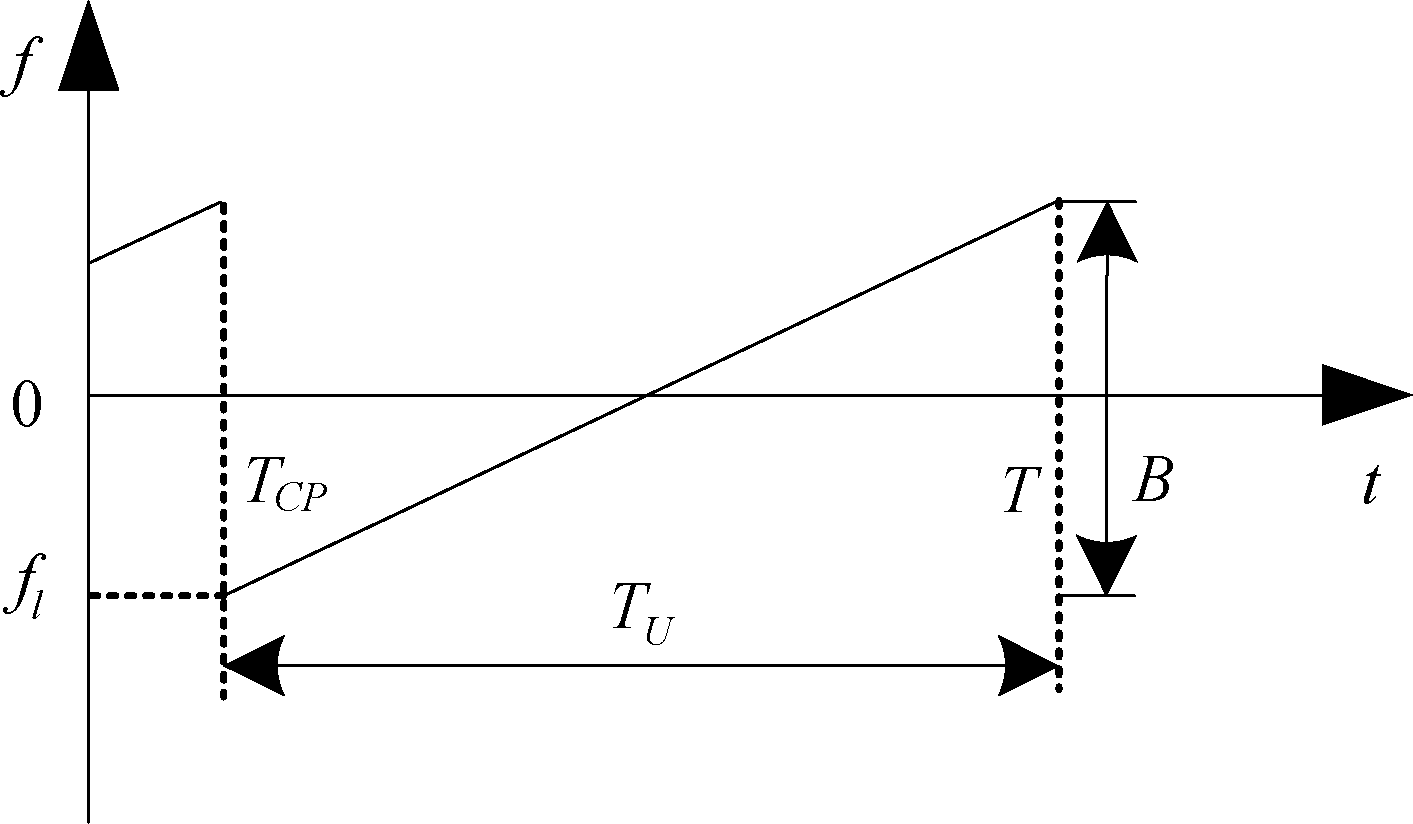
图2 CP-LFM信号的时频分布示意图
Fig.2 Time-frequency distribution diagram of CP-LFM signal
(1)
其中A表示信号的幅度,K=B/Tu为调频斜率,Tu为信号的调制周期,也为上述发射系统模型中的OFDM信号的有用符号周期。以采样率fs采样,得到离散信号可以表示为
(2)
其中P=fs/B表示过采样倍数,Nu=Tu fs。加循环前缀后,CP-LFM信号可以表示为
(3)
其中Nc=Tc fs,Tcp为循环前缀的周期,T=Tcp+Tu为系统的符号周期。
对于非合作接收方,接收信号存在时延、频率偏差以及信道噪声的影响,则接收信号模型可以表示为:
y(n)=Aej2πεnx(n-d)+w(n)
(4)
其中A表示接收信号幅度,d和ε分别表示时延和归一化频率偏差,w(t)表示均值为0,方差为σ2=N0/(2Es)的复值高斯白噪声,Es为平均符号能量,N0为噪声功率谱密度。对于非合作接收方而言,需要准确估计接收信号时延和频率偏差才能进一步对接收信号进行解调处理。
3 算法原理
3.1 基于循环前缀的最大似然估计
文献[3]利用循环前缀采用最大似然算法进行定时和频偏的联合估计。由于循环前缀是有用信号的部分信号的复制,因此循环前缀和有用信号的部分信号具有相关性,利用其相关性得到的定时和频偏最大似然联合估计为
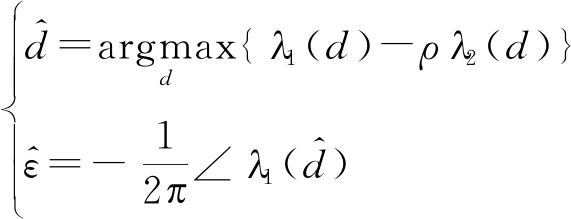
(5)
其中
基于循环前缀的最大似然估计受噪声的影响大,且对频偏的估计范围很小,只能获得小数倍子载波间隔的频率偏差,无法满足非合作接收的需求。
3.2 宽范围频偏粗估计
为了满足非合作接收中宽频率估计范围的需求,利用LFM信号的调频斜率特性进行频偏粗估计。LFM信号的模糊函数可以表示为[14]:
(6)
从上式可以看出,当且仅当π( fd-Kτd)(Tu-|τd|)=0时,模糊函数的幅度取得最大值|χ(τd, fd)|=1,即满足条件
fd=Kτd
(7)
当频率偏差fd=0时,模糊函数的幅值将在时延τd=0时取得最大。当fd≠0时,模糊函数的幅值将在时延
时取得最大,且峰值响应变小。通过上述分析可知,LFM信号模糊函数的时延和频偏相互耦合。对LFM信号做相关匹配检测时,匹配滤波输出的峰值出现在信号真实达到时刻附加一个频偏引起的耦合时延,且频偏越大,失配误差越大。因此为了估计LFM信号的频偏,首先需要确定LFM信号的真实到达时刻实现频偏与时延的解耦合,然后再确定由频偏引起的时延偏差实现频偏估计。
3.2.1 真实到达时刻的确定
由于信号中具有循环前缀,根据3.1节的描述可知,利用循环前缀可以确定符号周期的起点,且循环前缀相关峰值采用自相关,不受频率偏差大小的影响。为了更好地设置门限,采用归一化自相关函数作为检测统计量:
(8)
根据r(d)峰值出现的时刻,可以确定符号周期的起点d1,则LFM信号的起始时刻为d1+Nc,该时刻即为LFM信号的真实到达时刻。
3.2.2 基于时延差的频偏粗估计
为了确定由频偏引起的时延偏差,采用相关匹配检测方法。选择以零频为中心,带宽为B′,时长为T′的LFM波形作为本地参考波形。本地参考波形是原始LFM波形以零频为中心的部分截取,用sr(n)可以表示为:
(9)
其中
为参考波形的起始频率,
为T′的采样点数,且
只考虑LFM信号,将接收信号重新表示为
y′(n)=ej2πεnsr(n-d)+w(n)
(10)
用sr(n)与接收信号匹配相关,得到的互相关为
(11)
将式(9)和式(10)代入,可得
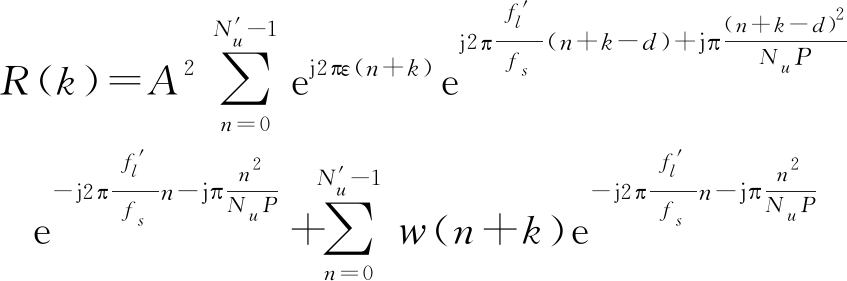
(12)
忽略噪声的影响,上式可进一步化简为
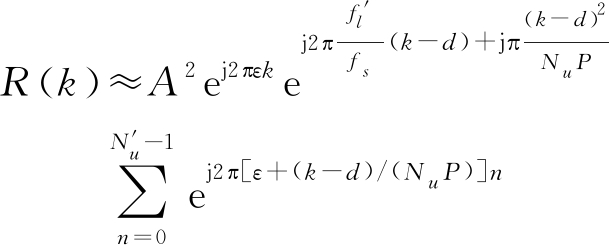
(13)
通过上式可知,当满足下式条件:
ε+(k-d)/(PNu)=mNu
(14)
互相关达到最大峰值,其中m为任意正整数,最大峰值所对应的时刻记为
该时刻为当前接收信号零频位置的时刻。当无频率偏差时,零频位置时刻应处于LFM信号的中点。根据3.2.1节的描述,可知无频偏条件下零频位置时刻为
根据式(14),利用两者的时间差可得到频率偏差估计。假设实际频率偏差不超过整个带宽,则m=0。由式(14)可以得到
(15)
将上式用频率偏差
表示时,可得
(16)
其中Ts=1/fs,上式与公式(7)的结论是一致的。
3.2.3 频偏估计范围与估计精度分析
在频偏粗估计过程中,接收信号与本地参考波形相关匹配时应保证无失配误差且具有大的频偏估计范围。根据式(16),频偏估计范围与d2的取值范围有关。在无失配误差条件下,应满足
因此,归一化频率偏差取值范围为
由此可见,相关匹配参考波形越短,频率偏差估计范围越大。在非合作接收中,为了获得宽范围频偏估计,通过缩短线性调频信号的相关匹配长度来扩大频偏估计范围。
在频偏估计精度方面,频偏估计精度与时差的估计精度有关。对d1和d2的估计依赖于循环前缀相关峰和匹配相关峰的检测。在无噪声条件下,相关峰检测的时间分辨率最高为一个采样点,因此归一化频率偏差ε的估计分辨率为1/(PNu)。受噪声的影响,峰值检测可能偏差若干个采样点,频偏估计精度难以满足要求。
3.3 残余频偏估计
为了进一步提高频偏估计的精度,在频偏粗估计的基础上进一步估计残余频偏。根据公式(10)的信号模型,在确定d2后接收信号与参考波形共轭相乘后的信号可以表示为
(17)
将式(9)和式(15)代入,化简后可得
(18)
其中θ为相位偏差,w′(n)为高斯白噪声与参考信号的乘积,可以等效为高斯白噪声。
即为残余频偏。公式(18)可以视为混入了高斯白噪声的复正弦信号,残余频偏估计等效为从高斯白噪声背景中估计出该正弦信号的频率。因此可以采用经典的高精度单频估计算法来提高频偏估计精度。常用的单频估计算法有L&R算法[15]、Fitz算法[16]、M&M算法[17]、DFT+L&R算法[18]等,其中DFT+L&R算法具有较高的估计精度和较宽的估计范围,残余频偏估计可以表示为
(19)
其中
DFT+L&R算法的估计范围为
能够满足残余频偏的需求。因此,最终频偏估计结果为
(20)
3.4 算法流程
综上所述,本文提出的宽范围高精度频偏估计算法的具体步骤如下表所示:
表1 算法的具体步骤
Tab.1 The concrete steps of the algorithm
步骤1 对接收信号下变频,得到存在频率偏差的复基带信号y(n);步骤2 根据公式(8)计算归一化自相关函数,根据相关峰得到符号周期起点d1;步骤3 根据公式(9)构造参考波形,按公式(11)对接收信号y(n)进行匹配相关处理,根据相关峰得到时刻d2;步骤4 根据公式(15)计算得到归一化频率偏差ε^;步骤5 选择接收信号中以d2为起点,长为N′u的序列与参考波形共轭相乘,得到的新序列z(n),利用DFT+L&R算法估计残余频偏Δε,最终频偏估计为εo=ε^+Δε。
需要指出,本文算法通过缩短线性调频信号的相关匹配长度来扩大频偏估计的范围。在估计精度上,通过与参考波形共轭相乘转化为单频信号后利用DFT+L&R算法提高估计精度,因此本文算法的估计方差由DFT+L&R算法决定。根据文献[15]和文献[18]可知,DFT+L&R的估计方差与信号相关长度有关,长度越短估计方差越大。因此,需要根据估计范围和估计精度的需求合理选择相关长度。
4 仿真实验与性能分析
本节将对本文算法的性能进行验证分析。仿真实验的条件设置为:线性调频信号的调制周期Tu=91.4 μs,调制带宽B=9.46 MHz,循环前缀长度Tc=0.8 μs,加性高斯白噪声信道。采样率设置为11.2 MHz,则Nu=1024,Nc=128。仿真实验中,每个信噪比下进行蒙特卡罗实验10000次。为避免采样率对评价指标的影响,采用如下的均方误差MSE评估文中方法的估计性能,定义为
(21)
其中P为估计次数,εfs/B表示相对于带宽的归一化频偏。
为测试本文算法在不同信噪比下的估计性能,在不同信噪比下与最大似然估计算法进行比较,接收信号频偏设置为1 kHz、10 kHz,根据公式(9)构造本地参考波形,选取长度分别为
仿真结果如图3所示。从图中可以看出,随着信噪比的提高,均方误差减小。当本文算法选取的长度等于LFM信号调制周期长度时,在相同信噪比下本文算法与最大似然估计算法的精度相当。随着相关匹配长度的减少,估计误差也将增大。这是由于本文算法在估计残余频偏时采用DFT+L&R算法,而该算法的估计精度与匹配相关长度有关。当频率偏差为10 kHz时,此时频率偏差大于子载波间隔的一半(11.2 MHz/1024/2=5.46875 kHz),最大似然估计算法失效,本文算法在
时与频偏1 kHz时的性能相当,这是因为此时频率偏差仍然在算法估计范围内。当
时本文算法估计范围缩小,匹配相关时存在失配误差,低信噪比情况下性能恶化,高信噪比情况下仍能有效估计。
为验证本文算法的频偏估计范围,在信噪比为5 dB和10 dB下对不同的频偏进行仿真实验,频偏取值范围从-0.5 B到0.5 B,仿真结果如图4所示。从图中可以看出,本文算法与最大似然估计算法相比具有很宽的估计范围。在相同匹配相关长度下,信噪比越高,均方误差越小。在相同的信噪比下,匹配相关长度越短,频偏估计范围越大。在匹配相关长度取1/4调制周期时,频偏估计范围达到0.4倍的信号带宽。虽然缩短匹配相关长度一定程度上增大了频偏估计方差,但获得了更大的频偏估计范围,在非合作接收条件下,大频偏范围的信号捕获能力具有很大的优势。
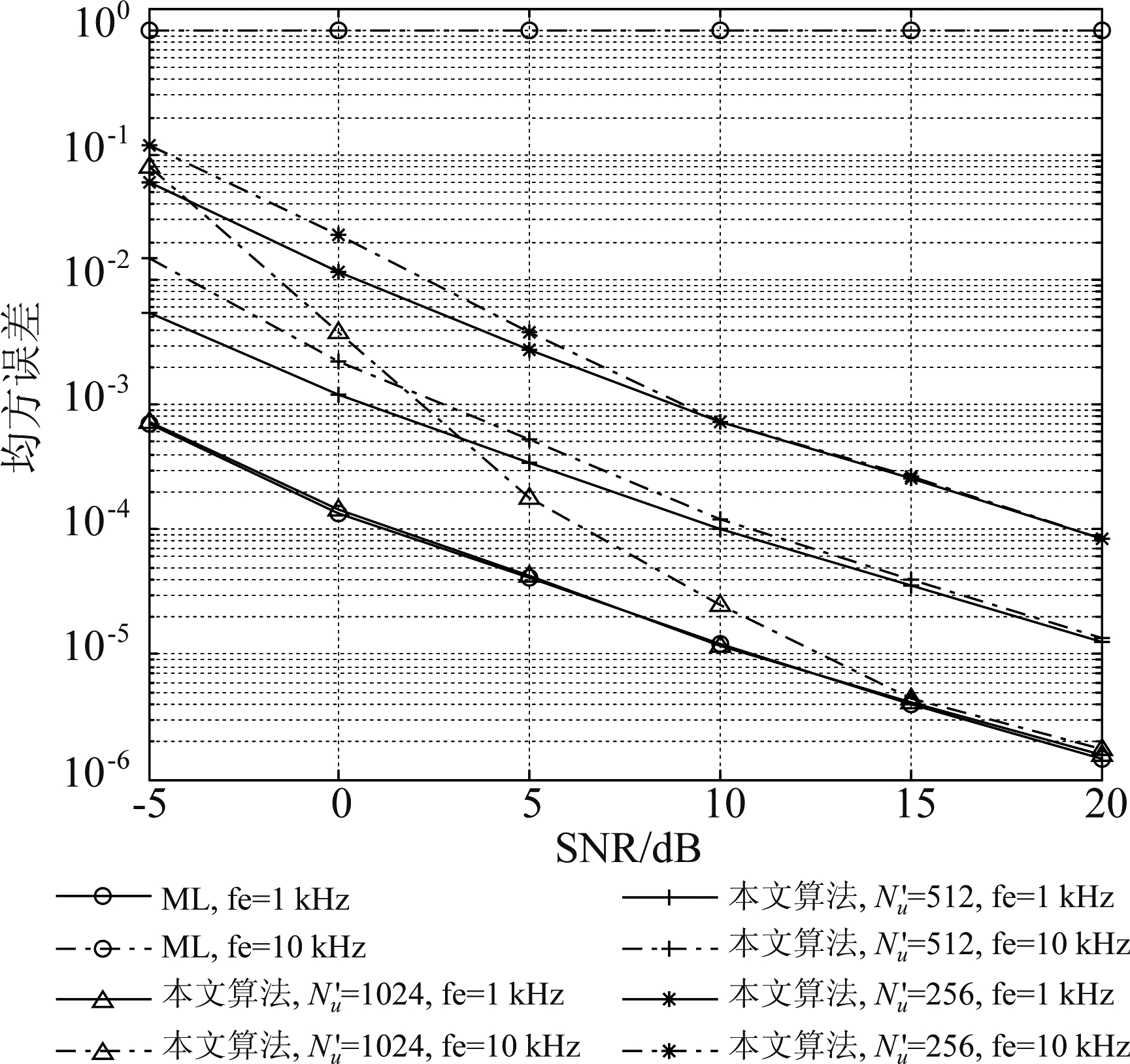
图3 不同信噪比下的估计均方误差 Fig.3 MSE of estimation for different SNR
图4 不同频偏下的估计均方误差 Fig.4 MSE of estimation for different frequency offset
5 结论
本文针对非合作通信中循环前缀线性调频信号的频率估计,利用循环前缀相关和部分线性调频相关的时延差计算频偏粗估计,从而扩展了频率估计的范围;然后利用DFT+L&R高精度单频估计算法估计相关匹配后波形的残余频偏,提高了算法的估计精度,从而得到了宽范围高精度的频率估计算法。仿真结果表明,本文算法在保证一定估计精度的同时大大提高了频率估计范围,更适用于非合作接收环境。
[1] Lin J. Least-Squares Channel Estimation for Mobile OFDM Communication on Time-Varying Frequency-Selective Fading Channels[J]. IEEE Transactions on Vehicular Technology, 2008, 57(6): 3538-3550.
[2] Park B, Cheon H, Ko E. A Blind OFDM Synchronization Algorithm based on Cyclic Correlation systems[J]．IEEE Signal Processing Letters, 2004, 11(2): 83- 85.
[3] Beek J J, Sandell M, Borjesson P O. ML estimation of time and frequency offset in OFDM systems[J]. IEEE Transactions on Signal Processing, 1997, 45(7): 1800-1805.
[4] 刘勇, 张国毅, 张旭洲. 线性调频连续波雷达信号的参数估计[J]. 信号处理, 2014, 30(7): 848- 855.
Liu Yong, Zhang Guoyi, Zhang Xuzhou. Parameter Estimation of LFMCW Radar Signal[J]. Journal of Signal Processing, 2014, 30(7): 848- 855.(in Chinese)
[5] Takahashi T, Kato Y, Isoda K, et al. A Novel Waveform for Joint Radar and Communication Systems[C]∥2019 International Symposium on Antennas and Propagation (ISAP), 2019: 1-3.
[6] Lin J C, Hsu H Y. Timing delay and frequency offset estimations for initial synchronisation on time varying Rayleigh fading channels[J]. IET Communications, 2013, 7(6): 562-576.
[7] Vishwanath T G, Parr M, Shi Z L, et al. Synchronization in mobile satellite systems using dual chirp waveform[P]. U.S.: 6418158,2002-7-9.
[8] Wei Wei, Hu Xiaoyi, Wang Deqing, et al. Performance comparison of time synchronization algorithms for OFDM underwater communication system[C]∥2007 14th International Conference on Mechatronics and Machine Vision in Practice, 2007: 104-107.
[9] 陈阳, 张艺朦, 陈凯, 等. 基于同步导频复用技术的OFDM水声通信[J]. 华中科技大学学报(自然科学版), 2011, 39(8): 80- 83.
Chen Yang, Zhang Yimeng, Chen Kai, et al. Synchronization and pilot reusing technology for OFDM in underwater acoustic communication[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(8): 80- 83.(in Chinese)
[10]樊军辉, 彭华, 付君, 等. 水声信道下Chirp信号参数与信道时延的联合估计[J]. 信息工程大学学报, 2018, 19(6): 685- 695.
Fan Junhui, Peng Hua, Fu Jun, et al. Joint Estimation of Chirp Parameters and Channel Time Delay for Underwater Acoustic Channels[J]. Journal of Information Engineering University, 2018, 19(6): 685- 695.(in Chinese)
[11]王鹏, 邱天爽, 李景春, 等. 基于高斯加权分数阶傅里叶变换的LFM信号参数估计[J]. 通信学报, 2016, 37(4): 107-115.
Wang Peng, Qiu Tianshuang, Li Jingchun, et al. Parameters estimation of LFM signal based on Gaussian-weighted fractional Fourier transform[J]. Journal on Communications, 2016, 37(4): 107-115.(in Chinese)
[12]Chen Yanli, Guo Lianghao, Gong Zaixiao. The concise fractional Fourier transform and its application in detection and parameter estimation of the linear frequency-modulated signal[J]. Chinese Journal of Acoustics, 2017, 36(1): 70- 86.
[13]Shen L R, Yin Q B, et al. Liner FM signal parameter estimation using STFT and FRFT[J]. Chinese Journal of Electronics, 2013, 22(2): 301-307.
[14]位寅生. 雷达信号理论与应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2011.
Wei Yinsheng. Radar signals: theory and application[M]. Harbin: Harbin Institute of Technology Press, 2011.(in Chinese)
[15]Luise M, Reggiannini R. Carrier frequency recovery in all-digital modems for burst-mode transmissions[J]. IEEE Transactions on Communications, 1995, 43(234): 0-1178.
[16]Fitz M P. Further results in the fast estimation of a single frequency[J]. IEEE Transactions on Communications, 1994, 42(2): 862- 864.
[17]Mengali U, Morelli M. Data-aided frequency estimation for burst digital transmission[J]. IEEE Transactions on Communications, 1997, 45(1): 23-25.
[18]李静, 彭华, 葛临东. 一种宽范围的最大似然载波频率同步算法[J]. 系统工程与电子技术, 2006, 28(3): 369-371.
Li Jing, Peng Hua, Ge Lindong. ML-based carrier frequency offset estimator with extended range[J]. Systems Engineering and Electronics, 2006, 28(3): 369-371.(in Chinese)
