1 引言
20世纪以来,计算机得到飞速的发展,从而对计算机的计算能力提出更高的要求,但是受制于半导体制作技术的极限,经典计算机的计算能力不会无限制的提高,计算机的未来如何将会是一个不得不去面对的问题。量子计算机理论为计算机的发展带来了希望。量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式,量子力学态叠加原理使得量子信息单元的状态可以处于多种可能性的叠加状态,基于量子力学的理论,量子计算机可以实现真正的并行运算,使得量子计算机信息处理效率比经典计算机信息处理效率更高。量子计算机的研究与发展受到计算机研究者和物理学家的关注,已提出若干实现量子计算机的方案及一些小规模的模型。
图像处理作为计算机信息处理领域的一个重要分支,主要对图像或图形信息进行存储、识别和分析等,其中图像信息隐藏技术是图像处理领域的一个研究热点,目的是保证秘密信息的安全传递。量子计算机强大的计算能力使得人们意识到量子计算机的实现是历史必然,图像信息隐藏作为图像处理领域必不可少的一个分支,在量子计算机上也必须得到重视和研究。在量子计算机上进行图像处理的首要工作就是研究量子图像的表示方法。迄今为止,研究者们提出了一系列的量子图像表示方法。2003年,Venegas-Andraca等[1]提出Qubit Lattice模型,模型借鉴经典数字图像的二维矩阵表示方法。2005年,Latorre[2]提出了Real Ket模型,将一幅图像存储在实矢量中。2011年,Le等[3]提出了量子图像灵活表示模型(flexible representation of quantum images, FROI),模型用经过角度编码后的1位量子比特|0〉和|1〉的叠加态来存储图像的像素信息,分别用n位量子比特的基态叠加表示图像的横纵坐标的位置信息,而位置坐标和对应像素之间的关系则通过量子纠缠表示。2013年,Zhang等[4]改进了FRQI模型的像素表示方法,提出了新颖的增强量子图像表示模型(novel enhanced quantum image representation, NEQR),相比于FRQI模型表示方法,NEQR模型用q个量子比特的基态表示颜色信息,图像最多可以表示2q种颜色信息。2017年,Sang等[5]提出的一种新的彩色数字图像量子表示(novel quantum representation of color digital images, NCQI)模型,分别用三个量子比特序列的基态存储彩色图像的RGB像素值。2018年,Li等[6]提出一种量子数字图像的位平面表示模型(bitplane representation of quantum images, BRQI),模型使用(n+4)或(n+6)个量子比特来存储2n个像素的灰度或RGB彩色图像,Sahin等[7]提出多波长的量子图像的表示模型(quantum representation of multi wavelength images, QRMW),模型使用多通道表示量子图像。2019年,Wang[8]等提出一种新的量子彩色图像表示模型(new quantum representation model of color digital images, QRCI),模型使用量子位序列的基本状态对颜色信息编码。同年,Wang[9]等提出一种量子索引图像的表示方法, 采用2种量子数据结构分别描述索引图像的数据矩阵和调色板。基于上述量子图像表示模型,可以在量子计算机上对图像进行表示和存储。
在经典图像处理领域,索引图像也可以承载彩色信息。不过与真彩色图像不同,索引图像由数据矩阵和调色板组成,数据矩阵的像素值是调色板的下标,每个下标对应调色板中的一种颜色。索引图像以高压缩比、便于网络传输等优点,被广泛应用于互联网环境中。但是,在信息安全领域中对量子索引图像的研究较少。作为量子索引图像的具体应用,本文提出一种基于SoC的量子索引图像信息隐藏算法。目前,在量子图像信息隐藏领域已有很多成果涌现。2015年,Jiang等[10]提出基于莫尔条纹的量子信息隐藏算法,在嵌入消息之前使用形变操作处理载体图像和消息图像。2016年Jiang等[11]提出量子最低比特位(least significant bit, LSB)信息隐藏算法,此算法是经典LSB信息隐藏方法的量子实现。2017年,Xiao[12]等人改进了一种经典的图像水印算法,将单色图像推广到彩色图像,提高了水印对象的幅度并给出了水印的嵌入和提取的量子策略。同年,Shang[13]等人提出一种水印图像和载体图像相互独立的水印嵌入和提取策略。2018年,Zhou[14]等提出一种基于LSB方法和NEQR模型的新型量子图像隐写算法,算法为提高安全性,使用位平面加扰和阿诺德加扰方法对原始信息图像进行加扰,并且由操作者控制的k1和k2执行嵌入过程和提取过程。2018年,Li等[15]提出使用反射格雷码将灰度图像隐藏到彩色量子图像中,获得了很好的效果。2018年,Sahin等[16]提出一种基于LSBq和QRMW的量子隐写算法,算法为提高安全性,在嵌入消息图像之前,用模数方法和希尔伯特置乱方法对消息图像进行处理。上述这些量子图像信息隐藏方法均基于灰度图像或真彩色图像进行信息隐藏。针对量子索引图像信息隐藏技术,本文提出一种SoC信息隐藏算法,通过改变量子索引图像的像素索引值进行信息隐藏,具有较好的安全性。
本文首先介绍了量子索引图像的表示模型[9],并将其与NEQR[4]和QRMW[7]量子表示模型进行比较分析。在此基础上给出量子索引图像SoC信息隐藏算法的线路实现,并对线路复杂度进行分析,通过仿真实验从视觉质量、鲁棒性、嵌入容量和安全性方面验证该算法的可行性和有效性。
2 量子索引图像的表示模型
经典索引图像包含数据矩阵和调色板矩阵两种数据结构。数据矩阵存储的是像素颜色值在调色板矩阵中的下标,每个下标对应调色板矩阵中一个颜色值。调色板矩阵存储的是颜色值,大小为m×3,3列分别表示R、G、B三个颜色分量,每个颜色分量由8位二进制数表示,m的值由数据矩阵的像素值域决定,通常为256。索引图像通常将数据矩阵和调色板矩阵一起存储。
量子索引图像表示模型包含量子数据矩阵|QData〉和量子调色板矩阵|QMap〉2种数据结构,均采用量子比特序列的基本态来存储信息。
2.1 量子数据矩阵
对于一幅大小为2n×2n,位深度为q的索引图像,其量子数据矩阵|QData〉表示为
(1)
其中,
为量子索引图像像素的二维位置坐标;
为像素索引值,即调色板矩阵的颜色下标。量子数据矩阵使用2n+q个量子比特。
2.2 量子调色板矩阵
对于位深度为q的索引图像,其量子调色板矩阵|QMap〉表示为
(2)
其中,
表示调色板矩阵的颜色下标;
分别为调色板中R、G、B三基色的颜色值。量子调色板矩阵使用q+24 个量子比特。
2.3 与其他量子彩色图像表示模型的比较
与文献[9]提出的量子索引图像表示模型类似,NEQR[4]和QRMW[7]均采用量子比特序列的基本态来表示量子彩色图像,因此从使用的量子比特数和制备复杂度方面对3种模型进行比较。以一幅大小为2n×2n,位深度为q,颜色范围为224的彩色图像为例,结果如表1所示。
从使用的量子比特数来看,量子索引图像表示模型使用2n+2q+24个量子比特,多于NEQR和QRMW;不过从制备复杂度来看,由于通常位深度q=8,与图像尺寸无关,因此,当n≥5时,即图像尺寸不小于32×32时,量子索引图像表示模型的制备复杂度低于NEQR和QRMW,且随着图像尺寸的增大,量子索引图像表示模型在制备复杂度上的优势越明显。
3 量子线路中的基本模块
本节对量子索引图像SoC信息隐藏算法中使用的基本量子线路模块进行说明与设计。其中,量子比较器(COMP)使用文献[17]中的量子线路,量子交换器(SWAP)使用文献[18]中的量子线路,量子减法器(SUB)使用文献[19]中的量子线路。
3.1 量子取差的绝对值模块
量子取差的绝对值模块(ABS-SUB)对于给定输入|a〉和|b〉,要求输出|abs(a-b)〉,abs表示取绝对值,
具体线路实现如图1所示。首先比较|a〉和|b〉的大小,当|a〉<|b〉时,交换|a〉和|b〉,使量子交换器的输出按降序排序,然后输入到量子减法器计算差值即可得到|abs(a-b)〉。
3.2 量子重复判别模块
量子重复判别模块(IS-REPEAT)的输入为|f0〉|A0〉|B0〉和|f1〉|A1〉|B1〉,输出为|f0〉|A0〉|B0〉
表1 量子索引图像表示模型与NEQR和QRMW的比较
Tab.1 Comparison of Quantum Indexed Image Representation Model with NEQR and QRMW
量子图像表示模型 使用的量子比特数制备复杂度 量子索引图像 QData>QMap>QData>+QMap>2n+qO(qn·22n)q+24O(12q·2q)2n+2q+24O(qn·22n+12q·2q)NEQR 2n+24O(24n·22n)QRMW 2n+10O(32(n+1)·22n)
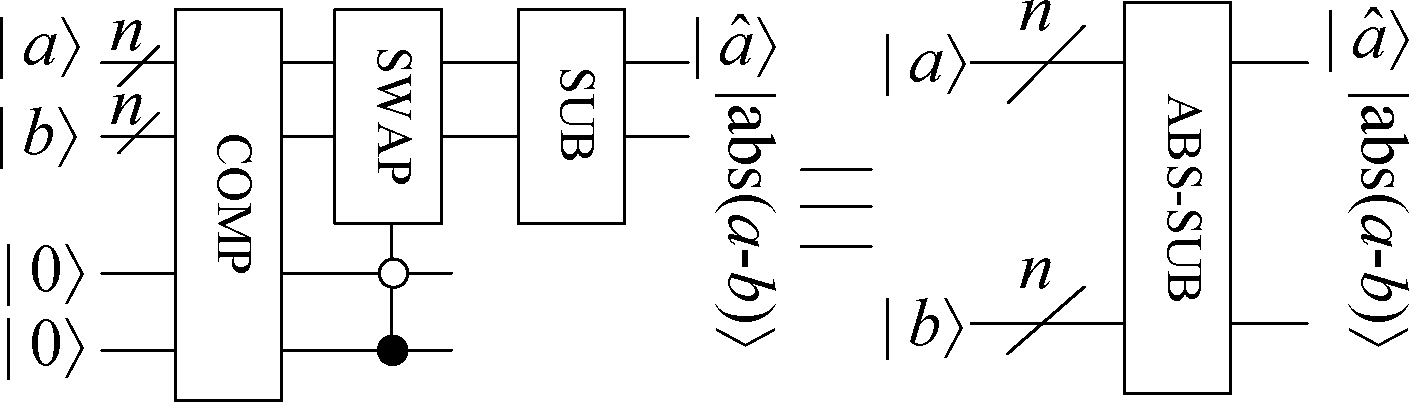
图1 量子取差的绝对值模块 Fig.1 Quantum absolute difference module
和
量子线路如图2所示,其功能为当|f0〉=|1〉且|f1〉=|1〉时,如果|A0〉=|A1〉,则置|f1〉=|0〉。其中
图2 量子重复判别模块 Fig.2 Quantum repeat discrimination module
4 基于SoC算法的量子索引图像信息隐藏
4.1 SoC信息隐藏算法
SoC算法是一种应用在索引图像上的信息隐藏算法,首先计算载体索引图像调色板矩阵中任意两个颜色值之间的欧式距离,然后求颜色值中R、G、B三个颜色分量的数值之和并对2求余数(1或0),也就是颜色值之和的奇偶性,记为e。当嵌入消息时,若消息比特位(1或0)与载体像素对应调色板中颜色值的e值相同,则该载体像素的颜色不发生变化。否则,将该载体像素的颜色替换为与其欧式距离最小且e值与消息比特位相同的颜色。当提取消息时,索引图像的像素对应调色板中颜色值的e值即为嵌入的消息。
4.2 基于SoC算法的量子索引图像信息嵌入
首先计算调色板中任意两个颜色值之间的距离,组成颜色对;其次对颜色对中两个颜色值e值不同的颜色对进行标记,初步确定有效颜色对;接着对颜色对进行拆分,按照距离对拆分后的颜色对进行升序排序;再次对排序后的颜色对进行筛选,最终确定2q对有效颜色对;最后将颜色对组装在一起,根据颜色对对载体图像进行消息嵌入。具体分为以下7个步骤。
(1)计算调色板中任意两个颜色值之间的距离。由于当前量子计算中还无法实现如开方等复杂运算,这里将计算颜色值(Ri,Gi,Bi)和(Rj,Gj,Bj)之间的欧氏距离
替换为计算曼哈顿距离dji=|Rj-Ri|+|Gj-Gi|+|Bj-Bi|。复制调色板矩阵
为量子态
和
以|QMapi〉和|QMapj〉作为输入,计算调色板矩阵中任意两个颜色值之间的距离,量子线路如图3所示。3个量子取差的绝对值模块分别用于计算R、G、B三基色的差的绝对值,2个量子加法器(ADDER)[19]用于对绝对值进行求和,最后得到量子颜色对矩阵
其中|dji〉≥|0〉为调色板矩阵中位置索引|j〉和|i〉上两个颜色值之间的距离,且|dji〉=|dij〉。这里,由于R、G、B三基色分别使用8位量子比特表示,经过2个量子加法器求和运算,|dji〉使用10位量子比特表示。
图3 计算任意两个颜色值之间的距离
Fig.3 Calculate the distance between any two color values
(2)比较颜色对|Qcolorpair〉中两个颜色值的|e〉值,相同则将有效标记位|fji〉置为|0〉,不同则置为|1〉。根据调色板矩阵|QMap〉中颜色值的|e〉值(即R、G、B颜色值二进制最低位的异或运算结果)确定颜色对|Qcolorpair〉中两个颜色值的|e〉值|ej〉和|ei〉。比较|ej〉和|ei〉,不同时将初值为|0〉的有效标记位|fji〉置为|1〉。最后得到量子态
具体线路如图4所示。这里,有效标记位|fji〉使用1位量子比特表示,|e〉值使用1位量子比特表示。
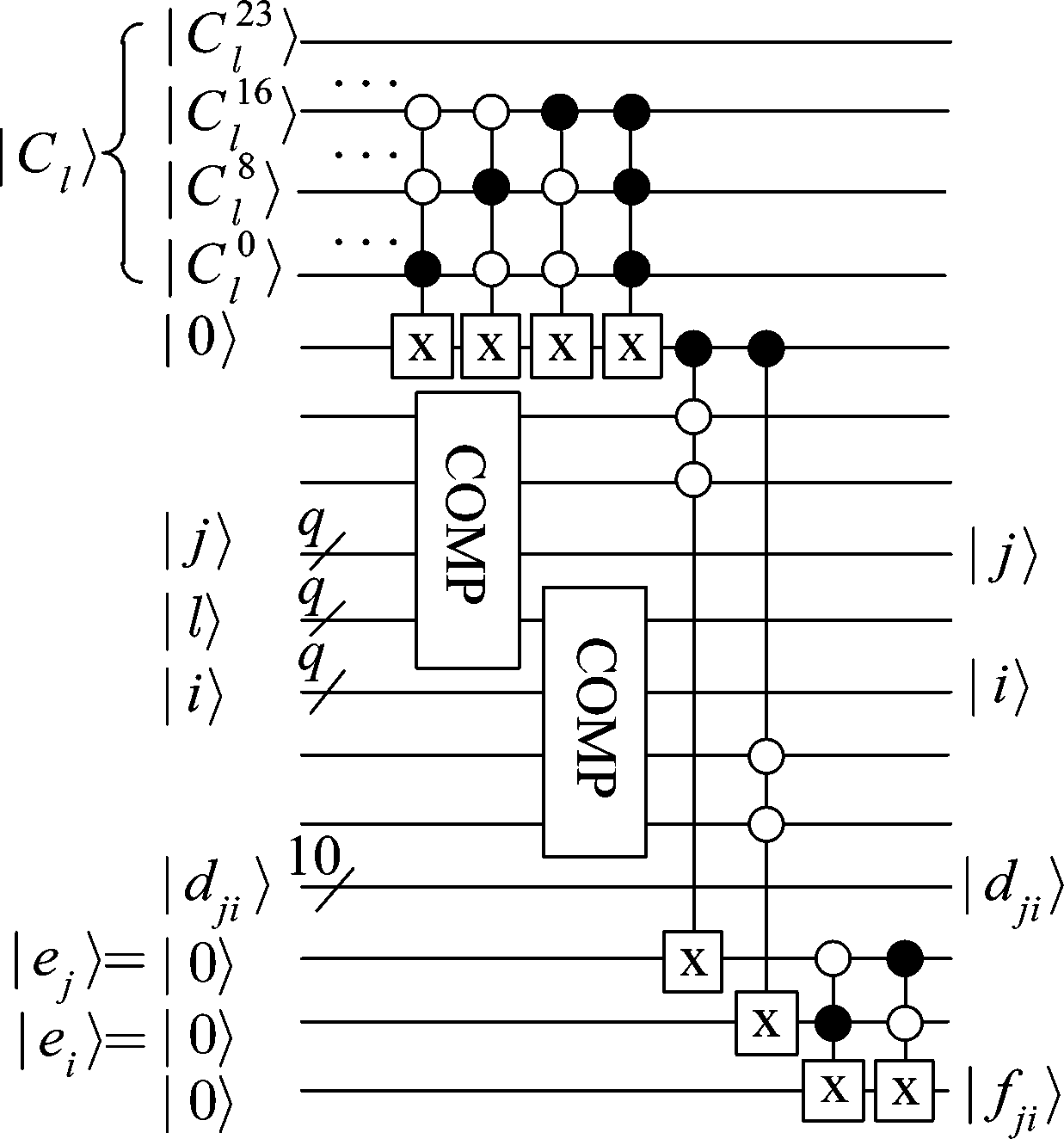
图4 确定有效标记位
Fig.4 Determine valid flag bit
(3)将量子态
拆分为2q×2q个独立量子态|d00〉|0〉|0〉|f00〉,|d01〉|0〉|1〉|f01〉,…,|d2q-1,2q-1〉|2q-1〉|2q-1〉|f2q-1,2q-1〉。比较叠加态|ji〉与|00〉,|01〉,…,|2q-1,2q-1〉,如果相等,将|d00〉,|d01〉,…,|d2q-1,2q-1〉分别设置为相应的|dji〉,同时也将|f00〉,|f01〉,…,|f2q-1,2q-1〉分别设置为相应的|fji〉,具体线路如图5所示。这里,|f00〉,|f01〉,…,|f2q-1,2q-1〉各使用1位量子比特表示。
(4)采用冒泡排序算法,利用量子比较交换(COMP-SWAP)模块[9],对|d00〉|00〉|f00〉,|d01〉|01〉|f01〉,…,|d2q-1,2q-1〉|2q-1,2q-1〉|f2q-1,2q-1〉按照距离|dji〉进行升序排序输出,具体线路如图6所示。
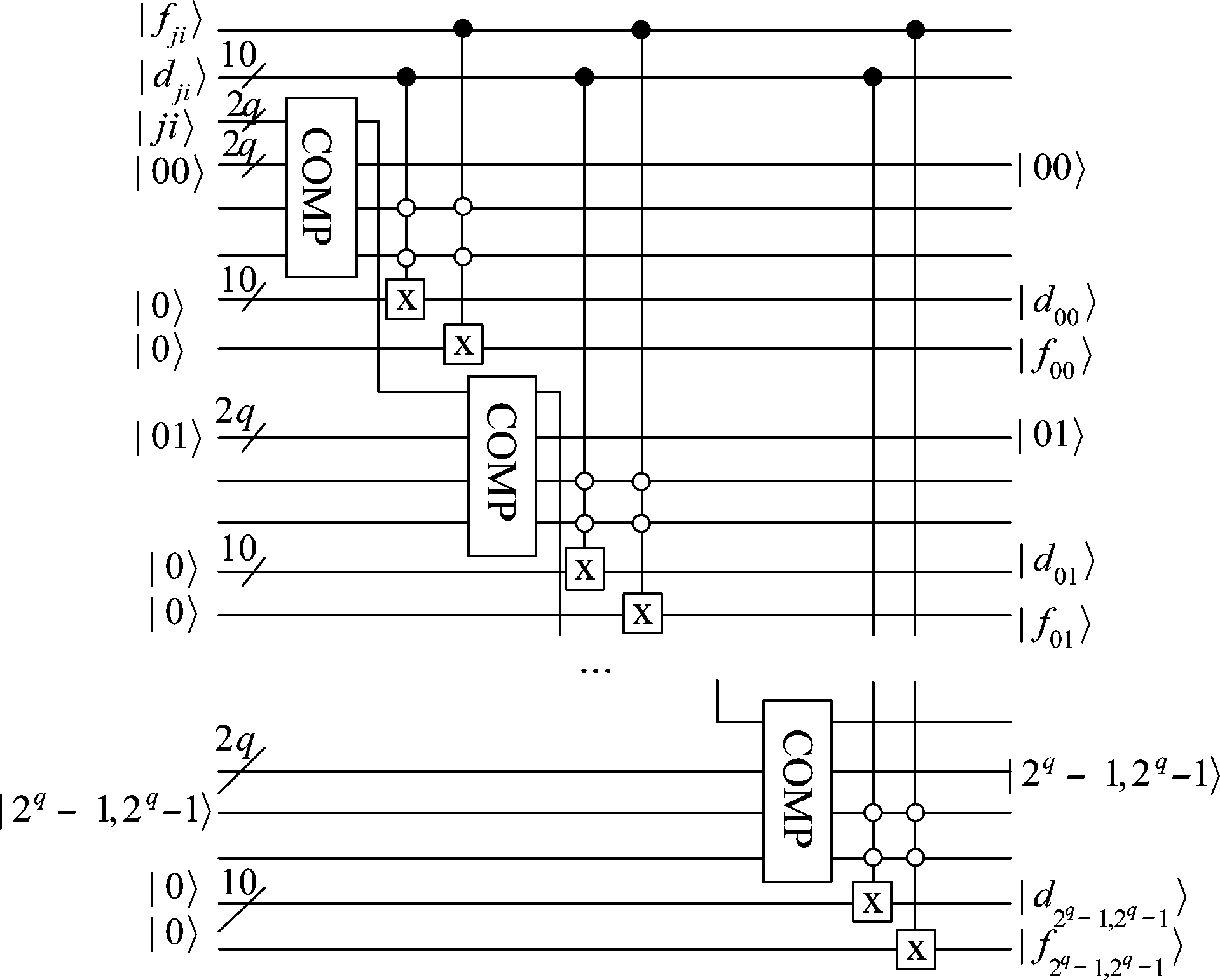
图5 拆分颜色对
Fig.5 Split color pairs
(5)按照颜色对距离最小且|e〉值相反的原则,对颜色对进行筛选,为每一个颜色均找到一个与它相匹配的颜色。利用量子重复判别模块,按照颜色对距离从小到大顺序,依次将每一对有效标记位
的颜色对与前面所有颜色对进行比较,如果该颜色对中第一个颜色从未在前面所有颜色对中有效标记位的第一种颜色中出现,则保持该颜色对的有效标记位
为|1〉不变,否则将置为|0〉。由于调色板矩阵中有2q个颜色,因此最终成功匹配的颜色对数量为2q。具体量子线路如图7所示。
(6)将步骤(5)得到的2q×2q个量子态组装成
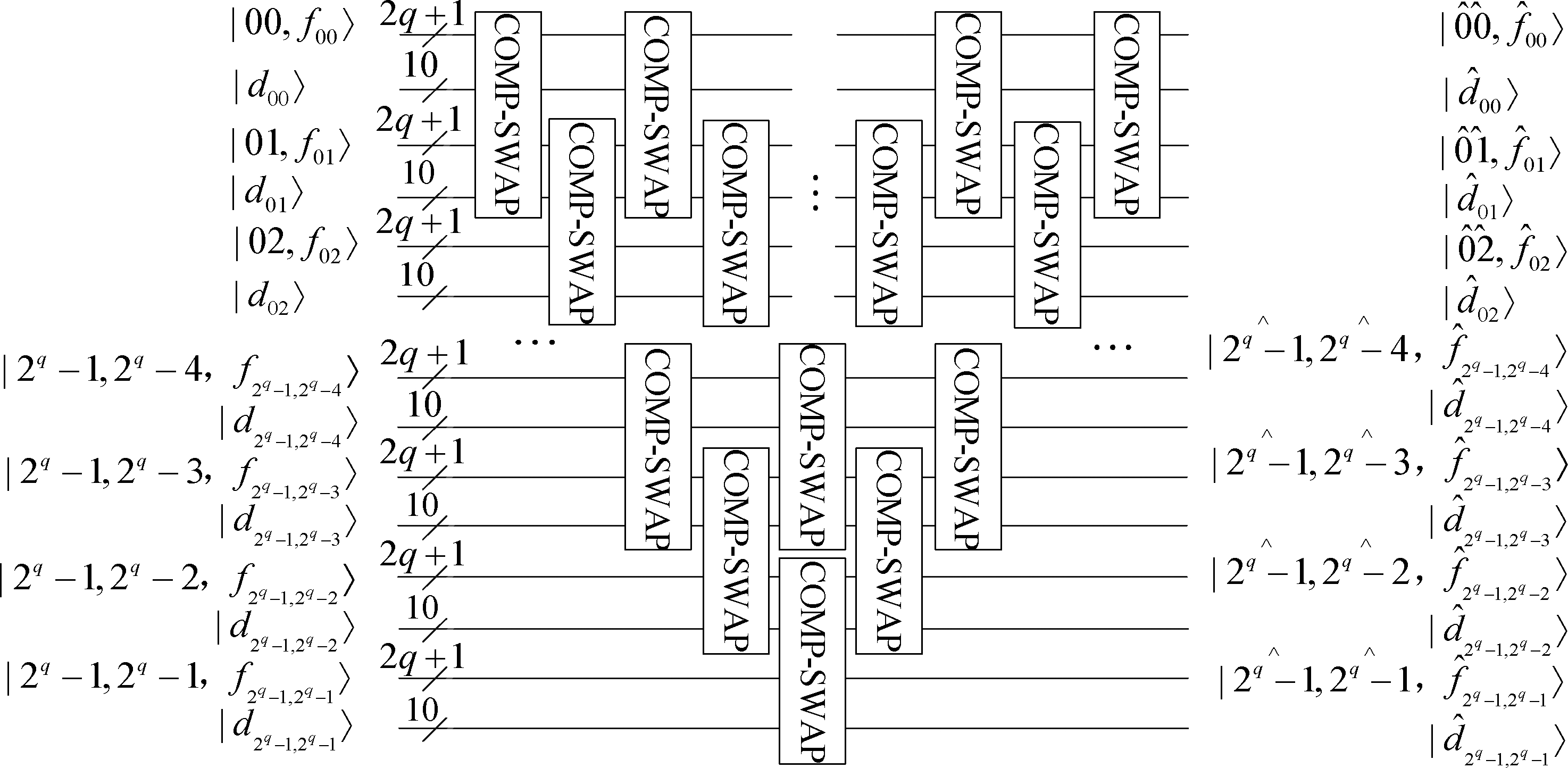
图6 按照距离对颜色对进行升序排序
Fig.6 Sort color pairs in ascending order by distance
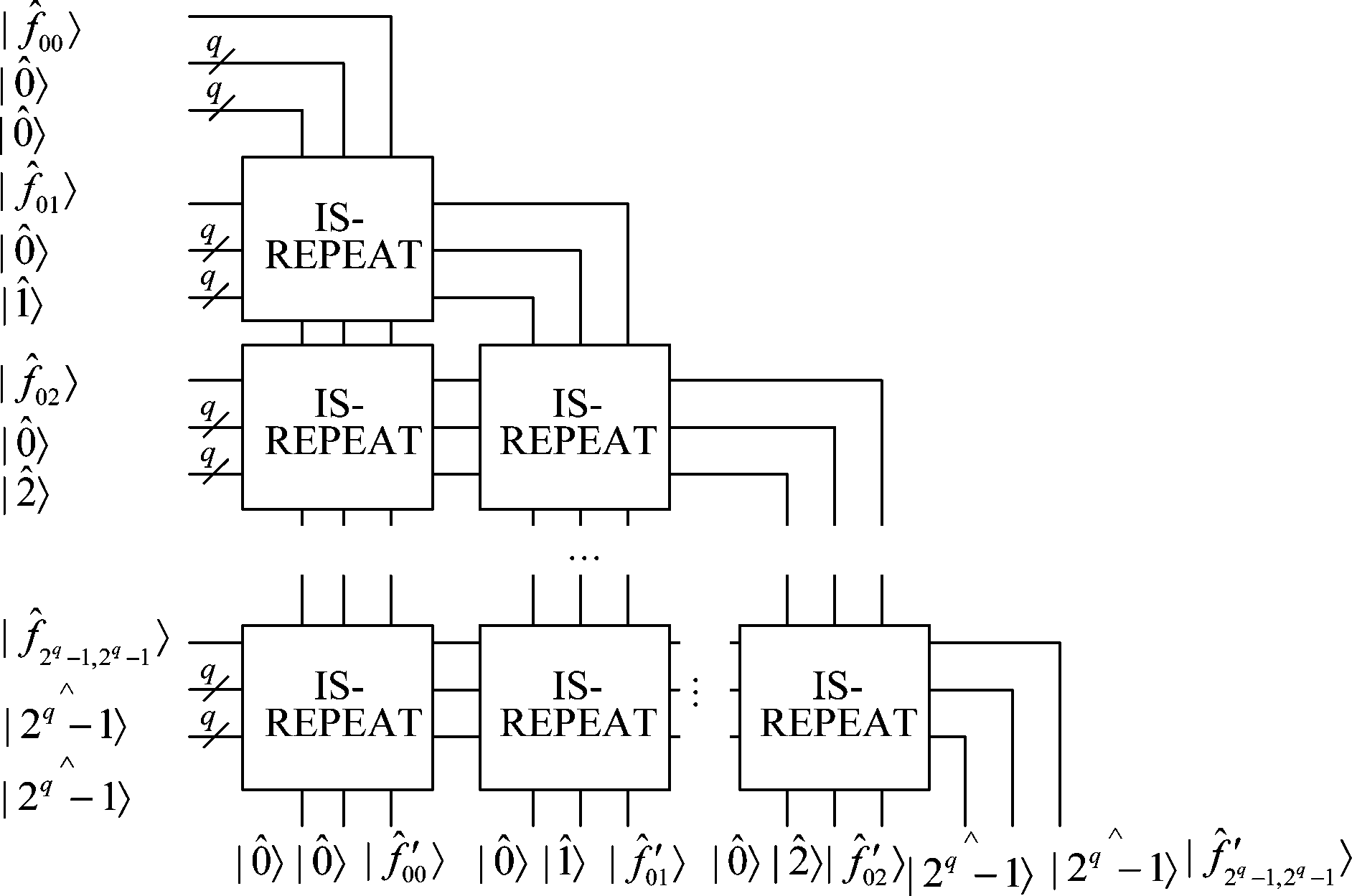
图7 筛选颜色对
Fig.7 Filter color pairs
具体线路如图8所示,其中辅助量子比特|gji〉使用1位量子比特表示。使用初值为|0〉的辅助量子比特|gji〉,与量子颜色对矩阵|Qcolorpair〉纠缠为量子态
来存储颜色对|ji〉的有效标记位。比较叠加态∑|j〉|i〉与
是否相等,如果相等则将
设置给相应的|gji〉。
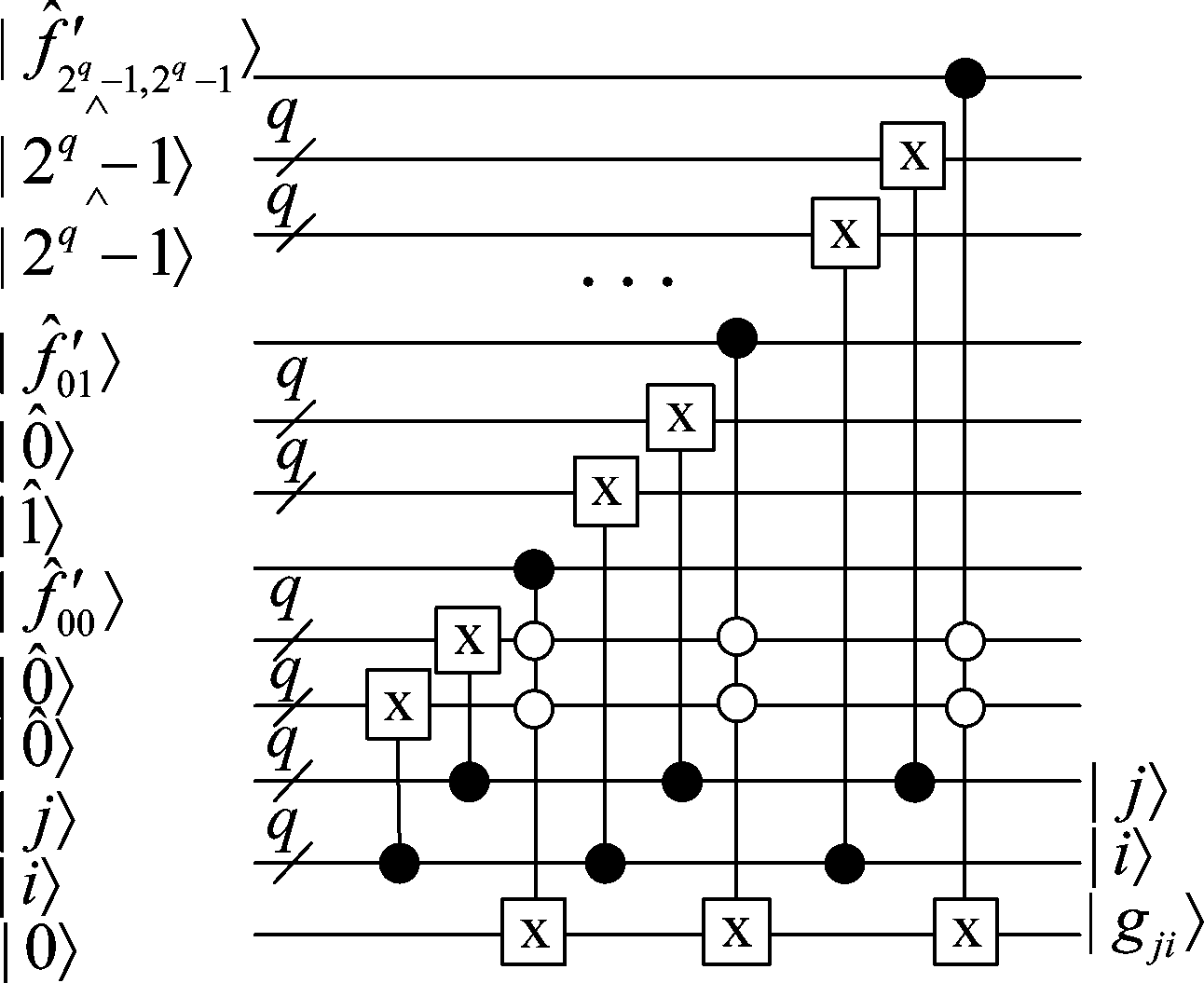
图8 组装颜色对
Fig.8 Assemble color pair
(7)嵌入消息。设待嵌入的2n×2n消息比特为
将|M〉嵌入到数据矩阵
中的过程如图9所示。首先,比较待嵌入的消息比特与载体索引图像像素的颜色值|e〉值,如果相等,则载体图像像素的索引值保持不变。否则,当|IYX〉=|j〉且|gji〉=|1〉时,将|IYX〉设置为|i〉,最后得到嵌入消息后的量子索引图像数据矩阵
图9 嵌入消息
Fig.9 Embed message
4.3 基于SoC算法的量子索引图像信息提取
待提取的消息即为量子索引图像数据矩阵中每个像素对应调色板中颜色值的|e〉值,提取消息的量子线路如图10所示。可以看出,该提取算法是一种盲消息提取算法,提取消息时只需嵌入消息后的量子索引图像即可。
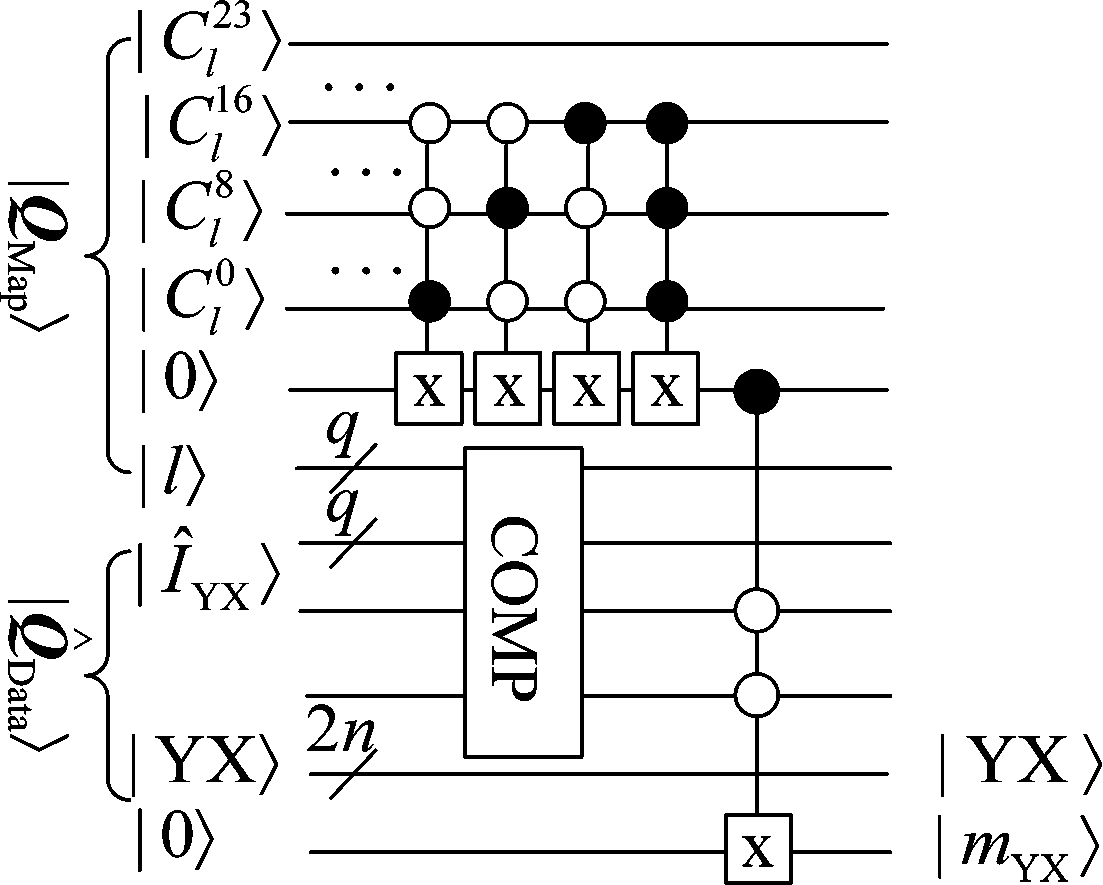
图10 提取消息
Fig.10 Extract message
4.4 线路复杂度分析
本文选用CNOT门和非门作为基本逻辑门。
(1) 逻辑门复杂度换算关系和基本模块的复杂度[19]
1个2-CNOT门等价于6个CNOT门,复杂度为6。1个交换门等价于3个CNOT门,复杂度为3。1个n-CNOT(n≥3)门的复杂度为12n-9。1个2-受控交换门可分解为3个3-CNOT门,复杂度为81。量子比较器的复杂度为48n2-36n+18。量子加法器和量子减法器的复杂度为28n-12。
(2) 量子基本模块的复杂度
量子取差的绝对值模块包含1个量子比较器,n个2-受控交换门和1个量子减法器,所以复杂度为48n2+73n+6。量子重复判别模块包含1个量子比较器,1个CNOT门,1个4-CNOT门,所以复杂度为192n2-144n+58。量子比较交换模块的复杂度为48m2+45m+81n+18[9]。
(3) 量子索引图像信息嵌入和提取过程的复杂度
图3所示线路包含3个量子取差的绝对值模块和2个量子加法器,复杂度为11438。图4所示线路包含2个量子比较器,6个3-CNOT门和2个2-CNOT门,复杂度为96q2-72q+210,即O(96q2)。图5所示线路包含22q个量子比较器和22q×11个3-CNOT门,复杂度为22q(192q2-72q+315),即O(192q2×22q)。图6所示线路包含
个量子比较交换模块,复杂度为(5349+162q)×(24q-1-22q-1),即O(162q×24q-1)。图7所示线路包含1+2+3+…+(22q-2q-1)=24q-23q+2q-1个量子重复判别模块,复杂度为106×(24q-23q+2q-1),即O(106×24q)。图8所示线路包含q×22q+1个CNOT门和q×22q个3-CNOT门,复杂度为29q×22q,即O(29q×22q)。图9所示线路包含2个量子比较器,3q个2-CNOT门,4个3-CNOT门和1个5-CNOT门,复杂度为192n2-72n+48q2-178+195,即O(192n2+48q2)。图10所示线路包含1个量子比较器和5个3-CNOT门,复杂度为48q2-36q+153,即O(48q2)。在索引图像中,由于位深度q通常为与图像尺寸无关的常数,因此上述复杂度均可认为是多项式级的。
5 仿真实验
目前还没有量子计算机,本文的所有实验都在经典计算机上使用Matlab(R2014a)软件进行仿真。实验数据来自USC-SIPI图像数据库。本文将从视觉质量、嵌入容量、鲁棒性和安全性4个方面对量子索引图像SoC信息隐藏算法进行评价与分析,并与文献[9]和文献[11]中提出的量子EzStego和量子LSB信息隐藏算法进行比较。利用图11(a)至图11(f)6幅彩色图像作为载体图像,图11(g)和图11(h)2幅黑白图像作为消息图像。首先利用MATLAB将这8幅图像大小转化为256×256,然后将tiff格式的载体图像转化为索引图像,消息图像转化为二值图像,在此基础上进行图像信息隐藏操作。
将图11(h)分别嵌入到图11(a)至图11(f)的效果如图12(a)至图12(f)所示。
(1)视觉质量
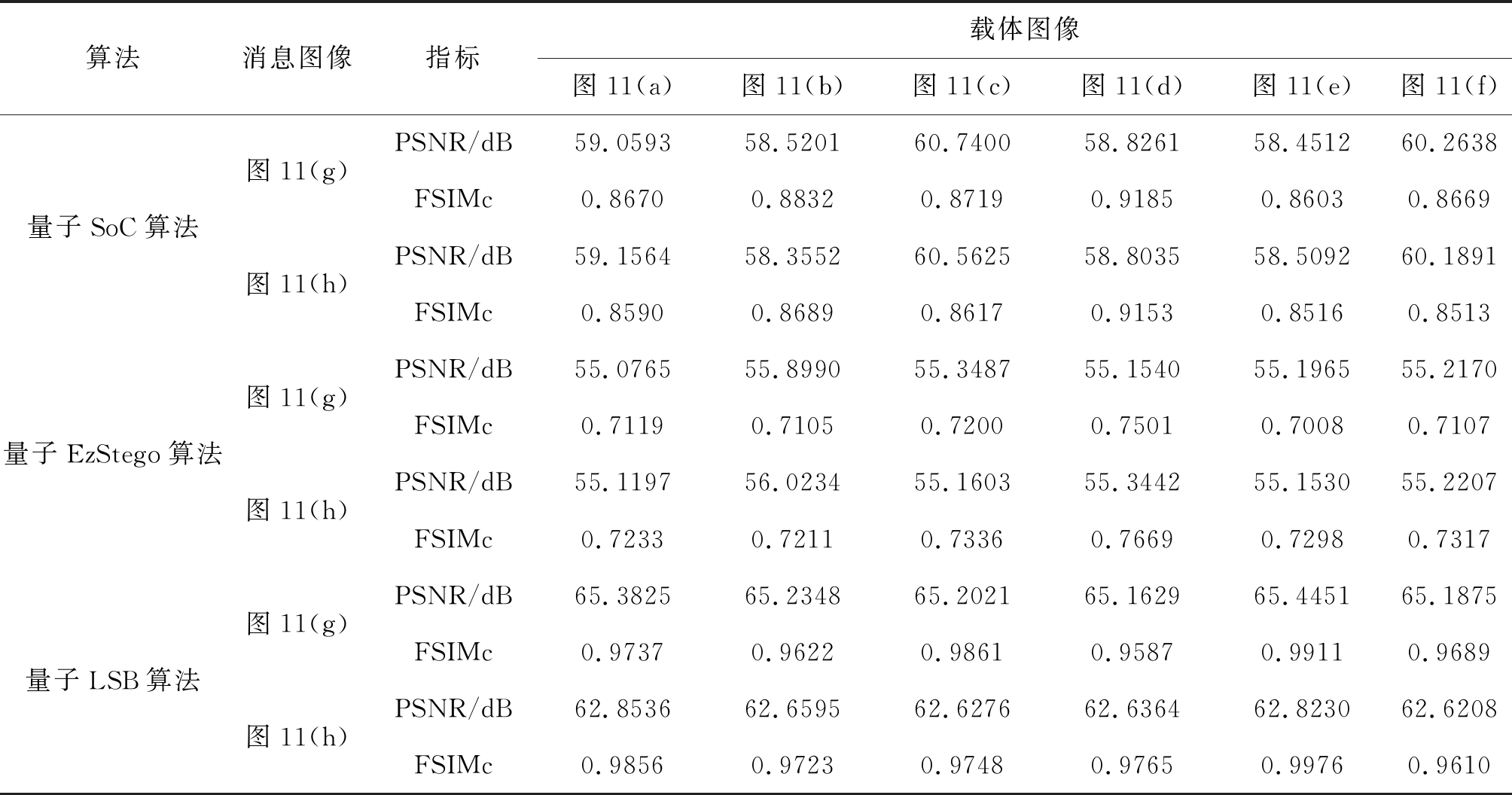
采用峰值信噪比(peak signal to noise ratio, PSNR)和特征相似性(feature similarity, FSIMc)衡量嵌入消息前后的量子索引图像的视觉质量效果。PSNR的计算公式参考文献[20],数值越接近100说明比较的两个图像越接近。FSIMc的计算公式参考文献[21],数值越接近1说明比较的两个图像越接近。分别采用量子SoC算法、量子EzStego算法
图11 载体图像和消息图像
Fig.11 Carrier images and message images
图12 嵌入图11(h)的载体图像
Fig.12 Carrier images embedded with
Fig.11(h)
表2 3种算法嵌入消息前后载体图像的PSNR和FSIMc
Tab.2 PSNR and FSIMc of carrier images before and after embedding message by 3 algorithms
算法消息图像指标载体图像图11(a)图11(b)图11(c)图11(d)图11(e)图11(f)量子SoC算法图11(g)图11(h)PSNR/dB59.059358.520160.740058.826158.451260.2638FSIMc0.86700.88320.87190.91850.86030.8669PSNR/dB59.156458.355260.562558.803558.509260.1891FSIMc0.85900.86890.86170.91530.85160.8513量子EzStego算法图11(g)图11(h)PSNR/dB55.076555.899055.348755.154055.196555.2170FSIMc0.71190.71050.72000.75010.70080.7107PSNR/dB55.119756.023455.160355.344255.153055.2207FSIMc0.72330.72110.73360.76690.72980.7317量子LSB算法图11(g)图11(h)PSNR/dB65.382565.234865.202165.162965.445165.1875FSIMc0.97370.96220.98610.95870.99110.9689PSNR/dB62.853662.659562.627662.636462.823062.6208FSIMc0.98560.97230.97480.97650.99760.9610
和量子LSB算法将图11(g)和图11(h)分别嵌入到图11(a)至图11(f)中并计算PSNR和FSIMc,结果如表2所示,这些数值都在可接受范围内。从表2可以看出,量子LSB算法的PSNR和FSIMc高于其他2种算法,量子EzStego算法的PSNR和FSIMc最低,表明量子LSB算法的视觉质量优于量子SoC算法和量子EzStego算法,而量子SoC算法的视觉质量优于量子EzStego算法。这是因为采用量子LSB算法进行消息嵌入时只改变载体图像像素值的最低位,不会对颜色值产生很大的影响,而在量子SoC算法和量子EzStego算法中进行消息嵌入时是将像素索引值直接替换为调色板中另一索引值,尽管2种索引颜色值接近,但也不会优于量子LSB算法中仅替换颜色值最低位的效果;在量子SoC算法中,颜色对是根据颜色值距离最近且e值相反的规则进行匹配的;与量子SoC算法相比,在量子EzStego算法中,颜色对是根据亮度值进行匹配的,但却存在2个颜色亮度值接近,却属于2种完全不同色系,颜色值差距很大的情况,因此量子EzStego算法视觉质量最差。
(2) 嵌入容量
嵌入容量是可嵌入的消息比特位的数量与整幅图像像素数量的比值。由于在量子SoC信息隐藏算法中,每个像素可嵌入1量子比特的消息,因此嵌入容量为100%。在量子EzStego算法和量子LSB算法中,每个像素也可嵌入1量子比特的消息,因此3种算法的嵌入容量是相等的。
(3)鲁棒性
在无噪声干扰情况下,量子索引图像SoC信息隐藏方案可无失真地提取出消息图像。但是在实际应用中不可避免的会产生噪声,本文使用椒盐噪声和几何攻击(平移、缩放、剪切)来测试算法的鲁棒性,采用误码率(bit error rate, BER)作为衡量鲁棒性的指标。在本文中,误码率是指在嵌入消息的载体图像中添加椒盐噪声后提取出的错误消息比特数量占总消息比特数量的百分比。误码率越小,鲁棒性越强。
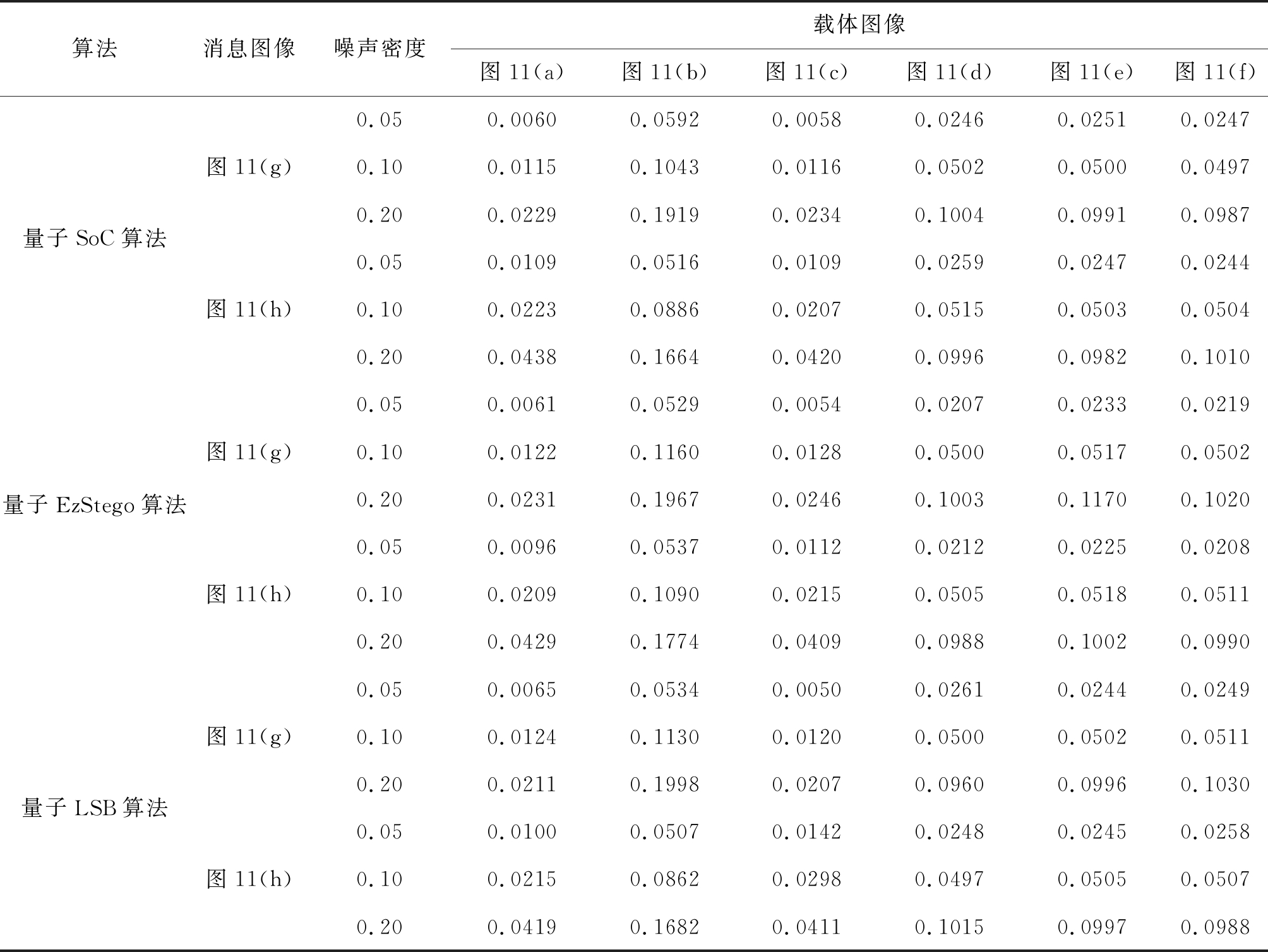
量子SoC算法、量子EzStego算法和量子LSB算法在不同噪声密度下的BER如表3所示。可以看出,添加椒盐噪声后,提取出的消息图像的误码率随着噪声密度的增加而增大。在本实验中,3种算法的鲁棒性基本一样。以向图11(d)中嵌入图11(g)为例,图13(a)至图13(c)分别给出了量子SoC算法、量子EzStego算法和量子LSB算法的BER随噪声密度的变化曲线。可以看出,BER和噪声密度基本成线性关系,3种算法的斜率都约为0.50,也就是大约有50%的椒盐噪声像素点会对提取出的消息图像产生影响。对此结果分析如下:采用量子SoC算法或量子EzStego算法提取消息依赖于索引图像像素颜色值的e值或颜色值亮度序号的最低位,添加椒盐噪声之后,即使像素索引值全部被改变,但索引值对应调色板中颜色值的e值(1或0)或颜色值亮度序号的最低位(1或0)却不会都被改变。采用量子LSB算法提取消息依赖于图像像素值的LSB(0或1),添加椒盐噪声后,虽然图像像素值被改变,在本实验中也仅有大约50%的椒盐噪声像素点的LSB被改变。
表3 3种算法在不同噪声密度下的BER
Tab.3 BER of 3 algorithms at different noise densities
算法消息图像噪声密度载体图像图11(a)图11(b)图11(c)图11(d)图11(e)图11(f)量子SoC算法图11(g)图11(h)0.050.00600.05920.00580.02460.02510.02470.100.01150.10430.01160.05020.05000.04970.200.02290.19190.02340.10040.09910.09870.050.01090.05160.01090.02590.02470.02440.100.02230.08860.02070.05150.05030.05040.200.04380.16640.04200.09960.09820.1010量子EzStego算法图11(g)图11(h)0.050.00610.05290.00540.02070.02330.02190.100.01220.11600.01280.05000.05170.05020.200.02310.19670.02460.10030.11700.10200.050.00960.05370.01120.02120.02250.02080.100.02090.10900.02150.05050.05180.05110.200.04290.17740.04090.09880.10020.0990量子LSB算法图11(g)图11(h)0.050.00650.05340.00500.02610.02440.02490.100.01240.11300.01200.05000.05020.05110.200.02110.19980.02070.09600.09960.10300.050.01000.05070.01420.02480.02450.02580.100.02150.08620.02980.04970.05050.05070.200.04190.16820.04110.10150.09970.0988
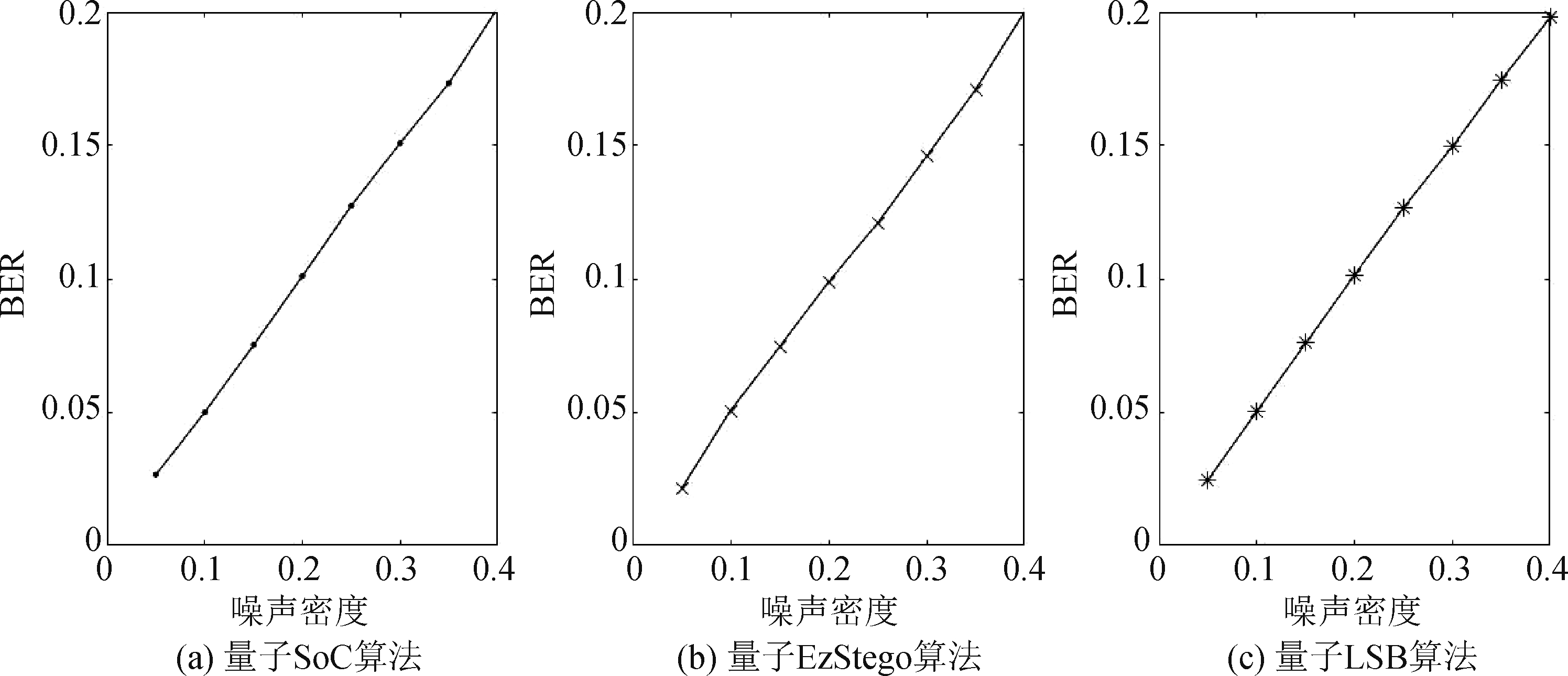
图13 3种算法在不同噪声密度下的BER曲线
Fig.13 BER curves of 3 algorithms at different noise densities
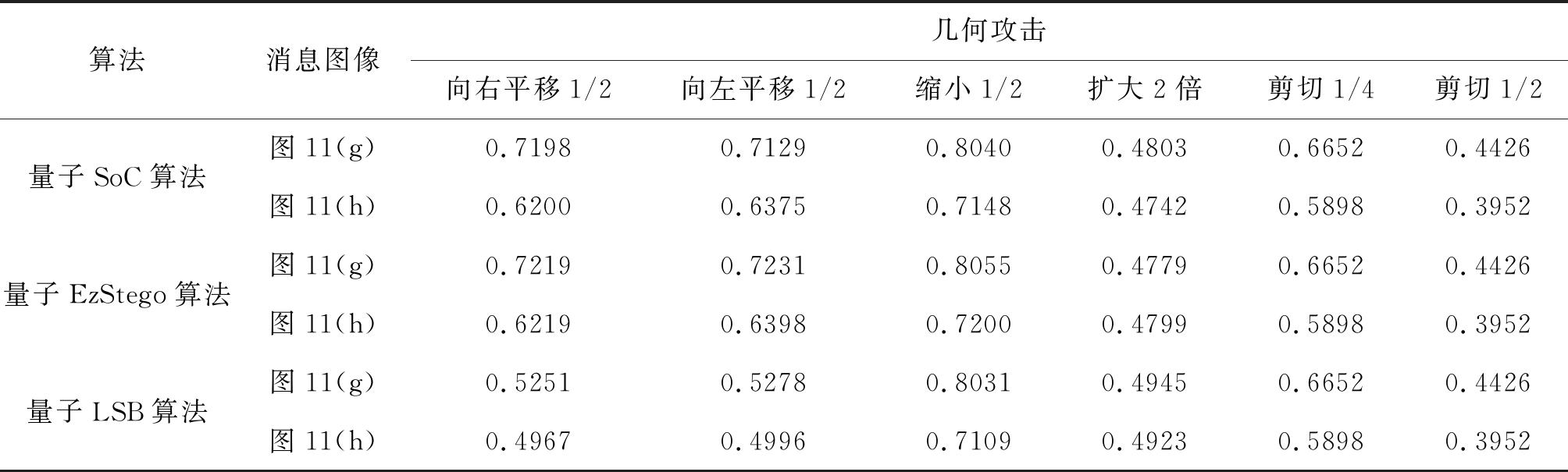
表4 3种算法在不同几何攻击下的BER
Tab.4 BER of 3 algorithms at different geometric attacks
算法消息图像几何攻击向右平移1/2向左平移1/2缩小1/2扩大2倍剪切1/4剪切1/2量子SoC算法图11(g)0.71980.71290.80400.48030.66520.4426图11(h)0.62000.63750.71480.47420.58980.3952量子EzStego算法图11(g)0.72190.72310.80550.47790.66520.4426图11(h)0.62190.63980.72000.47990.58980.3952量子LSB算法图11(g)0.52510.52780.80310.49450.66520.4426图11(h)0.49670.49960.71090.49230.58980.3952
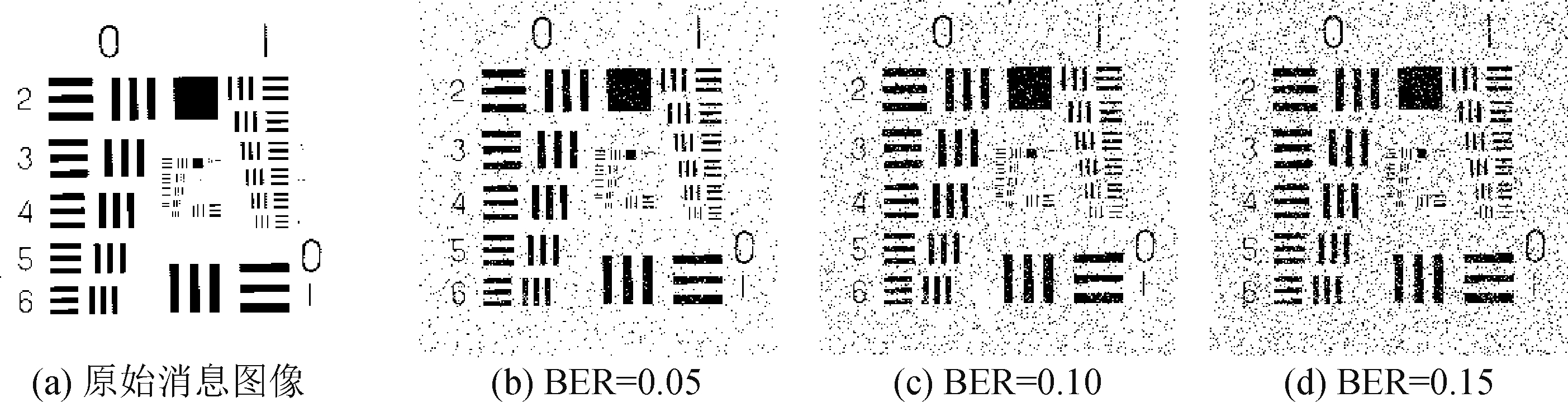
图14 量子SoC算法在不同噪声密度下提取的消息图像
Fig.14 Message images extracted under different noise densities by quantum SoC algorithm
以向图11(d)中嵌入图11(g)和(h)为例,表4给出了量子SoC算法、量子EzStego算法和量子LSB算法在不同几何攻击下的BER。可以看出,在添加不同类型的几何攻击后,3种算法的误码率都很大,说明3种算法对于几何攻击的抵抗性都很差。这是因为3种算法都是基于空域的信息隐藏算法,而空域算法的抗几何攻击性都比较差。基于变换域的算法和一些较复杂的空域算法的抗几何攻击性比较强,但是就目前对量子图像信息隐藏算法而言,较复杂的空域算法还无法使用量子方式实现。
以向图11(d)中嵌入图11(g)为例,量子SoC算法在不同噪声密度下提取出的消息图像如图14所示。可以看出,随着噪声密度的增加,提取出的消息图像逐渐模糊,但是仍然可以辨认出消息图像。
(4)安全性
与量子LSB算法相比,基于量子SoC算法和量子EzStego算法的量子索引图像信息隐藏方案具有更好的安全性。因为量子SoC算法和量子EzStego算法并没有真正的直接替换载体图像的LSB,而是改变了载体图像指向调色板矩阵的索引值。采用量子SoC算法和量子EzStego算法,以嵌入消息图像11(g)后的载体图像11(d)为例,分别对其调色板矩阵、数据矩阵以及转换为真彩色后的图像采用LSB算法进行消息提取,结果如图15(a)至图15(e)所示。采用量子LSB算法,同样将消息图像11(g)嵌入到载体图像11(d)中,提取出的消息图像如图15(f)所示。
图15(a)是与调色板等大的二值图像,大小为256×3,是一幅完全没有意义的图像。图15(b)至图15(e)是与载体图像等大的二值图像,可以从中看到载体图像的轮廓,但完全看不到消息图像的痕迹。而图15(f)是提取出的完整的消息图像。
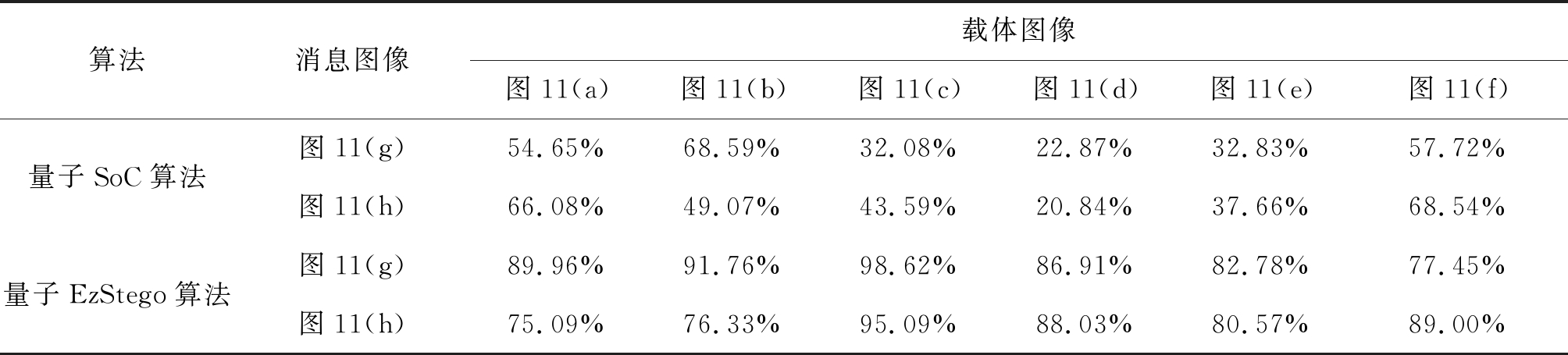
对于量子SoC算法和量子EzStego算法,本文采用成对分析法[22]进行安全性对比。通过对嵌入消息后的载体图像进行成对分析,得到估计的消息嵌入容量,结果如表5所示。可以看出,量子SoC算法的预测准确率小于量子EzStego算法,也就是说,量子SoC算法抵抗成对分析法的性能优于量子EzStego算法,具有更好的安全性。
图15 3种算法提取的消息的对比
Fig.15 Comparison of extracted message based on 3 algorithms
表5 基于成对分析法的预测嵌入容量
Tab.5 Predicted embedding capacity based on pairs analysis
算法消息图像载体图像图11(a)图11(b)图11(c)图11(d)图11(e)图11(f)量子SoC算法图11(g)图11(h)54.65%66.08%68.59%49.07%32.08%43.59%22.87%20.84%32.83%37.66%57.72%68.54%量子EzStego算法图11(g)图11(h)89.96%75.09%91.76%76.33%98.62%95.09%86.91%88.03%82.78%80.57%77.45%89.00%
6 结论
本文对量子索引图像的信息隐藏技术进行研究,提出基于量子索引图像的SoC信息隐藏算法。与量子LSB算法相比,尽管该方法在视觉质量方面并未优于量子LSB算法,不过该方法由于没有直接改变载体图像像素的LSB,而是改变载体图像指向调色板矩阵的索引值,因此具有更好的安全性。与量子EzStego算法相比,该方法的颜色对匹配方案更为合理,因此具有更好的视觉质量和安全性。与经典SoC隐藏算法相比,该方法虽然在视觉质量、嵌入容量、鲁棒性和安全性方面并未有所提高,但可在将来的量子计算机上执行,并且具有更高的并行性和处理速度。
本文提出的量子索引图像信息隐藏方法是量子图像处理的重要发展,其研究刚刚处于起步阶段。未来的研究方向将重点放在:(1)如何采用更少的量子比特进行量子索引图像的表示和存储,并且便于图像检索、颜色变换和几何变换等操作。(2)进行量子索引图像的应用研究,如进一步提高量子索引图像信息隐藏算法的性能、研究量子索引图像水印策略等。
[1] Venegas-Andraca S E, Bose S. Storing, processing and retrieving an image using quantum mechanics[C]∥ Proceedings of the SPIE: Society of Photo-Optical Instrumentation Engineers, Bellingham, USA, 2003, 5105: 137-147.
[2] Latorre J I. Image compression and entanglement. arXiv: quant-ph/0510031, 2005.
[3] Le P Q, Dong F, Hirota K. A flexible representation of quantum images for polynomial preparation, image compression, and processing operations[J]. Quantum Information Processing, 2011, 10(1): 63- 84.
[4] Zhang Yi, Lu Kai, Gao Yinghui, et al. NEQR: a novel enhanced quantum representation of digital images[J]. Quantum Information Processing, 2013, 12(8): 2833-2860.
[5] Sang Jianzhi, Wang Shen, Li Qing. A novel quantum representation of color digital images[J]. Quantum Information Processing, 2017, 12(6): 42.
[6] Li Haisheng, Chen Xiao, Xia Haiying, et al. A quantum image representation based on bitplanes[J]. IEEE Access, 2018, 6: 62396- 62404.
[7] 
ahin E, Yilmaz 
. QRMW: Quantum representation of multi wavelength images[J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2018, 26(2): 768-779.
[8] Wang Ling, Ran Qiwen, Ma Jing, et al. QRCI: a new quantum representation model of color digital images[J]. Optics Communications, 2019, 438: 147-158.
[9] 王兵, 郝梦奇, 李盼池, 等. 量子索引图像的描述方法与隐写算法[J]. 计算机辅助设计与图形学学报, 2019, 31(11): 1995-2006.
Wang Bing, Hao Mengqi, Li Panchi, et al. Description method and steganography of quantum indexed images[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(11): 1995-2006.(in Chinese)
[10]Jiang Nan, Wang Luo. A novel strategy for quantum image steganography based on Moiré pattern[J]. International Journal of Theoretical Physics, 2015, 54(3): 1021-1032.
[11]Jiang Nan, Zhao Na, Wang Luo. LSB based quantum image steganography algorithm[J]. International Journal of Theoretical Physics, 2016, 55(1): 107-123.
[12]肖红, 李盼池, 李滨旭. 改进的量子图像水印算法[J]. 信号处理, 2017, 33(2): 135-143.
Xiao Hong, Li Panchi, Li Binxu. Improved Quantum Image Watermarking Algorithm[J]. Journal of Signal Processing, 2017, 33(2): 135-143.(in Chinese)
[13]尚福华, 李盼池. 彩色图像的量子水印算法[J]. 信号处理, 2017, 33(11): 1424-1435.
Shang Fuhua, Li Panchi. Quantum watermarking algorithm for color images[J]. Journal of Signal Processing, 2017, 33(11): 1424-1435.(in Chinese)
[14]Zhou Rigui, Luo Jia, Liu Xingao, et al. A novel quantum image steganography scheme based on LSB[J]. International Journal of Theoretical Physics, 2018, 57(6): 1848-1863.
[15]Li Panchi, Lu Aiping. LSB-based steganography using reflected Gray code for color quantum images[J]. International Journal of Theoretical Physics, 2018, 57(5): 1516-1548.
[16]ahin E, Yilmaz . A novel quantum steganography algorithm based on LSBq for multi-wavelength quantum images[J]. Quantum Information Processing, 2018, 17(11): 319.
[17]王冬, 刘志昊, 朱皖宁, 等. 基于多目标扩展通用Toffoli门的量子比较器设计[J]. 计算机科学, 2012, 39(9): 302-306.
Wang Dong, Liu Zhihao, Zhu Wanning, et al. Design of quantum comparator based on extended general Toffoli gates with multiple targets[J]. Computer Science, 2012, 39(9): 302-306.(in Chinese)
[18]Li Panchi, Liu Xiande, Xiao Hong. Quantum image median filtering in the spatial domain[J]. Quantum Information Processing, 2018, 17(3): 17- 49.
[19]姜楠. 量子图像处理[M]. 北京: 清华大学出版社, 2016: 20-22, 49-50.
Jiang Nan. Quantum Image Processing[M]. Beijing: Tsinghua University Press, 2016: 20-22, 49-50.(in Chinese)
[20]Zhou Yang, Zhou Rigui, Liu Xingao, et al. A Quantum Image Watermarking Scheme Based on Two-Bit Superposition[J]. International Journal of Theoretical Physics, 2019, 58: 950-968.
[21]Zhang Lin, Zhang Lei, Mou Xuanqin, et al. FSIM: A feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378-2386.
[22]Chaeikar Shogae S, Ahmadi A. Ensemble SW image steganalysis: A low dimension method for LSBR detection[J]. Signal Processing: Image Communication, 2018, 70: 233-245.
