1 引言
杂波环境下的多目标跟踪问题是目标跟踪的难点之一,数据关联是有效的解决这一问题的主要方法[1]。由于杂波的干扰,回波的个数往往不等于目标的数目,导致无法判定量测数据是来自跟踪的目标还是来自于虚警。数据关联过程就是为了消除传感器观测和多目标跟踪环境中存在的不确定性和随机性,数据关联是否准确,直接影响了后续目标跟踪算法的估计结果。
在密集杂波环境下,概率数据关联(PDA)算法能较好的解决单目标跟踪问题,但无法对多目标同时进行跟踪[2];针对多目标跟踪问题,在概率数据关联算法的基础上,衍生出了联合概率数据关联(JPDA)算法,该方法综合考虑各个量测的目标来源情况,能够对密集杂波环境下的多目标进行有效跟踪。然而,JPDA算法较复杂,其可行联合事件的个数随回波数成指数增长,在拆分确认矩阵时会出现组合爆炸的现象[3],导致其计算量非常大。文献[4]利用模糊隶属度表示关联概率,避免拆分确认矩阵的拆分;文献[5]在经验JPDA算法的基础上,通过阈值处理,减少了可行联合事件的个数;文献[6]设计了一种新的确认矩阵,并结合模糊聚类方法计算量测与目标之间的互联概率;文献[7]同样利用模糊聚类方法,将隶属度作为关联概率,并分析了公共量测对目标的影响。
为了解决JPDA算法在杂波环境下计算过于复杂的问题,提高算法的实时性,本文设计了一种简化的JPDA算法。在密集杂波环境下,回波数量大,联合事件个数呈指数增长,JPDA算法在拆分确认矩阵时,计算量会急剧上升,而且JPDA算法的关联概率计算方法十分复杂,不利于工程实践。简化JPDA算法根据量测与目标之间的互联规则计算关联概率,避免了矩阵拆分,降低了运算量,并引入公共量测影响因子进行修正,最后利用关联概率加权对各目标的运动状态和协方差进行更新。
2 联合概率数据关联
JPDA算法具有较好的多目标跟踪性能,是一种有效的数据关联算法。JPDA算法按照多目标跟踪门之间的集合关系,划分多个聚,用确认矩阵Ω表示量测与多目标之间的复杂关系。确认矩阵Ω定义为:
(1)
式中,N为目标数;mk为k时刻量测数;ω=1表示量测j在目标t的跟踪门内,ω=0表示量测j不在目标t的跟踪门内。
JPDA算法的目的是计算每个量测与其可能的源目标之间的关联概率,为此对确认矩阵进行拆分得到互联矩阵,拆分时依据两个基本假设[8]:①每个量测有唯一的源,若某量测不源于任何目标,则必为杂波;②对于任意一个目标,最多只有一个真实量测。
设
为第k时刻的第i个联合事件,表示mk个量测匹配于各自目标的一种可能,
为量测j在第i个联合事件中来源于目标t的事件。互联矩阵
可表示为
(2)
第j个量测与目标t之间的关联概率βjt,可由下式计算得到
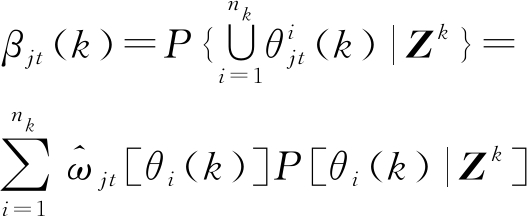
(3)
式中,nk为联合事件的个数,Zk为直到k时刻的累计量测集,P[θi(k)|Zk]为θi(k)的后验概率。
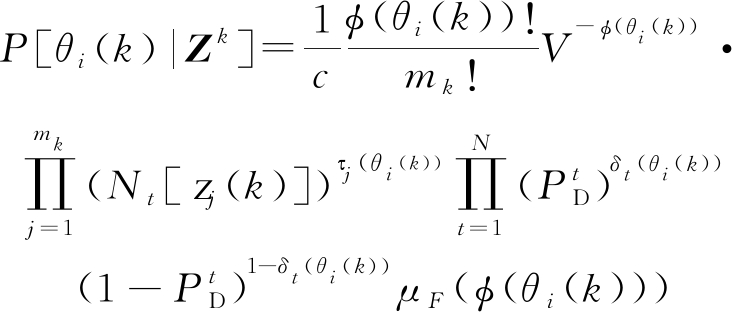
(4)
式中,c为归一化常数,zj(k)为k时刻量测j,τj(θi(k))为量测互联指示,表示量测j在联合事件θi(k)中是否与一个真实目标互联;δt(θi(k))为目标检测指示,表示在联合事件θi(k)中目标是否被检测;φ(θi(k))为杂波的数目;
为目标t的检测概率; μF(φ(θi(k)))为有 φ(θi(k))个虚警发生的概率。
JPDA算法的目标状态更新为
(5)
其中
表示k时刻第j个量测对目标t的状态估计。
JPDA算法的目标状态协方差更新为:
Pt(k|k)= 
(6)
式中,Pt(k|k-1)为k时刻目标t的状态预测协方差,Kt(k)为卡尔曼滤波增益矩阵,St(k)为残差协方差矩阵,β0t表示没有量测来源于目标t的可能性。
在回波数目较少的情况下,JPDA算法能有效地进行多目标跟踪,但JPDA算法的最大弊端就在于拆分确认矩阵时需要列举量测与目标之间所有可行联合事件,在杂波程度较高的环境下,随着量测数的增多,可行联合事件的个数会成指数增长,拆分确认矩阵时会出现组合爆炸的现象,导致计算量急剧增大,严重影响了算法的实时性。
3 简化JPDA算法
JPDA算法的关键在于关联概率的计算,由式(2)可知关联概率的计算过程十分复杂,本文提出了一种简化的关联概率的计算过程,并引入公共量测影响因子进行修正,以避免确认矩阵的拆分,降低计算量。
3.1 简化关联概率计算
假设跟踪区域中有N个目标,k时刻以N个目标的预测位置为中心建立跟踪门,一次扫描共有mk个量测落入跟踪门内,跟踪区域内目标与量测分布如图1所示 。
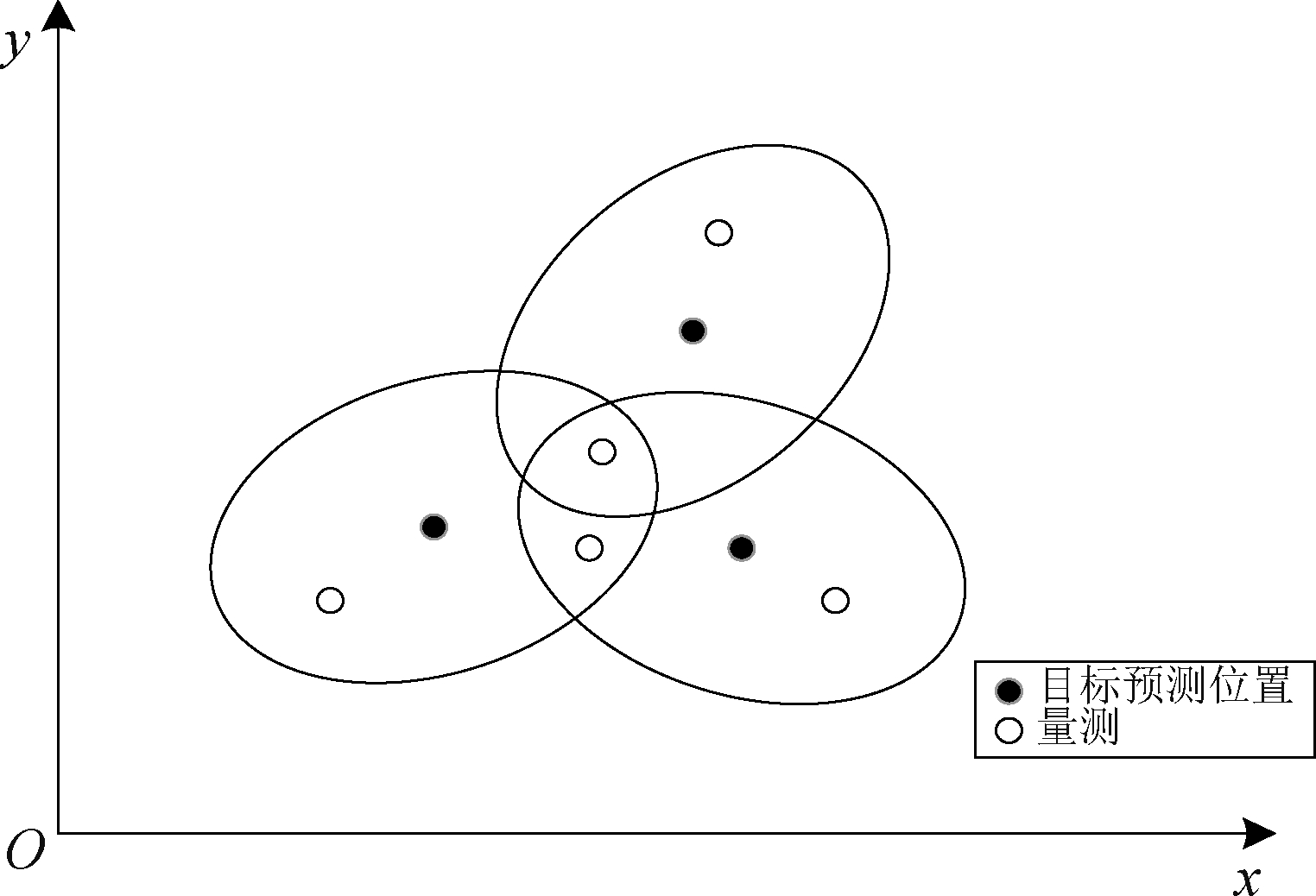
图1 目标跟踪门与量测
Fig.1 Target tracking gate and measurement
在定义简化关联概率的计算方法之前,应考虑以下2个关联规则[7]。
①每个目标跟踪门内的候选量测比其外部量测更可能来自该目标,所以其关联概率应与目标检测概率PD、真实量测落入跟踪门的概率的门概率PG成正比;
②假设目标在体积为V的跟踪门内至多只有1个此目标的真实量测,虚假量测均匀分布。定义βji时应考虑因子1/Vnt-1,表示目标t的跟踪门中有1个量测为目标的真实量测,其余量测均来自杂波,其中nt表示目标t跟踪门中的量测数量。
基于上述2条关联规则,定义简化关联概率为:
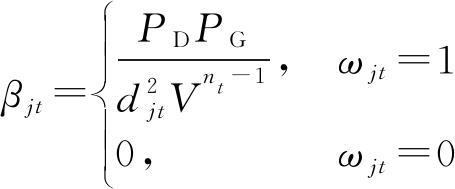
(7)
式中djt为马尔科夫距离,即
(8)
注意到当j=0时,即β0t表示目标t的跟踪门中所有量测全是来自于的关联概率,针对此类情况,补充定义
(9)
归一化处理:
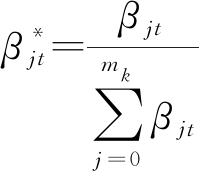
(10)
3.2 基于公共量测修正的关联概率
当一个量测落入多个目标的跟踪门时,即公共量测,在计算关联概率时不应该被单独处理,否则将会引起一定程度上的航迹重叠[4]。针对公共量测对目标的影响,在简化计算的关联概率的基础上,引入公共量测影响因子修正关联概率,以使公共量测更加准确地参与多目标的状态估计。
在k时刻,通过确认矩阵Ω找出所有的公共量测,建立公共量测集合pms,如式(11)
(11)
再次通过确认矩阵Ω找出每个公共量测所有可能的来源目标集合Tj,如式(12)
Tj={t|ωjt=1} j∈pms
(12)
(1)计算每个公共量测所有可能的源目标对关联概率的影响因子Ajt。
公共量测从属于多个目标,在计算可能源目标对公共量测的影响时,认为公共量测对每个可能的源目标的隶属程度是不同。若公共量测在某一源目标中的关联概率较大,认为公共量测更有可能来自于此目标,因此其他可能源目标在考虑此公共量测时,应减小其关联概率,反之则应该增大。因此定义所有可能的源目标对关联概率的影响因子Ajt为:
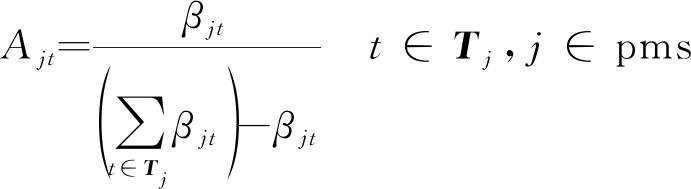
(13)
(2)在具有公共量测的目标跟踪门内,计算其他量测对于关联概率的影响因子Bt。
在计算其他量测对公共量测的影响时,需考虑公共量测数量与非公共量测数量的相对数量[7]。若公共量测数量少于非公共量测数量,表明两个目标相距较远,此时公共量测为真实量测的概率较小,应降低公共量测的权重;反之,应该增大公共量测的权重。因此定义影响因子Bt:
(14)
式中, ntp为目标t跟踪门内公共量测的数量。
利用影响因子Ajt和Bt修正关联概率,并做归一化处理:
(15)
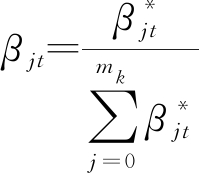
(16)
利用卡尔曼滤波算法计算各目标跟踪门中所有量测对于目标的状态估计,将修正后的关联概率带到式(5)、(6)中,进行加权计算,得到各个目标的最终状态估计。
4 仿真分析
为验证算法的有效性,在多目标并行伴飞的场景进行仿真实验。设目标t在k时刻的为状态向量为
其中x、y分别为x方向和y方向的位置,
分别为x方向和y方向的速度。目标的运动状态方程可表示为:
x(k)=Fx(k-1)+Gv(k)
(17)
式中,v(k)为过程噪声,服从均值为0,方差为Q(k)的高斯分布,且不同时刻过程噪声相互独立;F为状态转移矩阵;G为扰动矩阵。
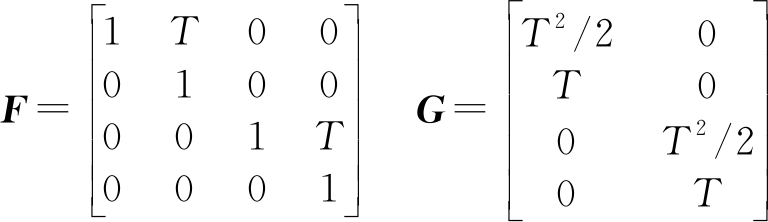
量测方程可表示为:
z(k)=γ(k)[Hx(k)+w(k)]
(18)
式中,w(k)为量测噪声,服从均值为0,方差为R(k)的高斯分布,且不同时刻量测噪声相互独立;H为量测矩阵,取值为
γ(k)表示k时刻传感器检测是否检测到目标。
(19)
仿真参数设置为:采样周期T=1 s;过程噪声标准差q=0.01 m,量测噪声标准差为r=15 m,检测概率为0.95,门概率为0.99;跟踪门限为9.12;杂波个数服从参数为λ的泊松分布,位置服从在以目标预测值为中心的均匀分布。
本节设置在杂波背景下跟踪4个并行伴飞的匀速目标的仿真环境,4个匀速飞行目标的初始状态的y方向位置不同,分别为[5 m, 15 m/s, d*i m, 50 m/s]T(i=1,2,3,4),运动时间为60 s,采用卡尔曼滤波算法进行滤波估计,蒙特卡洛仿真次数为100次,使用位置均方根误差比较JPDA、本文算法和文献[7]所提算法之间的估计精度。定义位置均方根误差如下:
RMSE= 
(20)
4.1 检验杂波密度对算法的影响
本节在目标间距适中(d=40 m)的仿真环境下,检验杂波密度对算法的影响。图2、图3,图4为杂波密度较为稀疏情况下(λ=2),多目标的跟踪。轨迹以及误差对比图;图5、图6、图7为杂波密度较为稀疏情况下(λ=8),多目标的跟踪轨迹以及误差对比图;图7为在不同杂波密度下算法的耗时图。
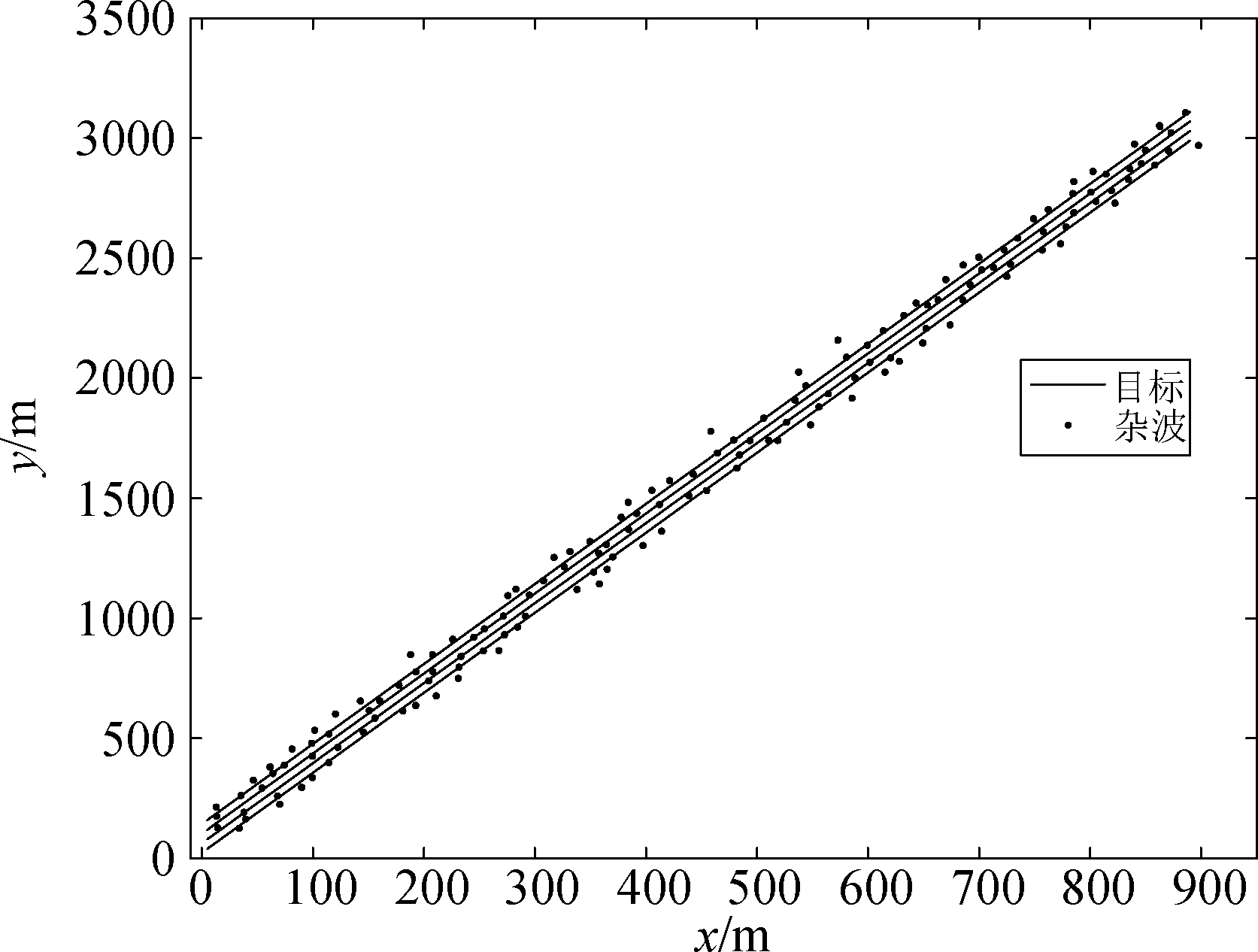
图2 目标真实运动轨迹(λ=2)
Fig.2 Target real motion trajectory(λ=2)
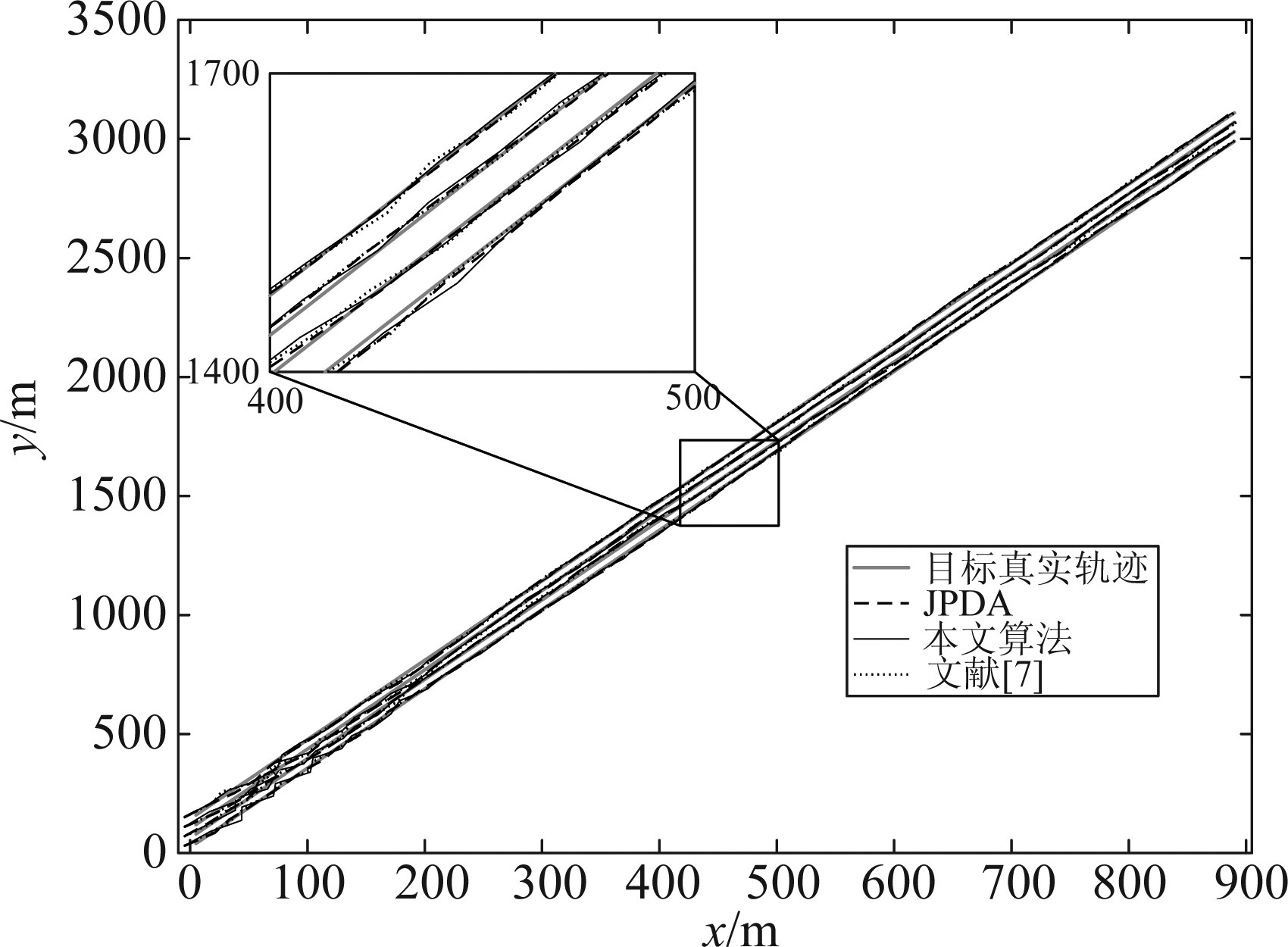
图3 目标跟踪轨迹(λ=2)
Fig.3 Target tracking trajectory(λ=2)
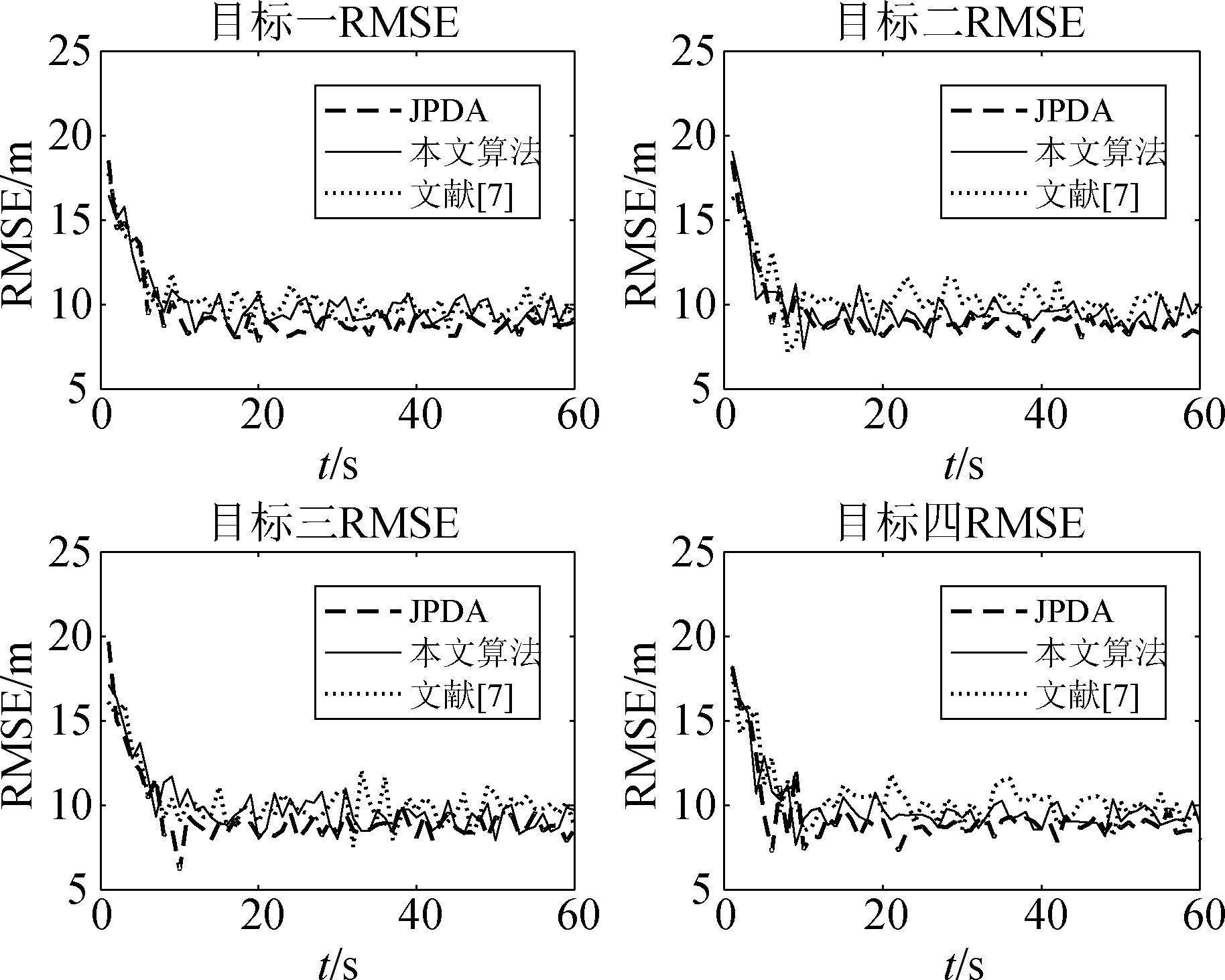
图4 各目标位置RMSE图(λ=2)
Fig.4 RMSE diagram of each target location(λ=2)
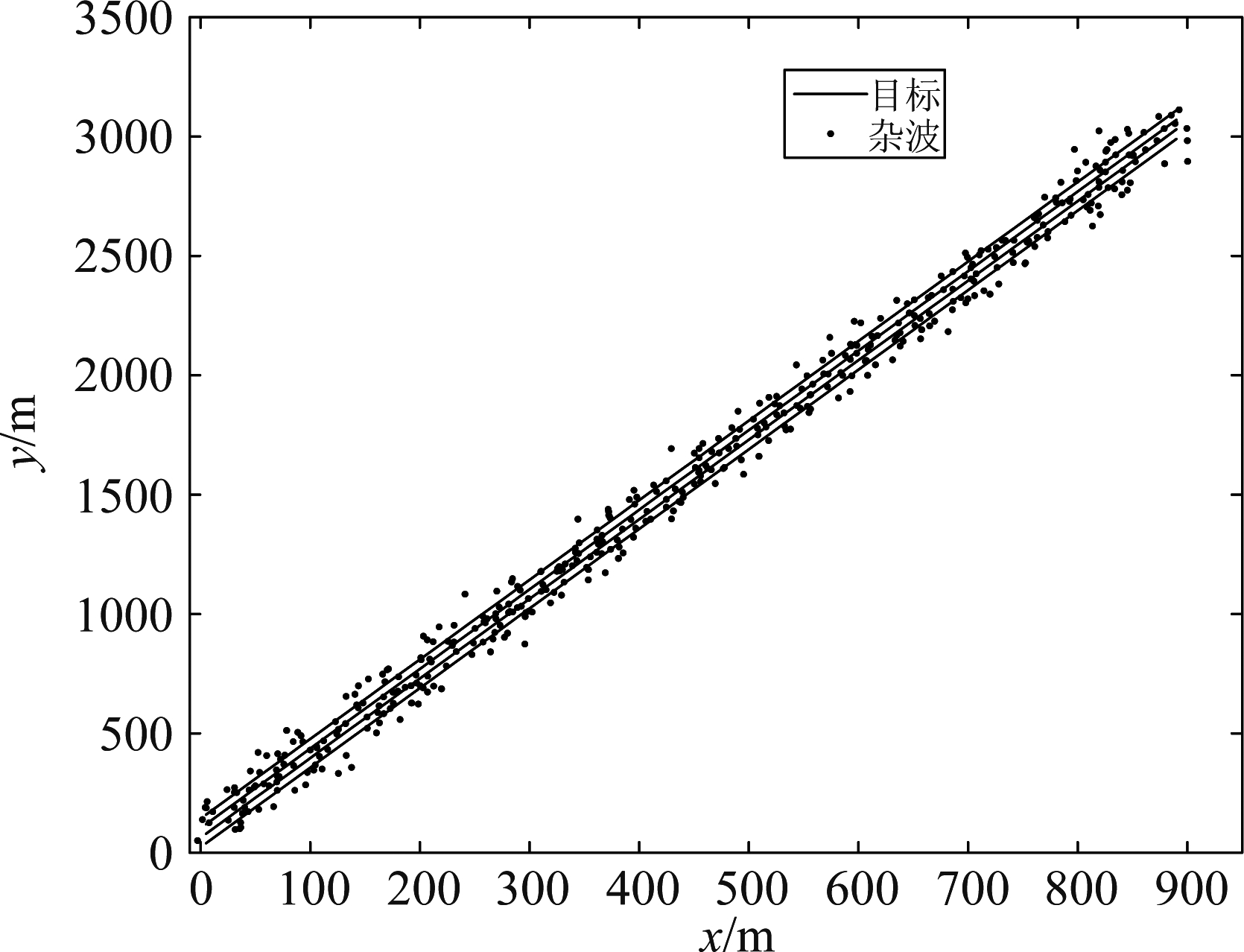
图5 目标真实运动轨迹(λ=8)
Fig.5 Target real motion trajectory(λ=8)
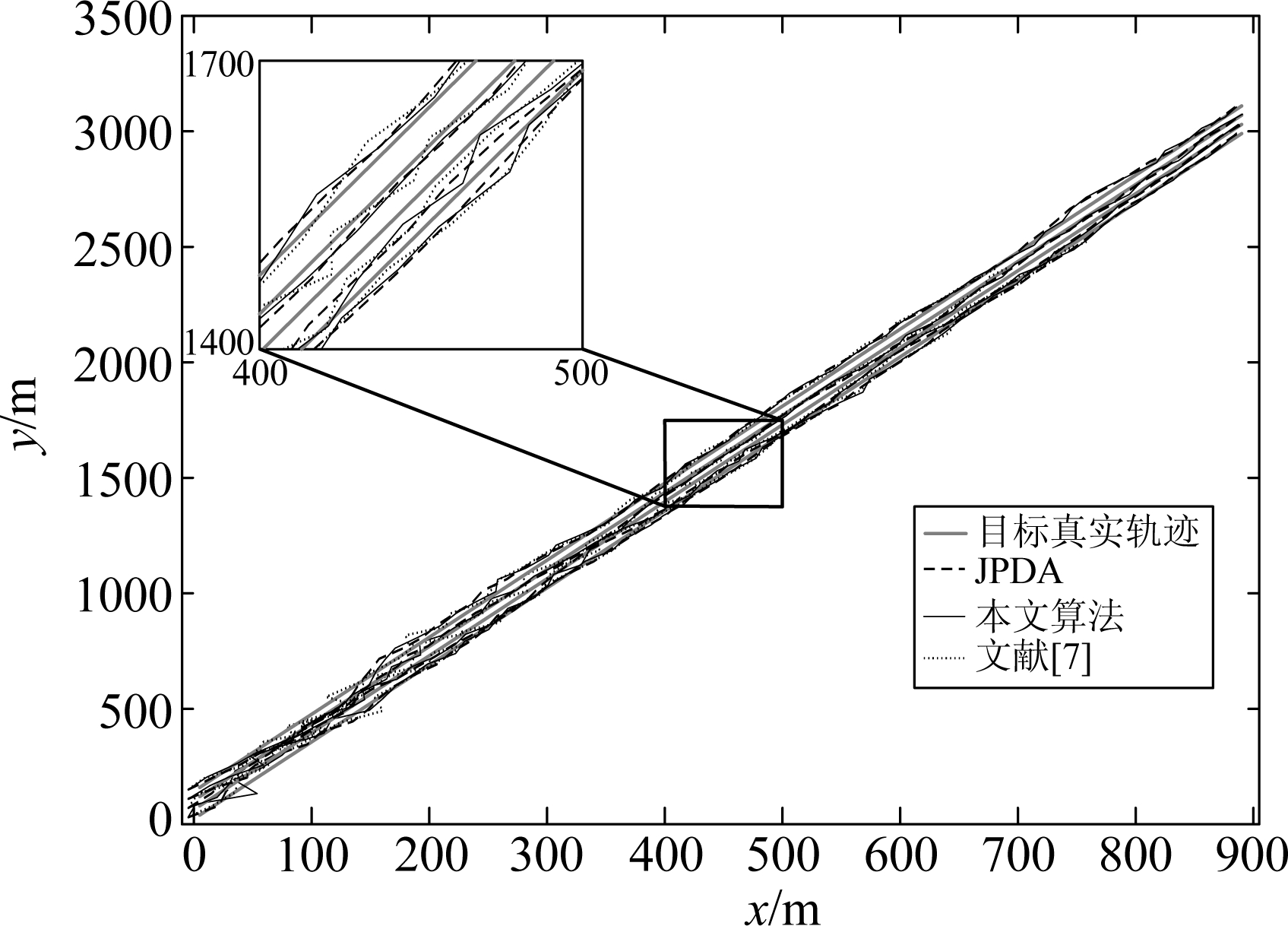
图6 目标跟踪轨迹(λ=8)
Fig.6 Target tracking trajectory(λ=8)
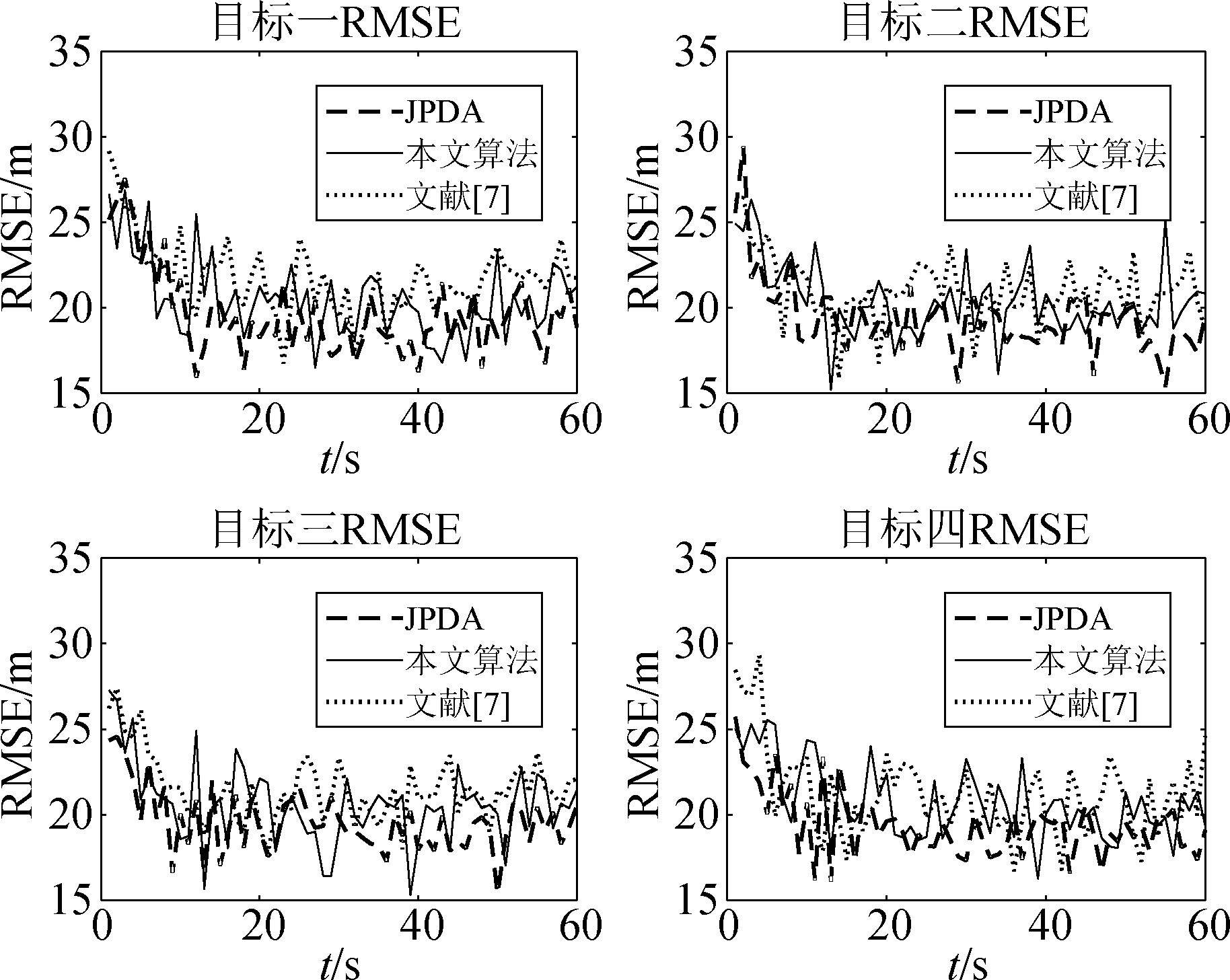
图7 各目标位置RMSE图(λ=8)
Fig.7 RMSE diagram of each target location(λ=8)
通过图4的对比,在稀疏杂波环境下,三种算法对多个目标进行跟踪的效果相当,由于文献[7]和本文算法计算关联概率的方式简单,因此误差要略大于传统JPDA算法,但总体上本文算法和文献[7]的跟踪精度与JPDA算法基本保持相当;通过图7的对比,在密集杂波的环境下,杂波密度的增大,使得参与目标状态估计的杂波数量增多,一定程度会减小真实量测的关联概率,因此三种算法的跟踪误差与误差的波动均有所增大,本文算法和文献[7]仍然可以保持与JPDA算法基本相同的跟踪精度。
通过图8的对比,本文算法和文献[7]算法的耗时较JPDA算法相比大大减少,这是由于本文算法和文献[7]在求解关联概率时避免了确认矩阵的拆分等复杂运算,简化算法流程,因此大幅缩短了计算时间,杂波密度的越大,越能体现出算法的实时性。由仿真结果分析可知,本文算法与JPDA算法的跟踪精度较为接近,算法耗时与文献[7]相同,但本文算法设计简单,更易于工程实现。
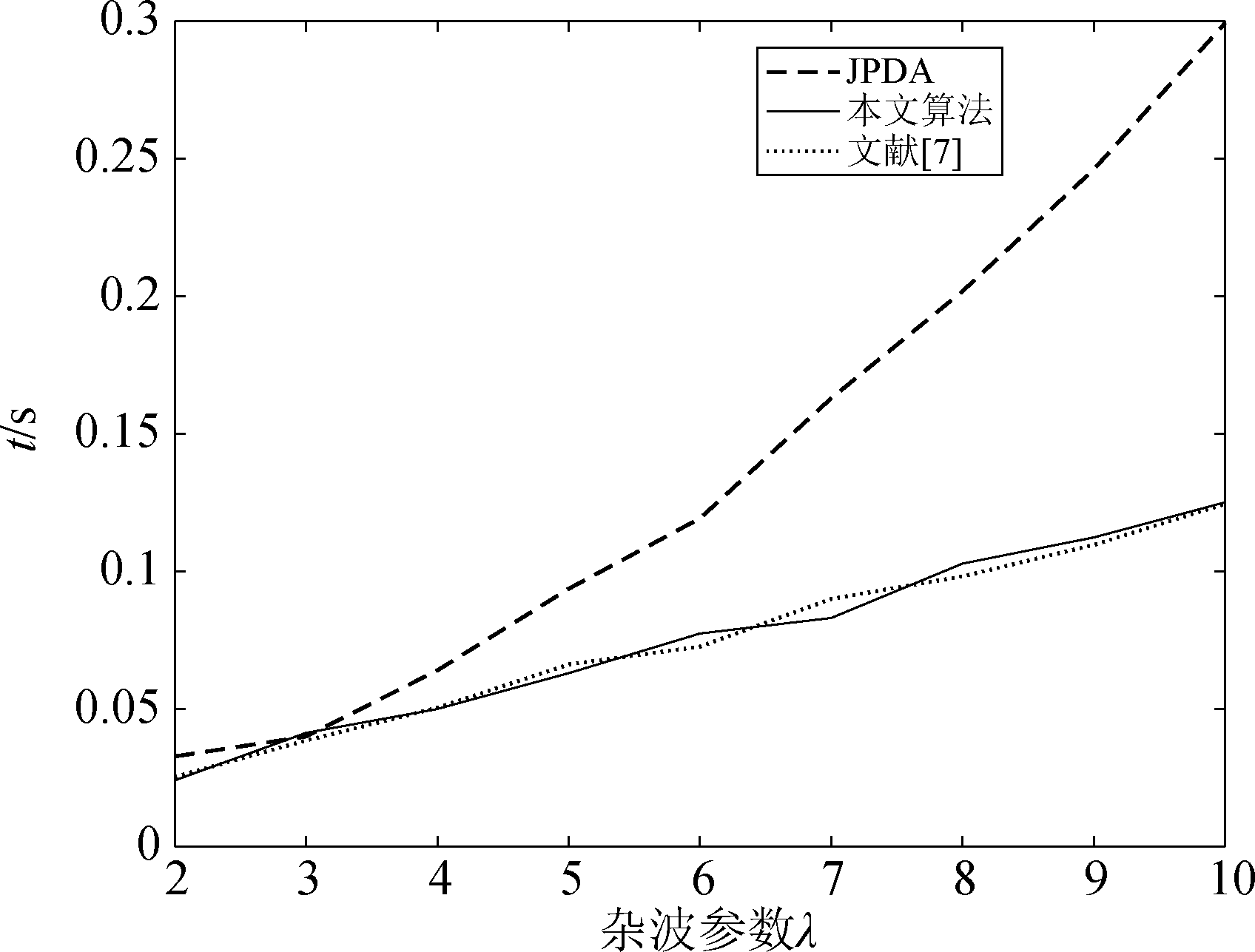
图8 算法耗时对比图
Fig.8 Time-consuming of algorithm
4.2 不同目标间距下影响因子对算法的影响
本节在密集杂波环境下λ=8,分别在目标间距离为20 m和100 m的情况下测试算法的性能,并检验公共量测影响因子的有效性,仿真结果如图9和图10。
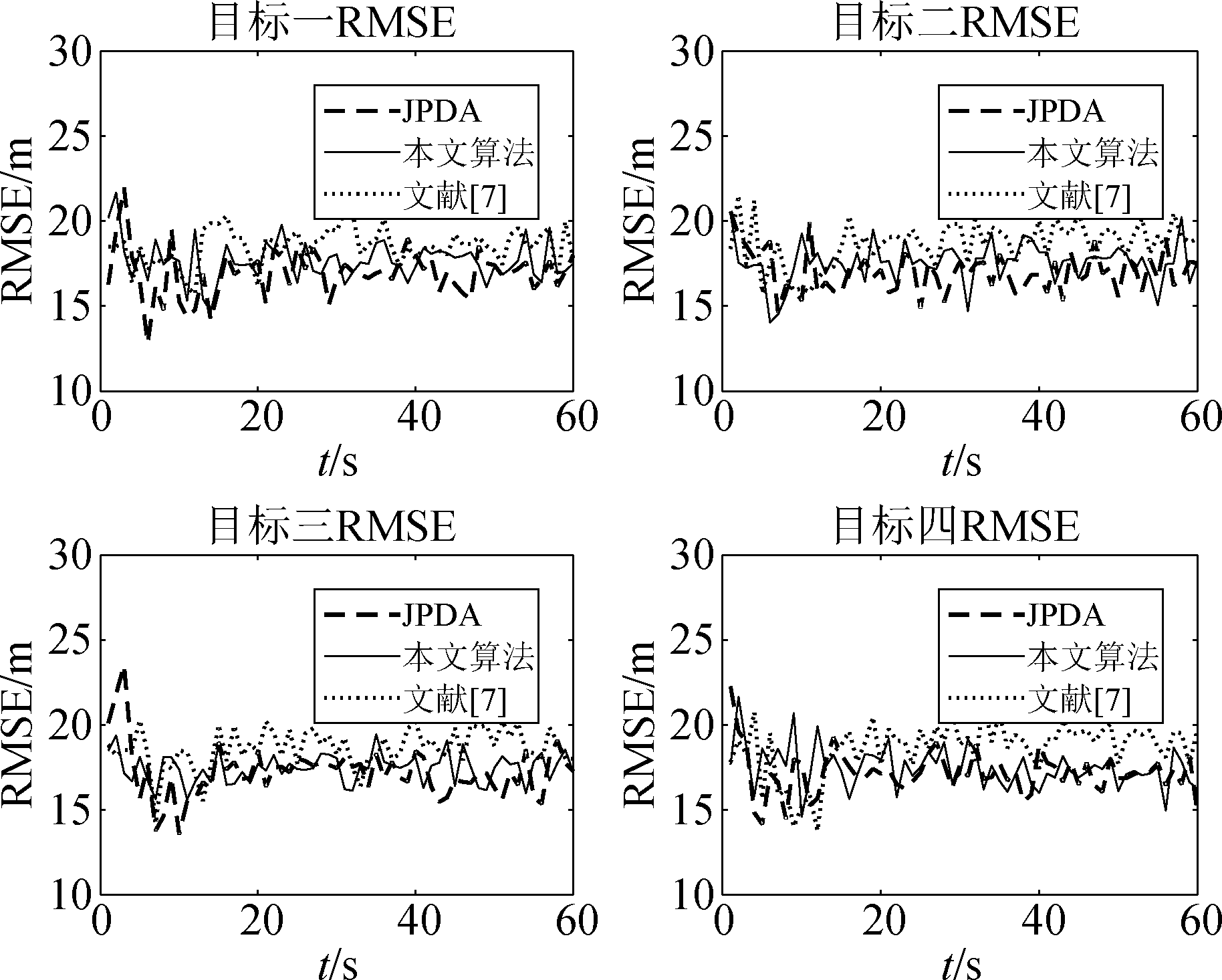
图9 各目标位置RMSE图(d=20 m)
Fig.9 RMSE diagram of each target location(d=20 m)
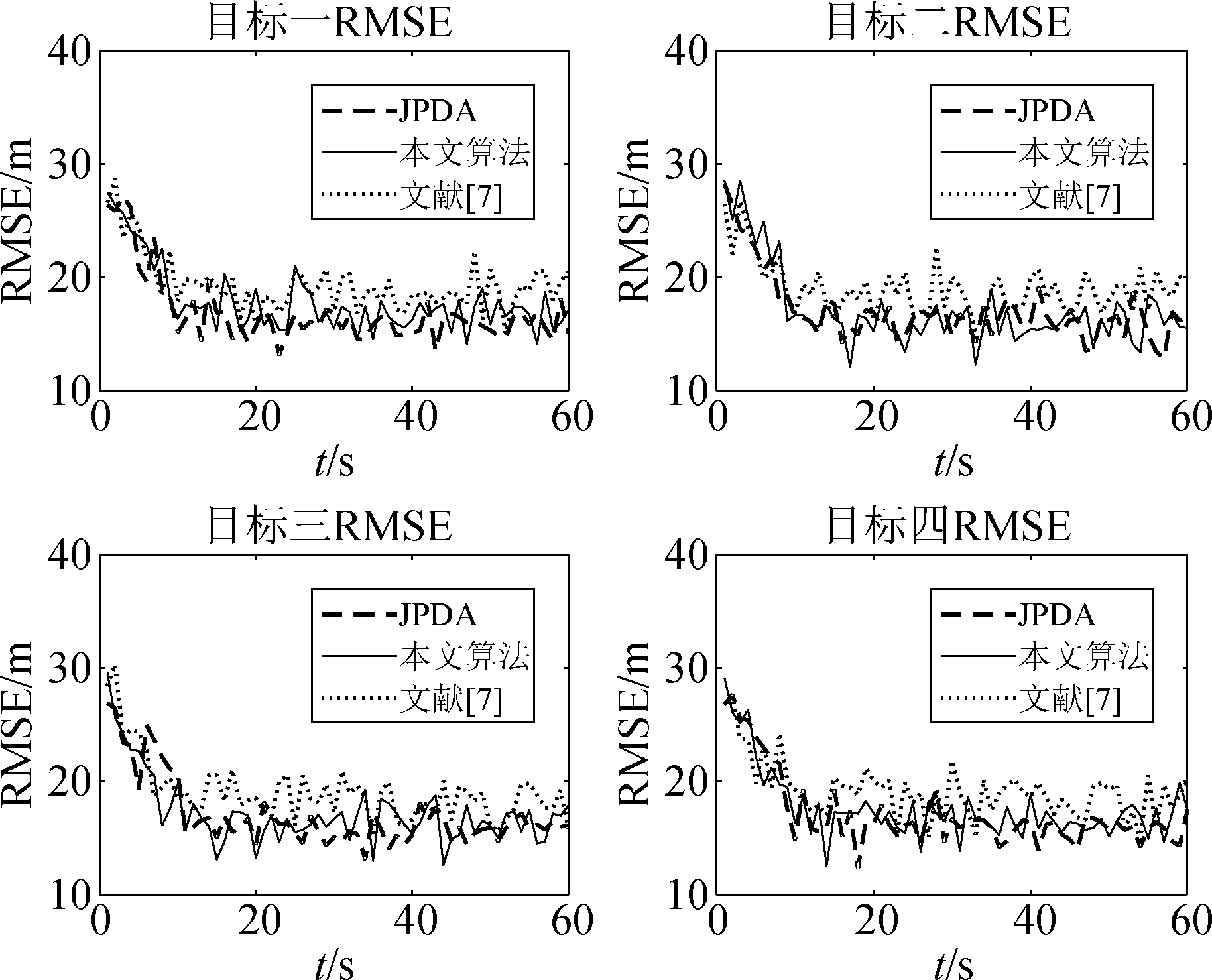
图10 各目标位置RMSE图(d=100 m)
Fig.10 RMSE diagram of each target location(d=100 m)
由以上仿真结果可知,在密集杂波环境下,当目标距离较近或较远时,未考虑公共影响的文献[7]算法有较大的误差。本文算法在通过对公共量测的分析,调整其参与目标状态估计的权重以提高估计精度,与文献[7]相比误差明显减小,误差波动也得到了明显的抑制,并且可以达到JPDA算法相同的精度。仿真结果证明在杂波密集环境下,通过公共量测影响因子的改进,使得算法能够对目标具有更为精确的跟踪效果。
4.3 检验检测概率对算法的影响
本节在λ=8、d=40 m的仿真环境下,检验检测概率对算法的影响,图11为不同检测概率下各目标的平均RMSE图。
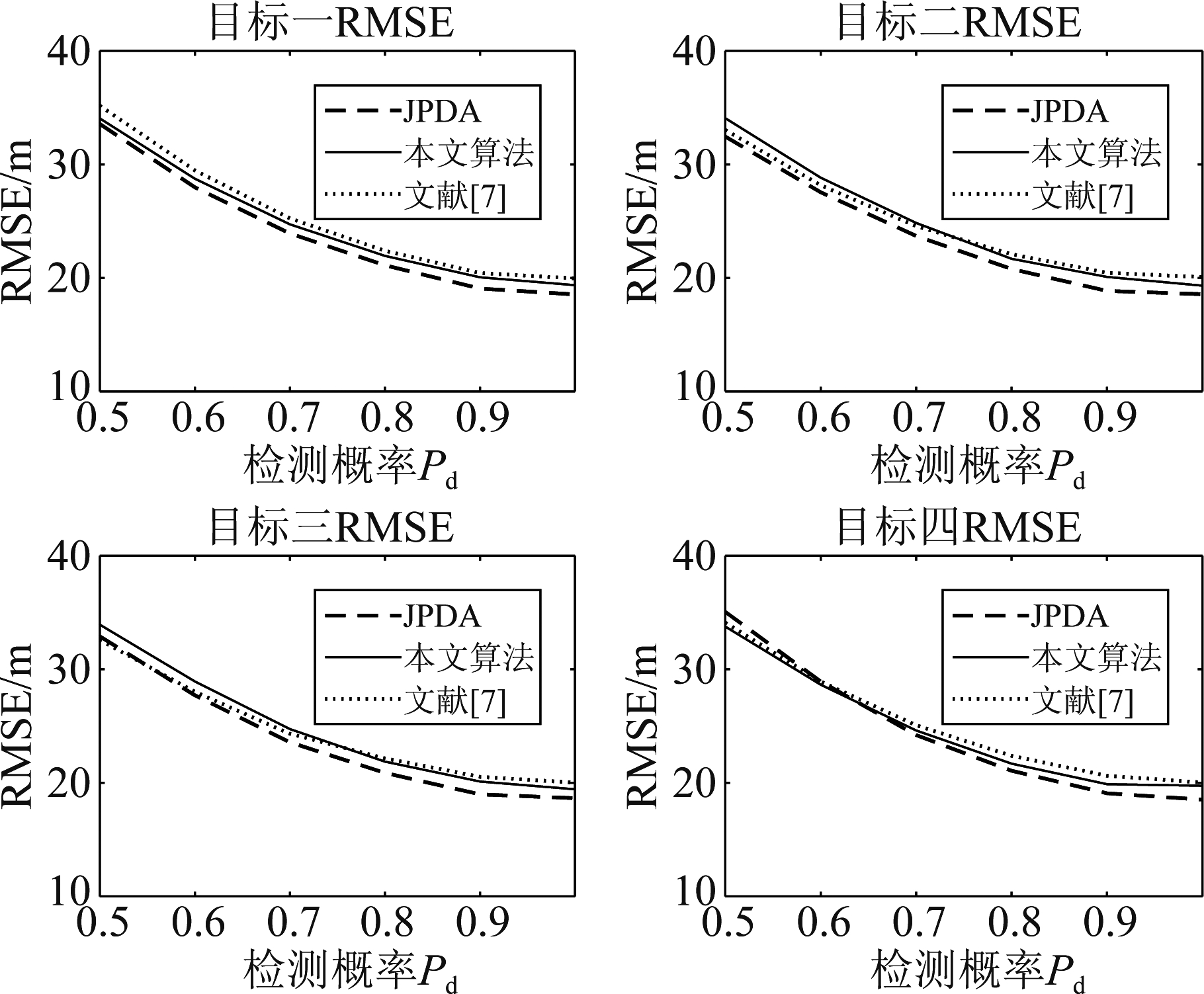
图11 不同检测概率下的RMSE
Fig.11 RMSE under different PD
分析图11可知,随着检测概率下降,真实量测参与目标估计的可能性就会减小,若某时刻无真实量测,则参与目标状态估计的量测全为杂波,在密集杂波环境下跟踪门内杂波数量较多,因此三种算法的跟踪精度都会随着检测概率降低而严重下降。
5 结论
本文针对JPDA算法计算量过大的问题,设计了一种新的JPDA简化算法,提出了一种新的计算关联概率的方式,并引入公共量测影响因子对其修正。在多目标并行运动的场景中,将本文算法与JPDA算法进行仿真实验对比。结果表明,简化JPDA算法的实时性要优于JPDA算法,而且在跟踪精度上两种算法较为接近,没有明显的下降,对于密集杂波下的多目标跟踪具有很好的工程实用价值,提供了一种新的多目标数据关联算法。
[1] 何友, 修建娟, 关欣. 雷达数据处理及应用(第三版)[M]. 北京: 电子工业出版社, 2013.
He You, Xiu Jianjuan, Guan Xin. Radar Data Processing With Applications(Third Edition)[M]. Beijing: Publishing House of Electronics Industry, 2013.(in Chinese)
[2] 靳标, 纠博, 苏涛, 等. 一种用于杂波中机动目标跟踪的自适应关联波门设计方法[J]. 西安交通大学学报, 2014, 48(10): 35- 41.
Jin Biao, Jiu Bo, Su Tao, et al. A Method to Design Adaptive Correlating Gate for Maneuvering Target Tracking in Clutter[J]. Journal of Xi’an Jiaotong University, 2014, 48(10): 35- 41.(in Chinese)
[3] Eui Hyuk Lee, Taek Lyul Song. Multi-sensor track-to-track fusion with target existence in cluttered environments, 2017, 11(7): 1108-1115.
[4] 陈晓, 李亚安, 蔚婧, 等. 基于最大熵模糊聚类的快速多目标跟踪算法研究[J]. 西北工业大学学报, 2017, 35(4): 629- 634.
Chen Xiao, Li Yaan, Yu Jing, et al. A Fast Multi-Target Tracking Algorithm Based on Maximum Entropy Fuzzy Clustering[J]. Journal of Northwestern Polytechnical University, 2017, 35(4): 629- 634.(in Chinese)
[5] 李首庆, 徐洋. 基于自适应聚概率矩阵的JPDA算法研究[J]. 西南交通大学学报, 2017, 52(2): 340-347.
Li Shouqing, Xu Yang. Joint Probabilistic Data Association Algorithm Based on Adaptive Cluster Probability Matrix[J]. Journal of Southwest Jiaotong University, 2017, 52(2): 340-347.(in Chinese)
[6] 康旭超, 何广军, 陈峰, 等. 密集杂波下的模糊数据关联多目标跟踪算法[J]. 探测与控制学报, 2019, 41(4): 56- 61.
Kang Xuchao, He Guangjun, Chen Feng, et al. Fuzzy Data Associated with Multi-target Tracking Algorithm under Dense Clutter[J]. Journal of Detection & Control, 2019, 41(4): 56- 61.(in Chinese)
[7] 刘俊, 刘瑜, 何友, 等. 杂波环境下基于全邻模糊聚类的联合概率数据互联算法[J]. 电子与信息学报, 2016, 38(6): 1438-1445.
Liu Jun, Liu Yu, He You, et al. Joint Probabilistic Data Association Algorithm Based on All-neighbor Fuzzy Clustering in Clutter[J]. Journal of Electronics and Information Technology, 2016, 38(6): 1438-1445.(in Chinese)
[8] Kuo-Chu Chang, Chee-Yee Chong, Bar-Shalom, Y. Joint probabilistic data association in distributed sensor networks[J]. Automatic Control IEEE Transactions on, 1986, 31(10): 889- 897.
[9] Mcgee J A, Luginbuhl T E, Dibiase J H, et al. A Modified PDAF Algorithm For Measurement Covariances that Vary within a Time Scan[J]. Aerospace & Electronic Systems IEEE Transactions on, 2012, 48(1): 906-912.
[10]Bae S H, Yoon K J. Robust Online Multiobject Tracking with Data Association and Track Management[J]. IEEE Transactions on Image Processing, 2014, 23(7): 2820-2833.
[11]Kemal Öksüz, Cemgil A T. The comparison of the performances of global nearest neighbor and probability hypothesis density filter for varying clutter rates[C]∥2016 24th Signal Processing and Communication Application Conference (SIU). IEEE, 2016.
[12]杜浩翠, 谢维信, 范建德. 基于PPP模型的多扩展目标跟踪的JPDA算法研究[J]. 信号处理, 2019, 35(6): 1079-1087.
Du Haocui, Xie Weixin, Fan Jiande. JPDA Algorithm for Multi-Extend Target Tracking Based on PPP Model[J]. Journal of Signal Processing, 2019, 35(6): 1079-1087.(in Chinese)
[13]尹成友, 杨斌. JPDA中联合事件概率的计算[J]. 信号处理, 2002, 18(6): 568-569, 573.
Yin Chengyou, Yang Bin. One kind of Modified Calculation Method of Joint-event Probability[J]. Journal of Signal Processing, 2002, 18(6): 568-569, 573.(in Chinese)
[14]王刚, 汪秋莹. 利用JPDA进行编队目标的多雷达航迹关联应用研究[J]. 现代雷达, 2019, 41(4): 39- 42.
Wang Gang, Wang Qiuying. Multi-radar Track Association of Formation Targets Based on JPDA[J]. Modern Radar, 2019, 41(4): 39- 42.(in Chinese)
[15]Turkmen I, Guney K. Cheap Joint Probabilistic Data Association with Adaptive Neuro-Fuzzy Inference System State Filter for Tracking Multiple Targets in Cluttered Environment[J]. AEU-International Journal of Electronics and Communications, 2004, 58(5): 349-357.
