1 引言
在毫米波大规模MIMO通信系统中,大量的设备接入网络,对数据高速传输的需求与日俱增,同时也对信息的安全性提出了更高的要求。然而,由于确保用户收到正确信息的协议不足等因素[1],使得系统极易受到攻击,如何保障系统的通信安全受到了普遍重视[2-3]。通常的方案是用加密算法对消息进行加密后再传输。加密算法主要分为对称加密和非对称加密[4-5]。对称加密简单高效,但是不能保证密钥的安全分发,容易被窃听者找到规律而破解。非对称加密通过使用公私密钥从而解决了对称加密中密钥分发的问题,缺点是加密过程比较复杂,不适合大量的数据加密。随着量子密钥分发技术(Quantum Key Distribution,QKD)的发展,利用量子态来保证系统安全被证明具有更高的安全性,因此,量子密钥分发技术受到了广泛关注[6]。
量子密钥分发基于量子态测不准原理和不可克隆原理,即使窃听者拥有无穷的计算能力也无法窃取到密钥,与一次一密(One-time-pad)体制相结合可以实现安全的保密通信[6]。量子密钥分发协议可以分为两类:第一类是制备和测量类型的方案,如BB84、B92[7]、六态协议[8]等方案;第二类是基于量子纠缠的方案,如Ekert91,BBM92[9]等方案。第一个量子密钥分发协议由Brassard和Bennett于1984年提出,即BB84协议,也称为四态协议。经过多年的发展,很多成熟的QKD系统已经投入到了商业市场,如瑞士的SwissQuantum量子网络、欧洲的SECOQC量子网络、中国合肥的量子通信网络等[10]。文献[11]将量子密钥分发用于电力通信接入网,保障了电网的安全与稳定运行;最近北京与上海之间也完成了2000KM的光纤量子链路。然而,QKD与通信结合的研究大部分都集中在有线通信上,将量子密钥分发用于无线通信网络中的相关研究相对较少。无线通信网络与有线通信网络不同,其信号是在自由空间中传播的,具有开放特性,这导致与有线通信系统相比,无线通信系统更容易受到窃听与攻击[12]。自由空间中的量子密钥分发技术相比于有线光纤中的量子密钥分发,自由空间对量子的衰减较小,且没有光纤中的双折射效应,这使得量子密钥分发能够传输的更远,误差也更小。“墨子”号量子卫星取得的一系列实验成果已经验证了无线通信中使用量子密钥分发的可行性,如7600KM的QKD实验,这也为将来组建无线量子通信网络奠定了基础[13]。
考虑到量子密钥分发技术在安全保密方面的巨大优势,本文提出利用量子密钥分发技术来保障无线通信系统的安全传输方案。在无线通信的收发两端使用量子密钥分发协议,结合一次一密,可以保障系统的安全性。此外,在无线通信的信号处理过程中,尤其是在毫米波大规模MIMO系统中,信道具有空间稀疏特性,通常都需要进行角度估计。角度估计在波束赋形、减少信道状态信息反馈、信道估计等方面都起到了重要的作用[14]。以往的无线环境中的量子密钥分发通常只将无线信道作为传输载体,而并没有考虑无线信道资源与QKD的结合,因此本文提出了将角度估计与量子密钥分发相结合的安全传输方案(Angle Estimation assisted QKD,AQKD)。与实际角度估计不同的是,本方案采用的是虚拟角度估计。相较于实际角度估计,虚拟角度估计具有计算复杂度低、受信噪比影响小、估计精确度高等优点[15]。本方案利用量子态的特性保障系统的安全性,同时利用角度估计产生的参考序列,作为收发两端量子密钥分发协议中制备用户态和选择测量基的依据。本方案与不结合角度估计的量子密钥分发协议相比,能够在保障通信安全的同时进一步的提高密钥生成效率。
文章结构如下:第2部分介绍了本文所提方案的系统模型。第3部分首先介绍了本方案采用的BB84量子密钥分发协议的基本过程;接着介绍了本方案采用的角度估计方法;最后说明了本方案将角度估计与量子密钥分发相结合的具体操作方法。第4部分是本方案整体流程的总结。第5部分为仿真实验。最后部分为本文的结论。
2 系统模型
图1为本文方案的系统模型。整个系统包含经典无线信道和量子信道两个部分。其中经典无线信道的作用有两个:一是用于进行角度估计产生参考序列,二是辅助完成量子密钥分发协议中收发两端选择量子基的对比。量子信道用于传输承载密钥信息的量子态,根据目前自由空间中量子密钥分发的研究现状[13],在短距离的覆盖范围内实现精确的量子密钥分发是可能的。图1中合法通信用户标记为Alice与Bob,窃听者标记为Eve,合法信道记为HA,HB,窃听信道记为HC,HD。首先Alice与Bob分别在相干时间内互相发送探测信号,在接收到对方的信号之后,Alice与Bob分别利用3.2小节中的角度估计方法生成各自的参考序列,在图1中表示为ZAK,ZBK。在采用时分双工模式(Time-division Duplex,TDD)的无线通信系统中,上下行信道之间存在信道互易性,即在信道相干时间内,可以认为上下行信道所经历的衰落相同,因此,在理想情况下得到的序列ZAK,ZBK是相同的[16]。AK是Alice随机生成的二进制序列。QKD设备用于发送和接收量子态。
根据信道的相干特性[17],只要Eve距离Alice和Bob超过半波长,HC,HD可被视为与HA,HB无关。由于毫米波的半波长仅处于毫米级别,在实际情况下,这一安全距离是完全可以实现的。因此,窃听者根据HC,HD获得的参考序列也就与ZAK,ZBK无关,由此保证了参考序列的安全性。
在得到ZAK后,Alice根据ZAK与AK选择制备的用户态,之后通过量子信道将量子态传递给Bob。在这一过程中,可能会有窃听者对量子态进行窃听。由于窃听者Eve得不到关于ZAK,ZBK的任何信息,所以只能随机的选取测量基进行窃听。根据量子测不准和不可克隆原理[18],只要窃听者选择的测量基与用户态的所属基的不一样,就有可能使Bob端产生误码。Bob在接收到量子态后根据ZBK选择测量量子态的测量基。Bob与Alice对比一部分密钥的误码率就能知道在量子态的传输过程中是否有窃听者的存在,从而选择相应的应对措施,保证了系统的安全传输。
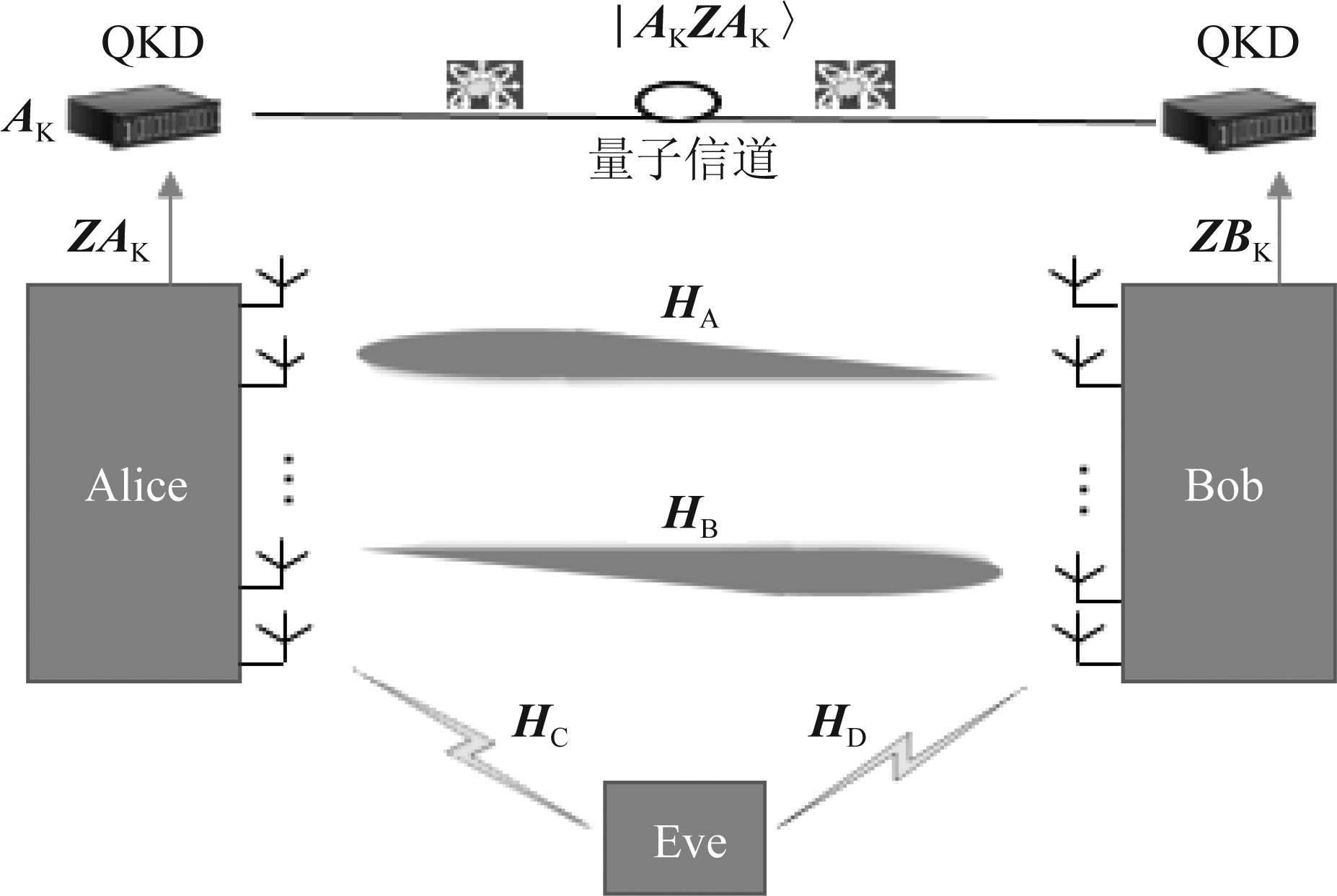
图1 系统模型
Fig.1 System model
3 量子密钥分发与角度估计
3.1 量子密钥分发协议
本文采用的量子密钥分发协议为经典的BB84协议[19],该协议是其他大部分量子密钥分发协议的基础。BB84协议利用量子的偏振态来传输密钥信息从而完成量子密钥分发,共包括四种偏振态:“+”基下的 |→〉态,|↑〉态和“×”基下的|
〉态和|
〉态。本文用“R”表示“+”基,用“D”表示“×”基。通过BB84协议,收发两端可以获得一致的而且安全的密钥。
表1 偏振态编码
Tab.1 Polarization state coding
测量基AK比特0用户态R0→〉R1↑〉D0↘〉D1↗〉
BB84协议的通信过程可以分为两个阶段:在第一阶段中,通过量子信道来进行密钥的通信;第二阶段是在经典信道中进行选基的对比、密钥协商以及检测窃听者是否存在,最终确定密钥。具体包括如下步骤:
1)发送端Alice选取随机序列AK和BK,接收端Bob选取随机序列CK。其中AK,BK和CK都是由0,1组成的二进制序列,K=1,...,N。
2)Alice首先根据AK,BK的取值向Bob发送量子态|AKBK〉。AK表示Alice期望传送的码值,对应同一对正交基中不同的偏振态。BK表示Alice选取的正交基。BK对应位置为0时选取基“R”,为1时选取基“D”。具体的量子态编码如表1所示。
3)Bob接收到Alice发送过来的量子态之后,根据序列CK来选取测量基对量子态进行测量。当CK对应位置为0时选择基“R”,为1时选择基“D”。
4)Bob在测量完Alice发送的量子态之后,收发两端通过经典信道公开自己的基,即公开序列CK和BK。接着收发两端对测量结果进行筛选,只保留下两端选基相同的部分,即BK和CK中相同的部分对应的测量结果。
5)Alice和Bob通过经典信道公开一部分筛选后的数据,并检测这部分数据的误码率。如果误码率大于设定的阈值,则说明窃听者存在,结束本次通信。若不超过阈值,则把公开的这部分数据舍弃掉,并将剩下的测量结果作为原始密钥。
6)Alice和Bob进行密钥协商。通过经典信道进行密钥纠错,使得误码率降低到合理水平。
7)Alice和Bob进行密钥放大,使窃听者获得的少量信息无效。
3.2 角度估计生成参考序列
在本方案中,利用估计到的角度信息来生成参考序列[15]。考虑非视距条件下的窄带和块衰落信道模型,其中块与块之间的信道被认为是独立的。通过毫米波测量验证的非视距窄带信道模型可以表示为公式(1):
(1)
其中ρ表示平均路径损失;Nr和Nt分别代表收发两端的天线数目;L表示散射路径数目;αl是符合零均值复高斯分布的衰落系数;变量φr.l,φt.l∈(0,2π)表示实际的信号到达角和离开角服从均匀分布;向量
和
分别表示收发两端的天线响应向量,在本文中选用了均匀线性阵列[20]。
毫米波大规模MIMO信道的虚拟信道表示可以写成:
(2)
其中
和
代表离散傅里叶变换矩阵。由于毫米波信道的有限散射特性,实际信道矩阵H中的每一对实际的离开角度和到达角度都对应于矩阵Ur和Ut中的一对虚拟到达角和离开角。当天线数目增多时,
变得越来越稀疏,虚拟矩阵中的到达角和离开角可以表示为网格中的L个脉冲,即数值较大的L个元素对应的坐标。通过估计相应的坐标值,可以得到和实际的到达角和离开角相对应的L对坐标。
假设在毫米波大规模MIMO信道中,在Alice端和Bob端分别配置有Nt和Nr根天线。Alice端接收信号记为
YA=HAXA+WA
(3)
信号可以在一个大小为Ta的时间窗口内被Alice接收到。
表示毫米波大规模MIMO信道。
是Bob端发送给Alice端的探测信号。同理可得Bob端接收到的由Alice端发送来的探测信号
假设信道具有完美的互易性,在这种情况下,可以把两个信道看作是彼此的转置,可得HB=HAT。根据公式(2)中虚拟信道的表达式,可以把公式(3)重写为公式(4)和(5)的形式。
(4)
(5)
公式(4)和(5)中
表示离散傅里叶变换矩阵,
由于信道互易性,Alice和Bob可以估计出公式(2)中虚拟矩阵的虚拟到达角和虚拟离开角对应的峰值,从而能够获得多组虚拟到达角和虚拟离开角的坐标。因为Alice端和Bob端具有相同的估计过程,所以用
来代替
和
用
来代替
和
用
来代替
和
接收信号的每一行都被独立处理,并寻找在每一行中的最大值。的第i行表示为
(6)
在公式(6)中,只包含了
的第i行,在这一行中具有最大峰值的虚拟离开角度按如下步骤可得:
首先,计算所有的探测信号与所选行的接收信号的内积。可得如下形式:
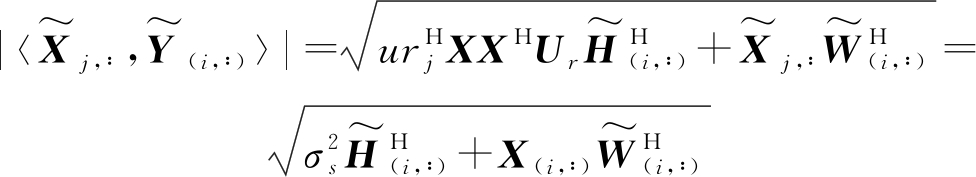
(7)
式中Ur=[ur1,ur2,...,urNr],urj∈Ur, j=1,...,Nr。可以选择正交探测信号X,因此满足
和
其中
是探测信号的功率。
随着信噪比的提高,所含的噪声部分
将趋向于零。实际上,部分的幅度与整体的幅度相比是很小的,基本可以忽略,因此公式(7)可以看作只包含虚拟信道的部分。根据公式(7),在虚拟矩阵
的第i行中,峰值出现在具有最大幅度的那一列上。首先保存每一行中可能的峰值的位置索引和幅度,这样能保证所有可能的峰值的列坐标被记录下来。之后再找出具有最大峰值的L个横坐标。最终得到上L个峰值对应的横坐标和纵坐标,这样就能获得虚拟角度坐标矩阵
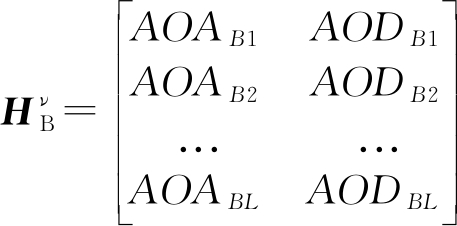
和
由发送端进行估计得到,
由接收端进行估计得到,和各包含了L对坐标。
(8)
(9)
这样,收发两端就都得到了L对坐标。接着把和写为向量的形式,得到:
(10)
(11)
把向量
和
中的每一个元素都用二进制的形式表示,得到ZAK,ZBK,这就是本文使用的参考序列。
此外,文献[15]证明了在毫米波通信中,虚拟角度符合均匀分布,即每个坐标出现的概率是相同的。那么在最终的参考序列中出现0或1的概率也是相同的,这一点和基本BB84协议中的随机等概选取0和1产生序列一致。因为窃听信道与合法信道是独立的[17],因此参考序列ZAK,ZBK只有收发两端知道,窃听者是得不到关于这两个信道的任何信息的。从而能够保证参考序列的安全性。通过角度估计方法得到的参考序列的一致率的高低会直接影响量子密钥分发协议的效率,一致率越高意味着密钥生成效率也就越高。参考序列的一致率定义为逐位对比收发两端的参考序列,两端元素相同的概率。
考虑到提取出来的序列的安全性和一致率,也有部分文献将从信道中提取出来的序列直接作为密钥[21-23],但是文献[21]表明,如果在静态网络中,信道变化缓慢,直接生成的序列是不适合作为密钥的。
3.3 角度估计辅助的量子密钥分发
为了提高无线通信系统的安全性,本文提出了利用角度估计辅助量子密钥分发的安全传输方案。该方案利用角度估计产生的参考序列作为收发两端制备用户态和选择测量基的依据。图2说明了该方案的具体过程。Alice在得到参考序列ZAK后,根据ZAK序列上每一个比特是0或是1来选择不同的基,若是0则选择R基,否则选择D基。随后Alice再根据自身随机生成的一串二进制序列AK来选择ZAK对应基中的不同偏振态。具体选择见表1。Alice按照ZAK和AK生成具体的量子态,通过量子信道发送给Bob。Bob端根据ZBK选择测量基,若是0选择R基,否则选择D基。如图2,在截取的长度为10的参考序列中,由于信道互易性的不完美和信道噪声,出现了1位不同,也因此,Bob端的测量基发生了错误。Alice制备的量子态经过Bob端的测量之后,生成了序列BK。这时收发两端同时公布自己的参考序列,经过对比,发现第6位不同,所以Alice舍弃AK中的第6位,同时Bob舍弃BK的第6位。最终分别得到密钥SA,SB。
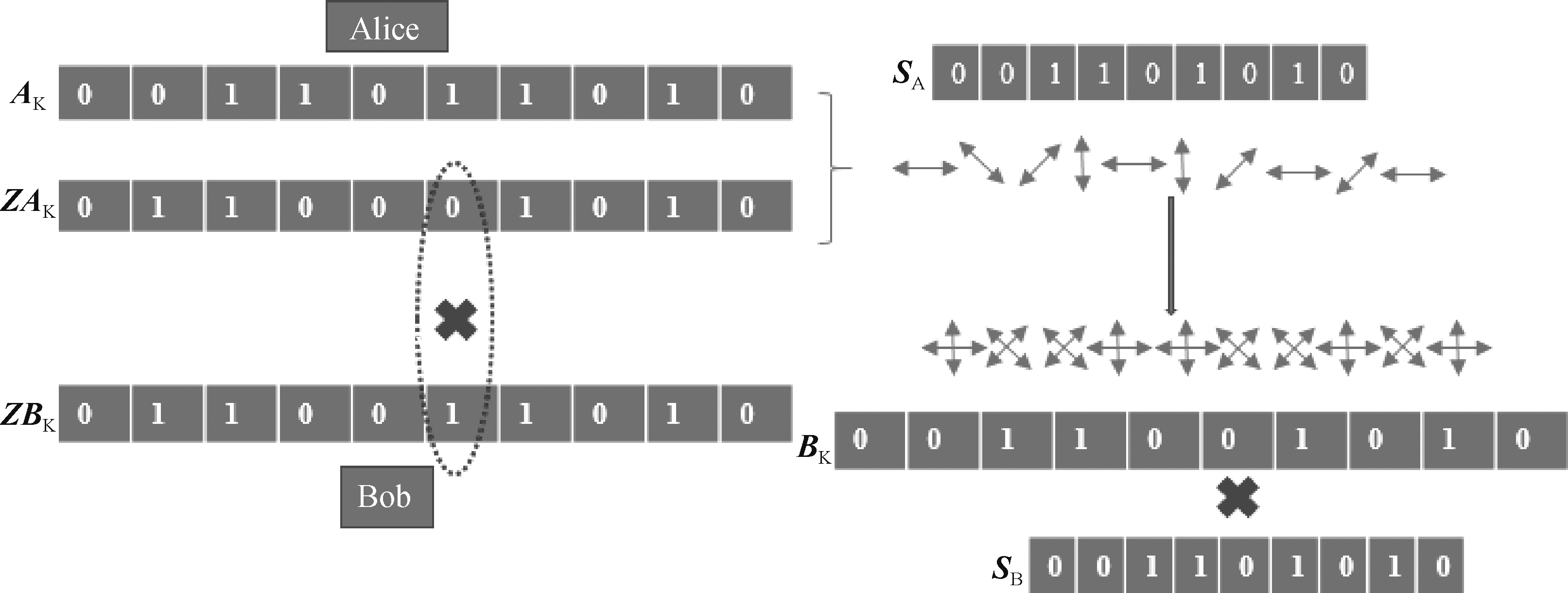
图2 角度估计辅助的量子密钥分发
Fig.2 Angle estimation assisted quantum key distribution
4 基于AQKD的毫米波大规模MIMO系统安全传输算法
基于AQKD的毫米波大规模MIMO系统安全传输算法设计如下,图3说明了该方案生成密钥的具体过程:
1)发送端Alice和接收端Bob在相干时间内互相发送探测信号。
2)在收发两端接收到彼此发送来的探测信号之后,利用角度估计得到的信息生成参考序列ZAK,ZBK。
3)Alice选取随机序列AK。其中AK是由0,1组成的二进制序列,K=1,...,N。
4)Alice首先根据AK,ZAK的取值向Bob发送量子态|AKZAK〉。AK表示Alice期望传送的码值,对应同一对正交基中不同的偏振态。ZAK表示Alice选取的正交基。ZAK对应位置为0时选取基“R”,否则选取基“D”。具体的量子态编码同表1,只需将BK替换为ZAK,量子态|AKBK〉替换为|AKZAK〉即可。
5)Bob接收到Alice发送过来的量子态之后,根据序列ZBK来选取测量基对量子态进行测量。当ZBK对应位置为0时选择基“R”,否则选择基“D”。
6)Bob在测量完Alice发送的量子态之后,收发两端通过经典信道公开自己的基,即公开序列ZAK和ZBK。接着收发两端对测量结果进行筛选,只保留下两端选基相同的部分,即ZAK和ZBK相同的部分对应的测量结果。
7)Alice和Bob通过经典信道公开一部分筛选后的数据,并检测这部分数据的误码率。如果误码率大于设定的阈值,则说明窃听者存在,结束本次通信。若不超过阈值,则把公开的这部分数据舍弃掉,并将剩下的数据作为原始密钥。
8)Alice和Bob进行密钥协商。通过经典信道进行密钥纠错,使得误码率降低到合理水平。
9)Alice和Bob进行密钥放大,使窃听者获得的
图3 基于AQKD的毫米波大规模MIMO系统安全传输算法
Fig.3 Secure transmission algorithm of millimeter wave massive MIMO system based on AQKD
少量信息无效,获得最终密钥。
10)使用最终密钥对消息进行加密,发送加密后的信息。
同时,本文所提方案不仅可用于BB84协议,还可用于基于多组测量基的量子密钥分发协议,如六态协议。在BB84协议中,由于该协议只用到了两组量子基,所以只需要一个比特就能表示基的选择。而在六态协议中,共包括3组量子基,因此需要将参考序列以2比特为一组进行分组,然后舍弃收发两端各自的序列中组元素为00的对应部分,因此得到的参考序列ZAK和ZBK全部由元素01,10,11构成,将这三个元素分别对应六态协议的三对量子态。其余步骤和与BB84协议结合的方案相同。
5 仿真实验与结果分析
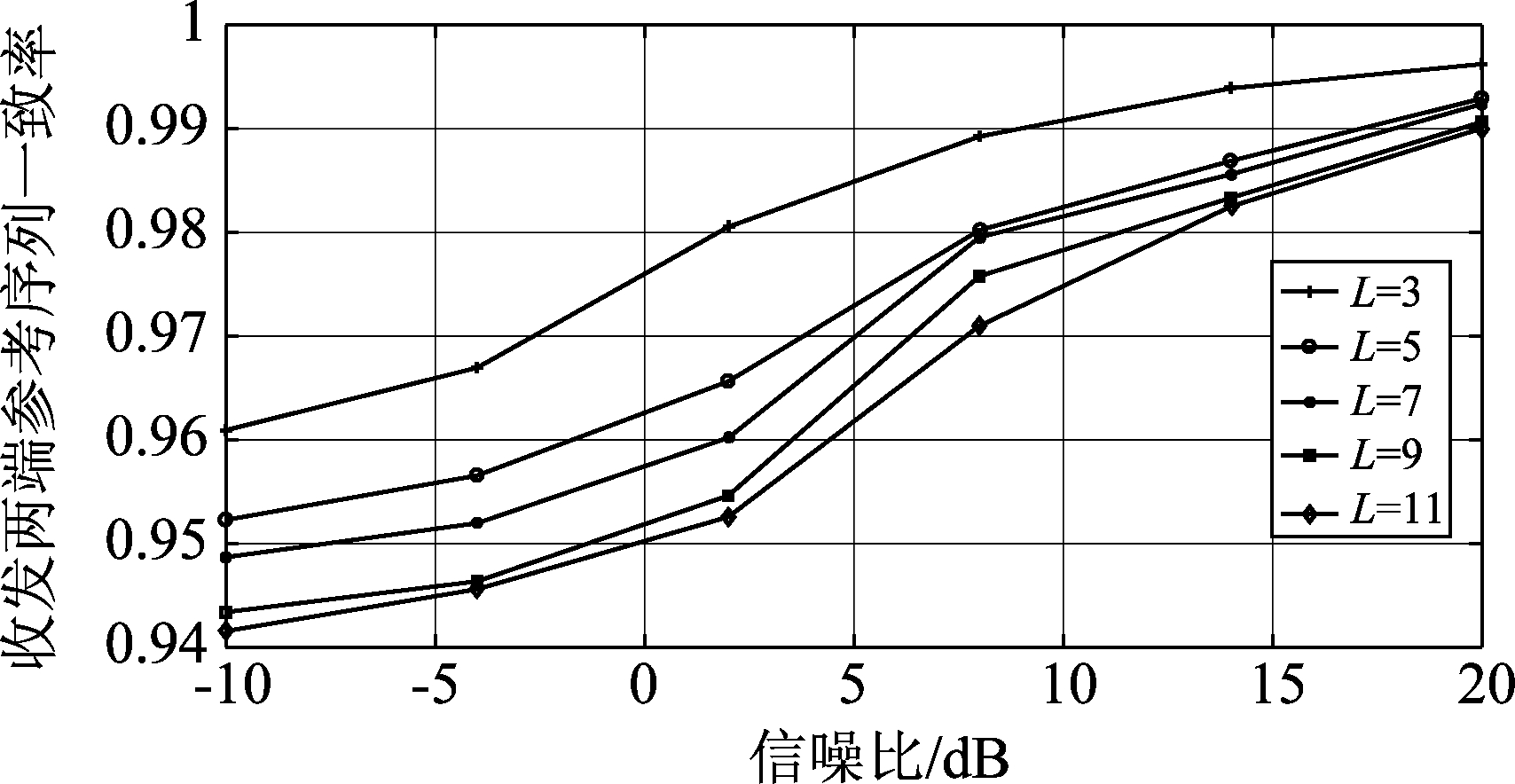
图4 不同稀疏度条件下的参考序列一致率对比
Fig.4 Comparison of reference sequence consistency under different sparsity
本小节对本文所提方案进行了对比仿真实验。在本文中,毫米波系统工作在28 GHz频段,信号的到达角和离开角分别在[0,2π]上均匀分布。散射路径数目设为L,每一条散射都被认为是单一的传播路径。设在发送端Alice和接收端Bob天线数目为Nt=Nr=128,信噪比范围设为-10 dB到20 dB。本文采用文献[15]中的虚拟角度估计算法来进行角度估计并生成参考序列,参考序列上的每个虚拟角度元素都由[0,Nt]上的一个整数表示。首先对利用角度估计生成的参考序列的一致率进行了仿真。在图4中,设散射路径数目L分别为3,5,7,9,11。在公式(1)中,因为毫米波大规模MIMO信道具有有限散射的稀疏特性,所以用散射路径数目L代表不同的信道稀疏度。实验结果表明,在信噪比较低的情况下,散射路径的增多会导致参考序列一致率的降低,这是由于散射路径越多会使虚拟矩阵的稀疏度降低,进而导致角度估计误差变高。但是,即使当L为11的情况下,参考序列一致率也很高。越高的一致率意味着收发两端制备用户态和选择测量基时,有更高的概率选择相同的基,即越高的一致率能够使AQKD算法的步骤(6)中ZAK和ZBK相同的部分占比更多,从而丢弃更少的测量结果,提高密钥的生成效率,更好的保障系统安全。
由于在实际的量子态传输过程中,自由空间对量子态也会产生影响,导致即使ZAK和ZBK选择相同,其对应的测量结果也有可能会不一致,即收发两端的密钥存在误码,需要进行密钥纠错来保障密钥的一致性,而这一过程会导致密钥效率的降低。因此,在图5中,比较了在不同误码率的情况下,不同的方案的最终密钥效率对比。在这里,定义最终密钥效率为在进行密钥纠错后获得的一致的密钥长度,与带误差的原始密钥长度的比值。考虑了在无线通信系统中直接使用量子密钥分发协议的方案,包括平衡选基的BB84协议和平衡选基的六态协议[10],不同基的选择概率相同;非平衡选基的BB84协议,两组基的选择概率分别设为P1,P2;非平衡选基的六态协议,三组基的选择概率分别设为P1,P2,P3。将上述方案与本文所提的角度估计辅助BB84协议和六态协议的量子密钥分发协议的方案进行了仿真对比。结果表明,本文所提的AQKD方案具有更高的密钥生成效率。另外可以发现,当误码率为0时,AQKD方案的最终密钥效率就等于参考序列的一致率。本方案借用了角度估计的信息作为参考序列来辅助生成密钥,而直接使用量子密钥分发是使用随机的序列来生成密钥。由于引入了角度估计的相关步骤,所以在生成参考序列上复杂度会提高,提高的程度取决于角度估计的算法。但是在得到参考序列之后的密钥生成上,复杂度是和直接使用量子密钥分发相同的,同时本方案对密钥生成效率的提高也可以降低量子密钥分发过程中的资源消耗。
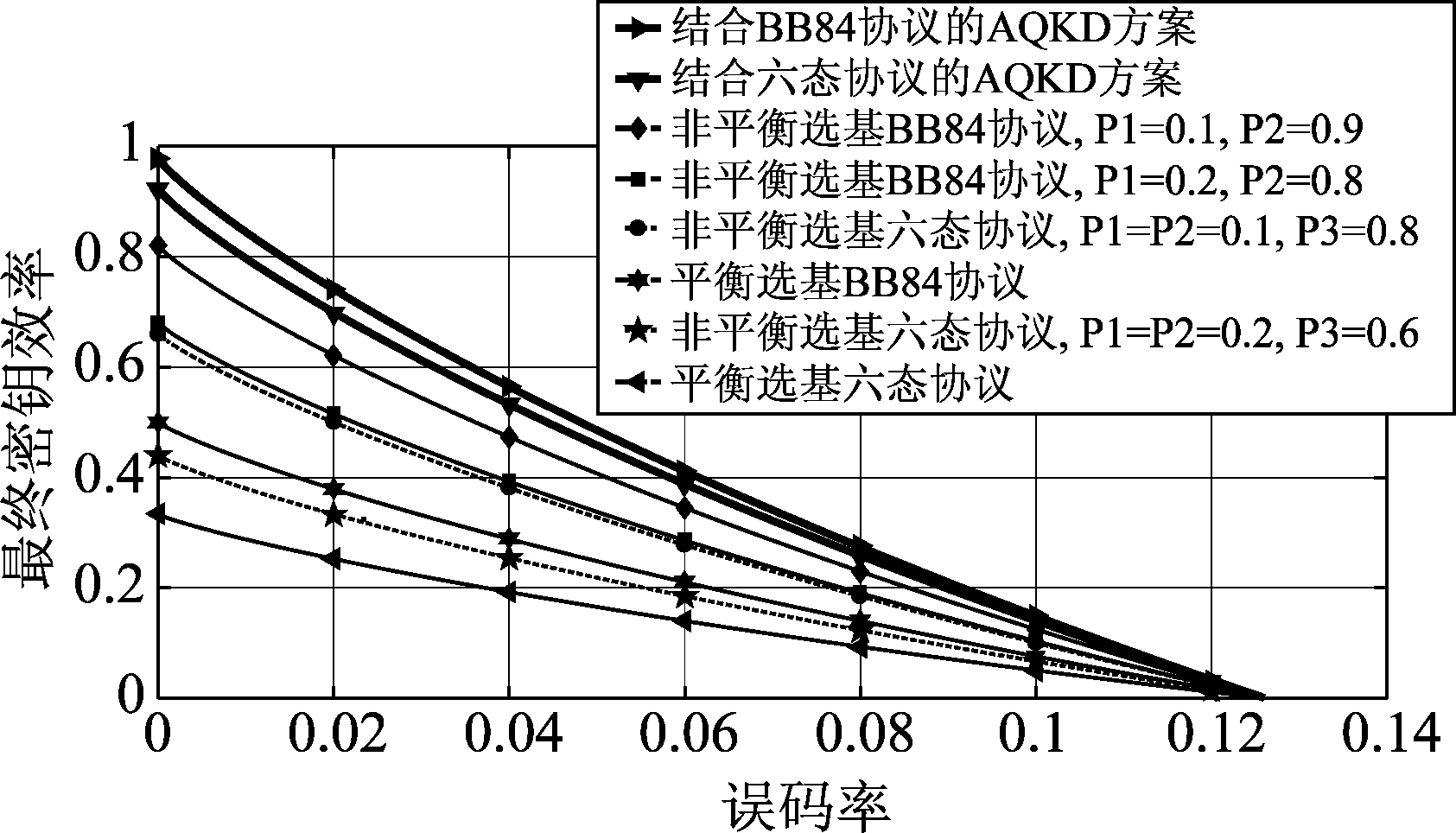
图5 最终密钥效率与误码率的关系对比
Fig.5 Comparison of the relationship between the final key efficiency and the bit error rate
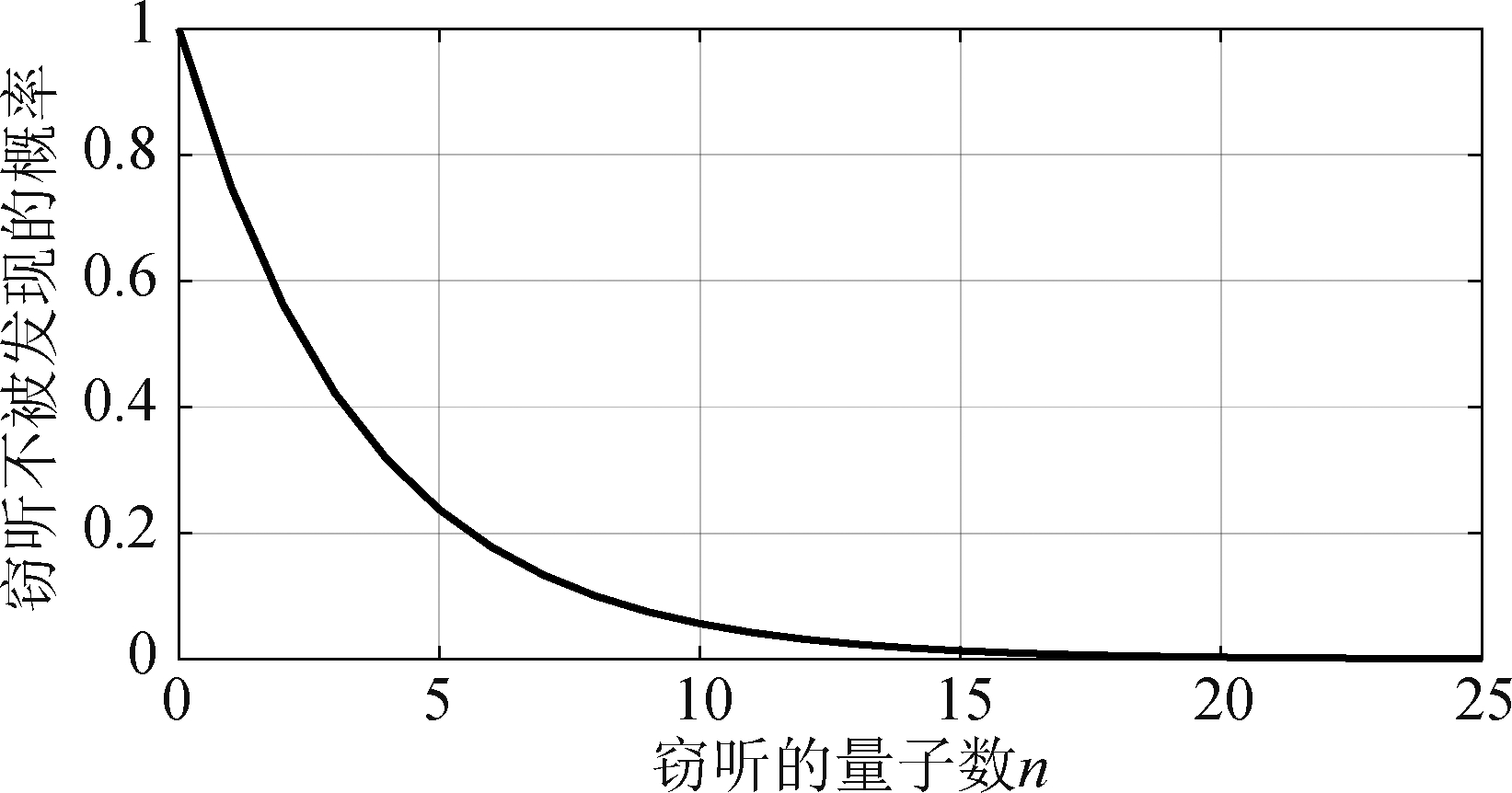
图6 窃听者不被发现的概率与窃听量子数量的关系
Fig.6 The relationship between the probability of eavesdropper not being found and the quantum quantity of eavesdropping
最后对窃听者不被发现的概率进行分析。由于窃听信道和合法信道是独立的,因此窃听者只能采取随机选基的方式来窃听。在BB84协议中不同的基选择的概率相同,当窃听者随机选择的基与收发两端的基一致时,量子态不会产生转换,因此也不会使接收端产生误码;当窃听者随机选择的基与收发两端不同时,量子态会随机的转化为窃听者的基所对应的状态中的一种,在接收端再次接收时,会再次进行转化,有一半的概率转化为正确的态,也有一半的概率转化为错误的态。因此,窃听者对单个量子态进行窃听,被发现的概率为选择了错误的测量基的同时又在接收端转化成错误的量子态的概率,即0.5×0.5=0.25,那么不被发现的概率即为0.75。当量子态的数目为n时,窃听者不被发现的概率为(0.75)n,当n逐渐变大时,窃听者不被发现的概率趋向于0,如图6所示。因此,系统的安全性能够得到保障。
6 结论
由于量子密钥分发技术在安全保密方面的巨大优势,为了进一步提高无线通信系统的安全性,本文提出了将无线通信的角度估计与量子密钥分发相结合的安全传输方案。利用量子态的测不准原理和不可克隆原理,可以发现窃听者,保证系统的通信安全。同时,与直接使用量子密钥分发的方案相比,由于本方案充分利用了无线信道的角度信息,因此在密钥的生成效率上也有显著提升。
[1] Akgun B, Krunz M, Ozan Koyluoglu O. Vulnerabilities of Massive MIMO Systems to Pilot Contamination Attacks[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(5): 1251-1263.
[2] Ziegler V, Wild T, Uusitalo M, et al. Stratification of 5G evolution and Beyond 5G[C]∥2019 IEEE 2nd 5G World Forum (5GWF). Dresden, Germany, 2019: 329-334.
[3] Ahmad I, Shahabuddin S, Kumar T, et al. Security for 5G and Beyond[J]. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3682-3722.
[4] Fernando E, Agustin D, Irsan M, et al. Performance Comparison of Symmetries Encryption Algorithm AES and DES with Raspberry Pi[C]∥2019 International Conference on Sustainable Information Engineering and Technology (SIET). Lombok, Indonesia, 2019: 353-357.
[5] Mallouli F, Hellal A, Sharief Saeed N, et al. A Survey on Cryptography: Comparative Study between RSA vs ECC Algorithms, and RSA vs El-Gamal Algorithms[C]∥2019 6th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud). Paris, France, 2019: 173-176.
[6] 方妍, 郭欣, 叶文景, 等. 经典通信信号的量子化处理: 现状与展望[J]. 信号处理, 2019, 35(10): 1615-1625.
Fang Yan, Guo Xin, Ye Wenjing, et al. Quantization processing of classical communication signals: current situation and prospect[J]. Journal of Signal Processing, 2019, 35(10): 1615-1625.(in Chinese)
[7] Bennett C H. Quantum cryptography using any two nonorthogonal states[J]. Physical Review Letters, 1992, 68(21): 3121-3124.
[8] Dagmar Bruss. Optimal eavesdropping in quantum cryptography with six states[J]. Physical Review Letters, 1998, 81(14): 3018-3021
[9] Bennett C H, Brassard G, Mermin N D. Quantum cryptography without Bell’s theorem[J]. Physical Review Letters, 1992, 68(5): 557-559.
[10]Chen T Y, Wang J, et al. Metropolitan all-pass and inter-city quantum communication network[J]. Optics Express, 2010, 18(26): 27217-27225.
[11]陈雅琳. 面向电力调度业务的量子密钥应用技术研究[D]. 华北电力大学(北京), 2019.
Chen Yalin. Research on application technology of quantum key for power dispatching service[D]. North China Electric Power University (Beijing), 2019.(in Chinese)
[12]Khan R, Kumar P, Jayakody D N K, et al. A Survey on Security and Privacy of 5G Technologies: Potential Solutions, Recent Advancements, and Future Directions[J]. IEEE Communications Surveys & Tutorials, 2020, 22(1): 196-248.
[13]Liao S K, Cai W Q, et al. Satellite-relayed intercontinental quantum network[J]. Physical Review Letters, 2018, 120(3): 030501.
[14]陈晓航, 张翔, 马晓峰, 等. 高性能空时二维角度估计改进算法[J]. 信号处理, 2017, 33(12): 1548-1554.
Chen Xiaohang, Zhang Xiang, Ma Xiaofeng, et al. Improved algorithm of high performance space-time two-dimensional angle estimation[J]. Journal of Signal Processing, 2017, 33(12): 1548-1554.(in Chinese)
[15]Jiao L, Tang J, Zeng K. Physical Layer Key Generation Using Virtual AoA and AoD of mmWave Massive MIMO Channel[C]∥2018 IEEE Conference on Communications and Network Security (CNS), Beijing, 2018: 1-9.
[16]Mathur S, Trappe W, Mandayam N, et al, Radio-telepathy: Extracting a secret key from an unauthenticated wireless channel[C]∥Proceedings of ACM Conference on Mobile Computing and Networking, San Francisco, 2008: 128-139.
[17]Sayeed A M. Deconstructing multiantenna fading channels[J]. IEEE Transactions on Signal Processing, 2002, 50(10): 2563-2579.
[18]Dai W, Peng T, Win M Z. Optimal Protocols for Remote Entanglement Distribution[C]∥2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 2020: 1014-1019.
[19]Razavi M, Leverrier A, Ma X, et al. Quantum key distribution and beyond: Introduction[J]. Journal of the Optical Society of America B, 2019, 36(3): QKD1-QKD2.
[20]Alkhateeb A, El Ayach O, Leus G, et al. Channel estimation and hybrid precoding for millimeter wave cellular systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 831- 846.
[21]Jana S. On the Effectiveness of Secret Key Extraction from Wireless Signal Strength in Real Environments[C]∥15th ACM Annual Int’l. Conf. Mobile Computing and Networking, 2009: 321-332.
[22]Du Y, Liu J, Chen M, et al. Mobility-based Physical-layer Key Generation Scheme for D2D Communications Underlaying Cellular Network[C]∥2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, 2018: 1-5.
[23]Badawy A, Khattab T, El-Fouly T, et al. Secret Key Generation Based on AoA Estimation for Low SNR Conditions[C]∥2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, 2015: 1-7.
