1 引言
现代信息化战场上的通信环境十分恶劣,存在各种各样的干扰,严重影响了通信质量。变换域通信系统作为认知无线电候补技术之一,已被应用于无线通信抗干扰[1]。但是,不同的变换域处理技术处理不同的通信干扰存在很大的效果差异[2]。因此,变换域的选取是变换域通信系统抗干扰性能的关键,研究变换域选择技术对变换域通信系统抗干扰能力有着重要意义。
目前,基于变换域思想的干扰处理问题相关研究较多。例如文献[3]研究了二进制小波变换,实现了时变干扰的剔除;文献[4]提出了基于小波包变换的干扰检测和干扰抑制技术,有效的抑制了干扰;文献[5]研究了分数阶傅里叶变换对扩频通信的线性快速调频干扰的抑制技术,获得了相对于傅里叶变换的较好的效果。但是,以上文献均是利用单一变换域,通过干扰检测等技术实现对特定干扰的抑制,其主要思想为:通过频谱感知得到干扰信号的多种特征值,经过归一化干扰的显著特征值得到干扰类别,进而据此选取变换域进行抗干扰。但这种方式很大程度依靠干扰检测技术的发展,且特征值等参数的选取往往依靠经验所得,故对变换域选取效果无法保证。针对上述缺点,人们将神经网络[6]等智能算法融合到干扰检测中,提高干扰检测准确性,但设计适当的神经网络也是一大难题,限制了其在变换域通信系统中的应用。
综上所述,变换域的选择主要是依靠干扰检测的结果,并且假定了敌方干扰机每次只采用一种干扰方式或在一种干扰方式下持续时间较长,干扰的方式预先设定。故,以上都属于静态的干扰对抗,发送方可以通过信号检测来选择适当变换域进行对抗或规避。但随着通信技术的发展,智能干扰、认知干扰等相继出现,干扰方也可以进行频谱侦测,双方均具有快速切换通信策略的能力,之前的静态对抗已经不合时宜,需要智能的抗干扰策略指导通信实践。
针对以上问题,本文引入博弈论的基本思想,研究通信双方在灵活干扰策略下的策略选择问题,获得了在完全信息下最佳策略组合及其盈利,实现了基于变换域优选的智能抗干扰,验证了利用博弈论分析变换域抗干扰的可能性,为变换域通信系统抗干扰性能的改进提供了理论支持。
2 通信干扰模型及优选变换域
干扰样式与变换域的选取有着紧密联系,针对不同干扰种类,变换域的选择也不尽相同。本文主要考虑通信方与具有频谱感知能力的敌恶意干扰机通信对抗的场景,双方可以根据对方选取的策略来及时更新自己的通信策略,适用于有限零合博弈的思想。
2.1 恶意干扰机可选干扰模型
本文研究的干扰类型和样式主要为变换域通信中常见的干扰[7],具体如下:
a) 单音干扰(Single Tone)
J(t)=J0exp(j(2πf0t+φ0))
(1)
b)多音干扰(Multiple Tone)
(2)
Jn为多音的第n个单音干扰的幅度, fn为第n个单音的干扰频率,φn为第n个单音信号的初始相位。
c) 部分频带干扰(Partial Band)
J(t)=Un(t)exp(j(2πf0t+φ0))
(3)
其中Un(t)为服从均值为0,方差为![]() 的高斯白噪声,φ0为[0,1]内分布且相互独立的相位。
的高斯白噪声,φ0为[0,1]内分布且相互独立的相位。
d) 线性调频干扰(Linear Frequency-modulated)
J(t)=Jexp[j(2πf0t+πkt2+φ)]
(4)
J是幅度、 f0是初始频率、k是调频系数、φ是初始相位。
2.2 通信方可选变换域处理技术
随着变换域通信技术的发展,变换域技术不再仅仅局限于傅里叶变换,发展到现在主流变换域主要有以下四种[8]:
(1)快速傅里叶变换(Fast Fourier transform)
FFT是经典变换域技术,被广泛应用于各个领域,常被用于处理平稳信号,缺点是无法将信号的时频局部特征描述清楚,下为FFT数学公式:
(5)
F(ω)=![]() f(t)e-jωtdt
f(t)e-jωtdt
(6)
(2)分数阶傅里叶变换(Fractional Fourier transform)
FFT 是将视角从时域转换到频域,而FRFT的视角是通过旋转时频面坐标轴,再利用观察频域的方法去分析信息。FRFT具有较强的处理非平稳信号的能力,能够选取信号能量集中的角度去分析,也就是在不同的分数阶得到的结果中选取幅值最大的那个结果,那么这个结果所存在的那个分数阶就是最优阶次。其数学公式为:
Xp(u)=![]() Kp(u,t)x(t)dt
Kp(u,t)x(t)dt
(7)
其核函数为:
Kp(u,t)= 
(8)
式中![]() 注意,核函数是p的连续函数。
注意,核函数是p的连续函数。
(3)离散小波变换
小波变换很早便被提出,但近些年才被广泛应用,可对信号低频部分分解,适合处理非平稳干扰信号,但是具有能量丢失和频点利用率低等缺点。其数学公式为:
(9)
其中小波函数为:
(10)
式中,m,n均为整数,a0>1,b0>0。
(4)离散小波包变换
小波包变换是利用分析树来表示小波包,通过多次迭代小波转换分析干扰信号的细节部分,可以理解为它是让信号通过一系列中心频率不同但带宽相同的滤波器。其数学公式为:
(11)
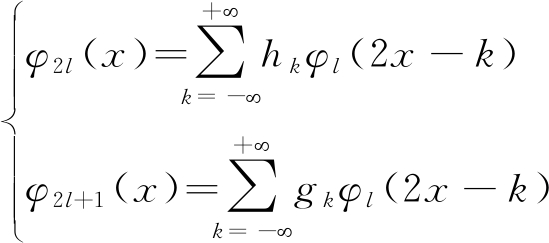
(12)
其中hk为低通滤波器,gk为高通滤波器。
3 基于有限零和博弈和变换域优选的智能抗干扰算法设计
3.1 博弈模型构建
将变换域通信抗干扰视为一个动态博弈,通信方T和干扰方G看作博弈双方,恶意干扰设备为了干扰正常通信,将用一切可能的干扰手段进行干扰,这些方式构成一个可选取的策略集SG=(G1,G2,G3…Gm),将通信方可选取的所有变换域构成一个策略集ST=(T1,T2,T3…Tn),为了便于表示,将Gm 记为干扰方纯策略,将Tn 记为通信方纯策略,又因为干扰机可选择的干扰方式和通信方可选取的变换域数量都是有限的。故SG和ST都是有限纯策略集。
恶意干扰机和通信设备在动态博弈过程中,博弈双方只要有盈利就有损失,通信方的盈利即干扰方的损失,干扰方的盈利即通信方的损失,博弈双方是不可调和的冲突关系,因此博弈双方是非合作竞争关系。故选取的博弈模型为非合作博弈[9-10]。假设,通信方采取的策略是Ti,干扰方采取的策略是Gj,则通信方获得的盈利为Uij,那么干扰方获得的盈利就为-Uij,故双方可以选择将同一函数作为效用函数,不过是一方求效用函数最大而另一方求效用函数最小。此时,可将博弈模型建模为有限零和博弈,即双方盈利之和为零,符号相反。模型可表达为如下数学公式:
(13)
UT=uT(ST,SG)
(14)
UG=uG(ST,SG)=-uT(ST,SG)=-UT
(15)
其中T表示通信方,G表示干扰方,ST表示通信方可选择的变换域策略集,SG表示干扰方可以选择的干扰策略集,UT表示通信方的盈利,UG表示干扰方的盈利,uG和uT分别表示干扰方和通信方的效用函数。
博弈模型构建的目标是通过博弈分析,求出博弈的纳什均衡解。纳什均衡解给出了双方策略选择的一个稳定点,该稳定点是对抗双方都能接受的策略组合。此时,双方均满足于通过博弈分析做出的选择,任意一方想通过改变策略都不能使自己的盈利变大。所以纳什均衡解对应的策略组合就是通过博弈论分析得到的最佳变换域和干扰方式的选择组合,并且博弈双方不论从哪种策略开始博弈,均会收敛于得出的纳什均衡解。
3.2 博弈模型的效用函数分析
博弈模型构建完成后,需要确定效用函数,选取不同的效用函数,博弈结果也不尽相同。本文将选取误码率作为博弈双方的效用函数,误码率是通信准确率最直观的参数,通信方想通过选取不同的变换域来降低误码率以保证通信的准确性,而干扰方则想尽一切办法来增大误码率,甚至导致通信中断。误码率还可以对不同的策略组合进行量化衡量,能够公平的比较每一种组合的好坏。故,本文选取的效用函数为误码率。
因为变换域通信系统具有类噪声性质,所以通常采用CSK调制,假设基于CSK调制的变换域通信系统的信号波形为S(n),经过信道,接收机接收到的信号为
R(n)=S(n)+Q(n)+n0
(16)
式中S(n)是发射信号,Q(n)是未被剔除干净的干扰信号,n0是噪声。
接收机接收到信号后,进行相关解调,得到解调信号:
w=r(n)×a*(n)=[S(n)+Q(n)+n0]×a*(n) =S(n)×a*(n)+Q(n)×a*(n)+n0×a*(n)
(17)
式中a*(n)是伪随机相位编码公式经过能量调整,得到的时域基函数。
故,接收机输出信号的信号干扰噪声比为:
(18)
即在有干扰时,基于CSK调制的变换域通信系统误码率为:
(19)
式中F(x) 是递减函数,故若SINR增加,则误码率降低。
3.3 算法设计
在确定博弈模型及其效用函数后需进行算法流程设计,计算出博弈盈利矩阵,求解出纳什均衡解。下为基于有限零和博弈和变换域优选的智能抗干扰算法:

算法:基于有限零和博弈和变换域优选的智能抗干扰算法Step 1 确定敌我双方对抗策略集;Step 2 确定博弈模型的效用函数,确定每种策略组合情况下的误码率数值,从而得出盈利矩阵;Step 3 若存在纯策略纳什均衡解,即根据纳什均衡解得出的策略组合进行选取变换域,博弈结束;Step 4 若不存在纯策略纳什均衡解,即计算出混合策略纳什均衡解,根据得出的结果选取混合策略组合,博弈结束。
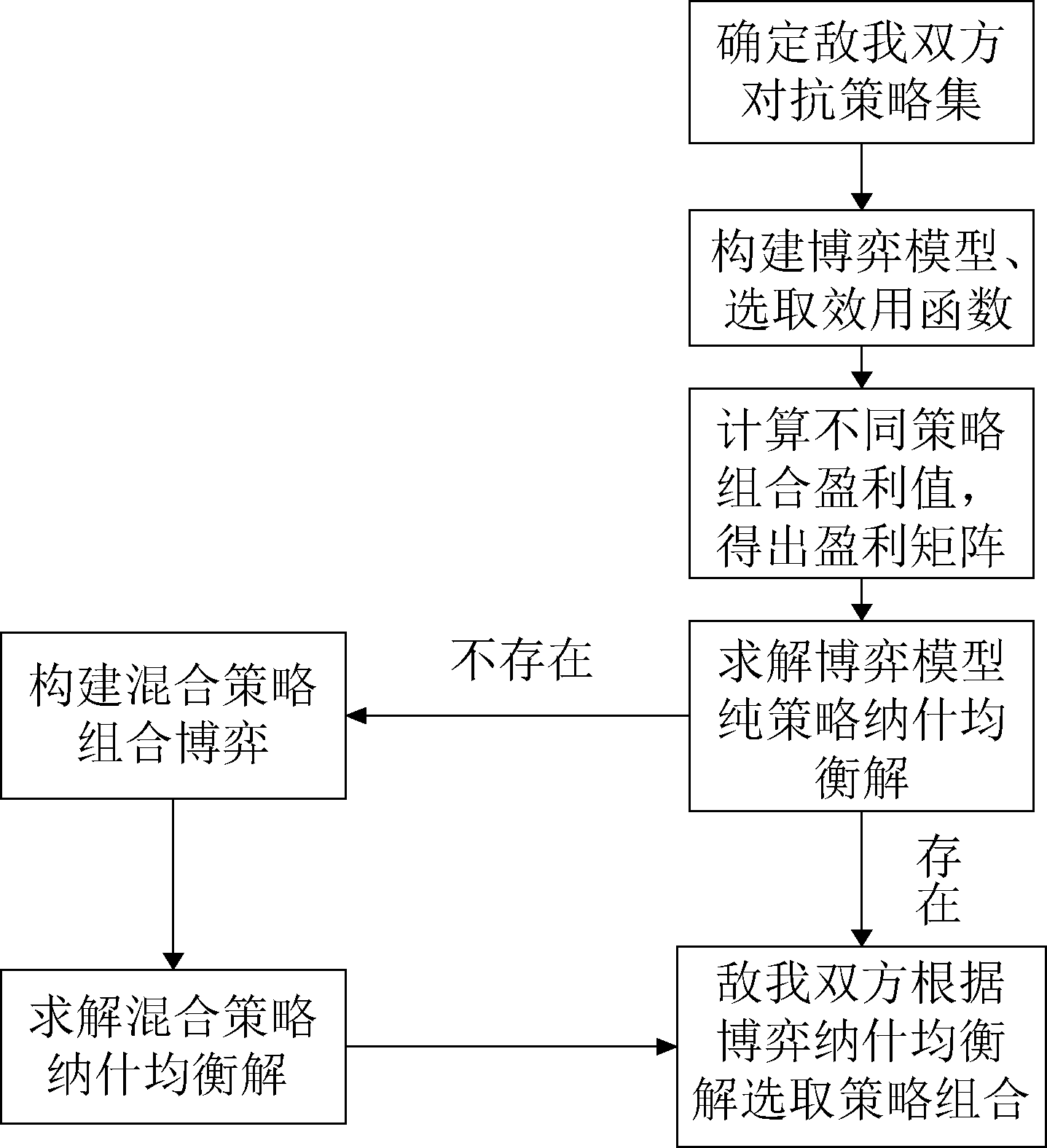
图1 基于有限零和博弈和变换域优选的智能抗干扰算法 Fig.1 Intelligent anti-interference algorithm based on finite zero-sum game and transform domain optimization
3.3.1 纳什均衡解的求解
设Uij是通信方选择策略Ti,干扰方采取的策略是Gj时通信方的盈利,那么干扰方的盈利为-Uij,由此,可以得到干扰对抗博弈盈利矩阵,如下表1所示。
表1 变换域通信干扰对抗博弈盈利矩阵Tab.1 Profit Matrix
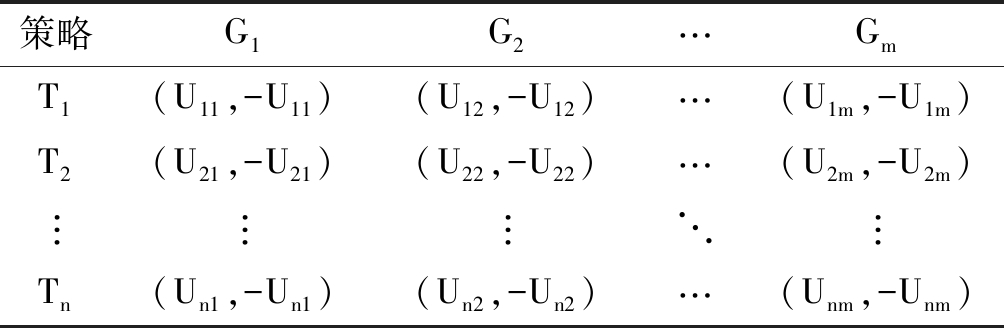
策略G1G2…GmT1(U11,-U11)(U12,-U12)…(U1m,-U1m)T2(U21,-U21)(U22,-U22)…(U2m,-U2m)︙ ︙︙⋱︙Tn(Un1,-Un1)(Un2,-Un2)…(Unm,-Unm)
其中通信方的优化问题可以表示为:
T*=arg max[Pe(Ti,Gj*)]
(20)
干扰方的优化问题可以表示为:
G*=arg max[-Pe(Ti*,Gj)]
(21)
若纳什均衡解在盈利矩阵中存在,由最小最大及最大最小值定理可知,盈利矩阵满足下式[11]:
(22)
当纳什均衡解在盈利矩阵中不存在,即不存在纯策略纳什均衡解,此时定存在一种混合策略,使得干扰方和通信方的盈利不低于某一个值,即混合策略纳什均衡解。
假设干扰方选取的纯策略Gj(j=1,2,…,m)的概率为yj,故可得到概率向量y=(y1,y2,…,ym); j=(1,2,…,m);yj≥0,∑yj=1是干扰方纯策略集SG的全体策略的一种概率选择。同理,概率向量x=(x1,x2,…,xn);i=(1,2,…,n);xi≥0,∑xi=1是通信方纯策略ST的全体策略的一种概率选择。则可称y为干扰方的混合策略,x为通信方的混合策略。根据混合策略,可得到通信方期望盈利:
(23)
干扰方期望盈利:
(24)
且由混合策略纳什均衡解定义可知,若策略组合为混合策略纳什均衡解,则其必满足以下方程组[12]:
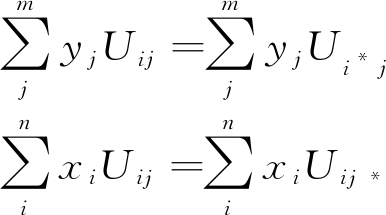
(25)
故解此方程组即可得出混合策略纳什均衡解。
4 基于有限零和博弈和变换域优选的智能抗干扰算法性能仿真分析
4.1 不同干扰在不同变换域下的效用函数仿真分析
为验证本文所提算法的有效性,此次仿真针对快速傅里叶变换域和分数阶傅里叶变换域以及单音干扰、多音干扰、部分频带干扰和线性调频干扰4种干扰信号数据集进行仿真实验。由于此部分仿真为理论基础验证性工作,不一一将结果列出,选取代表性结果进行详细分析。
仿真硬件平台是Inter(R) Core(TM),2.6 GHz,内存为8 GB的PC机,所有实验均在MATLAB R2016a环境下进行,对于不同的数据集,最佳参数的选取采取交叉验证的方法。通信方发送信号全部采用BCSK调制,在高斯信道下传输且干扰信号的总干扰功率不变。下面对在两种不同变换域系统下对抗不同干扰得到的误码率进行仿真。
表2 干扰信号仿真参数
Tab.2 Simulation parameters of interference signal

干扰信号类型干扰参数参数值部分频带干扰干扰频带/MHz带宽因子[200,450]20%,40%,60%单音干扰干扰频率/MHz100,200,300多音干扰干扰频率/MHz干扰音数[50,250]2,3,4,5线性调频干扰初始频率/MHz调频率100150,200
(1)MT-FFT: 在不同干信比下,多音干扰在快速傅里叶变换域系统下的误码率随信噪比变化曲线如图2所示。
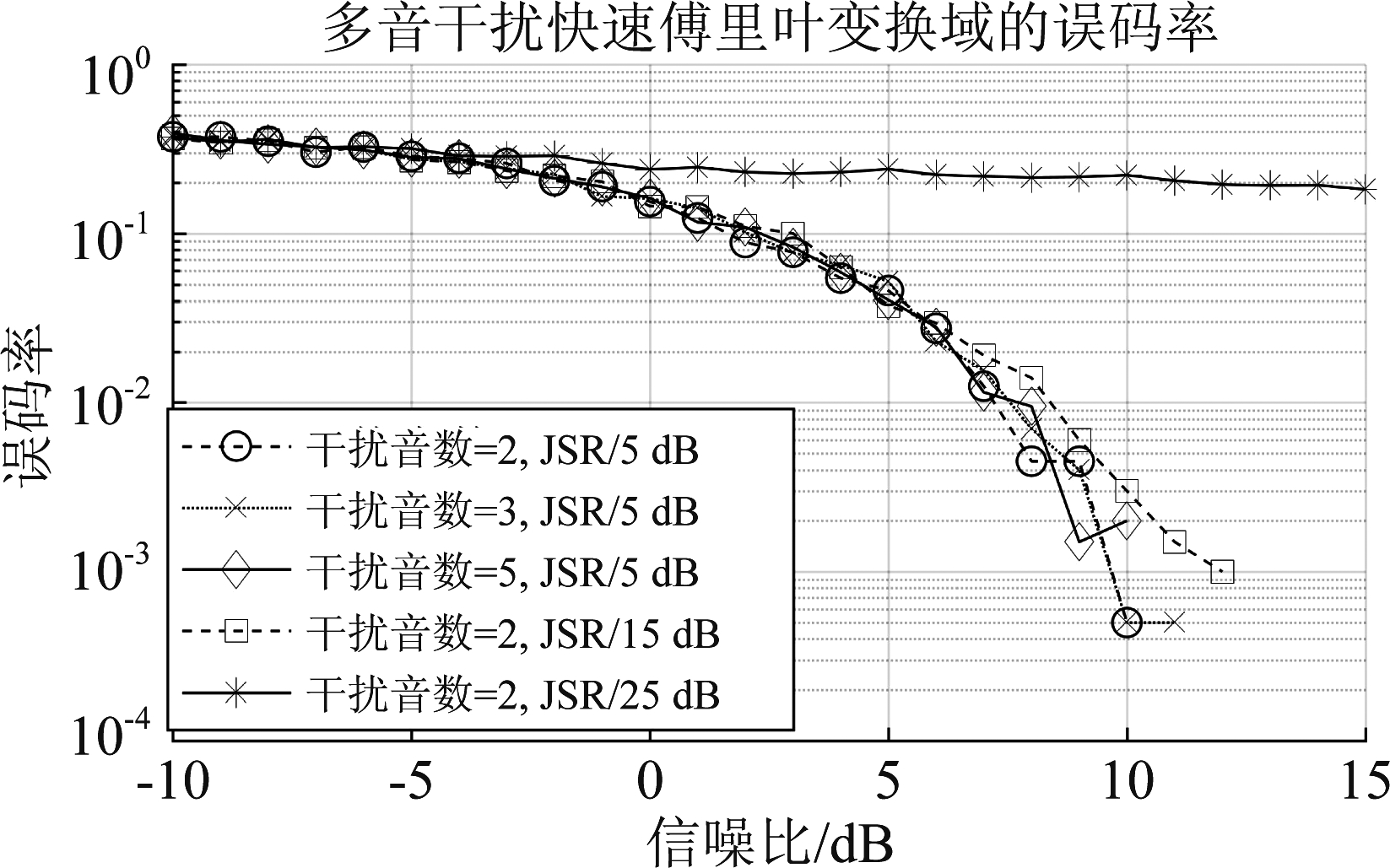
图2 多音干扰快速傅里叶变换域的误码率
Fig.2 Bit error rate in the multi-tone interference fast Fourier transform domain
仿真考虑的影响因素为多音干扰的干扰频点数及相同干扰频点数时在强干扰和弱干扰下误码率变化。由仿真结果可知,相同干信比和低信噪比时,不同干扰音数下的误码率区别不大,曲线几乎重合。但随着信噪比的增加,干扰音数多的误码率要略小于音数少的,这是因为干扰总功率不变前提下,干扰数目多,每个频点的干扰功率会降低,干扰效果下降。但频点数不变时,随着干信比增大,误码率变大。但是当干信比增大到一定程度时,误码率几乎不随着信噪比变化。因为强干扰下,噪音可忽略不计。
(2)LFM-FFT:在不同干信比下,线性调频干扰在快速傅里叶变换域系统下的误码率随信噪比变化曲线如图3所示。
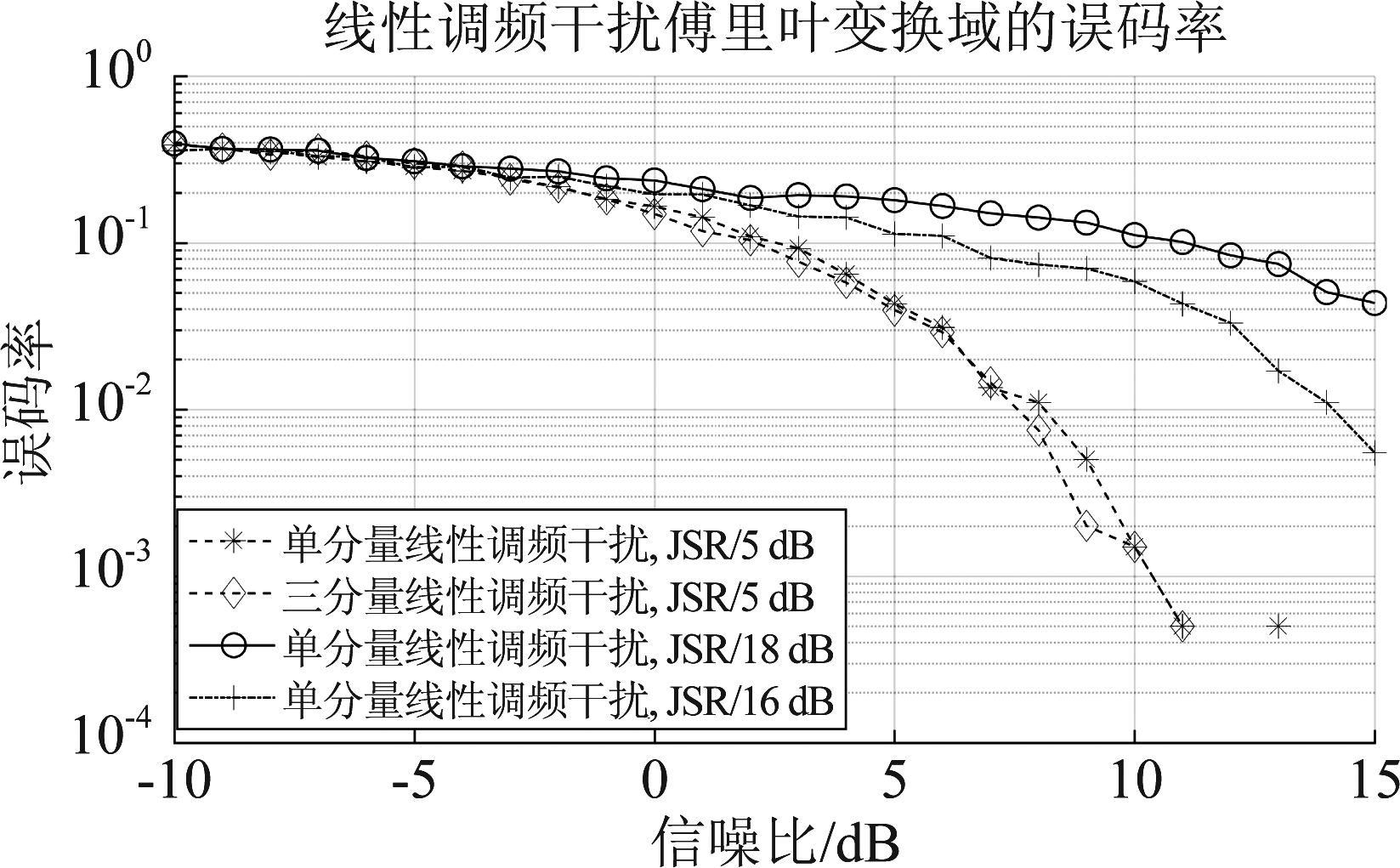
图3 线性调频干扰快速傅里叶变换域的误码率
Fig.3 Bit error rate in the chirped fast Fourier transform domain
从仿真结果可以得出,在低信噪比情况下,单分量线性调频干扰和三分量线性调频干扰的误码率曲线几乎重合。但当信噪比达到7 dB以后,曲线开始出现分叉,且单分量干扰的干扰效果相对较好,这是因为多分量干扰将干扰功率分散导致干扰效果降低,且对干信比较为敏感,干信比稍微增加,对曲线走向就有较大影响。
(3)MT-FRFT: 图4给出了干信比为5 dB,干扰音数分别为2、3、5的多音干扰以及干扰音数为2,干信比为15 dB、25 dB的多音干扰。从仿真图可以看出,与在傅里叶变换域下类似,在低信噪比时,误码率变化平缓,曲线几乎重合。高信噪比时音数少的干扰效果要好于音数多的,不过相较于快速傅里叶变换域对干信比变化敏感度较低,抗干扰效果更好一点。
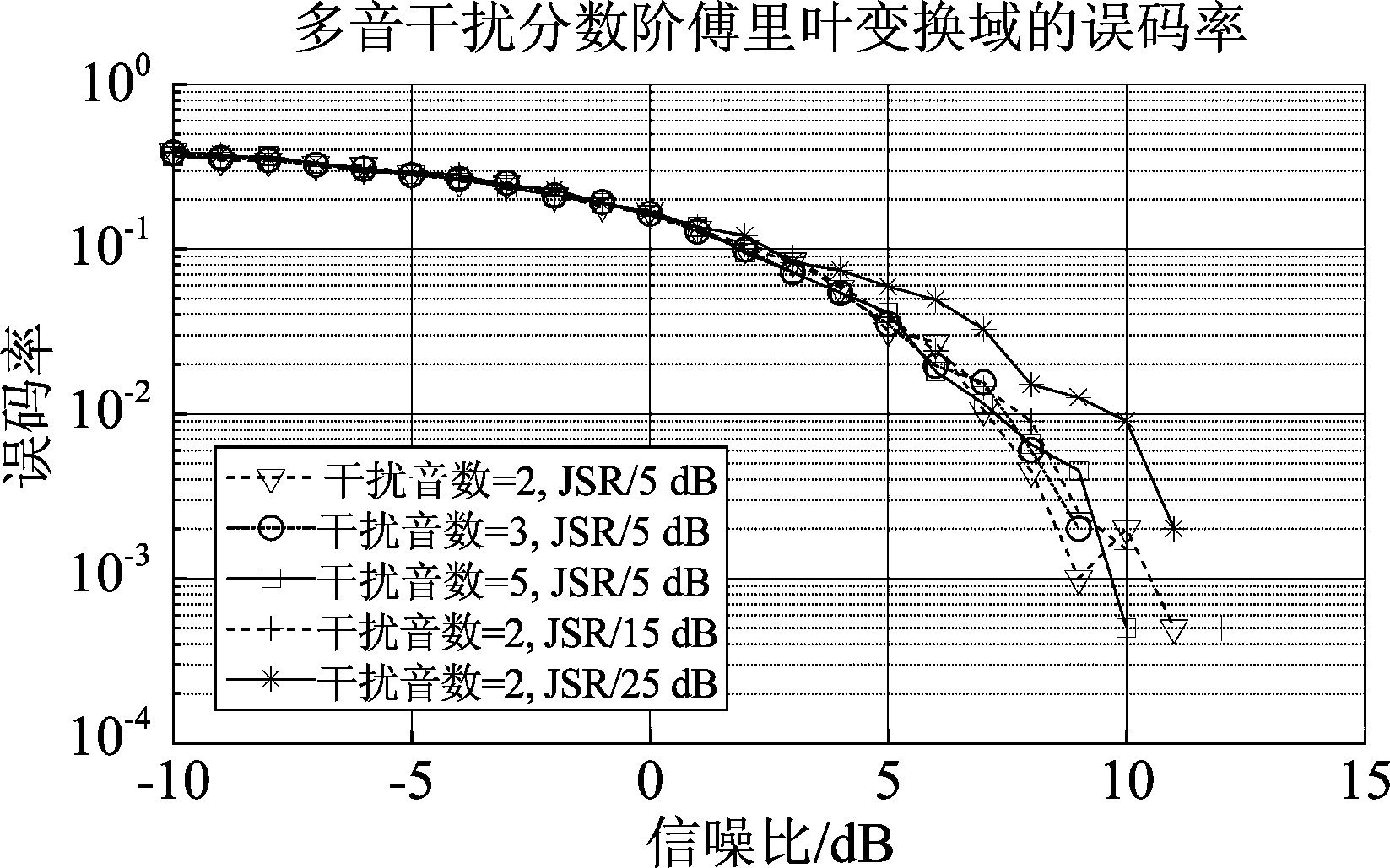
图4 多音干扰分数阶傅里叶变换域的误码率
Fig.4 Bit error rate in the fractional Fourier transform domain of multitone interference
(4)LFM-FRFT: 图5给出了干信比为5 dB时的单分量、三分量线性调频干扰以及单分量时,干信比为15 dB,19 dB的线性调频干扰。由仿真结果可知,低信噪比时,情况与快速傅里叶变换域类似,线性调频干扰对干信比变化敏感,稍微增加,就会增加很大的误码率,且敏感度要高于快速傅里叶变换域系统。但是相同干信比下,误码率相对较低。
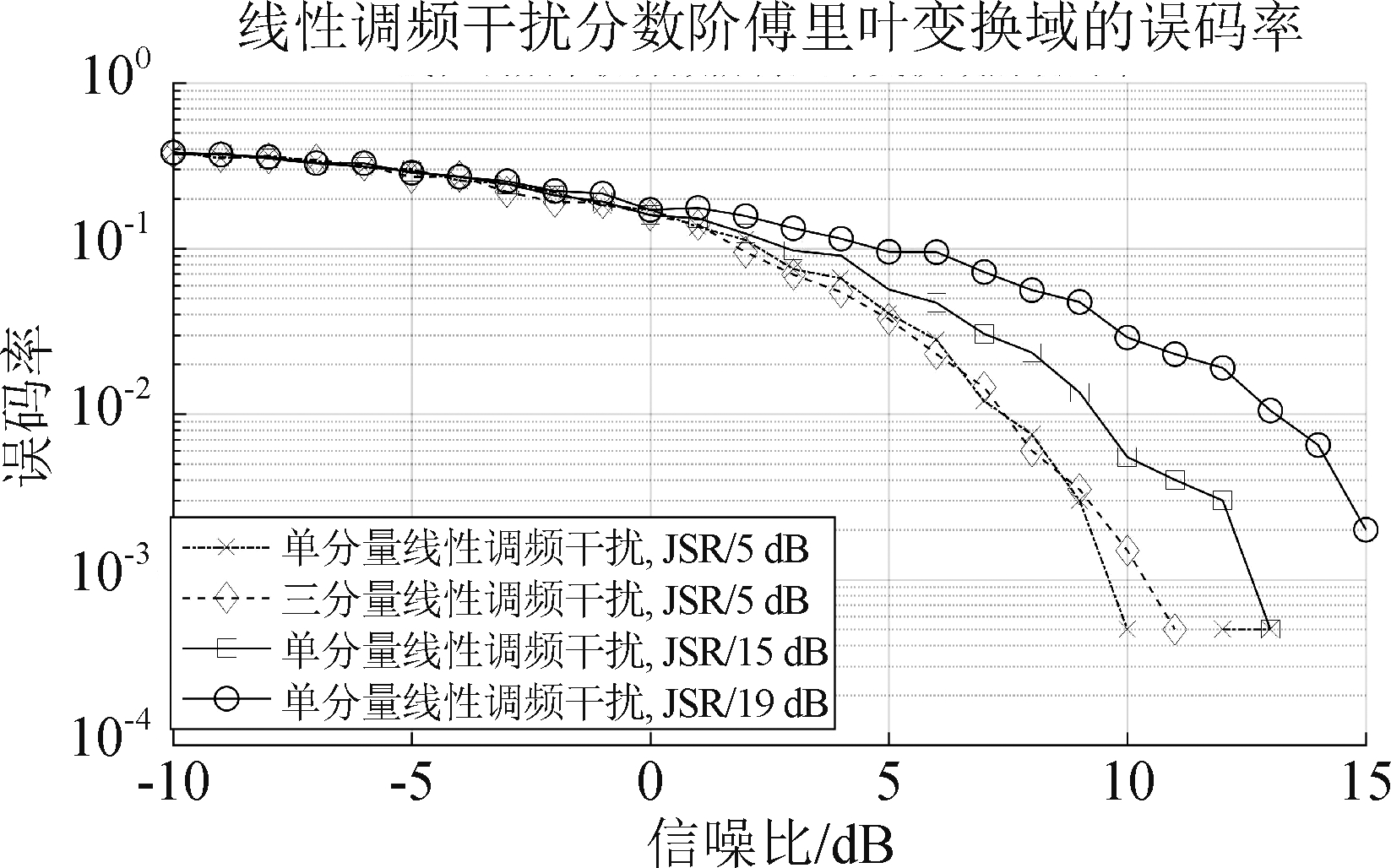
图5 线性调频干扰分数阶傅里叶变换域的误码率
Fig.5 Bit error rate in the chirp fractional Fourier transform domain
4.2 干扰对抗博弈策略决策动态仿真
上节仿真了干扰对抗博弈的效用函数,描绘了不同干扰在不同变换域系统下的误码率曲线,对它们的不同参数进行了纵向对比。此节则考虑的是在不同干扰场景下,对效用函数进行定值分析,从而得出零和博弈盈利矩阵。对干扰对抗博弈决策进行动态分析,最后求出纳什均衡解,从而选定对抗策略。
现假设仿真对抗双方条件及参数:发射机最大发射功率为25 kW,接收机与发射机间距35 km,发射频率为100 MHz,恶意干扰机距离接收机20 km,最大发射功率100 kW,通信方采用快速傅里叶变换域系统和分数阶傅里叶变换域系统两种变换域系统。故其纯策略集为ST=(FFT,FRFT),并且发送信号均采用BCSK调制。恶意干扰机采用的干扰策略为单音干扰、多音干扰、部分频带干扰和线性调频干扰,其干扰策略集为SG=(ST,DT,PB,LFM)。其中部分频带干扰包括带宽因子20%、40%、60%三种,多音干扰包括三音、四音、五音三种。线性调频干扰包括单分量和三分量两种。
下面针对不同对抗场景进行仿真,双方将会根据求解出的纳什均衡解,选择最佳对抗策略,以便得到自身效用函数最大化。
干扰场景1 恶意干扰机可选取的干扰方式为单音干扰、带宽因子为40%的部分频带干扰和单分量线性调频干扰。因为干扰功率的高低也会影响不同变换域的抗干扰效果,所以将分别考虑低干扰和强干扰的双方盈利矩阵。
(1)弱干扰:如图6为干信比为5 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。
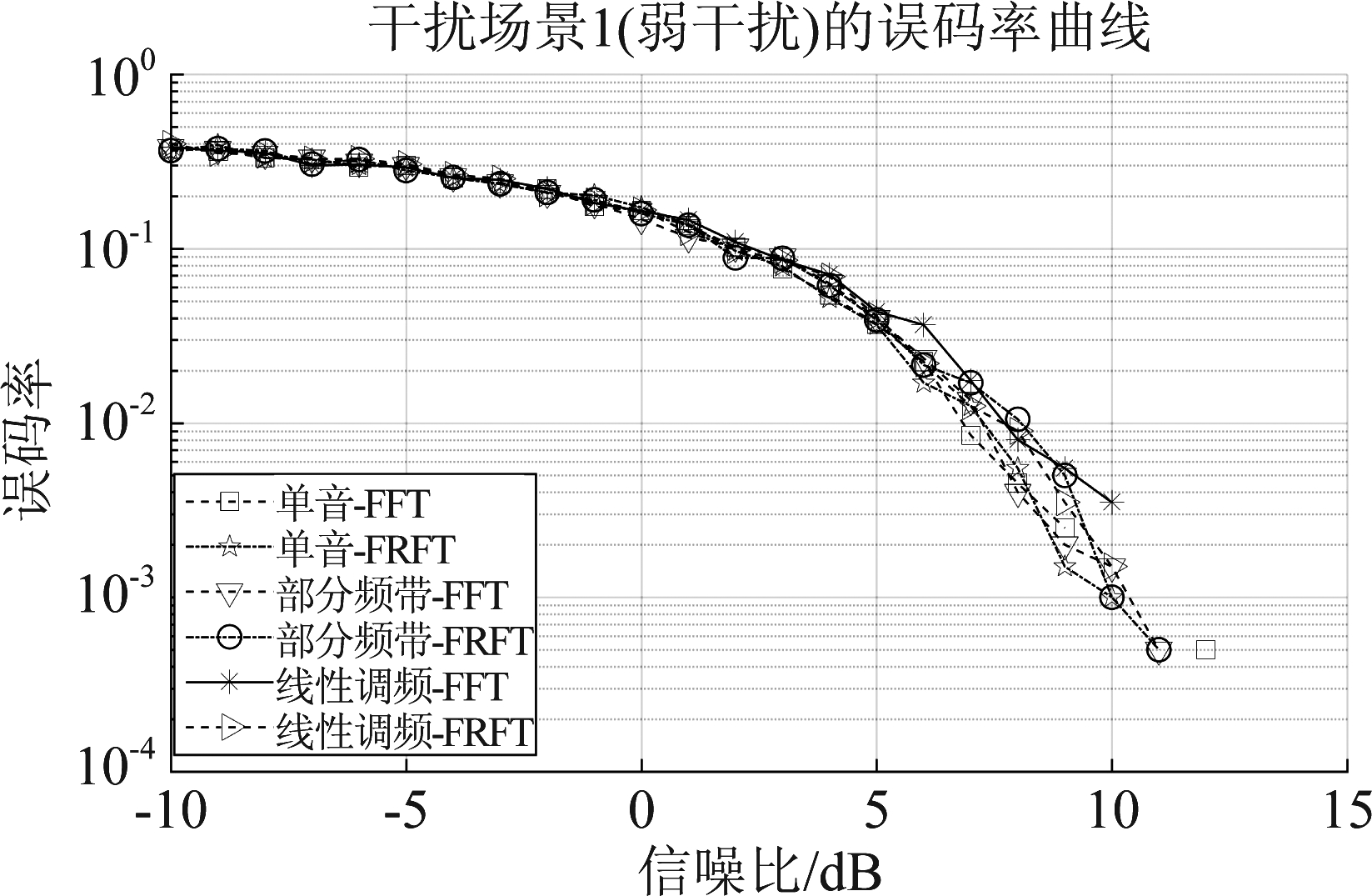
图6 干扰场景1(弱干扰)的误码率曲线
Fig.6 BER curve of interference scenario 1 (weak interference)
当信噪比为8 dB时:
1)恶意干扰机选取单音干扰时,通信方采用快速傅里叶变换域系统和分数阶傅里叶变换域系统的误码率分别为:Pe≈0.0045,Pe≈0.0055;
2)恶意干扰机选取部分频带干扰时,通信方采用快速傅里叶变换域系统和分数阶傅里叶变换域系统的误码率分别为:Pe≈0.004,Pe≈0.0105;
3)恶意干扰机选取线性调频干扰时,通信方采用快速傅里叶变换域系统和分数阶傅里叶变换域系统的误码率分别为:Pe=0.008,Pe=0.009。
表3为通过仿真得到的博弈对抗双方的盈利矩阵。
表3 博弈双方的盈利值矩阵1
Tab.3 Profitability matrix 1 for both players
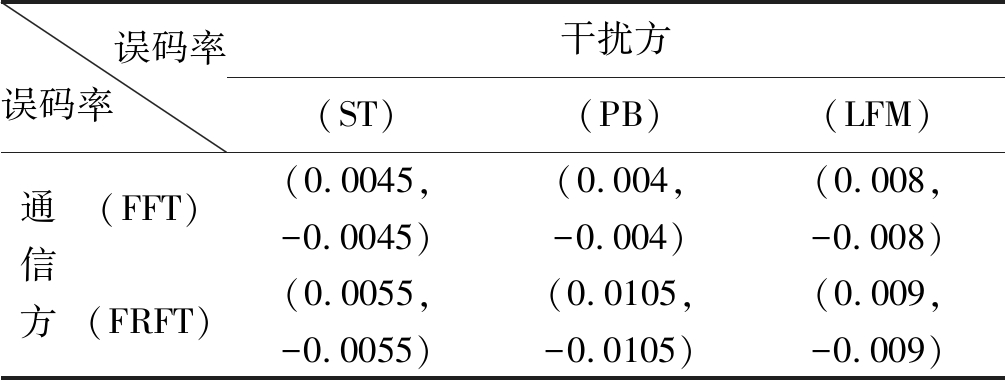
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.0045,-0.0045) (0.004,-0.004) (0.008,-0.008) (FRFT) (0.0055,-0.0055)(0.0105,-0.0105)(0.009,-0.009)
通信方希望传送的信息越准确越好,即接收机的误码率越低越好。对于干扰方,则希望阻碍消息的传送甚至中断,即接收机的误码率越大越好。在完全信息下,不知对方采取的何种策略。通信方为了保持最低通信效果,所采取的策略的结果是不管对方采用什么策略都不会使误码率高于一定值。同理,干扰方采取的策略的结果为无论对方采取什么策略都使误码率不低于一定值。
现若通信方初始状态为分数阶傅里叶变换域,通过频谱检测,干扰方定会采取使得误码率最大的干扰方式。通过盈利矩阵可知,干扰方会选取部分频带干扰,此时误码率为0.0105,干扰严重。这时通信方将会改变通信策略,故可预计下一个策略组合为(FFT,PB),更新策略后误码率降为0.004。那么干扰机也会改变策略去提高误码率,即策略组合变为(FFT,LFM),此时误码率为0.008。但是这时发现若通信方再次改变通信策略得到的误码率为0.009,大于此时的误码率。故通信方将不会改变策略,那么干扰方也会坚持使用此策略组合,即双方接受了此策略组合(FFT,LFM)。这便是根据最小最大值理论求出的零和博弈对抗的纯策略纳什均衡解。故双方采取的策略为快速傅里叶变换域和线性调频干扰,误码率为0.008,误码率相对于最差情况下的0.0105有所改善,降低了24%。
(2)强干扰:如图7为干信比为20 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。
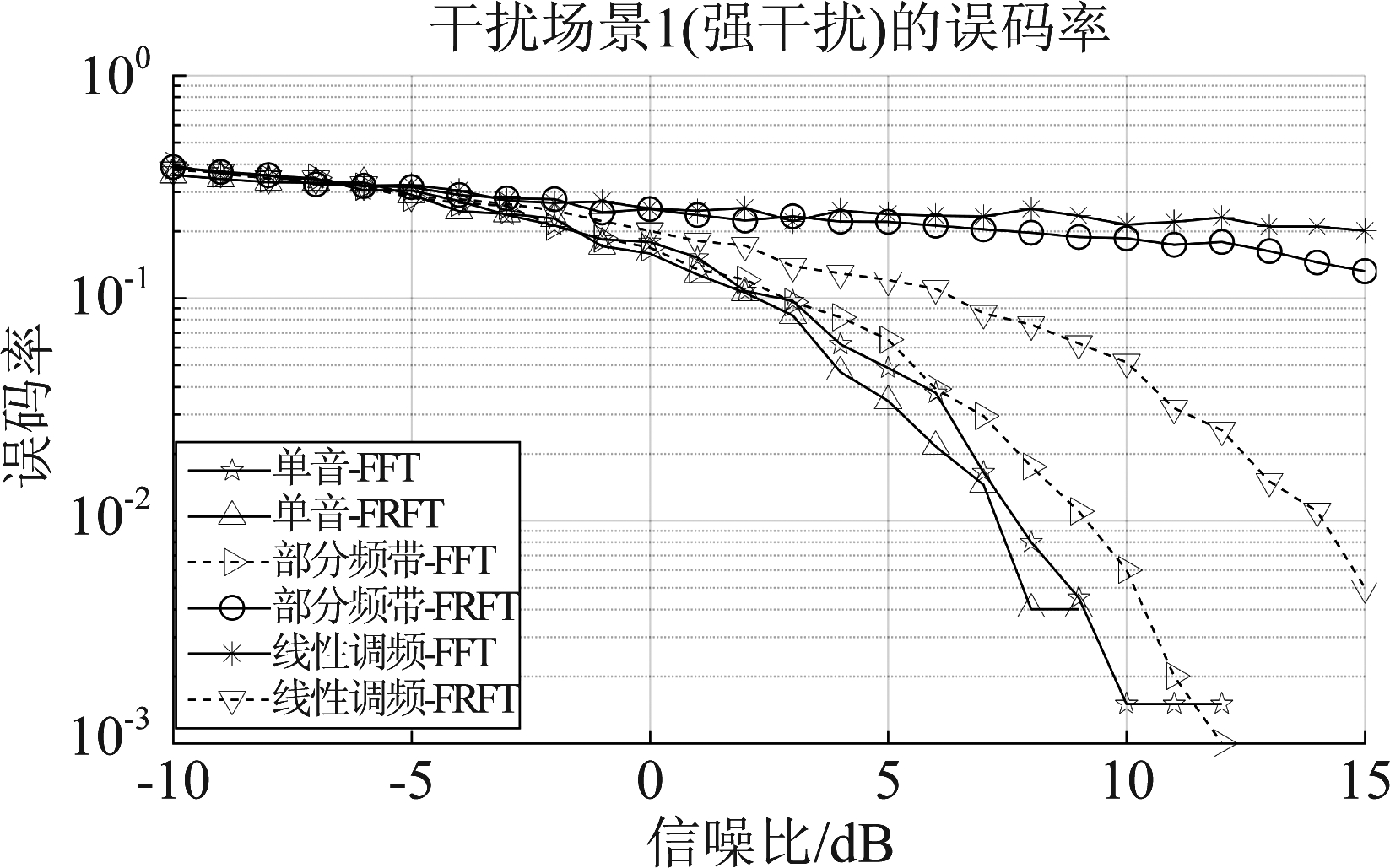
图7 干扰场景1(强干扰)的误码率曲线
Fig.7 BER curve of interference scenario 1 (strong interference)
当信噪比为8 dB时得到博弈对抗双方的盈利矩阵如表4所示。
表4 博弈双方的盈利值矩阵2
Tab.4 Profitability Matrix 2
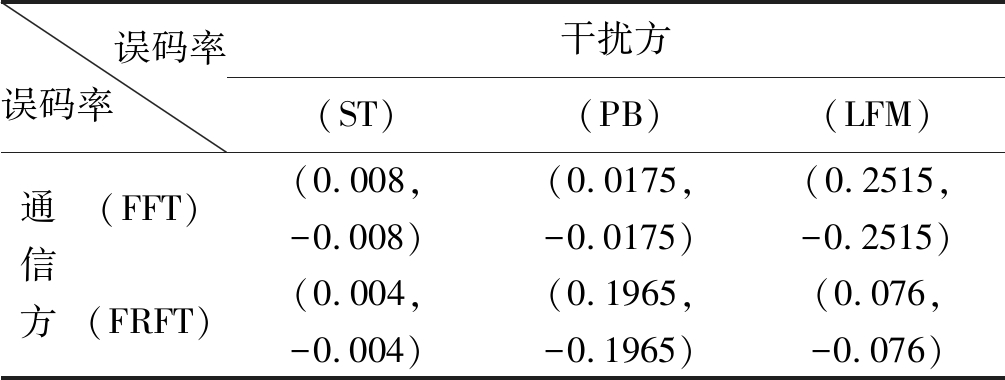
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.008,-0.008) (0.0175,-0.0175)(0.2515,-0.2515)(FRFT) (0.004,-0.004)(0.1965,-0.1965)(0.076,-0.076)
现假设干扰对抗博弈开始时通信方选取快速傅里叶变换域为初始状态,那么干扰方将会选取干扰效果最好的策略,即线性调频干扰,误码率为0.2515,干扰非常严重。通信方将改变通信方式以降低误码率,那么下一个状态为(FRFT,LFM),误码率为0.076,降低效果明显。此时干扰方继续改变干扰策略,使用部分频带干扰,误码率为0.1965。通信方为了寻求自己的利益继续改变通信方式,此时策略组合为(FFT,PB),误码率降为0.0175。那么干扰方又会选择线性调频干扰,双方经过一轮的对抗博弈,又回到最初的策略组合,进入无限循环,即不存在纯策略纳什均衡解,故将会考虑混合策略组合。
在混合策略博弈过程中,求出的纳什均衡解是每一种策略的概率向量。因为本次博弈双方有效策略空间为2,故设通信方策略(FFT,FRFT) 的概率向量为(p,1-p),干扰方策略(PB,LFM) 的概率向量为(q,1-q),将盈利值和概率向量带入式(25)的方程组。
通过解此不等式组得到通信方混合策略的混合概率为(49.5%,50.5%),干扰方混合策略的混合概率为(34%,66%)。即可理解为再次对抗博弈中通信方有49.5%的概率选择快速傅里叶变换域,50.5%的概率选择分数阶傅里叶变换;干扰方有34%的概率选择部分频带干扰,66%的概率选择线性调频干扰。或者可认为通信方有49.5%的时间选择快速傅里叶变换,50.5%的时间选择分数阶傅里叶变换域;干扰方有34%的时间选择部分频带干扰,66%的时间选择线性调频干扰。博弈对抗时间越长此混合策略结果越准确,相对于最差情况误码率降低32%。
干扰场景2 恶意干扰机可选取的干扰方式为音数为5的多音干扰、带宽因子为40%的部分频带干扰和三分量线性调频干扰。
(1)弱干扰:如图8为干信比为5 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。
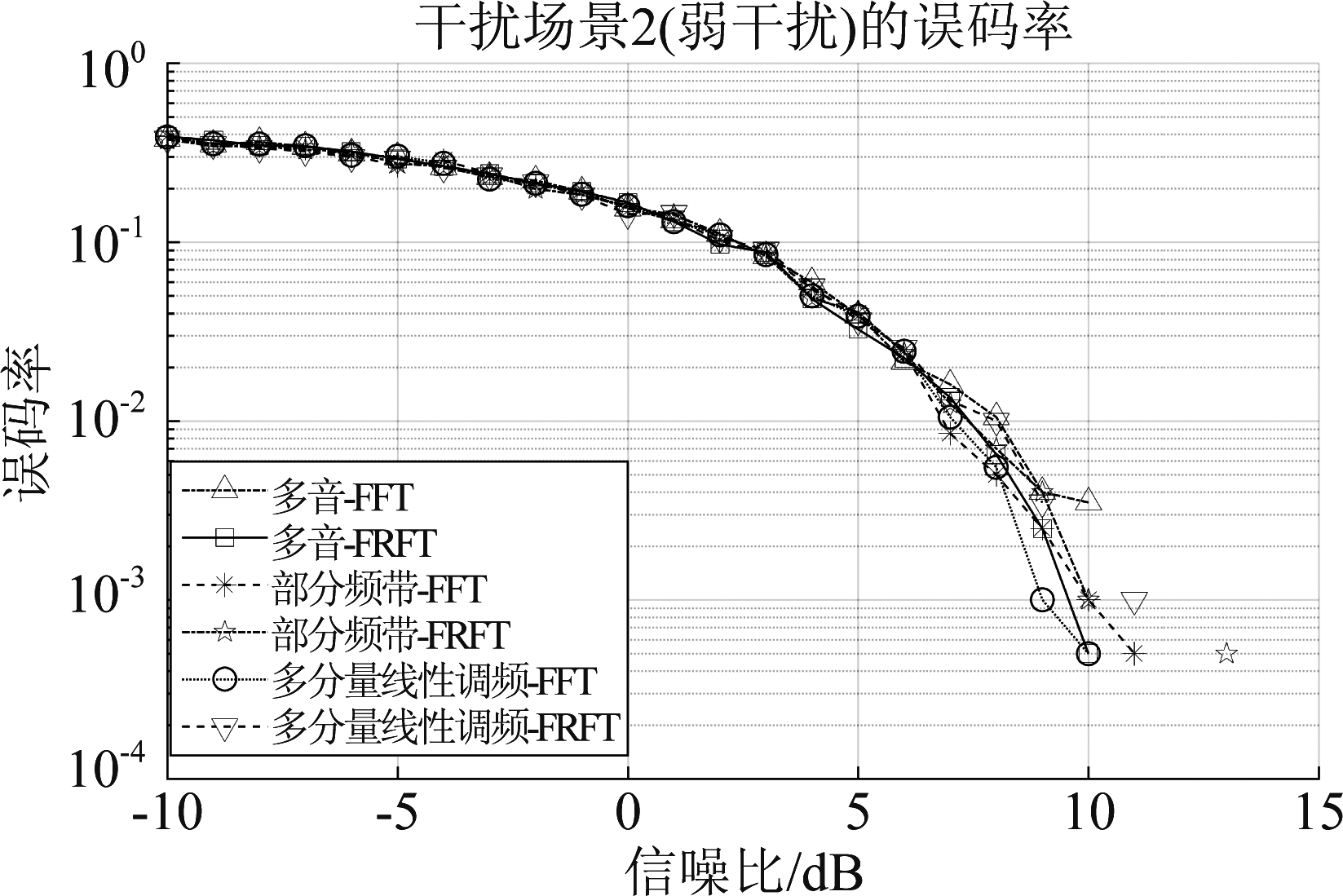
图8 干扰场景2(弱干扰)的误码率曲线
Fig.8 BER curve of interference scenario 2 (weak interference)
当信噪比为8 dB时由仿真得到博弈对抗双方的盈利矩阵如表5所示。
表5 博弈双方的盈利值矩阵3
Tab.5 Profitability matrix 3 for both players
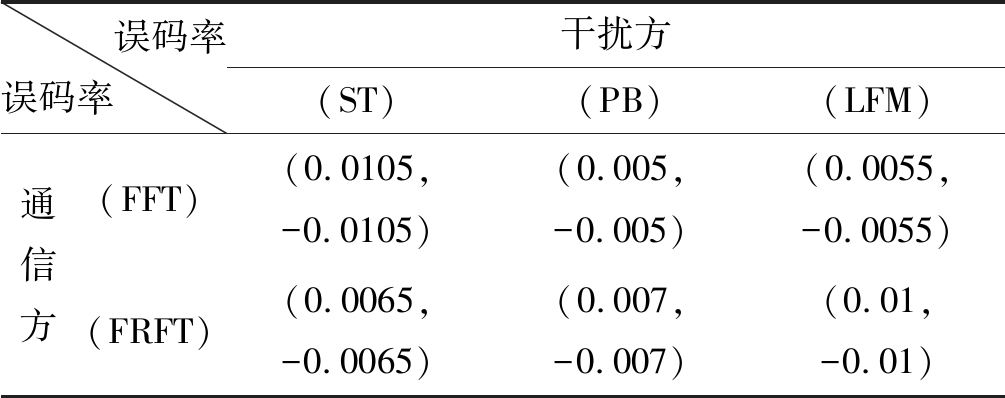
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.0105,-0.0105)(0.005,-0.005)(0.0055,-0.0055)(FRFT) (0.0065,-0.0065)(0.007,-0.007)(0.01,-0.01)
通过盈利矩阵分析不存在纯策略纳什均衡解,故求解混合策略纳什均衡解,利用上一小节同一方法求得干扰方混合策略是(ST,LFM),其对应的混合概率为(52.9%,47.1%),通信方混合策略为(FFT,FRFT),对应混合概率为(41.1%,58.9%);博弈混合纳什均衡解为(0.0081,-0.0081),相比较最差情况误码率降低22.4%。
(2)强干扰:如图9为干信比为20 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。

图9 干扰场景2(强干扰)的误码率曲线
Fig.9 BER curve of interference scenario 2 (strong interference)
当信噪比为10 dB时由仿真得到博弈对抗双方的盈利矩阵如表6所示。
表6 博弈双方的盈利值矩阵4
Tab.6 Profitability Matrix 4 of the Gamers
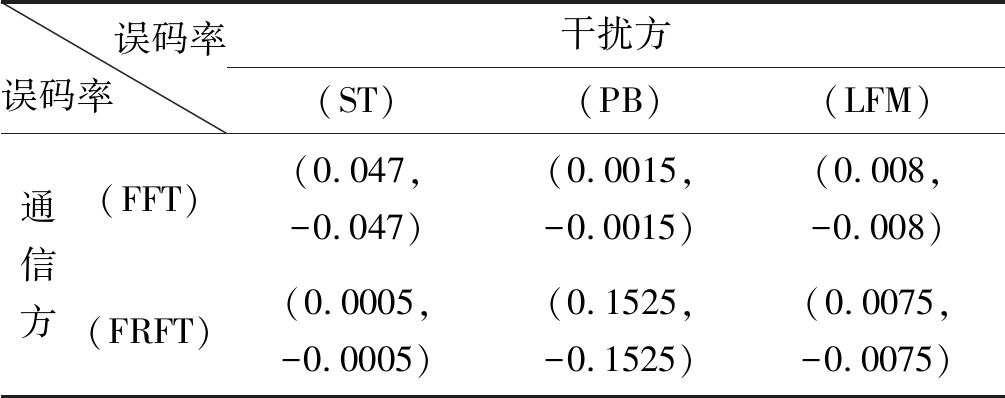
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.047,-0.047)(0.0015,-0.0015)(0.008,-0.008)(FRFT) (0.0005,-0.0005)(0.1525,-0.1525)(0.0075,-0.0075)
通过盈利矩阵分析不存在纯策略纳什均衡解,故求解混合策略纳什均衡解,利用上一小节同一方法求得干扰方混合策略是(ST,PB),其对应的混合概率为(76.5%,23.5%),通信方混合策略为(FFT,FRFT),对应混合概率为(76.9%,23.1%);博弈混合纳什均衡解为(0.036,-0.036),相比较最差情况误码率降低76.4%。
干扰场景3 恶意干扰机可选取的干扰方式为单音干扰、音数为5的多音干扰和单分量线性调频干扰。
(1)低干扰:如图10为干信比为5 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。
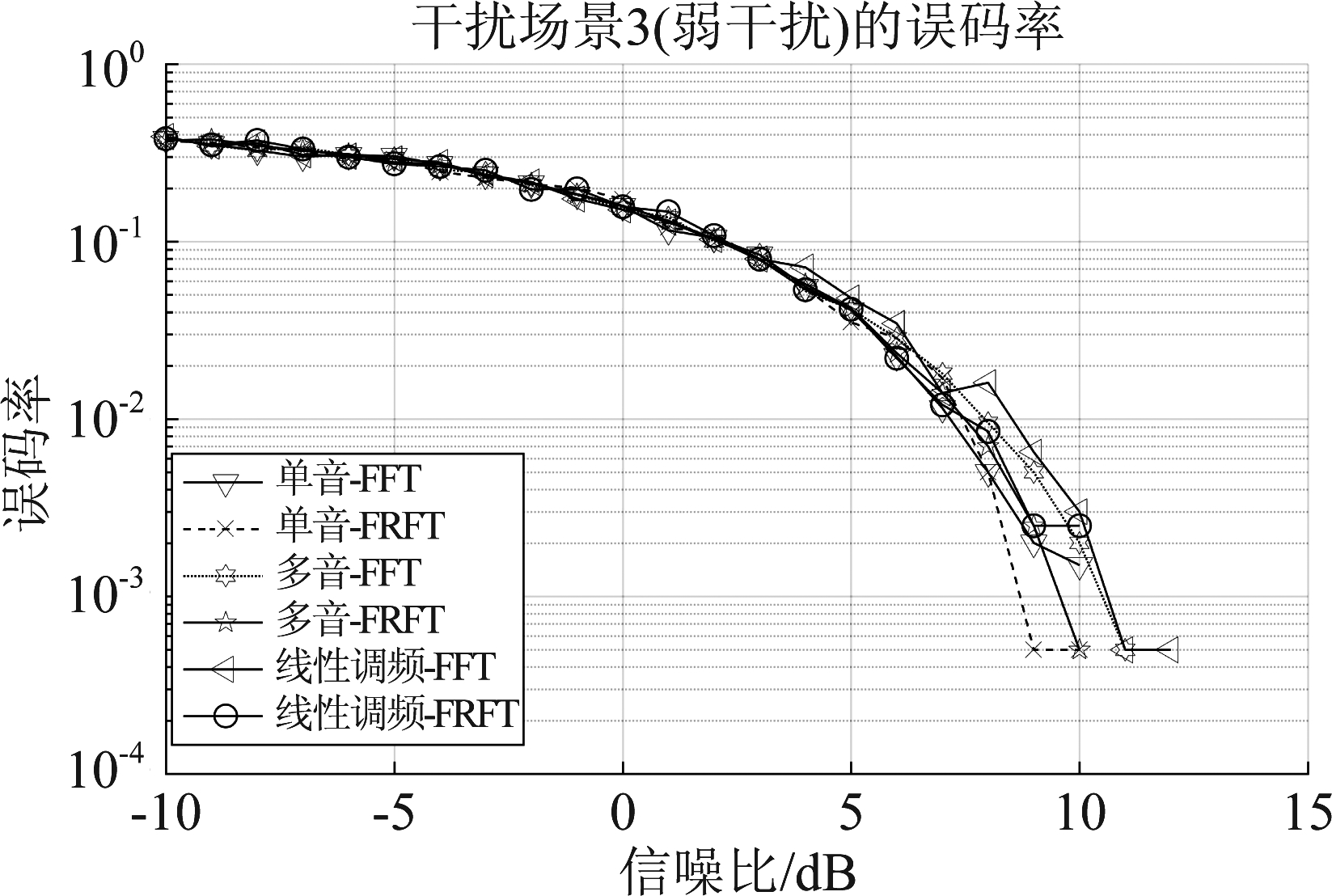
图10 干扰场景3(弱干扰)的误码率曲线
Fig.10 BER curve of interference scenario 3 (weak interference)
当信噪比为2 dB时由仿真得到博弈对抗双方的盈利矩阵如表7所示。
表7 博弈双方的盈利值矩阵5
Tab.7 Profitability Matrix 5
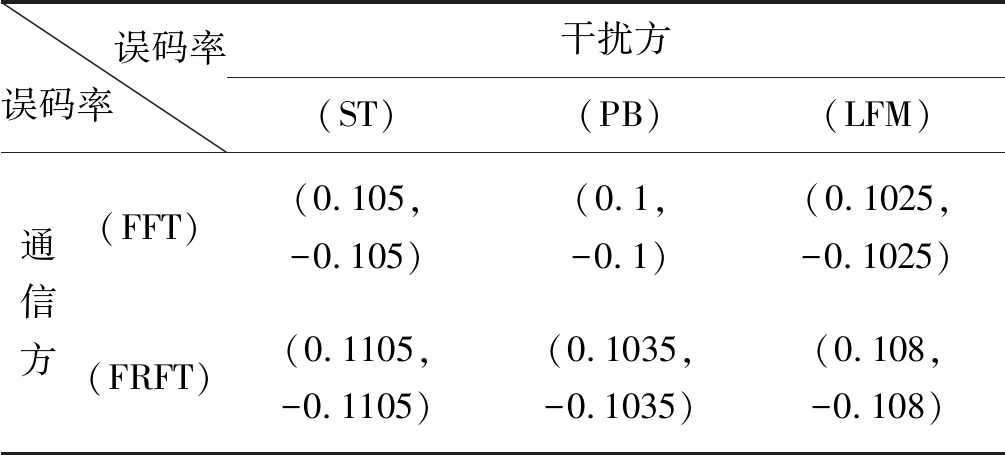
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.105,-0.105) (0.1,-0.1)(0.1025,-0.1025)(FRFT) (0.1105,-0.1105)(0.1035,-0.1035)(0.108,-0.108)
通过分析及最小最大值理论可知,此时的纳什均衡解为(0.105,-0.105),对应的策略组合为(FFT,ST),与通信最差情况相比误码率降低了4.9%。
(2)强干扰:如图11为干信比为20 dB时三种干扰在两种变换域系统下的误码率随信噪比变化曲线。
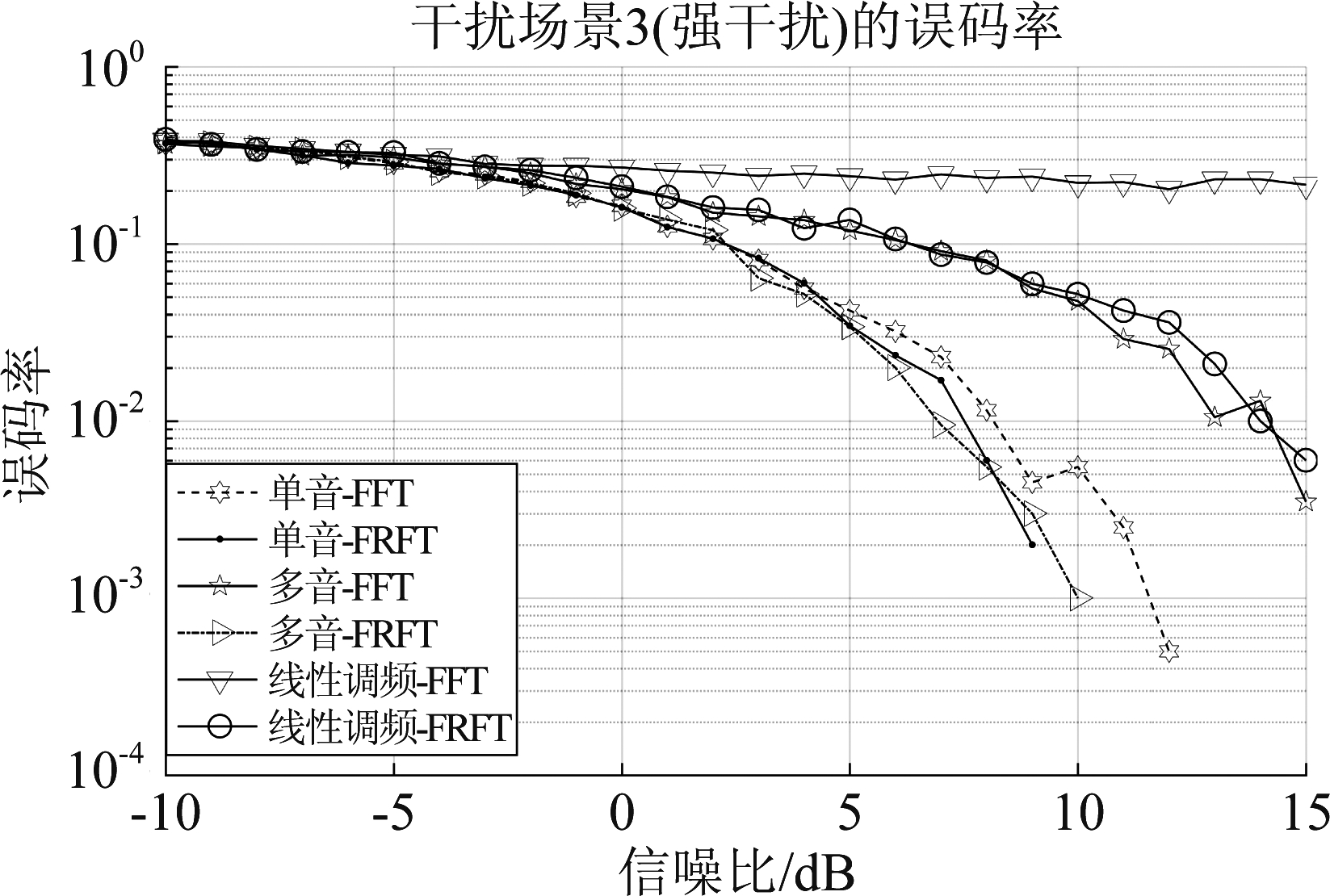
图11 干扰场景3(强干扰)的误码率曲线
Fig.11 BER curve of interference scenario 3 (strong interference)
当信噪比为8 dB时由仿真得到博弈对抗双方的盈利矩阵如表8所示。
表8 博弈双方的盈利值矩阵6
Tab.8 Profit matrix of both players
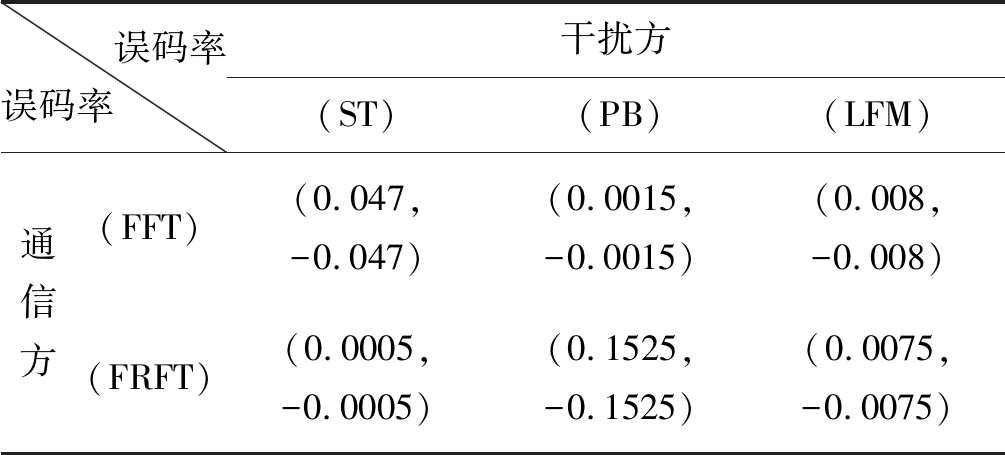
误码率误码率 干扰方(ST) (PB) (LFM) 通信方(FFT) (0.047,-0.047)(0.0015,-0.0015)(0.008,-0.008)(FRFT) (0.0005,-0.0005)(0.1525,-0.1525)(0.0075,-0.0075)
通过分析及最小最大值理论可知,此时的纳什均衡解为(0.0595,-0.0595),对应的策略组合为(FRFT,LFM),与通信最差情况相比误码率降低了75.2%。
5 结论
本文研究了变换域通信系统与恶意干扰机的对抗关系。他们的对抗过程实质为博弈过程,将可选择的变换域和可选择的干扰方式看作双方的策略集,选取误码率为效用函数,即构建了基于有限零和博弈和变换域优选的智能抗干扰算法。通过对在快速傅里叶变换域系统和分数阶傅里叶变换域系统下,采用单音干扰、多音干扰、部分频带干扰和线性调频干扰时的误码率进行仿真,比较了不同变换域对抗不同干扰性能的好坏,得到了博弈对抗双方的盈利矩阵。通过盈利矩阵分别考虑纯策略和混合策略两种情况,得到两种情况下的纳什均衡解,进而得到在双方均不知对方采取何种策略的情况下的最佳策略组合,实现了变换域的优选,使误码率相较于最差情况有了大幅降低,达到智能抗干扰的目的。证明本文算法可行性,为今后提高变换域通信系统抗干扰性能提供新思路以及理论支撑。
[1] Liu M, Wang J, Liu L. Research on Intelligent Anti-jamming Communication with Transform Domain Communication System[C]∥International Conference in Communications, Signal Processing, and Systems. Springer, Singapore, 2018: 949-955.
[2] 王桂胜, 任清华, 姜志刚, 等. 基于信号特征空间的TDCS干扰分类识别[J]. 系统工程与电子技术, 2017, 39(9): 1950-1958.
Wang G S, Ren Q H, Jiang Z G, et al. TDCS interference classification and recognition based on signal feature space[J]. System Engineering and Electronics, 2017, 39(9): 1950-1958.(in Chinese)
[3] 李宁, 蒋建中, 张东方, 等. 一种基于二进小波变换的抗时变干扰算法[J]. 信息工程大学学报, 2011, 12(1): 88-91, 102.
Li N, Jiang J Z, Zhang D F, et al. An anti-time-varying interference algorithm based on dyadic wavelet transform[J]. Journal of Information Engineering University, 2011, 12(1): 88-91, 102.(in Chinese)
[4] 王桁, 吕智勇, 杨龙. DSSS卫星通信中基于小波包变换的干扰抑制方法[J]. 系统工程与电子技术, 2016, 38(6): 1417-1422.
Wang H, Lu Z Y, Yang L. Interference suppression method based on wavelet packet transform in DSSS satellite communications[J]. System Engineering and Electronics, 2016, 38(6): 1417-1422.(in Chinese)
[5] 申丽然, 郭黎利, 尹清波. 基于分数阶傅里叶变换的直扩通信快速线性调频干扰抑制[J]. 科学技术与工程, 2014, 14(1): 59- 65, 71.
Shen L R, Guo L L, Yin Q B. Fast LFM Interference Suppression for DSSS Communication Based on Fractional Fourier Transform[J]. Science Technology and Engineering, 2014, 14(1): 59- 65, 71.(in Chinese)
[6] 冉雨, 程郁凡, 陈大勇, 等. 采用BP神经网络的智能抗干扰决策引擎研究[J]. 信号处理, 2019, 35(8): 1350-1357.
Ran Y, Cheng Y F, Chen D Y, et al. Study on intelligent anti-interference decision engine using BP neural network[J]. Journal of Signal Processing, 2019, 35(8): 1350-1357.(in Chinese)
[7] 王桂胜, 任清华, 刘洋, 等. 基于干扰模型的变换域优选算法研究[J]. 计算机仿真, 2017, 34(4): 66-71.
Wang G S, Ren Q H, Liu Y, et al. Research on transform domain optimization algorithm based on interference model[J]. Computer Simulation, 2017, 34(4): 66-71.(in Chinese)
[8] Chang C, Li Z, Yao G, et al. Multi-satellite Non-cooperative Communication Based on Transform Domain Communication System[C]∥International Conference on Wireless and Satellite Systems. Springer, Cham, 2019: 51-58.
[9] Scalabrin M, Vadori V, Guglielmi A V, et al. A zero-sum jamming game with incomplete position information in wireless scenarios[C]∥Proceedings of European Wireless 2015; 21th European Wireless Conference. VDE, 2015: 1- 6.
[10]于小宁, 刘咏梅. 基于博弈论的雷达抗干扰决策分析[J]. 机械与电子, 2017, 35(12): 14-17.
Yu X N, Liu Y M. Analysis of Radar Anti-jamming Decision Based on Game Theory[J]. Machinery and Electronics, 2017, 35(12): 14-17.(in Chinese)
[11]Xin Tian, Zhi Tian, Khanh Pham, 等. 空间通信认知干扰机的干扰/抗干扰博弈[J]. 通信对抗, 2016, 35(2): 57- 62.
Xin Tian, Zhi Tian, Khanh Pham, et al. Interference/anti-interference game of space communication cognitive jammer[J]. Communication Confrontation, 2016, 35(2): 57- 62.(in Chinese)
[12]曾勇. 基于博弈论的无线通信抗干扰关键技术研究[D]. 电子科技大学, 2014.
Zeng Yong. Research on key technologies of wireless communication anti-interference based on game theory[D]. University of Electronic Science and Technology of China, 2014.(in Chinese)


