1 引言
近年来,机器人在越来越多领域得到广泛应用。与单个机器人相比,使用多个机器人可以产生显着的性能提升[1-2]。因此,对机器人的研究逐渐从单机器人扩展到多机器人,多机器人系统的研究得到越来越多的关注。机器人任务分配是多机器人系统的主要研究问题之一[3]。多机器人任务分配是指设计一种分配方案将多个任务分配给系统中的不同机器人,以达到总的任务执行时间最短、消耗最小、任务完成度最高等目的[4]。随着对多目标同时优化的要求越来越高,多目标多机器人任务规划引起了研究者的关注。一般而言,在多目标优化问题中,一个目标的优化通常是以牺牲另一个目标为代价的。因此,如何在预定义约束下找到多个优化目标之间的最佳权衡对于多机器人系统的任务分配至关重要[5]。近年来,遗传算法被广泛应用于多目标优化问题并取得了巨大成功[6-7]。然而,传统遗传算法在求解时存在搜索范围小、易陷入局部最优等缺点,往往会导致求解质量不高等问题;另外,对于多目标优化问题,为了给决策者提供更多的决策选择,在求解多目标优化问题时需要考虑多目标解的多样性即多目标解集的覆盖度。为了进一步研究其他启发式算法在多目标优化问题上的表现,主要是为了研究如何提高多目标问题解集的质量和覆盖度,本文探索了一种新型群体智能优化算法——烟花算法在多目标优化问题上的应用。针对多目标多机器人任务分配问题,本文将烟花算法应用到多目标优化问题。为了提高多目标解集的质量和覆盖度,本文对烟花算法的排序和选择策略做了改进,并提出了一种基于改进烟花算法的多目标多机器人任务分配方法。
烟花算法(Firework Algorithm, FWA)最初由Tan等人提出[8]。烟花算法的寻优过程受烟花爆炸过程的启发,近年来得到广泛应用。不同于大多数研究将烟花算法应用于单目标优化问题,本文将烟花算法应用到解决多目标多机器人任务分配问题。根据多目标问题的特点,本文定义了爆炸火花数目和爆炸幅度的计算方法,并结合Pareto策略[9],改进了烟花算法的排序和选择操作。最后针对多目标多机器人任务分配问题提出了一种改进多目标烟花算法(multi-objective firework algorithm,MOFWA)。为了验证算法解决多目标多机器人任务分配问题的性能,本文将MOFWA算法和其他四种多目标算法在七种不同规模的实例上进行了对比实验。其他四种多目标算法分别为:NSGA-II[10]、SPEA2[11]、PESA[12]和一种改进的SPGA2算法;其中NSGA-II、SPEA2、PESA是三种经典的多目标算法,在求解多目标优化问题时得到了广泛应用;一种改进的SPGA2算法是指文献[13]针对多目标任务分配问题提出一种引入局部搜索的改进SPGA2算法,在下文统称SPGA2。实验结果表明该算法相比于其他四种多目标算法在解决多目标多机器人任务分配问题上具有一定优势。
本文剩余部分按照以下五部分展开:第2节讨论了一种多目标多机器人任务分配问题的数学模型;第3节回顾了烟花算法的寻优过程;第4节详细阐述了提出的一种改进多目标烟花算法的具体步骤;第5节对实验过程和实验结果进行分析;第6节对本文做了总结和展望。
2 问题描述和问题模型
2.1 多机器人系统的分类
通常从机器人类型、任务类型、任务分配实时性三方面描述一个多机器人系统。首先,机器人类型可以分为单任务机器人(Single-Task Robots, ST)和多任务机器人(Multi-Task Robots, MT)。单任务机器人每次最多执行一个任务,多任务机器人可以同时执行多个任务。其次,任务类型可以分为单机器人任务(Single-Robot Tasks, SR)和多机器人任务(Multi-Robot Tasks, MR)。单机器人任务需要单个机器人即可执行,多机器人任务需要多个机器人执行。最后,任务分配的时效性可以分为实时性分配(Instantaneous Assignment, IA)和非实时性分配 (Time-extended Assignment, TA)。实时性分配多用于系统当前环境快速变化的情况下,执行任务分配算法并快速给出合理的任务分配方案;非实时性分配多用于已知系统全局信息的情况下,执行任务分配算法并给出最优的任务分配方案[14]。对于多目标机器人任务分配问题,本文主要研究单任务机器人(ST)、单机器人任务(SR)、非实时性分配(TA)系统。本文中任务分配问题为任务多、机器人少的情况,即一个任务由一个机器人执行,每个机器人需要先后执行多个任务。
2.2 多目标多机器人任务分配的数学模型
假设机器人和任务分别用集合R={r1,r2,…,rM}和U={u1,u2,…,uN}表示,机器人和任务的数量分别为M和N,其中M≪N。矩阵T=(tij)表示机器人执行任务的时间,tij表示机器人i执行任务j需要的时间;矩阵C=(cij)表示机器人执行任务的消耗,cij表示机器人i执行任务j需要的消耗;矩阵P=(pij)表示机器人执行任务的完成程度,pij表示机器人i执行任务j的完成程度。
一个多目标机器人任务分配方案可以用一个N维向量V={ν1,ν2,…,νj,…νN}表示,其中νj∈[1,M]是介于1和M之间的整数,表示任务j由机器人rνj执行。不同机器人之间可以同时执行多个任务,而同一机器人必须按顺序依次执行多个不同的任务。因此在任务多、机器人少的情况下,多机器人系统完成所有任务需要的总时间与该系统中执行任务花费时间最长的机器人所花费的时间相等。机器人执行任务的时间、消耗和完成程度分别用公式(1)、(2)和(3)表示:
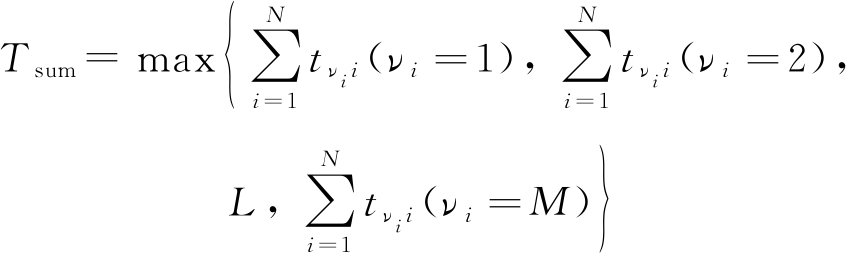
(1)
公式(1)中,![]() 是指1号机器人执行任务所需的时间;其中,νi=1是指任务i由1号机器人执行,tνii是指由1号机器人执行第i个任务所需的时间,
是指1号机器人执行任务所需的时间;其中,νi=1是指任务i由1号机器人执行,tνii是指由1号机器人执行第i个任务所需的时间,![]() 是指所有由1号机器人执行的任务所需的时间总和。
是指所有由1号机器人执行的任务所需的时间总和。
(2)
(3)
本文要解决的问题是在满足任务完成程度的约束条件下,同时最小化时间和消耗。因此,多目标多机器人任务分配的数学模型用公式(4)表示:
(4)
对于执行同一任务的机器人来说,当任务完成程度一定时,其所需时间越短,意味着执行速度越快,其相应的消耗越大。通常时间的缩短会导致消耗的升高,因此本文中的两个的优化目标是两个相互矛盾的变量,本文中多目标多机器人任务分配问题是一个典型的多目标优化问题。
3 烟花算法回顾
作为一种新型的群智能优化算法,烟花算法(firework algorithm, FWA)的寻优过程受烟花爆炸过程的启发[15]。在烟花算法寻优过程中,每个烟花和爆炸产生的火花都被看成一个可行解。质量好的烟花爆炸出的火花数目多,并且火花分布比较密集;相反质量差的烟花爆炸出的火花数目少,并且火花分布比较分散。在原始的烟花算法中,规定烟花爆炸产生两种火花——爆炸火花和高斯火花,爆炸火花的作用是进行邻域搜索,高斯火花的作用是利用高斯随机数保证解的多样性,然后选择质量好而且分布比较分散的烟花和火花进入下一代。烟花算法的具体过程描述如下:
3.1 初始化
假设烟花算法用来求解函数f(X)∈R的最小值,其中X=(x1,x2,…,xn)是函数的一个可行解,![]() 是变量xi的取值范围。每个烟花和火花代表一个可行解,在取值范围内随机生成Num个值作为初始烟花。
是变量xi的取值范围。每个烟花和火花代表一个可行解,在取值范围内随机生成Num个值作为初始烟花。
3.2 计算火花数目和爆炸幅度
在烟花的实际的爆炸过程,质量好的烟花爆炸产生更多的火花而且火花分布密集,质量差的烟花爆炸产生的火花数目少而且分布分散。在原始的烟花算法中,烟花Xi的质量用适应度f(Xi)表示,对于求最小值问题,适应度f(Xi)越小,烟花的质量越好。根据烟花Xi的适应度f(Xi),火花数目的计算公式用公式(5)、(6)表示,爆炸幅度的计算公式用公式(7)表示。
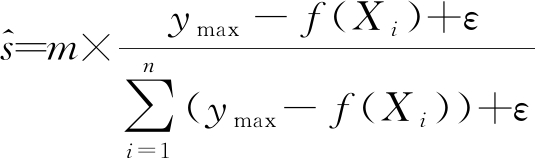
(5)

(6)
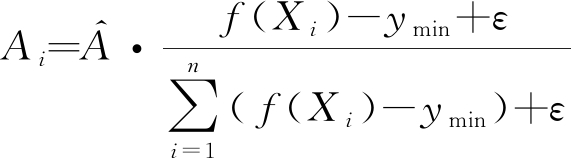
(7)
火花数目表征了一个烟花产生的邻域搜索的解的数目,爆炸幅度表征了烟花产生爆炸火花需要改变的维数。对于求最小值问题,ymax和ymin分别表示最差和最好适应度,m和![]() 分别表示每个烟花最多能产生的爆炸火花数和最大爆炸幅度。公式(6)保证了爆炸火花的数目在一个合理范围内。
分别表示每个烟花最多能产生的爆炸火花数和最大爆炸幅度。公式(6)保证了爆炸火花的数目在一个合理范围内。
3.3 爆炸操作
烟花爆炸产生两种火花,其中爆炸火花相当于执行邻域搜索,高斯火花被用来增加解的多样性。对于每个烟花Xi,产生![]() 个爆炸火花,每个爆炸火花的生成函数用算法1表示;在一次迭代中,产生
个爆炸火花,每个爆炸火花的生成函数用算法1表示;在一次迭代中,产生![]() 个高斯火花,并且
个高斯火花,并且![]() 是一个常数,每个高斯火花的生成函数用算法2表示。
是一个常数,每个高斯火花的生成函数用算法2表示。
其中![]() 表示烟花Xi爆炸产生的一个火花,
表示烟花Xi爆炸产生的一个火花,![]() 是火花
是火花![]() 的第n个维度。ai表示产生爆炸火花
的第n个维度。ai表示产生爆炸火花![]() 时,烟花Xi变化的维数,用公式(8)定义其计算方法。根据定义,烟花Xi的爆炸幅度越大,ai的取值范围越大,在产生爆炸火花时烟花Xi变化的维数越大。
时,烟花Xi变化的维数,用公式(8)定义其计算方法。根据定义,烟花Xi的爆炸幅度越大,ai的取值范围越大,在产生爆炸火花时烟花Xi变化的维数越大。![]() 表示烟花Xi爆炸产生的一个高斯火花,
表示烟花Xi爆炸产生的一个高斯火花,![]() 是火花
是火花![]() 的第n个维度。randn(0,1)表示满足均值为0、标准差为1的高斯分布的随机数。
的第n个维度。randn(0,1)表示满足均值为0、标准差为1的高斯分布的随机数。
ai=randn()%Ai+1
(8)
3.4 选择操作
爆炸操作之后,爆炸火花、高斯火花和烟花所对应的解都已经获得。选择操作就是在这些解中选择N个作为下次迭代的烟花。为了保证解的多样性,选择策略倾向于选择分布较分散的解。首先,质量最好的解被直接保留到下一代;其次,在剩下的解中,根据每个解与其他解的距离大小进行选择。距离越大表明这个解的分布越分散,被选择的概率较大;反之,被选择的概率较小。距离的定义很多,通常用欧氏距离来表示。
4 基于烟花算法的多目标多机器人任务分配方法
4.1 初始化
多目标多机器人任务分配问题的解是一系列可行的任务分配方案,因此在基于烟花算法的多目标多机器人任务分配方法中,每个烟花和火花表示一种任务分配方案,烟花和火花的每个维度表示一个任务被分配给某一个机器人执行。根据2.2节的数学模型,用公式(9)表示初始烟花X的定义:
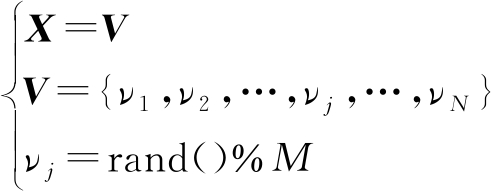
(9)
其中,初始烟花X是一个N维向量,代表一个任务分配方案;初始烟花X的一个维度νj∈[1,M]是介于1和M之间的整数,表示任务j由机器人rνj执行。根据公式(9)随机生成Num个初始烟花。
4.2 计算火花数目和爆炸幅度
和2.2节一样,爆炸火花数目和爆炸幅度根据解的适应度进行计算,其中最大爆炸幅度![]() 等于任务数量N。然而,对于多目标优化问题,目标通常不是一维的,因此烟花Xi的适应度f(Xi)需要根据多个目标进行定义。本文中,要解决的问题是在满足任务完成程度的约束条件下,同时最小化时间和消耗,因此本文把适应度定义为两个目标值的乘积,适应度值越小,解的质量越好。适应度值用公式(10)表示:
等于任务数量N。然而,对于多目标优化问题,目标通常不是一维的,因此烟花Xi的适应度f(Xi)需要根据多个目标进行定义。本文中,要解决的问题是在满足任务完成程度的约束条件下,同时最小化时间和消耗,因此本文把适应度定义为两个目标值的乘积,适应度值越小,解的质量越好。适应度值用公式(10)表示:
f(Xi)=Tsum(Xi)·Csum(Xi)
(10)
4.3 爆炸操作
根据烟花算法的寻优过程和多目标多机器人任务分配问题的数学模型可知,在基于烟花算法的多目标多机器人任务分配方法中,烟花产生爆炸火花和高斯火花的过程代表了在一次迭代中原始烟花对应的一个任务分配方案根据爆炸策略和高斯策略分别产生两种新的任务分配方案。爆炸策略和高斯策略的具体实现方式分别由算法1和算法2表示。
因此,和3.3节一样,每个烟花Xi根据算法1产生Si个爆炸火花,每次迭代根据算法2产生g个高斯火花。对于多机器人任务分配问题,爆炸火花![]() 的第n个维度
的第n个维度![]() 和高斯火花
和高斯火花![]() 的第n个维度
的第n个维度![]() 的计算方法分别用公式(11)和(12)表示:
的计算方法分别用公式(11)和(12)表示:
(11)
(12)
公式(11)、(12)表示给对应的任务重新分配一个机器人执行,以产生新的任务分配方案。

算法1 产生一个爆炸火花假设爆炸火花的初始位置为:X^nei=X^i随机产生要变化的维度数:ai对于X^nei的每一个维度: 如果 X^nei是之前选择的ai个维度中的其中一个:产生X^nei 结束判断结束

算法2 产生一个高斯火花假设高斯火花的初始位置为:X^gi=X^i对于X^ngi的每一个维度: 如果 randn(0,1)>0.5或randn(0,1)<-0.5:产生 X^ngi 结束判断结束
4.4 选择操作
在多目标优化问题中,目标向量的各个分量之间通常存在相互制约的关系,对一个目标分量的优化往往会导致其他目标分量的劣化。因此,传统烟花算法中解的质量评价方法不适用于多目标问题解的评价。对于多目标优化问题,解的质量通常根据Pareto优越性[16]进行度量;根据Pareto优越理论[17-18],所有多目标解被划分为不同的非支配等级,根据非支配等级来度量不同多目标解的优劣性。对于多目标优化问题,通常期望获得分散范围更广的多目标解集,以便给决策者提供更大的选择范围,因此多目标解集的覆盖范围与多目标解集的质量应该被同时考虑。因此,与传统烟花算法的选择操作相比,本文的选择操作在非支配等级排序的基础上增加了拥挤度c(Xi)和适应度f(Xi)两个指标对多目标多机器人任务分配问题的解的质量进行度量,旨在选择适应度好、分布分散,并且位于Pareto前沿的解进入下一代。相比于传统烟花算法的选择操作,本文的选择操作同时考虑多目标解集的质量和覆盖范围,在提高解集质量的同时扩大了解集的覆盖范围。
首先把所有多目标解划分为不同的非支配等级;然后计算同一非支配等级解的适应度和拥挤度,并且根据适应度和拥挤度对同一非支配等级的解进行度量;最后根据前两步的度量,选择下一代初始烟花和进入档案的解。
选择操作分为三个步骤进行,下面对每个步骤进行详细阐述。
第一步,根据Pareto优越理论把所有多目标解划分为不同的非支配等级。Pareto优越理论指出:对于两个多目标解S1、S2,如果S1的每个目标分量都优于S2,则称S2被S1支配,否则S2不被S1支配。首先,把所有的多目标解放入列表Q中,对于每一多目标解,如果它不被Q中其他的任一解所支配,则该多目标解的非支配等级记为1,并且将该解从列表Q中移除,移到列表P中,至此列表P中所有多目标解的非支配等级都记为1。其次,对于列表Q中剩下的解,继续上述过程,直到非支配等级为2的多目标解被找到。最后,重复上述过程,直到所有的多目标解都被分配一个非支配等级为止。根据非支配解的定义可知,非支配等级越低,解的质量越好。
第二步,计算同一非支配等级解的适应度和拥挤度。和2.2节一样,解的适应度用公式(10)定义;根据2.2节的数学模型,多目标多机器人任务分配问题的解有两个目标分量——时间Tsum和消耗Csum,在计算拥挤度之前,对于同一非支配等级的解,首先根据一个目标分量进行排序,同一非支配等级的解在Pareto图上的分布如图1所示。拥挤度c(Xi)定义如下:位于两端的两个解被随机分配一个拥挤度,其余解的拥挤度用公式(13)定义。
c(Xi)= ![]()
(13)
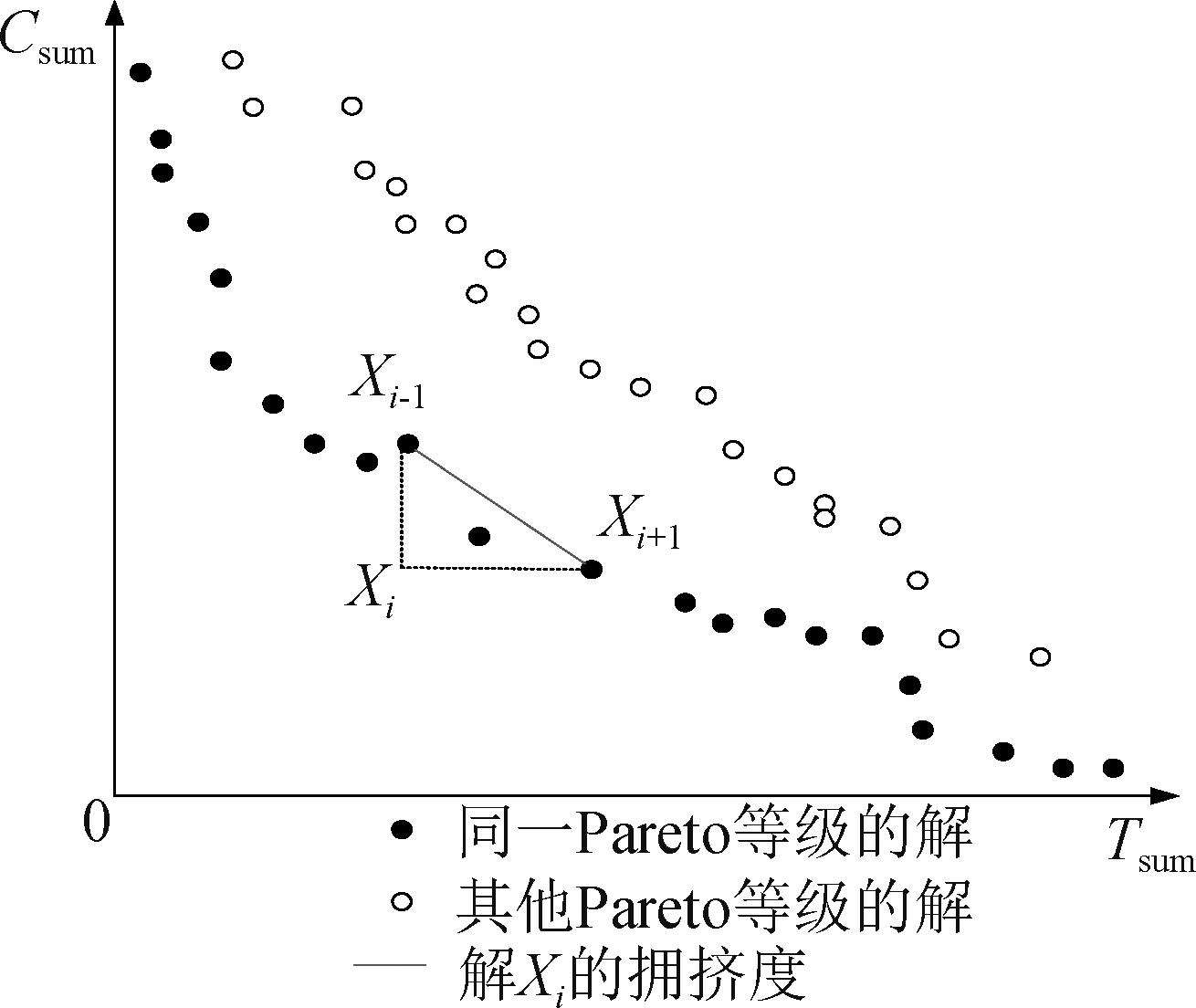
图1 Pareto解示意图
Fig.1 Pareto schematic diagram
根据定义,解Xi的拥挤度反映了解Xi前后两个解Xi-1、Xi+1之间的欧式距离,显然拥挤度越大,欧式距离越大,Xi附近的解的分布越分散;因此,拥挤度越大,解Xi越符合分散性条件,越容易被优先选择。
根据定义,适应度表征了解的质量,适应度越小,解的质量越好,对应的任务分配方案更满足时间短、消耗少的要求;拥挤度表征了解的分散性,拥挤度越大,解的分散性越好、解集的覆盖度越大,越能够提供差异化的任务分配方案。显然,对于多机器人任务分配问题,寻优的目的是找到质量更好、分散性更大的解集,只考虑适应度或拥挤度都不能兼顾解集的质量和分散性。因此,本文用适应度和拥挤度的综合指标f/c(Xi)对同一非支配等级的解排序,综合指标f/c(Xi)用公式(14)定义:
f/c(Xi)=f(Xi)/c(Xi)
(14)
根据定义,综合指标f/c(Xi)越小,说明解的质量和分散性越好。因此,在同一非支配顺序的解中综合指标f/c(Xi)小的解被认为更优。
第三步,根据前两步的度量,选择下一代初始烟花和进入本次迭代档案的解。
首先选择进入本次迭代档案的解。在分配非支配等级时,多目标解既包括本次迭代中所有的烟花和火花又包括上次迭代的档案中的解。首先,从最低非支配等级开始,把属于这一非支配等级的所有解存入档案,直到存档中的个体数目大于或等于存档规模Numb;然后将最后存入的一级非支配个体按照综合指标f/c(Xi)进行排序,并删除多余的个体,以维护一个固定大小的存档。
选择下一代初始烟花的方法与更新存档类似,不同的是,它仅从当前这一代烟花、爆炸火花和高斯火花组成的种群中按照非支配等级和综合指标f/c(Xi)选择前Num个作为下一代的初始烟花。在以后的每次迭代过程中,用都用当前个体对存档个体进行更新,以保证存档保存当前种群的最优个体。最后,输出最后一次迭代存档中的个体即为整个算法迭代输出的最优解。算法3给出了本文提出的一种基于改进烟花算法的多目标多机器人任务分配算法的流程。

算法3 MOFWA算法的伪代码开始 初始化种群中的n个烟花 当迭代次数iter<500: 对于每一个烟花Xi: 根据公式(10)计算出烟花的适应度值根据公式(5)、(6)计算出烟花的爆炸火花的数目根据公式(7)计算出烟花爆炸的幅度根据算法1生成一个爆炸火花结束对于k=0到^m: 根据算法2随机选择一个烟花并产生一个高斯火花结束找到所有烟花和火花的非支配前沿L=(L1,L2,L3,…)对于每一个烟花Xi、每一个爆炸火花X^ei和每一个高斯火花X^gi: 根据公式(10)、(13)和(14)计算综合指标结束i=1swarm=0∥swarm为下一次迭代的初始种群,swarm是种群中个体的数量当swarm≤Num: 如果swarm+Li≤Num: 将Li添加到种群swarm中 i=i+1 结束 如果swarm>Num:

根据综合指标对Li中的个体进行排序将Li中排名最高的(Num-swarm)个个体添加到种群swarm中 结束结束如果 迭代次数iter=1:archive=swarm 结束如果 迭代次数iter>1:找出本次迭代的所有烟花、火花以及上一次迭代存档中的非支配前沿L=(L1,L2,L3,…)i=1 archive=0∥archive是该存档中个体的数目当 archive≤Numb: 如果 archive+Li≤Numb:将Li添加到种群swarm中i=i+1 结束 如果 archive>Numb:根据综合指标对Li中的个体进行排序将Li中排名最高的(Numb-archive)个个体添加到种群swarm中 结束 结束结束 结束 返回最后一次迭代的存档结束
5 实验仿真与分析
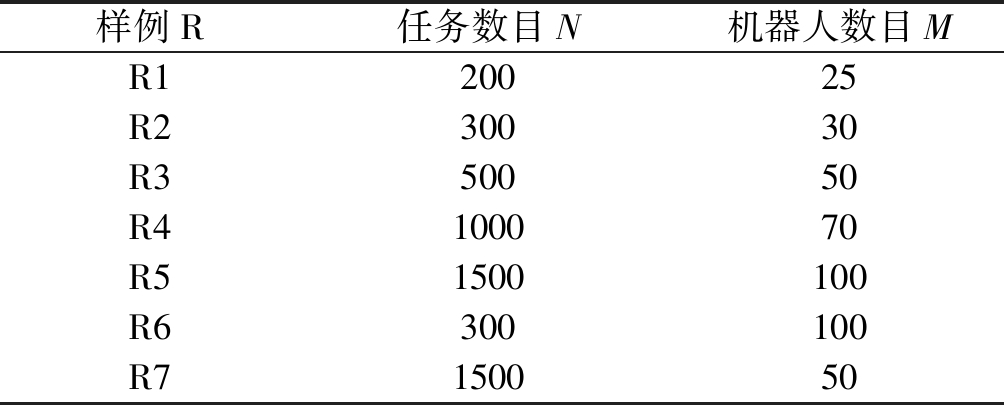
为了验证提出的MOFWA算法在解决多目标机器人任务分配问题时的性能,将本文提出的算法和其他四种多目标优化算法(NSGA-II, SPEA2, PESA和SPGA2)进行对比。这些算法是根据文献中的描述实现的,其他运算符(重组、变异、采样)保持相同。对于每个算法,我们使用相同的种群规模和存档大小,并在同一个运行环境、相同参数设置下将不同的算法运行多次获得最终结果,较好的保证了公平性。采用七种不同规模的数据集作为仿真样例,以式(4)作为多目标多机器人任务分配问题的数学模型。每个样例的任务数目和机器人数目如表1所示。
表1 数据集
Tab.1 Data set
样例R任务数目N机器人数目MR120025R230030R350050R4100070R51500100R6300100R7150050
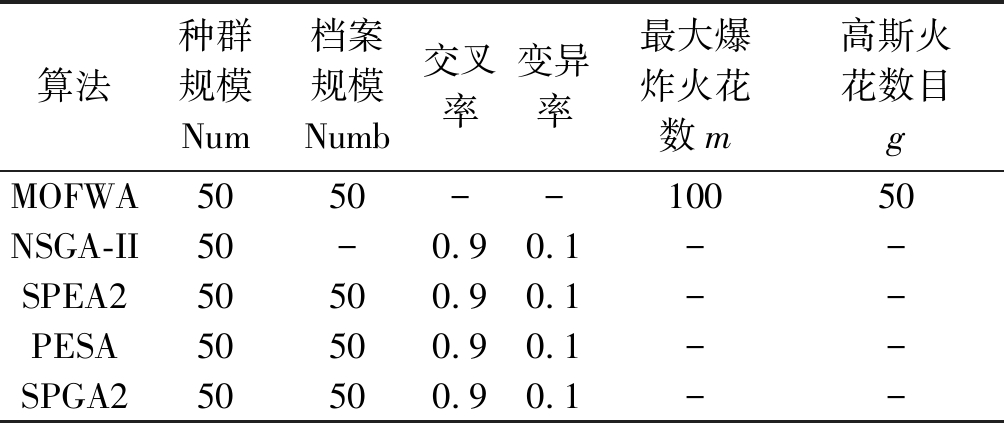
测试平台为PC计算机,处理器:Intel(R) Core(TM) i5-2310 CPU @2.90 GHz,内存:2.48 GB,操作系统版本:WINDOWS 7 旗舰版,编译软件版本:Microsoft Visual Studio 2010。对比实验方案如下:对于7种规模不同的样例,分别用这4种多目标算法对每个样例进行计算,每种算法在每个样例上均运行10次。该对比实验的4种算法的仿真参数设置如表2所示。其中,交叉率设置为0.9[10],变异率设置为0.1,种群规模和档案规模均设置为50,最大爆炸火花数和高斯火花数分别设为100和50。
表2 算法参数设置
Tab.2 Parameter settings
算法种群规模Num档案规模Numb交叉率变异率最大爆炸火花数m高斯火花数目gMOFWA5050--10050NSGA-II50-0.90.1--SPEA250500.90.1--PESA50500.90.1--SPGA250500.90.1--
为了评估算法的性能,本文使用了S-metric指标[21-22],它是由所有非支配点和客观空间中的参考点覆盖的超立方体的体积。根据定义,给定一个解集M={m1,m2,…,mn}和一个被M中的点支配的参考点xref,则解集M的评价指标S-metric的计算方法用公式(15)表示:
(15)
其中Λ表示勒贝格测度,并且m支配x、x支配xref。本文中,目标函数是二维的,两个目标分量分别为时间Tsum和消耗Csum;算法最后一次迭代产生的最优解即非支配解。则S-metric指标的计算方法为:首先根据一个目标分量对非支配解降序排列,然后计算公式(16)。
![]() |Tsum(Xi)-Tsum(Xref)|)
|Tsum(Xi)-Tsum(Xref)|)
(16)
其中,M表示算法最后一次迭代产生的最优解集,Numb表示最优解集中解的数量,Csum(Xi)和Tsum(Xi)表示解Xi的两个目标分量,并且在公式中,令参考点Xref等于X0。
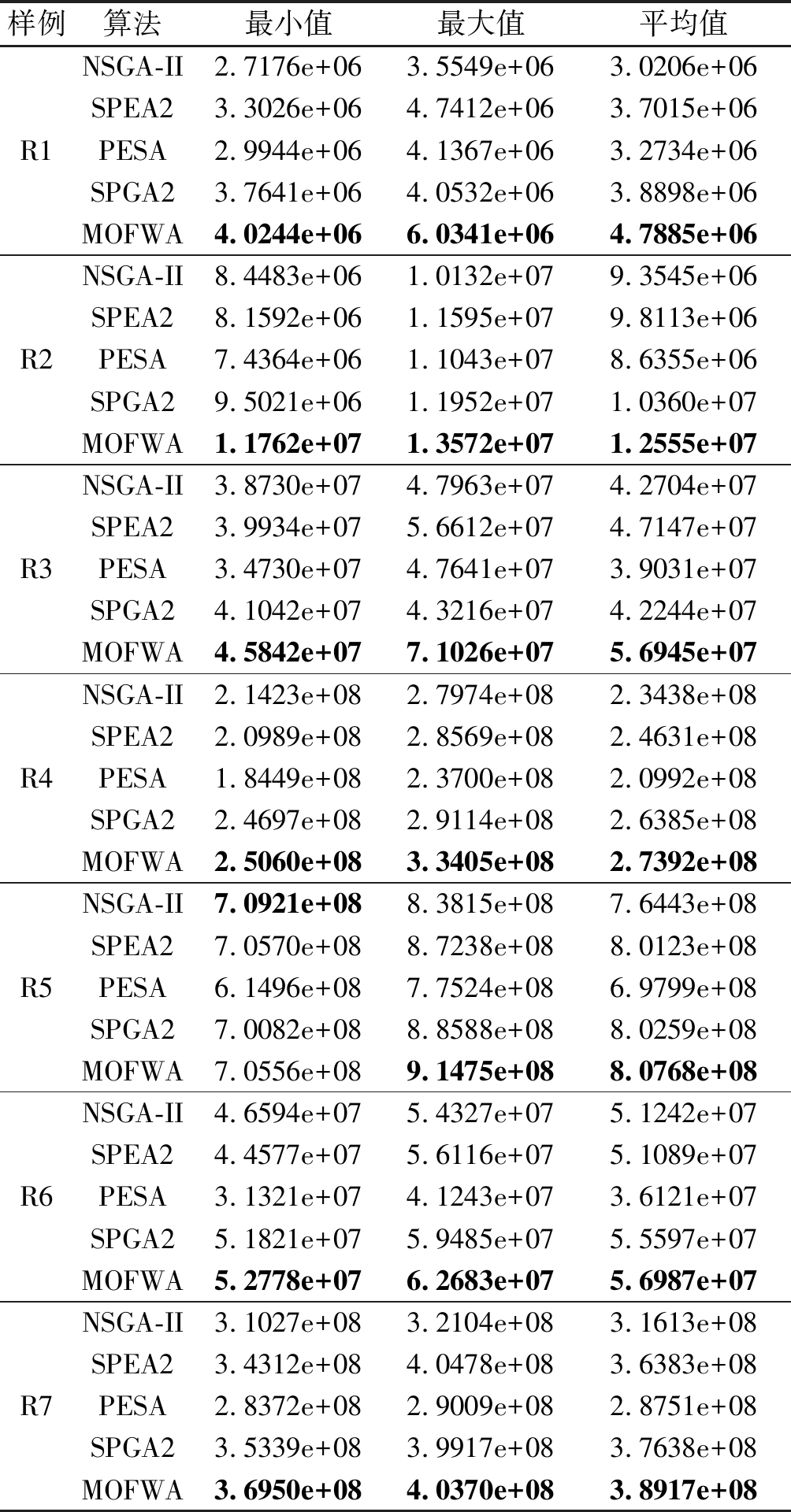
为了准确地对实验结果做出分析,本文中每个算法在每个样例上分别独立运行10次。分别计算每次运行结果的S-metric指标,表3列出了10次运行结果的最大值、最小值,和平均值。为了更直观地对比算法的性能,图2给出了运行10次得到的S-metric平均值的条形图。
表3 10次运行结果
Tab.3 Results of ten times’running
样例算法最小值最大值平均值R1NSGA-II2.7176e+063.5549e+063.0206e+06SPEA23.3026e+064.7412e+063.7015e+06PESA2.9944e+064.1367e+063.2734e+06SPGA23.7641e+064.0532e+063.8898e+06MOFWA4.0244e+066.0341e+064.7885e+06R2NSGA-II8.4483e+061.0132e+079.3545e+06SPEA28.1592e+061.1595e+079.8113e+06PESA7.4364e+061.1043e+078.6355e+06SPGA29.5021e+061.1952e+071.0360e+07MOFWA1.1762e+071.3572e+071.2555e+07R3NSGA-II3.8730e+074.7963e+074.2704e+07SPEA23.9934e+075.6612e+074.7147e+07PESA3.4730e+074.7641e+073.9031e+07SPGA24.1042e+074.3216e+074.2244e+07MOFWA4.5842e+077.1026e+075.6945e+07R4NSGA-II2.1423e+082.7974e+082.3438e+08SPEA22.0989e+082.8569e+082.4631e+08PESA1.8449e+082.3700e+082.0992e+08SPGA22.4697e+082.9114e+082.6385e+08MOFWA2.5060e+083.3405e+082.7392e+08R5NSGA-II7.0921e+088.3815e+087.6443e+08SPEA27.0570e+088.7238e+088.0123e+08PESA6.1496e+087.7524e+086.9799e+08SPGA27.0082e+088.8588e+088.0259e+08MOFWA7.0556e+089.1475e+088.0768e+08R6NSGA-II4.6594e+075.4327e+075.1242e+07SPEA24.4577e+075.6116e+075.1089e+07PESA3.1321e+074.1243e+073.6121e+07SPGA25.1821e+075.9485e+075.5597e+07MOFWA5.2778e+076.2683e+075.6987e+07R7NSGA-II3.1027e+083.2104e+083.1613e+08SPEA23.4312e+084.0478e+083.6383e+08PESA2.8372e+082.9009e+082.8751e+08SPGA23.5339e+083.9917e+083.7638e+08MOFWA3.6950e+084.0370e+083.8917e+08
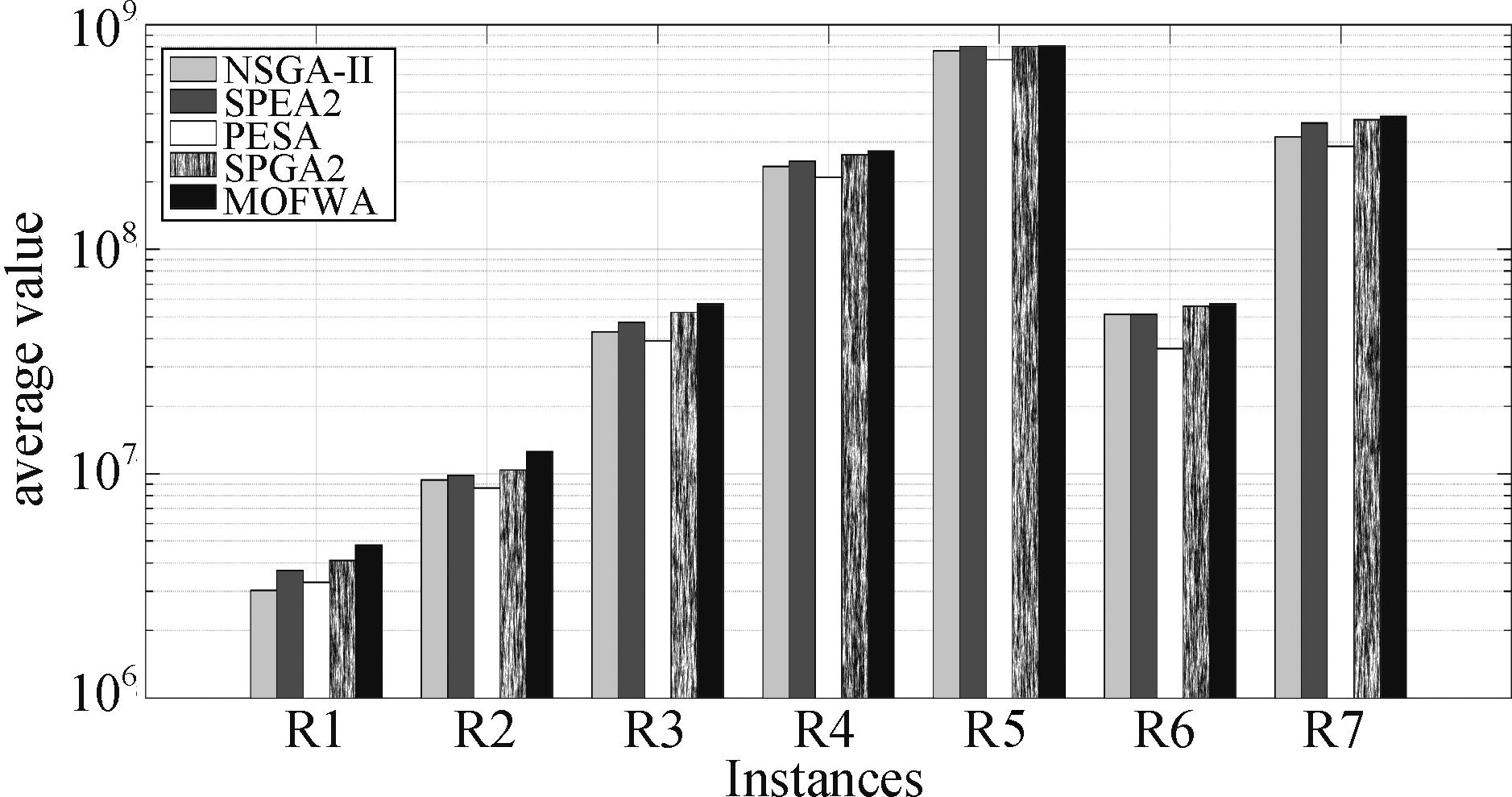
图2 S-metric平均值的条形图
Fig.2 Bar chart of the S-metric average
此外,为了比较算法复杂度,本文还对五种算法在七个样例上的运行时间做了比较,最大迭代次数均为500次。表4列出了五种算法在每个样例上运行10次的平均时间,单位为秒。
根据S-metric指标的定义可知,S-metric指标越大说明解的质量越好。表3中标红的值为S-metric指标最大的值。从表3和图2中能够看出,本文提出的MOFWA算法相比于其他四种算法在7个样例上都能得到最大的S-metric平均值,这说明本算法在解决多目标多机器人任务分配问题时,相比于其他三种多目标算法能够获得质量更高的运行结果。
根据表4可以看出,本文所提出的一种改进烟花算法在求解多目标多机器人任务分配问题时,运行时间高于NSGA-II和PESA算法,但是低于SPEA2和SPGA2算法。对于非实时性分配系统而言,以一定的时间代价来获得更优的任务分配方案更符合系统对性能的要求。从表3和图2中能明显看出,本文所提的改进多目标烟花算法与SPEA2算法和SPGA2算法相比于NSGA-II和PESA算法能获取更优的任务分配方案。
表4 10次运行平均时间
Tab.4 Average time of ten times’ running
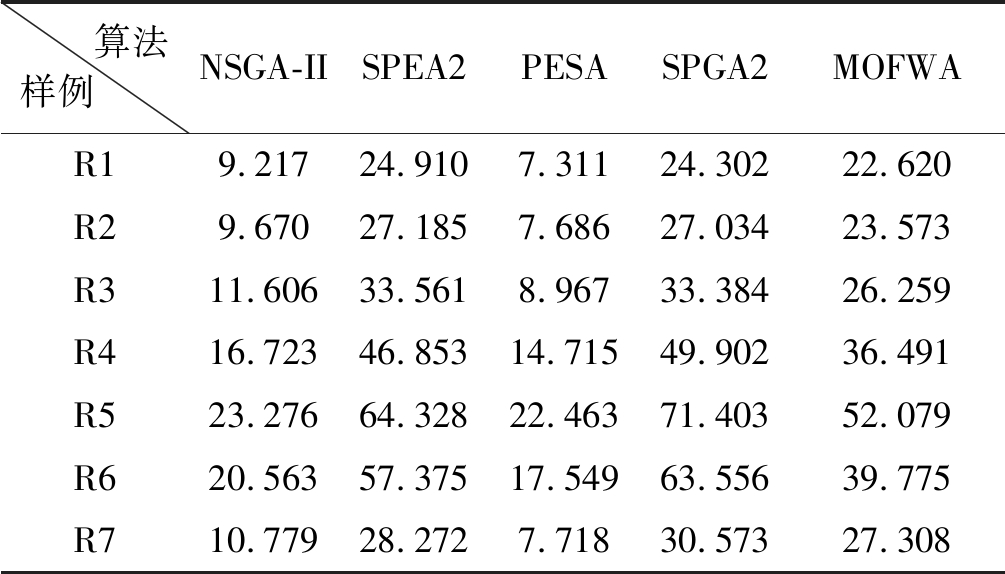
算法样例 NSGA-IISPEA2PESASPGA2MOFWAR19.21724.9107.31124.30222.620R29.67027.1857.68627.03423.573R311.60633.5618.96733.38426.259R416.72346.85314.71549.90236.491R523.27664.32822.46371.40352.079R620.56357.37517.54963.55639.775R710.77928.2727.71830.57327.308
图3给出了七种不同规模的样例在分别采用MOFWA与NSGA-II、SPEA2、PESA和SPGA2算法进行多目标多机器人任务分配求解时所求得的一个典型的多目标最优解集的情况。多目标最优解集的分布是按照所求的解在目标空间中的分布绘制的。在本算法中,约束条件为任务的完成度,目标分别是任务完成所需要的时间和相应的消耗。根据本文算法,可以分别获得解集中每个解在两个目标上的函数值。最后,通过将最终解集在目标空间中作图,得到最优解集的分布情况。
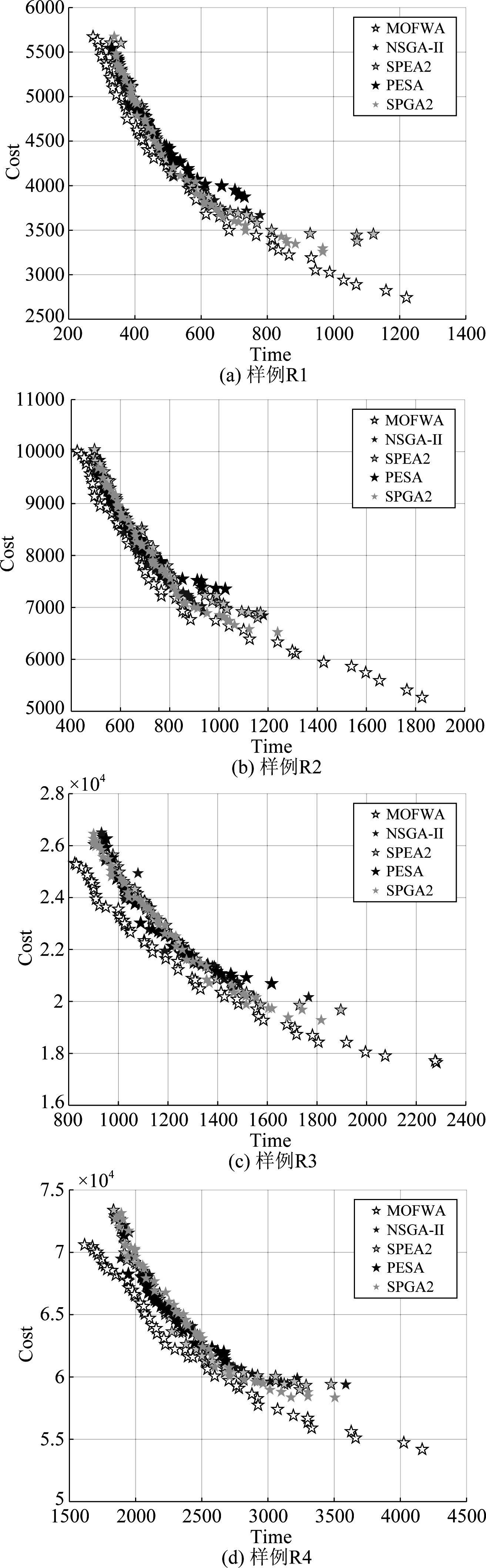
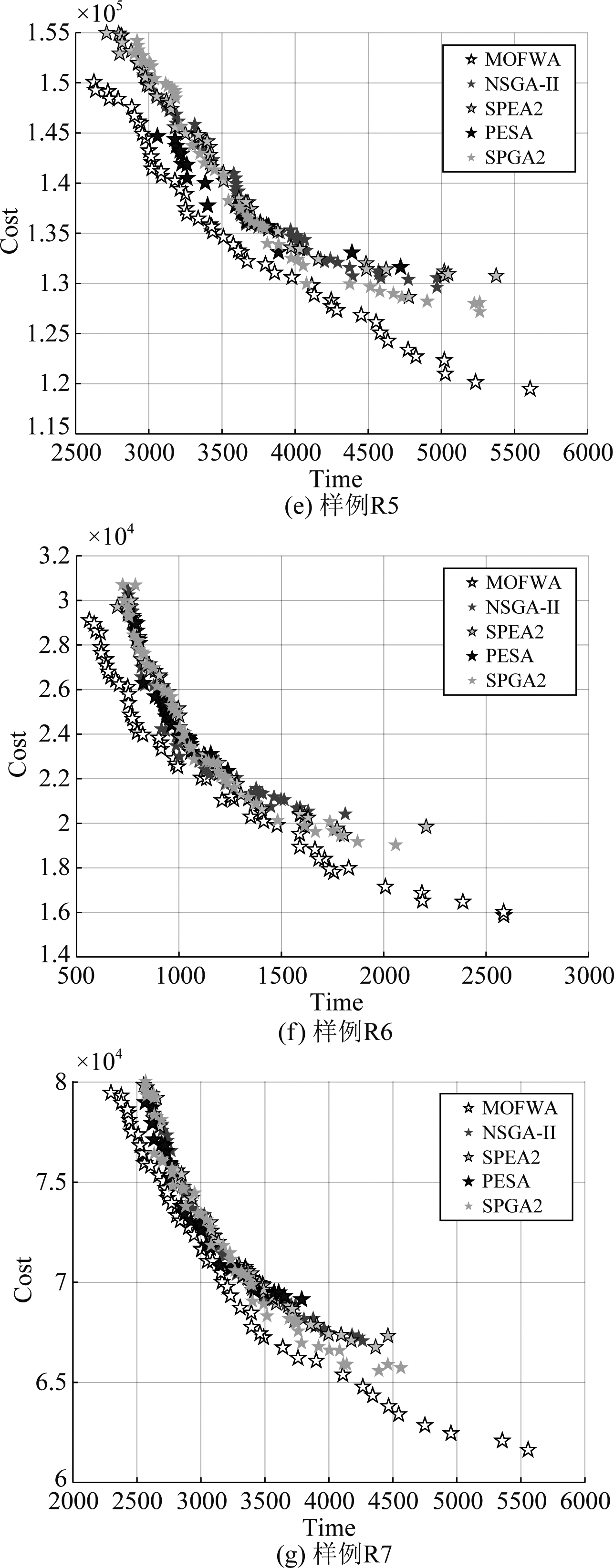
图3 多目标最优解集
Fig.3 Multi-objective optimal solution set
图3能够直观得出以下结论:在求解求多目标机器人任务分配问题时,相对于NSGA-II、SPEA2、PESA和SPGA2算法,MOFWA能得到更好质量的解;同时求得的解集覆盖的范围更大,能够提供更大范围的选择空间;而且随着任务规模的增加,这两个优势更明显。
以上实验结果充分说明,本文提出的MOFWA算法在求解多目标机器人任务分配问题时,相比于其他四种算法能够获得明显更优的解,这表明本文所提算法在解决多目标机器人任务分配问题时具有一定优势;对于多目标问题的求解,本文所提算法亦有参考意义。
6 结论
对于多目标多机器人任务分配问题,本文给出了以时间和消耗为优化目标、以任务完成度为约束条件的多目标多机器人任务分配模型。本文将Pareto优越性理论和烟花算法进行有效融合,并且对烟花算法的计算爆炸火花数目和爆炸幅度方法以及选择策略进行优化,提出一种基于改进烟花算法的多目标多机器人任务分配方法。最后将本文所提算法与其他四种多目标算法进行了对比实验,实验结果证实了本文所提算法在解集质量上和解集覆盖度上的优越性。
群体智能优化算法与多目标优化理论相结合,在解决多目标优化问题时具有广阔研究前景。然而在群体智能算法和多目标优化理论的研究中,仍然存在一些问题值得我们进一步探讨。例如,针对实际的工程问题如何构建更准确的数学模型;如何降低算法复杂度以适应实时性的要求等,这些问题的研究和探讨都将具有十分重要的理论和实际意义。
[1] Wei C, Hindriks K V, Jonker C M. Dynamic task allocation for multi-robot search and retrieval tasks[J]. Applied Intelligence, 2016, 45(2): 1-19.
[2] Juan Jesús Rold n, Miguel A Olivares-Méndez, Cerro J D, et al. Analyzing and improving multi-robot missions by using process mining[J]. Autonomous Robots, 2018, 42(6): 1187-1205.
n, Miguel A Olivares-Méndez, Cerro J D, et al. Analyzing and improving multi-robot missions by using process mining[J]. Autonomous Robots, 2018, 42(6): 1187-1205.
[3] Luo L, Chakraborty N, Sycara K. Provably-Good Distributed Algorithm for Constrained Multi-Robot Task Assignment for Grouped Tasks[J]. IEEE Transactions on Robotics, 2015, 31(1): 19-30.
[4] Chopra S, Notarstefano G, Rice M, et al. Distributed Version of the Hungarian Method for a Multirobot Assignment[J]. IEEE Transactions on Robotics, 2017, PP(99): 1-16.
[5] Itziar L T, Diana M, Sonia B, et al. Underwater Robot Task Planning Using Multi-Objective Meta-Heuristics[J]. Sensors, 2017, 17(4).
[6] Janakiraman N, Kumar P N. Multi-objective hardware/software partitioning technique for dynamic and partial reconfigurable system-on-chip using genetic algorithm[J]. International Journal of Engineering & Technology, 2014, 6(2).
[7] Govil N, Shrestha R, Chowdhury S R. A New Multi-objective Hardware-Software-Partitioning Algorithmic Approach for High Speed Applications[C]∥Hsinchu, Taiwan, 2017 International Symposium on VlSI Design & Test. Springer, Singapore, 2017.
[8] Tan Y, Zhu Y. Fireworks Algorithm for Optimization[C]∥Beijing, China, 2010 International Conference on Advances in Swarm Intelligence. Springer-Verlag, 2010: 355-364.
[9] Van den Berg, Ewout, Friedlander, Michael P. Probing the Pareto Frontier for Basis Pursuit Solutions[J]. Siam Journal on Scientific Computing, 2008, 31(2): 890-912.
[10]Deb, Kalyanmoy, Pratap, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[11]Kim M, Hiroyasu T, Miki M, et al. SPEA2+: Improving the Performance of the Strength Pareto Evolutionary Algorithm 2[J]. Parallel Problem Solving from Nature-PPSN VIII, 2004, 3242(4): 742-751.
[12]Corne D W, Knowles J D, Oates M J. The Pareto Envelope-Based Selection Algorithm for Multiobjective Optimization[C]∥Paris, France, 2000 International Conference on Parallel Problem Solving From Nature. Springer-Verlag, 2000: 839- 848.
[13]束柬, 梁昌勇, 徐健. 基于信任的云服务系统多目标任务分配模型[J]. 计算机研究与发展, 2018, 55(6): 53- 65.
Shu Jian, Liang Changyong, Xu Jian, et al. Trust-Based Multi-Objectives Task Assignment Model in Cloud Service System[J]. Journal of Computer Research and Development, 2018, 55(6): 53- 65.(in Chinese)
[14]Gerkey B P, ![]() Maja J. A Formal Analysis and Taxonomy of Task Allocation in Multi-Robot Systems[J]. International Journal of Robotics Research, 2004, 23(9): 939-954.
Maja J. A Formal Analysis and Taxonomy of Task Allocation in Multi-Robot Systems[J]. International Journal of Robotics Research, 2004, 23(9): 939-954.
[15]Li J, Zheng S, Ying T. The Effect of Information Utilization: Introducing a Novel Guiding Spark in the Fireworks Algorithm[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(1): 153-166.
[16]王芳, 饶运清, 唐秋华, 等. 多目标决策下Pareto非支配解的快速构造方法[J]. 系统工程理论与实践, 2016, 36(2): 454- 463.
Wang Fang, Rao Yunqing, Tang Qiuhua, et al. Fast construction method of Pareto non-dominated solution for multi-objective decision-making problem[J]. Systems Engineering-Theory & Practice, 2016, 36(2): 454- 463.(in Chinese)
[17]Bazgan C, Jamain F, Vanderpooten D. Approximate Pareto sets of minimal size for multi-objective optimization problems[J]. Operations Research Letters, 2015, 43(1): 1- 6.
[18]Wang Z, Rangaiah G P. Application and Analysis of Methods for Selecting an Optimal Solution from the Pareto-Optimal Front obtained by Multi-Objective Optimization[J]. Industrial & Engineering Chemistry Research, 2016, 56(2).
[19]Ishibuchi H, Yu S, Masuda H, et al. Performance of Decomposition-Based Many-Objective Algorithms Strongly Depends on Pareto Front Shapes[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(2): 169-190.
[20]Jaszkiewicz A, Lust T. Proper balance between search towards and along Pareto front: biobjective TSP case study[J]. Annals of Operations Research, 2017, 254(1-2): 1-20.
[21]Naujoks B, Beume N, Emmerich M. Multi-objective optimization using S-metric selection: application to three-dimensional solution spaces[C]∥Edinburgh, UK, 2005 IEEE Congress on Evolutionary Computation. IEEE, 2005: 1282-1289.
[22]Beume N. S-Metric calculation by considering dominated hypervolume as Klee’s measure problem[J]. Evolutionary Computation, 2014, 17(4): 477- 492.



