1 引言
卫星信号捕获是GPS(Global Positioning System)接收机跟踪定位的前提[1],目的是为了粗略估计出接收卫星信号的码相位和载波频率,并将其作为跟踪的初始化值。捕获过程是卫星信号接收机在工作时耗时最久的步骤,在进行该步骤时通常需要做数以万次的复数乘法,导致接收机功耗过高。未来,深空探测计划也将会受到卫星信号捕获速度的影响[2],因此对卫星信号快速捕获算法提出了更高的要求。
目前的卫星信号软件接收机常用的捕获方法是基于FFT(Fast Fourier Transform)的并行码相位捕获算法[3],通过快速傅里叶变换实现码相位的并行搜索,其运算复杂度为O(nlog2n)。由于卫星的伪随机码具有强自相关性,即当本地伪随机码相位与接收信号的伪随机码相位相近时,相关系数最大,其他情况下相关系数值很小,通常可以忽略不计。因此在进行卫星信号捕获时,某颗卫星的伪随机码的自相关值是具有稀疏特性的,从而可以将稀疏快速傅里叶变换(Sparse Fast Fourier Transform,SFFT)引入到并行码相位捕获算法中。
SFFT最早是由美国麻省理工学院的Hassanieh[4-5]等人提出的,它的主要思想是基于频域稀疏的特性,利用加窗-降采样-重构的原理,通过少数点的FFT重构出原信号的频谱,实现算法的亚线性处理。近年来,SFFT在信号处理和医学成像等领域得到广泛应用[6-7],也开始将其运用在卫星信号捕获中[8-12]。文献[8]首次将SFFT中降采样的原理应用于卫星信号的捕获工作中,提出一种快速捕获方法,降低了捕获运算量,且通过实测的卫星信号进行验证,但是没有给出具体的捕获结果。文献[9]使用实测的卫星信号数据对文献[8]中的降采样因子进行研究,结合相干积分时间给出了最优降采样因子,并且对捕获结果进行了详细地分析。文献[10]和文献[11]提出了一种基于SFT(Sparse Fourier Transform)的快速捕获与干扰抑制联合的算法,该算法将传统并行码相位捕获方法中的快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)替换为SFT,减少了IFFT的运算量,但没有分析其捕获概率,且没有捕获结果;文献[12]利用SFFT实现快速捕获,分析了算法随稀疏度变化的运行时间,并且分析了算法随信噪比变化的捕获概率,但由于卫星信号信噪比较低的特点,该文献直接使用SFFT导致估值误差较大,捕获成功概率较低,且该文中没有给出捕获结果图。
为了提高在SFFT算法下的捕获概率,本文提出一种基于相关的SFFT的快速捕获算法。该方法利用了卫星信号伪码的强自相关性,通过相关运算搜索最大峰值,取代了SFFT算法中的估值搜索峰值,从而避免在低信噪比下SFFT估值误差很大的情况。本文方法利用软件接收机进行捕获实验验证,实验结果表明该方法能有效的进行卫星信号快速捕获,捕获结果较好。
2 稀疏快速傅里叶变换原理
稀疏快速傅里叶变换的主要思想是通过对信号时域进行哈希映射,达到频域的降采样,根据信号频域稀疏特性,再通过哈希逆映射就可高概率恢复出整个信号的频谱,其处理流程图如下图1所示。
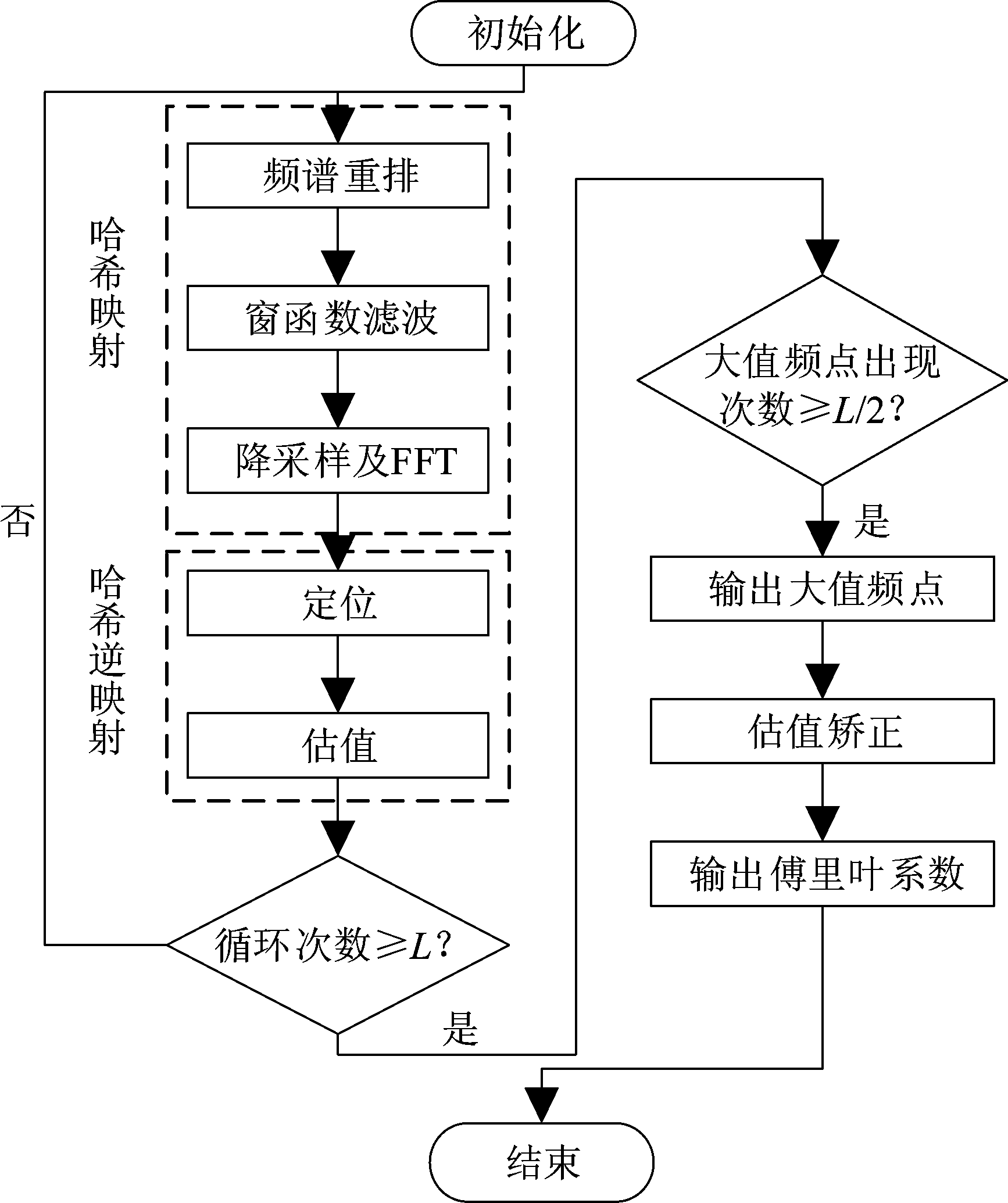
图1 SFFT算法流程图[4]
Fig.1 Flowchart of SFFT[4]
2.1 哈希映射
哈希映射的目的是通过信号的时域处理：对信号进行重排列、加窗和降采样,达到频域从N点映射到B点中,实现算法的亚线性运行时间。
2.1.1 频谱重排
对于一个N维向量x(i),定义变换Pσ,τ,可得序列为
(Pσ,τx)i=xσi+τ
(1)
对应的频域变换Pσ,τ为
(2)
式中,σ,τ为[0,N-1]的随机整数,σ为奇数且对N取模可逆。根据完全剩余系定理,(σi+τ)modN依然是完备的。对于频域,重排后
只改变了信号的相位,幅值没有发生变化,因此通过时域重排能实现频域重排。
2.1.2 窗函数滤波
窗函数是实现运算时间达到亚线性的关键步骤,但使用传统的窗函数对信号截断,会造成频谱泄露,所以本文的窗函数由高斯窗函数和矩形窗函数卷积得到,使得其在时域和频域的能量可以集中。所构造的平坦窗函数在时域用g表示,频域用G表示,参数为(1/B,1/(2B),δ,ω),K为信号的稀疏度,窗宽度为
且ω=O(Blog(N/δ))。Pσ,τx与g相乘得到序列y
y=Pσ,τx·g
(3)
2.1.3 频域降采样
根据傅里叶变化的性质：对信号时域混叠相当于频域降采样。对序列y时域混叠得到序列z
(4)
对应的频域变换
Zi=Yi(N/B) i∈[0,B-1]
(5)
其中B整除N。从公式(4)和公式(5)可以看到序列的频域由N维降到了B维,实现了高维序列到低维序列的转换。
2.2 哈希逆映射
通过哈希逆映射可以将B维的序列恢复出原始N维序列。定义哈希函数hσ(i)和偏移函数οσ(i),映射区间为[N]→[B]。
hσ(i)=round(σ·i·B/N)
(6)
οσ(i)=σ·i-hσ(i)·(N/B)
(7)
在2.1.3节对Zi取幅值最大的前d·K个坐标存于集合J,经哈希逆映射后得到J的原坐标I和对应的幅值估计X′(i)。
I={i∈[N] |hσ(i)∈J}
(8)
X′(i)=Zhσ(i)ωτ i/Gοσ(i)
(9)
2.3 循环估值定位
对2.1和2.2节做L=O(log2N)次循环,得到原像的集合Ir,r∈{1,…,L},统计每个频点坐标出现的次数si=|{r|i∈Ir}|,使出现次数大于L/2次的频点坐标作为最终的定位坐标,归入集合I′={i∈I|si≥L/2}。
在L次循环中,每个频点坐标i∈I′,取每次循环所得到的频率幅值X′(i)的中值作为最终的频率估计值,即X(i)=median({Xr(i)|r∈{1,...,L}})。
3 基于相关的稀疏快速捕获算法
通过对SFFT算法的分析,结合卫星信号的伪随机码的强自相关特性,在捕获过程中的IFFT的变换域具有稀疏特性,因此可以利用SFFT算法对FFT优化。
3.1 基于SFFT的快速捕获算法
基于SFFT的捕获算法是在基于FFT的并行码相位的捕获基础上,对传统捕获方法处理后的信号进行重排、加窗和降采样,将IFFT替换为SIFFT,进行捕获的。其算法流程图如图2所示。
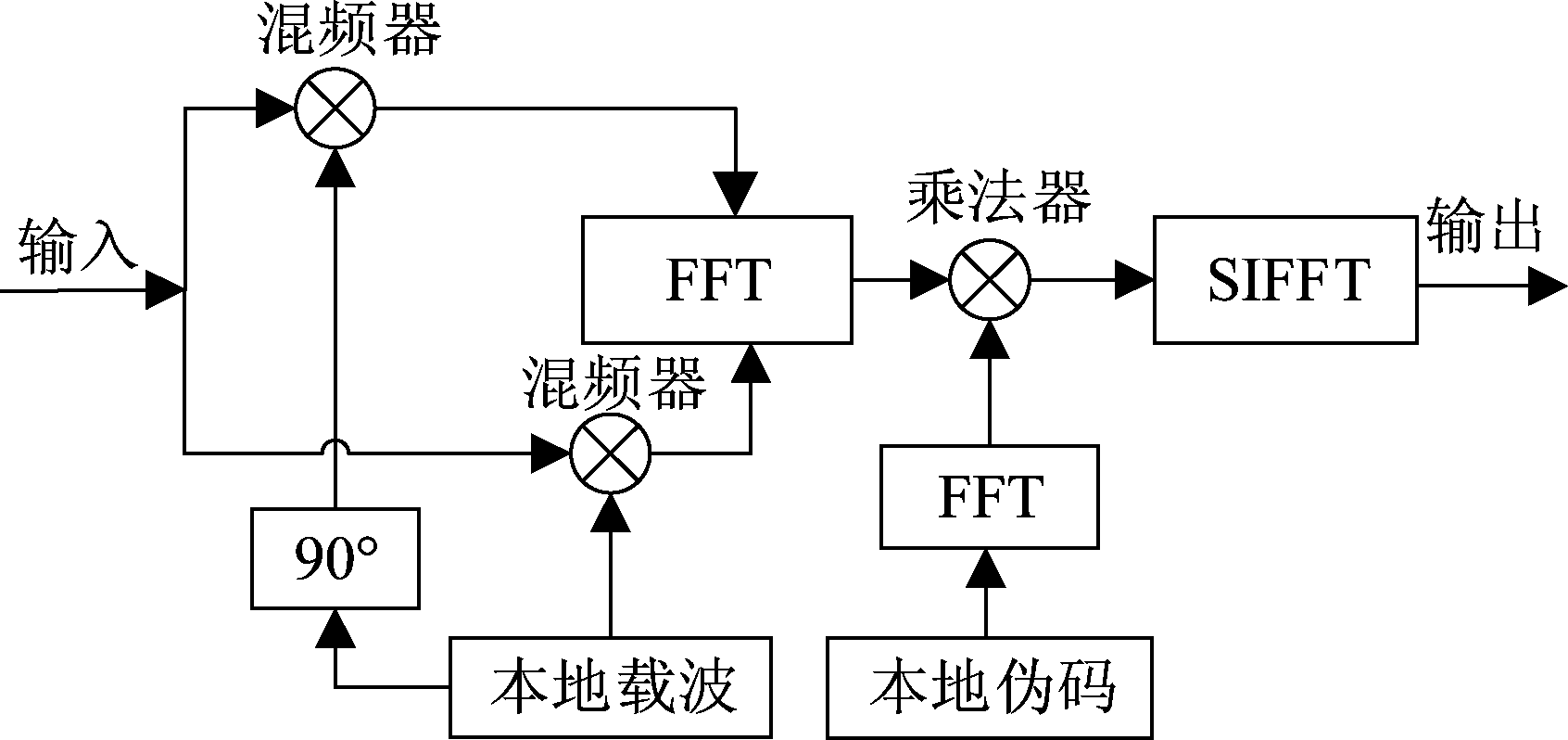
图2 SFFT捕获算法流程图
Fig.2 Flow chart of capture algorithm based on SFFT
接收到的中频信号和本地载波在经过图2处理后,将得到的信号进行SIFFT处理,通过估值处理,将每次捕获得到的最大值作为相关峰值,进而捕获卫星信号。
3.2 卫星信号中SFFT估值分析
用3.1节基于SFFT的快速捕获算法捕获卫星信号时,由于卫星信号的信噪比较低,通常是在-20 dB,通过公式(3)的加窗处理,其频域的每点幅值为N/B点的叠加,此时大值点的幅值会受到噪声很大的影响,与原信号的幅值已经相差很大;对其降采样和FFT后,再通过哈希逆映射中的公式(9)得到的Zhσ(i)的值也会与原信号的幅值误差很大,即使通过循环后取中值也不能正确估值。因此在低信噪比的情况下,通过SFFT算法的估值运算难以恢复原始信号的频谱,会降低捕获概率。
本文利用卫星信号的伪随机码的强自相关特性,通过传统时域串行捕获的方法,对SFFT输出的大值点对应的本地伪码与接收到的卫星信号做相关运算,可以提高捕获概率。
3.3 本文捕获算法
通过3.2节对SFFT算法的分析,其估值运算会降低卫星信号的捕获概率,所以通过相关运算来搜索卫星信号的捕获峰值。本文算法流程图如图3所示。
3.3.1 稀疏快速傅里叶逆变换
对中频信号与本地载波和伪码处理后得到的X(k)进行无估值的稀疏快速傅里叶逆变换,可以得到疑似大值点坐标,具体算法实现步骤如下：
步骤1 对算法进行初始化。设置输入信号长度为N,稀疏度为K,循环次数L=O(log2B),窗函数G的参数为(1/B,1/(2B),δ,ω)。
步骤2 利用完全剩余系定理对X(k)进行重排,得到Xσ,τ(k)。
步骤3 将Xσ,τ(k)与窗函数G相乘,得到Yσ,τ(k)=Xσ,τ(k)·G。
步骤4 对Yσ,τ(k)进行N/B点的混叠,得到
对Z(k)作IFFT,选择前d·K个最大的幅值的坐标,通过哈希逆映射找到对应的原像,将其存于集合I中。
步骤5 对上述四个步骤进行L次循环,得到集合Ir=I1∪…∪IL,r∈{1,…,L},统计每个大值频点出现的次数,并将其记录到集合sk=|{r|k∈Ir}|,将出现次数大于L/2的频点坐标归入集合I′,作为大值点坐标输出。
3.3.2 做相关后判决
由于信噪比低的情况下SFFT算法的估值部分误差较大,不能再通过公式(9)的估值运算进行估值,所以本文去掉公式(9)的估值部分,也不对其进行循环估值处理,利用时域串行捕获方法,对卫星信号进行捕获。
其中本地伪码用
表示,接收到的卫星信号用
表示,时域串行的捕获方法是根据卫星信号伪随机码的强自相关性的特点,计算出
和
相关性最大的移位
即为码相位。
(10)
所以将3.3.1节中集合I′的坐标对应处的本地伪码与接收到的卫星信号做相关运算,对其门限判决后,得到相关值最大的坐标点,其对应的载波频率和码相位即为捕获结果。
3.4 时间复杂度分析
基于FFT的并行码相位捕获方法进行一次FFT需要(N/2)×log2N次复数乘和N×log2N次复数加。其中对本地伪码做FFT可提前处理,所以完成一次完整的捕获需要N×(1+log2N)次复数乘和2N×log2N次复数加。为了提高信噪比,进行S次累加,传统捕获的时间复杂度为O(SN×log2N)。
基于SFFT的捕获算法中,通过S次累加来提高卫星信号捕获的信噪比。在稀疏快速傅里叶逆变换前的时间复杂度为O((SN/2)×log2N)。在稀疏快速傅里叶逆变换中,需要L次的定位和估值循环,其中得到混叠信号后,进行FFT的时间复杂度为O(Blog2B),得到大值点集合I的时间复杂度为O(Blog2B+dKN/B),估计I中对应的幅值X′(k)的时间复杂度为O(Blog2B+dKN/B),外循环计算中位值X(k)需要的时间复杂度为O(LdKN/B),其中参数
L=O(log2N),则SIFFT需要的时间复杂度[13]为O(log2N×
基于SFFT捕获的时间复杂度为
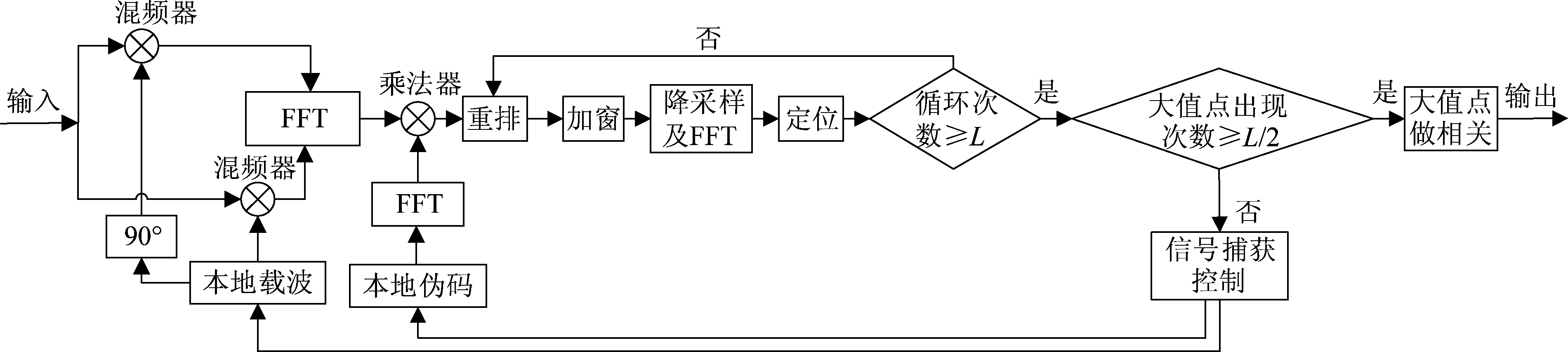
图3 捕获算法流程图
Fig.3 Flow chart of capture algorithm
在基于SFFT算法捕获的基础上,不对其进行估值,将I′所对应的本地伪码与中频信号做相关,则完成一次捕获的时间复杂度为
其中,a为I′中的个数。
4 实验结果及分析
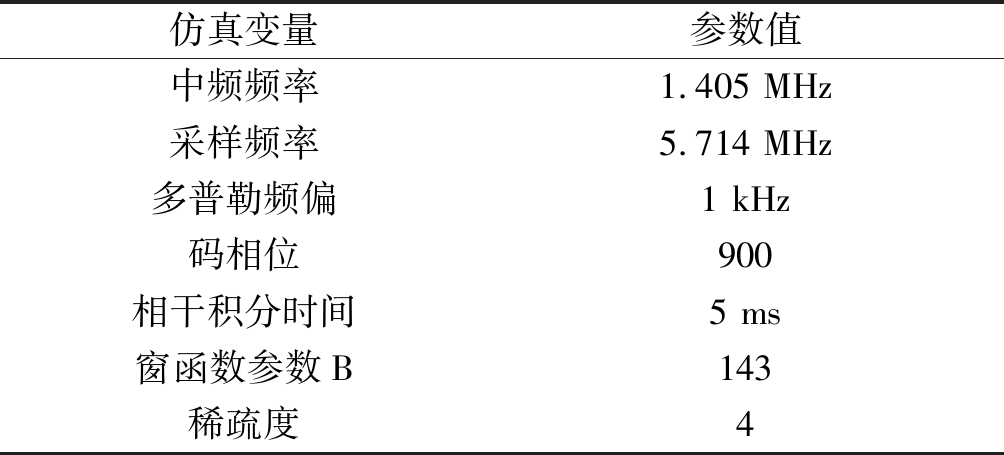
利用仿真的数据对本文方法进行测试。方法在基于MATLAB的软件接收机上实现。仿真实验的实验参数如下表1所示。
表1 仿真数据参数
Tab.1 Simulation data parameters
仿真变量参数值中频频率1.405 MHz采样频率5.714 MHz多普勒频偏1 kHz码相位900相干积分时间5 ms窗函数参数B143稀疏度4
为了验证本文方法的有效性,将方法与现有的文献[3]中基于FFT的并行码相位捕获方法和文献[12]中基于SFFT的捕获方法进行对比。
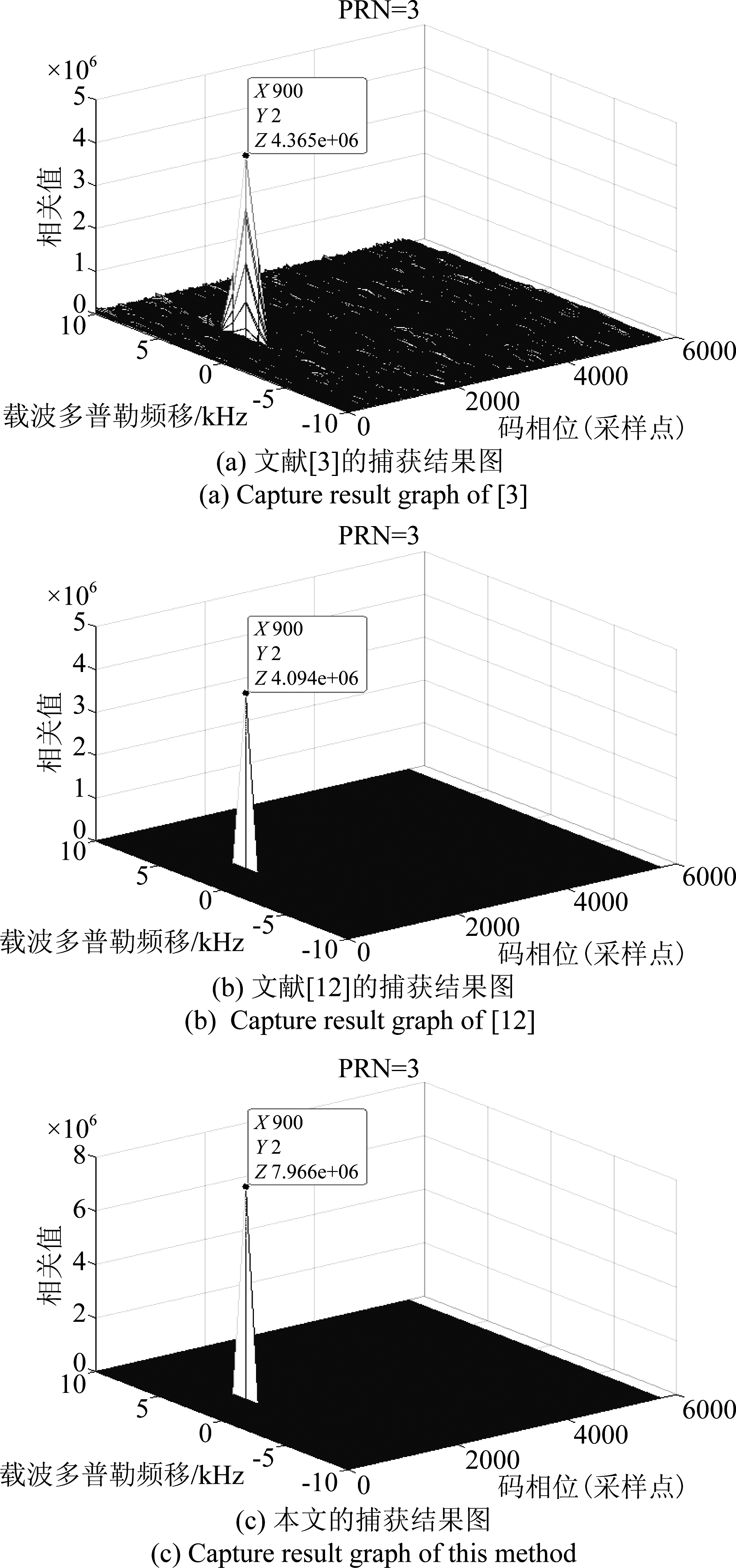
图4 SNR=-10 dB的实验结果及对比
Fig.4 Experimental results and comparison of SNR=-10 dB
首先在信噪比为-10 dB的情况下对三种方法进行了仿真实验对比,实验结果图如下图4所示。图4(a)为文献[3]的捕获结果图;图4(b)为文献[12]的捕获结果图;图4(c)为本文方法的捕获结果图。
从实验结果图中可以看出卫星信号在SNR=-10 dB时,文献[3]的捕获方法的噪底非常低,捕获结果很好;文献[12]的捕获性能也非常好,并且估值运算也比较准确,说明在信噪比高的情况下,SFFT的捕获方法是可行的;本文方法也能成功捕获卫星信号,只有一个独立峰值存在,捕获结果很好。
但在实际情况下,卫星信号的信噪比通常为-20 dB。所以在信噪比为-20dB的情况下进行了仿真实验对比，实验结果图如下图5所示。图5(a)为文献[3]的捕获结果图;图5(b)为文献[12]的捕获结果图,其中在本地伪码与接收卫星信号相关值最大时,SFFT的输出结果I′=[900,1148,5432],但由于SFFT在低信噪比的情况下估值误差大,所以当本地伪码与接收卫星信号的相关值最大的时候,估值运算后大值所在位置估为1148,而不是900;图5(c)为本文方法的捕获结果图。
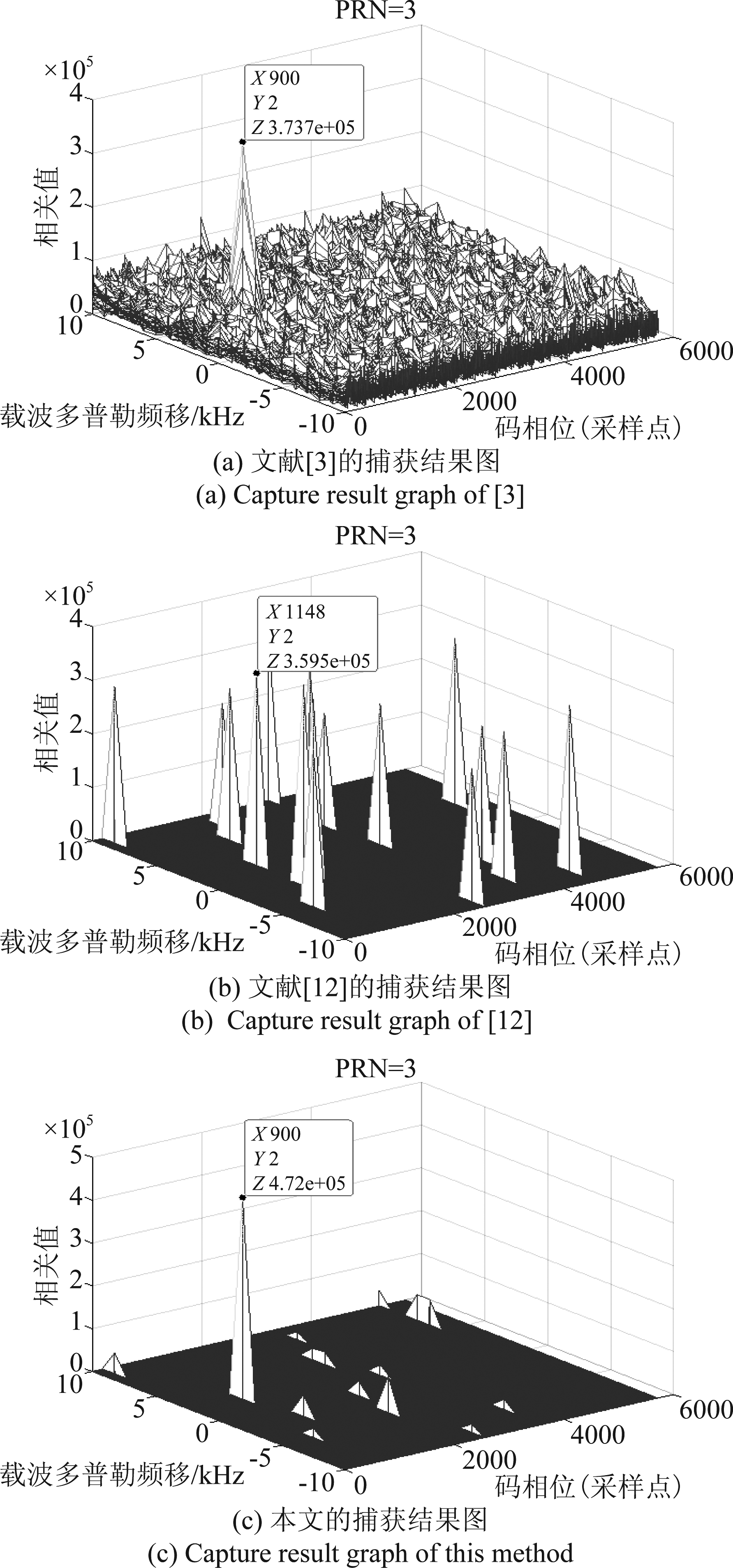
图5 SNR=-20 dB的实验结果及对比
Fig.5 Experimental results and comparison of SNR=-20 dB
从实验结果图中可以看出,本文方法相比文献[3]的捕获噪底很低,绝大多数情况下不需要做相关运算,峰值很干净;相比文献[12]的捕获算法可以看出,由于估值误差影响,SFFT的捕获算法在-20 dB情况下的捕获结果噪底很高,而且误差很大,所以本文的捕获概率要高于文献[12]的捕获概率。
在基于上述实验条件的情况下,表2在-20 dB情况下对三种方法的运算量进行统计对比。其中,本文方法平均每次SIFFT输出结果为5个大值,需要计算5个坐标点的相关值,则单次相关结果的复杂度为
文献[3]的单次相关结果的复杂度为O(SN×log2N);文献[12]的单次相关结果的复杂度为
表2 运算量比较
Tab.2 Comparison of calculation amount
实验方法运算次数文献[3]532480文献[12]274729本文算法303299
从上表2中可以看出：本文方法相比基于FFT的并行码相位的传统捕获方法减少了43%的运算量,相比基于SFFT的捕获方法增加了10%的运算量。
本文对三种捕获方法的捕获概率进行了分析,如下图6所示。
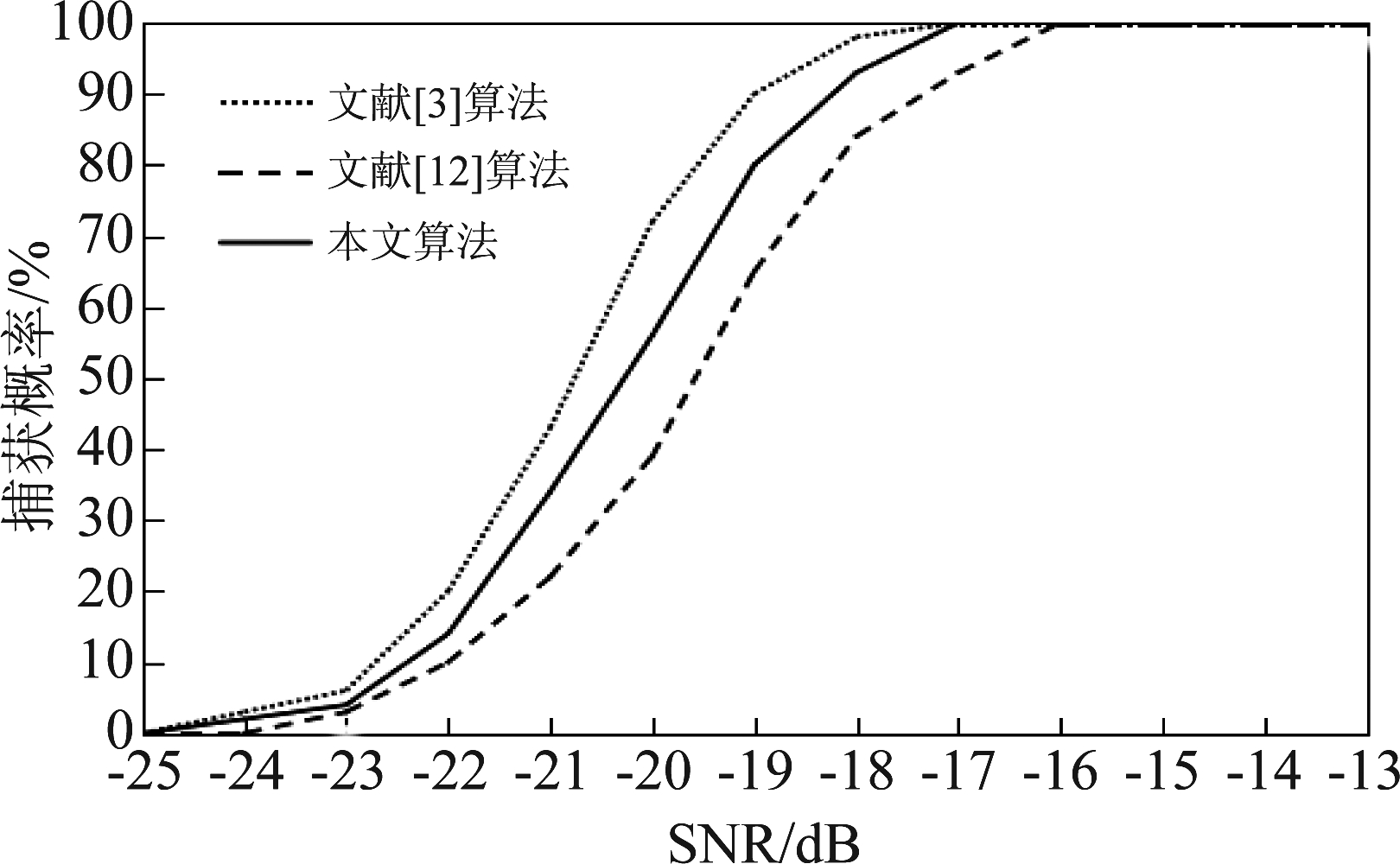
图6 捕获概率对比图
Fig.6 Comparison chart of capture probability
从图6中可以看出,文献[3]的捕获方法的捕获概率最高,其次是本文的捕获方法。当信噪比高于-18 dB时,本文方法与传统捕获方法的捕获概率相同,都是接近100%;当信噪比高于-17 dB时,三种方法的捕获概率相同,都为100%。
表3 -20 dB下三种算法5×103次实验下虚警次数对比
Tab.3 Comparison of false alarm times under 5×103 experiments with three algorithms under -20 dB
实验方法文献[3]文献[12]本文算法虚警次数083
从上表3可以看出：卫星信号的信噪比在-20 dB的情况下,三个捕获方法出现的虚警次数都很少,文献[3]出现的虚警次数最少,本文仅次于文献[3]。
结合表2、表3和图6的分析可以看出,文献[3]的捕获方法的捕获成功概率最高,运算次数最多,但出现虚警的次数最少;在文献[12]的捕获方法中,其运算量较文献[3]的方法降低了许多,但是其运用了估值步骤来恢复信号,导致捕获概率降低了许多且出现虚警的次数增多;而在本文算法中使用了部分SFFT步骤,将其融入到卫星信号捕获算法中,运算量与传统捕获方法相比降低较多,出现虚警的次数稍微增加。虽然本文算法运算量与基于SFFT的捕获方法相比有较少提高,但本文算法由于去掉了SFFT中的估值部分,改用直接对疑似大值进行相关运算的步骤,成功捕获到卫星信号的概率有大幅提高。
5 结论
本文在分析卫星捕获输出相关值具有稀疏的特性后,将稀疏快速傅里叶变换运用到卫星信号捕获中,给出了基于相关的SFFT的快速捕获方法。对传统捕获方法处理后的信号进行重排、加窗和降采样的哈希映射,找到大值点坐标;再对逆映射后的坐标点的伪码与输入信号做相关运算,最后通过门限判决进行捕获。通过实验对算法进行了验证,并与GPS信号捕获的经典方法和近年提出的新方法进行对比,结果表明本文方法捕获性能较好,在成功捕获信号的同时,能够降低运算量,减少捕获时间。但本文方法捕获概率仍有继续提高的空间,将在下一步工作中重点研究。
[1] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 349-375.
Xie Gang. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2009: 349-375.(in Chinese)
[2] 张颖一, 张伟. 国外载人深空探测现状及发展趋势分析[J]. 中国航天, 2019(11): 54-59.
Zhang Yingyi, Zhang Wei. Analysis of the Status and Development Trend of Manned Deep Space Exploration [J]. Aerospace China, 2019(11): 54-59.(in Chinese)
[3] Spangenberg S M, Scott I, Mclaughlin S, et al. An FFT-Based Approach for Fast Acquisition in Spread Spectrum Communication Systems[J]. Wireless Personal Communications, 2000, 13(1-2): 27-55.
[4] Hassanieh H, Indyk P, Katabi D, et al. Simple and Practical Algorithm for Sparse Fourier Transform[C]∥Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2011, San Francisco, California, USA, January 23-25, 2011. ACM, 2012.
[5] Hassanieh H, Indyk P, Katabi D, et al. Nearly Optimal Sparse Fourier Transform[J]. Proceedings of the Annual ACM Symposium on Theory of Computing, 2012: 563-578.
[6] 曹云, 陈洁. 基于稀疏傅里叶变换的涡街流量分析[J]. 工业控制计算机, 2019, 32(8): 32-33, 36.
Cao Yun, Chen Jie. Vortex Flow Analysis Based on Sparse Fourier Transform[J]. Industrial Control Computer, 2019, 32(8): 32-33, 36.(in Chinese)
[7] 黄浩. 基于S变换的医学影像降噪压缩及稀疏傅里叶变换理论研究[D]. 济南: 山东大学, 2016.
Huang Hao. Medical Image Denoising and Compression Using S Transform and Research on Sparse Fourier Transform[D]. Jinan: Shandong University, 2016.(in Chinese)
[8] Hassanieh H, Adib F, Katabi D, et al. Faster GPS via the Sparse Fourier Transform[C]∥International Conference on Mobile Computing & Networking. ACM, 2012.
[9] 张春熹, 李先慕, 高爽. 基于稀疏傅里叶变换的快速捕获方法[J]. 北京航空航天大学学报, 2018, 44(4): 670- 676.
Zhang Chunxi, Li Xianmu, Gao Shuang. Fast Acquisition Methods Based on Sparse Fourier Transform[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(4): 670- 676.(in Chinese)
[10]Ma Ying, Bu Xiangyuan, Gong Qiaoxian, et al. SFT-based Algorithm of Acquisition and Anti-jamming of GPS Signals[C]∥2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), 2014: 5.
[11]Ma Ying, Bu Xiangyuan, Han Hangcheng, et al. Combined Algorithm of Acquisition and Anti-jamming Based on SFT[J]. Journal of Systems Engineering and Electronics, 2015, 26(3): 431- 440.
[12]Xu D, Chen S, Shen F, et al. A Fast Acquisition Algorithm of GNSS Receiver Based on SFFT[C]∥2017 Forum on Cooperative Positioning and Service (CPGPS). IEEE, 2017.
[13]Schumacher J, Puschel M. High-performance Sparse Fast Fourier Transforms[C]∥2014 IEEE Workshop on Signal Processing Systems (SiPS). IEEE, 2014: 1- 6.
