1 引言
传统的多目标跟踪主要是基于数据关联的方法来实现,其存在计算量大的弊端。Mahler于2003年提出基于随机有限集(Random Finite Set,RFS)的概率假设密度(Probability Hypothesis Density,PHD)滤波算法[1],将目标状态与观测建模为随机有限集,并通过近似多目标后验分布一阶矩的方式实现对多目标跟踪,避免了传统算法中复杂的数据关联。随后,基于RFS的算法得到了广泛关注,众多学者投入研究,极大扩展了基于随机有限集滤波跟踪算法[2-10]。
多传感器多目标跟踪算法将单传感器滤波跟踪扩展至传感器网络的环境下,利用信息融合的方式处理网络中各传感器的跟踪信息,拥有可扩大跟踪范围与鲁棒性的特点。多传感器多目标跟踪主要分为集中式与分布式。集中式方法通过将各传感器探测数据汇总至融合中心进行统一融合,使信息损失最小化,但对计算与通讯资源均有较高的要求[11]。而分布式方法可依网络拓扑结构进行局部通信和融合,降低了通信与计算负载,且具有接近集中式方法的跟踪精度[12,18-21],这使得其更具研究价值。
分布式多传感器多目标跟踪算法目前广泛采用的信息融合方法为Mahler在文献[13]中提出的一种广义协方差交集算法(Generalized Covariance Intersection,GCI),其可适用于线性或非线性的多目标跟踪场景。GCI融合方法与随机有限集的滤波跟踪算法相结合的分布式算法在近些年来被各学者不断的创新与改进,并取得了不错的成果,其中较典型的如Murat Üney等在文献[14]中将随机有限集与GCI进行结合,建立了一种分布式多传感器多目标跟踪的一致性方法,降低了多假设跟踪(Multi-Hypothesis Tracking,MHT)和航迹至航迹(Track to Track)融合所需严格的网络要求,并给出基于RFS的指数混合密度(exponential mixture densities,EMD)显式公式以进行融合计算;文献[15]中提出基于粒子滤波的多伯努利(Multi-Bernoulli,MB)分布式GCI融合算法,并给出了GCI规则下的具体融合计算公式;在此基础上,文献[16]研究了基于GCI-MB的网络共识算法;文献[17]中提出带有航迹管理的分布式标签多伯努利(Labeled Multi-Bernoulli,LMB)滤波算法;文献[18]中对具有受限视野(field-of-view,FoV)传感器的分布式LMB滤波算法进行研究,并采用补偿策略及无标签(Label-free,LF)GCI算法(LF-GCI)进行融合以提高跟踪性能;文献[19]中提出基于混合高斯GCI融合策略,并对融合中的权重问题进行了讨论。然而,在真实跟踪场景中,受复杂环境以及各传感器探测能力和布站位置不同的影响,局部单传感器的跟踪能力不同,可能存在部分传感器漏跟等问题,这将直接影响GCI融合结果的准确性,导致融合精度降低,甚至恶化后续融合跟踪的过程。
针对上述问题,本文提出一种改进的基于多伯努利滤波的分布式多传感器多目标跟踪算法,主要工作包括以下几点:(1)提出决策级融合策略,以解决非理想融合场景下直接利用融合结果进行状态输出而导致状态估计失准的问题;(2)提出特征级融合反馈策略,以解决失准融合项直接反馈而影响后续跟踪的准确度问题并且降低虚警;(3)提出交互反馈策略,以改进单传感器滤波中可能存在的目标跟丢问题。通过不同阶段的融合和反馈,从而提高对复杂环境下数目变化的多目标跟踪精度。
2 GCI融合准则
假设在k时刻,有传感器1和2,其各自滤波得到多目标后验概率密度![]() 和
和![]() 融合两个后验概率密度,得到联合后验概率密度可表示为:
融合两个后验概率密度,得到联合后验概率密度可表示为:
(1)
但需要指出的是,如果采用两个相同类型的传感器,对于同一目标得到的概率分布,有着相同的过程噪声和观测噪声,因而![]() 和
和![]() 表示的分布具有一定的相关性,若直接融合会导致重复计算,此时将上式改为如下变体可解决相关性问题[15],即
表示的分布具有一定的相关性,若直接融合会导致重复计算,此时将上式改为如下变体可解决相关性问题[15],即
(2)
但在实际应用场景中,![]() 很难计算,为了解决该问题,Mahler提出GCI融合规则[13],并将随机有限集扩展到分布式环境下,将融合后验概率分布以几何平均的方式表示,即对各局部后验采用指数混合形式表示,
很难计算,为了解决该问题,Mahler提出GCI融合规则[13],并将随机有限集扩展到分布式环境下,将融合后验概率分布以几何平均的方式表示,即对各局部后验采用指数混合形式表示,
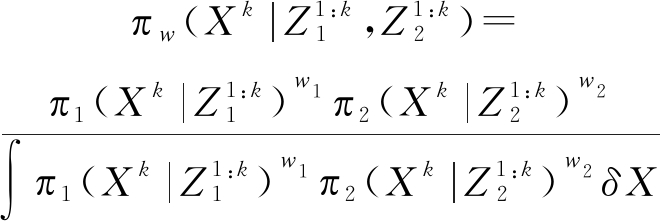
(3)
其中,w1和w2(w1+w2=1)分别表示各传感器对应的后验概率分布在融合中的相对权重。通过最小化KLD(Kullback-Leibler divergence)的加权和可获得最优融合结果,即
(4)
其中,DKL即表示KL散度,定义为
(5)
f(X)与g(X)分别表示不同的概率分布,式(5)中的积分为集合积分,积分结果表示概率分布f与g的差异大小。
3 传统GCI-MB算法问题分析
3.1 GCI-MB算法
多伯努利滤波主要是将跟踪场景中目标的状态与量测定义为随机有限集的形式,且在滤波过程中将多目标的后验概率建模为多伯努利分布,并根据贝叶斯原理进行迭代滤波,实现对数目未知且变化的多目标跟踪,具体实现过程参考文献[2]。基于多伯努利的传统GCI-MB融合算法[15]主要是对所有假设基数n(n小于最大伯努利项数)可能组合的融合分布进行加权求和,获得融合的后验分布,且分布满足广义多伯努利(Generalized Multi-Bernoulli,GMB)分布形式,表示为:
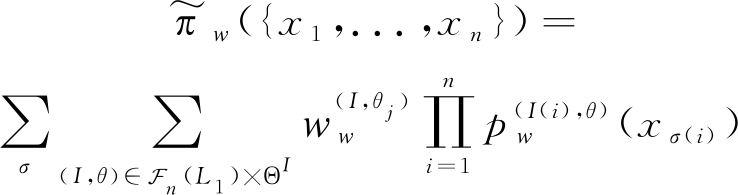
(6)
其中,
(7)
(8)
(9)
(10)
(11)
(12)
L1表示融合中本地传感器伯努利项索引集,ΘI表示伯努利子集I映射全体空间,![]() 与p(l,θ)(x)分别表示基于映射θ下融合所得GMB分量的权重和融合概率密度,w1与w2分别表示融合权重,I(i)表示取集合I中第i个元素,且满足
与p(l,θ)(x)分别表示基于映射θ下融合所得GMB分量的权重和融合概率密度,w1与w2分别表示融合权重,I(i)表示取集合I中第i个元素,且满足![]() 表示个数为n的子集。
表示个数为n的子集。
然后,采用基于一阶矩的匹配[15],将GMB分布近似为融合的MB分布πw,表示为
(13)
(14)
(15)
所得近似的πw用于状态提取,以及替代原本地后验多伯努利集用于后续时刻滤波。
3.2 问题分析
GCI融合技术的本质是分布间进行几何平均计算,其要求分布间具有较好的一致性[22],但分布的一致性在真实跟踪场景中往往很难得到保证。图1表示一维模型下两个基于MB滤波传感器融合前后示意图,图1(a)为漏跟场景,其中目标2被传感器2漏跟(传感器2滤波所得后验分布在目标2的位置没有带权粒子集构成的分布),而被传感器1正确检测并滤波,此时,采用GCI准则进行融合,会导致融合后目标2对应位置的融合伯努利项丢失,即目标2在融合后被漏跟;图1(b)为目标1被传感器2弱估计的情况,即目标1被传感器2漏检,使得目标1经漏检更新后,r值会低于提取状态的阈值,此时,伯努利项对应的rp(x)值较低,易导致融合后目标1对应伯努利项的rp(x)值低于被提取阈值,进而被漏跟踪;图1(c)为两个传感器对目标1均值位置估计差异较大的情况,即各传感器独立观测,且观测精度有较大差异时会出现此情况,此时,GCI融合后rp(x)值会趋近于0,导致目标1在融合时被漏跟。综上分析,在理想情况下,各个传感器对同一目标的后验分布都能如图1(b)中的目标2一样, GCI融合能获得较好的融合跟踪性能,但复杂环境下,采用GCI融合准则进行融合跟踪会导致跟踪结果不准确的问题。
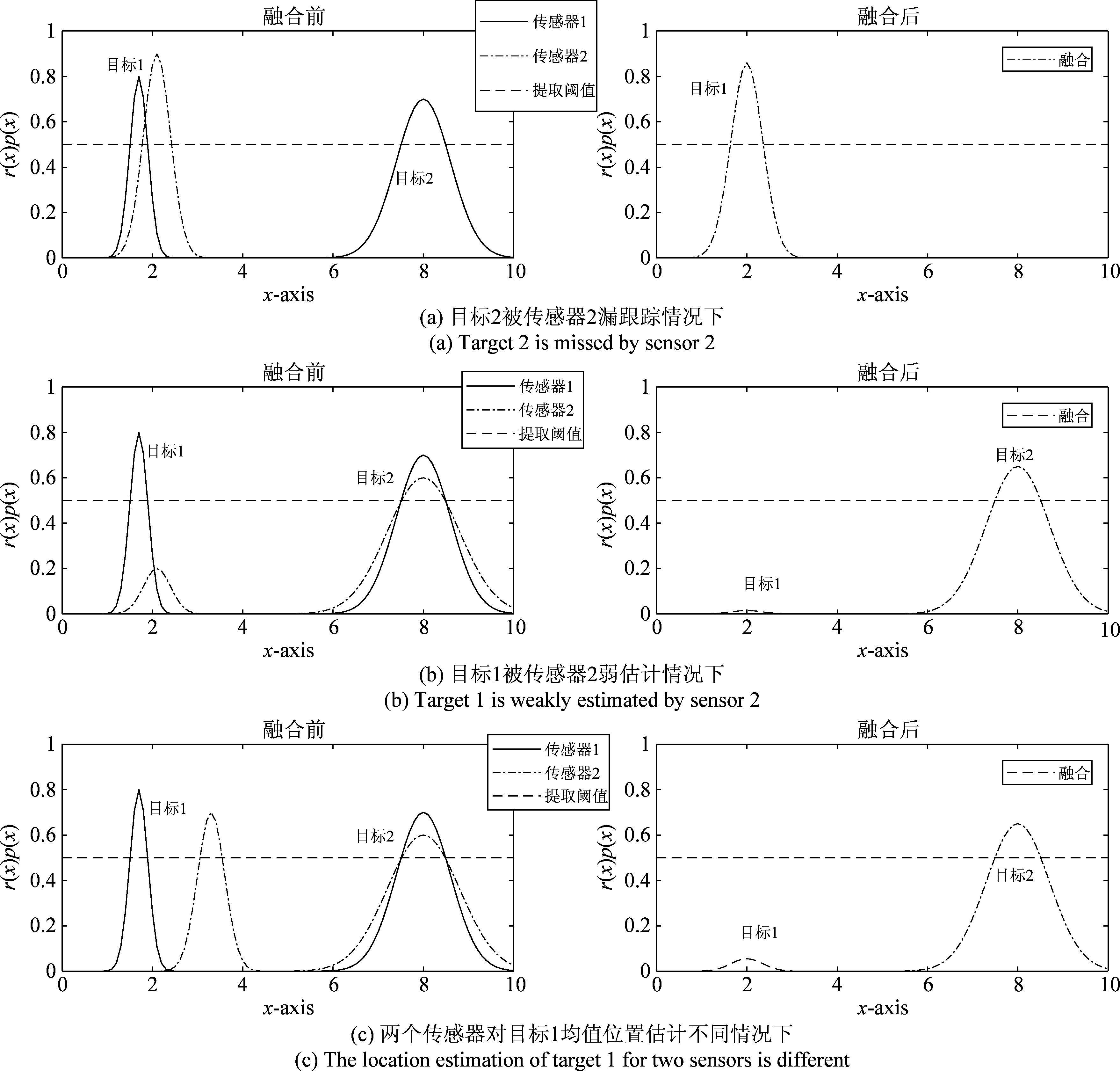
图1 一维模型下基于MB滤波的传感器融合前后示意图(融合前的图表示两个传感器的后验分布,融合后的 图表示基于GCI融合所得到的融合分布,分布高于蓝线虚线表示能够被作为真实目标提取)
Fig.1 Schematic diagram of sensor fusion based on MB filtering under one-dimensional model (the left
Figure shows the posterior distribution of the two sensors while the right
Figure shows the fusion distribution based on GCI fusion. The distribution curve higher than the blue dotted line indicates that it can be extracted as a real target)
4 提出改进的GCI-MB滤波算法
提出算法中,首先采用决策级融合策略以改善传统GCI-MB算法在复杂跟踪场景中的漏跟现象,然后进一步提出两种加强单传感器滤波效果的反馈策略,可间接提升融合性能。提出算法的总体流程框图如图2所示。
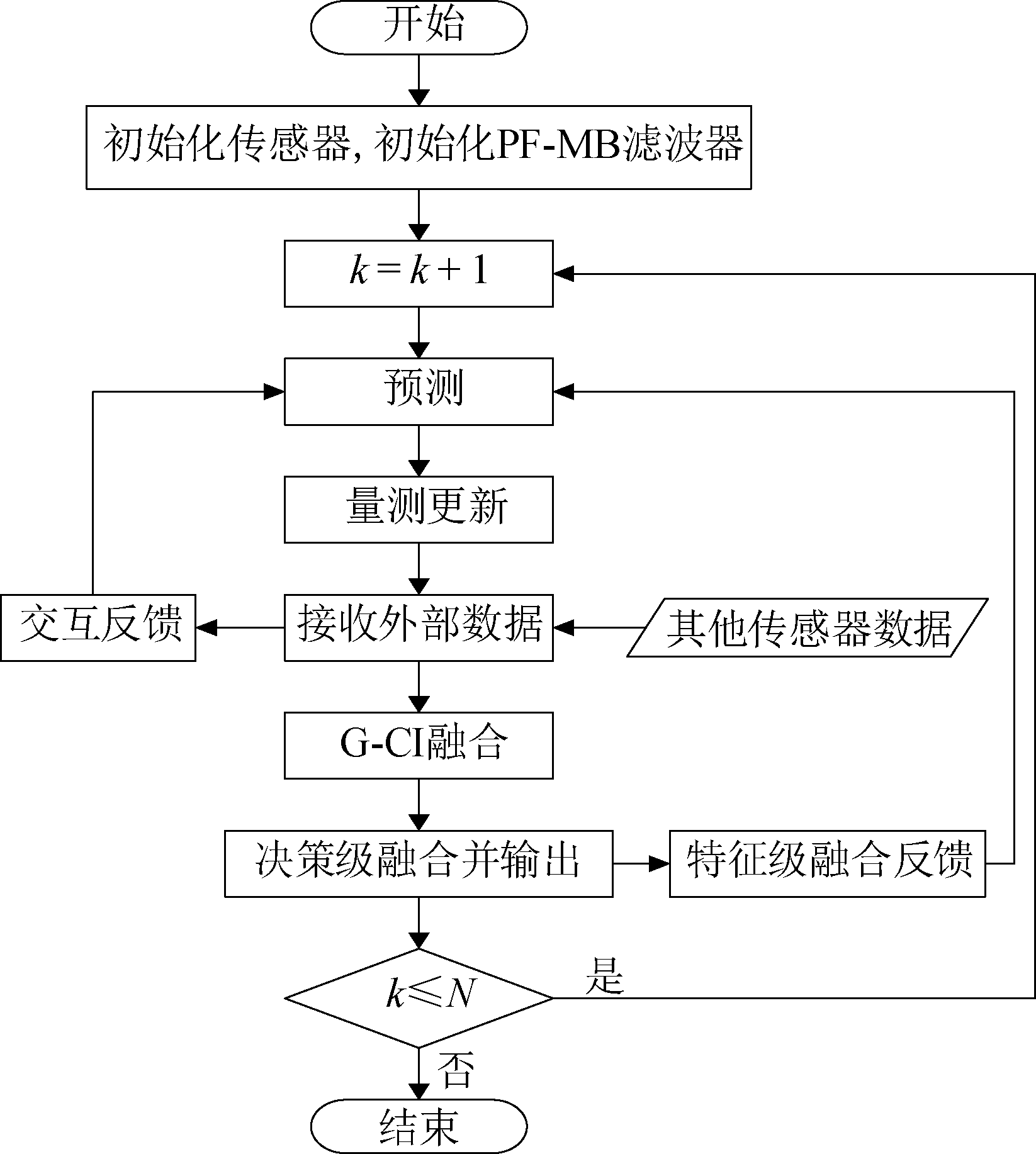
图2 提出算法的流程框图
Fig.2 Flow chart of the proposed algorithm
4.1 决策级融合策略
通过3.2节的问题分析可知,融合性能降低与否可以从融合前后势估计的变化中得到指示,若融合后势估计降低,则融合可能受到了不良影响。由此启发,本文提出决策级融合策略,根据融合前后势估计的变化,判断融合是否正常,如果,出现融合异常,依据融合前后提取项的势差异找出未能得到有效融合结果的“异常项”(如被某个传感器漏跟的目标项),由“异常项”与融合结果的提取项共同构成输出项;否则,认为GCI融合正确,依照融合结果进行状态提取。基于此思想,所得滤波输出既包含了正常融合的目标状态,同时也保留了异常项并输出,且保留的异常项将参与后续的跟踪,避免目标的漏跟。
显然,算法的关键在于如何寻找因错误融合而丢失掉分布信息的目标项,假设k时刻,本地传感器A采用PF-MB滤波后的多目标后验多伯努利参数集表示为:
(16)
其中,LA表示A传感器中所有伯努利项索引空间,![]() 为带权粒子集,Np表示粒子数,其势估计为NA,加权粒子可近似表示目标的后验概率密度分布[23]。
为带权粒子集,Np表示粒子数,其势估计为NA,加权粒子可近似表示目标的后验概率密度分布[23]。
假设将与A传感器进行融合的传感器B的多伯努利参数集表示为:
(17)
其中,LB为传感器B的伯努利项索引空间,且传感器B的势估计为NB。
根据式(6)~(12),若NA≥NB,则将LA记为L1,LB记为L2;否则,将LB视为L1,LA记为L2,令势估计更大的MB参数集为πmax,并提取多伯努利集πext={rl,pl}l∈Lext(其中,|Lext|=max(NA,NB),Lext⊂L1);势估计小的MB参数集记为πmin。
根据期望后验(EAP)可获得目标的状态估计为所有带权粒子的加权和,即
(18)
构造损失矩阵ML1×L2
(19)
其中,![]() 为πmax中第i个伯努利项对应目标的状态估计,
为πmax中第i个伯努利项对应目标的状态估计,![]() 则表示πmin中第j个目标的状态估计(i∈L1, j∈L2)。
则表示πmin中第j个目标的状态估计(i∈L1, j∈L2)。
由式(6)及文献[15]可知,随着伯努利项数的增加,![]() 以及Θ的数量均会呈指数级增加,导致计算量急剧增大。
以及Θ的数量均会呈指数级增加,导致计算量急剧增大。
为了降低计算量,受文献[5]中对GLMB更新剪枝的启发,通过Murty算法对ΘI(轨迹子集I与L2间的映射空间)进行选优。对任一![]() 算法利用ML1×L2以及一个数量参数Hn(用以限制融合映射的数量,为经验参数,取小于
算法利用ML1×L2以及一个数量参数Hn(用以限制融合映射的数量,为经验参数,取小于![]() 将ΘI的数量降低至Hn。此时,GMB简化为
将ΘI的数量降低至Hn。此时,GMB简化为
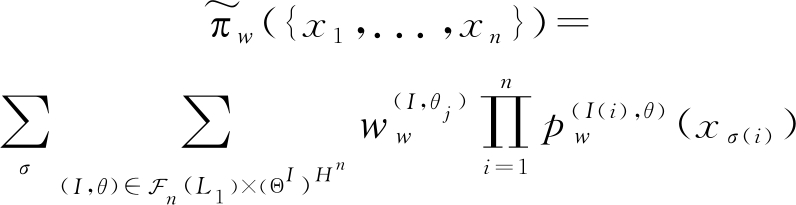
(20)
其中,(ΘI)Hn表示基于Murty算法得到的全体映射子集空间,满足|(ΘI)Hn|=Hn;减少ΘI的数量,本质上是对GMB分量进行了“剪枝”,且丢失的GMB分量不影响融合分布的一阶矩,即不会对融合精度产生不良影响。
由式(20)及(7)~(12)完成πA与πB间的GCI融合,然后根据式(13)~(15)及(20),对融合后验分布![]() 采用基于一阶矩匹配得到融合MB参数集表示为
采用基于一阶矩匹配得到融合MB参数集表示为![]() 计算出
计算出![]() 的势估计,表示为Nw,则基于融合结果提取MB参数集为πwext={rl,pl}l∈Lw(|Lw|=Nw)。
的势估计,表示为Nw,则基于融合结果提取MB参数集为πwext={rl,pl}l∈Lw(|Lw|=Nw)。
若Nw<|Lext|,取集合L3=Lext/Lw,并从πmax中依照索引集L3得到“异常项”集,定义为
πexc=πmax∩{rl,pl}l∈L3
(21)
否则取πexc={∅}。
按上述步骤,得到融合后的多伯努利参数集πw,表示为
(22)
当接收的数据源数量大于等于2时,则可利用πw作为πA重复上述算法步骤,直至迭代融合所有接收数据,再根据πw中的多伯努利参数进行目标提取,即可获得该时刻的状态输出,既可以提高对目标的估计精度,同时可以避免目标的漏跟。
4.2 特征级融合后的反馈策略
理想的融合环境中,各传感器滤波所得目标的分布均能如图1(b)中的目标2一样,此时,融合后的多目标分布较之融合前会更趋近于多目标真实的分布,因此可直接用融合后的多伯努利集替换原后验多伯努利集作为融合结果的反馈方式,即
(23)
其中,![]() 作为当前时刻的后验多伯努利集,用于下一时刻滤波。
作为当前时刻的后验多伯努利集,用于下一时刻滤波。
但在复杂跟踪环境中,各传感器受高噪声观测、目标紧邻运动或者虚警情况的影响,所得后验分布可能存在较大差异,采用GCI融合规则计算出的融合分布可能会偏离目标的真实分布,即融合结果精度降低,此时,若以式(23)的方式来反馈融合结果,会导致后验多伯努利分布中丢失真实目标的位置分布信息,使得PF-MB滤波器在下一时刻无法跟踪上真实目标,或者因高似然区域粒子过少而导致滤波精度下降。
基于上述分析,提出改进的反馈策略,即在式(23)的基础上,保留本地传感器后验多伯努利集中被提取为目标状态的多伯努利集,记为πA,ext,然后,修改πA,ext和融合后提取的多伯努利集πwext的存在概率,对于πA,ext,将其存在概率修改为新生分布的存在概率(如0.05),即将其视为下一时刻可能出现的新生目标对应的多伯努利参数集![]()
(24)
其中,|LA,ext|=NA,LA,ext⊂LA。
将融合后的多伯努利参数集πwext的存在概率设为经验参数(如0.15),表示为![]() 视为存活目标对应的多伯努利参数集,即
视为存活目标对应的多伯努利参数集,即
(25)
将反馈后的多伯努利后验分布表示为
(26)
![]() 的存在概率取为新生目标存在概率,以防止失准的融合分布可能在后续跟踪时导致目标被失跟(即量测点位置附近没有粒子)。
的存在概率取为新生目标存在概率,以防止失准的融合分布可能在后续跟踪时导致目标被失跟(即量测点位置附近没有粒子)。![]() 的存在概率取值为0.15,该经验参数可以保证,若融合结果准确,则在下一时刻,融合伯努利项进行MB滤波更新后,存在概率能够高于被提取的阈值,从而维持正确跟踪;若融合结果不准确,在后续时刻MB滤波过程中会因无对应目标量测更新,使得该伯努利分量的存在概率大幅下降而被剪枝掉,降低虚警的发生概率。
的存在概率取值为0.15,该经验参数可以保证,若融合结果准确,则在下一时刻,融合伯努利项进行MB滤波更新后,存在概率能够高于被提取的阈值,从而维持正确跟踪;若融合结果不准确,在后续时刻MB滤波过程中会因无对应目标量测更新,使得该伯努利分量的存在概率大幅下降而被剪枝掉,降低虚警的发生概率。
综上,基于式(26)表示的特征级融合反馈方式所得多伯努利后验分布用于下一时刻的预测和更新,可以起到避免虚警以及优化后续滤波跟踪性能的作用。
4.3 交互反馈
在实际跟踪场景中,传感器网络中各传感器的检测跟踪能力有所差异,可能存在同一个目标只被其中某一个或部分传感器跟踪上,即存在部分传感器漏跟该目标,此时,将所有传感器结果直接进行融合,难以有效提升精度。针对该问题,进一步提出交互反馈机制,以避免部分传感器因出现漏跟而影响后续跟踪。交互反馈的流程框图如图3所示。

图3 交互反馈机制
Fig.3 Interactive feedback mechanism
根据式(18)与式(19)所得到的损失矩阵MLA×LB,依次取每列,定义为ζ|·|,|i|,其中i∈LB,若
min(ζ|·|,|i|)>λ
(27)
则记录下索引i,其中λ表示距离阈值。最终筛选出的多伯努利集表示可能被本地传感器漏检(漏跟),而被互连传感器检测并跟踪上的目标。
将记录下的索引集定义为IC,且IC∈LB,根据IC定义多伯努利集πc,该集合中所包含的伯努利项即为要反馈的多伯努利集。
(28)
多伯努利参数集πc是从接收的互连传感器的后验数据中筛选出的,考虑到4.1节中异常项的获取方式,在NB>NA时,筛选出的多伯努利集与异常项可能会重合,导致冗余计算,因此,对πc与πexc作对称差运算,以消除冗余伯努利项,即πc=πc⊕πexc。
根据πc和式(26),交互反馈的多伯努利分布定义为
(29)
提出的交互反馈机制中,从互连传感器的后验多伯努利集中寻找与本地多伯努利集各项对应目标位置较远(以大于参数λ为准)的项,将其视为本地传感器可能漏跟的目标,并把这些项并入本地后验多伯努利集中,从而可以在复杂环境的分布式跟踪过程中保证传感器不会对目标长时间漏跟而导致跟踪失败。
πk+1是在融合反馈结果的基础上,进一步利用相邻传感器的有用信息以得到更好的后验多伯努利集,相较于4.2中的![]() 更有利于下一时刻的跟踪滤波。表1给出了提出算法的具体步骤。
更有利于下一时刻的跟踪滤波。表1给出了提出算法的具体步骤。
表1 提出算法步骤
Tab.1 Implementation steps of the proposed algorithm

① 初始化:初始化PF-MB滤波器《0={r=0.001,{x(i)l,w(i)l}Npi=1}1l=1,Np=300;② 传感器探测及滤波:k时刻,本地传感器A采用PF-MB滤波进行预测和更新后,得到式(16)所示的后验多伯努利集《A;③ 接收融合数据:计算式(17)所示传感器B的MB参数集《B及《A的势估计,并从势估计大的参数集中提取目标的MB参数集《ext={rl,pl}l∈Lext;④ GCI融合:由式(18)~(19)计算损失矩阵MLA×LB,并依据(7)~(15)及(20),对传感器A和B进行融合,计算融合MB参数集《〠w及其提取项MB参数集《wext={rl,pl}l∈Lw;⑤ 交互反馈:根据④中损失矩阵MLA×LB与(27)进行筛选并记录结果Ic,再由式(28)得到多伯努利集《c;⑥ 决策级融合:根据式(22)得到最终融合MB参数集《w=《〠w∪《exc。若迭代融合未结束(相邻传感器数量>1),重复步骤③~⑤,直至迭代完所有接收数据;⑦ 特征级融合反馈:根据式(24)与(25)分别修改《A,ext与步骤④所得《wext,得到《ιA,ext与《ιwext;⑧ 反馈:根据式(26)与式(29)所得的《k+1反馈用于下一时刻传感器滤波;⑨ 当k≤T时(T表示跟踪总时间),重复步骤②~⑧,否则停止跟踪。
5 实验结果与分析
为验证提出算法的有效性,本文采用如下典型的跟踪场景,目标平行运动和存在交叉的多目标运动场景,且分别考察低、中、高三种不同量测噪声强度,并与传统算法进行对比分析。
实验中,假定各传感器对目标的观测相互独立,且传感器观测精度和目标到传感器的距离和角度有关。假设传感器的量测参数采用极坐标方式给出,即(ρ,θ)的形式,如图4所示。
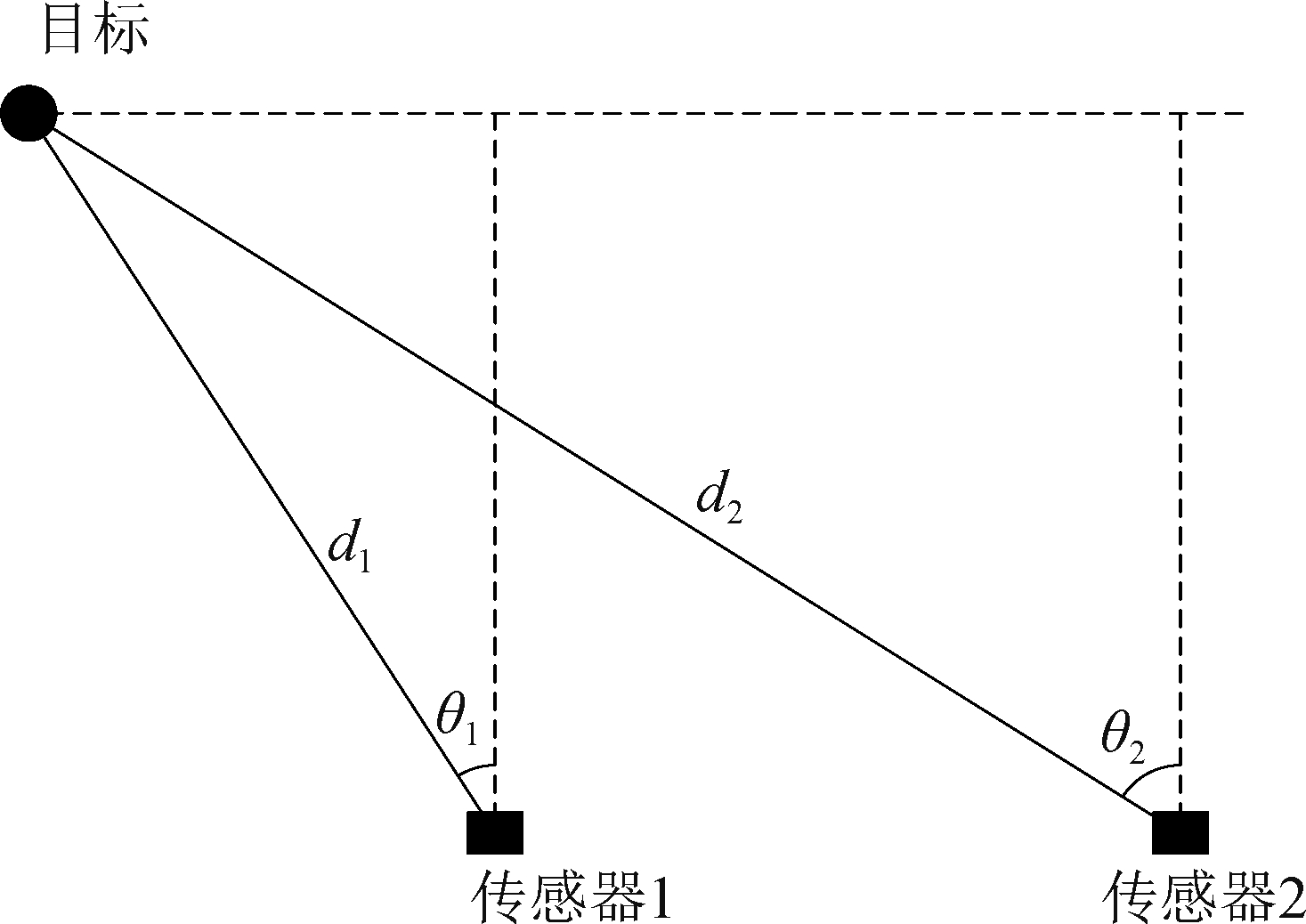
图4 传感器观测模型示意图
Fig.4 Schematic diagram of sensor observation model
设目标与传感器间的真实距离为d,与传感器垂直方向所形成的夹角为θ,则观测噪声协方差(COV)与观测z分别定义为:
(30)
z=xp+COV·randn
(31)
其中,σ表示观测噪声强度参数,xp为目标真实位置的极坐标参数[ρ,θ]T,randn~N([0,0]T,diag[1,1]),表示由二维标准正态分布产生的随机二维向量。
假设有两个传感器,位置坐标分别为(-300 m, 0 m)和(300 m, 0 m),新生目标伯努利项的存在概率设为r=0.05,检测概率pD=0.98,目标存活概率pS=0.99,粒子数Np∈[300,1000](即分配给单个伯努项构成其概率密度的粒子数,最低为300,上限为1000)。为测试不同观测噪声对算法的影响,分别假定观测噪声强度σ为0.01、0.025与0.05。杂波服从泊松分布,且泊松率λc=12,强度![]() 状态转移方程假设为xk=Fxk-1+Gνk,其中,F和G分别为状态转移矩阵和过程噪声矩阵[24],且νk~N([0,0]T,diag[1,1])。目标状态表示为x=[cx,νx,cy,νy]T,其中(cx,cy)表示目标在直角坐标系下的坐标值,(νx,νy)为目标在x与y方向上的速度。
状态转移方程假设为xk=Fxk-1+Gνk,其中,F和G分别为状态转移矩阵和过程噪声矩阵[24],且νk~N([0,0]T,diag[1,1])。目标状态表示为x=[cx,νx,cy,νy]T,其中(cx,cy)表示目标在直角坐标系下的坐标值,(νx,νy)为目标在x与y方向上的速度。
实验中采用最优次模式分配(OSPA)[25]来评估提出算法的跟踪精度,其中,参数c=100,p=1,实验中采用100次蒙特卡洛仿真,算法中GCI融合的权重采用Metropolis权重[26]。
5.1 目标作平行运动
假定两个目标的初始状态分别为[-500 m, 20 m/s, 150 m, 0 m/s]T和[-500 m, 20 m/s, 250 m, 0 m/s]T,作平行运动,运动总时长均为50 s,两个目标的运动轨迹如图5所示。
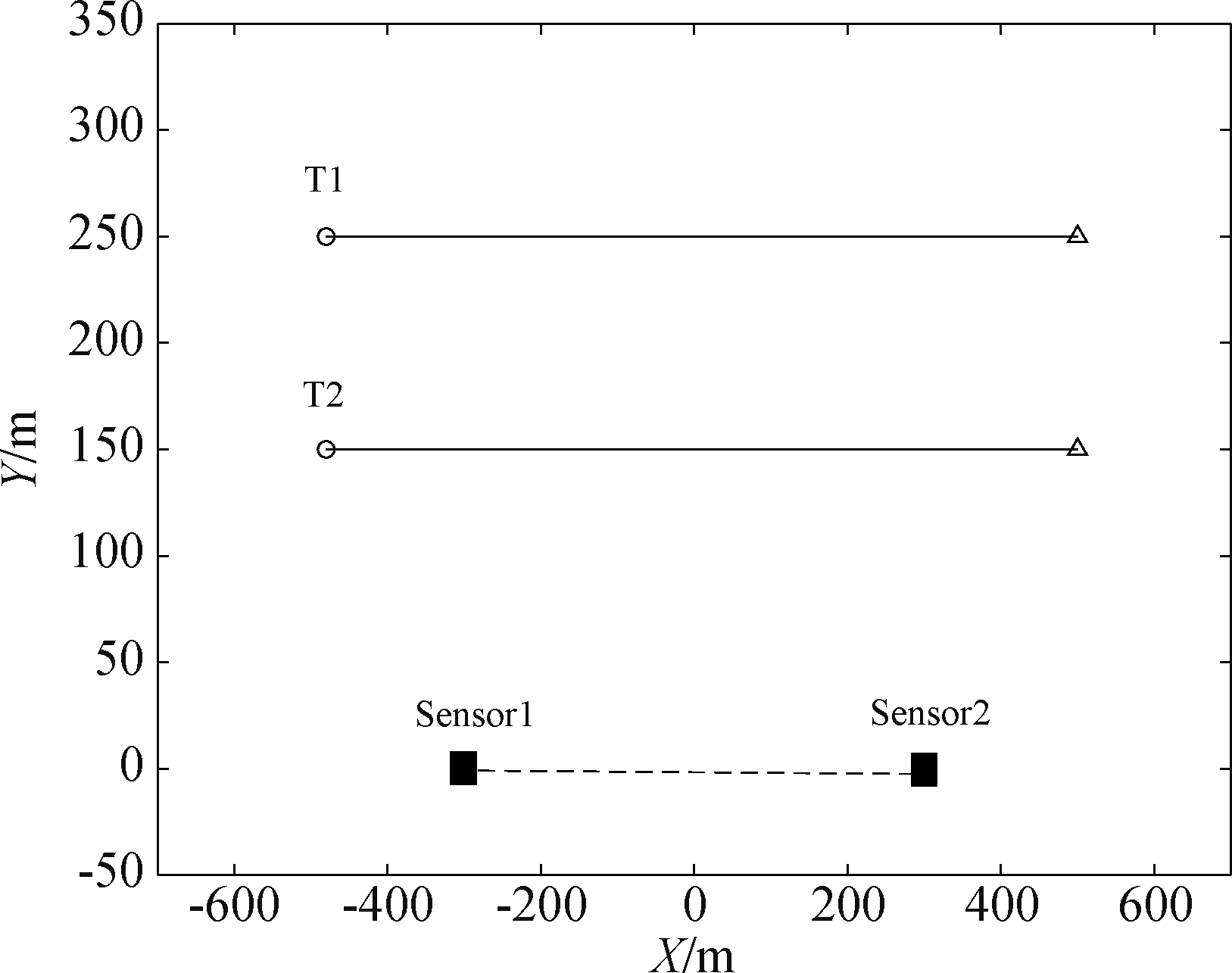
图5 目标平行运动场景,“○”表示目标 起始运动的点,“△”表示目标终止运动的点
Fig.5 Target parallel motion scene, in which “○” indicates the starting position of the target and “△” indicates the ending position of target
实验结果如图6~图9所示,分别给出了提出算法(Proposed Method)与粒子滤波多伯努利(Particle Filter Multi-Bernoulli,PF-MB)算法、粒子滤波交互反馈多伯努利算法(Particle Filter Interactive-Feedback Multi-Bernoulli,PF-IFMB)算法以及文献[15]中(GCI-MB)方法进行对比,给出不同观测噪声强度下的OSPA误差统计及多目标势估计对比。其中,PF-MB为传统的粒子多伯努利滤波算法,且传感器之间没有进行信息交互,每个传感器单独滤波;PF-IFMB算法表示在PF-MB算法的基础上,加入本文提出的传感器之间信息的交互反馈策略,为本文提出算法的过渡阶段。本文所提出方法是在PF-IFMB的基础上,进一步在GCI分布式融合基础上加入特征级融合反馈和决策级融合输出策略。
从图6(a)中可以看出,当噪声强度取σ=0.01时,提出算法的OSPA距离明显要低于其他算法,即提出算法的状态估计精度最优;从图6(b)的势估计图中可以看出,PF-MB算法存在势估计偏低的情况,而其他算法在该噪声强度下的势估计较为准确。
需要指出的是,图6(a)中PF-IFMB算法与GCI-MB算法的实验结果接近,因为在低观测噪声下,传感器探测精度较高,各传感器单独滤波所得状态估计也相对准确,因此,通过GCI融合也难以进一步提升跟踪的精度,但会存在部分异常情况,导致融合精度下降,如图1所示的融合情况。相比之下,提出算法采用决策级融合策略对GCI融合结果进行二次处理,依靠融合前后多伯努利集的势差判断有无异常融合情况产生,进而在状态输出时,可避免对目标的漏跟,即将筛选出的“异常项”也同时输出为目标状态,故可获得较高的状态估计精度;此外,同时利用特征级融合反馈策略将融合结果进行反馈,为提升后续时刻的目标跟踪精度奠定了基础。

图6 低观测噪声(σ=0.01)下的OSPA和势估计(S1和S2分别表示两个传感器)
Fig.6 The OSPA error and cadinality estimation of the algorithm with low observation noise (σ=0.01) (S1 and S2 indicates two sensors respectively)
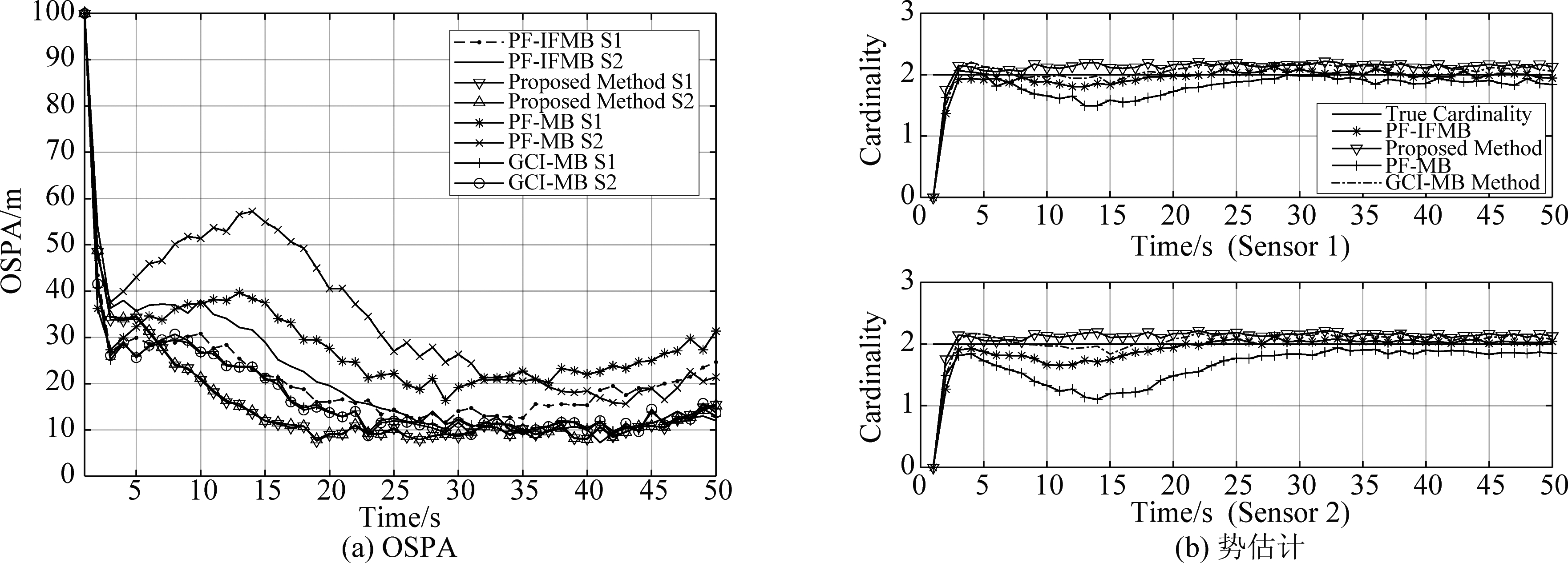
图7 中等观测噪声下(σ=0.025)各方法OSPA误差图及势估计图
Fig.7 The OSPA error and cardinality estimation of the algorithm with moderate observation noise (σ=0.025)
从图7(a)中可以看出,当噪声强度取σ=0.025时,提出算法的估计精度最高,其次是PF-IFMB算法与GCI-MB算法,结果最差的是PF-MB算法;从图7(b)中可看到,PF-MB的势估计存在偏低的情况,而其余算法的势估计在整个跟踪时段内均接近真实目标数。
需要指出的是,采用PF-MB算法与PF-IFMB算法的两个传感器(S1和S2)所得状态输出略有差异,因为目标相对于传感器的距离不同,传感器的跟踪精度也略有不同,该跟踪场景中,两个目标平行运动,先是离传感器S1比较近,当目标经过两个传感中间位置时,变成离传感器S2较近。从跟踪结果中明显可以看出,采用PF-MB和PF-IFMB算法,两个传感器单独跟踪精度在两个传感器中间位置前后发生了变化,且有较大的差异;而提出算法与GCI-MB算法所获得的状态估计,均融合了相邻传感器的后验多伯努利信息,且两个传感器的融合方式相同,所以两个传感器分别得到的输出状态具有较好的一致性。另外,从图中可以看出,GCI-MB算法所得误差曲线位于采用PF-IFMB算法的两个传感器所得结果的中间,因为,随着两个传感器观测精度下降,且距离真实目标的距离不同,两个传感器在不同位置的跟踪误差差异也变大,此时,采用GCI融合规则进行融合,则相当于对两个传感器的结果进行平均,即为一种折中思想,故所得结果会介于两传感器所得结果之间。而提出算法通过决策级融合输出策略进一步优化了状态估计,故相比较其他方法,OSPA更低,具有较高的跟踪精度。
从图8(a)和(b)中可以看出,当噪声强度继续增大取σ=0.05时,各算法的跟踪性能都有较大程度的下降,PF-MB算法的势估计最差,PF-IFMB与GCI-MB算法也出现不同程度的势估计偏低情况,而提出算法的势估计最准确。采用PF-MB和PF-IFMB算法的两个传感器跟踪结果OSPA的差异比中等观测噪声下更大。采用PF-MB算法的两个传感器在离目标较远时,OSPA误差值都比较大,GCI-MB算法的OSPA误差值介于采用PF-IFMB算法的两个传感器跟踪OSPA误差曲线的中间。提出算法的OSPA误差值明显要低于其他算法,表明提出算法的跟踪精度明显要高于其他算法,且采用提出算法的两个传感器所得结果基本一致,在实际跟踪场景中,两个传感器的跟踪结果都具有可靠的参考性,不像其他算法,在不同时刻、不同位置两个传感器的跟踪结果具有较大的差异。
表2给出了算法在不同噪声强度下的平均OSPA距离(为两个传感器滤波结果OSPA的平均值),明显可以看出,随着噪声强度的增大,算法的跟踪精度都有所下降,但提出算法的跟踪精度都明显要高于其他算法;此外,采用本文提出信息交互反馈策略的PF-IFMB算法的跟踪精度也略高于GCI-MB算法,而PF-MB算法的跟踪精度最低。图9给出提出算法在不同检测概率情况下的平均OSPA距离,同样可以看出,提出算法的跟踪精度都明显要高于PF-MB算法、PF-IFMB算法及GCI-MB算法。

图8 高观测噪声下(σ=0.05)算法的OSPA误差统计及势估计图
Fig.8 The OSPA error and cardinality estimation of the algorithm with high observation noise (σ=0.05)
表2 不同噪声强度下的位置/势估计平均OSPA
Tab.2 Average OSPA of location / cardinality estimation with different noise intensities

噪声强度/算法Proposed MethodPF-IFMBPF-MBGCI-MBσ=0.0112.9624/8.621716.9941/10.935724.4830/17.022718.1885/11.6193σ=0.02516.1463/9.562021.6616/12.481728.7582/21.632021.7689/13.0103σ=0.0525.3497/13.426037.4290/23.121052.3487/39.490537.8048/24.8760
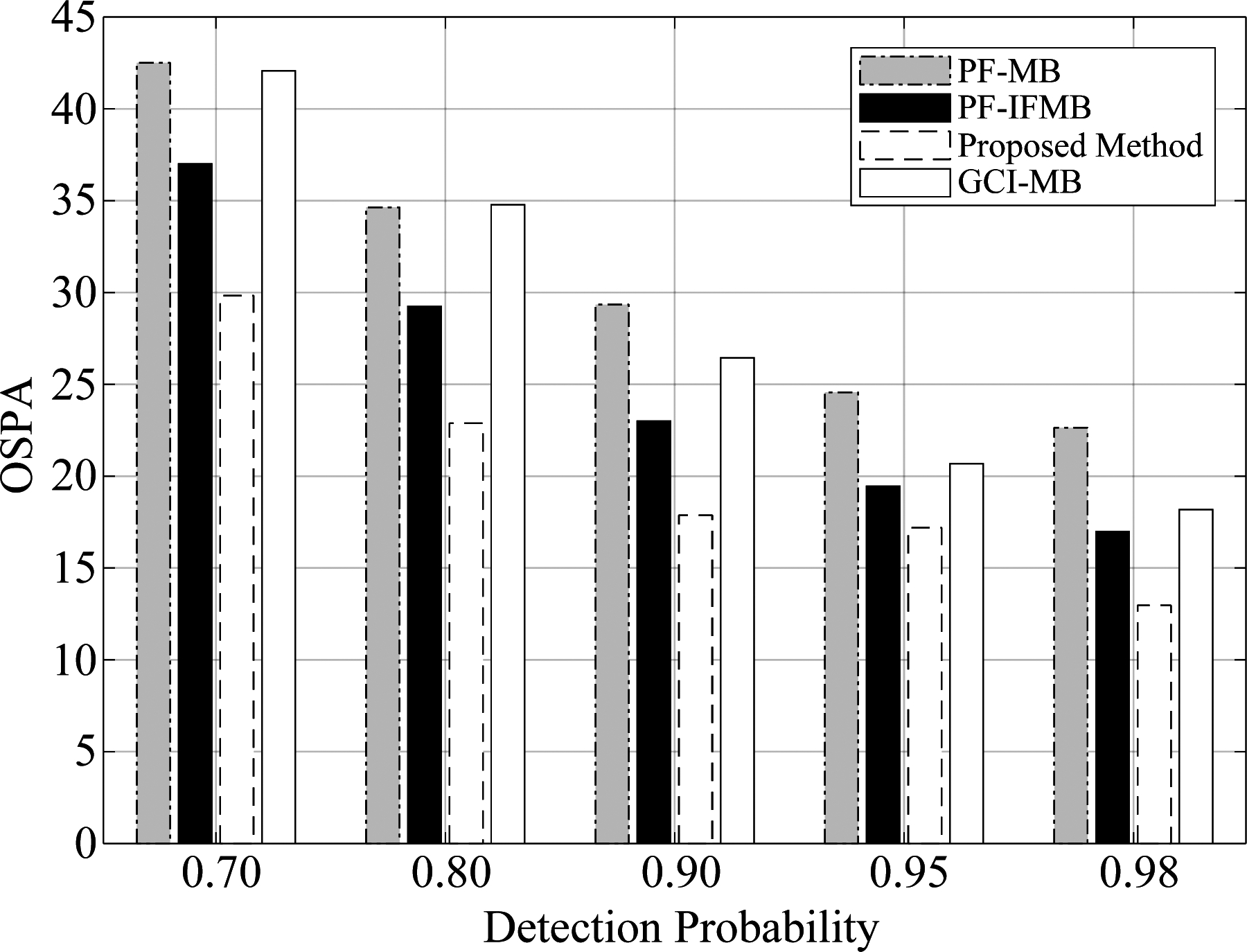
图9 低观测噪声(σ=0.01)下不同检测概率 下算法的平均OSPA图
Fig.9 Average OSPA of the algorithm based on different detection probability with low observation noise (σ=0.01)
5.2 数目变化的多目标作交叉运动
三个目标的初始状态分别为[-500 m, 10 m/s, 300 m,-4 m/s]T、[-500 m, 20 m/s, 200 m, 2 m/s]T和[500 m, -12 m/s, 200 m, -2 m/s]T,跟踪总时间为50 s。其中,目标T1在第1秒新生,第50秒消失;目标T2在第10秒新生,在第45秒消失;目标T3在第5秒新生,在第50秒消失。图10给出了目标运动的轨迹,实验结果如图11~图13所示,给出了目标运动存在交叉紧邻的情况下,三种不同噪声强度下提出算法和对比算法的OSPA误差统计及目标势估计图。
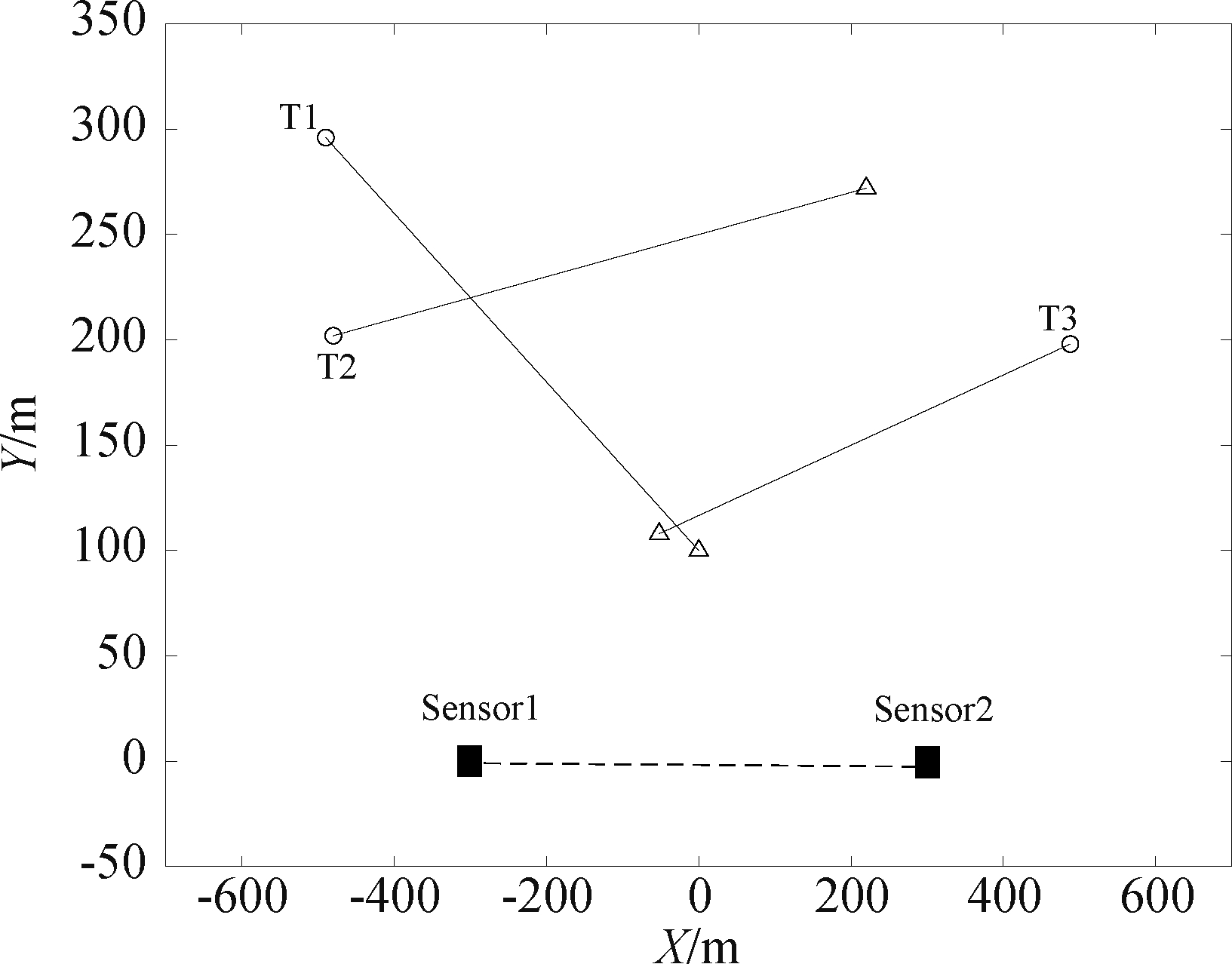
图10 目标交叉的运动场景 (“○”表示起点,“△”表示终点)
Fig.10 Cross motion scene of multi-target, in which “○” indicates the starting position of the target and “△” indicates the ending position of target
从图11(a)中可以看出,存在目标交叉和目标新生时,当观测噪声较小时(σ=0.01),各算法的跟踪精度比较接近,总体上来看,提出算法依然能保持相对较高的估计精度。图11(b)中给出了各算法在势估计上的比较,可以看出,在低噪声下,各个算法的势估计也都比较准确。
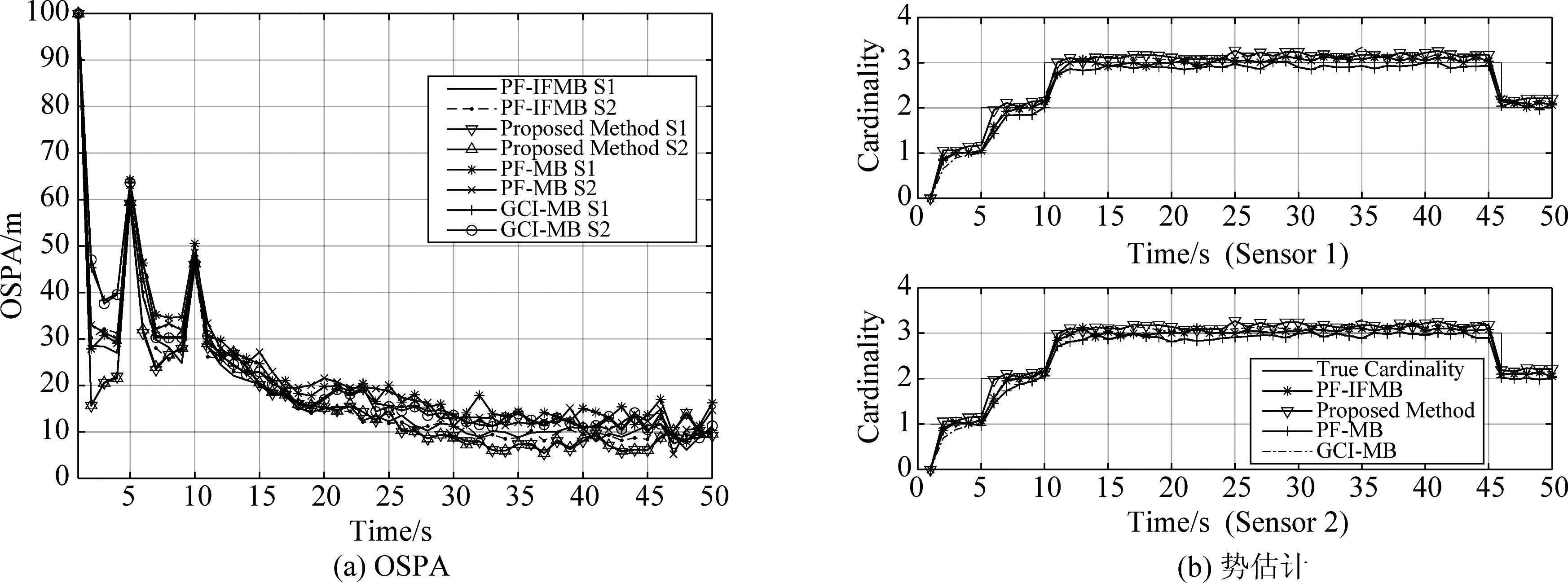
图11 低观测噪声下(σ=0.01)算法的OSPA及势估计图
Fig.11 The OSPA error and cardinality estimation of the algorithm with low observation noise (σ=0.01)
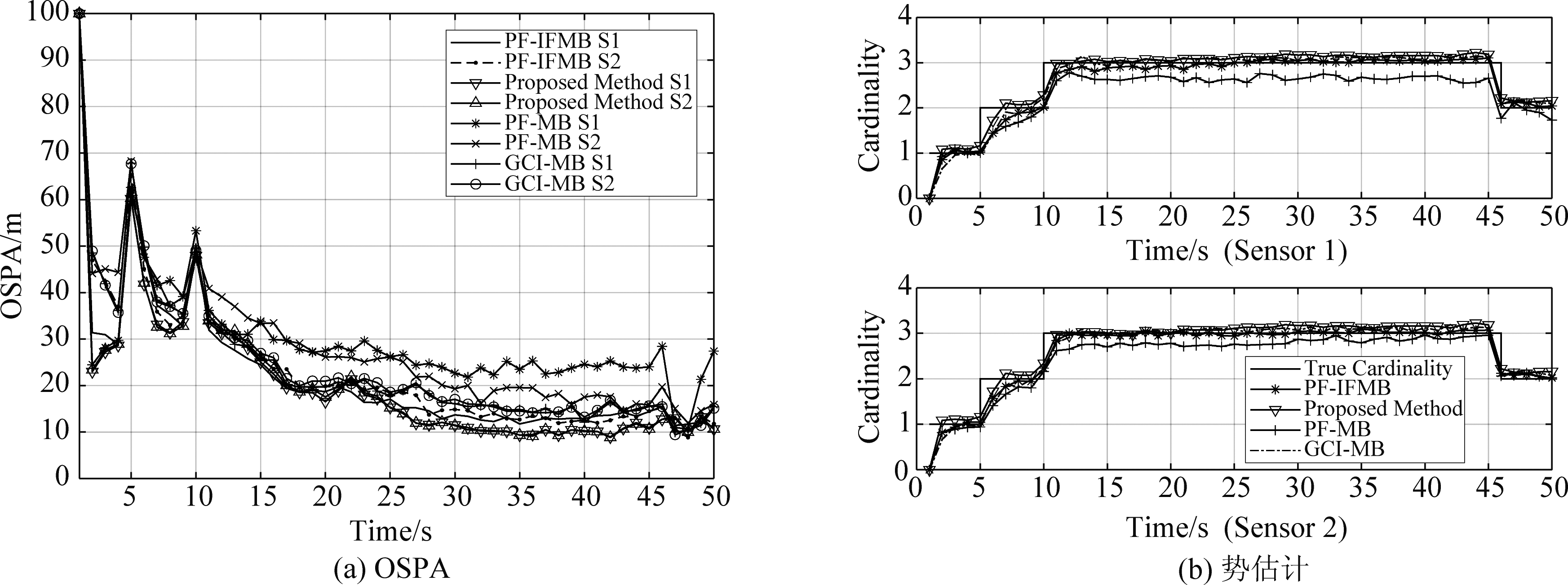
图12 中等观测噪声下(σ=0.025)各方法OSPA误差图及势估计图
Fig.12 The OSPA error and cardinality estimation of the algorithm with moderate observation noise (σ=0.025)
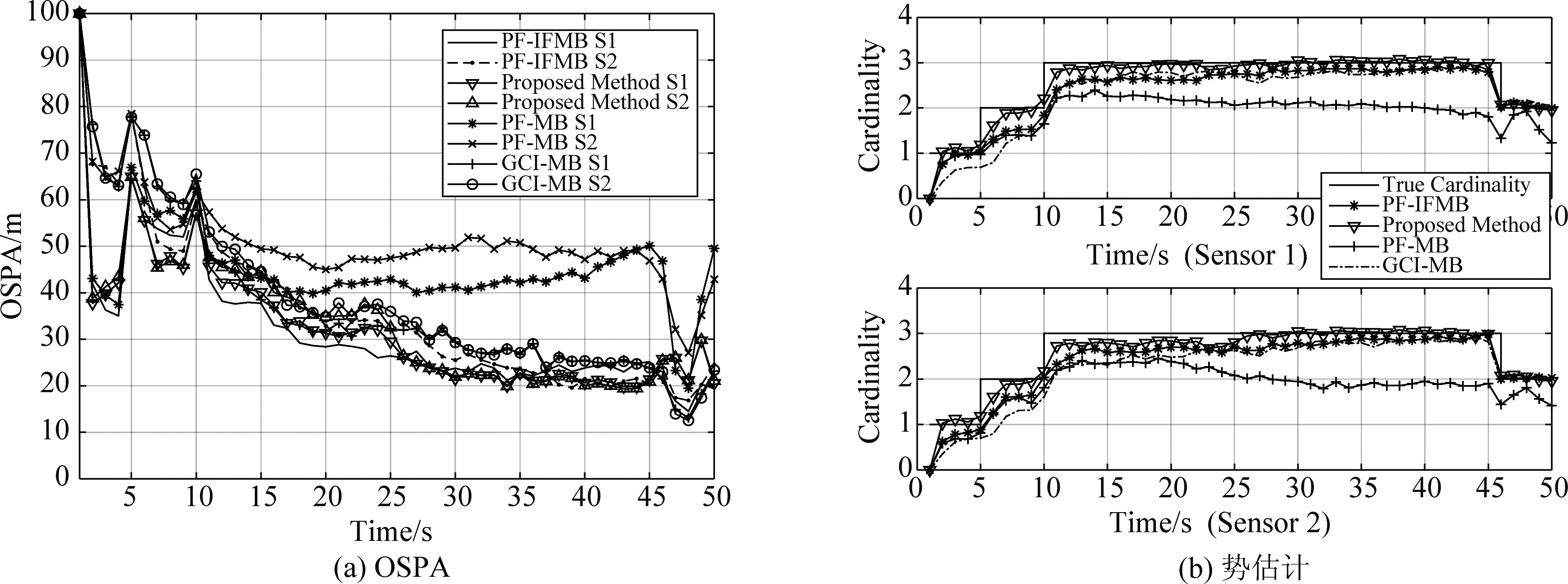
图13 高观测噪声下(σ=0.05)算法的OSPA及势估计图
Fig.13 The OSPA error and cardinality estimation of the algorithm with high observation noise (σ=0.05)
从图12所示的OSPA和势估计图中可以看出,当观测噪声取σ=0.025时,提出算法、PF-IFMB算法以及GCI-MB算法均明显优于PF-MB算法,其中,提出算法总体上更优,GCI-MB算法与PF-IFMB算法则较为接近。其中,由于GCI-MB算法缺少提出方法中的决策级融合策略对融合结果的二次处理,对于某些误差较大的融合结果进行反馈会进一步影响后续滤波与融合的精度,虽然势估计准确,但依然在精度上略低于PF-IFMB算法。
从图13(a)中可以看出,当观测噪声取值σ=0.05时,PF-MB算法的跟踪精度严重下降,势估计不准确,存在大量目标漏跟。而提出算法、PF-IFMB算法和GCI-MB算法在状态估计与势估计上都明显优于PF-MB,但采用PF-IFMB算法的不同传感器所获得的估计状态仍然存在较大的差异。总体来说,在高噪声的情况下,提出算法的跟踪精度也略高于PF-IFMB算法和GCI-MB算法,且跟踪性能比较稳定。从图13(b)势估计比较图中同样可以看出,提出算法的势估计明显要优于其他几种算法。
表3 不同噪声强度下的位置/势估计平均OSPA
Tab.3 Average OSPA of location / cardinality estimation with different noise intensities

噪声强度/算法Proposed MethodPF-IFMBPF-MBGCI-MBσ=0.0117.1692/9.437718.5681/11.839822.6385/14.636721.5107/13.4819σ=0.02520.8107/10.767222.9162/13.327329.8699/19.935024.6450/15.2088σ=0.0533.2339/15.263734.2717/19.816248.3401/33.796537.8048/24.0528
表3给出算法在不同噪声强度下的平均OSPA误差,可以看出,随着观测噪声的增大,平均OSPA误差均明显增大,但各观测噪声下提出算法的平均OSPA误差值均最低,表明提出算法的跟踪精度要明显高于其他几种算法。图14给出交叉运动场景下各对比算法在不同检测概率情况下的平均OSPA距离,同样可以看出,提出算法的跟踪精度都明显要高于PF-MB算法、PF-IFMB算法即GCI-MB算法。
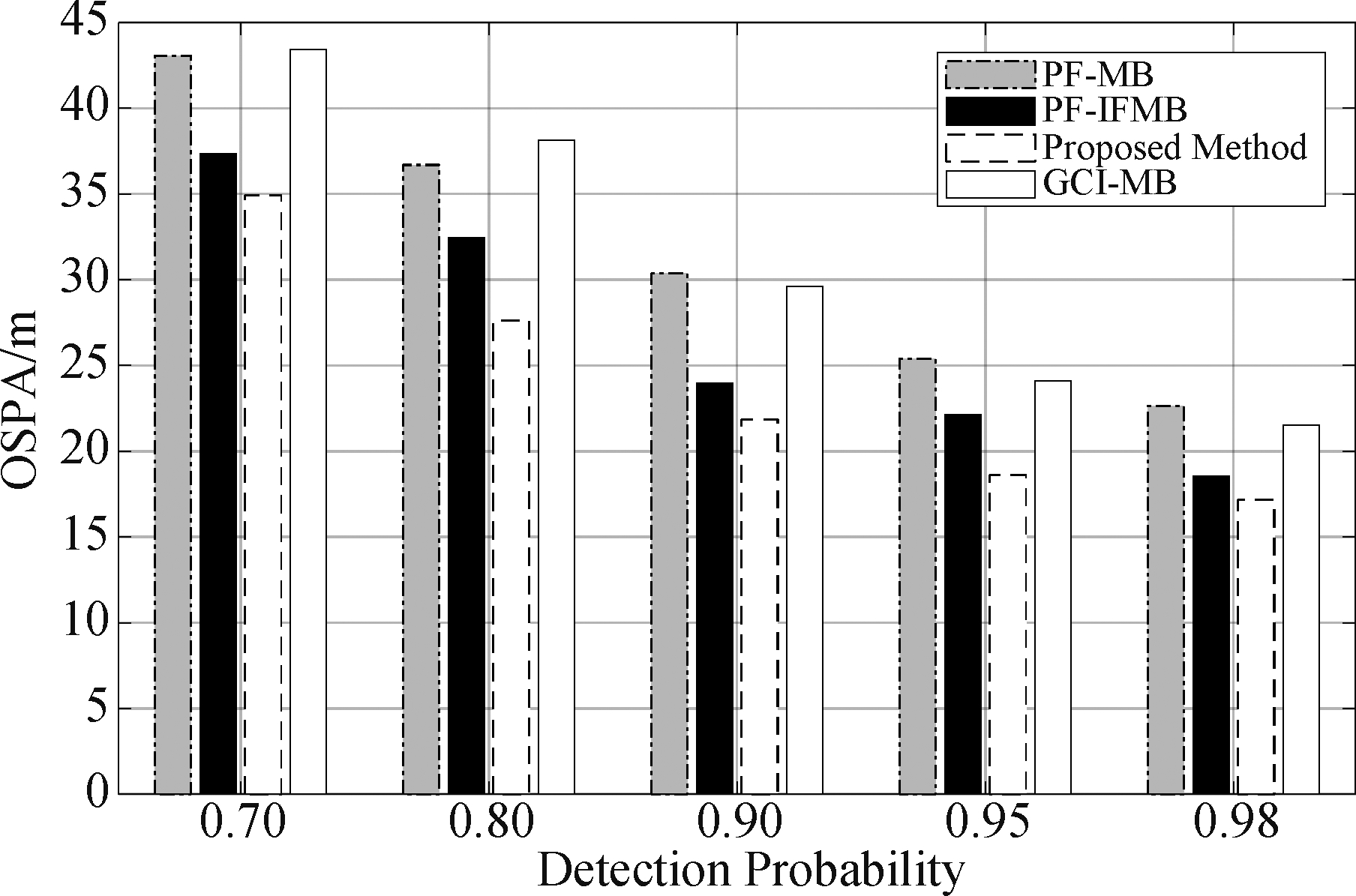
图14 低观测噪声(σ=0.01)下算法在不同 检测概率下的OSPA误差图
Fig.14 Average OSPA of the algorithm based on different detection probability with low observation noise (σ=0.01)
5.3 三传感器跟踪场景及算法时间复杂度分析
本实验场景包含5个运动目标和3个传感器,各目标初始状态分别为[-500 m, 20 m/s, 200 m, 2 m/s]T、[500 m, -12 m/s, 200 m, -2 m/s]T、[-500 m, 10 m/s, 300 m, -4 m/s]T、[400 m, -18 m/s, 160 m, 1.6 m/s]T和[-250 m, 20 m/s, 150 m, 1 m/s]T,传感器坐标分别为(0 m, 50 m)、(300 m, 0 m)以及(-300 m, 0 m)。其中,目标T1在第10秒新生,第45秒消失;目标T2在第5秒新生,在第50秒消失;目标T3在第1秒新生,在第50秒消失;目标T4在第15秒新生,在第40秒消失;目标T5在第20秒新生,在第35秒消失。图15给出了目标运动轨迹及传感器位置,图16给出了算法的OSPA统计和势估计的对比,表4给出了提出算法采用不同传感器数量的OSPA误差比较。图17中给出了在高杂波率下各算法的实验结果,并进行了分析与说明。表5给出了提出算法与传统GCI-MB算法的时间复杂度及实验实际运行时间。

图15 更复杂的目标运动场景(“○”表示起点, “△”表示终点,“虚线”表示传感器间可进行数据交换)
Fig.15 More complex target motion scene (“○” indicates the starting position of the target and “△” indicates the ending position of target, and “dashed line” indicates that data can be exchanged between sensors)
从图16可以看出,提出算法在复杂的多目标场景中仍然具有较好的跟踪性能,跟踪效果优于传统的GCI-MB算法以及普通单传感器MB滤波算法。
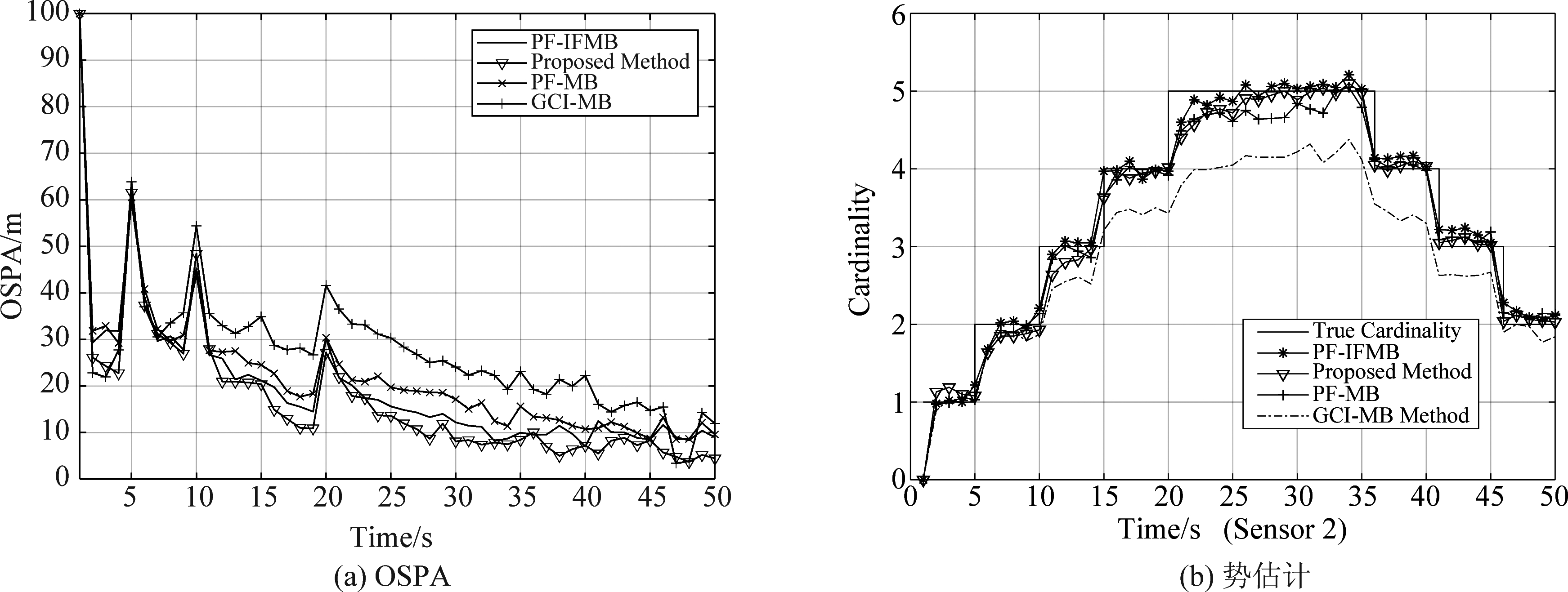
图16 三站跟踪场景下算法跟踪的OSPA及势估计(观测噪声σ=0.01)
Fig.16 OSPA and cardinality estimation of the proposed algorithm in three-sensor tracking scenario (σ=0.01)
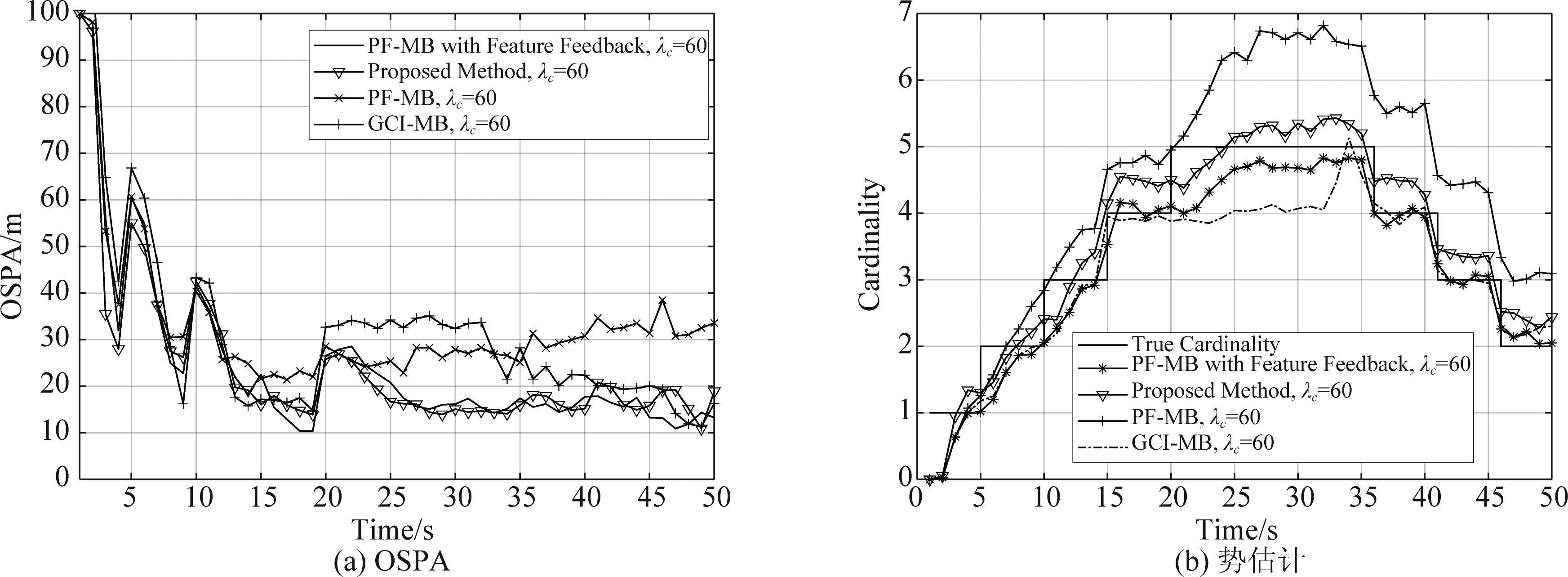
图17 高杂波率(λc=60)下算法跟踪的OSPA及势估计(观测噪声σ=0.01)
Fig.17 OSPA and cardinality estimation of proposed algorithm under high clutter rate (λc=60, σ=0.01)
传统GCI-MB算法在此场景下易出现图1所示的融合情况,且异常融合结果反馈会进一步恶化传感器的跟踪性能,故采用该算法的势估计明显偏低。从表4中可以看出,传感器数量的增加也可以进一步提升对目标的跟踪精度。
表4 提出算法在不同传感器数量下算法跟踪的OSPA
Tab.4 The OSPA error of the proposed algorithm with different sensor numbers

传感器数量123OSPA22.625318.231617.4811
图17为高杂波率下(λc=60)各算法的实验结果,其中,为了便于算法性能分析,在单传感器PF-MB算法基础上增加4.2节提出的特征级反馈步骤,算法记为PF-MB with Feature Feedback(FF-PF-MB)。从实验结果中可以看出,GCI-MB算法由于其状态输出完全依赖融合结果,高杂波率对势估计影响不大;而PF-MB算法在高杂波率下,会出现势估计严重偏高问题(MB滤波器本身具有高杂波率敏感特点),而FF-PF-MB算法可以有效降低高杂波率对MB滤波器的影响,从而能够保证提出算法采用4.1节决策级融合策略综合特征级融合反馈策略,在高杂波率下不会出现势估计严重偏高问题,具有良好的跟踪精度。
分布式算法主要的计算负载来自于融合计算,因此,本文仅分析融合计算时两种算法的计算复杂度。假设融合双方,索引集分别为L1与L2,GCI-MB算法中,需计算GMB项的数量为![]() 其中,
其中,![]() 假设|L1|=n,|L2|=m并且n≤m,每一个GMB项的计算复杂度假定相同为Ο(TGMB)(详细计算过程见文献[15]),则
假设|L1|=n,|L2|=m并且n≤m,每一个GMB项的计算复杂度假定相同为Ο(TGMB)(详细计算过程见文献[15]),则![]() 表示I对应融合映射空间,
表示I对应融合映射空间,![]() 可得到
可得到![]() 提出算法利用式(19)计算损失矩阵,复杂度为Ο(mn),再利用损失矩阵与一个自定义常量H结合Murty算法(时间复杂度为Ο(m4),具体原理见文献[5]),将需要计算的GMB项数降至H,则提出算法计算复杂度为Ο(m4+mn+H·TGMB),Ο(mn)显然小于其他两项,所以提出算法的复杂度为Ο(max{m4, H·TGMB})。
提出算法利用式(19)计算损失矩阵,复杂度为Ο(mn),再利用损失矩阵与一个自定义常量H结合Murty算法(时间复杂度为Ο(m4),具体原理见文献[5]),将需要计算的GMB项数降至H,则提出算法计算复杂度为Ο(m4+mn+H·TGMB),Ο(mn)显然小于其他两项,所以提出算法的复杂度为Ο(max{m4, H·TGMB})。
表5 提出算法与GCI-MB算法计算复杂度及运行时间
Tab.5 The execution time and computational complexity of the proposed method and GCI-MB

算法提出算法GCI-MB计算复杂度Ο(max{m4, H·TGMB})Ο(2n·Anm·TGMB)(单次)算法运行时间/min4.111615.6865
6 结论
在多伯努利滤波框架下,针对分布式多传感器GCI融合跟踪存在的问题提出一种改进的多目标跟踪算法,即在分布式融合过程中提出决策级融合策略、特征级融合反馈策略和交互反馈策略。其中,通过决策级融合输出策略,可以有避免直接利用融合结果进行状态输出而导致状态漏估问题,通过特征级融合反馈策略,有效降低错误融合对后续滤波过程的不良影响,通过交互反馈融合策略,进一步改进了局部单传感器滤波中可能存在的目标跟丢问题。最后,通过对不同场景下多目标跟踪的实验验证,提出算法明显要优于其他对比算法,表明提出算法在复杂环境下具有较好的跟踪性能。同时,标签滤波器LMB的分布式融合算法GCI-LMB在Lable-Free融合方案下会利用到GCI-MB的融合技术,因此,基于GCI-MB的改进算法可以扩展应用于GCI-LMB算法中,下一步的工作考虑将本方案与GCI-LMB相结合,研究更高效的基于标签滤波器的分布式多传感器多目标跟踪算法。
[1] Mahler R. Multitarget Bayes Filtering via First-Order Multitarget Moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.
[2] Vo B T, Vo B N, Cantoni A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.
[3] Mahler Ronald P S, Ebrary I. Statistical Multisource-Multitarget Information Fusion[M]. Norwood, MA: Artech House, 2007.
[4] Vo B T, Vo B N, Cantoni A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409-423.
[5] Vo B T, Vo B N. Labeled Random Finite Sets and Multi-Object Conjugate Priors[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3460-3475.
[6] Vo B T, Vo B N. The Labeled Multi-Bernoulli Filter[J]. IEEE Transactions on Signal Processing, 2014, 62(12): 3246-3260.
[7] Vo B N, Ma W K. The Gaussian Mixture Probability Hypothesis Density Filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.
[8] Zhang Huanqing, Ge Hongwei, Yang Jinlong, et al. A GM-PHD algorithm for multiple target tracking based on false alarm detection with irregular window[J]. Signal Processing, 2016, 120: 537-552.
[9] Wang Pin, Xie Weixin, Liu Zongxiang, et al. A Novel Gaussian Mixture PHD Filter for Nonlinear Models[J]. Acta Electronica Sinica, 2012, 40(8): 1597-1602.
[10]Li Wenling, Jia Yinming. Nonlinear Gaussian mixture PHD filter with an H∞ criterion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 2004-2016.
[11]Gao Xinbo, Chen Jinguang, Tao Dacheng, et al. Multi-Sensor Centralized Fusion without Measurement Noise Covariance by Variational Bayesian Approximation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 718-727.
[12]Leonard M R, Zoubir A M. Multi-target tracking in distributed sensor networks using particle PHD filters[J]. Signal Processing, 2019, 159: 130-146.
[13]Mahler R. Optimal/Robust distributed data fusion: a unified approach[C]∥Proceedings of Signal Processing, Sensor Fusion, and Target Recognition IX. International Society for Optics and Photonics, Orlando, USA, August 2000, 4052: 128-138.
[14]Uney M, Clark D E, Julier S J. Distributed Fusion of PHD Filters Via Exponential Mixture Densities[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 521-531.
[15]Wang Bailu, Yi Wei, Hoseinnezhad R, et al. Distributed Fusion with Multi-Bernoulli Filter based on Generalized Covariance Intersection[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 242-255.
[16]王佰录, 易伟, 李溯琪,等. 分布式多目标伯努利滤波器的网络共识技术[J]. 信号处理, 2018, 34(1): 1-12.
Wang Bailu, Yi Wei, Li Suqi, et al. Consensus for Distributed Multi-Bernoulli Filter[J]. Journal of Signal Processing, 2018, 34(1): 1-12.(in Chinese)
[17]Li Suqi, Yi Wei, Hoseinnezhad R, et al. Robust Distributed Fusion With Labeled Random Finite Sets[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 278-293.
[18]Li Suqi, Battistelli G, Chisci L, et al. Multi-sensor multi-object tracking with different fields-of-view using the LMB filter[C]∥Proceedings of 21st International Conference on Information Fusion (FUSION), IEEE, Cambridge, UK, July 2018.
[19]Yi Wei, Jiang Meng, Li Suqi, et al. Distributed sensor fusion for RFS density with consideration of limited sensing ability[C]∥Proceedings of 20th International Conference on Information Fusion (Fusion). IEEE, Xi’an, China, July 2017.
[20]Li Guchong, Battistelli G, Yi Wei, et al. Distributed Multi-sensor Multi-view Fusion based on Generalized Covariance Intersection[J]. Signal Processing, 2019, 166: 107246.
[21]Li Tiancheng, Hlawatsch F, ![]() P M. Cardinality-consensus-based PHD filtering for distributed multitarget tracking[J]. IEEE Signal Processing Letters, 2018, 26(1): 49-53.
P M. Cardinality-consensus-based PHD filtering for distributed multitarget tracking[J]. IEEE Signal Processing Letters, 2018, 26(1): 49-53.
[22]Gostar A K, Rathnayake T, Tennakoon R, et al. Cooperative sensor fusion in centralized sensor networks using Cauchy-Schwarz divergence[J]. Signal Processing, 2020, 167: 107278.
[23]Van Trees H, Bell K. A Tutorial on Particle Filters for Online Nonlinear/NonGaussian Bayesian Tracking[M]. Wiley-IEEE Press, 2007.
[24]Li X R, Jilkov V P. Survey of Maneuvering Target Tracking. Part I: Dynamic Models[J]. IEEE Transactions on Aerospace and Electronic System, 2003, 39(4): 1333-1364.
[25]Schuhmacher D, Vo B T, Vo B N. A Consistent Metric for Performance Evaluation of Multi-Object Filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
[26]Xiao L, Boyd S, Lall S. A scheme for robust distributed sensor fusion based on average consensus[C]∥Proceedings of Fourth International Symposium on Information Processing in Sensor Networks. IEEE, Boise, USA, April 2005.


