1 引言
近年来,无源定位系统由于其电磁隐蔽性高,抗干扰能力强[1]等优点,在电子支援系统及民用空防领域中占据着越来越重要的地位,并已被大量地应用于航空、航海、电子战、无人机反制等领域中。在多站无源定位系统中,多个接收站截获辐射源辐射的电磁波信号[2]并提取定位参数,如接收信号强度(Received Signal Strength, RSS)、到达角度(Angle Of Arrival, AOA)、到达时间(Time Of Arrival, TOA)、到达时间差(Time Difference Of Arrival, TDOA)等,以此建立并求解目标位置信息与定位参数之间的非线性方程,最终实现目标定位。其中,利用RSS的定位方法精度受信道环境影响较大[3- 4],在环境复杂的实战应用中定位性能较差;TOA联合AOA的定位方法则需要接收站与目标保持精确的时间同步[5],而且对硬件要求较高,多数应用场合无法满足其要求;TDOA定位由于其定位精度高,只要求基站间严格同步[6],系统构成简单等优点,逐渐成为一种常用的定位方法。TDOA定位技术通过测量源信号到达不同接收站的时间差获得距离差,并将其表示为一组双曲线方程,实际情况中,由于接收站布站形式的随机性和复杂性,在求解双曲线方程组时会遇到非线性问题,这会导致方程组求解产生模糊的定位结果。为解决这一问题,获得最优解,很多基于TDOA的算法被提出,如文献[7]提出的泰勒级数展开法将高度非线性的定位方程线性化处理,通过多次迭代求解目标位置,但该算法需要良好的初值作为全局最优的保证,在先验条件较少的情况下,算法性能无法保障。为了更好地适用于非合作目标的定位,文献[8]提出了一种利用两步加权最小二乘的代数解决方法,该算法不涉及初值拟定问题,避免了误差较大的初值对定位结果产生恶劣影响。
然而,上述文献都只考虑了TDOA测量误差[9],而假设接收站位置信息精确、已知。但在实际情况中,尽管接收站都携带有全球定位系统(Global Positioning System, GPS),但由于存在卫星时钟误差、星历误差、电离层和对流层影响以及多路效应等,GPS存在系统误差,其中的常值误差可通过信号接收、差分技术得到较好的抑制和消除[10],但自定位得到的接收站位置信息仍存在随机误差,即使是很小的误差也会大幅度降低算法的定位精度,K.C.Ho在文献[11]中证明了这一点。故在定位过程中不可忽略接收站的位置误差,否则将导致定位误差增大、精度降低。为弥补精度损失,文献[11]提出了考虑站址误差的两步加权最小二乘(Two-Stage Weighted Least Squares, TSWLS)算法,但由于该算法存在缺秩问题,当空间目标接近参考接收站的任何坐标轴时,算法的定位精度就会变差,稳健性低。最近,文献[12]提出了一种改进版本的TSWLS算法,该算法通过避开TSWLS算法第2步中导致误差增大的平方、开方等非线性操作,获得了更高的定位精度。但是文献[12]在其第1步粗估中进行了泰勒展开并忽略泰勒展开的二阶项,这在一定程度上会导致算法定位精度的降低。
为了进一步使定位模型贴近实际,提高定位精度,并改善现有算法稳健性,本文提出了一种改进算法。算法首先通过引入辅助变量线性化定位方程,利用加权最小二乘初步估计目标位置;然后利用辅助变量与目标位置之间的关系,构建新的等式方程,对步骤1结果的误差进行估计;最后用目标位置初步估计值减去误差估计值,得到最终解。与传统定位算法不同的是,本文算法的步骤2基于误差校正和泰勒展开构建定位方程,不仅消除了传统基于TSWLS算法中的非线性运算,而且巧妙地避免了该类算法中矩阵缺秩的问题。理论分析和仿真实验表明本文算法在噪声较小时可达到克拉美罗下界(Cramer-Rao Lower Bound, CRLB),且相比于现有算法,所提算法具有更好的抗噪性和稳健性。
本文包括的所有符号意义如下:斜体加粗表示矩阵和向量,[·]T和[·]-1表示矩阵的转置和矩阵的逆,E[·]表示数学期望,·表示二范数,(·)o表示真实值,(·)表示含噪声的测量值,
表示估计值,0i×j表示一个i×j维的零向量矩阵,Ii×j表示一个i×j维的单位矩阵。
2 定位模型
本文考虑三维辐射源定位场景,假设某无源定位系统中存在M个接收站,用以估计一个位于uo=[xo,yo,zo]T的目标位置。第i个接收站的真实位置表示为
令
由于实际场景中存在站址误差,我们只能获取到不准确的接收站位置
其中,si=[xi,yi,zi]T,为第i个接收站可利用的位置。接收站站址误差向量为
假设Δs是零均值高斯分布的,其协方差矩阵为E[ΔsΔsT]=Qs[11]。
根据上述定义,目标与接收站i之间的真实距离可表示为
(1)
不失一般性,本文将接收站s1作为参考站[5- 8],则目标到si与s1的距离差为
(2)
令ro=[r21,r31,…,rM1]T,由于实际场景中存在测量误差,我们有r=ro+n,其中,r=[r21,r31,…,rM1]T为TDOA测量向量, n=[n21,n31,…,nM1]T为噪声向量,假设n是零均值高斯分布的,且与Δs相互独立,其协方差矩阵表示为E[nnT]=Qn[11]。本文使用上述定义向量r和n实现对目标的定位。
3 定位算法
本文定位算法共分为两步,在TSWLS算法步骤1的基础上改进的步骤2是算法性能提升的关键,因此本节只给出第1步的简述,而详细给出步骤2的推导过程。
3.1 定位方程伪线性化初步定位
将
两边平方,用式(1)分别表示
并将
替换为
替换为si-Δsi,其中,ri1和si为含误差的测量值,忽略二阶误差项得
(3)
其中,εt,i是服从零均值高斯分布的等式误差,定义ε1=[εt,2,εt,3,…,εt,M]T,由式(3)可得
(4)
其中,
为待求向量,
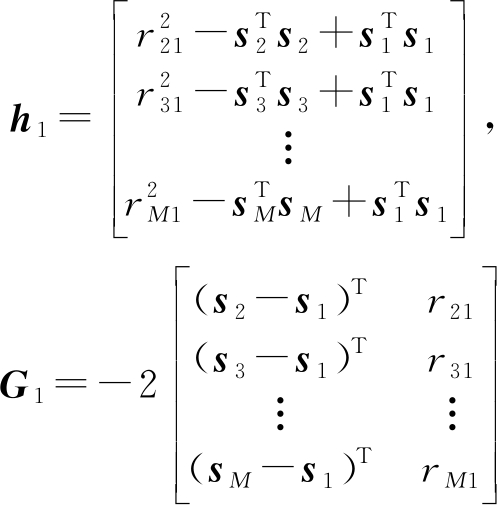
(5)
ε1还可以用n和Δs表示为
ε1=B1n+D1Δs
(6)
其中
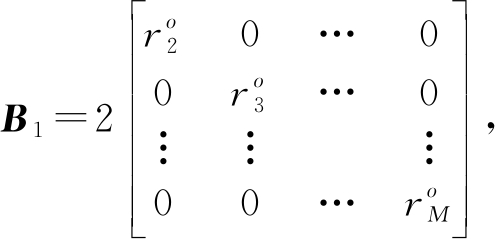D1=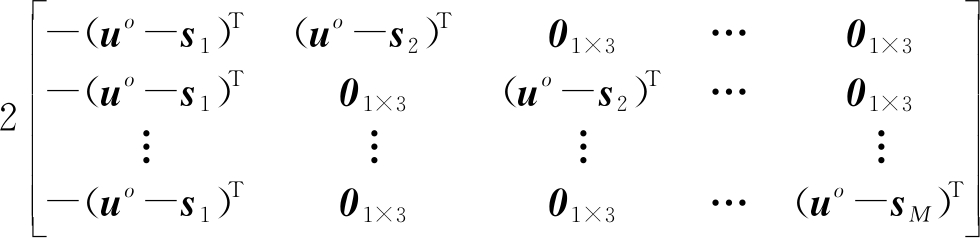 
(7)
由式(1)可知
与uo相关,式(4)是关于uo的非线性方程。如果假设与uo不相关,式(4)将变成关于
的线性方程,则可用加权最小二乘估计得
(8)
其中,加权矩阵
根据式(6)有
W1=E[(B1n+D1Δs)(B1n+D1Δs)T]-1= 
(9)
定义估计误差
表示为
(10)
由于n、Δs服从零均值高斯分布,故在噪声较小时,Δφ1均值近似为零,也就是说
是渐进无偏的,其协方差矩阵可表示为[13]
(11)
需要注意的是,由式(9)和式(7)可知加权矩阵W1的确定需要未知向量uo,在实际实现时,可将加权矩阵近似为
并将此W1带入式(8)中,得到初始估计值
再利用初估值更新加权矩阵W1,进而得到更好的估计值。
3.2 基于误差校正的高精度稳健定位
通过初步定位,我们得到了一个对目标位置的初步估计结果
为避免TSWLS算法步骤2中对平方,开方等非线性运算,以及忽略平方的二次误差项致使最终目标误差增大的操作,本文在步骤2中对泰勒展开,通过加权最小二乘估计步骤1的定位误差Δu,然后用初步定位结果
减去Δu,从而得到更准确的定位结果。
将在和s1处泰勒展开,并保留一阶项,有
(12)
其中,
且ρ2=-ρ1,设
下文中用
表示ρ1,ρ2。
将式(12)带入
得
(13)
由于Δφ1近似为零均值,故Δu近似也为零均值,有
03×1=Δu-Δu
(14)
结合(13)、(14)两式,令φ2=[Δu],构造步骤2矩阵方程
(15)
其中
(16)
式(15)的误差值ε2可用Δφ1、Δs表示为
ε2=B2Δφ1+D2Δs
(17)
其中
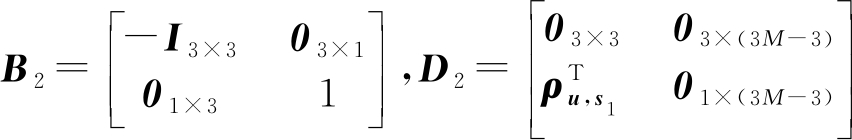
(18)
利用式(15),可得φ2的加权最小二乘解为
(19)
其中,加权矩阵
根据式(17)有
W2=E[(B2Δφ1+D2Δs)(B2Δφ1+D2Δs)T]-1= 
(20)
其中,cov(φ1)由式(11)给出。
的估计误差Δφ2为
(21)
其协方差为
(22)
最后,用步骤1的估计结果减去步骤2中Δu的估计值
可得目标位置的最终估计结果
(23)
综上所述,本文算法计算流程如下表 1所示。
表1 本文算法计算流程
Tab.1 Calculation steps of the proposed method
步骤步骤1 令W1=Q-1n,利用式(8)得到初估值φ^1;步骤2 将φ^1带入式(9)更新W1,重复计算式(8)得到更精确的估计值φ^1;步骤3 重复计算步骤2两次,利用式(11)计算估计值φ^1的协方差cov(φ^1);步骤4 将cov(φ^1)带入式(20)计算W2;步骤5 将W2带入式(19)计算φ^2;步骤6 将φ^2带入式(23)计算得到目标位置的最终估计结果。
4 性能分析
4.1 CRLB分析
CRLB是无偏线性估计器可实现的最小方差,是衡量一个无偏估计器的优良标准[14]。为了评估本文算法的估计性能,本节给出了本文定位场景下的新CRLB的推导与相关证明。
首先证明本文算法的渐进无偏性。将式(23)中的表示为uo+Δu,等号两边同时减去uo,可得
(24)
在噪声较小时,Δφ1、Δs均值都近似为0,故由式(21)、式(17)和式(24)可得
也就是说
是渐进无偏的。误差较小时,本文算法能提供目标位置的近似无偏估计。
下面证明本文算法在噪声较小时定位精度可以达到CRLB。从式(4)和式(7)可看出ε1正比于ro,故式(10)中的Δφ1也正比于ro,所以ε2的第一项起决定作用,即ε2≈B2Δφ1,因此
(25)
将式(9)中的W1,式(11)的cov(φ1)和式(25)中的W2带入式(22)中可得
(26)
其中,
由文献[11]可知,考虑站址误差TDOA定位的CRLB表达式为
CRLB(uo)-1=X-1-YZ-1YT
(27)
其中,
式(27)中,第一项X-1是不考虑站址误差时的CRLB,第二项是由于考虑了站址误差而增加的项。显然,式(26)与式(27)具有相同的矩阵形式。由文献[11]可知,在噪声较小的情况下,G4≈(∂ro/∂so),要证明本文算法定位精度可达CRLB,即cov(φ2)-1=CRLB(uo)-1,只需证G3≈∂ro/∂uo即可。G3可表示为
(28)
其中
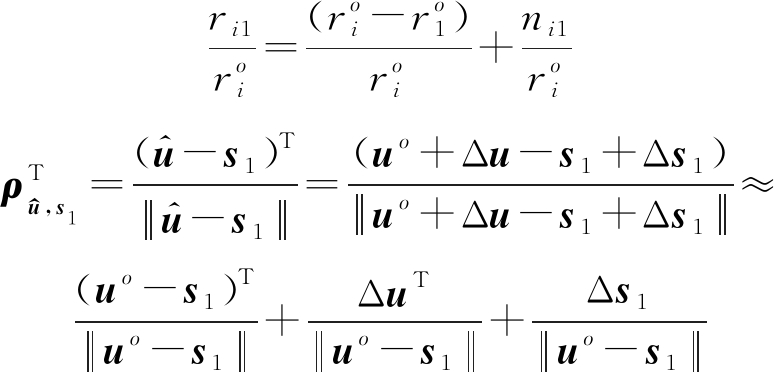
(29)
在噪声较小的情况下
有
(30)
故式(28)为
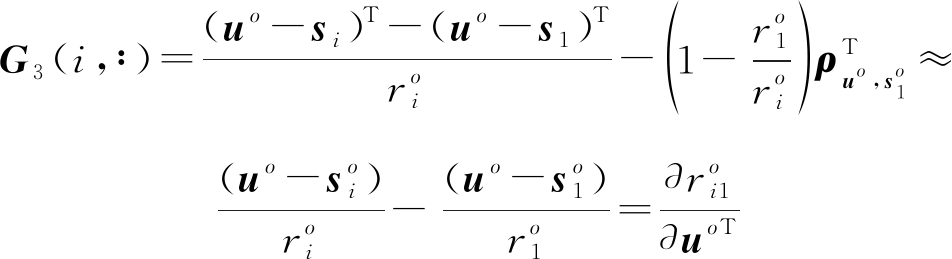
(31)
至此证得本文算法的定位精度在噪声较小的情况下可以达到考虑站址误差的CRLB。
4.2 定位精度分析
TSWLS算法的第2步利用与目标位置间的关系建立了新的等式方程以提高目标定位精度,在推导过程中,首先将第1步的估计值中的元素都平方,并忽略二阶误差项Δu⊙Δu和
表示为
(φ1(1∶3)-s1)⊙(φ1(1∶3)-s1)= (uo-s1)⊙(uo-s1)+2(uo-s1)⊙Δφ1(1∶3)
(32)
φ1(4)2=(uo-s1)T(uo-s1)+ 
(33)
用以估计新变量
再对估计结果进行开方等操作得到最终目标位置。其中,⊙代表矩阵的Schur积运算(元素和元素相乘)。TSWLS算法在目标位置求解过程中涉及平方、开方等非线性运算,可能会导致定位结果模糊或出现虚数解[15]。且在第2步求解时忽略了二阶误差项,但在噪声较大的情况下,二阶误差会显著增大以至于不能被忽略,故忽略二阶项可能会造成严重的定位精度下降。
本文算法的步骤2首先将在和s1处进行一阶泰勒展开,用以估计新变量
最后用第1步的估计值减去得到最终目标位置,避免了平方、开方等非线性操作以及由于忽略二次误差项造成的误差。尽管本文算法忽略了泰勒展开式的高阶相,但这些高阶项都和u-s1成反比,例如二阶项
(34)
由公式可见,当目标离接收站较远时,高阶相完全可以被忽略。故所提算法相比于文献[11]拥有更高的定位精度。
相比于文献[12]所提出的算法,本文没有在步骤1和步骤2分别对进行泰勒展开,而是统一在步骤2中进行展开,避免了两次忽略泰勒展开的高阶项造成的误差。且文献[12]在步骤1中计算ρuo,s1时,用的是存在较大误差的粗估值
因此所得的ρuo,s1误差也较大,而本文算法在步骤2中计算
时所用的已经是更新过三次误差较小的估计值。故本文的改动提高了算法的定位精度。
4.3 稳健性分析
由于空间目标位置的不确定性以及对定位连贯性的要求,在定位过程中,不能出现由于处在特殊地理位置而造成误差过大的目标点。
由式(19)可知的准确求解取决于
是否奇异,加权矩阵
算法中
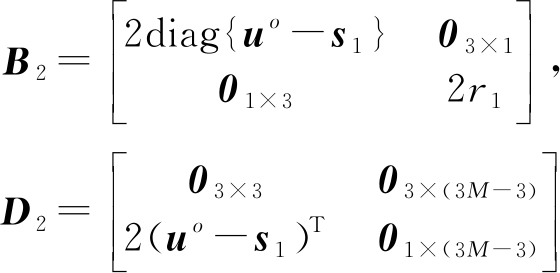
(35)
由式(35)可知,矩阵D2前三行元素全部为0,故是否奇异取决于B2是否奇异。对于TSWLS算法,当目标位置接近参考站的任一坐标轴时,(u-s1)中的某个元素接近为零,矩阵B2出现缺秩现象,所得为奇异矩阵,进而导致在这些特殊点附近无法得到准确的
定位误差增大。
本文算法中
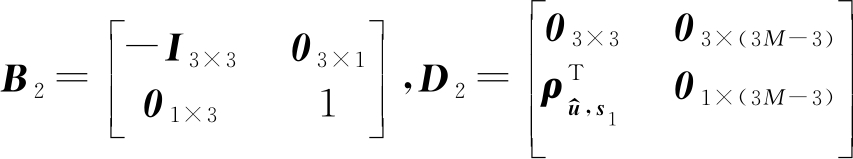
(36)
由式(36)可知,本文中D2前三行元素也全部为
是否奇异同样取决于B2,但本文算法中的B2在任何特殊点都不存在缺秩问题,都可以得到非奇异矩阵
进而得到准确的估计值
也就是说所提算法对空间目标定位的精度不受空间目标地理位置的影响,具有较强稳健性。
5 仿真结果与分析
本节利用仿真实验对比了TSWLS算法、文献[12]算法及本文所提算法的定位性能。对于以上三种算法,为了可以提供比较精确的估计值,需保证式(4)为非欠定方程[16],即在三维定位场景下需满足(M-1)≥(3+1),也就是说对于TSWLS算法、文献[12]算法及本文算法,定位至少需要5个接收站。考虑到实际应用的成本问题,本文仿真实验中选取M=5个接收站,其真实位置分别为
设TDOA观测向量r的协方差矩阵为
其中,σn为TDOA测量误差,R是(M-1)×(M-1)维矩阵,其对角线元素都为1,其余元素均为0.5;接收站位置向量s的协方差矩阵为
其中,σs为接收站站址误差,I是3M×3M维单位阵。
5.1 仿真一
仿真一的实验目的是验证本文所提算法的定位精度,实验通过比较各算法的均方根误差(Root Mean Squared Error, RMSE)来比较各算法的定位精度。对于目标位置的估计值
其中,uo是目标的真实位置, 
是第i次蒙特卡洛仿真得到的目标位置估计值[14],L是估计次数,实验中我们取L=500次。仿真一中,目标分为远场目标和近场目标两类,分别设两种目标的真实位置uo=[2000,2500,3000]T m,uo=[310,400,550]T m,TDOA测量误差σn=10-2 m,接收站站址误差σs=10-2～10 m,以小步进不断改变接收站站址误差水平,观察不同算法的定位性能。
图1给出了接收站站址误差从10-3 m到10 m 变化时,不同算法的定位RMSE和误差的变化情况。对于远场目标,当站址误差σs<0.631 m 时,所提算法定位精度完全可达CRLB,而TSWLS算法和文献[12]算法则分别在站址误差σs=0.316 m,σs=0.08 m时就已经偏离了CRLB。当站址误差σs=10 m时,所提算法的定位误差相比于TSWLS算法及文献[12]算法分别减少了166 m 及55.9 m。对于近场目标,当站址误差σs<3.981 m时,所提算法定位精度完全可达CRLB,而TSWLS算法和文献[12]算法则分别在站址误差σs=1.259 m,σs=1.995 m时就已经偏离了CRLB。当站址误差σs=10 m时,所提算法的定位误差相比于TSWLS算法及文献[12]算法分别减少了12.77 m及2.57 m。故相比于现有算法,在噪声较大的情况下,所提算法具有更高的定位精度,验证了4.2节中关于定位精度的分析。
另外,在图 1的子图(a)中TSWLS算法和文献[12]算法的RMSE并不是随站址误差的增大而单调增大,而是分别在站址误差为100.2 m和100.6 m处出现峰值后承下降趋势,这是因为在站址误差较大时,算法的估计结果是有偏的,其RMSE可能会出现低于CRLB的情况[17],故当站址误差增大到一定程度时算法的RMSE反而呈现下降趋势。而本文算法并未明显出现该种情况,具有更强的抗噪性。
5.2 仿真二
仿真二的实验目的是验证本文算法的稳健性。仿真中,设TDOA测量误差σn=10-2 m,接收站站址误差σs=10-1.5 m。为模拟现实情况中所有可能出现的情况,假定在高度为2000 m的情况下遍历二维平面所有点,为减少运算量,我们分别设置两种半径不同的源,R=2000 m和R=500 m,并假设其以z轴为中心,做圆周运动[18],模拟的运动轨迹为如图2所示,每隔10°在运动轨迹上抽取一个轨迹点进行定位,并计算定位的RMSE,这里蒙特卡洛实验次数L取50次即可,实验结果如下。
图3对比展示了本文算法与TSWLS算法的稳健性,我们可以看出,本文算法在目标位置方位角从0°变换到360°的过程中都可达到CRLB定位精度的要求,而对于TSWLS算法,在目标位置方位角为n×90°(n=0,1,…,4)时则出现明显误差增大的现象。如当
时,对于远场目标,(uo-s1)=(0,1700,2000)T,如4.3节中分析所述,由于TSWLS算法在该点产生矩阵缺秩现象,定位RMSE从个位数激增到十位数,在仿真图中呈现尖峰状。而本文算法得出的定位结果的RMSE则不随目标位置的改变而改变,故本文所提算法具有更强的稳健性。
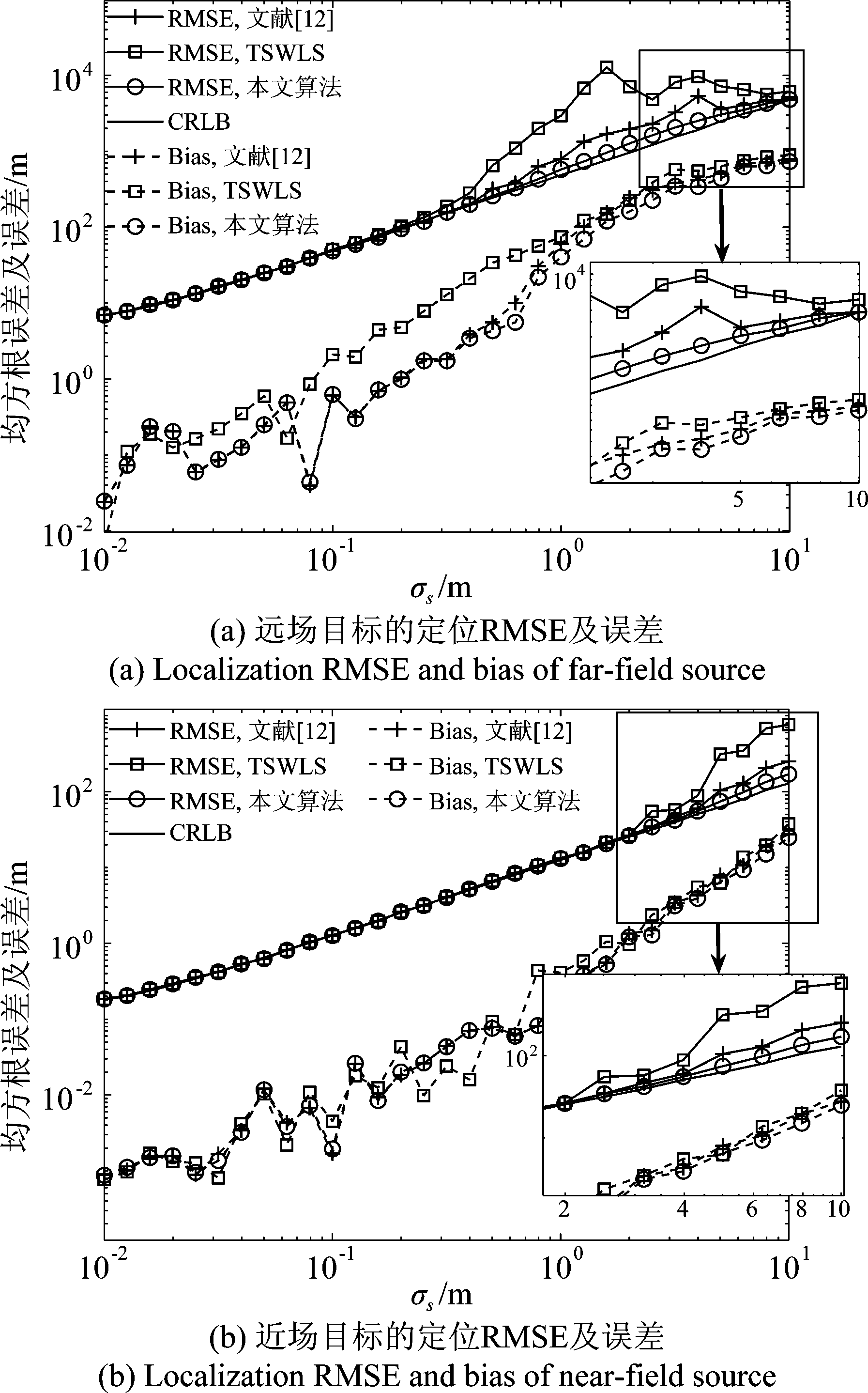
图1 目标定位误差随站址误差变化情况
Fig.1 Chang of positioning error among different sensor location error
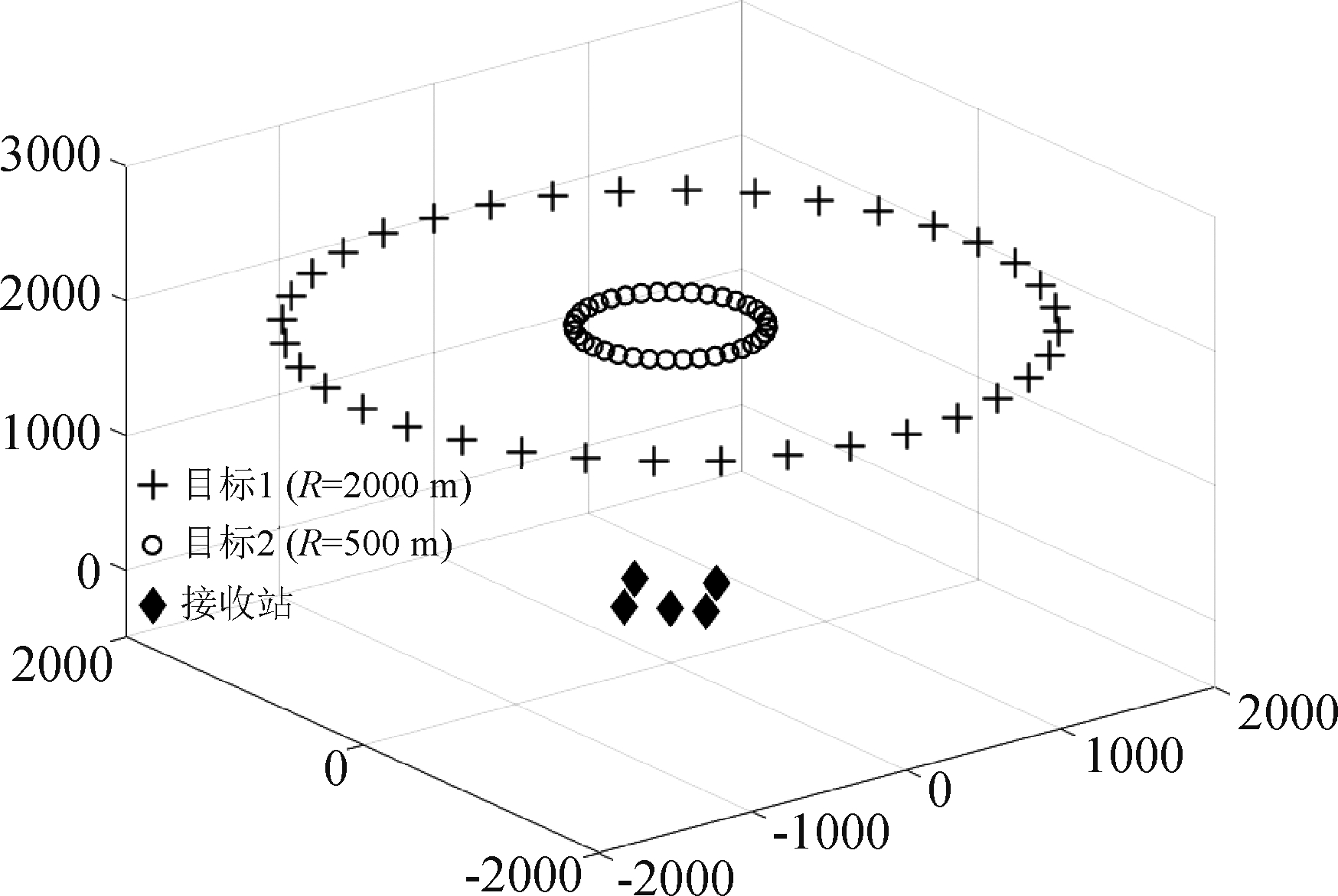
图2 接收站和目标的几何位置示意图
Fig.2 Geometric location of sensor and source
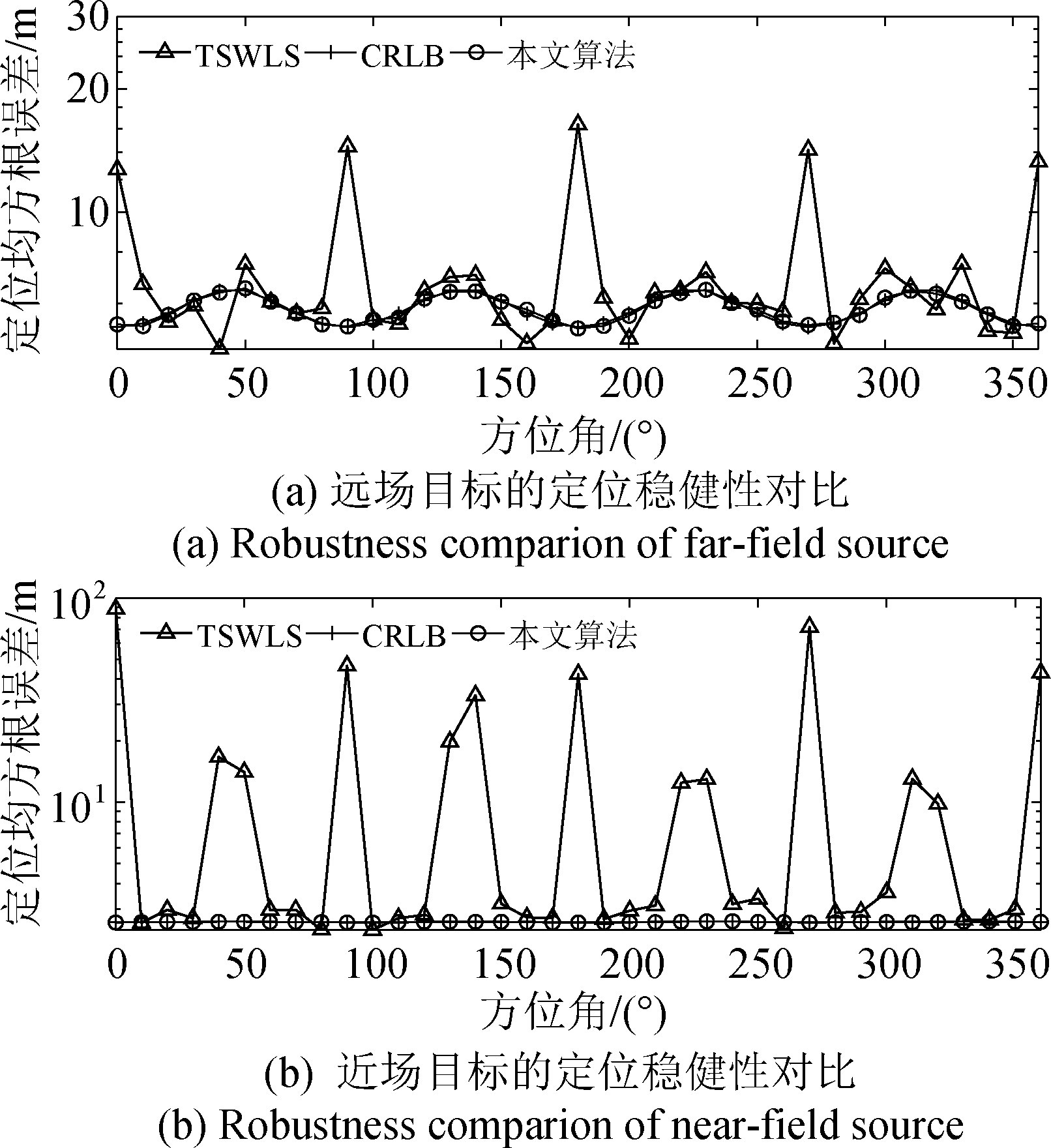
图3 不同算法稳健性比较
Fig.3 Robustness comparison among different methods
6 计算量分析
本节主要以算法涉及到的实数乘法次数为标准[19],对比分析了所提算法与其他算法的计算量。
首先分析所提算法步骤1的计算量：
1)计算W1:包括计算①
②
逆运算。以上每个步骤分别需要进行2(M-1)3、9(M-1)M2+3(M-1)2M以及(M-1)3次实数乘法。
2)计算
包括计算①
②
③
一共需要8(M-1)2+36(M-1)+64次实数乘法。
接着分析所提算法步骤2的计算量:
1)计算W2:包括计算①
③
④
⑤求逆运算。一共需要148M2+104M+464次实数乘法。
2)计算
包括计算①
②
③
一共需要207次实数乘法。
需要注意的是,所提算法步骤1中需要先初始化加权矩阵W1,并对其更新两次以得到更准确的估计结果,故步骤1中1)需要计算两次、2)需要计算三次,因此所提算法共需要(30M3+124M2+188M+773)次实数乘法。文献[11]中TSWLS算法在步骤2后仍需利用公式
得到最终定位结果,故相比于TSWLS算法,所提算法计算量稍小。而相比于文献[12]算法,由于所提算法在步骤2中多考虑了站址误差,在计算W2时比文献[12]多出148M2+104M+208次实数乘法,当M=5时,所提算法计算量大约为文献[12]的两倍,但考虑到所提算法定位精度的提升,一定计算量的牺牲是值得的。
7 结论
本文提出了一种考虑站址误差的稳健TDOA定位算法。算法首先引入辅助变量来伪线性化定位方程,利用加权最小二乘对目标位置进行初步估计,其次利用辅助变量与目标位置之间的关系,构建关于位置误差的定位方程,接着利用加权最小二乘对步骤1结果的误差进行估计,最后用第1步初步估计值减去误差估计值得到最终精确的目标位置结果。本文算法通过利用误差校正处理来构建定位方程,避免了传统基于TSWLS算法中的非线性运算及矩阵缺秩的问题,提高了算法的定位精度和稳健性。理论性能分析和仿真实验结果表明,本文所提算法具有更好的稳健性和抗噪性。由于本文算法单独利用TDOA进行目标定位,只适用于对静目标的定位解算,下一步将考虑对其进行扩展,实现对动目标的定位解算。
[1] 田中成, 刘聪锋. 无源定位技术[M]. 北京: 国防工业出版社, 2015: 8-12.
Tian Zhongcheng, Liu Congfeng. Passive Location Technology[M]. Beijing: National Defense Industry Press, 2015: 8-12.(in Chinese)
[2] 禹华钢, 汪汇川. 多校准站TDOA/FDOA无源定位方法[J]. 电讯技术, 2019, 59(1): 76- 81.
Yu Huagang, Wang Huichuan. A TDOA and FDOA Source Passive Localization Method Using Calibration Emitters[J]. Telecommunication Engineering, 2019, 59(1): 76- 81.(in Chinese)
[3] Beck B, Lanh S, Baxley R, et al. Uncooperative Emitter Localization Using Signal Strength in Uncalibrated Mobile Networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(11): 7488-7500.
[4] Tomic S, Beko M. Target Localization via Integrated and Segregated Ranging Based on RSS and TOA Measurements[J]. Sensors, 2019, 19(2): 230.
[5] Chen Xin, Wang Ding, Liu Ruirui, et al. Structural total least squares algorithm for locating multiple disjoint sources based on AOA/TOA/FOA in the presence of system error[J]. Frontiers of Information Technology & Electronic Engineering, 2018, 19(7): 917-936.
[6] 王生亮, 刘根友, 高铭, 等. 改进的自适应遗传算法在TDOA定位中的应用[J]. 系统工程与电子技术, 2019, 41(2): 254-258.
Wang Shengliang, Liu Genyou, Gao Ming, et al. Application of Improved Adaptive Genetic Algorithm in TDOA Location[J]. Systems Engineering and Electronics, 2019, 41(2): 254-258.(in Chinese)
[7] Foy W H. Position-Location Solutions by Taylor-Series Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(2): 187-194.
[8] Ho K C, Xu W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453-2463.
[9] Liu Zhixin, Wang Rui, Zhao Yongjun. A Bias Compensation Method for Distributed Moving Source Localization Using TDOA and FDOA with Sensor Location Errors[J]. Sensors, 2018, 18(11): 3747.
[10]杨海军, 郭美凤, 滕云鹤. GPS定位信号随机误差自适应模型[J]. 数值计算与计算机应用, 2000(1): 22-27.
Yang Haijun, Guo Meifeng, Teng Yunhe. Random Error Adaptive Model for GPS Positioning Signal[J]. Journal on Numerical Methods and Computer Applications, 2000(1): 22-27.(in Chinese)
[11]Ho K C, Lu X, Kovavisaruch L. Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors: Analysis and Solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684- 696.
[12]Liu Yang, Guo Fucheng, Yang Le, et al. An Improved Algebraic Solution for TDOA Localization with Sensor Position Errors[J]. IEEE Communications Letters, 2015, 19(12): 2218-2221.
[13]Sun M, Ho K C. An Asymptotically Efficient Estimator for TDOA and FDOA Positioning of Multiple Disjoint Sources in the Presence of Sensor Location Uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3434-3440.
[14]Liu Zhixin, Hu Dexiu, Zhao Yongsheng, et al. An algebraic method for moving source localization using TDOA, FDOA, and differential Doppler rate measurements with receiver location errors[J]. EURASIP Journal on Advances in Signal Processing, 2019, 2019(1): 1-15.
[15]邓兵, 孙正波, 杨乐, 等. 存在站址误差时的线性校正TDOA定位算法[J]. 西安电子科技大学学报(自然科学版), 2017(4): 106-111.
Deng Bing, Sun Zhengbo, Yang Le, et al. TDOA Localization with Linear-correction in the Presence of Sensor Position Errors[J]. Journal of Xidian University, 2017(4): 106-111.(in Chinese)
[16]孙霆, 董春曦, 董阳阳, 等. 一种基于观测站数目最小化的TDOA/FDOA无源定位算法[J]. 航空学报, 2019, 40(9): 265-275.
Sun Ting, Dong Chunxi, Dong Yangyang, et al. A TDOA/FDOA passive location algorithm with the minimum number of stations[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(9): 265-275.(in Chinese)
[17]Lin L, So H C, Chan F K W, et al. A new constrained weighted least squares algorithm for TDOA-based localization[J]. Signal Processing, 2013, 93(11): 2872-2878.
[18]Liu Zhixin, Hu Dexiu, Zhao Yongsheng, et al. An Improved Closed-Form Method for Moving Source Localization Using TDOA, FDOA, Differential Doppler Rate Measurements[J]. IEICE Transactions on Communications, 2019, 102(6): 1219-1228.
[19]孙霆, 董春曦. 传感器参数误差下的运动目标TDOA/FDOA无源定位算法[J]. 航空学报, 2020, 41(2): 262-271.
Sun Ting, Dong Chunxi. TDOA/FDOA Passive Localization Algorithm for Moving Target with the Sensor Parameter Errors[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(2): 262-271.(in Chinese)
