1 引言
线性调频(Linear Frequency Modulation, LFM)信号[1]作为一种成熟的宽带非平稳信号,具有大的时宽-带宽积,通过增加LFM信号的脉宽,提高信号的发射功率,能够获得更好的距离分辨率和更远的探测距离,被广泛使用在雷达[2]、声呐[3]和水声通信[4]等领域。在雷达和声呐中,通过对LFM信号做时延估计,可以实现对目标的方位估计[5],在水声通信中,LFM信号通常作为同步信号出现,通过对己方同步头信号的探测,可以实现有针对性地对通信信息的接收,通过对敌方同步头信号的侦察,可以判断出敌方发射同步头的方位,进而做出必要的应对,因此对LFM信号做目标方位估计(DOA)具有重要的意义[6]。
传统的傅里叶变换对LFM进行处理分析时,具有很大的局限性,它无法同时显示LFM携带的时频信息,因此FFT并不适合处理非平稳信号。对LFM类信号来说,分数阶傅里叶变换(Fractional Fourier Transform, FRFT)是一种很好的分析工具[7]。水下复杂的环境通常导致LFM信号的信噪比较低,这会增加DOA的难度,而FRFT的能量聚焦作用会对水下目标的估计精度产生积极影响,提高探测能力[8]。2005年,陶然等人提出了一种基于FRFT的混响抑制算法[9],并通过实验数据验证了该方法的可行性和有效性,而后陶然将其与MUSIC算法结合,提出了基于FRFT的MUSIC方法进行LFM信号的DOA估计。2014年,王瑞等人基于 FRFT提出了一种新的宽带 LFM 脉冲信号中心频率估计方法,并据此对基于 FRFT 的MUSIC 算法的DOA估计进行了改进[10]。Pei H提出了基于FRFT的Root-MUSIC算法用于主动声纳检测中的目标方位角估计[11],对MUSIC算法进行了不同的改进。Li B对FRFT中基于稀疏表示的DOA估计做了一些研究,将其与稀疏阵列相结合起来[12]。为了提高FRFT的实现计算速度,2015年Si C提出了一种新的离散算法[13],Liu S在原有快速离散算法的基础上进行了修改,使其在对多分量LFM信号分析时有更快的计算速度[14]。
DOA算法通常要求阵列流形精确已知,在此基础上进行准确估计,然而,由于海洋环境的多变性,受到波浪、流速等影响,水下探测阵列的阵列流形出现误差的概率更高,当出现阵元扰动时,FRFT的阶次搜索过程也会产生误差,该误差会影响对目标的估计精度,此时的DOA结果将不再准确。基于此,本文从稳健性出发将FRFT和稳健类波束形成算法相结合,利用稳健算法抑制外界因素和FRFT中带来的误差影响,以使在较低信噪比时获取更好的方位估计性能。文章共分为3部分,第一部分为基于FRFT预处理的DOA理论推导,第二部分为范数约束Capon波束形成(Norm Constrained Capon Beamforming, NCCB)算法的原理介绍,第三部分为该算法与传统FFT处理的对比分析。本文利用MATLAB仿真验证了算法的稳健性。
2 基于FRFT预处理的目标方位估计理论
分数阶傅里叶变换有若干等价的不同定义方式,其主要形式有三种,分别为:积分定义形式、特征函数定义形式、时频平面旋转定义形式,下面对积分定义形式进行简要介绍。作为一种线性积分运算,定义函数s(t)的分数阶傅里叶变换为
Fp(u)=![]() s(t)Kp(u,t)dt
s(t)Kp(u,t)dt
(1)
式中,p为阶数,Kp(u,t)被称为FRFT的核函数,即:
Kp(u,t)= 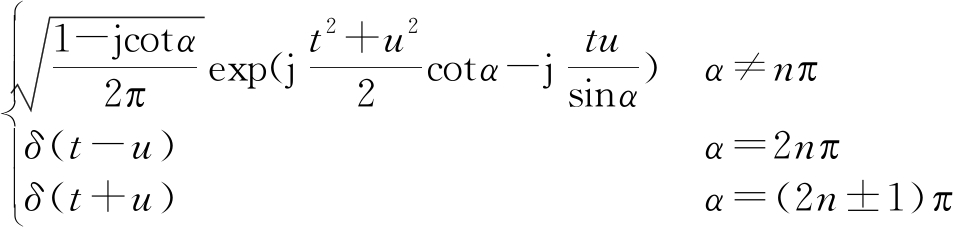
(2)
式中n为整数,α和p的关系为
(3)
从分数阶傅里叶变换积分定义可以看出,其相当于傅里叶变换的广义变换,由于二者基本积分运算类似,因此分数阶傅里叶变换与傅里叶变换的性质也基本相同。如图1所示,LFM信号在时频平面内可表示为具有一定角度的线段,t-f为时频平面,u-ν为FRFT平面。由于分数阶傅里叶变换具有旋转时频面的特性,因此可以得到u轴与LFM时频分布线段相垂直的FRFT平面,在这个FRFT平面中,LFM呈现冲激函数的形式,信号的能量全部聚集在u轴特定的点上。假设信号的调频斜率为k,则FRFT平面旋转角度α与k有下列关系
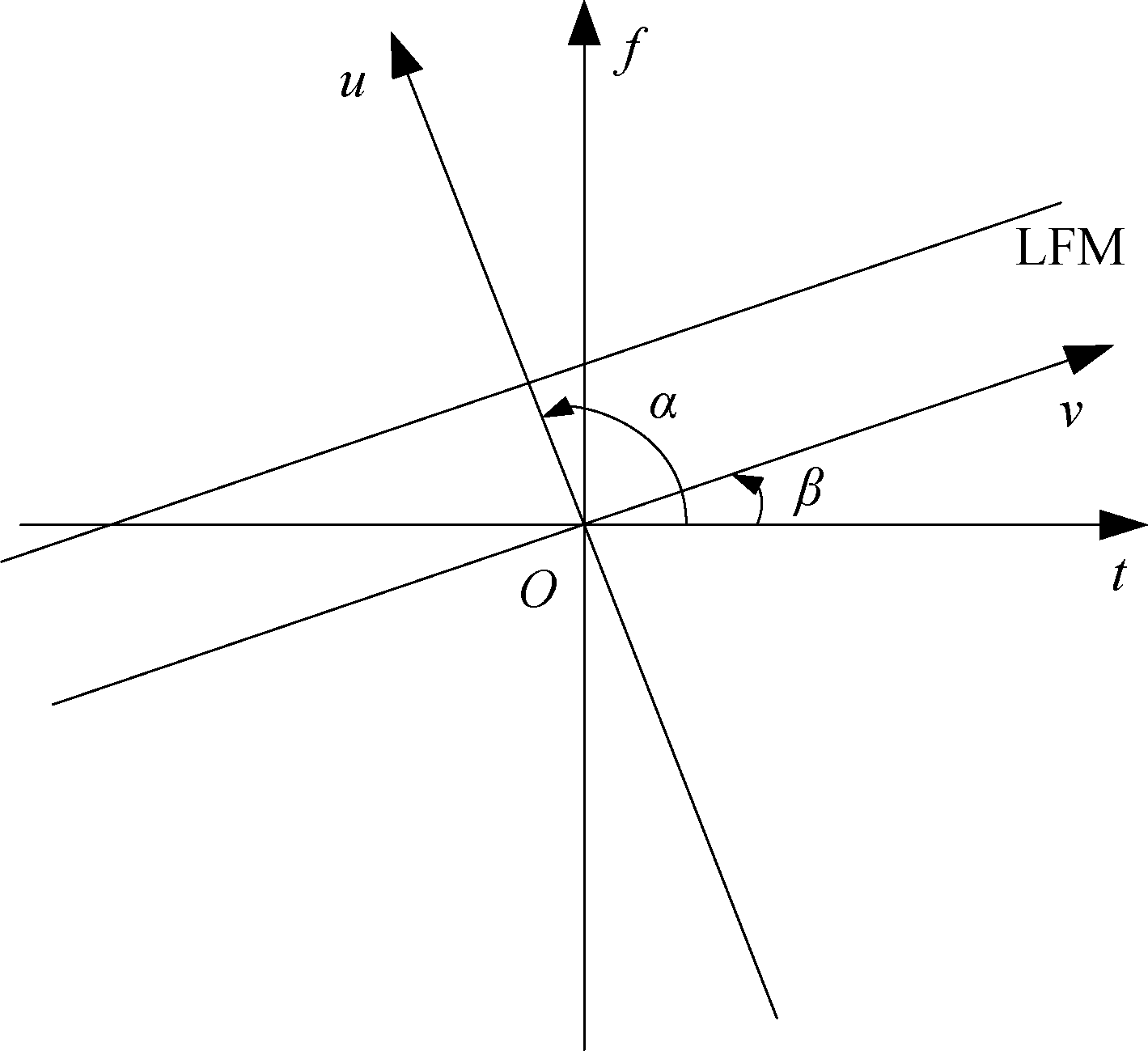
图1 LFM信号的时频分布与FRFT平面
Fig.1 The time-frequency distribution of LFM signal and FRFT plane
k=-cot α
(4)
通过对时频平面的旋转,LFM信号由时频面中宽带的形式转变为特定FRFT平面中窄带的形式,并且在这个过程中并不会丢失原始信号的方向角信息。
下面将利用FRFT处理LFM信号的这种独特优势,对均匀线列阵接收信号进行处理。假设有阵元间隔为d的M元均匀线列阵,将参考阵元设置在坐标原点,有Q个宽带LFM信号入射到基阵上,如图2所示。
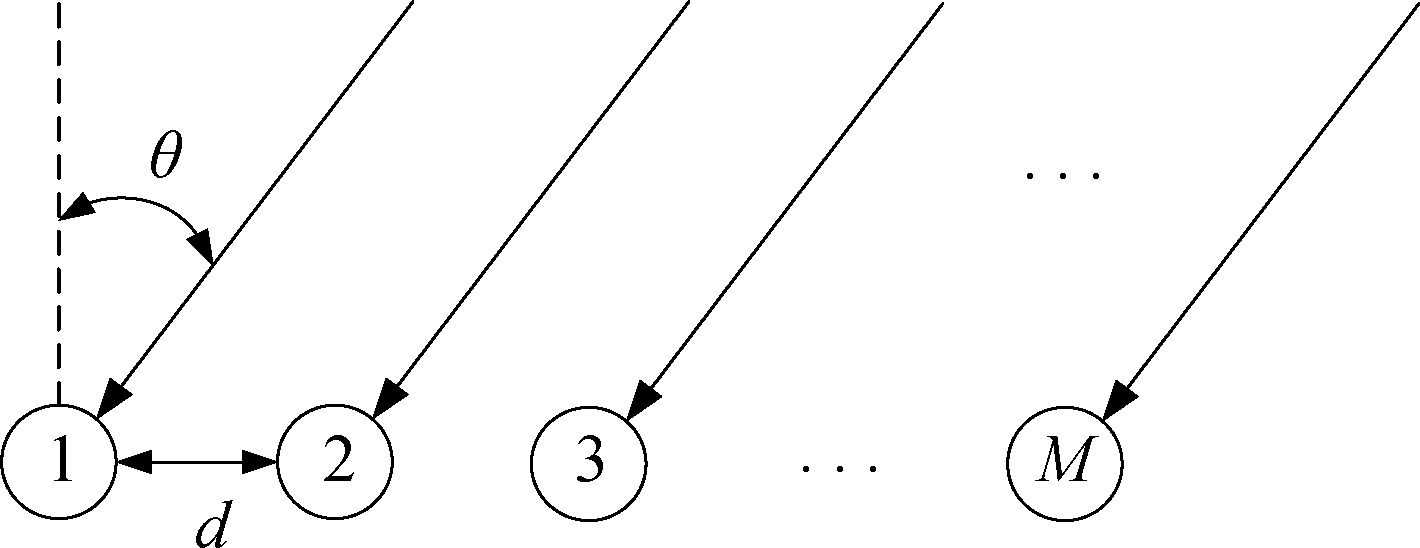
图2 均匀分布线阵信号接收示意图
Fig.2 Uniform linear array signal reception diagram
第k个阵元的信号输出为
(5)
其中,
sq(t)=ejπ(2fq0t+μqt2)
(6)
τk,q=(k-1)dsin θq/c
(7)
式中,sq(t)为源信号,fq0为LFM信号的初始频率,μq为信号的调频斜率,τk,q为第k个阵元接收信号sq(t)时相对参考阵元的时延,nk(t)为高斯白噪声。式(5)为单阵元输出信号,将所有阵元输出的信号写成向量的形式,并将式(6)代入式(5)可得
(8)
其中导向向量为
aq(t)= [1 ejπ[-2fq(t)τ1,q+μq(τ1,q)2] … ejπ[-2fq(t)τM,q+μq(τM,q)2]]
(9)
fq(t)=fq0+μqt
(10)
由式(9)可知导向向量并不是恒定的,它随着时间的改变而改变,因此无法应用于传统的DOA方法。但是通过分数阶傅里叶变换,可以得到恒定分数阶域的方向向量[15],下面进行简要推导。
对参考阵元而言,第q个接收信号sq(t)在μq=-cot αq0时能量聚集性最强,此时sq(t)的分数阶傅里叶变换为
Sq(α,u)= ![]()
(11)
式中,T为信号时间长度。由式(11)可知,当uq0=fq0/csc αq0时,Sq(αq0,u)可取得最大值
(12)
由此可得(αq0,uq0)与(fq0,μq)的关系如下:
(13)
上面推导了参考阵元接收信号的FRFT形式,下面对一般情况进行推导,由式(5)与式(6)可得,第k个阵元接收到第q个LFM信号为
sk,q(t)=sq(t-τk,q)= ejπ(-2fq0τk,q+μq(τk,q)2)ejπ(2(fq0-uqτk,q)t+μqt2)
(14)
由式(12)可知,LFM信号延时信号的调频斜率并没有改变,只是初始频率和相位发生了变化,令
Bq(τk,q)=ejπ(-2fq0τk,q+μq(τk,q)2)
(15)
式(15)是式(14)右侧的第一项,它作为常量仅与时延有关。
令Sk,q(α,u)=Fp[sk,q(t)],和参考阵元一样,Sk,q(α,u)也在αq0=-cot μq时能量聚集性最强,此时
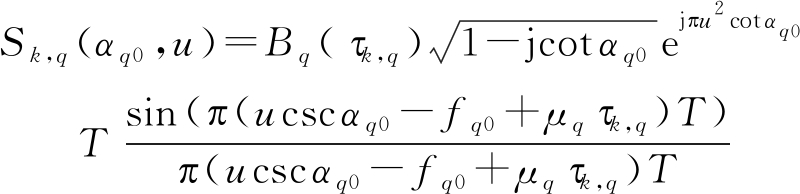
(16)
Sk,q(αq0,u)在(αq0,uk,q)处可得极大值,此时
(17)
uk,qcsc αq0=fq0-μqτk,q
(18)
由式(13)和式(18)可得
(19)
将式(13)、式(19)代入式(16)可得
Sk,q(αq0,uk,q)=Aq(τk,q)Sq(αq0,uq0)
(20)
其中
Aq(τk,q)= ejπ(-2uq0csc αq0τ-cot αq0(τk,q)2+2τk,quq0cos αq0cot αq0+cos 2αq0cot αq0(τk,q)2) =ejπ(-2τk,quq0sin αq0)e-jπ(τk,q)2sin αq0cos αq0
(21)
通过式(19)和式(20)可得到延时后的LFM信号在分数阶域的峰值幅度和位置情况。将经过分数阶傅里叶变换过的基阵输出写为向量形式,可得接收信号的分数阶域数据模型。
X=AS+N
(22)
X=[X1 X2 … XM]T
(23)
S=diag{S1(α10,u10) S2(α20,u20) … SQ(αQ0,uQ0)}
(24)
A=[A1 A2 … AQ]
(25)
式中,Aq为第q个LFM信号的分数阶域导向向量
Aq=[1 Aq(τ2,q) … Aq(τM,q)]T
(26)
3 范数约束Capon波束形成原理
经典的自适应波束形成算法为MVDR算法,当期望信号导向向量和噪声协方差矩阵精确已知的情况下,MVDR波束形成器具有很好的方位分辨力和干扰抑制能力。但是当噪声协方差矩阵与导向向量的估计值存在误差时,MVDR波束形成器会产生信号“自消”,将期望信号当成干扰来进行抑制,造成输出信干噪比下降严重,稳健性很差。为了改善MVDR波束形成器的稳健性,可采用对角加载类方法,NCCB算法便是一种稳健的对角加载类方法[16]。与MVDR加权向量求解过程类似,同样采用拉格朗日方法求解波束输出噪声方差的最小值,不同之处在于相比MVDR加权向量的求解增加了权向量范数约束的条件,即
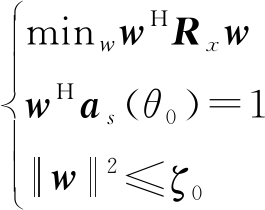
(27)
式中,w为加权向量,Rx为接收信号的自协方差矩阵,as(θ0)为θ0(观察方向)方向上的基阵响应向量,ζ0为加权向量范数约束值。由于波束形成器的灵敏度为
Tse=||w||2
(28)
灵敏度越大,波束形成器稳健性越差,因此可以通过控制ζ0的值来调节波束形成器的稳健性。而ζ0与白噪声增益损失Gwd存在以下的关系
(29)
因此可以通过设置白噪声增益损失来获得加权向量范数约束值,相较于普通对角加载法凭经验进行加载量的选取,采用NCCB方法的加载量的获取有了一定的数学依据。实验证明[17],白噪声增益损失设置为2 dB可获得较好的估计性能,然而也可以考虑角度分辨力和稳健性的实际需求,对白噪声增益损失进行折中确定。作为对角加载类方法的一种,NCCB方法的加权向量可写为
(30)
式中,λ为加载量。在利用NCCB算法进行波束扫描DOA估计时,首先利用式(31)来判断扫描方向上的加权向量范数是大于ζ0。如果式(31)成立,则MVDR与NCCB波束形成器的权向量的解相同,即λ=0;倘若不满足式(31),那么则需要对加载量λ进行求解。
(31)
对式(27)进行推导求解,可知加载量估计值![]() 满足下式
满足下式
(32)
可证明,在加权向量满足范数约束的情况下,式(32)有唯一正数解![]() 并且式(32)左侧为单调递减函数,因此可以用牛顿迭代法对其进行求解[16]。推导过程如下:首先对基阵接收数据协方差矩阵Rx进行特征分解,得到
并且式(32)左侧为单调递减函数,因此可以用牛顿迭代法对其进行求解[16]。推导过程如下:首先对基阵接收数据协方差矩阵Rx进行特征分解,得到
Rx=UΓUH
(33)
式中,Γ为特征值组成的对角阵,并且Γ=diag(γ1,γ2,…,γM),γ1≥γ2≥…≥γM。因此
(34)
令
(35)
因此,式(32)可写为
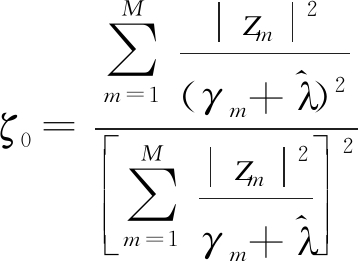
(36)
式中,zm为向量z的第m个元素,使用牛顿法对式(36)迭代求解即可得![]() 由式(30)可得,NCCB波束形成器的功率谱为
由式(30)可得,NCCB波束形成器的功率谱为
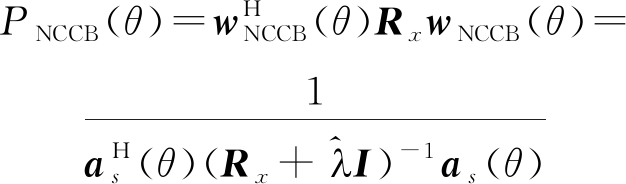
(37)
将上述算法在FRFT上进行实现,即可完成基于FRFT预处理的波束形成。当接收信号的调频斜率和初始频率已知时,可直接计算得到对应的最优阶次和聚焦谱峰的位置。当接收信号的参数不确定时,需要进行二维搜索来确定最优阶次和聚焦谱峰位置。由于存在多个目标时,最优阶次和峰值位置可能并不唯一,因此需要在多个最优阶次下进行搜索,以获得所有目标的数据。由于FRFT需要进行阶次搜索获取最优阶次,为加快运算速度,可以先在[0,2]的分数阶范围内进行FRFT粗扫,确定不同位置的峰值个数和相应最优分数阶,而后再对存在峰值的分数阶周围进行小范围的细扫,得到最终准确阶次以及各个峰值的准确位置,最后提取不同位置下的峰值数据来构造协方差矩阵。不同目标对应的导向向量有所不同,其与最优分数阶和峰值位置有关,因此将搜索得到的最优阶次和峰值位置数据代入式(21)即可得到每个信号的导向向量。综上所述,基于FRFT预处理的波束形成算法的主要步骤如下:
(1)对接收数据粗扫做FRFT,确定入射目标个数和相应最优阶次的粗略范围;
(2)对接收数据在最优阶次范围内进行细扫FRFT,获得准确的最优阶次和峰值位置;
(3)提取出峰值组成数据协方差矩阵,根据最优阶次和峰值位置构造相应导向向量;
(4)求解对角加载量后,由式(37)进行方位估计。
4 仿真结果
仿真中所用信号参数如下:信号采样频率1.2 kHz,LFM信号频率300 Hz~360 Hz,脉宽1 s。如图3所示,经过FRFT后,LFM信号在最优阶次附近能量开始逐渐聚焦,越接近最优阶次能量越集中,越远离最优阶次能量越分散,从而在扫描图中形成了交叉形式模型,交叉的中心即为最优阶次位置,图3(a)中所示的两个峰值点。正是因为FRFT的旋转特性,在[0,4]的一个周期内,LFM信号的时频分布线会与FRFT平面的u轴出现两次垂直的情况,所以也会出现两次聚焦,两个聚焦点仅位置不同,其余特征等效,因此实际搜索中,只需要对[0,2]范围内进行扫描即可。将最优阶次处对应的FRFT结果取出,即可得到图3(b),在后续的分数阶域波束形成中,将用其构成分数阶域的数据协方差矩阵。
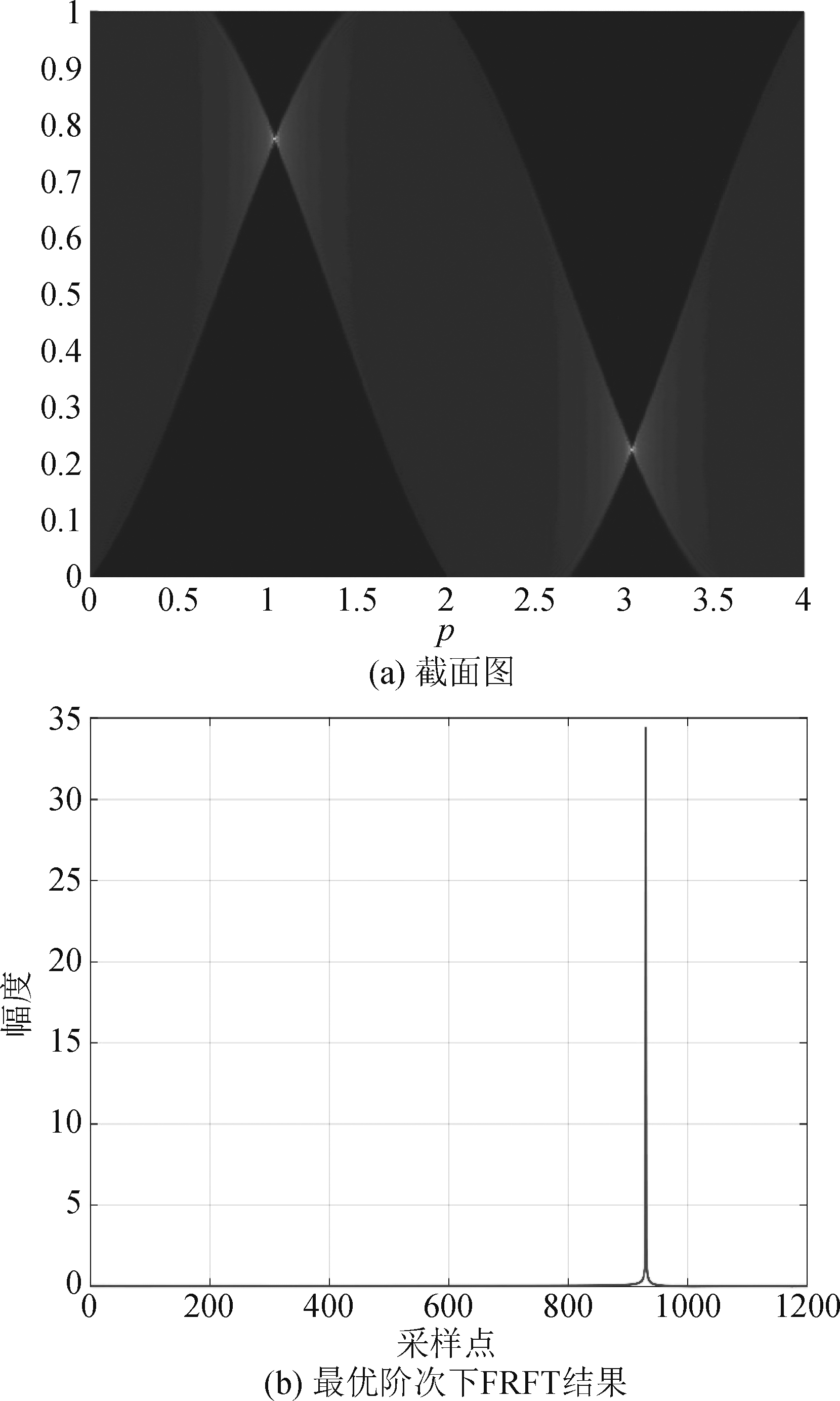
图3 基于FRFT的峰值搜索
Fig.3 Peak search based on FRFT
(1)分数阶域DOA估计方法仿真验证
基阵阵元数为10,半波长布阵,快拍数为100,目标方位10°,声速设置为1500 m/s。仿真中LFM信号主要参数如表1所示,信号采样率为12 kHz,白噪声增益损失为6 dB。
表1 LFM信号参数
Tab.1 LFM signal parameters

中心频率/kHz脉宽/ms带宽/Hz信噪比/dB信号2.91001000
图4给出了基于FRFT的NCCB算法方位谱图,图中虚线所示为目标实际方位。由图4可以看出,NCCB算法可以准确估计出目标方位,这与理论推导相符合,验证了基于FRFT预处理后对目标进行DOA估计是可行的。
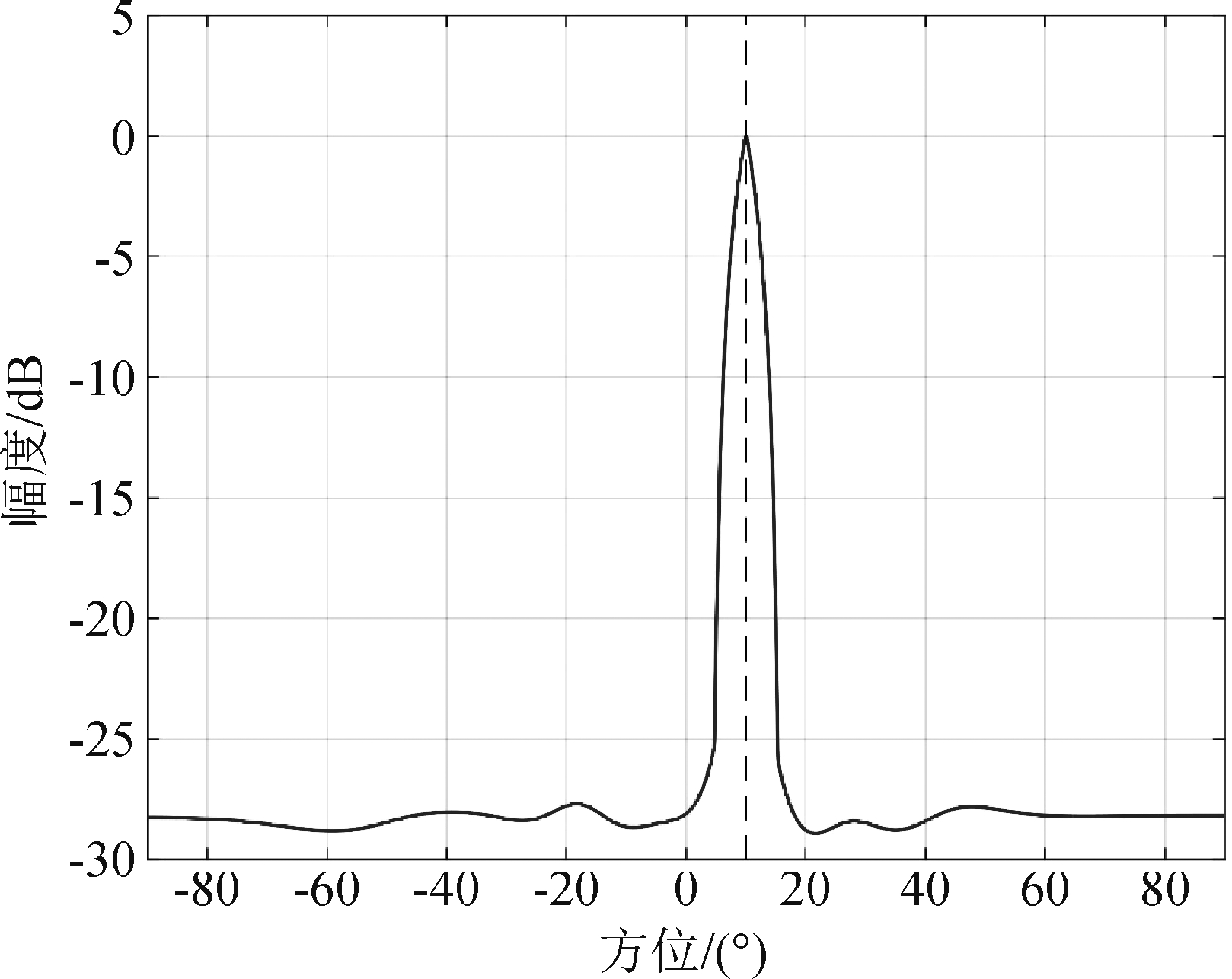
图4 基于FRFT的NCCB算法
Fig.4 NCCB algorithm based on FRFT
(2)FRFT域上不同算法波束图仿真对比
基阵阵元数为10,半波长布阵,快拍数为100。仿真中LFM主要参数如表2所示,其中信号1为期望信号,其余为干扰信号,信号采样率为12 kHz,白噪声增益损失为6 dB。
表2 信号参数
Tab.2 Signal parameters
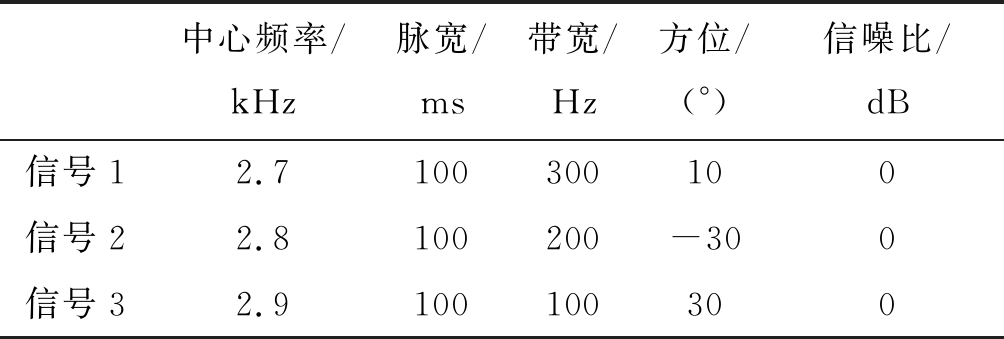
中心频率/kHz脉宽/ms带宽/Hz方位/(°)信噪比/dB信号12.7100300100信号22.8100200-300信号32.9100100300
在此次仿真中,选取了MVDR算法和NCCB算法进行对比分析。从图5可以看出,MVDR算法在波束图中出现了畸变,波束无法指向期望信号方位,性能有所下降,这种畸变随着快拍数的增加会逐渐消失,这也验证了MVDR算法对协方差矩阵较为敏感,需要精确构造才能取得好的结果,而NCCB算法则相对更为稳健,因此将NCCB算法与FRFT结合会获得更好的性能。
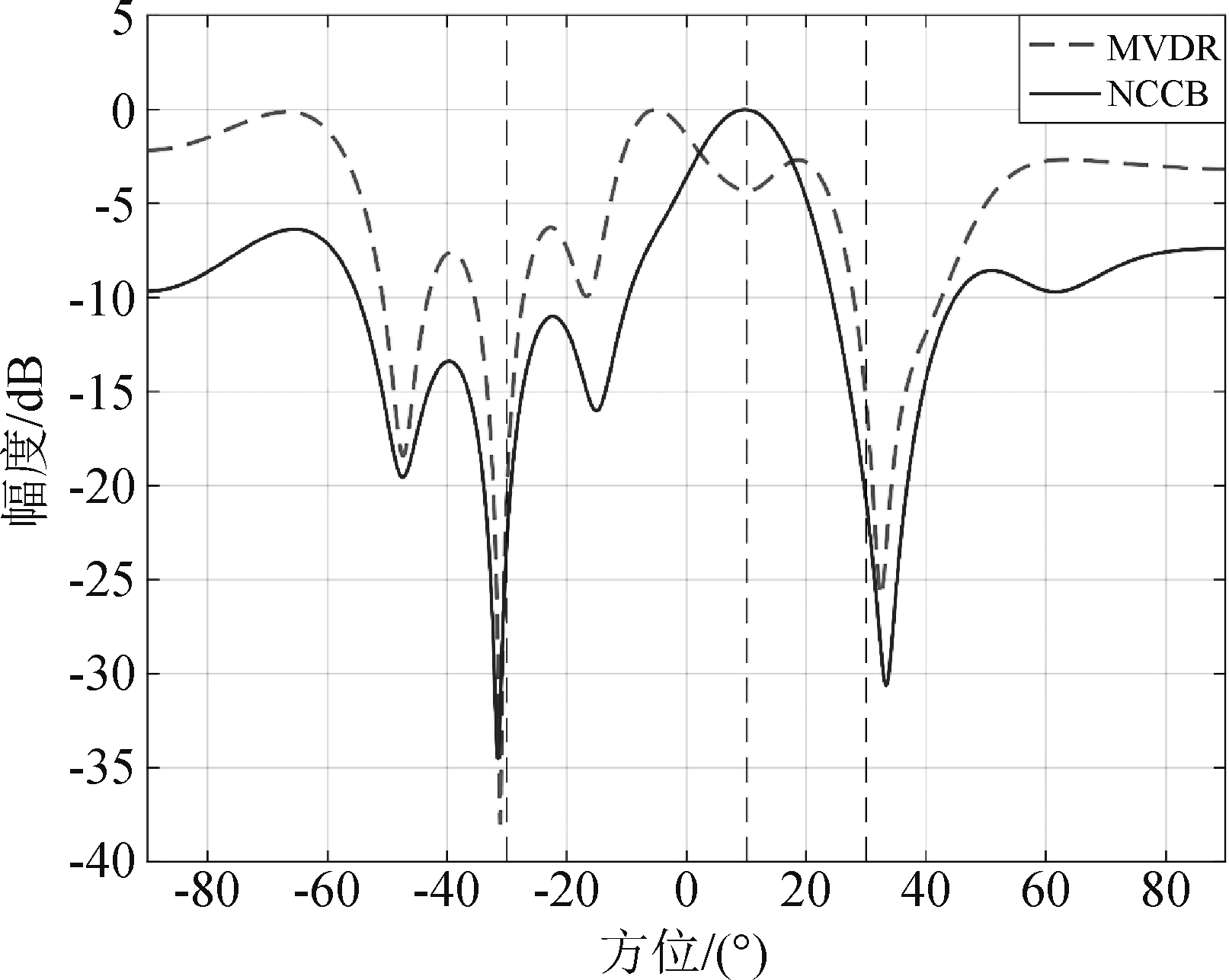
图5 MVDR和NCCB波束图对比
Fig.5 Comparison of MVDR and NCCB beam pattern
(3)分数阶域与频域DOA估计对比
取基阵阵元数为10,半波长布阵,快拍数为100,白噪声增益损失为6dB。仿真中LFM主要参数如表3所示,对频域宽带DOA估计与分数阶域DOA估计结果进行对比。
表3 信号参数
Tab.3 Signal parameters
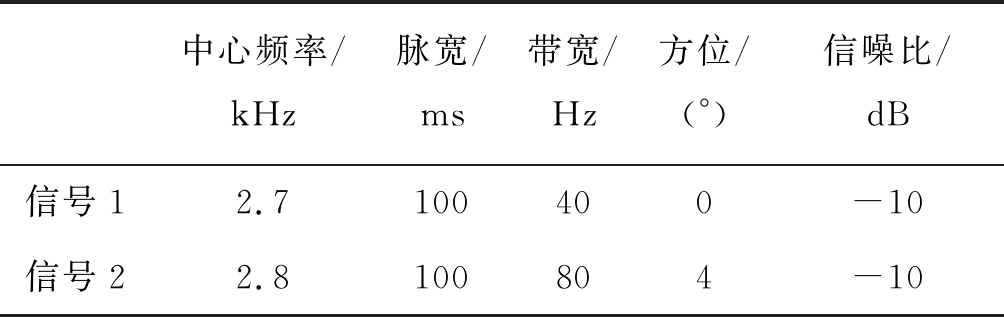
中心频率/kHz脉宽/ms带宽/Hz方位/(°)信噪比/dB信号12.7100400-10信号22.8100804-10
如图6中仿真结果所示,其中两条黑色虚线代表估计目标的方位。在低信噪比下,基于DFT的NCCB算法估计效果并不理想,估计出现误差,而利用FRFT预处理后,再用NCCB算法进行估计时,从左上的局部放大图中可以看出,此时实现了对两目标的精准估计,同时由于能量聚焦的作用,旁瓣级明显降低,输出信噪比有较大提高,效果要优于DFT处理。二者性能差异的主要原因在于噪声的影响程度不同,基于DFT的估计算法受到了所有子带叠加的噪声影响,而基于FRFT的DOA估计算法仅仅受峰值点处噪声的干扰,相当于间接提高了信噪比,因此获得了更优异的方位估计能力。需要注意的是,基于FRFT的DOA估计算法的性能与信号采样点数有很大关系,采样率和脉宽的增加都能提高能量聚集峰的高度,有利于谱峰搜索,而较少的采样点则会使得能量聚集峰被噪声掩盖,造成DOA估计性能大大降低。
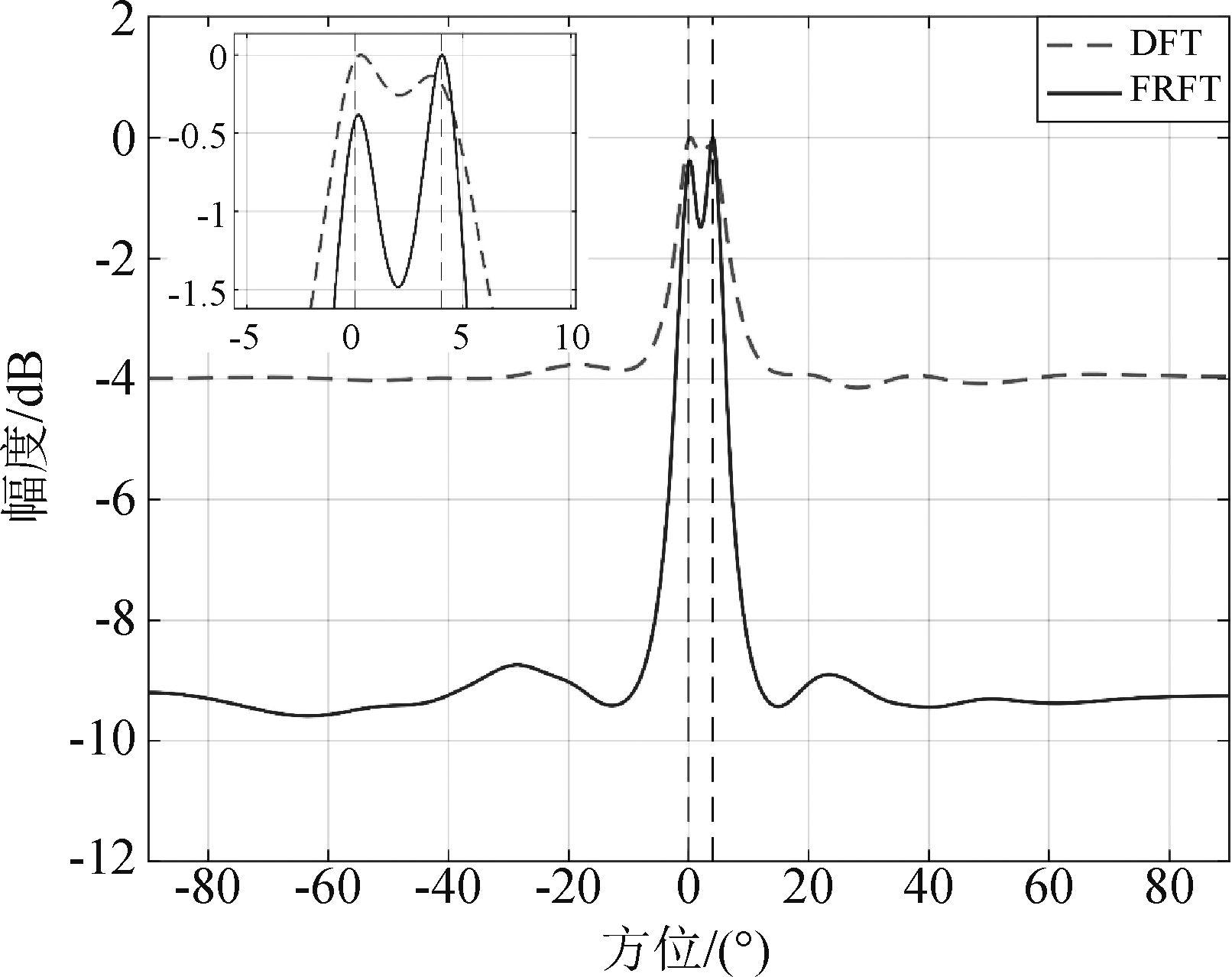
图6 DOA估计结果对比
Fig.6 DOA estimates results for comparison
除此之外,为了衡量传统频域和分数阶域DOA估计算法的运行效率,对本次仿真的运行时间进行了统计对比。计算机硬件采取Interi5-7300HQCPU,内存8G,仿真软件为MATLAB R2016a。可知传统频域NCCB算法的运行时间为38.95 s,而分数阶域NCCB算法的运行时间仅为21.01 s,大约为传统频域算法的一半,可知将接收信号在分数阶域处理显著提高了运行效率。因为频域NCCB算法要对所有信号带宽内的子带进行DOA估计,而分数阶域NCCB算法可视为仅对单个子带进行了DOA估计,即便增加了谱峰搜索的过程,但整体计算复杂度仍低于频域NCCB算法。
(4)快拍数和信噪比对估计性能的影响
基阵阵元数为10,半波长布阵,目标方位10°,声速设置为1500 m/s。LFM信号的中心频率为2.8 kHz,带宽100 Hz,脉宽100,信号采样率为6 kHz,快拍数为20,白噪声增益损失为6 dB。信号信噪比以1 dB为间隔从-20 dB变化到0 dB,波束扫描间隔为0.25°,当方位估计误差在0.5°以内时,可认为估计正确,在上述条件下,考察传统频域和分数阶域DOA估计方法的性能。由图7可知,随着信噪比的增大,两种算法的均方根误差均不断下降趋向于0,成功概率逐渐增大趋近于1,二者的性能差异逐渐减小。但在低信噪比下,分数阶域DOA估计方法的估计性能要远优于频域DOA估计方法。
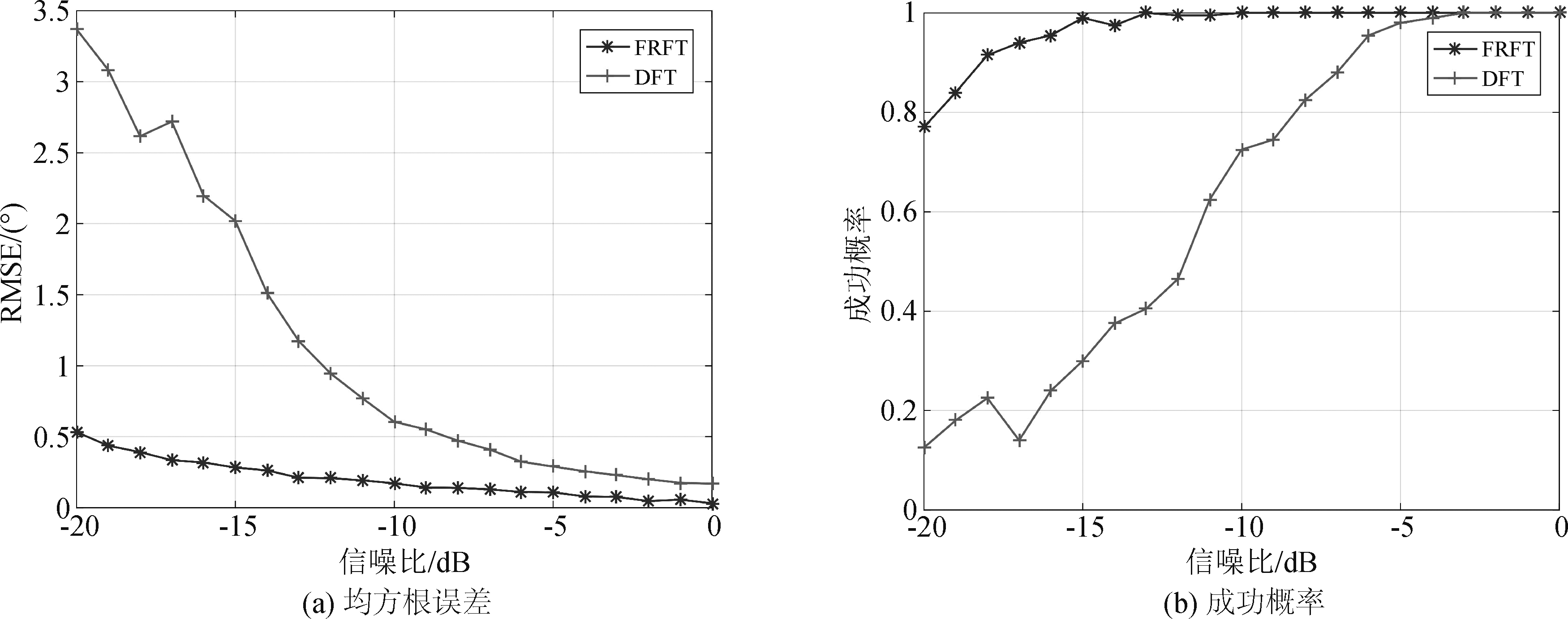
图7 信噪比对DOA估计精度的影响
Fig.7 Effect of SNR on DOA estimation accuracy
固定信号的信噪比为-10 dB,快拍数以5为间隔从10变化到100,波束扫描间隔为0.25°,当方位估计误差在0.25°以内时,可认为估计正确,在上述条件下,考察传统频域和分数阶域DOA估计方法的性能。如图8所示,与信噪比的影响类似,随着快拍数的增加,两种算法的方位估计性能均不断提高,二者间的差距不断缩小。在低快拍数下,分数阶域DOA估计方法的估计性能要远优于频域DOA估计方法。由此可得,相比于传统频域方法,分数阶域方法具有更低的快拍数和信噪比检测门限。
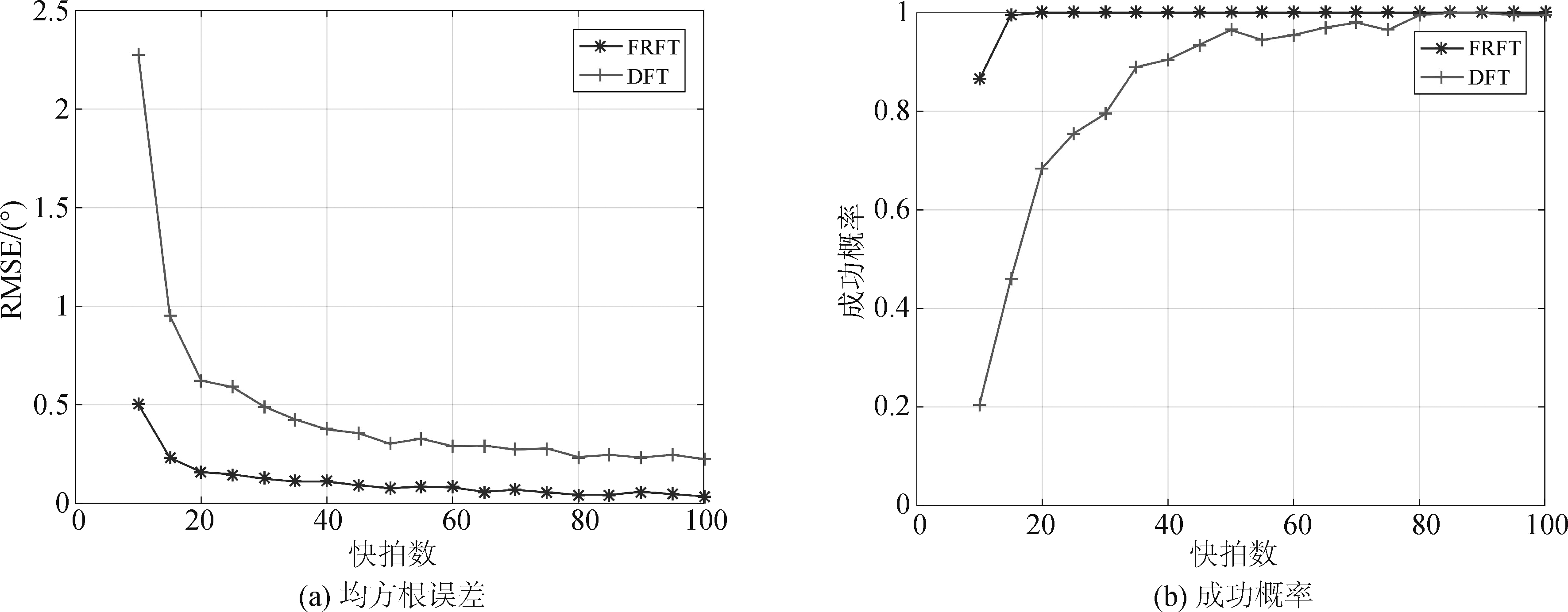
图8 快拍数对DOA估计精度的影响
Fig.8 Effect of the number of snapshot on DOA estimation accuracy
5 结论
本文通过对FRFT和稳健自适应波束形成技术进行研究,分析了将FRFT应用到DOA领域的可行性,发现利用FRFT对LFM类信号做处理时能起到能量聚焦的作用,与DOA算法结合后能够提高DOA的估计精度,降低旁瓣,提升信噪比。面对可能存在的误差因素,本文选择了一种稳健的波束形成算法与FRFT结合,利用算法的稳健性降低误差影响,从而得到更好的估计效果,最后用仿真进行了验证。
[1]Wang H, Fan X, You C, et al. Wigner-Hough transform based on slice′s entropy and its application to multi-LFM signal detection[J]. Journal of Systems Engineering & Electronics, 2017, 28(4): 634- 642.
[2]Gaglione D, Clemente C, Ilioudis C V, et al. Waveform design for communicating radar systems using Fractional Fourier Transform[J]. Digital Signal Processing, 2018, 80: 57- 69.
[3]Lee D H, Shin J W, Do D W, et al. Robust LFM Target Detection in Wideband Sonar Systems[J]. IEEE Transactions on Aerospace & Electronic Systems, 2017, 53(5): 2399-2412.
[4]马璐, 刘凇佐, 乔钢, 等. 水声正交频分复用异步多用户接入方法[J]. 声学学报, 2017, 42(4): 436- 444.
Ma Lu, Liu Songzuo, Qiao Gang, et al. Asynchronous multiuser reception for underwater acoustic orthogonal frequency division multiplexing communications[J]. Acta Acustica, 2017, 42(4): 436- 444.(in Chinese)
[5]Yang L, Su W, Hong G, et al. High-resolution velocity estimation and range profile analysis of moving target for pulse LFM UWB radar[J]. Signal Processing, 2011, 91(10): 2420-2425.
[6]Cui Y, Wang J, Qi J. Underdetermined DOA Estimation of Wideband LFM Signals Based on Gridless Sparse Reconstruction in the FRF Domain[J]. Sensors, 2019, 19(10): 2383.
[7]Zhou R, Liu A J, Pan X F, et al. An Improved Parameter Estimation Algorithm Based on FFT for LFM Signal[J]. Computer & Information Technology, 2014, 519-520: 998-1002.
[8]Diamant R, Lampe L. Low Probability of Detection for Underwater Acoustic Communication: A Review[J]. IEEE Access, 2018: 1-1.
[9]邓兵, 陶然, 齐林, 等. 基于分数阶傅里叶变换的混响抑制方法研究[J]. 兵工学报, 2005(6): 761-765.
Deng Bing, Tao Ran, Qi Lin, et al. Research on Reverberation Suppression Method Based on Fractional Fourier Transform[J]. Acta Armamentarii, 2005(6): 761-765.(in Chinese)
[10]Wang X, Li B, Yang H, et al. Off-Grid DOA Estimation for wideband LFM signals in FRFT Domain Using the Sensor Arrays[J]. IEEE Access, 2019, 7: 18500-18509.
[11]Yeh M H, Pei S C. A method for the discrete fractional Fourier transform computation[C]∥ IEEE International Symposium on Circuits & Systems, 2001.
[12]Hui Y, Li B, Zhao T. 4-weighted fractional Fourier transform over doubly selective channels and optimal order selecting algorithm[J]. Electronics Letters, 2015, 51(2): 177-179.
[13]Si C, Zhang S, Zhao H, et al. A New Chirp Scaling Algorithm for Highly Squinted Missile-Borne SAR Based on FrFT[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(8): 3977-3987.
[14]Liu S, Tao S, Zhang Y D, et al. A fast algorithm for multi-component LFM signal analysis exploiting segmented DPT and SDFrFT[C]∥ Radar Conference, 2015.
[15]陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 286-289.
Tao Ran, Deng Bing, Wang Yue. Fractional Fourier Transform and Its Applications[M]. Beijing: Tsinghua University Press, 2009: 286-289.(in Chinese)
[16]Li J, Stoica P, Wang Z A. Doubly constrained robust Capon beamformer[J]. IEEE Trans Signal Processing, 2004, 52(9): 2407-2423.
[17]Song H, Member, IEEE, et al. Null Broadening With Snapshot-Deficient Covariance Matrices in Passive Sonar[J]. IEEE Journal of Oceanic Engineering, 2003, 28(2): 250-261.

