1 引言
单载波频分多址(SC-FDMA, Single-carrier Frequency Division Multiple Access)是一种灵活高效的宽带无线通信技术[1],它不但具有多载波系统[2]的优势,如能够对抗信道频率选择性衰落效应,低复杂度的频域均衡,还具有单载波系统发送信号峰均比(PAPR, Peak-to-Average Power Ratio)低的优点[3],降低了对设备功耗和功放性能的要求,适合远距离传输。
多输入多输出(MIMO, Multiple-Input Multiple-Output)是现代宽带无线通信系统的重要技术之一[4],通过将数据符号转换为多条数据流并行传输,能在不增加发射功率和带宽的情况下获得比单入单出(SISO, Single-Input Single-Output)系统更高的系统容量,有效地提升频谱利用率。
MIMO系统中发送端按天线(空间)对数据流进行编码来获得分集增益。空时分组码(STBC, Space-Time Block Code)是一种常用的发送分集方案,它可与正交频分复用(OFDM, Orthogonal Frequency Division Multiplexing)或SC-FDMA技术结合使用[5-6],使MIMO系统获得对抗频率选择性衰落信道的能力,并保持原OFDM或SC-FDMA信号PAPR特性。而另一种同类发送分集方式——空频分组码[7](SFBC, Space-Frequency Block Code)对抗多普勒效应的能力比STBC更强[8],但与SC-FDMA的结合过程中,由于码字矩阵中符号顺序打乱,容易破坏信号的单载波特性,导致PAPR升高。为此,Ciochina等人提出了一种编码方式[9-10],将频域数据选点交错进行分组编码,组内元素在频域上不再连续,使其在时域仍然等效为单载波信号,PAPR与普通SC-FDMA相同,没有升高。
然而,该方法只给出了两发送天线正交编码[11]和四发送天线Jafarkhani准正交编码[12]的单载波传输方案。对于两根以上发送天线下可达到满分集增益的正交编码(OSFBC, Orthogonal SFBC),由于码字矩阵中多个列同时存在共轭、非共轭与0的形式,无法以单载波方式传输,目前仅与OFDM结合使用。如果直接使用SC-FDMA模式,在DFT操作后对频域数据符号按顺序进行OSFBC编码(下文将这种直观的做法称为“顺序SFBC方案”,用来与本文提出的方案做比较),将会导致3根有共轭形式符号的天线PAPR大幅升高,且各天线PAPR不一致,这将对天线系统的设计产生不利影响。因此,如何在多发送天线系统使用OSFBC并保证较低的PAPR是本文要解决的问题。
由于OSFBC码字矩阵上述特点,发送信号的PAPR将不可避免地较单载波有所升高,只能设法实现尽可能低的PAPR,使其接近单载波特性。由于OFDM信号的PAPR较高,即使针对OFDM存在数种PAPR降低技术[13],但大都对误码率性能有损失或实现复杂度较大,因此不考虑采用OFDM传输。本文以四发送天线为例,在SC-FDMA的基础上提出了一种使用多路DFT结构扩频的多天线OSFBC预编码方法,通过将多路单载波信号的频域数据交叉重叠进行编码,使其等效为多个单载波信号叠加的结果,有效降低了信号的PAPR。同时该方案未影响误码性能且复杂度不高,可作为多天线OSFBC低PAPR传输的一种解决方案。
2 顺序SFBC编码方案
发送信号在经过天线高功率放大器(HPA, High-Power Amplifier)时,高PAPR容易使功放进入非线性工作区间,导致信号失真而产生误码,所需的功耗也更大,因此对功放性能和设备供电能力提出了很高要求,带来体积、重量和成本等方面的上升。PAPR的定义式为:
(1)
xi为数字信号的离散样点值。
DFT-S-OFDM是SC-FDMA的一种经典结构,它将数据符号先经DFT转换到频域后再经IFFT转换到时域,对于单个天线发送的信号而言,仍然具有类似单载波的低PAPR特性。对于四发送天线的OSFBC,发送端结构图如图1所示。源数据符号经DFT处理后的频域符号按顺序进行SFBC编码。
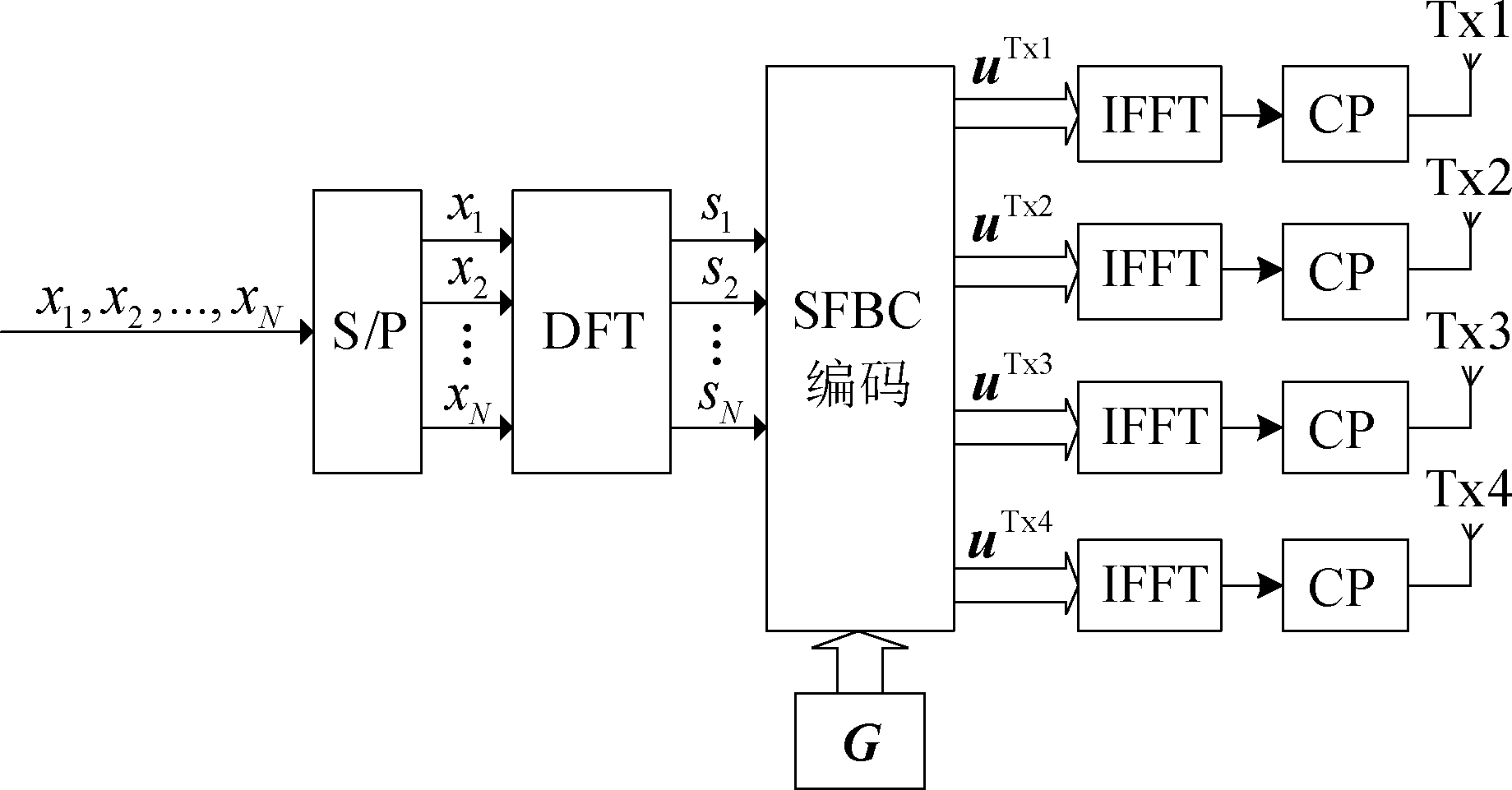
图1 顺序SFBC编码方案发送端
Fig.1 Transmitter of DFT-S-OFDM based SFBC
设要发送的数据符号为x1, x2,…, xN,其中N为3的整数倍。经串并转换后进行DFT,输出频域符号s1, s2,…,sN,按顺序将每3个频域符号划为一组,记作vk:
vk=[νk(0),νk(1),νk(2)]T=[s3k+1,s3k+2,s3k+3]T, ![]()
(2)
假设按式(3)的正交码字矩阵G进行编码,矩阵的行依次对应子载波,列依次对应各天线:
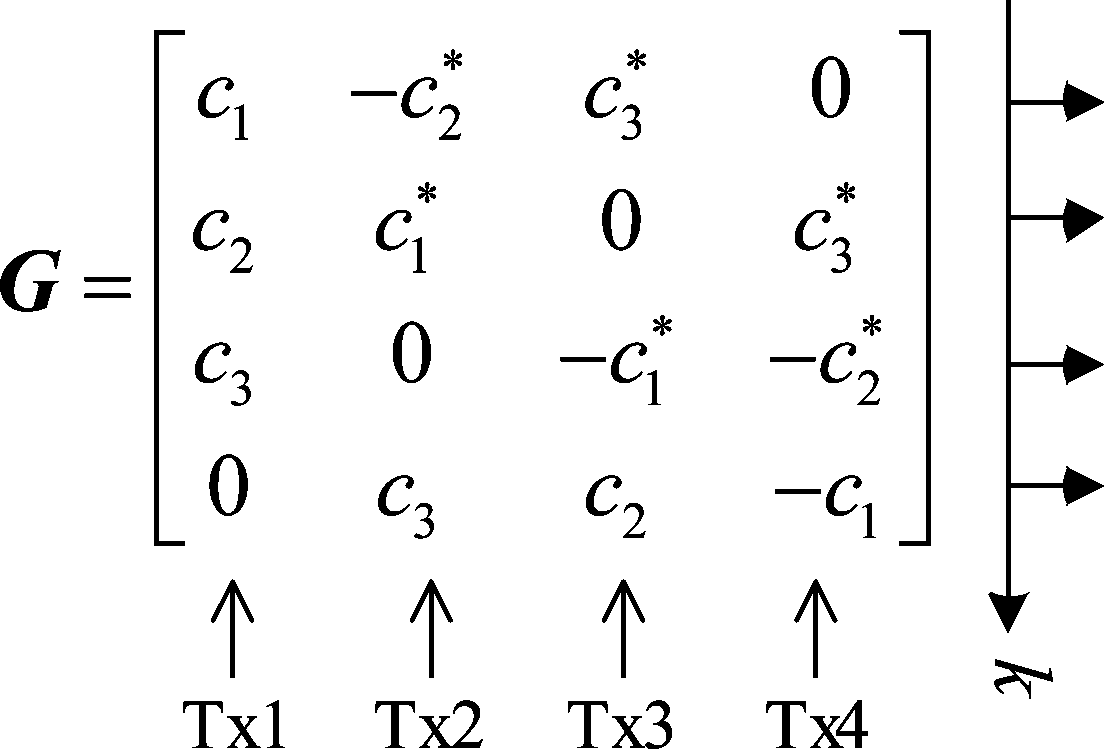
(3)
用fi(·), i=1, 2, 3, 4分别表示4根天线上的编码规则,有:
f1(vk)=[νk(0),νk(1),νk(2),0]T= [s3k+1,s3k+2,s3k+3, 0]T
(4)
(5)
(6)
(7)
则第i根天线上的SFBC编码输出:
uTxi=[fi(v0), fi(v1),…, fi(vM-1)]T
(8)
M=N/3表示数据符号分成的组数。编码完成后各天线上的编码结果经OFDM调制后送到天线端进行发送。该方案中,所有频域符号来自单个DFT的输出,但只有一根天线上的符号是按正序依次排列的,且全部非共轭,而其余天线上的情况并非如此,导致这些特殊形式天线的PAPR升高。
3 基于多路DFT扩频的编码方案
3.1 方案描述
为了避免顺序SFBC方案的上述缺陷,本文提出的多路DFT扩频的四天线OSFBC预编码方法发送端结构如图2所示。它将原顺序SFBC方案中的单个DFT替换为DFT组,并将它们的输出联合进行SFBC编码。

图2 本文方案发送端
Fig.2 Transmitter of proposed scheme
新方案将原方案1个DFT单元增加到K个DFT单元,K大于1且是3的倍数,每个DFT处理的点数M≥1,则经串并转换的数据符号总数为KM,且为3的倍数。这些符号被分成K组、每组M个分配给各DFT单元,其输入和输出分别表示为
![]() k=0,1,...,K-1
k=0,1,...,K-1
(9)
其中xk和sk表示第k+1个DFT单元的输入和输出向量。然后将输出的频域符号按每3个DFT为一簇划分,簇内各DFT相同位置的3个数据符号为一组相互交错编码,如图3所示,则第l+1簇的第m+1组符号可表示为
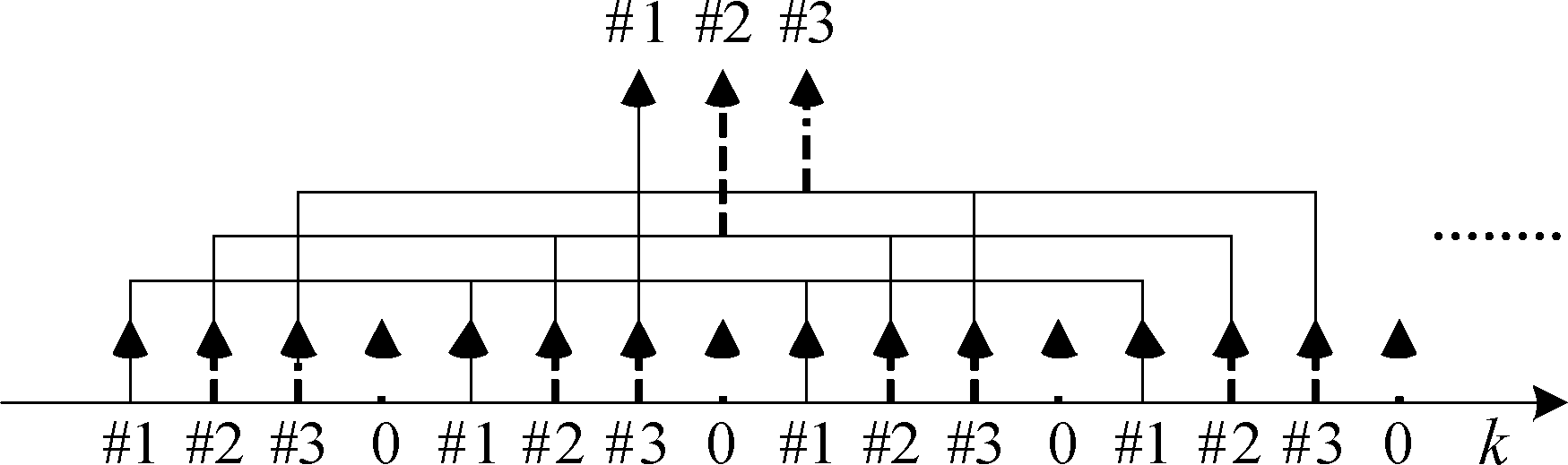
图3 频域数据交错排列示意图
Fig.3 Arrangement of frequency domain symbols
vl,m=[s3l(m),s3l+1(m),s3l+2(m)]T, ![]()
(10)
若第1根天线上的交错方式采用图3所示形式,后3根天线根据天线1的符号排列由码字矩阵G完成编码,则SFBC编码输出为
uTxi=[fi(v0,0),…, fi(v0,1), fi(v1,0),…, fi(v1,1),…, fi(vL-1,0),…, fi(vL-1,M-1)]T
(11)
其中L=K/3为总簇数。编码示意图如图4所示,是最终编码结果的一部分,其中zkj表示第k个DFT输出的第j个频域符号,即
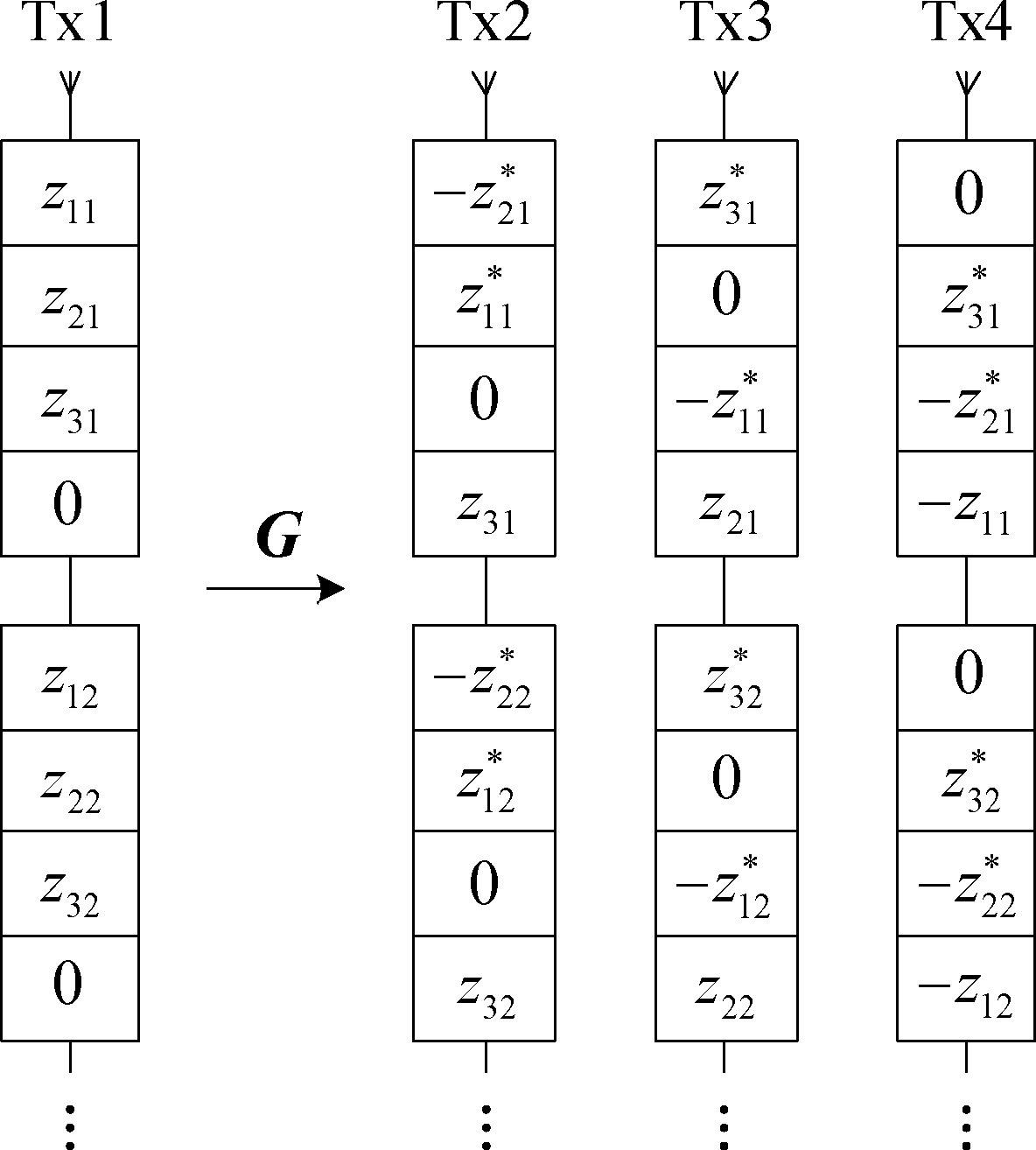
图4 本文方案编码结果示意图
Fig.4 Coding result of proposed scheme
zkj=νl, j(k)
(12)
不同组数据符号形成的编码矩阵向下延伸,最后形成完整编码结果。
本文方案在接收端的处理也无需过于复杂的结构,仅仅是发射端的逆过程,其结构如图5所示。接收端可以配备多根天线,接收信号依次经过去CP和FFT,接着利用信道估计结果进行SFBC译码,得到整个频域符号数据,然后根据交叉预编码的规则将其解映射为K组DFT数据,再分别按组进行IDFT处理,最后将得到的K组符号按顺序合在一起后转换为串行的数据符号完成整个接收译码过程。
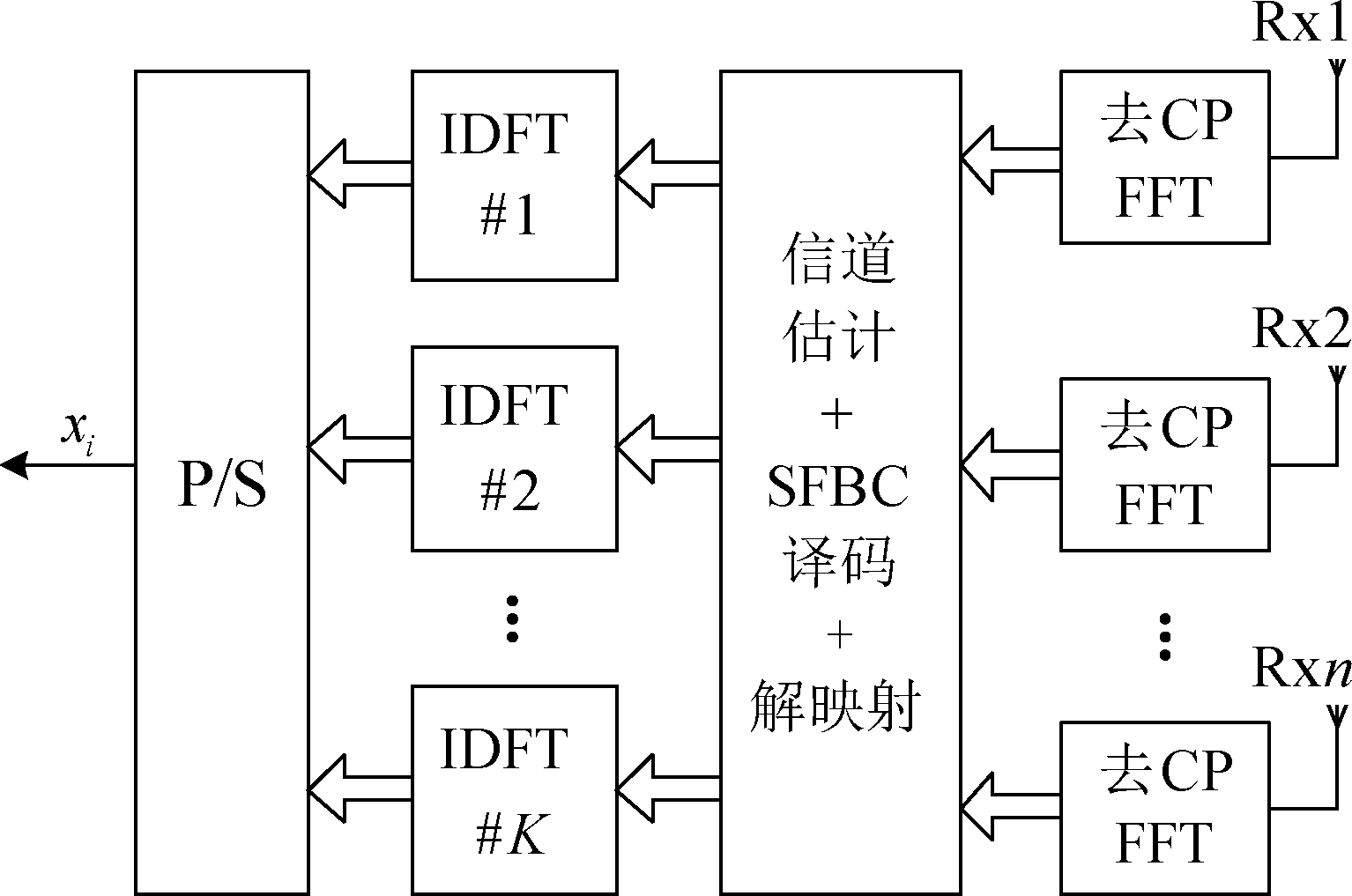
图5 本文方案接收端
Fig.5 Receiver of proposed scheme
3.2 PAPR性能分析
方便起见,现以DFT个数K=3来分析发送信号PAPR的情况。根据以上方案描述,每根天线上的频域信号是3路DFT输出的移位叠加。根据式(11),采用式(3)的码字矩阵,则第一根天线的频域序列表示为
(13)
![]() 表示
表示![]() 对FFT点数N的循环移位,
对FFT点数N的循环移位,![]() 是序列sk(n)经SFBC编码后的序列,即
是序列sk(n)经SFBC编码后的序列,即
 k=1,2,3,i=0,1,…,M-1
k=1,2,3,i=0,1,…,M-1
(14)
由于![]() 的傅里叶逆变换(IFFT)为
的傅里叶逆变换(IFFT)为
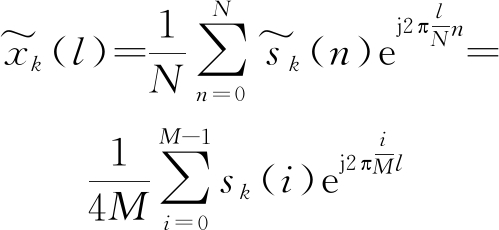
(15)
设l=qM+n,q是不小于0的整数,则
(16)
可以看出![]() 是xk(n)的周期重复。因此,根据DFT的线性相加和频移特性,第1根天线上的时域信号(不含CP)为
是xk(n)的周期重复。因此,根据DFT的线性相加和频移特性,第1根天线上的时域信号(不含CP)为
(17)
则
(18)
当点数N足够大时,
(19)
则发送信号的峰均比:
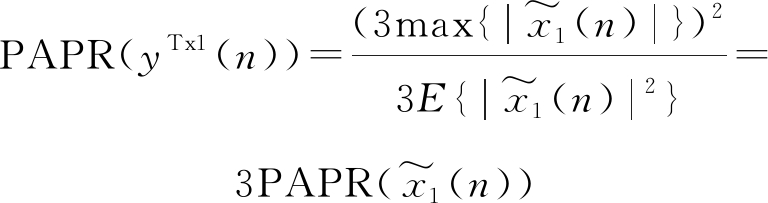
(20)
即为原单路信号PAPR的3倍。
同样地,剩余3根天线的频域序列为
(21)
(22)
(23)
经IFFT后的时域序列为
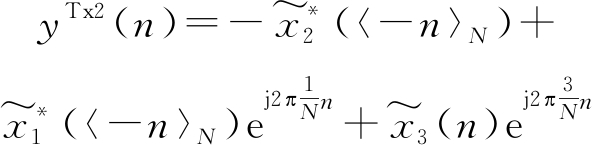
(24)
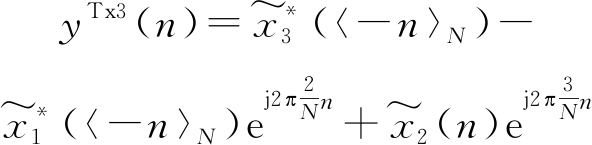
(25)
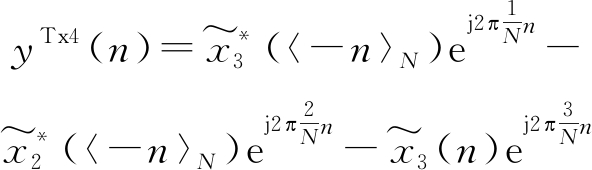
(26)
由于时域共轭反转并不改变信号星座点结构,那么每根天线最终发射信号均是原3路DFT时域信号的移相叠加,当右端各项幅值最大且相位相同时生成信号的幅度最大,其PAPR仅为原单路信号的3倍,即增加4.77 dB,且与单个DFT的点数无关。
对于DFT个数大于3个的配置情形,根据以上论述可以推断,发射信号PAPR至少为单路信号的K倍,因此本方案应尽量配置少个数的DFT单元,以实现低PAPR传输。而顺序SFBC方案3根特殊天线上的符号不但顺序被打乱,而且同时存在共轭与非共轭形式,其PAPR将高于多路单载波信号的叠加。
4 性能仿真分析
根据上文描述,对该方案的性能进行仿真验证。设单次串并转换的数据个数为384,DFT个数K=3,则每个DFT点数M=128,IFFT点数N=512,编码码字矩阵G采用式(3)的形式,调制方式为16QAM,通过蒙特卡洛仿真得到各发送天线的PAPR性能。
瞬时归一化功率(INP,Instantaneous Normalized Power)是衡量信号幅值的一种方式,用于评估信号PAPR性能。定义发送信号y的INP的互补累积分布函数(CCDF)为:
(27)
即信号样点的INP大于等于门限γ2的概率。它与信号的PAPR的关系为
(28)
图6是顺序SFBC编码方案特殊天线和本文方案各天线的PAPR性能对比,并以相同点数的SC-FDMA和OFDM作为参考。可以看出顺序SFBC编码方案特殊天线由于扩频作用,PAPR低于OFDM,但仍然比SC-FDMA高出较多,说明不规律的数据排列会破坏信号的单载波特性,使PAPR升高。本文的方案则改善了此现象,各天线都保持了较低的PAPR且大小一致,最大值约为7.3 dB,与理论相符(16QAM单载波信号PAPR为2.56 dB,加4.77 dB即7.33 dB)。与顺序SFBC方案相比,本文方案的INP范围收窄了大约1.7 dB,有利于发射天线系统的设计,降低了对功放非线性度的要求。
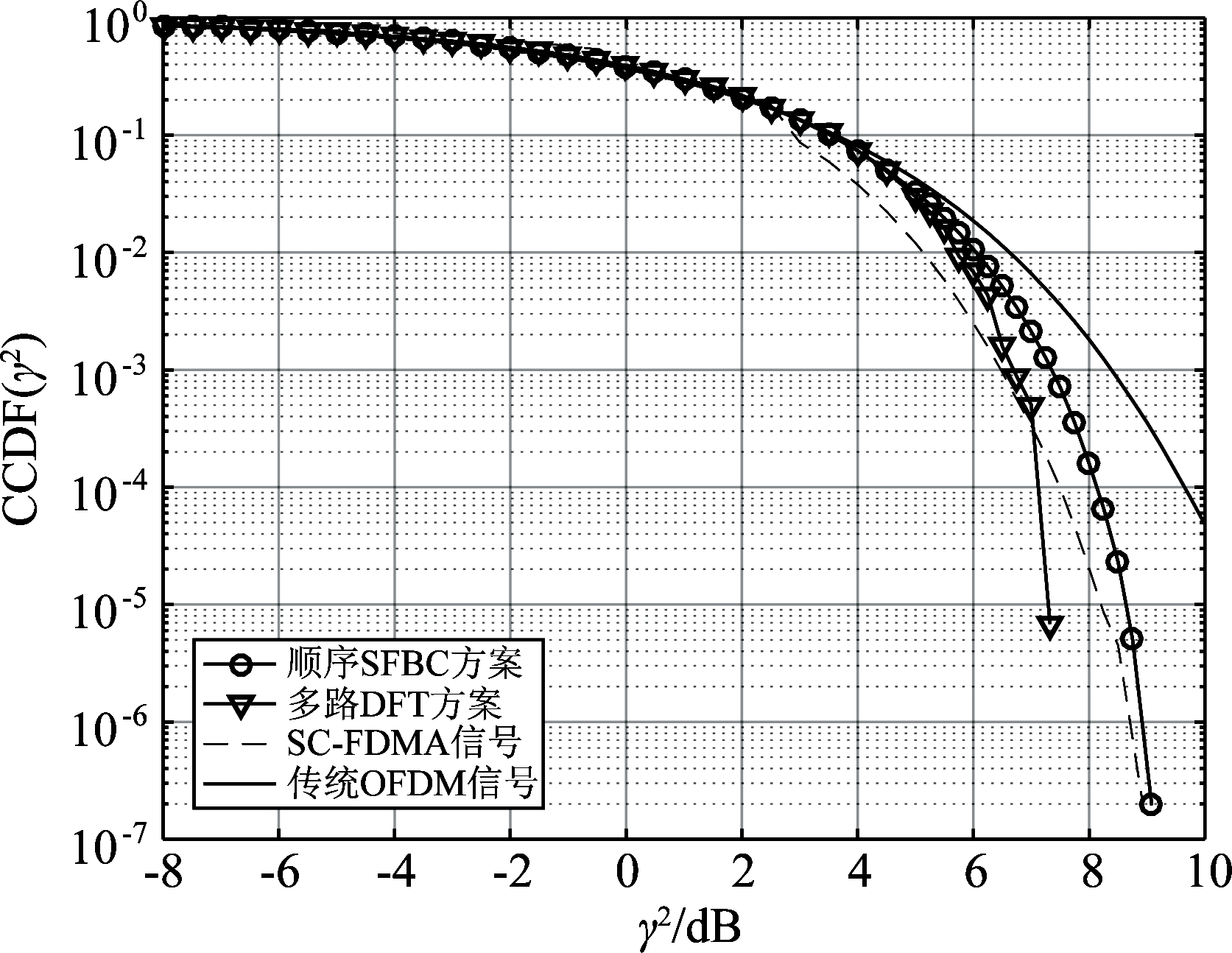
图6 顺序SFBC方案特殊天线与本文 方案各天线的PAPR性能仿真结果
Fig.6 PAPR performance of unique antennas of original scheme and proposed scheme
在与SC-FDMA和OFDM对比时,为了与本文方案保持一致,512点的IFFT中有384点承载数据,采用集中式映射在频域中央,其余为空载波。仿真结果显示,本文方案大幅优于OFDM,与SC-FDMA大致相当,互有高低,并在7 dB左右形成交点,在交点后的高PAPR段本文方案更低,且最大值低约1.9 dB。由于功放的非线性区间主要集中在此段,正常工作区间靠前端,即使曲线在7 dB前略高,本文方案PAPR变化对系统性能带来的影响也不会太大。
为进一步验证本文方案的思想,对不同DFT参数配置下的发送信号PAPR性能进行了仿真。图7中,在上文DFT个数K=3的配置基础上分别增加设置M=256、M=512,对应IFFT点数为1024、2048,仿真得到对应的CCDF曲线。
图7仿真结果显示,保持DFT个数不变,只增加各DFT的点数对PAPR几乎没有影响,并低于顺序SFBC方案(不同IFFT点数的顺序SFBC方案PAPR不变),与上文理论分析一致,从而验证了本文方案的思想。因此只要DFT的个数较少,无论单个DFT点数大小,信号PAPR都能够保持在较低水平。
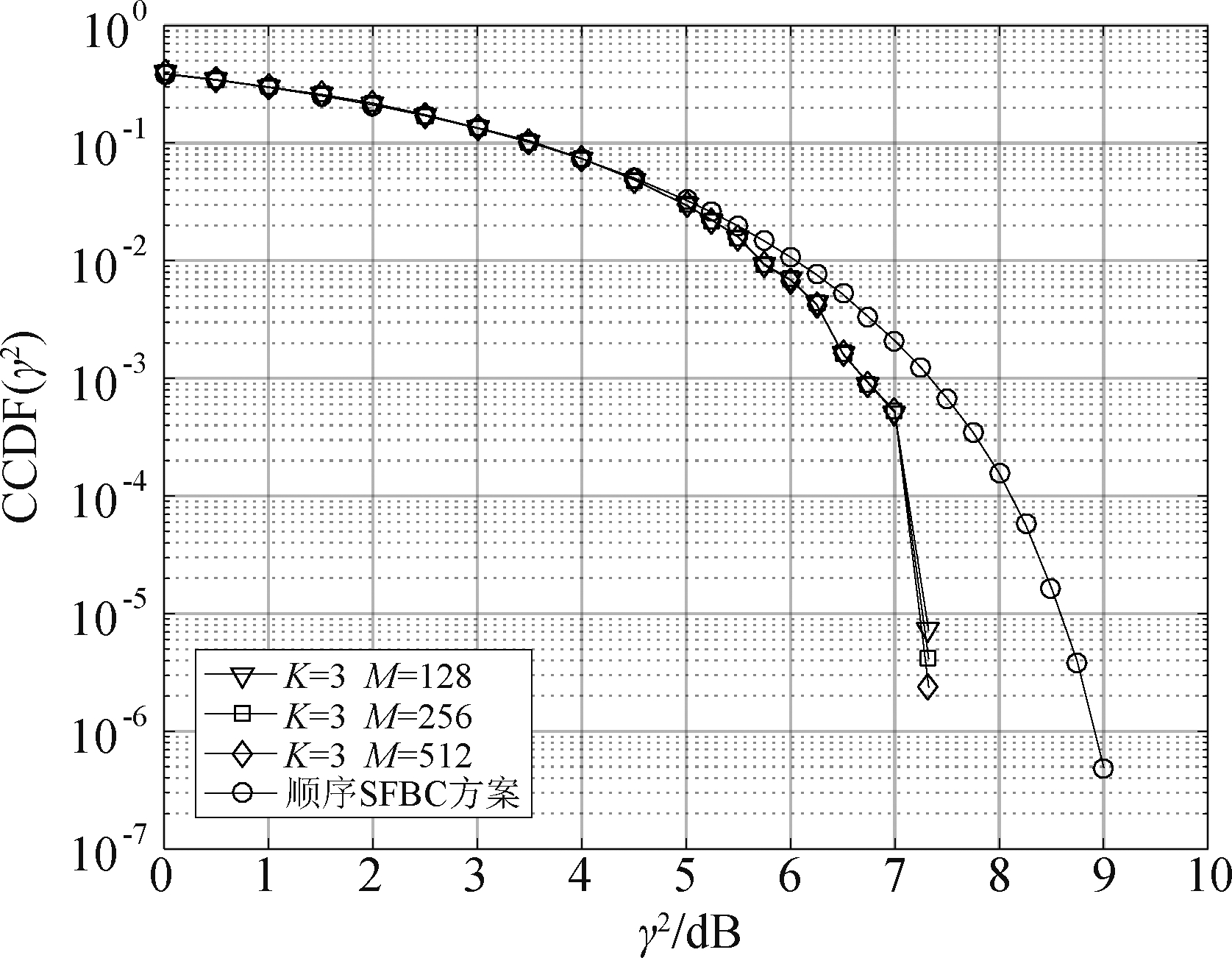
图7 不同参数配置下的PAPR性能结果
Fig.7 PAPR performance under different settings
本文还对新方案的误码率性能进行了仿真,参数如表1所示。认为收发天线间各信道相互独立,且位置相对静止,MIMO配置为四发一收,传输方式为DFT-S-OFDM,接收端拥有完整的信道状态信息,采用最小均方误差(MMSE)准则进行频域均衡。图8给出了本文方法、顺序SFBC方案、四发送天线SC-QOSFBC和OSTBC的平均BER性能。
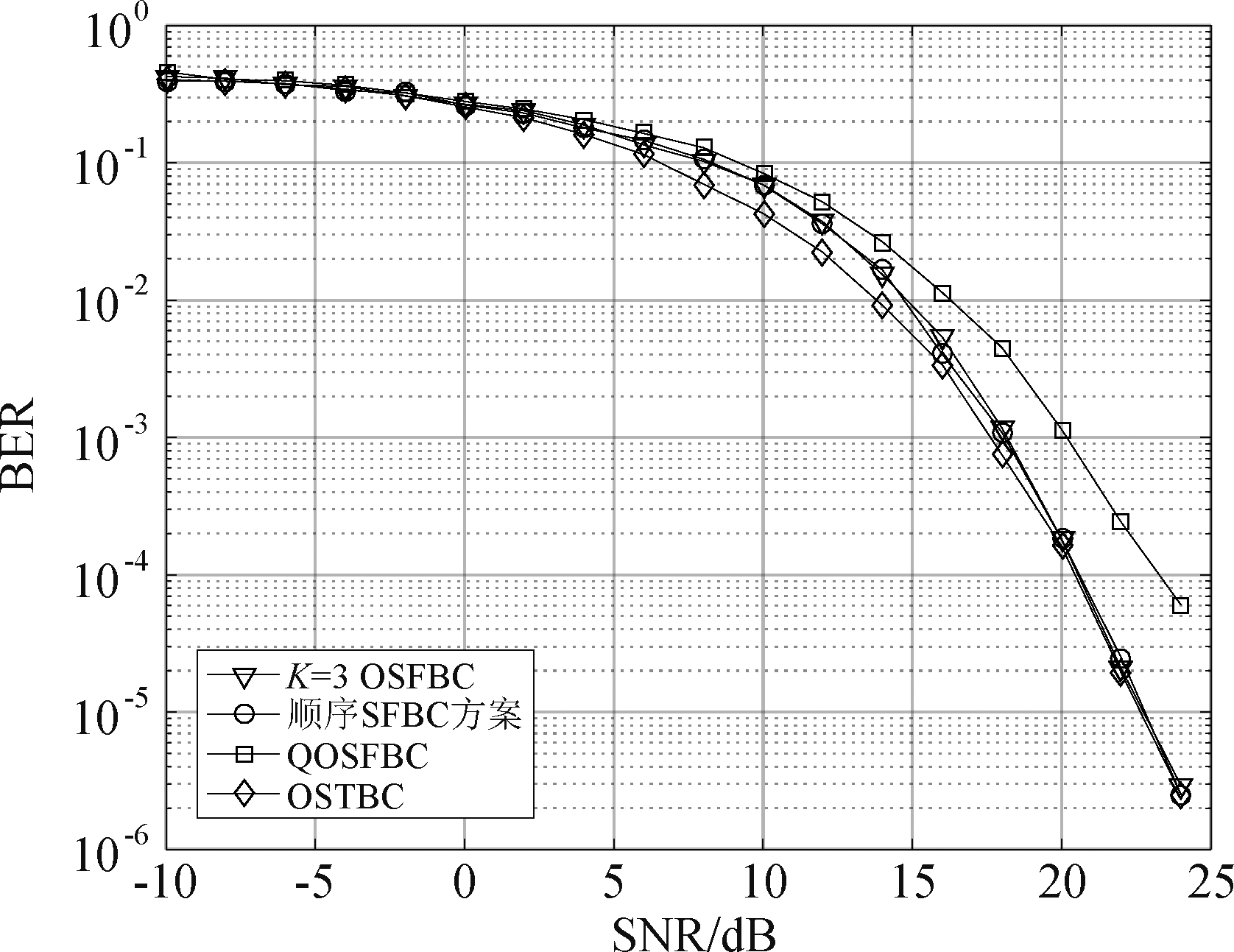
图8 不同传输方式的BER性能对比
Fig.8 BER performance of 4 transmission modes
表1 仿真参数
Tab.1 Simulation parameters

项目数值多径时延谱[0,30,70,90,110,190,410]ns时延功率谱[0,-1,-2,-3,-8,-17.2,-20.8]dB采样率15.36 MHzCP长度30IFFT点数512占用子载波个数384DFT个数K3DFT点数M128调制方式16 QAM数据速率43.53 Mbps
可见本文方法与顺序SFBC方案性能完全一致,并未造成性能的下降。曲线渐进斜率大于同为SFBC方式的QOSFBC,与OSTBC近似,说明其性能优于准正交编码,达到了相应的分集增益。需要注意的是,由于OSFBC在仿真信道下正交性被破坏,而OSTBC由于仿真未加入多普勒效应,信道时不变,仍然保持着正交性,因此其性能略优于SFBC。
5 结论
本文提出了一种适用于多天线OSFBC的低PAPR传输方法,并以四天线为例进行了介绍和分析。该方法与现有的DFT-S-FDMA系统结构类似,整体PAPR与同点数单载波信号大致相当,解决了原编码方案PAPR过高且各天线不一致的问题。理论分析与仿真结果表明,本文方案在最少个数DFT的配置下PAPR最低,有利于信号的传输,且每个DFT的点数几乎不影响PAPR,可以根据系统IFFT参数适当增大点数。同时,该低PAPR传输方法并未降低系统误码率性能,仍可取得相应发射分集增益。
[1]Lim J, Myung H G, Oh K, et al. Channel-Dependent Scheduling of Uplink Single Carrier FDMA Systems[C]∥IEEE Vehicular Technology Conference, Montreal, Que.: IEEE, 2007.
[2]Mrinalini, Singh K K. A SURVEY PAPER ON MULTICARRIER MODULATION TECHNIQUES[C]∥5th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gorakhpur: IEEE, 2018.
[3]Myung H G, Lim J, Goodman D J. Peak-To-Average Power Ratio of Single Carrier FDMA Signals with Pulse Shaping[C]∥2006 IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications. Helsinki: IEEE, 2006.
[4]Foschini G J, Gans M J. On limits of wireless communications in a fading environment when using multiple antennas[J]. Wireless Pers. Commun., 1998, 6(3): 311-335.
[5]Patil P, Patil M R, Itraj S, et al. A Review on MIMO OFDM Technology Basics and More[C]∥International Conference on Current Trends in Computer, Electrical, Electronics and Communication (CTCEEC), 2017: 119-124.
[6]Al-Dhahir N. Single-carrier frequency-domain equalization for space time block-coded transmissions over frequency-selective fading channels[J]. IEEE Commun. Lett., 2001, 5(7): 304-306.
[7]Jang J H, Won H C, Im G H. Cyclic prefixed single carrier transmission with SFBC over mobile wireless channels[J]. IEEE Signal Processing Letters, 2006, 13(5): 261-264.
[8]Singh D, Joshi H D. Performance analysis of SFBC-OFDM system with channel estimation error over generalized fading channels[J]. Transactions On Emerging Telecommunications Technologies, 2018, 29(3).
[9]Ciochina C, Castelain D, Mottier D, et al. A Novel Space-Frequency Coding Scheme for Single Carrier Modulations[C]∥IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens: IEEE, 2007.
[10]Ciochina C, Castelain, D, Mottier D, et al. A Novel Quasi-Orthogonal Space-Frequency Block Code for Single-Carrier FDMA[C]∥IEEE Vehicular Technology Conference, Singapore: IEEE, 2008: 1137-1141.
[11]Alamouti S M. A Simple Transmit Diversity Technique for Wireless Communications[J]. IEEE Journal on Select Areas in Communications, 1998, 16(8): 1451-1458.
[12]Jafarkhani H. A quasi-orthogonal space-time block code[J]. IEEE Transactions on Communications, 2001, 49(1): 1- 4.
[13]战非, 曹国震, 王建军, 等. OFDM系统降低峰值平均功率比研究[J]. 计算技术与自动化, 2017, 36(3): 35-39, 74.
Zhan Fei, Cao Guozhen, Wang Jianjun, et al. Research on Reducing the PAPR of OFDM system[J]. Computing Technology and Automation, 2017, 36(3): 35-39, 74.(in Chinese)


