1 引言
在大规模的机器类型通信(Machine-Type Communication,MTC)中,潜在用户的数量可能很大,活动用户的比率通常很低。为了利用MTC的大规模连接性和零星传输特性,前人积极探究了免调度非正交多址接入(Non-Orthogonal Multiple Access,NOMA)系统,每个设备无需基站调度即可发送信息,以减少调度过程的控制信令开销和传输延迟[1-2]。
针对免调度的NOMA系统,文献[3]提出了先进行导频辅助的联合活跃用户检测(Active User Detection,AUD)和信道估计(Channel Estimation,CE)算法,然后恢复活跃用户数据信息的方案。考虑到导频符号和数据符号在一帧时间内具有一致的(非)活跃状态,文献[4]直接以整个帧长为单位,在不需要事先知道用户活跃度的情况下为上行链路免调度NOMA系统提出了一种AUD,CE和多用户检测(Multiuser Detection,MUD)联合框架。文献[4]的作者在多重测量向量压缩感知(Multiple Measurement Vector-Compressive Sensing,MMV-CS)框架下建立CE和MUD联合问题,然后挖掘并利用潜在的帧结构化稀疏特性,将MMV-CS问题转换为块稀疏单一测量向量压缩感知(Block Sparse-Single Measurement Vector-Compressive Sensing,BS-SMV-CS)问题。最后,提出了块稀疏度自适应子空间跟踪(Block Sparsity Adaptive Subspace Pursuit,BSASP)重建算法来解决信道估计和多用户检测问题。此方案保证了较高的重建精度,但重建速度较慢。由于信道估计和多用户检测需要系统实时完成,如何提高估计和检测的速度是个有待解决的问题。
针对免调度NOMA系统多用户数据检测问题,与文献[4]相同本文直接在MMV-CS框架下解决CE和MUD联合问题。在传统的压缩感知模型下[5- 8],提出一种新的分布式自适应压缩感知重建算法,即门限辅助的分布式弱选择分段自适应匹配追踪(Thresholod Aided- Distributed Weak Selection Stagewise Adaptive Matching Pursuit,TA-DWSStAMP)算法。该算法引入阶段标识将整个过程分成两个部分,在开始的大步长阶段设计了一种幂函数型的变步长方法,可以更快地扩充支撑集的原子数量,减小算法的重建时间;当候选集的数量达到设定参数时,进入小步长阶段,用以保证更加准确地逼近真实稀疏度。另外,根据无线信道的物理特性,为了确保恢复信号的性能,该算法也采用了文献[4]中提出的基于高斯白噪声的迭代停止准则。仿真结果表明,针对免调度NOMA系统多用户数据检测,本文提出的算法与文献[4]提出的BSASP重建算法相比,算法复杂度显著下降,约为BSASP算法复杂度的10%,而重建性能接近。
2 基于MMV-CS框架的信道估计和多用户检测模型
我们考虑一个典型的上行免调度NOMA系统,其中K个用户(或发射机)将数据发送到基站(或接收机),所有终端均假定具有单个天线。在上行免调度NOMA系统中,一些发送端用户是活跃的,而其他发射端用户是处于非活跃状态的,这使得通信是零星的。本文假设用户在一个帧结构中处于同步状态,即在一帧内处于活动或不活动状态[9-10]。为了简单和不失一般性,我们考虑系统为平坦瑞利衰落信道,即一帧内全部时隙的信道状态保持不变。对于每个活跃用户,在一帧内首先发送一个导频符号,接着发送Jd个数据符号,并且所有不活动的用户在整个帧中不会传输任何符号,传输模型如图1所示。
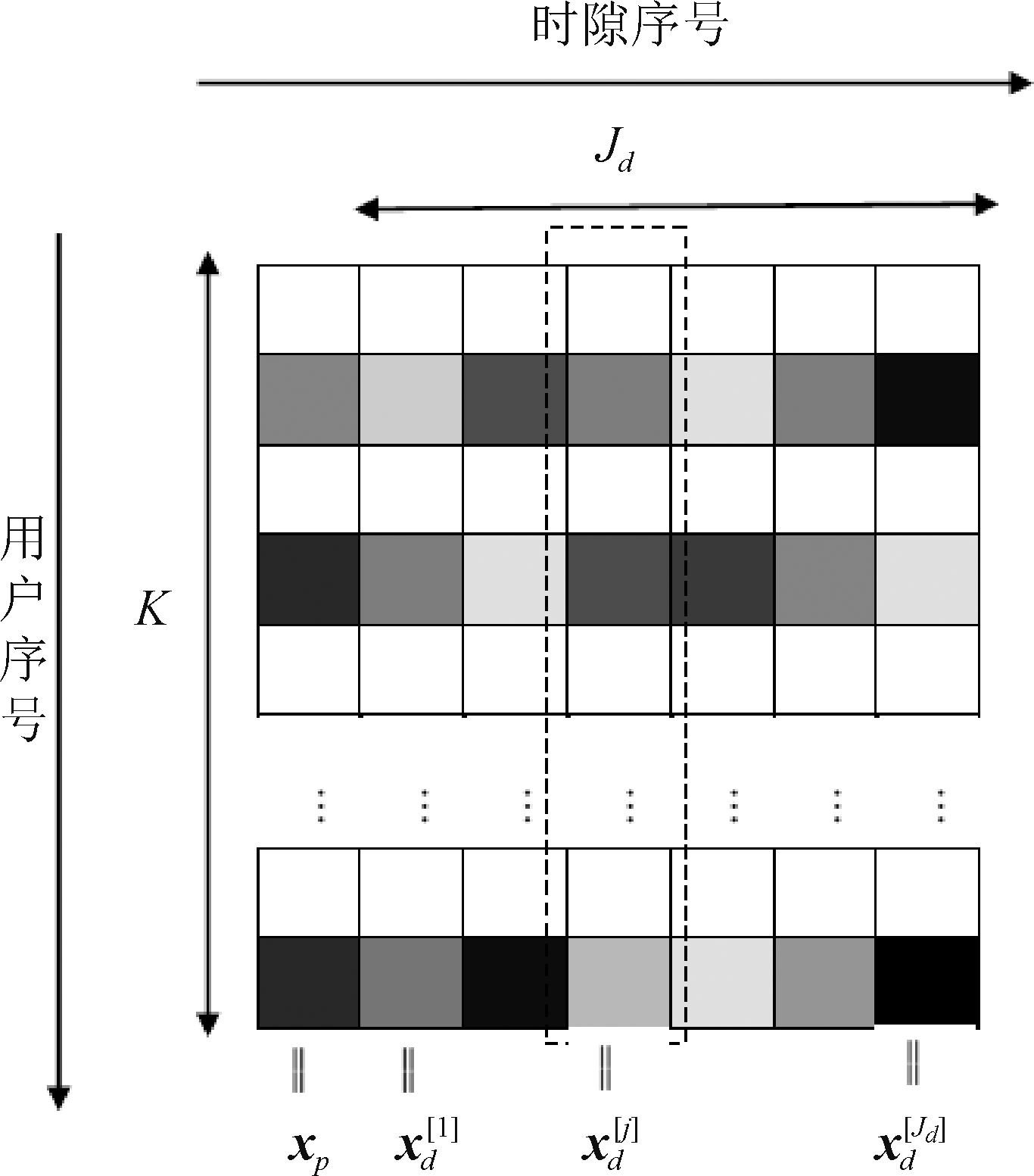
图1 基于帧结构化稀疏的传输模型
Fig.1 Transmission model based on frame structured sparse
因此,一帧内的联合稀疏特性可以表示为
(1)
其中,xp=(xp,1,xp,2,…,xp,K)T是导频符号向量,
表示第j个时隙上用户传输的数据符号向量。
是从增广复星座点集合χ
{χ0∪0}中提取的一个值,其中χ0表示复星座点集合,0表示用户为非活跃用户,等同于用户没有发送任何数据符号。supp(x)表示向量x的支撑集,即向量x中非零元素的索引。
在导频段,基站端接收到的信号可以表示为
(2)
其中,sk=(s1,k,s2,k,...,sN,k)T是用户k对应的扩频序列,N是扩展因子。为了适应MTC中大规模连接的需求,我们考虑了过载系统,即N<K。S=(s1xp,1,s2xp,2,…,sKxp,K)是测量矩阵,我们设导频符号向量xp=(xp,1,xp,2,…,xp,K)T中的导频符号xp,k为1,则S=(s1,s2,…,sK)代表扩频矩阵。 h=(h1,h2,...,hK)T是信道系数向量,h1,h2,...,hK之间相互独立并且都服从复高斯分布
是服从复高斯分布
的噪声向量,
是导频段噪声的方差。
在数据段,第j个时隙上基站端接收到的信号可以表示为
(3)
其中,
是服从分布
的复高斯噪声,
是数据段噪声的方差。事实上,由于信道状态信息h和数据符号
的支撑集是一样的,且除支撑集之外的位置上的元素为0。所以数据符号和其对应的信道状态信息h具有相同的支撑集为Γ,令
则
的支撑集也为Γ,此时式(3)可以重新表示为
(4)
这样,活跃用户的稀疏性可以反映在
中。因此,(3)被转移为单测量向量压缩感知(SMV-CS)模型(4)。
由于h与
的支撑集是一样的,我们以一帧为一个单位进行信号接收,从而就可以将式(2)和式(4)的两个稀疏信号重建问题合成一个新的稀疏信号重建问题。新的稀疏信号重建问题的表达式为
(5)
这样,两个基本的单一测量向量压缩感知(Single Measurement Vector-Compressive Sensing,SMV-CS)问题(式(2)和式(4))转化为了MMV-CS问题(式(5))。
令
则可以将式(5)转化为
Y=SX+Z
(6)
其中,S是N×K维的,X是K×J维的,其中J=Jd+1,Z是N×J维的,Y是N×J维的。
因此,我们可以在MMV-CS稀疏信号恢复框架下解决CE和MUD联合问题。
3 稀疏度自适应的压缩感知联合信道估计和多用户检测
本文提出了一种门限辅助的分布式弱选择分段自适应匹配追踪算法来恢复重建式(6)中的稀疏信号,由于式(6)中的稀疏信号X包含了信道状态信息h和用户信息
因此该算法可以联合解决信道估计和多用户检测问题,其中多用户检测包括活跃用户检测和数据检测。基于TA-DWSStAMP的联合信道估计和多用户检测算法步骤如下:
输入:接收信号矩阵
扩频矩阵S,初始步长d=1,时隙数J=Jd+1,Jd为发送数据信号的时隙数,高斯白噪声能量门限Pth。
输出:重建稀疏信号
步骤:
1) 初始化参数:支撑集Λ0=∅,索引集的大小U=d,迭代索引k=1,阶段标记δ=0,阶段stage=1,残差向量r0=Y。
2) 初选:Lk={|uk(j)|>α·umax},uk=abs[|SHrk-1|rows-∞]。其中,阈值参数α∈[0.5,1],rk为第k次迭代的残差向量,|·|rows-∞ 表示矩阵·按行取无穷范数,umax为uk元素中的最大值,初选的候选集Lk是uk元素中大于α·umax的值所对应的行标j构成的集合。
3) 更新候选集:Ck=Λk-1∪Lk。
4) 判断阶段标识值是否需要更新:如果size(Ck)>μ·N,则阶段标记δ=1。其中μ为标识阈值参数,size(Ck)表示候选集中元素的个数。
5) 终选:如果size(Ck)>U,则终选支撑集
否则F=Ck。其中
表示
的值按行取无穷范数中前U个最大值对应的行标所构成的集合。
6) 信号估计:
7) 计算残差向量:
8) 判断迭代停止条件:若
则转向步骤 11);否则继续向下迭代。其中,
表示
按行取二范数的平方后的最小值,是由终选支撑集F构成的估计信号矩阵,即
9) 判断是否更新步长、支撑集以及残差:
a) 若||rnew||2>||rk-1||2且δ=0,则stage=stage+1,U=U+「stageb⎤×d,Λk=Λk-1,rk=rk-1;
b) 若||rnew||2>||rk-1||2且δ=1,则U=U+d,Λk=Λk-1,rk=rk-1;
c) 否则,以固定支撑集大小迭代:rk=rnew,Λk=F。
10) 更新迭代次数:k=k+1。
11) 计算重建稀疏信号:
在获得式(6)的解后,我们可以得到估计的信道状态信息
和
从而我们可以根据式(3)获得用户数据符号的估计值
其中用户数据符号
中的非零值代表了活跃用户的数据,0值代表了非活跃用户。
本文提出的TA-DWSStAMP算法有如下几个特点:
第一,该算法在步骤2)进行原子初选的部分,只选出满足条件即相关性比α·umax大的原子,通过设置合适的阈值参数α使得每次选出的原子个数不固定,本文α可以取在0.7 ～0.95之间的值,确保选出的原子都具有较大的相关性,提高了重建精度。
第二,在第9) 步中通过阶段标记参数δ来确定支撑集大小U的改变。通过步骤4)中的size(Ck)>μ·N判断阶段标记参数δ是否需要更新,其中μ为标识阈值参数,根据1/4原则[11],μ的取值范围通常取小于 1/4 的值即可,本文中μ取0.085。本文通过可变步长的方法来增大支撑集U,当δ=0时,候选集的原子个数少,可以以大步长增大支撑集的大小,利用幂函数y=xb(0<b<1)是以逐渐减慢的速率递增的特性,设计了一种幂函数型的变步长方法来更快地扩大支撑集以逼近真实稀疏度[12],支撑集的大小U=U+「stageb⎤×d,「·⎤表示向上取整,b为设置的参数,一般取 0.4 ～ 0.6,本文取0.5,这样做有效地减少了算法的重建时间;当候选集的数量达到一定大小时,阶段标记更新为δ=1,为了避免过估计,以固定的小步长更新支撑集的大小U=U+d,这样可以更加准确地逼近真实稀疏度,保证较高的重建精度。
第三,为了提高算法重建信号的精度,在步骤8)中使用了文献[4]中提出的基于高斯白噪声的迭代终止条件。当检测出的活跃用户在一帧时间内能量的最小值小于JPth时,即<JPth,停止迭代。由大量的仿真实验表明,当得到真实用户活跃度时,如果继续下一次迭代,算法将会重构高斯白噪声,从而增加一个能量通常小于噪声能量门限的虚拟“非零值”部分,这会导致用户活跃度过估计。因此,使用基于高斯白噪声的迭代停止条件可以获得较为可靠的用户活跃度检测结果,确保了恢复信号的重建性能。
4 仿真结果和分析
本文是在有4GB RAM和1.80 GHz 的Intel(R) Core(TM) I3-3217U CPU的华硕笔记本运行Matlab2014a进行仿真实验的。仿真时的参数设置如下:一帧内的时隙数为J=7,其中有个Jd=6个时隙数用来发送数据信息;潜在用户数为K=200,采用的扩频序列是伪随机高斯序列,扩频序列长度为N=50,因此过载率为400%;信道为平坦瑞利衰落信道;仿真时调制方式采用QPSK。在信道估计和数据检测的联合框架中我们用所提出的TA-DWSStAMP算法来重建稀疏信号,算法中的μ值设置为0.085;在信噪比SNR分别为5 dB、10 dB、15 dB、20 dB、25 dB、30 dB的情况时,算法迭代终止条件中的门限Pth与文献[4]仿真中设定的数值相同,分别为0.21、0.07、0.035、0.014、0.0035、0.0014。在不同的信噪比条件下每次仿真进行2000次,然后取平均值得出各信噪比情况下的仿真结果。
先通过实验的方法考查阈值参数α对信号的成功活跃检测率(Successful Activity Detection Rate,SADR)的影响。α在0.7～0.95之间取值,分别取为0.7、0.8、0.9、0.95,仿真结果如图2所示,当α=0.9时,活跃用户的成功检测率最高,因此,之后的仿真都取α=0.9。
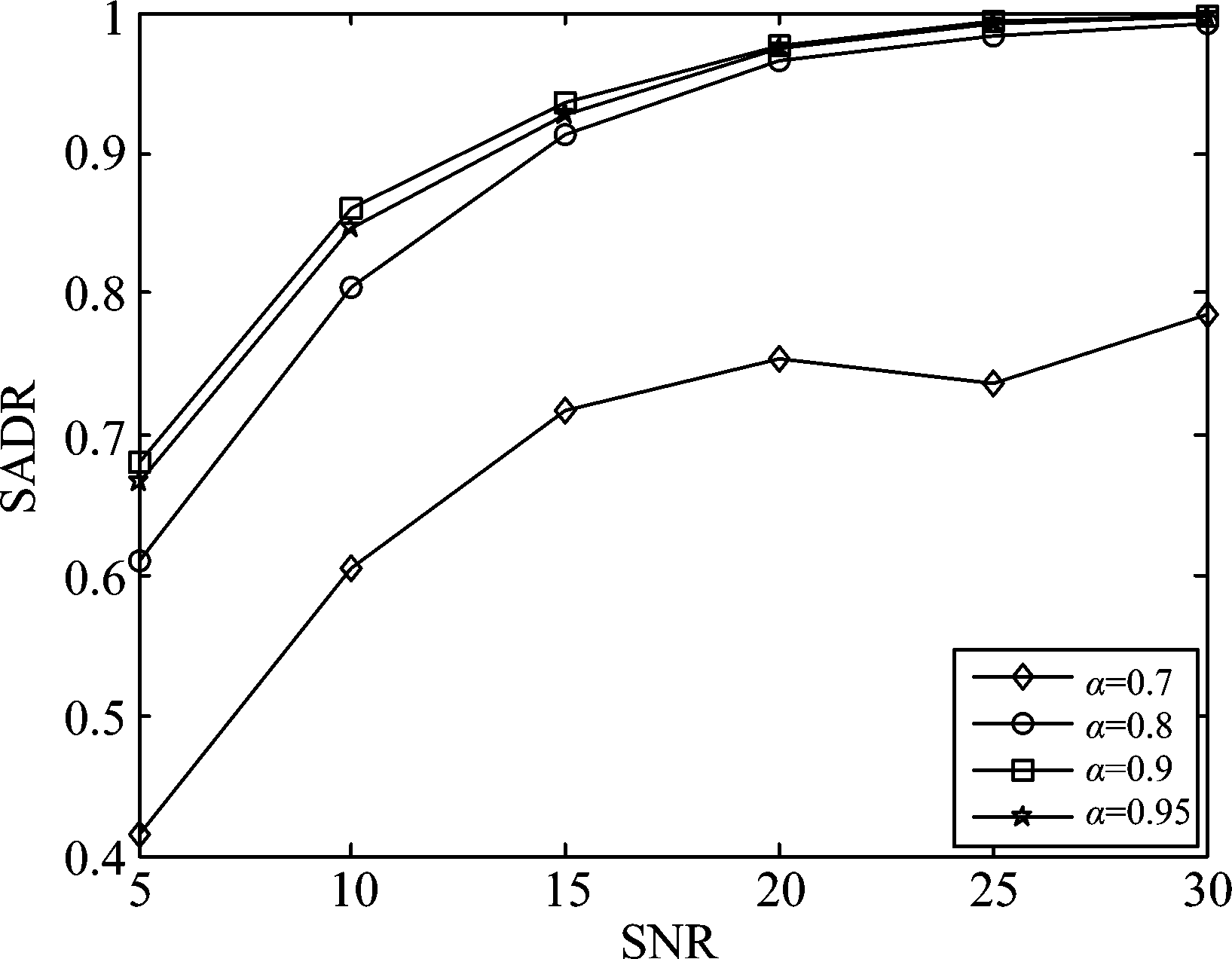
图2 不同阈值参数α下TA-DWSStAMP算法 的信号SADR性能比较
Fig.2 SADR performance comparison of TA-DWSStAMP algorithm under different threshold parameters
下面比较本文提出的TA-DWSStAMP算法与BSASP 算法进行稀疏信号重建的性能,具体有以下性能: SADR、误符号率性能(Symbol Error Rate,SER)、归一化均方误差(Normalized Mean Square Error,NMSE)以及算法复杂度。
4.1 SADR性能分析
本节比较各种算法在不同信噪比下的成功活跃检测率。图3所示为各算法在信噪比从5 dB到30 dB之间的数据成功活跃检测率曲线图。由图3可知,在信噪比大于8 dB时,TA-DWSStAMP算法的SADR性能都要优于BSASP 算法。这是由于TA-DWSStAMP算法采取了预选操作,通过设置α值选出了相关值较大的原子,提高了重建的精度。
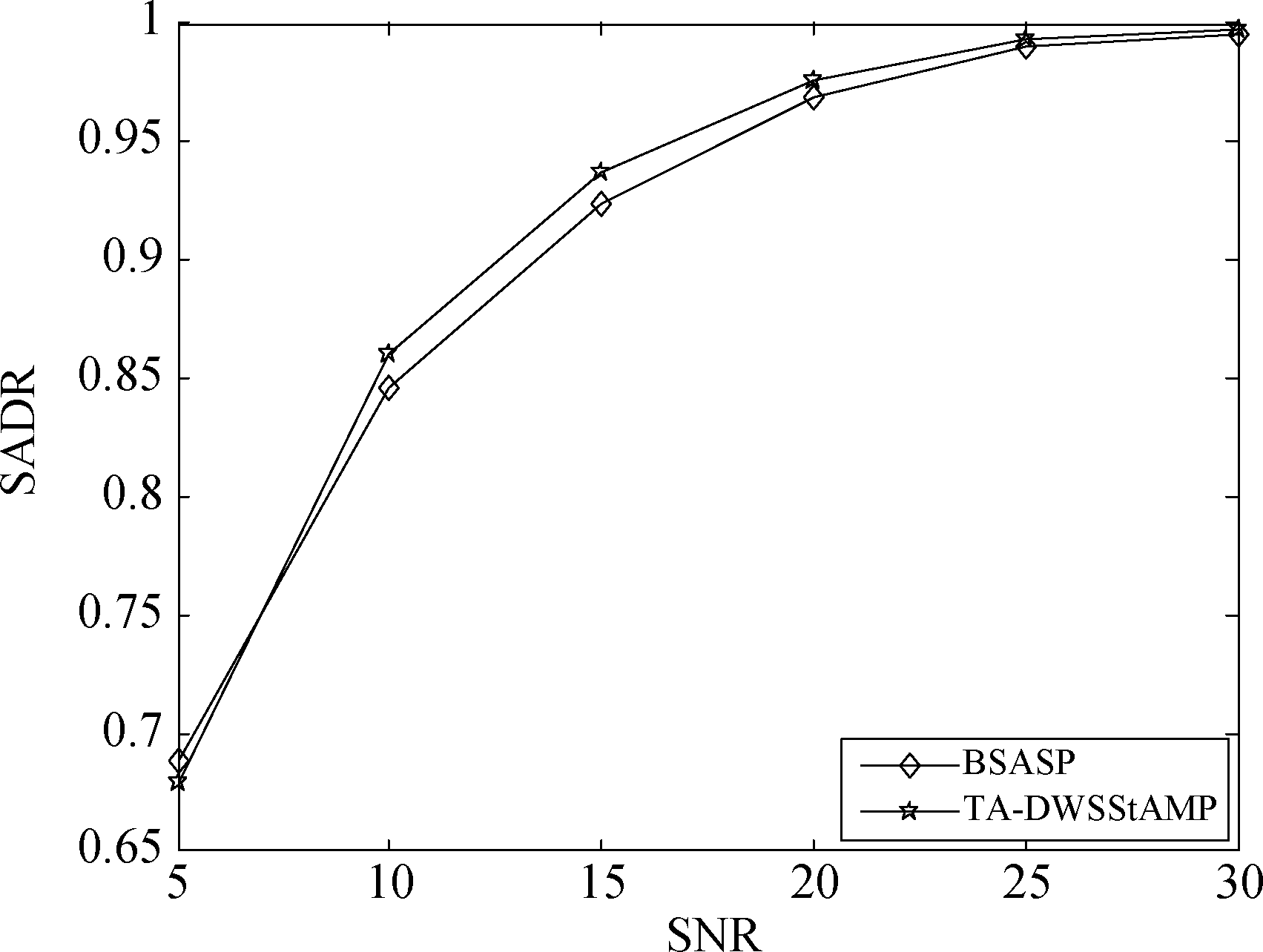
图3 各种算法在不同信噪比下的SADR性能对比
Fig.3 SADR performance comparison of various algorithms under different SNR
4.2 SER性能分析
本节比较各种算法在不同信噪比下的误符号率性能。图4所示为两种算法在不同信噪比下的误符号率曲线。从图4可以看出:TA-DWSStAMP算法与BSASP 算法的SER性能总体接近。当信噪比小于15时,TA-DWSStAMP算法比BSASP 算法的SER性能略差一点,这是由于在低信噪比阶段,噪声能量占比较大,通过预选选出的支撑集的原子有部分是噪声重建的,存在偏差;当信噪比大于15时,TA-DWSStAMP算法比BSASP 算法的SER低,且随着信噪比的增大,TA-DWSStAMP算法的SER性能优势越明显,这是由于TA-DWSStAMP算法有预选设计,在预选部分选出的原子相关性都是比较大的。
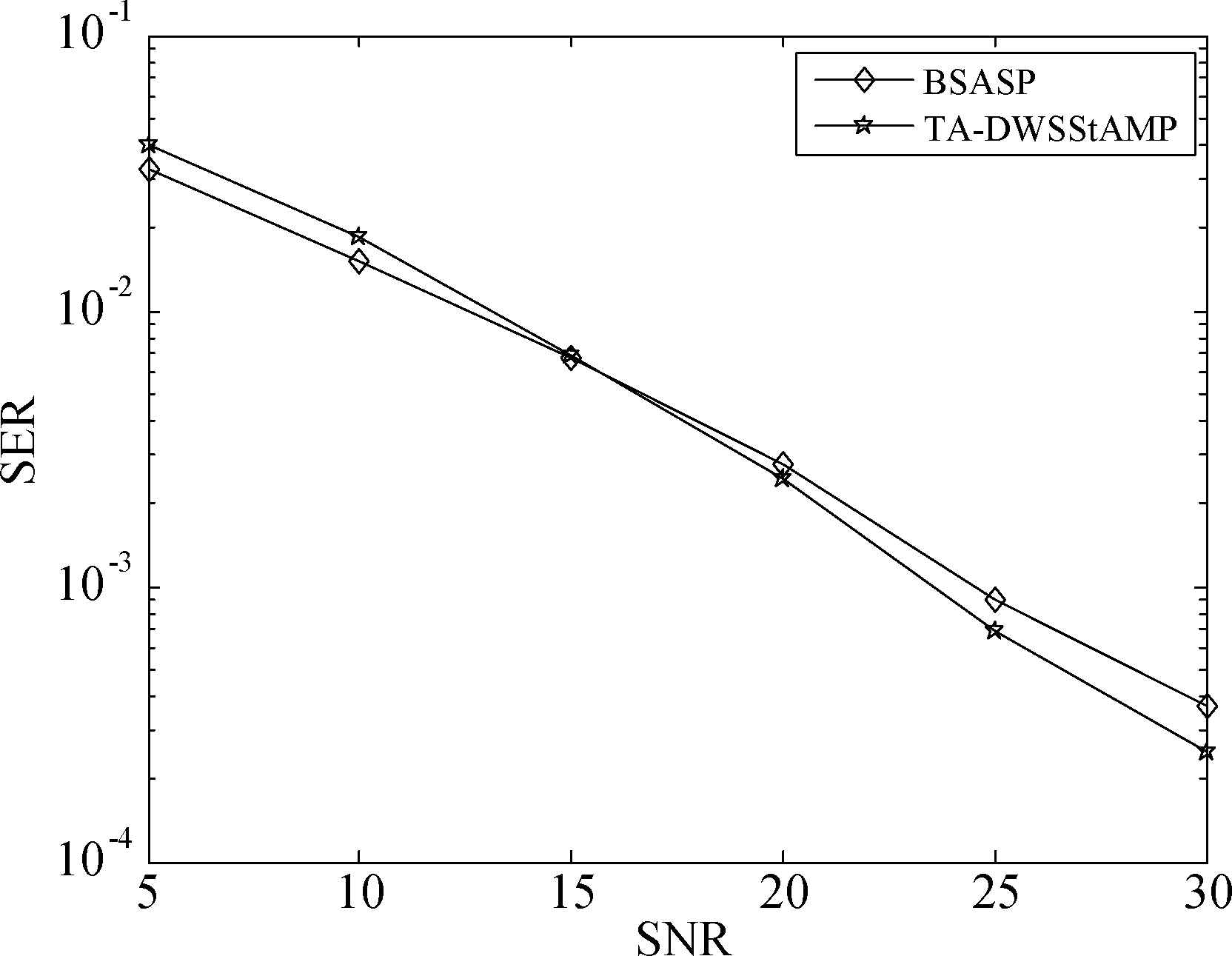
图4 各种算法在不同信噪比下的SER性能对比
Fig.4 SER performance comparison of various algorithms under different SNR
4.3 NMSE性能分析
本节通过衡量信道估计的归一化均方误差来比较仿真性能,NMSE的计算表达式为:
其中,h为信道系数向量,
为估计的信道系数向量,G是仿真的次数。图5显示的是两种算法在不同信噪比下NMSE仿真结果。结果表明:总体上来看,本文提出的TA-DWSStAMP算法在信道估计的NMSE性能上与BSASP 算法相接近。
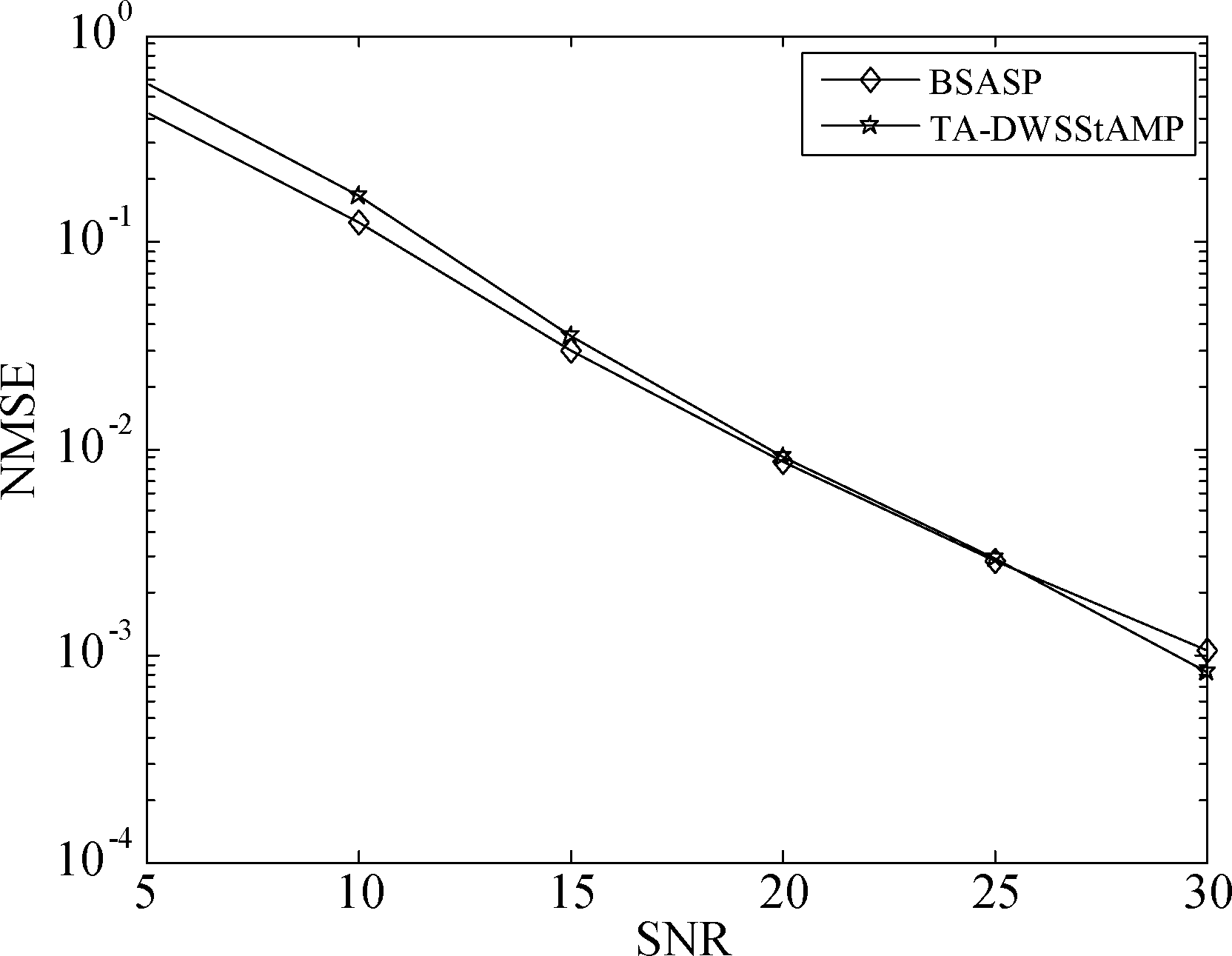
图5 各种算法在不同信噪比下的NMSE性能对比
Fig.5 NMSE performance comparison of various algorithms under different SNR
4.4 复杂度分析
由于信号的数据检测在NOMA系统中是实时进行的,所以如何降低算法的运算复杂度尤为重要。本文提出的TA-DWSStAMP算法单次迭代的复杂度主要来自于复乘数,则
的复杂度可以分别表示为O(KNJ)、O(s3+2Ns2+NJs)、O(s3+2Ns2+NJs)、O(KNJ)。因此,TA-DWSStAMP算法单次迭代的复杂度可以表示为O(KNJ+NJs+2Ns2+s3)。其中,s(0<s≤K)表示每个阶段算法所估计出来的稀疏度。而文献[4]提出的BSASP重建算法单次迭代的复杂度也主要来自于复乘数,复杂度可以表示为O(5K+3KJ+3KNJ2+2NJ(Js)2+(Js)3)。表1列出了s取不同值时两种算法的最大复乘次数,本论文在仿真时,K=200,N=50,J=7,可以看出本文提出的TA-DWSStAMP算法单次迭代的复杂度远小于BSASP重建算法单次迭代的复杂度。
表1 s取不同值时两种算法的最大复乘次数
Tab.1 Maximum multiplication times of two algorithms under different values of parameters s
s=5s=10s=15TA-DWSStAMP算法1.49×1051.69×1052.02×105BSASP算法2.81×1068.58×1061.88×107
另外,图6所示为两种算法在不同信噪比下的停止迭代次数。由图6可以直接看出,在相同的停止迭代条件下,本文提出的TA-DWSStAMP算法停止迭代所需的迭代次数比BSASP算法少很多。因此综合两种算法的单次迭代次数和达到停止迭代需要的迭代次数,本文提出的TA-DWSStAMP算法总复杂度比BSASP算法更低。
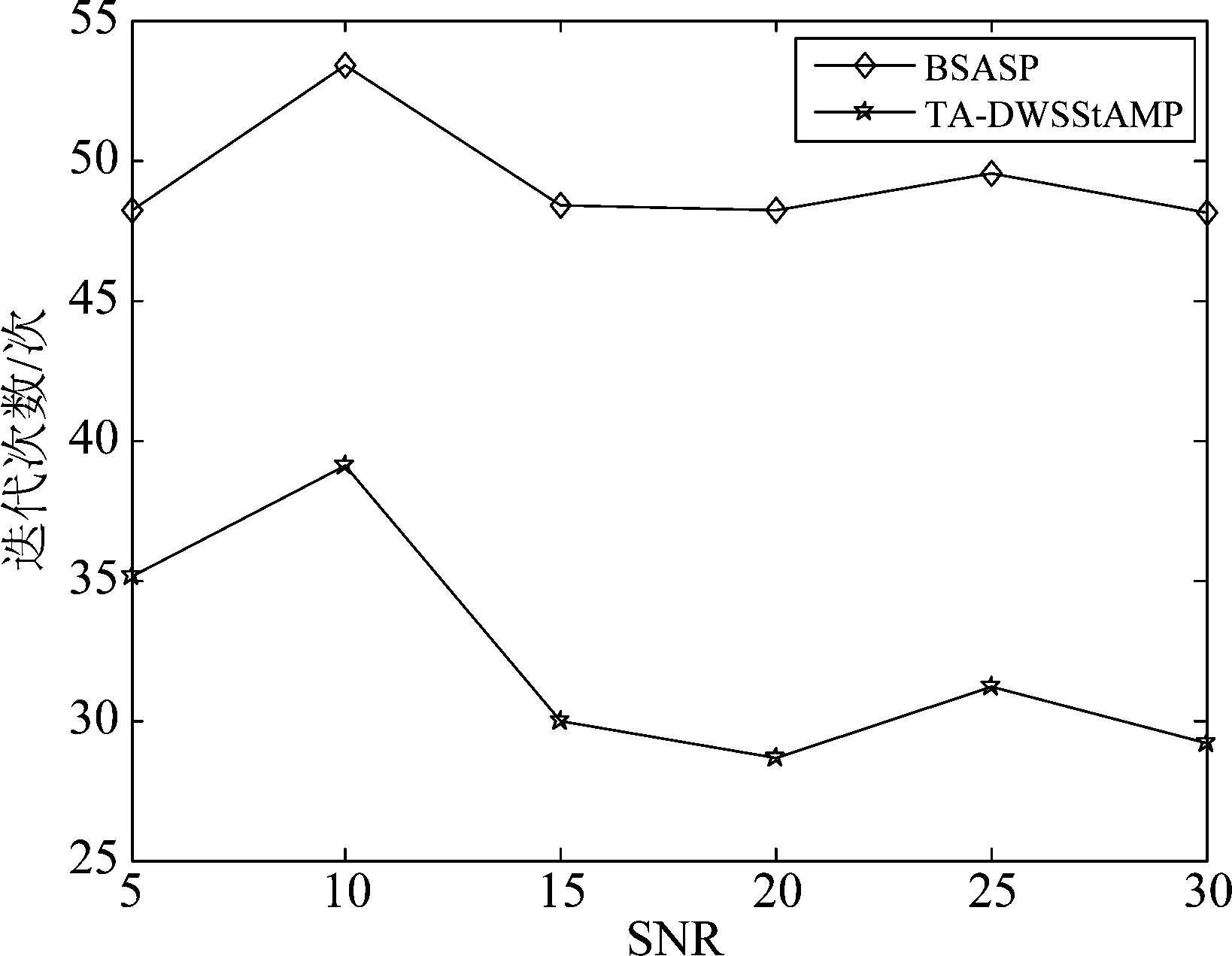
图6 不同算法的停止迭代次数图
Fig.6 Numbers of stopping iteration for various algorithms
图7是两种算法在不同信噪比情况下的运行时间对比图。从仿真图7中,我们也可以发现:在任何信噪比条件下,本文提出的TA-DWSStAMP算法的运算时间比BSASP算法的运算时间少得多。总体来看,本文提出的TA-DWSStAMP算法复杂度仅为文献[4]中提出的BSASP算法的10%,运算复杂度大大降低了。
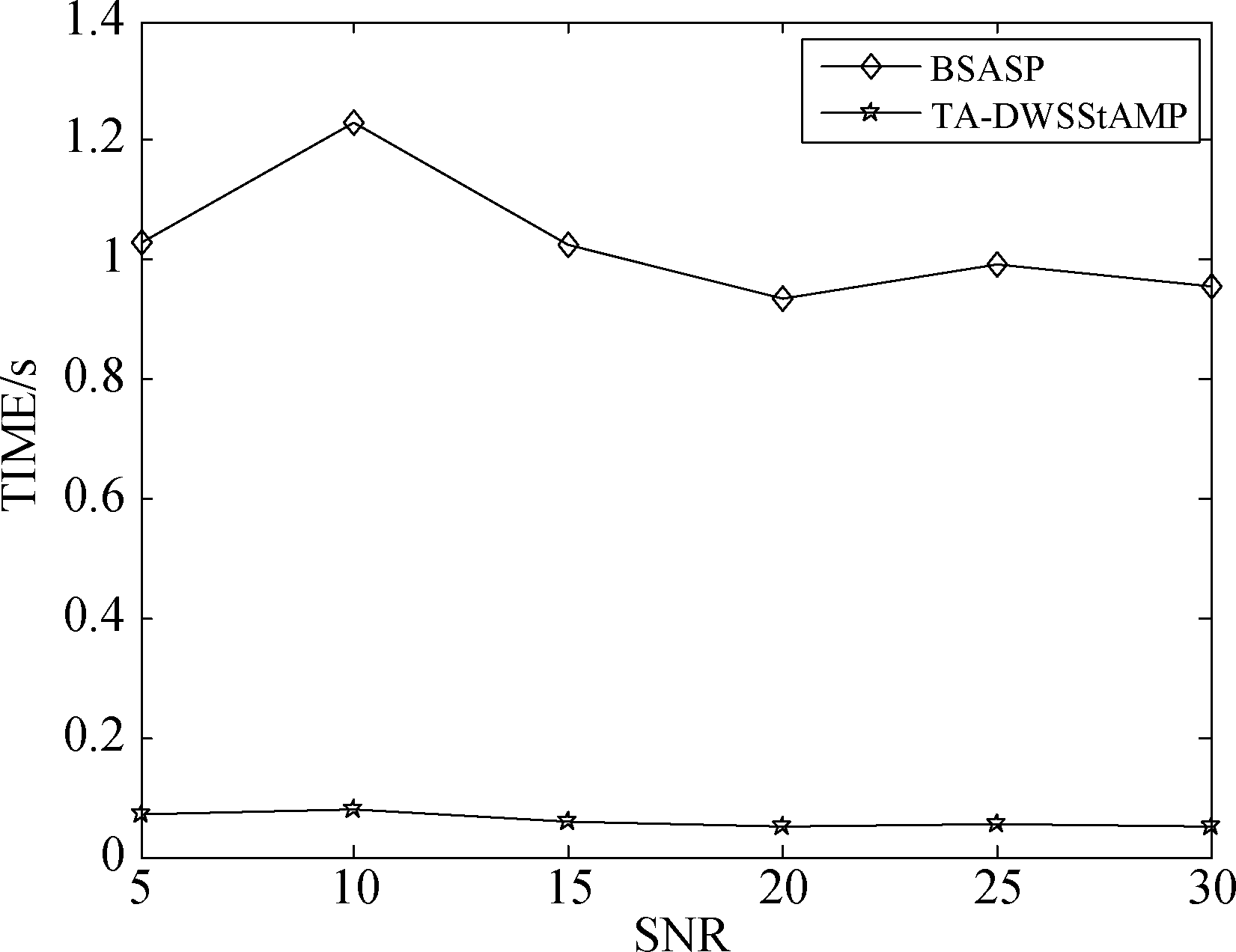
图7 两种算法运算时间的比较
Fig.7 Running time comparison of two algorithms
5 结论
本文针对上行免调度NOMA系统,提出了一种基于门限辅助的分布式弱选择分段自适应匹配追踪(TA-DWSStAMP)算法的联合信道估计和信号检测的解决方案。该方案可以利用一帧内导频符号和数据信息之间的联合稀疏特性,将活跃用户检测、信道估计及数据检测进行联合。本文提出的算法在开始的大步长阶段设计了一种幂函数型的变步长方法,当候选集的数量达到设定参数时,改变标记参数进入固定步长的小步长阶段。仿真结果表明,在上行免调度NOMA系统的联合信道估计和多用户检测的问题中,TA-DWSStAMP算法以极低的运算复杂度获得了与现有算法相近的估计性能。
[1]Du Yang, Cheng Cong, Dong Binghong, et al. Block-sparsity-based multiuser detection for uplink grant-free NOMA[J]. IEEE Transactions on Wireless Communications, 2018, 17(12): 7894-7909.
[2]Nikopour N, Baligh H. Sparse code multiple access[C]∥International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). UK: IEEE, 2013: 332-336.
[3]Hannak G, Mayer M, Jung A, et al. Joint channel estimation and activity detection for multiuser communication systems[C]∥International Conference on Communication Workshop(ICCW). UK: IEEE, 2015: 2086-2091.
[4]Du Yang, Dong Binghong, Zhu Wuyong, et al. Joint Channel Estimation and Multiuser Detection for Uplink Grant- Free NOMA[J]. IEEE Wireless Communications Letters, 2018, 7(4): 682- 685.
[5]Wang Qun, Liu Zhiwei. A robust and efficient algorithm for distributed compressed sensing[J]. Computers and Electrical Engineering, 2011, 37(6): 916-926.
[6]Duarte M F, Sarvotham S, Baron D, et al. Distributed Compressed Sensing of Jointly Sparse Signals[C]∥Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers. USA: IEEE, 2005: 1537-1541.
[7]Bi Xue, Chen Xiangdong, Zhang Yu, et al. Variable step size stagewise adaptive matching pursuit algorithm for image compressed sensing[C]∥International Conference on Signal Processing, Communication and Computing (IC-SPCC). China: IEEE, 2013: 1- 4.
[8]Song Yuming, He Xueyun, Gui Guan, et al. Novel Adaptive Distributed Compressed Sensing Algorithm for Estimating Channels in Doubly-Selective Fading OFDM Systems[J]. KSII Transactions on Internet and Information Systems, 2019, 13(5): 2400-2413.
[9]Wang Bichai, Dai Linglong, Mir Talha, et al. Joint user activity and data detection based on structured compressive sensing for NOMA[J]. IEEE Communication Letters, 2016, 20(7): 1473-1476.
[10]Wei Chao, Liu Huaping, Zhang Zaichen, et al. Approximate message passing-based joint user activity and data detection for NOMA[J]. IEEE Communications Letters, 2017, 21(3): 640- 643.
[11]Candes E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.
[12]费洪涛, 何雪云, 梁彦. 基于自适应压缩感知的OFDM稀疏信道估计研究[J]. 南京邮电大学学报(自然科学版), 2019, 39(2): 49-54.
Fei Hongtao, He Xueyun, Liang Yan. OFDM sparse channel estimation based on adaptive compressed sensing[J]. Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition), 2019, 39(2): 49-54.(in Chinese)
