1 引言
人脸识别技术是近些年来研究人员们不断研究的热门领域之一,由此涌现了大量的人脸识别算法[1-3]。随着图像处理技术不断地发展,当下的人脸识别系统在约束的条件下已经可以实现比较准确的识别效果。由于这些人脸识别系统采集的人脸图像尺寸较大,拥有丰富的便于识别的特征信息,因此可以实现令人满意的识别效果。但在很多实际监控场景中经常会遇到低分辨率的问题。有时由于监控视频中感兴趣的目标与摄像头距离较远,因此监控设备采集到的人脸图像会呈现出尺寸较小,视觉模糊等特点,这样的人脸图像称为低分辨率图像。它不像高分辨率人脸图像一样拥有丰富的面部特征信息,因此难以直接进行识别。对这类人脸图片的识别被称为低分辨率人脸识别。
目前针对低分辨率人脸识别问题的研究方法大多分为三类:低分辨率图像上采样法[4- 8];高分辨率图像下采样法[9-10];统一特征空间映射法[11-18]。低分辨率图像上采样法是通过上采样低分辨率图像来实现匹配。这类方法由于将图像数据从低维映射到了高维,因此会存在无用信息的干扰。高分辨率图像下采样法是通过下采样高分辨率图像来实现匹配。这类方法由于将图像数据从高维映射到了低维,而高维数据中的有用信息较多,因此映射过程会造成信息损失。第三类方法是统一特征空间映射法,这类方法是目前应用的最为广泛的低分辨率人脸识别方法。它是通过同时上采样低分辨率图像和下采样高分辨率图像来完成匹配,从而实现识别任务。与前两种方法相比,该类方法可以减弱映射过程中的信息损失和噪声干扰。2009年Li等人提出了一种局部保持的耦合映射方法(CLPM)[11],通过添加一个权重矩阵来保持高分辨率空间中样本的局部几何结构,在原始耦合映射算法的基础上提高了识别表现,然而该方法没有把类间图像信息考虑在内。后来shi等人提出了局部到全局的耦合子空间映射(LGCM)[15],在目标函数中加入了图像的类间信息和类内信息,使得识别表现再次得到了提升。Jiang等人提出了一种耦合可判别多元流行分析的方法(CDMMA)[17],引入了图的方法来保持样本的多元流行结构信息,实现了不错的识别效果。Chen等人提出了一种双层耦合局部保持映射的方法(DLCLPM)[18],在训练阶段通过引入多种不同的高分辨率图像,利用其丰富的信息来学习更精确的耦合空间。这些基于耦合映射的方法在解决低分辨率人脸识别问题上确实取得了不错的效果,但该类方法只是简单地将不同空间的数据进行了映射,没有明确的物理意义,在该类问题上没有较强的可解释性。低分辨率人脸识别的关键是如何将不同类型的数据进行匹配,而不同类型数据往往所处的特征空间是不同的,因此对于不同类型数据的匹配问题首先要考虑样本表示。在这方面, NMF[19-20](nonnegative matrix factorization)拥有不错的表现。
NMF在形式上只是一种简单的矩阵分解方法,但其本质上是一种特征提取方法。以图像为例,由于图像像素值非负,通过非负矩阵分解可以提取图像的局部特征,而这些局部特征又可以通过重新组合来表示原来的图像数据。因此,非负矩阵分解其实是一种基于局部表示的方法。目前,NMF算法通常用于提取高分辨率图像的特征,因为高分辨率图像的特征信息比较容易提取。由于低分辨率图像没有较多的特征信息,因此直接通过NMF来提取有用的特征比较困难。为了解决低分辨率人脸图像的特征提取问题,本文提出了一种新的RCNMF(relaxed coupled nonnegative matrix factorization)算法,该算法认为即使人脸图像的分辨率不同,但它们由各自的局部特征线性组合的方式是相似的。
本文的其余部分安排如下。第2部分主要介绍耦合映射和非负矩阵分解算法的相关工作。第3部分介绍提出的RCNMF算法。第4部分是对比实验,算法参数实验以及收敛性验证实验。最后,第5部分总结工作。
2 相关工作
本节将对耦合映射算法以及非负矩阵分解算法作一个简单的介绍。
2.1 耦合映射
耦合映射方法是目前常见的低分辨率人脸识别方法。基本的目标函数如下
(1)
其中,Nt表示样本的数量,hi∈RM与li∈Rm分别表示高低分辨率图像。由于高低分辨率图像的分辨率水平不一样,因此耦合映射利用PH∈RM×d与PL∈Rm×d将高低分辨率图像映射到一致的维度中,从而进行匹配。上式是基本的耦合映射算法,后来不断有研究人员在此基础上进行改进,提出新的方法。例如Li等人提出了CLPM[11]算法,Jiang等人提出了CDMMA[17]算法,Chen等人提出了DLCLPM[18]算法。这些方法在低分辨率图像目标识别问题作出了重要贡献。然而,该类方法仅仅从数据的角度和空间变换的角度,将不同维度的数据投影至同一维度空间中,并没有强烈的实际物理含义。此外,由于该类方法对原始数据进行了维度的变换,所以会导致信息的损失以及噪声的干扰,这无疑会对识别性能造成影响。
2.2 非负矩阵分解(NMF)
NMF的一般形式如下式
X≈BC
(2)
其中,X=[x1,x2,…,xn]∈Rm×n表示一组非负的数据,B=[b1,b2,…,bk]∈Rm×k是基矩阵,它的列表示基图像。C∈Rk×n是系数矩阵,C中的元素可表示为[c]ij。k是矩阵分解的中间维度,同时也是基图像的数量。因此,每一个样本xi都可表示为一组基图像的线性组合:xi=∑jcjibj,即每一个样本都可用局部特征的线性组合来表示。为了得到分解形式,一般构造的目标函数如下
s.t. B≥0,C≥0
(3)
对上式求解得到
Bt+1=Bt⊗(XCT)
(BtCCT)
(4)
Ct+1=Ct⊗(BTX)(BTBCt)
(5)
其中⊗表示点乘,表示点除。由于没有减法运算,因此在迭代过程可以保证计算的非负性。因为图像像素值非负,符合非负矩阵分解的要求,因此非负矩阵分解被广泛应用到图像处理的各个方面。此外,NMF也常被用作特征提取器。但在人脸识别领域,非负矩阵分解算法主要对高分辨率图像进行特征提取。目前还很少有研究人员通过NMF来解决低分辨率人脸识别问题。
3 松弛耦合非负矩阵分解算法
已有的低分辨率人脸识别方法中,应用较为广泛的是基于耦合映射的方法。但这类方法只是从数据方面进行了映射,没有较强的可解释性。非负矩阵分解算法在样本表示方面有着不错的表现,但目前通过该方法解决低分辨率人脸识别问题的研究还较少。因此,本文提出了一种松弛耦合非负矩阵分解算法用于解决低分辨率人脸识别问题。在提出的方法中,首先使高低分辨率图像局部特征的组合系数保持松弛耦合,然后,通过非负矩阵分解得到高低分辨率图像的基矩阵,最后通过基矩阵提取图像特征,进行识别任务。提出的RCNMF算法在保持高低分辨率图像的组合系数耦合的同时还增加了松弛的约束,是因为如果只对高低分辨率图像的组合系数保持耦合会使算法在迭代优化的过程中更加关注组合系数的一致性,从而减弱了基矩阵的学习。而加入松弛的约束不但可以适当增强算法的鲁棒性还可以提取原分辨率图像更多的局部特征信息。本文算法的结构图1所示。
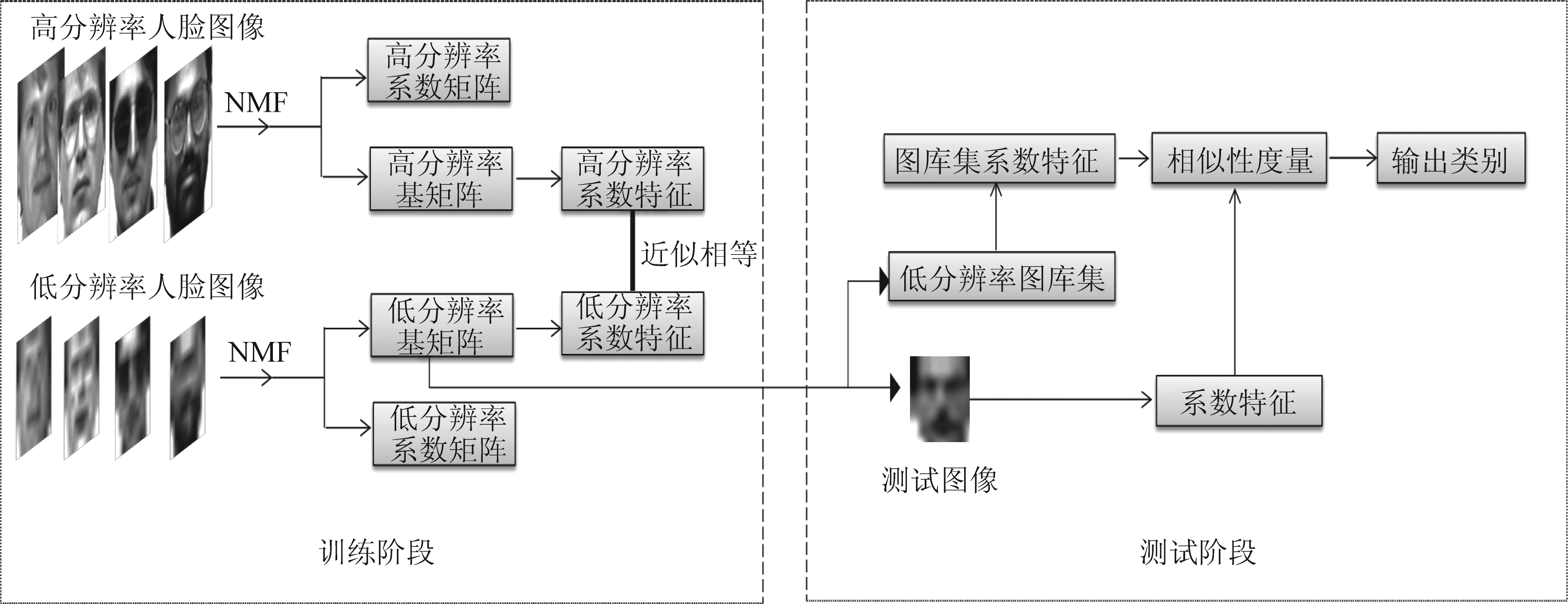
图1 本文算法示意图
Fig.1 Schematic diagram of algorithm in this paper
3.1 目标函数
给定一组高分辨率人脸图像H=[h1,h2,…,hn]∈RM×n和相应的低分辨率图像L=[l1,l2,…,ln]∈Rm×n,hi和li表示同一人脸的高分辨率图像和低分辨率图像。其非负矩阵分解的形式如下:
H≈BhCh
(6)
L≈BlCl
(7)
其中
和
分别表示高低分辨率图像的基矩阵,其中每一列表示一个基图像。K是分解的中间维度,也表示基图像的数量。
和
分别表示高低分辨率图像的系数矩阵。提出的目标函数如下:
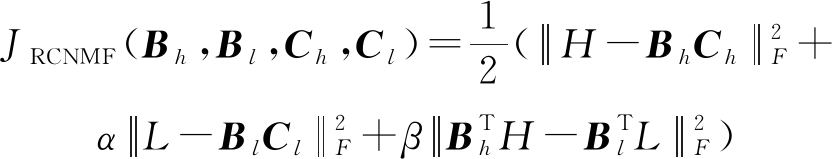
(8)
其中,α和β是权重参数。第一项表示高分辨率图像非负矩阵分解的误差项,第二项表示低分辨率图像非负矩阵分解的误差项,第三项表示高低分辨率图像组合系数松弛误差项。
3.2 目标函数优化求解
目标函数可以被重新写为
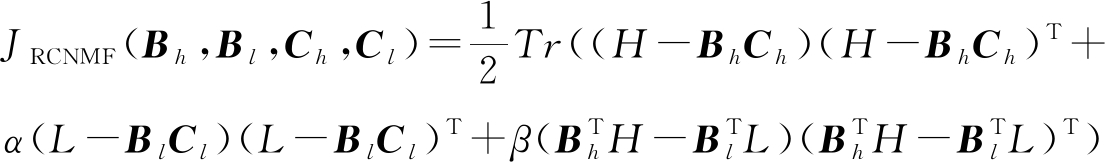
(9)
该目标函数的优化过程可以被规划为下式
s.t. Bh≥0,Bl≥0,Ch≥0,Cl≥0
(10)
该问题可以转化为对Bh,Bl,Ch,Cl 四个变量的优化求解,当优化其中一个变量时,其他三个变量固定。由梯度下降法得到Bh,Ch的更新公式
(11)
(12)
其中,ηBh和ηCh是步长矩阵。
和
可以由下式计算
(13)
(14)
从而得到Bh,Ch的迭代公式:
(15)
(16)
同理也可得到Bl,Cl的迭代公式:
(17)
(18)
3.3 特征提取
对于一张低分辨率训练样本li∈Rm,可以通过训练阶段得到的基矩阵Bl计算该样本在这组基下的组合系数Pi∈Rk,如下式:
(19)
对于所有的低分辨率训练样本L=[l1,l2,…,ln],可以得到相应的系数特征P
(20)
对于一张待测试的低分辨率图像,它在这组基下的系数特征应该与其所属类别样本的系数特征最为相似,从而可以根据相似性度量来判断类别。在本文算法中,上述相似性度量过程是通过计算欧氏距离来实现的,测试图像的类别由最小距离对应的图库人脸图片的标签唯一确定。从特征提取过程中可以发现并没有涉及到Bh,这是因为Bh中存储的是高分辨率图像的特征信息,如果其参与运算,提取的特征就会有冗余的特征信息,从而降低识别表现。
4 实验结果
本节通过实验来评估RCNMF算法的性能。先介绍数据集和参数设置。然后进行对比实验并对实验结果进行分析。最后针对算法本身设置了参数以及收敛性验证的实验。实验中高分辨率样本的大小为32×28。
4.1 人脸数据集
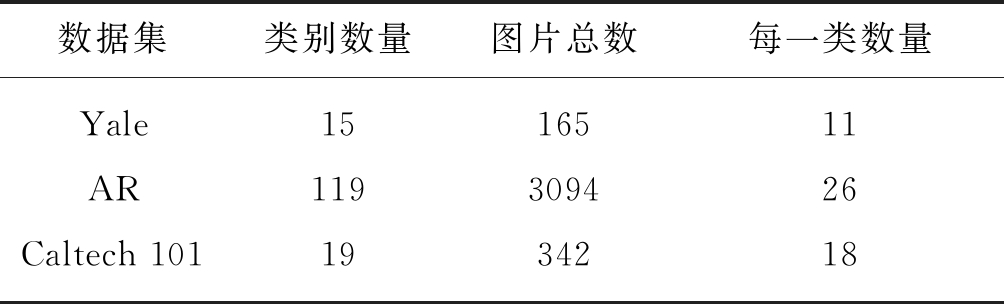
实验中一共用到了三种公开的人脸数据集,分别是Yale,AR 和 Caltech 101 人脸数据集。它们的类别数量,图片总数以及每一类图片的数量信息如表1所示。可以发现,AR人脸数据集的图片总数和类别总数最多,共有3094张人脸图片和119个不同的人脸目标。Yale人脸数据集图片总数和类别总数最少,只有165张图片和15个不同的人脸目标。这些人脸数据集中的人脸图片含有不同的光照条件,面部表情以及姿势变化等自然影响因素。实验中使用的部分高分辨率图片和低分辨率图片如图2所示。
表1 人脸数据集介绍
Tab.1 Face datasets introduction
数据集类别数量图片总数每一类数量YaleARCaltech 10115119191653094342112618
图2 部分人脸图片
Fig.2 Part face image
4.2 对比方法与参数设置
为了验证提出算法的性能,在实验中与CM[11],CLPM[11],LGCM[15],CDMMA[17],DLCLPM[18]五种基于耦合映射的算法进行了对比。这些对比方法以及本文算法在实验中参数的设置如表2所示。
表2 对比算法参数设置
Tab.2 Parameters setting
4.3 不同低分辨率的对比实验
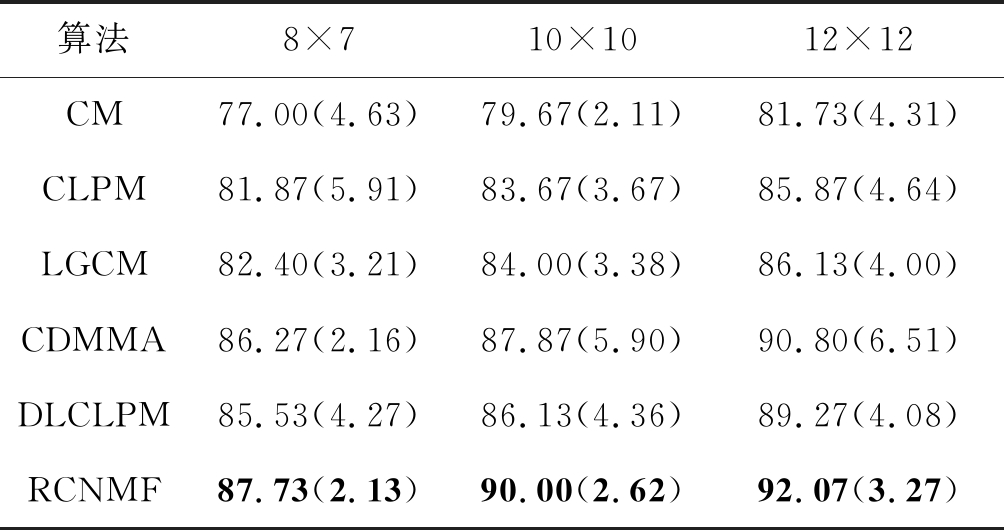
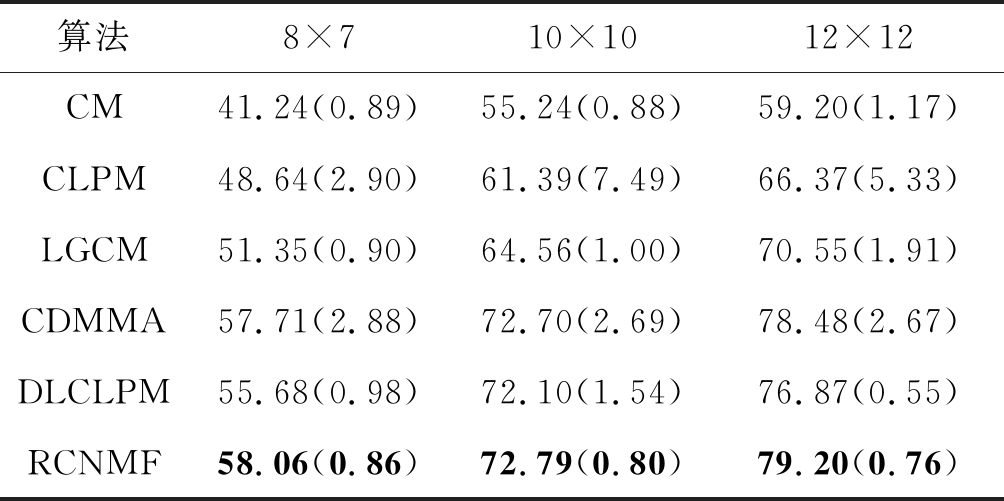
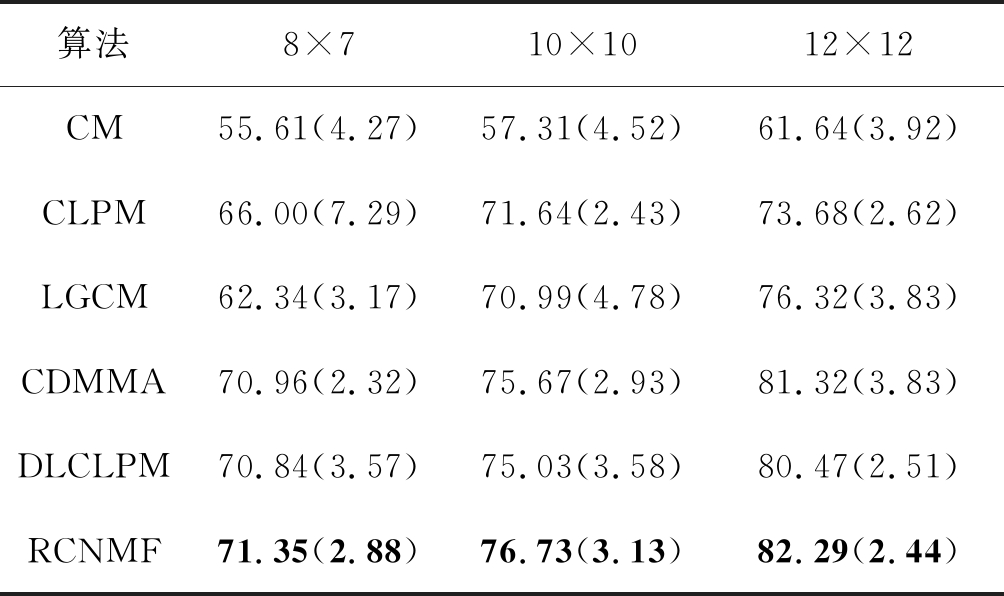
这部分实验中共设置了三种不同维度的低分辨率样本,尺寸分别为8×7,10×10以及12×12。训练与测试样本是按相等数量随机抽取得到的。在Yale,AR以及Caltech 101人脸数据集上的实验结果如表3～表5所示,表中数据表示百分制的识别结果并且每一个识别结果都是十次实验结果取均值得到的,括号内的数字表示这十次实验结果的标准差。从中可以发现,当低分辨率图像的维度增加时,每种算法的识别表现都会有所提高。另外,在几种耦合映射的方法中,CM算法的识别率最低。以12×12的尺寸为例,在三个人脸数据集上CM算法的识别率最高依次为81.73%,59.20%,61.64%,都比其他耦合映射方法最高的识别率低。这是因为CM算法只对数据进行了维度变换,没有考虑到样本的近邻结构以及几何空间结构等信息,因此性能相对较差。此外,在AR人脸数据集上,所有方法的识别表现都有所下降。因为该数据集中的图片含有更多的自然影响因素,使得人脸特征难以提取。但与所有耦合映射的方法相比,本文提出的RCNMF算法在三种人脸数据集上的识别表现都是最好的。说明提出的方法在多种低分辨率下都有较好的特征提取性能。此外,从标准差可以看出RCNMF算法是比较稳定的。
表3 Yale人脸数据集
Tab.3 Yale face database %
算法8×710×1012×12CM77.00(4.63)79.67(2.11)81.73(4.31)CLPM81.87(5.91)83.67(3.67)85.87(4.64)LGCM82.40(3.21)84.00(3.38)86.13(4.00)CDMMA86.27(2.16)87.87(5.90)90.80(6.51)DLCLPM85.53(4.27)86.13(4.36)89.27(4.08)RCNMF87.73(2.13)90.00(2.62)92.07(3.27)
表4 AR人脸数据集
Tab.4 AR face database %
算法8×710×1012×12CM41.24(0.89)55.24(0.88)59.20(1.17)CLPM48.64(2.90)61.39(7.49)66.37(5.33)LGCM51.35(0.90)64.56(1.00)70.55(1.91)CDMMA57.71(2.88)72.70(2.69)78.48(2.67)DLCLPM55.68(0.98)72.10(1.54)76.87(0.55)RCNMF58.06(0.86)72.79(0.80)79.20(0.76)
表5 Caltech 101人脸数据集 Tab.5 Caltech 101 face database %
算法8×710×1012×12CM55.61(4.27)57.31(4.52)61.64(3.92)CLPM66.00(7.29)71.64(2.43)73.68(2.62)LGCM62.34(3.17)70.99(4.78)76.32(3.83)CDMMA70.96(2.32)75.67(2.93)81.32(3.83)DLCLPM70.84(3.57)75.03(3.58)80.47(2.51)RCNMF71.35(2.88)76.73(3.13)82.29(2.44)
4.4 不同训练样本数量的实验
这部分实验通过改变训练样本的数量来观察算法识别性能的变化。实验中用的低分辨率图像的尺寸为8×7。图3是实验结果。可以发现,与4.3中的实验结果一致,在几种耦合映射的方法中,CLPM,LGCM,CDMMA,DLCLPM四种基于耦合映射的算法的识别表现仍然好于CM。另外,在不同的数据集和不同的样本数量下不同方法的识别性能也会不一样。以CLPM算法和LGCM算法为例,在AR人脸数据集上LGCM算法表现更好,然而在Caltech 101上CLPM方法表现更好。在Yale人脸数据集上,两种方法的识别率受训练样本数量影响而表现不同,样本数量少的时候CLPM方法的识别率更高,而样本数量多的时候LGCM方法识别率更高。从图3中的三个图来看,可以明显发现提出的RCNMF方法在三种数据集上的识别表现都要优于其他对比方法。其中,在Yale人脸数据集上,本文提出的算法在识别性能上的提升最为明显。在AR人脸数据集和Caltech 101人脸数据集上,当训练样本数量较少的时候,本文提出的方法有较为明显的提升。总的来说,从实验结果来看,提出的RCNMF算法可以有效地解决低分辨率人脸识别问题。
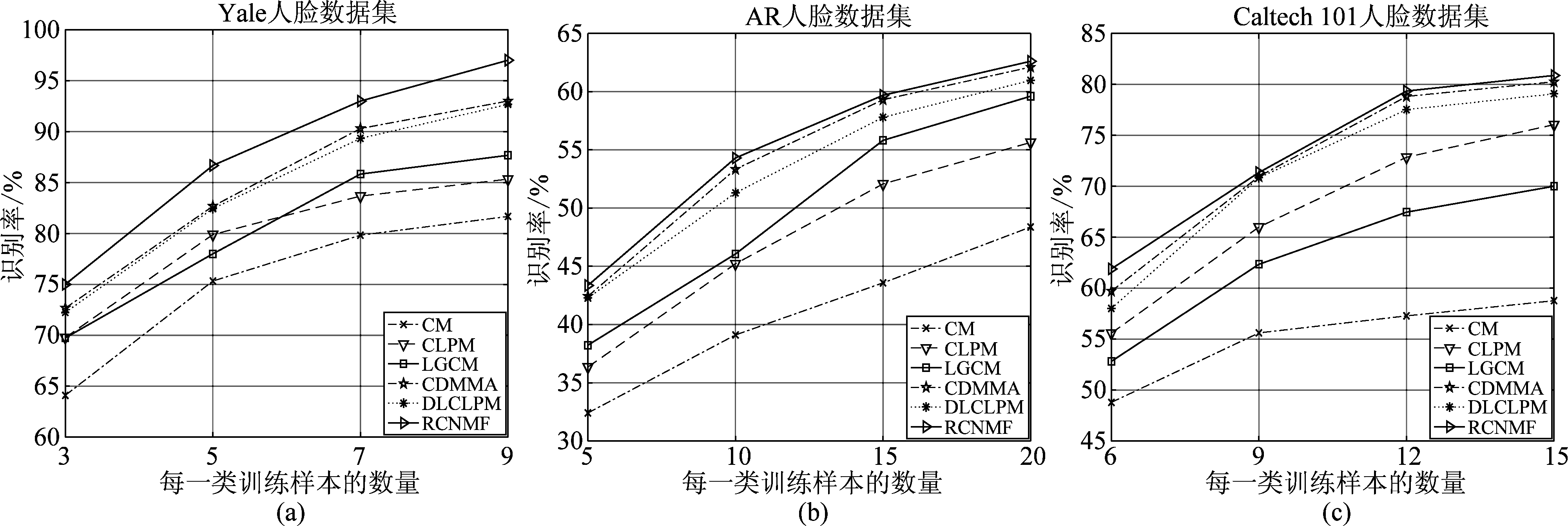
图3 训练数量的实验
Fig.3 Experiment of training number
4.5 基图像数量的实验
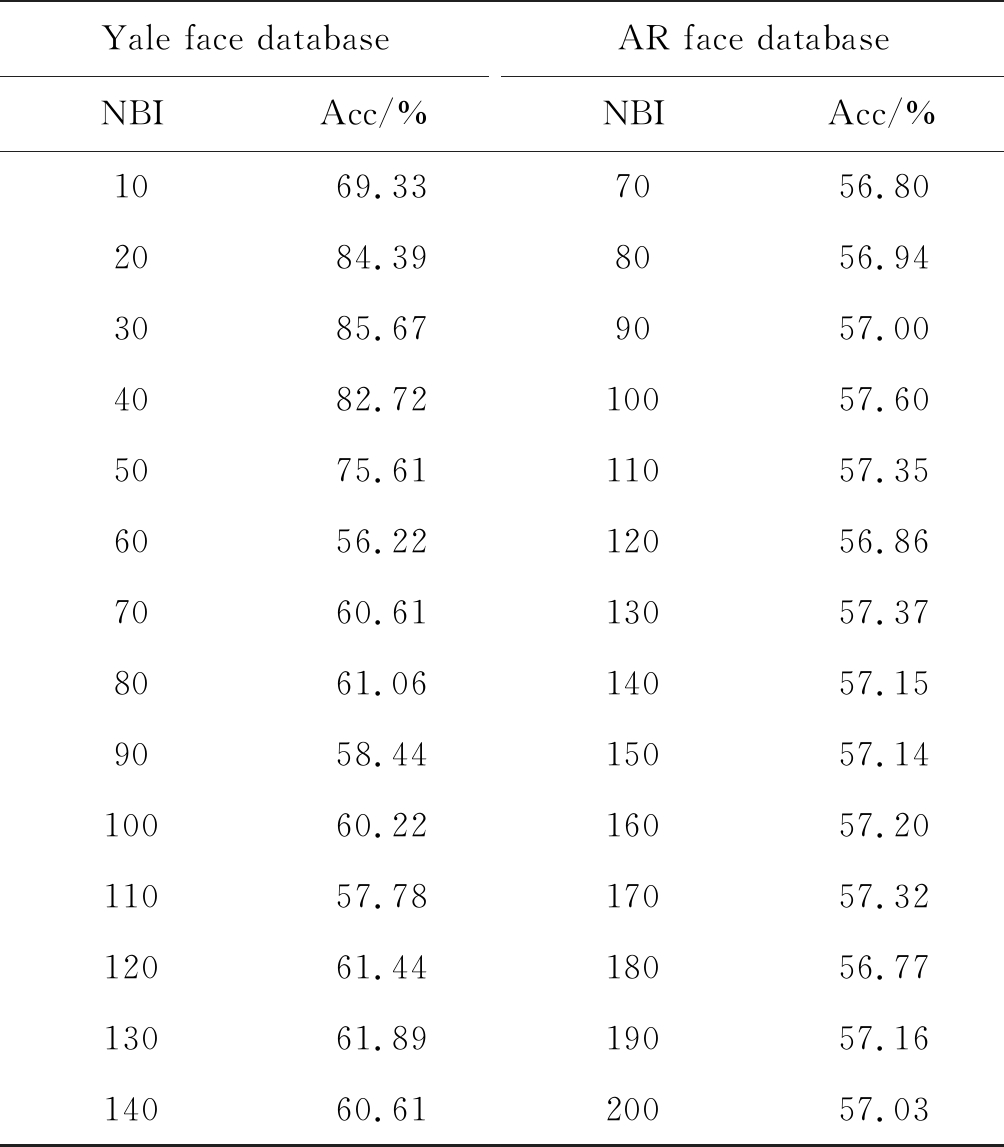
基图像表示经过训练阶段得到的关于人脸图像的局部特征。这部分通过实验来评估基图像的数量(number of basis image,后文简称NBI)对算法性能的影响。实验中用到了Yale和AR两种人脸数据集,在这两个人脸数据集上每一类的训练样本数量分别为5和13。每个识别率是二十次识别结果求均值的结果,表6是实验结果。从中可以发现,随着基图像数量的增加,本文提出的算法的识别率一开始会有明显增加,而后又会下降。以AR人脸数据集为例,一开始识别率从56.80%增加至57.60%,然后下降为56.86%,最后一直平稳地上下波动。这说明在提出的RCNMF方法中,基图像的数量并不是越多越好。这是因为基图像中存储了原图像的局部特征信息,而低分辨率图像的特征信息有限,如果基图像数量越多,则会导致学习到的基图像中冗余的特征信息会越来越多,这些无用的特征信息会降低算法的识别表现。
表6 不同基图像数量的实验
Tab.6 Experiments of different number of basis images
Yale face databaseNBIAcc/%AR face databaseNBIAcc/%1069.337056.802084.398056.943085.679057.004082.7210057.605075.6111057.356056.2212056.867060.6113057.378061.0614057.159058.4415057.1410060.2216057.2011057.7817057.3212061.4418056.7713061.8919057.1614060.6120057.03
4.6 参数实验
在这部分,我们将通过实验来评估提出的RCNMF算法中目标函数里的权重参数α,β对算法的影响。图4是实验结果。
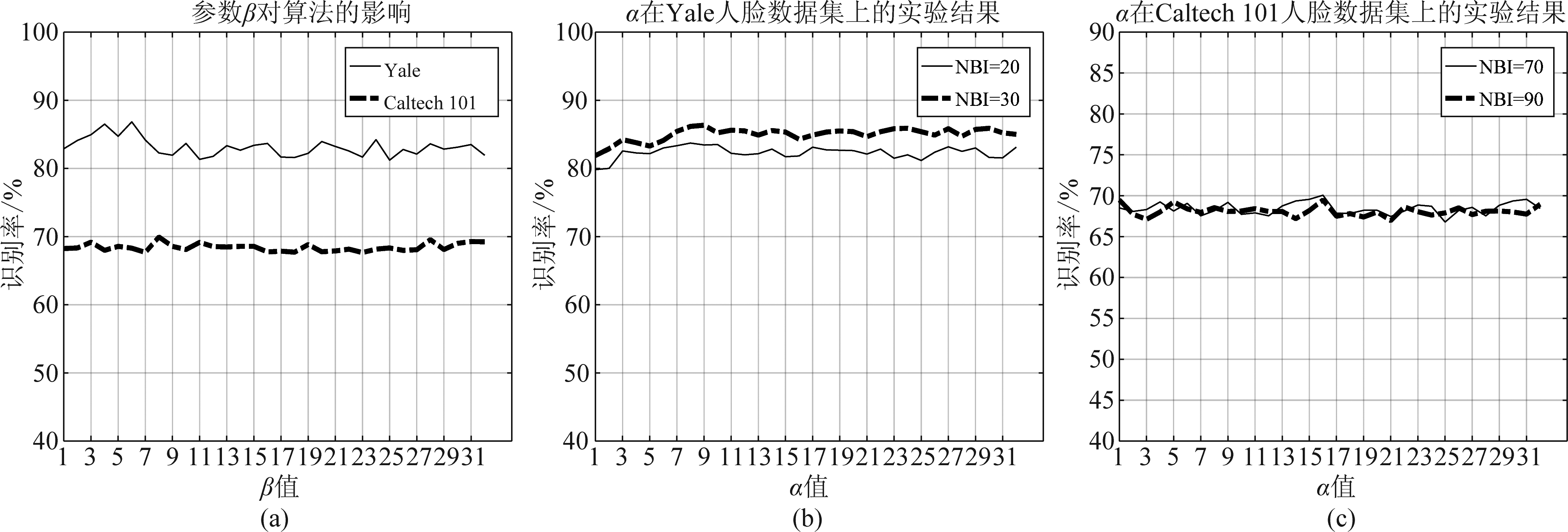
图4 α和β的实验
Fig.4 Experiment about α and β
参数β是目标函数中第三项(松弛误差项)的系数,控制这一项在目标函数中的比重。该参数对算法影响的实验结果如图(a)所示。可以看到, RCNMF算法的识别率随β的变化并没有较大的上升或下降变化。这说明本文提出的RCNMF算法对该参数不是很敏感。另外,在不同的人脸数据集上,本文提出的RCNMF算法的最佳β值并不相同,这是因为不同人脸数据集的特征信息是不同的。总体来看,β在[7,15]之间,算法比较稳定。
参数α是目标函数中第二项(低分辨率图像非负矩阵分解误差项)的系数,该参数对算法影响的实验结果如图(b)～(c)所示。实验中用的高分辨率图像的尺寸是32×28,低分辨率图像的尺寸是8×7,二者之间的比例为16∶1。该比例决定目标函数中相应误差项的比重。在这两个人脸数据集上的实验中,我们都选取了两种不同的NBI用于对比。从图中可以看到,无论在Yale人脸数据集还是在Caltech 101人脸数据集上,两条不同NBI的曲线的总体趋势是一致的,并且无较大起伏波动。另外,参数α在[1,16]之间时,算法可以取得最好的识别表现。这是因为在该范围内,目标函数中高分辨率图像非负矩阵分解误差项比重更大,从而算法更关注高分辨率图像的影响。高分辨率图像中含有更多有用的信息,从而更加有利于算法识别性能的提升。因此,实验中我们选取的α值的范围是[1,16]。
4.7 收敛性实验
这部分实验的目的是为了验证本文提出的RCNMF算法的收敛性。实验中我们在Yale,Caltech 101以及AR三个人脸数据集上都选取了三种不同维度的低分辨率样本,其尺寸分别为8×7,10×10以及12×12。图5是实验结果。可以看到,在三种人脸数据集上,8×7,10×10和12×12三种分辨率对应的曲线都是一开始下降得很快,而后逐渐趋于稳定,该结果说明了提出的RCNMF算法是收敛的。
图5 算法收敛性实验
Fig.5 Experiment of algorithm convergence
5 结论
针对实际监控场景中遇到的人脸图像分辨率较低的问题,本文提出了一种松弛耦合非负矩阵分解算法来解决低分辨率人脸识别问题。在提出的算法中,人脸可以视为由不同的人脸局部特征组合而成。虽然高低分辨率人脸图像的局部特征不同,但由这些局部特征表示原图像的组合方式可以认为是相似的。在算法的训练阶段,首先通过松弛耦合非负矩阵分解得到高低分辨率图像的基矩阵,然后通过基矩阵得到高低分辨率图像相应的系数特征。最后,通过得到的系数特征来实现分类任务。实验结果表明RCNMF算法可以有效解决低分辨率人脸识别问题。
[1]应自炉, 蔡淋波, 刘召义. 基于LBP的拉普拉斯特征映射人脸识别[J]. 信号处理, 2010, 26(8): 1230-1233.
Ying Zilu, Cai Lingbo, Liu Zhaoyi. Face Recognition With Laplacian Eigenmaps on Local Binary Pattern[J]. Journal of Signal Processing, 2010, 26(8): 1230-1233.(in Chinese)
[2]梁淑芬, 刘银华, 李立琛. 小波变换和LBP对数域特征提取的人脸识别算法[J]. 信号处理, 2013, 29(9): 1227-1232.
Liang Shufen, Liu Yinhua, Li Lichen. Face Recognition Based on Wavelet Transform and LBP in Logarithm[J]. Journal of Signal Processing, 2013, 29(9): 1227-1232.(in Chinese)
[3]朱建清, 葛主贝, 曾焕强, 等. 采用新型纹理特征的2DLDA人脸识别算法[J]. 信号处理, 2017, 33(6): 811- 818.
Zhu Jianqing, Ge Zhubei, Zeng Huanqiang, et al. 2DLDA Face Recognition Algorithm Using Novel Texture Features[J]. Journal of Signal Processing, 2017, 33(6): 811- 818.(in Chinese)
[4]Li Pei, Prieto L, Mery D, et al. On Low-Resolution Face Recognition in the Wild: Comparisons and New Techniques[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(8): 2000-2012.
[5]Ge Shiming, Zhao Shengwei, Li Chenyu, et al. Low-resolution face recognition in the wild via selective knowledge distillation[J]. IEEE Transactions on Image Processing, 2018, 28(4): 2051-2062.
[6]Mao Shanjun, Zhou Da, Zhang Yiping, et al. Weighted Patches Based Face Super-Resolution Via Adaboost[C]∥2018 International Conference on Machine Learning and Cybernetics (ICMLC). IEEE, 2018, 1: 234-239.
[7]Zou W W W, Yuen P C. Very Low Resolution Face Recognition Problem[J]. Image Processing, IEEE Transactions on, 2012, 21(1): 327-340.
[8]Zeng Xiao, Huang Hua, Qi Chun. Expanding training data for facial image super-resolution[J]. IEEE Transactions on Cybernetics, 2017, 48(2): 716-729.
[9]Mudunuri S P, Biswas S. Low resolution face recognition across variations in pose and illumination[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38 (5): 1034-1040.
[10]Wang Zhifei, Miao Zhenjiang, Wu Q M L, et al. Low-resolution face recognition: a review[J]. Visual Computer, 2014, 30(4): 359-386.
[11]Li Bo, Chang Hong, Shan Shiguang, et al. Low-resolution face recognition via coupled locality preserving mappings[J]. IEEE Signal Processing Letters, 2009, 17(1): 20-23.
[12]Biswas S, Bowyer K W, Flynn P J. Multidimensional scaling for matching low-resolution face images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 34(10): 2019-2030.
[13]Ren Chuanxian, Dai Daoqing, Yan Hong. Coupled Kernel Embedding for Low-Resolution Face Image Recognition[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3770-3783.
[14]Yang Fuwei, Yang Wenming, Gao Riqiang, et al. Discriminative multidimensional scaling for low-resolution face recognition[J]. IEEE Signal Processing Letters, 2017, 25(3): 388-392.
[15]Shi Jingang, Qi Chun. From local geometry to global structure: Learning latent subspace for low-resolution face image recognition[J]. IEEE Signal Processing Letters, 2014, 22(5): 554-558.
[16]Zhang Jiaqi, Guo Zhenhua, Li Xiu, et al. Large Margin Coupled Mapping for Low Resolution Face Recognition[C]∥Pacific Rim International Conference on Artificial Intelligence. Springer International Publishing, 2016.
[17]Jiang Junjun, Hu Ruimin, Han Zhen, et al. Coupled Discriminant Multi-Manifold Analysis with Application to Low-Resolution Face Recognition[C]∥International Conference on Multimedia Modeling. Springer International Publishing, 2015.
[18]Chen Hao, Zhao Yang, Pei Jihong. Double layer coupled locality preserving mappings for very low-resolution face recognition[C]∥In 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), IEEE, 2019: 63- 67.
[19]Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-788.
[20]Lee D D, Seung H S. Algorithms for non-negative matrix factorization[C]∥Proceedings of the 13th International Conference on Neural Information Processing Systems. MIT Press, 2000.
