1 引言
目标跟踪因其广泛的应用前景,在计算机视觉领域一直备受关注,算法在不断的得到改进和完善[1]。目标跟踪(本文指单目标跟踪)是指给定视频序列的初始帧并在初始帧上框出目标,在后续帧中提取目标的特征并进行预测评分,选择预测评分最高的目标作为最终的预测目标或者将评分进行融合获得最优的预测目标。目标跟踪广泛应用于军事和民用领域,军事领域有精确制导、战场监视、空中预警和无人飞行器等,民用领域有移动机器人、智能视频监控、人机交互和智能交通系统等。目标跟踪的广泛应用,使其一直是计算机视觉的研究热点之一。目标跟踪也是一个极具挑战性的难题,运动中的目标一直处于复杂的场景中且场景在不断的变化,同时目标本身也在不断的变化。这些复杂的变化加剧了跟踪任务的困难性。目前在目标跟踪领域中总结有几大挑战:背景相似干扰、光照影响、背景杂波、形变、遮挡、运动模糊、尺度变换等等[2-3]。所以如何在复杂的场景中准确跟踪不断变化的目标就成为亟待解决的问题。
在目标跟踪领域有两大跟踪算法,生成式模型跟踪算法[4-5]和鉴别式模型跟踪算法[6-7]。生成式模型跟踪算法是指在当前图像中对目标区域建模,在下一帧图像中搜索与当前算法模型最相似的区域,作为预测的位置,比较经典的算法有卡尔曼滤波[8]与粒子滤波[9]等。但是该类算法存在明显不足,不能全面利用图像中的信息,对于随机变化的目标达不到很好的鲁棒性,因此目前此类算法很少用。鉴别式模型跟踪算法是目前比较流行的跟踪算法,它是将目标模型和背景信息同时考虑在内,通过对比两者中信息的差异,将有用的目标信息从图像中提取出来从而获得目标的位置,常用的算法是基于核相关滤波的目标跟踪算法。
相关滤波最开始应用于信号处理,描述两个或者信号本身之间的相关性。应用于目标跟踪中是将输入图像通过滤波器映射出一个理想的响应图,响应图的最高峰对应的是目标的中心点。
相关滤波在目标跟踪领域的首次应用是在2010年Bolme等人提出的最小平方误差输出和滤波器(MOSSE)算法[10]。该算法的速度远超其他算法,显著的效果使相关滤波器跟踪算法备受关注,并得到不断的完善。
2012年Martins等人在MOSSE基础上提出了基于核函数与循环结构的CSK算法[11]。其速度保持较高,精度也有所提高。但是该算法运用的是单通道的灰度特征,对目标的外观描述能力明显不足。2014年Martins等人提出了多通道特征的KCF算法[12-13]。该算法提高了分类器的解释能力,同时增加了目标跟踪的场景,对光照变化、遮挡、形变、背景杂乱等情况的跟踪性能良好。
以上算法都在不断完善,但是这些算法对于尺度变化、快速运动等跟踪问题不够鲁棒。2014年浙江大学Yang等人提出一个较实用的跟踪算法-SAMF[14],它是CN算法[15]和KCF算法的多尺度扩展,同时增加尺度池方法,达到了尺度自适应的效果。另外,Danelljan等人于2014年也提出了针对尺度问题的DSST算法[16],该算法使用KCF的线性核版本即DCF算法进行平移位置检测,另单独增加一个尺度滤波器进行尺度训练,每一帧的尺度检测需要取样33种不同尺度的图像块。两种算法对尺度估计的精度都比较高,但速度有所降低。2019年胡正平等人提出位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法[17],跟踪的综合性能得到一定提升。
以上算法的跟踪性能一直在不断完善,但统一缺点是均使用了单一模板。2016年Bertinetto等人采用了信息融合方法提出了多模板特征的Staple算法[18-19],将颜色特征和多通道的HOG特征相融合。其融合方式是分别将两个特征进行训练和测试,在响应阶段将相应的概率图和滤波响应图以一定的固定比例进行融合,融合后的得分图作为目标的位置。Staple算法突破了单一的模板形式,以融合的新方法达到了互补的作用,扩展了跟踪的场景,同时其跟踪速度和精确度均保持很高,该算法在当时引起了较大的反响,对以后的算法也有很大的影响。但同时,也可以看到Staple算法的融合因子是固定的,这导致融合的效果无法达到最优。对于背景和目标相似、运动模糊以及形变等情况不够鲁棒,很容易造成跟踪框的漂移或者跟踪直接丢失。因此,为了解决上述问题,在Staple算法的基础上提出了颜色自适应的目标跟踪算法。将背景和目标的相似度值与融合因子相结合,使得融合因子按照每一帧的特征来匹配相应的权重,以此达到跟踪的最优匹配。
2 目标跟踪算法
2.1 KCF相关滤波算法
KCF算法主要利用岭回归函数进行训练,目的是寻找一个函数f(z)=ωT z可以使得误差函数最小,误差函数如下:
(1)
论文重点讲述了如何最小化此误差函数。
作者利用目标周围区域的循环矩阵采集正负样本,把图像向上、向下分别移动不同的像素得到新的样本图像,以此增加样本数量。然后利用核空间的脊回归训练目标检测器,假设非线性映射函数为φ(x),寻找的分类器为f(xi)=ωTφ(xi),其中{xi,f(xi)}为训练样本和回归值。可以得到一个权重系数为![]() 并令权重值为ω=∑iαiφ(xi)。文章下面用核函数求这个权重值,即α。用核函数求得的核空间的核矩阵K为:
并令权重值为ω=∑iαiφ(xi)。文章下面用核函数求这个权重值,即α。用核函数求得的核空间的核矩阵K为:
K=φ(X)φ(X)T
(2)
经过一系列计算,作者求得α值的共轭为:
α*=(K+λI)-1y
(3)
所以寻找的分类器为:
f(z)=ωTφ(z)=αTφ(X)φ(z)
(4)
在计算的过程中,作者通过核函数将复杂的线性空间映射到非线性核空间,解决了低维空间不可分问题,同时还使用傅氏对角化将样本循环矩阵转化为对角矩阵,大大降低运算量,提高计算的速度,满足了算法的实时性。
另外该文章的创新点还使用了多通道的HOG特征,提高了分辨力,使得分类器对待检测目标的解释能力更强。
KCF算法对光照强度、遮挡、背景杂乱等情况跟踪效果良好,但对于尺度变化、快速运动等的情况效果不佳。
2.2 Staple目标跟踪算法
Staple算法是在KCF算法上的改进,将KCF算法中的HOG特征和颜色直方图特征两种模板进行融合,在提升跟踪效果同时保持着较高的跟踪速度。该算法在当时引起了许多研究人员的关注,对后续算法的研究具有重要意义。
该算法的作者在论文开端放置了两张效果对比图,即DSST、DAT两个算法的跟踪效果图。如图1所示。

图1 原Staple算法跟踪效果图
Fig.1 Original Staple algorithm tracking effect map

图2 原Staple 算法与DSST、DAT两个算法的比较
Fig.2 Comparison of original Staple algorithm with DSST and DAT
从两张对比图中可以看出,当颜色对目标跟踪影响过大时,DSST算法的跟踪效果较好;当运动目标产生模糊对目标跟踪影响过大时,DAT算法跟踪效果较好。而Staple算法对两种情况均十分稳定,相当于两算法的结合。
在Staple算法中,使用HOG特征的算法对变形的目标十分敏感,而颜色直方图特征处理此类情况的效果较好;使用颜色直方图特征的算法对光照十分敏感,而HOG特征的算法对此情况的目标跟踪效果较好。Staple算法的结合并不是在算法训练和测试过程中,而是将HOG特征和颜色直方图特征分别进行训练、测试,然后将两者的结果使用融合因子进行融合,保持了较高的速度同时跟踪效果优异于之前的算法。
算法融合的公式:
f(x)=γtmpl ftmpl(x)+γhist fhist(x)
(5)
其中ftmpl(x)、 fhist(x)分别为使用的两种分类器对各自候选样本检测得到的响应。分别表示如下:
ftmpl(x;h)=∑u∈ h(u)Tφx[u]
h(u)Tφx[u]
(6)
![]()
![]() (β,ψ)[u]
(β,ψ)[u]
(7)
而两种分类器的训练过程表示为:
(8)
(9)
训练过程中的损失函数为:
(10)
最终的预测位置可以用以下函数表示:
(11)
将融合参数用一个因子代替为:
γtmpl=1-α
(12)
γhist=α
(13)
则最终预测位置函数为:
(14)
模板的在线更新函数为:
(15)
(16)
其中在模板更新过程中用到了汉明窗,而整个在线更新的思想实际上来自于DSST尺度滤波器算法。因此,这不仅最小化了边界效应,同时也适用于尺度变化的跟踪情况。
直方图的在线更新函数为:
(17)
(18)
其中ηtmpl、ηhist分别为模板学习率和直方图学习率。
3 颜色自适应目标跟踪算法
本文提出的STR-Staple算法是在原Staple算法基础上的改进,使用巴氏距离中的巴氏系数计算背景和前景的颜色直方图的相似度[20-21],设定相似度阈值,然后使用对数函数将相似度与融合因子结合。同时,在设定的阈值范围内,此对数函数在相似度值较高时可以降低相似度的值,相似度的值较低时可以提高其值。最后用每一帧所匹配的最优融合因子来限定相关滤波器和直方图分类器对算法的主导作用,从而使跟踪达到自适应状态,实现算法的最优融合。
3.1 颜色自适应的计算与表达
首先利用原算法的前景和背景的面积中每一点构成的矩阵计算出每个图像前景和背景的颜色直方图以及目标似然函数:
P_fg=P_O.*bg_mask
(19)
P_bg=P_O.*fg_mask
(20)
P_O=P_fg./(P_fg+P_bg)
(21)
fg_mask、bg_mask表示前景和背景的面积中每一点构成的矩阵,P_fg是前景的颜色直方图,P_bg是背景的颜色直方图,“.*”表示两个矩阵相乘;P_O是目标似然函数;“./”表示两个矩阵相除。
原图及求得似然图如下:
然后对前景、背景的似然函数进行规整以限定其范围,最后利用巴氏系数计算两者的相似度。
巴氏距离,是统计学中用于测量概率分布的函数。在离散分量的概率分布中巴氏距离被定义为:
D(n,m)=-ln(H(n,m))
(22)
其中![]() 是Bhattacharyya系数,范围设定如下
是Bhattacharyya系数,范围设定如下
0≤H≤1且0≤D≤
在连续分量的概率分布中定义如下:
(23)
0≤H≤1且0≤D≤

图3 原图以及所得的各似然图
Fig.3 Original image and obtained likelihood maps
Bhattacharyya Coefficient,中文是巴氏系数,可用来测量样本之间的相关性。巴氏系数可以积分或叠代出两个样本之间的重叠部分的面积,它是首先将样本划定指定的数量,然后分别进行积分或者叠代。叠代样本的公式如下:
(24)
其中,a,b为指定样本,n是叠代时分出的重叠块数量,ai, bi分别是在a,b中第i部分的叠代样本数。其中H会随着公式(23)中同时出现两个样本的公共部分的增多而增大。
在计算机视觉中,对图像相似度的计算主要是对两幅图像的内容的相似程度进行计算获得得分。相似度高,分数就高,反之则低。所以巴氏系数很适合用来计算前景和背景的颜色直方图的相似度。当前景和背景的巴氏系数大时,说明相似度比较高,跟踪就很容易产生错误,这时可以寻找一种函数将巴氏系数降低;反之提高巴氏系数。
通过大量的实验验证,确定一种对数函数十分适合以上的情况。寻找到的函数如下式所示:
H=1-log(H)-1.7133
(25)
H即为巴氏系数,函数的图形如图4所示。
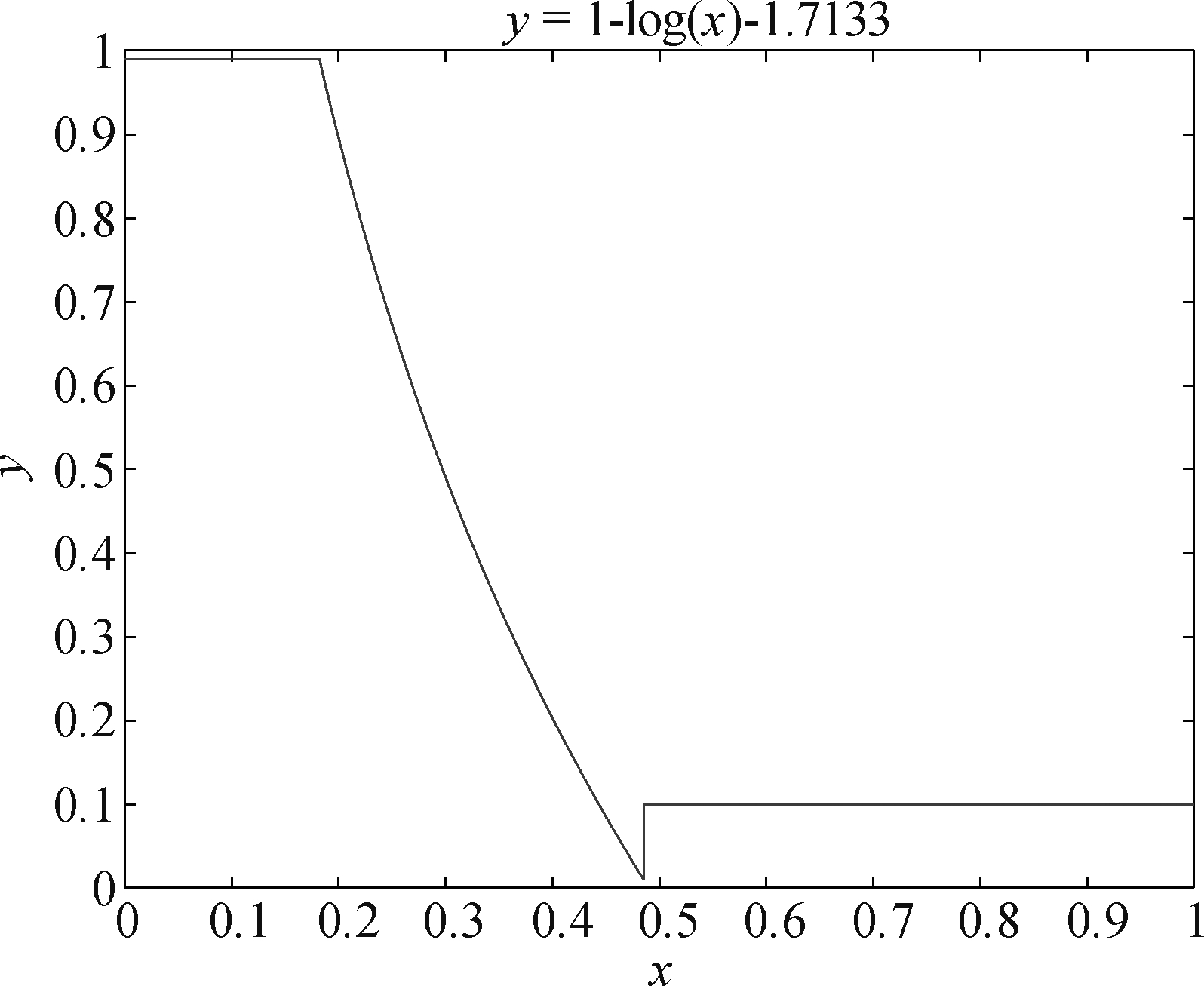
图4 对数函数图
Fig.4 Log function graph
然后将H与融合因子α相联系:
α=H
(26)
则最终的输出响应表示如下:
f(x)=(1-H)ftmpl(x)+Hfhist(x)
(27)
H会随着每帧之间的相似度的变化而变化,即每一帧图像可以匹配到相对应的融合因子α,然后用α控制相关滤波器和直方图分类器对算法的主导作用,使算法达到自适应的最优融合。
3.2 算法的整体流程
Step 1 输入图像,图像为xt。
Step 2 初始化。标定目标位置的矩形框Pt;确定滤波器模型:相关滤波器模型、尺度滤波器模型和直方图信息模型。
Step 3 对相关滤波器模板循环采样并训练和测试。
Step 4 对颜色直方图信息模板进行密集采样并训练和测试。
Step 5 计算目标和背景的相似度;计算自适应融合因子。
Step 6 将两个模板进行自适应融合。
Step 7 检测模板是否变化,考虑是否需要模型更新。如果需要更新,利用上文的模板和直方图的在线更新函数进行计算,求出当前帧的滤波器模板,并返回到步骤2继续算法的流程。

图5 算法流程框图
Fig.5 Algorithm flow chart
4 实验结果和分析
本文将改进的STR-Staple算法在OTB-13和OTB-15两个数据集上与CSK、KCF、DSST、SAMF、Staple五个算法进行实验对比。实验的评价指标为精确度、成功率。精确度指像素为20时占视频总帧数的比值,公式如下:
(28)
NI表示第t帧的帧数,Ns表示总帧数。
成功率指成功率曲线与坐标轴所包围的面积,公式如下:
(29)
rt表示预测框,ro表示人工标注框。
实验是在MATLAB R2018a,Inter(R) Core(TM) i5-3470 CPU @ 3.00GHz,内存为8.00GB环境下实现的。针对的情况有目标与背景极为相似、部分遮挡、光照变化、尺度变化等11种挑战。
实验参数设置为:HOG通道特征32维、HOG的cell大小为4×4,模板学习率ηtmpl=0.01、直方图学习率ηhist=0.04,颜色直方图的bins为32×32×32。
4.1 综合性能比较
算法使用的是OTB-13和OTB-15两个数据集,与五个目前比较流行的相关滤波类目标跟踪算法(CSK、KCF、SAMF、DSST、Staple)进行比较,实验结果如下图所示。
其中图6是算法在OTB-2013数据集上的实验结果,图7是算法在OTB-2015数据集上的实验结果。从两张实验对比图可以看出,基于核相关滤波器的颜色自适应目标跟踪算法的精确度和成功率在OTB-2013数据集上的结果分别为:0.871、0.814;而原Staple算法的结果分别为:0.837、0.801。因此,STR-Staple算法在精确度分数上比原算法提升5.7%,在成功率分数上提升3.6%,同时可以看出STR-Staple算法均优于其他算法;STR-Staple算法在OTB-2015数据集上的结果分别为:0.742、0.642,原算法的结果分别为:0.727、0.635,精确度分数和准确度分数分别提升了1.5%和0.7%,并且STR-Staple算法的结果仍然是最优的。该实验数据定性说明了STR-Staple算法的跟踪性能优于其他五种主流算法。
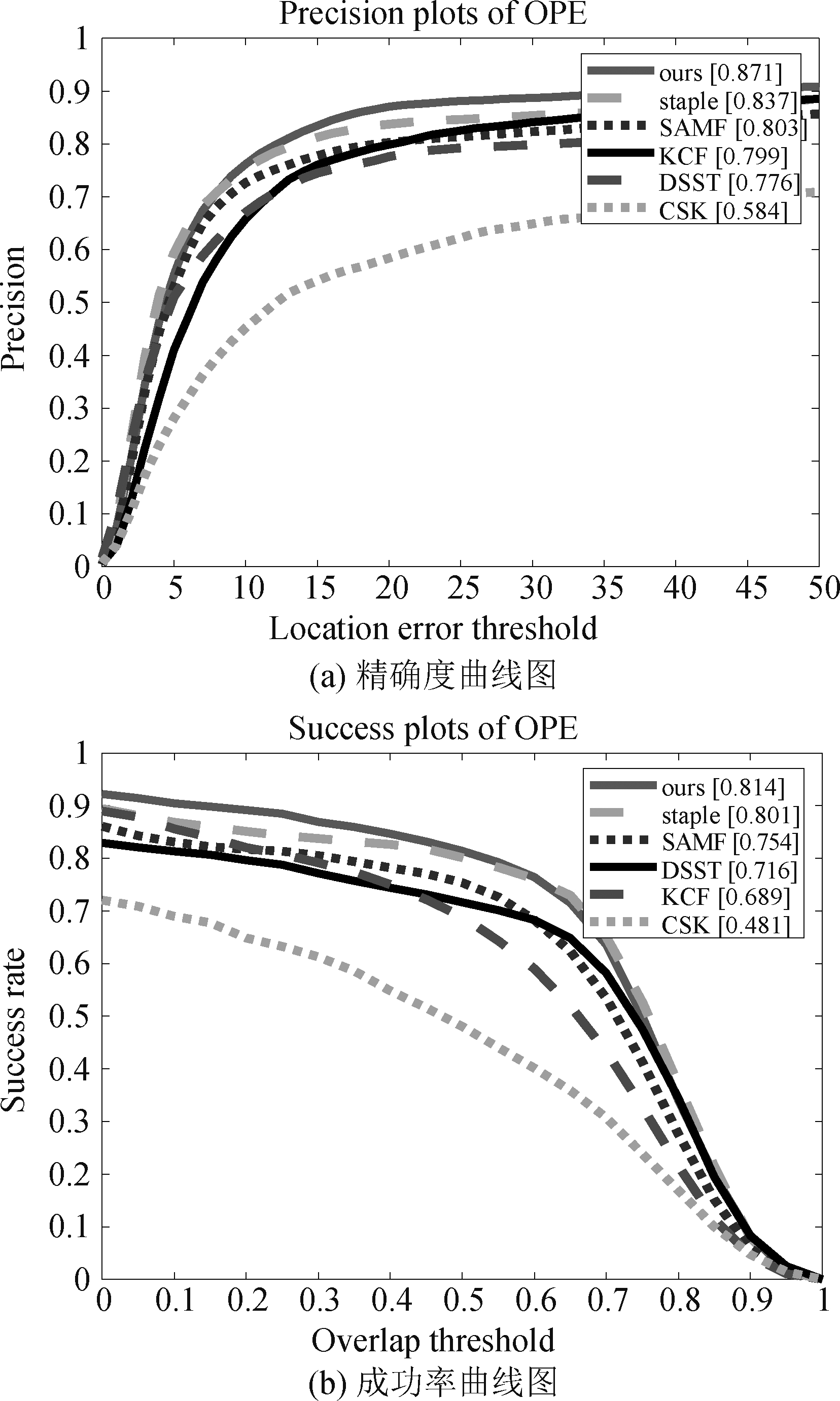
图6 OTB-2013综合评价曲线图
Fig.6 OTB-2013 Comprehensive Evaluation Curve
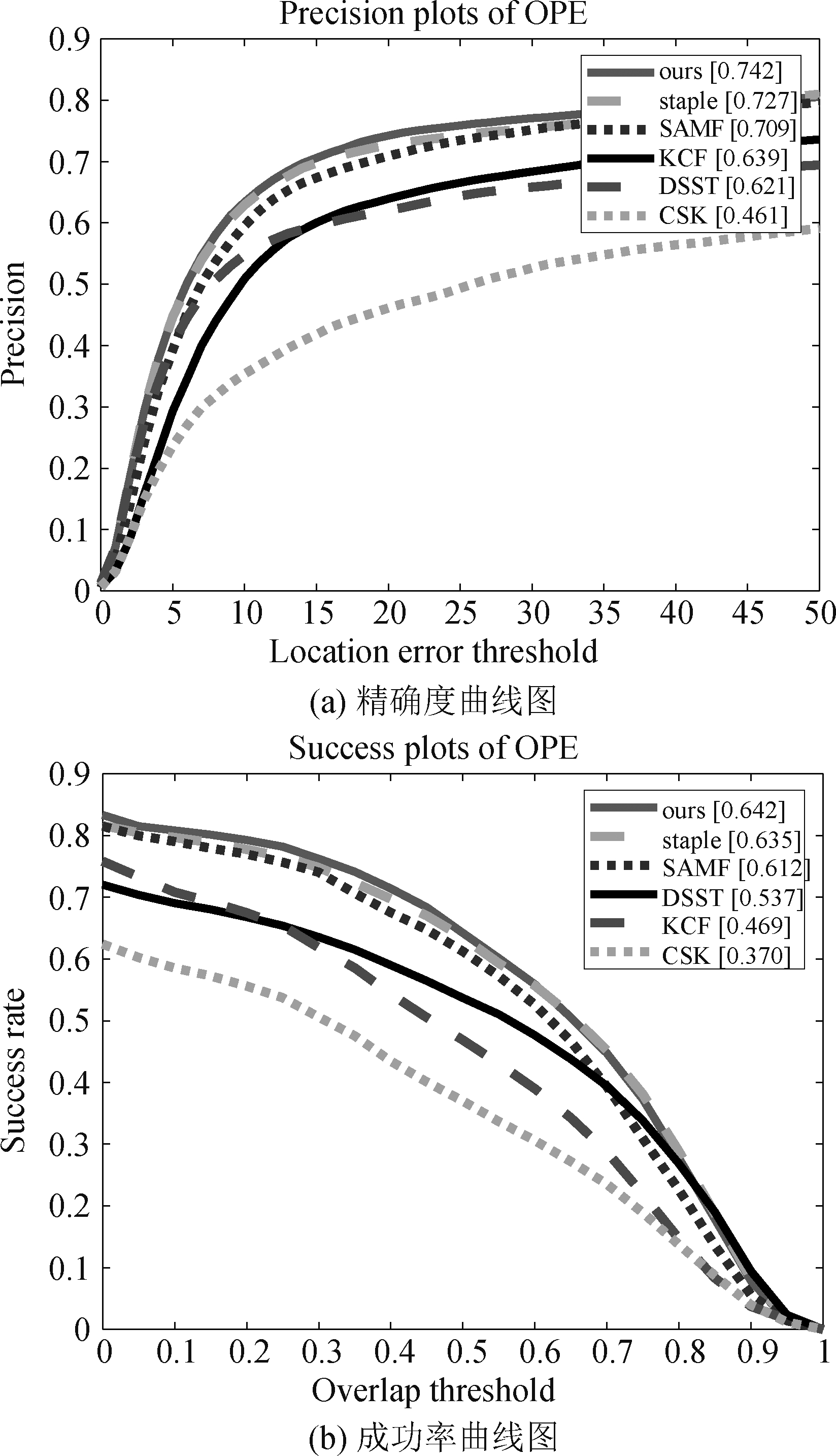
图7 OTB-2015综合评价曲线图
Fig.7 OTB-2015 Comprehensive Evaluation Curve
另外,在实验的过程中,根据文献[2]、[3]将跟踪分为11种挑战情况,分别为:光照变化(illumination variation,IV)、平面外旋转(out-of-plane rotation,OPR)、尺度变化(scale variation,SV)、遮挡(occlusion,OCC)、形变(deformation,DEF)、运动模糊(motion blur,MB)、快速运动(fast motion,FM)、平面内旋转(in-plane rotation,IPR)、移出视野(out of view,OFV)、背景杂波(background clutter,BC)、低分辨率(low resolution,LR)。这11种挑战的实验结果列于下表中。
其中表1和表2的加粗字体是排名第一的算法,斜体是排名第二的算法。从两个表中可以看出,我们的算法在11种跟踪挑战情况下均表现良好,其中IV、SV、OCC、DEF、MB、FM、BC7种情况的精确度和成功率最高。
表1 OTB-2013 误差阈值
Tab.1 OTB-2013 precision plots of OPE
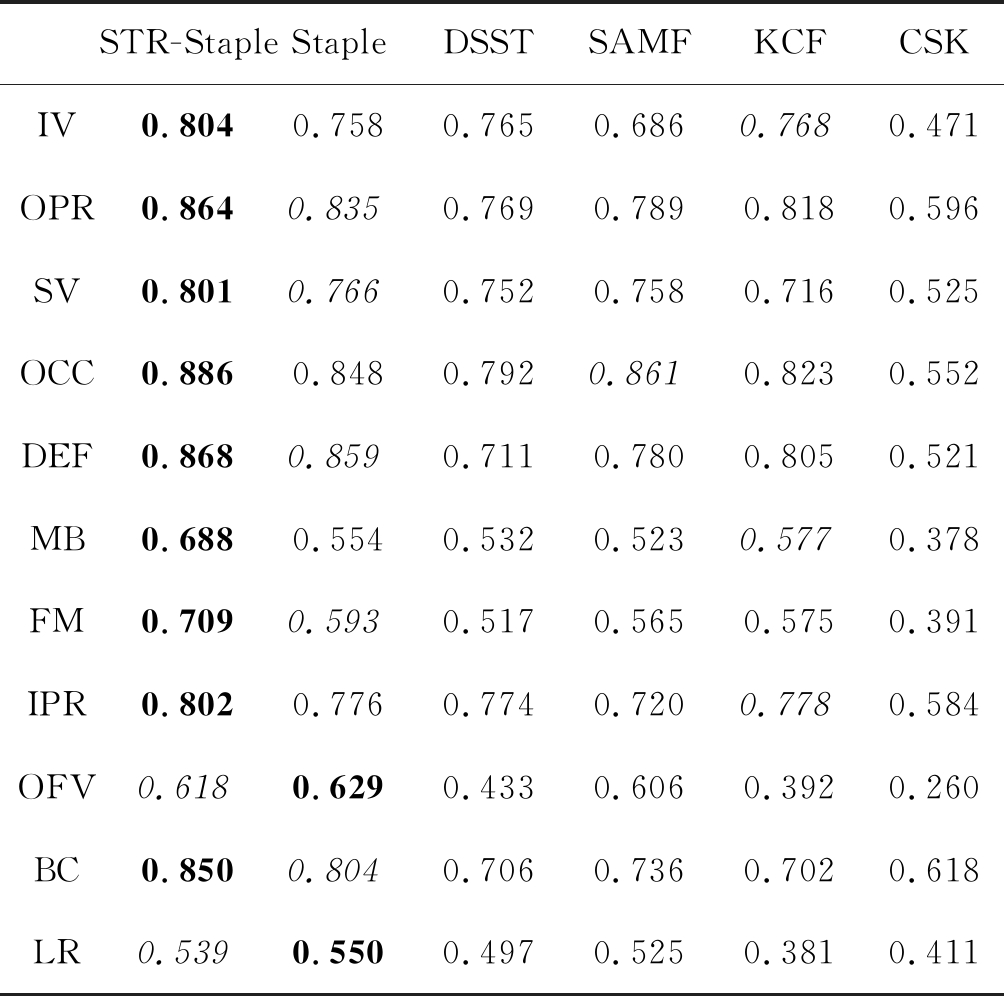
STR-StapleStapleDSSTSAMFKCFCSKIV0.8040.7580.7650.6860.7680.471OPR0.8640.8350.7690.7890.8180.596SV0.8010.7660.7520.7580.7160.525OCC0.8860.8480.7920.8610.8230.552DEF0.8680.8590.7110.7800.8050.521MB0.6880.5540.5320.5230.5770.378FM0.7090.5930.5170.5650.5750.391IPR0.8020.7760.7740.7200.7780.584OFV0.6180.6290.4330.6060.3920.260BC0.8500.8040.7060.7360.7020.618LR0.5390.5500.4970.5250.3810.411
表2 OTB-2013 重合阈值
Tab.2 OTB-2013 success plots of OPE
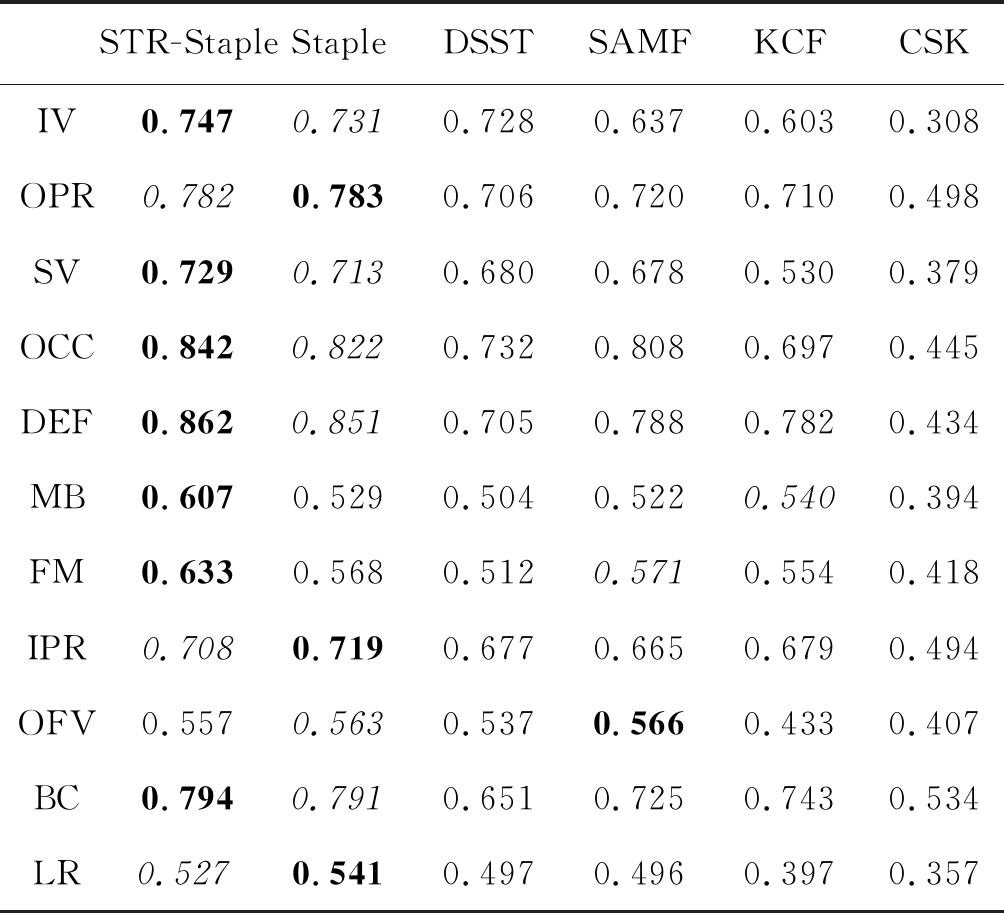
STR-StapleStapleDSSTSAMFKCFCSKIVOPRSVOCCDEFMBFMIPROFVBCLR0.7470.7820.7290.8420.8620.6070.6330.7080.5570.7940.5270.7310.7830.7130.8220.8510.5290.5680.7190.5630.7910.5410.7280.7060.6800.7320.7050.5040.5120.6770.5370.6510.4970.6370.7200.6780.8080.7880.5220.5710.6650.5660.7250.4960.6030.7100.5300.6970.7820.5400.5540.6790.4330.7430.3970.3080.4980.3790.4450.4340.3940.4180.4940.4070.5340.357
另外,OTB-2015数据集上的实验数据如下表:
其中表3,表4的加粗字体是排名第一的算法,斜体是排名第二的算法。从OTB-2015数据集上来看,STR-Staple算法与其他几种算法相比,跟踪效果仍然是最优的。
表3 OTB-2015 误差阈值
Tab.3 OTB-2015 Precision plots of OPE
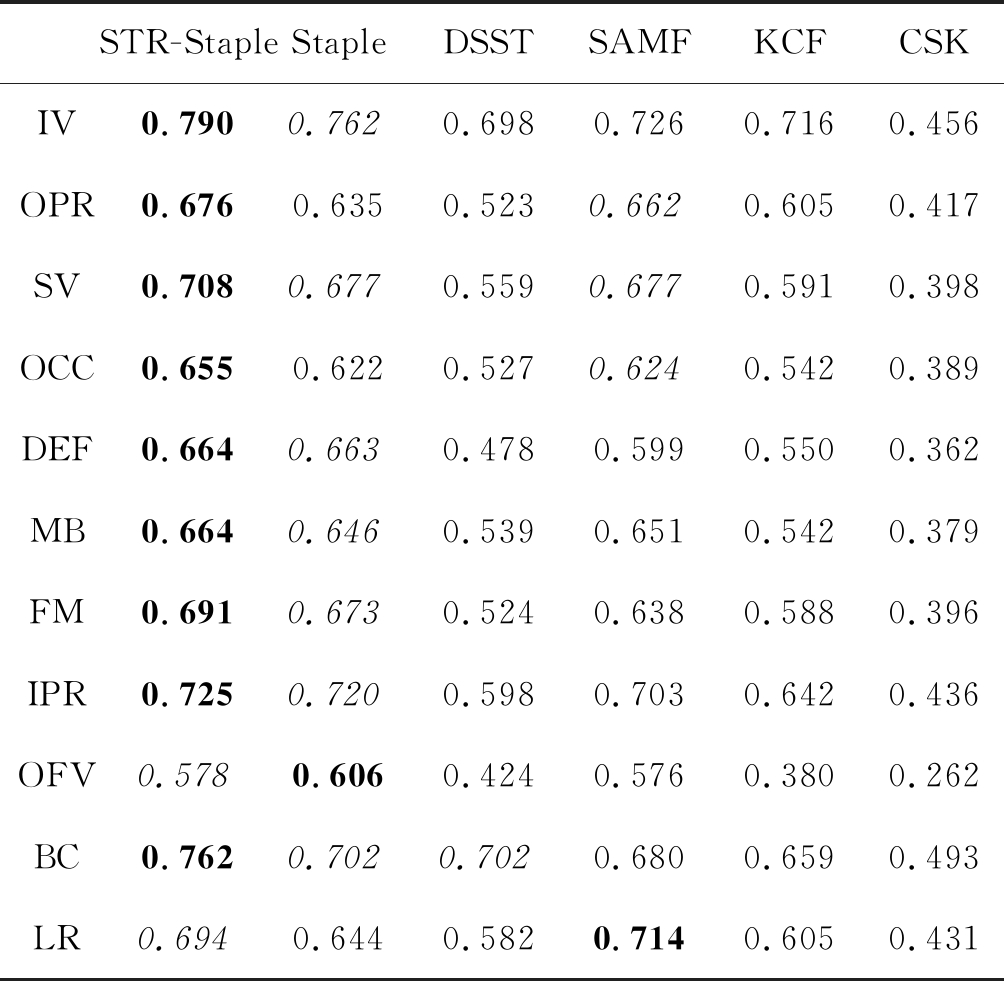
STR-StapleStapleDSSTSAMFKCFCSKIV0.7900.7620.6980.7260.7160.456OPR0.6760.6350.5230.6620.6050.417SV0.7080.6770.5590.6770.5910.398OCC0.6550.6220.5270.6240.5420.389DEF0.6640.6630.4780.5990.5500.362MB0.6640.6460.5390.6510.5420.379FM0.6910.6730.5240.6380.5880.396IPR0.7250.7200.5980.7030.6420.436OFV0.5780.6060.4240.5760.3800.262BC0.7620.7020.7020.6800.6590.493LR0.6940.6440.5820.7140.6050.431
表4 OTB-2015 重合阈值
Tab.4 OTB-2015 Success plots of OPE
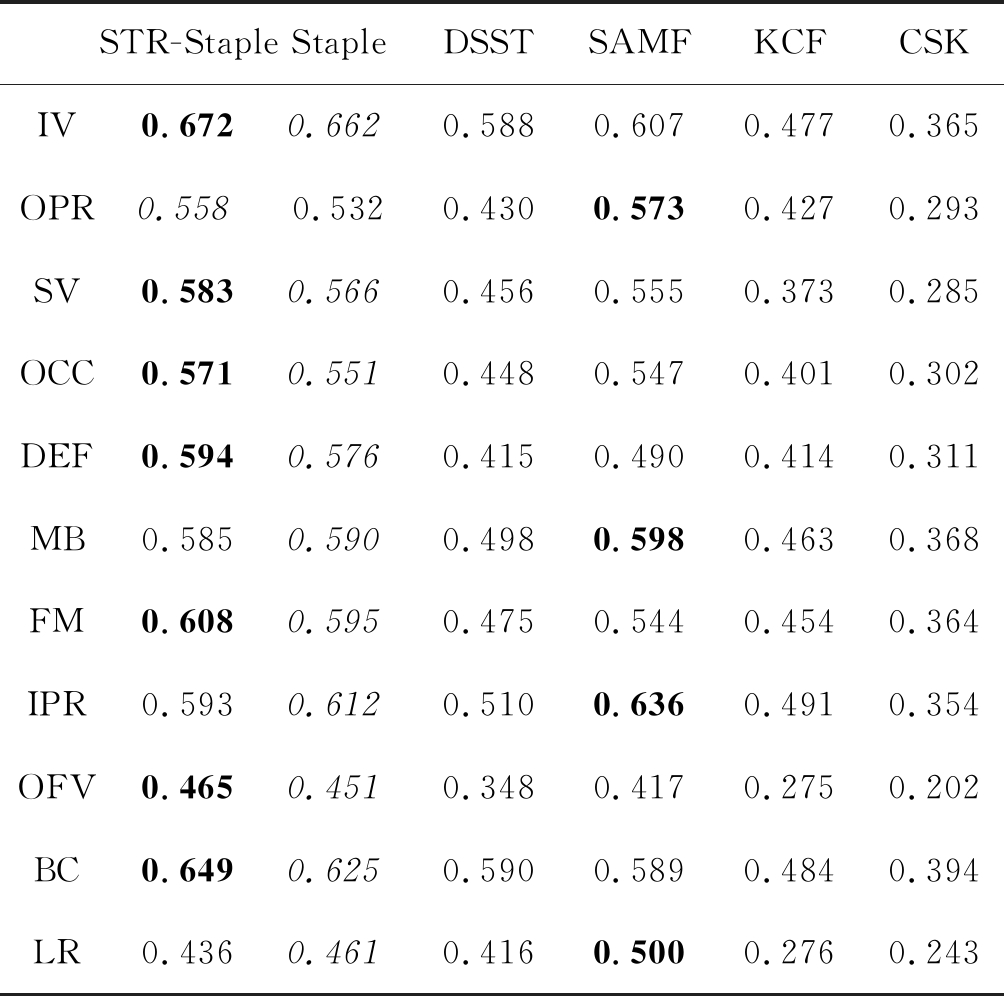
STR-StapleStapleDSSTSAMFKCFCSKIV0.6720.6620.5880.6070.4770.365OPR0.5580.5320.4300.5730.4270.293SV0.5830.5660.4560.5550.3730.285OCC0.5710.5510.4480.5470.4010.302DEF0.5940.5760.4150.4900.4140.311MB0.5850.5900.4980.5980.4630.368FM0.6080.5950.4750.5440.4540.364IPR0.5930.6120.5100.6360.4910.354OFV0.4650.4510.3480.4170.2750.202BC0.6490.6250.5900.5890.4840.394LR0.4360.4610.4160.5000.2760.243
STR-Staple算法表现最优主要有以下几点重要因素:(1)算法融合了HOG特征和颜色直方图特征,两种特征达到了互补的作用,当目标变形时颜色直方图特征起到跟踪的重要作用,当有光照变化时,HOG特征跟踪性能较好。这种互补的作用使得算法优于仅有单一模板的其他算法。(2)算法将目标的前景与背景的相似度达到一种实时的监控状态,并利用大量实验设定最恰当的阈值,同时将相似度值与融合因子相联系。当背景的颜色与目标十分相似导致目标丢失时,通过函数计算后降低相似度值,HOG特征做跟踪的主导作用;当背景与目标的相似度值很低时,颜色直方图特征做跟踪的主导作用。这种方式的跟踪性能的融合性进一步加强,对于背景杂波、快速运动、遮挡、形态变化等的跟踪效果明显提升。(3)算法的相似度值与融合因子的联系,使得跟踪达到实时的自适应,同时效果达到了最优的状态。因此,算法的鲁棒性也得到加强。
4.2 特定情况的性能比较
我们将部分具有代表性的视频序列单独列出来进行实验比较,这些视频均具有5种及以上的跟踪挑战性能,对我们的实验非常具有挑战性和说服力。其中,basketball包含有IV、OCC、DEF、OPR、BC五种挑战;blurbody包含有SV、DEF、MB、FM、IPR五种挑战;couple包含有SV、DEF、FM、OPR、BC五种挑战;clifbar包含有SV、OCC、DEF、FM、OPR、BC六种挑战;soccer包含有IV、SV、OCC、DEF、MB、FM、IPR、OPR、BC九种挑战。视频序列的最终结果如图8所示。

图8 6种跟踪算法在5个代表性视频上的跟踪效果图
Fig.8 Tracking effect of 6 tracking algorithms on 5 representative videos
从五组视频中看到,STR-Staple算法的跟踪性能始终是最稳定的、综合性能也保持最强。Basketball视频中间因为速度、光照、形变等因素导致另外五种算法存在漂移或者跟踪丢失;blurbody视频的摄像机镜头晃动剧烈,在视频极其模糊的情况下,Staple、SAMF、KCF、DSST四种算法不适合此种情况,完全跟丢,最终只有STR-Staple、CSK两个算法成功跟踪;couple视频因其晃动剧烈、变形快、速度快、杂波多以及背景相似干扰等多种复杂情况,导致到最后只有STR-Staple算法跟踪成功;DSST算法为专门的尺度算法,对clifbar视频跟踪效果相对较好,但是针对其他情况下的视频跟踪性能较弱;soccer视频内的干扰因素较多,而STR-Staple算法跟踪始终十分稳定。
下面的曲线图和表格记录了STR-Staple算法在这些具有代表性视频上的精确度和成功率的实验结果。
从图9中可以看到,该算法的精确度和成功率分别为0.902和0.740,比排在第二的Staple算法要高得多,并且每一个视频序列的精确度和成功率都相对较高,这表明STR-Staple算法的跟踪性能优于其他算法。
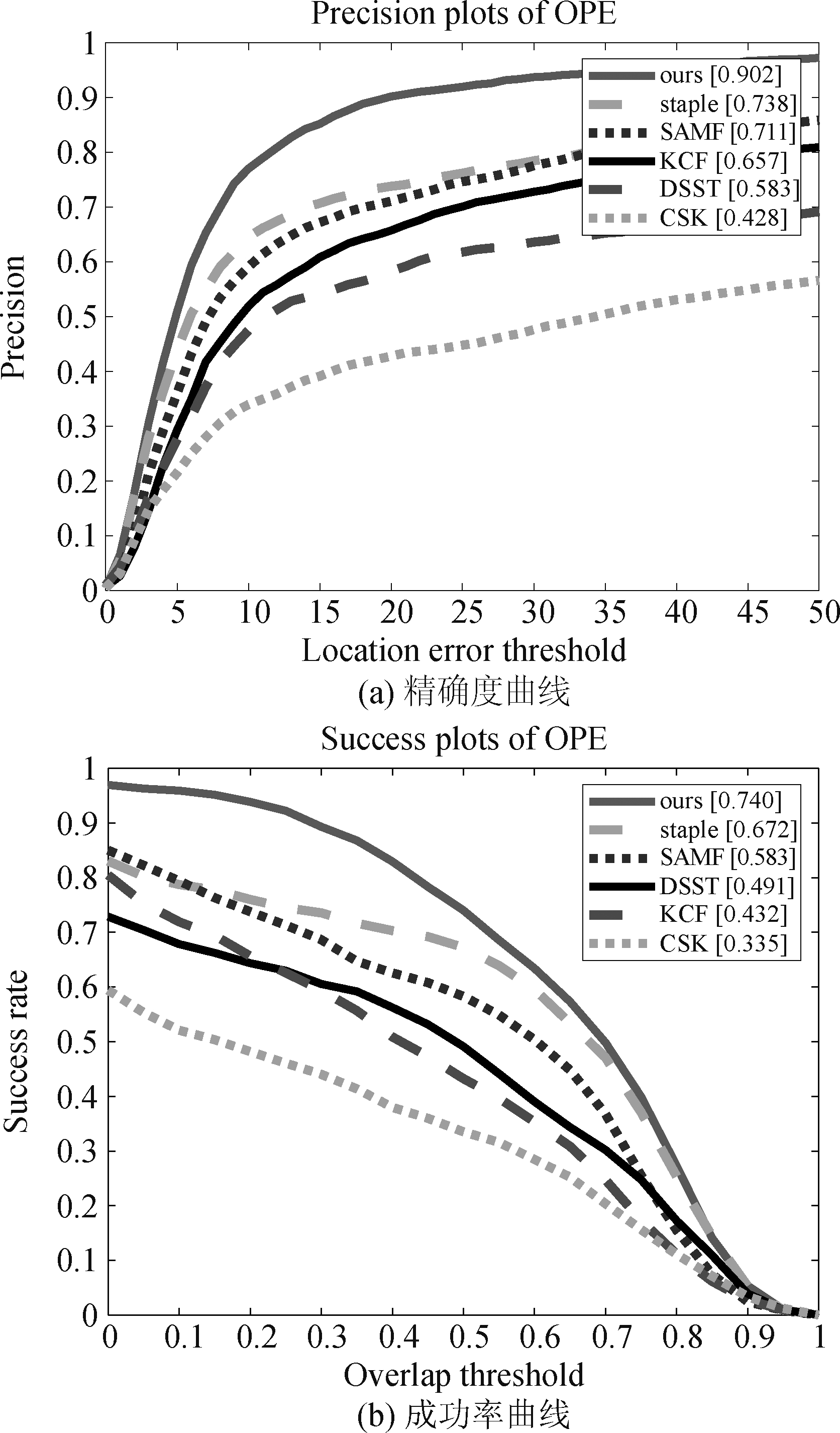
图9 部分具有代表性视频曲线图
Fig.9 Some representative video graphs
5 结论
本文的STR-Staple算法是在原Staple算法基础上的改进。通过利用巴氏距离中的巴氏系数方法计算前景和背景的相似度并设定相似度阈值,然后将适当的相似度值反馈给融合因子,得到自适应的融合因子,最后利用融合因子控制算法的两种模板,使算法达到最佳的自适应跟踪状态。通过在公开数据集OTB-13和OTB-15上的实验表明,STR-Staple算法的跟踪性能优于原Staple算法及其他几种主流算法,并且其精确度和成功率均得到了提高,对于背景与目标极为相似的情况跟踪十分稳定。另外,对于光照变化、尺度变化、遮挡、变形、背景杂波等的挑战情况也十分鲁棒。但同时该算法存在不足,当背景杂斑过多并出现目标的快速运动和快速变形的情况时,跟踪很容易出现漂移,导致目标丢失,后续需要对其进行改进。
[1]卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76.
Lu Huchuan, Li Peixia, Wang Dong. Survey of Target Tracking Algorithms [J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61-76.(in Chinese)
[2]Wu Y, Lim J, Yang M H. Online object tracking: A benchmark[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2013: 2411-2418.
[3]Wu Y, Lim J, Yang M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
[4]Chen Y, Park P S. A hybrid generative/ discriminative model based object tracking primary exploration[C]∥2015 SAI Intelligent Systems Conference (IntelliSys). IEEE, 2015: 765-772.
[5]黄文慧. 基于判别相关性滤波器的运动目标跟踪方法研究[D]. 山东大学, 2019.
Huang Wenhui. Research on moving target tracking method based on discriminative correlation filter [D]. Shandong University, 2019.(in Chinese)
[6]邵晴薇. 基于核相关滤波器的长期目标跟踪算法研究[D]. 南京理工大学, 2018.
Shao Qingwei. Research on long-term target tracking algorithm based on kernel correlation filter [D]. Nanjing University of Science and Technology, 2018.(in Chinese)
[7]Zhou B, Wang T, Luo M, et al. An online tracking method via improved cost-sensitive adaboost[C]∥2017 Eighth International Conference on Intelligent Control and Information Processing (ICICIP). IEEE, 2017: 49-54.
[8]Patnaik R. Distortion-invariant kernel correlation filters for general object recognition[D]. PhD thesis, Carnegie Mellon University, 2009.
[9]Nummiaro K, Koller-Meier E, Van Gool L. An adaptive color-based particle filter[J]. Image and Vision Computing, 2003, 21(1): 99-110.
[10]Bolme D S, Beveridge J R, Draper B A, et al. Visual object tracking using adaptive correlation filters[C]∥2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2010: 2544-2550.
[11]Jia X, Lu H, Yang M H. Visual tracking via adaptive structural local sparse appearance model[C]∥2012 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2012: 1822-1829.
[12]Henriques J F, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 37(3): 583-596.
[13]Gonz lez R C,Eddins S L and Woods R E, Digital Image Processing Using Matlab[J]. Digital Image Processing 3e. 2008, 21(84):197-199.
lez R C,Eddins S L and Woods R E, Digital Image Processing Using Matlab[J]. Digital Image Processing 3e. 2008, 21(84):197-199.
[14]Li Y, Zhu J. A scale adaptive kernel correlation filter tracker with feature integration[C]∥European Conference on Computer Vision. Springer, Cham, 2014: 254-265.
[15]Danelljan M, Shahbaz Khan F, Felsberg M, et al. Adaptive color attributes for real-time visual tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2014: 1090-1097.
[16]Danelljan M, Häger G, Khan F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,39(8): 1561-1575.
[17]胡正平, 尹艳华, 顾健新. 位置-尺度异空间协调的多特征选择相关滤波目标跟踪算法[J]. 信号处理, 2019, 35(12): 1979-1989.
Hu Zhengping, Yin Yanhua, Gu Jianxin. Multiple feature selection correlation filtering target tracking algorithm based on location scale coordination [J]. Journal of Signal Processing, 2019, 35(12): 1979-1989.(in Chinese)
[18]Bertinetto L, Valmadre J, Golodetz S, et al. Staple: Complementary learners for real-time tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1401-1409.
[19]Possegger H, Mauthner T, Bischof H. In defense of color-based model-free tracking[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 2113-2120.
[20]覃海松. 基于直方图巴氏距离的舌色分类[J]. 科技创新与应用, 2014(21): 71.
Qin Haisong. Classification of Tongue Color Based on Histogram Pappa Distance [J]. Science & Technology Innovation and Application, 2014(21): 71.(in Chinese)
[21]孙鹏, 冯鹏定, 于彤, 等. 基于巴氏距离的监控视频人体目标相似性度量[J]. 中国刑警学院学报, 2019(4): 119-123.
Sun Peng, Feng Pengding, Yu Tong, et al. Similarity Measures of Human Targets in Surveillance Video Based on Pappa Distance [J]. Journal of China Criminal Police College, 2019(4): 119-123.(in Chinese)


